Real-Time Hybrid Test Development and Application in Soil–Structure Interaction Systems

Abstract

Real-time hybrid testing is an efficient testing technique that combines physical testing with numerical calculations to jointly evaluate the performance of complex structures under different external excitations. This study conducted a quantitative bibliometric analysis of 121 RTHT articles published between 1992 and 2025. The survey revealed that only 8% of all test applications addressed soil–structure interaction systems, merely 3% employed finite element models exceeding 10,000 DOFs, and more than 90% of the interface equations were still based on lumped mass assumptions. An RTHT framework based on the branch modal method was proposed to overcome these limitations. Within this framework, the numerical soil substructure was reduced from thousands of DOFs to approximately one hundred DOFs, with a verified peak acceleration error of below 7%. This approach offers a practical reference for real-time hybrid testing of complex systems.

1. Introduction

Structural testing is an important means of determining the seismic performance of different structural systems. Currently, the testing methods commonly used in structural engineering include quasi-static, pseudo-dynamic, and shaking table tests. Owing to the high cost and difficulty in implementing dynamic testing on full-scale structures, most structural engineering dynamic tests are currently performed by using scaled models or by extending the time interval (pseudo-dynamic). The real-time hybrid test (RTHT) method is based on pseudo-dynamic testing and developed by introducing substructure technology and considering loading-rate-dependent device requirements [1,2]. This test method divides the original complete structural system into two parts: an experimental substructure and a numerical substructure. The experimental substructure is loaded using shaking tables or actuators, and the numerical substructure is simulated using software. The numerical and experimental substructure interact by exchanging data, thereby reducing the scale of the test while achieving the same effect as that under full loading (as shown in Figure 1).

As shown in Figure 1, the key points of RTHT comprise (1) physical substructure loading, where the accurate loading of physical substructures is a prerequisite for ensuring the RTHT outcomes match those of the overall model testing; (2) numerical substructure calculation, wherein the efficiency and accuracy of numerical substructures have a critical impact on the success of hybrid testing because data exchange in RTHT is typically controlled at the millisecond level; and (3) data exchange, wherein the data interaction or coupling of numerical and physical substructures has a significant impact on the difficulty, efficiency, and accuracy of the test method. Therefore, over the past three decades, researchers worldwide have conducted extensive studies on these aspects and expanded RTHT from its original focus on rate-dependent devices to more complex systems.

To sort out and summarize the current research status and main bottlenecks of RTHT, this paper conducted a quantitative bibliometric analysis of 121 RTHT articles published between 1992 and 2025. The literature search was conducted using major academic databases such as Web of Science, with keywords including “real-time hybrid testing” and “soil–structure interaction”. Data were extracted and analyzed based on four main aspects: experimental application, physical substructure loading, numerical substructure calculation, and data exchange. In this paper, the main achievements in RTHT were reviewed by categorizing them into the aforementioned four groups. The key deficiencies of the existing studies in data exchange methods and numerical modeling were analyzed, and a real-time hybrid testing scheme based on the branch modal method for soil–structure interaction (SSI) systems was proposed, serving as a reference for future studies.

2. Review of RTHT

2.1. RTHT Application

From the perspective of RTHT application, researchers are dedicated to the application and promotion of this new testing technology. RTHT is used to study rate-dependent structural properties, and its application is further extended to research on large and complex structures and even multidimensional and multipoint inputs. Furthermore, the application field has expanded from traditional structural engineering to electrical and marine engineering.

2.1.1. Vibration-Isolated Structures and Non-Vibration-Controlled Structures

Since Nakashima et al. first implemented the RTHT method, numerous researchers have applied it to structural systems with dampers or base isolation devices. The tests often utilized the advantages of RTHT in rate-dependent device research, selecting dampers or base isolation devices for the experimental substructure, and using numerical calculations for the remaining parts. Igarashi et al. [3] successfully implemented RTHT on a bridge pier structure with a tuned mass damper (TMD). They reported that the RTHT method has great potential, owing to the convenience of changing the numerical substructure. Using a five-story shear-type frame structure as the research object, with the top two stories as the experimental substructure and the bottom three stories as the numerical substructure, Lee et al. [4] derived hybrid testing implementation equations for a series of multi-DOF systems. In these equations, the excitation of the experimental substructure is the absolute acceleration at the top of the numerical substructure, and the reaction force of the numerical substructure is calculated using the inertial force of the absolute acceleration of the experimental substructure. They also applied RTHT to liquid dampers, using the liquid damper as the experimental substructure [5]. Because the damping force of an experimental substructure with a liquid damper is typically a nonlinear function of velocity, the reaction force of the experimental substructure was obtained via measurement. Reinhorn et al. [6] derived an RTHT implementation method using a series of three-DOF systems, designating the intermediate layer as the experimental substructure and the bottom and top layers as the numerical substructure. They conducted RTHT on a two-layer frame structure, using the first layer of the structure as the experimental substructure with a shaking table and actuator as the excitation device, and the second layer of the structure was represented by numerical calculations. Subsequent related studies are summarized in

Table 1. Summary of related main studies.

Researchers	Research Object	Experimental Substructure	Numerical Substructure
Zhu et al. [7], Wu et al. [8,9,10,11], Wang et al. [12], Riascos et al. [13], Chu et al. [14]	Vibration-isolated structures	Various dampers (TLD, MR, Piezoelectric)	Various systems (Single-DOF, Three-DOF, Lumped mass model)
Schellenberg et al. [15], Zhang et al. [16]	Interstory isolation structures	Various isolation bearings	Various frame structures (Single-story, Three-story), Lumped mass model
Park et al. [17], Shen et al. [18]	Vibration-isolated bridge structures	Bridge isolation bearings, High-damping rubber bearings	Bridge structure
Chi et al. [19,20], Tian et al. [21,22]	Non-vibration-controlled structures	Specific floors of the frame structure	Remaining floors

[-] refers to the reference number, and the same notation is used for other tables in the paper.

.

2.1.2. Electrical and Non-Structural Coupled Systems

Some researchers have applied substructure interaction data obtained from RTHT to seismic performance studies on both electrical and non-structural coupled systems. Mosalam et al. [23,24,25] conducted experimental studies on the performance of high-voltage electrical vertical circuit breakers. Initially, shaking table tests on the integral models of 245 and 550 kV vertical circuit breakers were performed separately. During the test, the acceleration response at the top of the support structure was calculated and used as the input signal for the experimental substructure. A shaking table RTHT was proposed and applied in seismic performance studies on the 245 kV breaker-support structure system. In the tests, the numerical substructure (i.e., support structure) was considered a single-DOF system, and the reaction force of the experimental substructure (i.e., high-voltage electrical vertical short-circuit breaker) on the numerical substructure was obtained through force sensors. Based on the principle of the branched mode method, Bi et al. [26] applied RTHT to a structural–equipment system, with the coupling terms between the structure and equipment considered to be the link between the numerical and experimental substructures. Xu et al. [27] used shaking tables and actuators to conduct RTHT on cable trays, reporting that the RTHT method has significant potential in the communication engineering field.

In addition, some researchers used RTHT for vehicle–bridge interactions. Guo et al. [28,29] used the RTHT method to study the interaction between trains, tracks, and bridges. The track–bridge–train system tested the train as an experimental substructure via shaking table testing, while the track–bridge structure participated in the experiment as a numerical substructure. This article proposes a method for real-time calculation of the dynamic response of the track–bridge system based on the moving load convolution integral method, which can efficiently complete numerical calculations. Wang et al. [30] advanced RTHT of high-speed train hunting dampers, significantly improving test fidelity. Xu et al. [31] developed an RTHT framework for vehicle–bridge interactions that incorporates vehicle-hopping effects, and experimental verification confirmed its capability in reproducing coupled dynamics. Some researchers have applied the RTHT method to assess the impact of wind-induced vibrations on buildings [32,33,34,35] as well as the structural performance of deep-water bridges in consideration of the fluid–structure dynamic interaction [36]. Moreover, RTHT has also been applied in marine/offshore engineering [37,38].

Based on the above research findings, the application of RTHT has expanded beyond the traditional field of structural seismic performance research to other disciplines, such as wind-induced vibrations. Because this testing method combines the advantages of traditional experiments and numerical simulations, while reducing the cost and difficulty of testing, RTHT has enormous potential for application.

2.1.3. SSI Systems

Although “real-time” in RTHT is proposed to address loading rate-related specimens, such as dampers and rubber seismic isolation devices, many researchers have also envisioned the application prospects of RTHT in complex structural systems such as SSI systems [39]. A few years after Nakashima et al. first performed RTHT, Konagai and Nogami [40] proposed connecting a circuit simulator to a shaking table system to simulate an infinite-domain foundation. The effect of the SSI on the superstructure of a 2 m high cantilever steel beam was studied using this system, further expanding the method to the nonlinear stage of soil. Subsequently, in 2002, Kobayashi et al. [41] applied RTHT to a bridge system. They used a shear soil box containing pile foundations as the experimental substructure, simplifying the bridge structure into a lumped mass system and considering the numerical substructure. A shaking table and actuators were used as the excitation devices for the experimental substructure. The rotational effect of soil on the superstructure was not considered, and the physical substructure was 30% that of the prototype because of the presence of the soil box. Subsequent related studies are summarized in

Table 2. Summary of existing SSI-RTHT studies.

Researchers	Research Object
Wang et al. [42,43], Zhou et al. [44], Fu et al. [45]	Frame structure–soil interaction system
Wang et al. [46]	Soil–structure–fluid dynamic interaction system
Li et al. [47,48], Chen et al. [49], Yan et al. [50,51]	Bridge structure–soil interaction
Xu et al. [52]	Storage tanks–soil interaction system
Li et al. [53]	Seismic isolation structures–soil interaction system

. The content of the numerical substructure model and the data interaction methods will be summarized and introduced in Section 3.1.

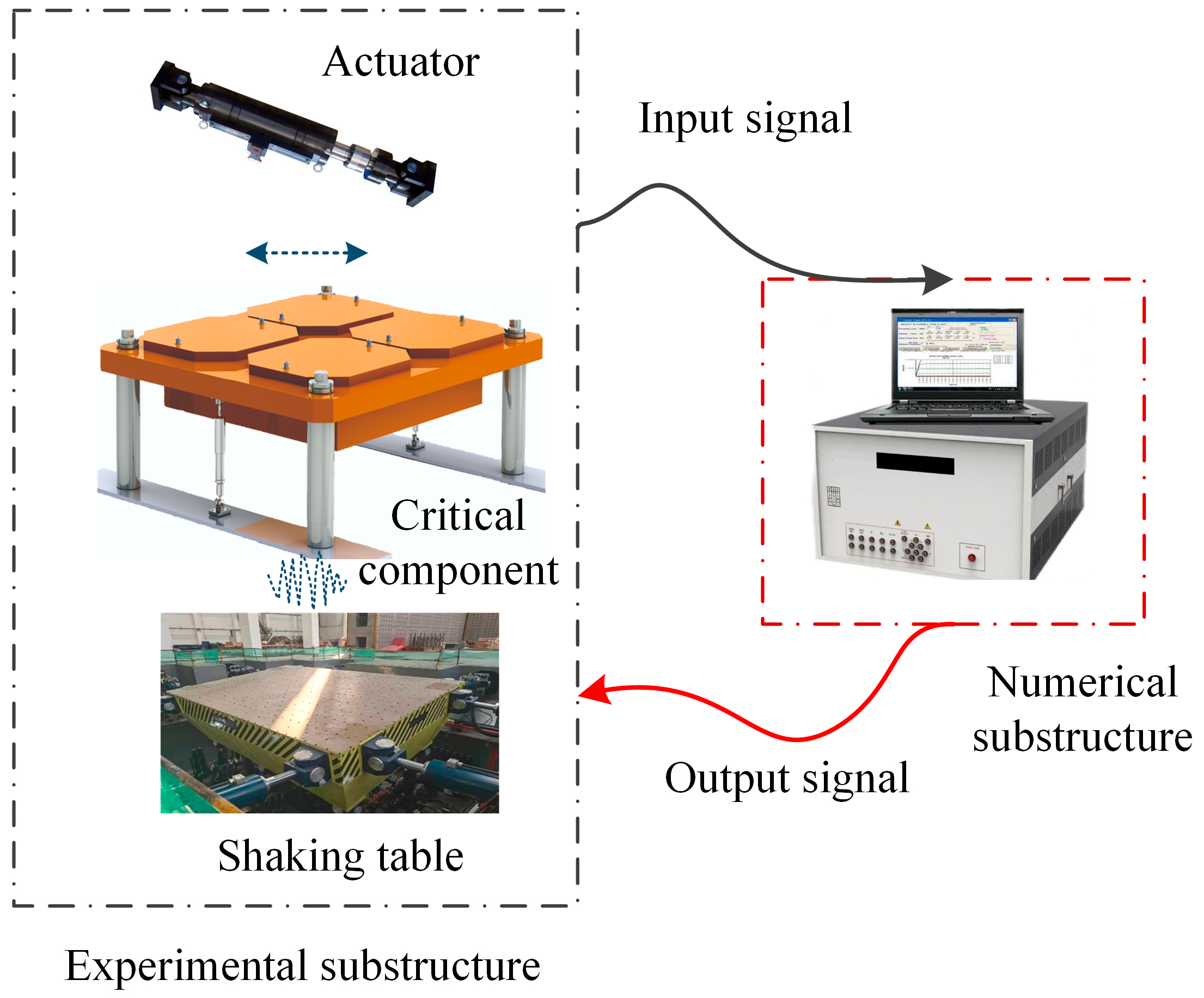
2.2. Experimental Substructure Loading

In RTHT, the experimental substructure refers to the part of the structure loaded by shaking tables or actuators during the experiment. The accurate loading of physical substructures is a prerequisite for ensuring the RTHT outcomes match those of the overall model testing. Research in this area has mainly focused on controlling the loading devices and methods for time-delay compensation, loading methods for physical substructures, and equivalent loading approaches.

2.2.1. Load Device Control and Time-Delay Compensation

Reliable control of the loading device and time-delay compensation must first be ensured to achieve accurate loading of the experimental substructure [54,55]. The time interval between receiving and executing commands in RTHT constitutes a time delay. Considering the development needs of the test specimen size, time-delay compensation and loading device stability remain important topics in RTHT research. Globally, scholars have proposed various time-delay compensation methods and studied the stability of time-delay compensation.

Horiuchi et al. [56] applied a time-delay effect compensation method in RTHT using an actuator (MTS Systems Co., Ltd., Eden Prairie, MN, USA), equating the time delay to the negative damping applied to the system. Subsequently, Neild et al. [57] reported on a control method using shaking tables as the excitation device, and Wallace et al. [58] analyzed time-delay stability in RTHT. Zakersalehi et al. [59] investigated methods for hysteresis compensation, numerical integration, and experimental stability evaluation in hybrid tests. Carrion et al. [60] investigated a model-based feedforward–feedback compensation control method using actuators as excitation devices and proved the reliability of this method in structures equipped with MR dampers. Chen and Ricles [61] proposed a time-delay compensation evaluation method based on equivalent discrete transfer functions, whereas Chen and Tsai [62] proposed a dual time-delay compensation strategy that combined phase compensation and restoring force compensation. Subsequently, Chen et al. [63] proposed an adaptive control method based on a model-based feedforward–feedback controller for specimen nonlinearity adaptation and improved tracking performance. Günay et al. [64] proposed a three-parameter control method and introduced the operator splitting method for numerical substructure integration, which was validated via RTHT on high-voltage equipment isolation switches. Gao et al. [65] proposed an H∞ loop control method, and Stefanaki et al. [66] improved the traditional control methods in RTHT by separating the controller and physical system, thus simplifying the RTHT system without requiring an explicit tracking controller. Chae et al. [67] used adaptive time series to compensate for time delays. Zhang et al. [68] studied the control method of the shaking table by considering the specimen-shaking table, whereas Nasiri and Safi [69] analyzed the system stability using both actuators and shaking tables via delay differential equations. Wu et al. [70,71] studied time-delay estimation and compensation methods, researched control methods based on equivalent force, introduced Kalman filters to filter noise in equivalent force feedback, and verified the reliability of the control methods in a series of RTHTs [72,73]. Chi et al. [19,74] analyzed time-delay stability and its influencing factors in single- and multi-DOF systems. They also studied the impact of actuator response delay on the tests and suggested solution methods. Zhu et al. [75,76] studied displacement prediction and force correction techniques during experimental loading and later used root locus techniques to study the time-delay stability of multi-DOF systems in RTHT. Maghareh et al. [77] proposed an adaptive control system that extended the application of RTHT to study structural nonstationary behavior. Guo et al. [78,79,80] studied the impact of the specimen–loading system interaction on the stability of hybrid tests as well as the stability prediction and analysis of the test system. Huang et al. [81] used the Takagi–Sugeno fuzzy model method and Lyapunov–Krasovskii stability theory to study the stability of RTHT under a combination of time-delay and nonlinearity effects. Based on the application of RTHT in high-speed rail–bridge structure-coupled systems [82], Liu et al. [83] developed a stability test strategy for vehicle–bridge-coupled systems.

2.2.2. Experimental Substructure Interface Load

Because the experimental substructure is derived from the overall model, the accurate loading of DOFs exposed in the experimental substructure is also an important topic in the implementation of RTHT. For interface loading implementation, the main methods include interface loading DOF reduction, loading boundary equivalence, and extension. Zhao et al. [84] studied the application of coordinate condensation transformation methods in hybrid tests. The number of DOFs between the numerical and experimental substructures was reduced by modifying the calculation matrix of the experimental substructure to that of the numerical substructure (achieved by adjusting the structural layout of the experimental substructure model), thus simulating the response of the original model with fewer loading devices. For test beams, columns, and substructures, some researchers have proposed applying a DOF reduction method to the test specimens or numerical substructure model, and by merging experimental substructures, extending or transferring loading interfaces to reduce the number of test loading devices, thus simulating collaborative displacements or rotational moments. Jia et al. [85,86] conducted in-depth research on the implementation of RTHT for large, complex structures and proposed a motion–stillness DOF separation and equivalence method, dividing the numerical substructure model into smaller substructure units and performing modal reduction on each substructure unit to improve computational efficiency. The simulation of complex boundary conditions in RTHT was also investigated. A complex boundary-effect simulation method that reduces the boundary DOFs of the test element was proposed, as well as a method for extending the boundary conditions of the experimental substructure. Thus, the collaborative control of horizontal DOF displacements and the application of vertical rotational moments in the experimental substructure were achieved. The feasibility of RTHT in large-scale engineering tests for the structure was verified with an isolated high-rise building. Tian et al. [87,88] combined experimental substructure units in RTHT, thus transferring the loading interface to ensure accurate simulation and effectively avoiding the handling of complex boundary conditions and reducing the number of actuators. Subsequently, an improved method using rubber block devices to simulate the long-period seismic response of high-level structures was studied from the perspective of interface force equivalence. To resolve the problem of a multidimensional test [89] involving the simultaneous loading of axial, shear, and bending DOFs, Amirali and Spencer [90] proposed a displacement-based multidimensional RTHT method that mainly included the following aspects: (1) numerical substructure calculation, (2) coordination between the boundaries of two substructures and the compensation of excitation devices, (3) experimental substructure loading, and (4) the coordinate transformation of the restoring forces between the two substructures. Using the load and boundary condition box of the University of Illinois at Urbana–Champaign, the proposed test loading method was verified using a single column in a steel-frame structure as the experimental substructure. Lin et al. [91] addressed the interaction problem between the shaking table and actuators by configuring two actuators on an existing large shaking table (6 m × 9 m) to establish a real-time coupled shaking table–actuator test platform. The reliability of the test platform was experimentally verified. Furthermore, for the division method between the two substructures, different division methods affect the loading difficulty and efficiency associated with the experimental substructure. Some researchers have utilized the concept of “overlap domain” [92] by setting an overlapping area between the two substructures to expand the exchange of information from merely node information between the two substructures to the exchange of information in the overlapping area, simplifying the meeting of experimental conditions and, thus, further simplifying experimental substructure loading and simultaneously making data interaction more accurate.

2.3. Numerical Substructure Calculation

The efficiency and accuracy of numerical substructures have a critical impact on the success of hybrid testing. Because of the high demand for RTHT data exchange, researchers have focused on maintaining the computational efficiency of numerical substructures via various methods. The focus of these achievements was primarily on numerical computing or numerical integration methods and their improvement techniques [93,94,95,96], as well as numerical substructure computation methods under complex working conditions [97,98,99] or large-scale structural systems [100,101]. Because finite element software has a significant advantage in numerical substructure modeling and nonlinear simulation, developing computational software [102,103] or embedding existing finite element software (e.g., Opensees 2.4.0) into RTHT systems [104] can also ensure the computational efficiency of numerical substructure computation. Another solution is to introduce finite element parallel computing into RTHT [105]. For instance, Tang et al. [106] proposed a GPU parallel computing method and built a numerical computing platform that increased the real-time solution scale of numerical substructures to 570,000 DOFs. Another method to alleviate the computational pressure on numerical substructures involves using different sampling frequencies on numerical and experimental substructures [107,108]. From another perspective, numerical substructure computation or experimental substructure loading can be performed separately if the experiment does not require high real-time performance. Based on the computed or measured data, the iterative computation or loading of the substructure can be completed; thus, adopting an offline hybrid testing method is also a solution [109,110]. Furthermore, from the perspective of the computational model, compressing the DOFs of numerical substructures via modal reduction is another way to improve the computational efficiency of numerical substructures [85,107], although research in this area has rarely been reported.

2.4. Data Exchange

The data interaction or coupling of numerical and physical substructures has a significant impact on the difficulty, efficiency, and accuracy of the test method. Summarizing the existing RTHT achievements, the implementation methods for RTHT typically assume a lumped mass model for formula derivation. The derivation methods mainly include the overall formula-splitting method using two or multiple DOFs and the separate numerical substructure motion equation method.

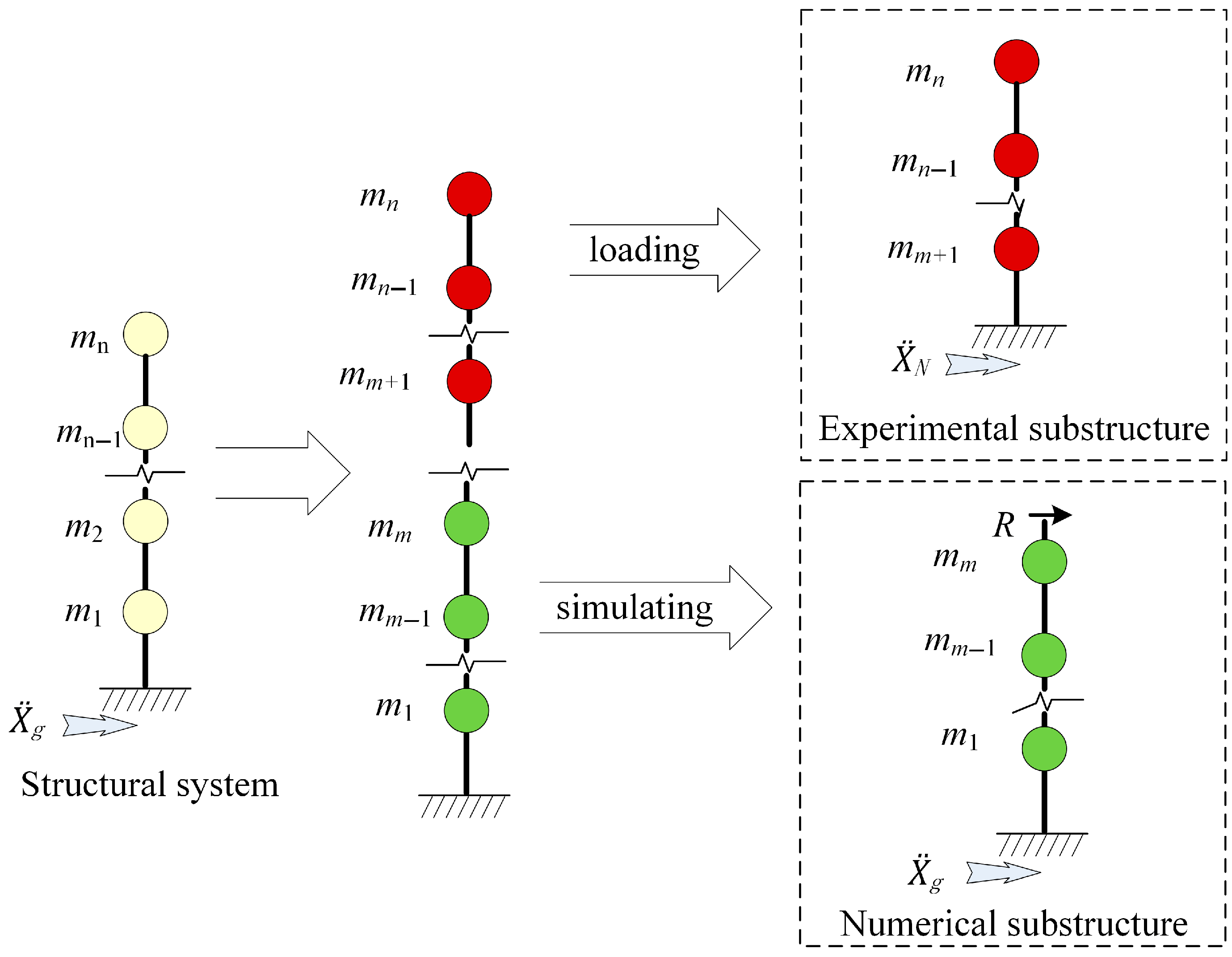
2.4.1. Derivation of Multi-DOF Systems [5,20]

In the derivation of equations for multi-DOF systems, the absolute acceleration value at the interface location of the numerical substructure is used as the excitation signal input to the experimental substructure, whereas the reaction force experienced by the numerical substructure can be obtained via testing or by adopting the total inertial force of the upper experimental substructure. The structural system represented by multiple DOFs is shown in Figure 2.

The motion equation of the overall system can be expressed as follows:

$$\left[M\right]\left\{\ddot{u}(t)\right\}+\left[C\right]\left\{\dot{u}(t)\right\}+\left[K\right]\left\{u(t)\right\}=\left\{F(t)\right\}$$

(1)

The system is divided into two substructures to conduct an RTHT: the experimental substructure (denoted by the subscript e) and the numerical substructure (denoted by the subscript n). The individual motion equations for each substructure are as follows:

$$\left[M_e\right]\left\{{\ddot{u}}_e(t)\right\}+\left[C_e\right]\left\{{\dot{u}}_e(t)\right\}+\left[K_e\right]\left\{u_e(t)\right\}=\left\{F_e(t)\right\}$$

(2)

$$\left[M_n\right]\left\{{\ddot{u}}_n(t)\right\}+\left[C_n\right]\left\{{\dot{u}}_n(t)\right\}+\left[K_n\right]\left\{u_n(t)\right\}=\left\{F_n(t)\right\}$$

(3)

where M_e, C_e, and K_e denote the mass, damping, and stiffness matrices of the experimental substructure, respectively; M_n, C_n, and K_n denote the mass, damping, and stiffness matrices of the numerical substructure, respectively; u_e and u_n denote the displacements of the two substructures, respectively; and F_e and F_n denote the external loads applied to the two substructures, respectively.

Based on the equilibrium condition of the numerical substructure, the interface force transferred from the experimental substructure can be obtained using Equation (4).

$$F_i(t)=C_{m+1}\left({\dot{u}}_{m+1}-{\dot{u}}_m\right)+K_{m+1}\left(u_{m+1}-u_m\right)$$

(4)

Because the interface force acting on the numerical substructure is related to the stiffness and damping parameters of the experimental substructure, direct measurement is typically adopted to obtain the interface force in RTHT with the loading-rate-dependent damping of the experimental substructure [5]. Alternatively, the motion equation can be continuously summed to express the total inertial load of the experimental substructure, thereby precluding the treatment of the stiffness and damping of the experimental substructure.

$$F_i(t)=-{\displaystyle \sum _{i=m+1}^n{M}_i}{\ddot{u}}_i$$

(5)

2.4.2. Derivation of Individual Numerical Substructure Motion Equation [15,111]

In the individual dynamic balance equation of the numerical substructure, the effect of the experimental substructure is reflected in the form of a restoring or external force, representing another method for implementing hybrid testing. The equations used are as follows:

$$\left[M_n\right]\left\{{\ddot{u}}_n(t)\right\}+\left[C_n\right]\left\{{\dot{u}}_n(t)\right\}+\left[K_n\right]\left\{u_n(t)\right\}+\left[R_e\right]=\left\{P_n(t)\right\}$$

(6)

where R_e is the restoring force vector, which can also appear as an external force. In this implementation method, the interaction force is typically obtained using force measurement devices.

In addition to obtaining the interface force through force sensors or summing the upper inertial forces, the interface force can also be obtained by calculating the interface force based on the response of the experimental substructure, combined with its stiffness and damping, or calculated by the strain of the experimental substructure [42,112], providing a further means of data acquisition.

3. Soil–Structure System RTHT

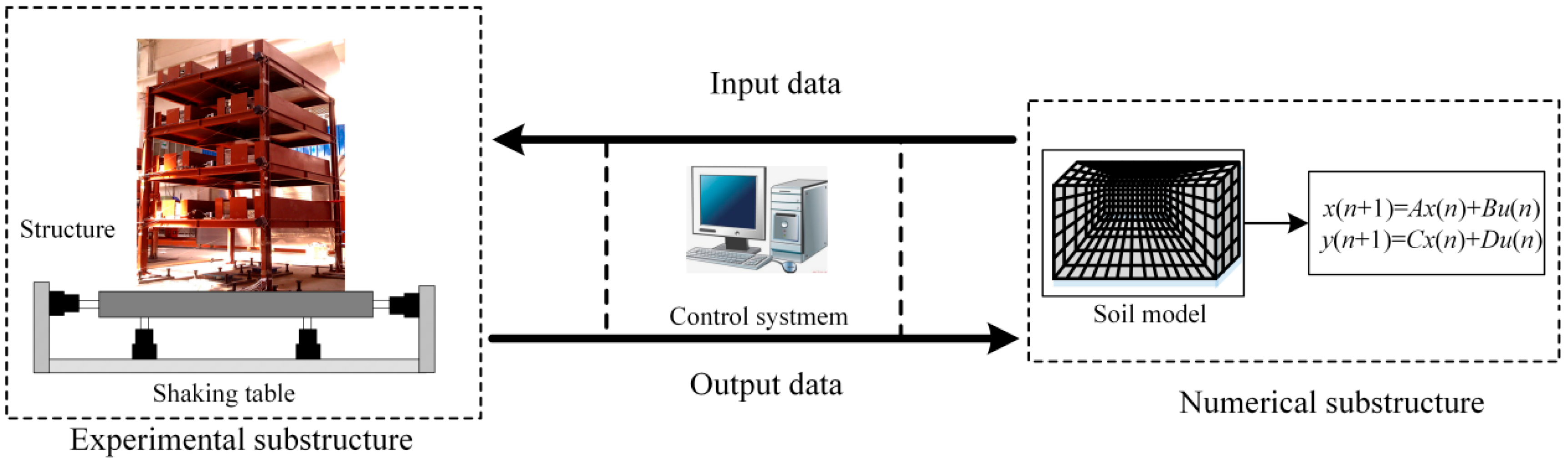
3.1. Review of Numerical Substructure Models and Date Exchanging Methods in Existing SSI-RTHT Studies

RTHT has attained certain achievements in the study of systems’ seismic performance, considering soil effects.

Table 3. Summary of numerical substructure models and date exchanging methods in existing SSI-RTHT studies.

Researchers	Experimental Substructure	Date Exchanging Methods
Wang et al. [42,43], Xu et al. [52]	Lumped parameter model for soil	Few existing studies have focused on the derivation of data interaction formulas. References [42,43] simplified the superstructure into a two-DOF concentrated mass system model to derive the method for RTHT
Wang et al. [46], Li et al. [53]
Zhou et al. [44]	Finite element analysis module with 132 DOFs
Li et al. [47]	Time-domain recursive model
Fu et al. [45]	200 quadrilateral plane elements

summarizes the main numerical substructure models and date exchanging methods in existing SSI-RTHT studies.

Soil is suitable as a numerical substructure because of its infinite nature. Although the finite element model better reflects actual conditions than the lumped parameter model, owing to current numerical calculation methods and the form of the numerical substructure model, relatively few achievements have been made in the utilization of soil finite element models in RTHT research. Furthermore, the model processing of numerical substructures has not received sufficient attention in current research. From a more direct perspective, adopting various means to reduce the DOFs of numerical substructures can effectively reduce the number of computational DOF in numerical substructures. However, few studies have been conducted in this regard. Regarding data interaction, the existing derivation of RTHT equations is not directly applicable to complex SSI systems, considering size effect still has a certain impact on the prediction of structural response in the RTHT [113]. Moreover, studies [114,115] have indicated that the current data interaction method for RTHT has certain limitations for data acquisition. Therefore, more reliable and convenient substructure data exchange methods need to be developed.

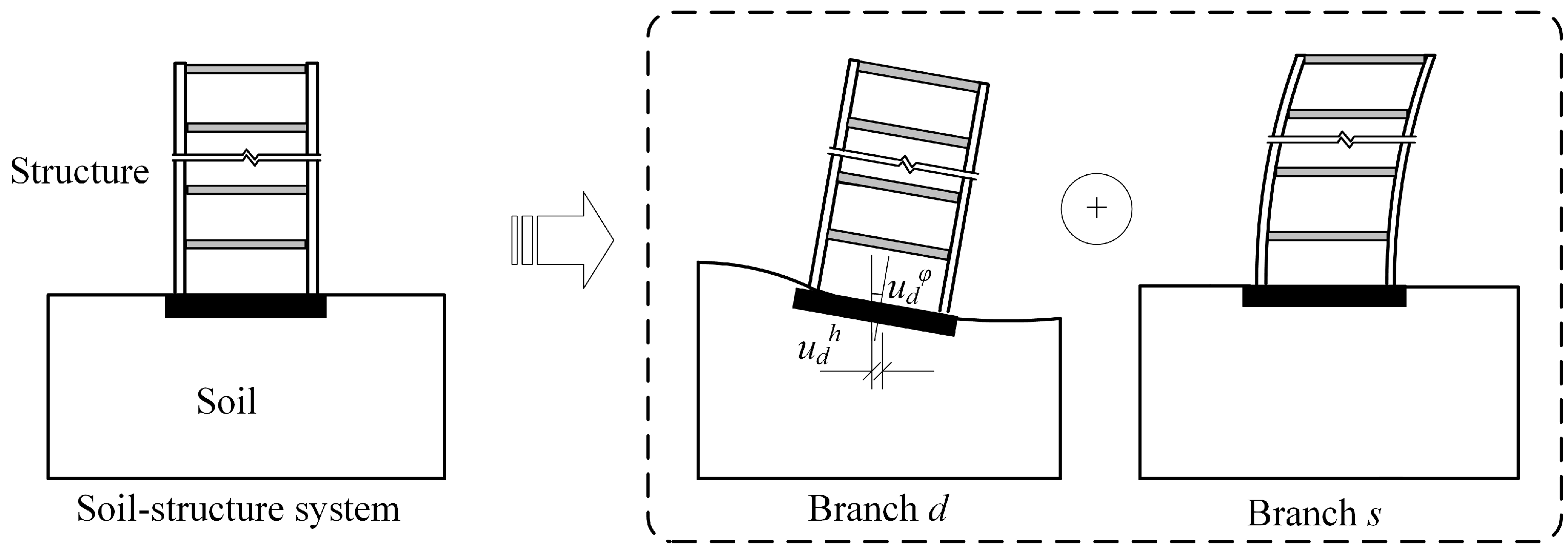
3.2. RTHT Method of SSI Based on Branch Modal Method

Owing to the current difficulties in the model processing of numerical substructures and the implementation of RTHT in large, complex structural systems, the motion equation of the soil–structure interaction system is derived using the branch modal substructure. Figure 3 shows the derivation principle diagram of the SSI system constructed using the branch modal method, where the soil is denoted by the letter ‘d’ and the upper structure by the letter ‘s’. The overall system is divided into two branches: (1) the rigid structure branch, d, on elastic soil, and (2) the elastic structure branch, s, on rigid soil.

First, the soil characteristic matrices m_d, k_d, and c_d are obtained using the finite element method and the finite element–infinite element coupled method, or other coupled methods, by performing a primary modal analysis on branch ‘d’ and calculating the eigenvalues of branch ‘d’ as follows:

$$\left[k_d\right]\left\{{\varphi }_d\right\}={\lambda }_d\left[m_d\right]\left\{{\varphi }_d\right\}$$

(7)

where λ_d is the eigenvalue, and {f_D} is the soil’s primary mode. The first m primary modes are selected to form the primary modal matrix [Φ_d] of branch ‘d’.

$$\left[{\mathit{\Phi }}_d\right]=\left[{\left\{{\varphi }_d\right\}}^1\cdots {\left\{{\varphi }_d\right\}}^i\cdots {\left\{{\varphi }_d\right\}}^m\right]$$

(8)

Furthermore, modal transformation can be performed on the soil characteristic matrices. The soil characteristic matrix after model transformation is shown below:

$$\begin{array}{l}\left[{\tilde{k}}_d\right]={\left[{\mathit{\Phi }}_d\right]}^T\left[k_d\right]\left[{\mathit{\Phi }}_d\right]\\ \left[{\tilde{m}}_d\right]={\left[{\mathit{\Phi }}_d\right]}^T\left[m_d\right]\left[{\mathit{\Phi }}_d\right]\\ \left[{\tilde{c}}_d\right]={\left[{\mathit{\Phi }}_d\right]}^T\left[c_d\right]\left[{\mathit{\Phi }}_d\right]\end{array}$$

(9)

Consequently, the computational DOFs of the soil numerical substructure can be significantly reduced, laying the foundation for its participation in RTHT.

Modal transformation is not performed considering the nonlinearities of the upper structure. Rather, modal synthesis is implemented based on the principle of inertial coupling in the branch modal method. Considering the rigid body modes of the upper structure, the displacement of the structure consists of two parts: displacement caused by the soil and its own displacement. Therefore, the physical coordinates of the soil and structure can be expressed as follows:

$$\left\{\begin{array}{c}{u}_d\\ u_s\end{array}\right\}=\left[\begin{array}{cc}{\Phi }_d& 0\\ R{\Phi }_d& I\end{array}\right]\left\{\begin{array}{c}{q}_d\\ q_s\end{array}\right\}$$

(10)

where u_d and q_d denote the displacements of the soil with respect to the physical and model coordinates, respectively; u_s and q_s denote the displacement of the structure with respect to the physical and model coordinates relative to the ground, respectively; and R is the rigid-body mode matrix of the superstructure of branch ‘d’, which can be obtained using the base point method.

Therefore, the overall motion equation of the soil–structure interaction system is shown in the following equation:

$$\left[\begin{array}{cc}{m}_s& m_{s}R{\Phi }_d\\ {{\Phi }_d}^T{R}^T{m}_s& {\tilde{m}}_d\end{array}\right]\left\{\begin{array}{c}{\ddot{q}}_d\\ {\ddot{q}}_s\end{array}\right\}+\left[\begin{array}{cc}{\tilde{c}}_s& 0\\ 0& {\tilde{c}}_d\end{array}\right]\left\{\begin{array}{c}{\dot{q}}_d\\ {\dot{q}}_s\end{array}\right\}+\left[\begin{array}{cc}{\tilde{k}}_s& 0\\ 0& {\tilde{k}}_d\end{array}\right]\left\{\begin{array}{c}{q}_d\\ q_s\end{array}\right\}=\left\{\begin{array}{c}{f}_s\\ {\tilde{f}}_d\end{array}\right\}$$

(11)

where f_s and f_d denote the load matrices of the structure and soil, respectively. By splitting the motion equations of the SSI system and moving the coupling terms to the right side of both equations in the form of loads, the following motion equations for the soil and structure can be obtained:

$${\tilde{m}}_d{\ddot{q}}_d+{\tilde{c}}_d{\dot{q}}_d+{\tilde{k}}_d{q}_d={\tilde{f}}_d-{\Phi }_d^T{R}_{sd}^T{m}_s{\ddot{q}}_s$$

(12)

$$m_s{\ddot{q}}_s+c_s{\dot{q}}_s+k_s{q}_s=f_s-m_s{R}_{sd}{\Phi }_d{\ddot{q}}_d$$

(13)

Thus, the motion equations of the SSI system are decoupled, with only the inertial coupling term existing between the two parts. During the test, the structure receives a unified acceleration excitation transmitted from the soil, and the interaction between the structure and soil is realized through acceleration excitation at the center of the foundation, thus achieving the convenient handling of the interaction in RTHT on complex SSI systems.

In [116], the soil is divided into near-field and far-field sections based on the soil characteristics, and the damping solvent extraction method is introduced to consider the impact of the far field. RTHT is realized based on the principle of the aforementioned branch modal method. Figure 4 shows a schematic of RTHT for the SSI system. Within this framework, the numerical soil substructure, which originally had thousands of degrees of freedom, was compressed to approximately one hundred DOFs, while the peak acceleration response of the reference points of the physical substructure had an error of less than 7% compared with the overall finite element simulation. This approach offers a practical reference for real-time hybrid testing of complex systems.

4. Discussion

This paper presents a systematic bibliometric review of 121 RTHT-related publications released between 1992 and 2025 and demonstrates the traditional modal synthesis method in RTHT.

4.1. Main Findings

In total, 46% of the publications focused on the extension and application of the test method, yet only 8% of these addressed complex systems such as SSI; 28% concentrated on physical substructure loading, and more than two-thirds of these studies were limited to three or fewer degrees of freedom; 18% dealt with numerical substructure computation, with merely three papers adopting finite element models exceeding 10,000 DOFs; and only 9% investigated data exchange strategies. The majority of these studies still relied on simplified lumped mass models.

4.2. Key Obstacles

• Limited numerical substructure modeling capacity: Existing studies rarely improve computational efficiency for large-scale finite element models, which severely restricts RTHT deployment in complex systems.
• Restricted delay-compensation accuracy: Current algorithms struggle to maintain high fidelity for heavy specimens or low-frequency structures.
• Poor generality of interface equations: Over 90% of existing RTHT implementations adopt lumped mass assumptions, making it difficult to couple three-dimensional continuum finite element models with experimental substructures.

4.3. Future Directions

• Model condensation: Modal synthesis strategies offer DOF reductions exceeding two orders of magnitude while safeguarding key modes within 5% deviation.
• Shared resources: Open-access, parameterized soil libraries integrated into real-time platforms can cut the model setup time and accelerate RTHT adoption for large-scale seismic assessment.

5. Conclusions

This paper reviews the current state of RTHT research across four key areas: test application, experimental substructure loading, numerical substructure calculation, and data exchange. It highlights deficiencies in numerical substructure processing and data exchange methods. Aiming to address these shortcomings in the context of reduced finite element soil models, this paper details an RTHT scheme for soil–structure interaction systems based on the branch modal method. The main conclusions are as follows:

• A quantitative review of 120 RTHT papers (1992–2025) revealed that SSI applications account for only 8% of all test applications, indicating a significant research gap in this complex area.
• The primary research obstacles were identified and quantified. Less than 3% of studies use numerical models with over 10,000 DOFs; large-mass specimens still struggle with delay compensation accuracy; and over 90% of interface equations rely on lumped mass assumptions.
• A branch modal RTHT framework is proposed, which compresses the DOFs of a soil model from thousands to one hundred DOFs, with a verified peak acceleration error of less than 7%, providing a viable pathway for large-scale SSI-RTHT.