Critical Damping Design and Vibration Suppression Research of Elastic Beam Coupled with Fractional-Order Inerter-Based Dampers
Abstract
1. Introduction
2. Modeling
2.1. The Constitutive Model of Fractional-Order Inerter
2.2. Elastic Beam Model Coupling FOIB-VMD
3. Critical Damping Design Based on Complex Modal Analysis
3.1. Complex Modal Analysis
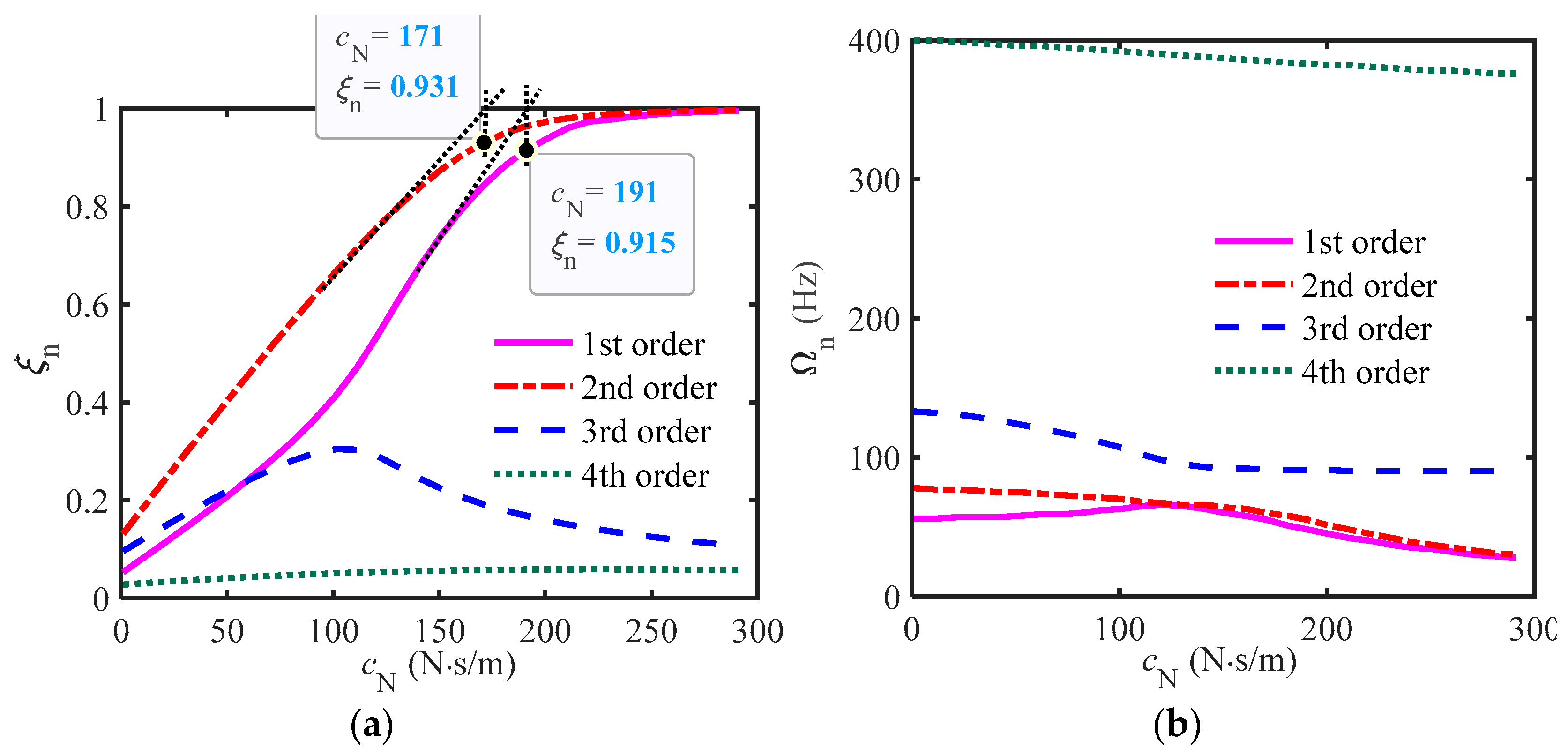
3.2. The Critical Damping Formula for Low-Order Modes
- (1)
- When αn ≠ 0, βn = 0, and the system damping ratio ξn = 0, then p = iωn, ωd = ωn, and the time-domain response is in the form of an equal amplitude oscillation, which is the undamped free vibration solution.
- (2)
- When αn ≠ 0, βn = 0, and ξn = 1, then p = −ωn, ωd = 0, s = = . Currently, the time-domain response of the system is in a monotonically decreasing form, which is the critical state where the frequency disappears, and the corresponding damping is the critical damping.
- (3)
- When αn tends to infinity and βn ≠ 0, the corresponding p, although complex, has a real part close to 0, ξn is close to 1 and ξn < 1, and ωd is close to 0. At this point, referring to the concept of second-order systems, it is called the underdamped ratio, and the response is in the form of oscillatory decay.
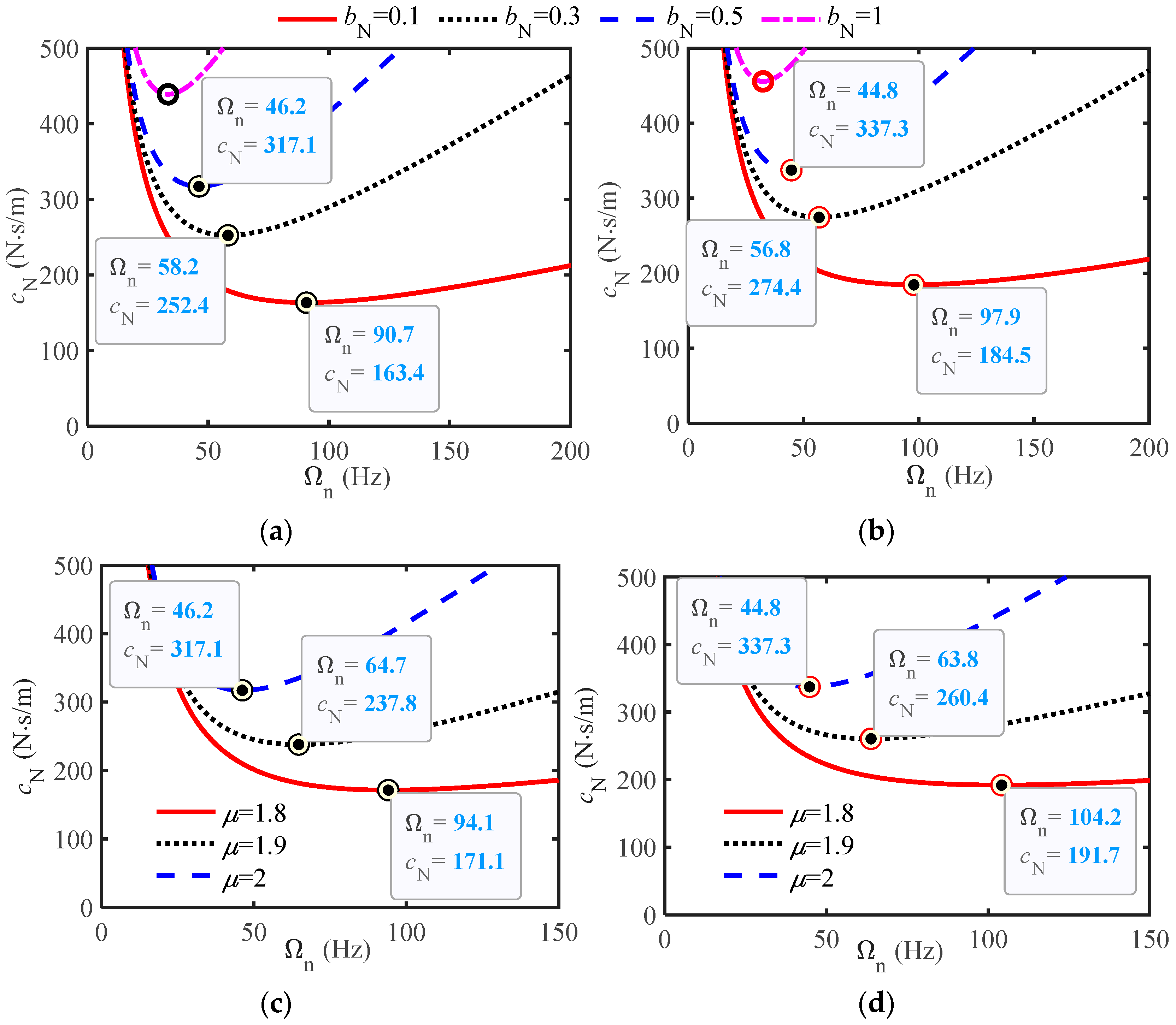
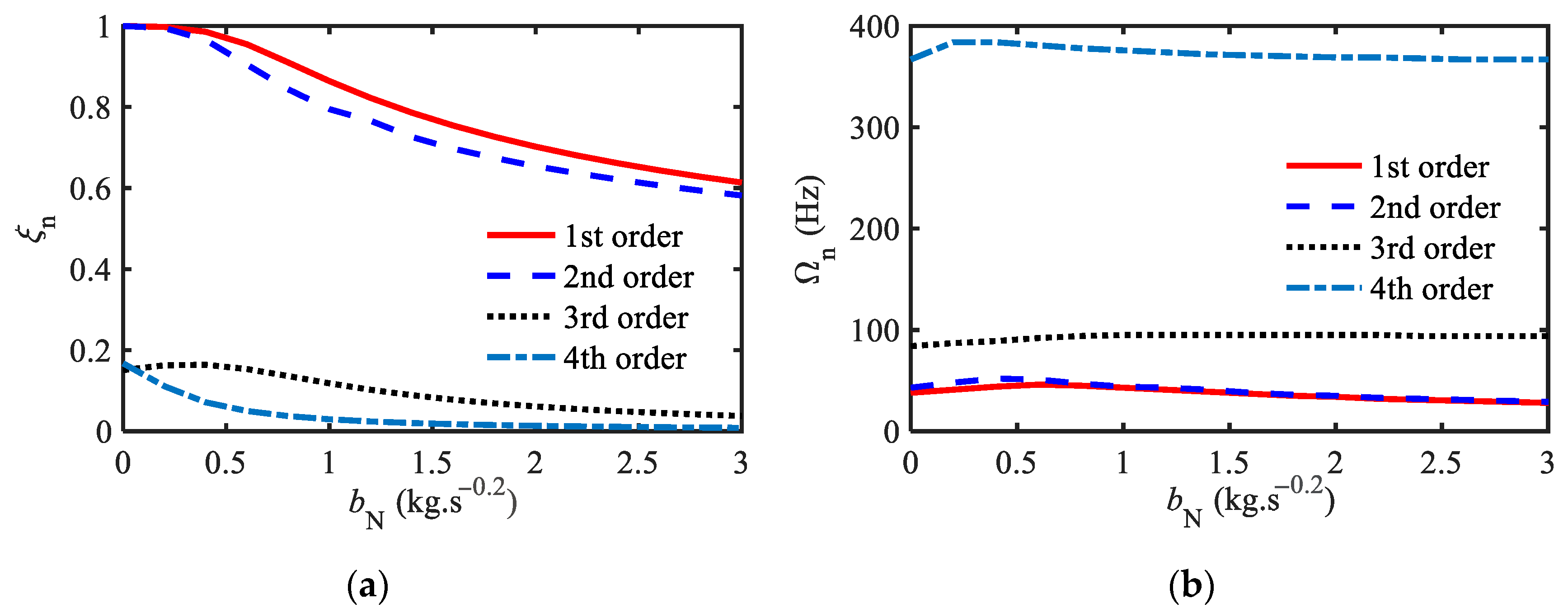
3.3. Verification of Critical Damping and the Influence of Parameters
4. Vibration Suppression Effect
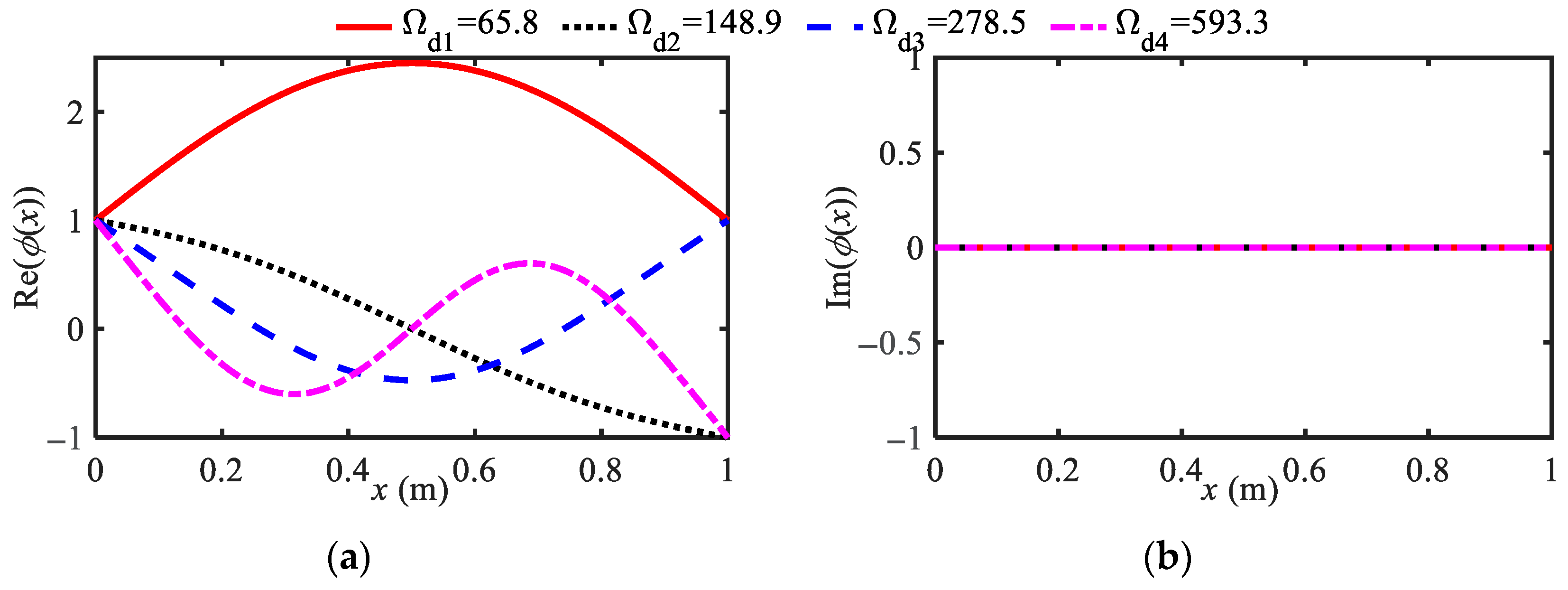
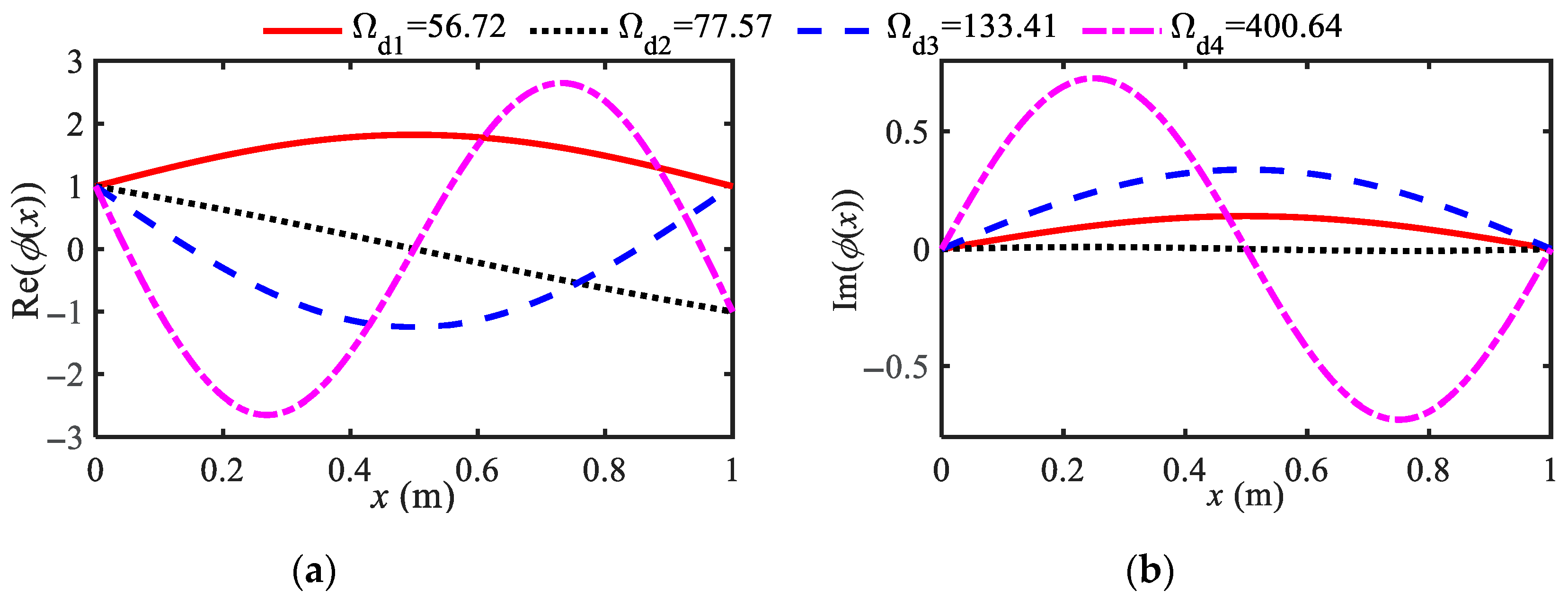
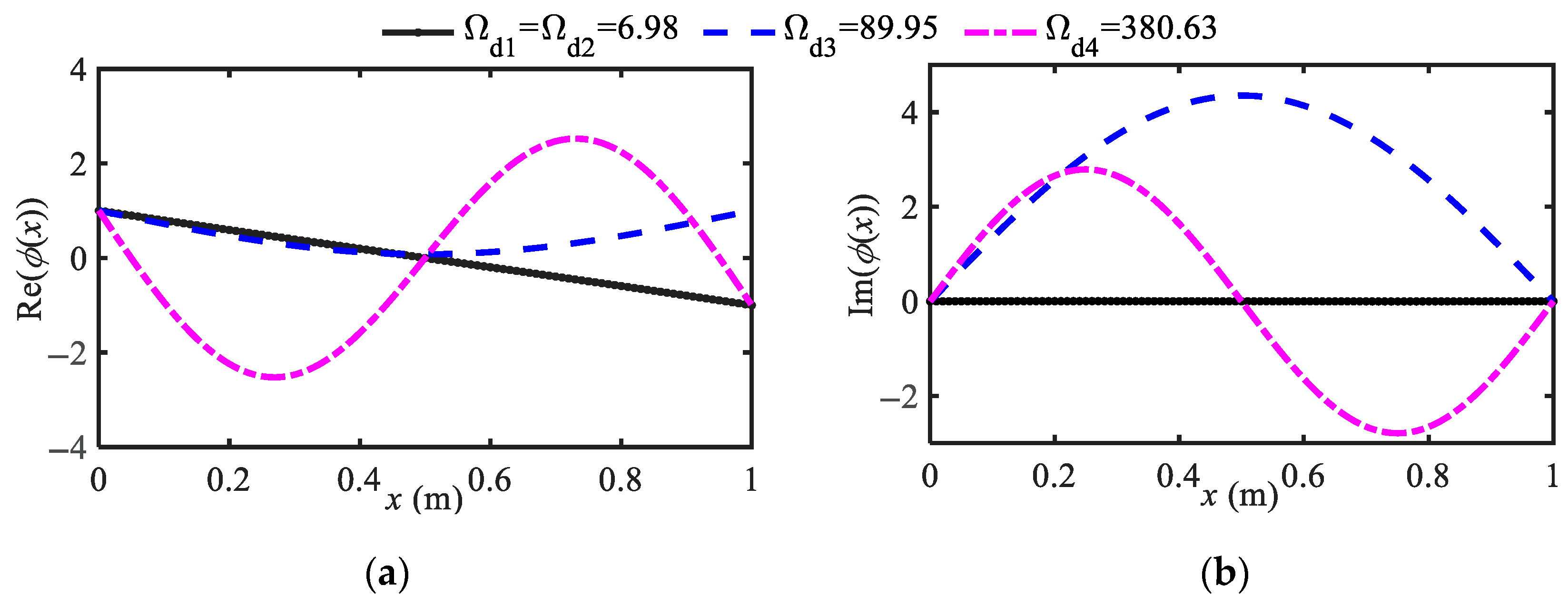
4.1. Vibration Mode Analysis
4.2. Galerkin Truncation Equation and Its Convergence
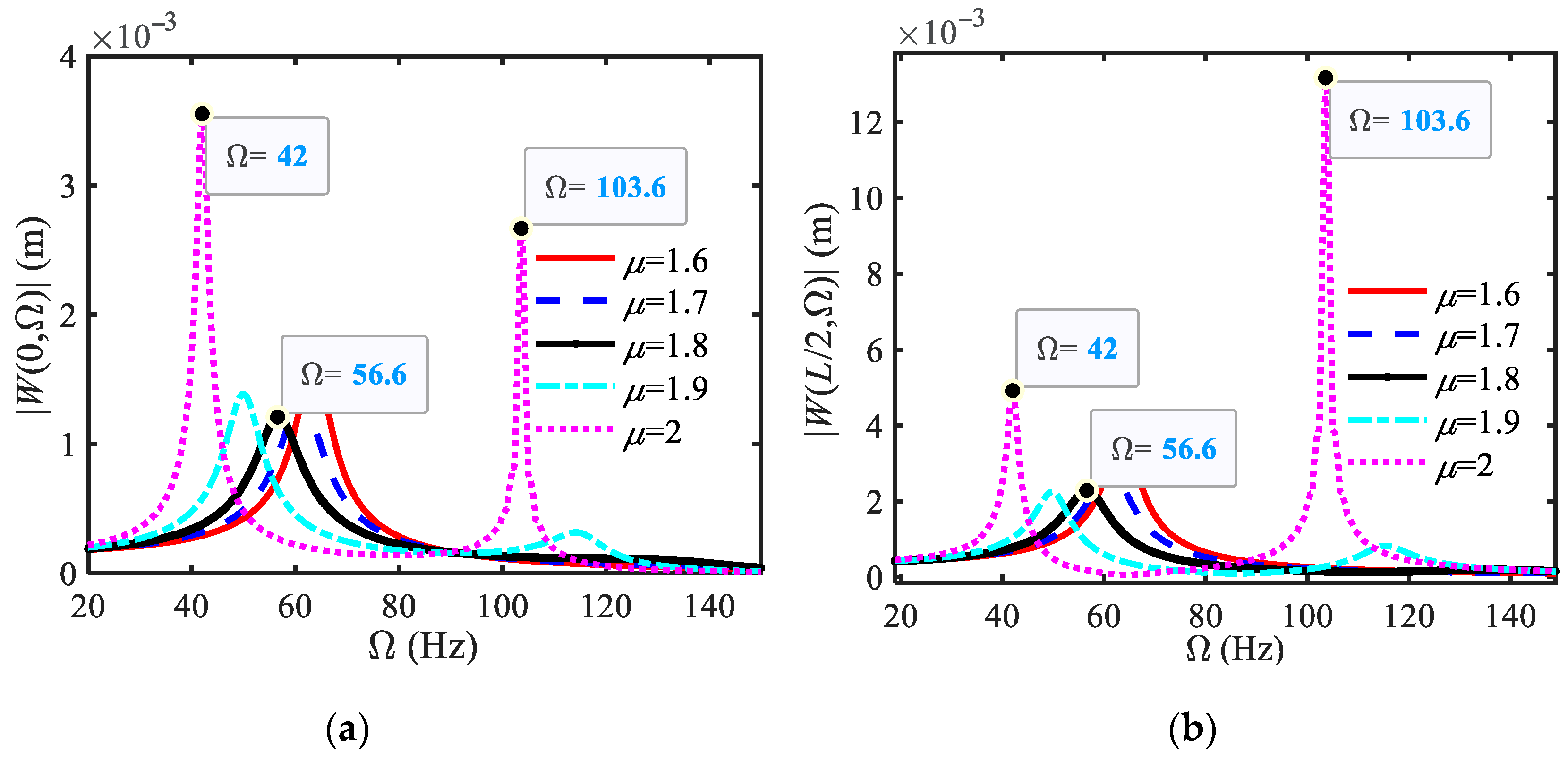
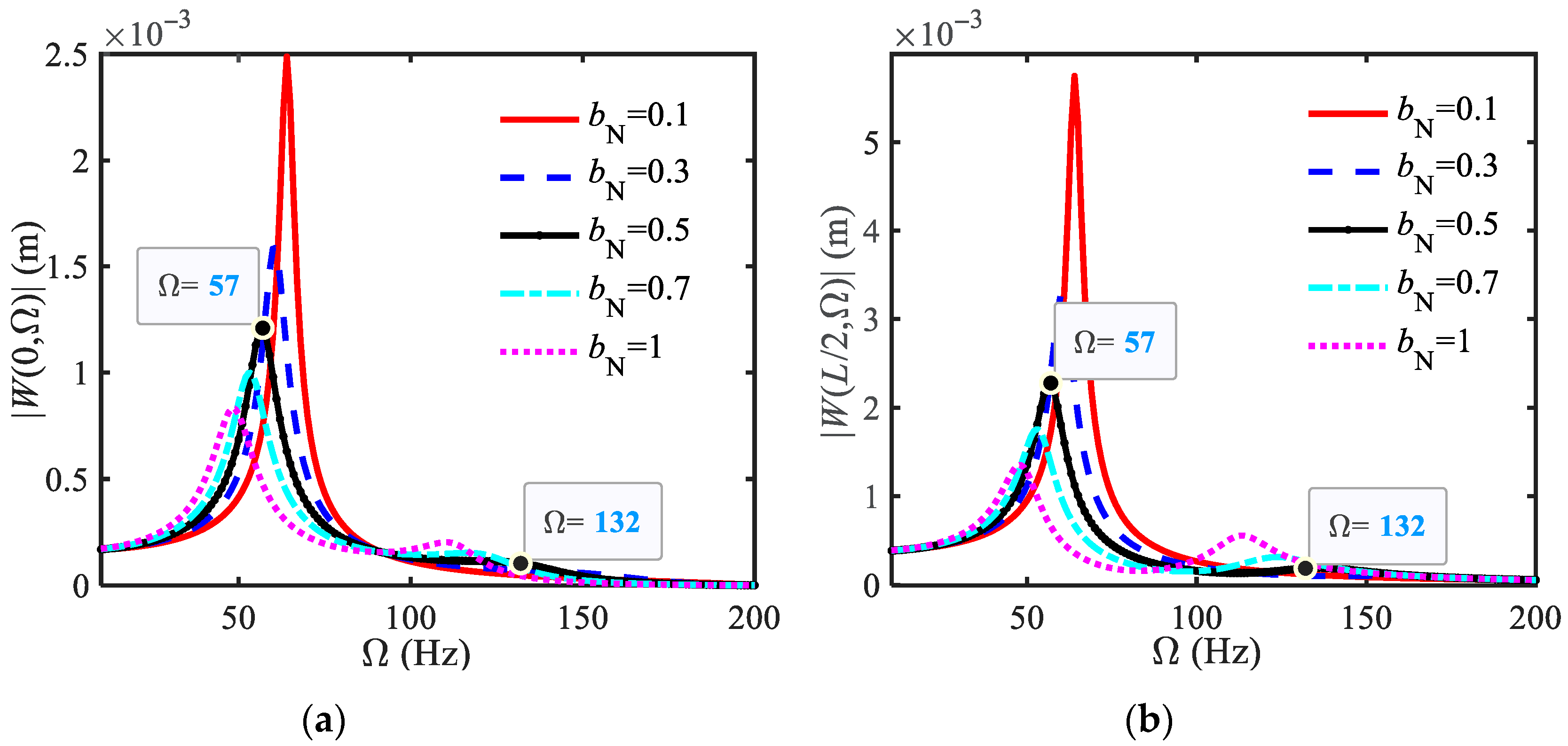
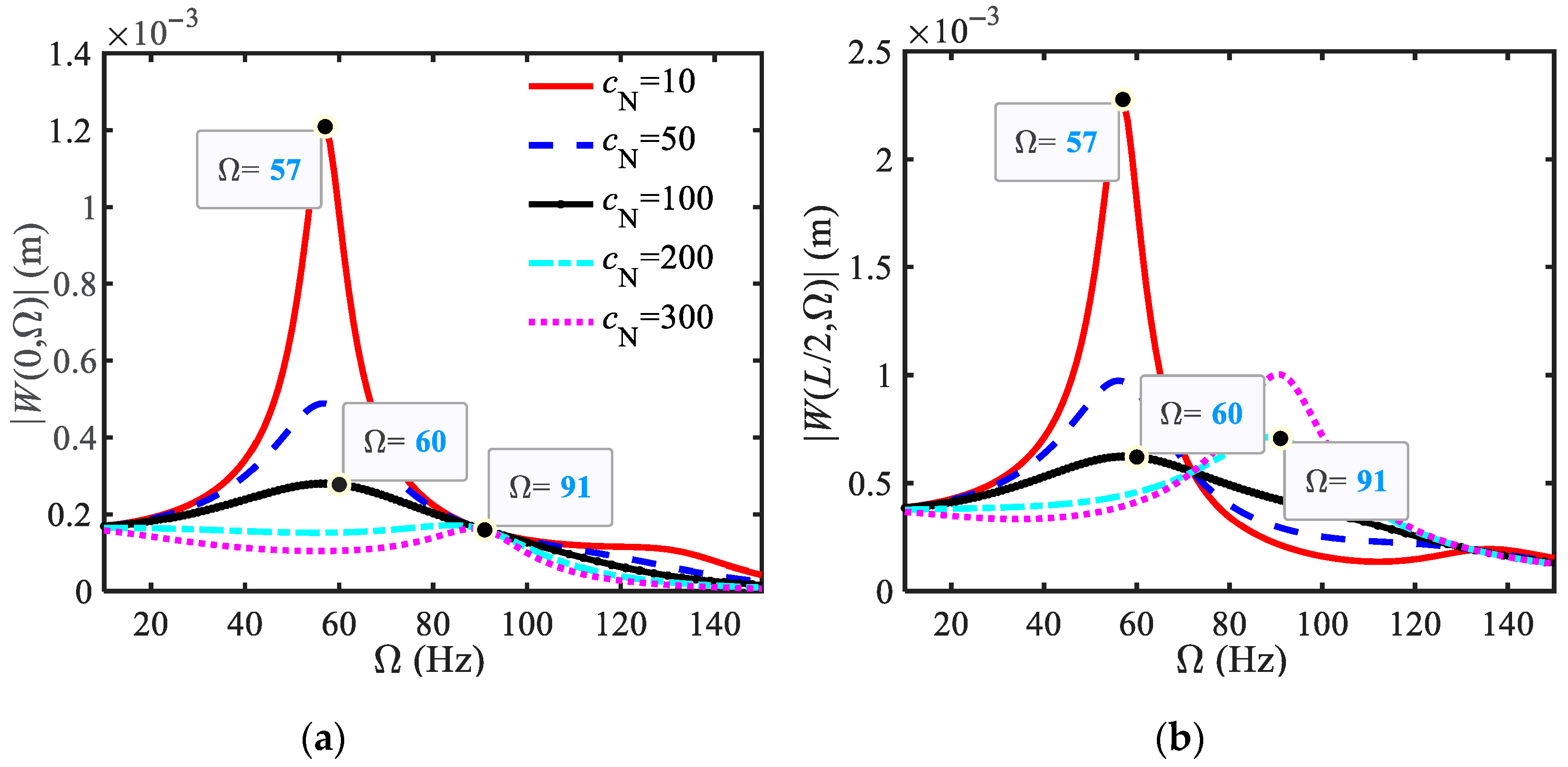
4.3. Analysis of Vibration Suppression Effect
- (1)
- Vibration suppression performance indicators
- (2)
- The influence of FOIB-VMD parameters on vibration suppression performance
5. Conclusions
- (1)
- By using the complex modal analysis method, a design method for the critical damping of an elastic beam with fractional-order inertial damping structures in the first-and second-order models was proposed for the first time, and the accuracy of the critical damping calculation formula was verified through specific examples.
- (2)
- Meanwhile, research has shown that the derivative order μ and inertance bN of fractional-order inerters have an beneficial impact on critical damping and primary resonance frequency. The higher μ and bN, the lower the main resonance frequency and the greater the critical damping. Conversely, the opposite is true, indicating that bN reflects the inertia characteristics, while μ reflects the proportion of attached damping.
- (3)
- Using the main resonance amplitude and frequency attenuation rate (RA and RΩ) as indicators, the impact of shock absorber parameters on vibration suppression was analyzed. (1) When using a fractional-order inerter, the vibration reduction effect is better than that of an integer-order inerter. However, expanding the vibration reduction bandwidth is slightly inferior, and the vibration reduction effect is best when μ is around 1.8. (2) The larger bN, the better. (3) Damping has a significant vibration reduction effect on beams when selecting under damping, and the critical damping proposed in this article helps us clarify the range of under damping. With first-order critical damping, the first-order main resonance frequency of the system disappears, while higher-order frequencies decrease, and the RA exceeds 99%. This demonstrates that the function of critical damping in traditional single-degree-of-freedom systems remains consistent. Based on the optimal average RA range (95–98%) and higher cost-effectiveness, selecting a damping value of 0.05~0.6 times the critical damping ensures better overall vibration suppression performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, A.L.; Li, C.H.; Liu, X.C.; Chen, X. Static performance of welded hollow spherical bolted joint with H-beams. Structures 2025, 76, 109039. [Google Scholar] [CrossRef]
- Hao, M.; Zhou, S.; Han, Y.; Zhu, Z.; Yang, Q.; Sun, P.; Fan, J. Performance Evaluation of Damaged T-Beam Bridges with External Prestressing Reinforcement Based on Natural Frequencies. Struct. Durab. Health Monit. 2025, 19, 399–415. [Google Scholar] [CrossRef]
- Rodrigues, R.; Alazard, D.; Sanfedino, F.; Mauriello, T.; Iannelli, P. Modeling and analysis of a flexible spinning Euler-Bernoulli beam with centrifugal stiffening and softening: A linear fractional representation approach with application to spinning spacecraft. Appl. Math. Model. 2025, 137 Pt B, 115699. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Chen, Y.; Liu, Y. Dynamic Behavior and Vibration Suppression of a Generally Restrained Pre-pressure Beam Structure Attached with Multiple Nonlinear Energy Sinks. Acta Mech. Solida Sin. 2023, 36, 116–131. [Google Scholar] [CrossRef]
- Wang, B.; Derbeli, M.; Barambones, O.; Yousefpour, A.; Jahanshahi, H.; Bekiros, S.; Aly, A.A.; Alharthi, M.M. Experimental validation of disturbance observer-based adaptive terminal sliding mode control subject to control input limitations for SISO and MIMO systems—ScienceDirect. Eur. J. Control. 2022, 63, 151–163. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Niu, M.Q.; Deng, L.F.; Fan, Y.; Chen, L.Q. Dynamic Analysis and Optimization on Passive/Active Vibration Reduction of a Beam Structure with Distributed Smart Foams. Int. J. Struct. Stab. Dyn. 2025, 25, 2550063. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Chen, J.; Zhang, W. Optimal placement of piezoelectric actuator/sensor pairs for active vibration control of beams with different boundary conditions. Mech. Based Des. Struct. Mach. 2025, 53, 2262–2279. [Google Scholar] [CrossRef]
- Chowdhury, S.; Adhikari, S. Structural vibration control using nonlinear damping amplifier friction vibration absorbers. Appl. Math. Mech. 2025, 46, 965–988. [Google Scholar] [CrossRef]
- Soltani, M.; Fesharaki, J.J.; Galehdari, S.A.; Esfahani, R.T.; Shahgholi, M.A. comprehensive evaluation of the vibration control approach of the multi-layer sandwich composite piezoelectric micro-beam using higher-order elasticity theory and surface energy. Structures 2024, 60, 105880. [Google Scholar] [CrossRef]
- Duc, D.M.; Hung, T.Q.; Tu, T.M. Analytical and mesh-free approaches to dynamic analysis and active control of smart FGP-GPLRC beam. Structures 2023, 56 (Suppl. C), 105020. [Google Scholar] [CrossRef]
- Fu, Y.; Li, H.B.; Reng, J.N. Research Progress of Damping and Vibration Reduction Technology Used in Aerospace. Mater. Res. Appl. 2022, 16, 656–662. [Google Scholar] [CrossRef]
- Kumar, K.R.; Narayanan, S. Active vibration control of beams with optimal placement of piezoelectric sensor/actuator pairs. Smart Mater. Struct. 2008, 17, 055008. [Google Scholar] [CrossRef]
- Khot, S.M.; Yelve, N.P.; Kumar, P.; Purohit, G.A.; Singh, D. Experimental investigation of performances of different optimal controllers in active vibration control of a cantilever beam. ISSS J. Micro Smart Syst. 2019, 8, 101–111. [Google Scholar] [CrossRef]
- Marian, L.; Giaralis, A. Optimal design of a novel tuned mass-damper–inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 2014, 38, 156–164. [Google Scholar] [CrossRef]
- Shi, X.; Shi, W.; Lin, K.; Xing, L.; Zhu, S. Optimal design of tuned inerter dampers with series or parallel stiffness connection for cable vibration control. Struct. Control. Health Monit. 2020, 28, e2673.1–e2673.26. [Google Scholar] [CrossRef]
- Shen, Y.; Hua, J.; Fan, W.; Liu, Y.; Yang, X.; Chen, L. Optimal design and dynamic performance analysis of a fractional-order electrical network-based vehicle mechatronic ISD suspension. Mech. Syst. Signal Process. 2023, 184, 109718. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Cheng, J.; Sheng, L.; Yao, Y. Adaptive stability mechanism of high-speed train employing parallel inerter yaw damper. Veh. Syst. Dyn. 2023, 61, 38–57. [Google Scholar] [CrossRef]
- Shen, Y.; Chen, L.; Yang, X.; Shi, D.; Yang, J. Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension. J. Sound Vib. 2016, 361, 148–158. [Google Scholar] [CrossRef]
- Swift, S.J.; Smith, M.C.; Glover, A.R.; Papageorgiou, C.; Gartner, B.; Houghton, N.E. Design and modelling of a fluid inerter. Int. J. Control 2013, 86, 2035–2051. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, J.; Tai, Y.; Xu, X.; Chen, N. Critical damping design method of vibration isolation system with both fractional-order inerter and damper. Mech. Adv. Mater. Struct. 2022, 29, 1348–1359. [Google Scholar] [CrossRef]
- Chen, Y.; Tai, Y.; Xu, J.; Xu, X.; Chen, N. Vibration Analysis of a 1-DOF System Coupled with a Nonlinear Energy Sink with a Fractional Order Inerter. Sensors 2022, 22, 6408. [Google Scholar] [CrossRef]
- Chen, Y.D.; Chen, N. A New Fractional-Order Constitutive Model and Rough Design Method for Fluid-Type Inerters. Materials 2025, 18, 2556. [Google Scholar] [CrossRef]
- Ding, H.; Zhu, M.H.; Chen, L.Q. Nonlinear vibration isolation of a viscoelastic beam. Nonlinear Dyn. 2018, 92, 325–349. [Google Scholar] [CrossRef]
- Ding, H.; Lu, Z.Q.; Chen, L.Q. Nonlinear isolation of transverse vibration of pre-pressure beams. J. Sound Vib. 2019, 442, 738–751. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z. Inclined Boundary Inertial Vibration Absorber for Elastic Beam. Open J. Acoust. Vib. 2025, 13, 22–36. [Google Scholar] [CrossRef]
- Sinha, A. Vibration of Mechanical Systems; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Wang, P.; Wang, Q.; Xu, X.; Chen, N. Fractional Critical Damping Theory and Its Application in Active Suspension Control. Shock. Vib. 2017, 2017 Pt 7, 2738976.1–2738976.8. [Google Scholar] [CrossRef]
- Zhou, Z.; Fan, S.; Cai, Y.; Luo, F. Effect of Noise Reduction on Thin-Walled Parts of Engine Using Damping Material Treatment. Trans. CSICE 2022, 40, 89–95. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice-Hall: Hoboken, NJ, USA, 2025. [Google Scholar]
- Bulatovic, R.M. On the critical damping in multi-degree-of-freedom systems. Mech. Res. Commun. 2002, 29, 315–319. [Google Scholar] [CrossRef]
- Main, J.A.; Jones, N.P. Free Vibrations of Taut Cable with Attached Damper. I: Linear Viscous Damper. J. Eng. Mech. 2002, 128, 1062–1071. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.; Tai, Y.; Xu, X.; Shi, G.; Chen, N. Vibration analysis of complex fractional viscoelastic beam structures by the wave method. Int. J. Mech. Sci. 2020, 167, 12. [Google Scholar] [CrossRef]
- Chen, W. Fractional Derivative Modeling of Mechanics and Engineering Problems; Science Press: Beijing, China, 2010. [Google Scholar]
- Xu, Y.; Xu, Z.D.; Hu, H.; Guo, Y.Q.; Huang, X.H.; Zhang, Z.W.; Zhang, T.; Xu, C. Experiment, Simulation, and Theoretical Investigation of a New Type of Interlayer Connections Enhanced Viscoelastic Damper. Int. J. Struct. Stab. Dyn. 2025, 25, 2550045. [Google Scholar] [CrossRef]
- Aghababaiyan, M.R.; Dehkordi, M.B.; Fallah, A. A new approach for nonlinear transient dynamic analysis of micro SMA beam considering size effect and instantaneous phase transformation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 2205–2214. [Google Scholar] [CrossRef]
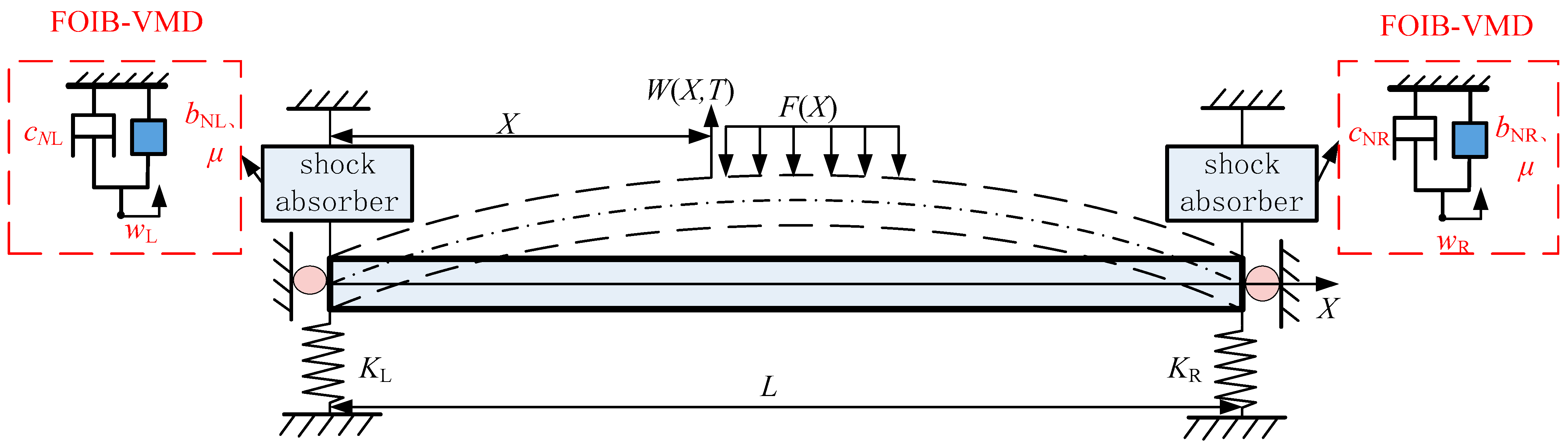



| Name | Symbol | Value (Unit) |
|---|---|---|
| Young’s modulus | E | 68.9 GPa |
| Density | ρ | 2800 kg/m3 |
| Viscous damping | Λ | 0 N s/m2 |
| Vertical stiffness | KL = KR | 46,025.2 N/m |
| Length | L | 0.5 m |
| Sectional area | A | 2 × 10−4 m2 |
| Sectional moment of inerter | I | 1.67 × 10−9 m4 |
| Damper damping coefficient | cN | N s/m |
| Inertance | bN | kg (μ = 2) kg sμ−2 (1 < μ < 2) |
| Derivative order of the inerter | μ | / |
| FOIB-VMD Parameters | Ωn (Hz) | Ωd (Hz) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 1st | 2nd | 3rd | 4th | ||
| cN = 0, bN = 0 | 65.8 | 148.9 | 278.5 | 593.3 | 65.8 | 148.9 | 278.5 | 593.3 | |
| μ = 2, cN = 0 | bN = 0.1 | 59.6 | 88.6 | 144.9 | 403.4 | 59.6 | 88.6 | 144.9 | 403.4 |
| bN = 0.2 | 53.8 | 68.6 | 120.1 | 383.7 | 53.8 | 68.6 | 120.1 | 383.7 | |
| bN = 0.3 | 48.9 | 57.9 | 110.0 | 376.4 | 48.9 | 57.9 | 110.0 | 376.4 | |
| μ = 1.8, cN = 0 | bN = 0.1 | 64.0 | 123.9 | 212.7 | 487.1 | 64.0 | 123.7 | 212.2 | 486.8 |
| bN = 0.2 | 62.2 | 106.8 | 178.2 | 444.3 | 62.2 | 106.4 | 177.5 | 443.9 | |
| bN = 0.3 | 60.4 | 94.5 | 157.4 | 422.4 | 60.4 | 94.0 | 156.7 | 422.1 | |
| bN = 0 | cN = 50 | 67.6 | 159.1 | 280.6 | 566.6 | 67.2 | 140.2 | 246.3 | 552.5 |
| cN = 100 | 73.5 | 102.8 | 157.3 | 423.5 | 0.0 | 0.0 | 154.6 | 393.7 | |
| cN = 150 | 54.6 | 67.9 | 80.9 | 375.9 | 0.0 | 0.0 | 79.5 | 365.7 | |
| cN = 200 | 38.8 | 43.7 | 84.9 | 367.8 | 0.0 | 0.0 | 83.9 | 362.6 | |
| FOIB-VMD Parameters | Ωn (Hz) | Ωd (Hz) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 1st | 2nd | 3rd | 4th | ||
| cN = 0, bN = 0 | 65.8 | 148.9 | 278.5 | 593.3 | 65.8 | 148.9 | 278.5 | 593.3 | |
| bN = 0.5, μ = 1.8 | cN = 10 | 56.9 | 77.7 | 132.7 | 400.1 | 56.7 | 76.4 | 131.8 | 400.0 |
| cN = 100 | 63.4 | 70.3 | 107.5 | 392.3 | 57.9 | 52.7 | 102.4 | 391.8 | |
| cN = 200 | 45.9 | 52.1 | 91.2 | 383.0 | 10.6 | 18.2 | 90.0 | 382.3 | |
| bN = 0.5, μ = 2 | cN = 10 | 41.7 | 46.2 | 101.7 | 370.1 | 41.7 | 46.1 | 101.7 | 370.1 |
| cN = 100 | 42.1 | 46.2 | 100.7 | 370.1 | 40.5 | 43.8 | 100.6 | 370.1 | |
| cN = 200 | 43.2 | 46.2 | 98.2 | 369.9 | 35.7 | 35.9 | 98.0 | 369.9 | |
| FOIB-VMD Parameters | RΩ (%) | |
|---|---|---|
| bN = 0.5, μ = 1.8 | cN = 10 | 13.83 |
| cN = 100 | 12.01 | |
| cN = 200 | 83.89 | |
| bN = 0.5, μ = 2 | cN = 10 | 36.63 |
| cN = 100 | 38.45 | |
| cN = 200 | 45.74 | |
| FOIB-VMD Parameters | RA (%) (Left End of the Beam) | RA (%) (Middle Position of the Beam) | Average Values of RA(%) on the Left and Middle Position of the Beam | |
|---|---|---|---|---|
| bN = 0.5, cN = 10 | μ = 1.7 | 96.72 | 93.05 | 94.89 |
| μ = 1.8 | 97.07 | 94.48 | 95.78 | |
| μ = 1.9 | 96.63 | 94.55 | 95.59 | |
| μ = 2 | 91.39 | 68.20 | 79.80 | |
| μ = 1.8, cN = 10 | bN = 0.1 | 93.97 | 86.07 | 90.02 |
| bN = 0.3 | 96.15 | 92.03 | 94.09 | |
| bN = 0.5 | 97.07 | 94.48 | 95.78 | |
| bN = 0.7 | 97.58 | 95.74 | 96.66 | |
| FOIB-VMD Parameters | Times of Critical Damping | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| μ = 2, bN = 0.5, cN = Times × 317 | 0 | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | 1.1 |
| Average values of RA (%) on the left and middle positions of the beam | |||||||||||||
| 65.40 | 91.27 | 94.54 | 96.57 | 97.38 | 97.84 | 98.12 | 98.25 | 98.27 | 98.29 | 98.27 | 98.21 | 98.15 | |
| μ = 1.8, bN = 0.5, cN = Times × 171 | 0 | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | 1.1 |
| Average values of RA (%) on the left and middle positions of the beam | |||||||||||||
| 93.31 | 95.78 | 96.63 | 97.72 | 98.26 | 98.58 | 98.78 | 98.93 | 99.02 | 99.07 | 99.05 | 99.02 | 98.97 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Chen, N. Critical Damping Design and Vibration Suppression Research of Elastic Beam Coupled with Fractional-Order Inerter-Based Dampers. Buildings 2025, 15, 2911. https://doi.org/10.3390/buildings15162911
Chen Y, Chen N. Critical Damping Design and Vibration Suppression Research of Elastic Beam Coupled with Fractional-Order Inerter-Based Dampers. Buildings. 2025; 15(16):2911. https://doi.org/10.3390/buildings15162911
Chicago/Turabian StyleChen, Yandong, and Ning Chen. 2025. "Critical Damping Design and Vibration Suppression Research of Elastic Beam Coupled with Fractional-Order Inerter-Based Dampers" Buildings 15, no. 16: 2911. https://doi.org/10.3390/buildings15162911
APA StyleChen, Y., & Chen, N. (2025). Critical Damping Design and Vibration Suppression Research of Elastic Beam Coupled with Fractional-Order Inerter-Based Dampers. Buildings, 15(16), 2911. https://doi.org/10.3390/buildings15162911






