Investigating the Double-Fissure Interactions of Hydraulic Concrete Under Three-Point Bending: A Simulation Study Using an Improved Meshless Method
Abstract
1. Introduction
2. Basic Principles of SPH
2.1. Kernel Function Approximation and Particle Approximation Method
2.2. Continuity Equation and Momentum Equation of SPH
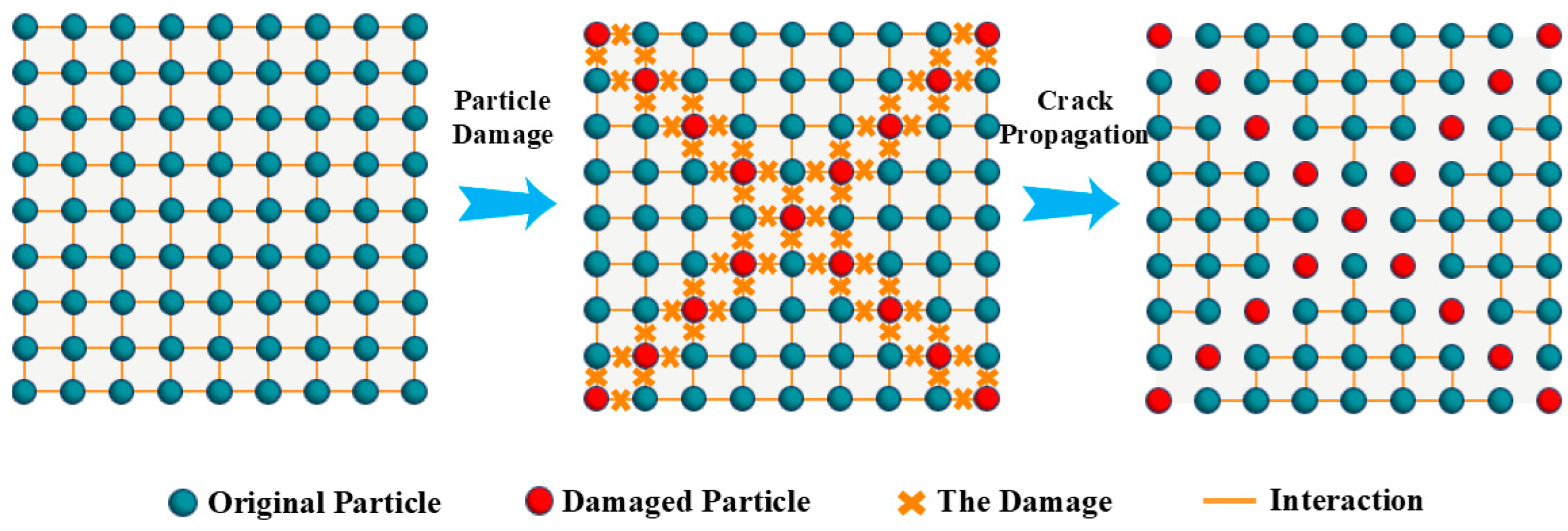
3. Numerical Treatment Method for Progressive Failure of SPH Particles
3.1. SPH Fracture Criterion
3.2. Treatment Method for SPH Particle Failure
4. Numerical Parameters and Schemes
4.1. Numerical Model and Parameters
4.2. Calculation Scheme
5. Analysis of Numerical Simulation Results
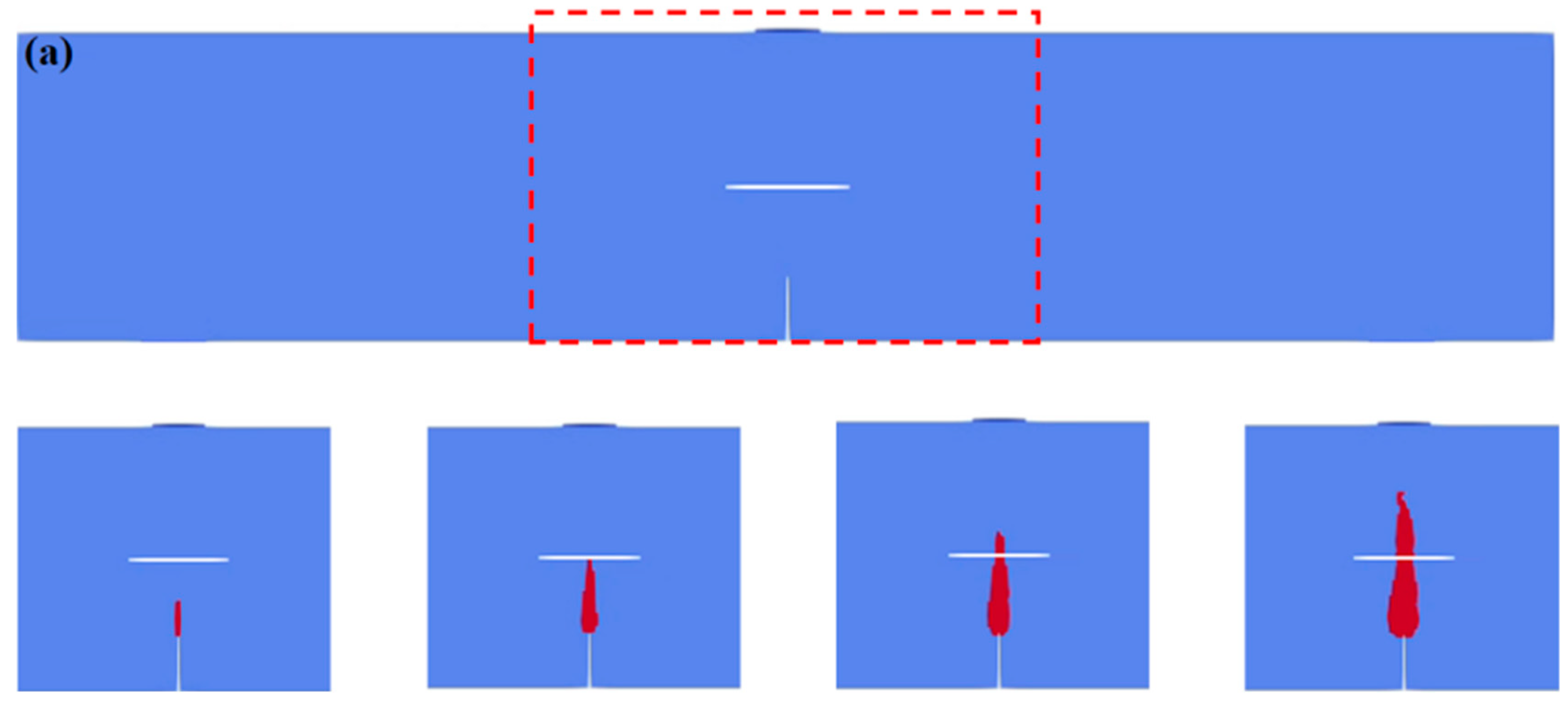
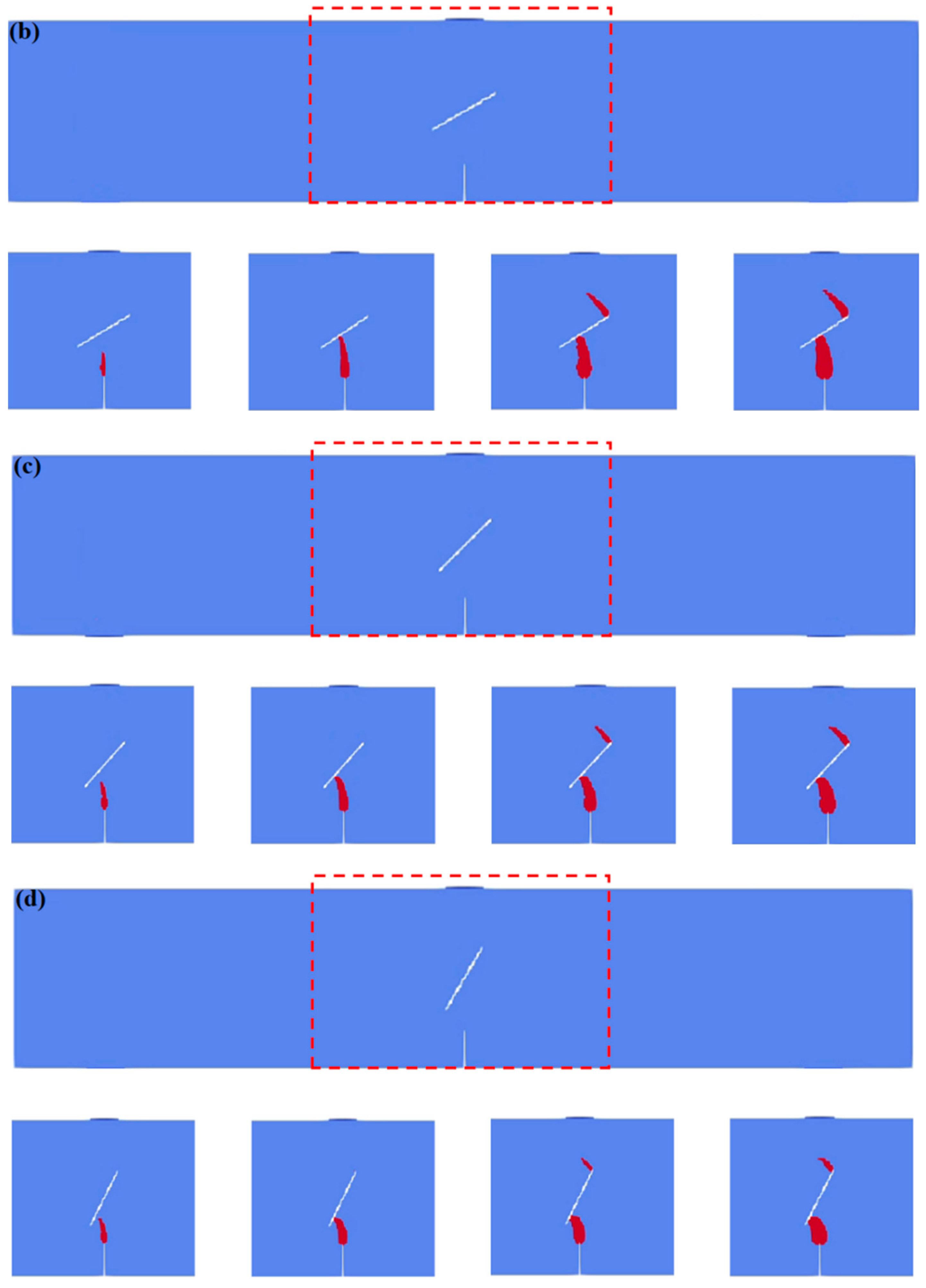
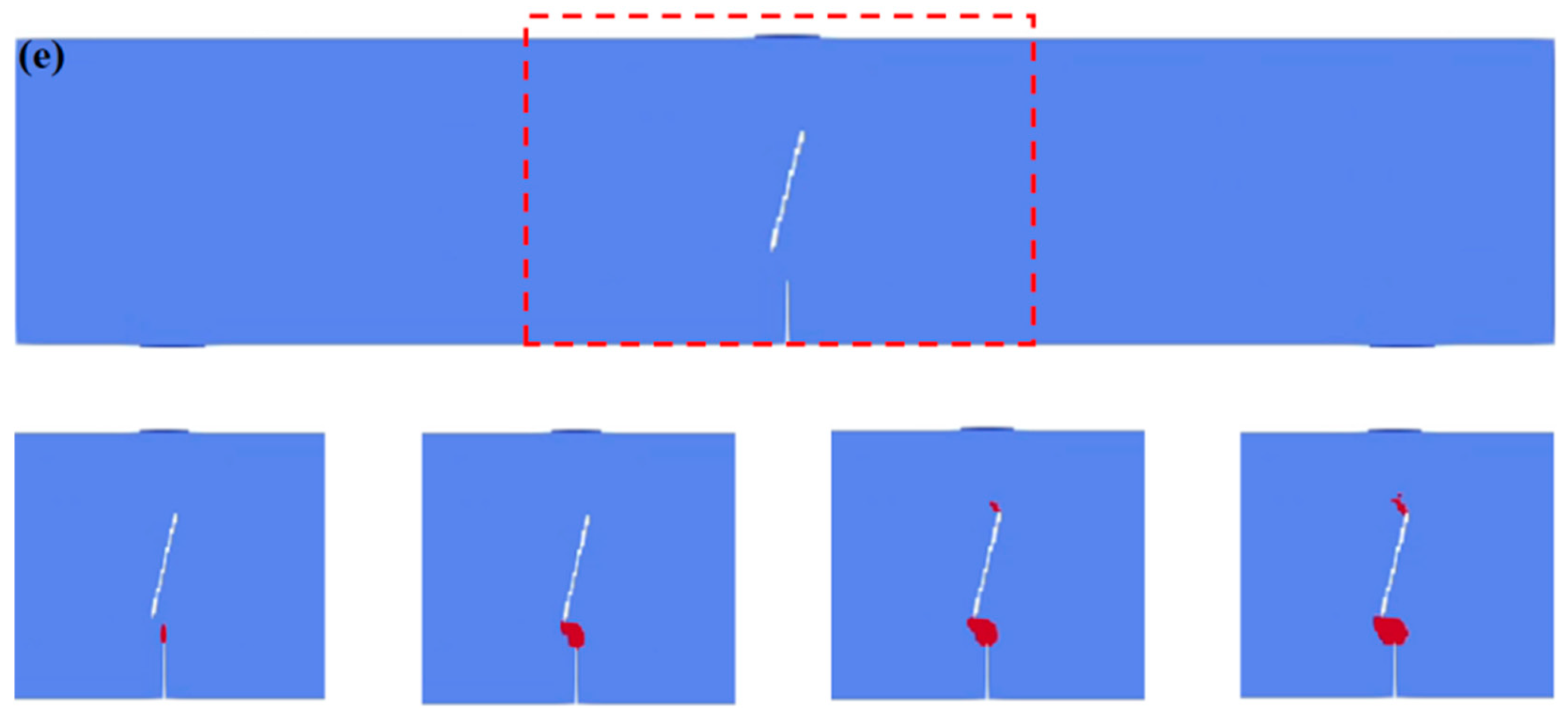
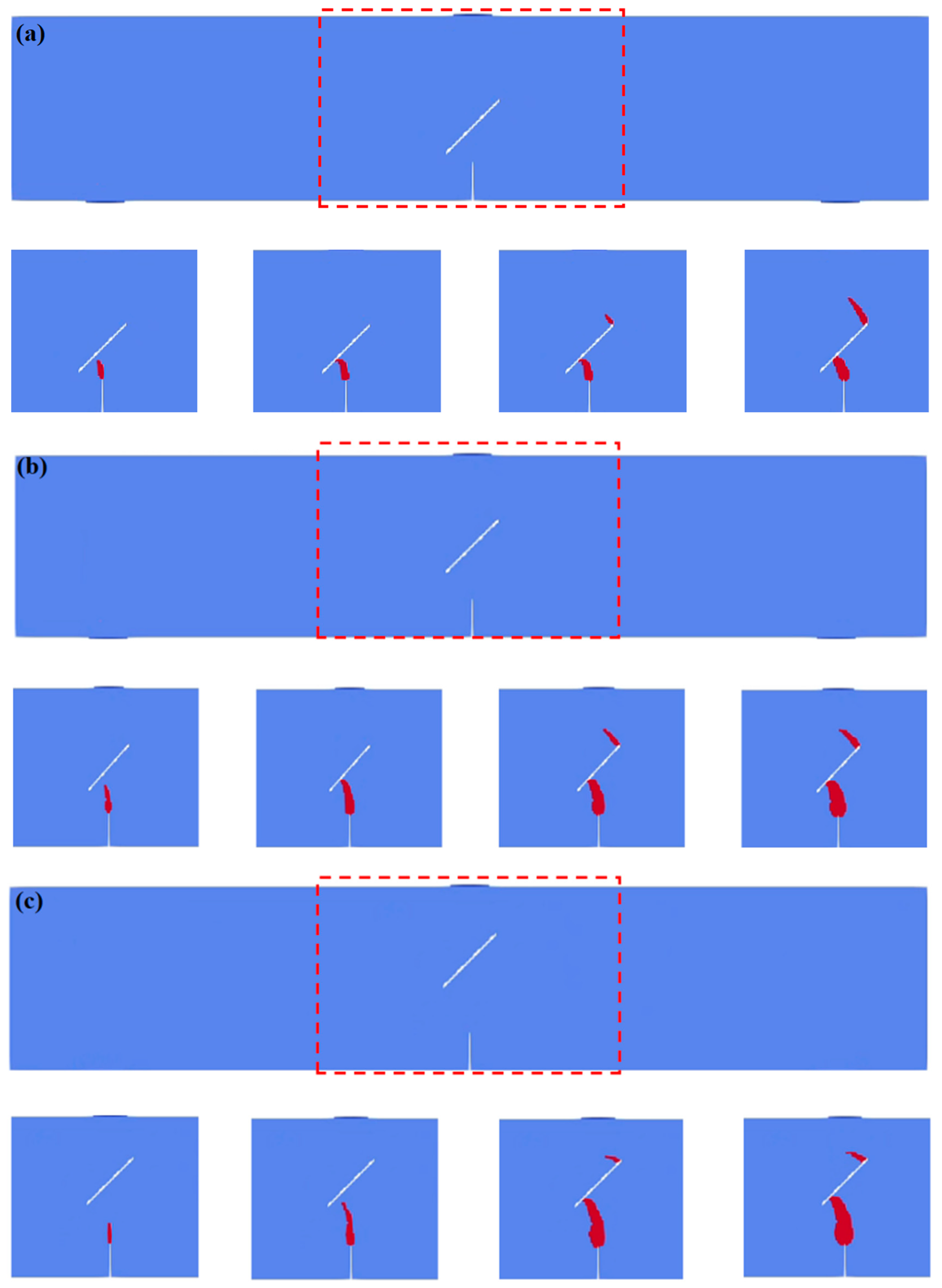
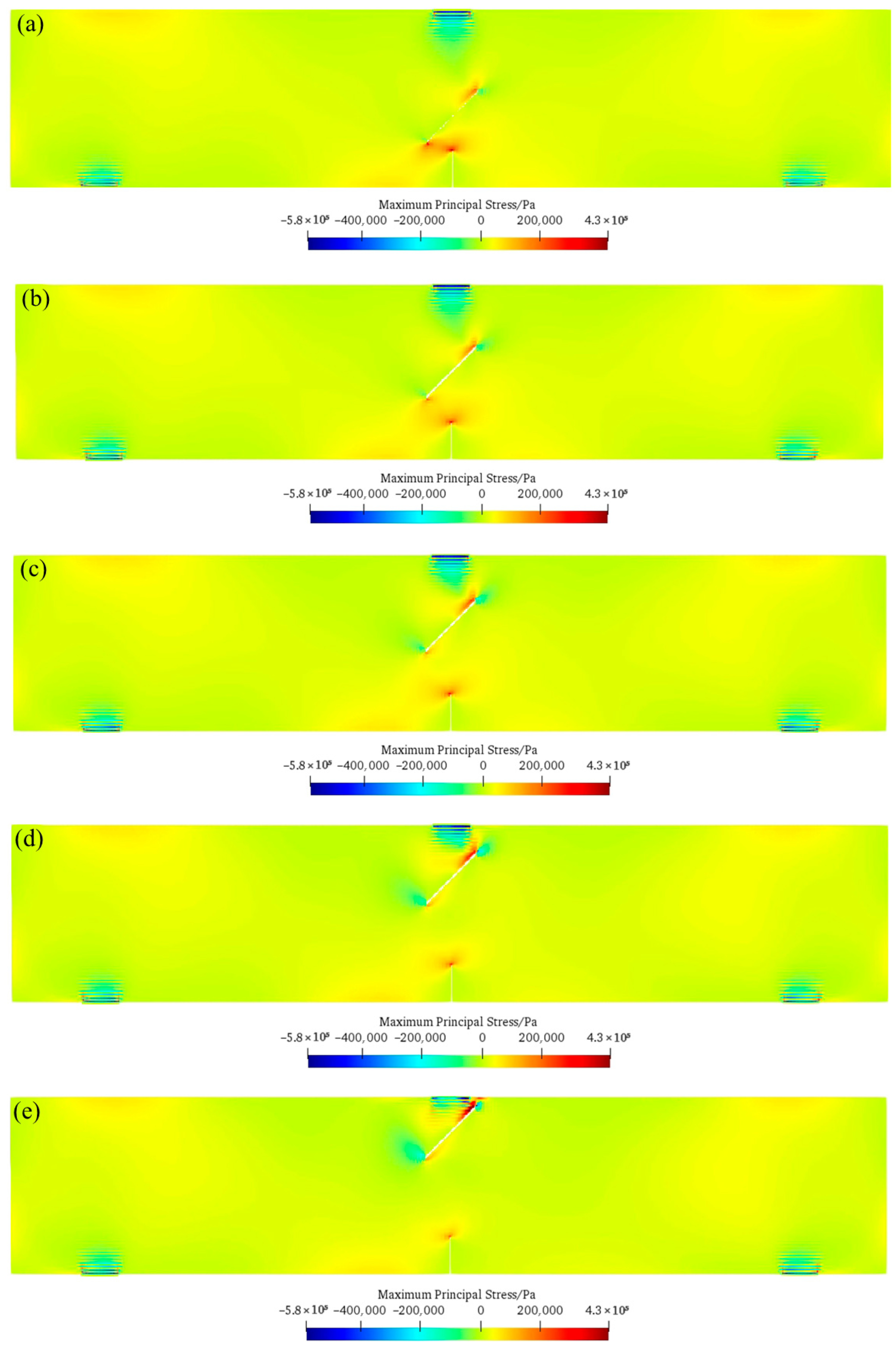
5.1. Influence of Different Precast Fissure Angles on Fissure Interaction in Concrete Beams
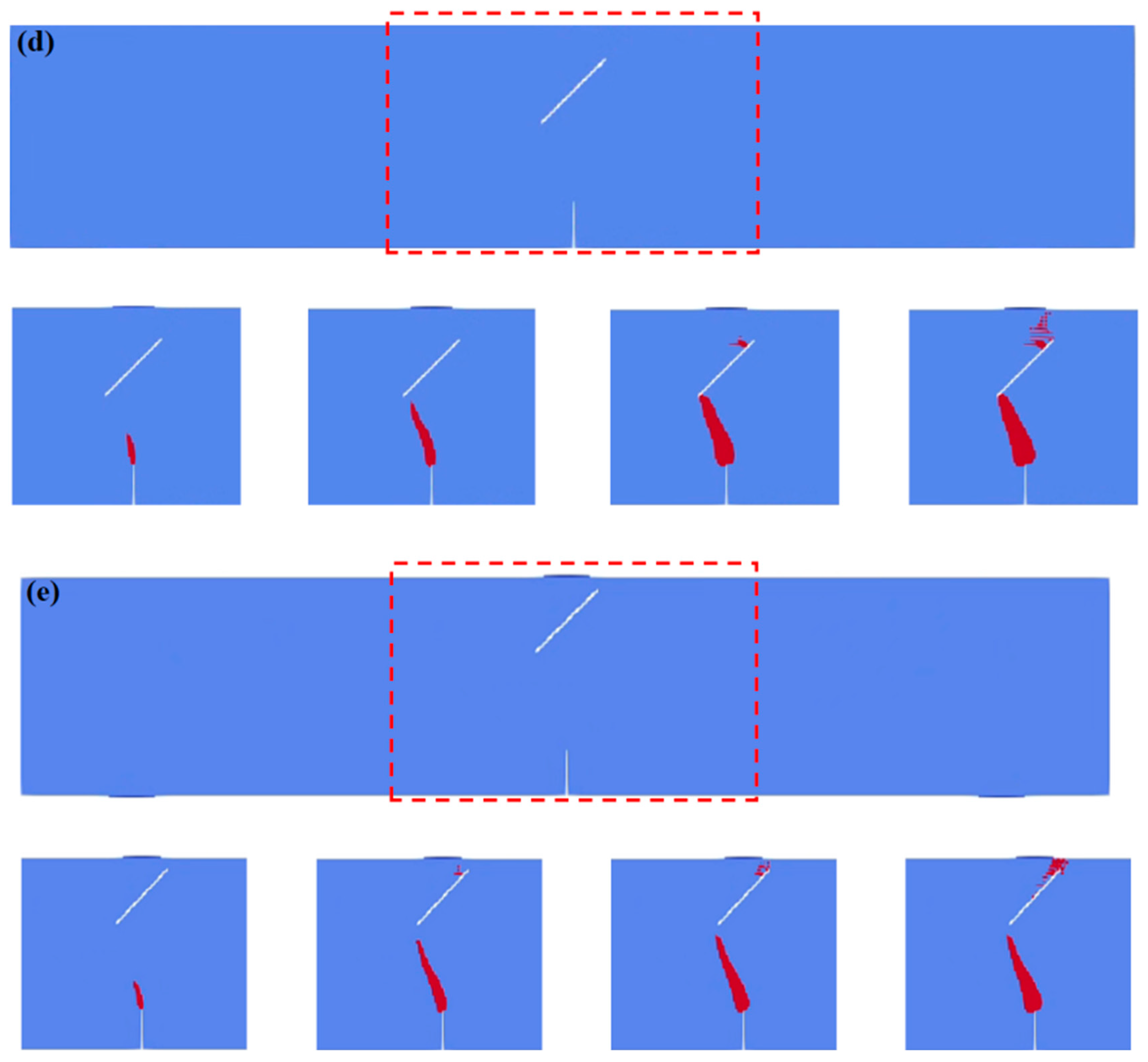
5.2. Influence of Different Obstacle Fissure Spacings on Fissure Interaction in Concrete Beams
6. Discussion
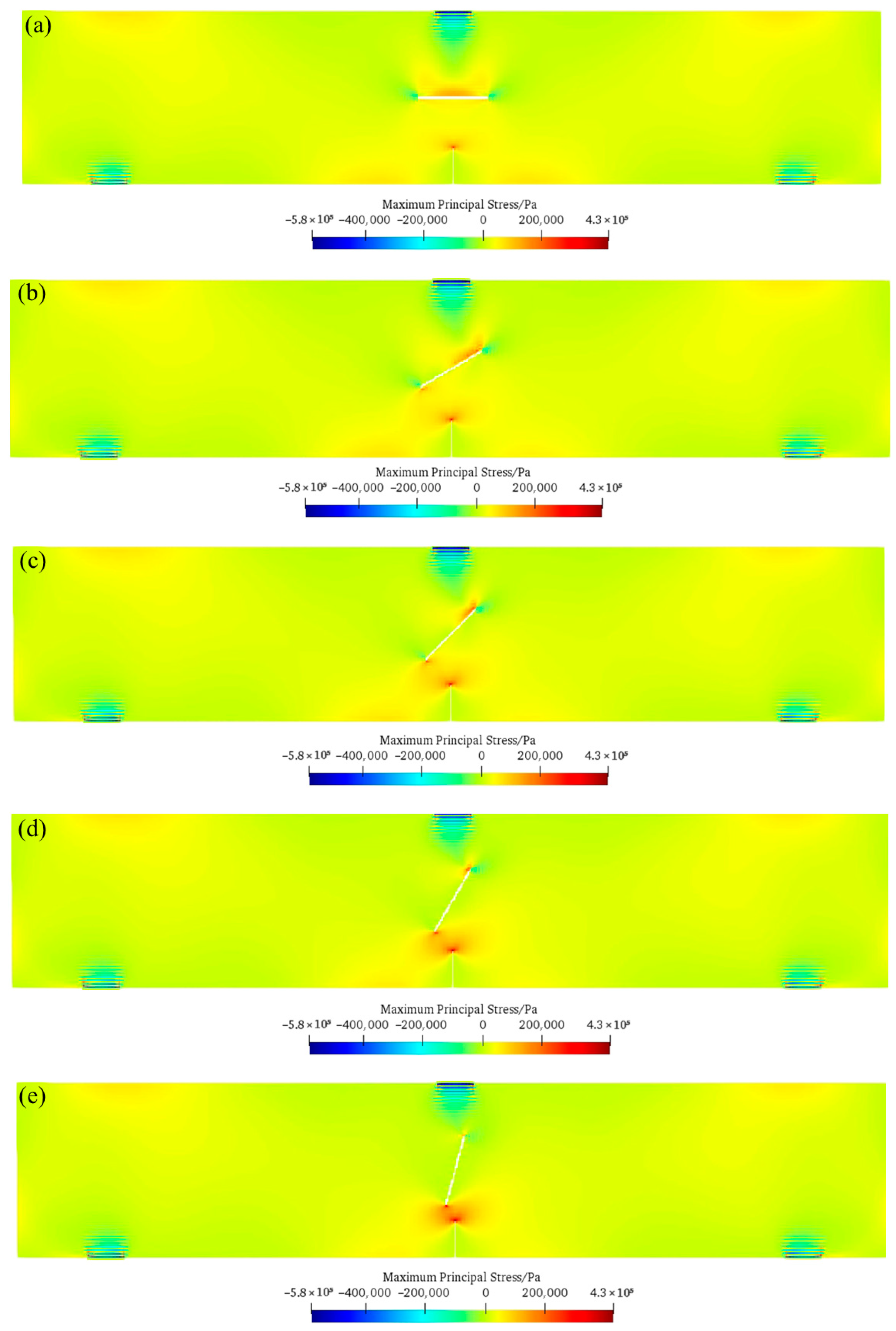
6.1. Crack Initiation Mechanism Under Different Obstacle Fissure Angles
6.2. Crack Initiation Mechanism Under Different Obstacle Fissure Spacings
6.3. Comparisons Between Numerical Results and Previous Experimental Results
6.4. Application Prospects of SPH Method to Simulation of Concrete Multi-Fissure Interaction
7. Conclusions
- (1)
- Aiming at the limitations of traditional SPH methods for handling the interaction of multiple fissures in concrete, the control equations were improved, and a particle progressive failure processing mechanism was introduced. By introducing the failure parameter ξ and improving the kernel function K, and combining them with the Mohr–Coulomb criterion, the simulation of the SPH particle failure process was realized. A meshless numerical model for the three-point bending of a concrete beam with double slits was established, and the interactive propagation process of cracks was successfully simulated, providing an effective numerical analysis method for revealing the evolution mechanism of concrete crack propagation.
- (2)
- The change in the obstacle fissure angle α directly regulates the crack initiation position and propagation path. When α = 0°, the crack initiates at the tip of the induced fissure and then propagates in the vertical direction to lap with the middle part of the obstacle fissure. As α increases to 30–75°, the tensile stress concentration transfers from the middle part of the obstacle fissure to both ends, the crack gradually deflects toward the lower end of the obstacle fissure, the lapping position migrates to its lower left end, and the propagation length shortens with a reduced lapping time. When α = 75°, the tensile stress concentration at the lower tip of the obstacle fissure is significantly enhanced, and the lower part of the structure fails first, presenting a through mode of “induced fissure–lower end of obstacle fissure–top”.
- (3)
- Under three-point bending loads, the obstacle fissure spacing d regulates crack propagation by changing the stress superposition effect. When d is small (e.g., 0.02 m), the tensile stress concentration at the tip of the induced fissure and at both ends of the obstacle fissure is significant, and the crack propagates vertically and rapidly laps with the lower end of the obstacle fissure. As d increases to 0.06 m, the tensile stress concentration at the tip of the induced fissure weakens, while the stress concentration at the upper end of the obstacle fissure is enhanced. The crack propagation path deflects toward the upper end of the obstacle fissure, the lapping position continues to migrate to the lower left end, and the horizontal propagation characteristic becomes more obvious, with the failure mode changing from “lower-end dominated” to “upper-end dominated”.
- (4)
- Compared with the finite element method and discrete element method, the SPH method has advantages, such as no mesh dependency; clear physical meanings of parameters; and strong adaptability to dynamic loading, which can effectively simulate the processes of crack initiation, propagation, and bifurcation. In the future, it will be necessary to further expand the three-dimensional SPH model, construct heterogeneous models with aggregates combined with CT scans, integrate multi-physical field coupling mechanisms, and improve the fracture energy dissipation model. This method is expected to become a core simulation tool in hydraulic engineering fields, such as crack prevention and control of concrete dams, anti-crack design of underground caverns, and durability evaluations of coastal structures, but it needs to be improved through experimental verification before application to three-dimensional heterogeneous scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, S.; Sun, Z.; Yu, J.; Yang, J.; Zhu, C. An improved meshless method for modeling the mesoscale cracking processes of concrete containing random aggregates and initial defects. Constr. Build. Mater. 2023, 363, 129770. [Google Scholar] [CrossRef]
- Yu, S.; Huang, S.; Li, Y.; Liang, Z. Insights into the frost cracking mechanisms of concrete by using the coupled thermo-hydro-mechanical-damage meshless method. Theor. Appl. Fract. Mech. 2025, 136, 104814. [Google Scholar] [CrossRef]
- Pan, J.; Xiong, S. Deformation, failure and restoration of the Trier arch dam in Switzerland. Dam Saf. 1987, 1, 2–22. [Google Scholar]
- Zhu, B. Re-discussion on the cause of fracture during construction of Xiaowan arch dam. Water Resour. Hydropower Eng. 2015, 46, 1–5. [Google Scholar]
- Ru, N.; Jiang, Z. Dam Accidents and Safety Arch Dams; China Water Resources and Hydropower Press: Beijing, China, 1995. [Google Scholar]
- Guo, W.; Yan, S.; Gao, G. Electro-Chemo-Mechanical coupled model for corrosion and crack propagation in reinforced concrete. J. Build. Eng. 2025, 108, 112988. [Google Scholar] [CrossRef]
- Wang, H.; Jia, M.; Yang, X.; Wang, Y.; Yu, R.C.; Wu, Z. Determination of fracture toughness of concrete based on actual critical crack length: Theoretical model and experimental validation. Eng. Fract. Mech. 2025, 318, 110966. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Z.; Feng, Y.; Yu, H. Meso-crack propagation of RC induced by non-uniform rebar corrosion and the predictive model of time to concrete cover cracking. Eng. Fail. Anal. 2024, 166, 108831. [Google Scholar] [CrossRef]
- Lei, J.; Xu, C.; Lü, C.; Feng, Q.; Zhang, H. A data-driven prediction for concrete crack propagation path based on deep learning method. Case Stud. Constr. Mater. 2024, 21, e03883. [Google Scholar] [CrossRef]
- Yousef, A.; Spyridis, P. Probabilistic analysis of cracking in concrete floor slabs under seismic loading and interactions with Power Actuated Fasteners (PAF). Structures 2025, 78, 109230. [Google Scholar] [CrossRef]
- Wang, D.; Tang, J. Assessment of thermal cracking and damage in concrete by ultrasonic velocity and Vp/Vs ratio. Cem. Concr. Res. 2025, 196, 107929. [Google Scholar] [CrossRef]
- Jia, M.; Wu, Z.; Jiang, X.; Yu, R.C.; Zhang, X.; Wang, Y. Modified Paris law for mode I fatigue fracture of concrete based on crack propagation resistance. Theor. Appl. Fract. Mech. 2024, 131, 104383. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Y.; Liu, X.; Yang, K. A review of crack research in concrete structures based on data-driven and intelligent algorithms. Structures 2025, 75, 108800. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Zhao, X.; Liang, Y. Propagation characteristics and prediction of blast-induced vibration on closely spaced rock tunnels. Tunn. Undergr. Space Technol. 2022, 123, 104416. [Google Scholar] [CrossRef]
- Xiao, W. Analytical theory on instability sliding of surrounding rock blocks in tunnel roof under stress wave actions. Chin. J. Theor. Appl. Mech. 2024, 56, 183–197. [Google Scholar]
- Wang, J.R.; Deng, J.; Ren, S.J.; Qu, G.Y.; Wang, C.P.; Guo, R.Q.; Zhao, X.Q. Acoustic wave propagation characteristics and spontaneous combustion warning of coal during oxidative warming of loose coal. Fuel 2025, 398, 135528. [Google Scholar] [CrossRef]
- Wang, Y.J.; Zeng, M.H.; Liu, H.B.; Yang, J.Q.; Li, X.X.; Hu, X. A comparative study of nil-SIF-based and initial fracture toughness-based criteria for prediction of mode-I crack propagation in concrete at low temperatures. Eng. Fract. Mech. 2025, 317, 110909. [Google Scholar] [CrossRef]
- Dong, W.; Wu, Z.; Zhou, X.; Wang, N.; Kastiukas, G. An experimental study on crack propagation at rock-concrete interface using digital image correlation technique. Eng. Fract. Mech. 2017, 171, 50–63. [Google Scholar] [CrossRef]
- Chen, B.; Yu, H.; Zhang, J.; Ma, H. Evolution law of crack propagation and crack mode in coral aggregate concrete under compression: Experimental study and 3D mesoscopic analysis. Theor. Appl. Fract. Mech. 2022, 122, 103663. [Google Scholar] [CrossRef]
- Li, D.; Huang, P.; Chen, Z.; Yao, G.; Guo, X.; Zheng, X.; Yang, Y. Experimental study on fracture and fatigue crack propagation processes in concrete based on DIC technology. Eng. Fract. Mech. 2020, 235, 107166. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, W.; Zhang, B. Experimental study on local crack propagation of concrete under three-point bending. Constr. Build. Mater. 2023, 401, 132699. [Google Scholar] [CrossRef]
- Nie, Z.; Yu, L.; Zhu, P.; Wu, N.; Zuo, D.; Gan, X. Experimental study on nonlinear ultrasonic characterization of concrete during crack propagation. J. Eng. Res. 2023, 11, 314–321. [Google Scholar] [CrossRef]
- Zeng, M.-H.; Wang, H.-W.; Wang, Y.-J.; Zheng, J.-J.; Wu, Z.-M. Meso-crack propagation process of concrete based on macro-fracture parameters: Numerical and experimental. Theor. Appl. Fract. Mech. 2024, 129, 104216. [Google Scholar] [CrossRef]
- Min, Q.; Li, M.; Zhang, M.; Lian, H.; Jacquemin, T.; Bordas, S.P.A. Node projection strategy for FEM simulating cross-scale crack propagation in massive concrete structures. Eng. Struct. 2023, 293, 116665. [Google Scholar] [CrossRef]
- Yang, S.T.; Li, K.F.; Li, C.Q. Numerical determination of concrete crack width for corrosion-affected concrete structures. Comput. Struct. 2018, 207, 75–82. [Google Scholar] [CrossRef]
- Lei, Y.; Yang, X.; Liu, Q. An enhanced polar-based GPGPU-parallelized contact detection algorithm for 3D FDEM and its application to cracking analysis of shield tunnel segmental linings. Tunn. Undergr. Space Technol. 2024, 148, 105782. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, D.; Wu, C.-T. Three dimensional fragmentation simulation of concrete structures with a nodally regularized meshfree method. Theor. Appl. Fract. Mech. 2014, 72, 89–99. [Google Scholar] [CrossRef]
- Nitka, M.; Rucka, M. 3D DEM modelling of acoustic emission in concrete: Insights into elastic waves initiated by microcracks. Ultrasonics 2025, 150, 107599. [Google Scholar] [CrossRef]
- Nitka, M.; Tejchman, J. Mesoscopic simulations of a fracture process in reinforced concrete beam in bending using a 2D coupled DEM/micro-CT approach. Eng. Fract. Mech. 2024, 304, 110153. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Chen, M.; Zhao, Z.; Zhu, F.; Jiang, Y.; Ren, J. Synergistic effects of aggregate-void distribution on low-temperature fracture performance and crack propagation of asphalt concrete under mode I and mode II fracturing. Eng. Fract. Mech. 2024, 307, 110352. [Google Scholar] [CrossRef]
- Zhang, Q.; Feng, C.; Wang, D.; Wu, Z.; Yang, L.; Yue, J. Investigation on the dynamic failure characteristics of concrete slab based on mesoscopic simulation and energy conversion analysis. Case Stud. Constr. Mater. 2024, 21, e03661. [Google Scholar] [CrossRef]
- Yang, X.; Xiang, J.; Latham, J.-P.; Naderi, S.; Wang, Y. Cracking and fragmentation in percussive drilling:Insight from FDEM simulation. J. Rock Mech. Geotech. Eng. 2025. [Google Scholar] [CrossRef]
- Tang, Z.-Q.; Yin, Z.-Y.; Jin, Y.-F.; Zhou, X.-W. A novel mesoscale modelling method for steel fibre-reinforced concrete with the combined finite-discrete element method. Cem. Concr. Compos. 2024, 149, 105479. [Google Scholar] [CrossRef]
- Wang, Y.; Xiong, Z.; Kou, L. Analysis of crack propagation in tunnel lining based on nonlinear dual-parameter bond-based peridynamics model. Structures 2025, 75, 108846. [Google Scholar] [CrossRef]
- Wang, G.; Lu, D.; Gao, Y.; Xie, Z.; Du, X. Viscoelastic peridynamic method for the interface in the reinforced concrete. Eng. Fract. Mech. 2025, 315, 110817. [Google Scholar] [CrossRef]
- Jin, Y.; Li, L.; Jia, Y.; Shao, J.; Rougelot, T.; Burlion, N. Numerical study of shrinkage and heating induced cracking in concrete materials and influence of inclusion stiffness with Peridynamics method. Comput. Geotech. 2021, 133, 103998. [Google Scholar] [CrossRef]
- Yu, S.; Wang, J.; Gao, Y. Effects of fissure properties on the tunnel damage evolutions: Insights from DIC-based 3D printing experiments and meshless numerical simulations. Tunn. Undergr. Space Technol. 2024, 149, 105817. [Google Scholar] [CrossRef]
- Xiang, Z.; Yu, S.; Wang, X. Modeling the Hydraulic Fracturing Processes in Shale Formations Using a Meshless Method. Water 2024, 16, 1855. [Google Scholar] [CrossRef]
- Hu, X.; Yu, S.; Gao, Y. Experimental and meshless numerical simulation on the crack propagation processes of marble SCB specimens. Eng. Fract. Mech. 2024, 308, 110354. [Google Scholar] [CrossRef]
- Hu, X.; Yu, S.; Ying, P. Effects of fissure locations on the crack propagation morphologies of 3D printing tunnel models: Experiments and numerical simulations. Theor. Appl. Fract. Mech. 2024, 133, 104631. [Google Scholar] [CrossRef]
- Yu, S.; Gao, Y. A total Lagrange meshless method for modeling the concrete damage evolutions under blast loading. Comput. Part. Mech. 2024, 12, 491–508. [Google Scholar] [CrossRef]
- Wang, S.; Yu, S.; Ren, Z. Modelling the blast cracking processes of rock masses using a total lagrange meshless method. Case Stud. Constr. Mater. 2024, 21, e03673. [Google Scholar] [CrossRef]
- Wang, S.; Yu, S.; Hu, X. Effects of folded fissure properties on tunnel model failure: Experiments and numerical simulations. Eng. Fract. Mech. 2024, 310, 110487. [Google Scholar] [CrossRef]
- Hu, S.; Huang, S.; Yu, S.; Li, Y.; Dong, J. Investigations on the fracture mechanisms of Z-shaped fissured rock-like specimens. Theor. Appl. Fract. Mech. 2024, 134, 104748. [Google Scholar] [CrossRef]
- Yu, S.; Ren, X.; Zhang, J. Modeling the rock frost cracking processes using an improved ice—Stress—Damage coupling method. Theor. Appl. Fract. Mech. 2024, 131, 104421. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, M.; Xue, X. Experimental and Numerical Investigations on Crack Intersection and Propagation of Concrete Structures. Int. J. Concr. Struct. Mater. 2022, 16, 67. [Google Scholar] [CrossRef]
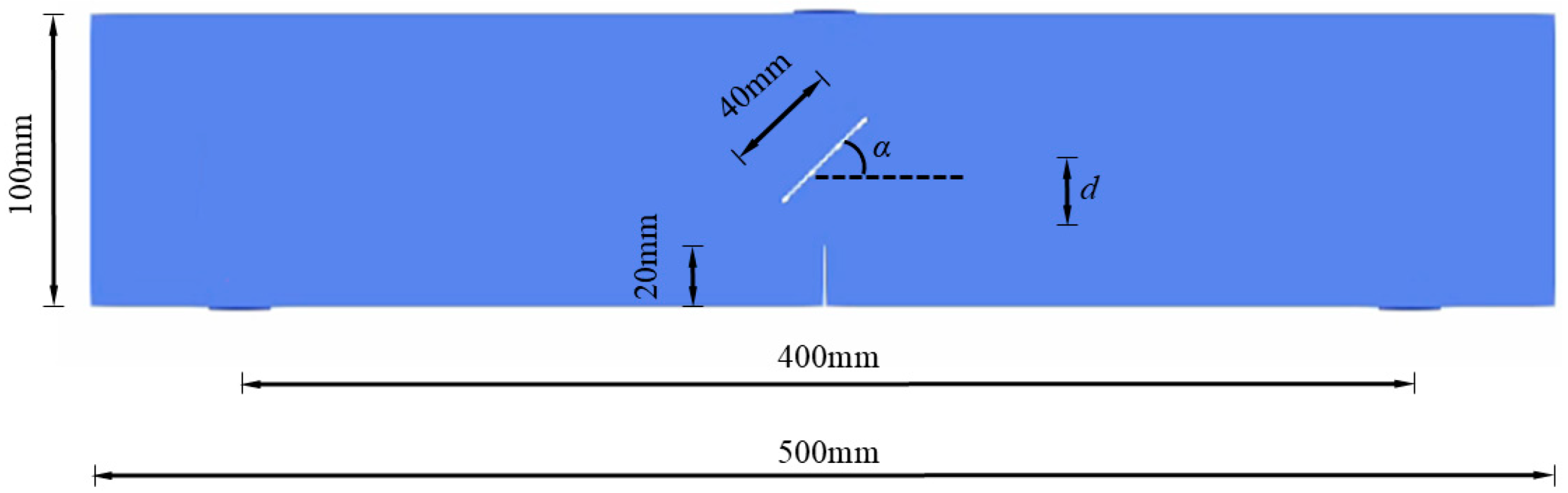

| Scheme | Details | Scheme | Details |
|---|---|---|---|
| A1 | α = 0° | B1 | d = 20 mm |
| A2 | α = 30° | B2 | d = 30 mm |
| A3 | α = 45° | B3 | d = 40 mm |
| A4 | α = 60° | B4 | d = 50 mm |
| A5 | α = 75° | B5 | d = 60 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Shi, Y.; Niu, D.; Xin, Y.; Qi, D.; Zhang, B.; Li, W.; Yu, S. Investigating the Double-Fissure Interactions of Hydraulic Concrete Under Three-Point Bending: A Simulation Study Using an Improved Meshless Method. Buildings 2025, 15, 2898. https://doi.org/10.3390/buildings15162898
Zhang H, Shi Y, Niu D, Xin Y, Qi D, Zhang B, Li W, Yu S. Investigating the Double-Fissure Interactions of Hydraulic Concrete Under Three-Point Bending: A Simulation Study Using an Improved Meshless Method. Buildings. 2025; 15(16):2898. https://doi.org/10.3390/buildings15162898
Chicago/Turabian StyleZhang, Hua, Yanran Shi, Dong Niu, Yongqiang Xin, Dunzhe Qi, Bufan Zhang, Wei Li, and Shuyang Yu. 2025. "Investigating the Double-Fissure Interactions of Hydraulic Concrete Under Three-Point Bending: A Simulation Study Using an Improved Meshless Method" Buildings 15, no. 16: 2898. https://doi.org/10.3390/buildings15162898
APA StyleZhang, H., Shi, Y., Niu, D., Xin, Y., Qi, D., Zhang, B., Li, W., & Yu, S. (2025). Investigating the Double-Fissure Interactions of Hydraulic Concrete Under Three-Point Bending: A Simulation Study Using an Improved Meshless Method. Buildings, 15(16), 2898. https://doi.org/10.3390/buildings15162898







