Small-Rib-Height Perfobond Strip Connectors (SRHPBLs) in Steel–UHPC Composite Beams: Static Behavior Under Combined Tension–Shear Loads
Abstract
1. Introduction
2. Experimental Program
2.1. Specimens Design
2.2. Specimen Fabrication
2.3. Material Properties
2.4. Test Setup and Instruments
3. Results and Discussions
3.1. Load–Slip and Load–Uplift Relationships
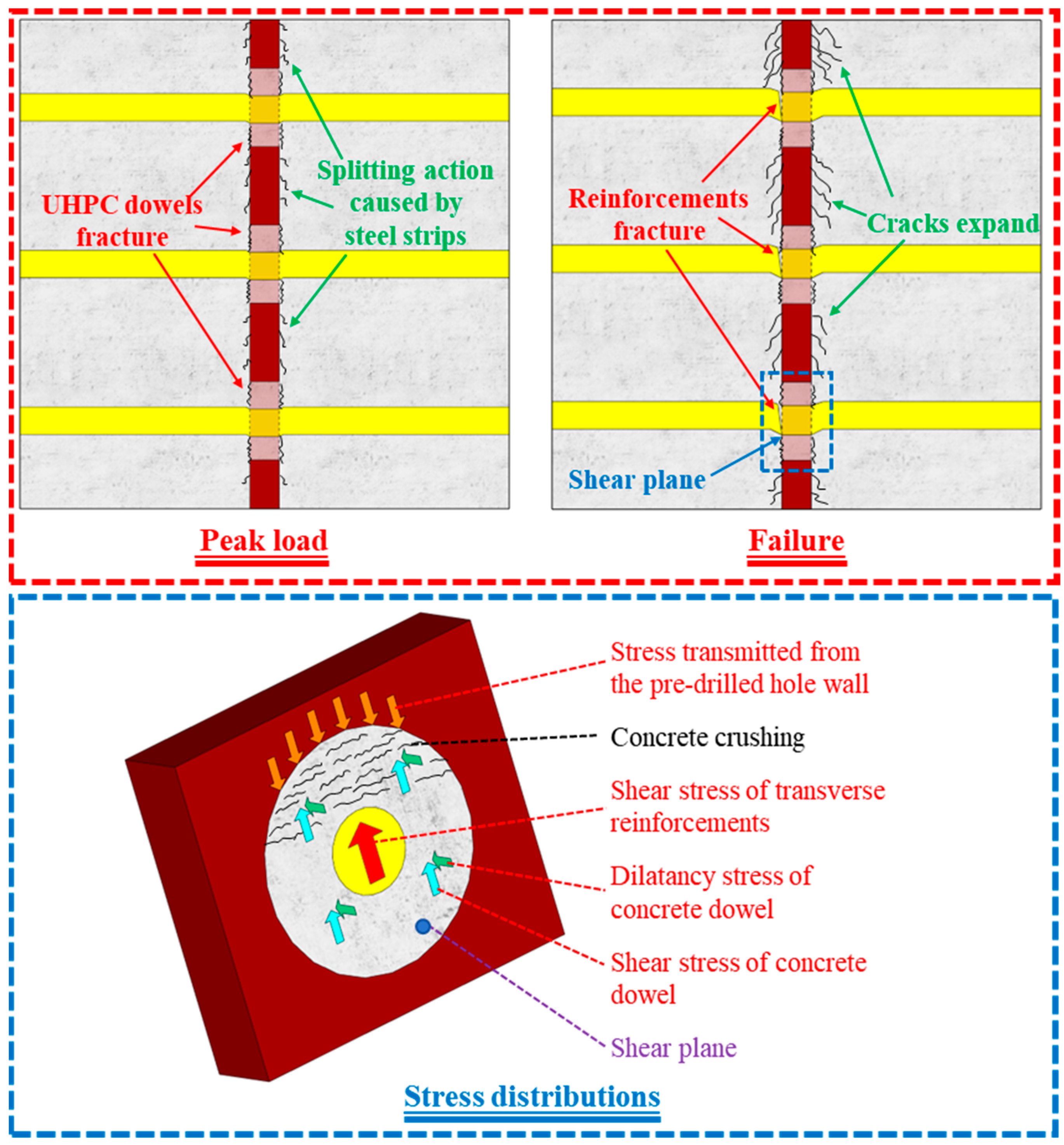
3.2. Crack Patterns and Failure Modes
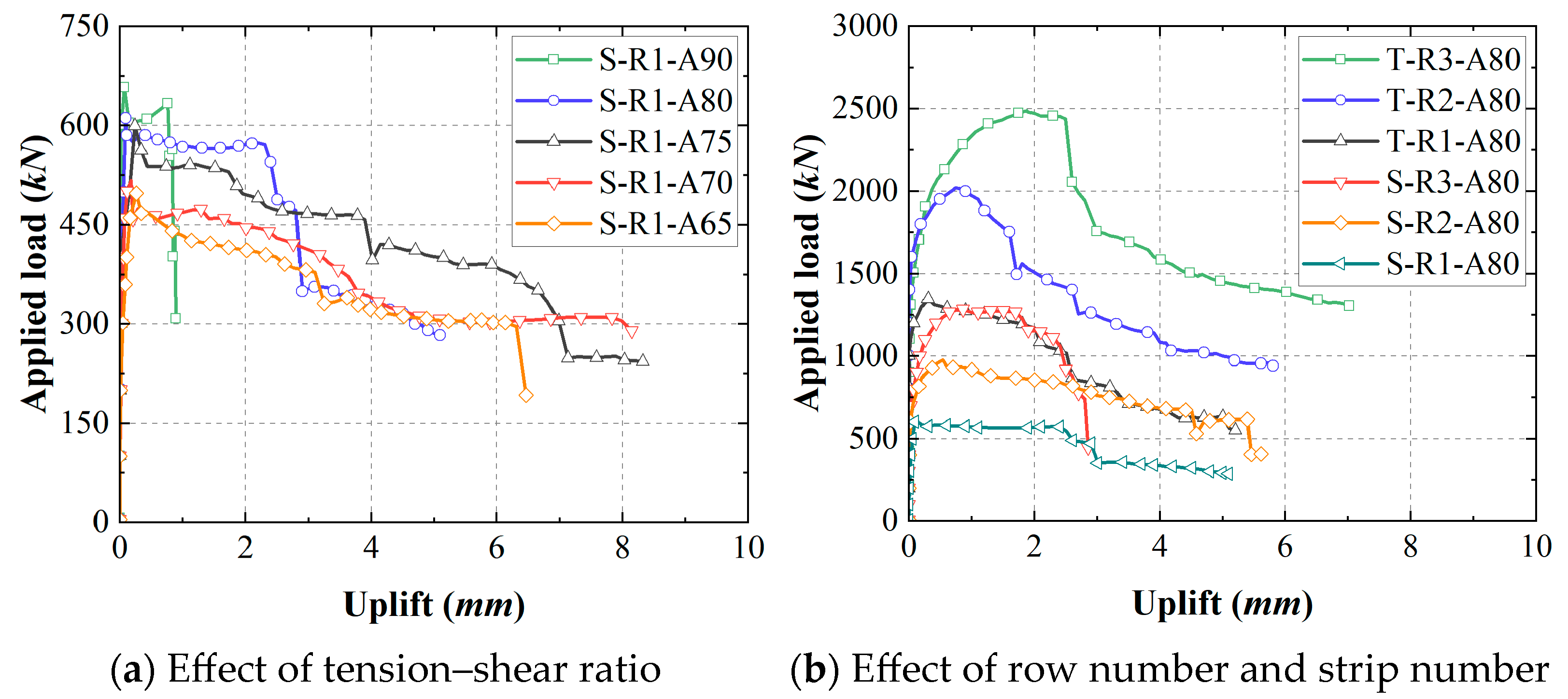
3.3. Static Behavior of SRHPBLs Under Combined Tension–Shear Loads
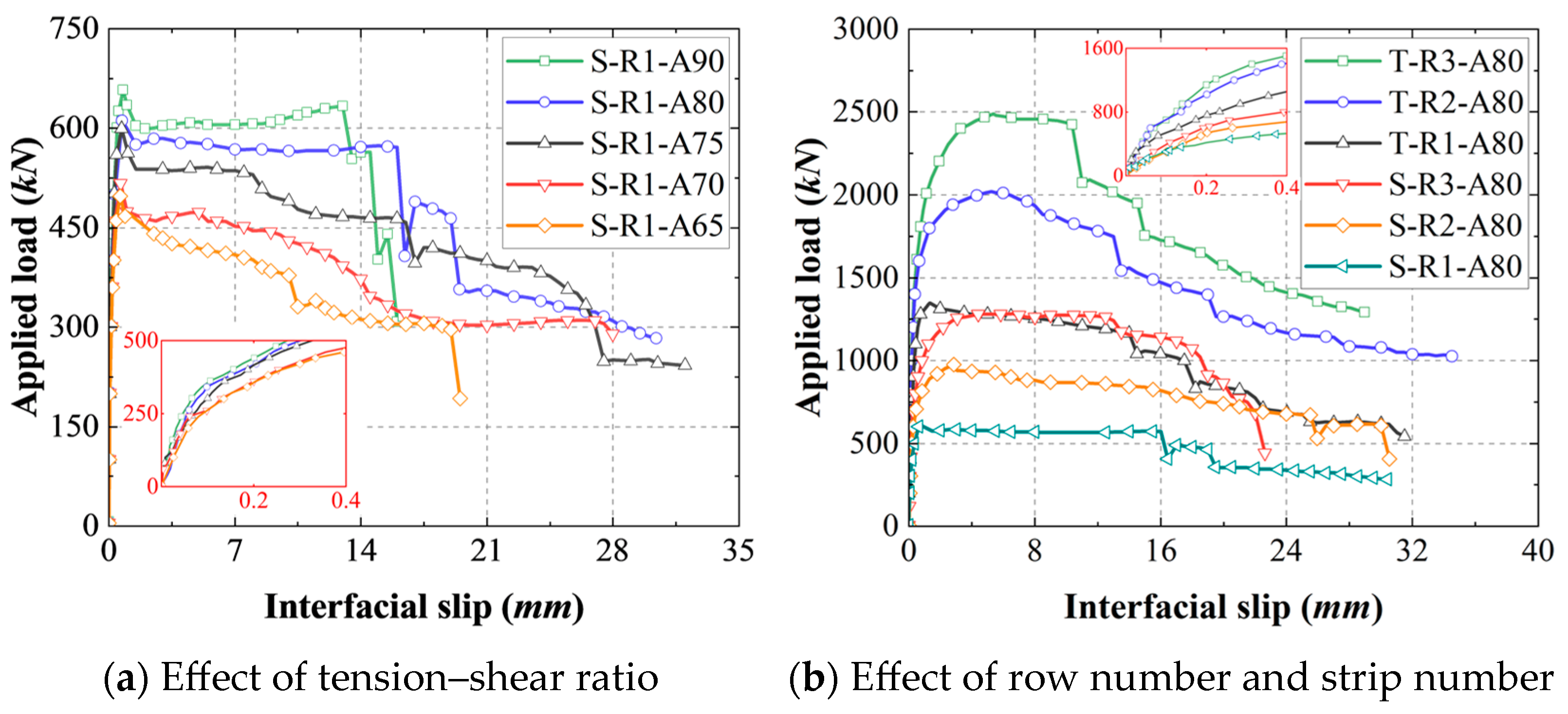
3.3.1. Influence of Tension–Shear Ratio
3.3.2. Influence of Row Number
3.3.3. Influence of Strip Number
4. Recommendations
4.1. Shear–Tension Interaction Relationships
4.2. Shear Capacity of SRHPBLs Under Combined Tension–Shear Loads
5. Conclusions
- (1)
- Most of the push-out tests demonstrated a similar failure mode, transverse reinforcements fracture, steel strip fracture, and excessive deformation of transverse reinforcements and steel strips. However, steel strip fracture was observed in three-row single-strip specimen. In addition, only UHPC dowel fracture and significant deformation in both steel strips and reinforcements were observed in specimens with excessive UHPC dowels.
- (2)
- The load–slip relationships showed similar five-stage behavior, including the initial elastic stage, the plastic stage induced by the breaking of SRHPBL–UHPC interfacial bonding, the softening stage due to UHPC dowel fracture, the ductile stage with strain hardening of transverse reinforcements, and the failure stage caused by transverse reinforcement fracture.
- (3)
- The tension–shear ratio exhibited a small effect on the static behaviors of SRHPBLs. When the tension–shear ratio was increased from 0 to 0.42, the shear capacity, initial shear stiffness, and slip at peak load of SRHPBLs decreased by 24.31%, 19.02%, and 22.00%, respectively. However, the increase in the tension–shear ratio substantially increased the uplift at the peak load of SRHPBLs.
- (4)
- Both row number and strip number exhibited a significant effect on the static behaviors of SRHPBLs. Compared to the single-row specimens, the shear capacity and initial shear stiffness of the three-row specimens increased by an average of 92.82% and 48.77%, respectively. The shear capacity and initial shear stiffness of the twin-strip specimens increased by an average of 103.84% and 87.80%, respectively, compared to the single-strip specimens.
- (5)
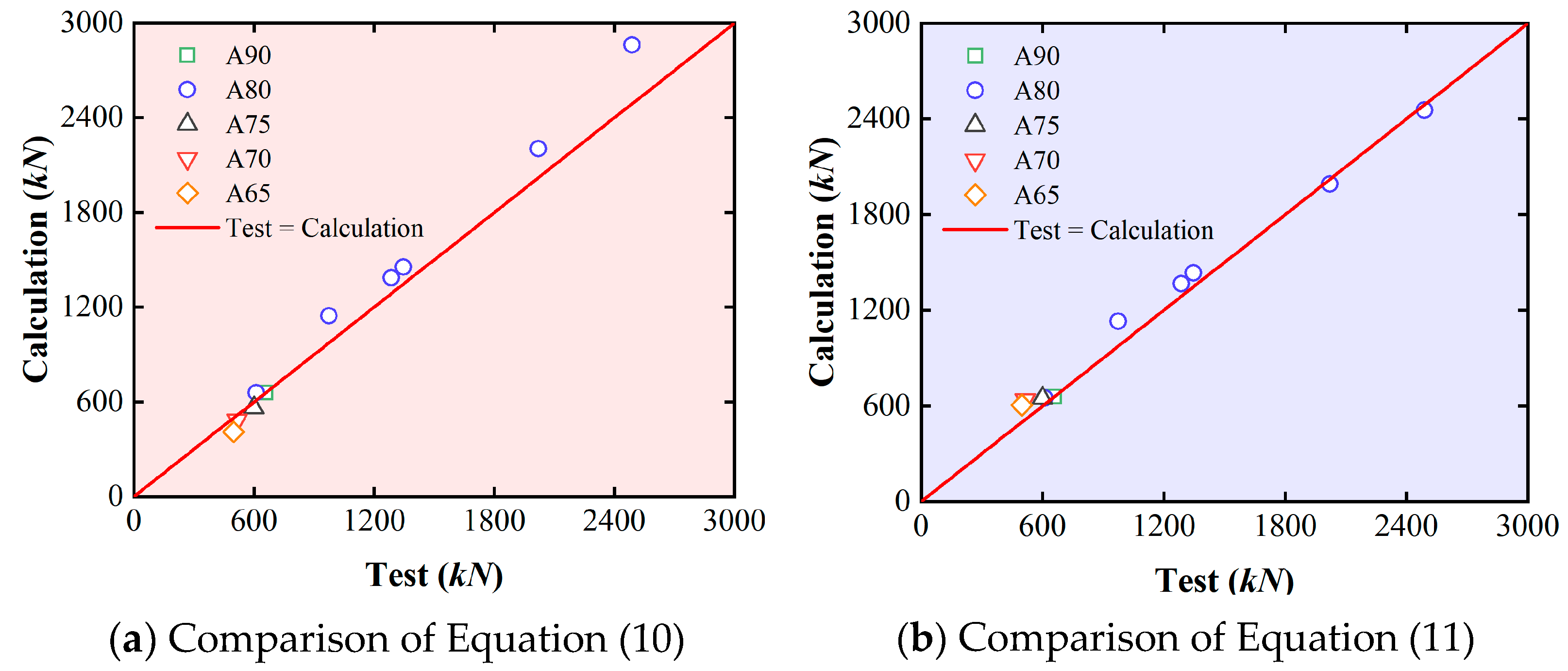
- A more accurate model was developed to predict the shear–tension interaction of SRHPBLs in UHPC slabs, with an error within 10%. Furthermore, considering the effect of tensile action on the ultimate shear capacity of SRHPBLs, a more accurate formula was developed, with an AVE, STDEV, and COV of the ratios between calculations and test results of 1.01, 0.04, and 0.04, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, J.; Wang, H.; Zhou, Z.; Liang, H.; Zhang, Z.; He, Z.; Zou, Y. Flexural behavior of prefabricated steel-UHPC composite beams with hollow UHPC bridge deck. J. Constr. Steel Res. 2025, 226, 109267. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, M.; Su, H.; Lu, W.; Zhang, L. Mechanical properties of plug-in perfobond strip connector in ultra-high-performance concrete. Structures 2025, 72, 108282. [Google Scholar] [CrossRef]
- He, S.; Zhou, D.; Bai, B.; Liu, C.; Dong, Y. Experimental study on shear performance of prefabricated HSS-UHPC composite beam with perfobond strip connectors. Eng. Struct. 2025, 324, 119318. [Google Scholar] [CrossRef]
- He, S.; Zhong, H.; Huang, X.; Xu, Y.; Mosallam, A.S. Experimental investigation on shear fatigue behavior of perfobond strip connectors made of high strength steel and ultra-high performance concrete. Eng. Struct. 2025, 322, 119181. [Google Scholar] [CrossRef]
- Kong, F.; Huang, P.; Han, B.; Wang, X.; Liu, C. Experimental study on behavior of corrugated steel-concrete composite bridge decks with MCL shape composite dowels. Eng. Struct. 2021, 227, 111399. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, Z.; Fang, Z.; Fang, S.; Tu, W.; Mo, F.; Xie, S.; Liu, J. Rapid hardening high performance concrete (RHHPC) for bridge expansion joints: From material properties to interfacial shear performance. Constr. Build. Mater. 2025, 458, 139638. [Google Scholar] [CrossRef]
- Zou, S.; Chen, R.; Wang, H.; Fang, Z.; Qu, C.; Zhang, C. Effect of shear key geometrical dimensions on seismic performance of prefabricated concrete piers with shallow socket connections. Structures 2025, 71, 107975. [Google Scholar] [CrossRef]
- Zou, S.; Wang, H.; Fang, S.; Fang, Z.; Wenliuhan, H.; Qu, C.; Zhang, C. Seismic isolation effect and parametric analysis of simply supported beam bridges with multi-level sliding friction adaptive isolation bearing. Soil Dyn. Earthq. Eng. 2025, 188, 109000. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, C.; Chen, B.; Yang, Y.; Liang, W.; Tang, Y.; Zheng, J. Long-term creep behavior of expansive agent core concrete in full-scale concrete-filled steel tube from the world’s largest span arch bridge study. Front. Struct. Civ. Eng. 2025, 19, 319–340. [Google Scholar] [CrossRef]
- Zhou, J.; Leng, J.; Yang, J.; Zhang, Z.; Du, J.; Zou, Y. Experimental investigation on shear behavior of damaged and acid rain-corroded RC T-beams strengthened with ultra-high-performance concrete. Eng. Struct. 2025, 327, 119618. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, H.; Zhang, Z.; Yang, J.; Wang, X.; Wang, X.; Zou, Y. Macro-micro investigation on the coefficient of friction on the interface between steel and cast-in-place UHPC. Eng. Struct. 2024, 318, 118769. [Google Scholar] [CrossRef]
- Wu, N.; Liao, S.; Pan, Z.; Fang, Z.; Fang, S.; Liu, F.; Li, L.; Xiong, Z. Shear performance of small-rib-height perfobond strip connector groups embedded in UHPC: Experimental investigations and design recommendations. Eng. Struct. 2024, 311, 118175. [Google Scholar] [CrossRef]
- Tan, X.; Fang, Z.; Yin, Y.; Yuan, R.; Liu, X.-H.; Liu, Q. Shear behavior of low-profile perfobond strip connectors for steel–thin UHPC composite deck structures. Eng. Struct. 2025, 322, 119204. [Google Scholar] [CrossRef]
- Xu, Y.; He, S.; Guan, P.; Mosallam, A.S.; Zeng, J.; Wan, Z.-Y. Shear behavior of flexible-sleeve perfobond strip connectors: Experimental and analytical studies. Eng. Struct. 2022, 264, 114380. [Google Scholar] [CrossRef]
- Su, Q.; Yang, G.; Bradford, M.A. Bearing capacity of perfobond rib shear connectors in composite girder bridges. J. Bridge Eng. 2016, 21, 06015009. [Google Scholar] [CrossRef]
- Kim, S.; Ahn, J.; Choi, K.; Jung, C. Experimental evaluation of the shear resistance of corrugated perfobond rib shear connections. Adv. Struct. Eng. 2011, 14, 249–264. [Google Scholar] [CrossRef]
- Su, Q.; Wang, W.; Luan, H.; Yang, G. Experimental research on bearing mechanism of perfobond rib shear connectors. J. Constr. Steel Res. 2014, 95, 22–31. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, B.; Cui, S.; Lui Eric, M. Experimental research on PBL connectors considering the effects of concrete stress state and other connection parameters. J. Bridge Eng. 2018, 23, 04017125. [Google Scholar] [CrossRef]
- Zhao, C.; Li, Z.; Deng, K.; Wang, W. Experimental investigation on the bearing mechanism of Perfobond rib shear connectors. Eng. Struct. 2018, 159, 172–184. [Google Scholar] [CrossRef]
- Zheng, S.; Liu, Y.; Yoda, T.; Lin, W. Parametric study on shear capacity of circular-hole and long-hole perfobond shear connector. J. Constr. Steel Res. 2016, 117, 64–80. [Google Scholar] [CrossRef]
- Xiao, L.; Li, X.; Ma, Z.J. Behavior of perforated shear connectors in steel–concrete composite joints of hybrid bridges. J. Bridge Eng. 2017, 22, 04016135. [Google Scholar] [CrossRef]
- Rodrigues, J.P.C.; Laím, L. Behaviour of Perfobond shear connectors at high temperatures. Eng. Struct. 2011, 33, 2744–2753. [Google Scholar] [CrossRef]
- Vianna, J.d.C.; Costa-Neves, L.F.; da S Vellasco, P.C.G.; de Andrade, S.A.L. Experimental assessment of perfobond and T-perfobond shear connectors’ structural response. J. Constr. Steel Res. 2009, 65, 408–421. [Google Scholar] [CrossRef]
- Zou, Y.; Zheng, K.; Zhou, J.; Zhang, Z.; Li, X. Mechanical behavior of perfobond connector group in steel–concrete joint of hybrid bridge. Structures 2021, 30, 925–936. [Google Scholar] [CrossRef]
- Cândido-Martins, J.P.S.; Costa-Neves, L.F.; Vellasco, P.C.G.d.S. Experimental evaluation of the structural response of Perfobond shear connectors. Eng. Struct. 2010, 32, 1976–1985. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q.; Cheng, Z.; Cui, C.; Tang, K. Study on the rational construction methods and mechanical properties of composite beams in transverse negative bending moment zones. Eng. Struct. 2025, 324, 119348. [Google Scholar] [CrossRef]
- Leng, J.; Yang, J.; Zhang, Z.; Zou, Y.; Du, J.; Zhou, J. Mechanical behavior of a novel compact steel-UHPC joint for hybrid girder bridges: Experimental and numerical investigation. J. Constr. Steel Res. 2024, 218, 108742. [Google Scholar] [CrossRef]
- Xiao, J.; Guo, L.; Nie, J.; Li, Y.; Fan, J.; Shu, B. Flexural behavior of wet joints in steel-UHPC composite deck slabs under hogging moment. Eng. Struct. 2022, 252, 113636. [Google Scholar] [CrossRef]
- Tan, X.; Fang, Z.; Xiong, X. Experimental study on group effect of perfobond strip connectors encased in UHPC. Eng. Struct. 2022, 250, 113424. [Google Scholar] [CrossRef]
- Tan, X.; Fang, Z.; Peng, Z.; Zheng, H.; Tang, S.; Liao, Y. Tensile behavior of a prefabricated Steel–UHPC composite deck system with notched perfobond strips. Eng. Struct. 2022, 268, 114737. [Google Scholar] [CrossRef]
- Xiao, J.; Yang, T.; Nie, X.; Li, B.; Fan, J.-S.; Shu, B. Experimental and numerical investigation on mechanical performance of continuous steel-UHPC composite slabs. Eng. Struct. 2022, 270, 114804. [Google Scholar] [CrossRef]
- Mai, G.; Xiong, Z.; Zhu, H.; Zhou, L.; Zhou, H.; Li, L.-J. Durability of GFRP bars embedded in seawater sea sand concrete in marine environments. Constr. Build. Mater. 2025, 458, 139488. [Google Scholar] [CrossRef]
- Chen, Z.; Su, J.; Luo, R.; Lin, J.; Chen, X.; Huang, P.; Guo, Y. Experimental investigation on fracture behavior of rubberized engineered cementitious composites under thermo-mechanical loadings. Eng. Fract. Mech. 2025, 315, 110838. [Google Scholar] [CrossRef]
- Wan, S.; Li, S.; Chen, Z.; Tang, Y. An ultrasonic-AI hybrid approach for predicting void defects in concrete-filled steel tubes via enhanced XGBoost with Bayesian optimization. Case Stud. Constr. Mater. 2025, 22, e04359. [Google Scholar] [CrossRef]
- Wang, J.; Liu, F.; Luo, Z.; He, M.; Chen, G.; Xiong, Z. Behaviour of FRP-rubber concrete-steel double-skin tubular slender columns under eccentric compression: An experimental and theoretical study. J. Build. Eng. 2025, 104, 112265. [Google Scholar] [CrossRef]
- Xiao, J.; Shuai, J.; Deng, W.; Liu, L.; Wang, P.; Li, L. Low-carbon and green materials in construction: Latest advances and prospects. Buildings 2025, 15, 1508. [Google Scholar] [CrossRef]
- Cao, X.; Feng, D. Probabilistic resilience assessment of structures considering the functional uncertainty: A case study for external prestressed subframe in strengthening. Eng. Struct. 2025, 332, 119968. [Google Scholar] [CrossRef]
- Cao, X.; Shen, D.; Ji, K.; Ju, J.W.; Xie, L. A novel stochastic IDA-CSM based design framework of the externally-attached sub-system for seismic upgrading. Bull. Earthquake Eng. 2025, 23, 1707–1735. [Google Scholar] [CrossRef]
- Cao, X.; Shen, D.; Ji, K.; Qu, Z.; Wang, C. Recovery resilience framework of replaceable AB-BRB for seismic strengthening during the aftershock stage. Thin-Walled Struct. 2024, 205, 112389. [Google Scholar] [CrossRef]
- Deng, K.; Wang, K.; Liang, H.; Zhao, C.; Cui, B. Experimental and analytical study on crack resistance of fully prefabricated steel-UHPC composite deck using PBL connectors. Eng. Struct. 2023, 275, 115249. [Google Scholar] [CrossRef]
- Luo, Z.; Zhao, H.; Qiao, D.; Zhang, Y.; An, J.; Tan, C.; Liang, L.; Liu, A.; Shao, X. Shear behavior on PBL shear connector with a relatively thin perforated steel plate in steel-UHPC composite bridge deck system. Eng. Struct. 2024, 316, 118583. [Google Scholar] [CrossRef]
- Xiao, R.; Song, C.; Sun, B.; Guo, R.; Chen, H. Design and experimental study of a replaceable steel-UHPC composite bridge deck. Structures 2022, 40, 1107–1120. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, L.; Wei, X.; Liao, X.; Wang, S. Investigation on fatigue performance and life prediction of PBL connectors in steel-UHPC composite structure. Eng. Struct. 2025, 329, 119762. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H.; Luan, L.; Xu, X.; Liu, Y.; Du, X. Three failure modes of High-Strength Steel (HSS) perfobond connector embedded in UHPC. Eng. Struct. 2023, 286, 116147. [Google Scholar] [CrossRef]
- Gao, X.; Shen, S.; Guo, Y.; Guo, J. Experimental study on the shear and slip behaviors of perfobond strip connectors with low elastic modulus material wrapped perforated rebars. Eng. Struct. 2024, 316, 118521. [Google Scholar] [CrossRef]
- Duan, M.; Zhang, S.; Wang, X.; Dong, F. Mechanical behavior in perfobond rib shear connector with UHPC-steel composite structure with coarse aggregate. KSCE J. Civ. Eng. 2020, 24, 1255–1267. [Google Scholar] [CrossRef]
- Ni, Y.; Hu, M.; Jia, Z.; Han, Q. Shear behavior of Y-shaped perfobond rib shear connector with UHPC grout. J. Struct. Eng. 2024, 150, 04024102. [Google Scholar] [CrossRef]
- Ding, J.; Zhu, J.; Shi, T. Performance of grouped stud connectors in precast steel-UHPC composite bridges under combined shear and tension loads. Eng. Struct. 2023, 277, 115470. [Google Scholar] [CrossRef]
- Shen, M.; Chung, K. Experimental investigation into stud shear connections under combined shear and tension forces. J. Constr. Steel Res. 2017, 133, 434–447. [Google Scholar] [CrossRef]
- Shen, M.; Chung, K.; Elghazouli, A.Y. Performance of stud shear connections under combined shear and pull-out forces. Structures 2023, 51, 415–434. [Google Scholar] [CrossRef]
- Zhan, Y.; Huang, W.; Li, Y.; Li, J.; Shao, J.; Tian, B. Experimental investigation on mechanical behavior of T-type perfobond rid shear connectors under combined shear and tension. J. Build. Eng. 2023, 73, 106840. [Google Scholar] [CrossRef]
- Huang, W.; Zhan, Y.; Zhang, C.; Lyu, W.; Li, Y.; Shao, J. Tensile resistance and shear-tension interaction relationship of T-type perfobond rid shear connectors. J. Build. Eng. 2024, 89, 109183. [Google Scholar] [CrossRef]
- Luan, L.; Xu, X.; Liu, Y.; Lin, W.; Du, X.; Liu, Y. Combined tensile and shear behavior of perfobond connectors embedded in UHPC with a new orthotropic rubber ring. J. Constr. Steel Res. 2024, 219, 108796. [Google Scholar] [CrossRef]
- Eurocode 4. EN 1994-1-1; Design of Composite Steel and Concrete Structures. Part 1.1: General Rules and Rules for Buildings. Europan Committee for Standardization: Brussels, Belgium, 2005.
- He, S.; Mosallam, A.S.; Fang, Z.; Sun, X.; Su, J. Experimental evaluation of shear connectors using reactive powder concrete under natural curing condition. Constr. Build. Mater. 2018, 191, 775–786. [Google Scholar] [CrossRef]
- Shoaib Karam, M.; Nakamura, H.; Yamamoto, Y.; Miura, T. Numerical evaluation of the perfobond (PBL) shear connector with transverse rebar using coupled rigid Body spring model (RBSM) and solid finite element method (FEM). Structures 2022, 45, 1544–1560. [Google Scholar] [CrossRef]
- TableASTM C1231/C1231M-15; Standard Practice for Use of Unbond Caps in Determination of Compressive Strength of Hardened Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM C496/C496M-11; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2011.
- ASTM C469/C469M-14e1; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM E8/E8M-22; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2022.
- Ahn, J.; Lee, C.; Won, J.; Kim, S. Shear resistance of the perfobond-rib shear connector depending on concrete strength and rib arrangement. J. Constr. Steel Res. 2010, 66, 1295–1307. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, H.; Liu, Y. Experimental and analytical study on tensile performance of perfobond connector in bridge engineering application. Structures 2021, 29, 714–729. [Google Scholar] [CrossRef]
- Harsányi, P.; Randl, N.; Tue, N.V. DIC-based failure analysis of high-strength continuous steel shear dowels for composite UHPFRC steel construction. Eng. Struct. 2021, 247, 113093. [Google Scholar] [CrossRef]
- Weng, R.; He, Z.; Liu, J.; Lei, B.; Huang, L.; Xu, J.; Liu, L.; Xiao, J. Shear performance of UHPC-NC composite structure interface treated with retarder: Quantification by fractal dimension and optimization of process parameters. Buildings 2025, 15, 2591. [Google Scholar] [CrossRef]
- Di, J.; Zou, Y.; Zhou, X.; Qin, F.; Peng, X. Push-out test of large perfobond connectors in steel–concrete joints of hybrid bridges. J. Constr. Steel Res. 2018, 150, 415–429. [Google Scholar] [CrossRef]
- Xian, B.; Wang, G.; Ma, F.; Fang, S.; Jiang, H.; Xiao, J. Shear performance of single embedded nut bolted shear connectors in precast steel–UHPC composite beams under combined tension-shear loads. Case Stud. Constr. Mater. 2024, 21, e03558. [Google Scholar] [CrossRef]
- McMackin, P.J.; Slutter, R.G.; Fisher, J.W. Headed steel anchor under combined loading. Eng. J. 1973, 10, 43–52. [Google Scholar] [CrossRef]
- Mirza, O.; Uy, B. Effects of the combination of axial and shear loading on the behaviour of headed stud steel anchors. Eng. Struct. 2010, 32, 93–105. [Google Scholar] [CrossRef]
- Takami, K.; Nishi, K.; Hamada, S. Shear strength of headed stud shear connector subjected to tensile load. J. Constr. Steel Res. 2000, 7, 233–240. [Google Scholar]
- Bode, H.; Roik, K. Headed studs-embedded in concrete and loaded in tension. Symp. Publ. 1987, 103, 61–88. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, Y.; He, J. Behavior of stud connectors under combined shear and tension loads. Eng. Struct. 2014, 81, 362–376. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Liu, A.; Chen, B.; Safaei, B.; Yang, Z. Study on the behavior of high-strength friction-grip bolts under combined shear and tensile forces. Structures 2022, 45, 854–866. [Google Scholar] [CrossRef]
- Pallarés, L.; Hajjar, J.F. Headed steel stud anchors in composite structures, Part II: Tension and interaction. J. Constr. Steel Res. 2010, 66, 213–228. [Google Scholar] [CrossRef]

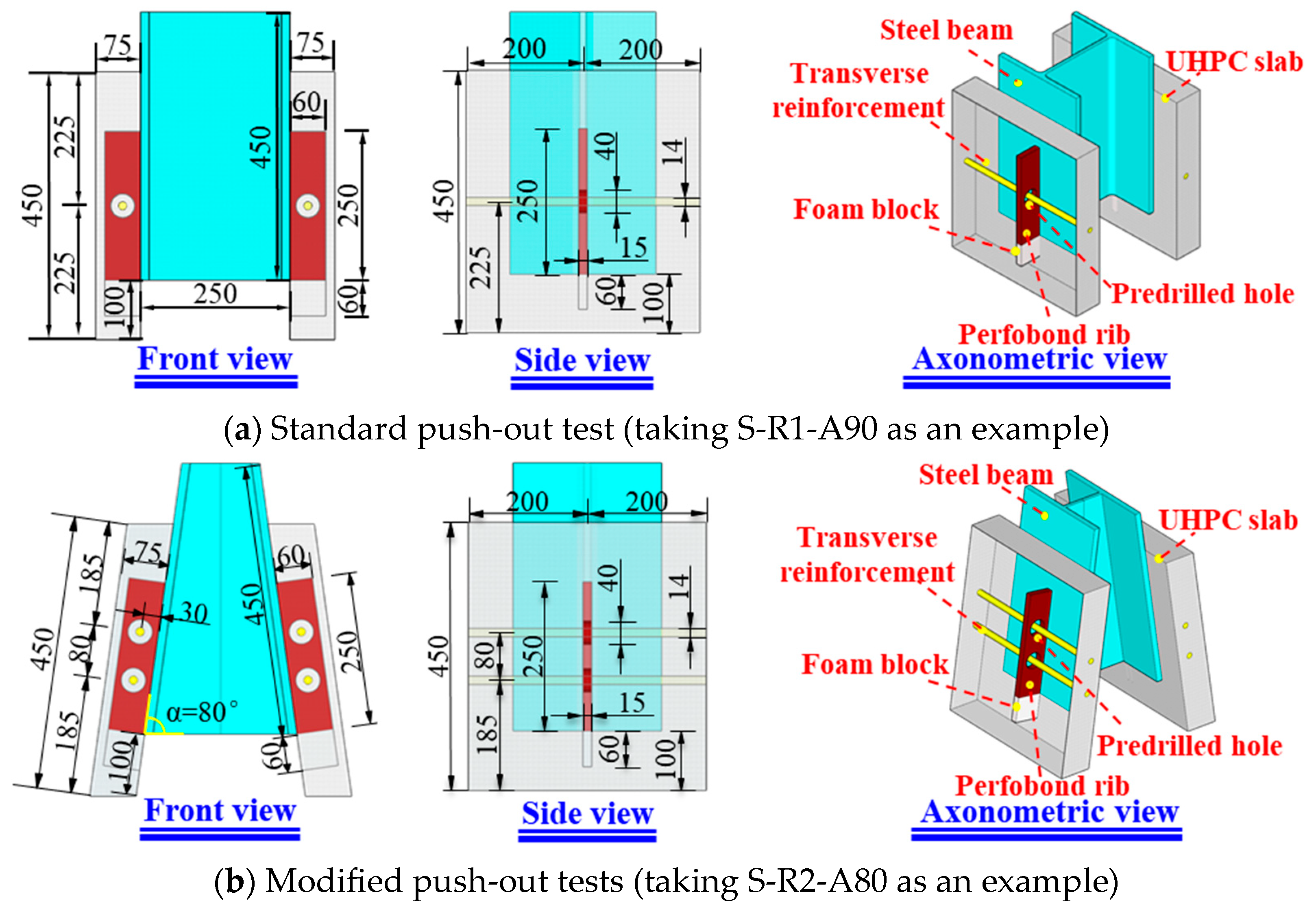
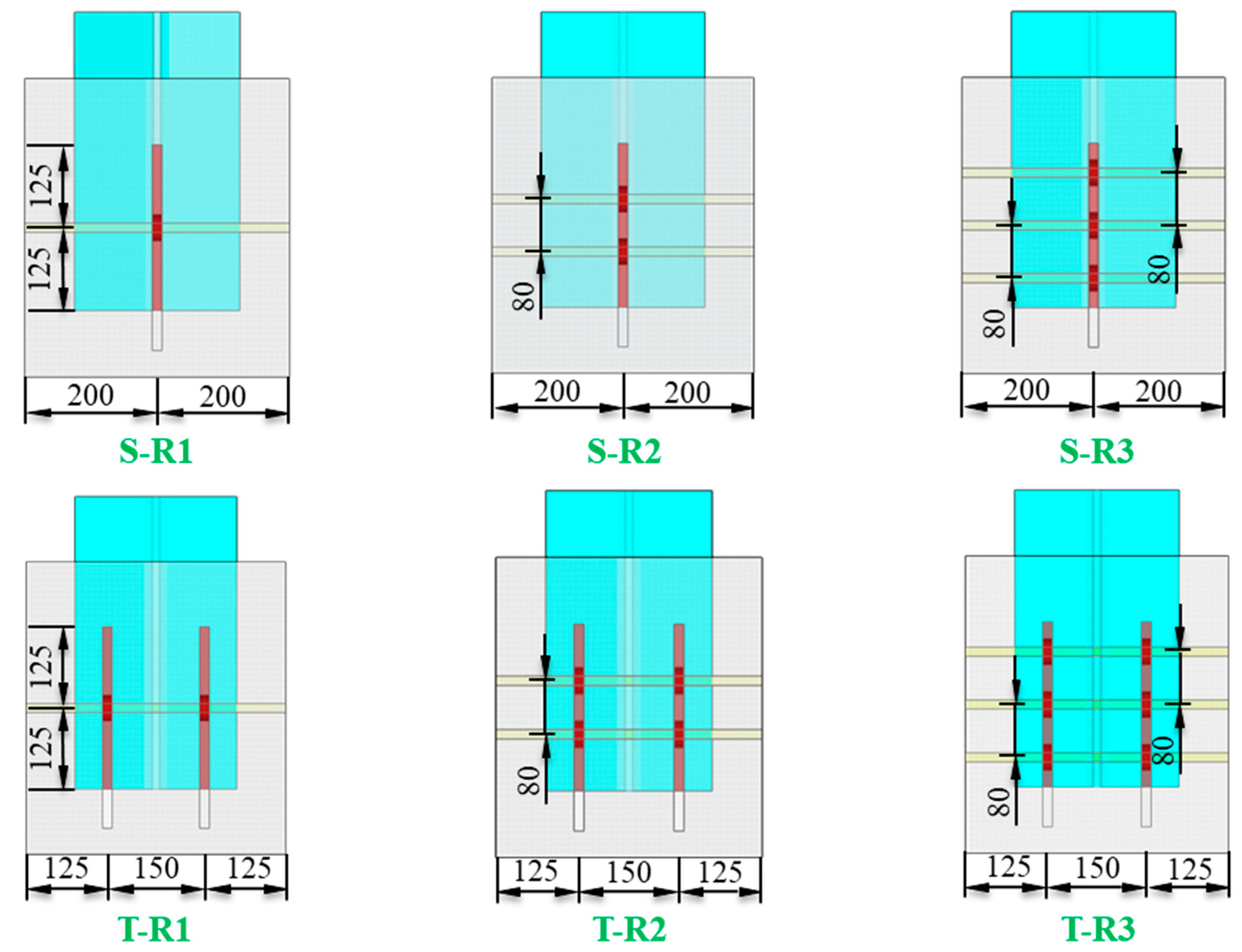


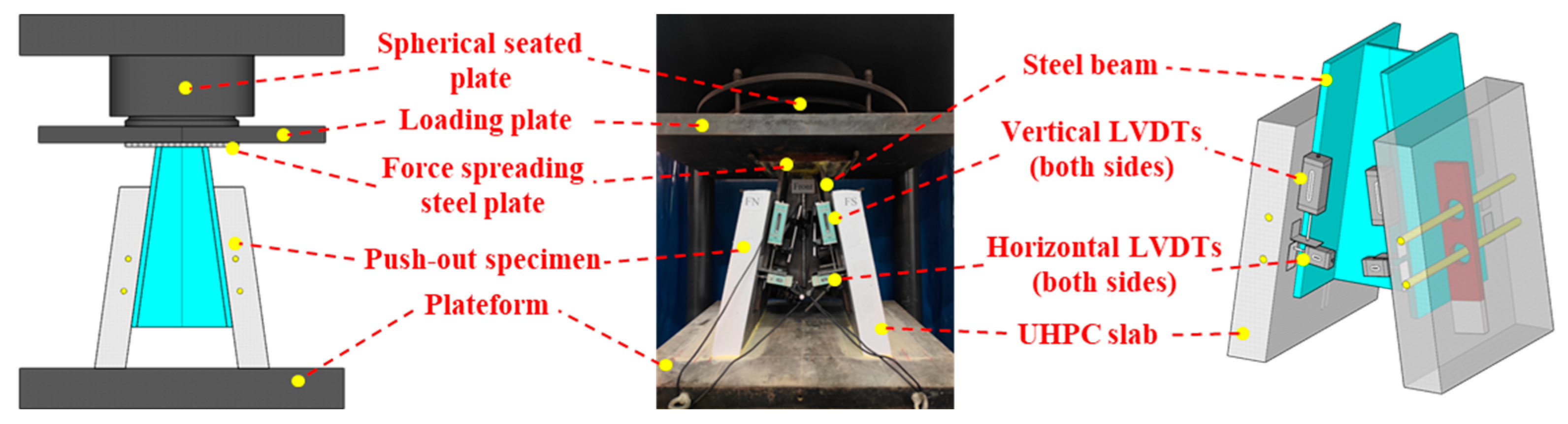






| Specimens | Strip Number | Row Number | Inclined Angle | Tension–Shear Ratio |
|---|---|---|---|---|
| S-R1-A90 | 1 | 1 | 90° | 0 |
| S-R1-A80 | 1 | 1 | 80° | 0.17 |
| S-R1-A75 | 1 | 1 | 75° | 0.26 |
| S-R1-A70 | 1 | 1 | 70° | 0.34 |
| S-R1-A65 | 1 | 1 | 65° | 0.42 |
| S-R2-A80 | 1 | 2 | 80° | 0.17 |
| S-R3-A80 | 1 | 3 | 80° | 0.17 |
| T-R1-A80 | 2 | 1 | 80° | 0.17 |
| T-R2-A80 | 2 | 2 | 80° | 0.17 |
| T-R3-A80 | 2 | 3 | 80° | 0.17 |
| Type | (MPa) | (Mpa) | (Gpa) | |||||
|---|---|---|---|---|---|---|---|---|
| COV | COV | COV | COV | |||||
| UHPC | 172.08 | 0.06 | 18.42 | 0.01 | 50.46 | 0.01 | 0.232 | 0.05 |
| Types | (MPa) | (Gpa) | (Mpa) | |||
|---|---|---|---|---|---|---|
| COV | COV | COV | ||||
| Steel beam | 274.65 | 0.02 | 202.11 | 0.01 | 462.66 | 0.01 |
| Steel strip | 292.99 | 0.01 | 199.25 | 0.05 | 419.85 | 0.01 |
| Transverse reinforcement | 447.31 | 0.01 | 197.23 | 0.02 | 634.99 | 0.01 |
| Push-Out Tests | (kN) | K (kN/mm) | (mm) | (mm) | |
|---|---|---|---|---|---|
| S-R1-A90 | 657.47 | 2190.55 | 0.800 | 0.071 | VC&HC&UF&RF |
| S-R1-A80 | 611.35 | 2081.15 | 0.726 | 0.107 | VC&HC&UF&RF |
| S-R1-A75 | 599.60 | 2049.76 | 0.709 | 0.159 | VC&UF&RF |
| S-R1-A70 | 517.08 | 1802.50 | 0.643 | 0.175 | VC&UF&RF |
| S-R1-A65 | 497.60 | 1773.89 | 0.624 | 0.266 | VC&UF&RF |
| S-R2-A80 | 975.10 | 2677.23 | 2.851 | 0.532 | VC&UF&RF |
| S-R3-A80 | 1286.64 | 2991.79 | 6.551 | 0.863 | VC&UF&SF |
| T-R1-A80 | 1346.72 | 3765.84 | 1.344 | 0.305 | VC&HC&RF&UF |
| T-R2-A80 | 2020.78 | 5082.09 | 5.245 | 0.740 | VC&HC&UF&ED |
| T-R3-A80 | 2489.00 | 5707.00 | 5.382 | 1.879 | VC&HC&UF&ED |
| Push-Out Tests | Equation (1) | Equation (2) | Equation (3) | Equation (4) | Equation (5) | Equation (6) | Equation (9) |
|---|---|---|---|---|---|---|---|
| S-R1-A90 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| S-R1-A80 | 0.96 | 0.98 | 0.94 | 0.93 | 0.96 | 0.93 | 1.01 |
| S-R1-A75 | 0.71 | 0.99 | 0.94 | 0.96 | 0.98 | 0.91 | 1.08 |
| S-R1-A70 | 0.87 | 0.89 | 0.84 | 0.89 | 0.88 | 0.80 | 1.02 |
| S-R1-A65 | 0.88 | 0.91 | 0.84 | 0.92 | 0.89 | 0.78 | 1.07 |
| S-R2-A80 | 0.88 | 0.89 | 0.86 | 0.85 | 0.88 | 0.85 | 0.93 |
| S-R3-A80 | 0.96 | 0.97 | 0.94 | 0.93 | 0.96 | 0.93 | 1.01 |
| T-R1-A80 | 0.96 | 0.97 | 0.94 | 0.93 | 0.96 | 0.93 | 1.01 |
| T-R2-A80 | 0.95 | 0.96 | 0.93 | 0.92 | 0.95 | 0.92 | 1.00 |
| T-R3-A80 | 0.90 | 0.91 | 0.88 | 0.87 | 0.90 | 0.87 | 0.95 |
| AVE | 0.91 | 0.95 | 0.91 | 0.92 | 0.94 | 0.89 | 1.01 |
| STDEV | 0.08 | 0.04 | 0.05 | 0.04 | 0.04 | 0.07 | 0.05 |
| COV | 0.09 | 0.04 | 0.06 | 0.05 | 0.05 | 0.08 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Shen, R.; Xian, B.; Wang, G.; Fang, S.; Jiang, H. Small-Rib-Height Perfobond Strip Connectors (SRHPBLs) in Steel–UHPC Composite Beams: Static Behavior Under Combined Tension–Shear Loads. Buildings 2025, 15, 2892. https://doi.org/10.3390/buildings15162892
Ma F, Shen R, Xian B, Wang G, Fang S, Jiang H. Small-Rib-Height Perfobond Strip Connectors (SRHPBLs) in Steel–UHPC Composite Beams: Static Behavior Under Combined Tension–Shear Loads. Buildings. 2025; 15(16):2892. https://doi.org/10.3390/buildings15162892
Chicago/Turabian StyleMa, Feiyang, Ruyu Shen, Bingxiong Xian, Guodong Wang, Shu Fang, and Haibo Jiang. 2025. "Small-Rib-Height Perfobond Strip Connectors (SRHPBLs) in Steel–UHPC Composite Beams: Static Behavior Under Combined Tension–Shear Loads" Buildings 15, no. 16: 2892. https://doi.org/10.3390/buildings15162892
APA StyleMa, F., Shen, R., Xian, B., Wang, G., Fang, S., & Jiang, H. (2025). Small-Rib-Height Perfobond Strip Connectors (SRHPBLs) in Steel–UHPC Composite Beams: Static Behavior Under Combined Tension–Shear Loads. Buildings, 15(16), 2892. https://doi.org/10.3390/buildings15162892









