Notch Frequency Prediction of Prestressed Seven-Wire Steel Strand Based on Ultrasonic Guided Wave
Abstract
1. Introduction
2. Theoretical Methodology for an Axially Stressed Rod
2.1. Acoustoelastic Theory of Axially Stressed Rod
- (1)
- The guided-wave medium is continuous and isotropic.
- (2)
- The waveguide is a hyper-elastic body, and the stress-strain constitutive relationship is nonlinear.
- (3)
- Under the action of loads, the perturbation of the waveguide to the acoustic wave is based on small deformations.
- (4)
- The material properties of the waveguide are not affected by external environments such as temperature.
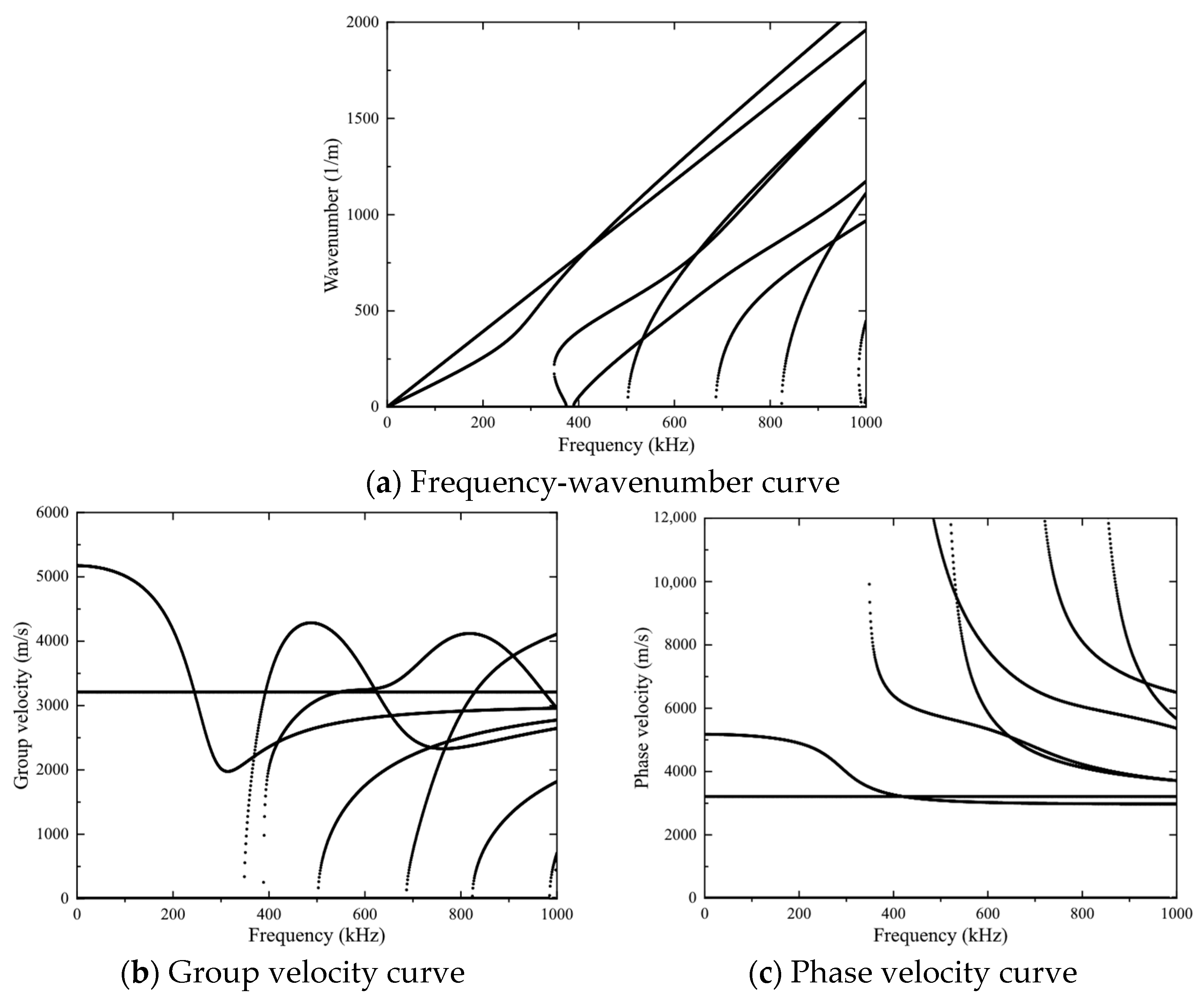
2.2. Theoretical Dispersion Curve of Cylindrical Rod
3. Finite Element Model
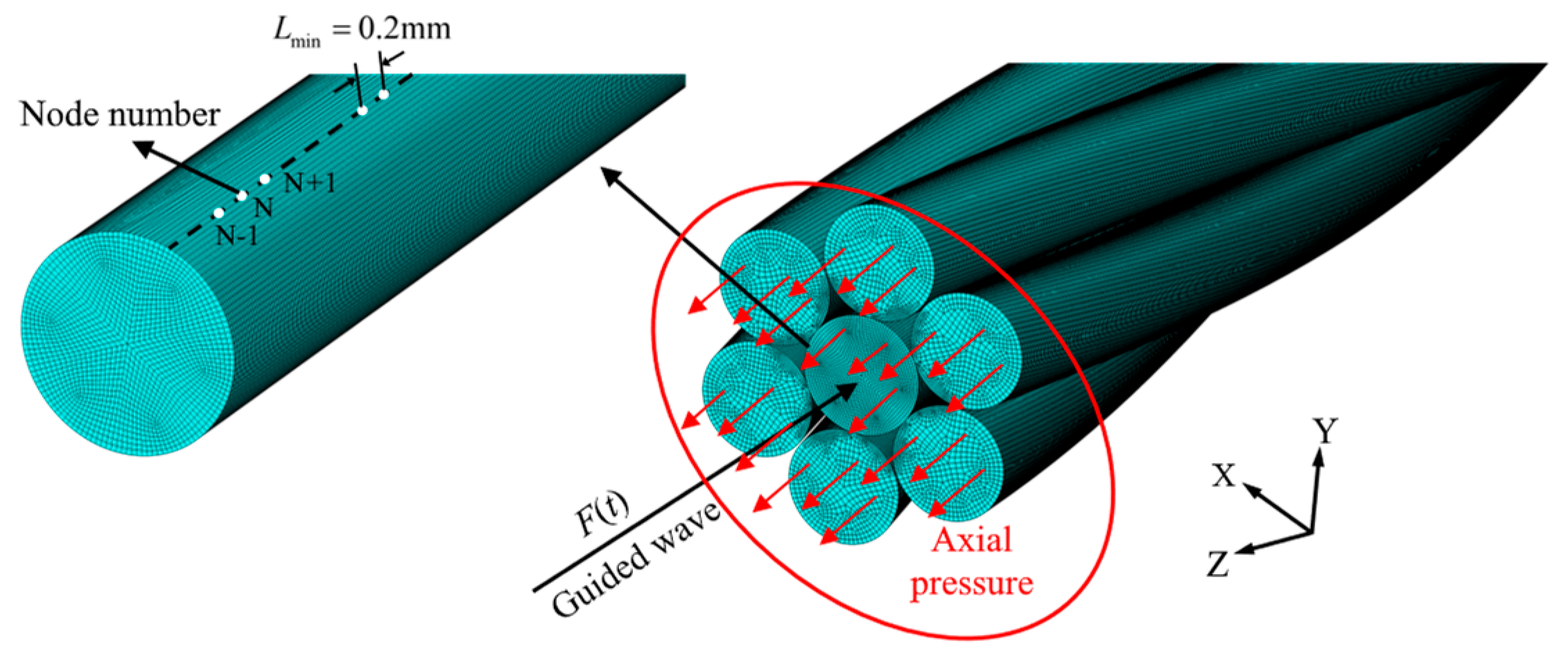
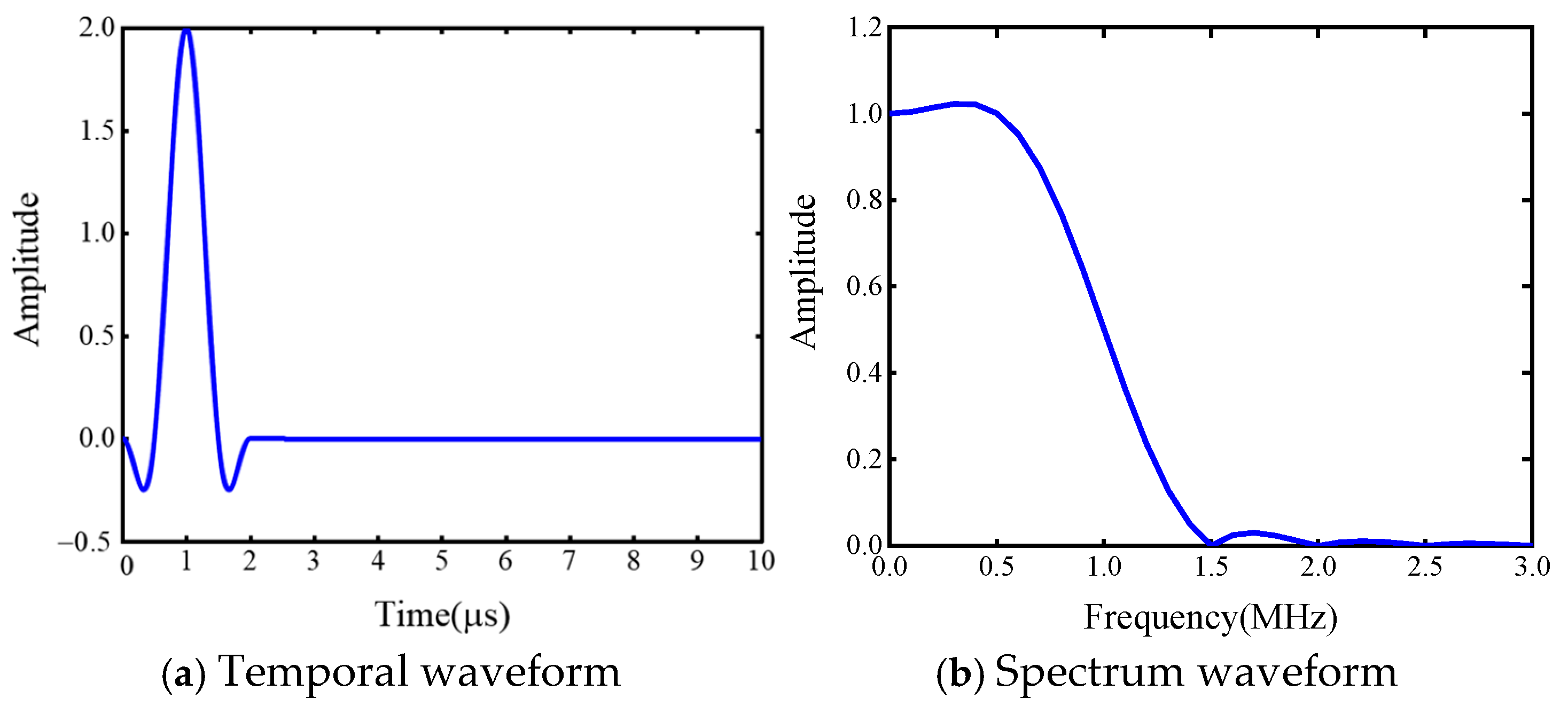
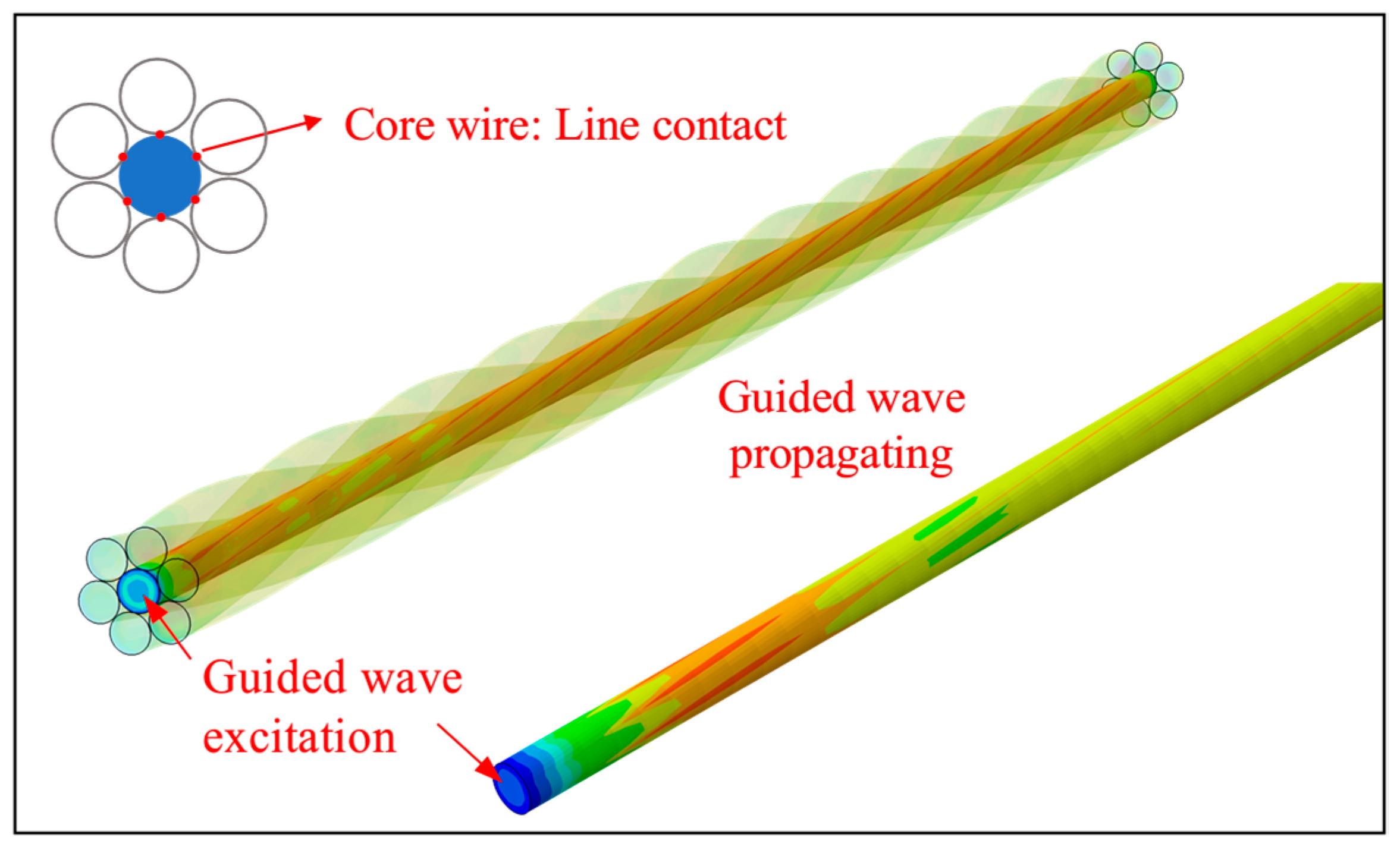
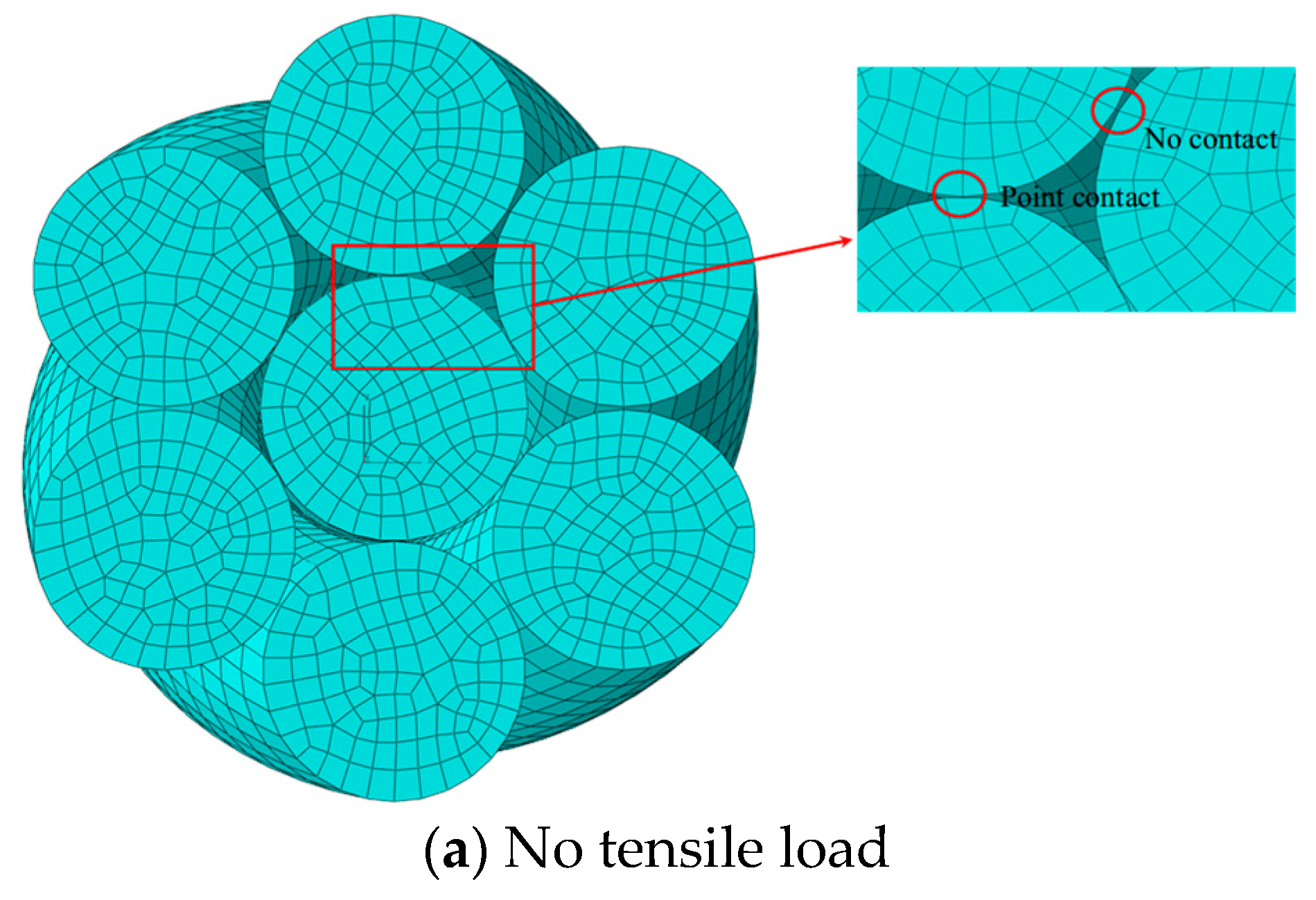
3.1. Finite Element Analysis of Guided Wave of Strand
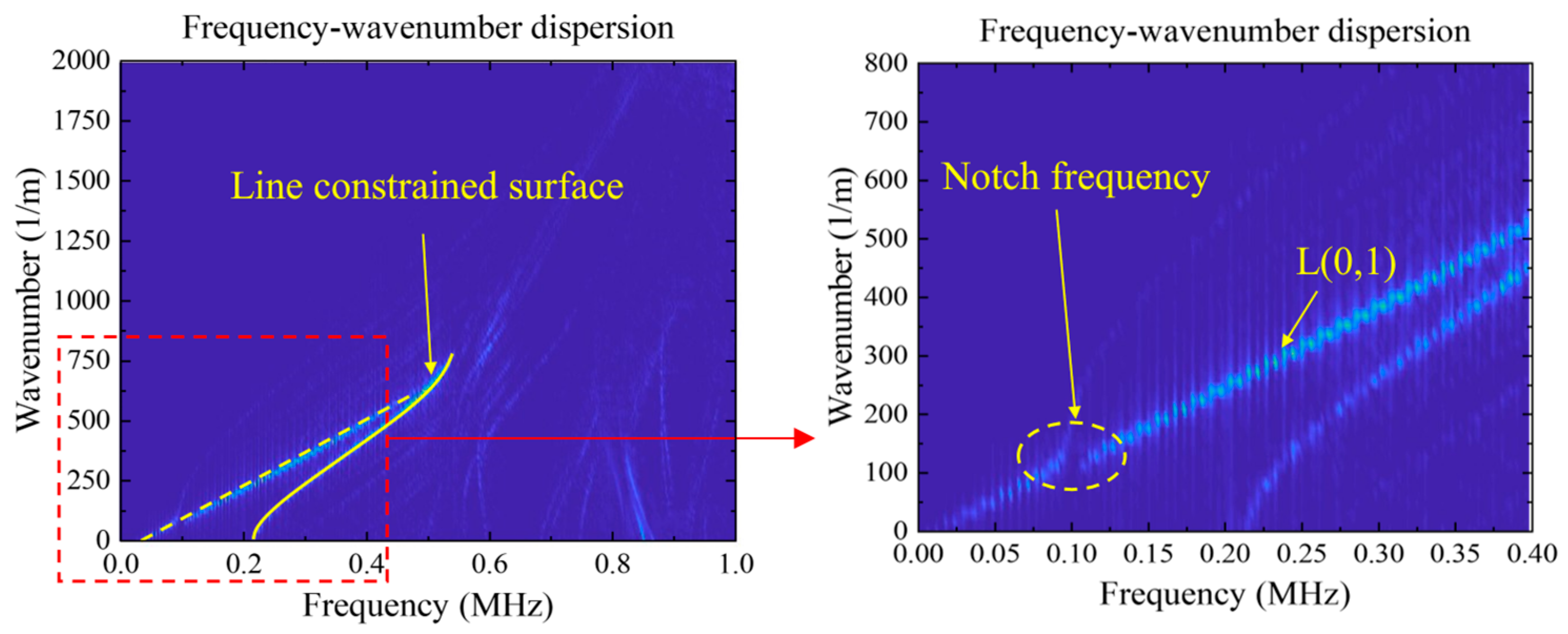
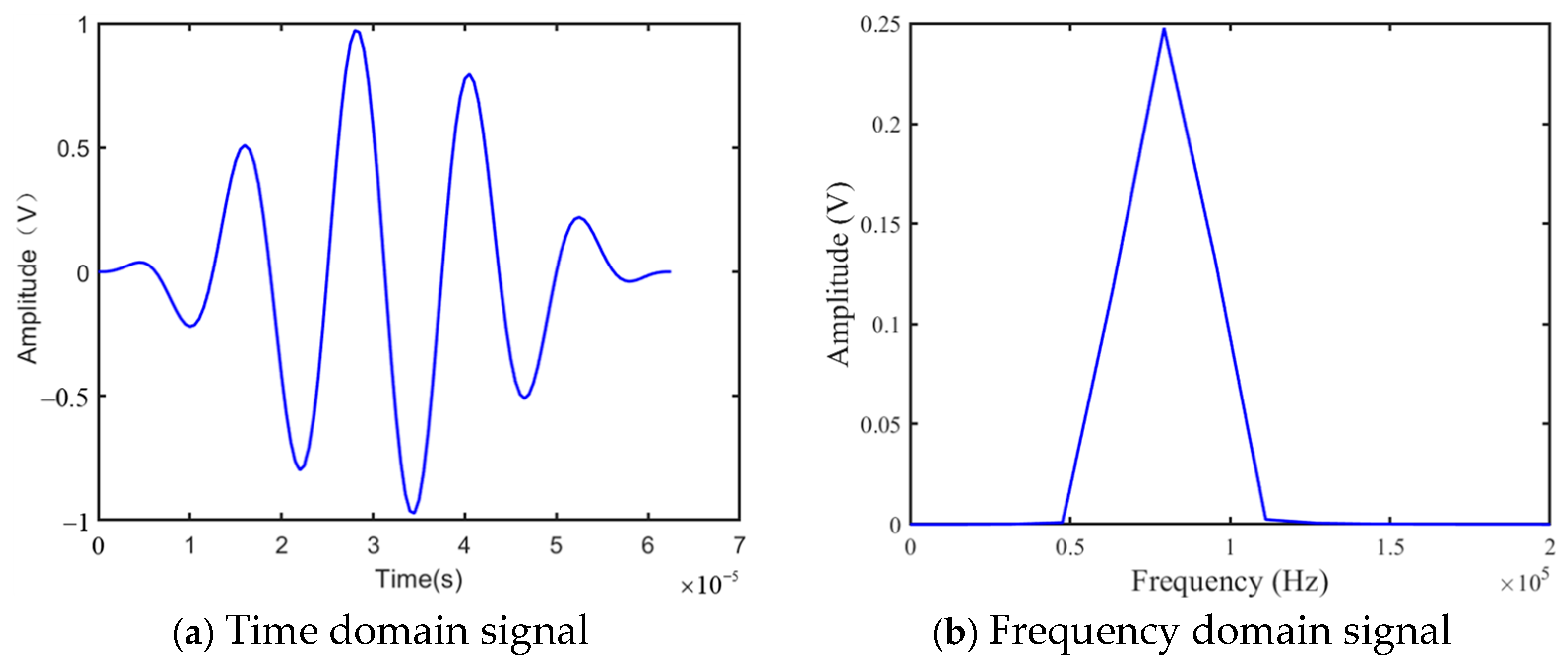
3.2. 2D-FFT Signal Analysis
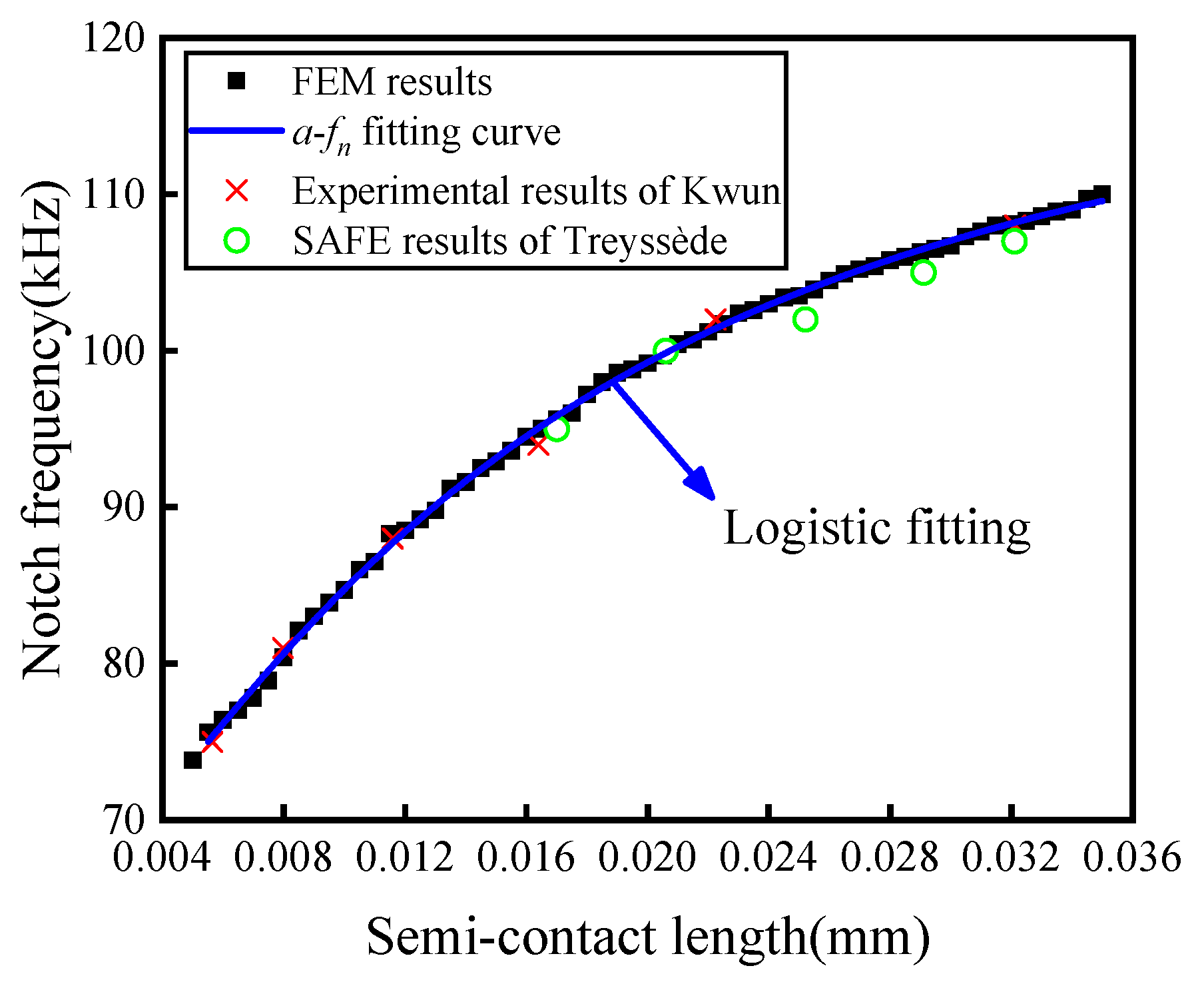
3.3. Simulation Results
4. Experimental Verification
4.1. Experimental Material
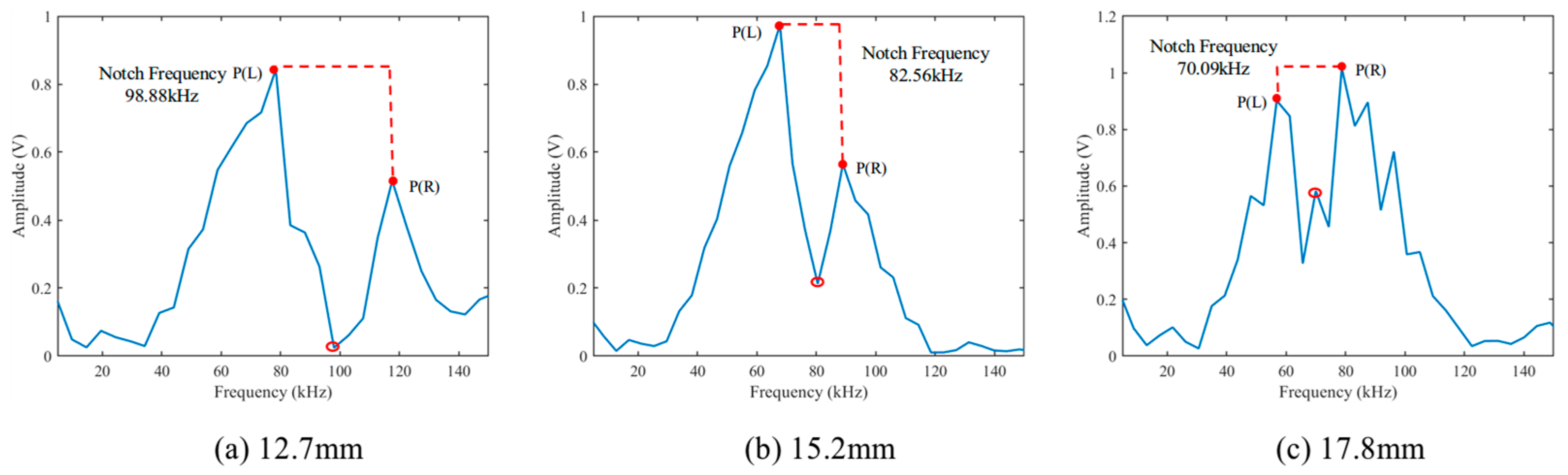
4.2. Experimental Result Analysis
5. Conclusions
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Al-Kaimakchi, A.; Rambo-Roddenberry, M. Flexural behavior of concrete bridge girders prestressed with stainless steel strands. ACI Struct. J. 2021, 118, 137–152. [Google Scholar] [CrossRef]
- Hou, J.; Wang, C.; Li, S. Study on propagation mechanism and attenuation law of acoustic emission waves for damage of prestressed steel strands. Measurement 2023, 219, 113240. [Google Scholar] [CrossRef]
- Obaydullah, M.; Jumaat, M.Z.; Alengaram, U.J. Prestressing of NSM steel strands to enhance the structural performance of prestressed concrete beams. Constr. Build. Mater. 2016, 129, 289–301. [Google Scholar] [CrossRef]
- Stefaniuk, D.; Mechaala, A.; Belarbi, A. Transfer length of stainless-steel strands in prestressed bridge elements: A combined experimental and numerical modeling approach. Eng. Struct. 2025, 325, 119482. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The current development of structural health monitoring for bridges: A review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Chen, J.; Wan, X.; Guo, Q. Monitoring of stress variation of strands in prestressed concrete by second harmonic generation measurements based on piezoelectric sensors. Smart Mater. Struct. 2021, 31, 015004. [Google Scholar] [CrossRef]
- Qian, J.; Li, J.; Liu, F.; Zhou, J.; Wang, X. Stress evaluation in seven-wire strands based on singular value feature of ultrasonic guided waves. Struct. Health Monit. 2021, 21, 518–533. [Google Scholar] [CrossRef]
- Pei, Y.; Zhang, J.; Yuan, Y.; Yang, D.; Au, F.T.K. Ultrasonic guided wave topological data analysis for corrosion characterization of steel strand based on Morse theory. Mech. Syst. Signal Process. 2025, 237, 113119. [Google Scholar] [CrossRef]
- Dubuc, B.; Ebrahimkhanlou, A.; Salamone, S. Data fusion approach for characterization of corrosion-induced stress change in prestressing strands using modulated higher-order guided ultrasonic waves. In Proceedings of the Health Monitoring of Structural and Biological Systems XIII, Denver, CO, USA, 1 April 2019; 10972, pp. 296–304. [Google Scholar]
- Dubuc, B.; Ebrahimkhanlou, A.; Salamone, S. Stress measurement in seven-wire strands using higher order guided ultrasonic wave modes. Transp. Res. Rec. 2018, 2672, 123–131. [Google Scholar] [CrossRef]
- Liu, S.; Sun, Y.; Ma, W. A new signal processing method based on notch filtering and wavelet denoising in wire rope inspection. J. Nondestruct. Eval. 2019, 38, 39. [Google Scholar] [CrossRef]
- Kwun, H.; Bartels, K.A.; Hanley, J.J. Effects of tensile loading on the properties of elastic-wave propagation in a strand. J. Acoust. Soc. Am. 1998, 103, 3370–3375. [Google Scholar] [CrossRef]
- Chaki, S.; Bourse, G. Stress level measurement in prestressed steel strands using acoustoelastic effect. Exp. Mech. 2009, 49, 673–681. [Google Scholar] [CrossRef]
- Bartoli, I.; Nucera, C.; Srivastava, A. Nonlinear ultrasonic guided waves for stress monitoring in prestressing tendons for post-tensioned concrete structures. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2009 SPIE, San Diego, CA, USA, 8–12 March 2009; Volume 7292, pp. 677–687. [Google Scholar]
- Cui, X.; Li, D.; Liu, J.; Ou, J. An NCFA-based notch frequency feature extraction method for guided waves and its application in steel strand tension detection. J. Bridge Eng. 2023, 28, 04023099. [Google Scholar] [CrossRef]
- Zhu, S.; Xu, X.; Han, J.; Luo, Y. Axial stress measurement of steel tubes using ultrasonic guided waves. Sensors 2022, 22, 3111. [Google Scholar] [CrossRef]
- Chen, X.; Xu, J.; Li, Y. Characteristic parameters of magnetostrictive guided wave testing for fatigue damage of steel strands. Materials 2023, 16, 5215. [Google Scholar] [CrossRef]
- Shen, S.; Yang, F.; Wang, H. Measurement of stress variation in unbonded and semi-bonded prestressing steel strands using the peak time shift of guided ultrasonic waves. J. Civ. Struct. Health Monit. 2025, 15, 2339–2358. [Google Scholar] [CrossRef]
- Frikha, A.; Cartraud, P.; Treyssede, F. Mechanical modeling of helical structures accounting for translational invariance. Part 1: Static behavior. Int. J. Solids Struct. 2013, 50, 1373–1382. [Google Scholar] [CrossRef]
- Treyssède, F.; Frikha, A.; Cartraud, P. Mechanical modeling of helical structures accounting for translational invariance. Part 2: Guided wave propagation under axial loads. Int. J. Solids Struct. 2013, 50, 1383–1393. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, J.; Hu, J. Nonlinear modeling of temperature-induced bearing displacement of long-span single-pier rigid frame bridge based on DCNN-LSTM. Case Stud. Therm. Eng. 2024, 53, 103897. [Google Scholar] [CrossRef]
- Huang, M.; Wan, N.; Zhu, H. Reconstruction of structural acceleration response based on CNN-BiGRU with squeeze-and-excitation under environmental temperature effects. J. Civ. Struct. Health Monit. 2025, 15, 985–1003. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, M.; Wan, N. Missing measurement data recovery methods in structural health monitoring: The state, challenges and case study. Measurement 2024, 231, 114528. [Google Scholar] [CrossRef]
- Yuan, Y.; Au, F.T.K.; Yang, D. An active learning Kriging-based Bayesian framework for probabilistic structural model exploration. J. Sound Vib. 2025, 596, 118730. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Hughes, D.S.; Kelly, J.L. Second-order elastic deformation of solids. Phys. Rev. 1953, 92, 1145. [Google Scholar] [CrossRef]
- Datta, D.; Kishore, N.N. Features of ultrasonic wave propagation to identify defects in composite materials modelled by finite element method. Ndt E Int. 1996, 29, 213–223. [Google Scholar] [CrossRef]
- Dreher, R.C. Studies of Friction and Wear Characteristics of Various Wires for Wire-Brush Skids; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1977.
- Li, G.; Zhang, J.; Cheng, J.; Wang, K.; Yang, D.; Yuan, Y. Multi-order mode excitation and separation of ultrasonic guided waves in rod structures using 2D-FFT. Sensors 2023, 23, 8483. [Google Scholar] [CrossRef] [PubMed]
- Treyssède, F.; Laguerre, L. Investigation of elastic modes propagating in multi-wire helical waveguides. J. Sound Vib. 2010, 329, 1702–1716. [Google Scholar] [CrossRef]








| Geometric Characteristic | Mechanical Characteristic | ||
|---|---|---|---|
| Core wire diameter (mm) | 5.4 | Elastic modulus E (GPa) | 210 |
| Helical wire diameter (mm) | 5.22 | Poisson’s ratio | 0.3 |
| Strand diameter D (mm) | 15.7 | Ultimate tension strength (MPa) | 1860 |
| Pitch of helical wire (mm) | 240 | Dilatational wave velocity (m/s) | 6001 |
| Helix lay angle (deg) | 7.9 | Shear wave velocity (m/s) | 3207.7 |
| Performance Parameter | Maximum Output Frequency | Number of Channels | Vertical Resolution | Sampling Rate | Arbitrary Waveform Length |
|---|---|---|---|---|---|
| Value (Unit) | 10 MHz | 2 CH | 16 bit | 125 Msa/s | 2 M (8 M opt.) |
| Performance Parameter | Symbol | Performance Indicator (Unit) |
|---|---|---|
| Electromechanical coupling coefficient | KP | 0.62 |
| K31 | 0.36 | |
| k33 | 0.8 | |
| k15 | 0.68 | |
| kt | 0.47 | |
| Relative permittivity | er3T | 3400 |
| er1T | 3800 | |
| Dielectric loss | tgd | 2.3 |
| Capacitance | F | 0.9 nf |
| No. | Force (kN) | Diameter (mm) | Elastic Modulus (GPa) | Helix Pitch (mm) | Measured Notch Frequency (kHz) | Simulated Notch Frequency (kHz) | Discrepancy (%) |
|---|---|---|---|---|---|---|---|
| 1 | 50 | 12.7 | 210 | 240 | 97.8 | 98.88 | 1.1 |
| 2 | 80 | 12.7 | 210 | 240 | 102.5 | 103.54 | 1.01 |
| 3 | 110 | 12.7 | 210 | 240 | 105.7 | 104.67 | −0.97 |
| 4 | 50 | 15.2 | 210 | 240 | 80.2 | 82.56 | 2.94 |
| 5 | 80 | 15.2 | 210 | 240 | 87.3 | 89.45 | 2.46 |
| 6 | 110 | 15.2 | 210 | 240 | 89.5 | 91.83 | 2.6 |
| 7 | 50 | 17.8 | 210 | 240 | 70.1 | 70.09 | −0.02 |
| 8 | 80 | 17.8 | 210 | 240 | 73.2 | 74.27 | 1.46 |
| 9 | 110 | 17.8 | 210 | 240 | 76.41 | 77.51 | 1.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, Y.; Xu, P.; Zhang, J.; Yang, S.; Wu, X. Notch Frequency Prediction of Prestressed Seven-Wire Steel Strand Based on Ultrasonic Guided Wave. Buildings 2025, 15, 3166. https://doi.org/10.3390/buildings15173166
Pei Y, Xu P, Zhang J, Yang S, Wu X. Notch Frequency Prediction of Prestressed Seven-Wire Steel Strand Based on Ultrasonic Guided Wave. Buildings. 2025; 15(17):3166. https://doi.org/10.3390/buildings15173166
Chicago/Turabian StylePei, Yao, Pengkai Xu, Jing Zhang, Shuping Yang, and Xiaohuan Wu. 2025. "Notch Frequency Prediction of Prestressed Seven-Wire Steel Strand Based on Ultrasonic Guided Wave" Buildings 15, no. 17: 3166. https://doi.org/10.3390/buildings15173166
APA StylePei, Y., Xu, P., Zhang, J., Yang, S., & Wu, X. (2025). Notch Frequency Prediction of Prestressed Seven-Wire Steel Strand Based on Ultrasonic Guided Wave. Buildings, 15(17), 3166. https://doi.org/10.3390/buildings15173166






