Characterization of the Physical, Mechanical, and Thermal Properties of Cement and Compressed Earth Stabilized Blocks, Incorporating Closed-Loop Materials for Use in Hot and Humid Climates
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
- Stiff clay soil (SCS) and spill way dirt (SWD), clayey local soils purchased clean of wood sticks and big rocks.
- Mississippi river sand (MRS).
- Recycled glass (R-G) sand, produced by crushing bottles and jars of a variety of colors.
- C&DW, produced from demolished structures, construction waste, and other sources of crushed concrete (CDW).
- Pea gravel (PG), naturally weathered rocks with predominantly smooth and round forms.
- Limestone (LS) #8, a sedimentary rock with a laminar appearance.
- Portland Cement (PCs) Type I/II No, 1124 manufactured by Quikrete ® Atlanta, GA, USA, which complies with ASTM C150 [28].
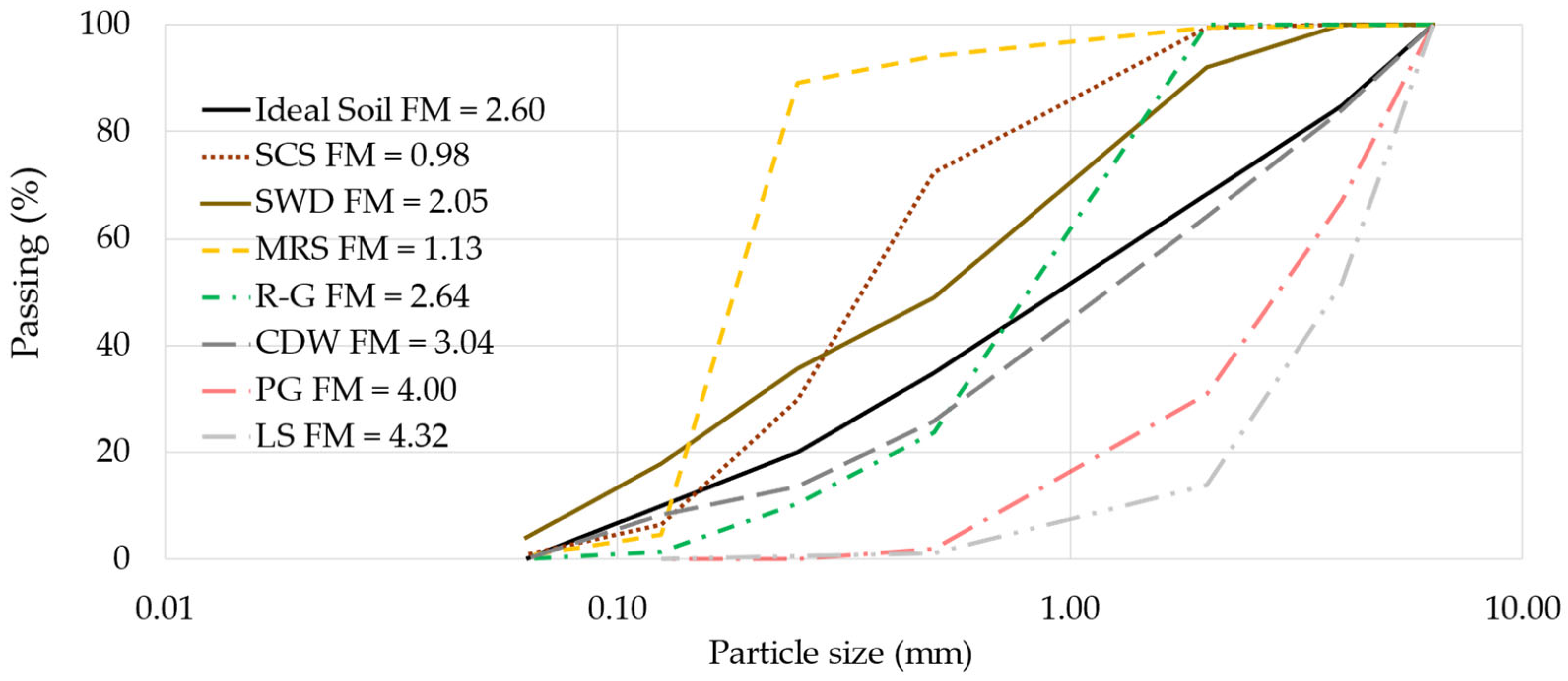
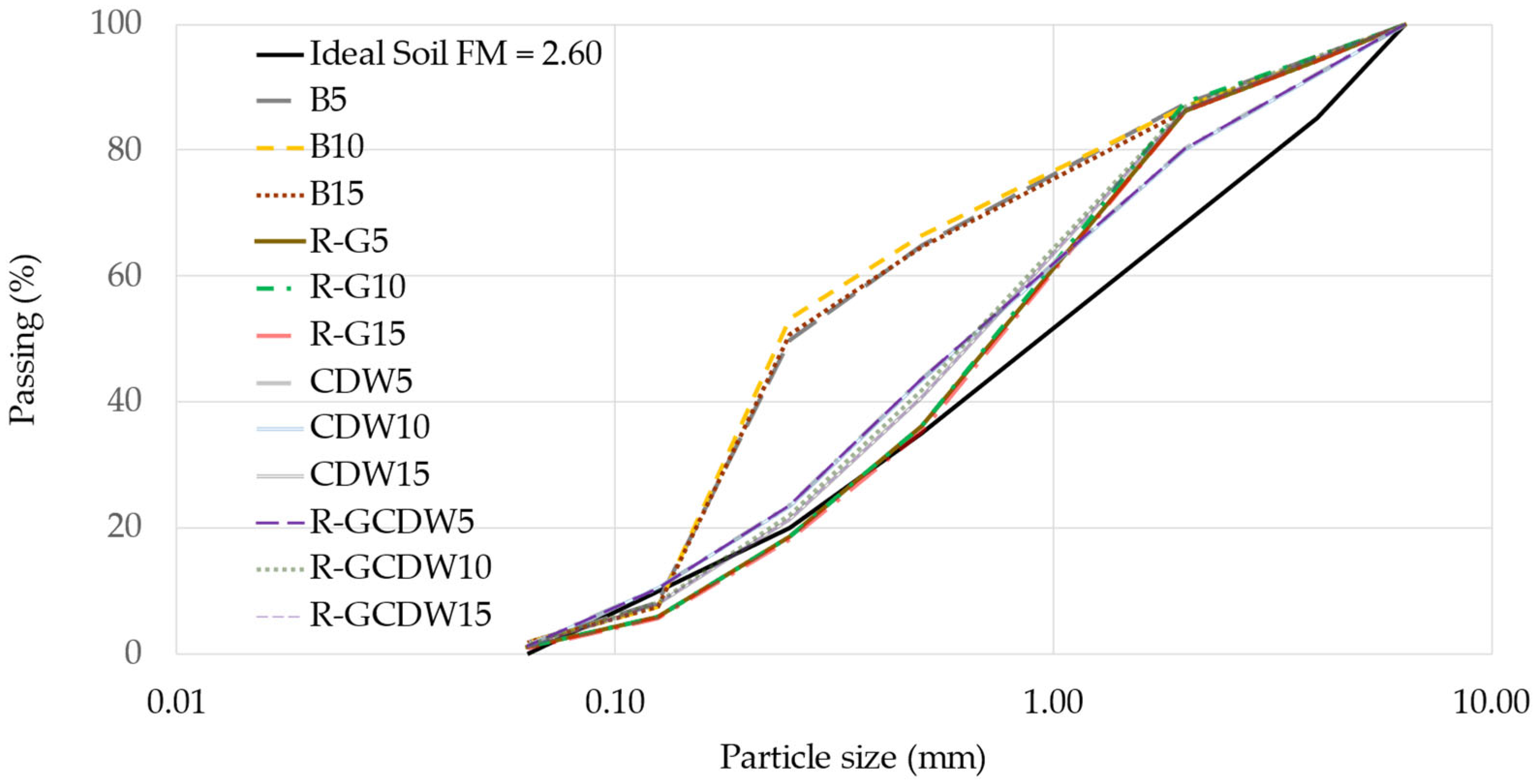
2.2. Characterization of Aggregates
2.3. Formulation of the CSEBs
2.4. Manufacture of the CSEB
2.5. Setting
2.6. Characterization of the CSEB
3. Results and Discussion
3.1. Density
3.2. Apparent Porosity
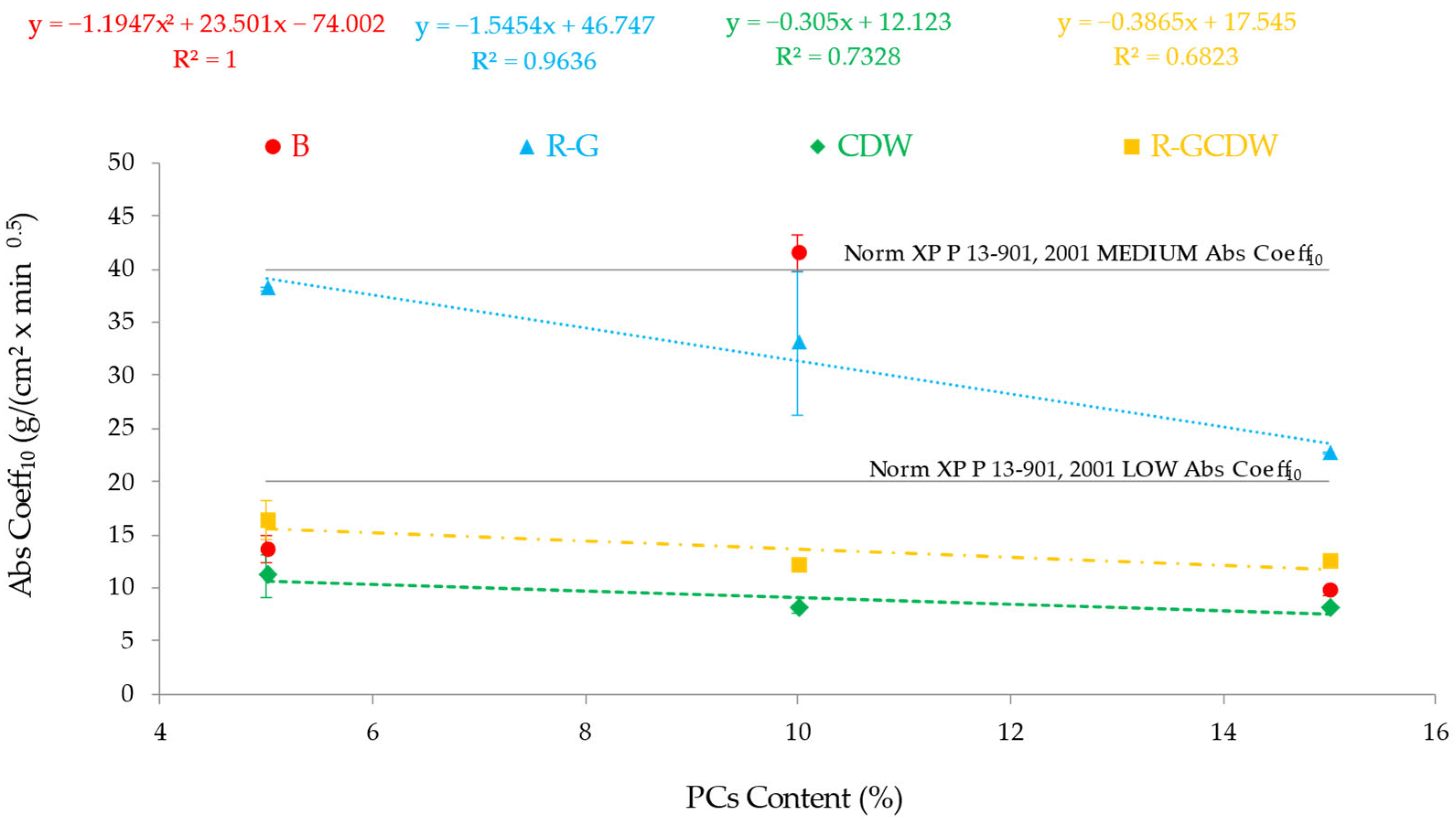
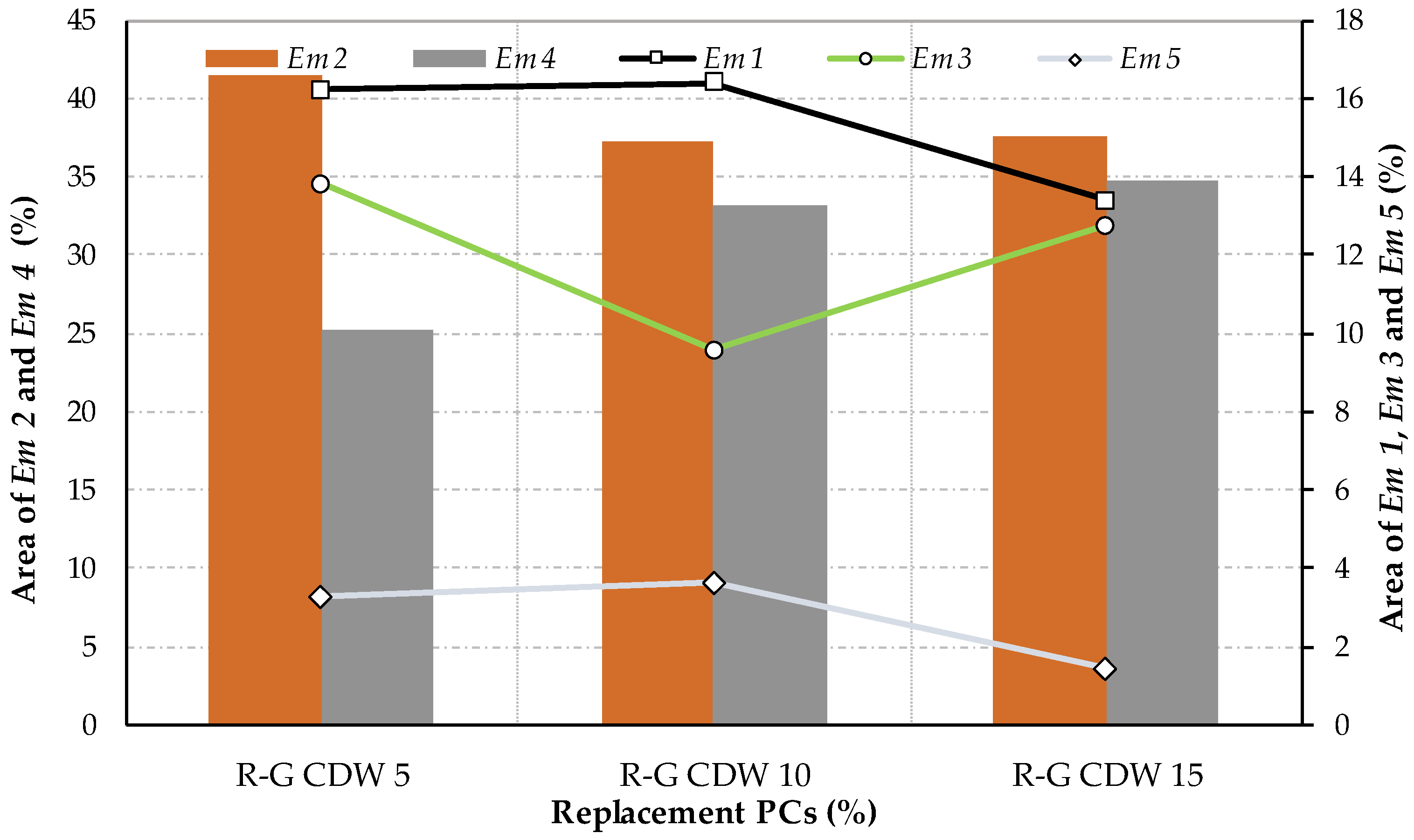
3.3. AbsCoeff10
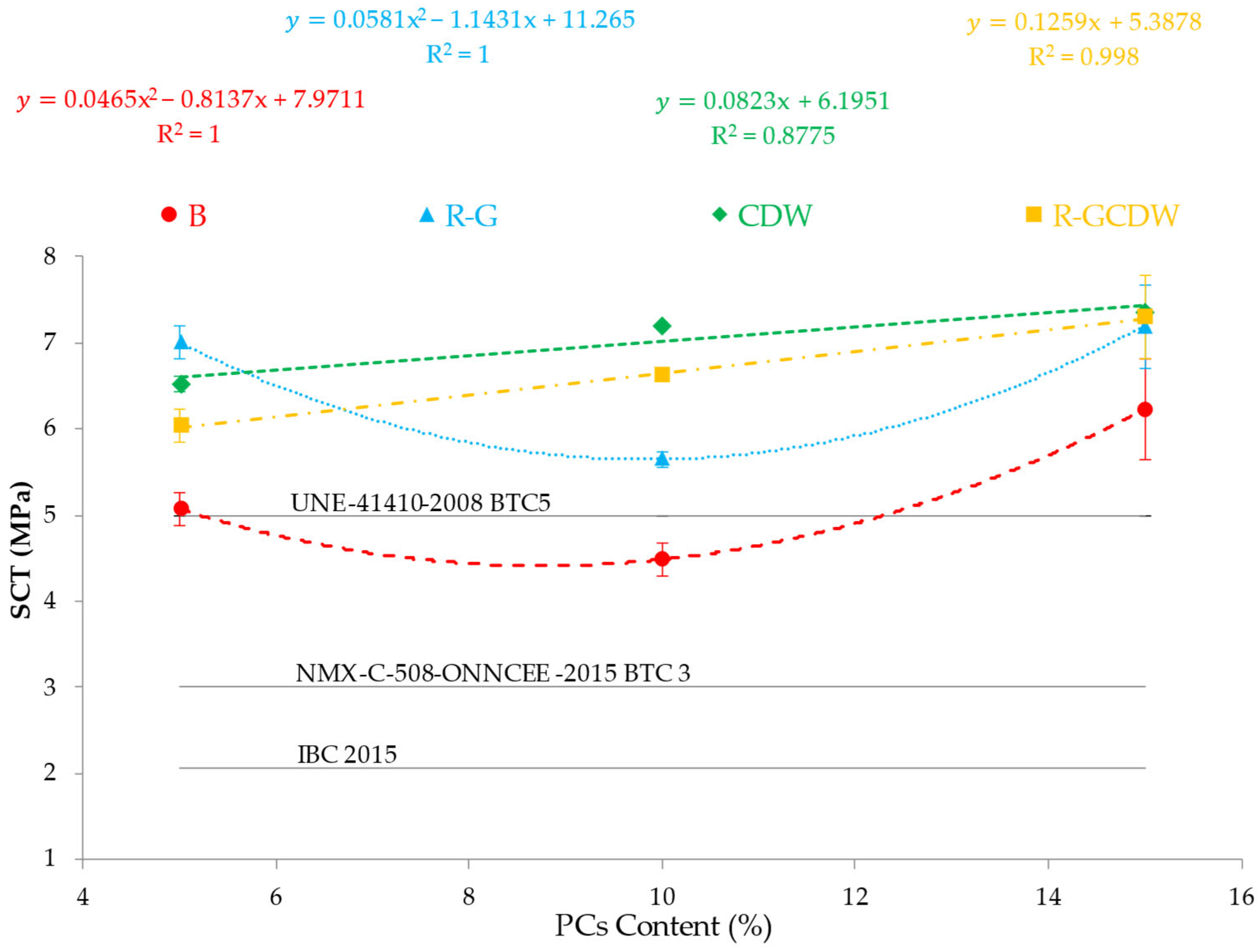
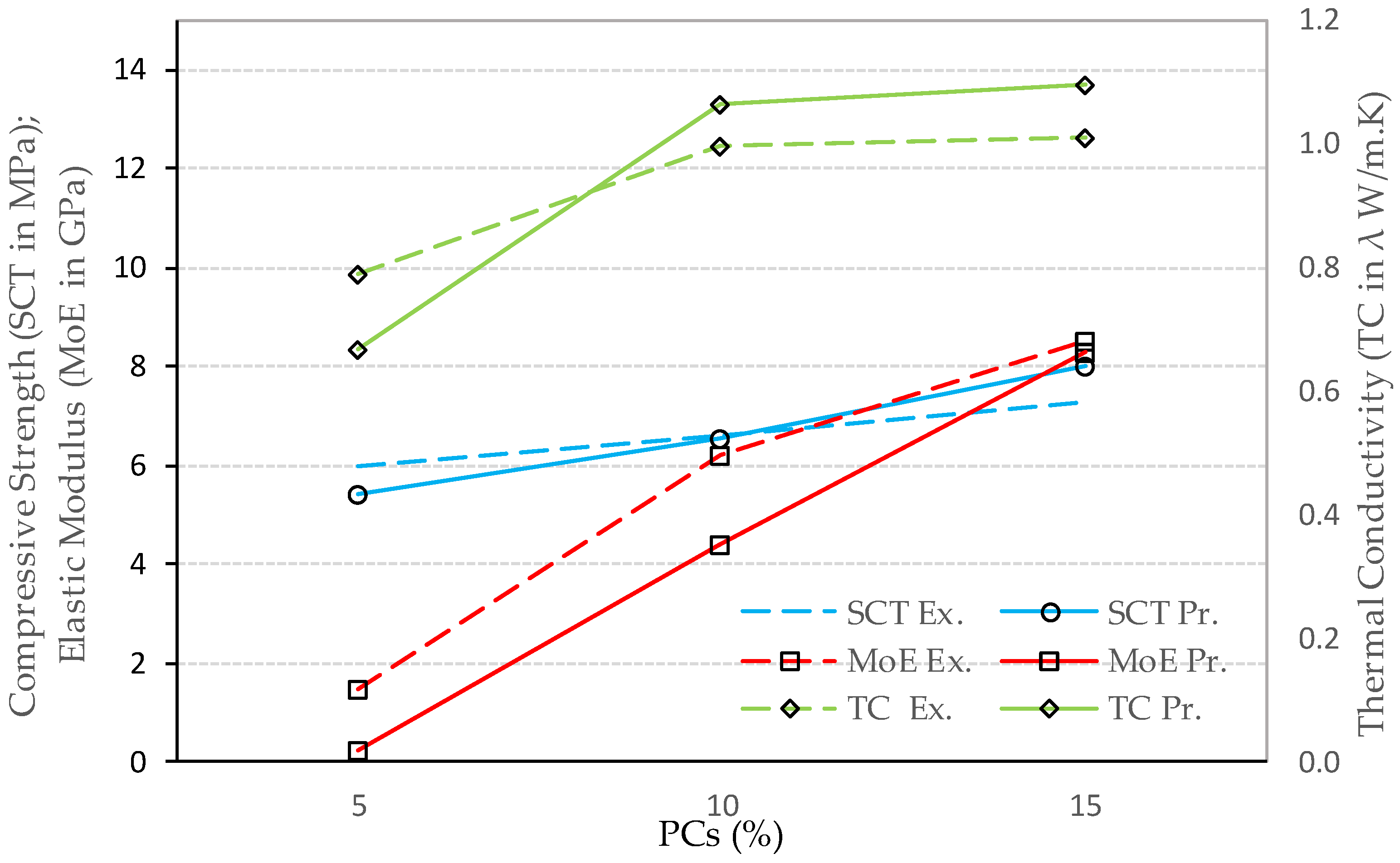
3.4. Simple Compression Tests (SCT)
3.5. MoE
3.6. TC
3.7. Microstructural Components of CSEBs
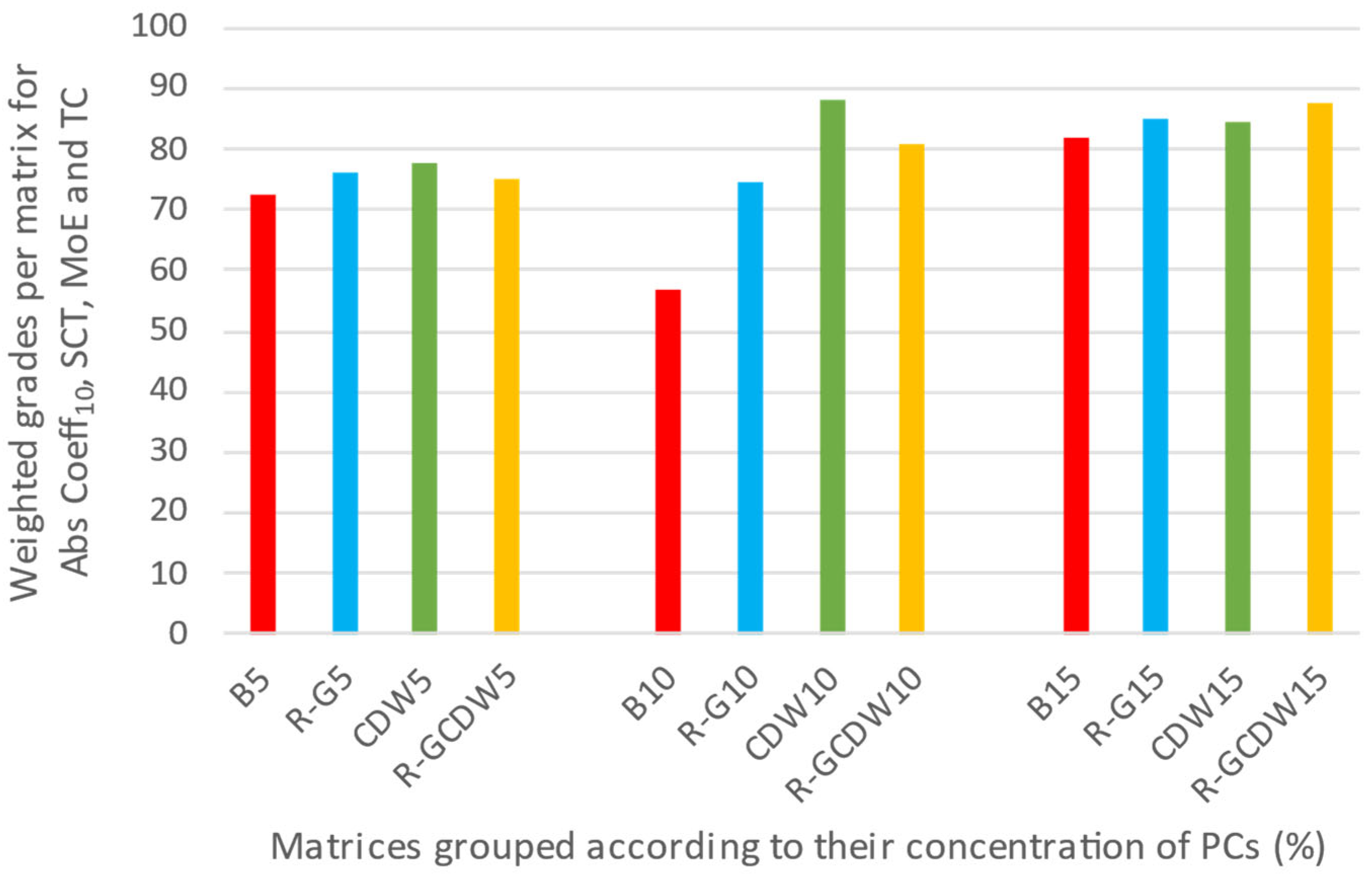
3.8. Rating
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Morel, J.C.; Mesbah, A.; Oggero, M.; Walker, P. Building houses with local materials: Means to drastically reduce the environmental impact of construction. Build. Environ. 2001, 36, 1119–1126. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, S.; Quan, D.; Fang, K.; Wang, B.; Ma, Z. Properties of Sustainable Earth Construction Materials: A State-of-the-Art Review. Sustainability 2024, 16, 670. [Google Scholar] [CrossRef]
- EPA United States Environmental Protection Agency. Sustainable Management of Construction and Demolition Materials. Available online: https://www.epa.gov/smm/sustainable-management-construction-and-demolition-materials (accessed on 24 September 2024).
- Louisiana Department of Environmental Quality Office of Environmental Services Waste Permits Division (LDEQ Louisiana), 2023. 2021 Biennial Solid Waste Capacity Report (Fiscal Year 2020 & Fiscal Year 2021) to the House Natural Resources and Environment Committee and Senate Committee on Environmental Quality. Available online: https://www.deq.louisiana.gov/assets/docs/Land/CapacityReport2021.pdf (accessed on 24 September 2024).
- Federal Highway Administration, Publications, Research Publications. User Guidelines for Waste and Byproduct Materials in Pavement Construction. Publication Number: FHWA-RD-97-148. Available online: https://www.fhwa.dot.gov/publications/research/infrastructure/pavements/97148/053.cfm (accessed on 24 September 2024).
- Panghal, H.; Kumar, A. Sustainable Concrete: Exploring Fresh, Mechanical, Durability, and Microstructural Properties with Recycled Fine Aggregates. Period. Polytech. Civ. Eng. 2024, 68, 543–558. [Google Scholar] [CrossRef]
- González-Martínez, M.A.; Gómez-Soberón, J.M.; Leal-Castañeda, E.J. Permeable Concrete with Recycled Aggregates. Study of Its Mechanical and Microstructural Properties. Materials 2025, 18, 770. [Google Scholar] [CrossRef]
- Wei, M.; Chen, L.; Lei, N.; Li, H.; Huang, L. Mechanical properties and microstructures of thermally activated ultrafine recycled fine powder cementitious materials. Constr. Build. Mater. 2025, 475, 141195. [Google Scholar] [CrossRef]
- Marey Mahmoud, H.H.; Kamel, A.M.A.; Ali, M.F. Developing Low-Cost Eco-friendly Restoration Mortars for Historic Lime-based Stucco and Building Materials. Period. Polytech. Civ. Eng. 2024, 68, 657–668. [Google Scholar] [CrossRef]
- Aninda, S.S.; Islam, M.S. Effectiveness of waste concrete powder in fabricating compressed stabilized earth blocks: Strength, durability and thermal assessment. J. Build. Eng. 2023, 80, 107989. [Google Scholar] [CrossRef]
- Coherent, M.I. United States Container Glass Market Size and Share Analysis—Growth Trends and Forecasts (2025–2032). 2023. Available online: https://www.coherentmi.com/industry-reports/united-states-container-glass-market (accessed on 24 September 2024).
- Wildman, J.C. Laboratory Evaluation of Recycled Crushed Glass Cullet for Use as an Aggregate in Beach Nourishment and Marsh Creation Projects in Southeastern Louisiana. Master’s Thesis, University of New Orleans, New Orleans, LA, USA, December 2018. Available online: https://scholarworks.uno.edu/td/2565 (accessed on 20 May 2024).
- Mohajerani, A.; Vajna, J.; Cheung, T.H.H.; Kurmus, H.; Arulrajah, A.; Horpibulsuk, S. Practical recycling applications of crushed waste glass in construction materials: A review. Constr. Build. Mater. 2017, 156, 443–467. [Google Scholar] [CrossRef]
- Alducin-Ochoa, J.M.; Martín-del-Río, J.J.; Torres-González, M.; Flores-Alés, V.; Hernández-Cruz, D. Performance of mortars based on recycled glass as aggregate by accelerated decay tests (ADT). Const. Build. Mater. 2021, 300, 124057. [Google Scholar] [CrossRef]
- Gómez-Soberón, J.M.; Cabrera-Covarrubias, F.G.; Luis Almaral-Sánchez, J.; Gómez-Soberón, M.C. Fresh-State Properties of Mortars with Recycled Glass Aggregates: Global Unification of Behavior. Adv. Mater. Sci. Eng. 2018, 2018, 1386946. [Google Scholar] [CrossRef]
- Cabrera-Covarrubias, F.G.; Gómez-Soberón, J.M.; Almaral-Sánchez, J.L.; Arredondo-Rea, S.P.; Mendivil-Escalante, J.M. Mechanical and Basic Deformation Properties of Mortar with Recycled Gass as a Fine Aggregate Replacement. Int. J. Civ. Eng. 2018, 16, 107–121. [Google Scholar] [CrossRef]
- Redondo-Pérez, N.M.; Redondo-Mosquera, J.D.; Abellán-García, J. A Comprehensive Overview of Recycled Glass as Mineral Admixture for Circular UHPC Solutions. Sustainability 2024, 16, 5077. [Google Scholar] [CrossRef]
- Larbi, S.; Khaldi, A.; Maherzi, W.; Abriak, N.E. Formulation of compressed earth blocks stabilized by glass waste activated with NaOH solution. Sustainability 2022, 14, 102. [Google Scholar] [CrossRef]
- Ellwood, B.B.; Warny, S.; Hackworth, R.A.; Ellwood, S.H.; Tomkin, J.J.; Bentley, S.J.; Braud, D.H.; Clayton, J. The LSU Campus Mound with construction beginning at ~11,000 BP, are the oldest known extant man-made structures in the Americas. Am. J. Sci. 2022, 322, 795–827. [Google Scholar] [CrossRef]
- Smith, E.W.; Austin, G.S. Adobe, Pressed-Earth, and Rammed-Earth Industries in New Mexico; Revised Edition; Bulletin 159; New Mexico Bureau of Mines & Mineral Resources: Socorro, NM, USA, 1996. [Google Scholar]
- Montoya-Pino, M.P.; Ramírez-Nieto, J.V.; Aravecchia-Botas, N.C. CINVA: Un proyecto latinoamericano 1951–1972 (CINVA: A Latin-American Project 1951–1972). 2024. Radio Podcast from Universidad Nacional de Colombia, radio UNAL. Available online: https://radio.unal.edu.co/detalle/cinva-un-proyecto-latinoamericano-1951-197 (accessed on 25 September 2024).
- Galindo-Díaz, J.; Escorcia-Oyola, O.; González-Calderón, A.J. The Inter-American Housing Center (CINVA) and the origins of the experimentation with compressed earth blocks (CEB) in social dwelling (1953–1957). Inf. Constr. 2023, 75, 570. [Google Scholar] [CrossRef]
- Peña Rodríguez, M.L. El Programa CINVA y la acción communal (The CINVA program and the community action). Bit. Urb. Terr. 2008, 12, 185–192. [Google Scholar]
- Kimmons, G.L.; Ferm, R.L.; Matteson, R. Asphalt-stabilized building blocks. Ind. Eng. Chem. Prod. Res. Dev. 1969, 8, 3. [Google Scholar] [CrossRef]
- Reyna-Ruiz, C.; Gómez-Soberón, J.M.; Rojas-Valencia, M.N. Feasibility and Application of Local Closed-Loop Materials to Produce Compressed and Stabilized Earth Blocks. Materials 2024, 17, 3358. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, S.; Darras, G.; Losa, N. Evaluation of the pressing process in the manufacture of compressed earth blocks. Inf. Constr. 2024, 76, 574. [Google Scholar] [CrossRef]
- Walker, P.; Stace, T. Properties of some cement stabilized compressed earth blocks and mortars. Mater. Struct. 1997, 30, 545–551. [Google Scholar] [CrossRef]
- ASTM-C 150-07; Standard Specification for Portland Cement. ASTM International: West Conshohocken, PA, USA, 2007.
- ISO 2591-1:1988; International Standard ISO 2591-1, First Edition 1988 12-01. Test sieving—Part 1: Methods Using Test Sieves of Woven Wire Cloth and Perforated Metal Plate. International Organization for Standardization: Geneva, Switzerland, 1998.
- Maïni, S. Production and Use of Compressed Stabilized Earth Blocks, Code of Practice; Auroville Earth Institute: Auroville, India, 2010. [Google Scholar]
- NMX-C-508-ONNCE-2015; Norma Mexicana-Industria de la Construcción—Bloques de Tierra Comprimida Estabilizados con Cal—Especificaciones y Métodos de Ensayo (Mexican Norm for the Construction Industry, Compressed Earth Blocks, Stabilized with lime—Specifications and Test Methods). Organismo Nacional de Normalización y Certificación de la Construcción y la Edificación, S.C.: Ciudad de México, México, 2015.
- UNE 41410-2008; Bloques de Tierra Comprimida para Muros y Tabiques. Definiciones, Especificaciones y Métodos de Ensayo. Norma Española: Madrid, Spain, 2008.
- Kaifan, A.; Gani, F.A.; Irham; Munardy. The Stabilization of Compressed Stabilized Earth Blocks using rice husk ash-lime-cement to reduce environmental pollution. IOP Conf. Ser. Earth Environ. Sci. 2025, 1510, 012091. [Google Scholar] [CrossRef]
- Sadouri, R.; Kebir, H.; Benyoucef, M. The Effect of Incorporating Juncus Fibers on the Properties of Compressed Earth Blocks Stabilized with Portland Cement. Appl. Sci. 2024, 14, 815. [Google Scholar] [CrossRef]
- Labiad, Y.; Meddah, A.; Beddar, M. Performance of sisal fiber-reinforced cement-stabilized compressed-earth blocks incorporating recycled brick waste. Innov. Infrastr. Solut. 2023, 8, 107. [Google Scholar] [CrossRef]
- Kumar, N.; Barbato, M. Effects of sugarcane bagasse fibers on the properties of compressed and stabilized earth blocks. Constr. Build. Mater. 2022, 315, 125552. [Google Scholar] [CrossRef]
- Kasinikota, P.; Tripura, D.D. Prediction of physical-mechanical properties of hollow interlocking compressed unstabilized and stabilized earth blocks at different moisture conditions using ultrasonic pulse velocity. J. Build. Eng. 2022, 48, 103961. [Google Scholar] [CrossRef]
- Ma, J.; Abdelaal, A.; Zhang, H.; Zhou, A.; Fu, Y.; Xie, Y.M. Ultra-compressed earth block stabilized by bio-binder for sustainable building construction. Case Stud. Constr. Mater. 2024, 21, e03523. [Google Scholar] [CrossRef]
- Sathiparan, N.; Tharuka, R.A.N.S.; Jeyananthan, P. Prediction of moisture content of cement-stabilized earth blocks using soil characteristics, cement content, and ultrasonic pulse velocity. J. Eng. Appl. Sci. 2024, 71, 187. [Google Scholar] [CrossRef]
- Cruz, R.; Bogas, J.A.; Balboa, A.; Faria, P. Water Resistance of Compressed Earth Blocks Stabilised with Thermoactivated Recycled Cement. Materials 2024, 17, 5617. [Google Scholar] [CrossRef] [PubMed]
- WU Weather Underground. Kenner, LA Weather History. Available online: https://www.wunderground.com/history/monthly/us/la/kenner/KMSY/ (accessed on 30 June 2023).
- Nshimiyimana, P.; Hema, C.; Sore, S.O.; Zoungrana, O.; Messan, A.; Courard, L. Durability Performances of Compressed Earth Blocks Exposed to Wetting-Drying Cycles and High Temperature. WIT Trans. Built Environ. 2022, 210, 141–149. [Google Scholar] [CrossRef]
- Nshimiyimana, P.; Djibo, K.B.; Sore, S.O.; Coulibaly, Y.; Pru’Homme, E.; Zhao, Z.; Messan, A.; Courard, L. High-Temperature Performances of Compressed Earth Blocks Stabilized with Cementitious Binders. In Second RILEM International Conference on Earthen Construction. ICEC 2024, Edinburgh, UK, 8–10 July 2024; Beckett, C., Bras, A., Fabbri, A., Keita, E., Perlot, C., Perrot, A., Eds.; RILEM Book Series; Springer: Cham, Switzerland, 2024; Volume 52. [Google Scholar] [CrossRef]
- UNE-EN-ISO 18754:2022; Cerámicas Técnicas (cerámicas avanzadas, cerámicas técnicas avanzadas) Determinación de la densidad y de la porosidad aparente. Asociación Española de Normalización: Madrid, Spain, 2022.
- NMX-C-037-ONNCCE-2013; Industria de la Construcción—Mampostería—Determinación de la absorción total y la absorción inicial de agua en bloques, tabiques o ladrillos y tabicones—Método de Ensayo. Norma Mexicana: Naucalpan de Juárez, Mexico, 2013.
- NMX-C-036-ONNCCE-2013; Industria de la Construcción—Mampostería—Resistencia a la compresión de bloques, tabiques o ladrillos y tabicones y adoquines—Método de ensayo. Norma Mexicana: Naucalpan de Juárez, Mexico, 2013.
- Speevak, T.; Yu, A.K. Multiple Attributes Sampling Acceptance Plans Involving Destructive Testing. Technometrics 1987, 29, 103–107. [Google Scholar] [CrossRef]
- Warren, W.G. Sampling Strategies for Destructive Tests; Environment Canada, Forestry Directorate, Western Forest Products Laboratory: Vancouver, BC, Canada, 1975. [Google Scholar]
- Bayiha, B.N.; Kenmogne, F.; Bahel, B.; A’Paglan Bidime, É.Y.; Bell, E.Y.; Billong, N. Development and characterization of a composite material with geopolymer matrix obtained by incorporation of microparticles from plastic bottles. Heliyon 2024, 10, e30801. [Google Scholar] [CrossRef]
- Adesina, F.; Mohammed, T.I.; Ojo, O.T. Design and Fabrication of a Manually Operated Hydraulic Press. Open Access Libr. J. 2018, 5, e4522. [Google Scholar] [CrossRef]
- Debele, A.D.; Demeke, S.; Bekele, T.; Malimo, M. Recycling and reusing potential of disposable low-density polyethylene plastic waste for flexible paver tile construction for outdoor application. Heliyon 2024, 10, e29381. [Google Scholar] [CrossRef] [PubMed]
- Khatib, M.I.; Ahmed, R.Z.; Uddin, M.S.; Abdul Rahman, M.; Shareef, M.R.; Akber, S.; Khan, M.; Shaikh, S. Design and Fabrication of 5 Ton Hydraulic Press Machine. Int. J. Sci. Res. Sci. Eng. Technol. 2020, 7, 22–30. [Google Scholar] [CrossRef]
- Sumaila, M.; Okonigbon, A.; Ibhadode, A. Design and Manufacture of a 30-ton Hydraulic Press. Au J. Technol. 2011, 14, 196–200. [Google Scholar]
- ASTM C597-22; Standard Test Method for Ultrasonic Pulse Velocity Through Concrete. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM E494-15; Standard Practice for Measuring Ultrasonic Velocity in Materials. ASTM International: West Conshohocken, PA, USA, 2015.
- Bowen, P.K. Engineering Elastic Constants from Ultrasonic Wave Velocity. Deringer-Ney Tech Briefs. 2015. Available online: https://deringerney.com/engineering-elastic-constants-from-ultrasonic-wave-velocity (accessed on 15 February 2025).
- Hak-Chul, S.; Yoonseok, C. Determination of Coefficient of Thermal Expansion Effects on Louisiana’s PCC Pavement Design. Department of Civil and Environmental Engineering, Louisiana State University, Baton Rouge Louisiana, 70803 2011, State Project No 736-99-1450 conducted for Louisiana Department of Transportation and Development Louisiana Transportation Research Center. Available online: https://rosap.ntl.bts.gov/view/dot/23571 (accessed on 4 August 2025).
- He, H.; Dyck, M.; Lv, J. The heat pulse method for soil physical measurements: A bibliometric analysis. Appl. Sci. 2020, 10, 6171. [Google Scholar] [CrossRef]
- Solver, version 2025 Q1; Frontline Solvers: Reno, NV, USA, 2025. Available online: https://www.solver.com (accessed on 6 May 2025).
- SLS 1328:1:2009; Specification for Compressed Stabilised Earth Blocks: Part 1: Requirements. Sri Lanka Standards Institution: Colombo, Sri Lanka, 2009.
- Malkanthi, S.N.; Wickramasinghe, W.G.S.; Perera, A.A.D.A.J. Use of construction waste to modify soil grading for compressed stabilized earth blocks (CSEB) production. Case Stud. Constr. Mater. 2021, 15, e00717. [Google Scholar] [CrossRef]
- Davis, L.K.; Maïni, S. Feasibility Report for Compressed Stabilized Earth Block (CSEB) Production and Use in the North and East of Sri Lanka; 2014 Office of the European Union: Luxembourg, 2017. [Google Scholar] [CrossRef]
- Venkatarama, R.B.V.; Gupta, A. Characteristics of soil-cement blocks using highly sandy soils. Mater. Struct. 2005, 38, 651–658. [Google Scholar] [CrossRef]
- Hall, E.; Pulatsu, B.; Erdogmus, E.; Skourup, B. Compression, Tension, and Fracture Energy Properties of Compressed Cement-Stabilized Earth Blocks. J. Archit. Eng. 2022, 28, 06021005. [Google Scholar] [CrossRef]
- Morel, J.C.; Pkla, A.; Walker, P. Compressive strength testing of compressed earth blocks. Constr. Build. Mater. 2007, 21, 303–309. [Google Scholar] [CrossRef]
- Kumar, B.M.V.; Ananthan, H.; Balaji, K.V.A. Experimental studies on cement stabilized masonry blocks prepared from brick powder, fine recycled concrete aggregate and pozzolanic materials. J. Build. Eng. 2017, 10, 80–88. [Google Scholar] [CrossRef]
- Lavie Arsène, M.I.; Frédéric, C.; Nathalie, F. Improvement of lifetime of compressed earth blocks by adding limestone, sandstone and porphyry aggregates. J. Build. Eng. 2020, 29, 101155. [Google Scholar] [CrossRef]
- Sekhar, D.C.; Nayak, S. Utilization of granulated blast furnace slag and cement in the manufacture of compressed stabilized earth blocks. Constr. Build. Mater. 2018, 166, 531–536. [Google Scholar] [CrossRef]
- Islam, M.S.; Elahi, T.E.; Shahriar, A.R.; Mumtaz, N. Effectiveness of fly ash and cement for compressed stabilized earth block construction. Constr. Build. Mater. 2020, 255, 119392. [Google Scholar] [CrossRef]
- XP P 13-901; Normalisation Française. Blocs de terre comprimée pour murs et cloisons. AFNOR: La Plaine Saint-Denis, France, 2001.
- Goutsaya, J.; Ntamack, G.E.; d’Ouazzane, S.C.; Li, X. Damage Modelling of Compressed Earth Blocks Stabilised with Cement. Adv. Civ. Eng. 2022, 2022, 3342661. [Google Scholar] [CrossRef]
- Islam, M.S.; Elahi, T.-E.; Shahriar, A.R.; Asce, S.M.; Nahar, K.; Hossain, T.R. Strength and Durability Characteristics of Cement-Sand Stabilized Earth Blocks. J. Mater. Civ. Eng. 2020, 32, 04020087. [Google Scholar] [CrossRef]
- Elahi, T.E.; Shahriar, A.R.; Islam, M.S.; Mehzabin, F.; Mumtaz, N. Suitability of fly ash and cement for fabrication of compressed stabilized earth blocks. Constr. Build. Mater. 2020, 263, 120935. [Google Scholar] [CrossRef]
- Elahi, T.E.; Shahriar, A.R.; Alam, M.K.; Abedin, M.Z. Effectiveness of saw dust ash and cement for fabrication of compressed stabilized earth blocks. Constr. Build. Mater. 2020, 259, 120568. [Google Scholar] [CrossRef]
- 2015 International Building Code (IBC). International Code Council Inc. 2015. Available online: https://codes.iccsafe.org/content/IBC2015 (accessed on 1 December 2024).
- Akoglu, H. User’s guide to correlation coefficients. Turkish J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
- Udo, M.; Esezobor, D.; Afolalu, A.; Onovo, H.; Ongbali, S.; Okokpujie, I.P. Investigation of Balling Characteristics of Mixture of Iron Oxide Bearing Wastes and Iron Ore Concentrates. IOP Conf. Ser. Mater. Sci. Eng. 2018, 413, 012042. [Google Scholar] [CrossRef]
- Qiu, Z.; Chen, F.; Yu, Y.; Gu, Y.; Wang, X.; Wang, Y. Effects of water-cement ratio and particle diameter on the mechanical properties of cement paste particles. Opt. Lasers Eng. 2025, 187, 108874. [Google Scholar] [CrossRef]
- Elahi, T.E.; Shahriar, A.R.; Islam, M.S. Engineering characteristics of compressed earth blocks stabilized with cement and fly ash. Constr. Build. Mater. 2021, 277, 122367. [Google Scholar] [CrossRef]
- Zakham, N.; Younes, E.L.; Ammari, A.; Cherraj, M.; Bouabid, H.; Gueraoui, K.; Samaouali, A.; Mzerd, A. Influence of cement content on the thermal properties of compressed earth blocks (CEB) in the dry state. MATEC Web Conf. 2018, 149, 01059. [Google Scholar] [CrossRef][Green Version]
- Sindanne, A.S.; Sanga, L.R.; Sallaboui, K.E. Thermophysical characterization of earth blocks stabilized by cement, sawdust and lime. J. Build. Mater. Struct. 2014, 1, 58–64. Available online: http://journals.lagh-univ.dz/index.php/jbms/article/view/12/ (accessed on 7 March 2024). [CrossRef]
- Saidi, M.; Cherif, A.S.; Zeghmati, B.; Sediki, E. Stabilization effects on the thermal conductivity and sorption behavior of earth bricks. Constr. Build. Mater. 2018, 167, 566–577. [Google Scholar] [CrossRef]
- Bachar, M.; Azzouz, L.; Rabehi, M.; Mezghiche, B. Characterization of a stabilized earth concrete and the effect of incorporation of aggregates of cork on its thermo-mechanical properties: Experimental study and modeling. Constr. Build. Mater. 2015, 74, 259–267. [Google Scholar] [CrossRef]
- Rasooli, A.; Itard, L. In-situ rapid determination of walls’ thermal conductivity, volumetric heat capacity, and thermal resistance, using response factors. Appl. Energy 2019, 253, 113539. [Google Scholar] [CrossRef]
- Casapino-Espinoza, C.A.; Gómez-Soberón, J.M.; Gómez-Soberón, M.C. The Use of Steatite Powder Waste as an Aggregate for the Manufacture of Earth Blocks—An Evaluation of Its Impact on Physical, Mechanical and Thermal Conductivity Properties. Buildings 2025, 15, 1605. [Google Scholar] [CrossRef]
- Casapino-Espinoza, C.A.; Gómez-Soberón, J.M.; Gómez-Soberón, M.C. The Effect of Recycled Crushed Brick Aggregate on the Physical–Mechanical Properties of Earth Blocks. Buildings 2025, 15, 145. [Google Scholar] [CrossRef]
- Cabrera-Covarrubias, F.G.; Gómez-Soberón, J.M.; Almaral-Sánchez, C.J.L.; Arredondo-Rea, S.P.; Gómez-Soberón, M.C.; Corral-Higuera, R. An Experimental Study of Mortars with Recycled Ceramic Aggregates: Deduction and Prediction of the Stress-Strain. Materials 2016, 9, 1029. [Google Scholar] [CrossRef]
- Huang, Z.; Luo, Y.; Zhang, W.; Ye, Z.; Li, Z.; Liang, Y. Thermal insulation and high-temperature resistant cement-based materials with different pore structure characteristics: Performance and high-temperature testing. J. Build. Eng. 2025, 101, 111839. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhu, T.; Chen, J.; Shan, K.; Li, J. Relationship Between Pore-Size Distribution and 1D Compressibility of Different Reconstituted Clays Based on Fractal Theory. Fractal Fract. 2025, 9, 235. [Google Scholar] [CrossRef]
- Meijering, J.V.; Kern, K.; Tobi, H. Identifying the methodological characteristics of European green city rankings. Ecol. Indic. 2014, 43, 132–142. [Google Scholar] [CrossRef]
- Santos, W. Effect of moisture and porosity on the thermal properties of a conventional refractory concrete. J. Eur. Ceram. Soc. 2003, 23, 745–755. [Google Scholar] [CrossRef]
- Limami, H.; Manssouri, I.; Cherkaoui, K.; Khaldoun, A. Mechanical and physicochemical performances of reinforced unfired clay bricks with recycled Typha-fibers waste as a construction material additive. Clean. Eng. Technol. 2021, 2, 100037. [Google Scholar] [CrossRef]
- Kim, J.H.; Bae, Y.H.; Kim, S.S.; Lee, M.; Ho, S.H. Formative Usability Evaluation of a Three-Way Digital Healthcare System for the People with Disabilities and Their Caregivers: A Cross-Sectional Study. Healthcare 2022, 10, 2325. [Google Scholar] [CrossRef]
- Singh, S.; Upadhyay, S.P.; Powar, S. Developing an integrated social, economic, environmental, and technical analysis model for sustainable development using hybrid multi-criteria decision-making methods. Appl. Energy 2022, 308, 118235. [Google Scholar] [CrossRef]
- Wiehle, P.; Brinkmann, M. Material behavior of unstabilised earth block masonry and its components under compression at varying relative humidity. Case Stud. Constr. Mater. 2022, 17, e01663. [Google Scholar] [CrossRef]
- Raimondo, M.; Dondi, M.; Gardini, D.; Guarini, G.; Mazanti, F. Predicting the initial rate of water absorption in clay bricks. Constr. Build. Mater. 2009, 23, 2623–2630. [Google Scholar] [CrossRef]
- Fabbri, A.; Soudani, L.; McGregor, F.; Morel, J.C. Analysis of the water absorption test to assess the intrinsic permeability of earthen materials. Constr. Build. Mater. 2019, 199, 154–162. [Google Scholar] [CrossRef]
- Kameni Nematchoua, M.; Ricciardi, P.; Reiter, S.; Yvon, A. A comparative study on optimum insulation thickness of walls and energy savings in equatorial and tropical climate. Int. J. Sustain. Built Environ. 2017, 6, 170–182. [Google Scholar] [CrossRef]
- Gratzl, S.; Lex, A.; Gehlenborg, N.; Pfister, H.; Streit, M. LineUp: Visual Analysis of Multi-Attribute Rankings. IEEE Trans. Vis. Comput. Graph. 2013, 19, 2277–2286. [Google Scholar] [CrossRef]
- Belayali, F.; Maherzi, W.; Benzerzour, M.; Abriak, N.E.; Senouci, A. Compressed Earth Blocks Using Sediments and Alkali-Activated By products. Sustainability 2022, 14, 3158. [Google Scholar] [CrossRef]
- Raj, A.; Sharma, T.; Singh, S.; Sharma, U.; Sharma, P.; Singh, R.; Sharma, S.; Kaur, J.; Kaur, H.; Salah, B. Building a Sustainable Future from Theory to Practice: A Comprehensive PRISMA-Guided Assessment of Compressed Stabilized Earth Blocks (CSEB) for Construction Applications. Sustainability 2023, 15, 9374. [Google Scholar] [CrossRef]
- Shalini, S.; Honnalli, S.; Pavan, G.S. Determining elastic properties of CSEB masonry using FEA-based hominization technique. Mater. Today Proc. 2023, in press. [Google Scholar] [CrossRef]

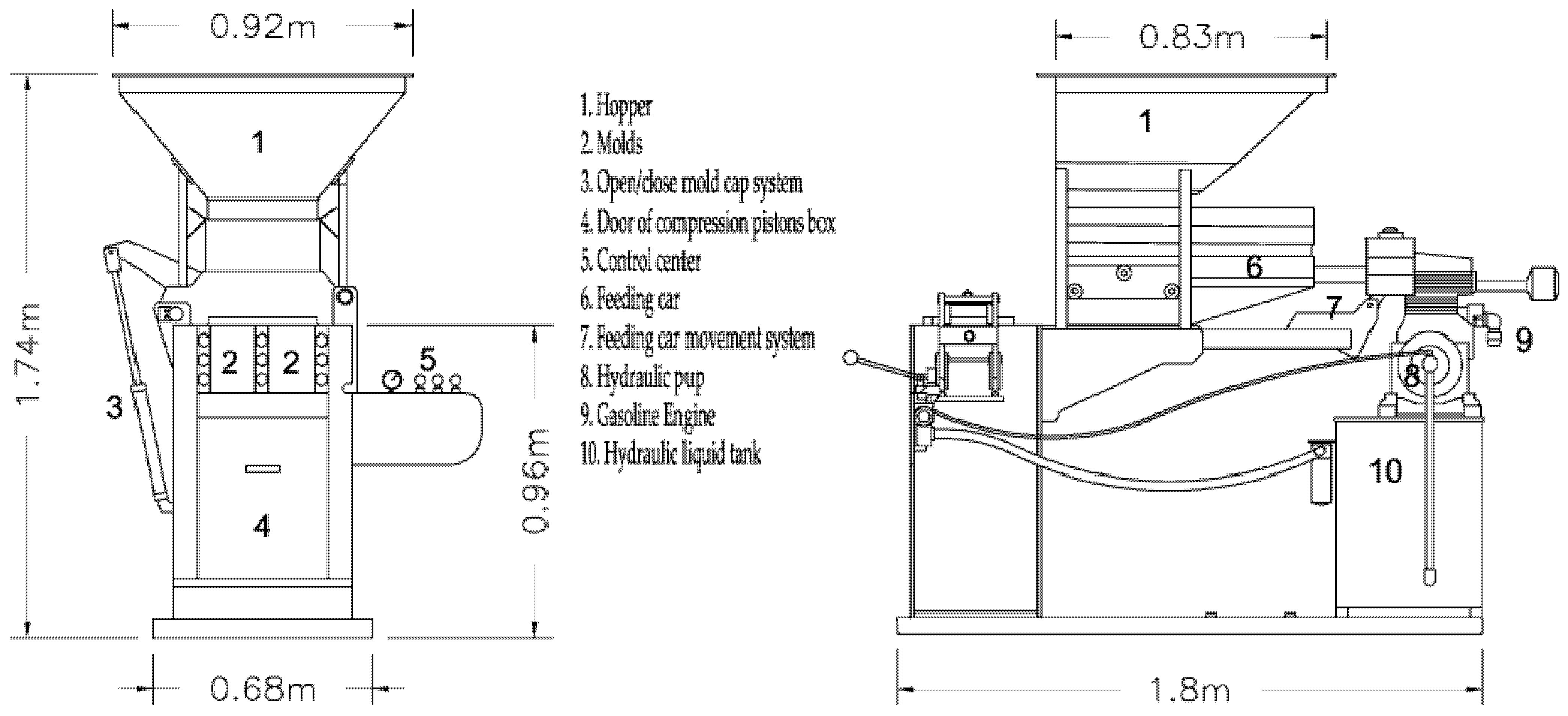



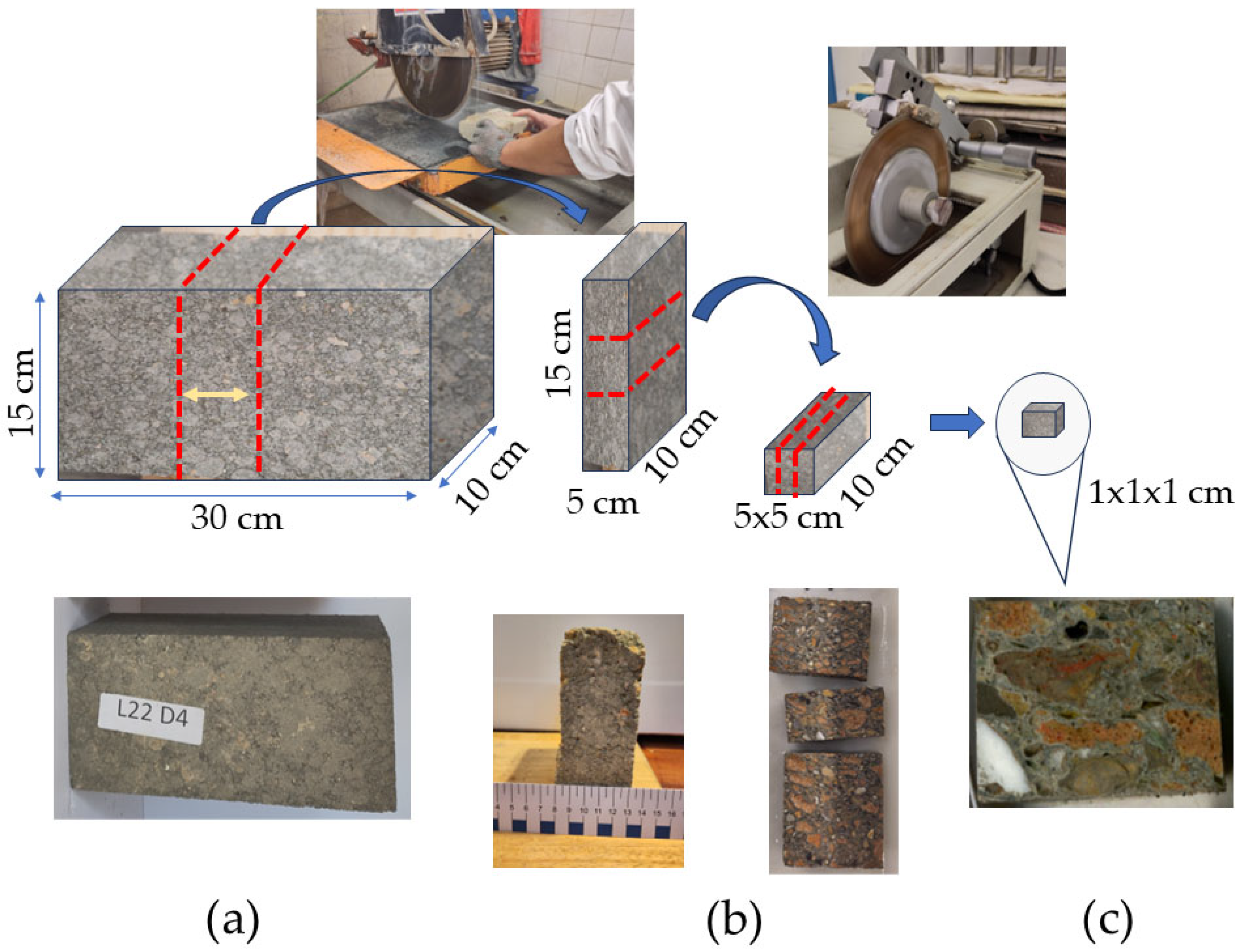




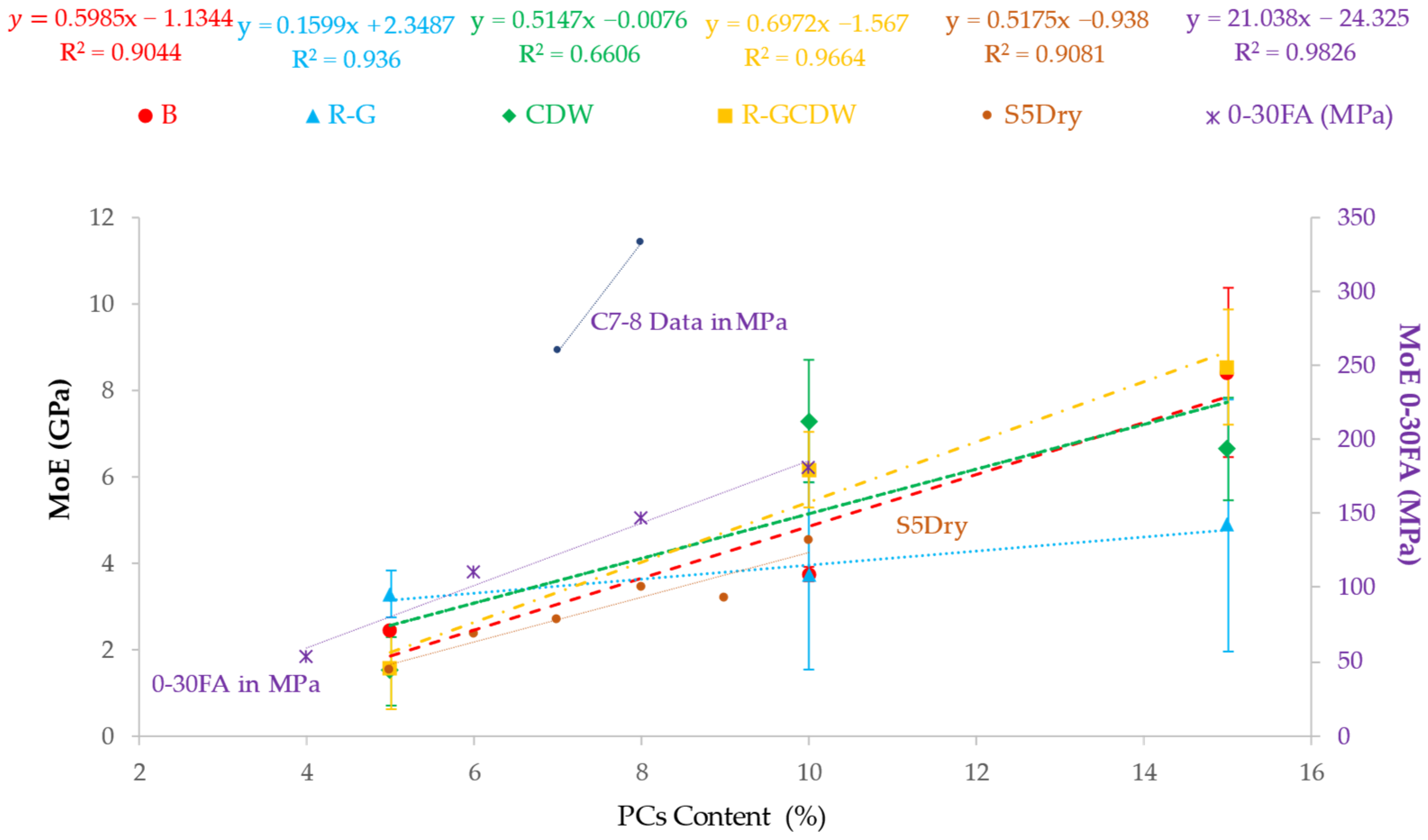
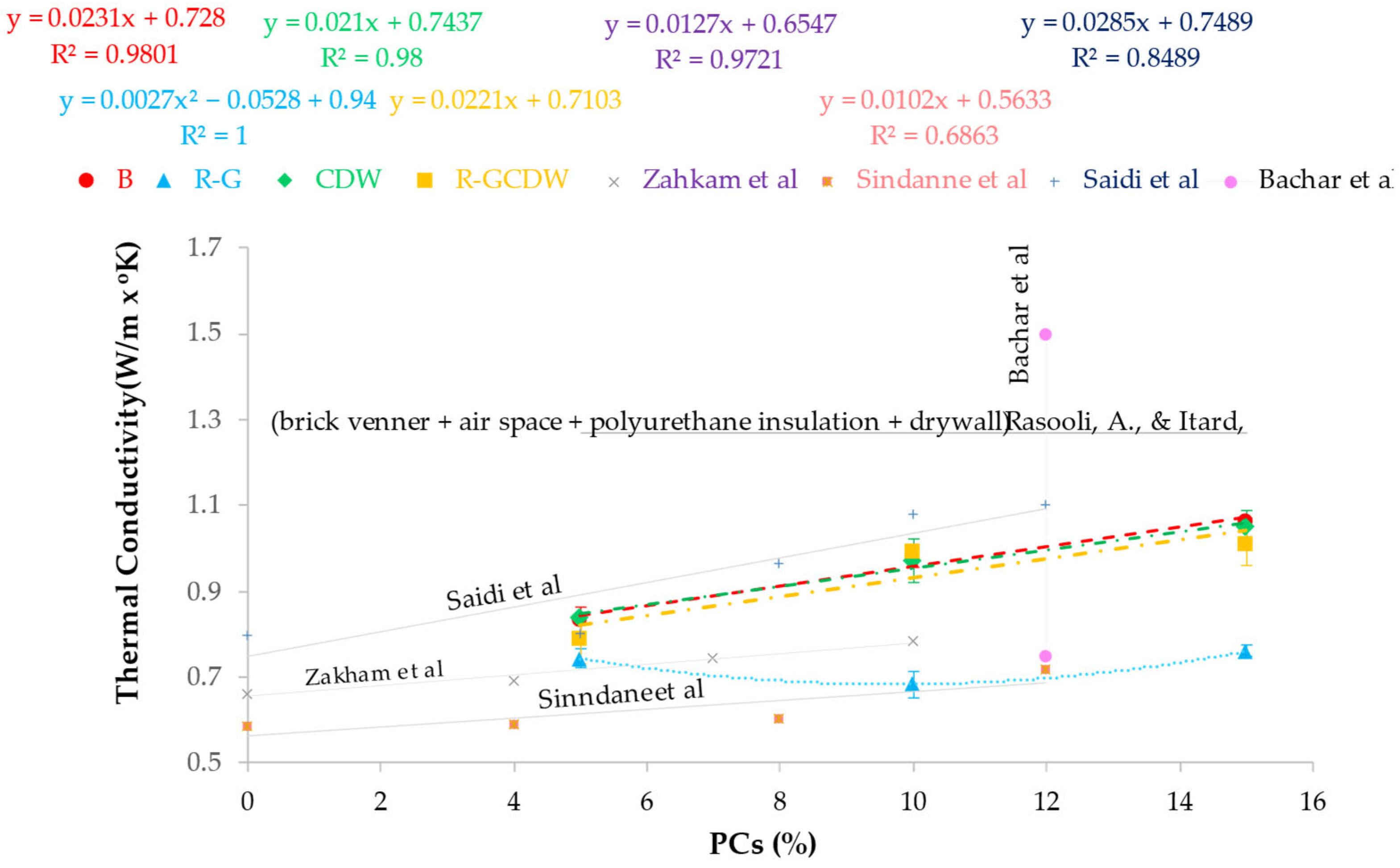



| Parameter | SCS | SWD |
|---|---|---|
| Proctor test values | 2157 kg/m3 at moisture of 12.05 (%) | 2174 kg/m3 at moisture of 13.2 (%) |
| Liquid limit (LL) | 23.55 | 20.09 |
| Plastic limit (PL) | 8.10 | 11.77 |
| Plastic index (PI) | 15.45 | 8.30 |
| Shrinkage limit (SL) | 8.30 | 5.10 |
| B5 | B10 | B15 | R-G5 | R-G10 | R-G15 | CDW5 | CDW10 | CDW15 | R-G CDW5 | R-G CDW10 | R-G CDW15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PCs 1 | 5 | 10 | 15 | 5 | 10 | 15 | 5 | 10 | 15 | 5 | 10 | 15 |
| MRS 1 | 31.6 | 36 | 31 | - | - | - | - | - | - | - | - | - |
| R-G 1 | - | - | - | 34 | 34.4 | 31 | - | - | - | 13 | 13.6 | 13.3 |
| PG 1 | 6.4 | 7 | 7 | 7 | 6 | 6.5 | - | - | - | 2.7 | 2.7 | 2.7 |
| LS 1 | 6.4 | 7 | 7 | 7 | 6 | 6.5 | - | - | - | 2.7 | 2.7 | 2.7 |
| CDW 1 | - | - | - | - | - | - | 40.2 | 39 | 36 | 18.6 | 19 | 18.6 |
| SCS 2 | 19.3 | 15 | 15 | 19 | 17.3 | 16 | 20.4 | 19 | 18 | 23 | 20 | 17.6 |
| SDW 2 | 19.3 | 15 | 15 | 19 | 17.3 | 16 | 20.4 | 19 | 18 | 23 | 20 | 17.6 |
| Water 2 | 12 | 10 | 10 | 9 | 9 | 9 | 14 | 13 | 13 | 12 | 12 | 12.5 |
| Matrix/ Batch | Weight (kg) at T2 | V (cm3) at T2 | Density (kg/m3) | AP (%) | CiW (%) T1-T2 | CiV (%) T1-T2 | Abs Coeff10 | SCT (MPa) | MoE (GPa) | TC (W/m·K) |
|---|---|---|---|---|---|---|---|---|---|---|
| B5 | 9.98 | 5042 | 1979 | 17.1 | −8.66 | −0.8 | 13.6 | 5.1 | 2.4 | 0.834 |
| B10 | 10.99 | 5688 | 1932 | 15.7 | −4.74 | −0.8 | 41.5 | 4.5 | 3.7 | 0.978 |
| B15 | 10.92 | 5489 | 1989 | 14.2 | −4.88 | −0.4 | 9.7 | 6.2 | 8.4 | 1.065 |
| R-G5 | 10.79 | 5666 | 1906 | 18.5 | −4.87 | −0.2 | 38.2 | 7.0 | 3.3 | 0.744 |
| R-G10 | 10.72 | 5752 | 1864 | 17.0 | −5.33 | −0.7 | 33.0 | 5.6 | 3.7 | 0.684 |
| R-G15 | 10.88 | 5674 | 1918 | 17.6 | −4.18 | −0.3 | 22.7 | 7.2 | 4.9 | 0.760 |
| CDW5 | 9.13 | 4916 | 1858 | 22.4 | −9.94 | −0.8 | 11.1 | 6.5 | 1.5 | 0.840 |
| CDW10 | 9.59 | 4976 | 1928 | 19.2 | −7.27 | −1.0 | 8.0 | 7.2 | 7.3 | 0.971 |
| CDW15 | 10.44 | 5408 | 1931 | 18.6 | −6.05 | −0.4 | 8.1 | 7.3 | 6.6 | 1.050 |
| R-GCDW5 | 9.89 | 5153 | 1920 | 15.3 | −7.40 | −0.9 | 16.4 | 6.0 | 1.5 | 0.789 |
| R-GCDW10 | 10.82 | 5567 | 1945 | 17.4 | −5.13 | −0.2 | 12.2 | 6.6 | 6.2 | 0.995 |
| R-GCDW15 | 11.10 | 5693 | 1951 | 16.5 | −4.48 | −0.1 | 12.5 | 7.3 | 8.5 | 1.010 |
| CPCs Coefficients for the Properties of the R-GCDW | |||
|---|---|---|---|
| PCs Matrix | SCT | MoE | TC |
| PCs 5 | 0.168 | 0.054 | 1.267 |
| PCs 10 | 0.185 | 0.223 | 1.598 |
| PCs 15 | 0.204 | 0.306 | 1.622 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reyna-Ruiz, C.; Gómez-Soberón, J.M.; Rojas-Valencia, M.N. Characterization of the Physical, Mechanical, and Thermal Properties of Cement and Compressed Earth Stabilized Blocks, Incorporating Closed-Loop Materials for Use in Hot and Humid Climates. Buildings 2025, 15, 2891. https://doi.org/10.3390/buildings15162891
Reyna-Ruiz C, Gómez-Soberón JM, Rojas-Valencia MN. Characterization of the Physical, Mechanical, and Thermal Properties of Cement and Compressed Earth Stabilized Blocks, Incorporating Closed-Loop Materials for Use in Hot and Humid Climates. Buildings. 2025; 15(16):2891. https://doi.org/10.3390/buildings15162891
Chicago/Turabian StyleReyna-Ruiz, Catalina, José Manuel Gómez-Soberón, and María Neftalí Rojas-Valencia. 2025. "Characterization of the Physical, Mechanical, and Thermal Properties of Cement and Compressed Earth Stabilized Blocks, Incorporating Closed-Loop Materials for Use in Hot and Humid Climates" Buildings 15, no. 16: 2891. https://doi.org/10.3390/buildings15162891
APA StyleReyna-Ruiz, C., Gómez-Soberón, J. M., & Rojas-Valencia, M. N. (2025). Characterization of the Physical, Mechanical, and Thermal Properties of Cement and Compressed Earth Stabilized Blocks, Incorporating Closed-Loop Materials for Use in Hot and Humid Climates. Buildings, 15(16), 2891. https://doi.org/10.3390/buildings15162891