Study on the Bearing Characteristics of a Novel Inner Support Structure for Deep Foundation Pits Based on Full-Scale Experiments
Abstract
1. Introduction
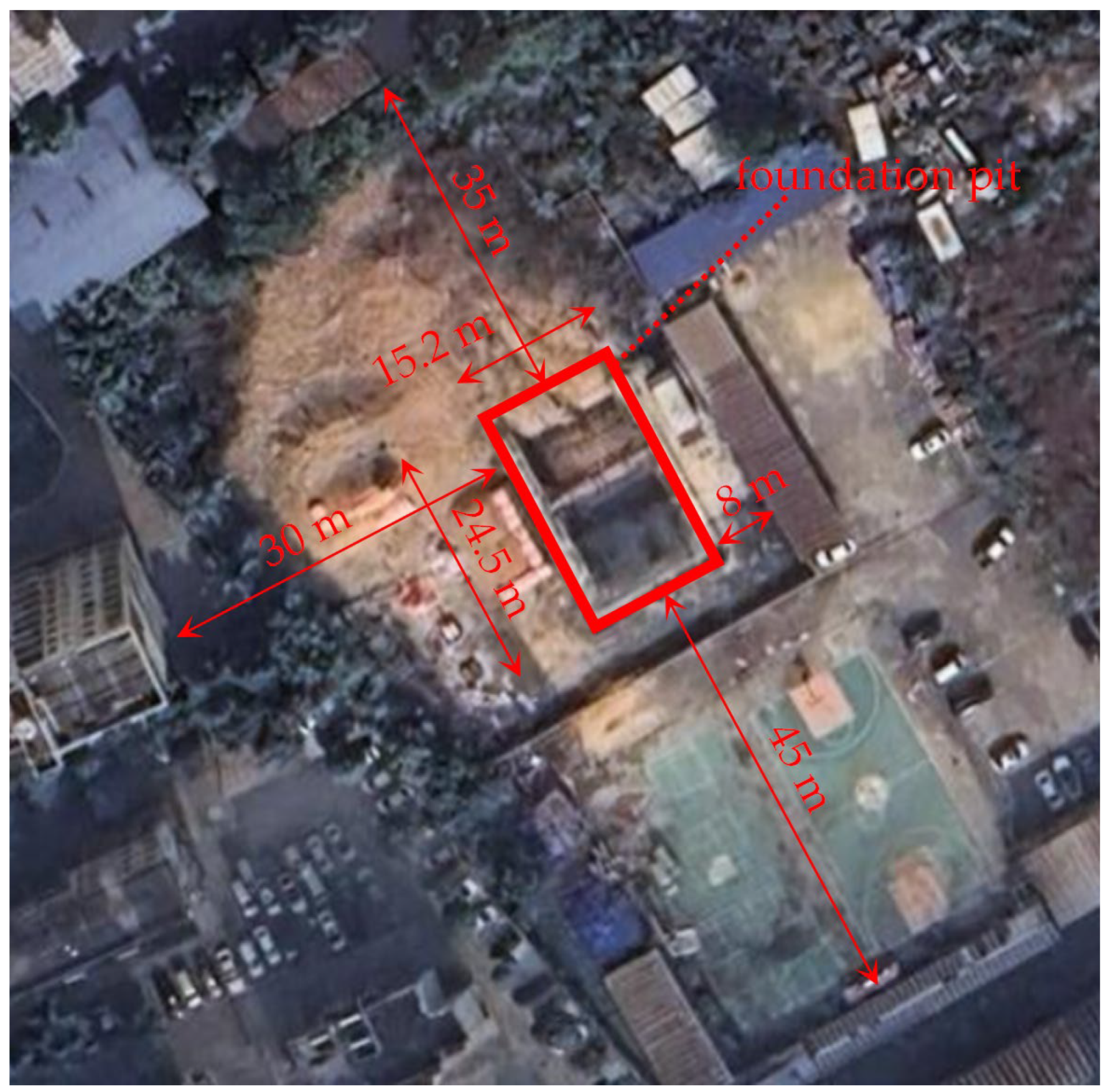
2. Structure and Experimental Program
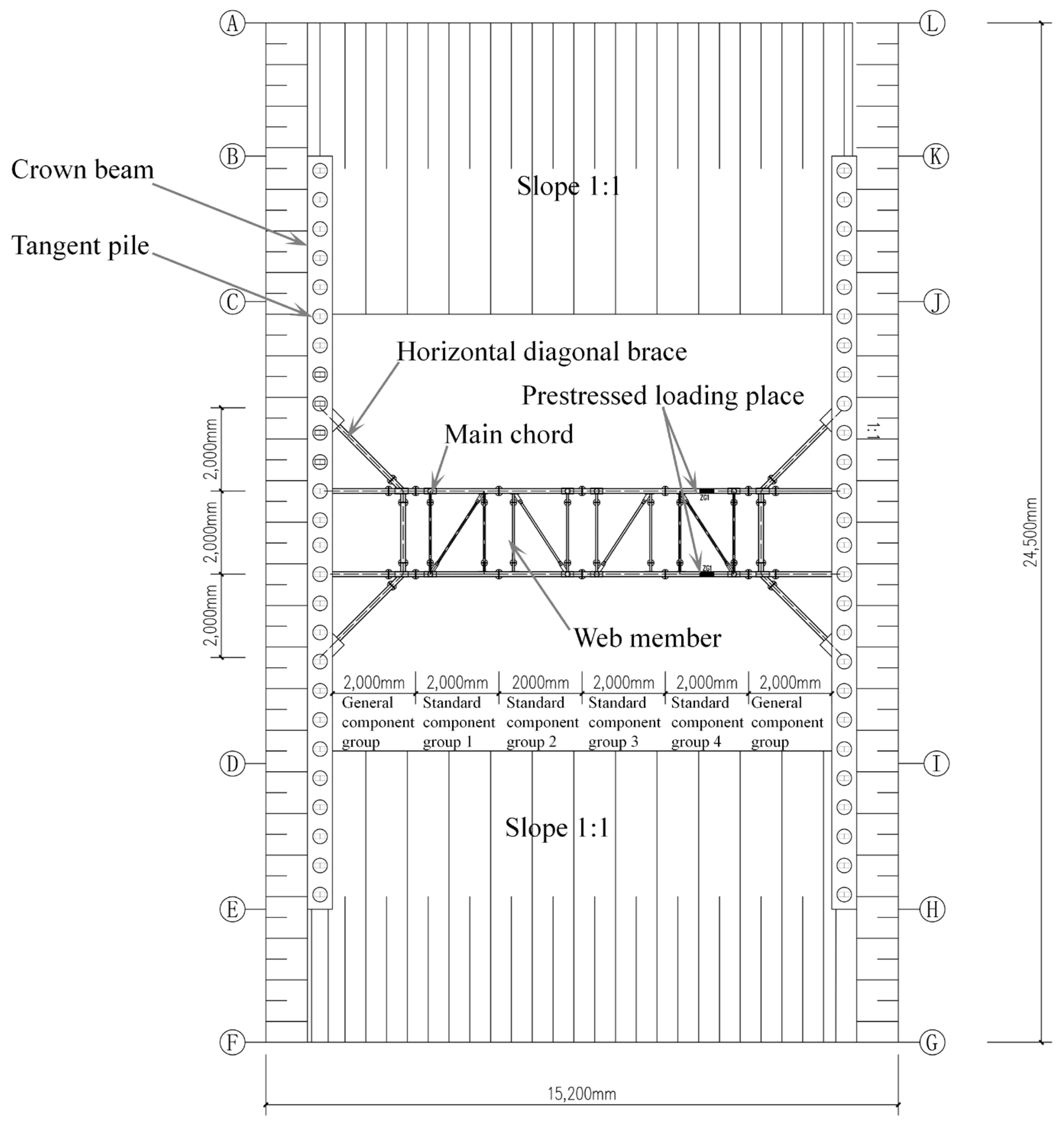
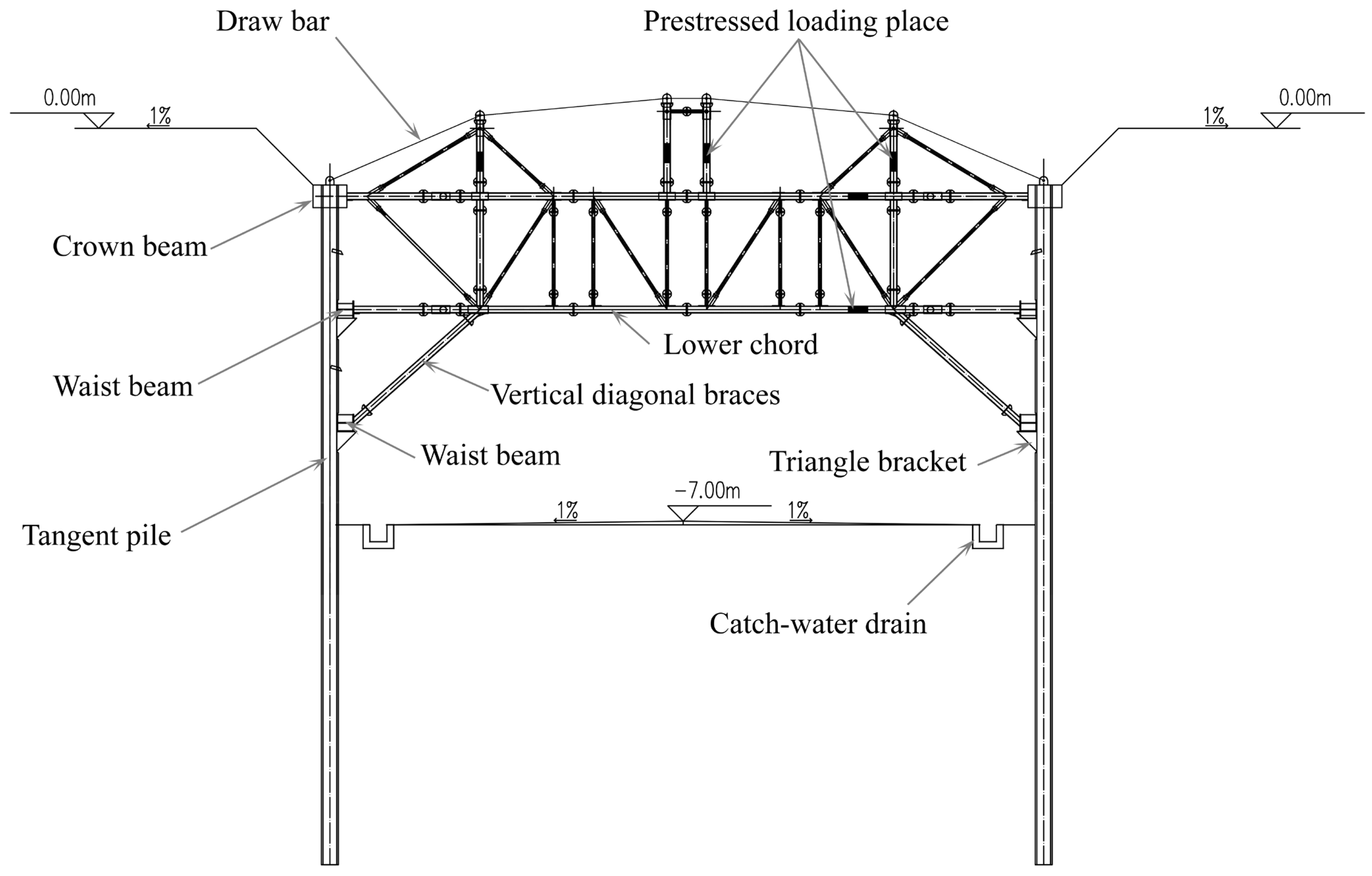
2.1. Structural System
2.1.1. Structure Composition
2.1.2. The Force Transmission Path
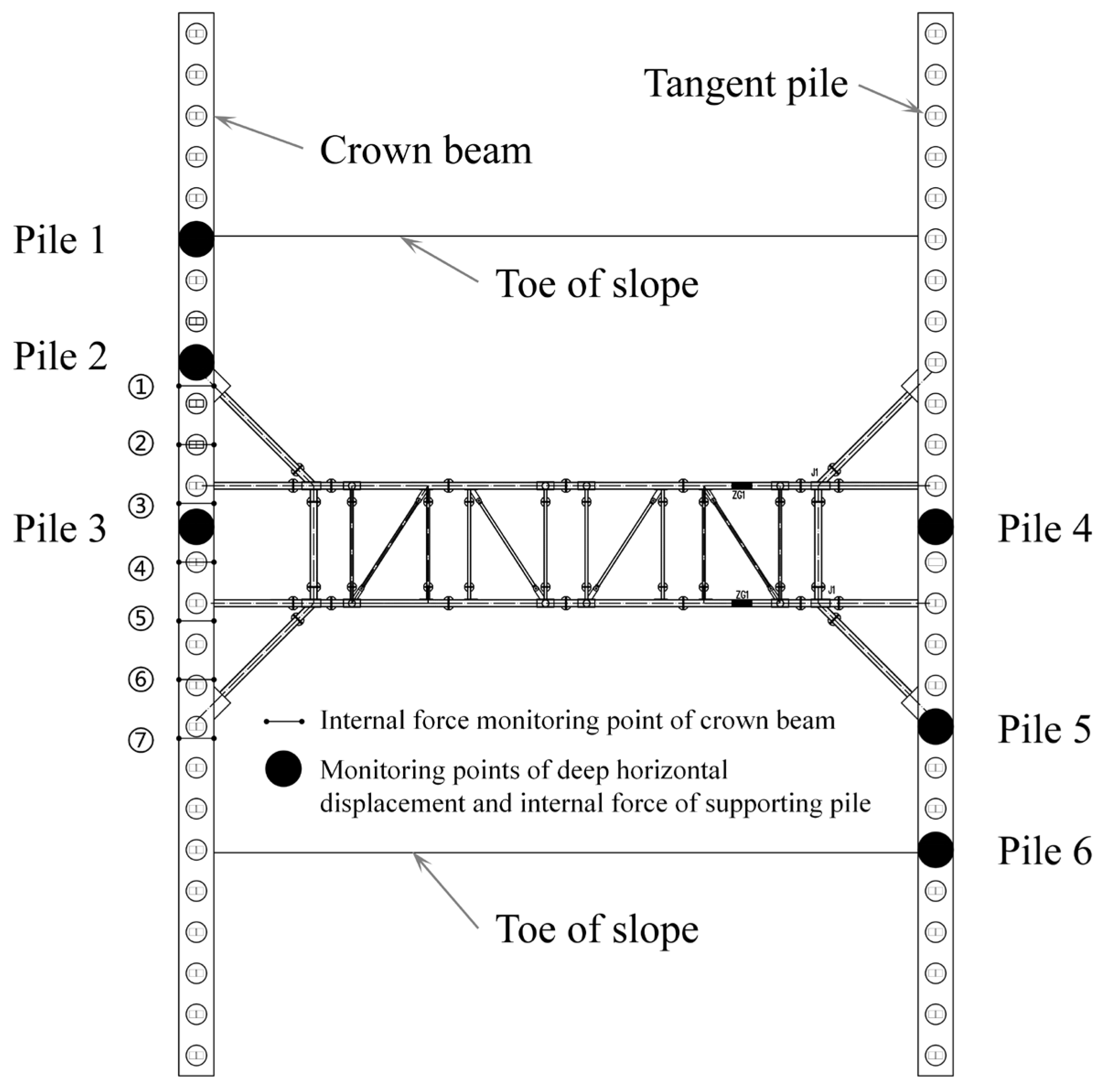
2.2. Experiment Procedure and Monitoring
- Construct a support pile and a crown beam;
- Excavate the site elevation to −4 m and install the internal support;
- The first application of horizontal prestress (winding bar: 30 kN; lower chord: 60 kN);
- Excavate the site elevation to −6 m, install the second waist beam, and use inclined support;
- The second application of horizontal prestress (winding bar: 60 kN; lower chord: 120 kN);
- The overall site elevation is excavated to −7 m;
- Vertical prestressing (40 kN).
2.3. Derivation of Stiffness Calculation Formula
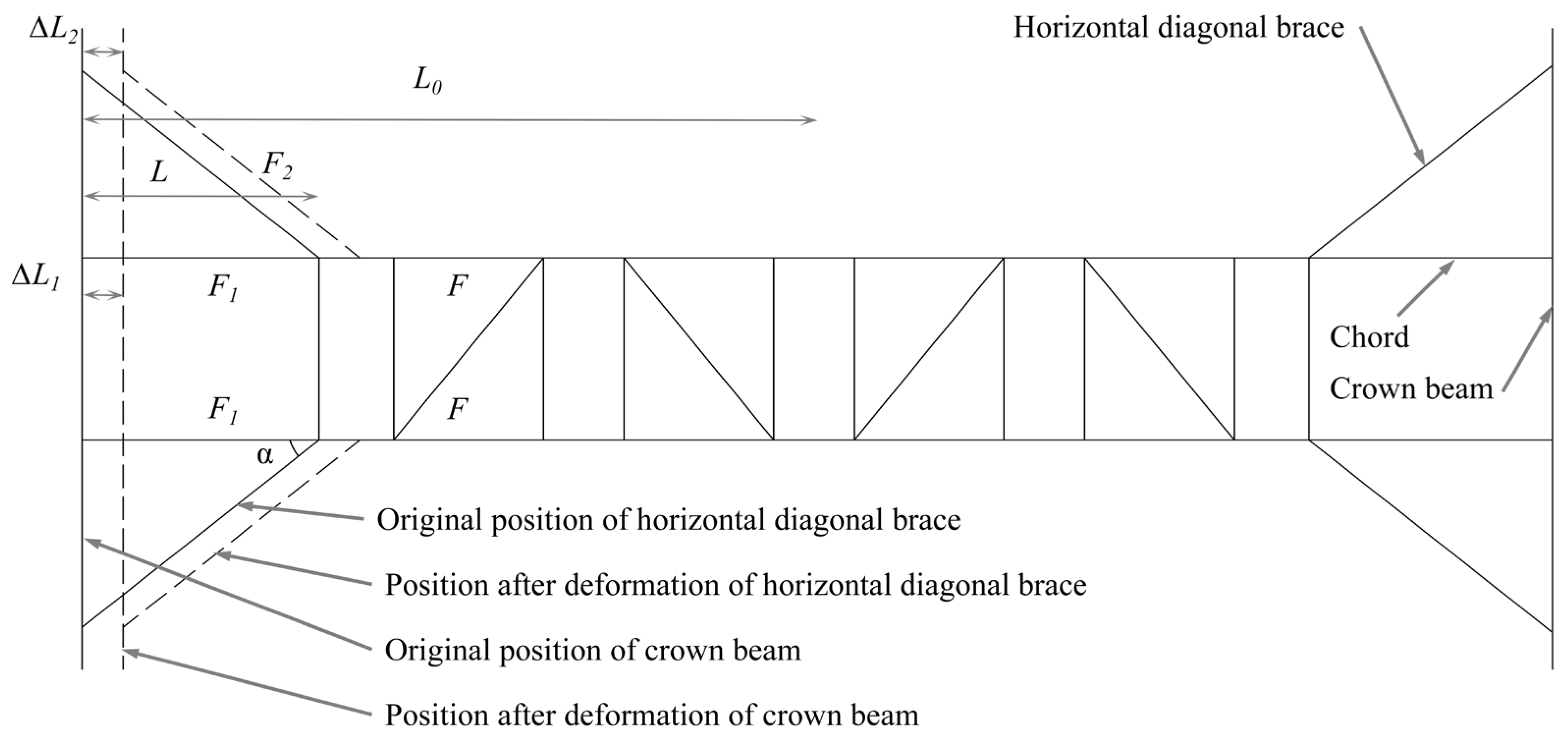
2.3.1. Derivation of Stiffness Formula of Non-Vertical Diagonal Brace
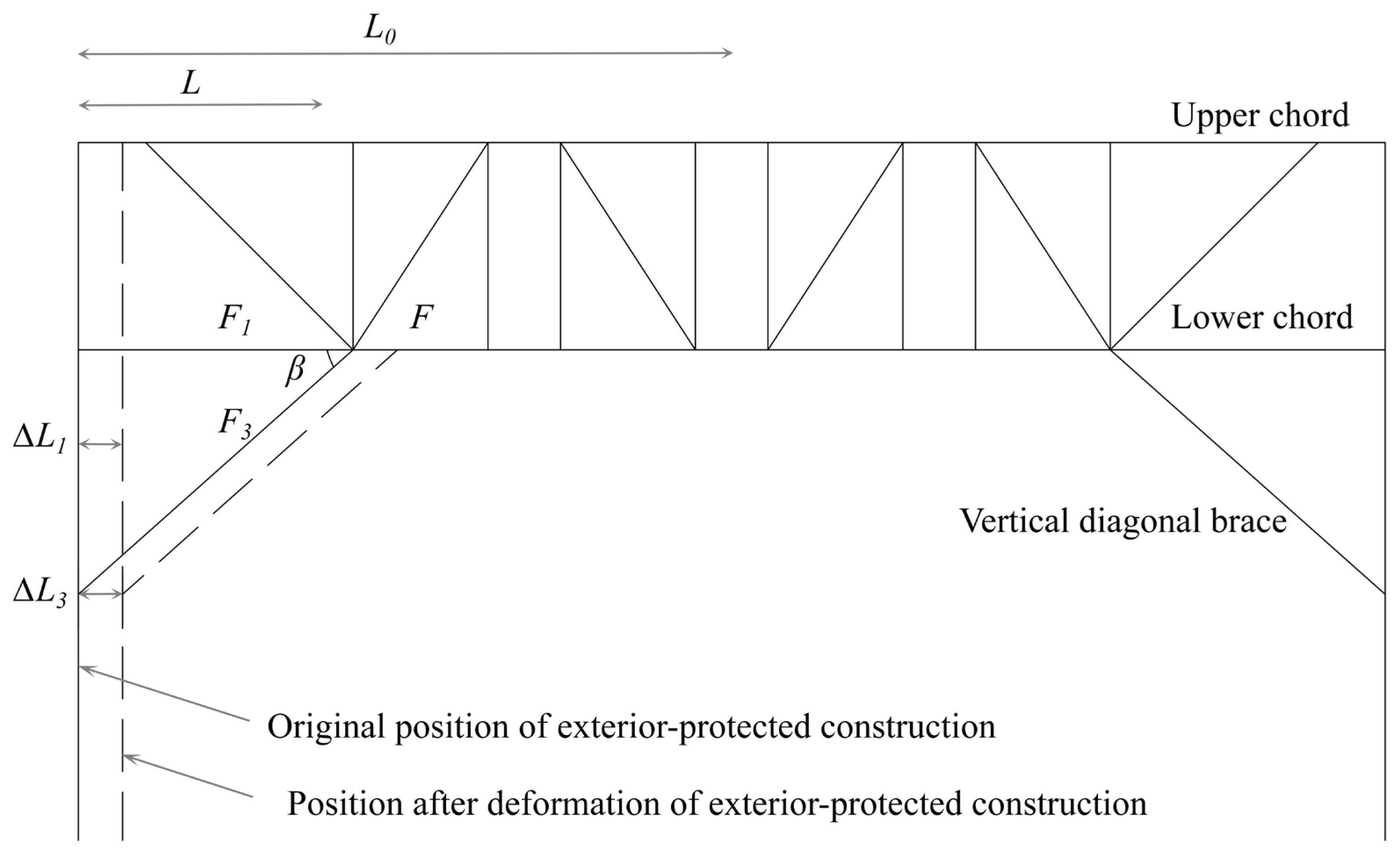
2.3.2. Derivation of Stiffness Formula of Steel Truss with Vertical Diagonal Brace
2.3.3. Rationality Analysis of Stiffness Formula
3. Results and Analysis
3.1. Supporting Piles
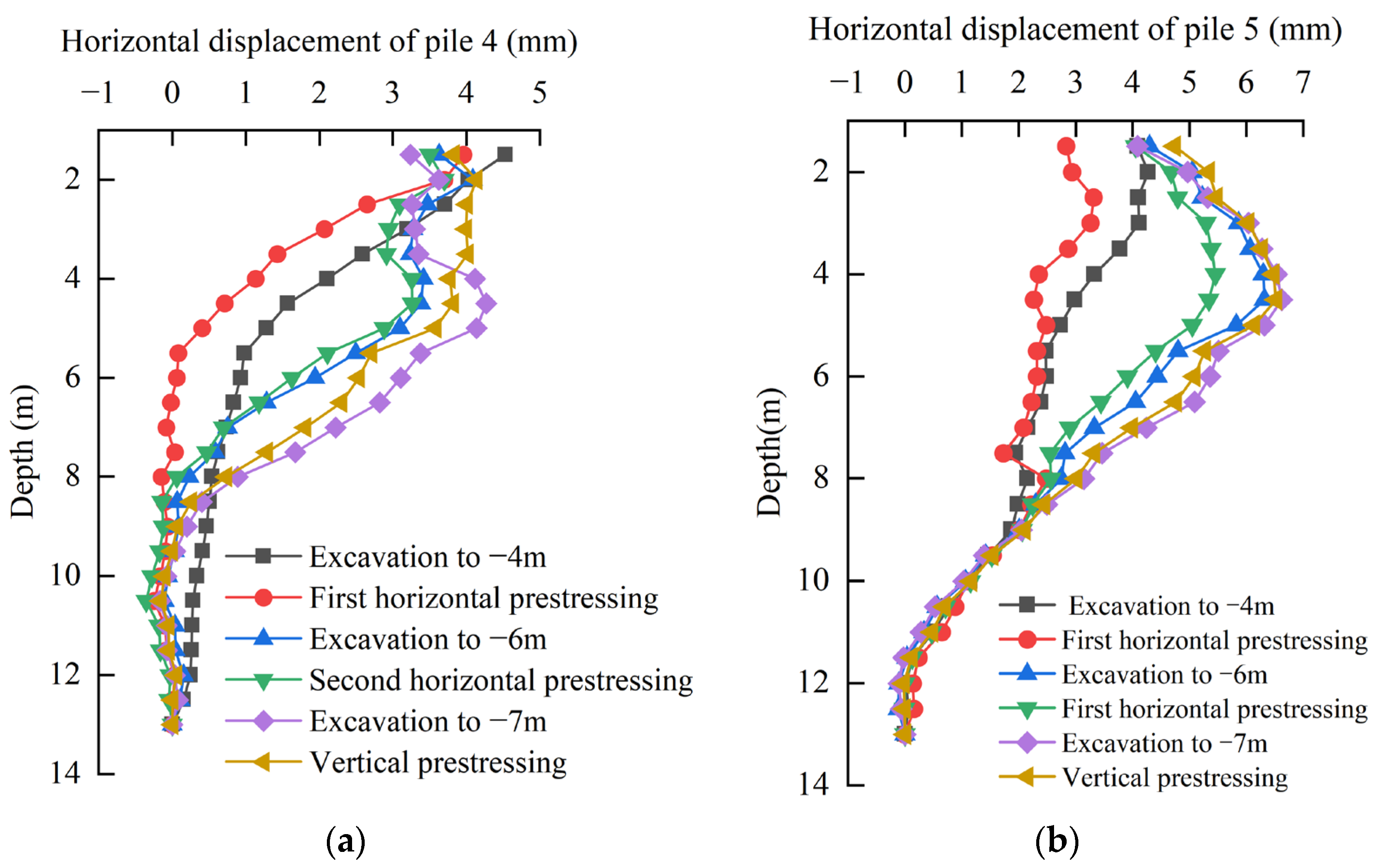
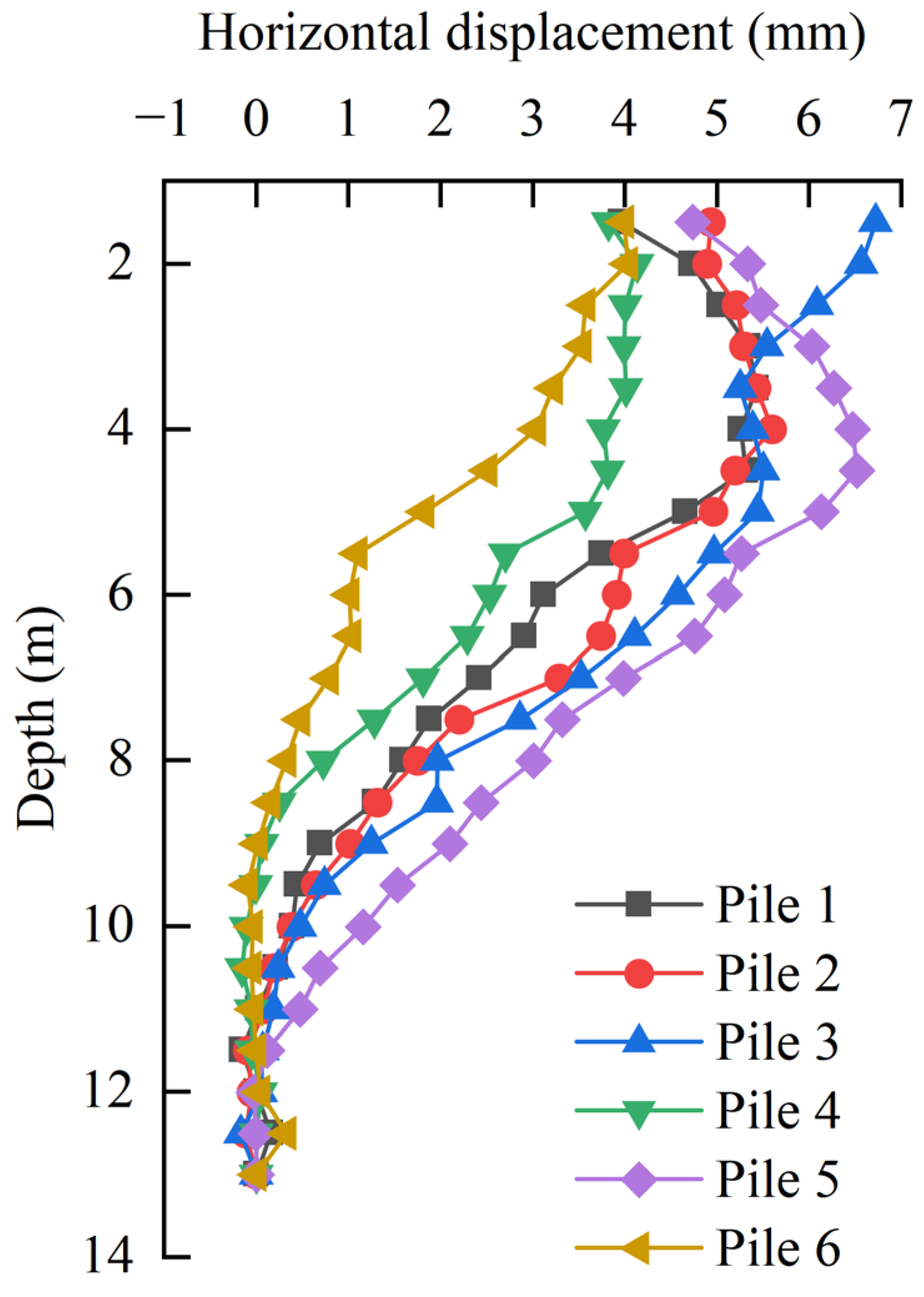
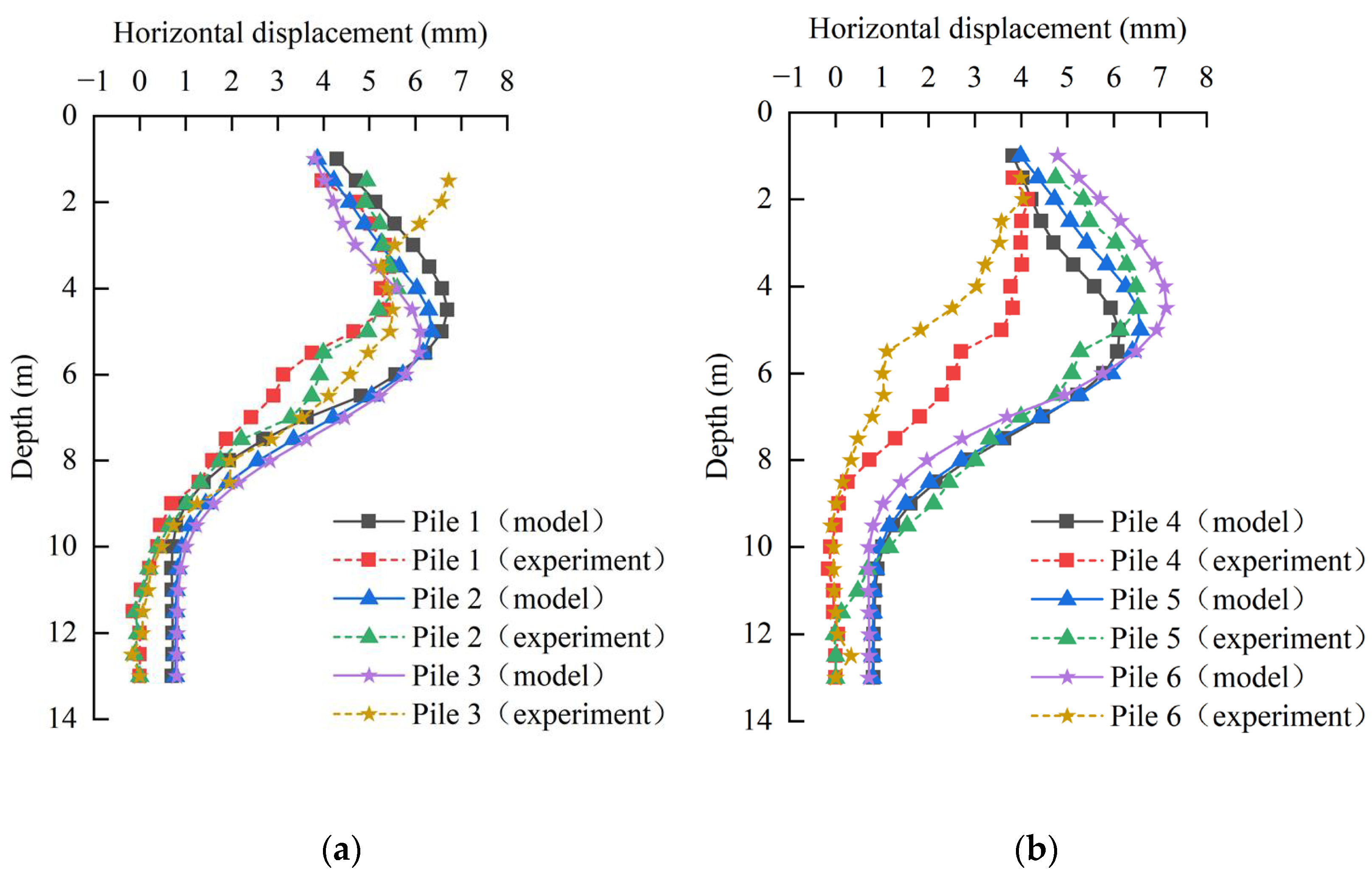
3.1.1. Displacement
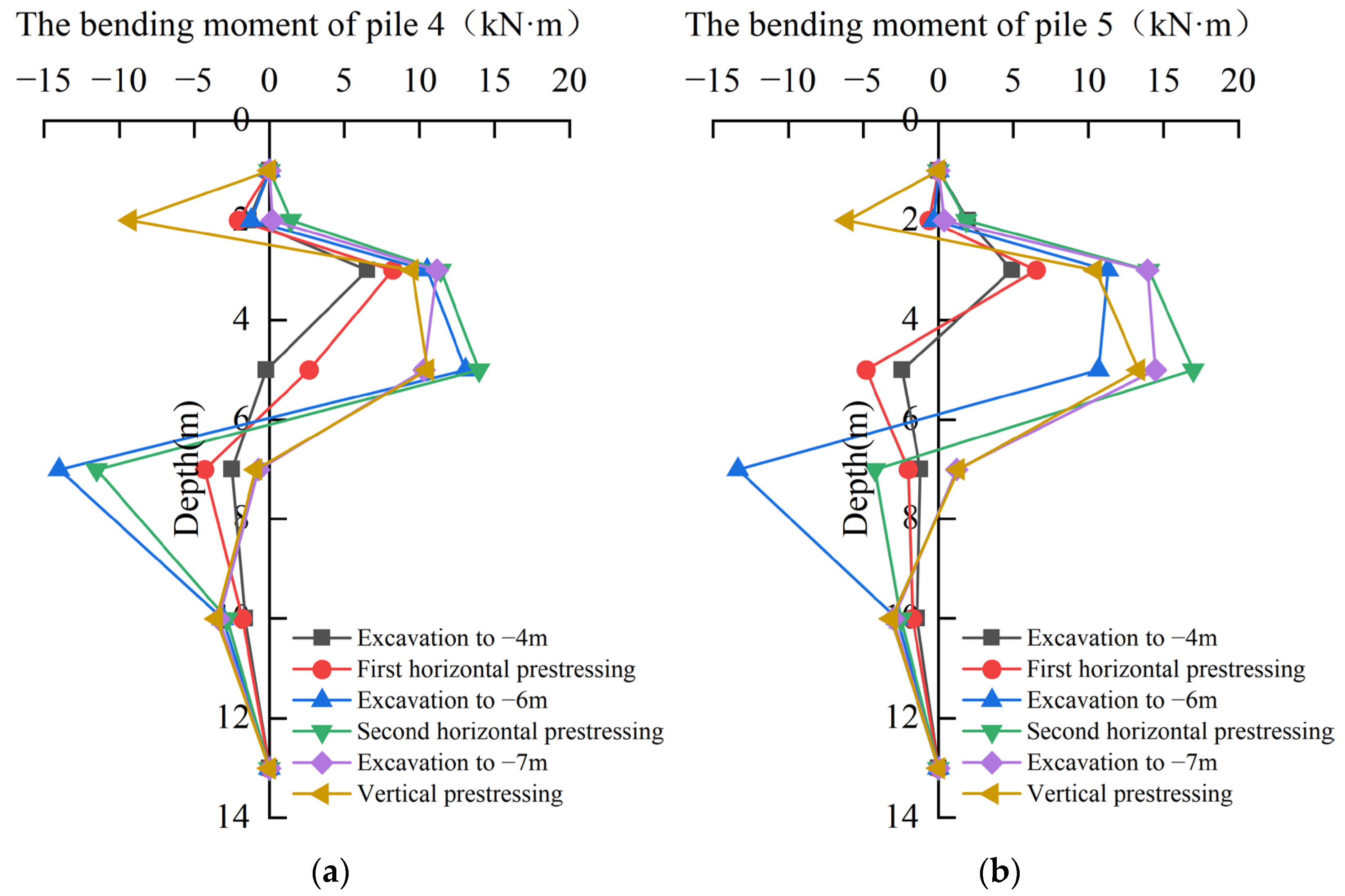
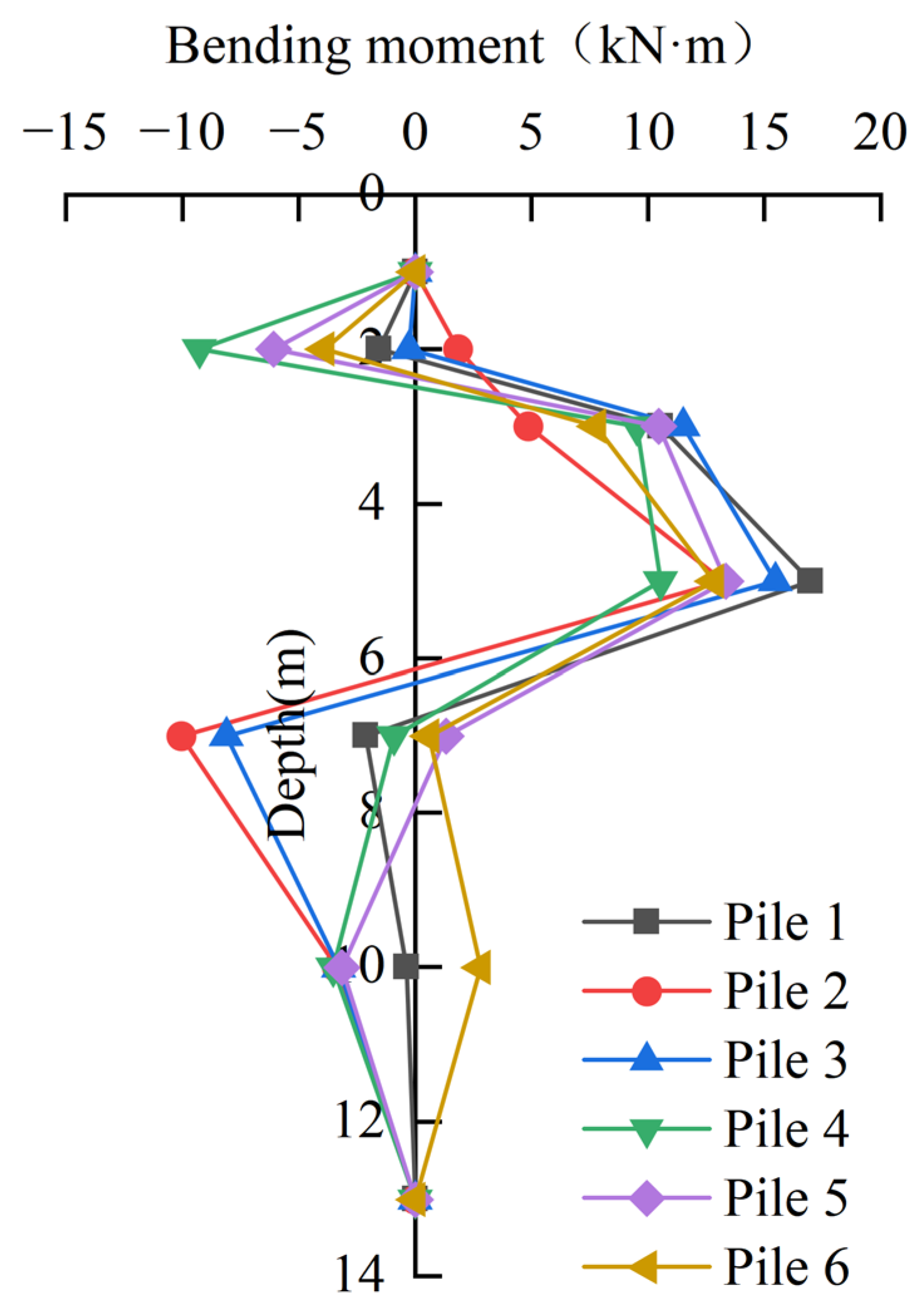
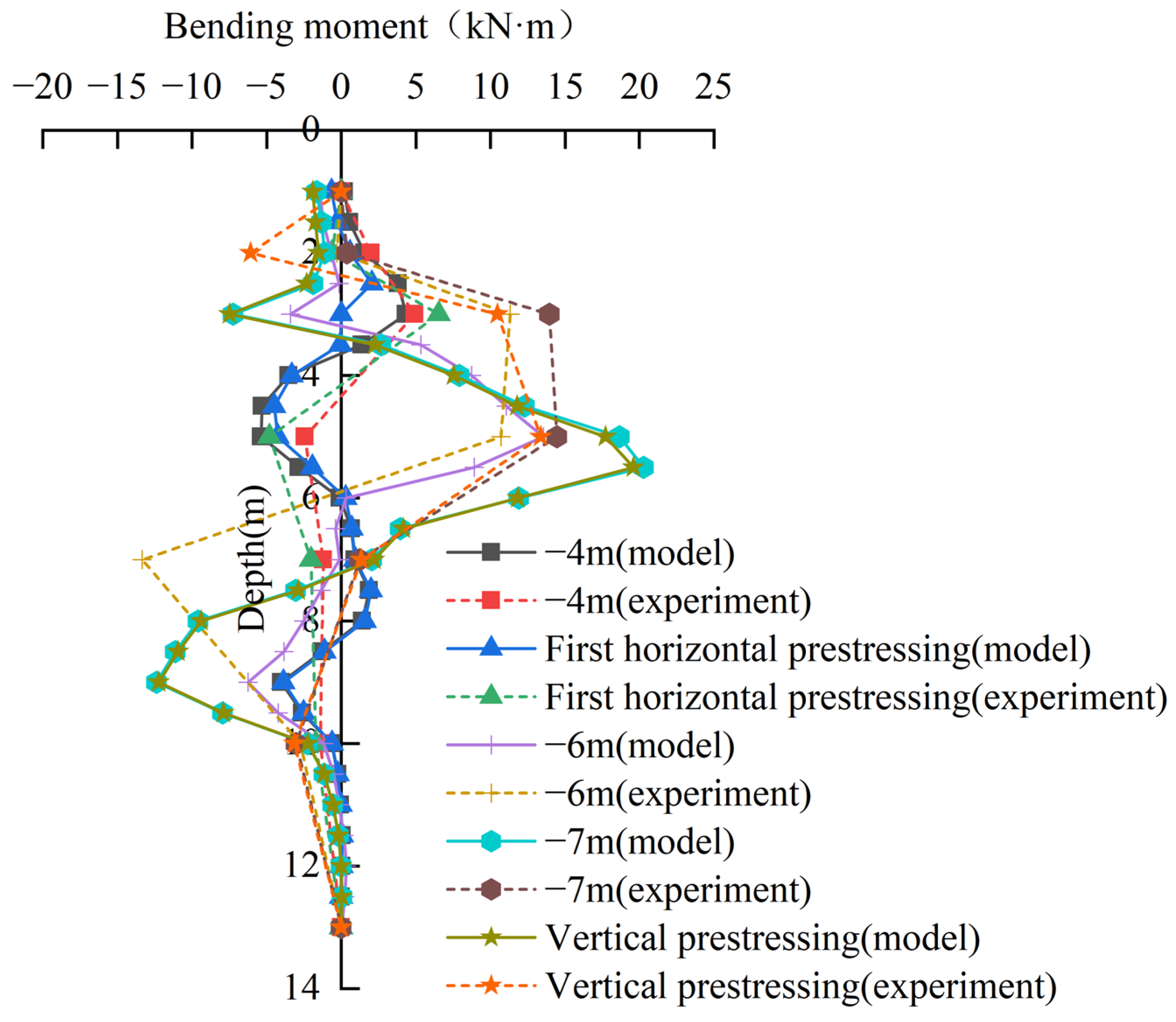
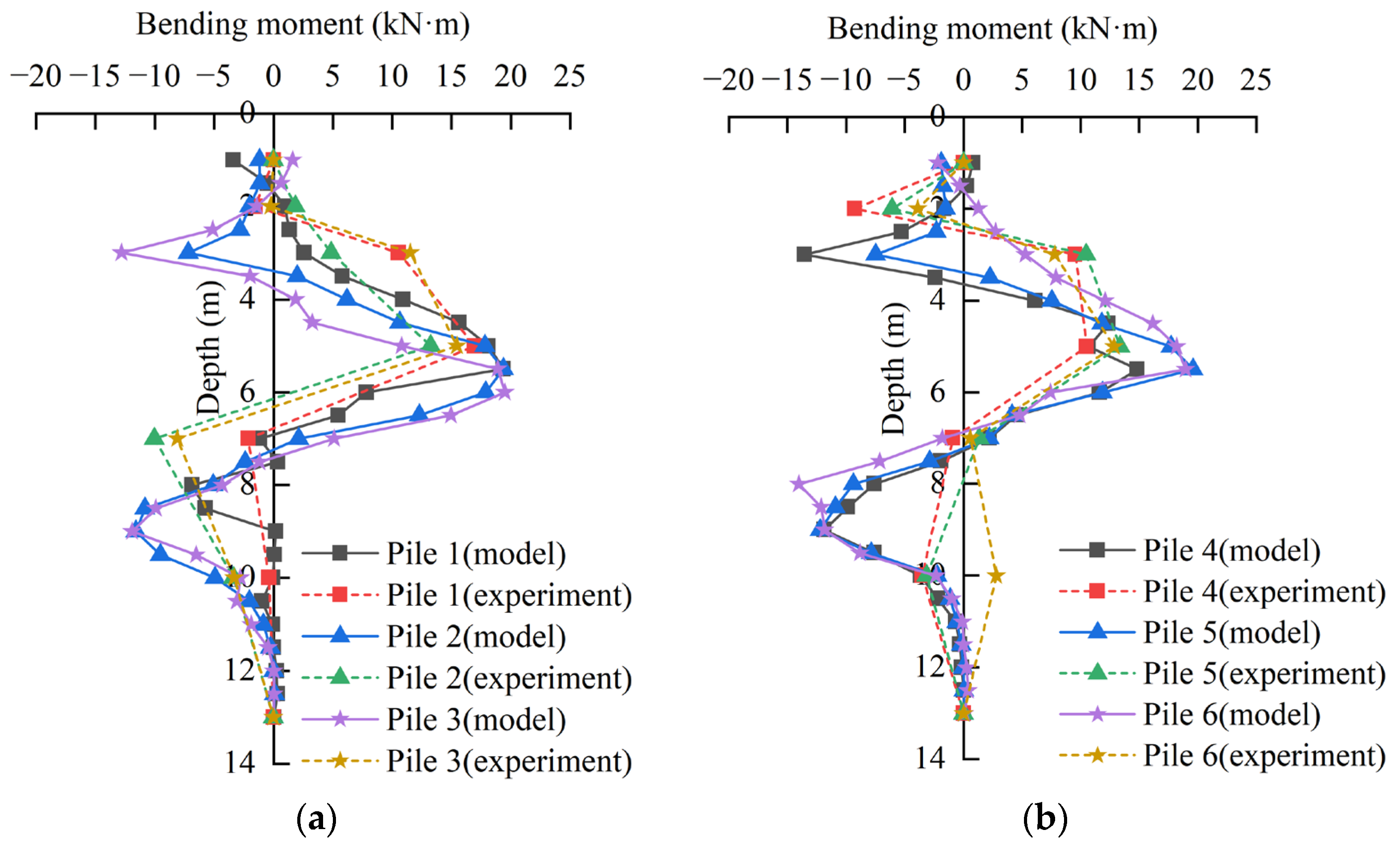
3.1.2. Bending Moment
3.2. Crown Beam
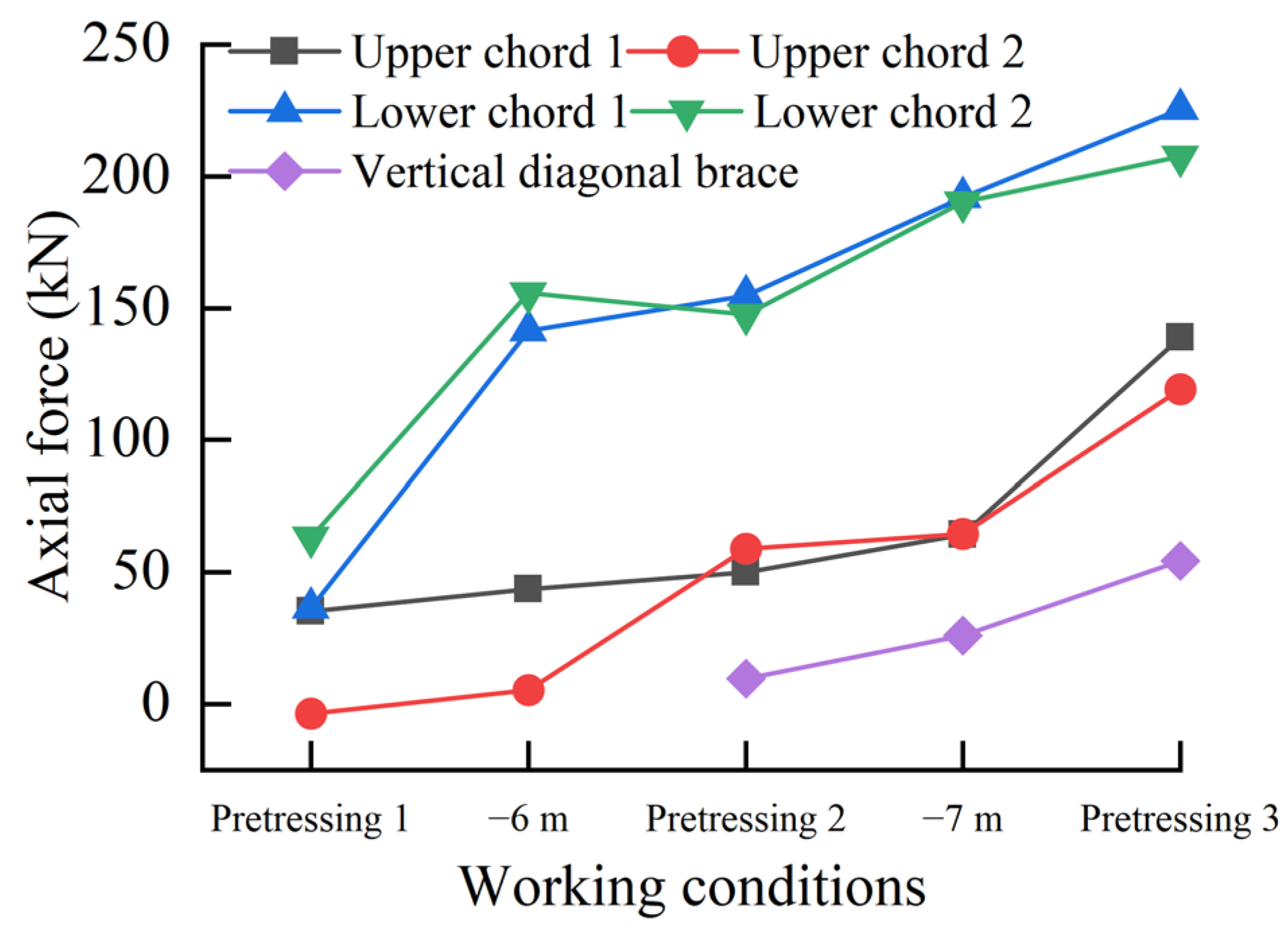
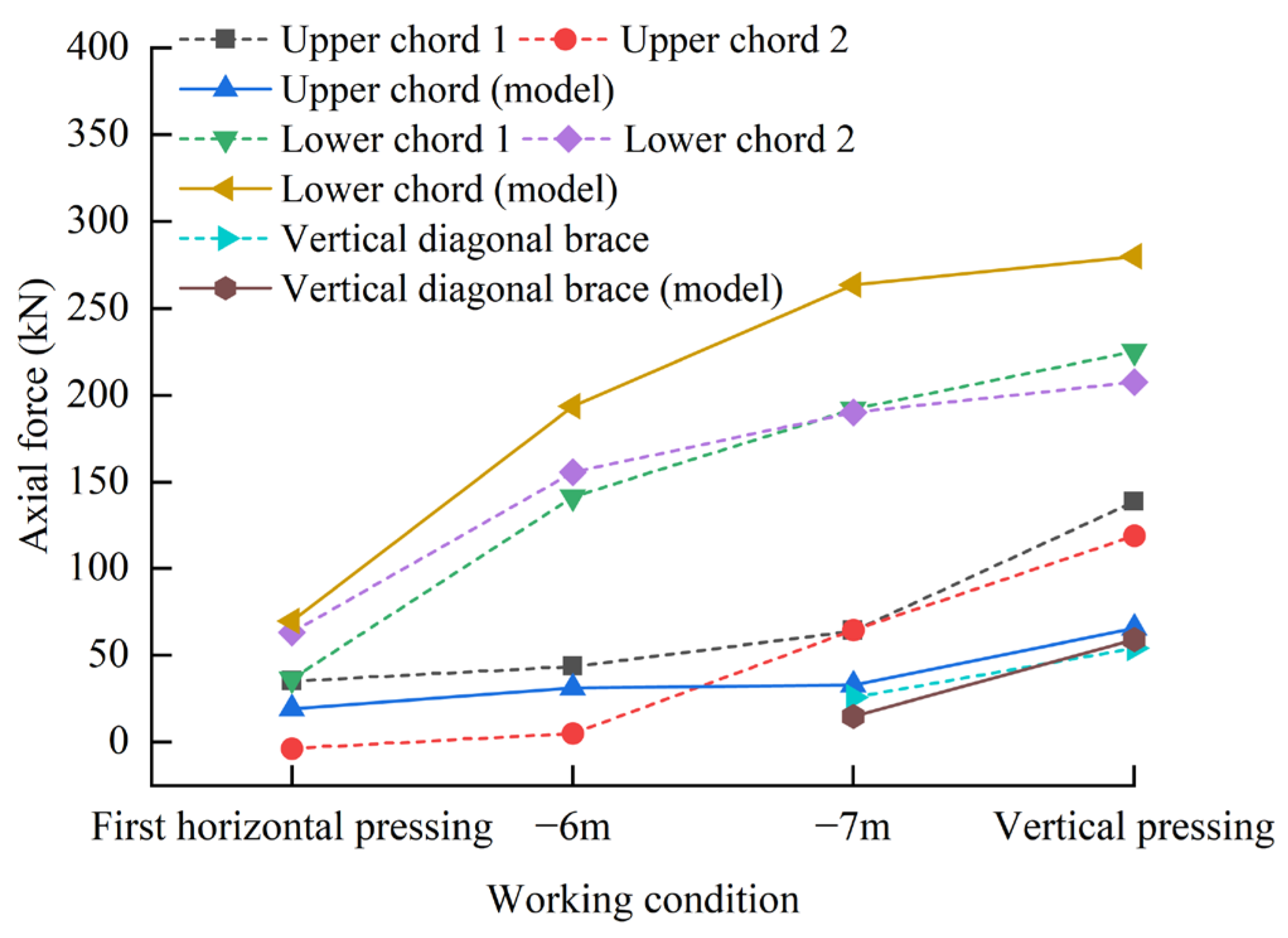
3.2.1. Axial Force
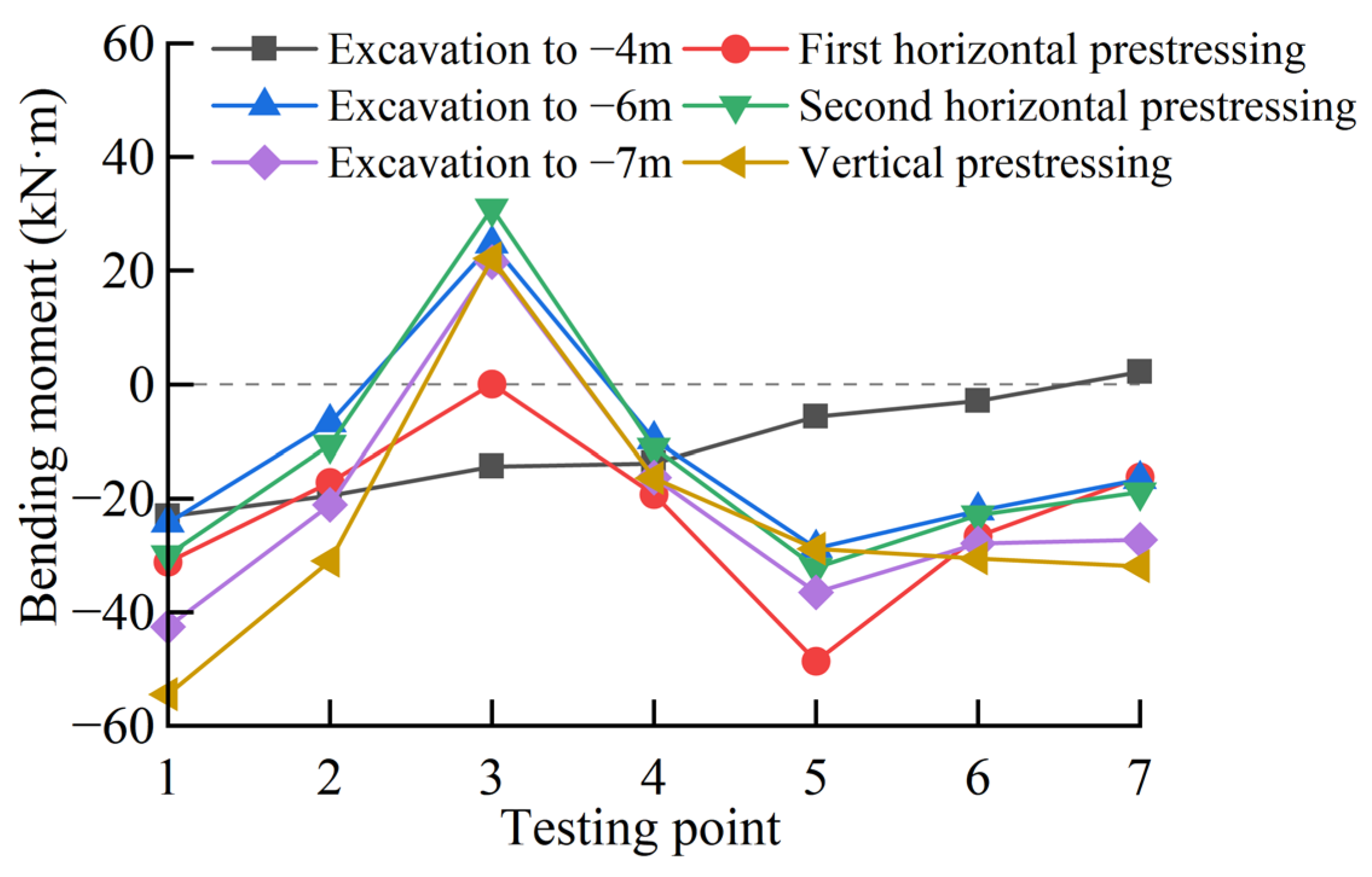
3.2.2. Bending Moment
3.3. Comparative Analysis of Numerical Simulation Results and Measured Results
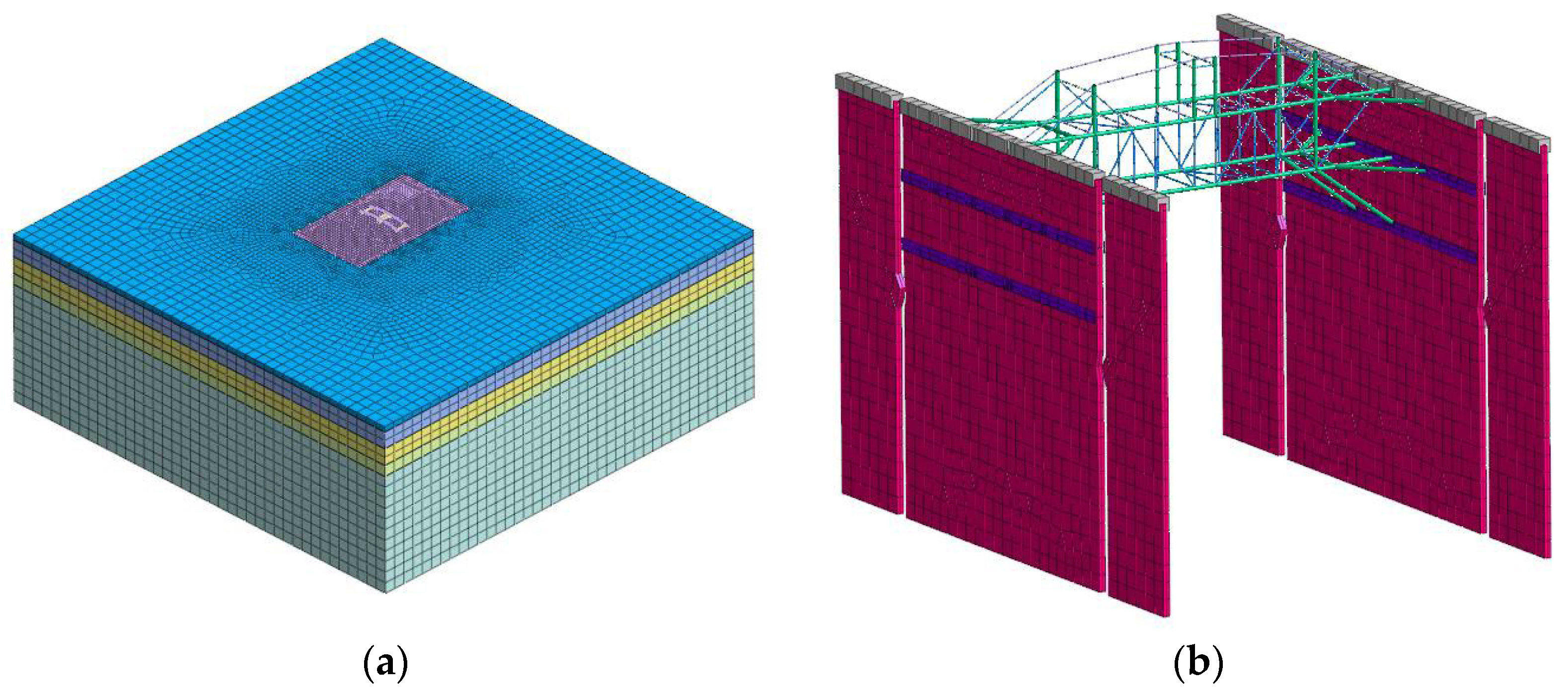
3.3.1. Modeling Methodology
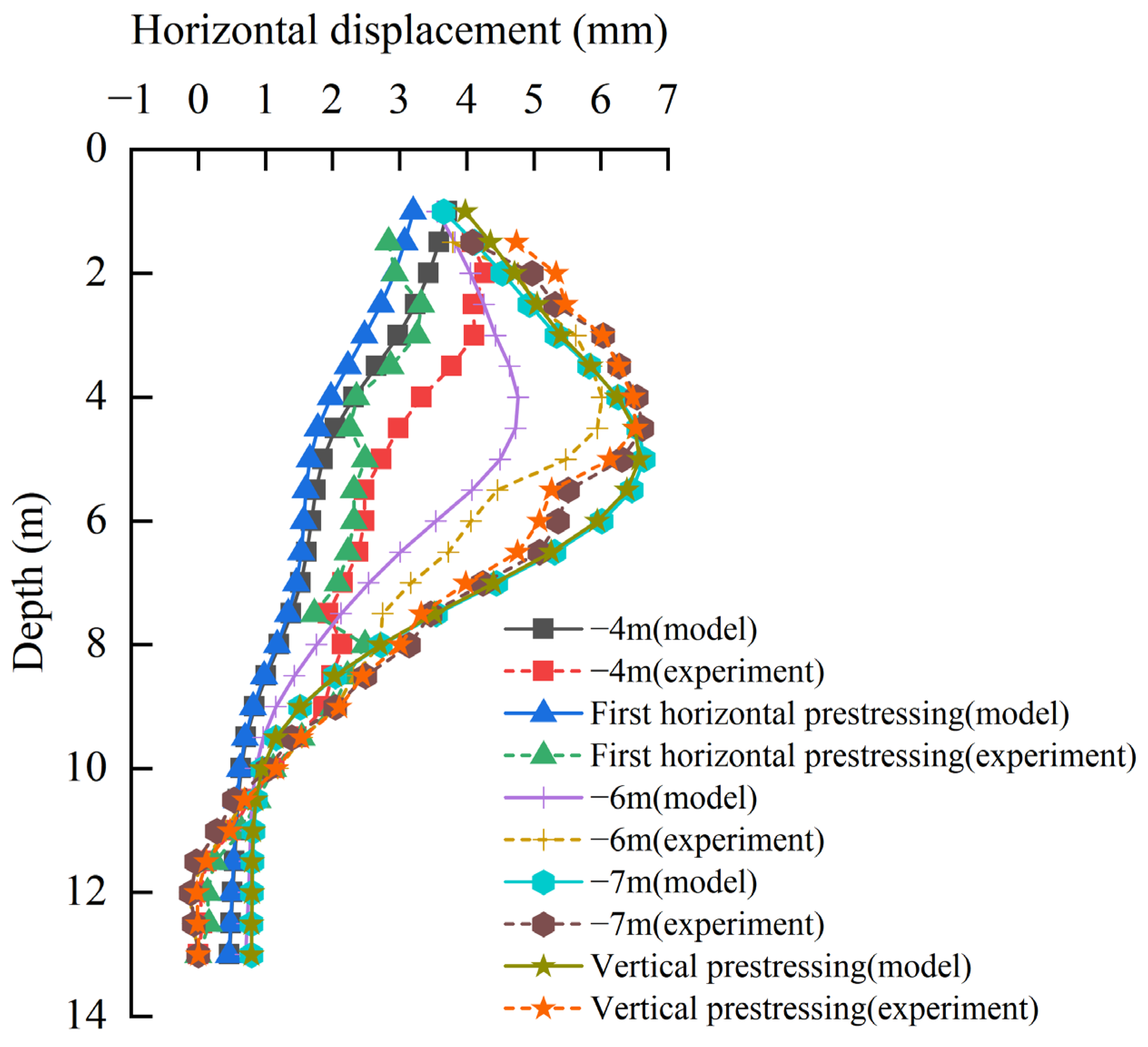
3.3.2. Comparative Analysis of Horizontal Displacement
3.3.3. Comparative Analysis of Bending Moment
3.3.4. Comparative Analysis of Steel Support Axial Force
3.3.5. Future Prospects
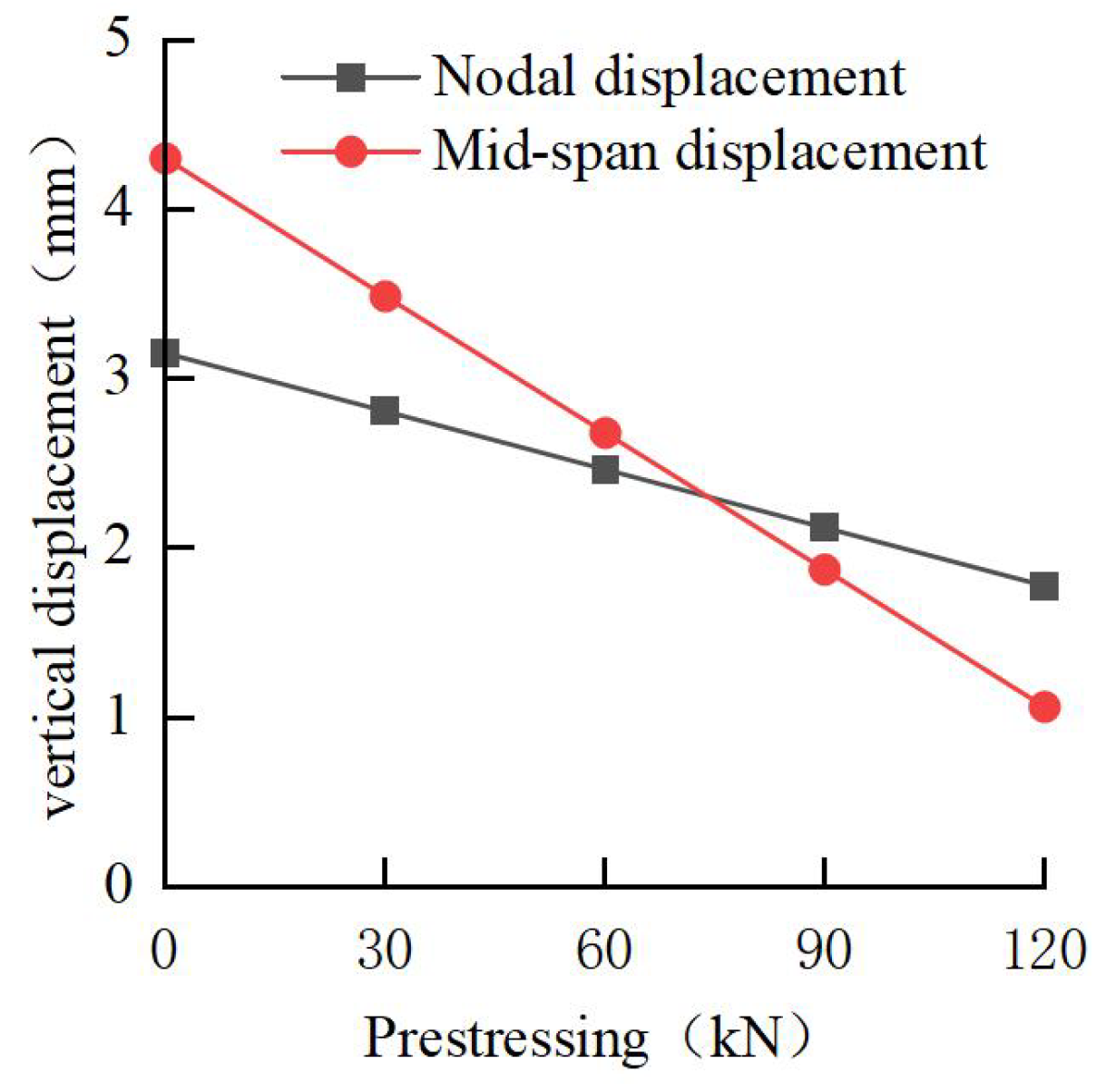
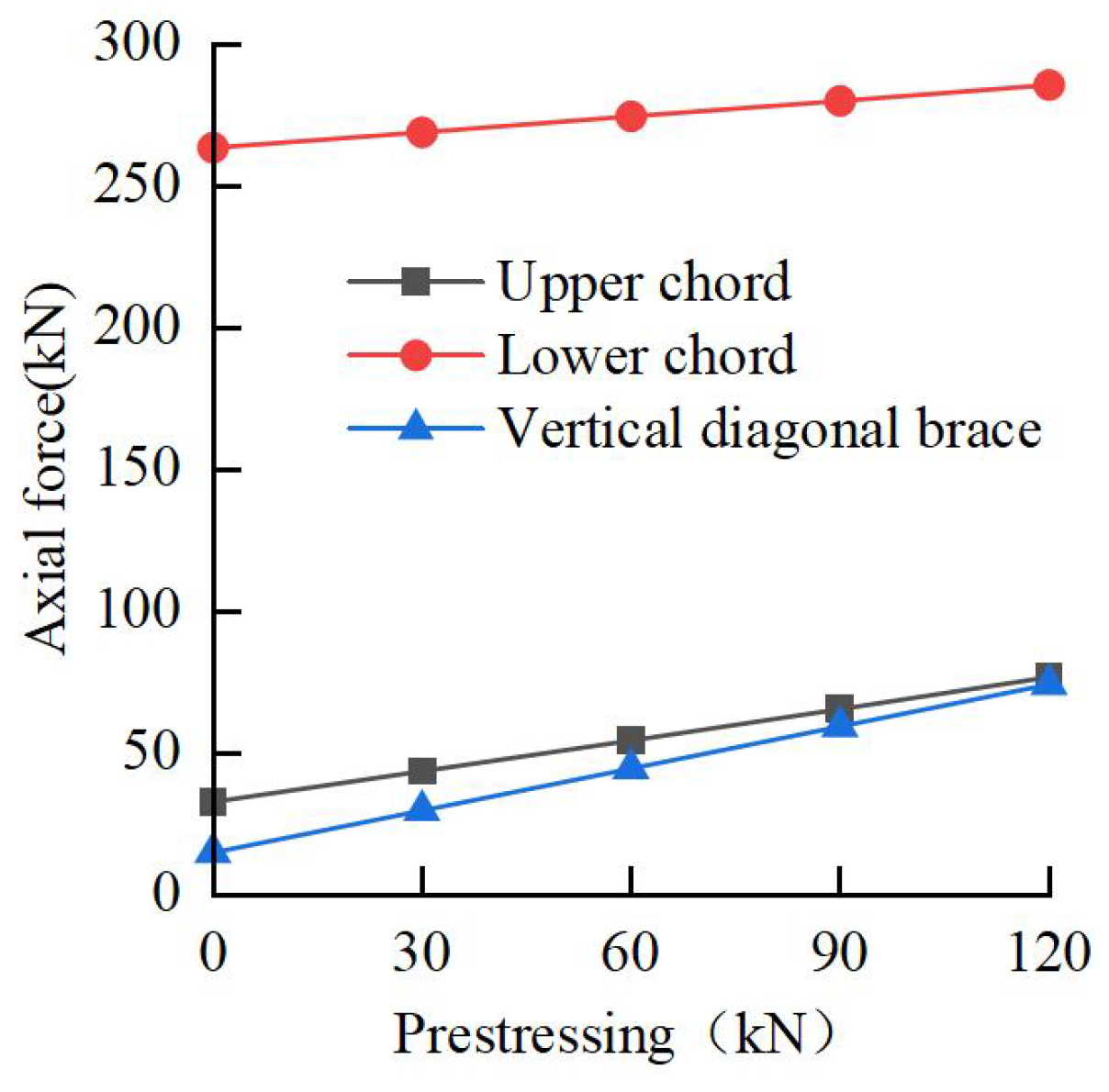
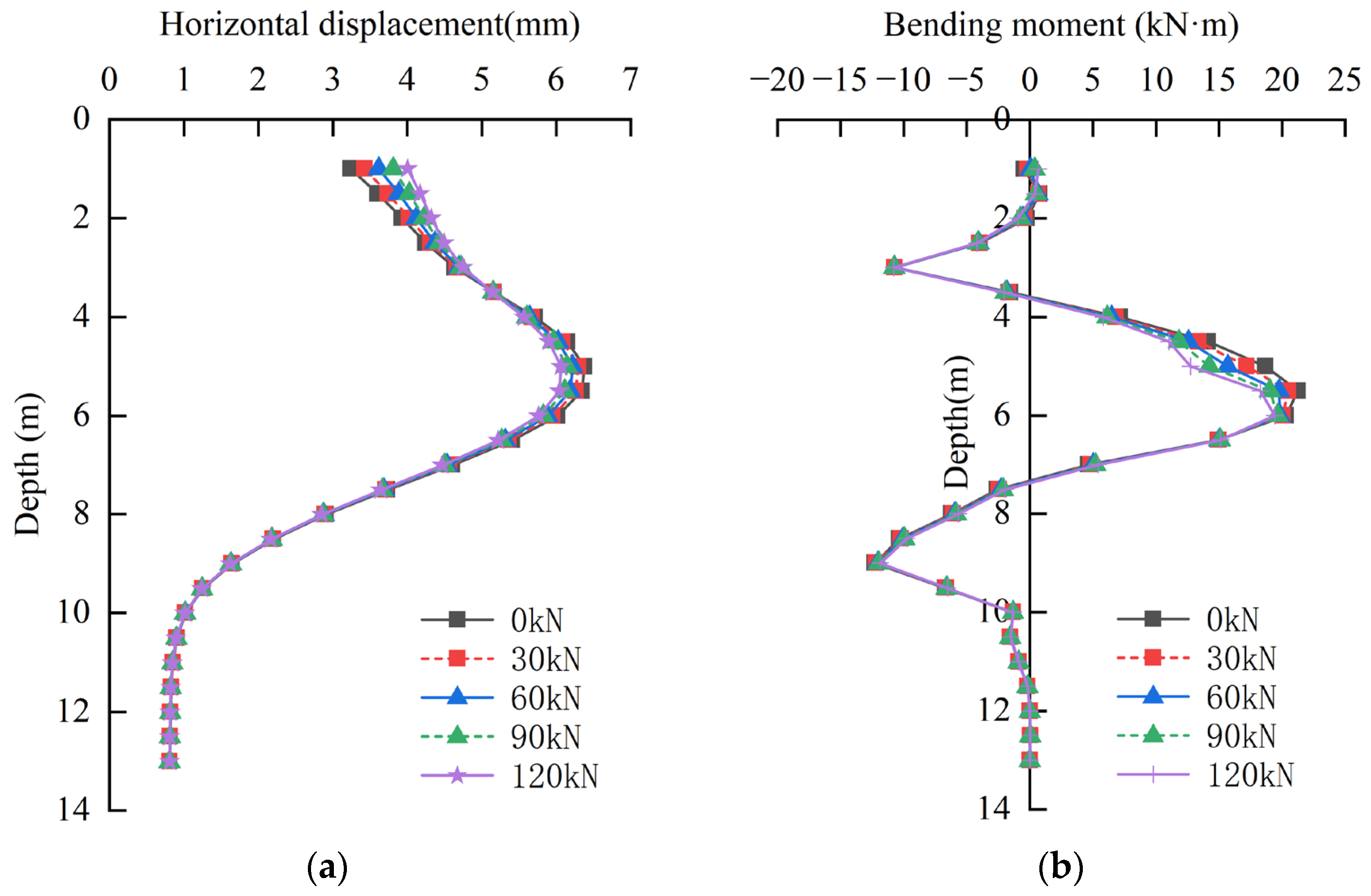
3.4. Control Mechanism of Vertical Prestress
3.4.1. Influence on Support Characteristics
3.4.2. Influence on Pile Displacement and Bending Moment
3.5. Comparison with Conventional Support Systems
4. Conclusions
- (1)
- According to the vertical force transmission path of the new space steel joist internal support structure system for a deep foundation pit, the prestress in both horizontal and vertical directions is applied to realize the balance of force and deformation control. The accuracy of the derived stiffness theoretical formula is high. The design of the vertical diagonal brace increases the stiffness of the lower chord support by 28.24%, which can be used to guide the engineering design calculations of the new internal support structure.
- (2)
- The results of the model test show that the new space steel joist internal support structure system for a deep foundation pit can effectively restrain the deformation of the supporting pile. When the prestress is applied, the horizontal displacement of the supporting pile is reduced, the supporting axial force is increased, and the bending moment of the crown beam is increased. Under the tension of the steel tie rod and the compression of the vertical diagonal brace, the axial force of the upper chord and the vertical diagonal brace increases further.
- (3)
- Based on the rationality of the numerical model, the vertical prestress is applied by tensioning the steel rod in the model, which can effectively restrain the arch displacement of the support and ensure the vertical stability of the support. With the increase in the prestress of the steel tie rod, the maximum horizontal displacement of the pile body and the vertical arch displacement of the support show a decreasing trend, and the axial force of each main support and the displacement of the pile top show an increasing trend. The applied value of vertical prestress should be considered comprehensively according to support displacement, axial force, and pile displacement.
- (4)
- Although this investigation yields valuable findings, certain limitations merit consideration. The numerical model adopted simplified assumptions, such as fully rigid joints and the use of a linear elastic–plastic Mohr–Coulomb soil model, which may not fully reflect realistic soil–structure interaction behaviors. Additionally, the field test and numerical validation focused on a 7 m deep excavation under a specific geological condition, which may limit the generalizability of the findings.
- (5)
- Future research should investigate the performance of the proposed support system in deeper excavations (e.g., >10 m), under more complex geological conditions, and in the presence of groundwater or dynamic loads. Advanced soil constitutive models (e.g., Hardening Soil and Modified Cam-Clay) and flexible joint behavior should be incorporated to enhance predictive accuracy and assess the adaptability of the system in broader engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notation
| F | Force on the outer chord of the horizontal diagonal brace |
| F1 | Force acting on the chord |
| F2 | Force acting on the horizontal diagonal brace |
| F3 | Force of the vertical diagonal brace |
| ε | Linear strain |
| Compression deformation of the chord is not in the horizontal diagonal brace section | |
| Compression deformation of the chord of the horizontal diagonal brace | |
| Vertical compression deformation of the crown beam in the direction of the vertical diagonal brace | |
| Compression deformation of vertical diagonal brace perpendicular to the direction of the crown beam | |
| Total compression | |
| K | Horizontal stiffness coefficient |
| E | Elastic modulus |
| A | Cross-sectional area |
References
- Lu, J.; Li, Y.; Yao, A. Bearing characteristics and ground deformation computation of recyclable Steel-Pipe piles during pit excavation. Appl. Sci. 2024, 14, 5727. [Google Scholar] [CrossRef]
- Pan, Y.; Fang, H.; Li, B.; Wang, F. Stability analysis and full-scale test of a new recyclable supporting structure for underground ecological granaries. Eng. Struct. 2019, 192, 205–219. [Google Scholar] [CrossRef]
- Hong, L.; Wang, X.; Zhang, W.; Li, Y.; Zhang, R.; Chen, C. System reliability-based robust design of deep foundation pit considering multiple failure modes. Geosci. Front. 2024, 15, 101761. [Google Scholar] [CrossRef]
- Nejjar, K.; Dias, D.; Cuira, F.; Chapron, G.; Le Bissonnais, H. Numerical modelling of a 32 m deep excavation in the suburbs of Paris. Eng. Struct. 2022, 268, 114727. [Google Scholar] [CrossRef]
- Tang, W.; Tang, L.; Ling, X.; Kong, X.; Zhang, Y. Long-term performance of subway tunnels induced by the symmetrical excavation of semicircular deep foundation pits in the Northeast Region hard silty clay. Tunn. Undergr. Space Technol. 2024, 154, 106052. [Google Scholar] [CrossRef]
- Ge, C.; Yang, M.; Li, P.; Zhang, M.; Zhang, Z. Performance and environmental impacts of deep foundation excavation in soft soils: A field and modeling-based case study in Nanjing, China. Undergr. Space 2024, 18, 218–238. [Google Scholar] [CrossRef]
- Bryson, L.S.; Zapata-Medina, D.G. Method for estimating system stiffness for excavation support walls. J. Geotech. Geoenviron. Eng. 2012, 138, 1104–1115. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, J.; Hu, X. Study on synthesis stiffness of inner supported deep excavation in soft soil area. IOP Conf. Ser. Earth Environ. Sci. 2019, 283, 12001. [Google Scholar] [CrossRef]
- Li, S.L.; Ge, Y.X. Calculation method of retaining piles with annular beams elastic support stiffness coefficient forcircular foundation pit. Chin. J. Undergr. Space Eng. 2017, 13, 129–134. [Google Scholar]
- Lin, Z.; Jiang, Y.; Xiong, Y.; Xu, C.; Guo, Y.; Wang, C.; Fang, T. Analytical solution for displacement-dependent active earth pressure considering the stiffness of cantilever retaining structure in cohesionless soil. Comput. Geotech. 2024, 170, 106258. [Google Scholar] [CrossRef]
- Jin, Y.B.; Liu, D. Analytical methods for horizontal stiffness coefficient at pivots of inner support structures in deep foundation pits. Chin. J. Geotech. Eng. 2019, 41, 1031–1039. [Google Scholar]
- Zheng, G.; Lei, Y.W.; Cheng, X.S.; Li, X.Y.; Wang, R.Z. Experimental study on progressive collapse mechanism in braced and tied-back retaining systems of deep excavations. Can. Geotech. J. 2021, 58, 540–564. [Google Scholar] [CrossRef]
- Di, H.; Jin, Y.; Zhou, S.; Zhang, X.; Wu, D.; Guo, H. Experimental study on the adjustments of servo steel struts in deep excavations. Acta Geotech. 2023, 18, 6615–6629. [Google Scholar] [CrossRef]
- Huang, M.; Zhien, Z.; Chen, B.; Wang, H. Field experimental study on mechanical properties of frame support structure composed of subway foundation pit retaining pile and steel strut rigid joint. Adv. Civ. Eng. 2022, 2022, 1243282. [Google Scholar] [CrossRef]
- Ezzeldin, I.; El Naggar, H. Earth pressure distribution around flexible arch pipes. Eng. Struct. 2021, 237, 112226. [Google Scholar] [CrossRef]
- Pan, W.H.; Tong, J.Z.; Guo, Y.L.; Wang, C.M. Optimal design of steel buckling-restrained braces considering stiffness and strength requirements. Eng. Struct. 2020, 211, 110437. [Google Scholar] [CrossRef]
- Yu, X.; Ji, T.; Zheng, T. Relationships between internal forces, bracing patterns and lateral stiffnesses of a simple frame. Eng. Struct. 2015, 89, 147–161. [Google Scholar] [CrossRef]
- Sun, J.; Bai, T.; Liao, S. Active control of deep foundation pit deformation based on coherence of supporting axial force. Chin. J. Undergr. Space Eng. 2021, 17, 529–540. [Google Scholar]
- Gil-Martín, L.M.; Hernández-Montes, E.; Shin, M.; Aschheim, M. Developments in excavation bracing systems. Tunn. Undergr. Space Technol. 2012, 31, 107–116. [Google Scholar] [CrossRef]
- Cao, X.S.; Lu, X.Y.; Gu, Y.M. Variation of axial force of steel struts in deep excavations. Chin. J. Geotech. Eng. 2022, 44, 1988–1997. [Google Scholar]
- Zheng, G.; Zhao, J.; Cheng, X.; Yu, D.Y.; Wang, R.Z.; Zhu, X.W.; Yi, F. Mechanism and control measures of the vertical progressive collapse of deep excavations retained by a multilayer strutting system. J. Tianjin Univ. (Sci. Technol.) 2021, 54, 1025–1038. [Google Scholar]
- Haundi, T.; Nangulama, H.K.; Mbewe, V.R. Site characterisation, deep basement support, construction, and deformation control. Geotech. Geol. Eng. 2024, 42, 1611–1622. [Google Scholar] [CrossRef]
- Lu, X.; Song, E.; Ji, L.; Sui, F. 3-Dimensional FEA for the interaction between supporting structure of excavation and soil in a very deep pit. Chin. J. Geotech. Eng. 2003, 25, 488–491. [Google Scholar]
- Zhang, M.; Yang, M.; Li, P.; Gao, Y. Mechanical behaviors of a symmetrical bolt fasten wedge active joint for braced excavations. Symmetry 2020, 12, 140. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, X.; Hu, B.; Huang, L.; Lu, G.; Yao, H. Automatic monitoring and control of excavation disturbance of an ultra-deep foundation pit extremely adjacent to metro tunnels. Tunn. Undergr. Space Technol. 2023, 142, 105445. [Google Scholar] [CrossRef]
- Ren, B.; Shen, Y.; Zhao, T.; Li, X. Deformation monitoring and remote analysis of ultra-deep underground space excavation. Undergr. Space 2023, 8, 30–44. [Google Scholar] [CrossRef]
- Rao, A.S.; Radanovic, M.; Liu, Y.; Hu, S.; Fang, Y.; Khoshelham, K.; Palaniswami, M.; Ngo, T. Real-time monitoring of construction sites: Sensors, methods, and applications. Autom. Constr. 2022, 136, 104099. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, D.; Wang, Y.; Wang, N.; Xu, W. Design optimization and observed performance of a super-large foundation pit excavation subjected to unsymmetrical loading in water-rich floodplain: A case study. Soils Found. 2023, 63, 101329. [Google Scholar] [CrossRef]
- Cui, X.; Li, Z.; He, H.; Ma, S. Improved calculation method for corresponding characteristics of foundation pit excavation on the diaphragm wall. Alex. Eng. J. 2024, 103, 251–265. [Google Scholar] [CrossRef]
- Wang, Y. Design and construction of foundation support in urban underground space Development—A review of new advances in geotechnical engineering for urban underground space development. Chin. J. Mod. Urban Res. 2025, 4, 124. [Google Scholar]
- Zhang, C.; Liu, S. A review on the research of prefabricated structures in underground space. J. Basic. Sci. Eng. 2022, 30, 236–245. [Google Scholar]
- Long, Z.; Ye, S.; Li, X.; Guo, Z. Model box test and numerical simulation analysis of supporting performance of Loess-Based composite slurry soil nailing wall. Buildings 2025, 15, 2090. [Google Scholar] [CrossRef]
- Yan, H.; Long, J.; Yang, Y.; Shi, Q.; Yang, B. Model test study on bearing characteristics of pile foundation in red clay. Buildings 2024, 14, 2316. [Google Scholar] [CrossRef]
- Wu, K.; Xing, Z. Stability of imperfect prestressed stayed beam-columns under combined axial load and bending. Eng. Struct. 2021, 245, 112891. [Google Scholar] [CrossRef]
- Xu, Q.; Xie, J.; Lu, L.; Wang, Y.; Wu, C.; Meng, Q. Numerical and theoretical analysis on soil arching effect of prefabricated piles as deep foundation pit supports. Undergr. Space 2024, 16, 314–330. [Google Scholar] [CrossRef]
- Liu, M.; Meng, F.; Liu, Z.; Chen, R. Observed soil arching-induced ground deformation and stress redistribution behind braced excavation. Can. Geotech. J. 2024, 61, 12. [Google Scholar] [CrossRef]
- Wu, L.; He, K.; Guo, L.; Zhang, J.; Sun, L.; Jia, Y. Research on the excavation stability evaluation method of Chaqishan ancient landslide in China. Eng. Fail. Anal. 2022, 141, 106664. [Google Scholar] [CrossRef]
- Elgamal, A. Guidelines for geotechnical Finite-Element modeling. Open Civ. Eng. J. 2021, 15, 424–440. [Google Scholar] [CrossRef]
- Ibrahim, E.; Soubra, A.; Mollon, G.; Raphael, W.; Dias, D.; Reda, A. Three-dimensional face stability analysis of pressurized tunnels driven in a multilayered purely frictional medium. Tunn. Undergr. Space Technol. 2015, 49, 18–34. [Google Scholar] [CrossRef]
- Meschke, G.; Ninić, J.; Stascheit, J.; Alsahly, A. Parallelized computational modeling of pile–soil interactions in mechanized tunneling. Eng. Struct. 2013, 47, 35–44. [Google Scholar] [CrossRef]
- Han, G.; Zhang, Y.; Zhang, J.; Zhang, H. Numerical analysis and optimization of displacement of enclosure structure based on MIDAS finite element simulation software. Buildings 2025, 15, 1462. [Google Scholar] [CrossRef]
- Liang, L.; Xu, C.; Fan, X.; Chen, Q. Hyperbolic stress-strain behaviour of sandy soil under plane strain unloading condition and its application on predicting displacement-dependent active earth pressure. Comput. Geotech. 2023, 155, 105219. [Google Scholar] [CrossRef]
- Yong, Y.; Qiaozhi, S.; Xi, C. Dynamic shear modulus degradation of saturated soil analysis: From the perspective of phase field theory. Comput. Struct. 2024, 305, 107568. [Google Scholar] [CrossRef]
- Liu, K.; Chen, W.; Feng, W.; Tan, D.; Zhou, C.; Yin, J. Variation of secant young’s modulus in an unsaturated Gap-Graded granular fill. Transp. Geotech. 2024, 49, 101416. [Google Scholar] [CrossRef]
- Kong, G.Q.; Gu, H.W.; Che, P.; Ren, L.W.; Peng, H.F. Impact of pile shaft shapes on vertical bearing capacity of belled piles. Rock Soil Mech. 2017, 38, 361–367. [Google Scholar]
- Xu, S.C.; Zhang, X.G.; Ma, F.R.; Chen, Z.X. Analysis of model test and failure of slope reinforced by soil-cement pile. Rock Soil Mech. 2017, 38, 3187–3196. [Google Scholar]
- Zhang, S.; Lu, Y.; Lu, L. A new method for evaluating the stability of retaining walls. Buildings 2025, 15, 1732. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, B. Retaining and protection structural design and monitoring for foundation pit of Guangzhou CTF Finance Centre. Build. Struct. 2019, 49, 104–110. [Google Scholar]
- Zhuo, Z.; Fu, W.; Zhou, H.; Feng, S.; Zhou, K. Design example of deep excavation of a high-rise building. Chin. J. Geotech. Eng. 2012, 34, 687–691. [Google Scholar]
- Song, J.; Li, L.; Tong, Y. Monitoring and analysis on composite support system with soil nailing wall-pile anchor-inner bracing. J. Archit. Civ. Eng. 2018, 35, 120–126. [Google Scholar]



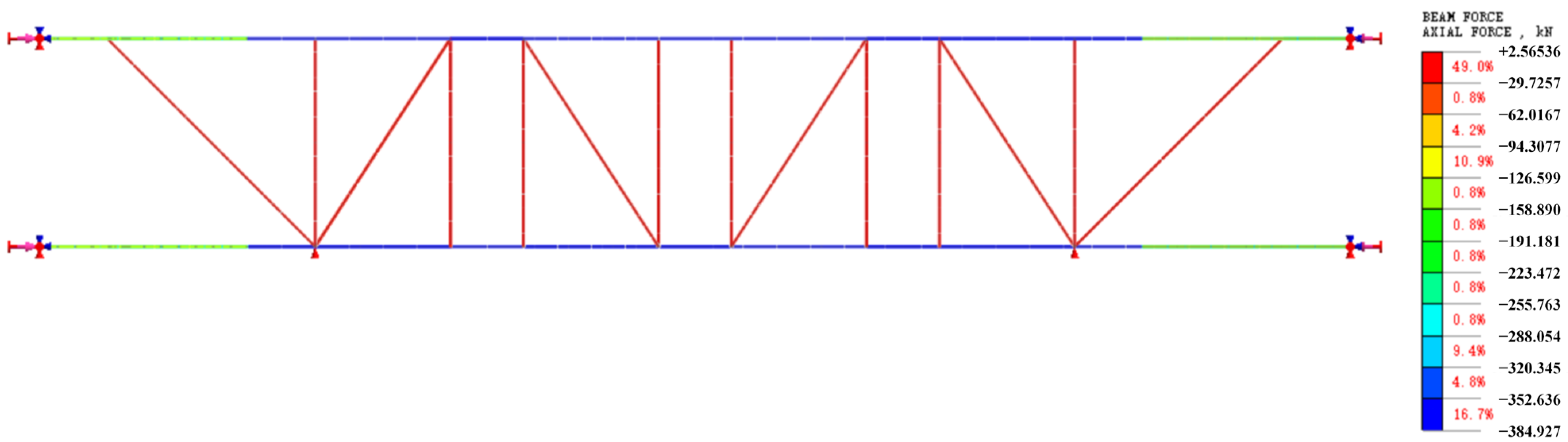
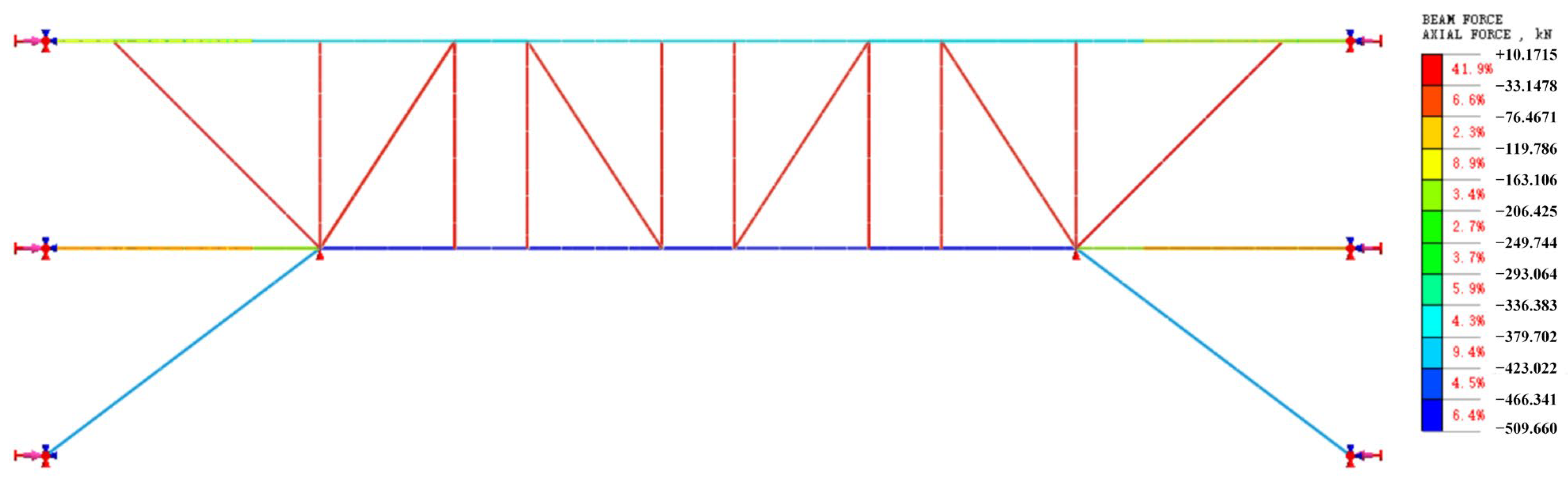

| With or Without Vertical Diagonal Brace | Bracing Component | Calculation Method | Support Stiffness (MN/m) | Error |
|---|---|---|---|---|
| Without | Upper chord | T | 81.58 | 5.98% |
| F | 76.98 | |||
| Lower chord | T | 81.58 | 6.33% | |
| F | 76.72 | |||
| With | Upper chord | T | 81.58 | 5.71% |
| F | 77.17 | |||
| Lower chord | T | 104.62 | 2.90% | |
| F | 101.67 | |||
| vertical diagonal brace | T | 25.66 | 4.22% | |
| F | 26.79 |
| Component | Bracing Component | Poisson Ratio | Elastic Modulus (GPa) |
|---|---|---|---|
| Tangent pile | Plate unit | 0.2 | 31.5 |
| Sprayed concrete | Plate unit | 0.2 | 31.5 |
| Crown beam | Beam unit | 0.2 | 31.5 |
| Waist beam | Beam unit | 0.274 | 210 |
| Steel pipe support | Beam unit | 0.274 | 210 |
| Steel tie rod | Tension-only truss unit | 0.274 | 210 |
| Soli | Thickness (m) | Gravity (kN/m3) | Poisson Ratio | Force of Cohesion (kPa) | Friction Angle (°) | Secant Modulus (MPa) | Tangent Modulus (MPa) | Unloading Modulus (MPa) |
|---|---|---|---|---|---|---|---|---|
| Miscellaneous fill | 1 | 18.5 | 0.40 | 10.0 | 5.0 | 3.5 | 3.5 | 14 |
| Clay | 3 | 19.3 | 0.31 | 44.2 | 15.2 | 11.0 | 11.0 | 30 |
| Silty clay 1 | 3 | 19.8 | 0.32 | 40.2 | 14.6 | 10.7 | 10.7 | 29 |
| Silty clay 2 | 2 | 19.7 | 0.33 | 20.0 | 10.1 | 9.0 | 9.0 | 28 |
| Rounded gravel | Not debunked | 22.5 | 0.30 | — | 35.0 | 30.0 | 30.0 | 120 |
| Construction Condition | Maximum Horizontal Displacement (mm) | ||
|---|---|---|---|
| Simulated Values | Measured Values | Differentials | |
| Excavation to −4 m | 3.712 | 4.085 | 0.373 |
| Apply the first prestress | 3.180 | 2.834 | 0.346 |
| Excavation to −6 m | 4.725 | 6.014 | 1.290 |
| Excavation to −7 m | 6.603 | 6.618 | 0.015 |
| Apply vertical prestress | 6.533 | 6.518 | 0.015 |
| Performance Metric | Conventional System | Proposed System | Improvement (%) |
|---|---|---|---|
| Max horizontal displacement (mm) | 15.5 | 6.618 | 57% |
| Equivalent lateral stiffness (MN/m) | 80 | 101 | 25% |
| Reusability of bracing components | custom-welded components | standardized modular | Significantly improved |
| Estimated unit cost (CNY/m) | 50,000 | 30,000 | 40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liang, J.; Wei, G.; Liang, C.; Yan, L.; Han, W.; Zhang, Y.; Tian, Y.; Zhang, H. Study on the Bearing Characteristics of a Novel Inner Support Structure for Deep Foundation Pits Based on Full-Scale Experiments. Buildings 2025, 15, 2887. https://doi.org/10.3390/buildings15162887
Zhang X, Liang J, Wei G, Liang C, Yan L, Han W, Zhang Y, Tian Y, Zhang H. Study on the Bearing Characteristics of a Novel Inner Support Structure for Deep Foundation Pits Based on Full-Scale Experiments. Buildings. 2025; 15(16):2887. https://doi.org/10.3390/buildings15162887
Chicago/Turabian StyleZhang, Xingui, Jianhang Liang, Gang Wei, Chengkao Liang, Li’e Yan, Wei Han, Yidan Zhang, Yingzhi Tian, and Huai Zhang. 2025. "Study on the Bearing Characteristics of a Novel Inner Support Structure for Deep Foundation Pits Based on Full-Scale Experiments" Buildings 15, no. 16: 2887. https://doi.org/10.3390/buildings15162887
APA StyleZhang, X., Liang, J., Wei, G., Liang, C., Yan, L., Han, W., Zhang, Y., Tian, Y., & Zhang, H. (2025). Study on the Bearing Characteristics of a Novel Inner Support Structure for Deep Foundation Pits Based on Full-Scale Experiments. Buildings, 15(16), 2887. https://doi.org/10.3390/buildings15162887






