Investigating Three-Dimensional Auxetic Structural Responses to Impact Loading with the Generalized Interpolation Material Point Method
Abstract
1. Introduction
2. NPR Modeling and Simulation Methodology
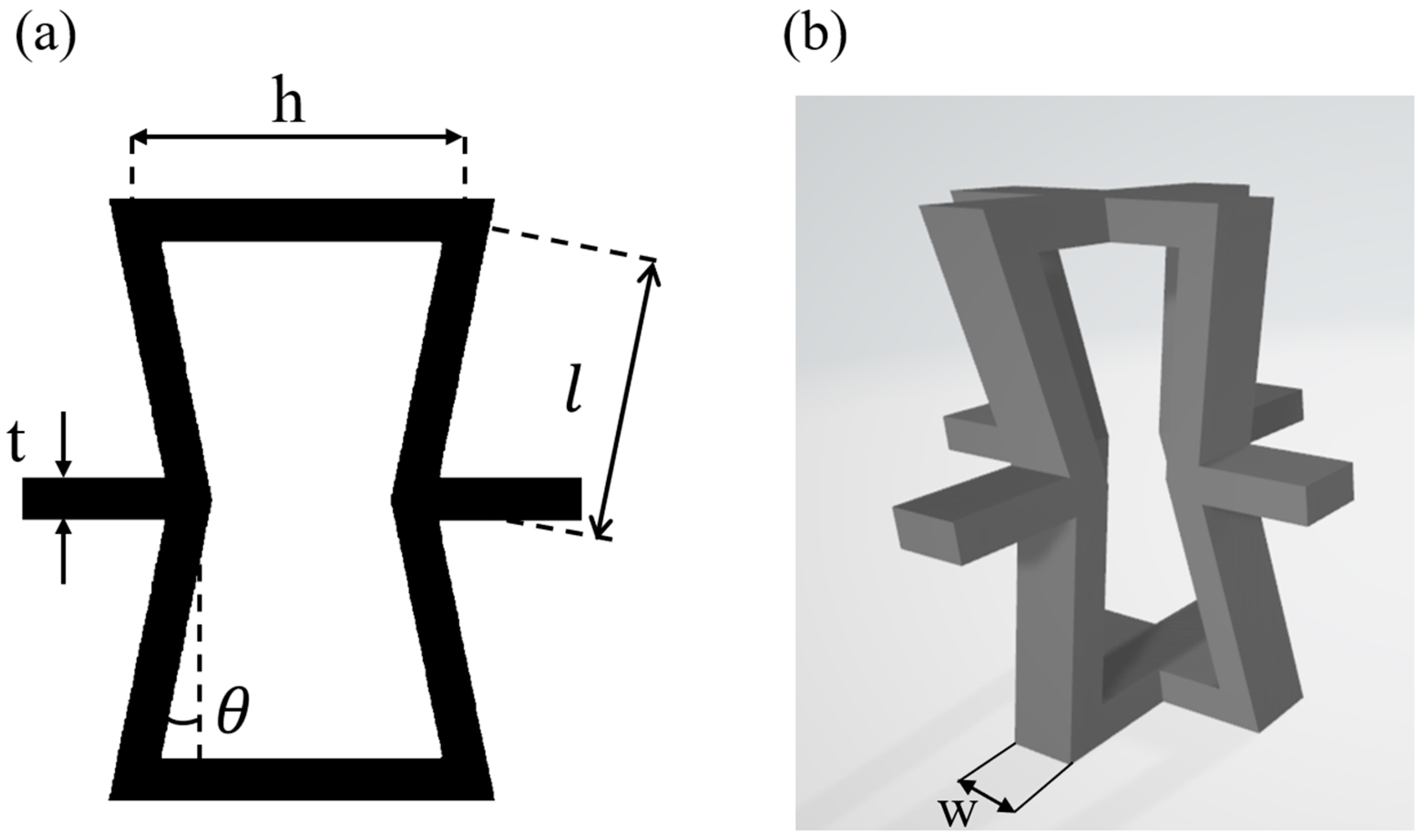
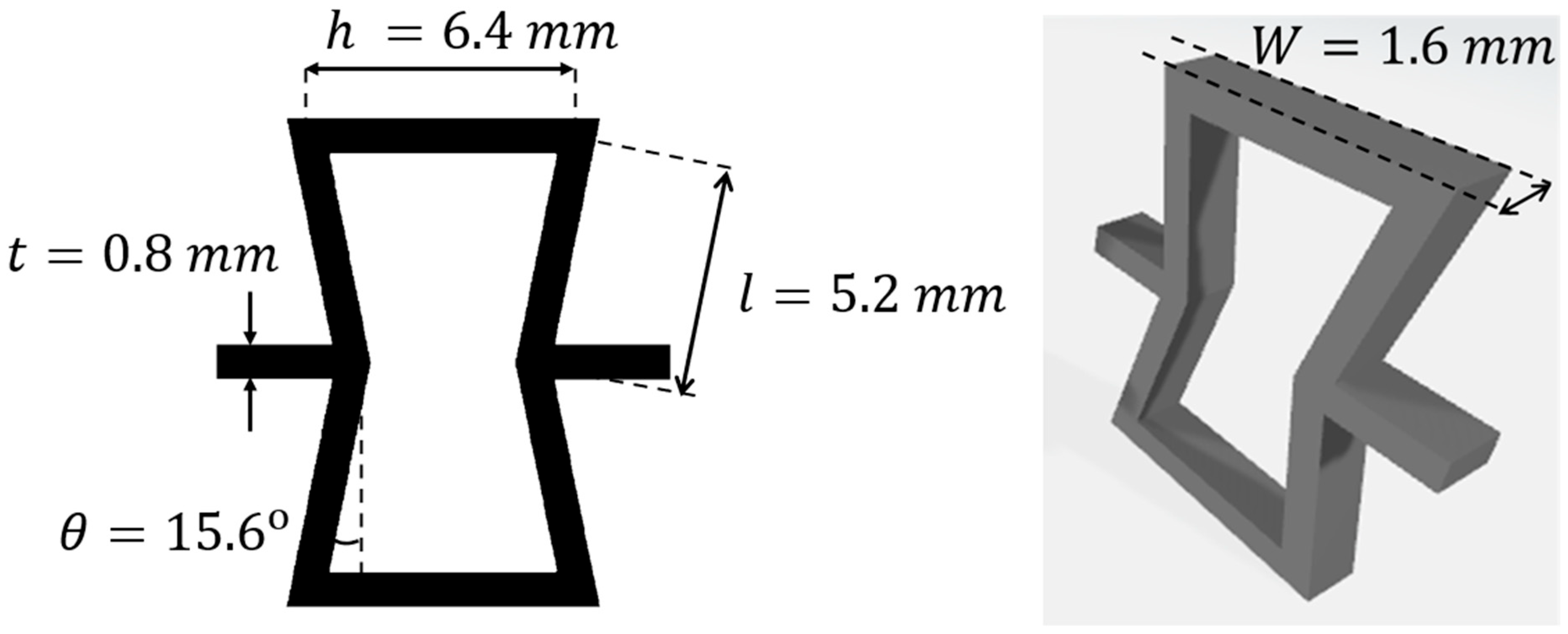
2.1. NPR Modeling with Re-Entrant Honeycomb Structures
2.2. Simulation Methodology with the GIMP
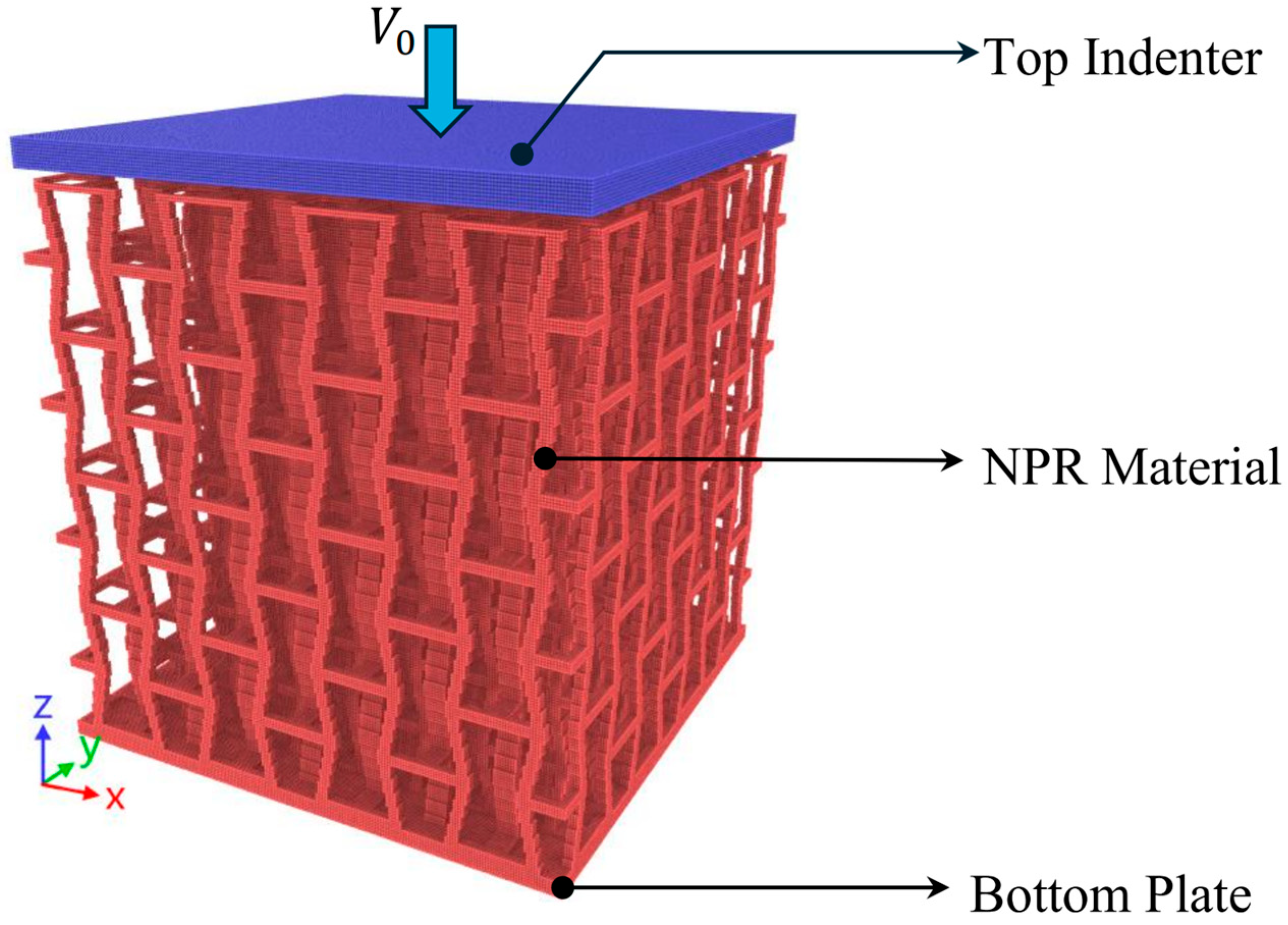
3. Computational Setting
4. Verification of NPR
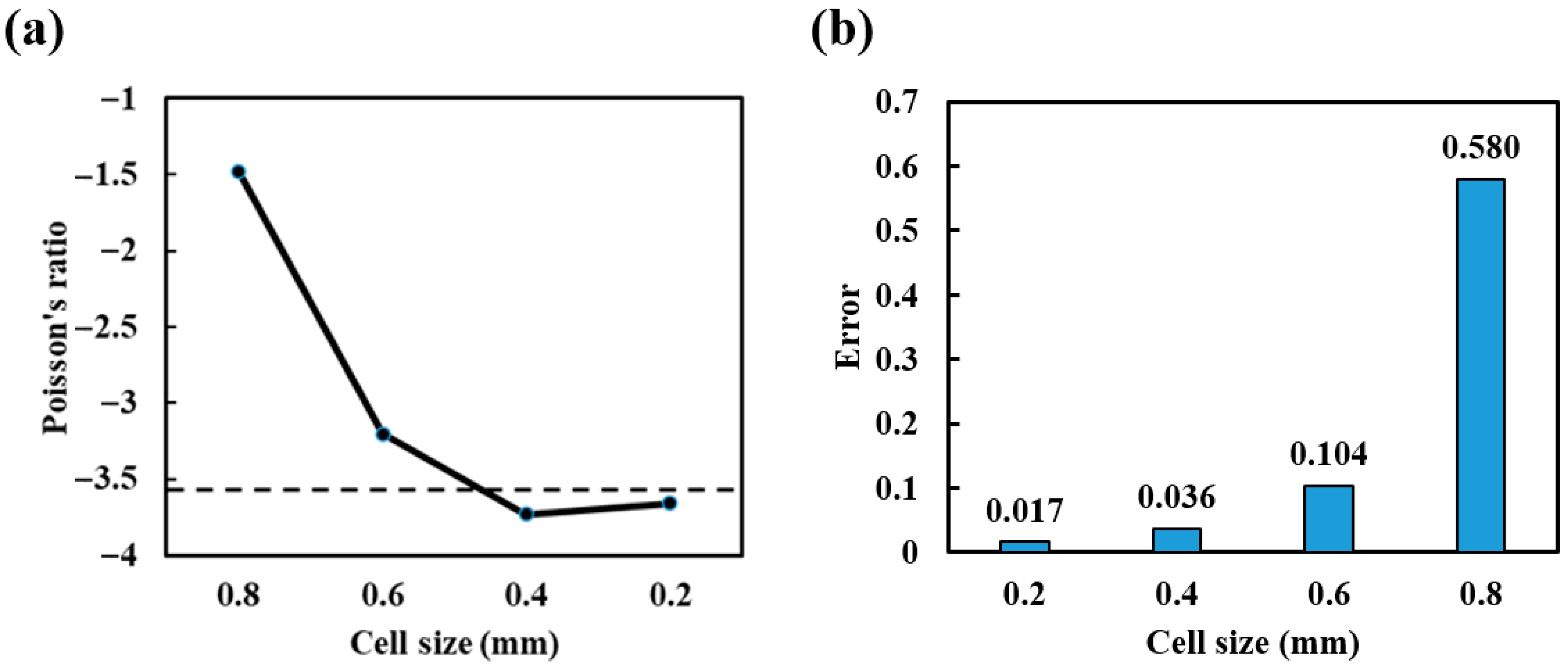
4.1. Convergence Study
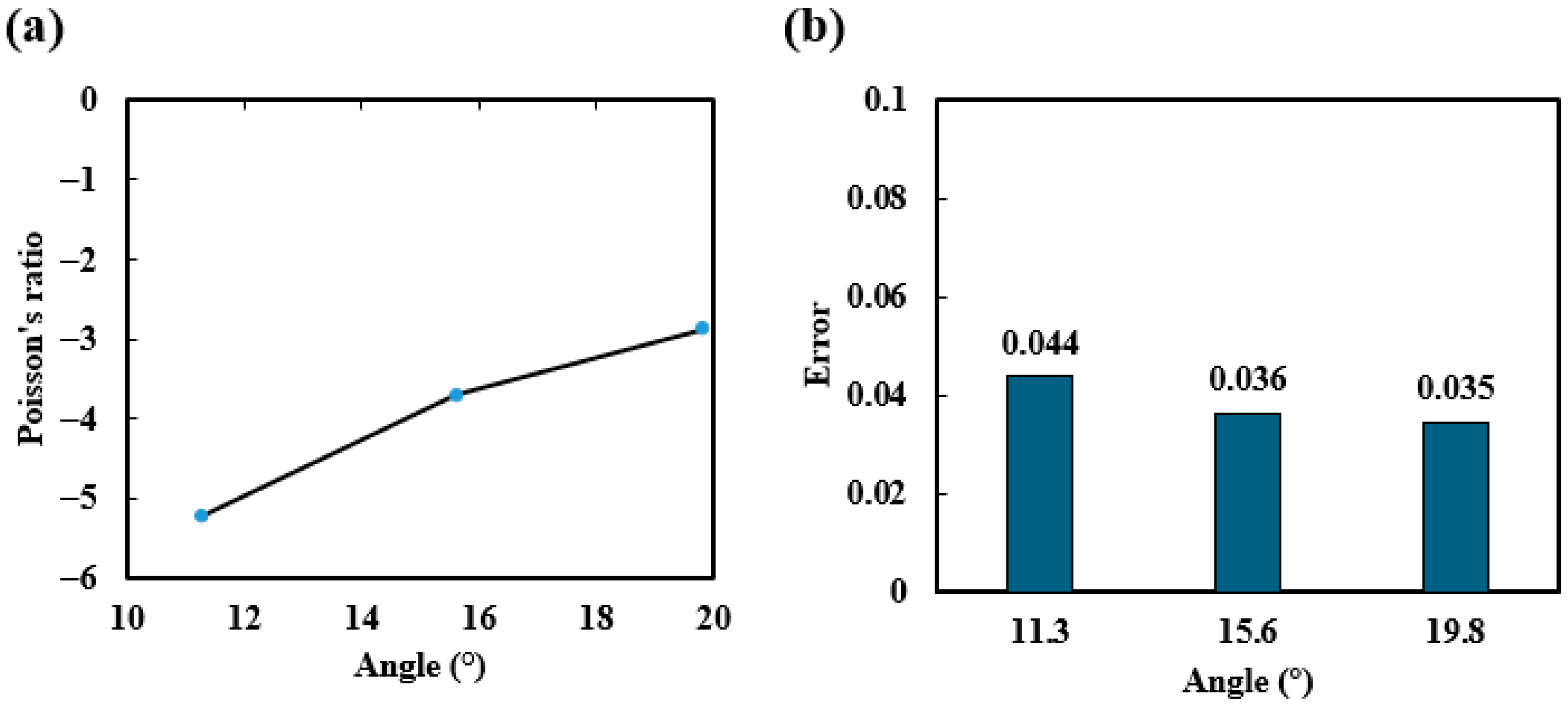
4.2. Verification of NPR with Different Angles
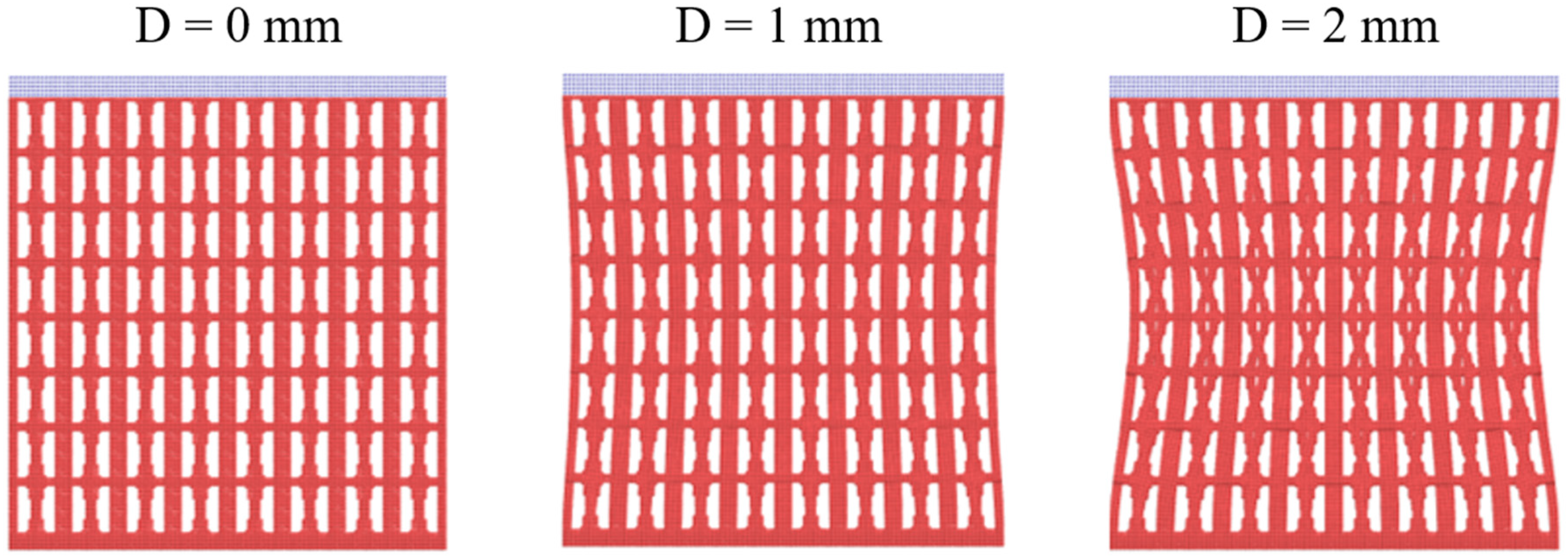
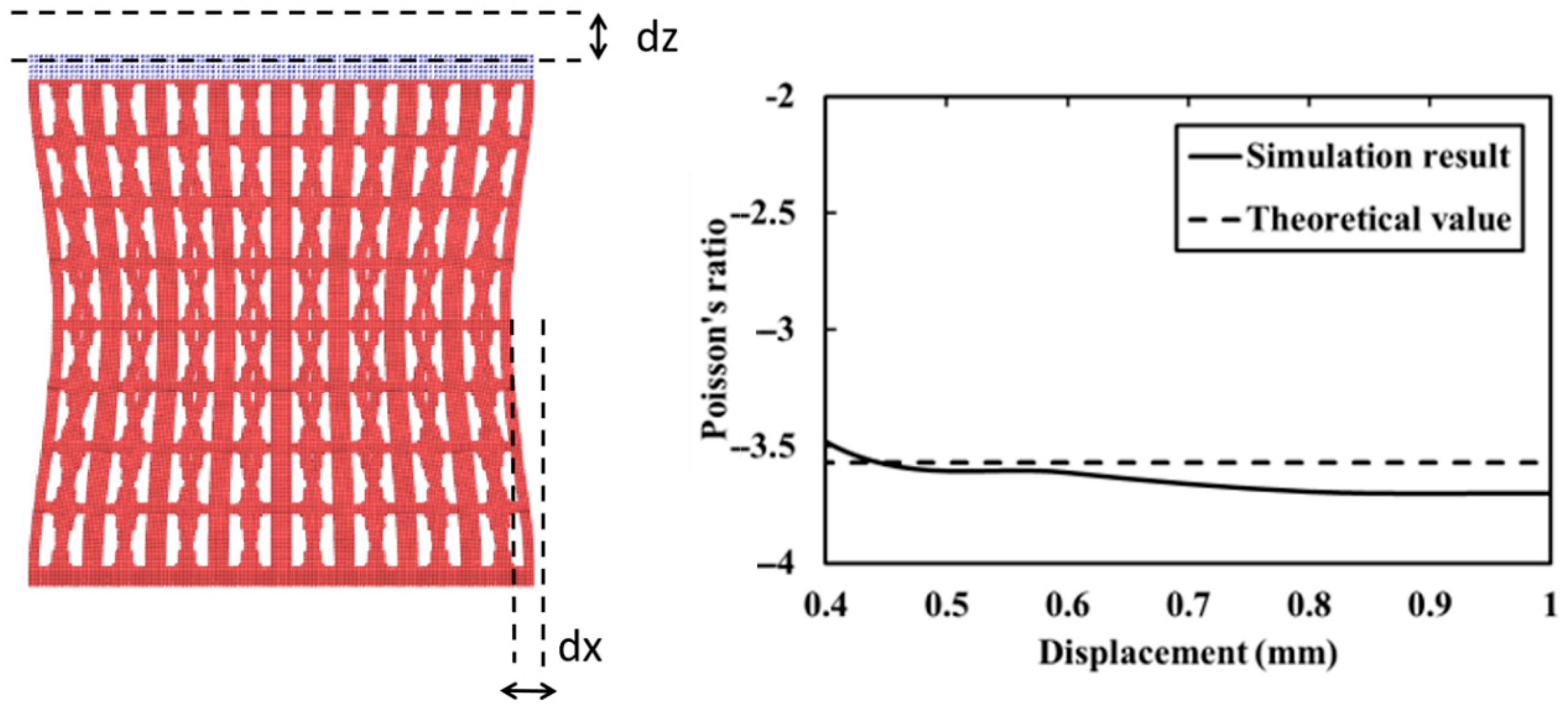
4.3. Verification of NPR with a Larger Model
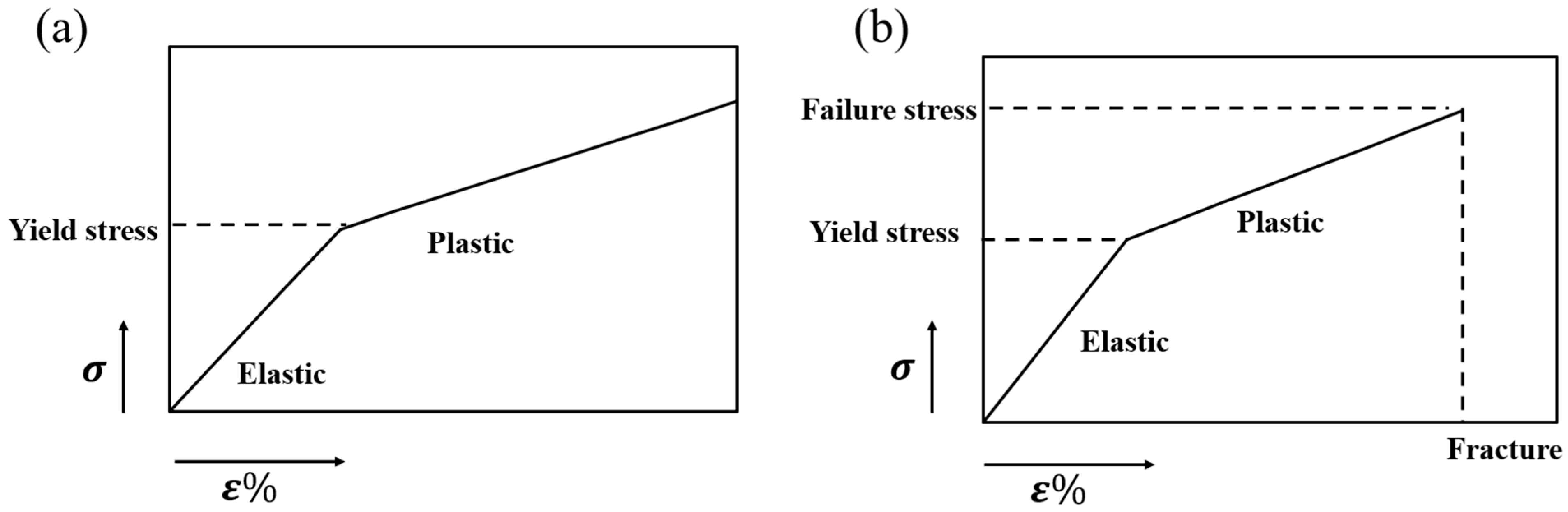
5. Constitutive Effect
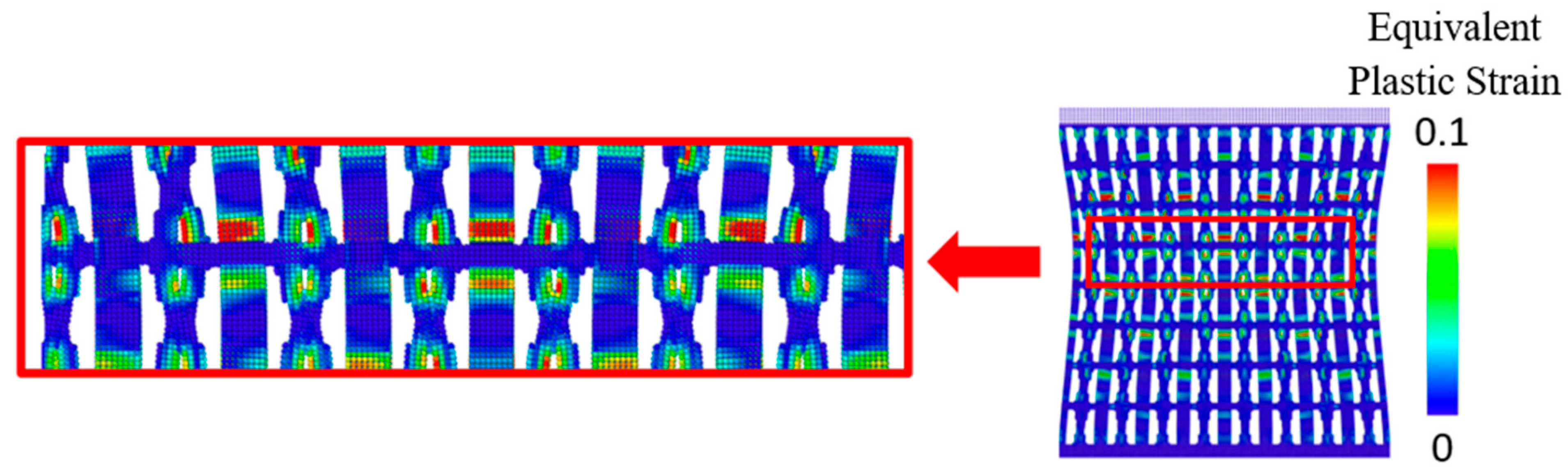
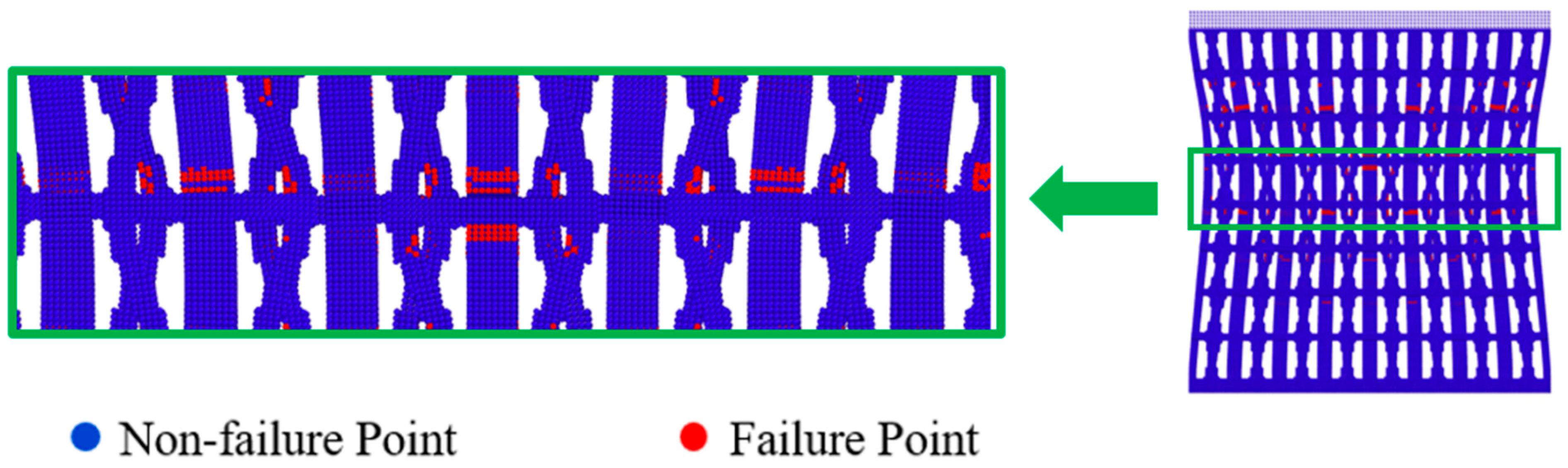
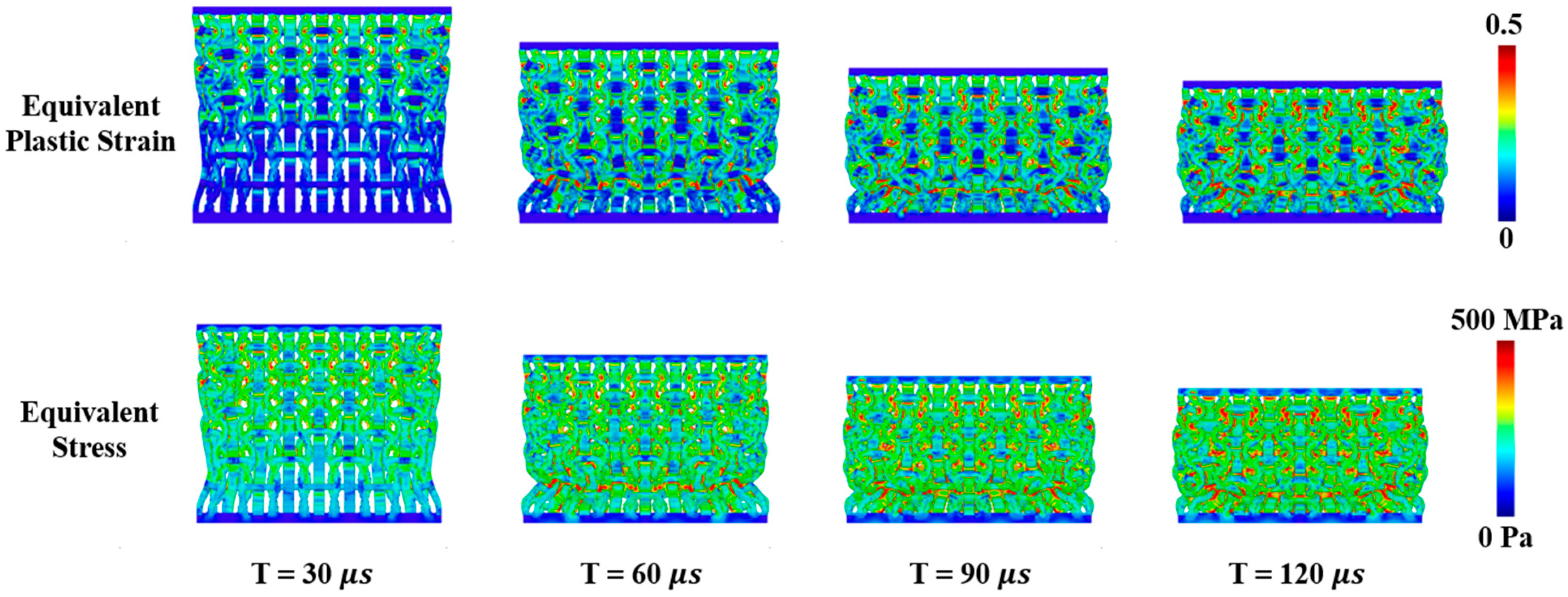
5.1. Comparison of Failure Evolution Patterns
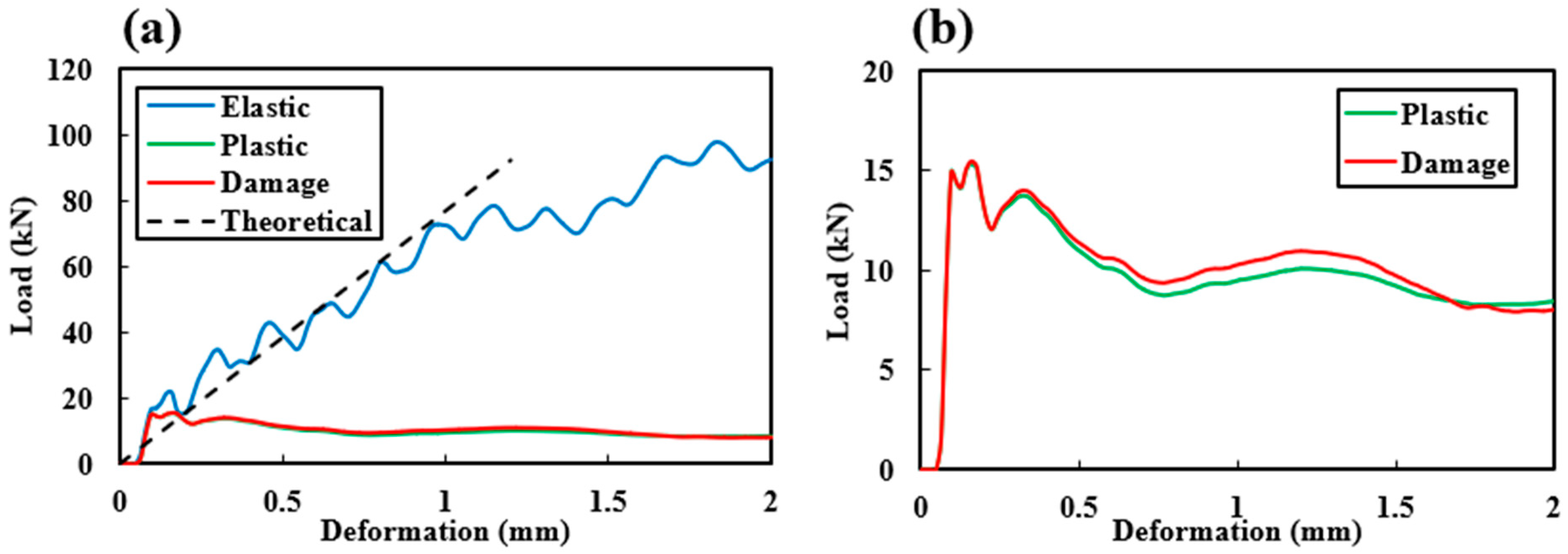
5.2. Verification of the Equivalent Elastic Modulus
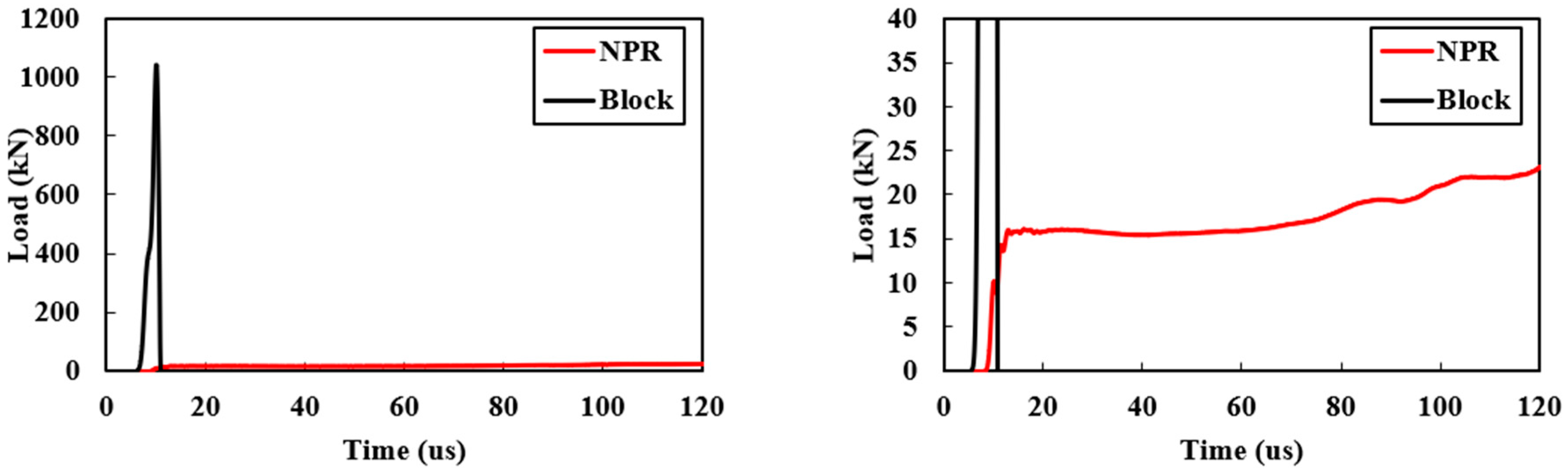
6. NPR Effect on Impact Resistance
7. Conclusions
- Three different constitutive models for structural materials are adopted to investigate the constitutive effects on the failure evolution patterns and reaction load–displacement relations. Within the elastic range, the load–displacement relationship is linear and aligns with the analytical prediction. The inelastic models demonstrate that higher equivalent plastic strains and damaged material points are more concentrated at the joints between the horizontal and oblique lattice members. It indicates that the specially designed joints promote noticeable lateral contraction under compression. The difference between elastoplasticity and damage models for structural materials is not significant in governing the impact responses, which indicates the important role of process–structure–property relationships in impact-resistant composite designs.
- Under high-speed impact, the NPR material transfers most of the impact kinetic energy into the re-entrant honeycomb structures. In contrast, the kinetic energy propagates through the solid block to the bottom plate. As a result, the NPR material significantly reduces the load transmitted to the bottom plate. The GIMP could effectively capture the impact resistance characteristics of the NPR materials with lattice structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.D.; Winwood, K.; Allen, T.; Alderson, A. Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection. Appl. Sci. 2018, 8, 941. [Google Scholar] [CrossRef]
- Madke, R.R.; Chowdhury, R. Anti-Impact Behavior of Auxetic Sandwich Structure with Braided Face Sheets and 3D Re-Entrant Cores. Compos. Struct. 2020, 236, 111838. [Google Scholar] [CrossRef]
- Kim, Y.; Son, K.; Lee, J. Auxetic Structures for Tissue Engineering Scaffolds and Biomedical Devices. Materials 2021, 14, 6821. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zulifqar, A.; Hu, H. Auxetic composites in aerospace engineering. In Advanced Composite Materials for Aerospace Engineering; Woodhead Publishing: Cambridge, UK, 2016; pp. 213–240. [Google Scholar]
- Saxena, K.K.; Das, R.; Calius, E.P. Three Decades of Auxetics Research−Materials with Negative Poisson’s Ratio: A Review. Adv. Eng. Mater. 2016, 18, 1847–1870. [Google Scholar] [CrossRef]
- Choudhry, N.K.; Panda, B.; Dixit, U.S. Energy Absorption Characteristics of Fused Deposition Modeling 3D Printed Auxetic Re-Entrant Structures: A Review. J. Mater. Eng. Perform. 2023, 32, 8981–8999. [Google Scholar] [CrossRef]
- Faraci, D.; Driemeier, L.; Comi, C. Bending-Dominated Auxetic Materials for Wearable Protective Devices Against Impact. J. Dyn. Behav. Mater. 2021, 7, 425–435. [Google Scholar] [CrossRef]
- Wang, T.; An, J.; He, H.; Wen, X.; Xi, X. A Novel 3D Impact Energy Absorption Structure with Negative Poisson’s Ratio and Its Application in Aircraft Crashworthiness. Compos. Struct. 2021, 262, 113663. [Google Scholar] [CrossRef]
- Lian, J.; Xu, L.; Wu, D.; Wang, Z. Study on Re-Entrant Hierarchical Honeycombs in-Plane Impact. Sci. Rep. 2023, 13, 21423. [Google Scholar] [CrossRef]
- Choi, J.B. Fracture Toughness of Re-Entrant Foam Materials with a Negative Poisson’s Ratio: Experiment and Analysis. Int. J. Fract. 1996, 80, 73–83. [Google Scholar] [CrossRef]
- Logakannan, K.P.; Ramachandran, V.; Rengaswamy, J.; Ruan, D. Dynamic Performance of a 3D Re-Entrant Structure. Mech. Mater. 2020, 148, 103503. [Google Scholar] [CrossRef]
- Plewa, J.; Płońska, M.; Feliksik, K.; Junak, G. Experimental Study of Auxetic Structures Made of Re-Entrant (“Bow-Tie”) Cells. Materials 2024, 17, 3061. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Shi, B.Q.; Wang, B.; Yu, G.Q. Crushing Response and Optimization of a Modified 3D Re-Entrant Honeycomb. Materials 2024, 17, 2083. [Google Scholar] [CrossRef]
- Baroutaji, A.; Nikkhah, H.; Arjunan, A.; Pirmohammad, S.; Robinson, J. In-Plane Compressive Responses of Non-Homogenous Re-Entrant Honeycombs Fabricated by Fused Deposition Modelling. Micromachines 2024, 15, 694. [Google Scholar] [CrossRef]
- Cui, Z.; Qi, J.; Duan, Y.; Tie, Y.; Zheng, Y.; Yang, J.; Li, C. Low-Velocity Impact Resistance of 3D Re-Entrant Honeycomb Sandwich Structures with CFRP Face Sheets. Polymers 2023, 15, 1092. [Google Scholar] [CrossRef]
- Taşdemir, M.; Toktaş, İ.; Motameni, A.; Evis, Z. Experimental and Numerical Investigation of Mechanical Properties of PLA-Based Auxetic Structures. Int. J. Adv. Manuf. Technol. 2025, 137, 83–103. [Google Scholar] [CrossRef]
- Lian, J.; Wang, Z. Impact Response of Re-Entrant Hierarchical Honeycomb. Materials 2023, 16, 7121. [Google Scholar] [CrossRef]
- Rad, M.S.; Hatami, H.; Ahmad, Z.; Yasuri, A.K. Analytical Solution and Finite Element Approach to the Dense Re-Entrant Unit Cells of Auxetic Structures. Acta. Mech. 2019, 230, 2171–2185. [Google Scholar] [CrossRef]
- Nečemer, B.; Glodež, S.; Novak, N.; Kramberger, J. Numerical Modelling of a Chiral Auxetic Cellular Structure under Multiaxial Loading Conditions. Theor. Appl. Fract. Mech. 2020, 107, 102514. [Google Scholar] [CrossRef]
- Lira, C.; Innocenti, P.; Scarpa, F. Transverse Elastic Shear of Auxetic Multi Re-Entrant Honeycombs. Compos. Struct. 2009, 90, 314–322. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Schury, F.; Stingl, M.; Wein, F.; Singer, R.F.; Körner, C. Mechanical Characterisation of a Periodic Auxetic Structure Produced by SEBM. Phys. Status Solidi B Basic Res. 2012, 249, 1347–1352. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Z.; Liu, Y. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chen, Z.P.; Zhang, X.; Sze, K.Y.; Kan, L.; Qiu, X.M. V-p Material Point Method for Weakly Compressible Problems. Comput. Fluids 2018, 176, 170–181. [Google Scholar] [CrossRef]
- Andersen, S.; Andersen, L. Modelling of Landslides with the Material-Point Method. Comput. Geosci. 2010, 14, 137–147. [Google Scholar] [CrossRef]
- Liang, Y.; Chandra, B.; Soga, K. Shear Band Evolution and Post-Failure Simulation by the Extended Material Point Method (XMPM) with Localization Detection and Frictional Self-Contact. Comput. Methods Appl. Mech. Eng. 2022, 390, 114530. [Google Scholar] [CrossRef]
- Stomakhin, A.; Schroeder, C.; Chai, L.; Teran, J.; Selle, A. A Material Point Method for Snow Simulation. ACM Trans. Graph. 2013, 32, 1–10. [Google Scholar] [CrossRef]
- Xie, M.; Navas, P.; López-Querol, S. An Implicit Locking-Free B-Spline Material Point Method for Large Strain Geotechnical Modelling. Int. J. Numer. Anal. Methods Geomech. 2023, 47, 2741–2761. [Google Scholar] [CrossRef]
- Li, J.G.; Hamamoto, Y.; Liu, Y.; Zhang, X. Sloshing Impact Simulation with Material Point Method and Its Experimental Validations. Comput. Fluids 2014, 103, 86–99. [Google Scholar] [CrossRef]
- Bardenhagen, S.G.; Kober, E.M. The Generalized Interpolation Material Point Method. Comput. Model. Eng. Sci. 2004, 5, 477–496. [Google Scholar]
- Tao, J.; Zheng, Y.; Chen, Z.; Zhang, H. Generalized Interpolation Material Point Method for Coupled Thermo-Mechanical Processes. Int. J. Mech. Mater. Des. 2016, 12, 577–595. [Google Scholar] [CrossRef]
- Tao, J.; Zhang, H.; Zheng, Y.; Chen, Z. Development of Generalized Interpolation Material Point Method for Simulating Fully Coupled Thermomechanical Failure Evolution. Comput. Methods Appl. Mech. Eng. 2018, 332, 325–342. [Google Scholar] [CrossRef]
- Lei, X.; He, S.; Abed, A.; Chen, X.; Yang, Z.; Wu, Y. A Generalized Interpolation Material Point Method for Modelling Coupled Thermo-Hydro-Mechanical Problems. Comput. Methods Appl. Mech. Eng. 2021, 386, 114080. [Google Scholar] [CrossRef]
- Chen, Z.; Su, Y.C.; Rajendran, A.M.; Su, H.; Liu, Y.; Jiang, S. Study of Constituent Effect on the Failure Response of Fiber Reinforced Composites to Impact Loading with the Material Point Method. Compos. Struct. 2020, 252, 112751. [Google Scholar] [CrossRef]
- Mohammad, Z.; Gupta, P.K.; Baqi, A. Experimental and Numerical Investigations on the Behavior of Thin Metallic Plate Targets Subjected to Ballistic Impact. Int. J. Impact Eng. 2020, 146, 103717. [Google Scholar] [CrossRef]
- Giraldo-Londoño, O.; Muñetón-López, R.A.; Barclay, P.L.; Zhuang, X.; Zhang, D.Z.; Chen, Z. Toward Engineering Lattice Structures with the Material Point Method (MPM). Eng. Comput. 2025, 41, 1637–1655. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, X.; Zhang, X.; Yu, T.X. Response of Woodpecker’s Head during Pecking Process Simulated by Material Point Method. PLoS ONE 2015, 10, e0122677. [Google Scholar] [CrossRef]
- Krzyzanowski, J.; Wójcik, M.; Tejchman, J. Numerical Modelling of Shear Localization in Granular Bodies Using MPM and Non-Local Hypoplasticity. AIP Conf. Proc. 2020, 2239, 020023. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, X.; Su, Y.-C.; Chen, Z. Investigating Three-Dimensional Auxetic Structural Responses to Impact Loading with the Generalized Interpolation Material Point Method. Buildings 2025, 15, 2878. https://doi.org/10.3390/buildings15162878
Zhuang X, Su Y-C, Chen Z. Investigating Three-Dimensional Auxetic Structural Responses to Impact Loading with the Generalized Interpolation Material Point Method. Buildings. 2025; 15(16):2878. https://doi.org/10.3390/buildings15162878
Chicago/Turabian StyleZhuang, Xiatian, Yu-Chen Su, and Zhen Chen. 2025. "Investigating Three-Dimensional Auxetic Structural Responses to Impact Loading with the Generalized Interpolation Material Point Method" Buildings 15, no. 16: 2878. https://doi.org/10.3390/buildings15162878
APA StyleZhuang, X., Su, Y.-C., & Chen, Z. (2025). Investigating Three-Dimensional Auxetic Structural Responses to Impact Loading with the Generalized Interpolation Material Point Method. Buildings, 15(16), 2878. https://doi.org/10.3390/buildings15162878





