Study on the Empirical Probability Distribution Model of Soil Factors Influencing Seismic Liquefaction
Abstract
1. Introduction
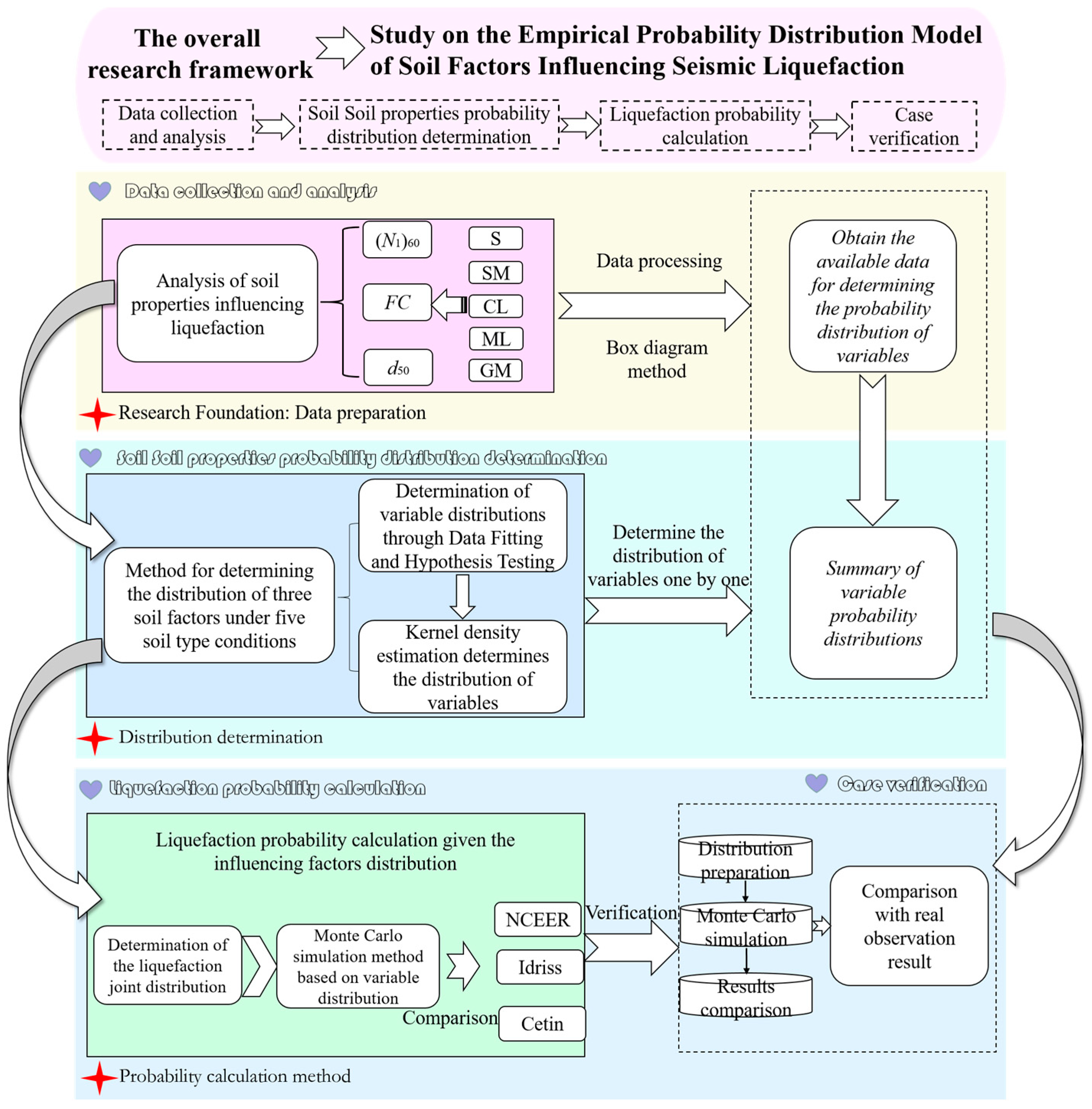
2. Analysis of Liquefaction Influencing Factors and the Collection and Processing of Field Liquefaction Investigation Cases
2.1. Analysis of Soil Properties via Liquefaction Influencing Factors
2.2. Collection and Processing of Field Liquefaction Investigation Cases Based on SPT
3. Study on the Soil Property Variables’ Probability Distribution
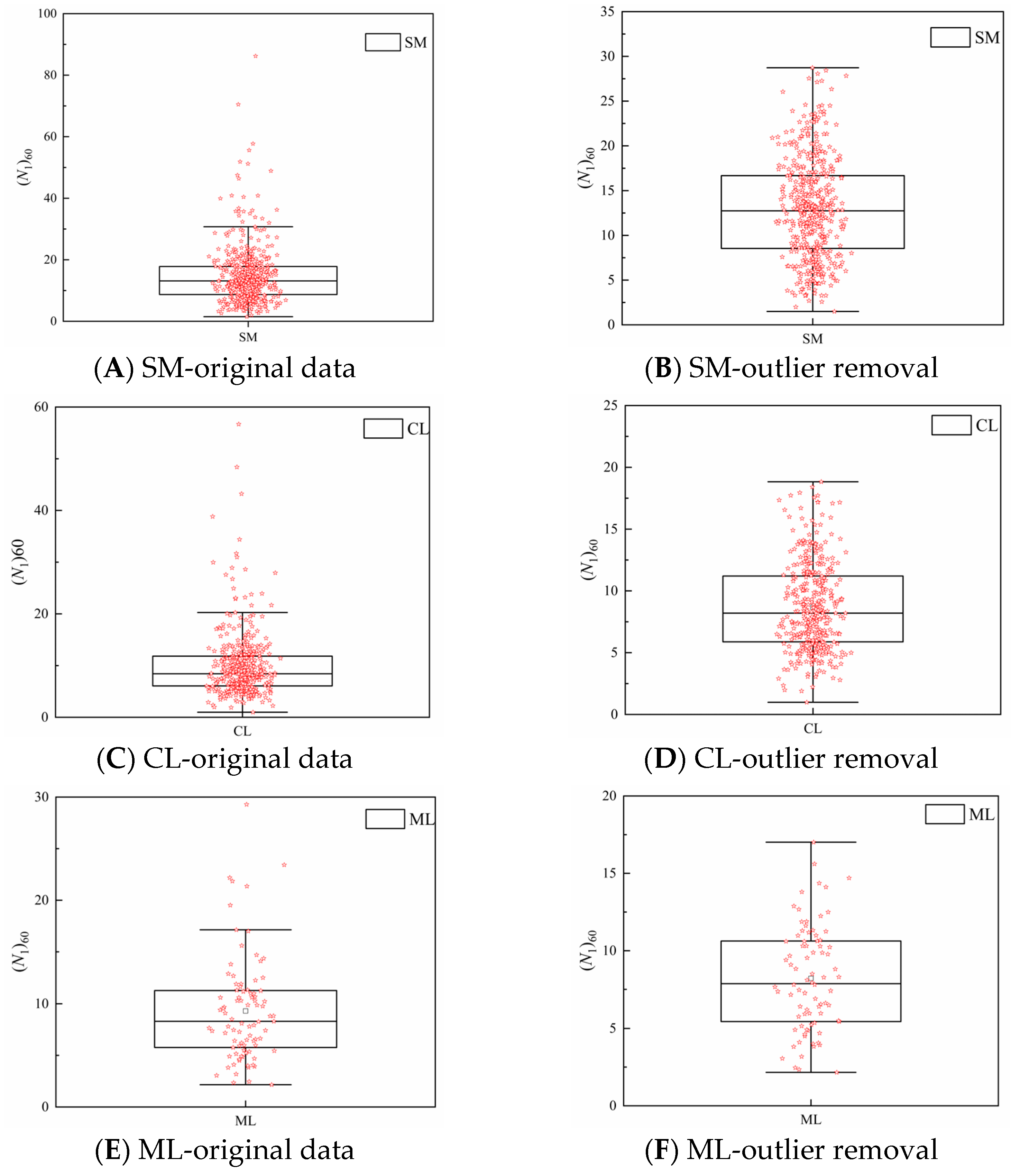
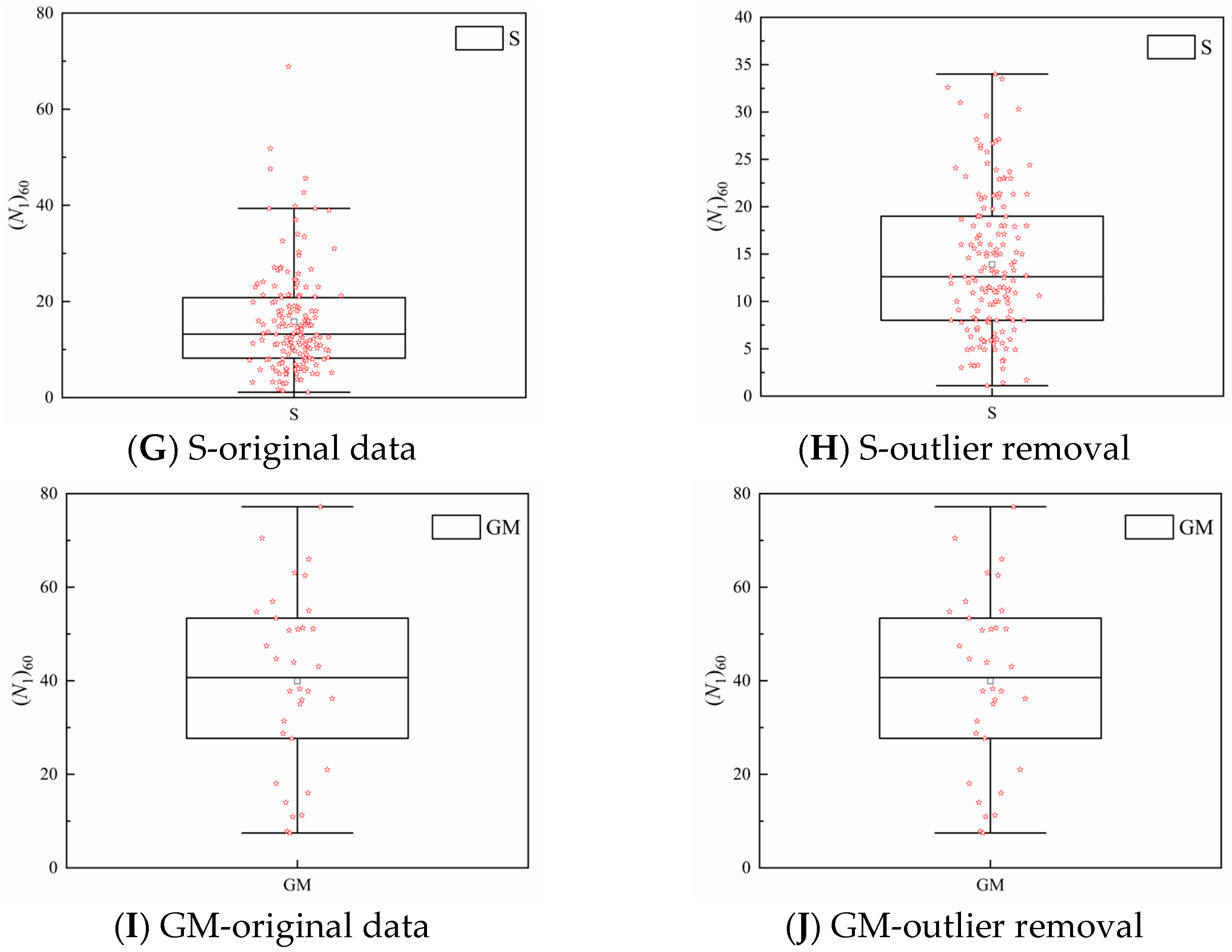
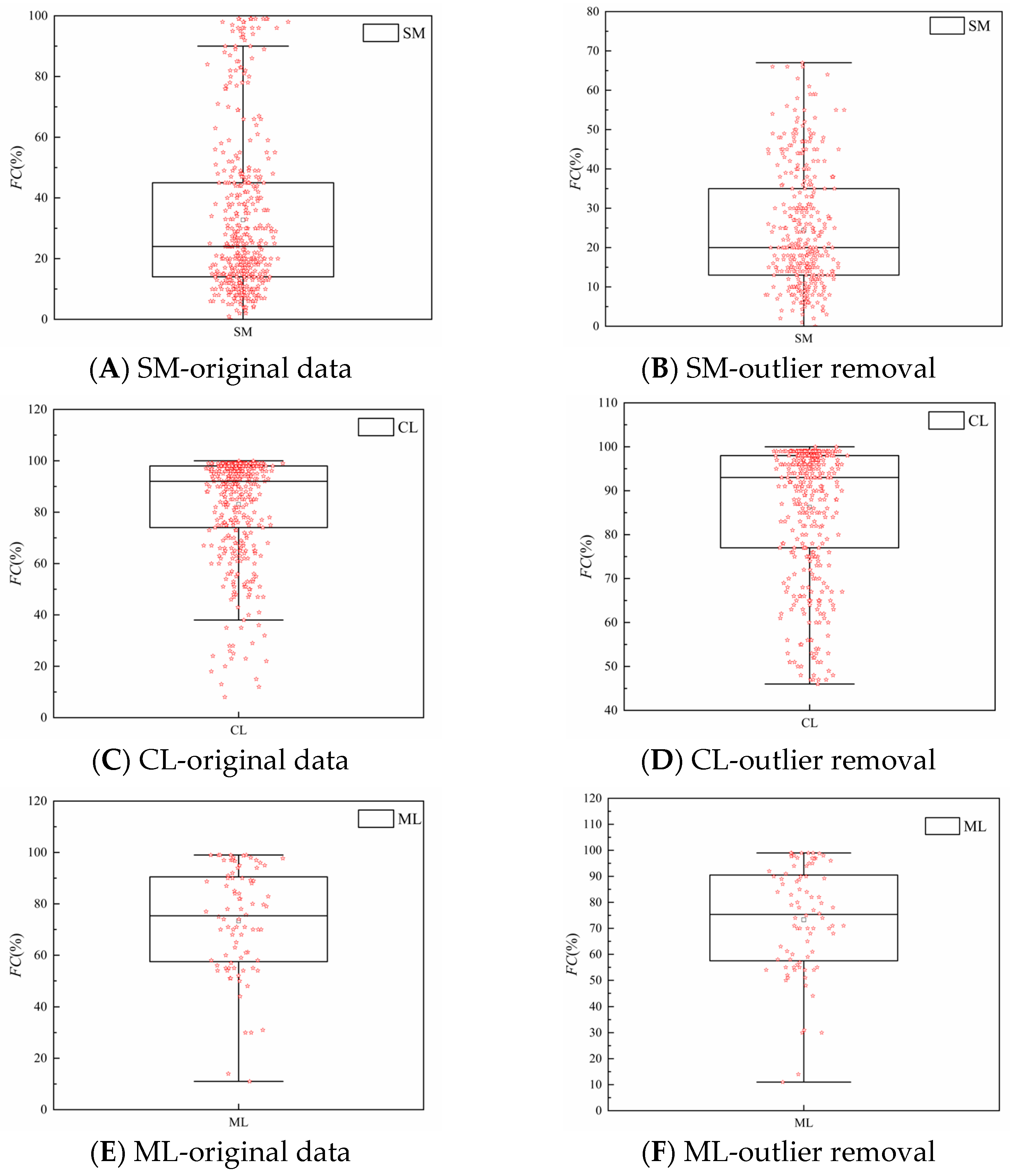
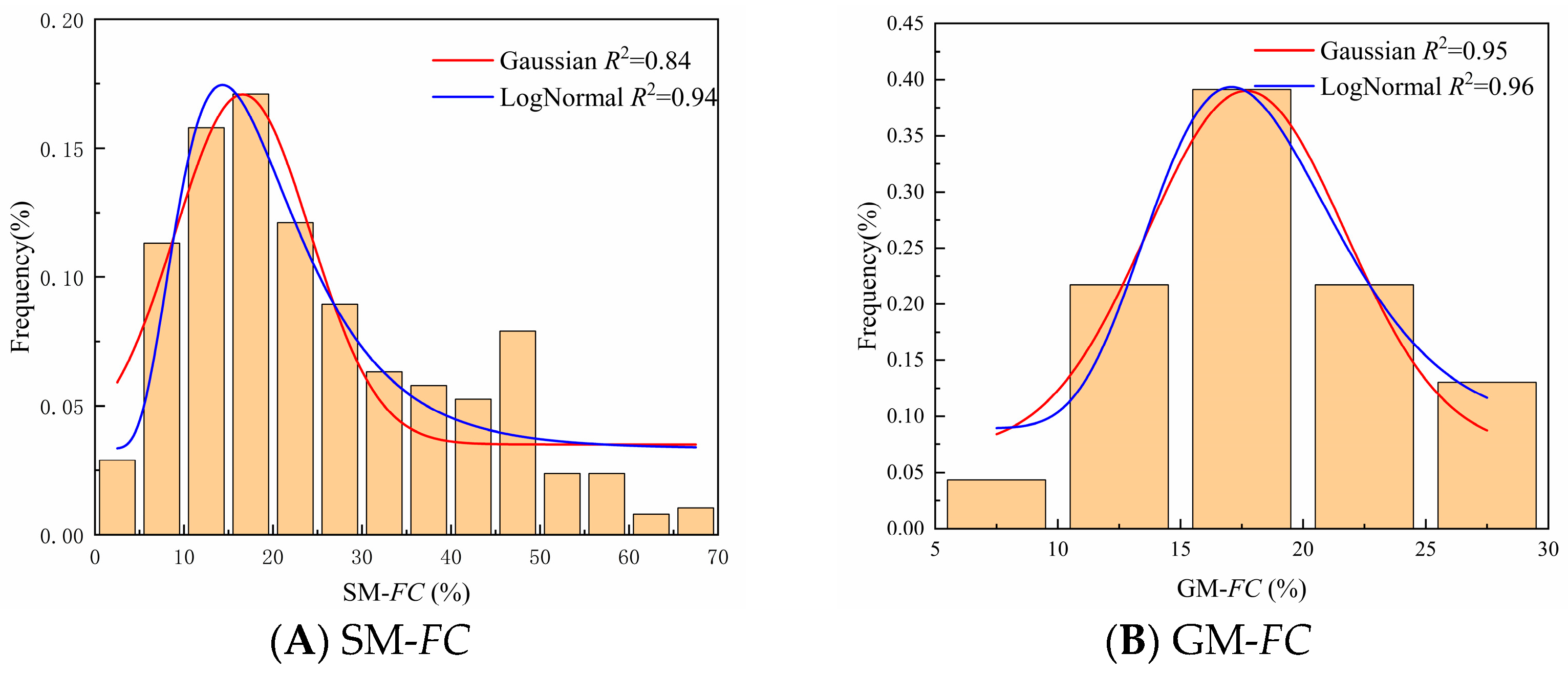
3.1. Interval Discretization and Probability Distribution Fitting
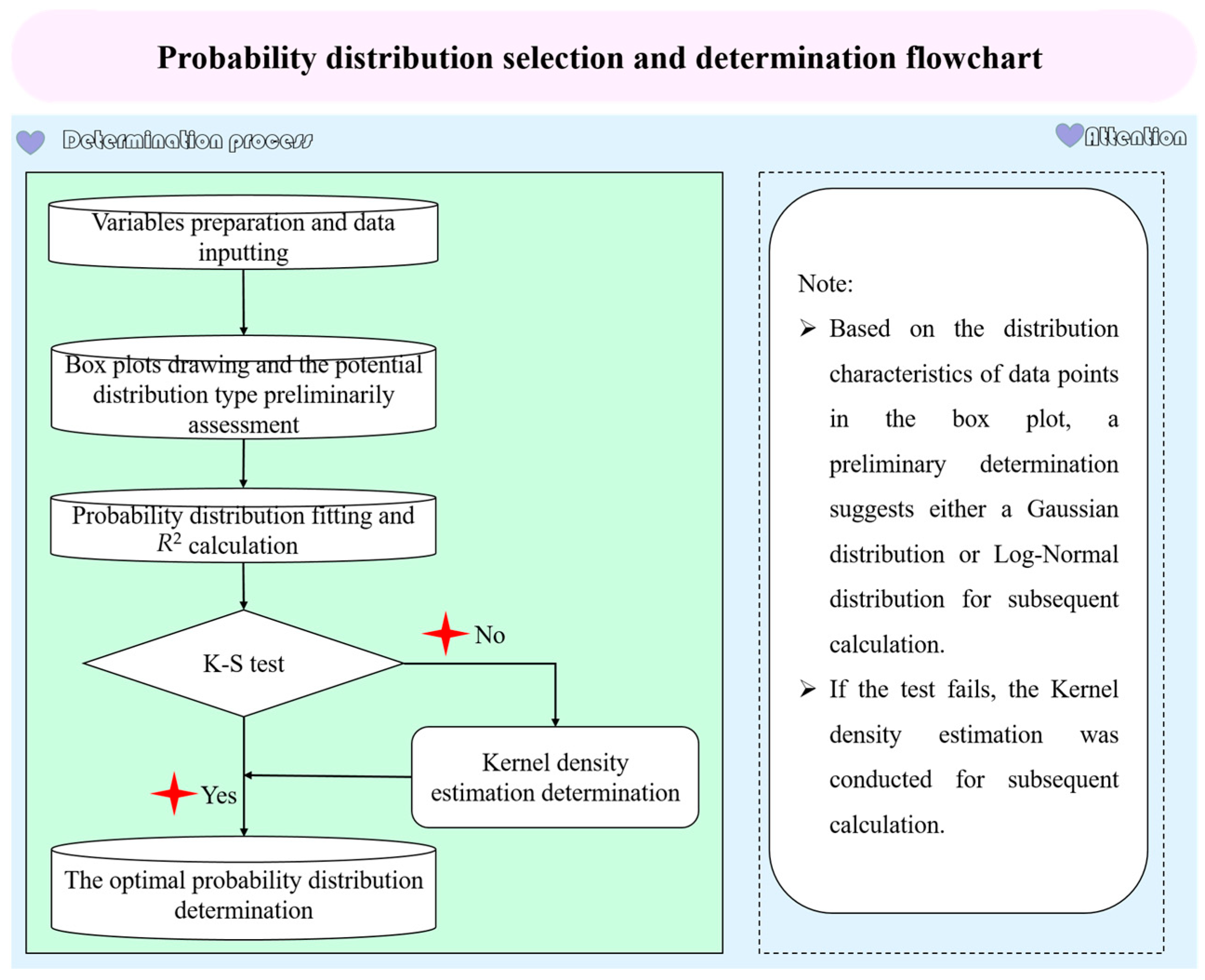
3.2. Probability Distribution Hypothesis Test
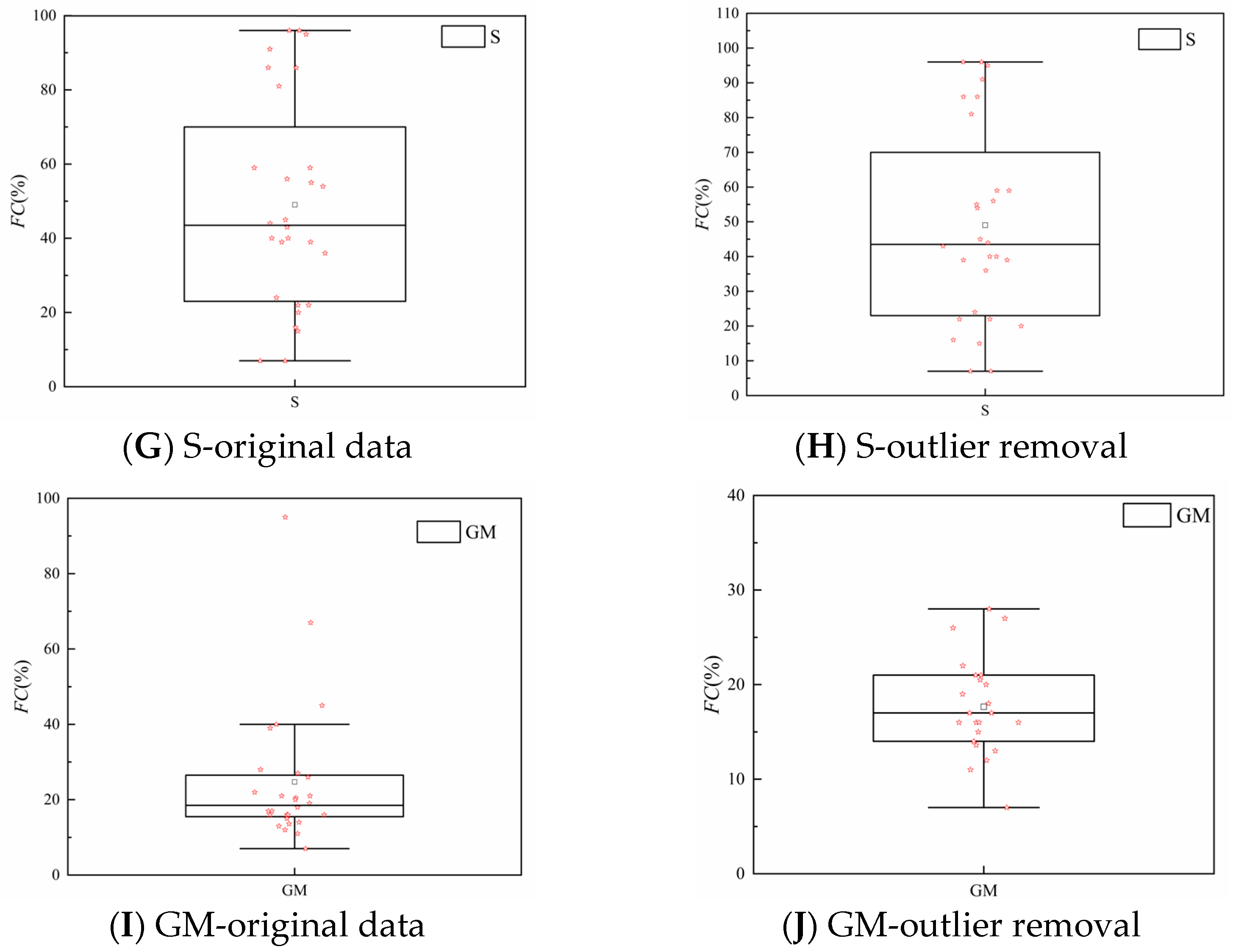
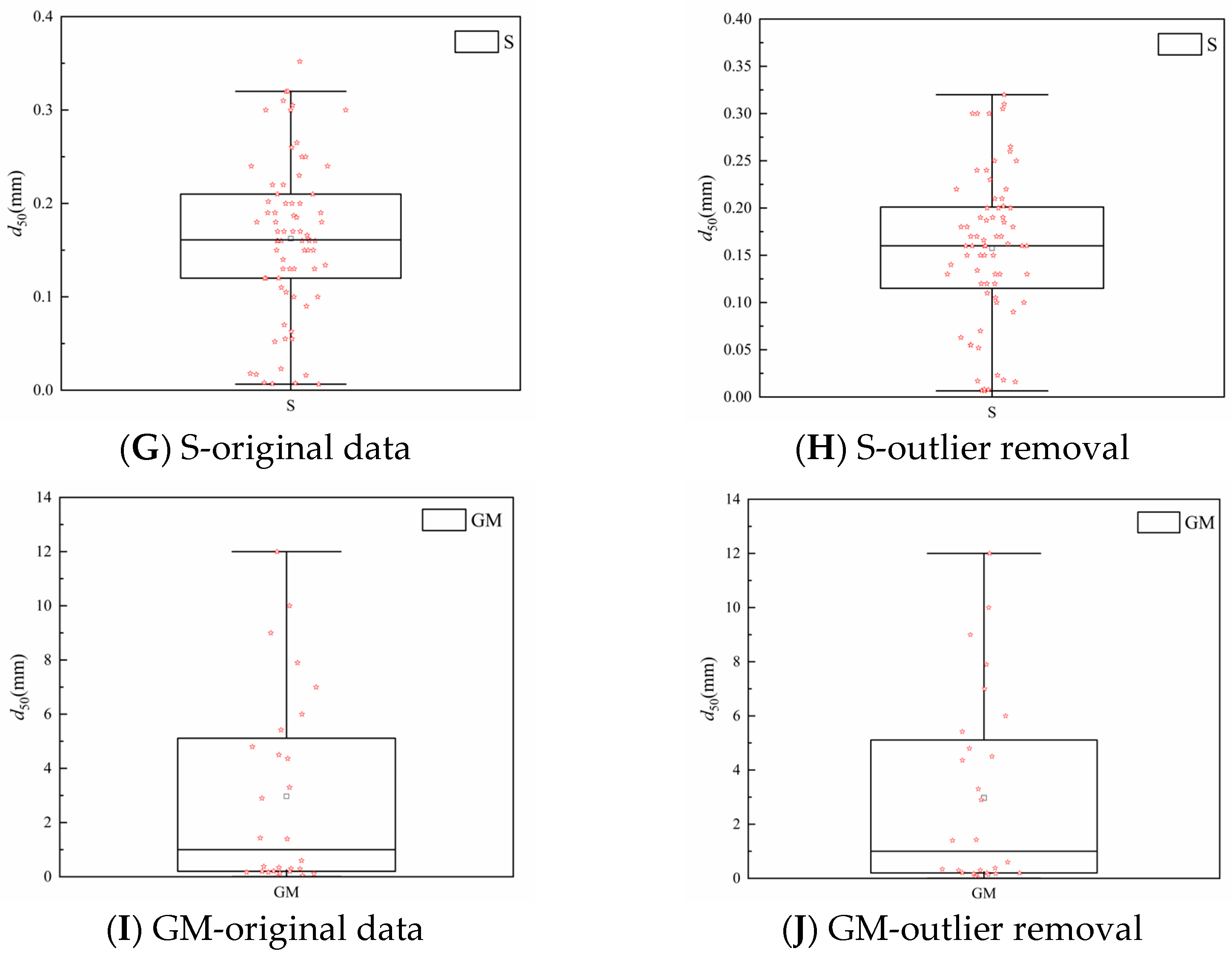
3.3. Further Analysis of Factors Whose Probability Distribution Failed the Hypothesis Test
4. Probability Distribution Determination Results
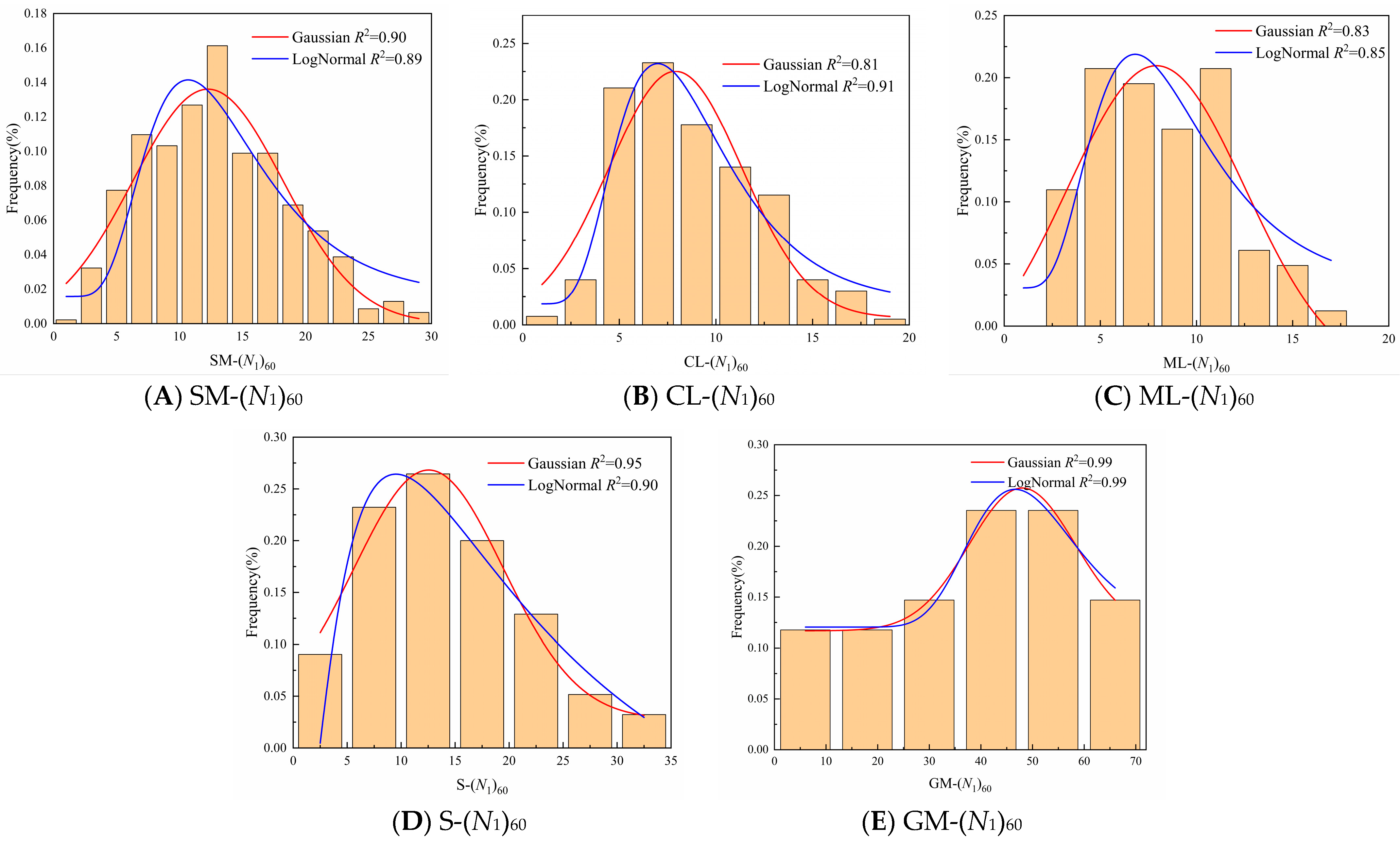
4.1. Probability Distribution Fitting
4.2. Probability Distribution Hypothesis Testing Results
4.3. Further Analysis of the Factors That Failed the Hypothesis Test
5. Liquefaction Probability Calculation Given the Distribution of Influencing Factors
5.1. Method for Determining Liquefaction Probability Based on Variable Distributions
5.2. The Principle and Process of Liquefaction Probability Calculations Using Monte Carlo Method
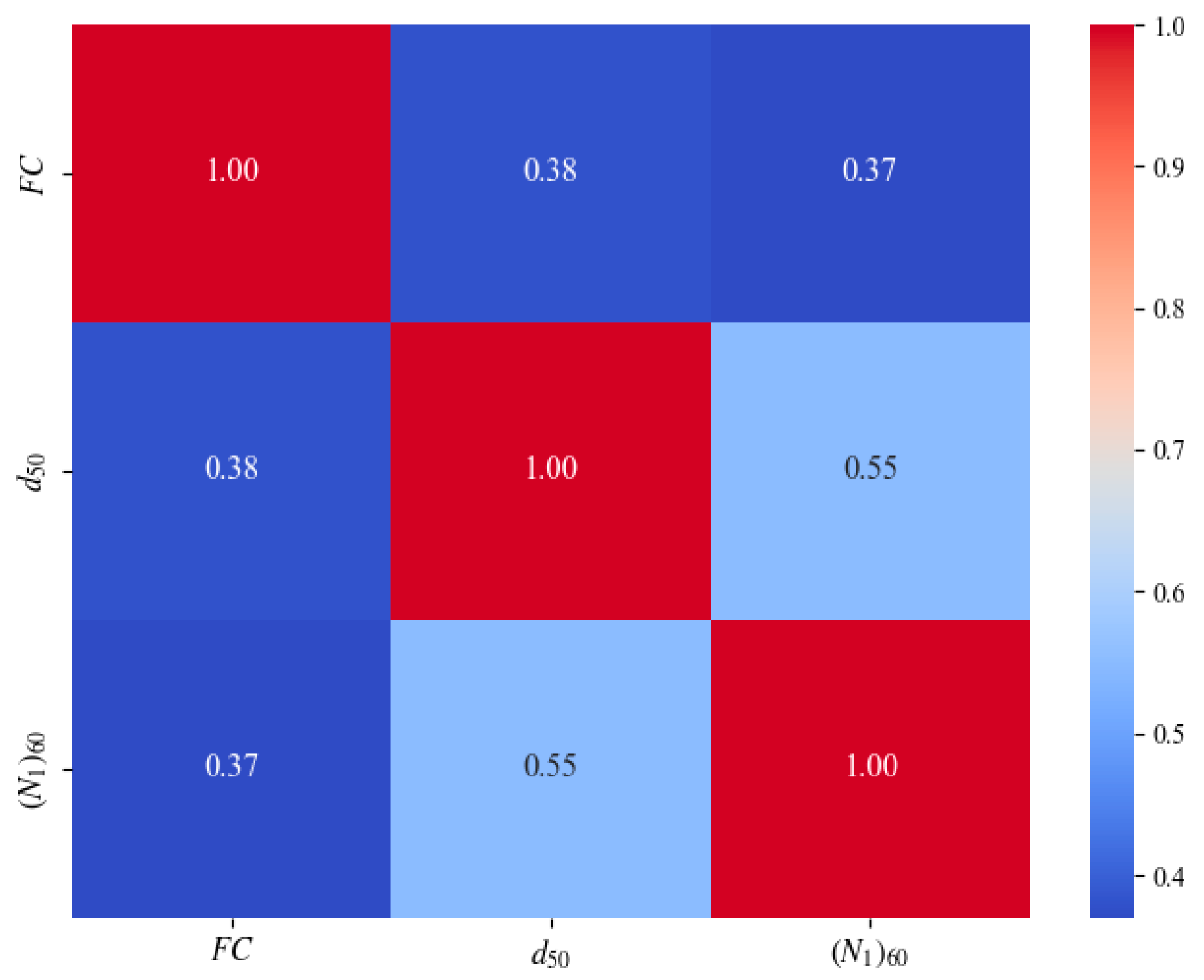
- Step 1: Determination of correlations among the variables in the joint distribution
- Step 2: Sample generation with a certain correlation using the Monte Carlo method
- Step 3: Liquefaction probability calculation with the generated samples
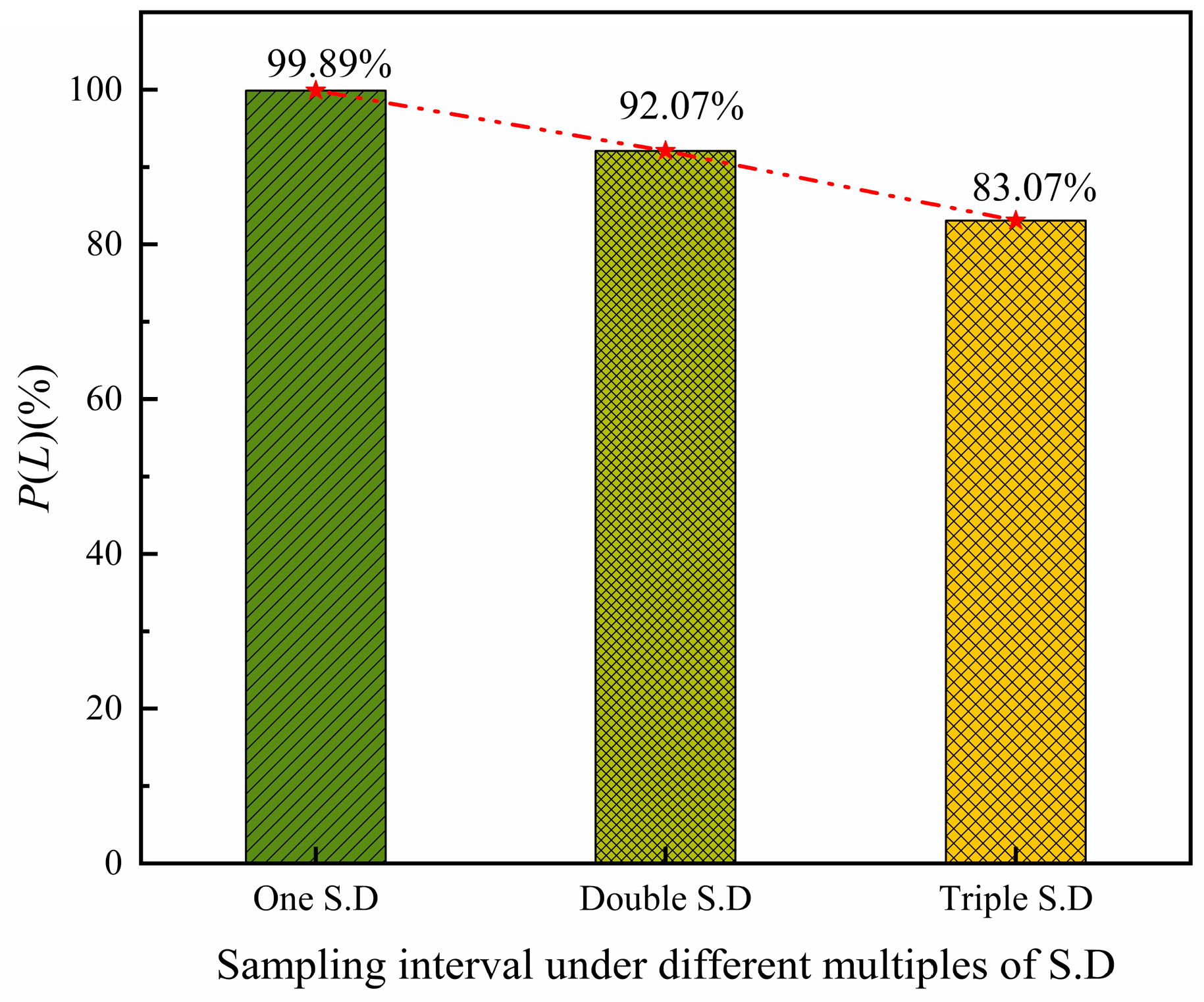
5.3. Case Verification Clculation
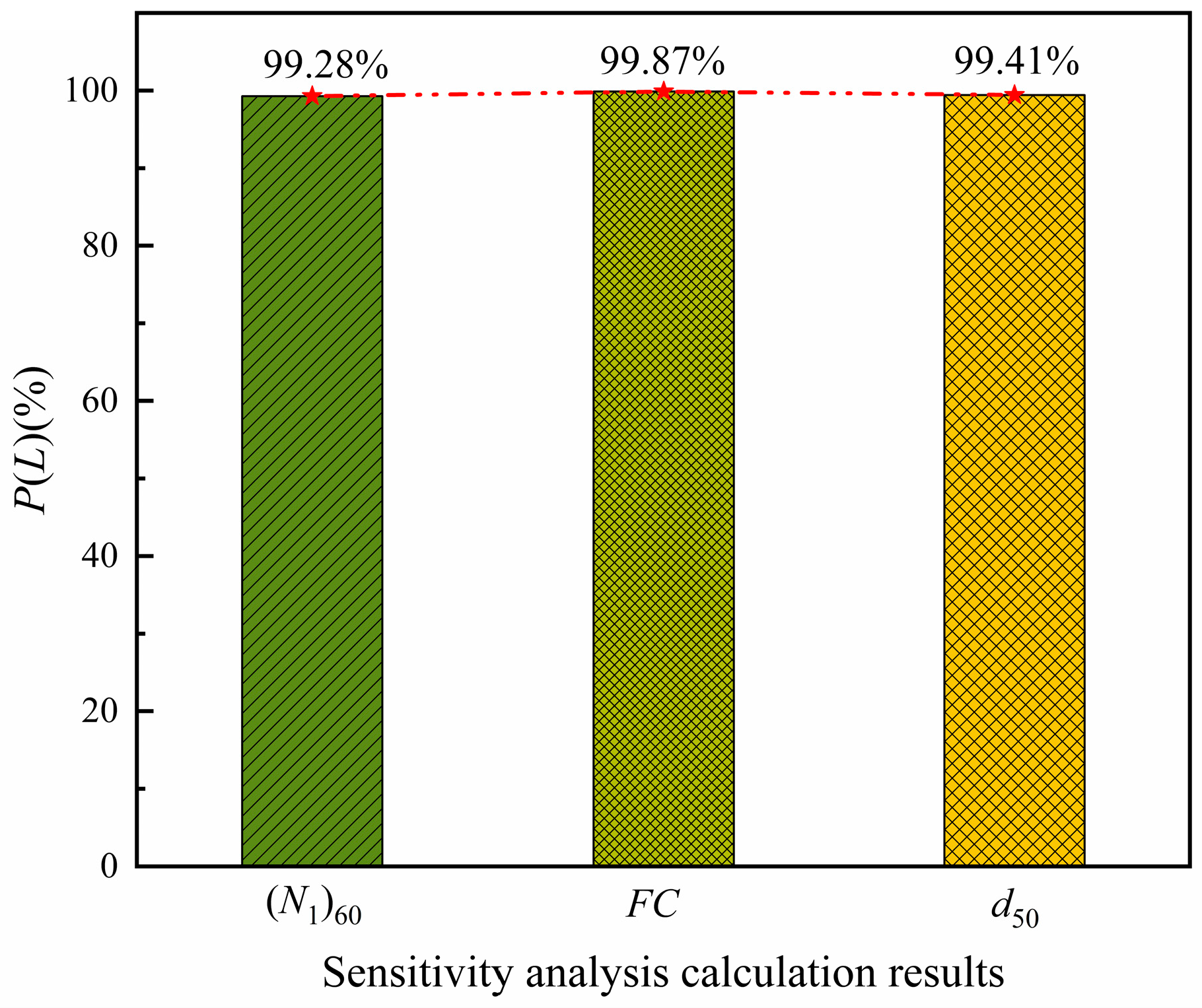
5.4. Sensitivity Analysis
6. Discussion
7. Conclusions
- (1)
- The probability distributions of the same variable under different soil types were not identical. (N1)60, SM, S, and GM followed a Gaussian distribution, while CL and ML followed a lognormal distribution. FC, SM, and GM followed a lognormal distribution, while d50, ML, and S followed the Gaussian and lognormal distributions, respectively. The distribution curves of FC under CL, ML, S, and d50 under SM, CL, and GM can be calculated by the kernel density estimation;
- (2)
- The method of calculating liquefaction probability by using Monte Carlo simulations was feasible. The liquefaction probability calculation result of the case was similar to the existing probability model and consisted with the actual situation, indicating that the proposed methods are reliable;
- (3)
- Regional differences can be considered by introducing the normal distribution error term. The liquefaction probability accuracy can be improved to a certain extent. The method proposed in this paper can either regard amax and M as fixed values to calculate the liquefaction probability at a specific seismic level, or substitute the joint distribution P(amax, M) to determine the total probability within a certain period in the future.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seed, H.B.; Idriss, I.M. Analysis of Soil Liquefaction: Niigata Earthquake. J. Soil Mech. Found. Div. 1967, 93, 83–108. [Google Scholar] [CrossRef]
- Kramer, S.L.; Seed, H.B. Initiation of Soil Liquefaction Under Static Loading Conditions. J. Geotech. Geoenviron. Eng. 1988, 114, 412–430. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified Procedure for Evaluating Soil Liquefaction Potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar] [CrossRef]
- Fiegel, G.L.; Kutter, B.L. Liquefaction Mechanism for Layered Soils. J. Geotech. Geoenviron. Eng. 1994, 120, 737–755. [Google Scholar] [CrossRef]
- Wang, J.P.; Teng, C.C.; Sung, C.Y.; Xu, Y. Weighing the Influence of Geological and Geotechnical Factors in Soil Liquefaction Assessments. Nat. Hazards Rev. 2024, 25, 04024030. [Google Scholar] [CrossRef]
- Özener, P.T.; Özaydin, K.; Berilgen, M. Numerical and Physical Modeling of Liquefaction Mechanisms in Layered Sands. In Geotechnical Earthquake Engineering and Soil Dynamics IV; Proceedings; ASCE Library: Reston, VA, USA, 2012; pp. 1–12. [Google Scholar]
- Seed, H.B.; Idriss, I.M.; Arango, I. Evaluation of Liquefaction Potential Using Field Performance Data. J. Geotech. Geoenviron. Eng. 1983, 109, 458–482. [Google Scholar] [CrossRef]
- Cetin, K.O.; Seed, R.B.; Der Kiureghian, A.; Tokimatsu, K.; Harder Jr, L.F.; Kayen, R.E.; Moss, R.E. Standard Penetration Test-Based Probabilistic and Deterministic Assessment of Seismic Soil Liquefaction Potential. J. Geotech. Geoenviron. Eng. 2004, 130, 1314–1340. [Google Scholar] [CrossRef]
- Youd, T.L.; Idriss, I.M.; Andrus, R.D.; Arango, I.; Castro, G.; Christian, J.T.; Dobry, R.; Finn, W.D.L.; Harder Leslie, F.; Hynes Mary, E.; et al. Liquefaction Resistance of Soils: Summary Report from the 1996 NCEER and 1998 NCEER/NSF Workshops on Evaluation of Liquefaction Resistance of Soils. J. Geotech. Geoenviron. Eng. 2001, 127, 817–833. [Google Scholar] [CrossRef]
- Cetin, K.O.; Youd, T.L.; Seed, R.B.; Bray, J.D.; Stewart, J.P.; Durgunoglu, H.T.; Lettis, W.; Yilmaz, M.T. Liquefaction-Induced Lateral Spreading at Izmit Bay During the Kocaeli (Izmit)-Turkey Earthquake. J. Geotech. Geoenviron. Eng. 2004, 130, 1300–1313. [Google Scholar] [CrossRef]
- Cetin, K.O.; Seed, R.B.; Kayen, R.E.; Moss, R.E.S.; Bilge, H.T.; Ilgac, M.; Chowdhury, K. SPT-based probabilistic and deterministic assessment of seismic soil liquefaction triggering hazard. Soil Dyn. Earthq. Eng. 2018, 115, 698–709. [Google Scholar] [CrossRef]
- Han, X.; Gong, W.; Juang, C.H. Probabilistic evaluation of earthquake-induced liquefaction using Bayesian network based on a side-by-side SPT–CPT database. Can. Geotech. J. 2024, 61, 2653–2666. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. SPT-based probabilistic evaluation of soil liquefaction potential considering design life of civil infrastructures. Comput. Geotech. 2022, 148, 104807. [Google Scholar] [CrossRef]
- Acharya, I.P.; Subedi, M.; KC, R. Liquefaction Hazard Assessment of Kathmandu Valley Using Deterministic and Probabilistic Approaches. In Geo-Risk 2023; Proceedings; ASCE Library: Reston, VA, USA, 2023; pp. 307–317. [Google Scholar]
- Karagiannakis, G.; Di Sarno, L.; Necci, A.; Krausmann, E. Seismic risk assessment of supporting structures and process piping for accident prevention in chemical facilities. Int. J. Disaster Risk Reduct. 2022, 69, 102748. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, J.; Cheng, J.; Yang, S. Dimension-Reduction Spectral Representation of Soil Spatial Variability and Its Application in the Efficient Reliability Analysis of Seismic Response in Tunnels. Reliab. Eng. Syst. Saf. 2024, 248, 110175. [Google Scholar] [CrossRef]
- Kameshwar, S.; Cox, D.T.; Barbosa, A.R.; Farokhnia, K.; Park, H.; Alam, M.S.; van de Lindt, J.W. Probabilistic decision-support framework for community resilience: Incorporating multi-hazards, infrastructure interdependencies, and resilience goals in a Bayesian network. Reliab. Eng. Syst. Saf. 2019, 191, 106568. [Google Scholar] [CrossRef]
- Jas, K.; Mangalathu, S.; Dodagoudar, G.R. Evaluation and analysis of liquefaction potential of gravelly soils using explainable probabilistic machine learning model. Comput. Geotech. 2024, 167, 106051. [Google Scholar] [CrossRef]
- Makdisi, A.J.; Kramer, S.L. Framework for Mapping Liquefaction Hazard–Targeted Design Ground Motions. J. Geotech. Geoenviron. Eng. 2024, 150, 04024123. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. Probabilistic Assessment of Soil Liquefaction Potential Using CPT-Based Smart Site Investigation Strategy. In Geo-Risk 2023; Proceedings; ASCE Library: Reston, VA, USA, 2023; pp. 145–154. [Google Scholar]
- Liao, S.S.C.; Veneziano, D.; Whitman, R.V. Regression Models For Evaluating Liquefaction Probability. J. Geotech. Geoenviron. Eng. 1988, 114, 389–411. [Google Scholar] [CrossRef]
- Yang, H.; Liu, Z.; Xie, Y. Probabilistic Liquefaction Assessment Based on an In-situ State Parameter Considering Soil Spatial Variability and Various Uncertainties. KSCE J. Civ. Eng. 2023, 27, 4228–4239. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G.; Wu, M.; Liu, S. CPT-based fully probabilistic seismic liquefaction potential assessment to reduce uncertainty: Integrating XGBoost algorithm with Bayesian theorem. Comput. Geotech. 2022, 149, 104868. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J. Prediction of liquefaction of gravelly soils based on a cost-sensitive Bayesian network combined with rough set weighting. Gondwana Res. 2024, 131, 57–68. [Google Scholar] [CrossRef]
- Cruz, A.; Karimzadeh, S.; Chieffo, N.; Sandoval, E.; Lourenço, P.B. A Review of Probabilistic Approaches for Assessing the Liquefaction Hazard in Urban Areas. Arch. Comput. Methods Eng. 2024, 31, 4673–4708. [Google Scholar] [CrossRef]
- Sianko, I.; Ozdemir, Z.; Khoshkholghi, S.; Garcia, R.; Hajirasouliha, I.; Yazgan, U.; Pilakoutas, K. A practical probabilistic earthquake hazard analysis tool: Case study Marmara region. Bull. Earthq. Eng. 2020, 18, 2523–2555. [Google Scholar] [CrossRef]
- Wang, F.; Huang, H.; Yin, Z.; Huang, Q. Probabilistic characteristics analysis for the time-dependent deformation of clay soils due to spatial variability. Eur. J. Environ. Civ. Eng. 2021, 26, 6096–6114. [Google Scholar] [CrossRef]
- Lifshitz, S.G.; Urlainis, A.; Moyal, S.; Shohet, I.M. Seismic Resilience in Critical Infrastructures: A Power Station Preparedness Case Study. Appl. Sci. 2024, 14, 3835. [Google Scholar] [CrossRef]
- Huang, F.K.; Wang, G.S. A Method for Developing Seismic Hazard-Consistent Fragility Curves for Soil Liquefaction Using Monte Carlo Simulation. Appl. Sci. 2024, 14, 9482. [Google Scholar] [CrossRef]
- Wang, F.Y.; Zhai, W.Z.; Man, J.H.; Huang, H.W. A hybrid cohesive phase-field numerical method for the stability analysis of rock slopes with discontinuities. Can. Geotech. J. 2025, 62, 1–16. [Google Scholar] [CrossRef]
- Urlainis, A.; Ornai, D.; Levy, R.; Vilnay, O.; Shohet, I.M. Loss and damage assessment in critical infrastructures due to extreme events. Saf. Sci. 2022, 147, 105587. [Google Scholar] [CrossRef]
- Wang, Z.; Cudmani, R.; Pena, O.; Andres, A.; Zhang, C.; Zhou, P. Leveraging Bayesian methods for addressing multi-uncertainty in data-driven seismic liquefaction assessment. J. Rock Mech. Geotech. Eng. 2024, 17, 2474–2491. [Google Scholar] [CrossRef]
- Jain, A.; Oommen, T. Significance of Quantifying Uncertainties in Probabilistic Modeling and a Possible Approach to Select the Best: A Study Using SPT- and CPT-Based Liquefaction Case Histories. In Advances in Soil Dynamics and Foundation Engineering; Proceedings; ASCE Library: Reston, VA, USA, 2014; pp. 83–96. [Google Scholar]
- Tang, X.W.; Hu, J.L.; Qiu, J.N. Identifying significant influence factors of seismic soil liquefaction and analyzing their structural relationship. KSCE J. Civ. Eng. 2016, 20, 2655–2663. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Wu, W.; Sun, Y.; Huang, M.; Zhao, Z.; Zheng, Q. Quantitative study of the effects of loading conditions and physical parameters on the liquefaction properties of saturated sandy soils: A DEM and experimental investigation. Soil Dyn. Earthq. Eng. 2025, 190, 109187. [Google Scholar] [CrossRef]
- Klu, A.K.; Affam, M.; Ewusi, A.; Ziggah, Y.Y.; Boateng, E.K. Site classification and soil liquefaction evaluation based on shear wave velocity via HoliSurface approach. J. Afr. Earth Sci. 2025, 225, 105574. [Google Scholar] [CrossRef]
- Boulanger, R.W.; Idriss, I.M. Probabilistic Standard Penetration Test–Based Liquefaction–Triggering Procedure. J. Geotech. Geoenviron. Eng. 2012, 138, 1185–1195. [Google Scholar] [CrossRef]
- Gu, X.; Zuo, K.; Hu, C.; Hu, J. Liquefaction resistance and small strain stiffness of silty sand: Effects of host sand gradation and fines content. Eng. Geol. 2024, 335, 107546. [Google Scholar] [CrossRef]
- Yu, T.; Fleureau, J.M.; Souli, H.; Kong, X. The improved cyclic resistance of bio-treated sands with various gradations for liquefaction mitigation: Density increase and/or cementation? Soil Dyn. Earthq. Eng. 2024, 185, 108894. [Google Scholar] [CrossRef]
- El Ahmad, M.; Hubler, J. Investigating the Influence of Sand Particle Morphology on Post-Liquefaction Volumetric Strain of Two Uniform Sands. In Geo-Congress 2024; Proceedings; ASCE Library: Reston, VA, USA, 2024; pp. 415–424. [Google Scholar]
- Yang, S.; Huang, D. Understanding the influence of drained cyclic preloading on liquefaction resistance of sands using DEM-clump modeling. Comput. Geotech. 2024, 176, 106800. [Google Scholar] [CrossRef]
- Xu, M.Q.; Pan, K.; Duan, B.; Wu, Q.X.; Yang, Z.X. Investigating the influence of particle shape on discrete element modeling of granular soil under multidirectional cyclic shearing. Soil Dyn. Earthq. Eng. 2025, 189, 109097. [Google Scholar] [CrossRef]
- Molina, G.F.; Viana, F.A.; Ferreira, C.; Caicedo, B. Insights into the assessment and interpretation of earthquake-induced liquefaction in sands under different degrees of saturation. Earth-Sci. Rev. 2024, 258, 104925. [Google Scholar] [CrossRef]
- Upadhyaya, S.; Maurer, B.W.; Green, R.A.; Rodriguez-Marek, A.; van Ballegooy, S. Surficial liquefaction manifestation severity thresholds for profiles having high fines-content, high-plasticity soils. Can. Geotech. J. 2022, 60, 642–653. [Google Scholar] [CrossRef]
- Duan, W.; Congress, S.S.C.; Cai, G.; Zhao, Z.; Pu, S.; Liu, S.; Dong, X.; Wu, M.; Chen, R. Characterizing the in-situ state of sandy soils for liquefaction analysis using resistivity piezocone penetration test. Soil Dyn. Earthq. Eng. 2023, 164, 107529. [Google Scholar] [CrossRef]
- Jas, K.; Dodagoudar, G.R. Explainable machine learning model for liquefaction potential assessment of soils using XGBoost-SHAP. Soil Dyn. Earthq. Eng. 2023, 165, 107662. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Yang, Z.; Qi, X. Estimation of site-specific multivariate probability distribution of soil properties using a mixed sampling technique. Comput. Geotech. 2024, 166, 105956. [Google Scholar] [CrossRef]
- Porwik, P.; Dadzie, B.M. Detection of data drift in a two-dimensional stream using the Kolmogorov-Smirnov test. Procedia Comput. Sci. 2022, 207, 168–175. [Google Scholar] [CrossRef]
- Harrop-Williams, K. Probability Distribution of Strength Parameters in Uniform Soils. J. Eng. Mech. 1986, 112, 345–350. [Google Scholar] [CrossRef]
- Chen, W.; Ding, J.; Shi, C.; Wang, T.; Connolly, D.P. Geotechnical correlation field-informed and data-driven prediction of spatially varying geotechnical properties. Comput. Geotech. 2024, 171, 106407. [Google Scholar] [CrossRef]
- Zhang, J.; Han, S.; Li, M.; Li, H.; Zhao, W.; Wang, J.; Liang, H. CasMDN: A deep learning-based multivariate distribution modelling approach and its application in geotechnical engineering. Comput. Geotech. 2024, 168, 106164. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Probabilistic Modeling of Soil Profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Gao, D.Z. Reliability Principle of Soil Mechanics; China Architecture & Building Press: Beijing, China, 1989. [Google Scholar]
- Ding, J.H.; Liang, J.G.; Zhang, J.P.; Chang, W.J. Reliability Design Principle and Application of Foundation Engineering; China Water & Power Press, Intellectual Property Publishing House: Beijing, China, 2010. [Google Scholar]
- Zacchei, E.; Molina, J.L. Probabilistic Seismic Hazard Analysis for Andalusian Dams in Southern Spain Using New Seismogenic Zones. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2022, 8, 04022034. [Google Scholar] [CrossRef]



| Factors | Influencing Factors | |||
|---|---|---|---|---|
| Method | Dynamic Loading | Environmental Factors | Soil Factors | |
| Deterministic method | NCEER | M, amax | ds, dw, σ, σ’ | (N1)60, FC, DR |
| Chinese code | M, amax, R | ds, dw | N, ρc | |
| Probabilistic method | Idriss | M, amax | ds, dw, σ, σ’ | (N1)60, FC, DR |
| Liao | amax | σ, σ’ | N | |
| Cetin | M, amax | σ, σ’ | (N1)60, FC | |
| Chen | M, amax | σ, σ’ | (N1)60, FC, DR | |
| Machine learning method | Support vector machine | M, ED, R | ds, dw | N |
| Neural network | M, amax | ds, dw, σ, σ’ | (N1)60, FC, d50 | |
| Bayesian network | M, amax, R | ds, dw, σ, σ’ | (N1)60, FC, d50, ST | |
| Soil Type | Factors | Minimum Value | Maximum Value | Mean Value | Variance | Variation Coefficient |
|---|---|---|---|---|---|---|
| SM | (N1)60 | 1.5 | 86 | 14.74 | 86.85 | 0.63 |
| FC | 0 | 99 | 32.75 | 674.33 | 0.79 | |
| d50 | 0.0028 | 96 | 0.55 | 20.59 | 8.18 | |
| CL | (N1)60 | 0.98 | 56.68 | 9.92 | 39.43 | 0.63 |
| FC | 8 | 100 | 83.07 | 398.91 | 0.24 | |
| d50 | 0.002 | 5 | 0.043 | 0.06 | 5.74 | |
| ML | (N1)60 | 2.16 | 29.28 | 9.30 | 25.63 | 0.54 |
| FC | 5.73 | 99 | 72.50 | 477.35 | 0.30 | |
| d50 | 0 | 0.22 | 0.045 | 0.001 | 0.80 | |
| S | (N1)60 | 1.1 | 68.87 | 15.78 | 111.92 | 0.67 |
| FC | 7 | 96 | 49.22 | 832.64 | 0.59 | |
| d50 | 0.0065 | 15 | 0.57 | 4.08 | 3.54 | |
| GM | (N1)60 | 7.46 | 77.20 | 39.94 | 357.83 | 0.47 |
| FC | 7 | 95 | 24.72 | 344.59 | 0.75 | |
| d50 | 0.0055 | 12 | 2.97 | 12.64 | 1.20 |
| Distribution Name | Gaussian | Lognormal | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SM | CL | ML | S | GM | SM | CL | ML | S | GM | |
| (N1)60 | 0.31 | 0.02 | 0.51 | 0.25 | 0.80 | 0.00 | 0.69 | 0.76 | 0.18 | 0.13 |
| FC | 0.00 | 0.00 | 0.00 | 0.00 | 0.76 | 0.28 | 0.00 | 0.00 | 0.00 | 0.88 |
| d50 | 0.00 | 0.00 | 0.23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.53 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Fan, M.; Li, J.; Liu, X.; Zhao, J.; Yang, H. Study on the Empirical Probability Distribution Model of Soil Factors Influencing Seismic Liquefaction. Buildings 2025, 15, 2861. https://doi.org/10.3390/buildings15162861
Yang Z, Fan M, Li J, Liu X, Zhao J, Yang H. Study on the Empirical Probability Distribution Model of Soil Factors Influencing Seismic Liquefaction. Buildings. 2025; 15(16):2861. https://doi.org/10.3390/buildings15162861
Chicago/Turabian StyleYang, Zhengquan, Meng Fan, Jingjun Li, Xiaosheng Liu, Jianming Zhao, and Hui Yang. 2025. "Study on the Empirical Probability Distribution Model of Soil Factors Influencing Seismic Liquefaction" Buildings 15, no. 16: 2861. https://doi.org/10.3390/buildings15162861
APA StyleYang, Z., Fan, M., Li, J., Liu, X., Zhao, J., & Yang, H. (2025). Study on the Empirical Probability Distribution Model of Soil Factors Influencing Seismic Liquefaction. Buildings, 15(16), 2861. https://doi.org/10.3390/buildings15162861





