Inspection Data-Driven Machine Learning Models for Predicting the Remaining Service Life of Deteriorating Bridge Decks
Abstract
1. Introduction
2. Literature Review
2.1. National Frameworks for Assessing Bridge Deck Deterioration
2.2. Concrete Bridge Deck Damage Mechanism
2.2.1. Corrosion Initiation Due to Chloride Ingress and Carbonation
- Cd = Design chloride concentration at depth x and time t
- Ci = Initial chloride concentration (maximum value)
- Cs = Surface chloride concentration determined from measurements
- Erf = Error function (
- Dd = Effective diffusion coefficient of chloride ions
- x = Concrete cover depth to reinforcing steel
- t = service years
- Tcr = Time to crack initiation
- Wcrit = Critical mass of corrosion products
- ρrust = Density of corrosion products
- ρsteel = Density of steel
- α = Ratio of molecular weight between steel and corrosion products
- D = Diameter of the reinforcing bar
- Cs = Chloride concentration measured at the concrete surface
- c = Thickness of the concrete cover
- ft = Tensile strength of concrete
- E = Elastic modulus of concrete
- a = Distance from the center of the reinforcing bar to the boundary of the void region between the rebar and the concrete
- b = Distance from the center of the reinforcing bar to the concrete surface
- υc = Poisson’s ratio of concrete at the service limit state
- d0 = Thickness of the porous zone
2.2.2. Machine Learning-Based Studies on Bridge Deck Deterioration
3. Methodology
3.1. Definition of Deterioration for Bridge Deck
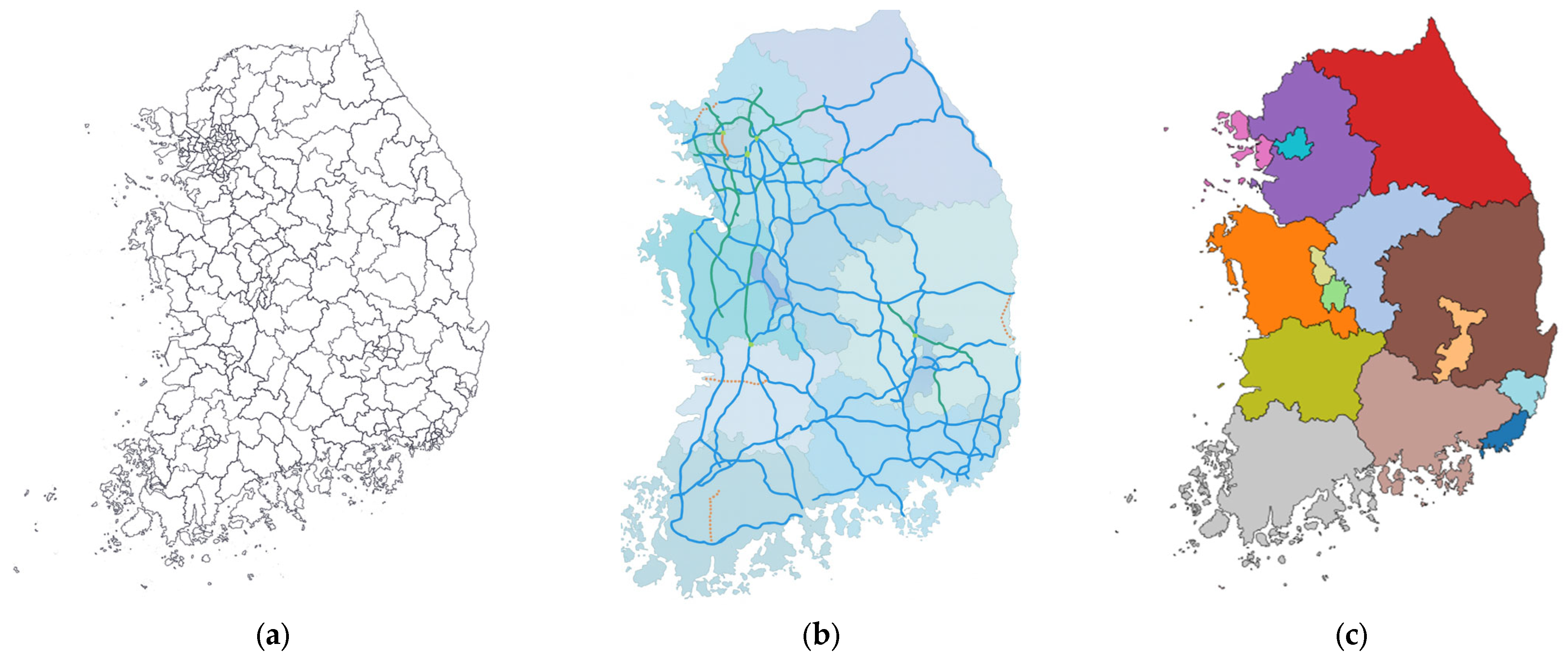
3.2. Data Zoning
3.2.1. Zoning for Dataset
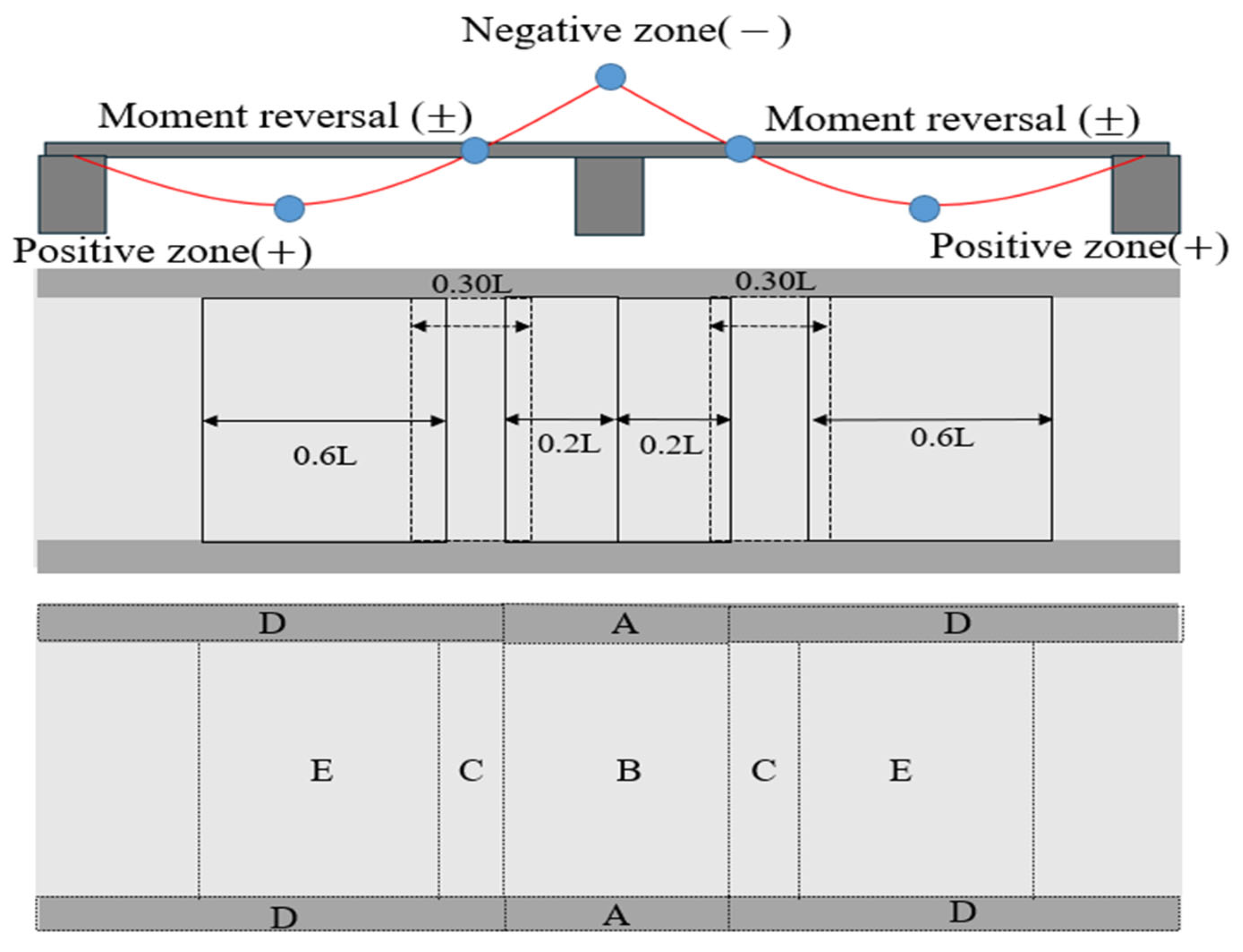
3.2.2. Zoning for Load Conditions in the Bridge Span
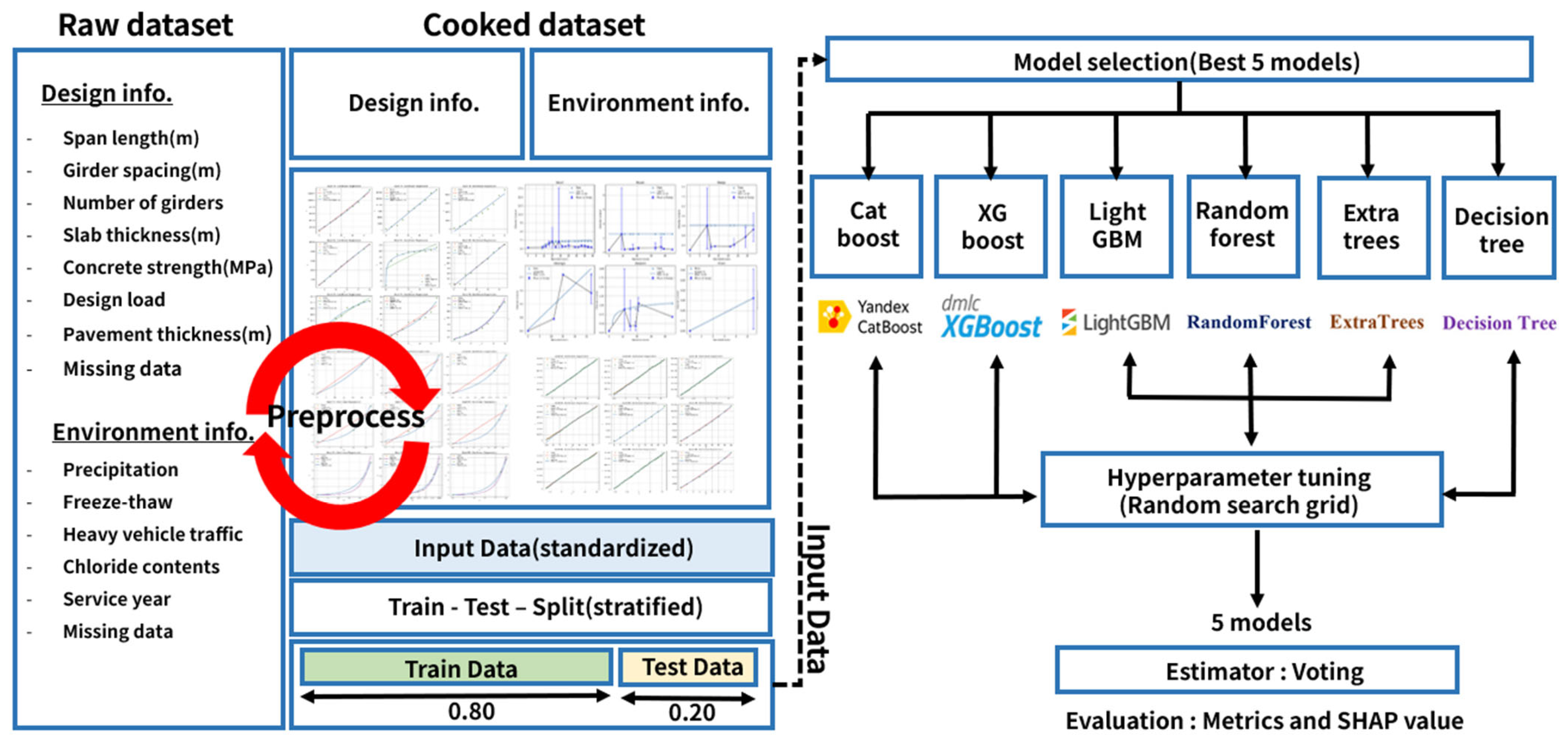
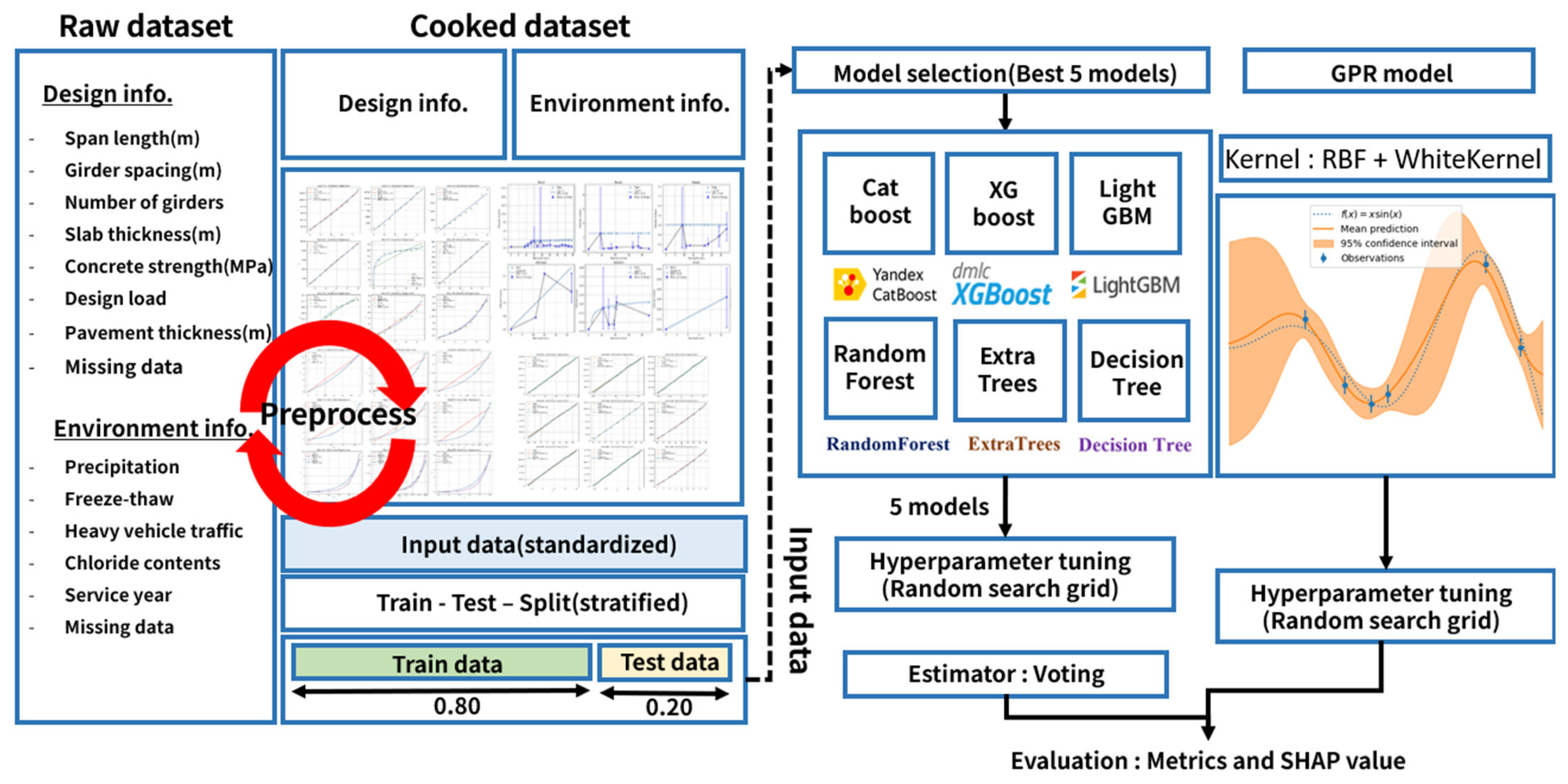
3.3. Machine Leaning Model
- TP: Number of positive samples correctly predicted
- TN: Number of negative samples correctly predicted
- FP: Number of negative samples incorrectly predicted as positive
- FN: Number of positive samples incorrectly predicted as negative
- : Actual observed value
- : Predicted value
- n: Number of data points
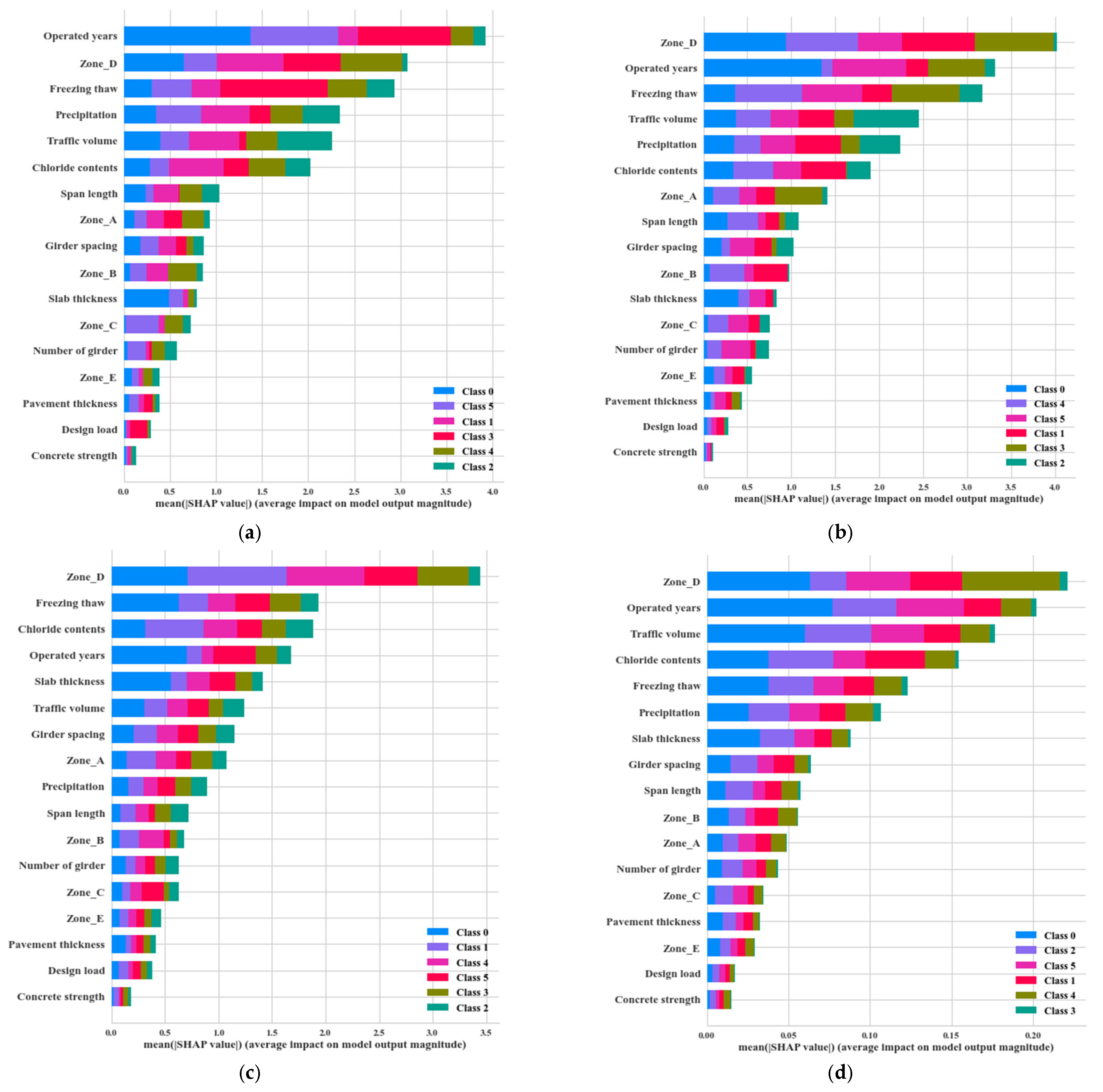
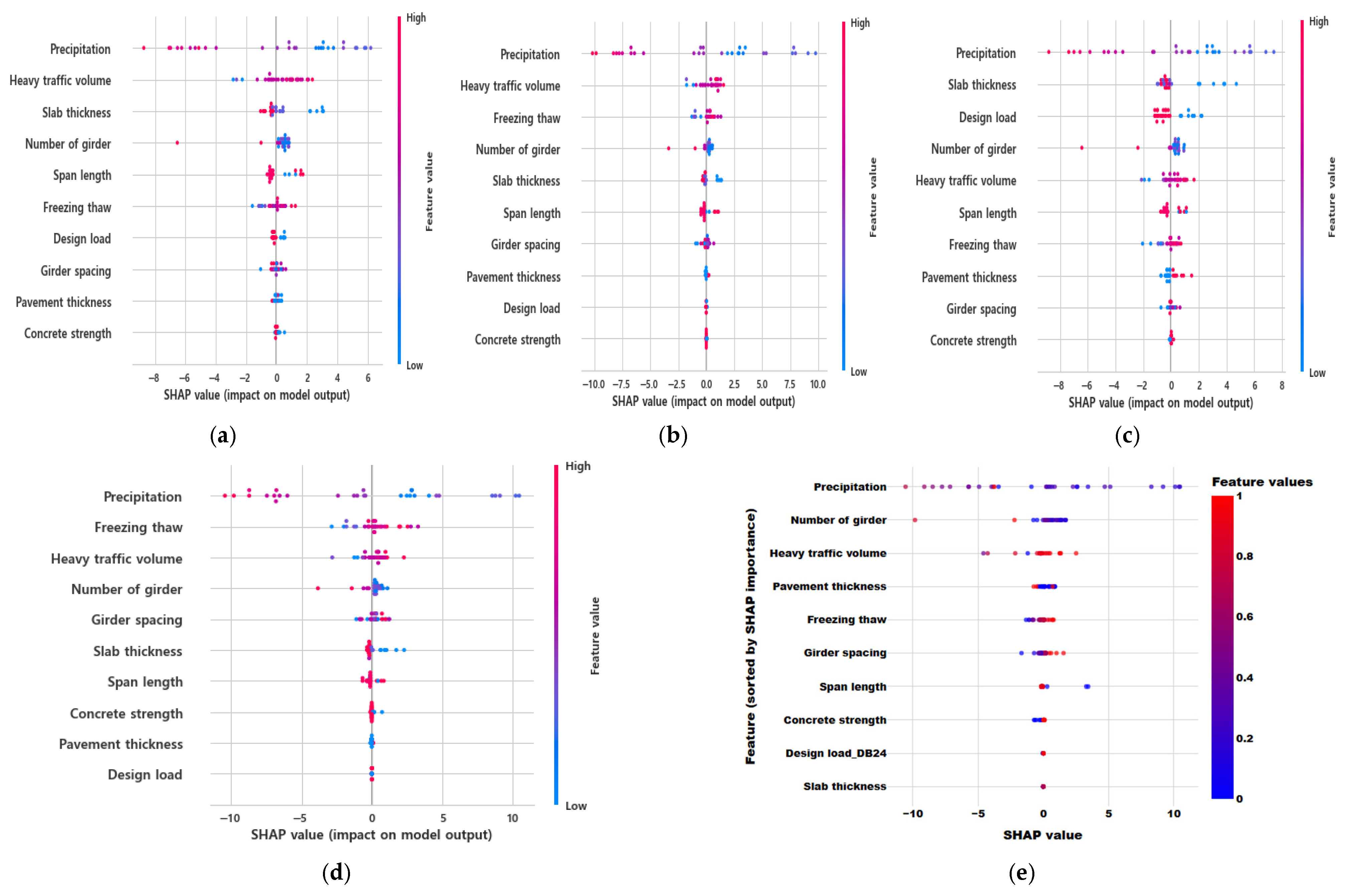
3.4. Feature Importance (SHAP—SHapley Additive exPlanations)
4. Data Collection for Machine Learning
4.1. Data Composition
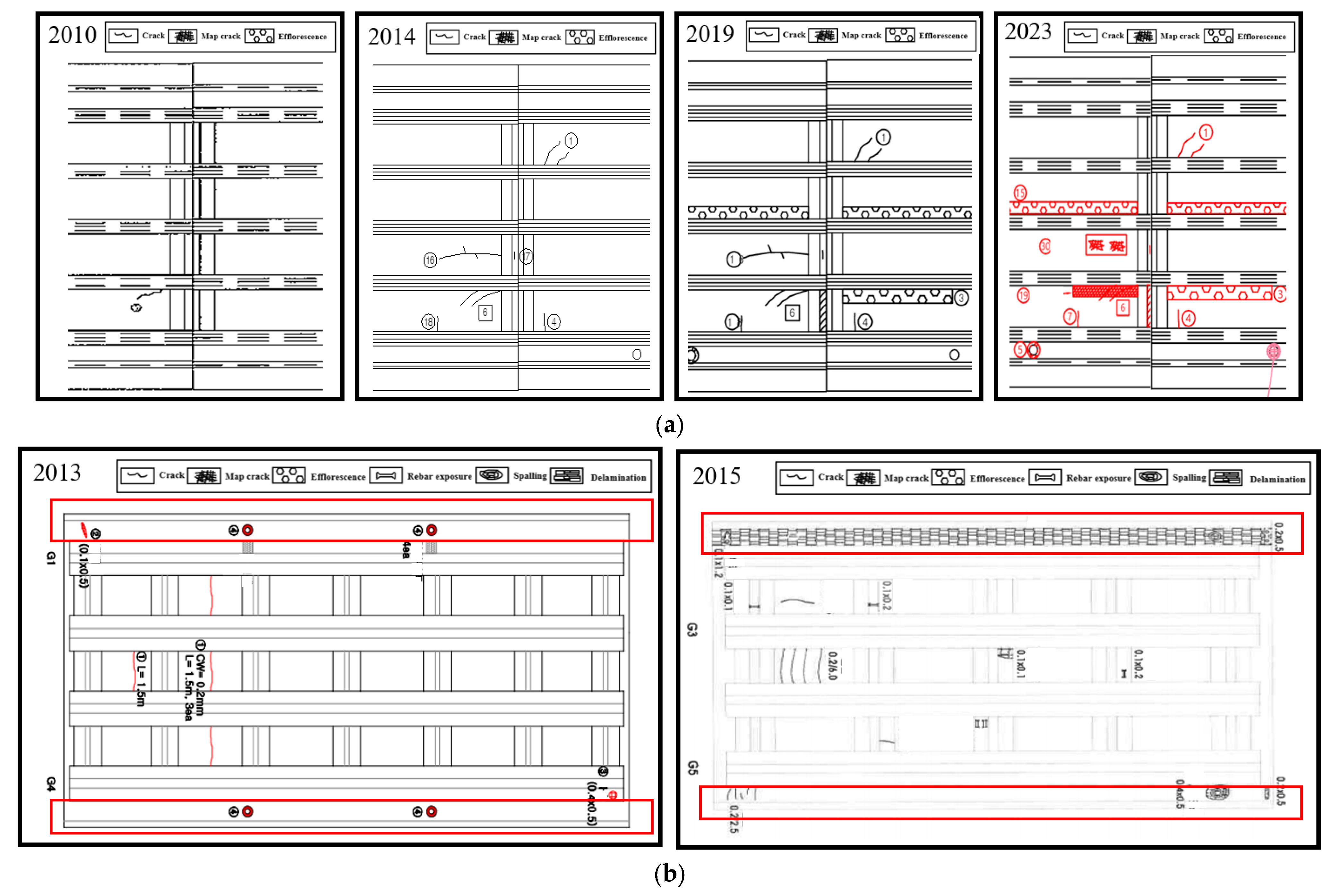
- The occurrence time of deterioration visible in the visual inspection map is defined as the inspection year recorded in the map.
- Initial transverse cracks in the deck are assumed to occur at the time of bridge completion.
- The progression from map cracking to efflorescence is assumed to result from water penetration through full-depth cracks from the surface, which initiates corrosion of the internal reinforcement and gradually accelerates its spread.
- Since the characteristics of deck data extracted from bridges vary depending on location, the deck is divided into five zones according to load characteristics. Each zone is assumed to have uniform loading and environmental conditions.
- The onset of delamination and spalling is assumed to coincide with the initiation of surface cracking caused by corrosion-induced expansion of reinforcement.
- Initial material defects in concrete are assumed to be absent, and the compressive strength is taken as the design strength.
- Chemical data obtained from the deck are represented by the median value of the dataset, regardless of the sampling location.
- Although negative moments may also occur in the direction perpendicular to the bridge axis, this study considers only the longitudinal (bridge axis) moment.
- Only zones with three or more consecutive inspection records were included in the analysis, while zones with insufficient data were excluded.
- Time-series records showing abnormal reversals or improvements in deterioration states (e.g., from State 5 to State 2) were deemed logically inconsistent and removed.
- To prevent distortion of deterioration trends and maintain the predictive accuracy of the model, no interpolation was applied to missing segments in the time series.
4.2. Bridge Structural Information
4.3. Deterioration Data on the Bridge Inspection Map
4.4. Environmental Data (Accumalted Data over Time)
4.4.1. Traffic Volume
4.4.2. Precipitation
4.4.3. Carbonation
4.4.4. Chloride Contents
4.4.5. Freezing-Thaw
4.5. Dataset for ML
5. ML for Remaining Life of Bridge Deck
5.1. ML Classification
5.1.1. ML for Classification with All Integrated Data
5.1.2. ML for Classification with Dataset for Each Zone A~E
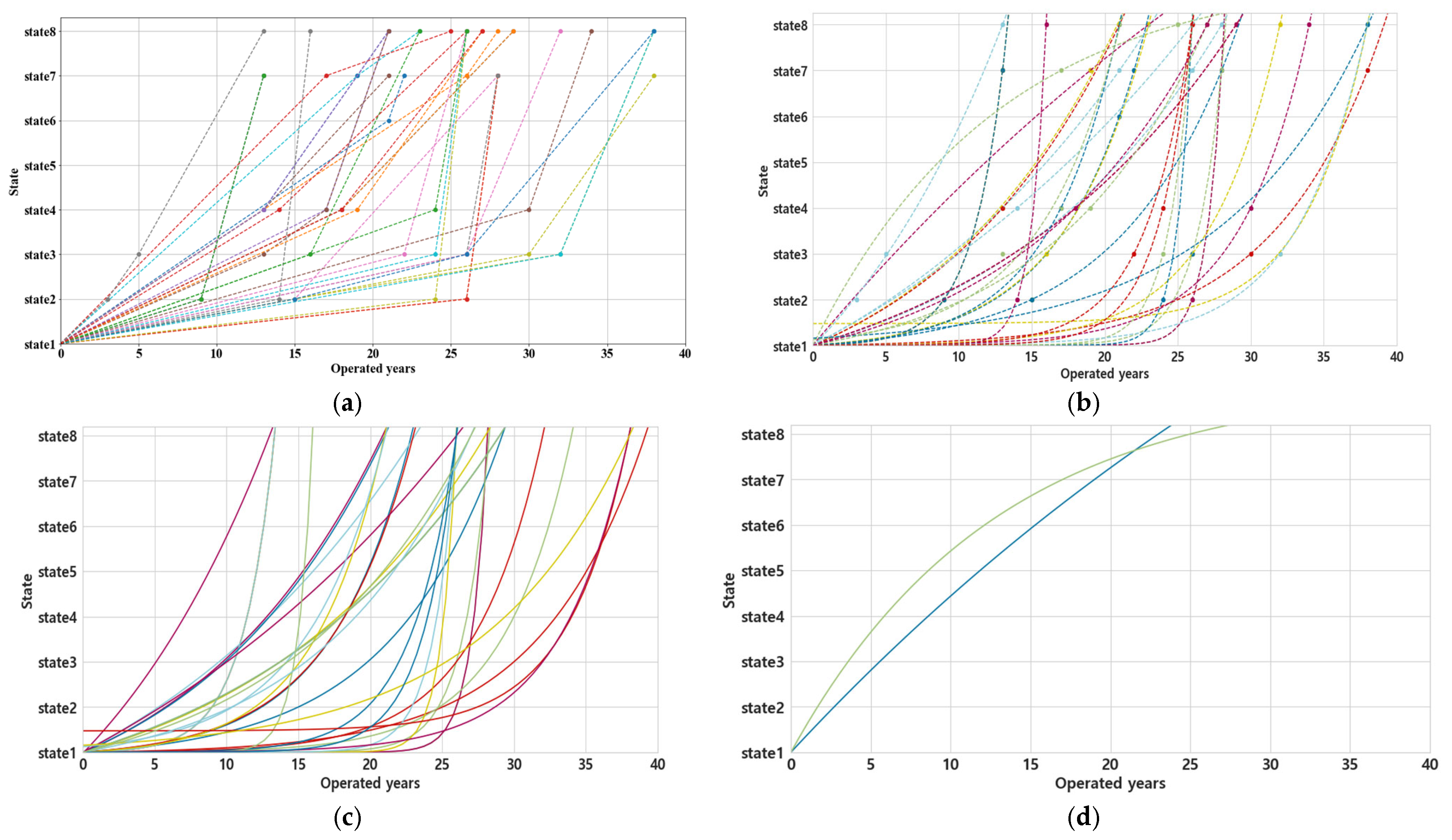
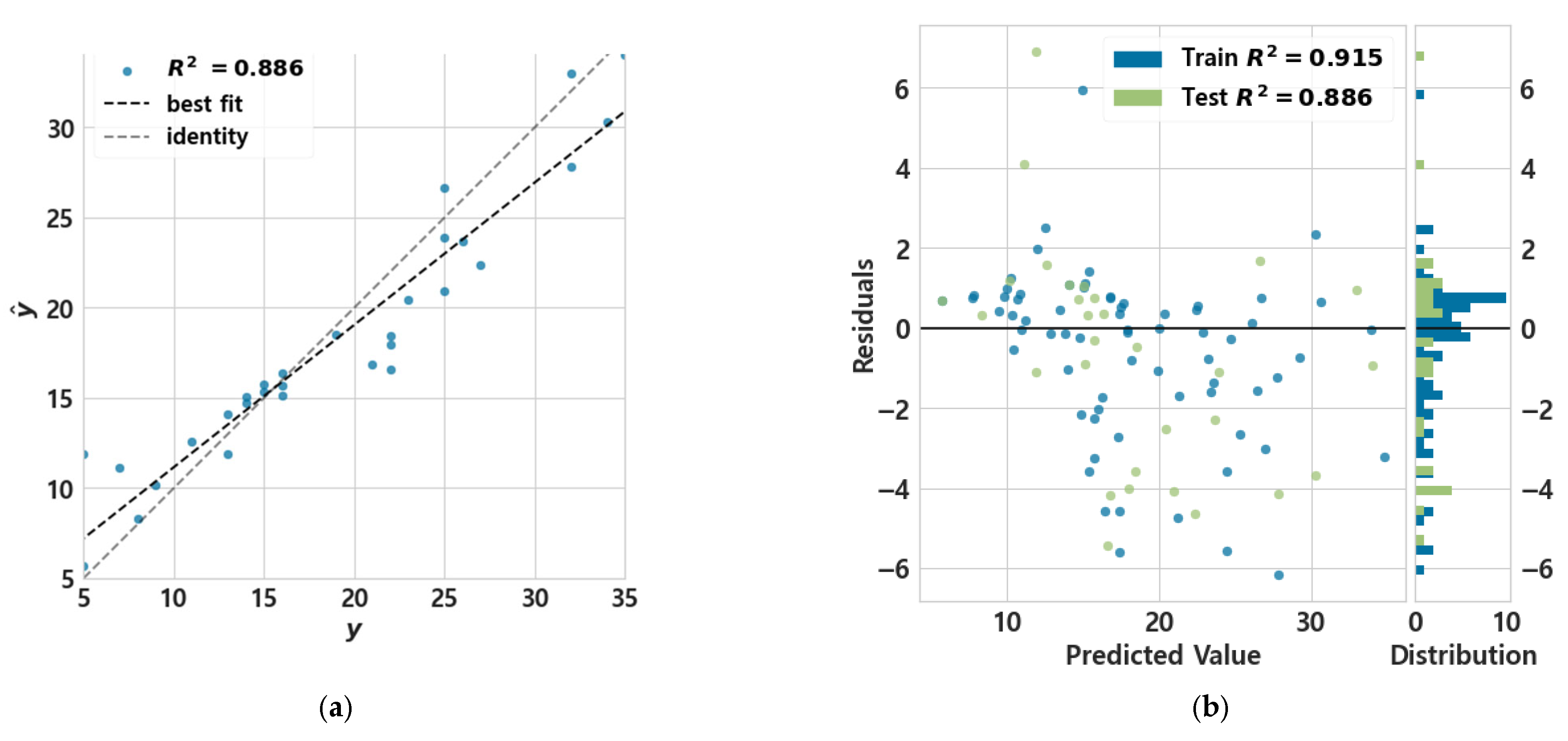
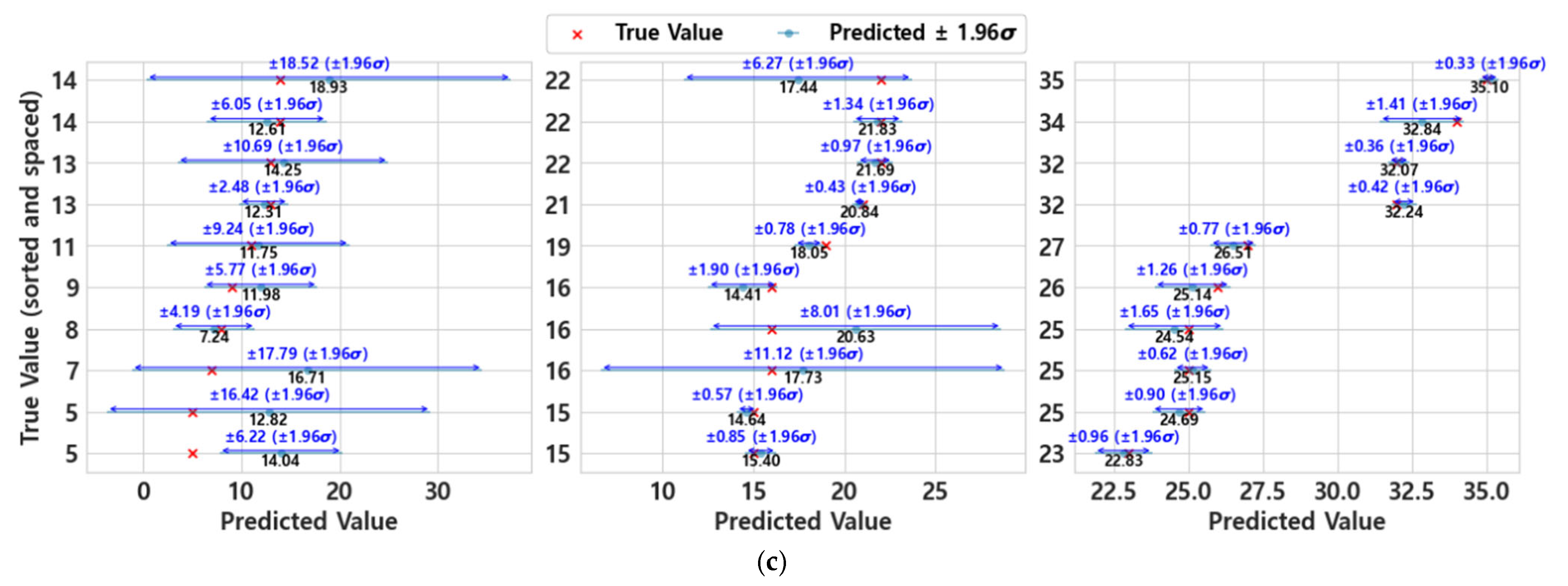
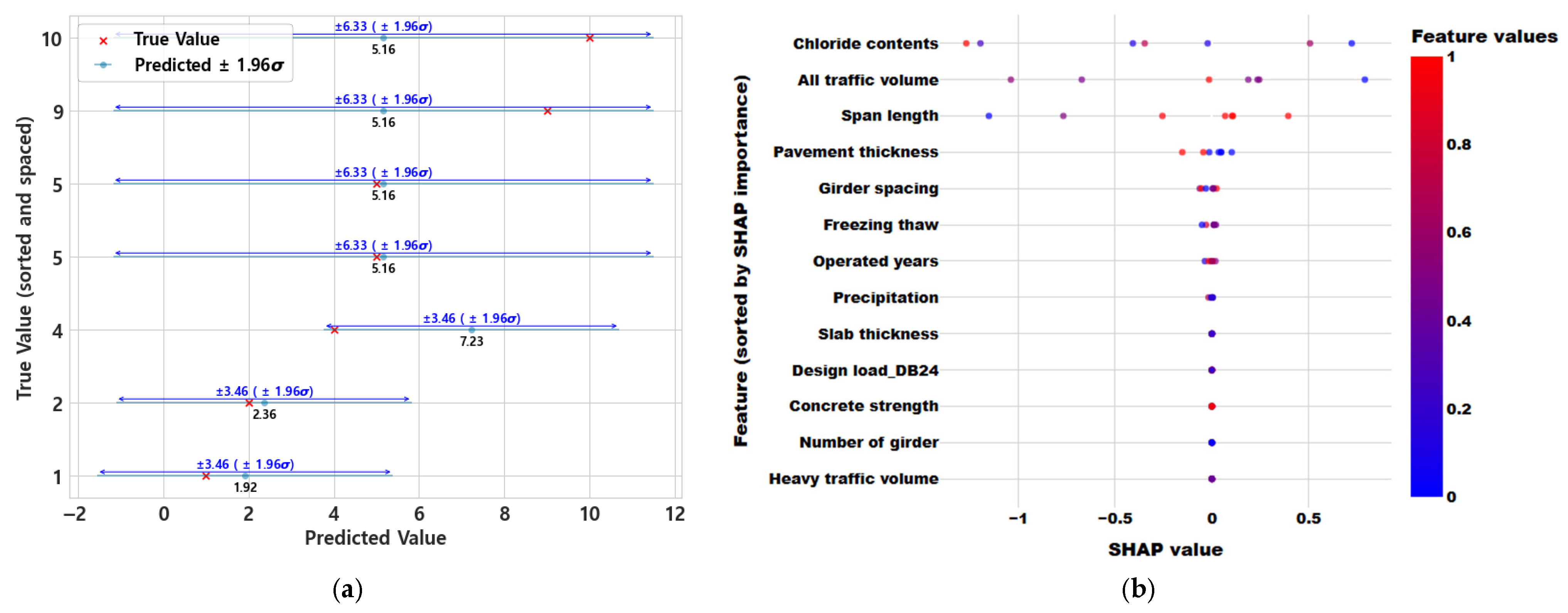
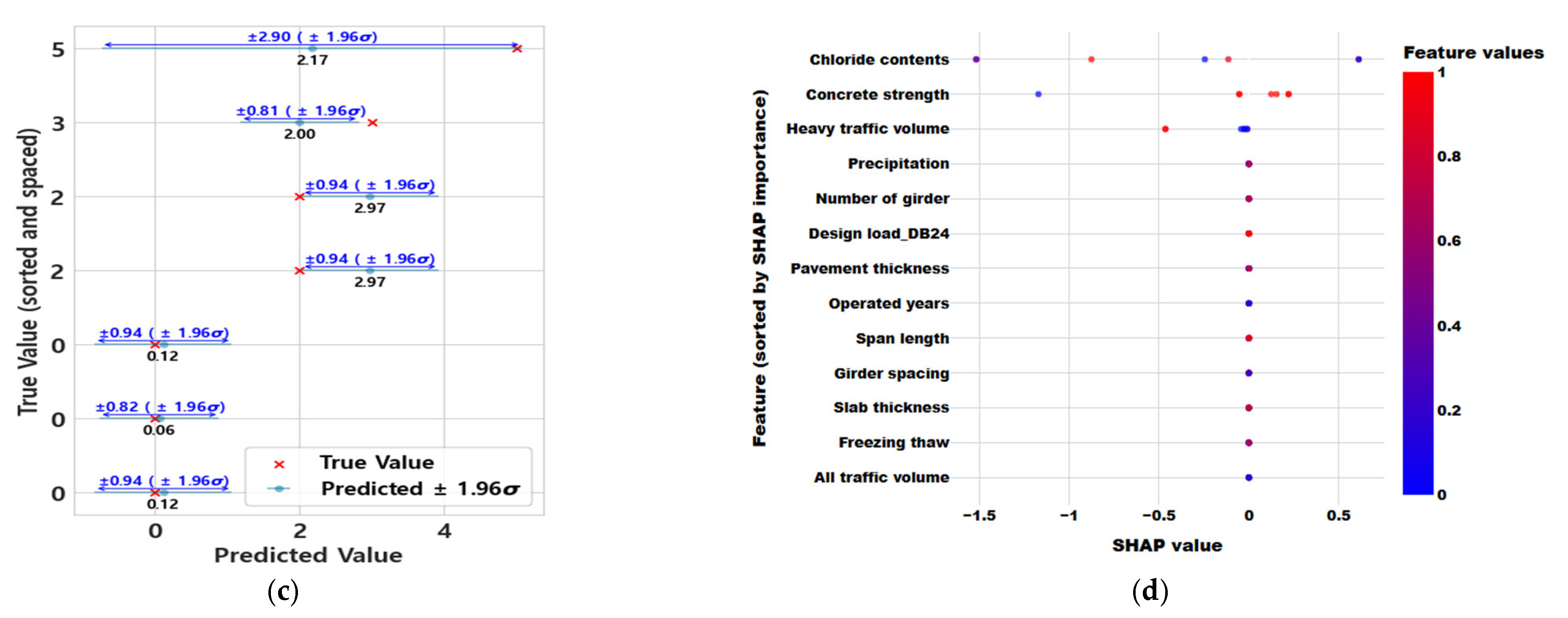
5.2. Regression ML Model for Service Remained Life for Bridge Deck
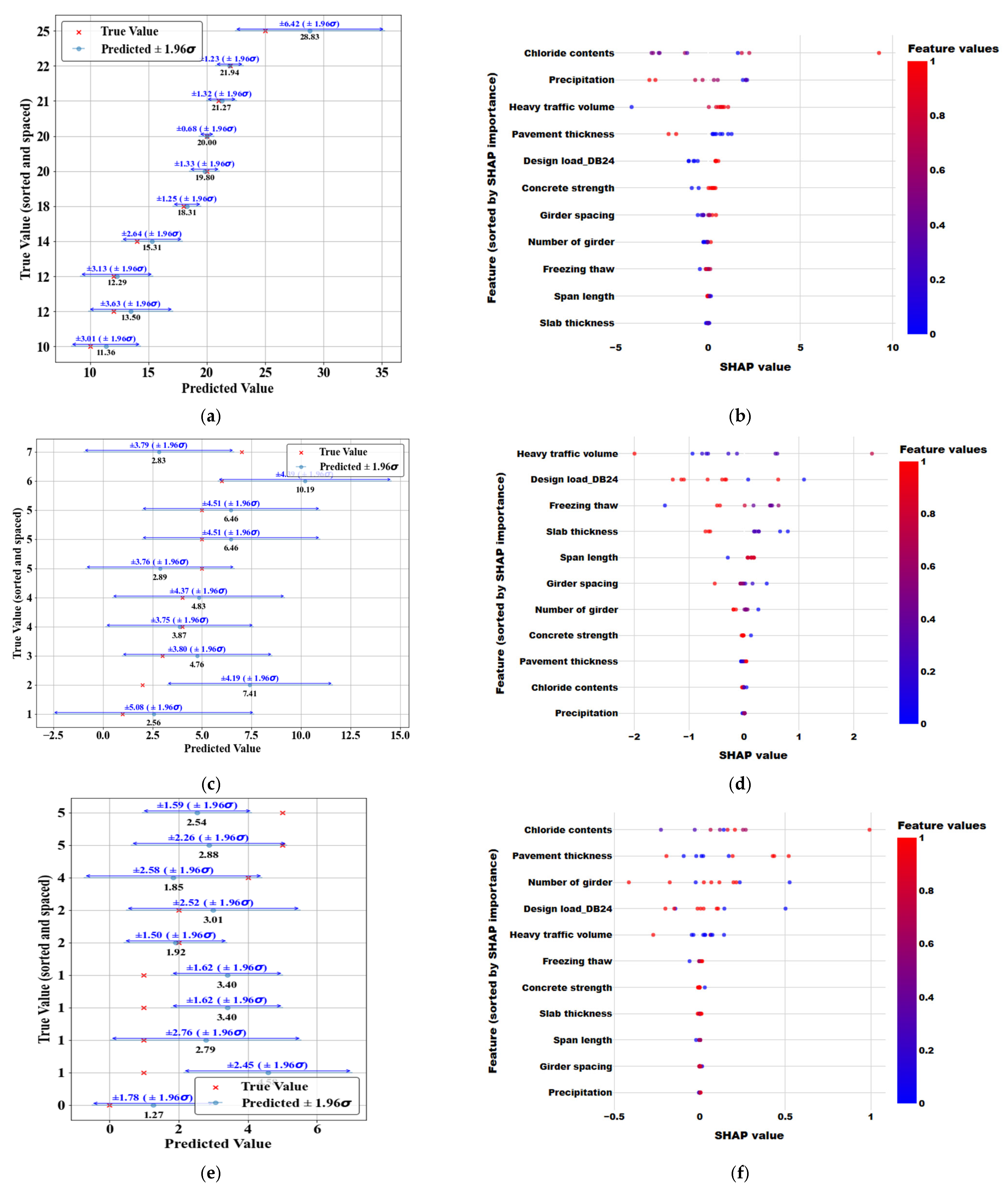
5.2.1. ML Regression Model for Exponential Trends in the Moment Zone
5.2.2. ML Regression Model in the Cantilever Zone
Exponential Trends
Logarithmic Trends
6. Discussion
7. Conclusions
- Traditional chloride models are based on diffusion equations, which primarily account for the influence of diffusion coefficients while excluding the combined effects of multiple factors. These models attempt to predict the initiation and progression of corrosion under simplified assumptions. However, when considering the direct impact of additional environmental factors such as rainfall, de-icing salts, and freeze–thaw cycles, it becomes evident that deterioration prediction requires a model that reflects the actual progression of deterioration over time using real inspection data.
- Although the deterioration of bridge decks is caused by various factors such as precipitation, freeze–thaw cycles, and chloride content, the magnitude of these values differs by region and zone. Therefore, appropriate consideration of these differences is essential during evaluation. Sensitivity analysis of the data is necessary to accurately classify the factors influencing deterioration, and it is important to develop a prediction model by grouping data with similar patterns to estimate remaining service life effectively.
- In data-driven ML models, the application of explainable AI techniques is essential to obtain reliable results. Using SHAP values—a widely used method in ML—this study assessed both the accuracy of the model and the importance of variables influencing the learning process. When training was performed without considering zoning in the bridge deck, it was found that the zoning variable had the greatest influence on the results. This suggests the critical need for incorporating deck zoning into the model. Furthermore, when the data were divided by zone and the remaining service life was analyzed based on deterioration patterns, it was observed that in exponential deterioration patterns, factors such as precipitation, heavy traffic volume, and slab thickness appeared in varying combinations, indicating the influence of multiple interacting variables. On the other hand, in zones where logarithmic deterioration patterns were found—typically limited to cantilever regions—environmental factors emerged as the most influential variables.
- The deterioration patterns of the bridge deck vary depending on whether the zone is a cantilever region or a moment region. In moment regions, deterioration generally progresses due to environmental factors following typical structural cracking. However, in cantilever regions, many cases of reinforcement corrosion, delamination, or spalling were observed without the presence of visible structural cracks. This indicates that, in order to properly define the serviceability life cycle of bridge decks, separate evaluation and modeling for moment regions and cantilever regions are required.
- General deterioration patterns can be classified into structural damage and environmental degradation. Once structural damage occurs, environmental factors tend to accelerate the deterioration process, particularly from the stages of map cracking or efflorescence. Therefore, it is crucial to implement timely maintenance and rehabilitation at the transition point between structural and environmental deterioration stages. In addition, for cantilever regions where deterioration may progress without visible signs, continuous monitoring of drainage systems and appropriate maintenance strategies are necessary to prevent unseen damage.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, K.H.; Nam, M.S.; Hwang, H.H.; Ann, K.Y. Prediction of Remaining Life for Bridge Decks Considering Deterioration Factors and Propose of Prioritization Process for Bridge Deck Maintenance. Sustainability 2020, 12, 10625. [Google Scholar] [CrossRef]
- Song, H.H.; Kim, K.Y.; Shin, J.H.; Roh, G.T.; Shim, C.S. A Digital Twin Framework for Bridge Slab Deterioration: From 2D Inspection Data to Predictive 3D Maintenance Modeling. Buildings 2025, 15, 1979. [Google Scholar] [CrossRef]
- Frosch, R.J.; Kreger, M.E.; Byl, E.A.; Lyrenmann, J.P.; Pollastrini, A.S. Development of a Cost-Effective Concrete Bridge Deck Preservation Program: Volume 1—Development and Implementation of the Experimental Program; FHWA/IN/JTRP-2016/22; Joint Transportation Research Program Publication: West Lafayette, IN, USA, 2016. [Google Scholar] [CrossRef]
- Guo, C.; Farzaneh, A. Fatigue Behavior of Reinforced Concrete Bridge Decks under Moving Wheel Loads: A State-of-the-Art Review. J. Bridge Eng. 2024, 29, 03124003. [Google Scholar] [CrossRef]
- Kobayashi, A.; Matsui, S. A Study on Prediction Method of Fatigue Life of RC Highway Bridge Slabs Strengthened with FRP. Sheets. Struct. Civil Eng. Ser. A 2016, 62A, 1261–1271. [Google Scholar] [CrossRef]
- Yang, C.; Lou, P.; Nassif, H. Correlation of Bridge Deck Deterioration with Truckload Spectra Based on NBI Condition Rating and Weigh-In-Motion Data; FHWA-HRT-24-032; U.S. Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2024. [CrossRef]
- Ministry of Land, Infrastructure and Transport (MOLIT). Facility Safety and Maintenance Implementation Guidelines: Inspection and Diagnosis Part; MOLIT: Sejong, Republic of Korea, 2021. (In Korean)
- AASHTO. The Manual for Bridge Evaluation, 3rd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2018. [Google Scholar]
- Sachidanand, J.; Sitarama, R.S. Enhancement in Indian Bridge Management System Using Analytics within BIM Data Model. In Proceedings of the IABSE Symposium Prague 2022, Prague, Czech Republic, 25–27 May 2022; pp. 903–910. [Google Scholar]
- Kim, H.-S.; Shin, S.-W.; Lee, H.-S. Analysis on the Characteristics of Deterioration and Durability of Reinforced Concrete Deck in Railway Bridge. J. Korean Soc. Railw. 2019, 22, 48–56. [Google Scholar] [CrossRef]
- Broomfield, J.P. Corrosion of Steel in Concrete: Understanding, Investigation and Repair; CRC Press: London, UK, 2006. [Google Scholar]
- Liu, T.; Weyers, R.W. Modeling the Dynamic Corrosion Process in Chloride Contaminated Concrete Structures. Cem. Concr. Res. 1998, 28, 365–379. [Google Scholar] [CrossRef]
- Liu, Y. Modeling Time-to-Corrosion Cracking in Chloride Contaminated Reinforced Concrete Structures. ACI Mater. J. 1999, 96, 611–613. [Google Scholar]
- Ouzaa, K.; Oucif, C. Numerical Model for Prediction of Corrosion of Steel Reinforcements in Reinforced Concrete Structures. Undergr. Space 2019, 4, 72–77. [Google Scholar] [CrossRef]
- Kwon, T.H.; Kim, J.; Park, K.T.; Jung, K.S. Long Short Term Memory Based Methodology for Predicting Carbonation Models of Reinforced Concrete Slab Bridges: Case Study in South Korea. Appl. Sci. 2022, 12, 12470. [Google Scholar] [CrossRef]
- Liu, Y.; Xiang, S.; Wang, D. Real-Time Evaluation and Prediction of Spatial Temperature Field and Temperature Effect of Steel-Concrete Composite Bridge Deck System Based on BP-LSTM Hybrid Model. Tumu Gongcheng Xuebao/China Civ. Eng. J. 2021, 54, 57–70, 78. [Google Scholar]
- Jeon, C.-H.; Kwon, T.-H.; Kim, J.-H.; Jung, K.-S.; Park, K.-T. Quantitative Evaluation of Reinforced Concrete Slab Bridges Using a Novel Health Index and LSTM-Based Deterioration Models. Appl. Sci. 2024, 14, 10530. [Google Scholar] [CrossRef]
- Roh, G.T.; Vu, N.; Jeon, C.-H.; Shim, C.S. Augmented Data-Driven Machine Learning for Digital Twin of Stud Shear Connections. Buildings 2024, 14, 328. [Google Scholar] [CrossRef]
- Rashidi Nasab, H.; Elzarka, H. Optimizing Machine Learning Algorithms for Improving Prediction of Bridge Deck Deterioration: A Case Study of Ohio Bridges. Buildings 2023, 13, 1517. [Google Scholar] [CrossRef]
- Ruggieri, N.; Tran, V.; De Domenico, D. Physics-informed deep learning for modeling nonlinear stress–strain behavior of concrete under uniaxial compression. Eng. Struct. 2023, 285, 116190. [Google Scholar] [CrossRef]
- Li, D.; Chen, Q.; Wang, H.; Shen, P.; Li, Z.; Nettis, A.; He, W. Deep learning-based acoustic emission data clustering for crack evaluation of welded joints in field bridges. Autom. Constr. 2024, 165, 105540. [Google Scholar] [CrossRef]
- Nettis, A.; Nettis, A.; Ruggieri, S.; Uva, G. Corrosion-induced fragility of existing prestressed concrete girder bridges under traffic loads. Eng. Struct. 2024, 314, 118302. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, W.; Su, Y.; Jia, F.; Long, X. Plastic damage prediction of concrete under compression based on deep learning. Acta Mech. 2024, 235, 255–266. [Google Scholar] [CrossRef]
- Fard, F.; Naieni Fard, F.S. Development and Utilization of Bridge Data of the United States for Predicting Deck Condition Rating Using Random Forest, XGBoost, and Artificial Neural Network. Remote Sens. 2024, 16, 367. [Google Scholar] [CrossRef]
- Kang, D.H.; Roh, G.T.; Shim, C.S.; Lee, K.C. Fatigue Life Prediction for Stud Shear Connectors Based on a Machine Learning Model. Buildings 2024, 14, 3278. [Google Scholar] [CrossRef]
- Korea Agency for Infrastructure Technology Advancement (KAIA). Open Traffic Volume Data from the Traffic Information Service System. Available online: https://www.road.re.kr (accessed on 30 June 2025).
- Korea Meteorological Administration (KMA). Annual Statistics of Precipitation and Snowfall Days (1991–2024). Available online: https://data.kma.go.kr/stcs/grnd/grndRnList.do?pgmNo=69 (accessed on 30 June 2025).


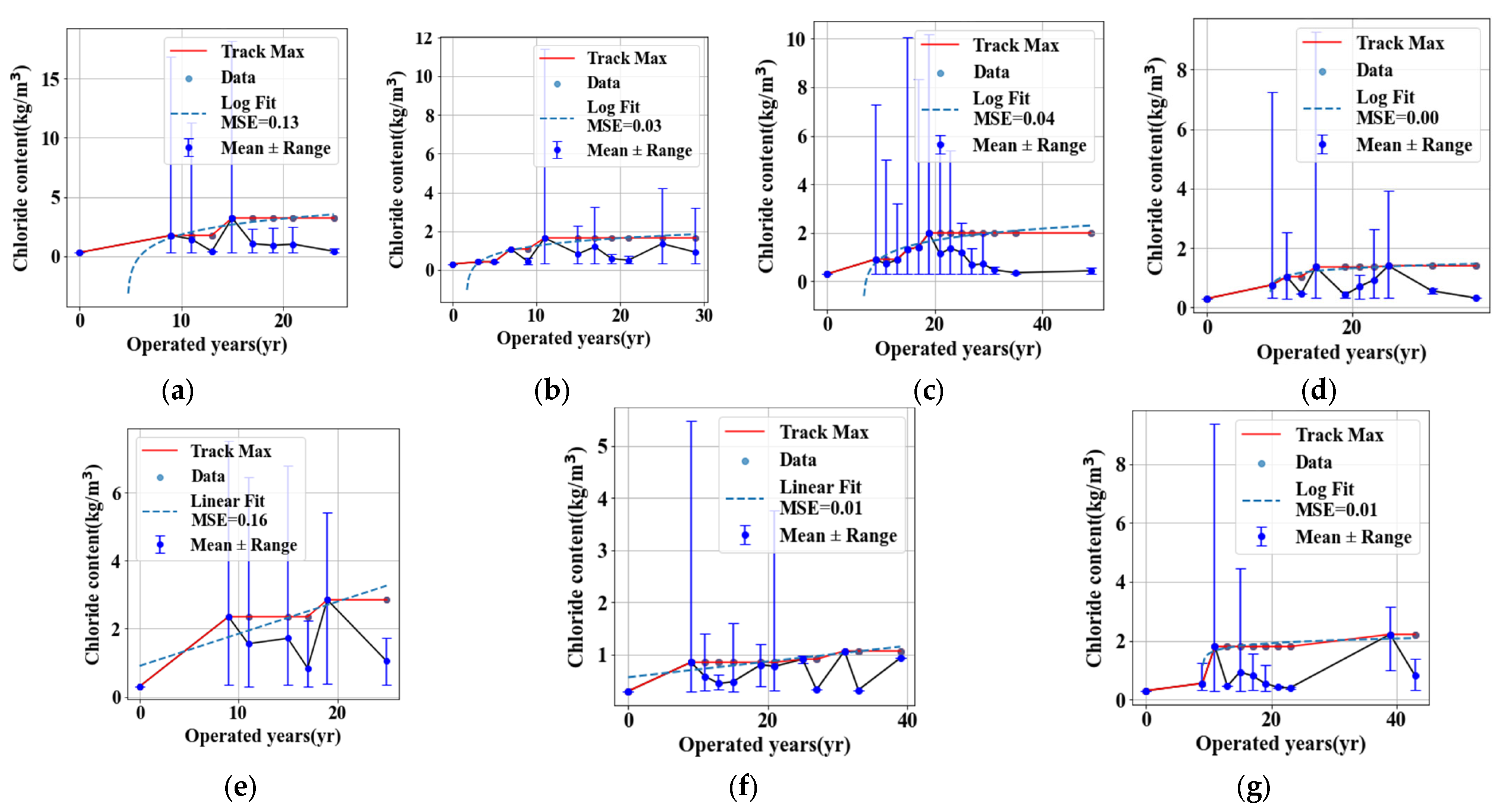



| Condition | State |
|---|---|
| A | Perfect, no problems |
| B | Minor problems in secondary elements, needs of small repairs for improvement in durability |
| C | Minor problems in primary elements or extensive problems in secondary elements, needs of repairs in primary elements or of rehabilitations in secondary elements |
| D | Problems in primary elements, needs of emergency repairs/rehabilitations |
| E | Serious problems in primary elements, out of service, needs of rehabilitations/replacements |
| Rating | Description |
|---|---|
| 9 | No Visual Distress |
| 8 | Presence of Micro cracks |
| 7 | Extensive micro cracks |
| 6 | Micro Cracks change to Cracks |
| 5 | Cracks widening |
| 4 | Start of delamination |
| 3 | Delamination extensive and start of spalling |
| 2 | Spalling extensive and loss of section |
| 1 | Sectional reduction in the core concrete |
| 0 | Section failed |
| Index | Condition | Explanation |
|---|---|---|
| N | Not Applicable | - |
| 9 | Excellent Condition | No problem noted |
| 8 | Very good Condition | No problem noted |
| 7 | Good Condition | Some minor problems |
| 6 | Satisfactory Condition | Structural elements show minor deterioration |
| 5 | Fair Condition | All primary structural elements are sound but may have minor section loss, cracking, spalling, or scour |
| 4 | Poor Condition | Advanced section loss, deterioration, spalling, or scour |
| 3 | Serious Condition | Loss of section, deterioration, spalling, or scour have seriously affected primary structural components |
| 2 | Critical Condition | Advanced deterioration of primary structural elements, fatigue cracks in steel or shear cracks in concrete may be present |
| 1 | “Imminent” Failure Condition | Major deterioration or section loss present in critical structural components, or obvious vertical or horizontal movement affecting structural stability |
| 0 | Failed Condition | Out of service, beyond corrective action |
| Phase | Deterioration Stage | Description | Remarks |
|---|---|---|---|
| Phase 1 | State 1 | Transverse crack (Crack width < 0.1 mm) | |
| State 2 | Transverse crack (0.1 mm < Crack width < 0.3 mm) | ||
| State 3 | Map crack, transverse crack (Crack width > 0.3 mm) | ||
| State 4 | Efflorescence near cracks | ||
| Phase 2 | State 5 | Corrosion condition | Leakage, chloride (>0.4%), carbonation depth (>cover) |
| State 6 | Corrosion initiation | Rust stains on the concrete surface | |
| Phase 3 | State 7, 8 | Delamination and spalling | Service life limit |
| Zone | Location |
|---|---|
| A | Cantilever (Adjacent to negative moment region) |
| B | Negative moment region (Near Support) |
| C | Moment reversal region |
| D | Cantilever section |
| E | Positive moment region (Mid-span) |
| Class | When the Chloride Penetration Reaches 2.5 (kg/m2) | Chloride Penetration Cr (kg/m2) |
|---|---|---|
| A | 30 years < T | Cr ≥ 0.3 |
| B | 20 years < T ≤ 30 years | 0.3 < Cr < 0.6 |
| C | 10 years < T ≤ 20 years | 0.6 < Cr < 1.2 |
| D | 5 years < T ≤ 10 years | 1.2 < Cr < 2.5 |
| E | 5 years ≥ T | 2.5 ≤ Cr |
| Classification | Factor | Detail | Unit |
|---|---|---|---|
| Basic Information | Province and city | Do/ Si/ Gun | - |
| Number of bridge | Bridge Name (1–52) | - | |
| Girder type | PSC-I | - | |
| bridge line | Highway/Expressway/National road/Provincial road | - | |
| Operated years | - | yrs | |
| Structural factors | Span length | 25.0~35.0 | m |
| Girder spacing | 1.7~3.0 | m | |
| Number of girders | 3~25 | - | |
| Concrete strength | 24.0~27.0 | MPa | |
| Design load | DB18/DB24 (Standard load for road bridge design (18 t/24 t)) | - | |
| Pavement type | Asphalt pavement | ||
| Pavement thickness | 50–80 | m | |
| Slab thickness | 180–250 | mm | |
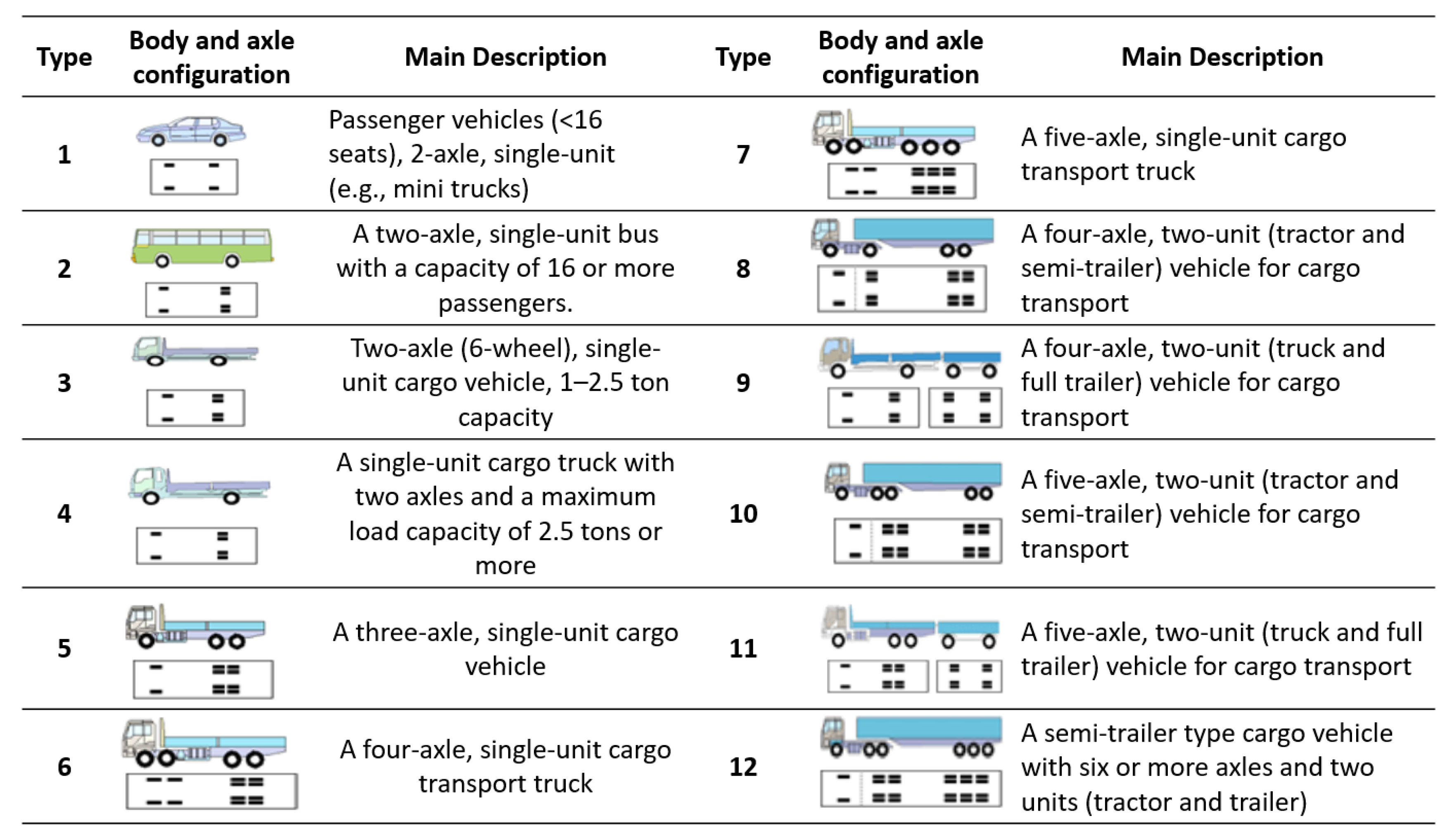
| Mechanical factors | Total vehicle volume | Type 1~12 | - |
| Heavy vehicle traffic | Type 1~5 | - | |
| Chemical factors | Precipitation | Average annual precipitation per year | mm |
| Freezing thaw | Average number of freeze–thaw cycles per year | - | |
| Chloride contents | Annual De-icing chemicals application per km | kpf/cm2 |
| Voting | Feature Importance | ||||||
|---|---|---|---|---|---|---|---|
| Accuracy | AUC | Recall | SHAP 1 | SHAP 2 | SHAP 3 | SHAP 4 | |
| A | 0.71 | 0.92 | 0.71 | Operated years | Freezing thaw | Chloride contents | Precipitation |
| B | 0.69 | 0.92 | 0.69 | Operated years | Traffic volume | Slab thickness | Chloride contents |
| C | 0.83 | 0.97 | 0.83 | Chloride contents | Slab thickness | Traffic volume | Freezing thaw |
| D | 0.59 | 0.87 | 0.59 | Chloride contents | Operated years | Traffic volume | Freezing thaw |
| E | 0.74 | 0.93 | 0.74 | Operated years | Chloride contents | Traffic volume | Freezing thaw |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roh, G.; Shim, C.; Song, H. Inspection Data-Driven Machine Learning Models for Predicting the Remaining Service Life of Deteriorating Bridge Decks. Buildings 2025, 15, 2799. https://doi.org/10.3390/buildings15152799
Roh G, Shim C, Song H. Inspection Data-Driven Machine Learning Models for Predicting the Remaining Service Life of Deteriorating Bridge Decks. Buildings. 2025; 15(15):2799. https://doi.org/10.3390/buildings15152799
Chicago/Turabian StyleRoh, Gitae, Changsu Shim, and Hyunhye Song. 2025. "Inspection Data-Driven Machine Learning Models for Predicting the Remaining Service Life of Deteriorating Bridge Decks" Buildings 15, no. 15: 2799. https://doi.org/10.3390/buildings15152799
APA StyleRoh, G., Shim, C., & Song, H. (2025). Inspection Data-Driven Machine Learning Models for Predicting the Remaining Service Life of Deteriorating Bridge Decks. Buildings, 15(15), 2799. https://doi.org/10.3390/buildings15152799







