Research on the Causes of the Concave Shapes of Traditional Chinese Building Roofs from the Construction Perspective

Abstract

Exploring the causes of the concave curved form of the roofs in traditional Chinese architecture is key to understanding its unique esthetics and structural logic. Regarding its causes, the academic community offers various explanations, including esthetics and function, but research that delves deeply into specific construction techniques and material limitations and systematically explains how they lead to the precise roof forms is relatively insufficient, which limits our comprehensive understanding of the deep generative logic of this unique form. This study aimed to bridge this gap by systematically exploring the causes of the concave curved form of roofs in traditional Chinese architecture (such as flying eaves, upturned corners, and Ju zhe) from the perspective of construction technology. Through a systematic review of historical literature (especially Yingzao fashi (Treatise on Architectural Methods)); the empirical investigation and analysis of typical architectural examples; detailed research on the structural practices, material properties (especially the creep behavior of timber), and construction techniques of key timber components such as flying rafters, hip rafters, and rafters; and mechanical principles and computational simulation, this study found that the concave curved forms of different parts of the roof, such as the eaves (flying rafters), corners (corner upturn), and main body (Ju zhe), are not purely esthetic choices but are, to a large extent, technical responses or inevitable results stemming from objective construction constraints of the time, including limitations on timber length, component connection methods, structural load distribution, and long-term deformation. Based on these findings, this study proposes the concept of “Passive Form” to summarize this form-generation mechanism, emphasizing that architectural forms are not solely determined by subjective will but are rooted in the adaptation and transformation of real constraints in construction, providing a technical perspective rooted in practice for understanding the forms of Chinese traditional architecture.

1. Introduction

1.1. Background

Chinese timber-framed architecture has undergone millennia of inheritance and evolution, achieving remarkable geographical dispersion across diverse regions [1]. The most distinctive feature of traditional Chinese architecture is its large roofs with upturned eaves, considered the the most majestic and beautiful element of the building system, fundamentally distinguishing it from other architectural traditions [2]. The graceful curves on traditional Chinese roofs are designed to avoid rigid straight lines while maintaining expansive flow, effectively reducing the visual weight caused by the massive roof structure [3]. These distinctive roof features embody the esthetic essence of traditional Chinese architecture and have become an iconic representation of China’s architectural heritage. Recognized as a national architectural style in the early 20th century, this form remains frequently referenced in modern designs. Its enduring influence has prompted cross-cultural academic investigations into its historical development.

Traditional Chinese timber-framed buildings exhibit diverse roof forms, which can be categorized into several types based on the structural features of the ridges and eaves. These include the Overhanging Gable Roof and Flush Gable Roof with Bofeng boards at both ends, the Hipped Roof with four-sided eaves and four main ridges, the Hip-and-Gable Roof combining characteristics of both overhanging and hipped roofs, and the Pyramidal Roof with multiple slopes converging at a central point. Additionally, more grandiose or significant structures often employ double-eaved designs (e.g., double-eaved pyramidal, hipped, or hip-and-gable roofs), enhancing their volumetric hierarchy, grandeur, and solemnity (Figure 1). All these roof types feature distinctive concave curvatures or upturned eaves.

Regarding the causes of the concave curved form of the roofs in Chinese traditional architecture, there are three main types of explanations in the academic community. The first type is from the perspective of esthetics and cultural symbolism. It is believed that the roof curves are imitations of natural forms, pursuits of specific cultural images (such as flying birds, dragons, and phoenixes), or manifestations of the ancient people’s creation of artistic conception and charm [5,6]. The second type is functional explanations. Scholars like Yang Hongxun have systematically analyzed the practical advantages of curved roofs in rapid and effective drainage, as well as optimizing lighting and ventilation under the eaves [7]. The third type is construction-based explanations, which focus on the influence of material properties, structural principles, and construction techniques on the roof form. For example, Mr. Le Jiazao once proposed that the formation of roof curves might result from certain objective technical limitations or material properties during the construction process, and such forms were adopted and developed due to their rationality or esthetic appeal [8]. Mr. Wang Tian determined that the Roof Curvature could more effectively prevent the reverse suction of rainwater in the tile joints, which was beneficial for roof waterproofing [9]. Other studies have also analyzed the potential technical advantages of roof curves in reducing the sliding force of tiles and improving the overall stability of the roof [10,11]. These construction-based analyses provide strong technical evidence. However, existing research remains limited in systematically and meticulously tracing how precise concave profiles in specific roof areas (e.g., the eaves, corners, and main bays) emerged from material or structural constraints. In particular, there is a lack of in-depth analysis that systematically integrates these local technical treatments with the mechanism by which the overall roof contour is formed.

1.2. Objectives

This study aimed to make up for the deficiencies of existing research in the aspect of refined technical explanations and systematically analyze the causes of the concave curved form of the roofs in Chinese traditional architecture from the perspective of construction. The research focused on the key components and construction techniques in the roof system, aiming to demonstrate that the concave curved forms of the eaves, corners, and main body of the roof are, to a large extent, technical responses or inevitable results of the objective limitations of the materials’ properties at that time (such as the natural properties of timber) and construction techniques. This study proposes the concept of “Passive Form” to summarize this form-generation mechanism, emphasizing that architectural forms are not solely determined by subjective will but are rooted in the adaptation and transformation of the real constraints in construction. Specifically, this study addressed the following key questions: (1) What are the technical relationships between the formation of the flying eaves and upturned corners and the structural treatments and material properties of components such as flying rafters and hip rafters? (2) Is there a technical causal relationship between the Roof Curvature of the main part of the roof and the arrangement and structural treatments of the rafters? This study verified these technical explanations by analyzing historical literature, such as Yingzao fashi (Treatise on Architectural Methods), and typical architectural examples.

This study provides a technical perspective rooted in construction practice, which helps us to gain a deeper understanding of the generation logic of the forms of Chinese traditional architecture. It goes beyond single-dimensional functional or esthetic explanations, reveals the dialectical relationship between technical rationality and formal beauty hidden in simple construction wisdom, and also offers new ideas for contemporary architectural design on how to draw inspiration from tradition; forms may stem from the creative transformation of constraints.

To assist readers with specialized terminology, a glossary of Chinese architectural terms and their English explanations can be found in Appendix A.

2. Materials and Methods

This study aimed to explore in depth the causes of the unique forms of the roofs in Chinese traditional architecture, especially the Concave Curved Form of the Eaves (Flying Rafters), the Hip Rafter Upturn (Corner Upturn), and the Main Roof Curvature (Ju zhe), from the perspective of construction. This research adopted a multi-dimensional approach, integrating historical literature analysis, empirical investigations and data analysis for existing architectural examples, studies on the characteristics of building materials, and the application of structural and construction principles.

2.1. Literature and Historical Case Analysis

First, this study conducted a systematic review of ancient Chinese architectural literature, with the Yingzao fashi by Li Jie [12] as the core. As an official architectural technical standard promulgated during the Northern Song Dynasty, this book meticulously records the design and construction regulations for timber structure buildings, providing a crucial basis for understanding the dimensional settings, proportional relationships, and construction methods of roof components. Supplementary literature includes other publications on ancient woodworking techniques, architectural history, and survey research [8,11,13].

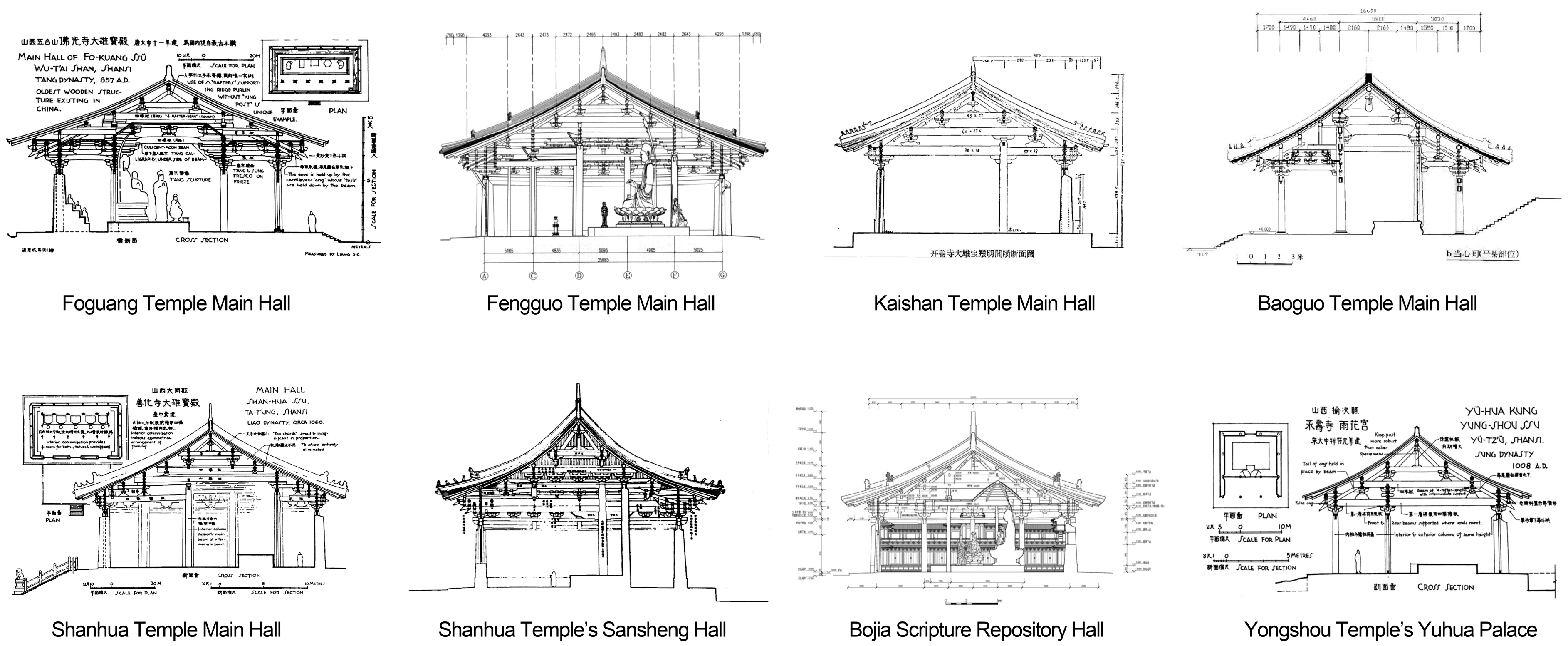
Secondly, representative examples of traditional Chinese timber structure buildings were selected for analysis, with a focus on the Tang and Song dynasties, when the technical and institutional systems were relatively mature. The selection of these examples (including but not limited to the Main Hall of Foguang Temple, the Main Hall of Shanhua Temple, the Main Hall of Kaishan Temple, the Main Hall of Fengguo Temple in Yixian, and parts of the Huayan Temple in Datong) was based on their state of preservation, typicality, and the availability of detailed existing survey data. Detailed analysis was conducted on the actual dimensions, slopes, construction nodes, and overall form of key components in these buildings, such as Eave Rafters, Hip Rafters, and Roof Curvature. These analyses relied on published architectural survey reports, archeological excavation data, and measured data and graphic records from relevant academic studies [4,14,15,16,17,18]. By comparing these actual data with the specifications in the Yingzao fashi, potential deviations in historical building practices and the motivations behind technical choices are revealed.

2.2. Material Selection and Properties

This study thoroughly examined the inherent physical and mechanical properties of timber, the primary material used in traditional Chinese timber-framed buildings. Particular attention was paid to how the natural growth limitations of timber influence the possible dimensions of timber-based building components. For example, the relationship between tree height and diameter at breast height (DBH), as well as the clear bole height available for material extraction, were considered. By referring to relevant forestry research data [19], the feasibility of sourcing specific components (such as long eave rafters) was evaluated, which helps to explain the possible reasons for the emergence of structures like flying rafters.

Furthermore, the creep behavior of timber under sustained load was analyzed [13]. This study explored the potential influence of this material property on the long-term deformation of the roof profile (such as the sagging phenomenon in the central roof section observed by Le Jiazao [8]) and its potential association with the design of the Roof Curvature construction.

2.3. Structure and Construction Principles Analysis

This study analyzed the stress states of roof components in the traditional timber-framed system. Based on previous analysis results for relevant structures reported by predecessors, it explored how the structural forms meet the requirements of structural stability and functionality. This includes referring to the calculations and analyses of the bending moments of eave rafters and hip rafters, as well as the sliding force of roof tiles, by scholars such as Wang Tian and Guo Ning Error! Reference source not found [9,11]. In particular, the model of the roof sliding force proposed by scholars like Guo Ning is used to assist in understanding the mechanical performance of different roof forms and is correlated with the purpose of the Roof Curvature structure.

This study further conducted computational simulation analysis to investigate the long-term deformation characteristics of roof components under actual loads and their impact on the overall roof morphology. The simulation aimed to quantitatively analyze the bending and creep behavior of rafters under their self-weight and tile load. In the simulation, a 3D geometric model of an idealized straight-sloped roof was first established, with Fir wood selected as the material. The analysis was performed using the Static Structure module within ANSYS 2022 software, and fixed constraints were applied at the support surfaces of the model. The applied loads included gravity along the Y-axis direction and a vertical pressure representing the self-weight of the tiles. The tile self-weight was estimated at 100 kg/m², and considering that the actual load-bearing area of the rafters accounts for approximately 1/6 of the total roof area, the vertical pressure on the model was set to 5880 Pa. The analysis clearly revealed that, for a roof initially designed with a continuous straight slope, the creep deformation of the eave rafters leads to bending and sagging, creating undesirable outward bulges at the rafter joints, thereby compromising the roof’s flatness and drainage efficiency. Through comparison, the simulation further elucidated how the traditional Ju zhe (Main Roof Curvature) construction, with its pre-set concave inflections, effectively mitigates the adverse effects of rafter creep. This allows the roof to maintain a generally coherent concave curved form under long-term loading, highlighting the functional advantage of Ju zhe (Main Roof Curvature) in addressing the material properties of wood.

On this basis, this study focused on analyzing the specific construction techniques and structural logics that form the concave curved forms of the eaves, corners, and main body of the roof. These include the methods for connecting flying rafters to the lower-layer rafters, the dimensional ratios and overlapping methods of hip rafters (Principal Hip Rafter and Upper Hip Rafter), and the auxiliary components (such as Pad Blocks) used to adjust the elevation of the components. It analyzed how these construction practices physically achieve the changes in the eave line, roof corners, and roof slopes, and discusses their functionality in dealing with material limitations, realizing roof continuity and drainage, and ensuring overall structural stability (for example, hip rafters balance the stress of components through the lever effect). By explaining these delicate construction techniques and their applications under specific constraints, it reveals how these structural treatments directly lead to the iconic concave curved form of the roof.

3. Results

3.1. Concave Curved Form of the Eaves (Flying Rafters)

To protect wooden components, deep-overhanging eaves are necessary. Eave rafters are the main components for achieving overhanging eaves, and they need to be relatively long. The measured lengths of Eave Rafters in existing timber structure buildings from the Tang and Song dynasties are consistently close to 5–7 m (

Table 1. Calculated Eave Rafter lengths for selected Tang and Song dynasty timber structures (unit: cm).

Building/Hall Name	Horizontal Distance: Lower Purlin to Eave Column Center (cm)	Horizontal Distance: Bracket Set Projection + Eave Overhang + Flying Rafter (cm)	Eave Slope (°)	Calculated Eave Rafter Length (Incl. Flying Rafter) (cm)
Fengguo Temple Main Hall (奉国寺大殿)	224	412.8	21.5	684.42
Guangji Temple San Dashi Hall (广济寺三大士殿)	223	217	17.7	461.86
Kaishan Temple Main Hall (开善寺大殿)	231	266.5	24.2	545.43
Huayan Temple Bojia Jiao Zang Hall (华严寺薄伽教藏殿)	234	279	19.7	544.89
Shanhua Temple Main Hall (善化寺大殿)	225	310	24.5	587.94
Huayan Temple Haihui Hall (华严寺海会殿)	232	229	17.5	483.37
Foguang Temple Wenshu Hall (佛光寺文殊殿)	217	255	14.6	487.75
Huayan Temple Main Hall (华严寺大殿)	290	376	21.6	716.30
Shanhua Temple Sansheng Hall (善化寺三圣殿)	216	352	21.1	608.82

Redrawn by the authors based on data from [21].

). However, commonly used timber (such as Chinese fir) is restricted by the laws of natural growth. When meeting the requirements for rafter diameter (for example, a Chinese fir with a breast–height diameter of 14–16 cm is needed for the rafter diameter of 12.5 cm in Fengguo Temple), the available length of knot-free timber (the height under the branches, estimated to be about 5.6–6.1 m on average at 52%) [20] often fails to meet the needs of long eave rafters. Moreover, it is difficult and costly to obtain long timber.

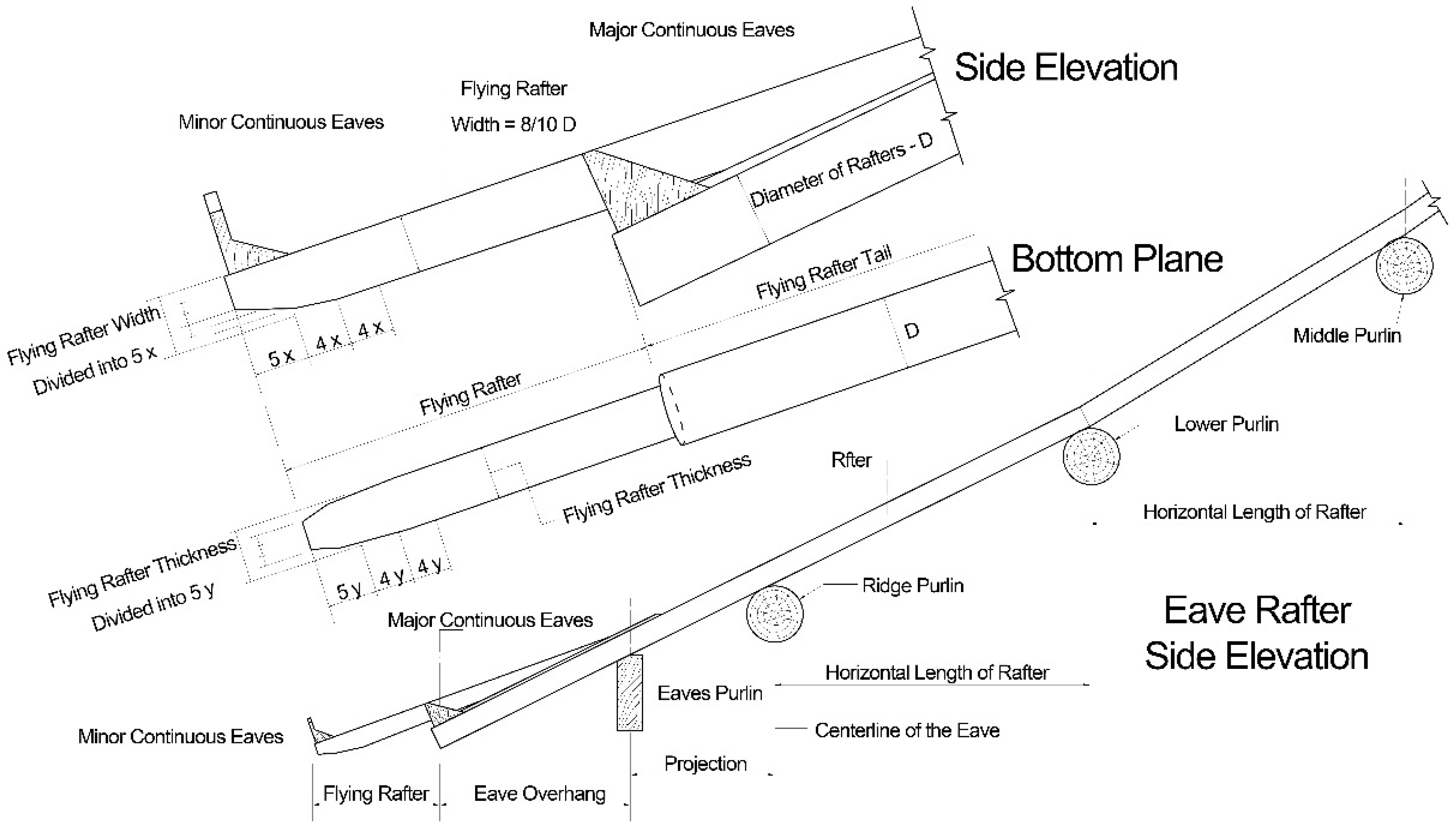
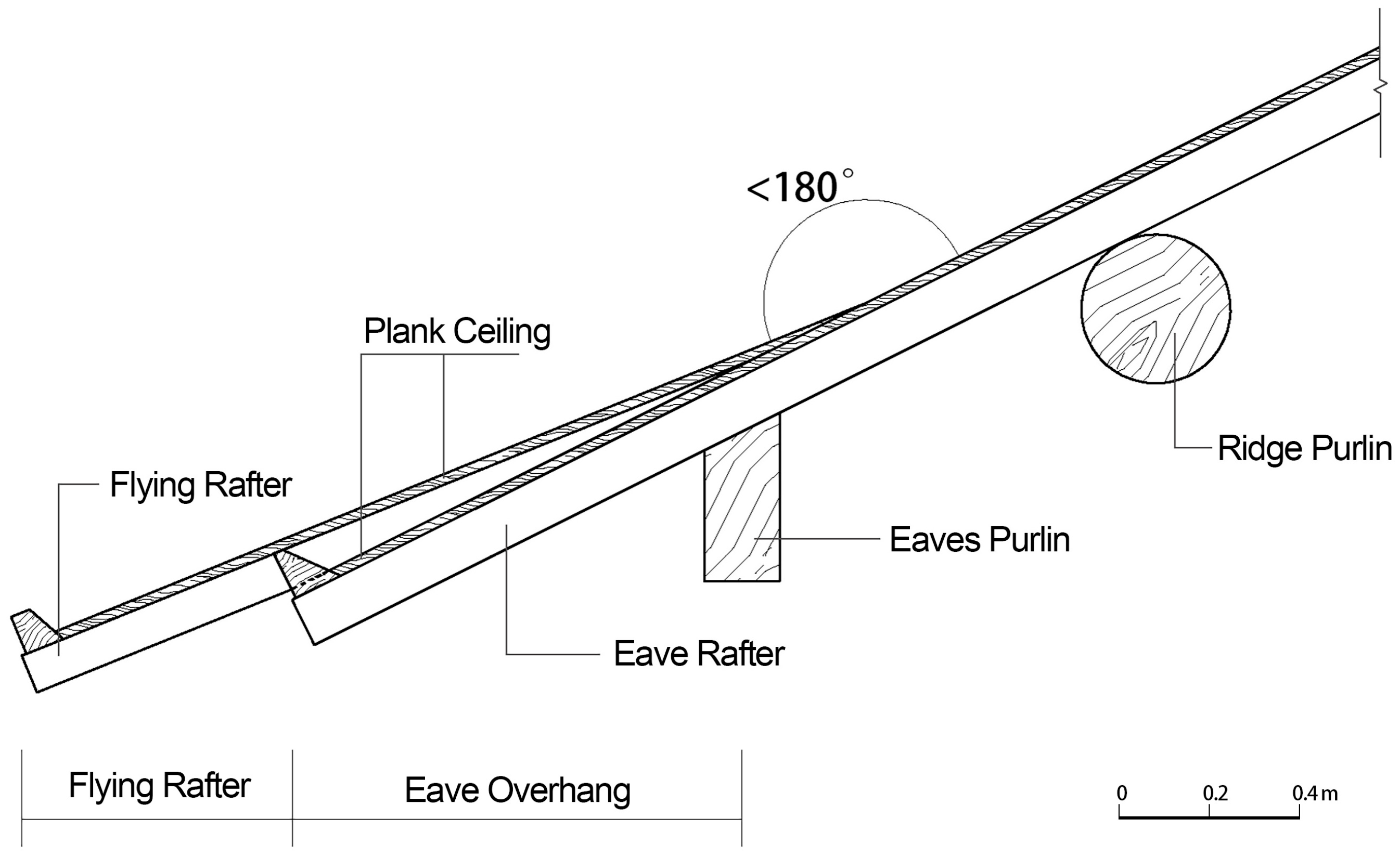
To increase the projection depth of the eaves, a secondary rafter with a square cross-section, known as the flying rafter (fei chuan), is nailed to the outer end of the existing round cross-section eave rafter. This component is also referred to as feiyan chuan and was termed feizi during the Song Dynasty (Figure 2). The use of flying rafters first appeared in the Northern Wei Grottoes (386–534 CE) [22] and became increasingly common during the Tang Dynasty (618–907 CE). However, even in the late Tang period, some large-scale buildings did not incorporate them; they only became widespread after the Tang Dynasty [23]. The depth of the eaves’ overhang is effectively enhanced through the implementation of flying eaves. This design solution ensures that the eaves adequately fulfill their functional requirements for weather protection and the safeguarding of components beneath them (Figure 3).

Taking Fengguo Temple in Yi County as an example, the eave rafter length (including flying rafters) measures approximately 7 m, with a rafter diameter of 12.5 cm. To produce rafters of this diameter, fir trees with a breast height diameter (BHD) of 14–16 cm are required. This specification is determined based on two factors: (1) the debarked breast height diameter (BHD) is measured as 0.93 times the bark-on BHD [19], and (2) the standard measurement of BHD (defined at 1.3 m above ground level) requires additional reduction adjustments due to the natural tapering of tree trunks—wider at the base and narrower toward the apex.

According to fir tree height–diameter correlation tables (

Table 2. Height–diameter correlation for fir trees by size class.

Breast Height Diameter (BHD) (cm)	10	12	14	16	18	20	22	24
Mean Tree Height (m)	9.2	10.3	11.2	12.2	12.5	13.4	15.2	16.1

Redrawn by the authors based on data from [26].

), trees within this diameter range typically attain heights of 11.2–12.2 m. The clear bole height (measured as 52% of the total tree height) is calculated as 5.6–6.1 m. However, due to limitations in historical logging techniques that restricted access to lower trunk sections, the actual usable lengths were likely shorter than the theoretical calculations. While larger-diameter trees could provide longer clear boles, choosing them would contradict the principles of optimal resource utilization. Traditional Chinese architecture required numerous eave rafters, yet longer timber lengths became progressively scarce within same-diameter stock [25]. When rafter lengths proved insufficient for eave projection requirements, the addition of flying rafters at eave terminals emerged as a functionally adaptive solution.

The Yingzao fashi [Building Standards, 1103] provides specific technical guidelines for eave projections and flying rafters: “The construction of eaves should extend outward from the center of the purlin. For rafters with a diameter of 3 cun (ancient Chinese unit of length, 1 cun ≈ 1/10 chi, approximately 31.2 mm), the eave projection should measure 3 chi 5 cun. For rafters with a diameter of 5 cun, the eave projection should range from 4 chi to 4 chi 5 cun. An additional flying rafters should extend 6 cun outward for every 1 chi of eave projection.” Regarding flying rafters, the text specifies the following: “The width of a feizi should be 8/10 of the rafter diameter, and its thickness 7/10. Variations in size should follow proportional adjustments.” It further details the following: “The tail of the feizi must align diagonally with the eave. Two feizi should be constructed as a continuous unit, first removing material at both ends to fit within the bracket joints, then shaping the central portion to follow the eave’s curvature. Near corners, feizi must curve upward to align their backs with the lower eave purlin (xiao lianyan).” [12] (pp. 265–278).

The ratio of the flying rafter’s head-to-tail length generally exceeds 1:2. While the flying rafter head projects outward, its tail must be nailed to the underlying eave rafter. To ensure structural stability and maintain roof continuity, part of the flying rafter tail is carved away to create sufficient contact area with the eave rafter. The flying rafters are fastened to the eave rafters with nails, forming a cohesive unit with a continuous form. This angled joint generates a concave curvature in the eave line (Figure 4), resulting in the characteristic curved eave form commonly seen today.

3.2. Hip Rafter Upturn (Corner Upturn)

According to archeological evidence, large-scale buildings prior to the Eastern Han Dynasty (25–220 CE) primarily relied on eave columns or bracket-arm supports to sustain eave projections. The overhang of eave rafters was minimal, and the cross-sectional safety margin of the rafters themselves was substantial. Hip rafters required no increase in cross-sectional size compared to regular rafters and could meet projection demands when identical to rafters. Consequently, both the roof surface and corners remained straight without upward curvature [15]. However, this structural system was imperfect. Eave columns and bracket-arm supports near the eaves were prone to water damage due to inadequate protection from rainwater [27]. This led to subsequent developments in timber framing (damuzuo), where eave projections gradually increased, and supporting structures receded inward to shelter the main structural components under the eaves [28].

Traditional architectural eave projections at roof corners are structurally far more complex than those at principal eaves. First, the actual projection length of hip rafters is √2 times that of principal eave rafters. With additional extensions, the projection becomes even longer. The bending moment of these components is proportional to the square of their projection length, while the relative deflection is proportional to the cube of the projection length.

As eave projections increasingly relied on the self-supporting capacity of eave rafters, the dimensional disparity between hip rafters and eave rafters grew. Scholars note that, when this disparity remained small, two methods could maintain straight roof corners: (1) enlarging the roof ridge (chuiji) to encapsulate the protruding hip rafter within the ridge structure and (2) carving out a section of the eave purlin (liaoyan fang) to embed the hip rafter, aligning its back with the eave rafter.

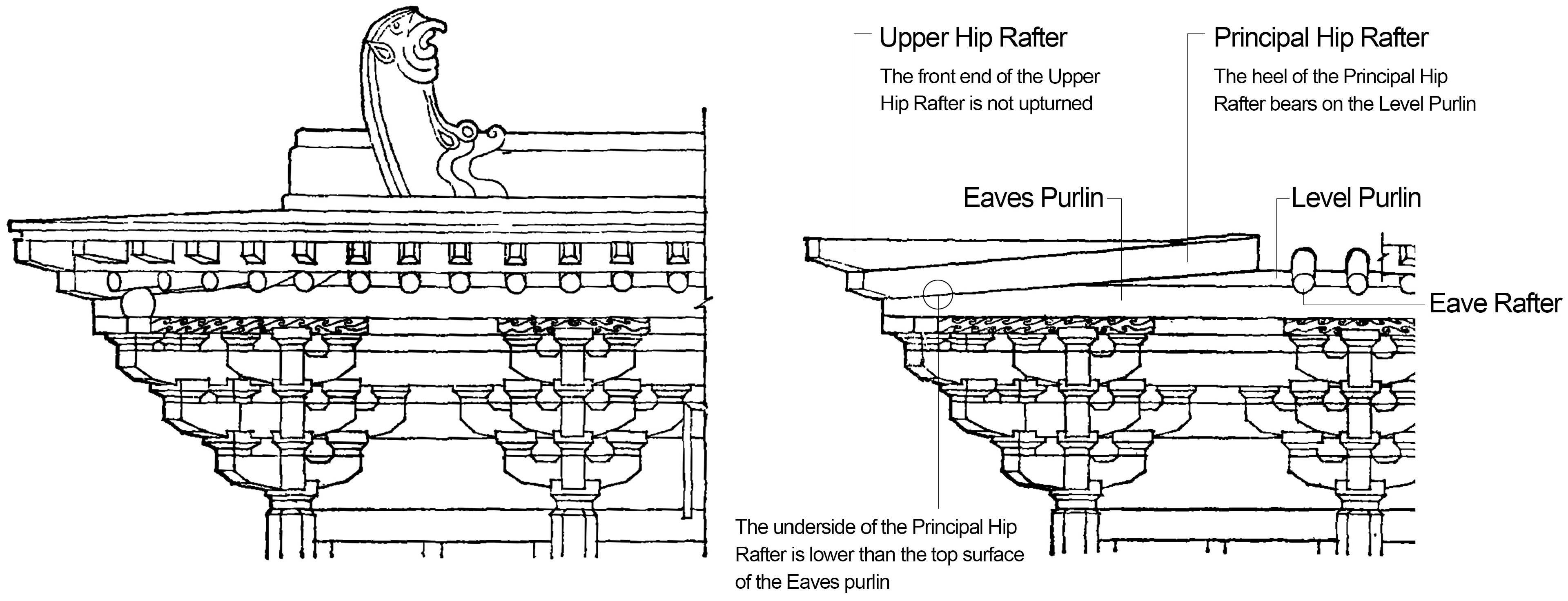
Examples include three early Song Dynasty cave-eaves (kuyan) at Dunhuang. These structures feature hip roofs (wudian ding), where principal eave rafters are circular in cross-section and transition to square flying rafters. At the corners, the height of the principal hip rafters slightly exceeds the diameter of the eave rafters, but the difference is negligible. The principal hip rafters are partially embedded into the eave purlin, aligning their backs with those of the eave rafters. The rear ends of the principal hip rafters rest on the lower purlin, mirroring the slope of the eave rafters. The upper hip rafters share similar dimensions and angles with the flying rafters, allowing seamless transitions at corners without angular adjustments [29]. Thus, the entire roof corner remains straight (Figure 5).

Traditional wooden architecture matured by the Song Dynasty. “Yingzao fashi” stipulated the materials for the corner beams as follows: a Main Corner Beam with a width of 28–30 fen (a subdivision within the cai–fen modular system defined in the Yingzao fashi) and a thickness of 18–20 fen, while the Subsidiary Corner Rafter was specified with a width of 18–20 fen and a thickness of 15–17 fen. It also stipulated the dimensions for common rafters: Palace/Pavilion Rafters with a diameter of 9–10 fen, Hall Rafters with a diameter of 7–8 fen, and Rafters for other buildings with a diameter of 6–7 fen. The height of the Main Corner Beam is generally three times the diameter of the eave rafters. According to Mr. Wang Tian’s calculations in Preliminary Study on Static Mechanics of Ancient Timber Structures [Gudai damuzuo jingli chutan], the height of the Main Corner Beam and the diameter of the eave rafters stipulated by the Song Dynasty’s “Yingzao fashi” precisely meet the static requirements for the corner and the horizontal eave overhang. The dimensional differences between these two components result in the back of the Main Corner Beam and the back of the eave rafters not being level, creating the first obstacle for the straight construction of the roofs.

Another structural challenge lies in the inclination angle of the principal hip rafter. The Yingzao fashi (Building Standards) provides ambiguous guidelines on hip rafter construction within the damuzuo (large timber framing) system. Critical details—such as how the principal hip rafter interfaces with the eave purlin and lower purlin, or connects to the upper hip rafter and concealed hip rafter—are either omitted or inadequately explained. Surviving examples reveal diverse practices, primarily categorized by whether the principal hip rafter is horizontally placed or angled. A horizontally placed rafter rests its tail beneath the lower purlin, whereas an angled rafter sits on top of it.

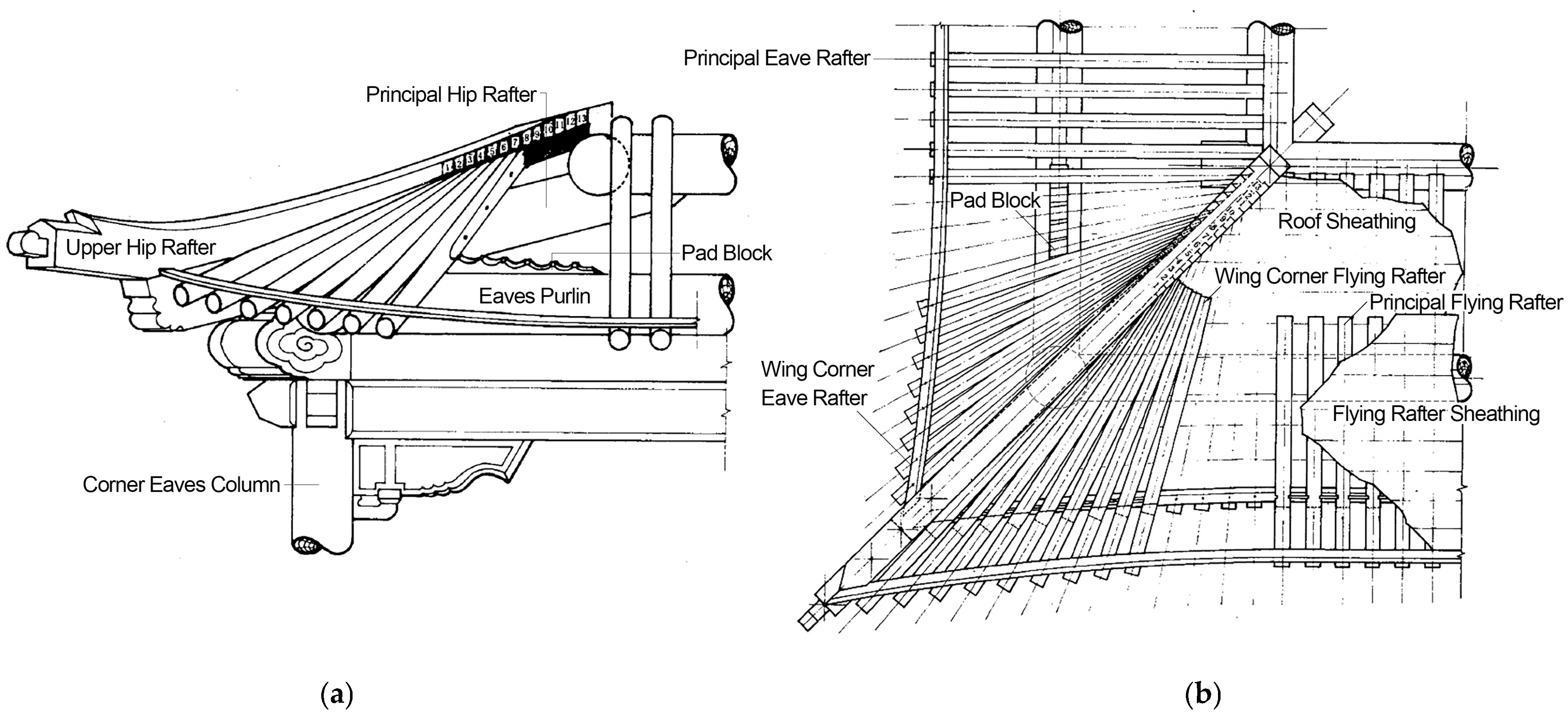
Yue et al. [30] systematically analyzed principal hip rafter configurations in damuzuo structures from the late Tang to Yuan dynasties north of the Yangtze River (

Table 3. Structural and corner-upturning typology of major timber buildings in northern China (late Tang to Yuan dynasties).

Basic Information			Structure Type		Warpage
Name	Era	Location	Principal Hip Rafter	Upper Hip Rafter
Wulong Temple Main Hall (五龙庙正殿)	831	Rui Cheng, Shanxi	Obliquely set above purlin	Straight	Gentle curvature
Foguang E. Hall (佛光寺东大殿)	857	Wutai, Shanxi	Obliquely set above purlin	Straight	Gentle curvature
Tiantai Nunnery Hall (天台庵正殿)	Late Tang Dynasty	Ping Shun, Shanxi	Obliquely set above purlin	Straight	Pronounced curvature II
Zhenguo Wofo Hall (镇国寺万佛殿)	961	Pingyao, Shanxi	Obliquely set above purlin	Straight	Gentle curvature
Jidu Temple Bedchamber (济源济渎庙寝宫)	973	Jiyuan, Henan	Horizontally placed below purlin	Straight	Pronounced curvature I
Chongqing Qianfo Hall (崇庆寺千佛殿)	1016	Jincheng, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature I
Yuanqi Temple Hall (原起寺大殿)	1068–1085	Changzhi, Shanxi	Intersecting between Xitoufu and purlin	Straight	Gentle curvature
Cui Fujun Gate (崔府君庙山门)	Middle Northern Song Dynasty	Lingchuan, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Kaihua Main Hall (开化寺大雄宝殿)	1073	Gaoping, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Xiaohuiling Erxian Hall (小会岭二仙庙大殿)	Middle to Late Northern Song Dynasty	Jincheng, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Longmen Temple Hall (五龙庙正殿)	1098	Changzhi, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature I
Jin Temple Shengmu Hall (龙门寺大殿)	1102	Taiyuan, Shanxi	Obliquely set above purlin	Straight	Gentle curvature
Xiaonancun Erxian Hall (小南村二仙庙大殿)	1107	Jincheng, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Chongshou Temple Hall (崇寿寺大殿)	1119	Changzhi, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Shaolin Chuzu Hall (少林寺初祖庵大殿)	1125	Dengfeng, Henan	Horizontally placed below purlin	Straight	Pronounced curvature I
Bojiao Scripture Hall (薄伽教藏殿)	1138	Datong, Shanxi	Obliquely set above purlin	Straight	Gentle curvature
Huayan Main Hall (华严寺大雄宝殿)	1140	Datong, Shanxi	Obliquely set above purlin	Straight	Gentle curvature
Zhenze Erxian Rear Hall (真泽二仙宫后殿)	1142	Lingchuan, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Xilimen Erxian Hall (西里门二仙庙中殿)	1157	Lingchuan, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Jin Temple Xian Hall (晋祠献殿)	1168	Taiyuan, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Shanhua Sansheng Hall (善化寺三圣殿)	Jin Dynasty	Datong, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature I
Chongfu Guanyin Hall (崇福寺观音殿)	Jin Dynasty	Shuozhou, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature I
Nanchantou Erxian Hall (南禅头二仙庙大殿)	Late Jin Dynasty	Lingchuan, Shanxi	Horizontally placed below purlin	Straight	Pronounced curvature II
Cisheng Main Hall (慈胜寺大雄宝殿)	Yuan Dynasty	Wen County, Henan	Horizontally placed below purlin	Straight	Pronounced curvature II
Daming Central Hall (大明寺中佛殿)	Yuan Dynasty	Jiyuan, Henan	Horizontally placed below purlin	Straight	Pronounced curvature II
Tangdi Temple Hall (汤帝庙汤帝殿)	Yuan Dynasty	Bo’ai, Henan	Horizontally placed below purlin	Straight	Pronounced curvature II

Figure created by the author.

). Their data show that horizontally placed examples dominate, likely due to structural reactions from wing corner eave rafters.

Unlike principal eave rafters, which anchor securely to the lower purlin, wing corner eave rafters fan out along the principal hip rafter. Those closer to the corner exhibit shorter tails, destabilizing their balance without rafter support. The load differential across the eave purlin—greater externally than internally—creates a forward-tilting tendency in wing corner eave rafters, exacerbated by seismic or climatic risks. Horizontally placing the principal hip rafter beneath the lower purlin forms a lever mechanism, enhancing structural stability.

Furthermore, the principal hip rafter’s greater cross-sectional height compared to eave rafters prevents the alignment of their backs on the eave purlin. Additionally, differing slopes arise because the eave rafters rest on the lower purlin (steeper slope), while the principal hip rafter typically sits beneath it (gentler slope). This elevates the front–back height of the principal hip rafter significantly above that of eave rafters. To ensure a continuous roof surface for roof sheathing (wangban), a triangular pad block (shengtou mu, also called chentou mu) is inserted near the corner on the purlin’s backside. This progressively elevates the wing corner eave rafters, generating the corner’s characteristic curvature (Figure 6).

3.3. Main Roof Curvature (Ju Zhe)

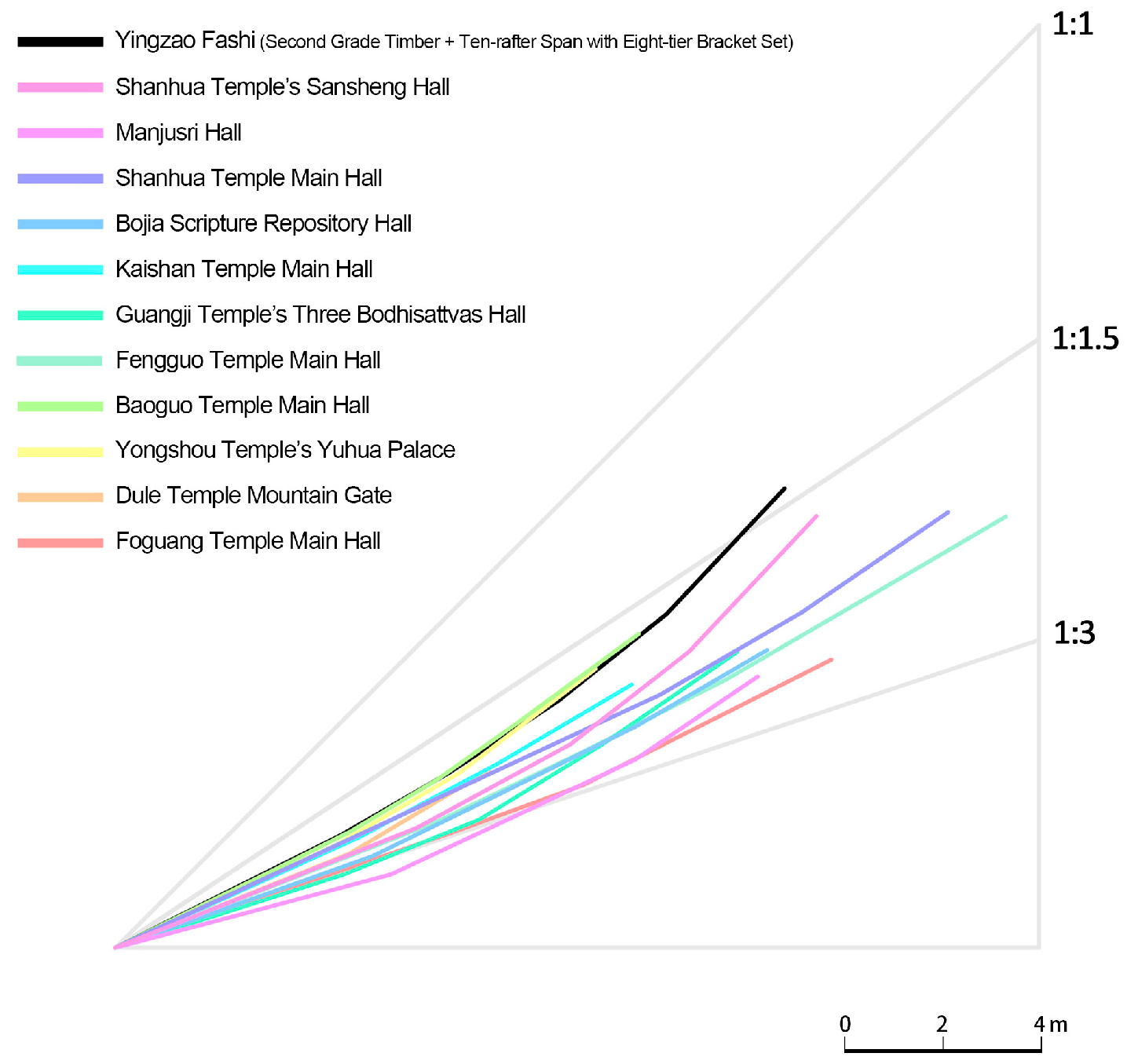
This study analyzed several typical roof examples documented in Liang Sicheng: A Pictorial History of Chinese Architecture. These cases, such as the Main Hall of Kaishan Temple and the Mahavira Hall of Fengguo Temple, represent invaluable data acquired by Mr. Liang Sicheng and his team through arduous field surveys and research during the 1930s and 1940s. They stand as rare and remarkably preserved classic (typical) examples of Tang and Song dynasty timber-frame architecture in China (Figure 7). Upon comparing the cross-sections of 11 typical Tang and Song architectural examples with the standard roof practices detailed in the Yingzao fashi (Treatise on Architectural Methods) and subsequently plotting the roof curves of these various buildings together, it is evident that the roof pitch of these architectural relics fundamentally exhibits a distinct concave curvature, typically ranging between 1:3 and 1:1.5 (Figure 8). This characteristic is commonly referred to as “Ju zhe”.

From these case studies, it can be observed that the line connecting the rafters from the eaves to the ridge is not a straight line but, rather, a concave polyline formed by individual rafters positioned at varying angles. This design choice is clearly intentional, not merely a consequence of construction error. Such a practice can be discussed in terms of material creep characteristics, roof waterproofing mechanisms, and the mechanical properties associated with preventing tile slippage.

For a single rafter, under its self-weight and the gravitational load of the tiles, the rafter body undergoes downward bending creep. As the rafter ends are securely fixed to the purlins, experiencing minimal displacement, the bending-deformed rafter body and its relatively fixed ends generate a new angle of inclination. If the initial roof surface were a continuous straight line, then upon bending, the central sag of the rafters would result in an undesirable outward bulge or kink at the intersection of two rafters. This would cause the entire roof surface to appear undulating and wavy, not only detracting from its esthetic appeal but also proving detrimental to proper tiling. To investigate this, we conducted modeling and simulation validation as follows: (1) A 3D geometric model of a straight-sloped roof was established, and its material was defined (fir wood was selected). (2) Stress analysis was performed using the Static Structure module in ANSYS, with fixed constraints applied to the support surfaces. (3) Earth’s gravity and a vertical roof load were applied in the -Y-axis direction (the self-weight of a tiled roof is approximately 100 kg/m²; considering that the stressed area of the rafters accounts for about 1/6 of the total roof area, a pressure of 5880 Pa was set on the model). (4) The deformation results and stress distribution were analyzed. The simulation analysis intuitively demonstrated the deformation trend of an ideal straight-sloped roof (Figure 9). In contrast, with a Ju zhe roof, a concave polyline is predefined from the outset. Consequently, even when the rafters undergo bending deformation due to creep, the roof does not exhibit outward convex kinks but instead maintains a fundamentally continuous concave curve.

In terms of roof waterproofing mechanisms, Wang T. [9], in his seminal work Preliminary Study on Static Mechanics of Ancient Timber Structures [Gudai damuzuo jingli chutan], computationally demonstrated that the roof curvature bears no mechanical relationship with timber frame load-bearing systems. His analysis further revealed that the persistent adoption of roof curvature in Chinese traditional architecture likely originated from its hydrological superiority when employing semi-cylindrical interlocking tiles (tongban tiles). The curved roof geometry created by roof curvature enhances water resistance through optimized tile overlap patterns, outperforming linear-sloped roofs in precipitation management. Mechanistically, Wang T. attributed this waterproofing advantage to roof curvature’s capacity to disrupt capillary water flow within tile joints. The technique effectively prevents the tile edge uplift phenomenon, a common failure mode in straight-sloped roofs where tiles separate at their leading edges. This protective mechanism becomes particularly crucial when considering rafter creep deformation, as discussed in preceding sections. The author warned that convex surfaces formed at intersecting rafters due to creep could paradoxically intensify tile edge uplift, thereby elevating leakage risks despite the inherent waterproofing benefits of roof curvature.

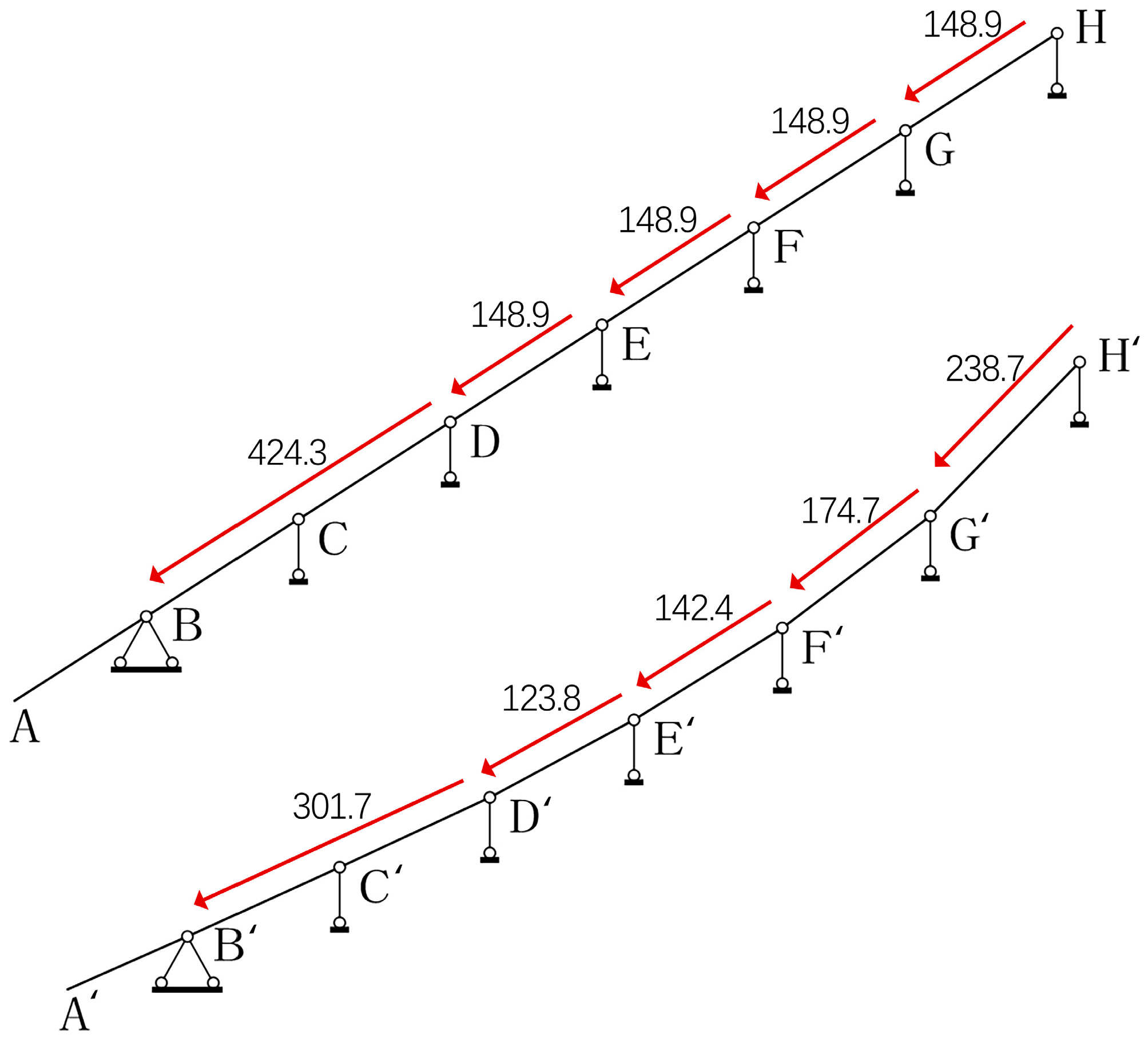
Regarding the mechanical characteristics that prevent roof tiles from sliding down, Guo Ning, in his article “A New Exploration into the Causes of Curved Roofs in Ancient Chinese Architecture” [10], demonstrates through calculations that a curved roof is superior to a straight roof in reducing the downward sliding force generated by the roof load. Furthermore, at the curved sections of a curved roof, the roof structure produces a certain reaction force that counteracts a portion of the downward sliding force of the roof. The actual value of the downward sliding force is therefore less than a simple summation of values, where letters such as A, B, C represent the points of force application, and the data on the arrows represent the downward sliding force (Figure 10,

Table 4. Calculation Table of Roof Downward Sliding Force (Unit: KG).

Roof Type	AD Segment	DE Segment	EF Segment	FG Segment	GH Segment	Total
Curved Roof	301.7	123.8	142.4	174.7	238.7	981.3
Straight Roof	424.3	148.9	148.9	148.9	148.9	1019.9

Figure created by the author.

). This analysis may explain why early roof slopes close to a straight line were relatively gentle because of concerns about the risk of sliding due to the downward force of shingle loads on a straight line roof under the superimposed effect of snow loads or seismic forces. The emergence of roof curvature breaks down the downward force on each roof joist and reduces the cumulative transfer of downward force from the upper roof to the lower roof. The refinement of the roof curvature technique supports the steep correction of the roof slope in Yingzao fashi (Treatise on Architectural Methods), especially the steepest slope near the ridge. This may be due to the fact that these roofing bays do not have to share the downward force of the upper roof; only their own gravity balance considerations have to be addressed. This has the advantage that the increase in the slope of the roof lifts the roof profile, widens the scale of the roof, and enhances the expressive power of the roof (Figure 11).

Compared to rectilinear designs, the concave Ju zhe roof form enhanced structural rationality and safety. It also reduced the demands on construction precision and provided inherent allowance for inevitable future deformation. This flexible construction strategy represents valuable experience garnered by traditional artisans through extensive building practices, embodying the pragmatic wisdom of the ancients in understanding and shaping their world.

4. Discussion and Conclusions

Based on the comprehensive analysis of the construction methods of flying rafters, upturned roof corners, and roof curvature, it can be found that the formation of the concave curved form of the roofs in Chinese traditional architecture is closely related to solving specific technical problems and adapting to the characteristics of building materials. At the eaves, the use of flying rafters to extend the overhang and ensure lap joints naturally results in an upward curve. At the roof corners, due to the size and installation requirements of the corner beams, the rafters are raised by the corner blocks, creating an upturned effect. For the main body of the roof, the adoption of roof curvature is related to multiple factors such as adapting to wood creep, improving waterproof performance, reducing sliding force, and lowering the requirements for construction accuracy. The internal logic of these three parts of the structure works together to shape the classic form of the overall concave curved roof with upturned eaves and corners.

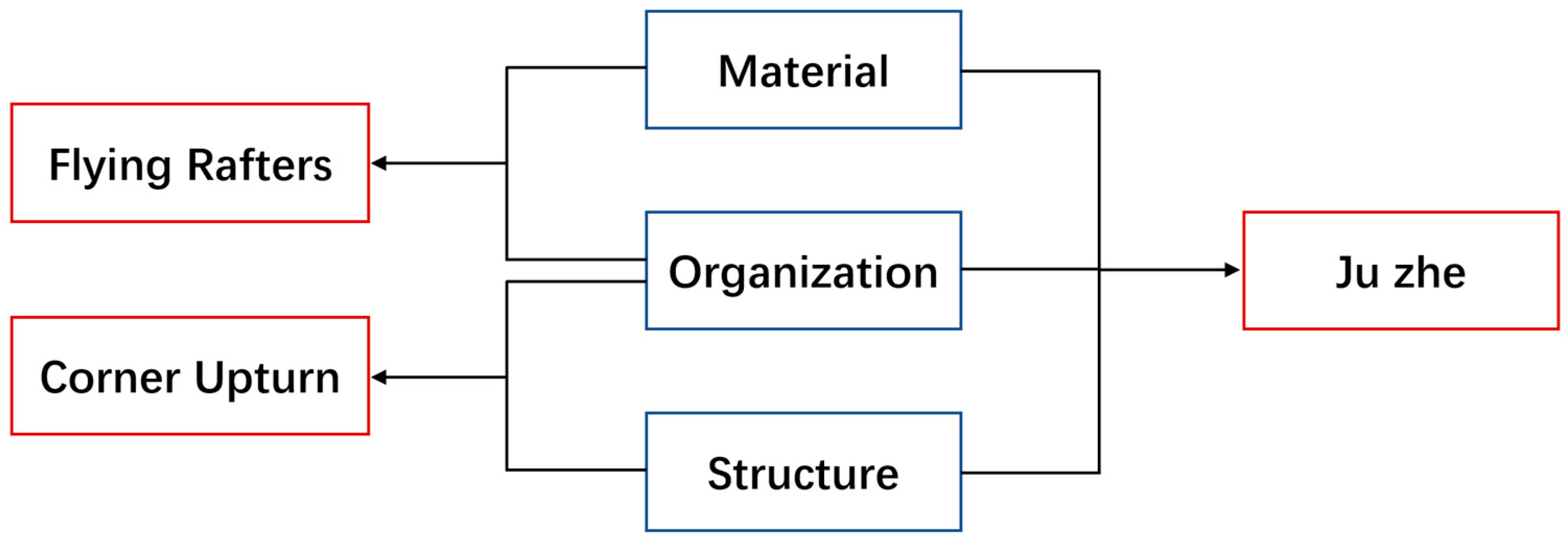
Among these elements, the flying rafters exhibit a strong correlation with material properties and construction methods. The corner upturn demonstrates a significant relationship with construction and structural design. Furthermore, Ju zhe (Main Roof Curvature) is profoundly connected to materials, construction, and structural principles (Figure 12). Under the combined influence of the intrinsic logic pertaining to materials, construction, and structure, these three elements—the flying rafters, corner upturn, and Ju zhe—collectively shaped the classic form of traditional Chinese architectural roofs, characterized by their overall concave curvature and distinctive upturned eaves.

This confirms the concept of “passive form” proposed in this paper: The form of architecture is not always derived from a priori esthetic concepts or symbolic intentions. Instead, it is often the natural result of reasonable and effective solutions found by craftsmen when dealing with objective constraints such as the environment, materials, structure, and construction. Initially, the concave curved form of the roof may not have been an actively pursued esthetic goal but rather a morphological manifestation brought about by technical strategies that had to be accepted or chosen during the construction process.

Although previous scholars have explained the roof curves from perspectives such as water drainage and light intake, as well as cultural interests (such as the image of phoenixes), the analysis from the construction perspective reveals its deeper-seated technical roots. The limitations and requirements of construction are the foundation for the emergence of form. Subsequently, this form may be endowed with cultural and esthetic meanings and, in turn, influence subsequent development and choices. However, the starting point of its occurrence may lie in the construction itself.

The emergence of architectural forms shaped by construction constraints and functional demands is not unique to Chinese architecture but represents a universal phenomenon observed globally.

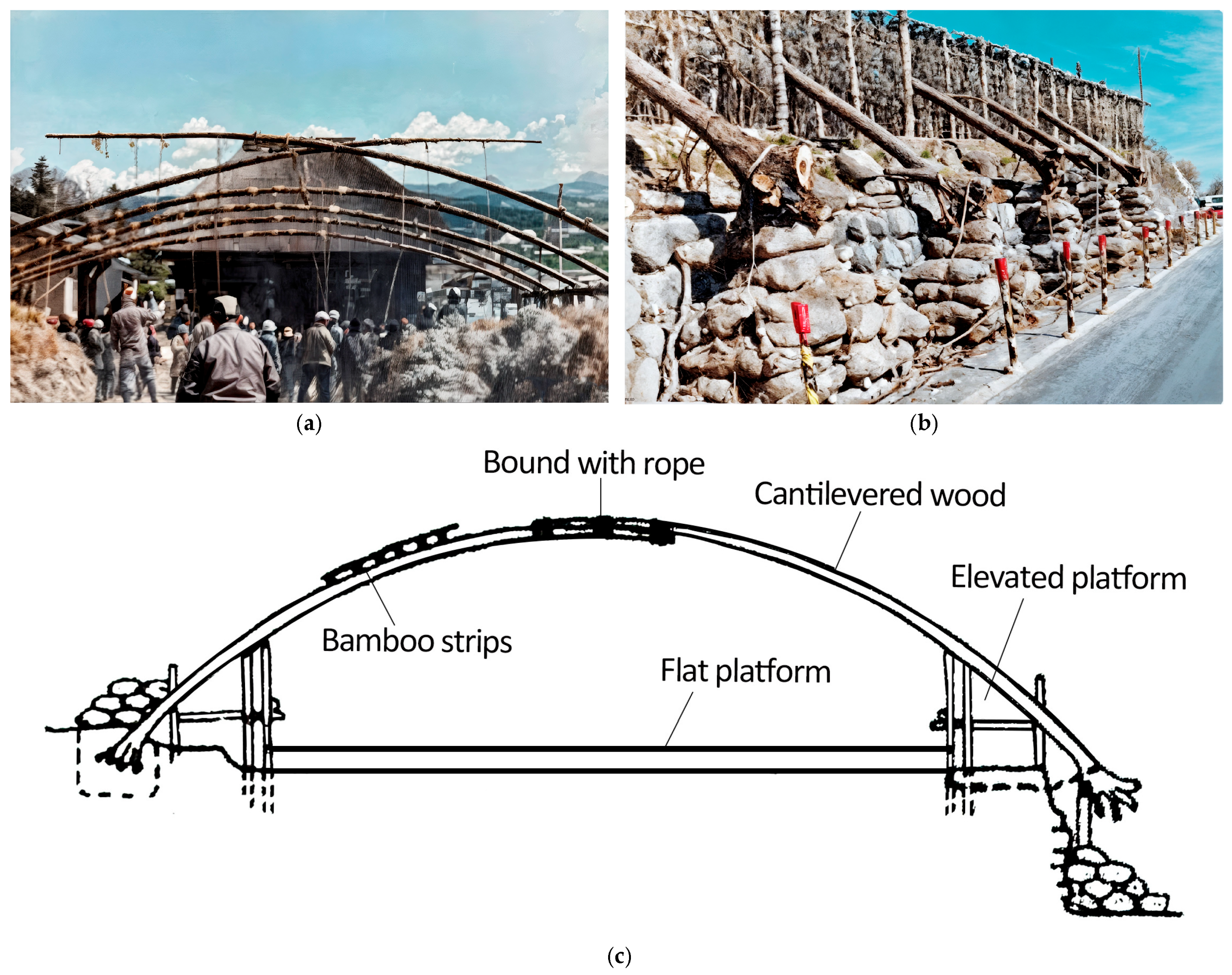
In Development and Outlook of Space Structures, Kimao Saito investigated the roofs of traditional Japanese rural stages, unveiling the structural logic and functional requirements behind their form generation [32]. Using the Mihara stage as an example, the temporary large roof covering the audience employed a unique construction technique (Figure 13). Logs felled from nearby forests were utilized, leveraging the surrounding high viewing stands as fulcrums. These logs were cantilevered from both ends, acting as cantilever beams. The cantilevered ends were forcibly depressed and firmly bound together to form an arched roof structure, which was then covered with thatch. This natural arch, formed by the “single bending” of the components and serving as the structural system, represents an ingenious solution developed under the constraints of a short construction duration, limited rural labor, and cost. It effectively utilized readily available local materials (such as logs, bamboo, ropes, and thatch) and simple jointing methods (rope lashing). After the performance, the materials were disassembled and reused. This form is a direct outcome of responding to material characteristics, temporary requirements, labor conditions, and economic constraints, making it a quintessential example of a building form dictated by construction constraints and demands.

In the history of European architecture, particularly during periods addressing challenges related to large-span structures, form was also profoundly driven by structural demands. The dome of Florence Cathedral, an iconic Renaissance structure, serves as a prime example where its unique form and structural system precisely reflect Brunelleschi’s creative response to the technical challenges of that era. Due to the lack of massive, thick walls to resist the significant lateral thrust of the massive dome, Brunelleschi employed a double-shell structure, supplemented by ringed stone and timber ribs (Figure 14), and borrowed techniques such as Gothic pointed arches (which effectively reduce lateral thrust), thereby ensuring structural stability and safety [33]. This double-shell structure effectively reduced the required volume of material and self-weight and was capable of withstanding complex internal forces. The dome’s “voluminous” form and its ingenious internal structural system fundamentally represent the optimal solution given the limitations of structural forces, material characteristics, and construction techniques of that era. This was not a purely esthetic choice but rather the shaping of form dictated by structural demands.

These examples spanning different cultures and eras reveal the underlying construction logic of architectural form. As emphasized by theorists such as Kenneth Frampton in their concept of Tectonics [36], architecture is more than mere space or facade, but rather the artistic expression of structure and construction. While Tectonics theory encompasses active esthetic choices, the concept of “passive form” emphasizes how the practical limitations and technical challenges encountered during the construction process are directly translated into architectural form. This perspective also resonates with the Materialism perspective of Gottfried Semper and others [37], namely that architectural form is rooted in materials, technology, and craftsmanship themselves.

In ancestral halls and other social buildings, technical logic and cultural needs form an interwoven dialectic. For example, although the odd number of bays system in Lingnan ancestral halls is constrained by the pillar-and-beam frame modular system, it precisely aligns with the spatial ethics of the ritual system regarding “axial symmetry”; similarly, although the span and height of the main hall are limited by timber construction techniques, the achievement of its “monumental scale” is essentially still a breakthrough in material properties and craftsmanship [38]. Cultural demands are, in effect, the proposers of technical problems, while material properties and craft tradition are the sole path to solving them. Decorative art likewise follows this logic: the choice of pigments for murals must consider not only the symbolic meaning of colors but also their durability, adhesion, and compatibility with wall materials, which involves a series of complex craft techniques such as the grinding, preparation, and fixing of mineral pigments. Another example is the decorations on the roof ridge, which commonly include “ridge-end beasts” or “finials”. In some regions, “Ji cha” (also called “ridge cylinder” or “bamboo shoot”) is also used. This is a decorative component erected vertically on the roof ridge, usually made of ceramic or stone, symbolizing the warding off of evil spirits, protecting the dwelling, and praying for good fortune. The installation of these roof ridge decorations requires intricate mortise-and-tenon joinery and stable fixing techniques to ensure that they remain stable under the erosion of wind and rain [39]. The expression of cultural meaning is always dependent on the material carrier enabled by material technology.

The concept of “passive form” underscores the ontological authenticity of architectural practice, embodying three interconnected virtues: (1) Truth (zhen): The form emerges as an honest expression of material properties (e.g., timber creep), constructional logic (e.g., purlin-rafter load redistribution), and structural rationality (e.g., curvature-induced torsion mitigation in wing corner flying rafters). (2) Goodness (shan): It addresses functional imperatives—resolving gravitational deflection in principal eave rafters, optimizing rainwater drainage, and mediating human–environmental symbiosis through incremental adaptations like pad block adjustments. (3) Beauty (mei): It cultivates a “refined simplicity” where technical necessity begets meaningful details (e.g., the rhythmic concave polyline of ju-zhe), transforming structural pragmatism into poetic spatial experiences.

This trinity of zhen–shan–mei coalesces into an architectural sensibility that transcends mere construction, anchoring buildings in cultural meaning and enduring value. The “passive form” thus serves not as a limitation but as a generative framework, proving that architectural significance arises from the dialectic between constraint and creativity.