Thermal Performance and Energy Efficiency Evaluation of Building Envelopes Incorporating Trombe Walls, PCM, and Multi-Alveolar Structures in Tunisian Climate
Abstract
1. Introduction
1.1. Trombe Wall Incorporated into the Buildings’ Façade
1.2. Phase Change Materials Incorporation into the Building Envelope
1.3. Integration of the Trombe Walls That Includes a Phase Change Material
1.4. Multi-Alveolar Envelope Systems
2. Materials and Methods
- -
- Model 1: Corresponds to the reference model: traditional wall with a layer of bricks and plaster (Figure 1a).
- -
- Model 2: Consists of a wall integrating a Trombe wall on the south face to enhance passive solar heating (Figure 1b).
- -
- Model 3: Consists of a wall featuring a MAS designed to improve thermal insulation and inertia (Figure 2a).
- -
- Model 4: Consists of a wall incorporating PCM to store and release heat to stabilize indoor temperatures (Figure 2b).


2.1. Characteristics of PCM
2.2. Characteristics of Multi-Alveolar Envelopes
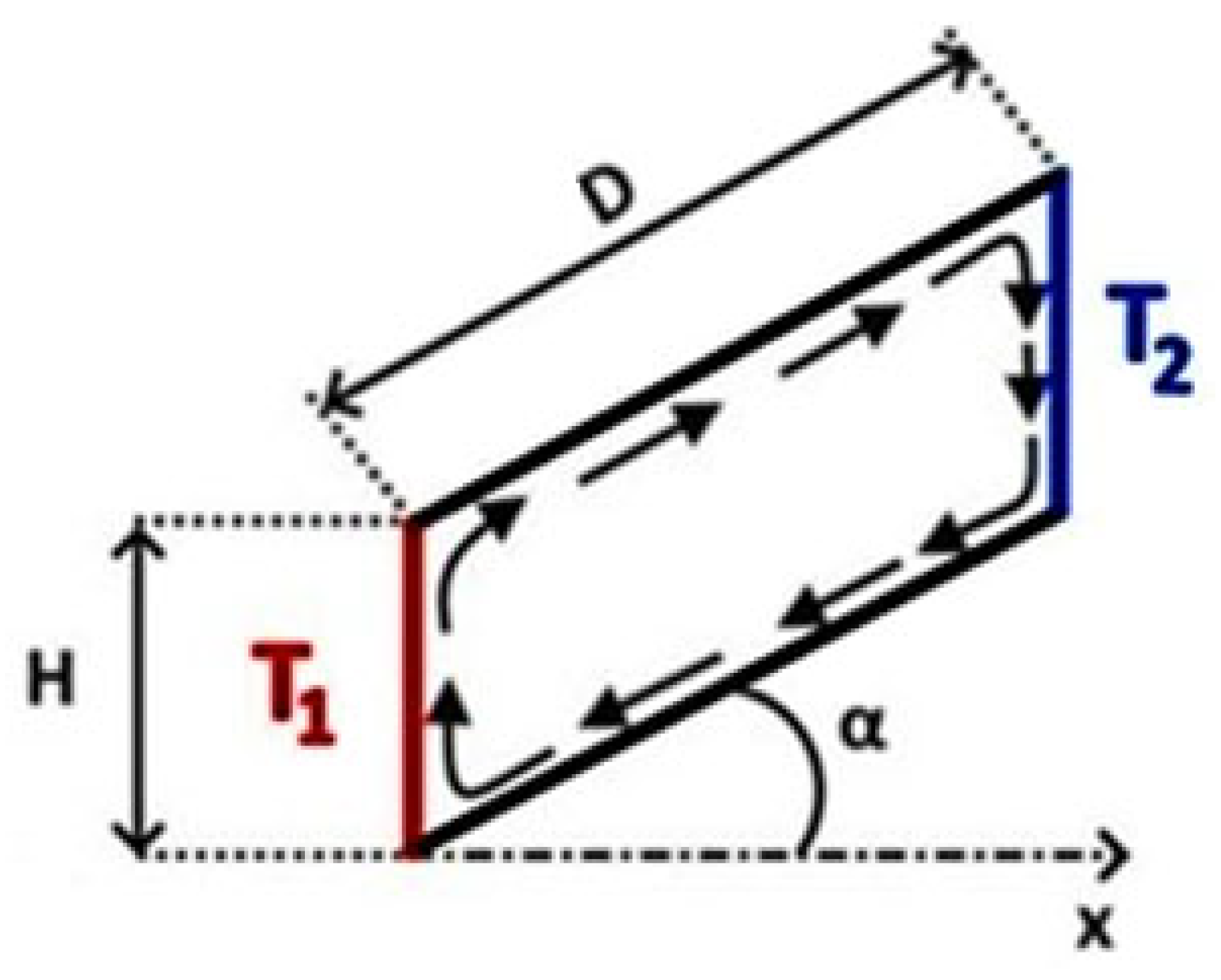
2.3. Heat Transfer Coefficient in Inclined Cavities of MAS
- γ: coefficient influenced by several factors, including the direction of heat transfer, the angle at which the slats are inclined relative to the horizontal, and the emissivity characteristics of the slat surfaces, whether they are low- or high-emissive.
- : Temperature gradients (°C)
2.4. Mathematical Formulation
2.4.1. The Hypotheses
- -
- Heat transmission occurs in only one direction.
- -
- The thermophysical characteristics of the materials are the same in both zones and remain stable.
- -
- Each layer is homogeneous and isotropic.
- -
- The layers that make up the envelope walls are perfectly in contact with each other.
- -
- There are no thermal bridges.
- -
- Within these two zones, the air temperature remains constant.
- -
- The incident solar flux is constant over the entire face.
2.4.2. Formulation and Discretization of the Problem
2.5. Conditions of Thermal Boundaries
2.5.1. External Boundary Conditions
Weather and Temperature Conditions
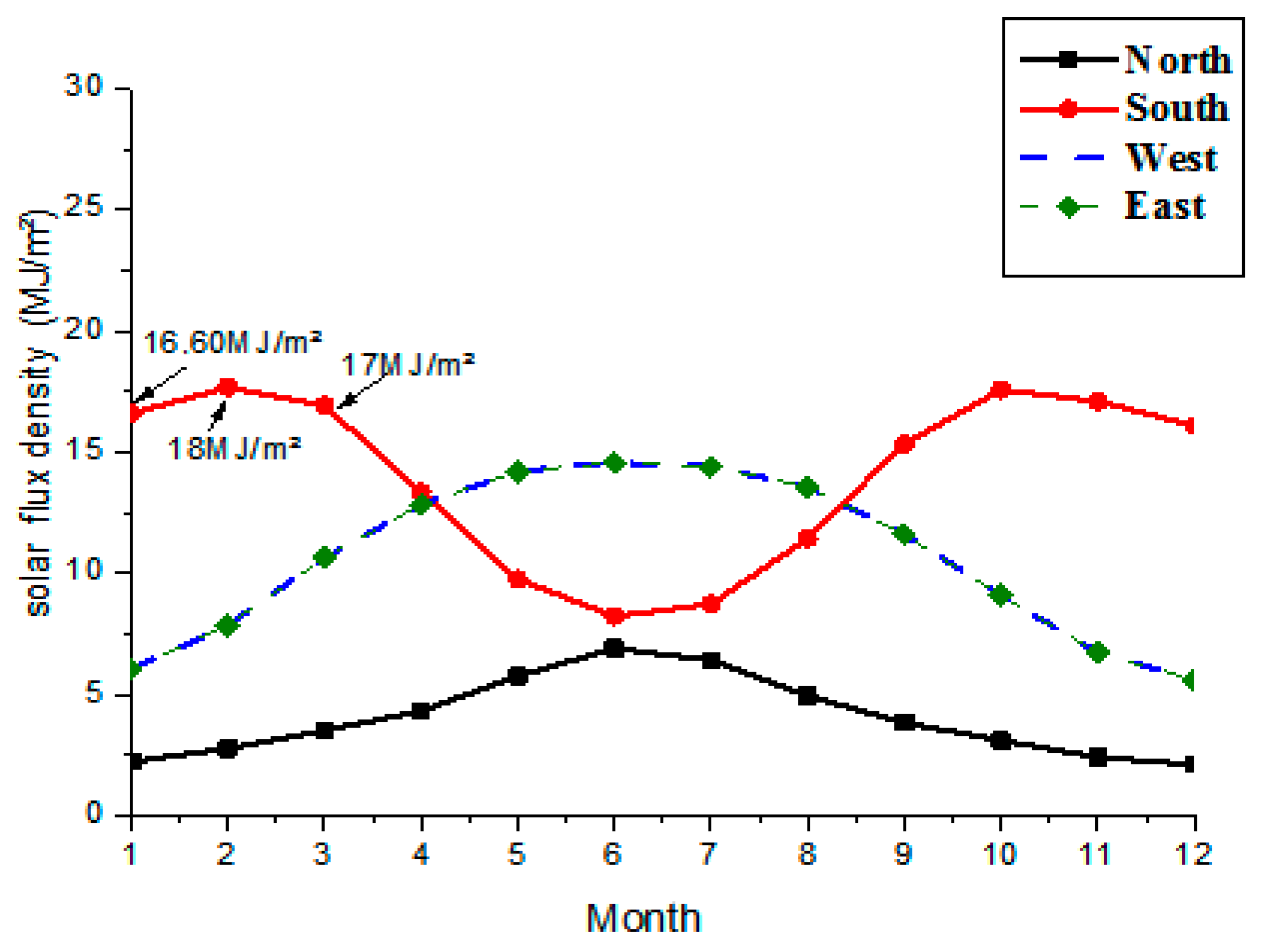
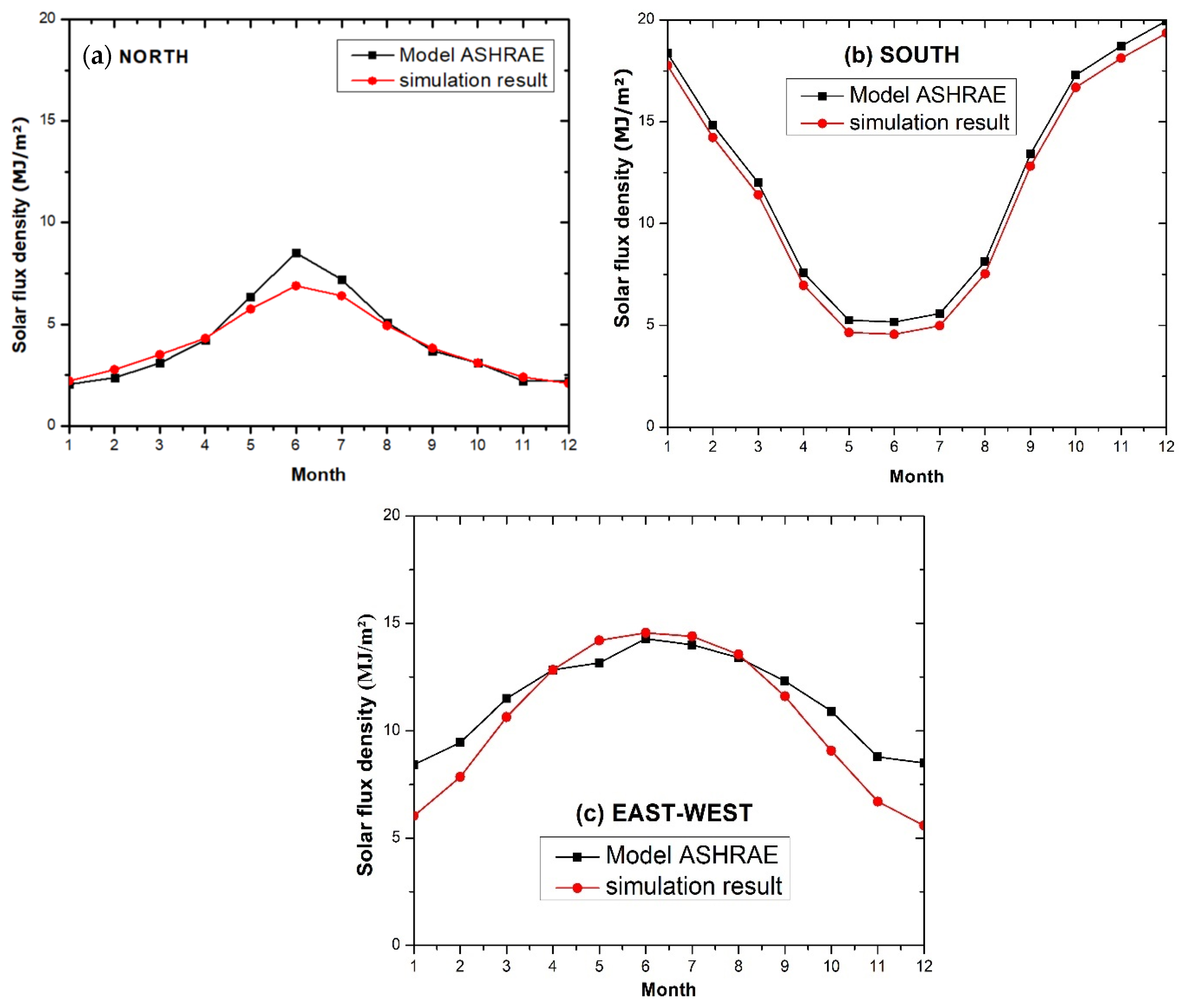
The Modeling of the Global Solar Radiation Density Was Validated
External Thermal Convective Coefficient
2.5.2. Internal Boundary Conditions
2.6. Comfort and Building Response
2.6.1. Building Thermal Comfort
2.6.2. Thermal Response of the Building
3. Results and Discussion
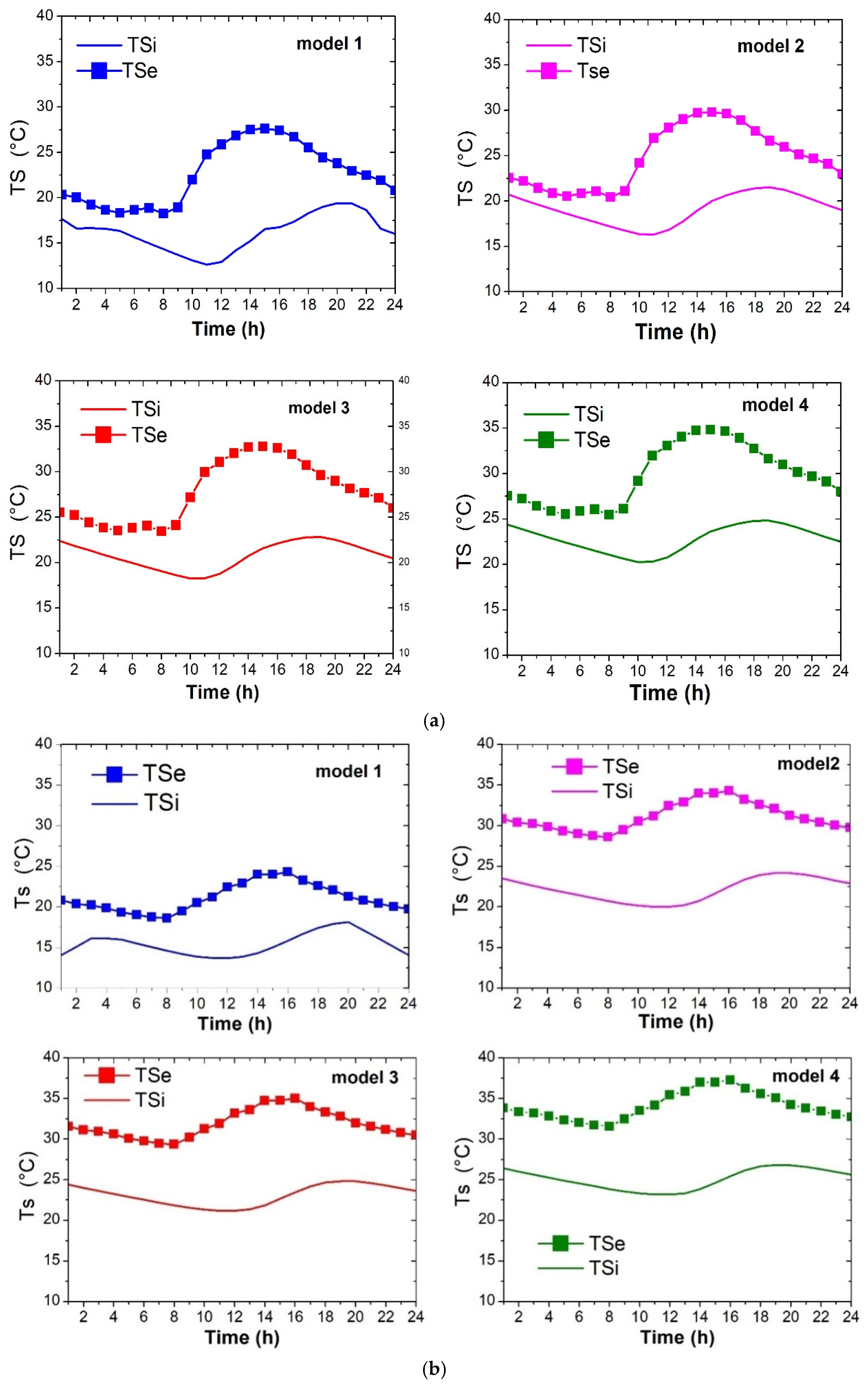
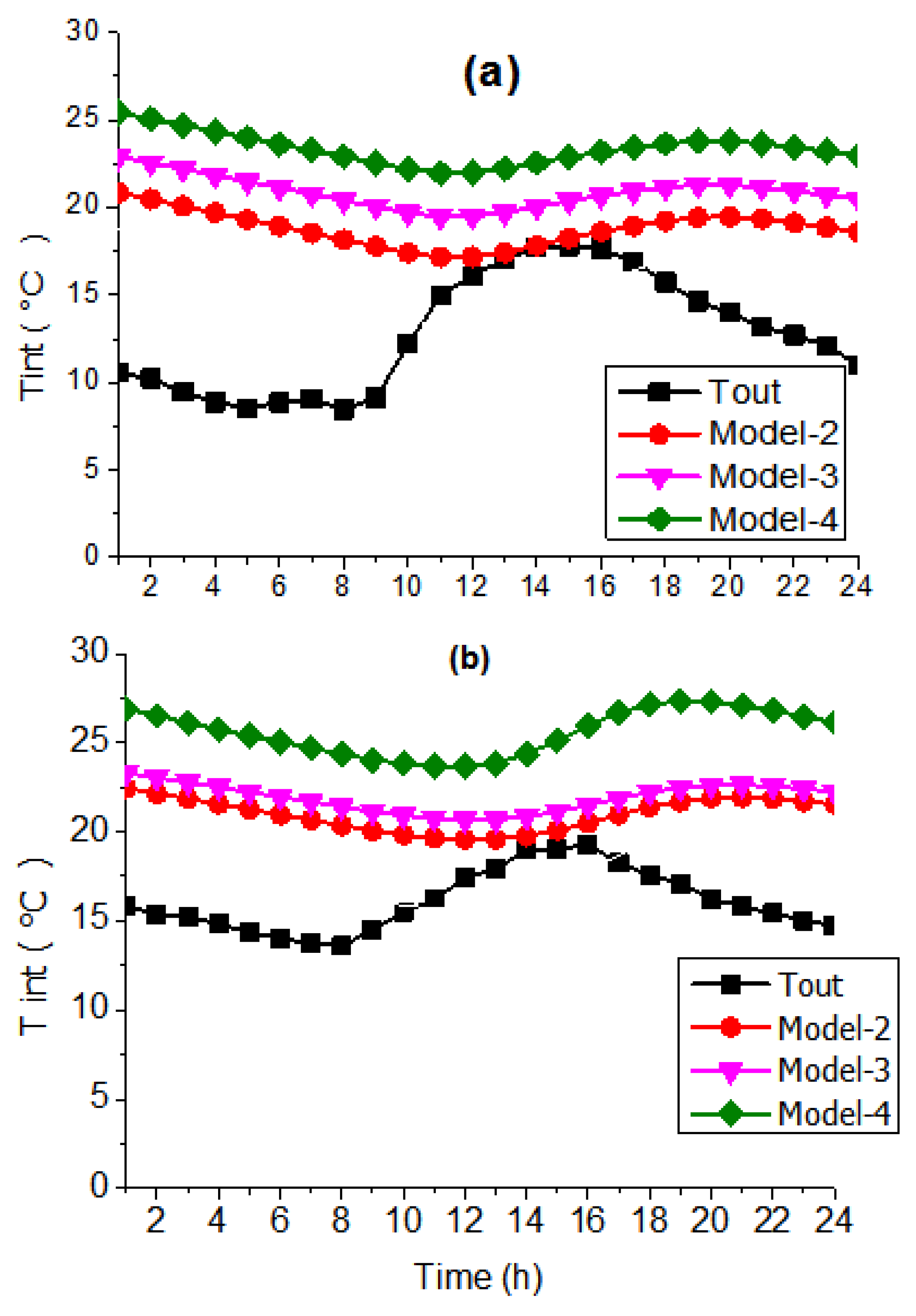
3.1. Case of Free Indoor Air Temperature
3.2. Situation Where the Temperature Inside Is Set
3.3. Impact of Occupant Presence
4. Conclusions
- -
- Model 4 (Trombe wall + PCM + MAS) achieved optimal thermal stability, showing a 6-h phase shift and damping factors of 40% (January) and 50% (March). This configuration reduced indoor temperature fluctuations by 40% compared to Model 1 (conventional wall).
- -
- Model 3 (MAS) demonstrated intermediate performance, with phase shifts of 5.1–5.5 h and damping factors of 50–66%, underscoring the contribution of alveolar structures to thermal inertia.
- -
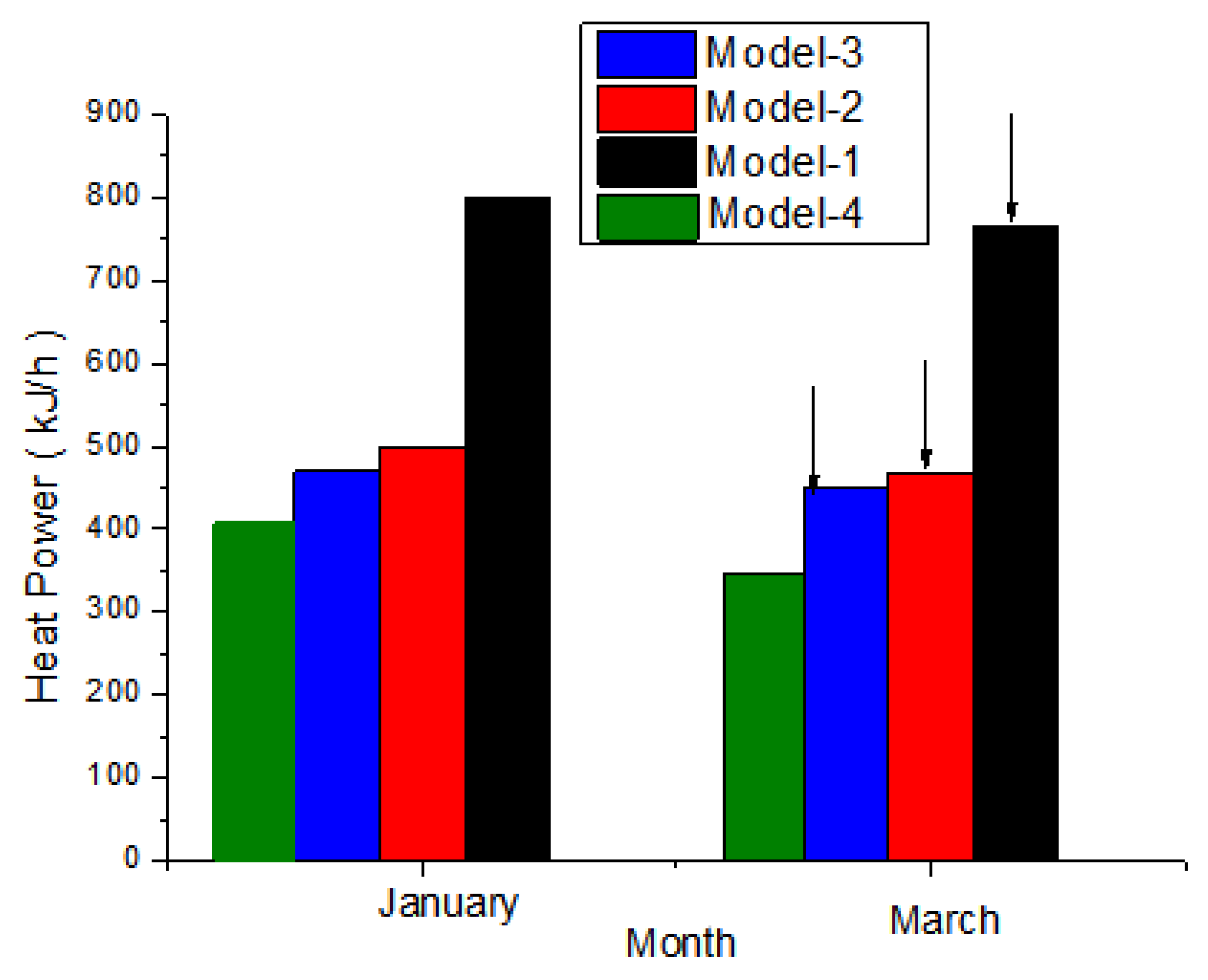
- The heating power demand of Model 4 was 400 kJ/h in January and 300 kJ/h in March, representing a 50% reduction compared to Model 1 (800 kJ/h in January).
- -
- Model 2 (Trombe wall) reduced heating demand by 37.5% (500 kJ/h), highlighting the additional benefits of PCM and MAS integration.
- -
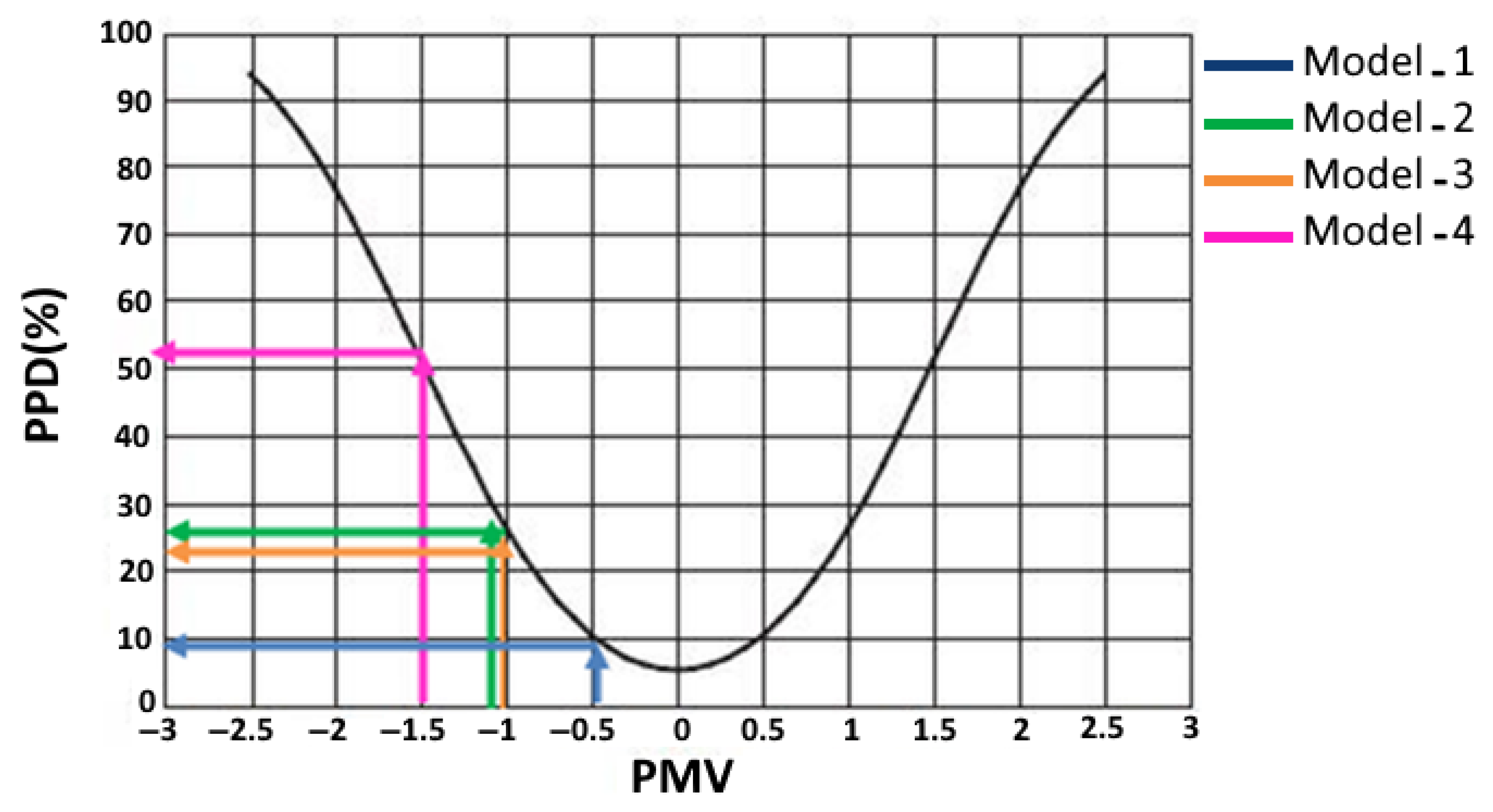
- Thermal comfort in Model 4 (PMV: −0.5; PPD: 9.8%) complied with the ISO 7730 standards, whereas Model 1 exhibited inferior performance (PMV: −1.5; PPD: 51%).
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Corasaniti, S.; Manni, L.; Russo, F.; Gori, F. Numerical simulation of modified Trombe-Michel Walls with exergy and energy analysis. Int. Commun. Heat Mass Transf. 2017, 88, 269–276. [Google Scholar] [CrossRef]
- Boyer, H.; Lucas, F.; Miranville, F.; Bastide, A.; Morau, D. Simulations de dispositifs du type Mur Trombe avec CODYRUN. In Proceedings of the ESIM, Toronto, ON, Canada, 3–5 May 2006; pp. 81–233. [Google Scholar]
- Stazi, F.; Mastrucci, A.; De Perna, C. Experimental and numerical study on the performance of solar walls in Mediterranean climates. World Renew. Energy Congr. 2011, 57, 1938–1945. [Google Scholar]
- Simões, N.; Manaia, M.; Simões, I. Energy performance of solar and Trombe walls in Mediterranean climates. Energy 2021, 234, 121197. [Google Scholar] [CrossRef]
- Briga-Sá, A.; Martins, A.; Boaventura-Cunha, J.; Lanzinha, J.C.; Paiva, A. Energy performance of Trombe walls: Adaptation of ISO 13790: 2008 to the Portuguese reality. Energy Build. 2014, 74, 111–119. [Google Scholar] [CrossRef]
- Figueiredo, A.; Vicente, R.; Lapa, J.; Cardoso, C.; Rodrigues, F.; Kämpf, J. Indoor thermal comfort assessment using different constructive solutions incorporating PCM. Appl. Energy 2017, 208, 1208–1221. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M. Energetic and thermal comfort assessment of phase change material passively incorporated building envelope in severe hot climate. Appl. Energy 2022, 314, 118957. [Google Scholar] [CrossRef]
- Gobinath, S.; Senthilkumar, G.; Beemkumar, N. Comparative study of room temperature control in buildings with and without the use of PCM in walls. Energy Sources Part A 2018, 40, 1765–1771. [Google Scholar] [CrossRef]
- Kharbouch, Y.; Mimet, A.; El Ganaoui, M. A simulation-based optimization method for energy efficiency of a multi-zone house integrated PCM. Energy Procedia 2017, 139, 450–455. [Google Scholar] [CrossRef]
- Khdair, A.I.; Rumman, G.A.; Basha, M. The art of writing a scientific article. J. Build. Eng. 2022, 48, 103923. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Zhu, Z.; Zhu, J.; Luo, J.; Peng, F.; Sun, X. The impact of Trombe wall integrated with phase change materials on thermal comfort in buildings. Energy Built Environ. 2024, 5, 58–69. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, Z.; Peng, Z.; Luo, J.; Sun, X.; Li, J.; Peng, F. The Trombe wall equipped with PCMs for the enhancement of the indoor thermal quality. Energy Build. 2023, 297, 113407. [Google Scholar] [CrossRef]
- Zhou, Y.; Wah Yu, C. The year-round thermal performance of a new ventilated Trombe wall integrated with phase change materials. Indoor Built Environ. 2019, 28, 195–216. [Google Scholar] [CrossRef]
- Sadineni, S.B.; Madala, S.; Boehm, R.F. Passive building energy savings: A review of building envelope components. Renew. Sustain. Energy Rev. 2011, 15, 3617–3631. [Google Scholar] [CrossRef]
- Elsaid, A.M.; Hashem, F.A.; Mohamed, H.A.; Ahmed, M.S. The energy savings achieved by various Trombe solar wall enhancement techniques. Sol. Energy Mater. Sol. Cells 2023, 254, 112228. [Google Scholar] [CrossRef]
- Mazurek, M. Annual Thermal Performance of the Trombe Wall with Phase Change Heat Storage under Climate Conditions of Uzbekistan. Appl. Sol. Energy 2022, 58, 55–64. [Google Scholar] [CrossRef]
- Tenpierik, A.; Turrin, M.; van der Spoel, R. Phase Change Materials in Facades of Buildings for Solar Heating and Cooling. In Proceedings of the CLIMA 2022, Rotterdam, The Netherlands, 22–25 May 2022. [Google Scholar]
- Zhou, D.; Song, X.; Liu, H.; Zhao, J. Structure and Regional Optimization of a Phase Change Material Trombe Wall System. Energy 2024, 305, 117977. [Google Scholar] [CrossRef]
- Askari, M.; Jahangir, M. Evaluation of Thermal Performance and Energy Efficiency of a Trombe Wall Improved with Dual Phase Change Materials. Energy 2023, 284, 119027. [Google Scholar] [CrossRef]
- Zhou, D.; Liu, H.; Song, X.; Zhao, J. Heating and Energy Performances of a Dynamic Trombe Wall Incorporating Phase Change Materials. J. Build. Eng. 2024, 95, 107458. [Google Scholar] [CrossRef]
- Vázquez-Beltrán, M.; Herrera-Vázquez, R.; Araiza-Aguilar, J.J. Thermal Evaluation of a Trombe Wall with Phase Change Material for Heating in the Cold Season. J. Build. Eng. 2025, 100, 107174. [Google Scholar]
- Seki, N.; Fukusako, S.; Yamaguchi, A. An experimental study of free corrective heat transfer in a parallelogrammic enclosure. J. Heat Transf. 1983, 105, 433–439. [Google Scholar] [CrossRef]
- Vullierme, J.J.; Boukadida, N. Study of Structure with a Diode Thermal Effect. In Proceedings of the IJTH Congress, Rabat, Morocco, 2–5 April 1985; pp. 781–789. [Google Scholar]
- Lajimi, N.; Boukadida, N. Numerical study of the thermal behavior of bi-zone buildings. Comptes Rendus Phys. 2015, 16, 708–720. [Google Scholar] [CrossRef]
- Lajimi, N.; Ben Taher, N.; Boukadida, N. Numerical study of the energy efficiency of the building envelope containing multi-alveolar structures. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 931–946. [Google Scholar] [CrossRef]
- ISO 10456:2007; Building Materials-Thermal Properties. International Organization for Standardization: Geneva, Switzerland, 2007.
- Dolzycki, B.; Jaczewski, M.; Szydlowski, C. The long-term properties of mineral-cement-emulsion mixtures. Constr. Build. Mater. 2017, 156, 790–798. [Google Scholar] [CrossRef]
- Biwole, P.H.; Eclache, P.; Kuznik, F. Phase-change materials to improve solar panel’s performance. Energy Build. 2013, 62, 59–67. [Google Scholar] [CrossRef]
- Al-Sanea, S.A.; Zedan, M.F.; Al-Ajlan, S.A. Adjustment factors for the ASHRAE clear-sky model. Appl. Energy 2004, 79, 215–237. [Google Scholar] [CrossRef]
- ISO 7730:1994; Moderate Thermal Environments-Determination of the PMV and PPD Indices. International Organization for Standardization: Geneva, Switzerland, 1994.
- Hamdani, M.; Bekkouche, S.M.A.; Benouaz, T.; Cherier, M.K.; Benamrane, N.; Benkhalifa, R.D.A. Étude de la ventilation naturelle transversale sur un bâtiment semi-collectif. In Proceedings of the 5th International Seminar on New and Renewable Energies, Ghardaïa, Algeria, 24–25 October 2018. [Google Scholar]
- Aste, N.; Angelotti, A.; Buzzetti, M. The influence of the external walls thermal inertia. Energy Build. 2009, 41, 1181–1187. [Google Scholar] [CrossRef]
- Cianfrini, M.; Corcione, M.; de Lieto Vollaro, R.; Habib, E.; Quintino, A. Thermal inertia of hollow wall blocks. In Proceedings of the CISBAT 2015 Proceedings, Lausanne, Switzerland, 9–11 September 2015; pp. 149–154. [Google Scholar]
- Saboor, S.; TP, A.B. Effect of air space thickness within the external walls. Energy Procedia 2015, 79, 766–771. [Google Scholar] [CrossRef]
- Bungău, T.; Bungău, C.C.; Bendea, C.; Hanga-Fărcaș, I.F.; Prada, M.F. Bibliometric Analysis of Thermal Comfort and Environmental Quality: A Framework for Sustainable Construction. J. Appl. Eng. Sci. 2024, 22, 45–58. [Google Scholar] [CrossRef]
- Bungau, C.C.; Bendea, C.; Bungau, T.; Radu, A.-F.; Hanga-Farcas, I.F.; Vesa, C.M. The Relationship between the Parameters That Characterize a Built Living Space and the Health Status of Its Inhabitants. Sustainability 2024, 16, 1771. [Google Scholar] [CrossRef]
- Sánchez, E.D.P.; Grindlay, A.L.; Agulló, M.J.C. Triple Helix Model for Sustainable Regional Innovation. Sustainability 2022, 14, 15728. [Google Scholar] [CrossRef]

| Walls | Components (from Inside to Outside) | Thickness (m) | Density (kg/m3) | Specific Heat (kJ/kg·K) | Thermal Conductivity (kJ/h·m·K) |
|---|---|---|---|---|---|
| Components of vertical walls of Mode 1 | Plaster coating [26] | 0.005 | 1500 | 1 | 1.264 |
| Brick [27] | 0.126 | 1800 | 1 | 3.2 | |
| Components of the vertical walls of Model 2 | Plaster coating | 0.005 | 1500 | 1 | 1.264 |
| Brick | 0.126 | 1800 | 1 | 3.2 | |
| Air gap | 0.013 | 1 | 1.227 | 0.289 | |
| Glass | 0.013 | 2490 | 0.83 | 4.188 | |
| Components of the vertical walls of Model 3 | Plaster coating | 0.005 | 1500 | 1 | 1.264 |
| PCM [28] | 0.02 | 814 | 2.15 | 0.35 | |
| Brick | 0.126 | 1800 | 1 | 3.2 | |
| Air gap | 0.013 | 1 | 1.227 | 0.289 | |
| Glass | 0.013 | 2490 | 0.83 | 4.188 | |
| Components of the vertical walls of Model 4 | Plaster coating | 0.005 | 1500 | 1 | 1.264 |
| PCM | 0.02 | 814 | 2.145 | 0.04 | |
| Brick | 0.126 | 1800 | 1 | 3.2 | |
| MAS [24] | 0.057 | 2490 | 0.83 | 4.188 | |
| Glass | 0.013 | 2490 | 0.83 | 4.188 | |
| Roof | Concrete | 0.240 | 2400 | 0.8 | 7.56 |
| Insulation | 0.16 | 40 | 0.8 | 5 | |
| Floor | Floor | 0.005 | 800 | 1 | 0.252 |
| Stone | 0.06 | 2000 | 1 | 5 | |
| Concrete | 0.240 | 2400 | 0.8 | 7.56 | |
| Insulation | 0.080 | 40 | 0.8 | 5 |
| State | ||||
|---|---|---|---|---|
| Solid PCM | 1.26 | 2150 | 814 | - |
| Liquid PCM | 0.54 | 2150 | 750 | 223 |
| Criteria | Model-2 (Trombe Wall) | Model-3 (MAS) | Model-4 (PCM + MAS + Trombe) | Comparative Analysis |
|---|---|---|---|---|
| Average Temperature (°C) | ||||
| January | 18.2 | 19.8 | 21.4 | Model-4 maintains a higher temperature (21.4 °C) compared to Model 2 (18.2 °C). |
| March | 22.2 | 23.8 | 25.4 | Model-4 reaches the highest temperature (25.4 °C) compared to Model2 (20.5 °C). |
| Months | January | March | ||
|---|---|---|---|---|
| φ (h) | F (%) | φ (h) | F (%) | |
| Model-1 | 3 | 75 | 4 | 80 |
| Model-2 | 4.25 | 57 | 5 | 71 |
| Model-3 | 5.12 | 50 | 5.5 | 66 |
| Model-4 | 6.02 | 40 | 6.12 | 50 |
| Configuration | Model-1 | Model-2 | Model-3 | Model-4 |
|---|---|---|---|---|
| PMV | −1.5 | −1.2 | −1 | −0.5 |
| PPD | 51% | 25% | 20% | 9.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lajimi, N.; Boukadida, N.; Maatki, C.; Hadrich, B.; Hassen, W.; Kolsi, L.; Ben Aissia, H. Thermal Performance and Energy Efficiency Evaluation of Building Envelopes Incorporating Trombe Walls, PCM, and Multi-Alveolar Structures in Tunisian Climate. Buildings 2025, 15, 2575. https://doi.org/10.3390/buildings15142575
Lajimi N, Boukadida N, Maatki C, Hadrich B, Hassen W, Kolsi L, Ben Aissia H. Thermal Performance and Energy Efficiency Evaluation of Building Envelopes Incorporating Trombe Walls, PCM, and Multi-Alveolar Structures in Tunisian Climate. Buildings. 2025; 15(14):2575. https://doi.org/10.3390/buildings15142575
Chicago/Turabian StyleLajimi, Nour, Noureddine Boukadida, Chemseddine Maatki, Bilel Hadrich, Walid Hassen, Lioua Kolsi, and Habib Ben Aissia. 2025. "Thermal Performance and Energy Efficiency Evaluation of Building Envelopes Incorporating Trombe Walls, PCM, and Multi-Alveolar Structures in Tunisian Climate" Buildings 15, no. 14: 2575. https://doi.org/10.3390/buildings15142575
APA StyleLajimi, N., Boukadida, N., Maatki, C., Hadrich, B., Hassen, W., Kolsi, L., & Ben Aissia, H. (2025). Thermal Performance and Energy Efficiency Evaluation of Building Envelopes Incorporating Trombe Walls, PCM, and Multi-Alveolar Structures in Tunisian Climate. Buildings, 15(14), 2575. https://doi.org/10.3390/buildings15142575










