Finite Element Modeling and Performance Evaluation of a Novel 3D Isolation Bearing
Abstract
1. Introduction
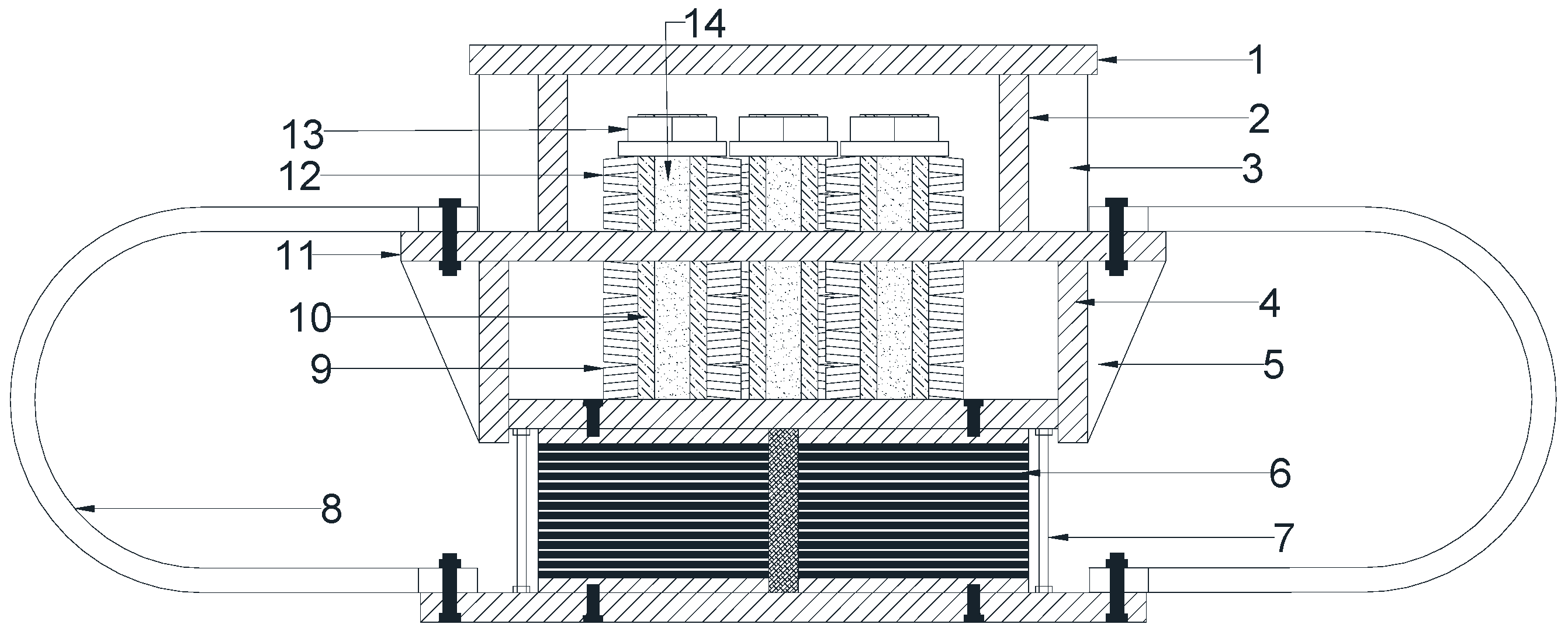
2. Configuration and Working Mechanism of Bearing
2.1. Configuration
2.2. Working Mechanism
3. Introduction to Specimen Design
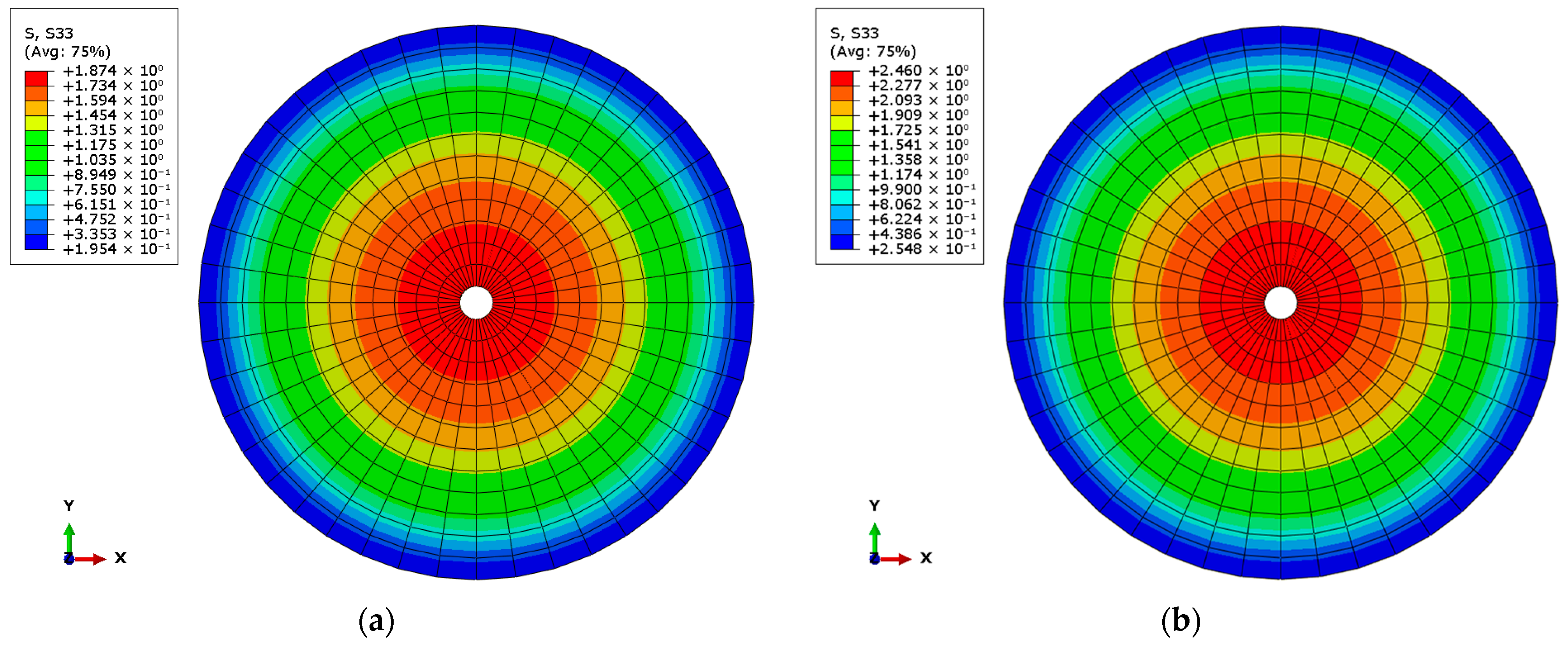
3.1. Design of LRB
3.2. Disc Spring Groups 1 and 2
3.3. U-Shaped Dampers
3.4. Sleeves and Other Plates
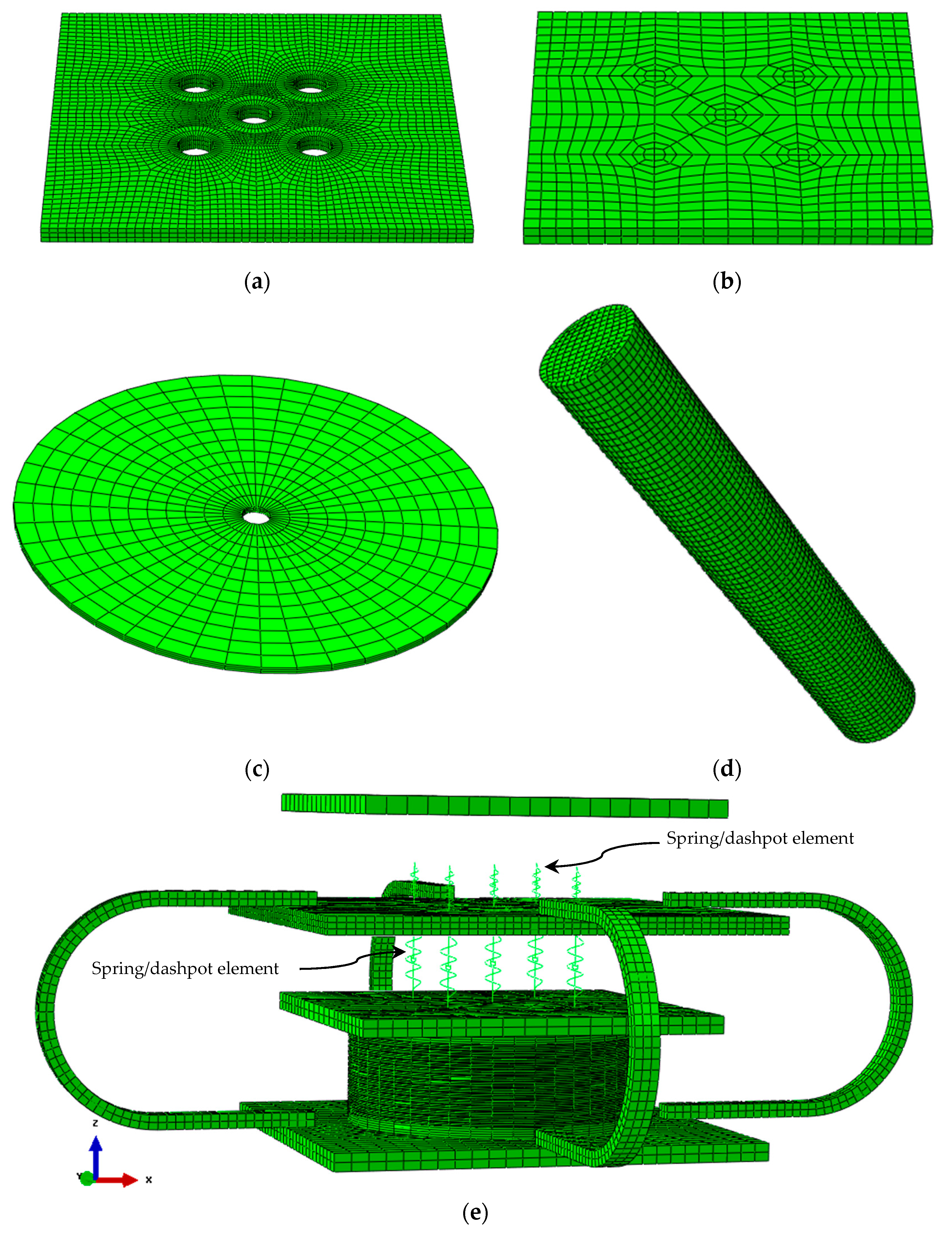
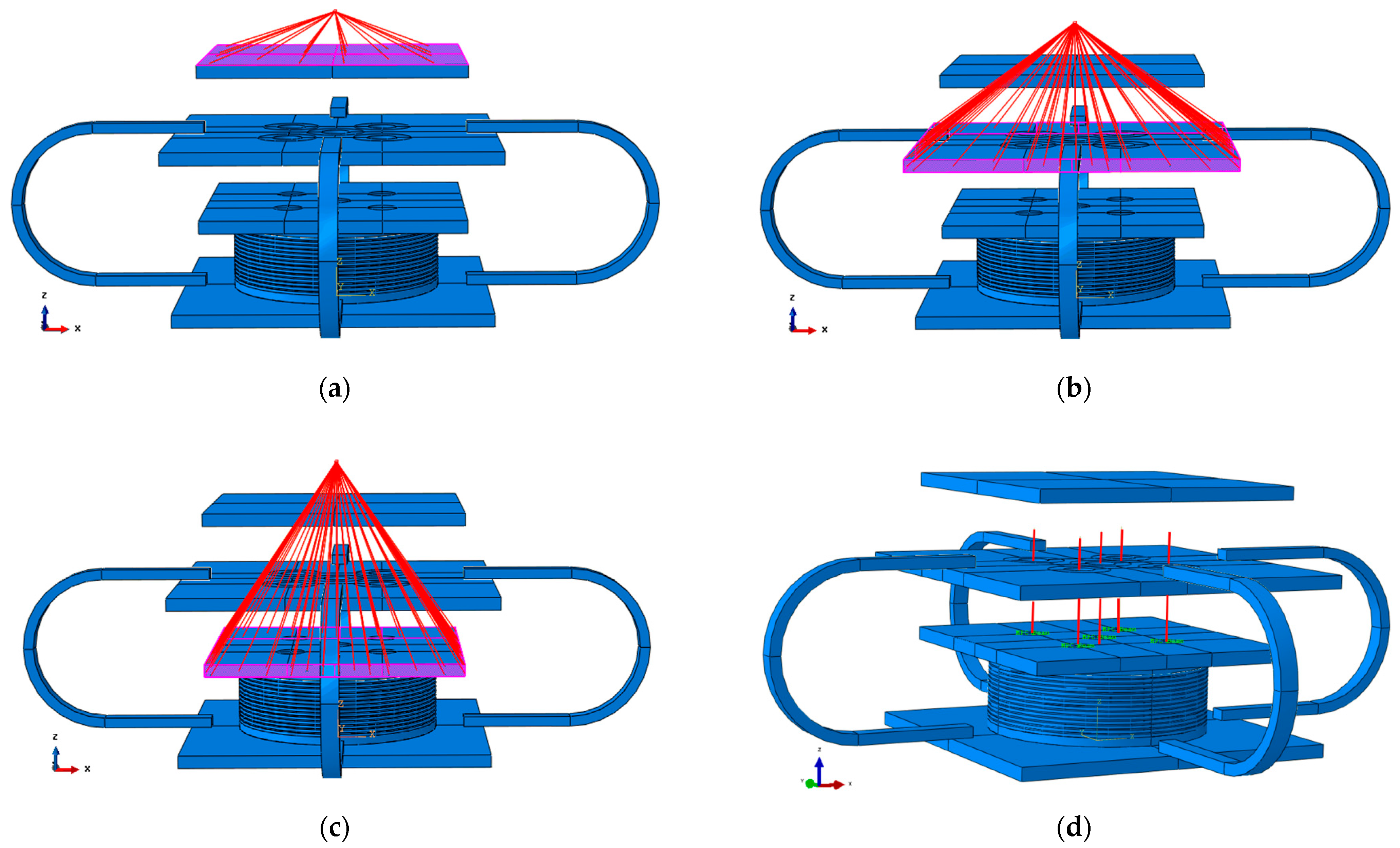
4. Finite Element Modeling
4.1. Material Constitutive Model
4.2. Element Type and Meshing
4.3. Definition of Interaction and Boundary Conditions
5. Validation of FE Model
6. Horizontal Performance Analysis
6.1. Different Vertical Loads
6.2. Different Horizontal Shear Strains
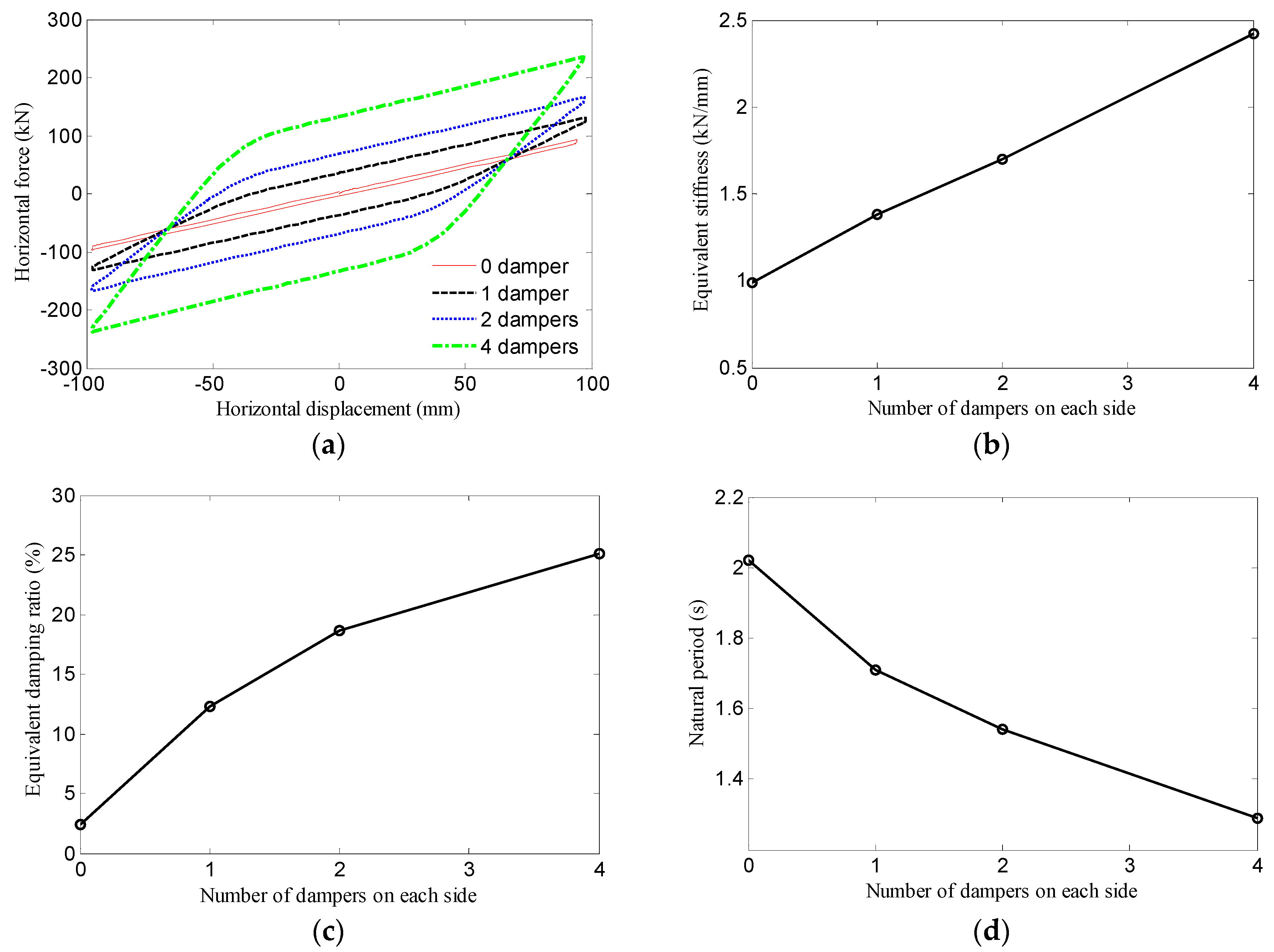
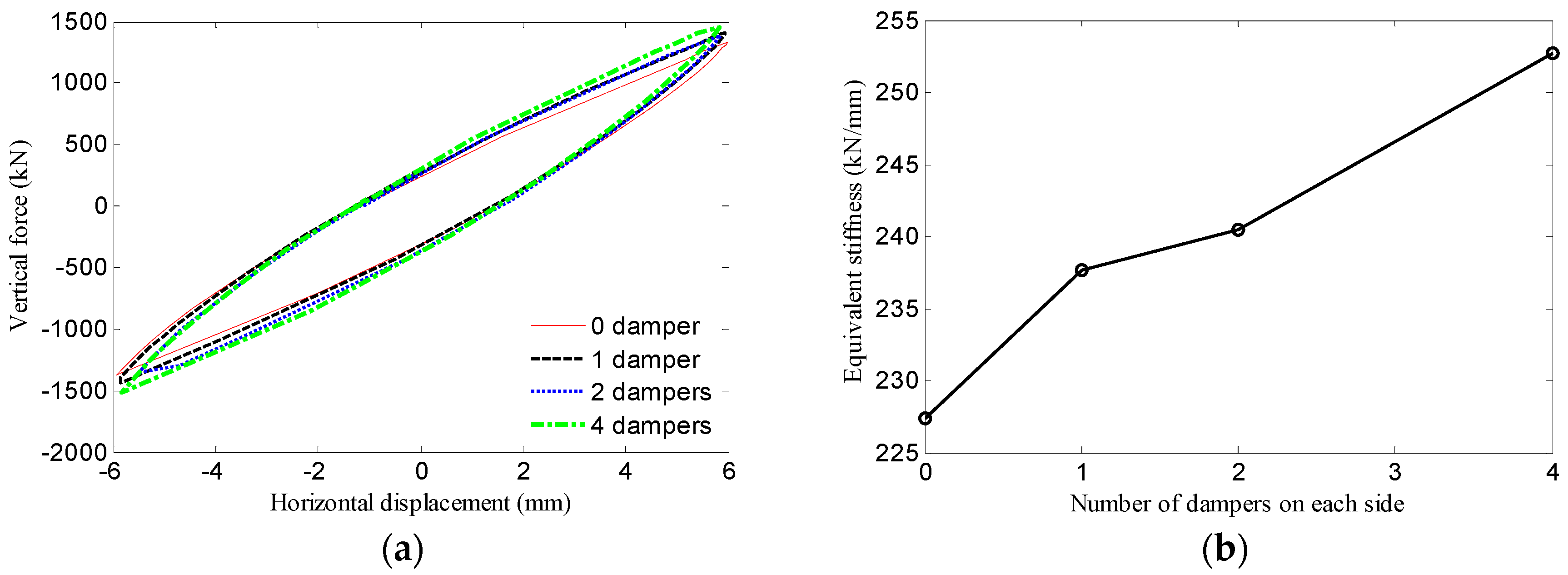
6.3. Different Numbers of U-Shaped Dampers
7. Vertical Performance Analysis
7.1. Different Vertical Displacements
7.2. Different U-Shaped Dampers
8. Conclusions
- (1)
- A finite element model of the 3D isolation bearing is established. Given the structural complexity of the bearing, certain components, such as the stiffened sleeves, disc springs, and support shafts, are simplified during the modeling process. The validity of the model is confirmed through comparison with existing experimental data. The results indicate that the finite element model can accurately predict the mechanical behavior of the bearing.
- (2)
- In terms of load-bearing capacity, the numerical analysis demonstrates that the proposed bearing provides stable load-carrying performance. The distribution of vertical loads between the LRB and U-shaped dampers can be flexibly adjusted by varying the number of dampers.
- (3)
- Under compressive-shear loading conditions, the bearing exhibits reliable energy dissipation characteristics. Although the small lead core design imposes limitations on energy dissipation, increasing the number of U-shaped dampers significantly enhances this capability. Specifically, compared with the bearing without U-shaped dampers, the energy dissipation capacity of the bearing increases by 628%, 1300%, and 2581% when employing 1, 2, and 4 dampers on each side, respectively.
- (4)
- With respect to vertical performance, the numerical results show that when the bearing is subjected to a tensile displacement of 6 mm, the displacement of the LRB remains within the range of 4.43 to 4.67 mm. This indicates that the disc spring group design effectively mitigates the tensile deformation of the LRB, thereby improving its tensile resistance. Additionally, the U-shaped dampers contribute minimally to vertical energy dissipation compared to their impact on the vertical stiffness and load-bearing capacity.
- (5)
- This study primarily employs finite element analysis to conduct a preliminary investigation into the mechanical properties of a new 3D bearing. To facilitate further research and practical application, future studies should include vertical performance testing, shaking table experiments, and theoretical analysis, which are urgently needed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pan, P.; Zeng, Y.; Cao, Y.R.; Ai, H.H.; Wang, H.S. State-of-the-art of research on the building structure isolation technologies. Eng. Mech. 2024, 41, 39–54. (In Chinese) [Google Scholar]
- Collier, C.J.; Elnashai, A.S. A procedure for combining vertical and horizontal seismic action effects. J. Earth Eng. 2001, 5, 521–539. [Google Scholar] [CrossRef]
- Li, N.; Liu, H.G.; Liu, P.; Li, Z.X.; Xie, L.L. Statistical analysis of vertical ground motion characteristics in near-fault regions. Chin. Civ. Eng. J. 2020, 53, 120–128. (In Chinese) [Google Scholar]
- Seigenthaler, R. Earthquake-proof building supporting structure with shock absorbing damping elements. Schweiz. Bauztg. 1970, 20, 211–219. [Google Scholar]
- Aiken, I.D.; Kelly, J.M.; Tajirian, F.F. Mechanics of Low Shape Factor Elastomeric Seismic Isolation Bearings; Report No. UCB/EERC-89/13; University of California: Berkeley, CA, USA, 1989. [Google Scholar]
- Lu, Z.; Liang, Q.Y.; Zhou, Y.; Luo, W.L.; Li, J.R.; Jiang, K. Novel thick layer damping rubber bearing (TLDRB) with reduced vertical stiffness: Laboratory tests and mechanical models. J. Build. Struct. 2024, 94, 109839. [Google Scholar] [CrossRef]
- Huffmann, G. Full base isolation for earthquake protection by helical springs and viscodampers. Nucl. Eng. Des. 1985, 84, 331–338. [Google Scholar] [CrossRef]
- Fujita, S.; Minagawa, K.; Tanaka, G.; Shimosaka, H. Intelligent seismic isolation system using air bearings and earthquake early warning. Soil Dyn. Earthq. Eng. 2011, 31, 223–230. [Google Scholar] [CrossRef]
- Mo, Z.; Lai, B.L.; Shu, G.P.; Yang, T.Y.; Ventura, C.E.; Richard Liew, J.Y. Enhancing seismic resilience in modular steel building through three-dimensional isolation. Eng. Struct. 2025, 323, 119269. [Google Scholar] [CrossRef]
- Zhou, Z.G.; Wong, J.; Mahin, S. Potentiality of using vertical and tree-dimensional isolation systems in nuclear structures. Nucl. Eng. Technol. 2016, 48, 1237–1251. [Google Scholar] [CrossRef]
- Fujita, S.; Kato, E.; Kashiwazaki, A.; Shimoda, I.; Sasaki, K. Shake table tests on three-dimensional vibration isolation system comprising rubber bearing and oil spring. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996; pp. 23–28. [Google Scholar]
- Xiong, S.S. Theoretical and Experimental Research of Three-Dimensional Seismic Base Isolation System. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2004. (In Chinese). [Google Scholar]
- Zhao, Y.M.; Su, J.Y.; Lu, M. Experimental study on three-dimensional base-isolated model with 3DIB. Adv. Mater. Res. 2011, 255–260, 2325–2329. [Google Scholar] [CrossRef]
- Yan, X.Y.; Zhang, Y.S.; Wang, H.D.; Wei, L.S. Experimental study on high-rise structure with three-dimensional base isolation and overturn resistance devices. J. Build. Struct. 2009, 30, 4–11. (In Chinese) [Google Scholar]
- Xue, S.D.; Chang, L.H.; Li, X.Y.; Liang, S.Z. Research on mechanical characteristics of anti-extraction three-dimensional seismic isolation bearing. Build. Struct. 2022, 52, 81–87. (In Chinese) [Google Scholar]
- Jia, J.F.; Ou, J.P.; Liu, M.; Zhang, Z. Mechanical performance tests of a novel three-dimensional isolation bearing. J. Civ. Archit. Environ. Eng. 2012, 34, 29–34, 53. (In Chinese) [Google Scholar]
- Liu, H.Q. SMA Strands-Laminated Rubber Compound Bearing and Its Seismic Isolation Behavior. Ph.D. Thesis, Tianjin University, Tianjin, China, 2006. (In Chinese). [Google Scholar]
- Kashiwazaki, A.; Tanaka, M.; Tokuda, N. Shaking test of seismic isolation floor system by using 3-dimensional isolator. In Proceedings of the Ninth World Conference on Earthquake Engineering, Tokyo and Kyoto, Japan, 2–9 August 1988; pp. 845–850. [Google Scholar]
- Shu, G.P.; Lai, B.L.; Ventura, C.E.; Yang, T.Y. Experimental behavior, numerical modeling and parameters evaluation of three-dimensional seismic isolation device. J. Constr. Steel Res. 2024, 220, 108817. [Google Scholar] [CrossRef]
- Liu, W.G.; Xu, H.; He, W.F.; Yang, Q.R. Static test and seismic dynamic response of an innovative 3D seismic isolation system. J. Eng. Struct. 2018, 144, 04018212. [Google Scholar] [CrossRef]
- Xu, H.; He, W.F.; Zhang, L.L.; Liu, W.G. Shaking table test of an novel three-dimensional seismic isolation system with inclined rubber bearings. Eng. Struct. 2023, 293, 116609. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, Y.; Shi, Y. A vertical isolation device with variable stiffness for long-span spatial structures. Soil Dyn. Earthq. Eng. 2019, 123, 543–558. [Google Scholar] [CrossRef]
- Liang, Q.H.; Luo, W.L.; Zhou, Y.; Ke, X.B.; Li, J.R. Seismic performance of a novel three-dimensional isolation bearing. J. Build. Struct. 2022, 57, 104818. [Google Scholar] [CrossRef]
- Wei, Y.Y.; Wang, X.P.; Wu, H.B.; Liu, B.; Zhu, N.H. A new sliding three-dimensional seismic isolation bearing mechanical model and its seismic performance. Structures 2025, 72, 108216. [Google Scholar] [CrossRef]
- Luo, W.L.; Liang, Q.H.; Zhou, Y.; Lu, Z.C.; Li, J.R.; He, Z.M. A novel three-dimensional isolation bearing for buildings subject to metro- and earthquake-induced vibration: Laboratory test and application. J. Build. Eng. 2024, 86, 108798. [Google Scholar] [CrossRef]
- Gao, Y. Design and Research of a Three-Dimensional Seismic Isolation Bearing. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2019. (In Chinese). [Google Scholar]
- Ge, G.Y. Study on the Mechanical Properties and Isolation Performance of Three-Dimensional Isolation Support. Master’s Thesis, Xihua University, Chengdu, China, 2006. (In Chinese). [Google Scholar]
- Han, Q.; Jing, M.; Lu, Y.; Liu, M. Mechanical behaviors of air spring-FPS three-dimensional isolation bearing and isolation performance analysis. Soil Dyn. Earthq. Eng. 2021, 149, 106872. [Google Scholar] [CrossRef]
- Cao, Y.; Pan, P.; Sun, J.; Wang, H. Mechanical properties and isolation effect of disc spring-single friction pendulum 3D vibration isolation device. J. Build. Struct. 2022, 7, 44–53. [Google Scholar]
- Cao, Y.R.; Pan, P.; Wang, H.S.; Sun, J.B.; Xiao, G.Q.; Zuo, Z.F. Development of an innovative three-dimensional vibration isolation bearing. Eng. Struct. 2023, 295, 116890. [Google Scholar] [CrossRef]
- Kitayama, S.; Lee, D.H.; Constantinou, M.C.; Kempner, L., Jr. Probabilistic seismic assessment of seismically isolated electrical transformers considering vertical isolation and vertical ground motion. Eng. Struct. 2017, 152, 888–900. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, P.; Mosqueda, G. Numerical studies of Three-Dimensional isolated structures with vertical Quasi-Zero stiffness property. J. Earthq. Eng. 2022, 26, 3601–3622. [Google Scholar] [CrossRef]
- Yu, T.H.; Zhang, C.; Huang, Z.Q.; Huang, W.Y.; Wang, S.Y.; Zhong, G.Q.; Qu, D.T. Experimental and numerical studies of a novel three-dimensional isolation device incorporating disc springs with U-shaped dampers. Soil Dyn. Earthq. Eng. 2023, 174, 108164. [Google Scholar] [CrossRef]
- Yu, T.H.; Huang, Z.Q.; Zhang, C.; Huang, W.Y.; Bao, W.; Liu, Y.Y. Numerical investigation of three-dimensional isolator and mitigation for single-layer lattice shell structure. Structures 2024, 62, 106235. [Google Scholar] [CrossRef]
- Sha, M.; Guan, M.S.; Lin, M.J.; Tan, X.Y.; Chen, X.S. Experimental study on the performance of innovative self-centering three-dimensional isolation bearing. Structures 2024, 69, 107587. [Google Scholar] [CrossRef]
- GB/T 1972.1-2023; Disc Spring—Part 1: Calculation. China National Standards: Beijing, China, 2023. (In Chinese)
- GB/T 1972.2-2023; Disc Spring—Part 2: Technical Specifications. China National Standards: Beijing, China, 2023. (In Chinese)
- Mu, J.J. Design and Mechanical Property Research of a New Three-Dimensional Seismic Isolation Bearing. Master’s Thesis, Hainan University, Haikou, China, 2024. (In Chinese). [Google Scholar]
- ABAQUS. ABAQUS Standard User’s Manual; Version 6.12; Dassault Systems Simulia Corporation: Providence, RI, USA, 2012. [Google Scholar]
- Xing, J.H.; Huang, H.; Zhang, J.Y.; Yang, Q.S. Mechnical properties of disc springs. J. Vib. Shock 2015, 34, 167–172. (In Chinese) [Google Scholar]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of Seismic Soil-Pile-Structure Interaction on Mid- and High-Rise Steel Buildings Resting on a Group of Pile Foundations. Int. J. Geomech. 2018, 18, 04018103. [Google Scholar] [CrossRef]
- Asgari, A.; Ranjbar, F.; Bagheri, M. Seismic resilience of pile groups to lateral spreading in liquefiable soils: 3D parallel finite element modeling. Structures 2025, 74, 108578. [Google Scholar] [CrossRef]
- GB/T 20688.1-2007; Rubber Bear—Part 1: Seismic-Protection Isolators Test Methods. China National Standards: Beijing, China, 2007. (In Chinese)
- Benzoni, G.; Casarotti, C. Effects of vertical load, strain rate and cycling on the response of Lead-Rubber seismic isolators. J. Earthq. Eng. 2009, 13, 293–312. [Google Scholar] [CrossRef]
- Kircher, C. Chapter 12: Seismically Isolated Structures. In FEMA P-751, 2009 NEHRP Recommeded Provisions: Design Examples; BSSC: Washington, DC, USA, 2012; pp. 1–63. [Google Scholar]









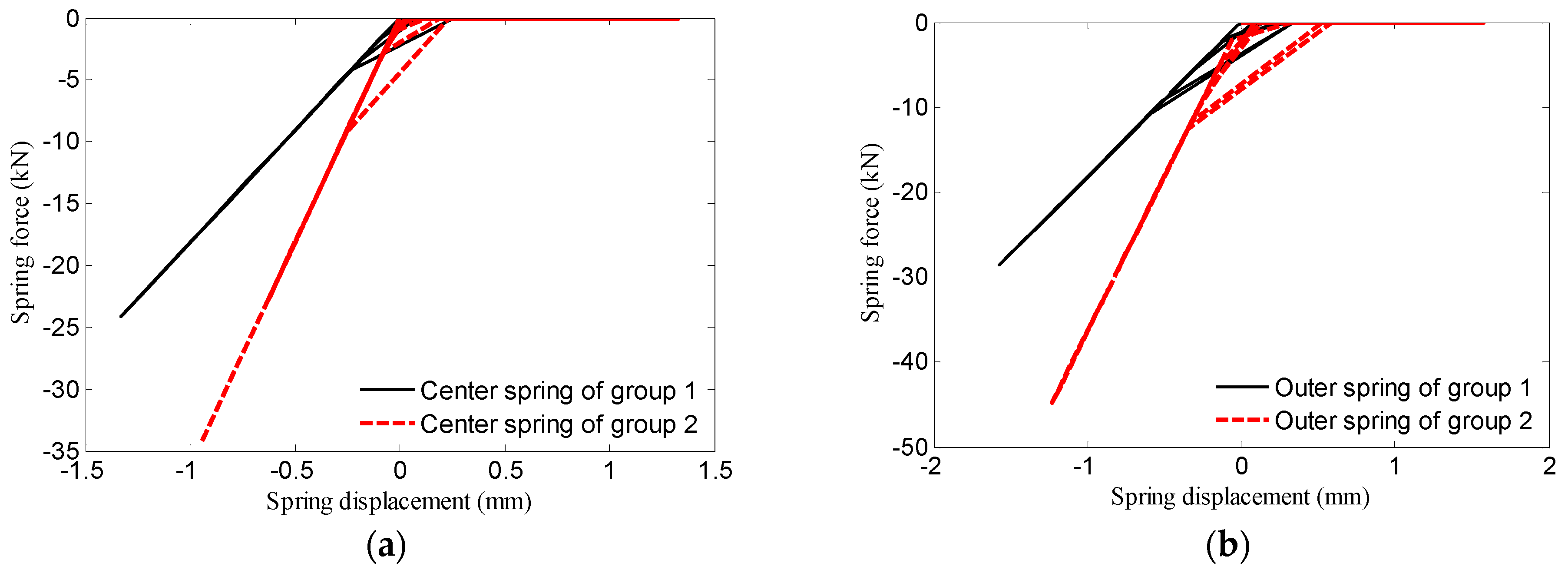


| Diameter (mm) | Lead Core Diameter (mm) | Thickness of Rubber Layer (mm) | Internal Plate Thickness (mm) | Rubber Layer Numbers | Rubber Shear Modulus (MPa) |
|---|---|---|---|---|---|
| 500 | 30 | 7 | 3 | 14 | 0.4 |
| Outside Diameter (mm) | Inside Diameter (mm) | Thickness (mm) | Ultimate Displacement (mm) | Free Altitude (mm) | Bearing Capacity (kN) |
|---|---|---|---|---|---|
| 140 | 72 | 8 | 3.2 | 11.2 | 85.3 |
| Radius of Arc Segment (mm) | Breadth (mm) | Thickness (mm) | Straight Section Length (mm) |
|---|---|---|---|
| 175 | 40 | 25 | 220 |
| Material | Elastic Modulus (GPa) | Poisson’s Ratio | Yield Stress (MPa) | Hardening Modulus (MPa) |
|---|---|---|---|---|
| Steel plate | 206.00 | 0.30 | 355 | - |
| Lead | 17.00 | 0.42 | 8.50 | 17.00 |
| U-shaped damper | 206.00 | 0.30 | 298.88 | 2060 |
| Parameter Classification | Load Case Number | Constant Vertical Force (kN) | Horizontal Displacement (mm) | Equivalent Horizontal Stiffness (kN/mm) | Equivalent Horizontal Damping ratio (%) | Horizontal Natural Period (s) |
|---|---|---|---|---|---|---|
| Vertical load | 1 | 1000 | [−98, +98] | 1.38 | 12.28 | 1.71 |
| 2 | 1200 | [−98, +98] | 1.37 | 12.34 | 1.88 | |
| 3 | 1500 | [−98, +98] | 1.36 | 12.53 | 2.11 | |
| Shear strain | 4 | 1000 | [−47, +47] | 1.71 | 12.06 | 1.53 |
| 5 | 1000 | [−74, +74] | 1.47 | 13.27 | 1.66 | |
| 6 | 1000 | [−98, +98] | 1.38 | 12.28 | 1.71 | |
| 7 | 1000 | [−123, +123] | 1.28 | 11.41 | 1.77 | |
| 8 | 1000 | [−147, +147] | 1.24 | 10.38 | 1.80 | |
| 0 damper | 9 | 1000 | [−98, +98] | 0.99 | 2.35 | 2.02 |
| 1 damper | 10 | 1000 | [−98, +98] | 1.38 | 12.28 | 1.71 |
| 2 dampers | 11 | 1000 | [−98, +98] | 1.70 | 18.62 | 1.54 |
| 4 dampers | 12 | 1000 | [−98, +98] | 2.42 | 25.05 | 1.29 |
| Parameter Classification | Load Case Number | Vertical Displacement (mm) | Equivalent Vertical Stiffness (kN/mm) | Equivalent Vertical Damping Ratio (%) | Vertical Vibration Period (s) |
|---|---|---|---|---|---|
| Vertical displacement | 1 | [−1, +1] | 232.68 | 9.59 | 0.132 |
| 2 | [−2, +2] | 220.80 | 11.53 | 0.146 | |
| 3 | [−4, +4] | 229.34 | 10.36 | 0.137 | |
| 4 | [−6, +6] | 237.66 | 9.34 | 0.130 | |
| 0 damper | 5 | [−6, +6] | 227.36 | 9.08 | 0.133 |
| 1 damper | 6 | [−6, +6] | 237.66 | 9.34 | 0.130 |
| 2 dampers | 7 | [−6, +6] | 240.49 | 10.55 | 0.129 |
| 4 dampers | 8 | [−6, +6] | 252.72 | 9.65 | 0.126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Sun, L.; Wu, Y.; Chen, Y.; Quan, D.; Lei, T.; Dong, S. Finite Element Modeling and Performance Evaluation of a Novel 3D Isolation Bearing. Buildings 2025, 15, 2553. https://doi.org/10.3390/buildings15142553
Li J, Sun L, Wu Y, Chen Y, Quan D, Lei T, Dong S. Finite Element Modeling and Performance Evaluation of a Novel 3D Isolation Bearing. Buildings. 2025; 15(14):2553. https://doi.org/10.3390/buildings15142553
Chicago/Turabian StyleLi, Jianjun, Lvhong Sun, Yanchao Wu, Yun Chen, Dengzhou Quan, Tuo Lei, and Sansheng Dong. 2025. "Finite Element Modeling and Performance Evaluation of a Novel 3D Isolation Bearing" Buildings 15, no. 14: 2553. https://doi.org/10.3390/buildings15142553
APA StyleLi, J., Sun, L., Wu, Y., Chen, Y., Quan, D., Lei, T., & Dong, S. (2025). Finite Element Modeling and Performance Evaluation of a Novel 3D Isolation Bearing. Buildings, 15(14), 2553. https://doi.org/10.3390/buildings15142553





