The Validation and Discussion of a Comparative Method Based on Experiment to Determine the Effective Thickness of Composite Glass
Abstract
1. Introduction
2. Methodology
2.1. Glass Materials
2.2. Four-Point Bending Test
2.3. Strain Measurements
2.4. The Method for Determining the Effective Thickness of Composite Glass
2.5. Mechanical Properties of Polymeric Interlayers
3. Results
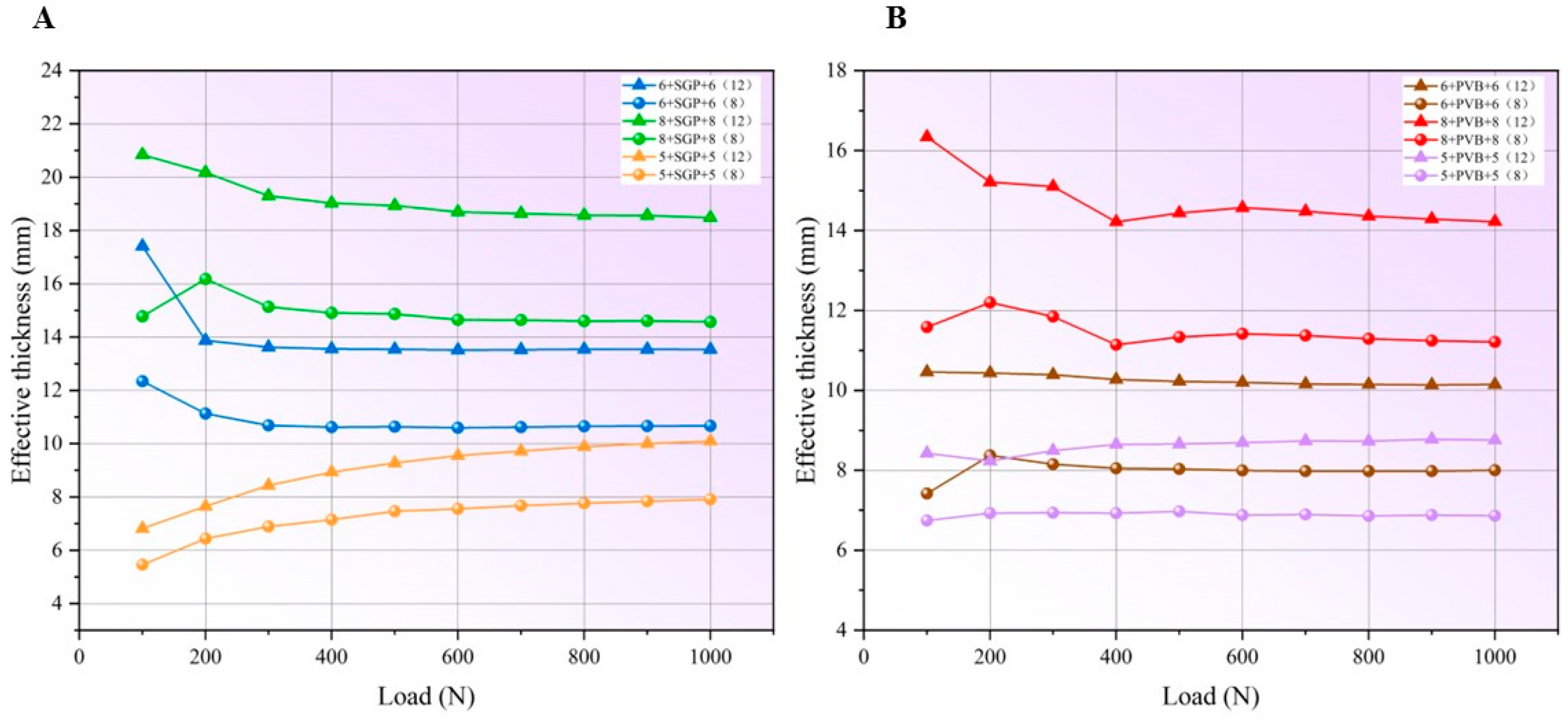
3.1. The Effective Thickness and Stress State of PVB and SGP Laminated Glass
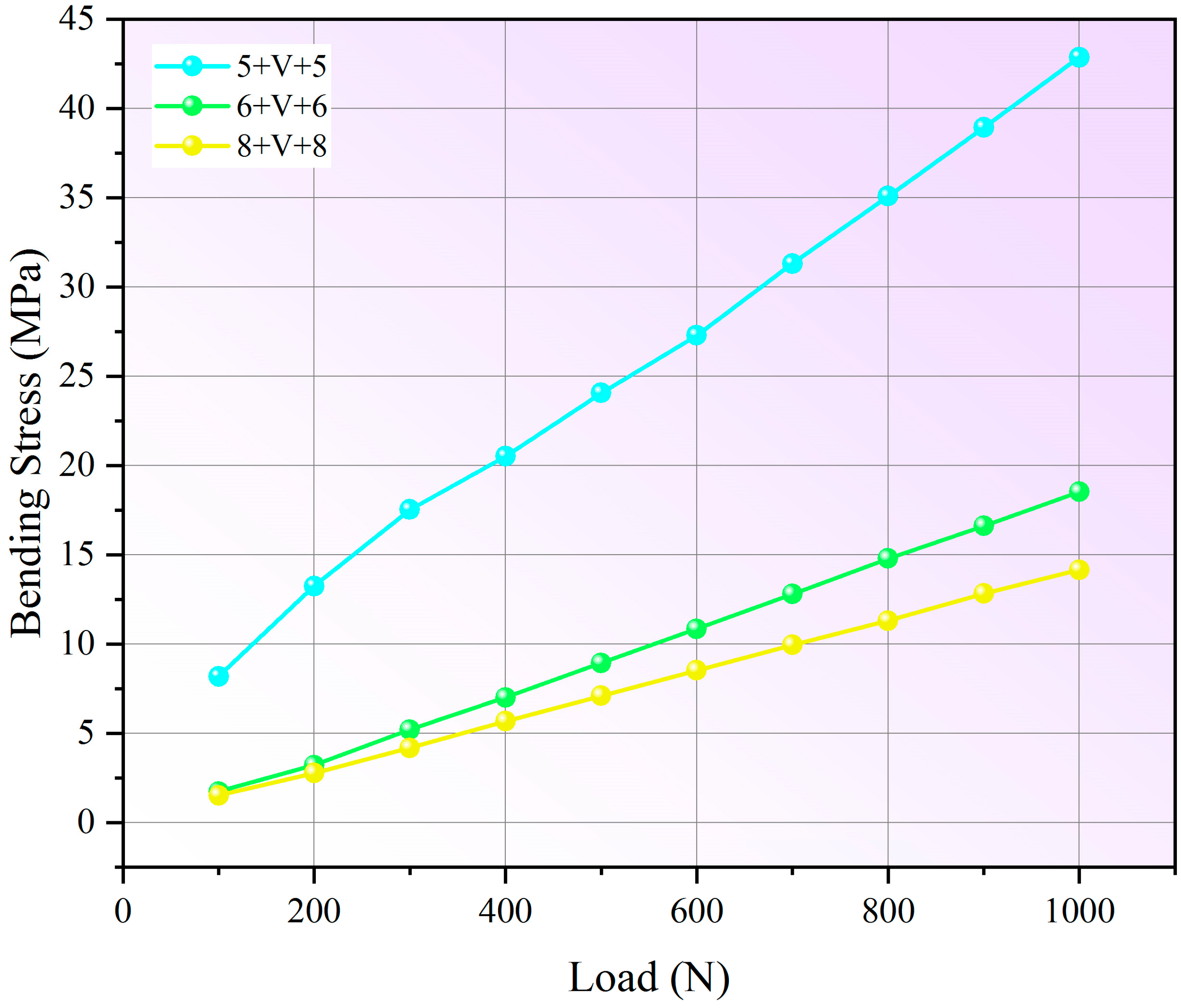
3.2. The Effective Thickness and Stress State of Vacuum Glazing
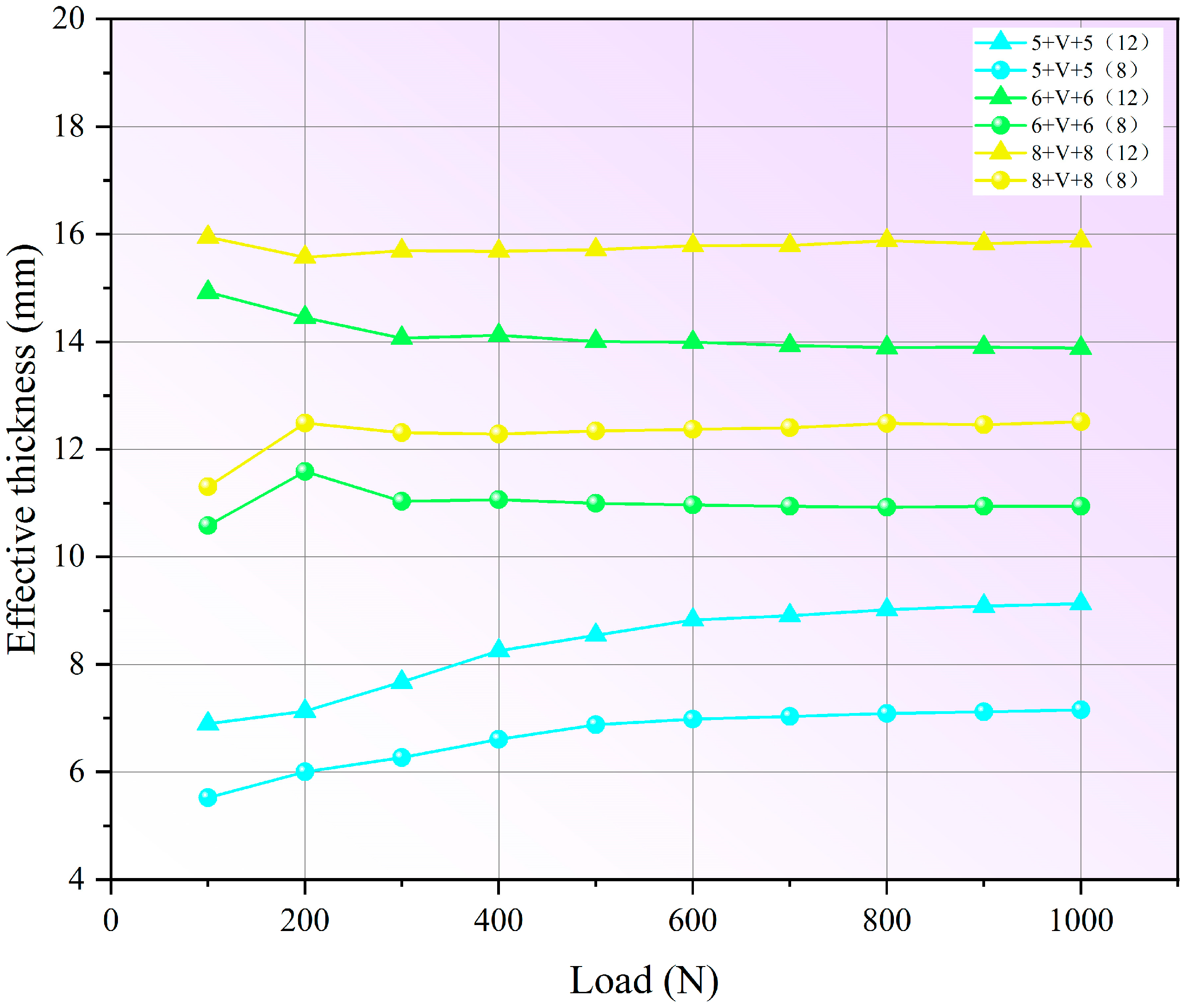
3.3. Validation of Comparative Method for Determining the Effective Thickness of Composite Glass
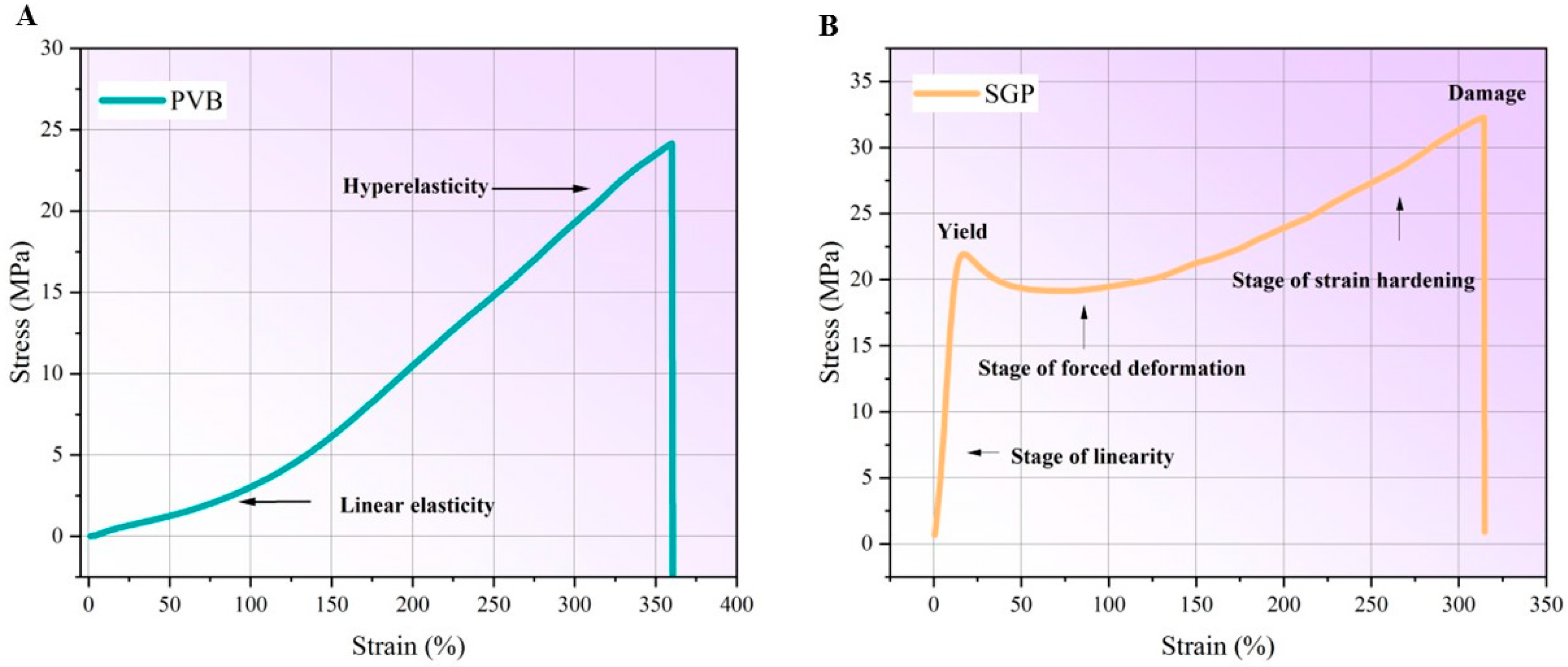
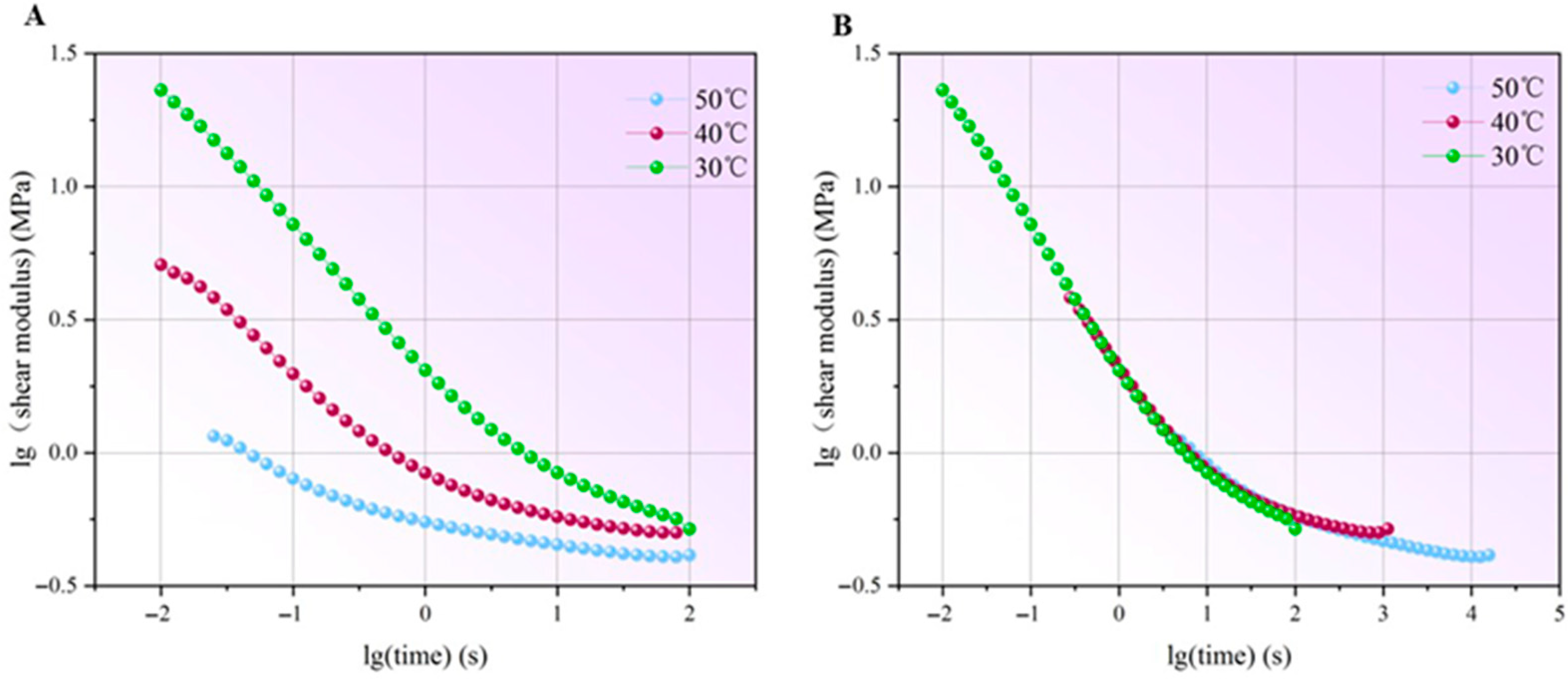
3.4. The Mechanical Properties of PVB and SGP
4. Discussions
4.1. Polymeric Laminated Glass
4.2. Polymertic Interlayers
4.3. Vacuum Glazing
4.4. Discussion of Appropriate Use of the Proposed Method
5. Conclusions
- The SGP laminated glass and vacuum glazing exhibit significantly lower bending stress compared to PVB laminated glass under identical loading levels, attributed to their enhanced stiffness. The SGP and vacuum glazing exhibit monolithic-like behavior, indicating superior load-bearing capacity.
- The proposed method enables the precise determination of the effective thickness of PVB and SGP laminated glass and vacuum glazing. The results are compared with the results from the prEN and the empirical formula. The results from the proposed method demonstrate the superior accuracy.
- Bending stress calculated using derived effective thickness shows a strong correlation with experimental measurements. It is also found that the selection of reference monolithic glass thickness can critically influence the accuracy of the proposed method. Using a 12 mm reference glass can obtain the optimal results. Experimenting using 12 mm reference glass can minimize the errors caused by large-deflection effects and inaccurate strain measurement.
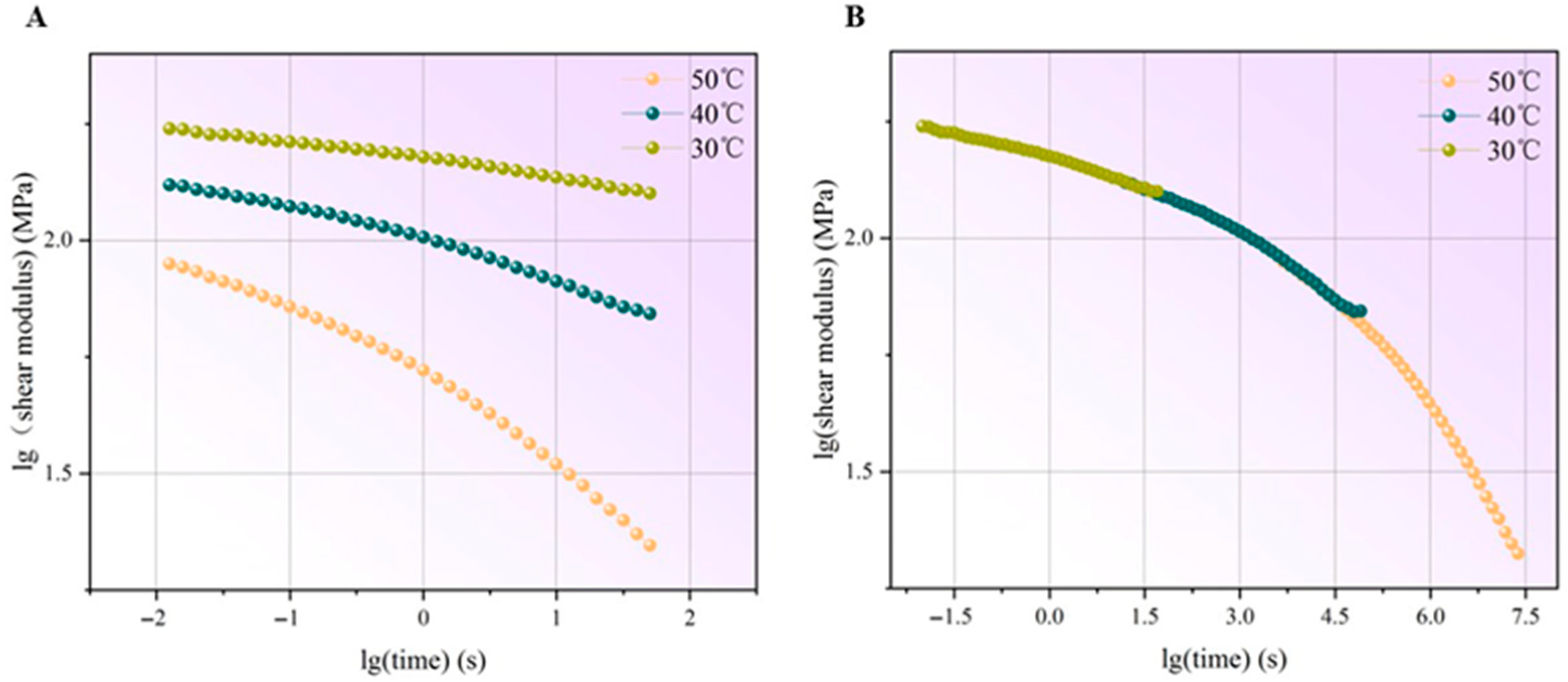
- By static tensile test, the SGP interlayer provides higher tensile strength and lower tensile deformation compared to that of PVB. Substantially different tensile behavior of SGP and PVB is evident from their respective stress–strain profiles. Furthermore, the TTSP analysis reveals that the evolution of shear modulus of PVB and SGP over time shows a distinct difference. PVB undergoes a dramatic reduction in shear modulus over a short duration, whereas the shear modulus of SGP shows a minimal change over a relatively extended period. Additionally, it is also found that there is negligible shear modulus change of both interlayers during 30 s intervals, so the 30 s holding time in the proposed method could not be affected so much.
- A guideline for providing accurate results by using the proposed method is established, which is to avoid using the early loading stage data due to the nonlinearity caused by the gaps between the fixtures. The optimal results can be obtained from the middle to later loading range (500 N–1000 N). The methodology also accounts for material defects through three mechanisms. This integrated approach ensures that derived effective thickness values reflect actual structural performance while accommodating inherent material variability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Martín, M.; Centelles, X.; Solé, A.; Barreneche, C.; Fernández, A.I.; Cabeza, L.F. Polymeric interlayer materials for laminated glass: A review. Constr. Build. Mater 2020, 230, 116897. [Google Scholar] [CrossRef]
- Bennison, S.J.; Qin, M.H.; Davies, P.S. High-performance laminated glass for structurally efficient glazing. In Proceedings of the Innovative Light-Weight Structures and Sustainable Facades Conference, Hong Kong, China, 7 May 2008; pp. 1–12. Available online: https://www.researchgate.net/profile/Phillip-Davies/publication/237263030_High-performance_laminated_glass_for_structurally_efficient_glazing/links/5eb10af592851cb267741cf8/High-performance-laminated-glass-for-structurally-efficient-glazing.pdf (accessed on 10 July 2025).
- Galuppi, L.; Royer-Carfagni, G.F. Effective thickness of laminated glass beams: New expression via a variational approach. Eng. Struct. 2012, 38, 53–67. [Google Scholar] [CrossRef]
- Norville, H.S.; King, K.W.; Swofford, J.L. Behavior and strength of laminated glass. J. Eng. Mech. 1998, 124, 46–53. [Google Scholar] [CrossRef]
- Behr, R.A.; Minor, J.E.; Norville, H.S. Structural behavior of architectural laminated glass. J. Struct. Eng. 1993, 119, 202–222. [Google Scholar] [CrossRef]
- Simko, T.M.; Fischer-Cripps, A.C.; Collins, R.E. Temperature-induced stresses in vacuum glazing: Modelling and experimental validation. Sol. Energy 1998, 63, 1–21. [Google Scholar] [CrossRef]
- Collins, R.E.; Turner, G.M.; Fischer-Cripps, A.C.; Tang, J.Z.; Simko, T.M.; Dey, C.J.; Clugston, D.A.; Zhang, Q.C.; Garrison, J.D. Vacuum glazing—A new component for insulating windows. Build. Environ. 1995, 30, 459–492. [Google Scholar] [CrossRef]
- Pont, U.; Wölzl, M.; Schober, P.; Khosravi, S.N.; Schuss, M.; Mahdavi, A. Recent progress in the development of windows with vacuum glass. MATEC Web Conf. 2019, 282, 02020. [Google Scholar] [CrossRef]
- Ali, H.; Hayat, N.; Farukh, F.; Imran, S.; Kamran, M.S.; Ali, H.M. Key design features of multi-vacuum glazing for windows: A review. Therm. Sci. 2017, 21, 2673–2687. [Google Scholar] [CrossRef]
- Liu, X.G.; Bao, Y.W.; Wan, D.T.; Qiu, Y.; Wang, X.F.; Xu, H. Bearing behavior and strength design for building vacuum glazing. J. Cent. South Univ. 2011, 42, 349–355. [Google Scholar]
- Galuppi, L.; Royer-Carfagni, G. The effective thickness of laminated glass plates. J. Mech. Mater. Struct. 2012, 7, 375–400. [Google Scholar] [CrossRef]
- Bennison, S.J.; Stelzer, I. Structural Properties of Laminated Glass; Glass Performance Days: Tampere, Finland, 2009; pp. 12–15. [Google Scholar]
- prEN 16612; Glass in Buildings—Determination of the Load Resistance of Glass Panes by Calculation and Testing, European Standard. European Commission: Brussels, Belgium, 2013.
- Liu, X.G.; Qi, S.; Sun, Y.K. Stress Analysis and Strength Design of Vacuum Glazing. Bull. Chin. Ceram. Soc. 2022, 41, 1141–1147. [Google Scholar]
- Hoffmann, K. An introduction to stress analysis and transducer design using strain gauges. HBM Test Meas. 2012, 257. Available online: https://www.kk-group.ru/help/Strain_Gauge_Measurements_Book_2012_01.pdf (accessed on 10 July 2025).
- Rouxel, T. Elastic properties and short-to medium-range order in glasses. J. Am. Ceram. Soc. 2007, 90, 3019–3039. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Shi, Y.; Cui, J. The mechanical properties of Polyvinyl Butyral (PVB) at high strain rates. Constr. Build. Mater. 2015, 93, 404–415. [Google Scholar] [CrossRef]
- Krasnopol’skii, B.I.; Chesnokov, A.G.; Chesnokov, S. A Numerical modeling and analysis of strength properties in glass. Glass Ceram. 2005, 62, 375–378. [Google Scholar] [CrossRef]
- Serafinavicius, T.; Kvedaras, A.K.; Sauciuvenas, G. Bending behavior of structural glass laminated with different interlayers. Mech. Compos. Mater. 2013, 49, 437–446. [Google Scholar] [CrossRef]
- Wang, S.; Wan, C.; Li, D.; Wang, J. Research on the Design Method of Equivalent Thickness of Architectural Vacuum Glass. Bull. Sci. Technol. 2025, 41, 56–63. [Google Scholar]
- Sable, L.; Kalnins, K. Evaluation of Glass in Design of Load Bearing Structures. In Proceedings of the 4th International Conference Civil Engineering`13 Proceedings Part I Structural Engineering, Jelgava, Latvia, 16–17 May 2013; pp. 46–52. [Google Scholar]
- Sable, L.; Japins, G.; Kalnins, K. Evaluation of Behaviours of Laminated Glass. IOP Conf. Ser. Mater. Sci. Eng. 2015, 96, 012077. [Google Scholar] [CrossRef]
- Naya, S.; Meneses, A.; Tarrío-Saavedra, J.; López-Beceiro, J.; Gracia-Fernández, C.; Artiaga, R. New method for estimating shift factors in time-temperature superposition models. J. Therm. Anal. Calorim. 2013, 113, 453–460. [Google Scholar] [CrossRef]
- Bennison, S.J.; Smith, C.A.; Duser, A.V.; Jagota, A. Structural performance of laminated glass made with a “stiff” interlayer. ASTM Int. Glass Build. 2002, 1434, 57–65. [Google Scholar]
- Wang, X.E.; Yang, J.; Liu, Q.; Zhao, C. Experimental investigations into SGP laminated glass under low velocity impact. Int. J. Impact Eng. 2018, 122, 91–108. [Google Scholar] [CrossRef]
- Xu, X. Research on Influence of Polymer Interlayer on Mechanical Characteristics and Fracture Mechanism of Laminated Glass; Tsinghua University: Beijing, China, 2017. [Google Scholar]
- Shao, X.; Chen, S. Review on studies on mechanical properties of SGP. Hans J. Civ. Eng. 2015, 4, 143–150. [Google Scholar] [CrossRef]
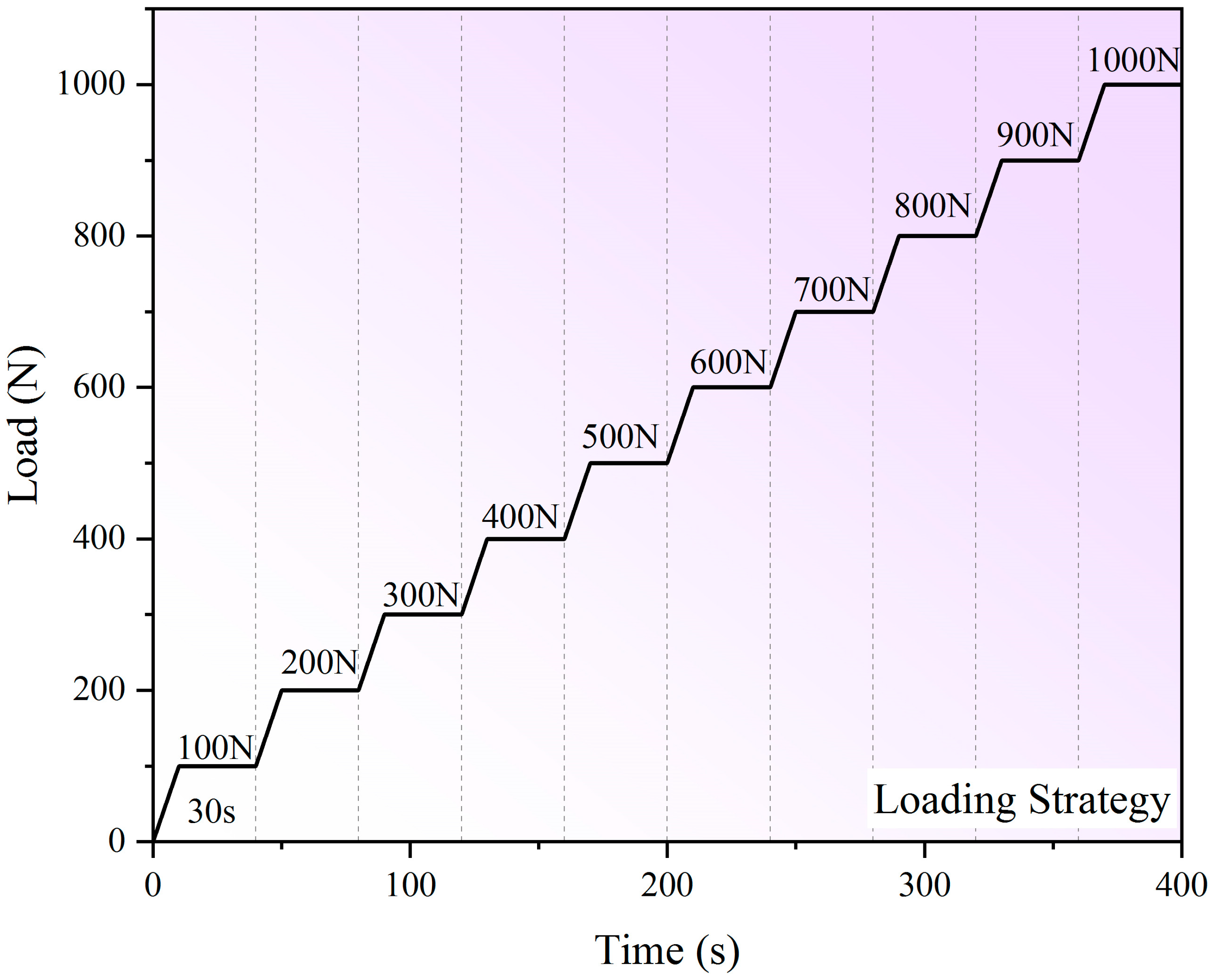
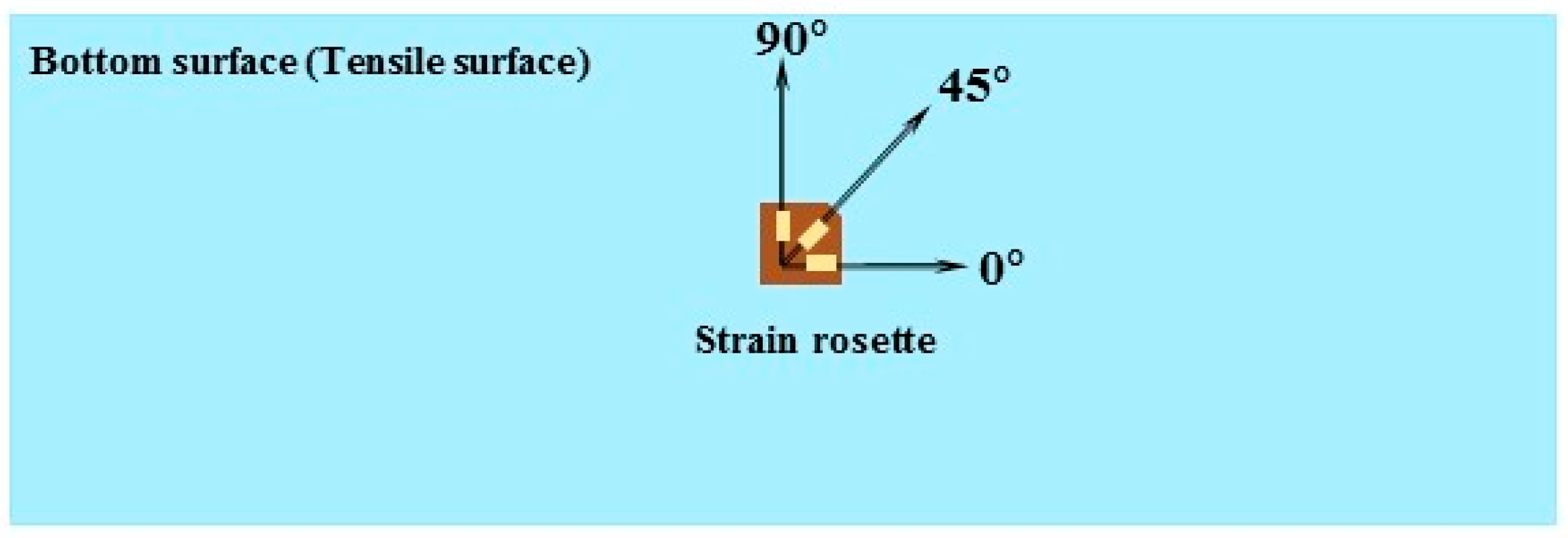

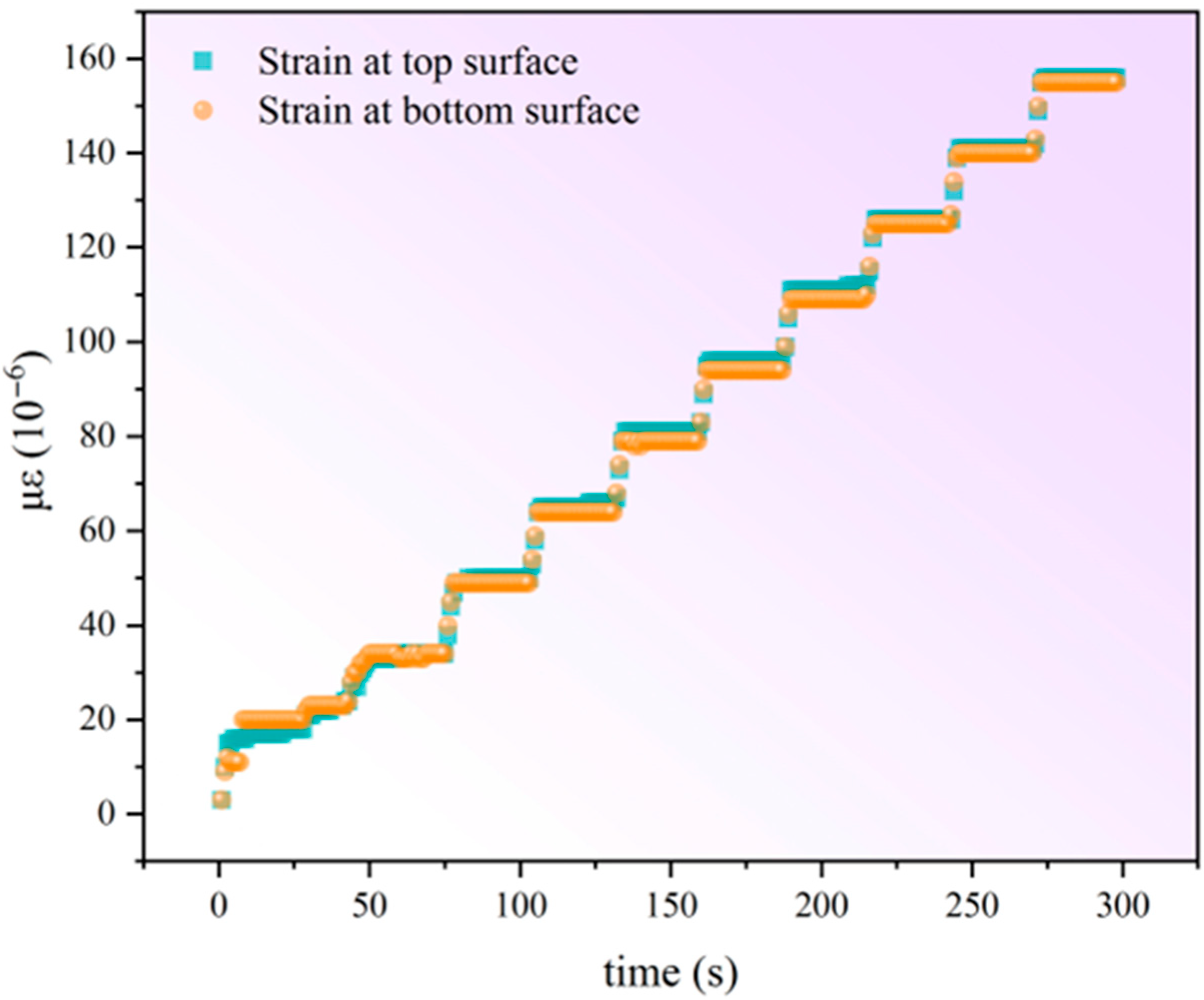




| Structure | Thickness (mm) |
|---|---|
| Glass + PVB interlayer + Glass | 5 + 1.52 + 5 |
| 6 + 1.52 + 6 | |
| 8 + 1.52 + 8 | |
| Glass + SGP interlayer + Glass | 5 + 1.52 + 5 |
| 6 + 1.52 + 6 | |
| 8 + 1.52 + 8 | |
| Glass + Vacuum + Glass | 5 + V + 5 |
| 6 + V + 6 | |
| 8 + V + 8 | |
| Reference monolithic glass | 8 |
| 12 |
| Effective thickness of 5 + PVB + 5 | (mm) | 9.99 |
| Effective thickness of 6 + PVB + 6 | 11.8 | |
| Effective thickness of 8 + PVB + 8 | 14.8 | |
| Effective thickness of 5 + SGP + 5 | 13.2 | |
| Effective thickness of 6 + SGP + 6 | 15.7 | |
| Effective thickness of 8 + SGP + 8 | 20.5 |
| Effective Thickness of 5 + V + 5 | Effective Thickness of 6 + V + 6 | Effective Thickness of 8 + V + 8 |
|---|---|---|
| (mm) | ||
| 8.10 | 9.72 | 13.0 |
| Corresponding Load | Calculated Bending Stress by the Method Using 12 mm Reference Glass | Calculated Bending Stress by the Method Using 8 mm Reference Glass | Calculated Bending Stress by the Results from prEN or Empirical Formula | Experimental Bending Stress |
|---|---|---|---|---|
| (N) | (MPa) | (MPa) | (MPa) | (MPa) |
| 5 + PVB + 5 | ||||
| 1000 | 45.6 | 73.5 | 35.2 | 46.6 |
| 900 | 41.0 | 66.1 | 31.9 | 41.7 |
| 800 | 37.1 | 59.4 | 28.6 | 37.5 |
| 700 | 32.7 | 51.8 | 25.2 | 32.6 |
| 600 | 28.6 | 45.0 | 21.9 | 28.1 |
| 500 | 24.4 | 37.0 | 18.5 | 23.4 |
| 400 | 19.9 | 30.5 | 15.2 | 18.7 |
| 300 | 16.0 | 23.4 | 11.9 | 14.3 |
| 200 | 12.1 | 16.5 | 8.52 | 9.94 |
| 100 | 6.88 | 10.0 | 5.21 | 5.49 |
| 6 + PVB + 6 | ||||
| 1000 | 34.2 | 54.4 | 43.5 | 34.7 |
| 900 | 31.0 | 49.4 | 39.4 | 31.3 |
| 800 | 27.7 | 44.2 | 35.2 | 27.7 |
| 700 | 24.4 | 38.9 | 31.1 | 24.1 |
| 600 | 21.0 | 33.6 | 26.9 | 20.4 |
| 500 | 17.7 | 28.1 | 22.8 | 16.8 |
| 400 | 14.4 | 22.9 | 18.6 | 13.2 |
| 300 | 11.0 | 17.3 | 14.5 | 9.6 |
| 200 | 7.88 | 11.7 | 10.3 | 6.18 |
| 100 | 4.80 | 8.54 | 6.20 | 3.56 |
| 8 + PVB + 8 | ||||
| 1000 | 17.8 | 28.2 | 25.7 | 17.7 |
| 900 | 16.0 | 25.4 | 23.3 | 15.7 |
| 800 | 14.2 | 22.5 | 20.8 | 13.8 |
| 700 | 12.4 | 19.7 | 18.4 | 11.9 |
| 600 | 10.7 | 17.0 | 16.0 | 10.0 |
| 500 | 9.27 | 14.6 | 13.6 | 8.43 |
| 400 | 7.89 | 12.4 | 11.2 | 6.91 |
| 300 | 5.60 | 8.68 | 8.79 | 4.52 |
| 200 | 4.09 | 5.99 | 6.38 | 2.91 |
| 100 | 2.37 | 4.07 | 3.97 | 1.46 |
| 5 + SGP + 5 | ||||
| 1000 | 34.5 | 55.6 | 20.5 | 35.0 |
| 900 | 31.8 | 51.2 | 18.6 | 32.1 |
| 800 | 29.2 | 46.6 | 16.7 | 29.2 |
| 700 | 26.6 | 42.0 | 14.8 | 26.3 |
| 600 | 23.9 | 37.5 | 12.9 | 23.3 |
| 500 | 21.4 | 32.4 | 11.0 | 20.4 |
| 400 | 18.8 | 28.7 | 9.04 | 17.5 |
| 300 | 16.2 | 23.7 | 7.13 | 14.5 |
| 200 | 13.8 | 18.9 | 5.22 | 11.5 |
| 100 | 9.87 | 14.6 | 3.31 | 8.38 |
| 6 + SGP + 6 | ||||
| 1000 | 19.6 | 31.0 | 14.7 | 19.5 |
| 900 | 17.7 | 28.1 | 13.3 | 17.5 |
| 800 | 15.9 | 25.2 | 12.0 | 15.6 |
| 700 | 14.1 | 22.4 | 10.6 | 13.6 |
| 600 | 12.3 | 19.6 | 9.28 | 11.6 |
| 500 | 10.4 | 16.5 | 7.93 | 9.57 |
| 400 | 8.61 | 13.6 | 6.58 | 7.61 |
| 300 | 6.74 | 10.5 | 5.23 | 5.56 |
| 200 | 4.79 | 7.04 | 3.88 | 3.50 |
| 100 | 2.15 | 3.68 | 2.52 | 1.28 |
| 8 + SGP + 8 | ||||
| 1000 | 10.8 | 17.0 | 8.83 | 10.5 |
| 900 | 9.70 | 15.3 | 8.03 | 9.32 |
| 800 | 8.72 | 13.8 | 7.24 | 8.28 |
| 700 | 7.70 | 12.1 | 6.45 | 7.15 |
| 600 | 6.70 | 10.6 | 5.66 | 6.08 |
| 500 | 5.62 | 8.78 | 4.86 | 4.90 |
| 400 | 4.65 | 7.23 | 4.07 | 3.86 |
| 300 | 3.64 | 5.58 | 3.28 | 2.77 |
| 200 | 2.55 | 3.68 | 2.48 | 1.65 |
| 100 | 1.65 | 2.77 | 1.69 | 0.90 |
| 5 + V + 5 | ||||
| 1000 | 42.0 | 67.7 | 53.1 | 42.9 |
| 900 | 38.4 | 61.8 | 48.0 | 38.9 |
| 800 | 34.8 | 55.7 | 42.9 | 35.1 |
| 700 | 31.5 | 49.8 | 37.8 | 31.3 |
| 600 | 27.8 | 43.7 | 32.8 | 27.3 |
| 500 | 25.0 | 37.9 | 27.7 | 24.1 |
| 400 | 21.8 | 33.3 | 22.6 | 20.5 |
| 300 | 19.4 | 28.4 | 17.5 | 17.5 |
| 200 | 15.7 | 21.6 | 12.4 | 13.3 |
| 100 | 9.68 | 14.3 | 7.35 | 8.19 |
| 6 + V + 6 | ||||
| 1000 | 18.6 | 29.5 | 33.8 | 18.5 |
| 900 | 16.9 | 26.8 | 30.6 | 16.6 |
| 800 | 15.1 | 24.0 | 27.4 | 14.8 |
| 700 | 13.3 | 21.2 | 24.2 | 12.8 |
| 600 | 11.5 | 18.3 | 21.0 | 10.9 |
| 500 | 9.81 | 15.5 | 17.8 | 8.96 |
| 400 | 7.99 | 12.6 | 14.6 | 7.01 |
| 300 | 6.36 | 9.88 | 11.4 | 5.21 |
| 200 | 4.46 | 6.55 | 8.21 | 3.22 |
| 100 | 2.73 | 4.71 | 5.01 | 1.75 |
| 8 + V + 8 | ||||
| 1000 | 14.4 | 22.8 | 19.4 | 14.2 |
| 900 | 13.1 | 20.8 | 17.6 | 12.8 |
| 800 | 11.7 | 18.6 | 15.8 | 11.3 |
| 700 | 10.5 | 16.7 | 14.0 | 9.96 |
| 600 | 9.19 | 14.6 | 12.2 | 8.53 |
| 500 | 7.92 | 12.4 | 10.7 | 7.11 |
| 400 | 6.59 | 10.3 | 8.56 | 5.68 |
| 300 | 5.23 | 8.09 | 6.76 | 4.19 |
| 200 | 3.93 | 5.75 | 4.96 | 2.78 |
| 100 | 2.46 | 4.23 | 3.15 | 1.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, D.; Liu, X.; Yang, Z.; Huang, J.; Xu, M.; Wan, D. The Validation and Discussion of a Comparative Method Based on Experiment to Determine the Effective Thickness of Composite Glass. Buildings 2025, 15, 2542. https://doi.org/10.3390/buildings15142542
Cao D, Liu X, Yang Z, Huang J, Xu M, Wan D. The Validation and Discussion of a Comparative Method Based on Experiment to Determine the Effective Thickness of Composite Glass. Buildings. 2025; 15(14):2542. https://doi.org/10.3390/buildings15142542
Chicago/Turabian StyleCao, Dake, Xiaogen Liu, Zhe Yang, Jiawei Huang, Ming Xu, and Detian Wan. 2025. "The Validation and Discussion of a Comparative Method Based on Experiment to Determine the Effective Thickness of Composite Glass" Buildings 15, no. 14: 2542. https://doi.org/10.3390/buildings15142542
APA StyleCao, D., Liu, X., Yang, Z., Huang, J., Xu, M., & Wan, D. (2025). The Validation and Discussion of a Comparative Method Based on Experiment to Determine the Effective Thickness of Composite Glass. Buildings, 15(14), 2542. https://doi.org/10.3390/buildings15142542





