Finite Element Analysis of the Mechanical Performance of an Innovative Beam-Column Joint Incorporating V-Shaped Steel as a Replaceable Energy-Dissipating Component
Abstract
1. Introduction
2. Joint Structure and Design Methods
2.1. Joint Structure and Construction Process
2.2. Design Principles
3. Establishment and Verification of Finite Element Model
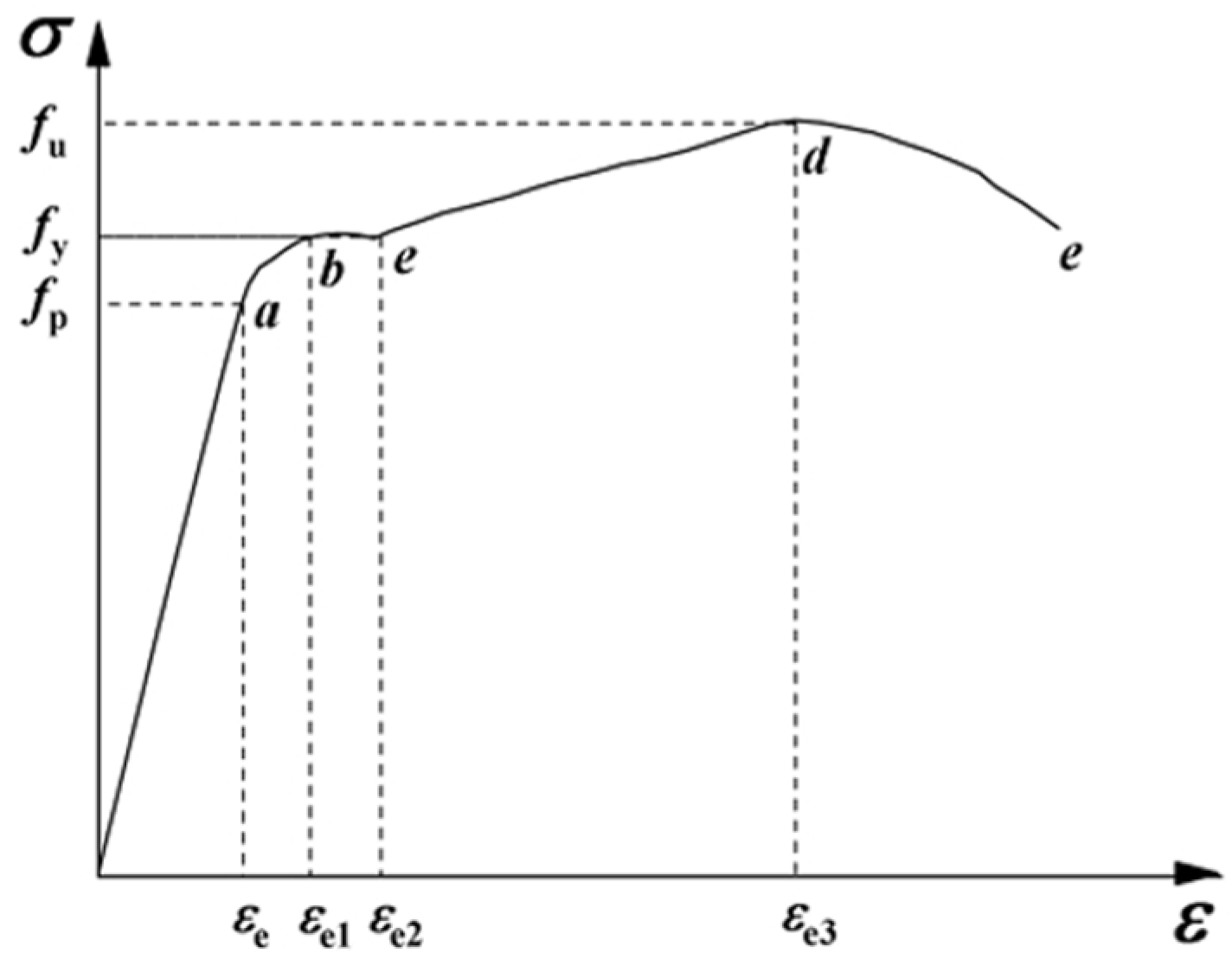
3.1. Material Constitutive Models
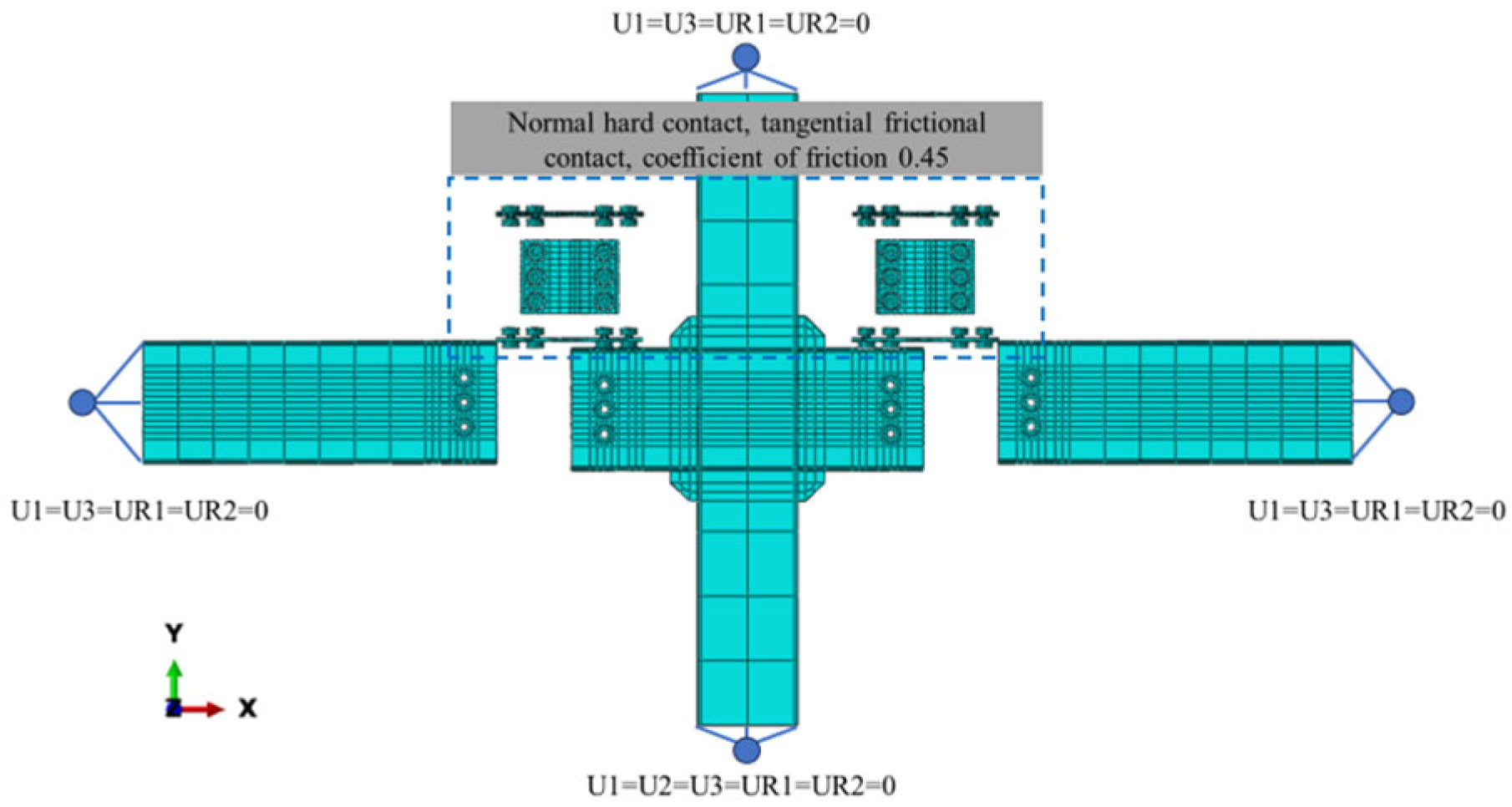
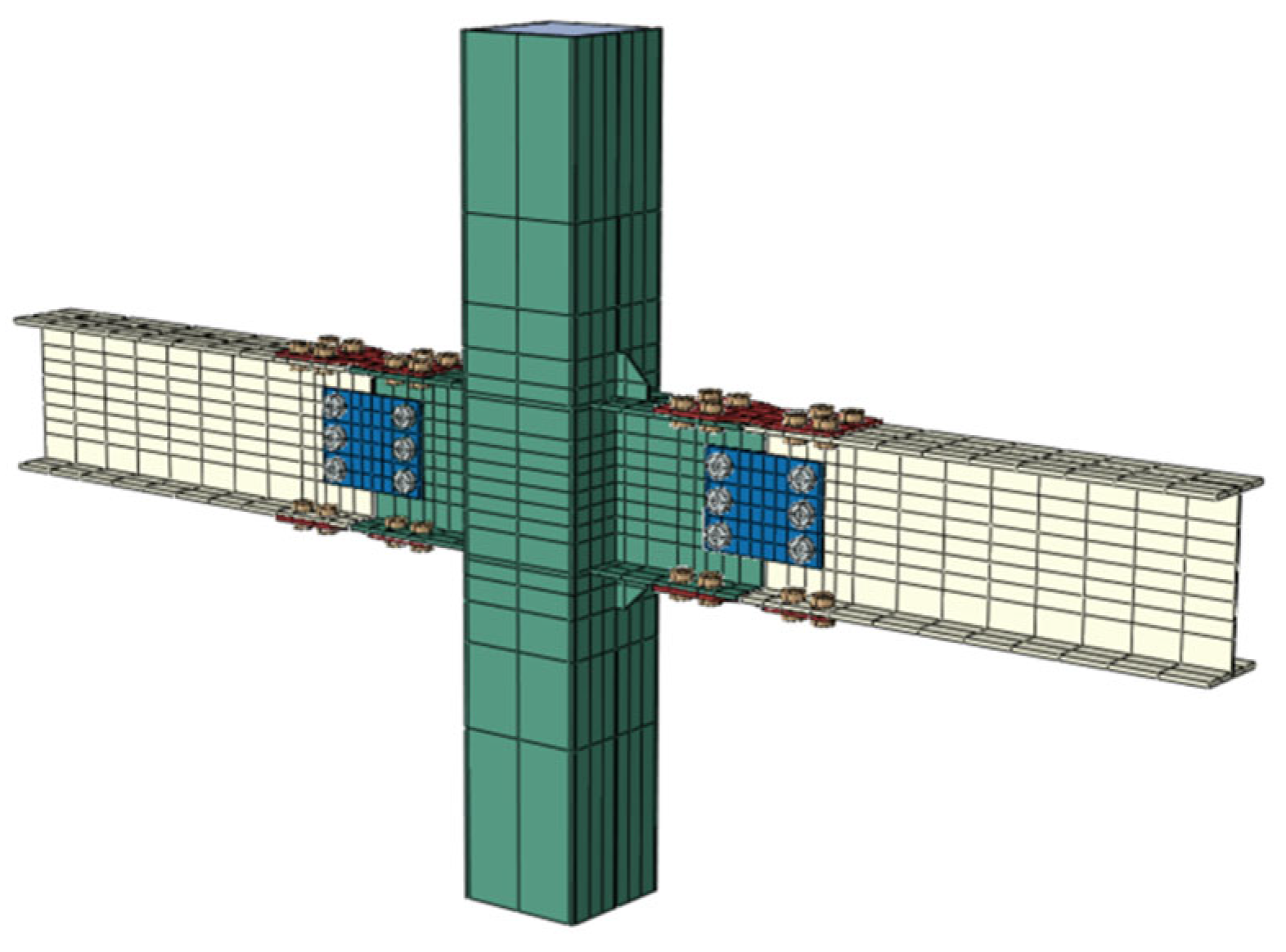
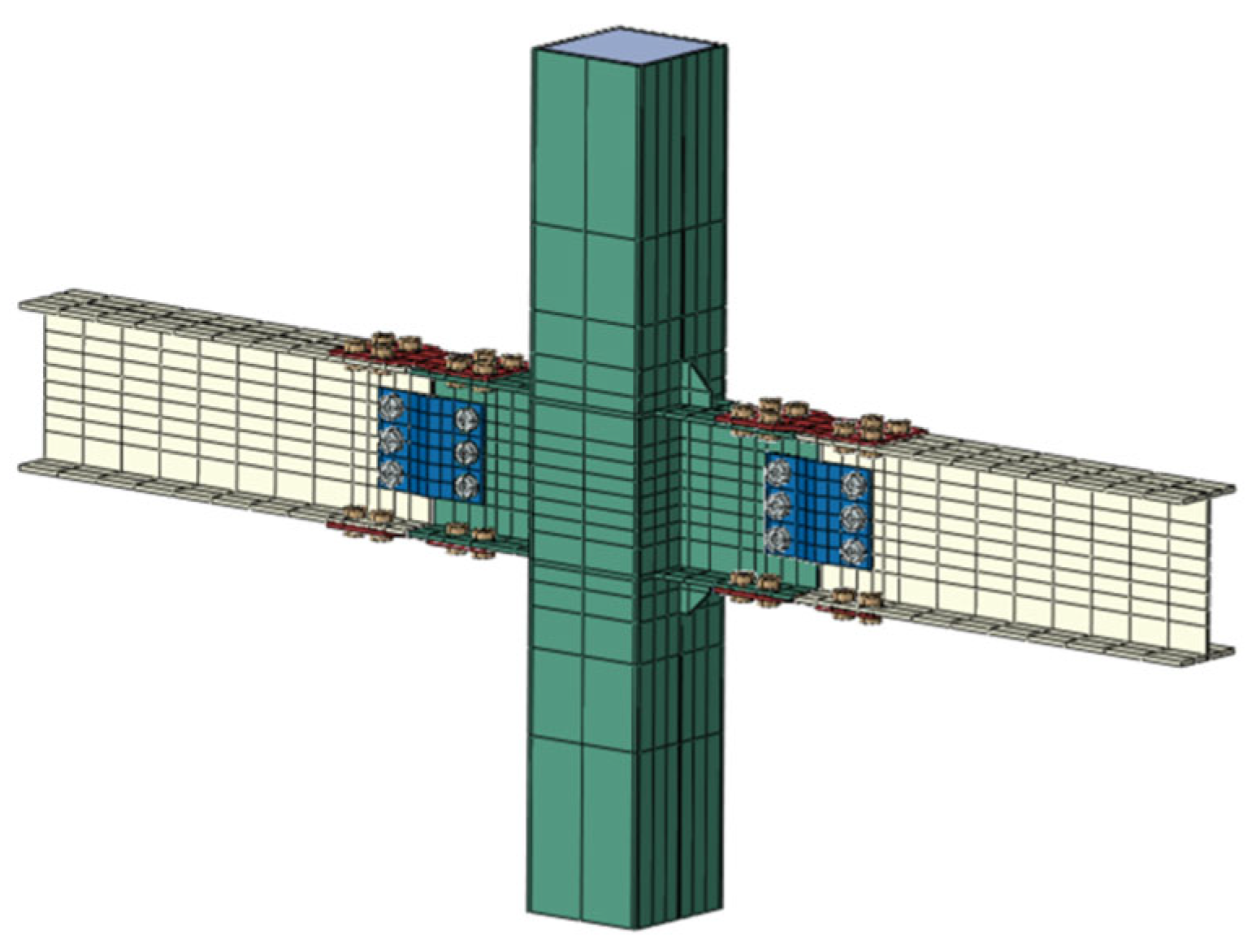
3.2. Model Building
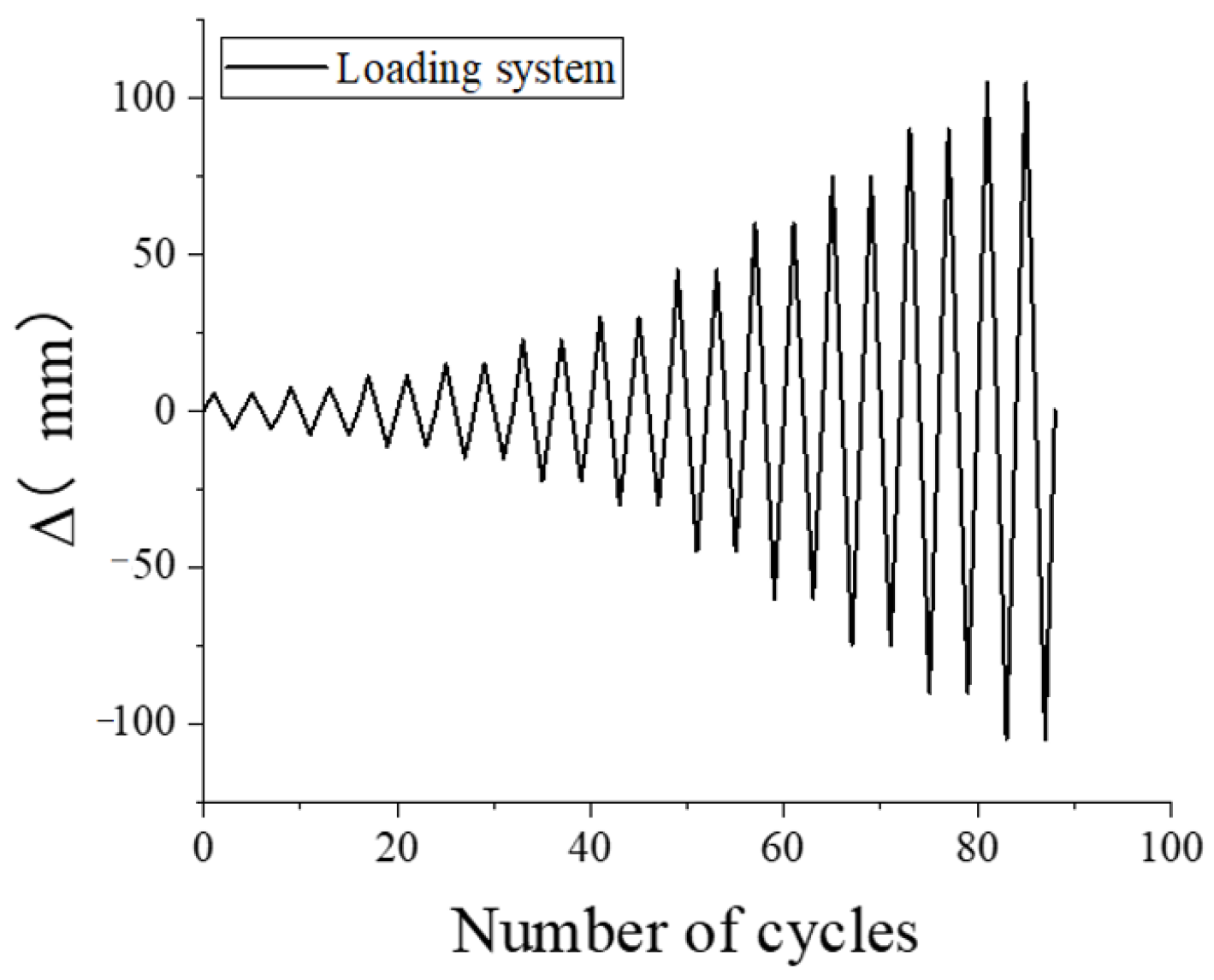
3.3. Loading Procedure
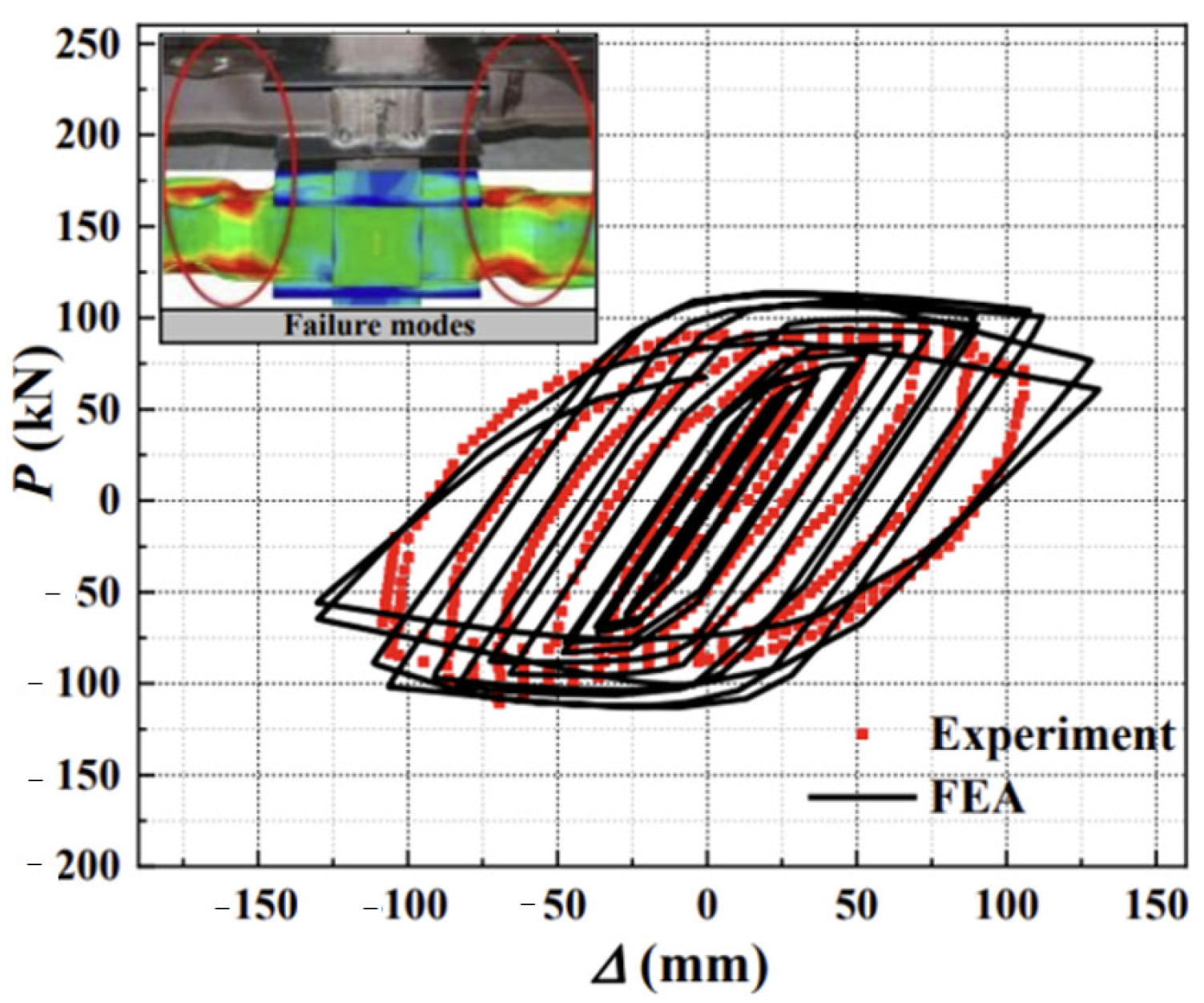
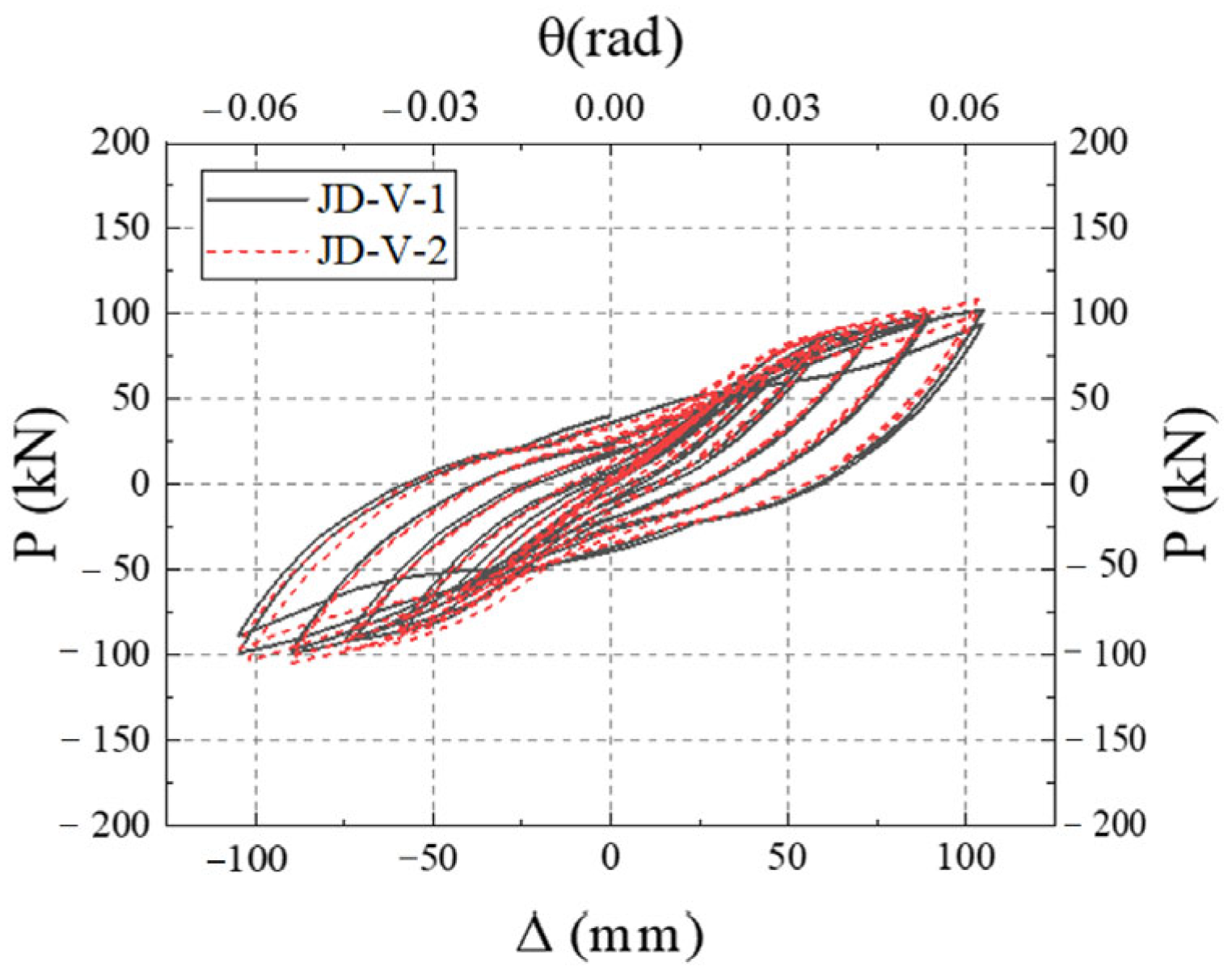
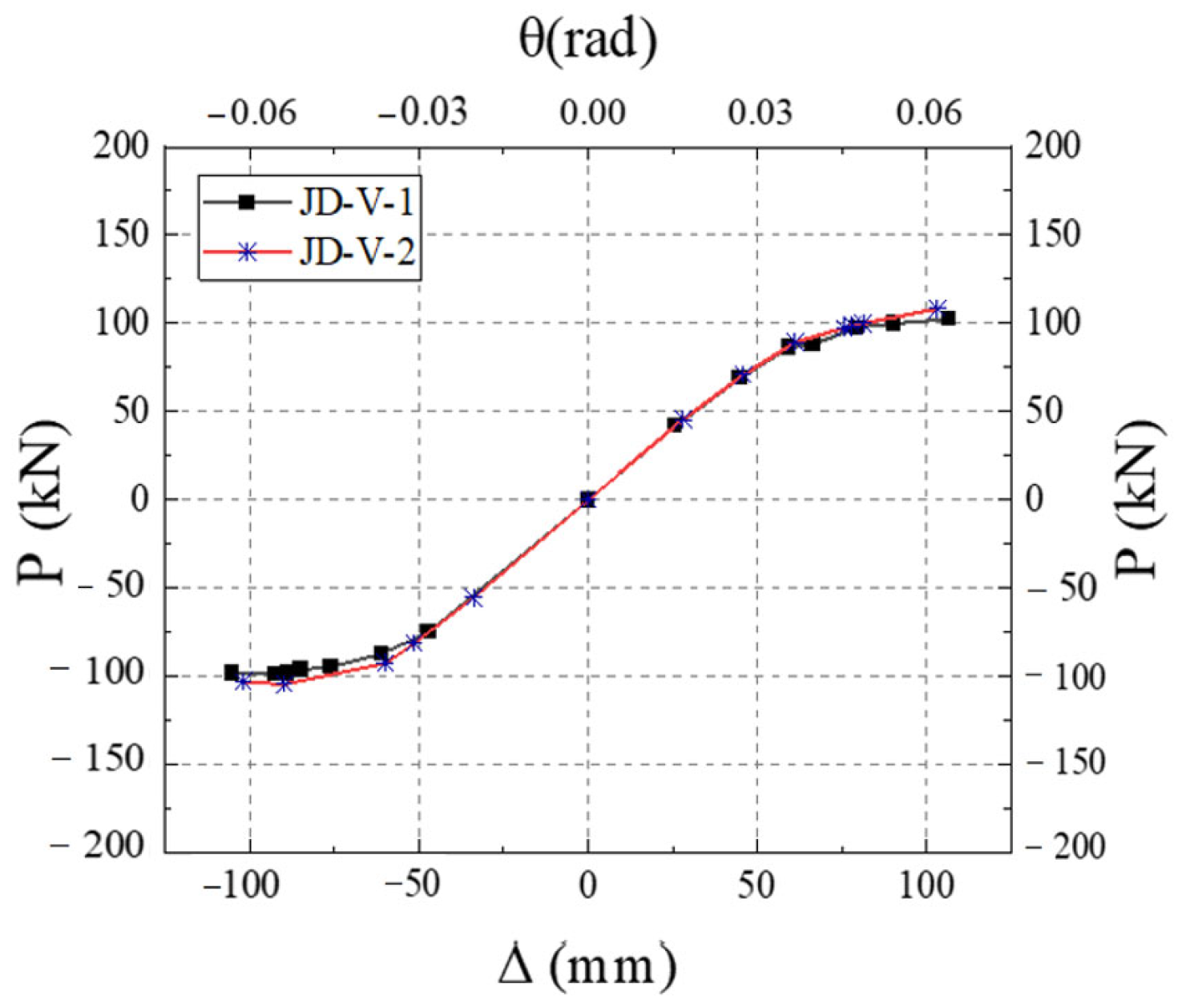
3.4. Finite Element Model Verification
4. Finite Element Simulation Analysis
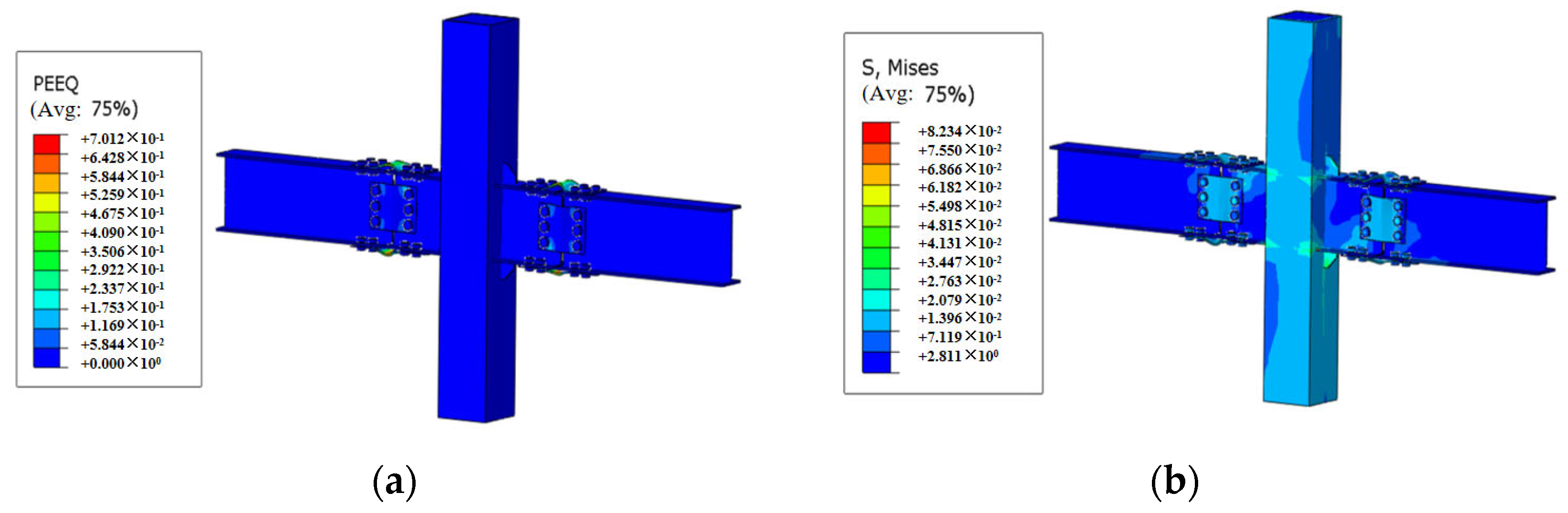
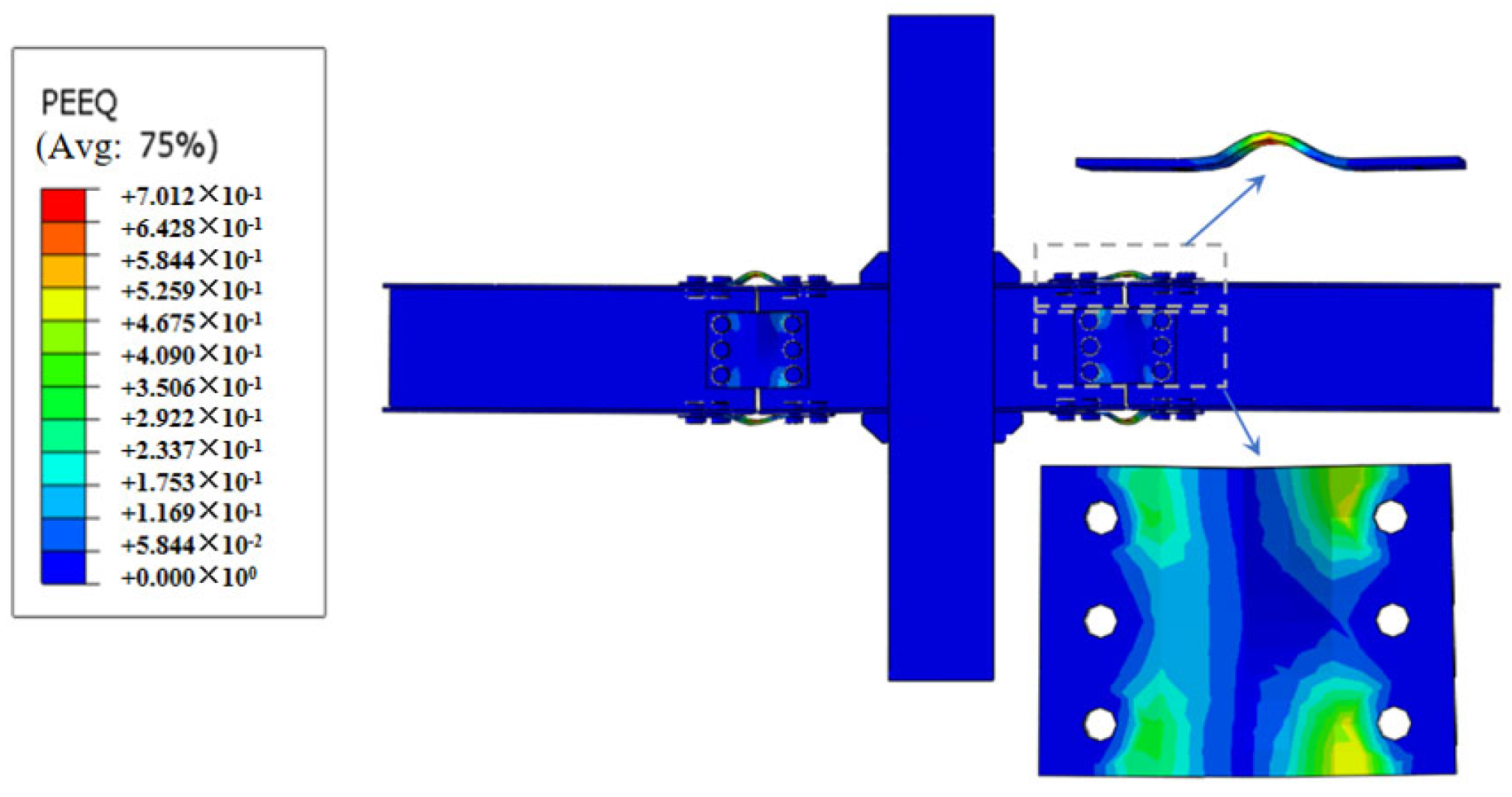
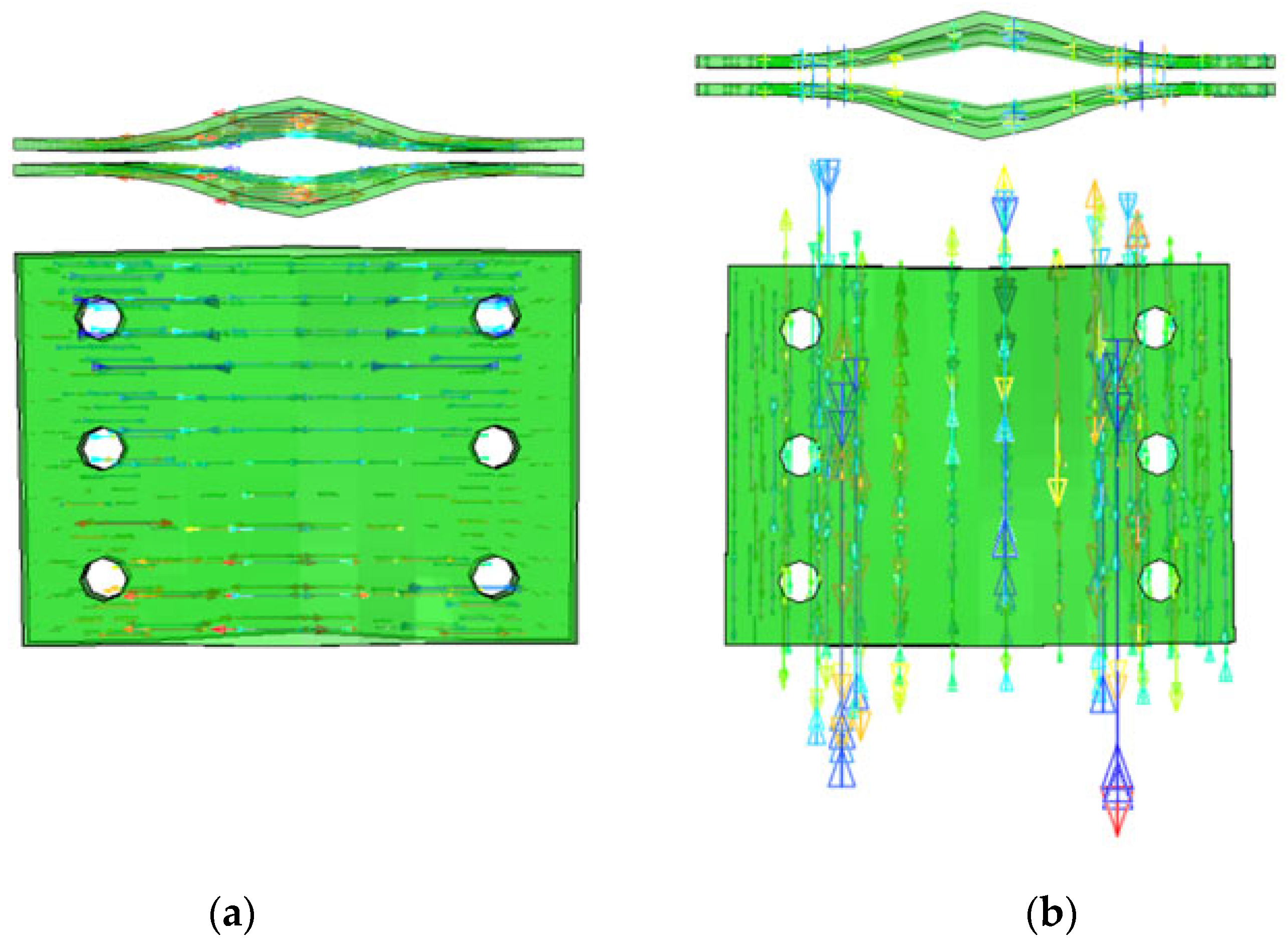
4.1. Analysis of Failure Mode of Typical Member
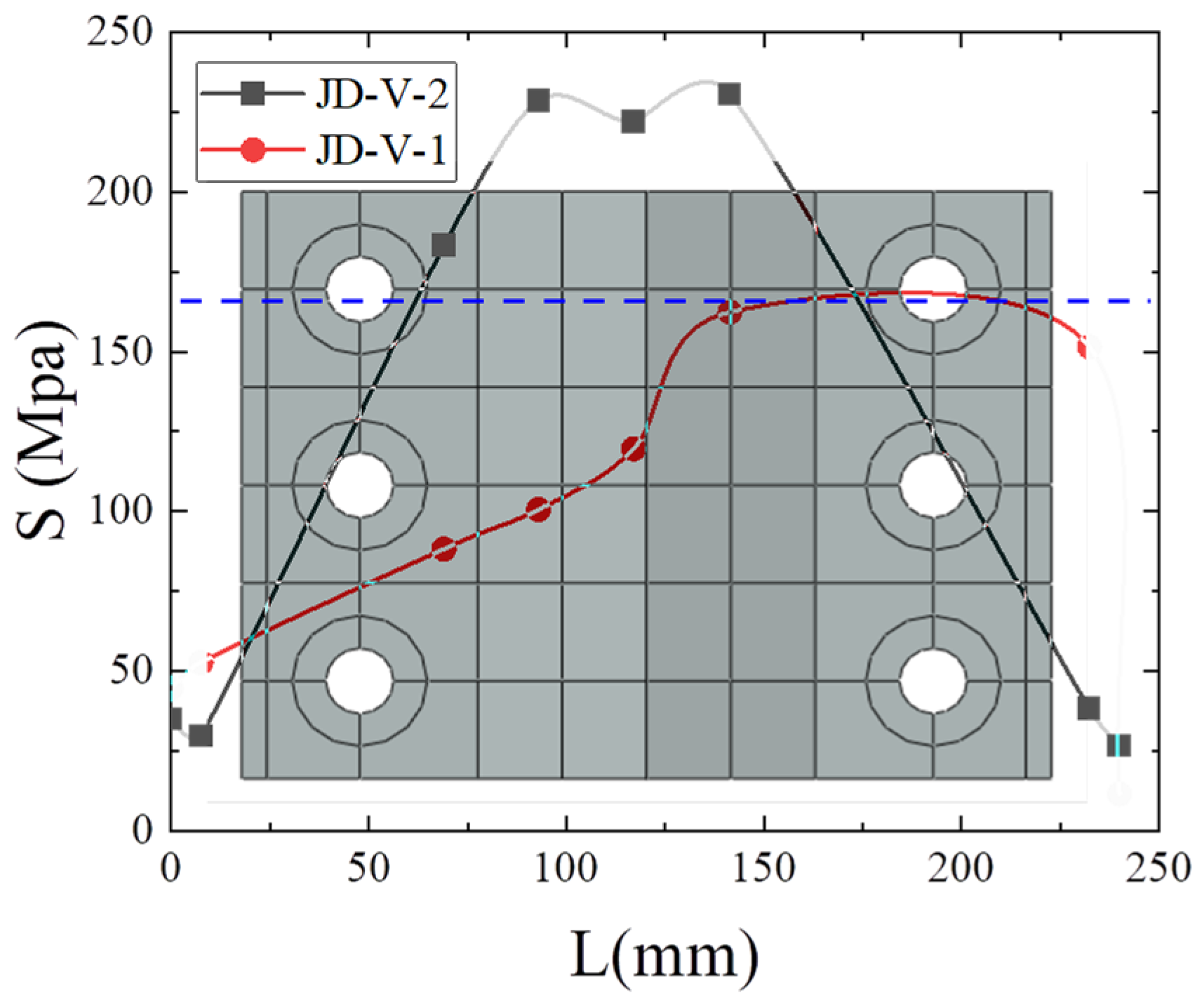
4.2. Stress Distribution
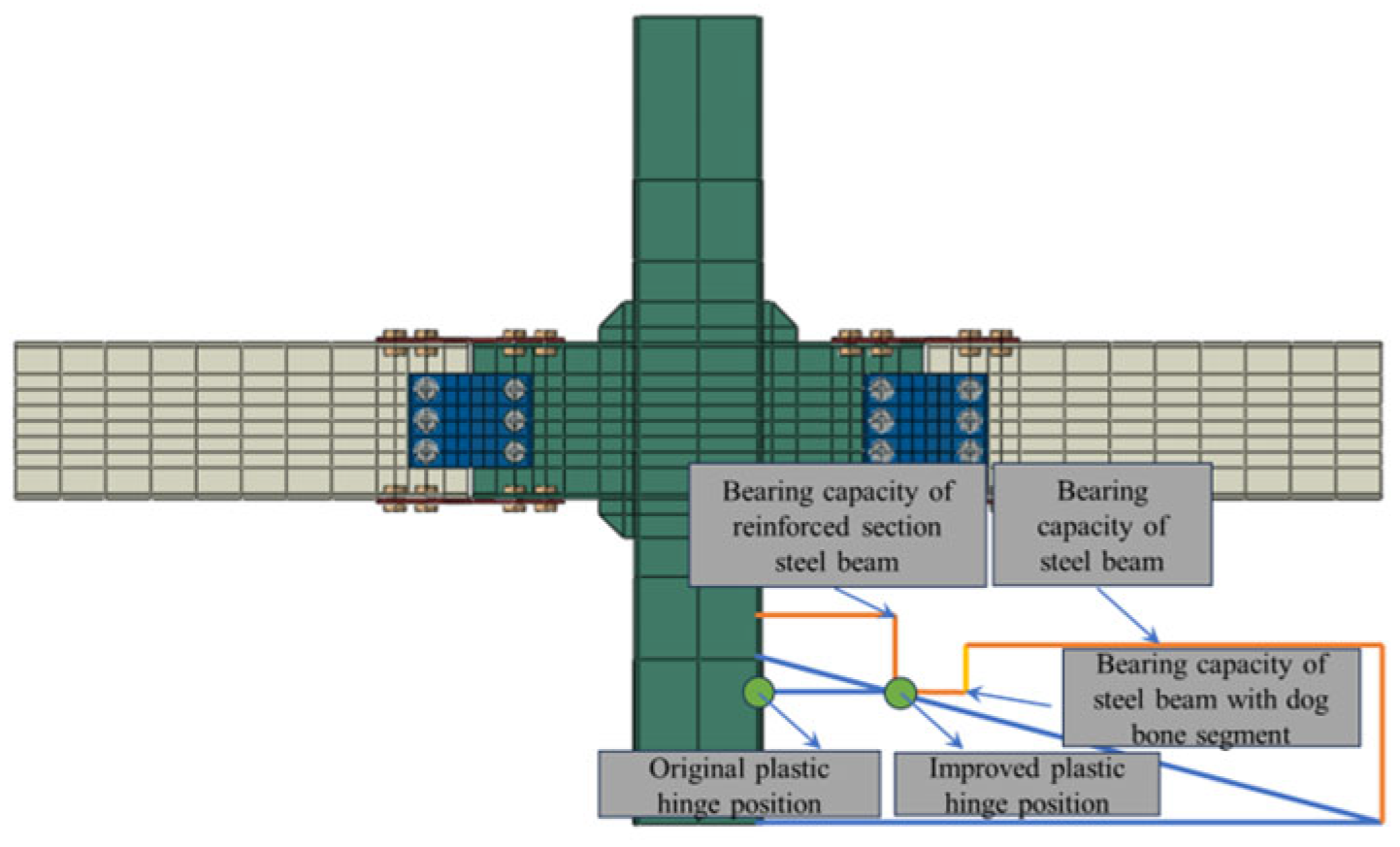
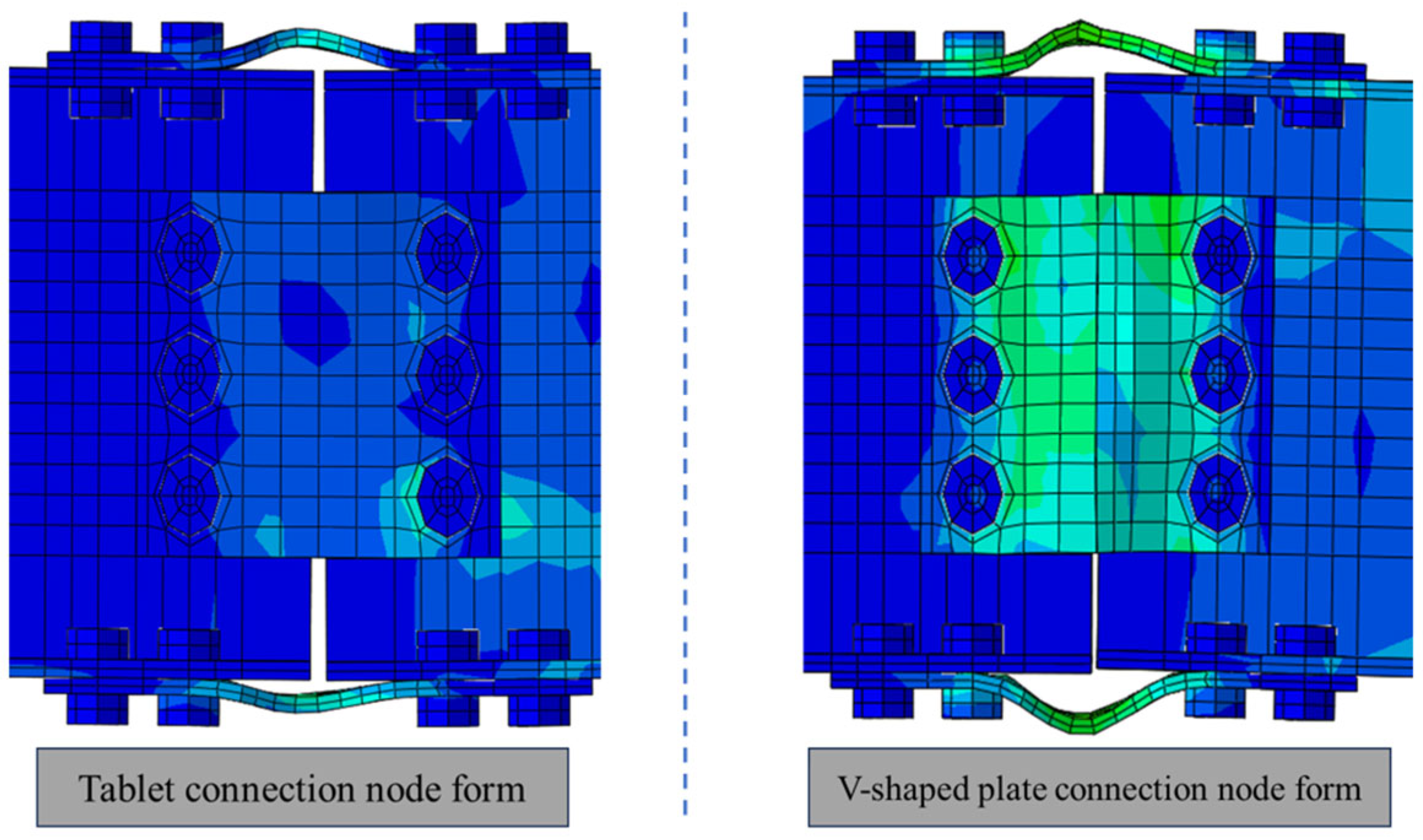
4.3. Comparative Analysis of Node Forms
5. Parameter Analysis
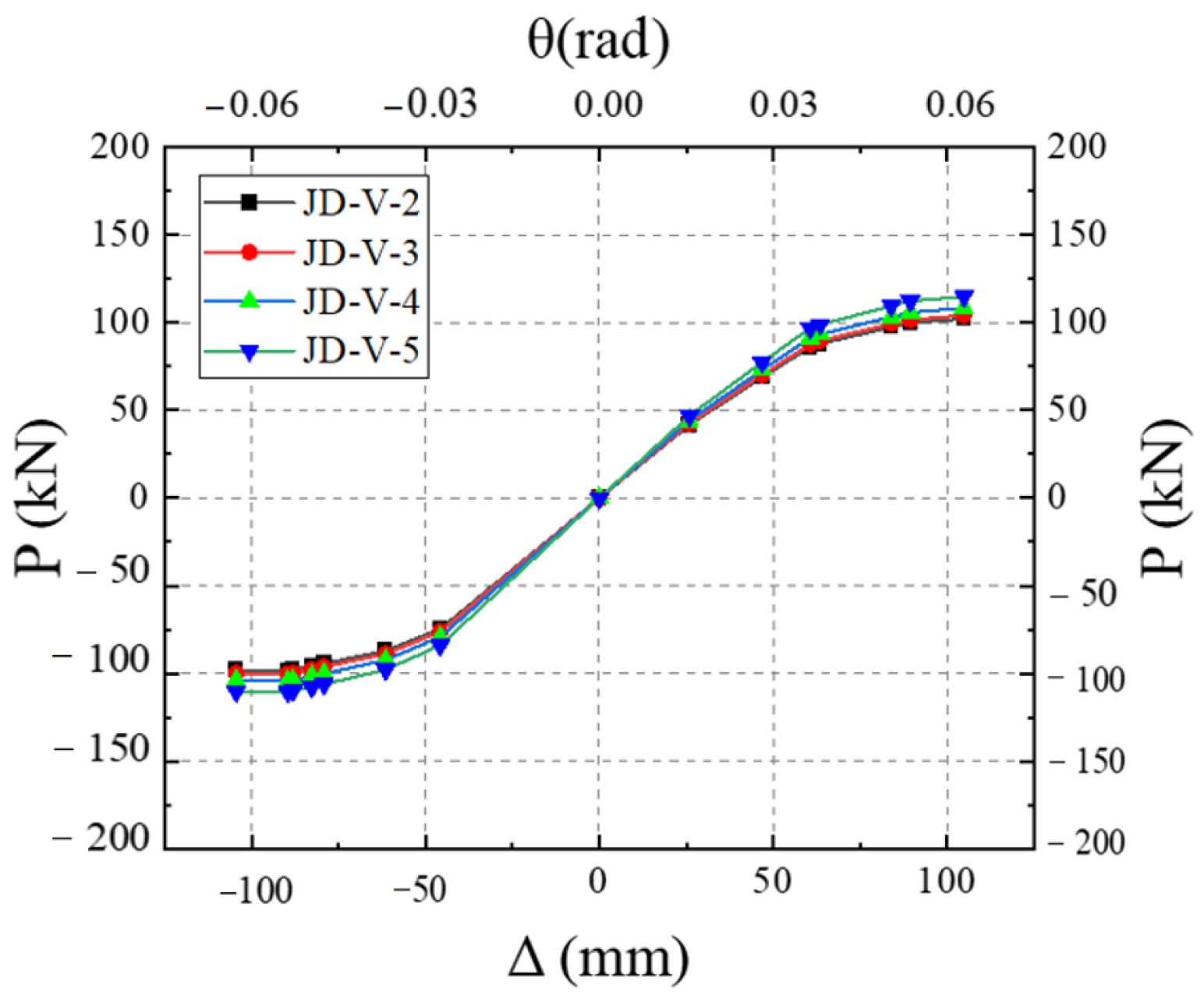
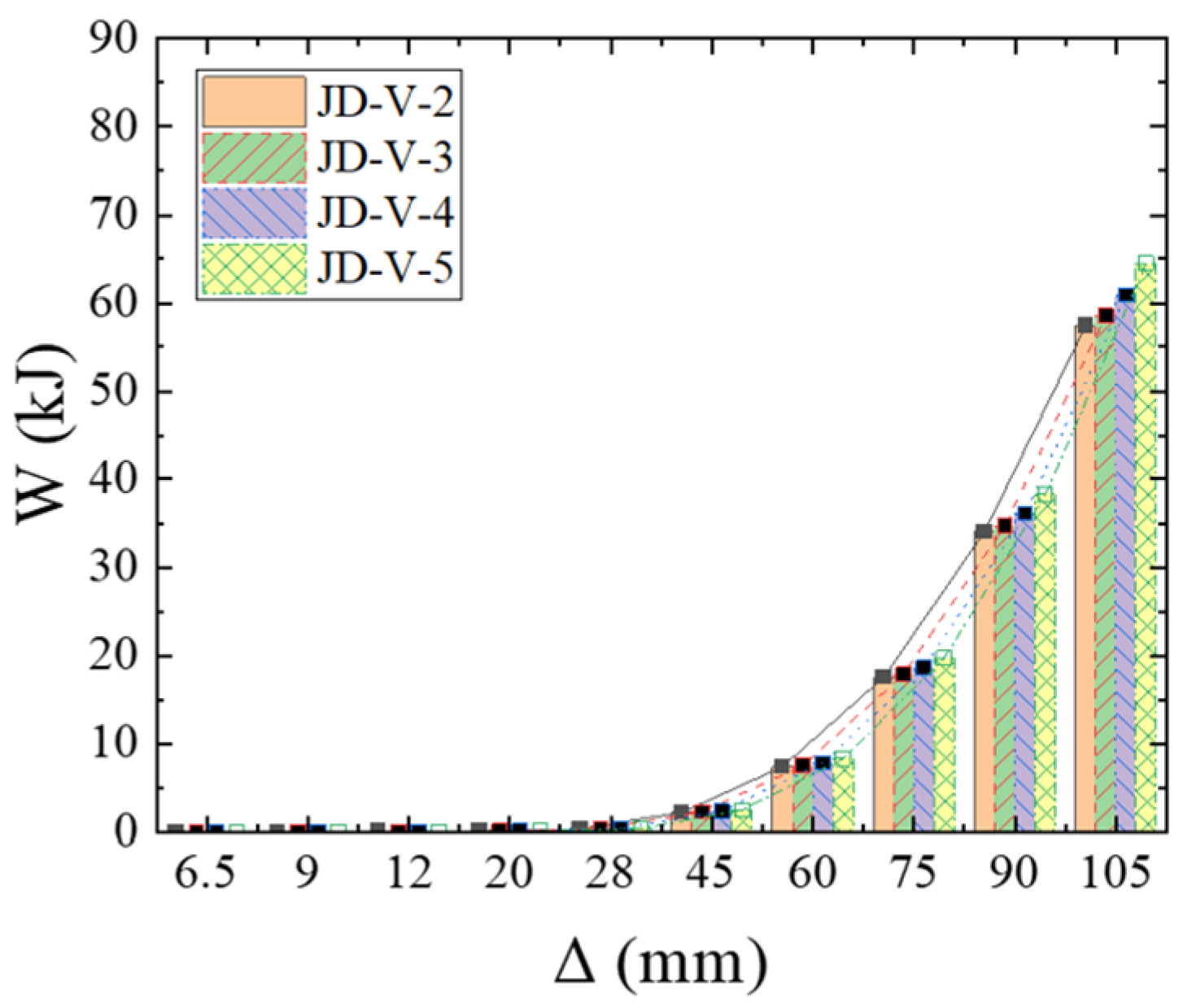
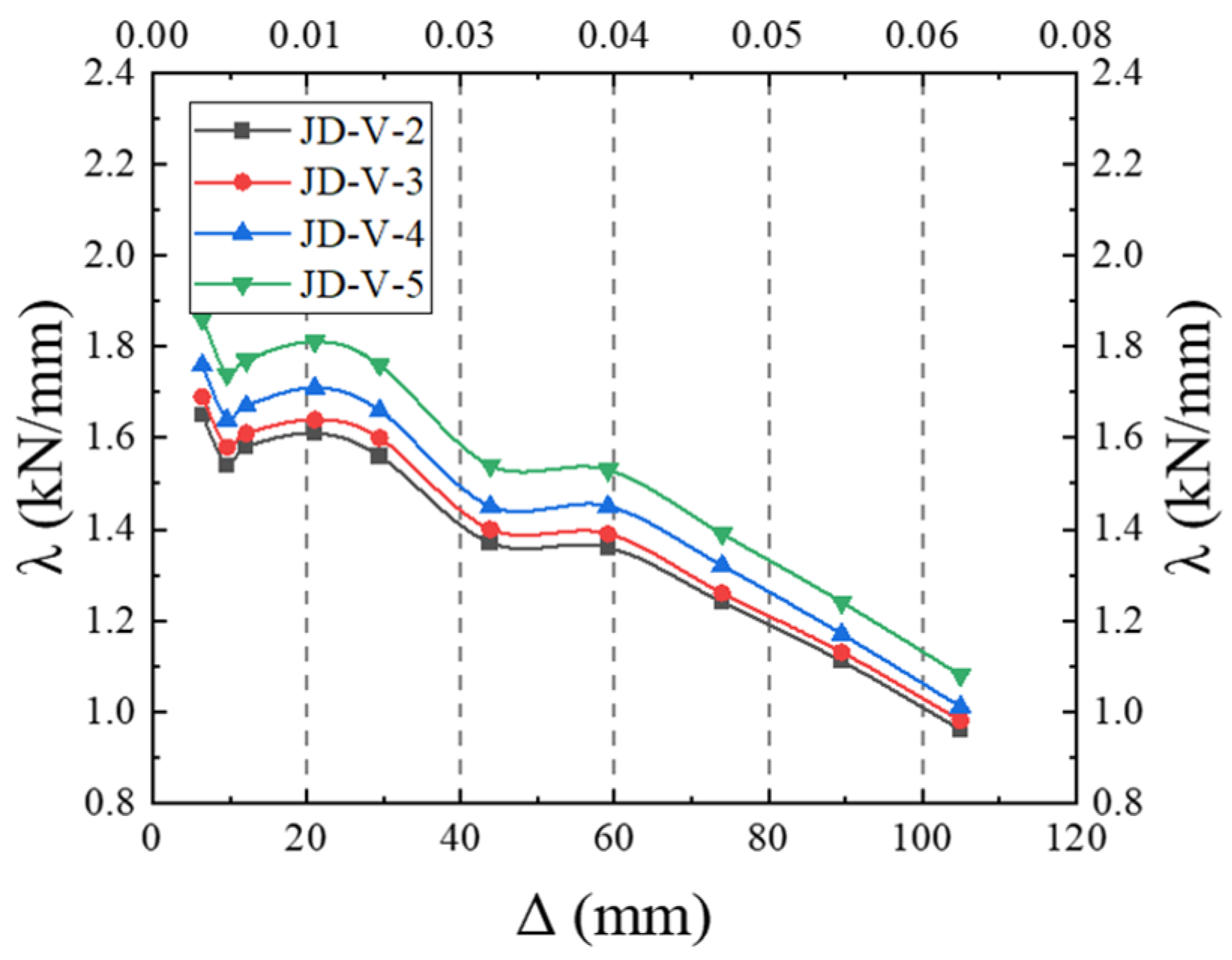
5.1. Effect of V-Shaped Steel Connector Thickness
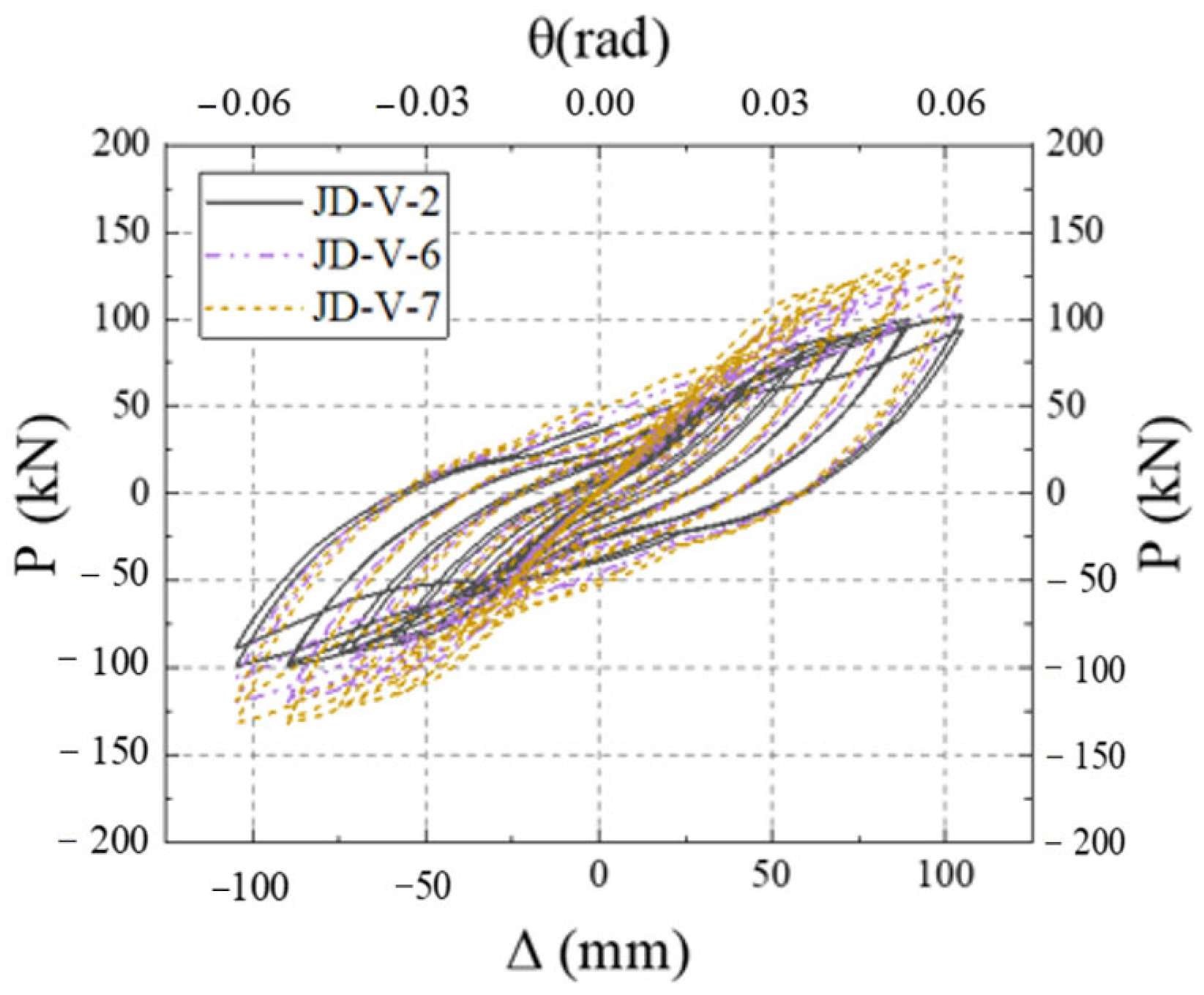
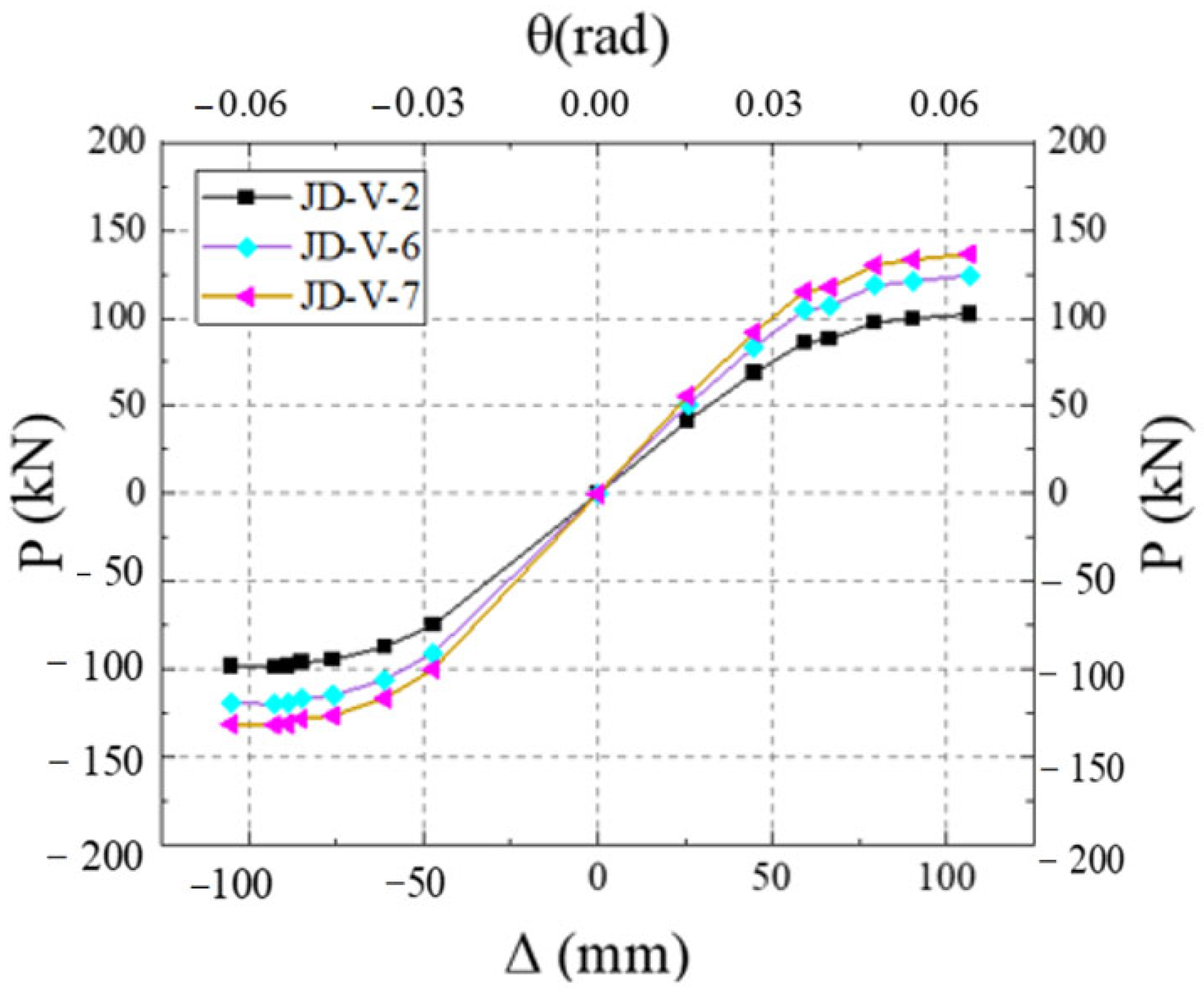
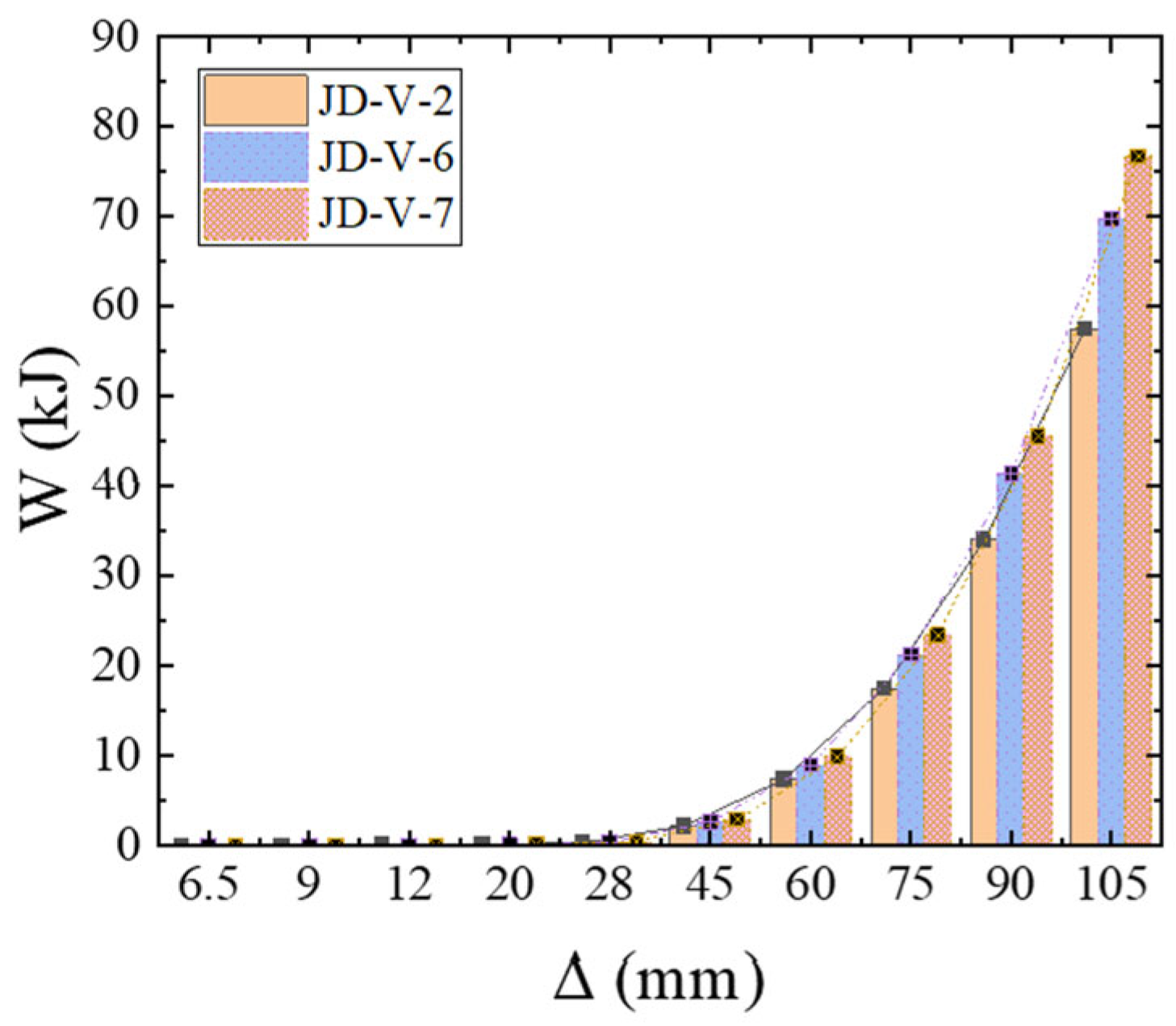
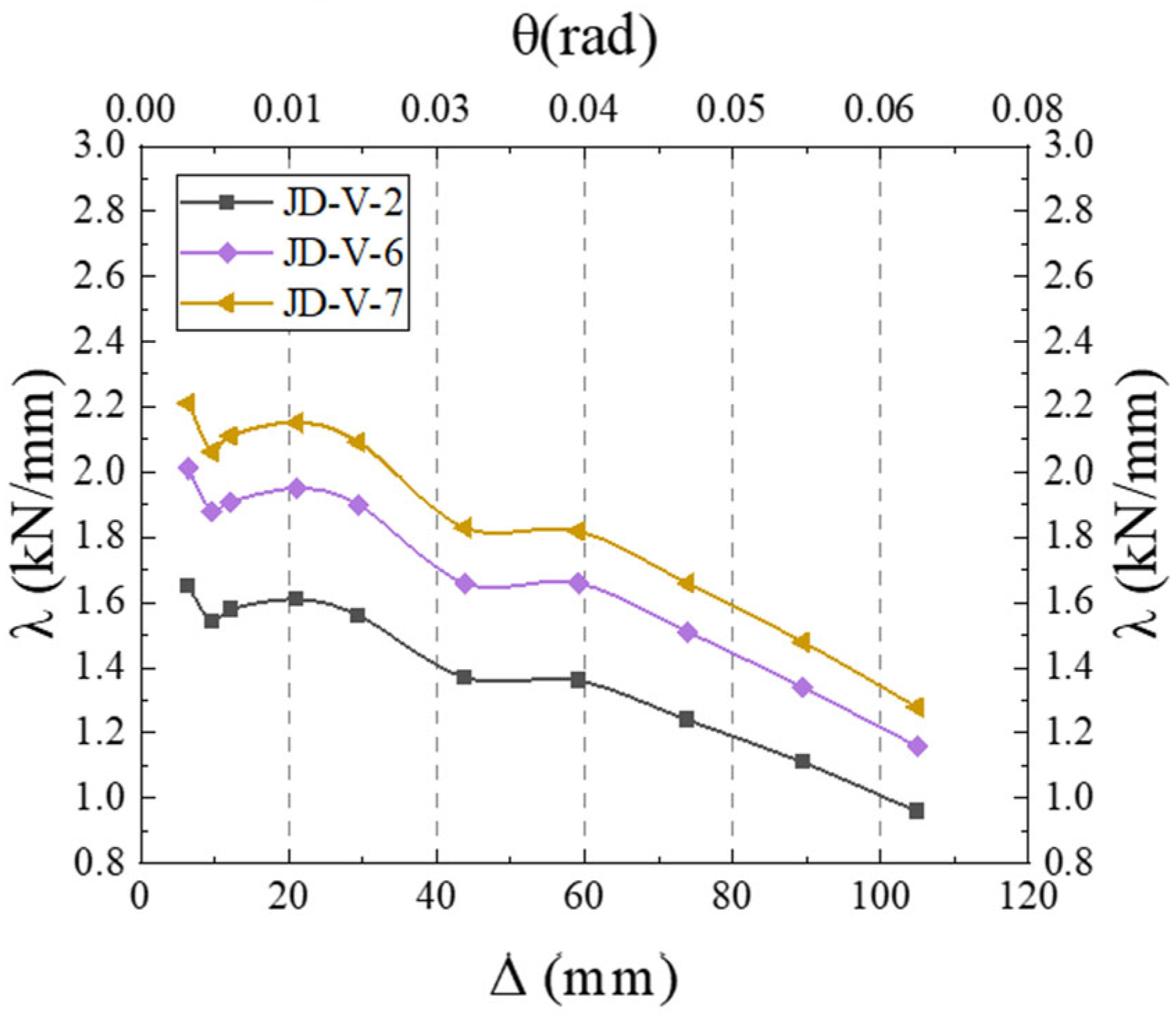
5.2. Effect of V-Shaped Steel Connector Strength
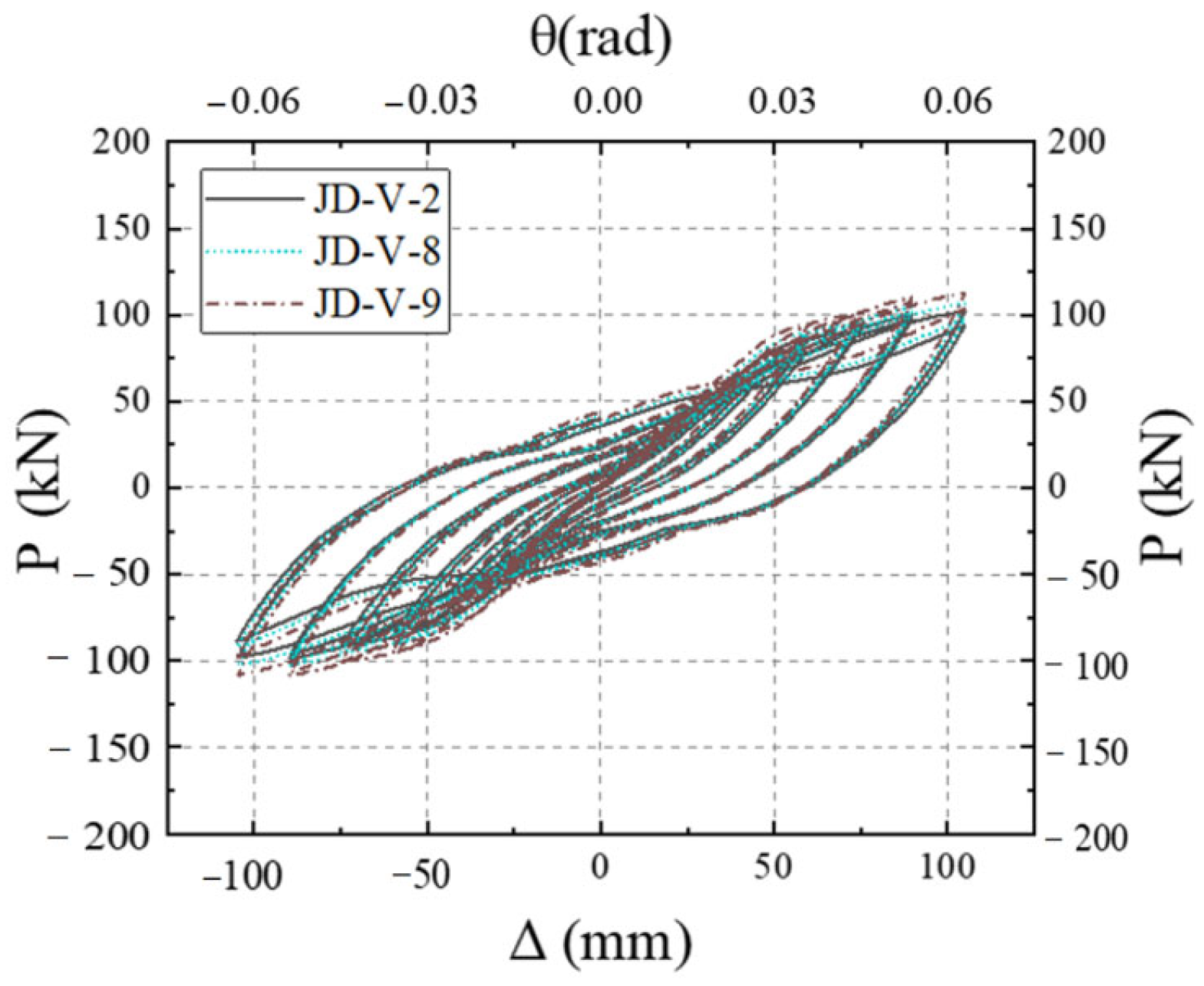
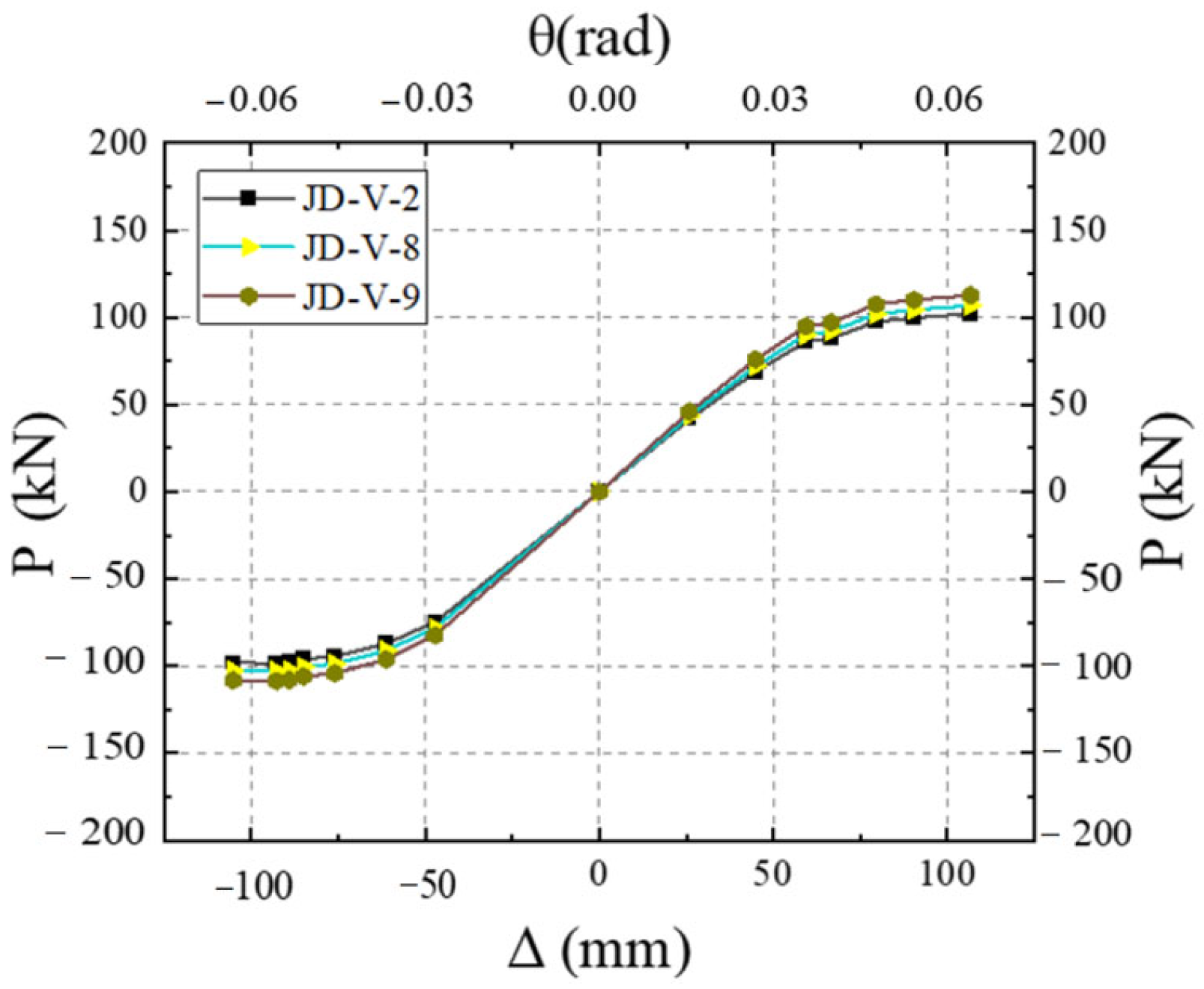
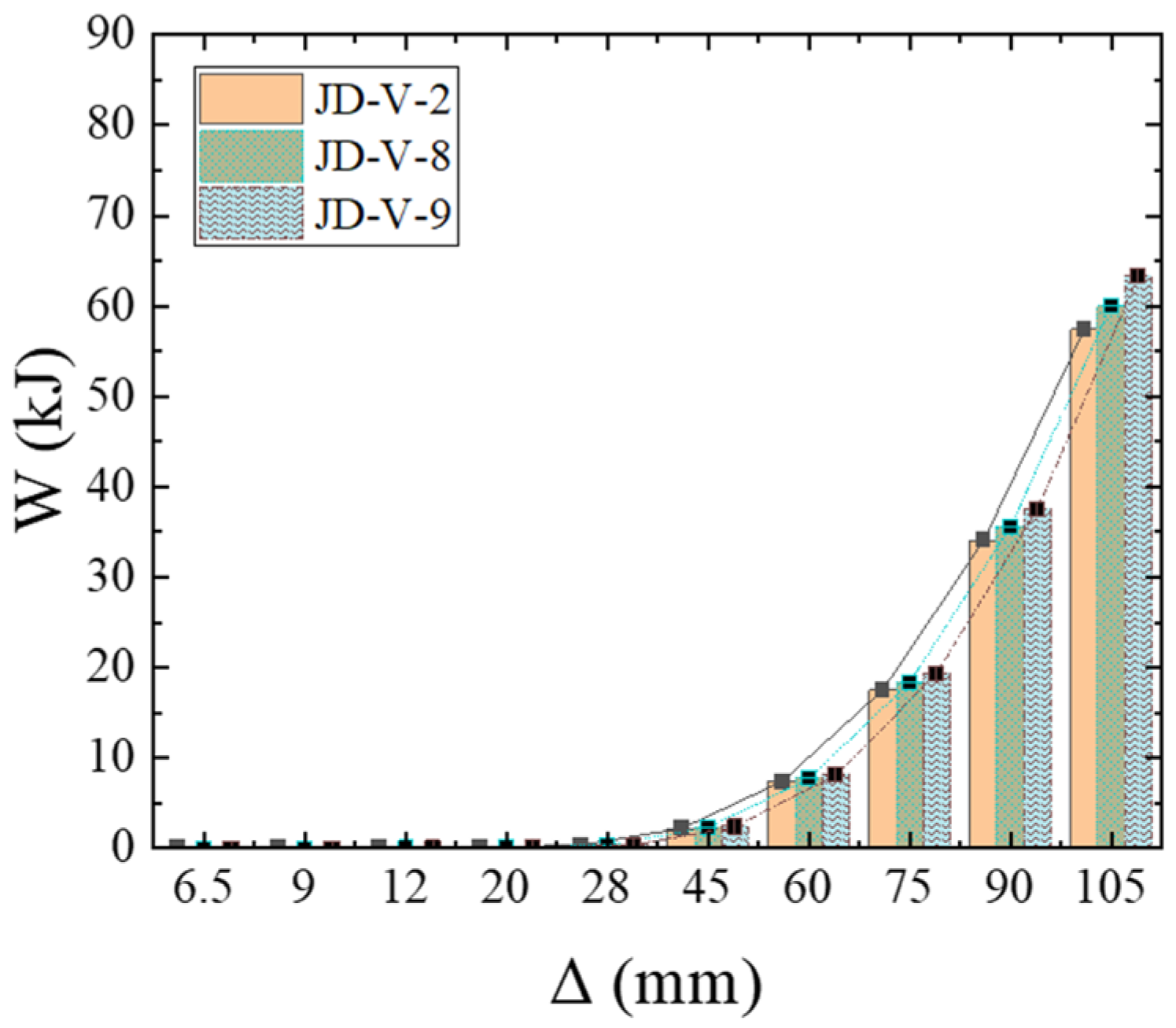
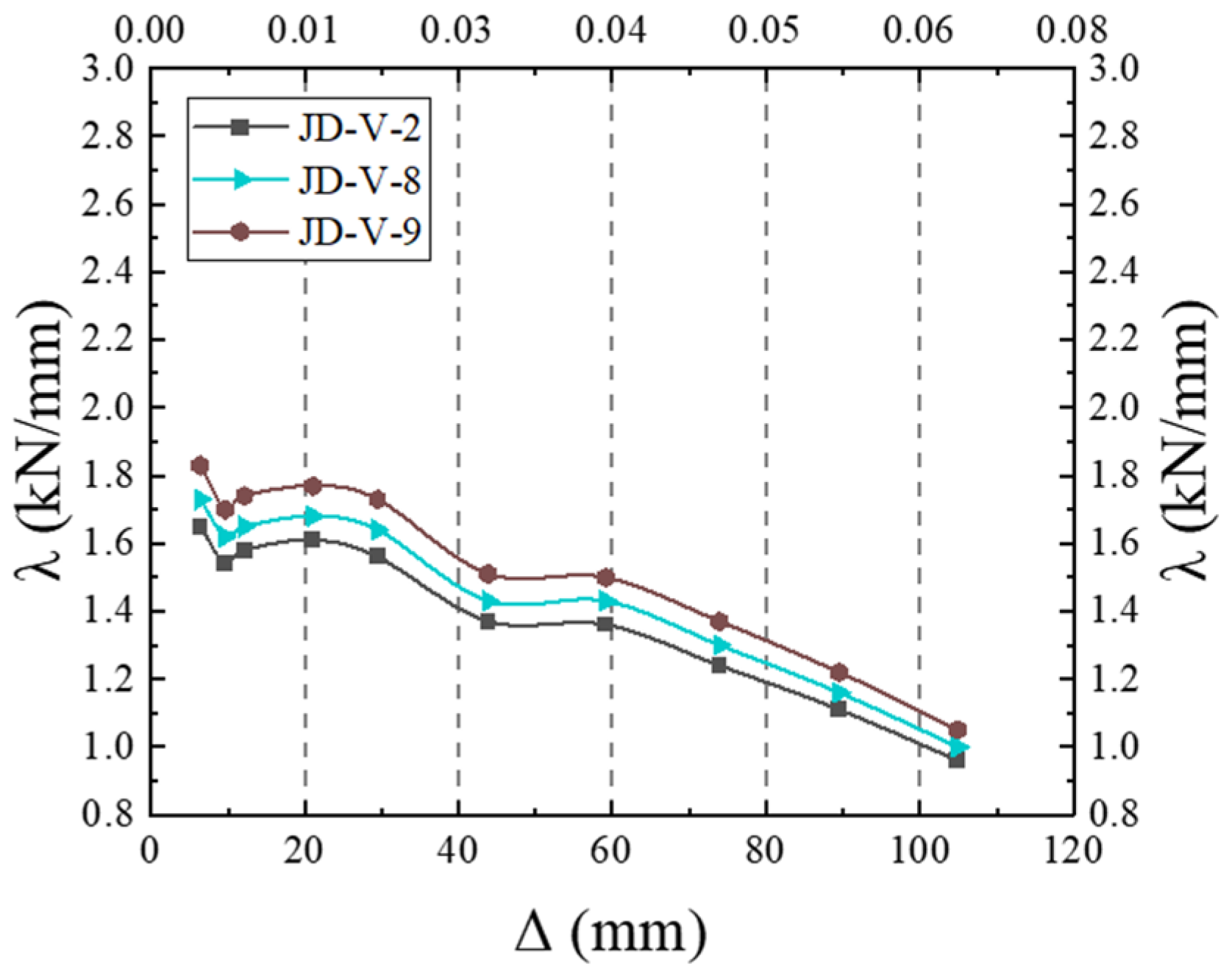
5.3. Effect of Weakening Size of Dog-Bone End
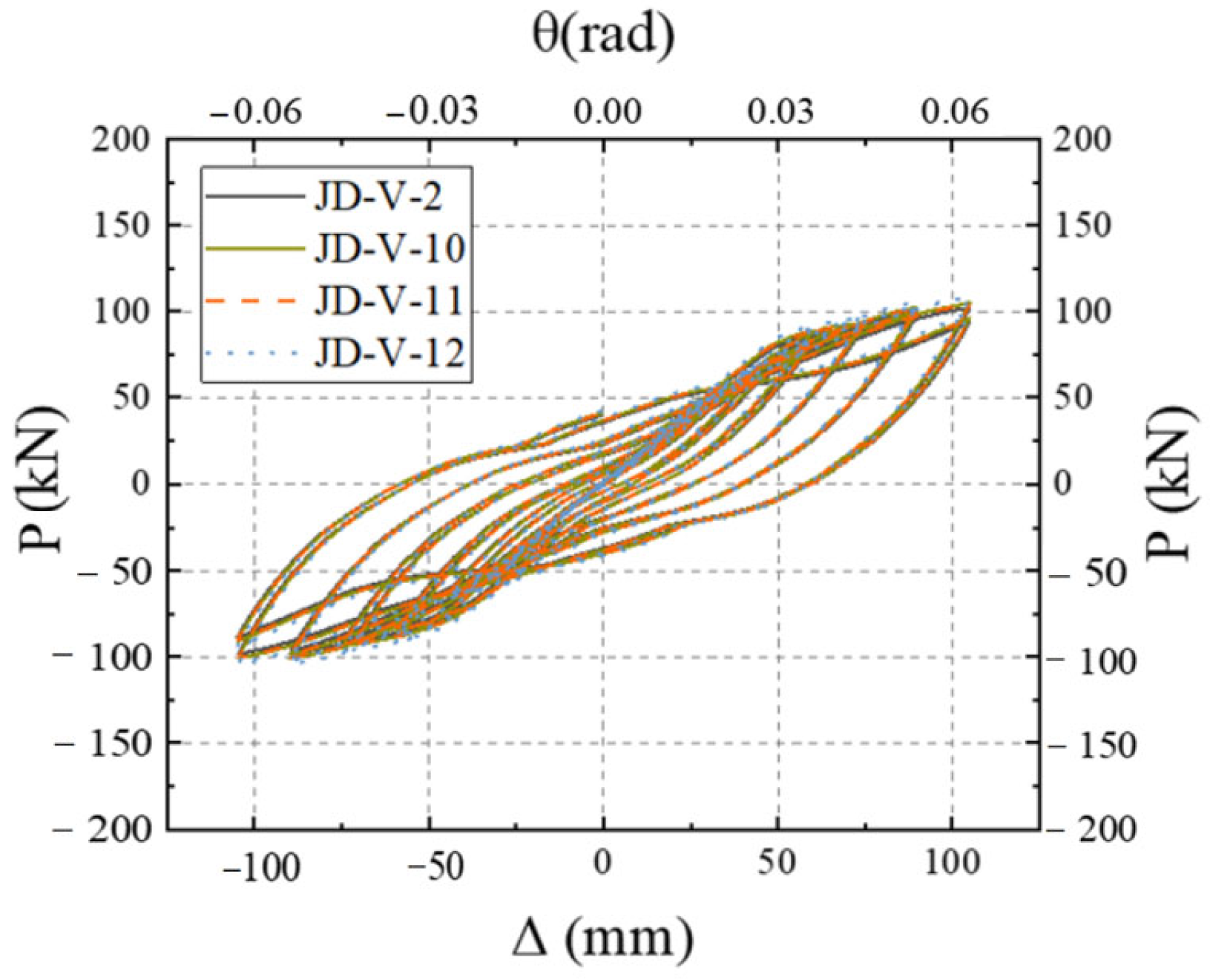
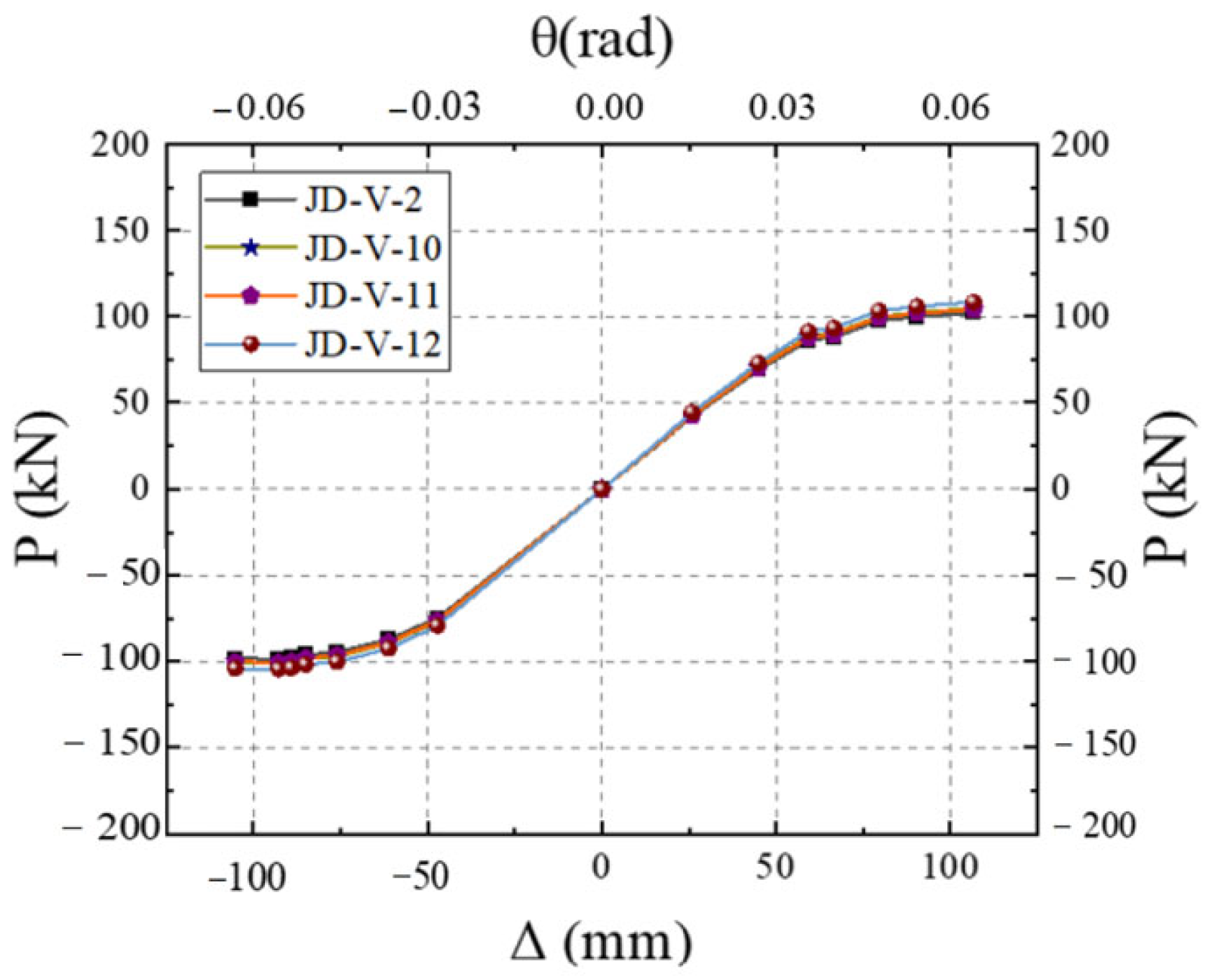
5.4. Effect of Dog-Bone Weakened Connector Thickness
5.5. Effect of Dog-Bone Weakened Connector Strength
6. Discussion
7. Conclusions
- The novel joint achieves a synergistic design integrating dual energy-dissipation mechanisms and plastic hinge relocation through V-shaped steel connecting dampers, which complies with the seismic design principles of strong column–weak beam and strong joint–weak component. Moreover, it enables completely bolted on-site assembly connections.
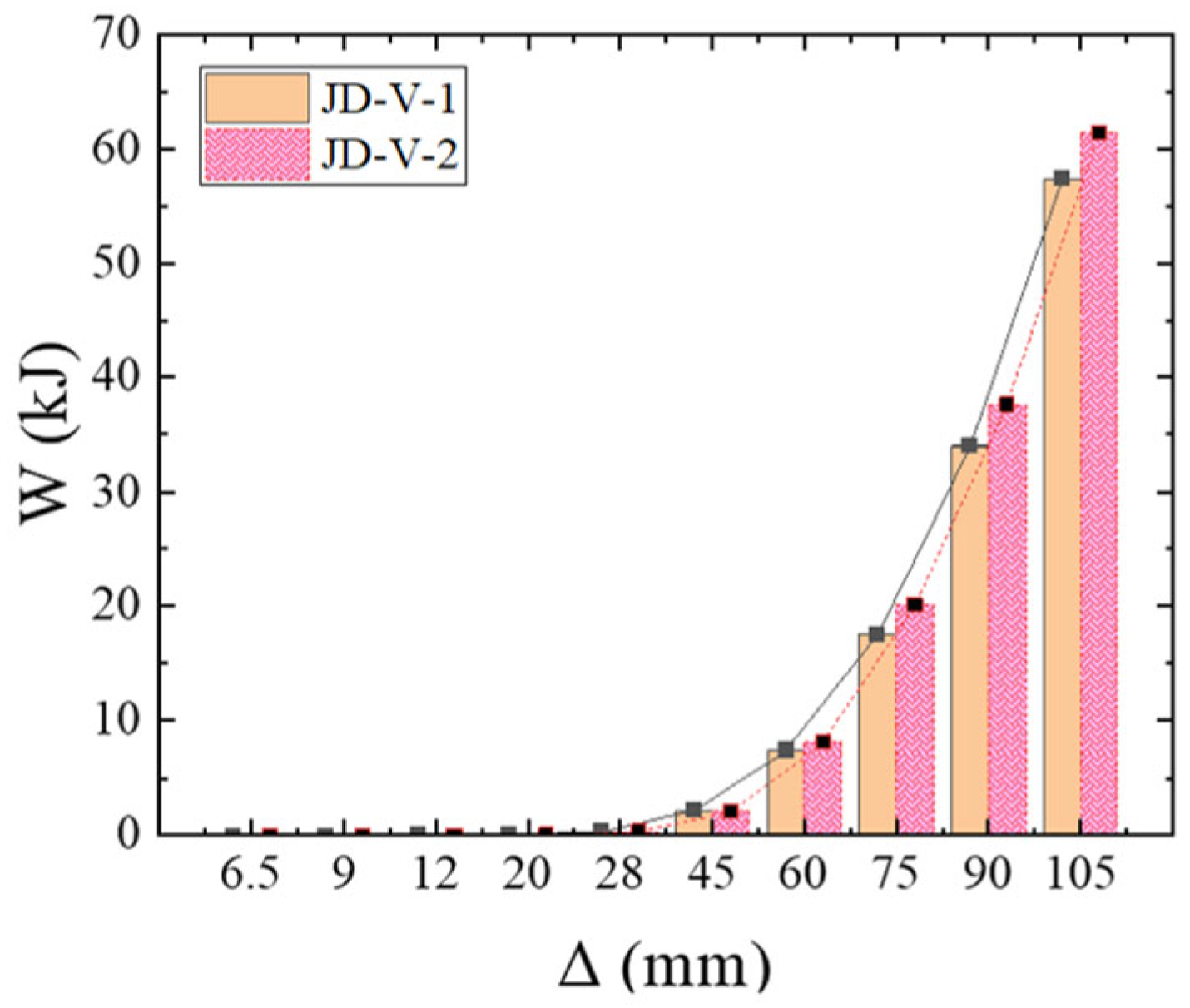
- Compared with joint configurations using flat plate connectors at the web, the joint with V-shaped steel connectors demonstrates superior energy dissipation capacity through flexural deformation of the V-shaped components during the elastoplastic stage, exhibiting more stable and fuller hysteresis loops. The failure mode concentrates on the dog-bone weakened connections and plastic hinge formation in the beam sections at V-shaped connectors, while the joint core zone maintains elastic column sections without significant concrete damage. This configuration achieves the seismic performance objectives of controllable damage and post-earthquake replaceability, while ensuring reliable and well-defined force transfer paths.
- The beam-column joint equipped with V-shaped replaceable energy-dissipating components demonstrates superior performance compared to conventional flat plate connection joints, exhibiting a 1.7% increase in initial stiffness and a 1.3% enhancement in ultimate load-bearing capacity. More significantly, the proposed configuration achieves a 9% improvement in ductility and a 7.53% increase in cumulative energy dissipation capacity. These results confirm that the innovative design effectively enhances both the ductile behavior and energy dissipation capability of the joint, while maintaining its fundamental stiffness and load-bearing characteristics.
- The strength and dimensions of both the V-shaped steel connectors and dog-bone weakened connections were identified as critical parameters affecting the joint’s seismic performance. Based on comprehensive analysis, the recommended specifications are that V-shaped connectors should adopt LY160 steel with a thickness of 2–4 mm, while dog-bone weakened connections should use Q235 steel with a thickness of 6–10 mm and a weakened zone dimension of 15–20 mm. However, practical applications face three major challenges: stringent construction accuracy requirements, insufficient environmental durability, and relatively high initial costs. These limitations will be systematically addressed through further research and experimental optimization in subsequent studies.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Chen, W.; Hao, H.; Xia, Y. Damage evaluation of a welded beam–column joint with surface imperfections subjected to impact loads. Eng. Struct. 2022, 261, 114276. [Google Scholar] [CrossRef]
- Nelson, N.R.; Prasad, N.S.; Sekhar, A. Structural integrity and sealing behavior of bolted flange joint: A state of art review. Int. J. Press. Vessel. Pip. 2023, 204, 104975. [Google Scholar] [CrossRef]
- Hou, N.; Ding, N.; Qu, S.; Guo, W.; Liu, L.; Xu, N.; Tian, L.; Xu, H.; Chen, X.; Zaïri, F.; et al. Failure modes, mechanisms and causes of shafts in mechanical equipment. Eng. Fail. Anal. 2022, 136, 106216. [Google Scholar] [CrossRef]
- Popov, E.P.; Bertero, V.V. Cyclic Loading of Steel Beams and Connections. J. Struct. Div. 1973, 99, 1189–1204. [Google Scholar] [CrossRef]
- Shen, J.; Kitjasateanphun, T.; Srivanich, W. Seismic performance of steel moment frames with reduced beam sections. Eng. Struct. 2000, 22, 968–983. [Google Scholar] [CrossRef]
- Chen, S.-J.; Yeh, C.H.; Chu, J.M. Ductile Steel Beam-to-Column Connections for Seismic Resistance. J. Struct. Eng. 1996, 122, 1292–1299. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, Y.; Zhang, T. A novel damage-control PC beam-column joint with fully precast slab: Experimental investigation. J. Build. Eng. 2025, 106, 112513. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, L.; Liu, W.; Zhang, M. Seismic performance of earthquake-damaged HSRAC beam-column interior joints rehabilitated by bonding steel plates in the plastic hinge of beams. Structures 2024, 69, 107357. [Google Scholar] [CrossRef]
- Du, Y.; Li, F.; Li, H.; Hong, N.; Chi, P. Seismic behavior and resilience assessment of prefabricated beam–column joint with replaceable graded-yielding energy-dissipating connectors. Eng. Struct. 2024, 319, 118814. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.; Ma, B.; Peng, G.; Wang, C.; Zhou, L. Seismic performance of a novel steel-concrete composite beam-column joint. J. Constr. Steel Res. 2025, 229, 109479. [Google Scholar] [CrossRef]
- Jafari, A.; Shahmansouri, A.A.; Pourshamsian, S.; Bengar, H.A.; Zhou, Y. Post-tensioned coupling beams: Mechanics, cyclic response, and damage evaluation. Soil Dyn. Earthq. Eng. 2025, 188, 109082. [Google Scholar] [CrossRef]
- Chen, P.; Pan, J.; Hu, F.; Wang, Z. Experimental investigation on earthquake-resilient steel beam-to-column joints with replaceable buckling-restrained fuses. J. Constr. Steel Res. 2022, 196, 107413. [Google Scholar] [CrossRef]
- Yu, J.; Peng, J.; Wang, Y.H.; Luo, W.W.; Li, C.Y.; Wang, L.P. Study on seismic performance of steel frame beam-slab-column joint based on angle unilateral connection. Eng. Struct. 2025, 330, 119888. [Google Scholar] [CrossRef]
- Li, G.; Qin, Z.; Li, X.; Liu, M. Numerical study on the seismic performance of H-beam to built-in CFRP circular tube CFST column joint with replaceable energy dissipation angle steel. Structures 2024, 67, 106793. [Google Scholar] [CrossRef]
- Men, J.; Li, T.; Zhou, Q.; Zhang, H.; Huang, C.H. Structural fuse performance and earthquake-resilient performance of beam-column joints with replaceable T-stub. J. Constr. Steel Res. 2023, 206, 107943. [Google Scholar] [CrossRef]
- Cui, W.B.; Liu, X.C.; Chen, X.; Guo, L.X. Seismic performance of bolted beam-to-column composite joints with integrated precast edge composite hollow floor slab. J. Build. Eng. 2025, 105, 112438. [Google Scholar] [CrossRef]
- Feng, Y.; Han, C.; Chen, W. Theoretical, experimental and numerical studies of a novel tension-compression bolt (TCB) for single-sided beam-column joints. Thin-Walled Struct. 2025, 212, 113172. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, S.; An, R.; Wang, Z. Seismic performance of a newly assembled joint between shaped steel beams and square steel tubular columns. J. Build. Eng. 2025, 100, 111748. [Google Scholar] [CrossRef]
- Yi, W.; Zhu, L.; Wang, Z.; Sun, H.; Yin, F. Experimental and numerical study on seismic performance of H-beam to HSST column joints connected by elliptical head one-sided bolts. J. Build. Eng. 2025, 102, 111855. [Google Scholar] [CrossRef]
- Hou, G.; Shang, Y.; Zhang, L.; Sun, L.; Wu, J.; Lu, Y.; Zhu, A.; Mou, Y. Bending performance of bolted beam-column joints with T-stubs. J. Constr. Steel Res. 2025, 226, 109280. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Zhao, J.; Du, Q.; Chen, H. Seismic performance of CFDST column to steel beam welded-bolted joint with slab. J. Constr. Steel Res. 2025, 226, 109192. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Zhao, J.; Du, Q.; Bwalya, J. Experimental and numerical investigation on ring-plate CFDST column to steel beam bolted-welded joint. Structures 2024, 69, 107586. [Google Scholar] [CrossRef]
- Rasoulitabar, M.; TahamoliRoudsari, M.; Memarzadeh, P.; Fathi, F. Experimental investigation of the cyclic behavior of bolted T-stub steel connections. Steel Compos. Struct. 2025, 55, 397. [Google Scholar] [CrossRef]
- Yin, L.; Zhu, Y.; Cai, X.; Xu, Z.; Zhang, J. Seismic performance of self-centering precast concrete buckling-restrained braced frame sub-assembly. J. Build. Eng. 2025, 107, 112690. [Google Scholar] [CrossRef]
- Xiong, S.; Yang, N.; Guan, H.; Shi, G.; Luo, M.; Deguchi, Y.; Cui, M. Combination of plasma acoustic emission signal and laser-induced breakdown spectroscopy for accurate classification of steel. Anal. Chim. Acta 2025, 1336, 343496. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Nie, J.-H.; Wang, H.; Yu, T.; Kuang, K.S.C. Path planning and topology-aided acoustic emission damage localization in high-strength bolt connections of bridges. Eng. Struct. 2025, 332, 120103. [Google Scholar] [CrossRef]
- Tang, H.; Peng, J.; Peng, H.; Yang, Y.; Gao, Q.; Xiao, L.; Li, H.; Zheng, L.; Chen, Z.; Yang, Z. Test and Theoretical Investigations on Flexural Behavior of High-Performance H-Shaped Steel Beam with Local Corrosion in Pure Bending Zone. Steel Res. Int. 2025, 96, 2400640. [Google Scholar] [CrossRef]
- GB50011-2010; Seismic Design Code of Building. China Building Industry Press: Beijing, China, 2016. (In Chinese)
- GB50017-2017; Steel Structure Design Standard. China Building Industry Press: Beijing, China, 2017. (In Chinese)
- Nagesh; Gupta, N.K. Response simulations of clamped circular steel plates under uniform impulse and effects of axisymmetric stiffener configurations. Int. J. Impact Eng. 2022, 159, 104049. [Google Scholar] [CrossRef]
- Zhou, J.; Ren, J.; Feng, Y.; Tian, W.; Shi, K. A modified parallel-sided shear zone model for determining material constitutive law. Int. J. Adv. Manuf. Technol. 2017, 91, 589–603. [Google Scholar] [CrossRef]
- Feng, Y.; Li, W. Seismic performance of SMA-prestressed self-centering beam-column joints: Experimental and numerical study. J. Constr. Steel Res. 2025, 226, 109272. [Google Scholar] [CrossRef]
- JGJ/T101-2015; Code for Seismic Test of Buildings. China Building Industry Press: Beijing, China, 2015. (In Chinese)
- Zuo, B. Pseudo-Static Experimental Study of H-Shaped Beams to Cold-Formed Square Steel Tube Columns Connections with Different Outer Diaphragm. Master’s Thesis, Qingdao Technological University, Qingdao, China, 2014. (In Chinese). [Google Scholar]
- Yuan, Z.R. The Research on the Mechanical Performance of the Square Concrete Filled Steel Tube with T-Stub Connector. Master’s Thesis, Hunan University, Changsha, China, 2013. (In Chinese). [Google Scholar]
- Sarfarazi, S.; Saffari, H.; Fakhraddini, A. Shear behavior of panel zone considering axial force for flanged cruciform Columns. Civ. Eng. Infrastruct. J. 2020, 53, 359–377. [Google Scholar] [CrossRef]







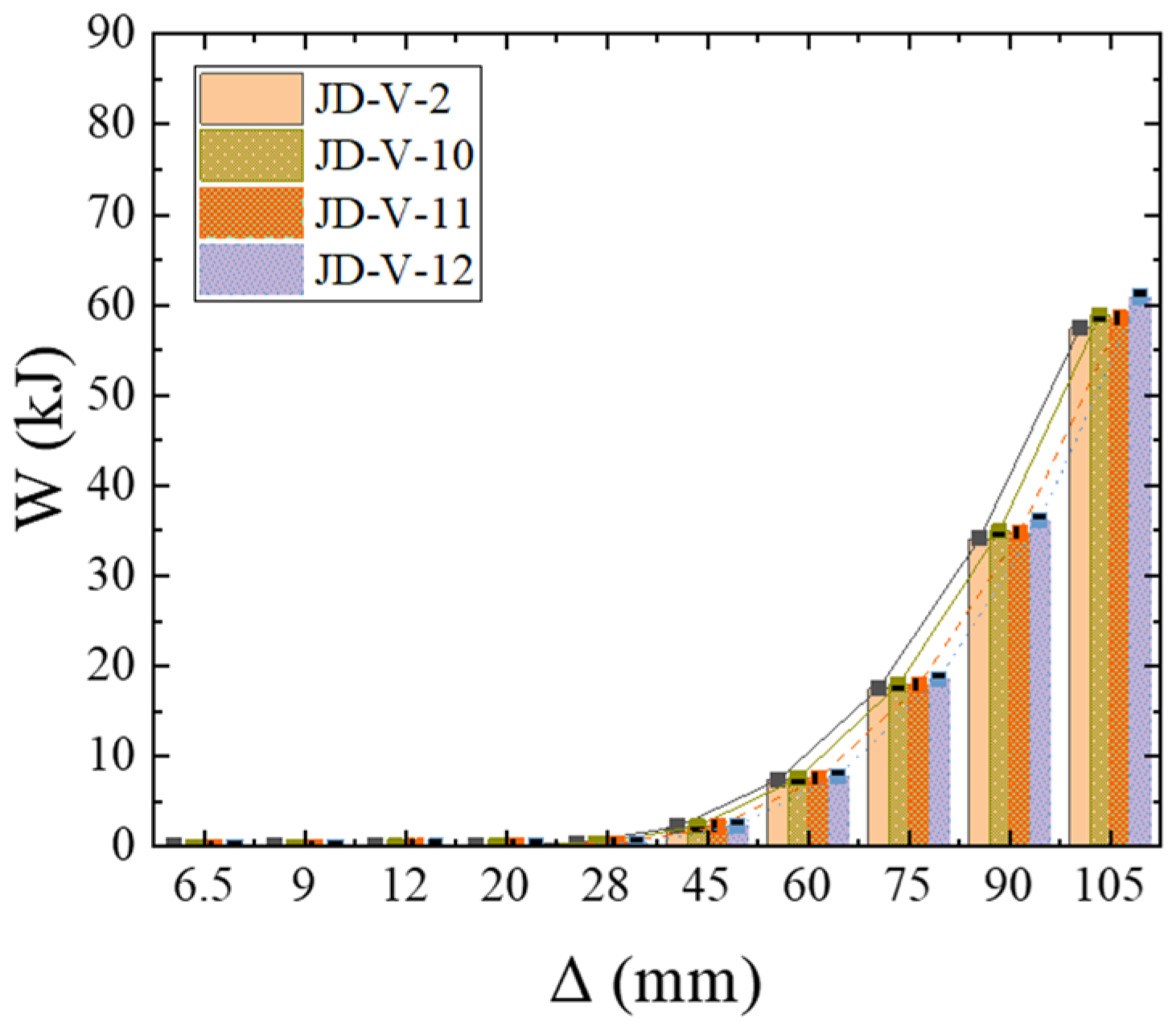

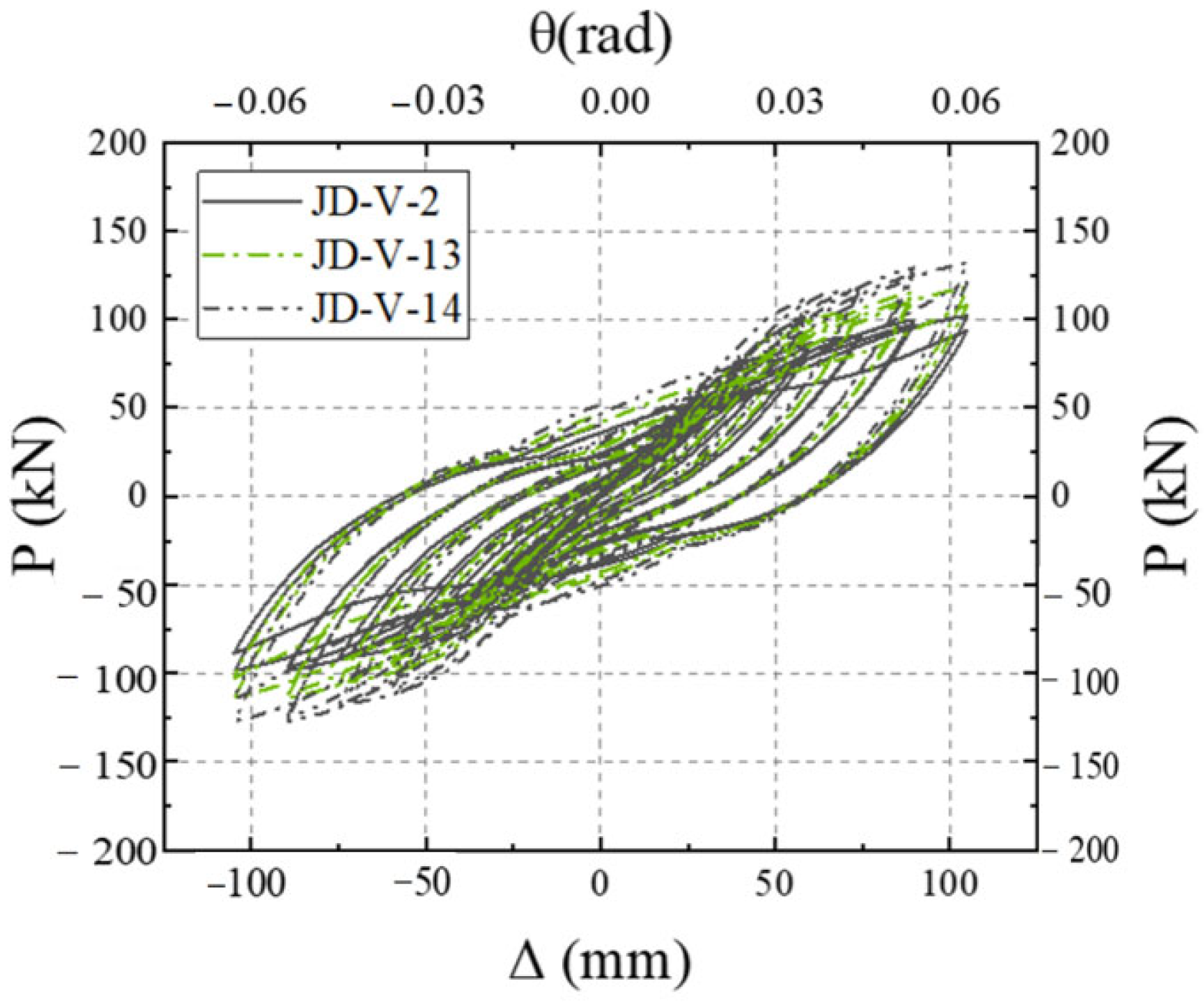
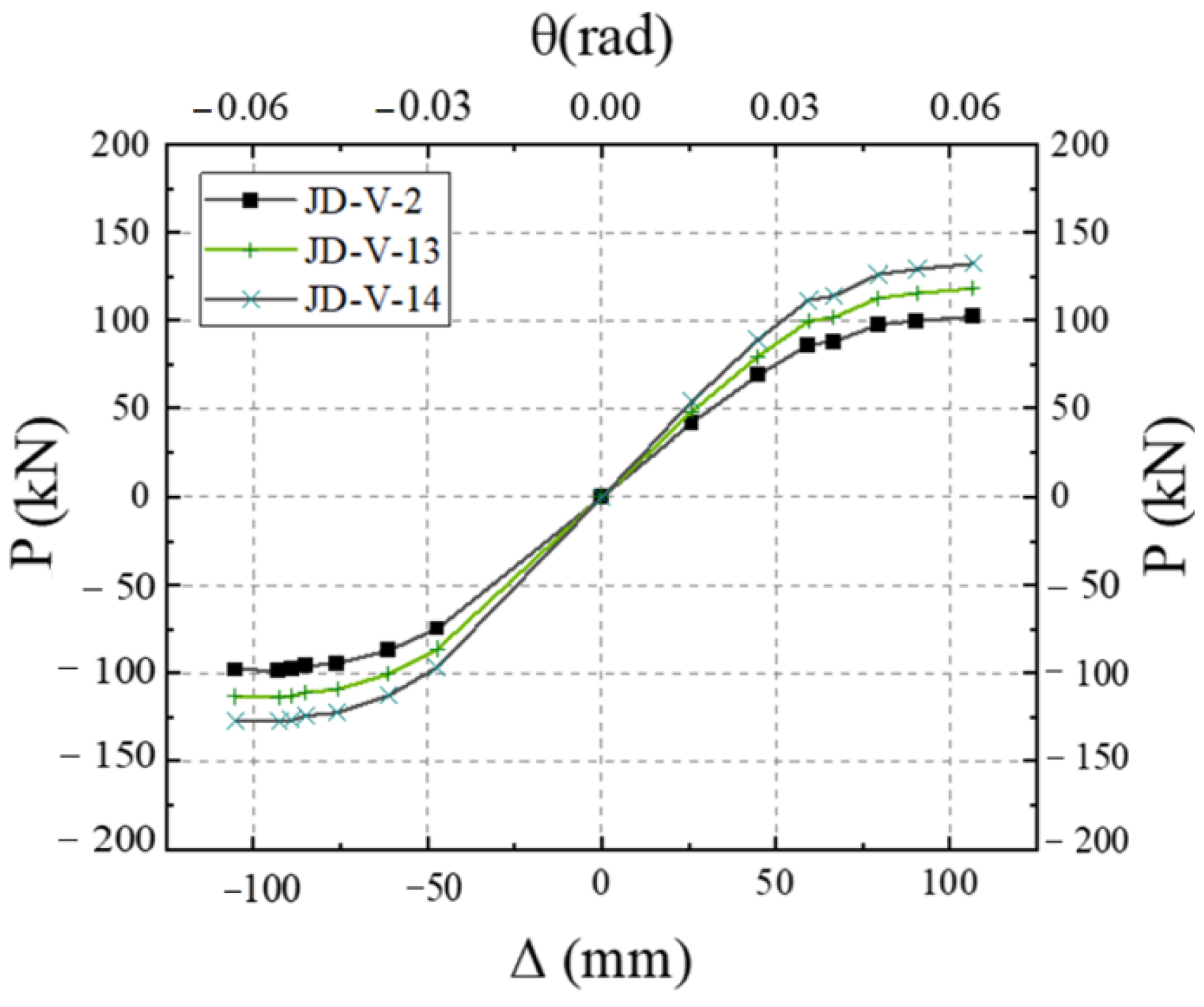
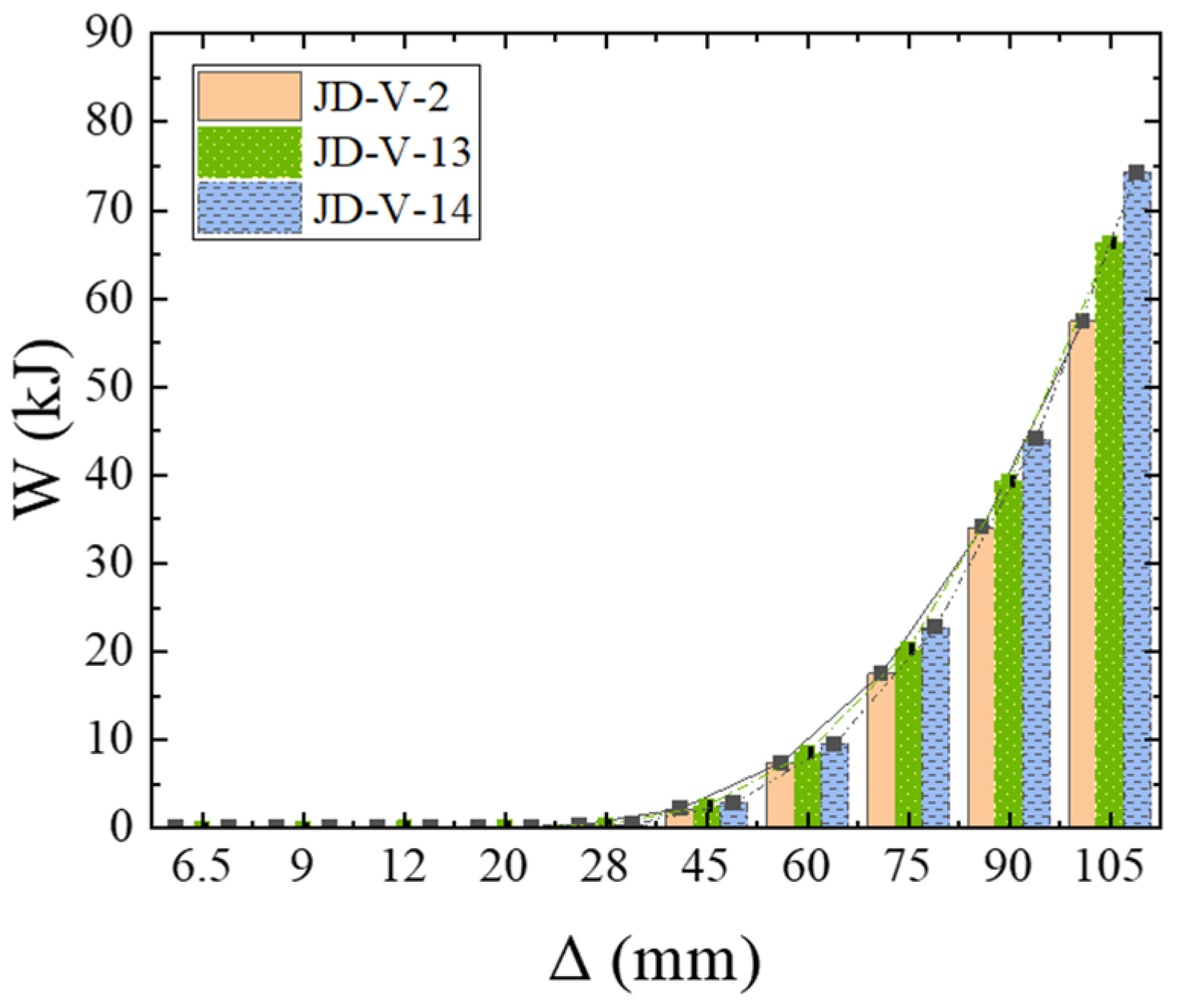

| Serial Number | Steel Tube Dimensions | Steel Beam Dimensions | Web Joint Types | V-Shaped Piece Thickness | Strength of V-Shaped Steel Connectors | Reduced Section Dimensions of Dog-Bone Connections | Thickness of Dog-Bone Reduced Connections | Strength of Dog-Bone Reduced Connections |
|---|---|---|---|---|---|---|---|---|
| JD-V-1 | 250×250×8 | 300 × 150 × 6.5 × 9 | Standard connection | 2 | LY160 | 25 | 8 | LY160 |
| JD-V-2 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 25 | 8 | LY160 |
| JD-V-3 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 3 | LY160 | 25 | 8 | LY160 |
| JD-V-4 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 4 | LY160 | 25 | 8 | LY160 |
| JD-V-5 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 5 | LY160 | 25 | 8 | LY160 |
| JD-V-6 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | Q235 | 25 | 8 | LY160 |
| JD-V-7 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | Q355 | 25 | 8 | LY160 |
| JD-V-8 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 15 | 8 | LY160 |
| JD-V-9 | 250×250×8 | 300 × 50 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 20 | 8 | LY160 |
| JD-V-10 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 25 | 6 | LY160 |
| JD-V-11 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 25 | 10 | LY160 |
| JD-V-12 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 25 | 12 | LY160 |
| JD-V-13 | 250×250×8 | 300 × 150 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 25 | 8 | Q235 |
| JD-V-14 | 250×250×8 | 300 × 50 × 6.5 × 9 | V-shaped steel connector | 2 | LY160 | 25 | 8 | Q355 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Hou, Y.; Wang, Y. Finite Element Analysis of the Mechanical Performance of an Innovative Beam-Column Joint Incorporating V-Shaped Steel as a Replaceable Energy-Dissipating Component. Buildings 2025, 15, 2513. https://doi.org/10.3390/buildings15142513
Zhang L, Hou Y, Wang Y. Finite Element Analysis of the Mechanical Performance of an Innovative Beam-Column Joint Incorporating V-Shaped Steel as a Replaceable Energy-Dissipating Component. Buildings. 2025; 15(14):2513. https://doi.org/10.3390/buildings15142513
Chicago/Turabian StyleZhang, Lin, Yiru Hou, and Yi Wang. 2025. "Finite Element Analysis of the Mechanical Performance of an Innovative Beam-Column Joint Incorporating V-Shaped Steel as a Replaceable Energy-Dissipating Component" Buildings 15, no. 14: 2513. https://doi.org/10.3390/buildings15142513
APA StyleZhang, L., Hou, Y., & Wang, Y. (2025). Finite Element Analysis of the Mechanical Performance of an Innovative Beam-Column Joint Incorporating V-Shaped Steel as a Replaceable Energy-Dissipating Component. Buildings, 15(14), 2513. https://doi.org/10.3390/buildings15142513





