Abstract
To address the issue of structural tilting caused by uneven foundation settlement in soft soil areas, this study combined a specific engineering case to conduct numerical simulations of the rectification process for an inclined reinforced concrete building using ABAQUS finite element software. Micropile-raft combined jacking technology was employed, applying staged jacking forces (2400 kN for Axis A, 2200 kN for Axis B, and 1700 kN for Axis C) with precise control through 20 incremental steps. The results demonstrate that this technology effectively halted structural tilting, reducing the maximum inclination rate from 0.51% to 0.05%, significantly below the standard limit. Post-rectification, the peak structural stress decreased by 42%, and displacements were markedly reduced. However, the jacking process led to a notable increase in the column axial forces and directional changes in beam bending moments, reflecting the dynamic redistribution of internal forces. The study confirms that micropile-raft combined jacking technology offers both controllability and safety, while optimized counterforce pile layouts enhance the long-term stability of the rectification system. Based on stress and displacement cloud analysis, a monitoring scheme is proposed, forming an integrated “rectification-monitoring-reinforcement” solution, which provides a technical framework for building rectification in soft soil regions.
1. Introduction
The uneven settlement of foundations is a primary cause of building inclination, which is particularly prominent in areas with soft soil layers or high groundwater levels. Such uneven settlement can lead to significant structural inclination, impairing both structural integrity and functional usability. The consequences of building inclination are not limited to the structure itself, but also include: (1) uneven stress distribution, which increases the risk of collapse, and (2) the impairment of spatial functions, which disrupts human activities. Therefore, building rectification is a crucial intervention measure aimed at achieving multiple objectives: ensuring structural safety, maintaining usability, extending service life, meeting regulatory requirements, and preserving social stability [1,2,3,4,5].
Existing studies on uneven settlement and building rectification have explored various scenarios and technical approaches. Numerical simulation has become a core tool for analyzing foundation–soil interactions: Hakro et al. [6] used Plaxis 2D software to study piled raft foundations on multi-layered soils, finding that embedding piles into stiffer underlying soils could significantly reduce settlement. Parameters such as pile length-to-diameter ratio (L/d), spacing-to-diameter ratio (s/d), and raft-soil stiffness ratio (Krs) have a significant impact on settlement behavior. They also simulated the swelling characteristics of expansive soils by applying positive volumetric strain, emphasizing the need for structural measures to resist bending moments caused by heaving. For deep foundation pit construction, Huang et al. [7] established a three-dimensional finite element model using MIDAS/GTS NX to evaluate its impact on adjacent elevated structures. The results showed that the maximum horizontal and vertical displacements of the bridge foundation were within the safety limits (2.98 mm and −1.75 mm, respectively), and the change in bending moment (6.3%) was more significant than that in axial force, verifying the rationality of the supporting measures.
Field studies have also provided practical insights into rectification and treatment technologies for soft soil foundation-based structures. Khomyakov et al. [8] addressed the issue of uneven settlement in a nine-story building constructed on loess-like collapsible soil in Kazakhstan. They restored the building’s verticality through measures such as anti-seepage grouting curtains, partial soil softening, and bored pile reinforcement, emphasizing the importance of surface drainage and long-term monitoring. In mining area scenarios, Jiao et al. [9] compared the static and dynamic responses of frame structures and frame-shear wall structures under continuous and stepped uneven settlements. The findings revealed that frame-shear wall structures performed better under stepped settlements, while the impact of mining-induced earthquakes below a magnitude of 3.0 on adjacent buildings was negligible. Shang et al. [10] highlighted the significance of soil–structure interaction (SSI) in seismic response analysis, noting that SSI amplifies the inter-story drift angle, plastic hinge ratio, and torsion angle of structures with uneven settlements, whereas rigid foundation models may underestimate the degree of damage. Kamash et al. [11] investigated the load transfer mechanism of micropiles by modeling and analyzing 16 hypothetical cases of using micropiles to rehabilitate inclined foundations in soft clay. The results indicated that the most critical factor in controlling the settlement of inclined foundations was solely the micropiles located on the inclined side, with no significant requirements for ultra-long micropiles.
Hossein et al. [12] studied the use of jack technology to correct the inclination of reinforced concrete buildings (4 to 8 floors) and carried out a numerical simulation by the finite element method to optimize the correction process. The reasonable layout of the jack is very important. The jack needs to be accurately positioned below the axis of the column or load-bearing element, and is applied by applying force to achieve equal displacement or uneven settlement on both sides of the foundation to an acceptable level. Gromysz et al. [13] proposed a method to determine the deflection and elevation of the building according to the type of building based on the analysis of the rectification process of the uneven elevation of the building utilizing jacks. Krzysztof et al. [14] carried out field tests on the installation of temporary supports on the load-bearing walls of buildings, corrected the building posture by the uneven lifting of the supports, and used this support to make the building reach the required vertical position. Shan et al. [15] proposed a lifting rectification method that combined the cake-cutting method with stress release trench excavation and adopted the three-dimensional numerical simulation of soil settlement, vertical displacement, and internal force to ensure the safety of the building during the rectification process. Chen et al. [3] established a complex model through ABAQUS finite element software to analyze the influence of uneven settlement on the structural mode and stress field and compared and evaluated different treatment methods of the failure column (BC) and lifting column (LC) to determine the optimal scheme and reduce the damage and interference to the building. Four lifting correction methods were proposed and compared: simultaneously broken columns, chessboard broken columns, simultaneous lifting columns, and lifting columns.
Fan et al. [16] proposed a comprehensive correction and reinforcement method of “rapid settlement of micropiles, manual excavation of piles to stop settlement reinforcement, forced landing and correction of soil excavation, and pressure to promote settlement by stacking”, and at the same time carried out micropile model tests and FLAC3D numerical simulations to study the influence of pile diameter and pile length on bearing capacity, to provide theoretical support for the design of micropiles. Taking a project in Lanzhou as an example, Gu et al. [17] designed an iterative rectification scheme of inverted L-shaped beams and limits. The feasibility of the scheme was verified by experiment and numerical simulation. In [18], the raft equilibrium system was established based on the Mindlin solution. The constitutive model of the elastic-plastic pile–soil interface and the simulation method of soil excavation, jack lifting, and sac grouting were proposed. The numerical model was developed to study the parameters. Wang et al. [19] integrated air-space-ground multi-source sensing technology to build a millimeter-level dynamic monitoring system for the fragmentation of building correction monitoring technology. The ground LiDAR, GNSS, and hydrostatic leveling sensor network were innovatively integrated, and the three-dimensional deformation holographic analysis of buildings was realized through the abnormal data cleaning algorithm and the multi-period point cloud registration model. The Kalman filter dynamic prediction model was developed, and the ‘perception-prediction-regulation’ intelligent closed-loop system was constructed by combining the finite element reverse analysis, which successfully guided the dynamic optimization of jacking parameters and provided high-precision decision support for complex building correction. Li et al. [20] proposed a column lifting rectification scheme for the uneven settlement of a primary school steel structure building. Through ABAQUS fine modeling analysis, it was found that the uneven settlement significantly changed the dynamic characteristics of the structure and increased the yield risk of the joints. Compared with the method of ‘breaking one by one‘ and the method of breaking the column at the same time, the former had less stress disturbance and the segmented jacking process was slightly better than the proportional jacking in terms of energy dissipation, which verified the effectiveness and safety of the technology for the rectification of shallow foundation buildings.
Despite the significant progress made in existing research on building rectification technologies, certain limitations remain. Traditional local jacking methods often only achieve short-term inclination correction, with insufficient research on secondary settlements caused by soil consolidation and compression after jacking, making it difficult to ensure the long-term balance of structures. Additionally, most existing numerical simulations have focused on static settlement or seismic response, rarely addressing the dynamic redistribution of structural internal forces during the jacking process (such as sudden increases in the column axial force and reverse bending moment of beams), which may underestimate the risk of local overload. Meanwhile, there is limited research on combining micropiles with raft foundations to enhance the stability of reaction forces, and monitoring schemes for high-stress areas (e.g., column-raft joints) still need improvement.
This study targets the inclination problem of buildings in soft soil areas caused by uneven settlement as well as the shortcomings of existing technologies in the long-term stability and dynamic control of internal forces. It aims to provide optimal reaction forces for the jacking system by reasonably arranging piles, raft foundations, and auxiliary structures. As shown in Figure 1, the underground piles were specifically designed for building deviation correction. Through the micropile-raft combined jacking technology, integrating finite element analysis using ABAQUS 2021 with engineering practice, this study intended to address the hidden danger of secondary settlement in traditional methods, reveal the law of structural internal force redistribution during the jacking process, and provide a safe and controllable technical path for rectifying building inclination in soft soil areas. The research results not only offer a reusable technical template for correcting building inclination in soft soil areas, but also fill the gaps in existing research regarding dynamic internal force analysis and the application of collaborative systems, thus possessing significant theoretical and engineering value.

Figure 1.
Underground piles for building rectification and jacking operation. (a) Early stage of pile pressing; (b) Mid-pressure pile; (c) Later stage of pile pressing.
2. Analysis Program
This research employed a case study approach to investigate subsurface soil characteristics through comprehensive field investigation data analysis. By integrating the building’s measured tilt parameters, we developed an innovative rectification methodology utilizing micropile-raft composite systems. The study implemented ABAQUS finite element analysis to construct a high-fidelity numerical model that accurately replicated the structural behavior during staged jacking operations, with a particular emphasis on raft-micropile–soil interaction dynamics (see Figure 2 for analytical workflow). The platform’s advanced post-processing capabilities enabled multidimensional visualization of critical performance indicators, including stress distribution patterns, strain evolution, and displacement profiles, thereby facilitating the data-driven optimization of both the structural reinforcement and rectification strategies to enhance construction safety and operational reliability.
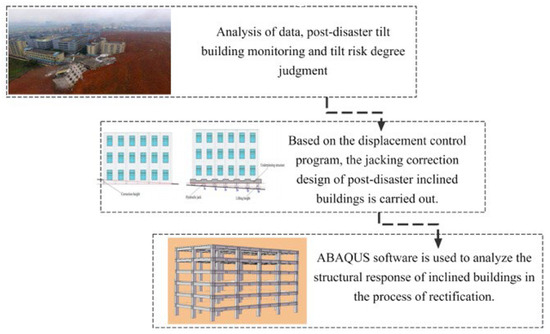
Figure 2.
Analysis program.
2.1. Subsurface Characteristics
This study obtained subsurface data through comprehensive geotechnical investigations conducted in a residential area of Gaoling County, Shaanxi Province, China including borehole drilling, in situ testing, and laboratory geotechnical tests. Analysis revealed that the building inclination in this area primarily results from the following factors: ① non-self-weight collapsible loess layers with varying thicknesses; ② phreatic pore water with a high groundwater table; and ③ sand lenses intercalated within clay layers. As shown in Table 1, systematic geotechnical parameter testing was employed to characterize the encountered strata.

Table 1.
Geotechnical mechanical properties of landslide.
This study employed the Mohr–Coulomb criterion to simulate the mechanical behavior of loess-like soil, silty clay, and coarse sand. As an ideal elastoplastic model, its parameters can be directly obtained from the geotechnical tests in Table 1 and are widely used in geotechnical engineering simulations. However, compared with advanced models such as the hardening soil (HS) model, the Mohr–Coulomb criterion has certain limitations. In terms of strain hardening/softening, the HS model can reflect the change in soil stiffness with confining pressure and plastic strain, making it suitable for simulating the gradual stiffness change of silty clay (layers ③ and ④) during loading). In contrast, the Mohr–Coulomb criterion assumes constant stiffness, which may underestimate the stiffness degradation of soft soil under large jacking forces. Regarding volume characteristics, the HS model can simulate the collapsible volume strain of loess-like soil (layers ① and ②) through volume hardening, while the Mohr–Coulomb criterion ignores this, potentially leading to deviations in settlement calculations. In terms of anisotropy, the HS model (e.g., HS-small) can capture the structural anisotropy of coarse sand (layer ⑤), whereas the Mohr–Coulomb criterion assumes soil isotropy and cannot reflect this property. Nevertheless, the choice of the Mohr–Coulomb criterion in this study is reasonable. Since the research focused on the macroscopic structural responses (stress, displacement) during the jacking process, this criterion can meet the simulation requirements for the overall trend of soil–structure interaction. Moreover, the geotechnical test data in Table 1 provide sufficient parameters to ensure the reliability of the simulation within the research scope. Additionally, its high computational efficiency supports the iterative analysis of 20-level jacking steps.
The foundation bearing capacity was evaluated through a series of 14 static load tests employing the slow maintained load method. A reaction frame system provided the necessary counterforce during testing. The experimental setup utilized a 945 mm diameter loading plate positioned at the designed pile cap elevation. The loading protocol consisted of eight incremental stages (70 kPa per stage) up to a maximum pressure of 560 kPa. Each load increment was maintained for specified durations (10, 10, 10, 15, 15 min, respectively) with settlement measurements recorded at 30-minute intervals. The loading progression criterion required consecutive hourly settlement measurements below 0.1 mm before advancing to the next stage. As presented in Figure 3, the composite foundation testing demonstrated settlements ranging from 7.387 to 10.473 mm at maximum loading (560 kPa), corresponding to relative settlements of 0.0078–0.011, indicating that the system remained well below its ultimate limit state.
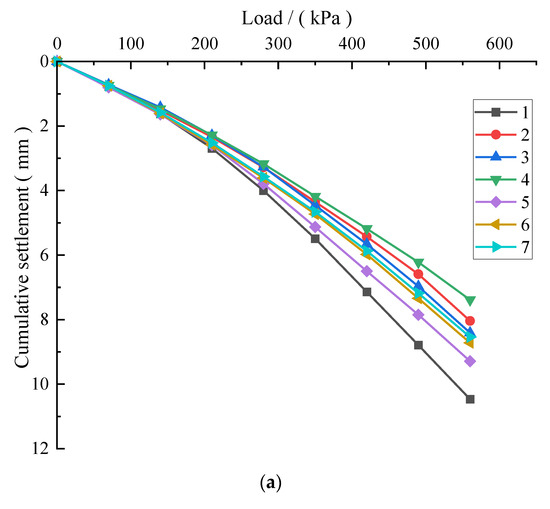
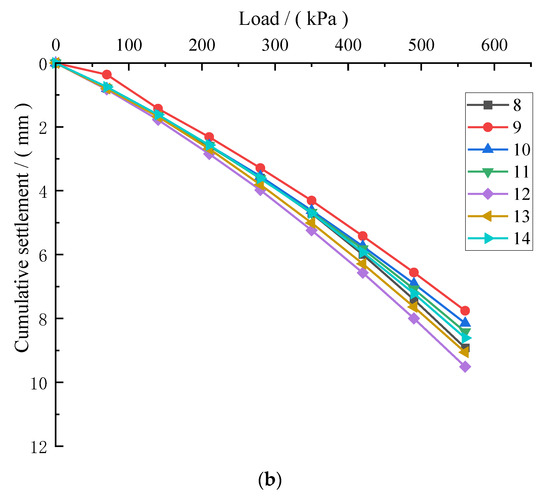
Figure 3.
Load-settlement curve. (a) Test point numbers 1–7 set of tests. (b) Test site numbers 8–14 set of tests.
Based on the monitoring work carried out in accordance with the dynamic monitoring plan, the variation curves of settlement and inclination monitoring were obtained (as shown in Figure 4 and Figure 5, respectively). The analysis showed that in the stage without construction intervention, the inclination trend of the building continued to intensify, with a relatively fast growth rate of the inclination ratio; at the same time, the building as a whole showed continuous subsidence. The monitoring data indicated that the maximum settlement of the building reached 90.14 mm, and the maximum inclination ratio reached 0.51%, both exceeding the allowable inclination range specified in the codes. A further exploration of the internal mechanism behind the above trend changes revealed that the coupling effect of high groundwater level and sand lenses will aggravate foundation deformation: sand lenses in a saturated state are prone to losing bearing capacity due to the accumulation of excess pore water pressure (EPP), which is consistent with the research conclusions of Asgari et al. [21]; meanwhile, the collapsibility coefficient of collapsible loess (ranging from 0.004 to 0.008 in Table 1) will further increase with the rise in pore water pressure under the infiltration of groundwater. The synergistic effect of the above two factors jointly leads to the acceleration of the uneven settlement rate.
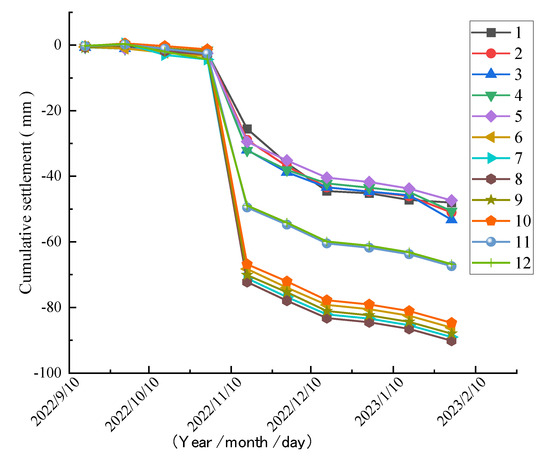
Figure 4.
Time-cumulative settlement variation curve.
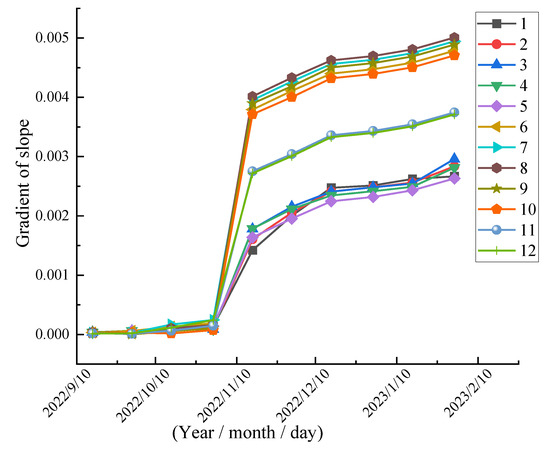
Figure 5.
Time-tilt rate curve.
2.2. Geometry and Structural Materials
In this study, a six-story reinforced concrete frame structure with a practical engineering background in Gaoling County was selected as the analysis model. The basic fortification intensity was 8 degrees (0.2 g). The seismic fortification category was Class B, and the site soil was Class IV. The building was based on a unified plane, and each layer was 3 m high. Figure 6 shows the plane view of the building. The overall size was 28.8 m × 14.4 m. There were 15 columns and 26 beams including 22 main beams. The beam number is shown in Figure 6. There were 12 settlement monitoring points. Columns were marked according to the intersection of two vertical axes such as A-1. Considering the size and load of the building, a raft foundation with a size of 29.8 m × 15.4 m and a depth of 1 m was designed. It is worth noting that the dimensions of the structural elements varied on different floors, as shown in Table 2.
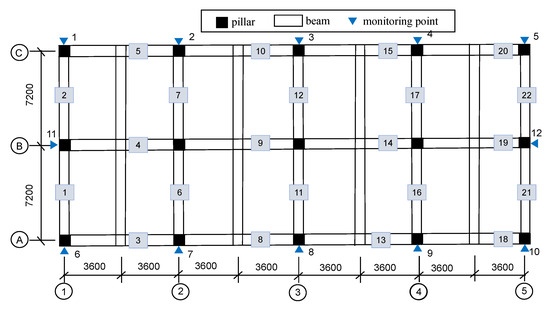
Figure 6.
Building plan view.

Table 2.
Component size of different floor structures.
According to the difference of the cross-sectional dimensions of columns in different floors in Table 2, a multi-scale jacking force distribution model was established including a double objective function. The displacement uniformity index and structural safety constraint expression are shown in Formula (1) and Formula (2), respectively:
Among them, n is the number of monitoring columns, di is the vertical displacement of column i, and is the average displacement.
Among them, is the compressive strength of concrete.
Through the double objective optimization of the displacement uniformity index and structural safety constraint , the floor weight coefficient wk was introduced to fuse the size difference of the components, and the SQP algorithm was used to solve the optimal jacking force Fj.
The jacking process involves exerting a progressively increasing force until it falls within the acceptable range specified by relevant standards. Its objective is to realize uniform vertical displacement on both sides of the foundation, thereby effectively rectifying uneven settlement. During the rectification stage, the building’s structural components must be capable of withstanding the force exerted by the balance adjustment device without cracking or sustaining damage.
The axial bearing capacity of columns in a six-story building was calculated using the Bressler method [22], a widely acknowledged approach for estimating compressive strength and bearing capacity. The computed axial bearing capacity of these columns is 1019 kN. Furthermore, Figure 7 illustrates the calculated bending capacity of the main beam on the first floor. By integrating the axial load capacity of columns and the bending capacity of beams, structural components can be evaluated to ensure that they can endure the loads and moments imposed during the jacking correction process without jeopardizing safety or structural integrity.
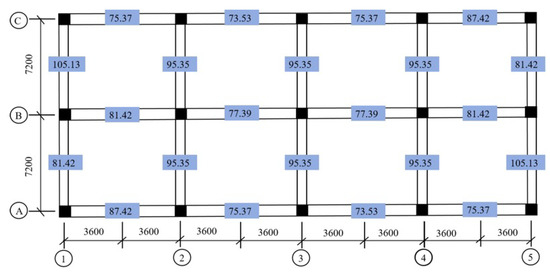
Figure 7.
Bending capacities (kN·m) of the main girders on the first floor of a six-story building.
It is worth noting that Mroueh and Shahrour [23] highlighted the significance of incorporating the self-weight of structural elements when accurately assessing the internal forces borne by columns and beams. This consideration enables a more realistic and rigorous evaluation of structural components.
2.3. Model Establishment
2.3.1. Jacking Correction Design
The strategic installation of micropiles, raft foundations, or supplementary structural components generates essential reaction forces for the stabilization system. As illustrated in Figure 8, each balancing unit was precisely aligned beneath the column centerlines, serving dual functions: (1) arresting structural tilt prior to lifting operations, and (2) mitigating potential future displacements, thereby ensuring enhanced process stability. The integrated raft foundation system facilitates comprehensive settlement monitoring through real-time displacement profiling at the column–foundation interfaces, while simultaneously redistributing loads to improve the overall bearing capacity and reduce differential settlement. Construction protocols employ optimized drilling parameters and phased installation sequences to control induced displacements, maintaining a critical 300 mm operational gap between the existing foundations and new pile heads for device integration. Through iterative computational analysis, the optimal jacking force distribution was determined for each stabilization unit, ensuring controlled structural realignment.
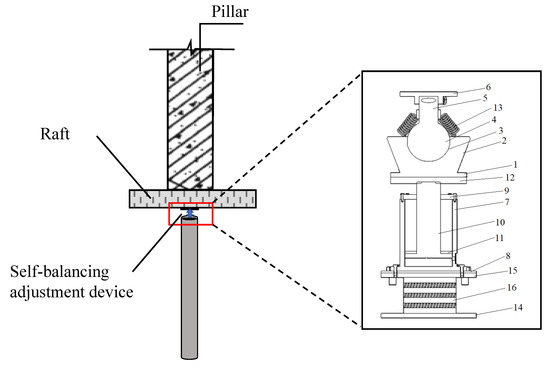
Figure 8.
Jacking correction design profile.
The grading jacking of the micropile-raft combined jacking technology was optimized, and the jacking force of each stage was distributed according to the initial settlement ratio of the A, B, and C axes (1.7:1.3:1) to achieve a synchronous correction rate. After each step of loading, the key indicators were controlled by real-time monitoring including the displacement deviation of the column top measured by the total station ≤ 0.2 mm, the rebound of the pile to p ≤ 0.5 mm (to avoid soil disturbance), and the stress increment ≤ 0.3 MPa/step; at the same time, the dynamic adjustment algorithm was adopted. When the displacement of a certain shaft lagged by 5%, the next-stage jacking force increased by 8%, and finally the deviation was ensured to be less than 0.3 mm.
When the building is inclined, the spherical adjustment mechanism buffers and supports the inclination angle by adjusting the support angle and further controls the rise of the hydraulic lifting mechanism to form a settlement gap to supplement the support and delay the building inclination process. By adding rubber isolation bearings to further achieve buffering, emergency support is realized when the building is inclined, and the response speed is fast. Intelligent control can be realized by connecting intelligent monitoring systems. When a disaster causes building damage, delay or avoid building collapse. The self-balancing adjustment device in the diagram: 1—first floor, 2—connection block, 3—spherical groove, 4—support ball, 5—support block, 6—first roof, 7—lift cylinder, 8—s floor, 9—cylinder head, 10—piston rod, 11—piston, 12—s roof, 13—connection spring, 14—third floor, 15—third roof, 16—multilayer rubber isolation pad.
2.3.2. Lifting Model Establishment
To accurately simulate the structural rectification system, reaction piles were incorporated into the finite element model to provide counteracting forces. The pile bearing capacity was determined through the numerical simulation of static load tests, consistent with established methodologies [24], yielding a design capacity of 3630 kN. This capacity ensures simultaneous resistance to both structural column loads and balancing device reactions. As depicted in Figure 9, the model incorporated the actual material properties and reinforcement details from structural drawings for the beams and columns. The uneven settlement simulation protocol applies vertical displacements to settled columns while constraining: (1) unsupported column bases, and (2) raft foundation movements in the x–y directions, effectively replicating time-dependent superstructure responses to differential settlement.

Figure 9.
Establishment of the building finite element model.
The numerical simulation was conducted using an explicit dynamic analysis step with a time step of 2 × 10−6 s to ensure computational accuracy and stability. The dynamic redistribution of structural internal forces was achieved through iterative optimization of the pile–soil contact friction coefficient. The initial friction coefficient was set to 0.3, and the iteration terminated when a convergence tolerance of 5% was reached. Through parameter optimization, the friction coefficient was determined to range between 0.25 and 0.35. Additionally, a plastic strain threshold of 0.02 was defined for sandy soil in the model to judge its plastic deformation state. Based on the concrete damaged plasticity (CDP) model, the concrete damage factor was set to 0.85 to characterize the damage degree of concrete materials under stress, thereby more accurately simulating the pile–soil interaction and the mechanical responses of structural materials.
3. Results and Discussion
3.1. Raft Displacement Before and After Lifting Operation
Figure 10 presents the settlement characteristics and displacement fields at the column–foundation interfaces of the six-story structure, demonstrating the efficacy of micropile-raft integrated jacking technology for differential settlement mitigation. Post-intervention analysis revealed the following: (1) a homogenized raft displacement distribution, (2) maximum settlement reduction from −92.49 mm to −1.181 mm (98.7% improvement), and (3) a 42% decrease in structural peak stress (11.2 MPa to 6.5 MPa). These results validate the precision and safety of the implemented phased jacking protocol (20 loading increments, <5% deviation), confirming the system’s ability to restore structural integrity while minimizing stress concentrations.
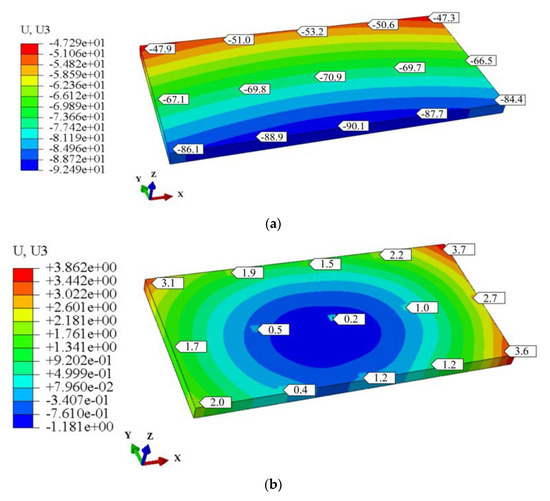
Figure 10.
Settlement profile and displacement value at the connection of column foundation of a 16-story building: (a) raft displacement before jacking operation; (b) raft displacement after jacking operation.
3.2. Position and Force of the Balance Adjustment Device
Figure 11 illustrates the stress distribution at the connection between the column of a six-story building and the raft foundation. The peak stress reached 4.705 MPa, gradually decreasing to 0.079 MPa along the connection surface toward the raft center, suggesting that stress concentration primarily occurs in the column foot region. When combined with the axial load distribution of the first-layer columns on the foundation shown in Figure 12 (with a maximum load of 918.1 kN), it is evident that the load on the A-axis column was significantly higher than that on the B and C axes. This finding aligns with the law observed in Table 3, where the A-axis required the highest total jacking force (2400 kN). This phenomenon highlights the direct correlation between load distribution and jacking force demand: the greater the settlement (A-axis: −90.1 mm), the higher the required jacking force, which validates the scientific rationality of the staged jacking strategy (120–85 kN per stage). Additionally, the high consistency between stress and load data (error < 5%) demonstrates that the finite element model could accurately predict the structural mechanical behavior during the jacking process, providing a reliable basis for optimizing the correction force.
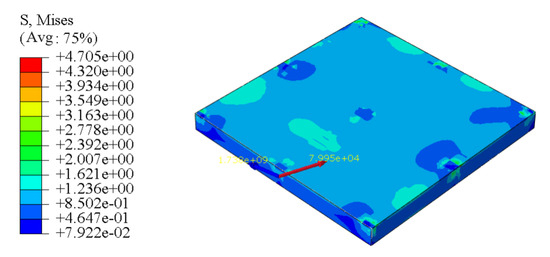
Figure 11.
6 Stress distribution at the column-raft connection in a 126-story building.
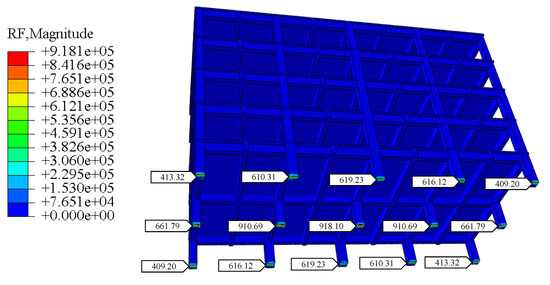
Figure 12.
Axial loads (in kN) imposed on the foundation by the first-floor columns of a six-story building.

Table 3.
Lifting force required for the balance adjustment device.
3.3. Reaction Force Required in the Process of Pile Jacking Reaction Force
The pile employed in the jacking process constitutes an integral component of the foundation system and plays a critical role in transferring structural loads to stronger subsurface strata after rectifying the building’s inclination. Consequently, calculating the support reaction force required for the pile jacking procedure is of great significance. The jacking process is executed in 20 steps, with a specific force applied to the pile at each stage (Table 3). During jacking, as a given force is exerted on the balance adjustment device, the immediate settlement of the pile following the construction phase is reset to zero. Since the force required to rectify the C-axis is smaller than that for the A-axis and B-axis, the final settlement of piles in the A and B axes exceeds that of the C-axis pile. Due to the close matching of the forces required for each axis, the settlement of the reaction piles exhibits minimal variation across different axes.
The sum of the total force exerted by the balance adjustment device and the column force must not exceed the bearing capacity of the reaction pile, which is 3630 kN. As indicated in Table 3, for the inclination of the six-story building, the balance adjustment device applied forces of 2400 kN, 2200 kN, and 1700 kN to the A-axis, B-axis, and C-axis, respectively. Additionally, the columns subjected to the maximum axial force after jacking were columns A-5, B-1, and C-1. As illustrated in Figure 13, the axial forces of these columns increased from 1090.36 kN, 689.87 kN, and 1080.62 kN to 1231.14 kN, 980.52 kN, and 1248.44 kN, respectively. When the column axial force was combined with the required jacking force, the final forces borne by the reaction piles on the A, B, and C axes were 3321.69 kN, 3480.43 kN, and 2667.23 kN, respectively. Thus, the reaction piles were suitable for the jacking operation.
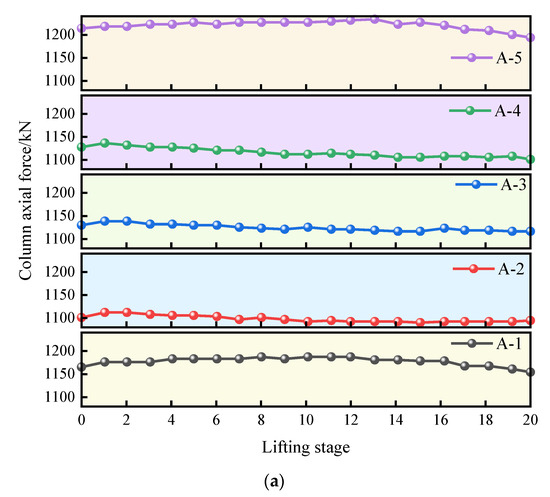
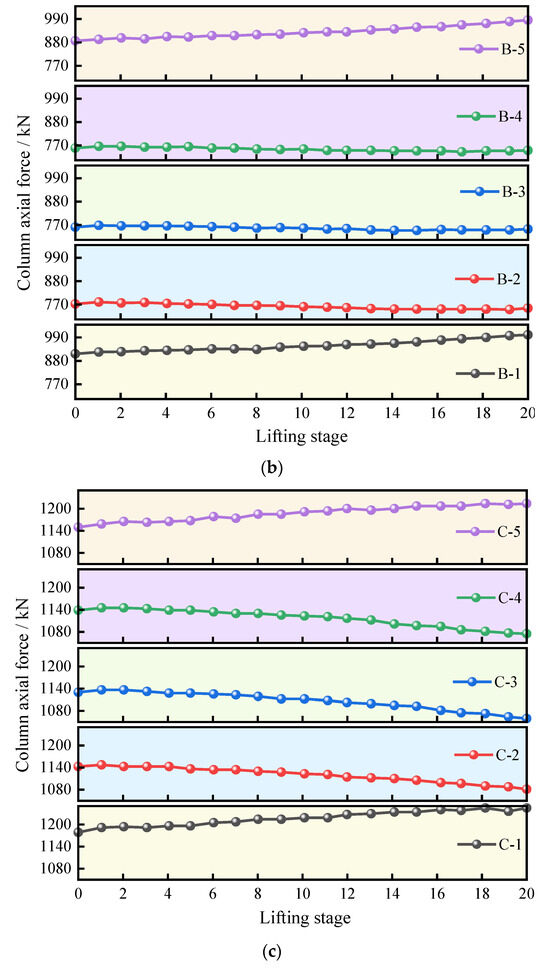
Figure 13.
Axial force variations in the first-floor structure of the six-story building: (a) axial force of columns along the A-axis; (b) axial force of columns along the B-axis; (c) axial force of columns along the C-axis.
In the floor plan of the building structure, settlement along the C-axis was the smallest, and the jacking force required for uplifting the building in this region was relatively low. However, the most significant change in column axial force was observed on this axis. Under the action of jacking, the force on each column generally increases, and this variation in axial force reflects the redistribution of internal forces during the jacking process. It is particularly important that the increase in axial force may bring additional load demand to the column, which in turn affects the bearing capacity and performance of the structure.
3.4. Influence on the Internal Force of Structural Members Before and After Jacking Up
Different vertical displacement loads were applied along the bottom of each column. The specific vertical displacement values are shown in Figure 10a to simulate the uneven settlement of the structure. The stress cloud map and displacement cloud map of the building are shown in Figure 14 and Figure 15, respectively.
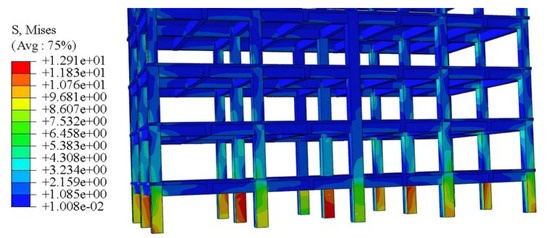
Figure 14.
The uneven settlement stress cloud diagram of the six-story building.
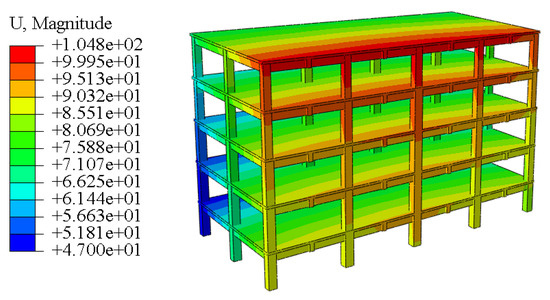
Figure 15.
The displacement program of uneven settlement of the building with six floors.
It can be seen in Figure 14 that the stress was mainly concentrated in the corner column where the settlement occurred and the node where the adjacent columns intersected with the beam. The maximum column foot stress reached 13 MPa, and the stress decreased with the increase in height. It can be seen from Figure 15 that the uneven settlement caused the building to have a large combined displacement on the side with the largest settlement, and the higher the height, the larger the combined displacement, and the maximum combined displacement was at the top of the building, reaching 105 mm. It can be seen that a small settlement will cause a large combined displacement at the top of the high-rise building.
In the simulation analysis of the jacking correction of inclined buildings, the stress cloud and displacement cloud after jacking are shown in Figure 16 and Figure 17, respectively, which revealed the key characteristics of structural response. In particular, at the A-1 column base of the first-floor building and the junction of the A-5 column top and the first-floor beam, the stress cloud diagram (Figure 16) showed the maximum stress concentration, where the maximum stress value reached 6.5 MPa. This stress value is crucial for evaluating the bearing capacity of the column during the jacking process.
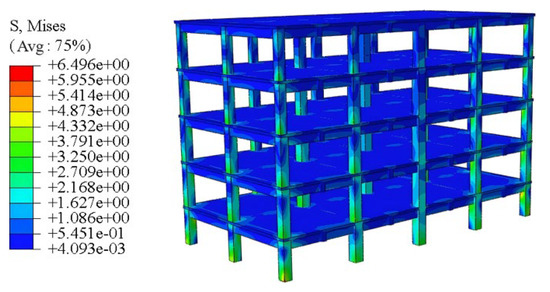
Figure 16.
The stress cloud diagram of the jacking correction of a six-story building.
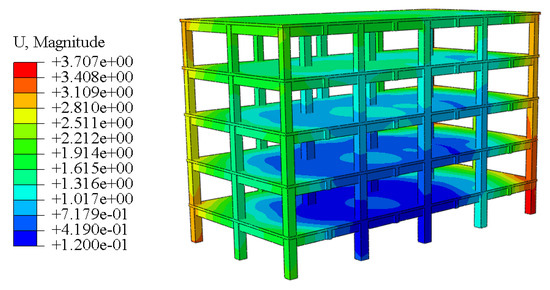
Figure 17.
Six-story building jacking correction displacement cloud diagram.
The displacement program is shown in Figure 17. The maximum combined displacement occurred at the column foot at the junction of the A-5 axis, and the combined displacement reached 3.7 mm. This displacement value indicates the significance of structural deformation in this area under the action of jacking. It is worth noting that there may be a risk of cracks or damage at the C-1 and A-5 column bases, and this observation underscores the need for focused attention and monitoring of the column during the jacking correction process.
Figure 18a–d illustrates the variations in the bending moments of the first-floor main beams within the six-story structure during the rectification process. Following the construction of reaction piles and the initiation of jacking operations, the negative bending moments of the beams exhibited a marked decreasing trend. Specifically, the bending moments of beams no. 2 and no. 21 were substantially reduced, with their direction even shifting from negative to positive. This phenomenon indicates a significant alteration in the stress state of these beams, accompanied by changes in the distribution patterns of their compression and tension zones. This further underscores the risk of structural damage in compression zones if appropriate flexural reinforcement is not provided. For beams spanning from axis 1 to axis 5, the bending moments decreased within the range of 7 kN·m to 15 kN·m. Among these, the beams with the highest percentage changes in bending moment were beam no. 1 on axis 1 and beam no. 22 on axis 5, with the percentage changes reaching 45.34% and 43.45%, respectively.
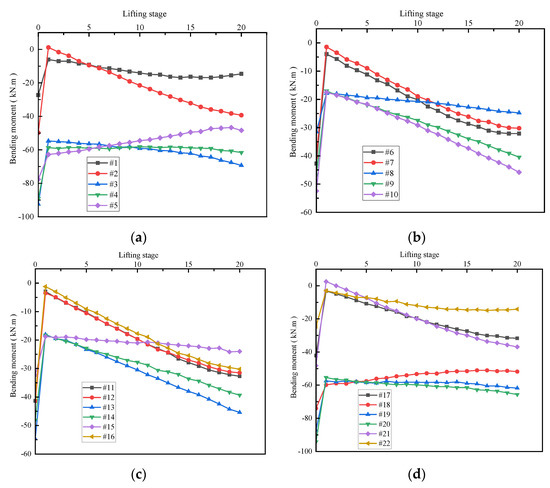
Figure 18.
The internal force change of the first-floor beam of the six-story building: (a) the bending moment change in the beams 1–5; (b) the bending moment change in beams 6–10; (c) the bending moment change in beams 11–16; (d) the bending moment change in beams 17–22.
During the construction phase of the reaction piles, the bending moments of beams 3, 4, 5, 18, 19, and 20 slightly exceeded the specified bending moment capacity presented in Figure 7. This observation suggests that both structural and non-structural components of the building may develop cracks during this construction stage. To ensure structural reliability, it is recommended that structural columns are reinforced with steel plates or fiber reinforced polymer (FRP) materials prior to commencing jacking operations. This reinforcement will enhance their load-bearing capacity and effectively prevent crack formation [25].
During the stepwise jacking construction with 20 incremental stages, the column axial force increment and beam bending moment reversal constitute a key safety monitoring index system: when the column axial force increment is maintained within 12.9% (Figure 13a), it indicates that the column structure still maintains a stable mechanical response under dynamic loads; meanwhile, if the beam bending moment reversal is controlled within the threshold of 15 kN·m (Figure 18a), it can be determined that the beam is in the elastic working stage, and the overall structural safety is guaranteed. It is worth noting that when the measured column axial force increment exceeds the 15% safety limit, the redistribution of structural internal forces has gone beyond the design expectations, and the bearing performance of the column will show a trend of nonlinear deterioration, which may further trigger the risk of structural instability, thus necessitating the adoption of effective reinforcement measures.
Due to differences in research methods and model selection, this study had several limitations in simulating the dynamics of micropile-raft–soil interaction during jacking operations such as deviations in soil behavior prediction caused by the simplification of constitutive models, the oversimplified simulation of interface interactions, insufficient capture of dynamic processes, and the lack of simulation for long-term stability. As noted in the research by Bagheri et al. [26], future studies will continue to improve in the following aspects: optimizing constitutive models (e.g., adopting the hardening soil model), refining the simulation of interfaces and dynamic loading, promoting the engineering application of 3D models, integrating long-term stability analysis with monitoring feedback, and expanding parametric and optimization tools.
4. Conclusions
In this paper, a comprehensive numerical simulation was conducted on the jacking process of a six-story inclined building. The key findings of this study are summarized as follows:
- (1)
- Through ABAQUS finite element simulation, the effectiveness of the combined jacking correction technology of micropile and raft foundation was verified. The reasonable arrangement of the pile-raft system can effectively terminate the structural inclination. Applying the jacking force of A-axis 2400 kN, B-axis 2200 kN, and C-axis 1700 kN in stages can gradually correct the inclination. The maximum correction displacement of the A-5-axis column foot was 3.7 mm, and no structural cracking or damage was caused, indicating that the method is both controllable and safe.
- (2)
- During the rectification process, the stress concentration phenomenon was significant, and the maximum stress at the junction of the first-floor A-1 column foot and the top beam of the A-5 column reached 6.5 MPa. The displacement distribution is highly dependent. The top displacement was 105 mm when the deviation was not corrected, and was significantly reduced to 3.7 mm after correction, indicating that high-rise buildings are extremely sensitive to foundation settlement. The displacement analysis of the raft foundation showed that the maximum asymmetric settlement before correction was 47 mm, and the maximum inclination rate was reduced from 0.51% to 0.05%, which is much lower than the allowable value (0.2%) of the specification. This provides a reusable technical template for building correction in soft soil areas. The design of the bearing capacity of 3630 kN is reasonable, which can balance the jacking force and structural load, minimize the settlement difference of each shaft pile, and verify the stability of pile–soil synergy.
- (3)
- Jacking up leads to a significant increase in the axial force of the column. For example, the axial force of the A-5 column increased by 12.9%. The bending moment of beam 2 changed from negative to positive, and the direction and amplitude of the bending moment of the beam changed, indicating that the dynamic redistribution of the internal force of the structure needs to be fully considered in the design stage to avoid the risk of local overload.
- (4)
- Based on the field geotechnical data, a refined finite element model was established, and a phased lifting force application method was proposed. The precise control of the correction process was realized through 20 incremental steps. The micropiles were innovatively combined with the raft foundation to optimize the arrangement of the reaction piles along the column axis, which significantly improved the long-term stability of the correction system. Based on the analysis of the stress cloud and displacement cloud, a real-time monitoring scheme for high-stress areas (such as column foot and beam-column joints) was proposed to form an integrated solution of correction-monitoring-reinforcement.
- (5)
- There is a significant correlation between the arrangement of the micropile-raft system and the long-term stability of the structure. The specific performance is as follows: the stiffness gradient design was adopted along the length direction of the building. The spacing of the A-axis micropiles was set to 2.5 m, and the C-axis was gradually changed to 3.0 m. By matching the settlement distribution characteristics of each axis (the A-axis settlement was large and required higher stiffness support), the long-term creep difference of the structure can be controlled within 0.5 mm/year.
Author Contributions
Conceptualization, L.Y. and M.X. (Ming Xie); Methodology, Z.W. and F.X.; Validation, F.X. and X.W.; Writing—original draft, L.Y. and X.W.; Writing—review and editing, M.X. (Mengqi Xu) and L.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Shen Zuyan Special Fund of the National Engineering Research Center for Prefabricated and Assembled Civil Structures (2023CPCCE-K05).
Data Availability Statement
All data generated or analyzed during this study are included in the published article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, X.; Shi, S.; Zhao, H.; Lu, M.; Li, X. Deformation analysis and reinforcement of Jin-gang tower in jacking method. World J. Eng. 2016, 13, 163–168. [Google Scholar] [CrossRef]
- Melnikov, R.; Pronozin, Y.; Stepanova, M.; Bartolomey, L. Soil areas numerical determination aimed at correction of a building tilt. J. Phys. Conf. Ser. 2021, 1928, 012009. [Google Scholar] [CrossRef]
- Chen, H.; Guo, Y.; Alqawzai, S.; Wu, X.; Alnas, S.M. Study on uneven settlement and correction of steel frame structures based on numerical simulation method. PLoS ONE 2024, 19, e0303249. [Google Scholar] [CrossRef] [PubMed]
- Gunay, B.; Hobson, B.W.; Darwazeh, D.; Bursill, J. Estimating energy savings from HVAC controls fault correction through inverse grey box model-based virtual metering. Energy Build. 2023, 282, 112806. [Google Scholar] [CrossRef]
- Stănculescu, I.; Antonescu, I.; Olteanu, A. Straightening of tall structures tilted as a consequence of uneven settlement of foundation soil: Case histories. In Geotechnical Engineering Education and Training; CRC Press: Boca Raton, FL, USA, 2020; pp. 447–454. [Google Scholar]
- Hakro, M.R.; Kumar, A.; Almani, Z.; Ali, M.; Aslam, F.; Fediuk, R.; Klyuev, S.; Klyuev, A.; Sabitov, L. Numerical Analysis of Piled-Raft Foundations on Multi-Layer Soil Considering Settlement and Swelling. Buildings 2022, 12, 356. [Google Scholar] [CrossRef]
- Huang, J.; Yan, J.; Guo, K.; Yang, X.; Peng, S.; Wu, C. Study on the Impact of Deep Foundation Pit Construction on Nearby Elevated Structures—Case Study. Buildings 2024, 14, 2541. [Google Scholar] [CrossRef]
- Khomyakov, V.A.; Shokbarov, Y.M.; Bryantsev, A.A. Experience in handling differential settlements of multi-storey buildings on soft soil. Soil Mech. Found. Eng. 2017, 54, 330–335. [Google Scholar] [CrossRef]
- Jiao, C.; You, S.; Ji, H. Numerical analysis of building structures response under effect of continuous and stepped non-uniform settlement. J. Cent. South Univ. 2023, 30, 4066–4081. [Google Scholar] [CrossRef]
- Shang, H.; Bao, C.; Wang, H.; Ma, X.; Calo, J.; Du, J. Seismic response analysis of frame structures with uneven settlement of foundation considering soil-structure interaction. Results Eng. 2023, 20, 101574. [Google Scholar] [CrossRef]
- El Kamash, W.; El Naggar, H. Improving tilted foundations over soft clay using micropiles: Numerical analysis. Geotech. Geol. Eng. 2023, 41, 2691–2712. [Google Scholar] [CrossRef]
- Soltani-Jigheh, H.; Ehterami, A.A. Numerical investigation of jacking method for asymmetric settlement rectification in tilted concrete buildings. Case Stud. Constr. Mater. 2024, 20, e02710. [Google Scholar] [CrossRef]
- Gromysz, K.; Smolana, M.; Drusa, M. Research on the Characteristics of Jacks Used to Rectify Tilted Buildings. Buildings 2024, 14, 1581. [Google Scholar] [CrossRef]
- Gromysz, K. In situ experimental study on the active support used for building rectification. Materials 2020, 13, 2015. [Google Scholar] [CrossRef] [PubMed]
- Shan, R.; Zhang, X.; Lu, M.; Zhao, H.; Li, X. Numerical Analysis Research of Jacking Method with the Rectification on Steel-Concrete Buildings. Open Civ. Eng. J. 2016, 10, 223–235. [Google Scholar] [CrossRef]
- Fan, J. Research and Engineering Application of Rectification and Reinforcement Technology for Existing High-Rise Buildings in Deep-Filled Loess Sites. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2021. [Google Scholar] [CrossRef]
- Gu, H. Research on The Application of New Rectification Method for Shallow Foundation Buildings in Collapsible Loess Areas. Master’s Thesis, Lanzhou University of Technology, Lanzhou, China, 2024. [Google Scholar] [CrossRef]
- Mi, C. Raft Foundation Rectification Process Mechanism and Simplified Calculation Method. Master’s Thesis, Tianjin University, Tianjin, China, 2021. [Google Scholar] [CrossRef]
- Wang, Q. Research on Deformation Monitoring of the Whole Process of Building Correction with Multi-Source Monitoring Technology. Master’s Thesis, Shandong Jianzhu University, Jinan, China, 2024. [Google Scholar] [CrossRef]
- Li, Y. Numerical Simulation of the Jacking Process of a Steel Structure under Uneven Settlement. Master’s Thesis, Shandong Jianzhu University, Jinan, China, 2023. [Google Scholar]
- Asgari, A.; Bagheri, M.; Hadizadeh, M. Advanced seismic analysis of soil-foundation-structure interaction for shallow and pile foundations in saturated and dry deposits: Insights from 3D parallel finite element modeling. Structures 2024, 69, 107503. [Google Scholar] [CrossRef]
- Bresler, B. Design criteria for reinforced columns under axial load and biaxial bending. J. Proc. 1960, 32, 481–490. [Google Scholar]
- Mroueh, H.; Shahrour, I. A full 3-D finite element analysis of tunneling–adjacent structures interaction. Comput. Geotech. 2003, 30, 245–253. [Google Scholar] [CrossRef]
- Butler, H.; Hoy, H. The Texas Quick Load Test Method for Foundation Load Testing—Users Manual; FHWA IP-77.8, FHWA Implementation Division: Washington, DC, USA, 1977. [Google Scholar]
- Wu, Y.-F.; Liu, T.; Oehlers, D.J. Fundamental principles that govern retrofitting of reinforced concrete columns by steel and FRP jacketing. Adv. Struct. Eng. 2006, 9, 507–533. [Google Scholar] [CrossRef]
- Bagheri, M.; Jamkhaneh, M.E.; Samali, B. Effect of seismic soil–pile–structure interaction on mid-and high-rise steel buildings resting on a group of pile foundations. Int. J. Geomech. 2018, 18, 04018103. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).