Intelligent Optimization Method for Rebar Cutting in Pump Stations Based on Genetic Algorithm and BIM
Abstract
1. Introduction
1.1. Intelligent Optimization of Rebar Cutting
1.2. BIM-Assisted Construction Technologies
2. Rebar-Cutting Optimization Model for Pump Station Based on an Improved Genetic Algorithm
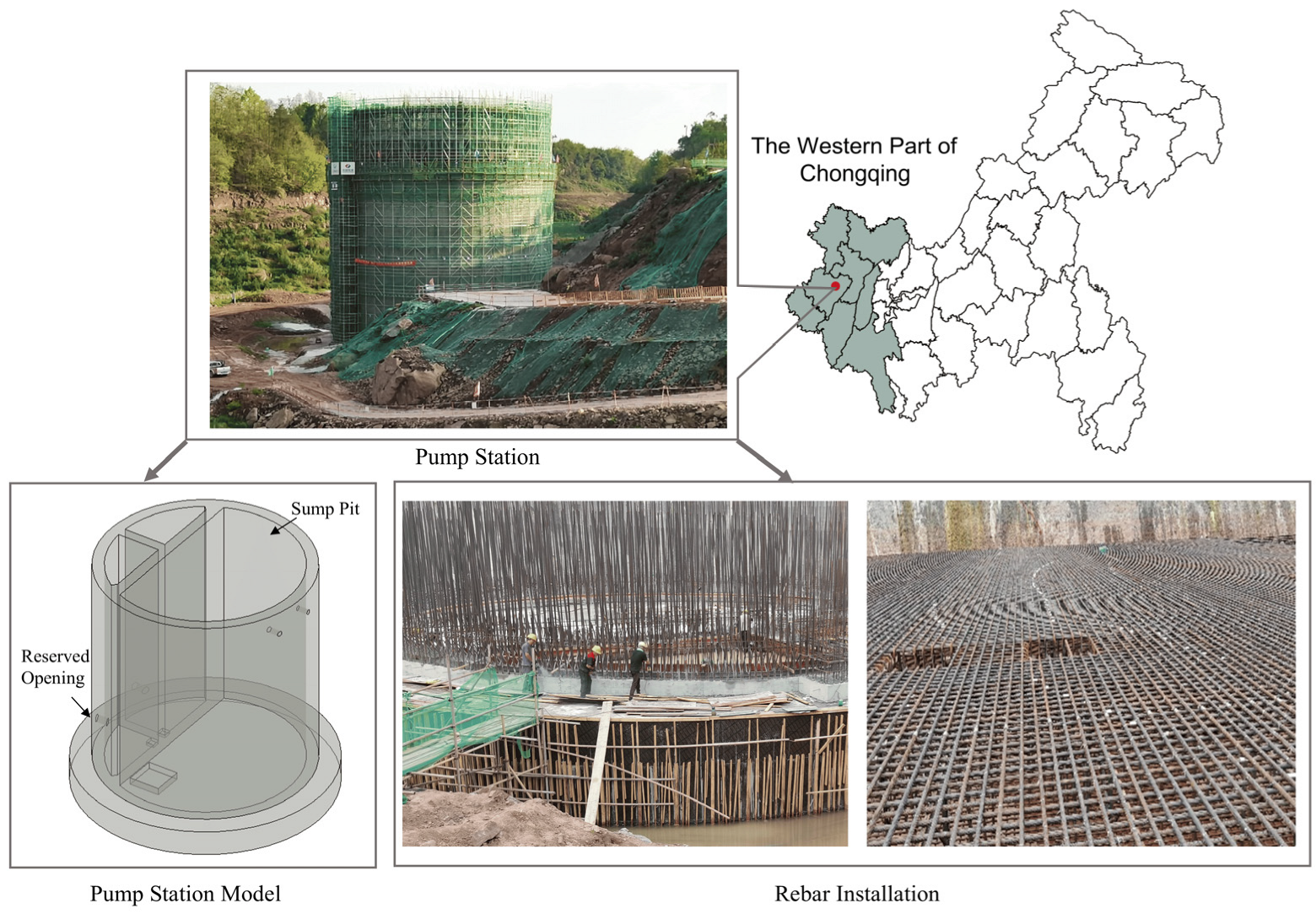
2.1. Rebar Detailing for the Pump Station
2.1.1. Pump Station Sidewall
2.1.2. Pump Station Bottom Slab
2.2. Improved Genetic Algorithm for the Cutting Stock Problem
2.2.1. Mathematical Model of the Cutting Stock Problem
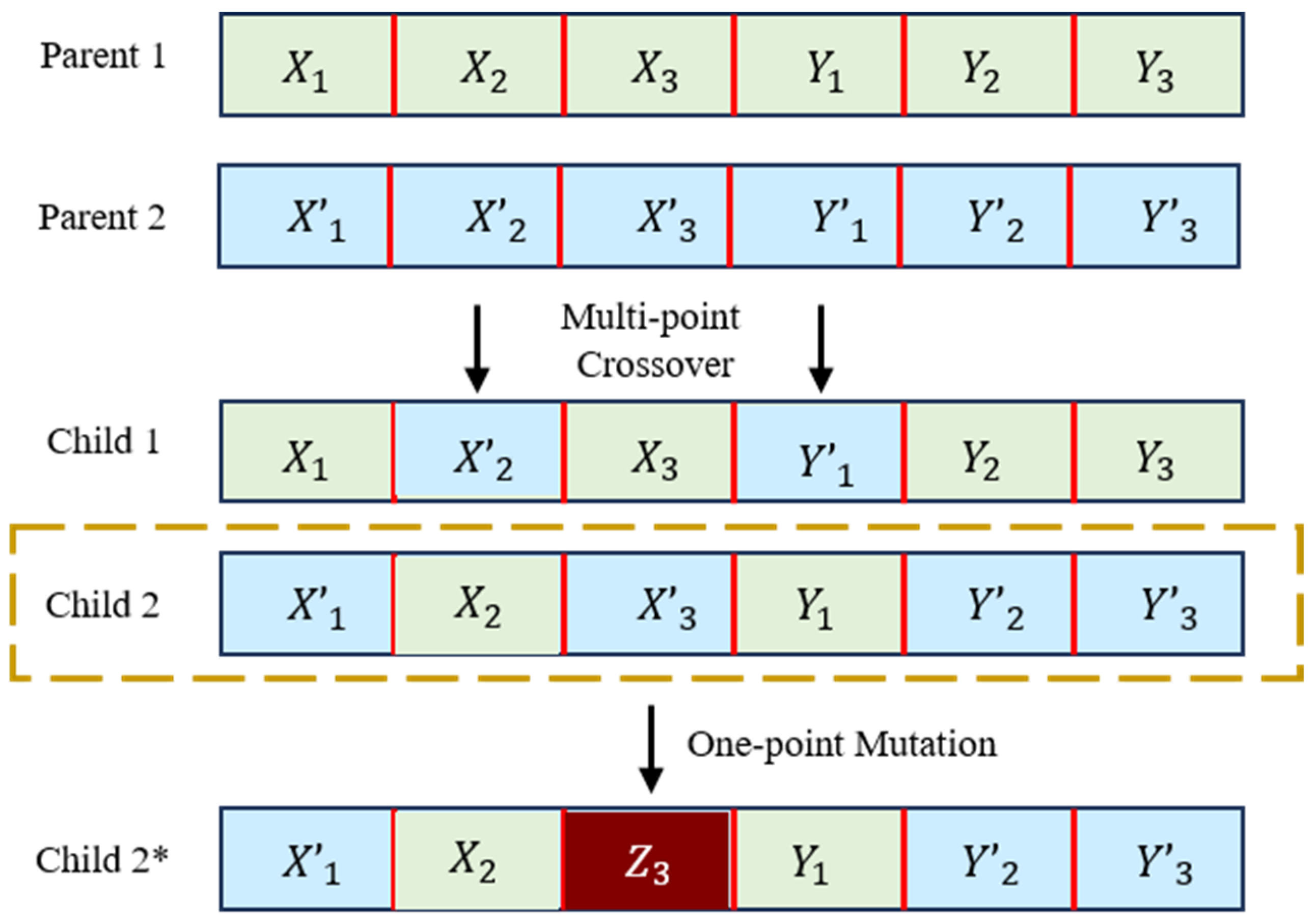
2.2.2. Genetic Algorithm Improvement
| Algorithm 1. Selection | |
| Input: | Population and corresponding fitness values |
| 1: | Calculate the total fitness of all individuals in the current population. |
| 2: | For each individual, compute its selection probability as its fitness divided by the total fitness; construct the basic roulette wheel accordingly. |
| 3: | For to population size, do: |
| 4: | Generate a random number uniformly in the interval . |
| 5: | Starting from the first individual, accumulate the selection probabilities until the sum exceeds . The individual at this point is selected. |
| 6: | End for |
| Output: | New population after selection. |
| Algorithm 2. Crossover | |
| Input: | Population and crossover probability |
| 1: | For to population size, perform crossover operations equal to the population size. |
| 2: | Randomly select two individuals to serve as parents. |
| 3: | Generate a random number and compare it with the crossover probability: - If crossover probability: skip crossover, return to step 1. - If crossover probability: continue with crossover. |
| 4: | Randomly generate two integers , and sort them so that . The interval is used as the crossover range. |
| 5: | Exchange the gene segments between the two parents within the range. |
| 6: | End for |
| Output: | Population after crossover. |
| Algorithm 3. Mutation | |
| Input: | Population and mutation probability |
| 1: | For to population size, perform mutation operations equal to the population size. |
| 2: | Randomly select one individual for mutation. |
| 3: | Generate a random number and compare it with the mutation probability: - If mutation probability: skip mutation, return to step 1. - If mutation probability: continue with mutation. |
| 4: | Randomly generate an integer , representing the gene position to be mutated. |
| 5: | Determine the maximum allowable value for this gene, then generate a random integer and replace the gene at position aaa with . |
| 6: | End for |
| Output: | Population after mutation. |
3. Development of Rebar Batch Generation and Query Components
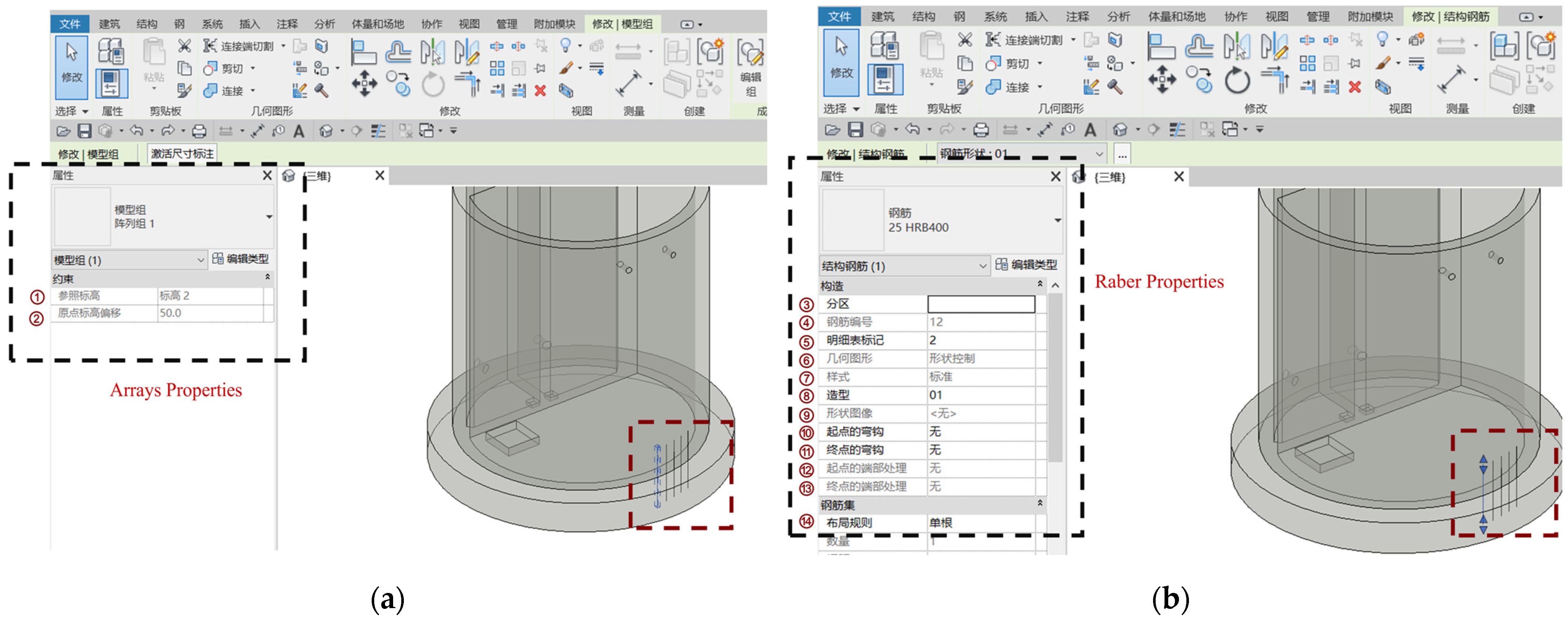
3.1. Rebar Batch Generation via Revit Secondary Development
- R.CFRS—Creation based on existing system rebar shapes;
- R.CFC—Creation based on custom curves;
- R.CFCAS—Creation based on rebar shape curves.
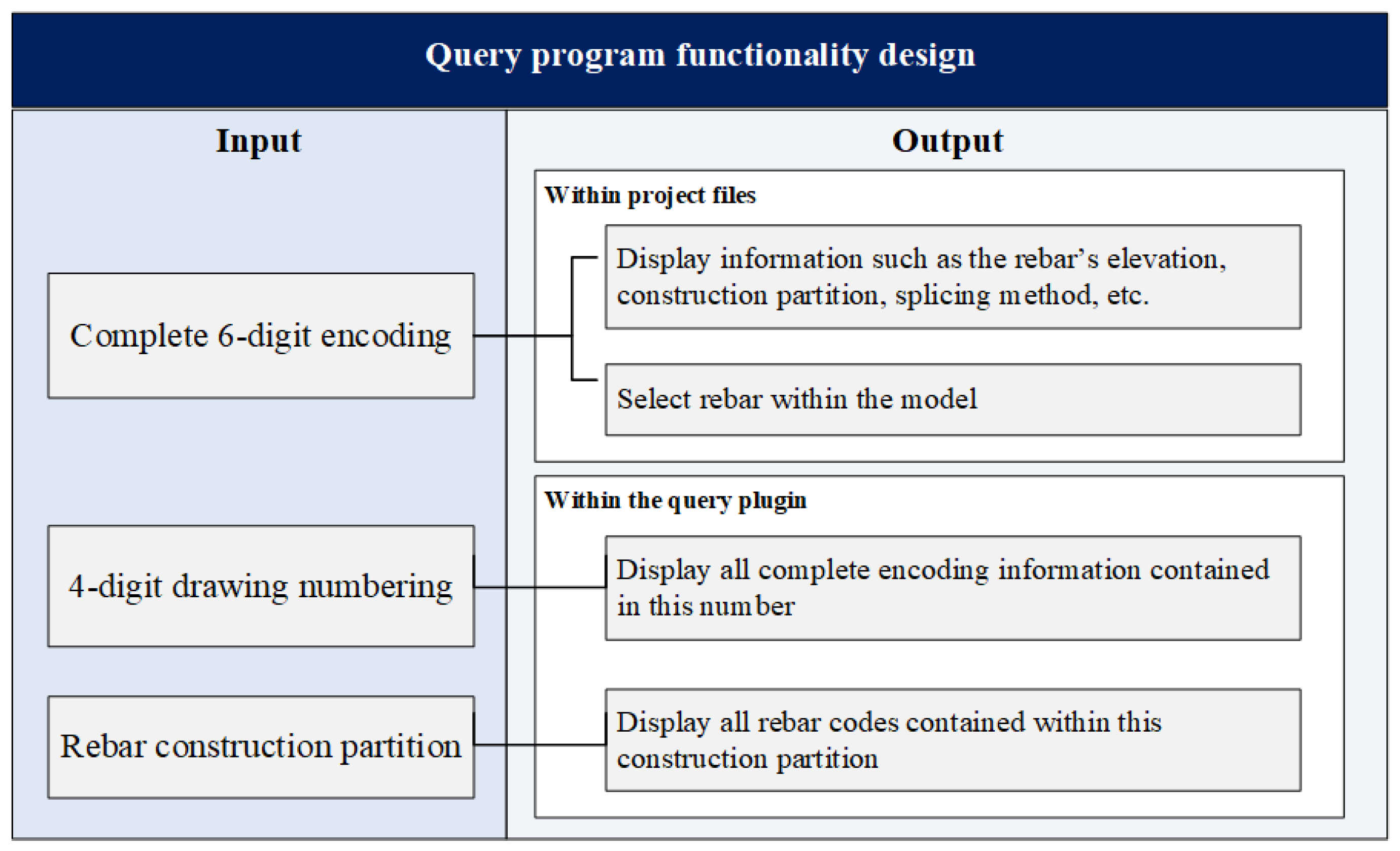
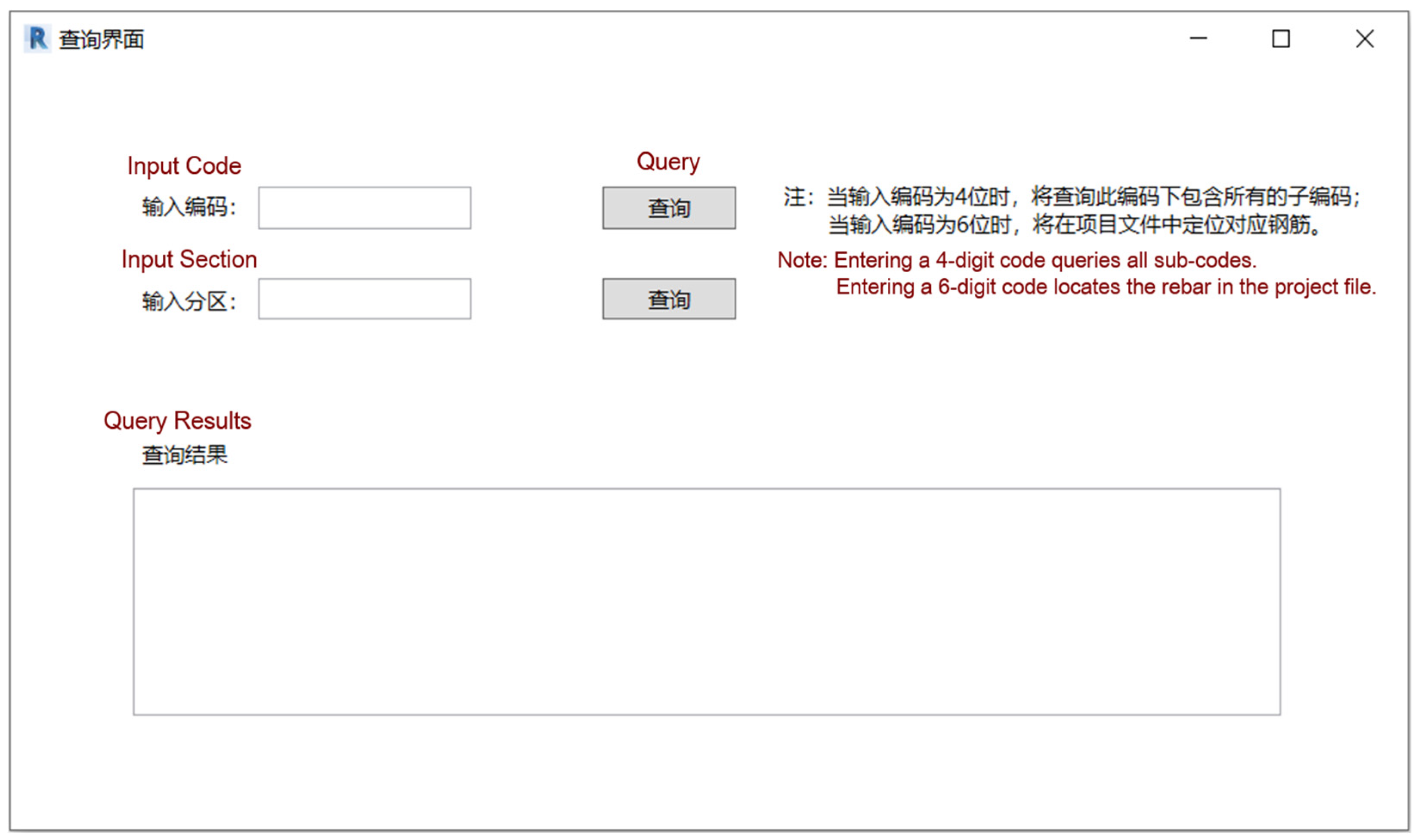
3.2. Development of Rebar Query Component
- Query by first four digits of the code: returns all rebars under the same drawing number, allowing for specific individual queries.
- Query by full six-digit code: selects the corresponding rebar element in the document and displays its annotation.
- Query by partition: returns all rebar codes contained within a given zone.
4. Results
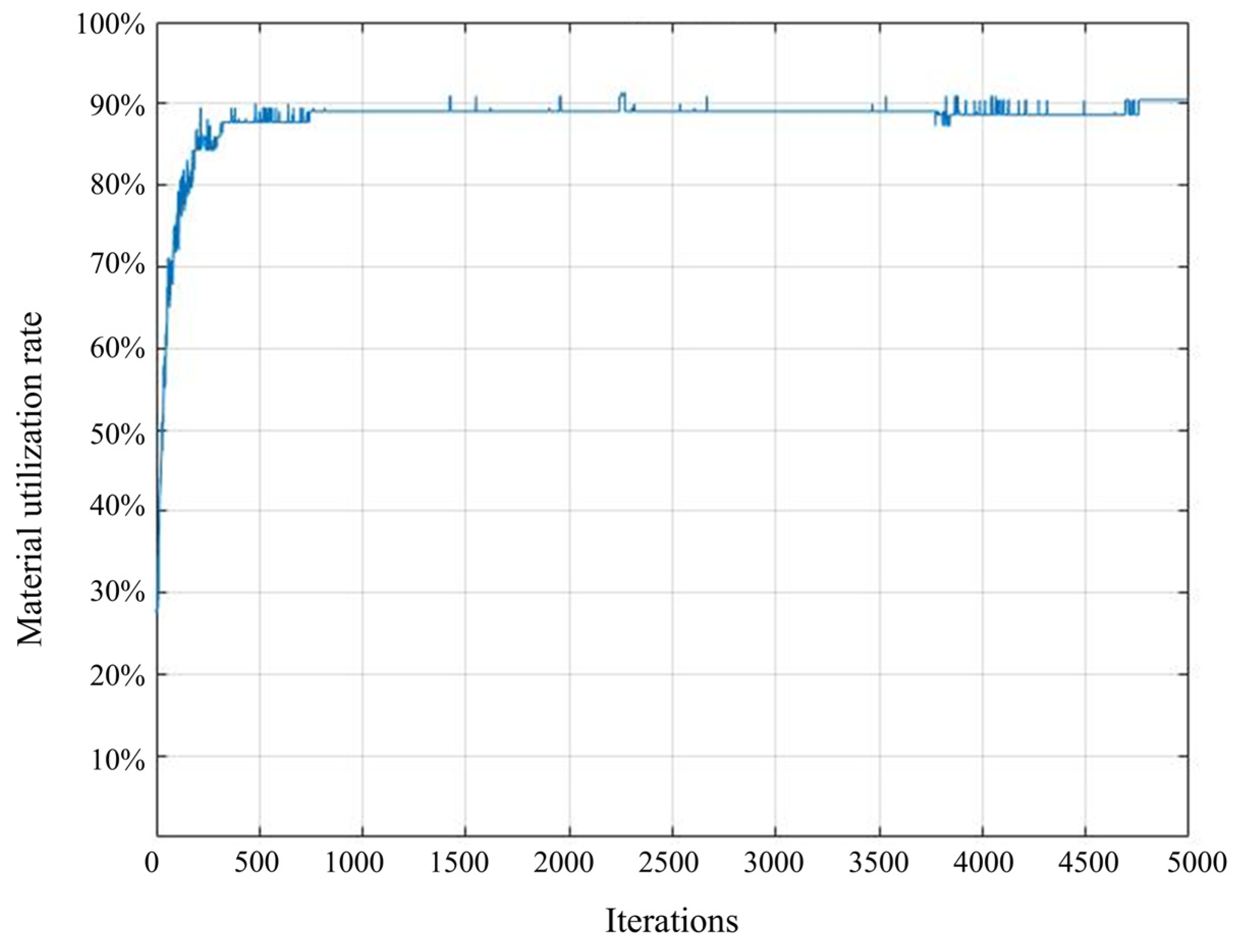
4.1. Optimization Results of the Improved Genetic Algorithm
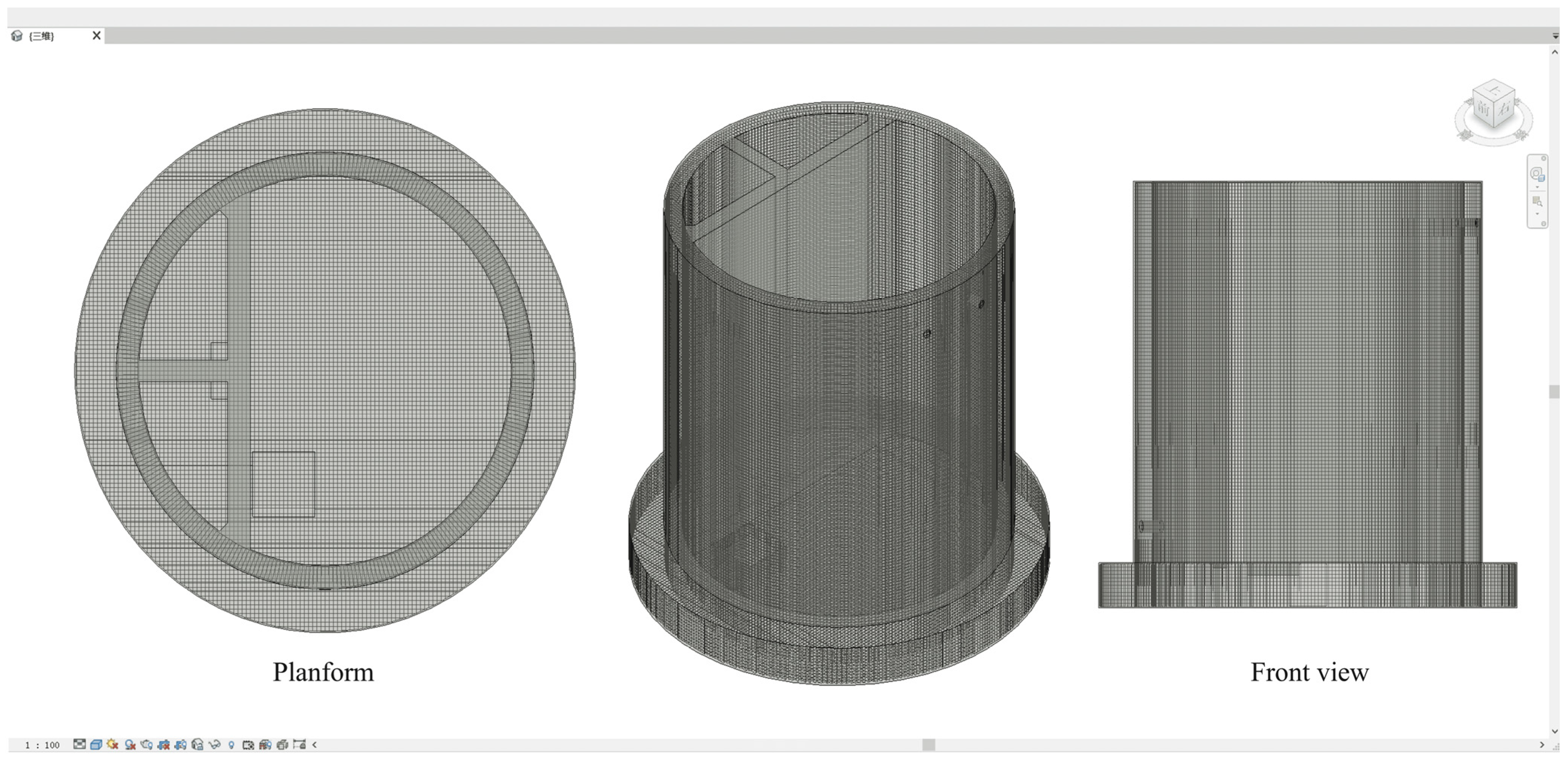
4.2. Application Example of Batch Rebar Generation
4.3. Application of Rebar Query Component
5. Conclusions and Future Prospects
- A one-dimensional rebar-cutting optimization model was developed, incorporating a novel real-number encoding strategy within the genetic algorithm framework. Using a pump station project as a case study, the proposed method successfully maximized material utilization. The results demonstrated a rebar utilization rate of 86.76% for 32 mm rebars and 93.90% for 16 mm rebars—significantly higher than the actual utilization rate of 78% observed in the project.
- Leveraging Revit-based secondary development, a total of 5560 rebar elements were generated for the bottom slab and sidewalls of the pump station through one-click automation. Each rebar was assigned a unique identifier, establishing a bidirectional link between the digital model and physical construction elements. This ensured accurate rebar placement and facilitated information-driven construction management throughout the project lifecycle.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| ID | Position Code | Total Length (m) | Bending Length 1 (cm) | Part 1 (m) | Part 2 (m) | Bending Length 2 (cm) | Quantity |
|---|---|---|---|---|---|---|---|
| 1-4 | 4 | 20.06 | 235 | 8.06 | 12 | 193 | 1 |
| 5 | 20.05 | 235 | 12 | 8.05 | 193 | 1 | |
| 6 | 20.03 | 235 | 8.03 | 12 | 193 | 1 | |
| 7 | 20.01 | 235 | 12 | 8.01 | 193 | 1 | |
| 8 | 19.99 | 235 | 7.99 | 12 | 193 | 1 | |
| 9 | 19.97 | 235 | 12 | 7.97 | 193 | 1 | |
| 10 | 19.94 | 235 | 7.94 | 12 | 193 | 1 | |
| 11 | 19.91 | 235 | 12 | 7.91 | 193 | 1 | |
| 12 | 19.87 | 235 | 7.87 | 12 | 193 | 1 | |
| 13 | 19.83 | 235 | 12 | 7.83 | 193 | 1 | |
| 14 | 19.79 | 235 | 7.79 | 12 | 193 | 1 | |
| 15 | 19.74 | 235 | 12 | 7.74 | 193 | 1 | |
| 16 | 19.69 | 235 | 7.69 | 12 | 193 | 1 | |
| 17 | 19.64 | 235 | 12 | 7.64 | 193 | 1 | |
| 18 | 19.58 | 235 | 7.58 | 12 | 193 | 1 | |
| 1-7 | 25 | 13.64 | 235 | 6 | 7.64 | 153 | 1 |
| 26 | 13.55 | 235 | 4.55 | 9 | 153 | 1 | |
| 27 | 13.45 | 235 | 9 | 4.45 | 153 | 1 | |
| 28 | 13.35 | 235 | 4.35 | 9 | 153 | 1 | |
| 25 | 13.64 | 153 | 4.64 | 9 | 235 | 1 | |
| 26 | 13.55 | 153 | 4.55 | 9 | 235 | 1 | |
| 27 | 13.45 | 153 | 9 | 4.45 | 235 | 1 | |
| 28 | 13.35 | 153 | 6 | 7.35 | 235 | 1 | |
| 1-10 | 1 | 20.63 | 153 | 12 | 8.63 | 235 | 1 |
| 2 | 20.63 | 153 | 8.63 | 12 | 235 | 2 | |
| 3 | 20.63 | 153 | 12 | 8.63 | 235 | 2 | |
| 4 | 20.62 | 153 | 8.62 | 12 | 235 | 2 | |
| 5 | 20.61 | 153 | 12 | 8.61 | 235 | 2 | |
| 6 | 20.59 | 153 | 8.59 | 12 | 235 | 2 | |
| 7 | 20.57 | 153 | 12 | 8.57 | 235 | 2 | |
| 1-13 | 20 | 16.22 | 193 | 7.22 | 9 | 235 | 1 |
| 21 | 16.15 | 193 | 9 | 7.15 | 235 | 1 | |
| 22 | 16.08 | 193 | 7.08 | 9 | 235 | 1 | |
| 23 | 16 | 193 | 9 | 7 | 235 | 1 | |
| 24 | 15.92 | 193 | 6.92 | 9 | 235 | 1 | |
| 25 | 15.84 | 193 | 9 | 6.84 | 235 | 1 | |
| 26 | 15.75 | 193 | 6.75 | 9 | 235 | 1 | |
| 27 | 15.65 | 193 | 9 | 6.65 | 235 | 1 | |
| 28 | 15.55 | 193 | 6.55 | 9 | 235 | 1 | |
| 29 | 15.45 | 193 | 9 | 6.45 | 235 | 1 | |
| 30 | 15.34 | 193 | 6.34 | 9 | 235 | 1 |
References
- Kantorovich, L.V. Mathematical Methods of Organizing and Planning Production. Manag. Sci. 1960, 6, 366–422. [Google Scholar] [CrossRef]
- Gilmore, P.C.; Gomory, R.E. A Linear Programming Approach to the Cutting-Stock Problem. Oper. Res. 1961, 9, 849–859. [Google Scholar] [CrossRef]
- Gilmore, P.C.; Gomory, R.E. A Linear Programming Approach to the Cutting Stock Problem—Part II. Oper. Res. 1963, 11, 863–888. [Google Scholar] [CrossRef]
- Alves, C.; Valério de Carvalho, J.M. A stabilized branch-and-price-and-cut algorithm for the multiple length cutting stock problem. Comput. Oper. Res. 2008, 35, 1315–1328. [Google Scholar] [CrossRef]
- Martinovic, J.; Scheithauer, G.; Valério de Carvalho, J.M. A comparative study of the arcflow model and the one-cut model for one-dimensional cutting stock problems. Eur. J. Oper. Res. 2018, 266, 458–471. [Google Scholar] [CrossRef]
- Cui, Y.; Yang, Y. A heuristic for the one-dimensional cutting stock problem with usable leftover. Eur. J. Oper. Res. 2010, 204, 245–250. [Google Scholar] [CrossRef]
- Umetani, S.; Yagiura, M.; Ibaraki, T. One-dimensional cutting stock problem to minimize the number of different patterns. Eur. J. Oper. Res. 2003, 146, 388–402. [Google Scholar] [CrossRef]
- Haessler, R.W. A Heuristic Programming Solution to a Nonlinear Cutting Stock Problem. Manag. Sci. 1971, 17, B-793–B-802. [Google Scholar] [CrossRef]
- Haessler, R.W. Controlling Cutting Pattern Changes in One-Dimensional Trim Problems. Oper. Res. 1975, 23, 483–493. [Google Scholar] [CrossRef]
- Wäscher, G.; Haußner, H.; Schumann, H. An improved typology of cutting and packing problems. Eur. J. Oper. Res. 2007, 183, 1109–1130. [Google Scholar] [CrossRef]
- Delorme, M.; Iori, M.; Martello, S. Bin packing and cutting stock problems: Mathematical models and exact algorithms. Eur. J. Oper. Res. 2016, 255, 1–20. [Google Scholar] [CrossRef]
- Belov, G.; Scheithauer, G. Setup and Open-Stacks Minimization in One-Dimensional Stock Cutting. Inf. J. Comput. 2007, 19, 27–35. [Google Scholar] [CrossRef]
- Mukhacheva, E.; Belov, G.; Kartak, V.; Mukhacheva, A. Linear one-dimensional cutting-packing problems: Numerical experiments with the sequential value correction method (SVC) and a modified branch-and-bound method (MBB). Pesqui. Oper. 2000, 20, 153–168. [Google Scholar] [CrossRef]
- Chen, Q.; Yaodong, C.; Chen, Y. Sequential value correction heuristic for the two-dimensional cutting stock problem with three-staged homogenous patterns. Optim. Methods Softw. 2016, 31, 68–87. [Google Scholar] [CrossRef]
- de Lima, V.L.; Alves, C.; Clautiaux, F.; Iori, M.; Valério de Carvalho, J.M. Arc flow formulations based on dynamic programming: Theoretical foundations and applications. Eur. J. Oper. Res. 2022, 296, 3–21. [Google Scholar] [CrossRef]
- Onwubolu, G.C.; Mutingi, M. A genetic algorithm approach for the cutting stock problem. J. Intell. Manuf. 2003, 14, 209–218. [Google Scholar] [CrossRef]
- Gracia, C.; Andrés, C.; Gracia, L. A hybrid approach based on genetic algorithms to solve the problem of cutting structural beams in a metalwork company. J. Heuristics 2013, 19, 253–273. [Google Scholar] [CrossRef]
- Kang, M.; Oh, J.; Lee, Y.; Park, K.; Sangchul, P. Selecting Heuristic Method for One-dimensional Cutting Stock Problems Using Artificial Neural Networks. Korean J. Comput. Des. Eng. 2020, 25, 67–76. [Google Scholar] [CrossRef]
- Jahromi, M.H.M.A.; Tavakkoli-Moghaddam, R.; Makui, A.; Shamsi, A. Solving an one-dimensional cutting stock problem by simulated annealing and tabu search. J. Ind. Eng. Int. 2012, 8, 24. [Google Scholar] [CrossRef]
- Bressan, G.M.; Pimenta-Zanon, M.H.; Sakuray, F. A Tree-Based Heuristic for the One-Dimensional Cutting Stock Problem Optimization Using Leftovers. Materials 2023, 16, 7133. [Google Scholar] [CrossRef]
- Fang, J.; Rao, Y.; Luo, Q.; Xu, J. Solving One-Dimensional Cutting Stock Problems with the Deep Reinforcement Learning. Mathematics 2023, 11, 1028. [Google Scholar] [CrossRef]
- Barragan-Vite, I.; Medina-Marin, J.; Hernandez-Romero, N.; Anaya-Fuentes, G.E. A Petri Net-Based Algorithm for Solving the One-Dimensional Cutting Stock Problem. Appl. Sci. 2024, 14, 8172. [Google Scholar] [CrossRef]
- Martin, M.; Yanasse, H.H.; Salles-Neto, L.L. Pattern-based ILP models for the one-dimensional cutting stock problem with setup cost. J. Comb. Optim. 2022, 44, 557–582. [Google Scholar] [CrossRef]
- Adjei-Kumi, T.; Retik, A. A library-based 4D visualisation of construction processes. In Proceedings of the IEEE Conference on Information Visualization (Cat. No.97TB100165), London, UK, 27–29 August 1997; pp. 315–321. [Google Scholar]
- Azhar, S. Building Information Modeling (BIM): Trends, Benefits, Risks, and Challenges for the AEC Industry. Leadersh. Manag. Eng. 2011, 11, 241–252. [Google Scholar] [CrossRef]
- Volk, R.; Stengel, J.; Schultmann, F. Building Information Modeling (BIM) for existing buildings—Literature review and future needs. Autom. Constr. 2014, 38, 109–127. [Google Scholar] [CrossRef]
- Sacks, R.; Kaner, I.; Eastman, C.M.; Jeong, Y.-S. The Rosewood experiment—Building information modeling and interoperability for architectural precast facades. Autom. Constr. 2010, 19, 419–432. [Google Scholar] [CrossRef]
- Succar, B. Building information modelling framework: A research and delivery foundation for industry stakeholders. Autom. Constr. 2009, 18, 357–375. [Google Scholar] [CrossRef]
- Hartmann, T.; Gao, J.; Fischer, M. Areas of Application for 3D and 4D Models on Construction Projects. J. Constr. Eng. Manag. 2008, 134, 776–785. [Google Scholar] [CrossRef]
- Toyin, J.; Mewomo, M.; Mogaji, I.; Oyewole, M. An Overview of BIM as a Material Management Tool in the Construction Industry. In Proceedings of the International Conference on Construction in the 21st Century, Arnhem, The Netherlands, 8–11 May 2023. [Google Scholar]
- Lee, D.-G.; Park, J.-Y.; Song, S.-H. BIM-Based Construction Information Management Framework for Site Information Management. Adv. Civ. Eng. 2018, 2018, 5249548. [Google Scholar] [CrossRef]
- Bortolini, R.; Formoso, C.T.; Viana, D.D. Site logistics planning and control for engineer-to-order prefabricated building systems using BIM 4D modeling. Autom. Constr. 2019, 98, 248–264. [Google Scholar] [CrossRef]
- Şerban, C.; Dumitriu, C.Ş.; Bărbulescu, A. Solving Single Nesting Problem Using a Genetic Algorithm. Analele Ştiinţifice Univ. “Ovidius” Constanţa Ser. Mat. 2022, 30, 259–272. [Google Scholar] [CrossRef]







| ID | Diameter (mm) | Length (m) | Segment Composition (cm) | Quantity | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | ||||
| 2-4 | 25 | 14.55 + 1 | \ | \ | \ | 355 | 400 | 400 | 400 | 300 + 100 | 158 |
| 15.85 + 1 | \ | \ | \ | 385 | 400 | 400 | 400 | 400 + 100 | 158 | ||
| 2-5 | 25 | 14.55 | \ | \ | \ | 355 | 400 | 400 | 400 | 300 | 142 |
| 15.85 | \ | \ | \ | 385 | 400 | 400 | 400 | 400 | 142 | ||
| 3-4 | 25 | 14.55 + 1 | \ | \ | \ | 355 | 400 | 400 | 400 | 300 + 100 | 78 |
| 15.85 + 1 | \ | \ | \ | 385 | 400 | 400 | 400 | 400 + 100 | 78 | ||
| 2-3 | 32 | 8.9 | 245 | 435 | 470 | \ | \ | \ | \ | \ | 300 |
| 10.2 | 375 | 435 | 470 | \ | \ | \ | \ | \ | 300 | ||
| 3-3 | 32 | 8.9 | 245 | 435 | 470 | \ | \ | \ | \ | \ | 78 |
| 10.2 | 375 | 435 | 470 | \ | \ | \ | \ | \ | 78 | ||
| Diameter (mm) | Length (m) | Quantity | Diameter (mm) | Length (m) | Quantity |
|---|---|---|---|---|---|
| 22 | 3.35 | 22 | 16 | 5.56 | 65 |
| 22 | 3.95 | 22 | 16 | 3.12 | 18 |
| 22 | 3.9 | 22 | 16 | 3.37 | 20 |
| 25 | 3.55 | 378 | 16 | 2.78 | 12 |
| 25 | 3.85 | 378 | 32 | 2.45 | 378 |
| 25 | 3.00 | 142 | 32 | 3.75 | 378 |
| 25 | 4.00 | 1512 | 32 | 4.35 | 756 |
| 25 | 5.00 | 236 | 32 | 4.70 | 756 |
| Num | Len (m) | Part 1 | Part 2 | Part 3 | Num | Len (m) | Part 1 | Part 2 | Part 3 | Num | Len (m) | Part 1 | Part 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 28.80 | 12.00 | 12.00 | 4.80 | 23 | 27.14 | 9.00 | 12.00 | 6.14 | 45 | 21.16 | 9.16 | 12.00 |
| 2 | 28.80 | 4.80 | 12.00 | 12.00 | 24 | 26.97 | 5.97 | 12.00 | 9.00 | 46 | 20.73 | 12.00 | 8.73 |
| 3 | 28.79 | 12.00 | 12.00 | 4.79 | 25 | 26.81 | 9.00 | 12.00 | 5.81 | 47 | 20.26 | 8.26 | 12.00 |
| 4 | 28.77 | 4.77 | 12.00 | 12.00 | 26 | 26.63 | 5.63 | 12.00 | 9.00 | 48 | 19.78 | 12.00 | 7.78 |
| 5 | 28.75 | 12.00 | 12.00 | 4.75 | 27 | 26.24 | 9.00 | 12.00 | 5.44 | 49 | 19.27 | 7.27 | 12.00 |
| 6 | 28.72 | 4.72 | 12.00 | 12.00 | 28 | 26.24 | 5.24 | 12.00 | 9.00 | 50 | 18.72 | 12.00 | 6.72 |
| 7 | 28.68 | 12.00 | 12.00 | 4.68 | 29 | 26.04 | 9.00 | 12.00 | 5.04 | 51 | 18.15 | 6.15 | 12.00 |
| 8 | 28.64 | 4.64 | 12.00 | 12.00 | 30 | 25.82 | 4.82 | 12.00 | 9.00 | 52 | 17.53 | 12.00 | 5.53 |
| 9 | 28.59 | 12.00 | 12.00 | 4.59 | 31 | 25.60 | 9.00 | 12.00 | 4.60 | 53 | 16.87 | 4.87 | 12.00 |
| 10 | 28.53 | 4.53 | 12.00 | 12.00 | 32 | 25.37 | 4.37 | 12.00 | 9.00 | 54 | 16.16 | 12.00 | 4.16 |
| 11 | 28.47 | 12.00 | 12.00 | 4.47 | 33 | 25.12 | 9.00 | 12.00 | 4.12 | 55 | 15.39 | 6.39 | 9.00 |
| 12 | 28.39 | 4.39 | 12.00 | 12.00 | 34 | 24.86 | 3.86 | 12.00 | 9.00 | 56 | 14.54 | 9.00 | 5.54 |
| 13 | 28.32 | 12.00 | 12.00 | 4.32 | 35 | 24.60 | 9.00 | 12.00 | 3.60 | 57 | 13.59 | 4.59 | 9.00 |
| 14 | 28.23 | 4.23 | 12.00 | 12.00 | 36 | 24.32 | 6.32 | 9.00 | 9.00 | 58 | 12.51 | 9.00 | 3.51 |
| 15 | 28.14 | 12.00 | 12.00 | 4.14 | 37 | 24.02 | 9.00 | 9.00 | 6.02 | 59 | 11.22 | 11.22 | \ |
| 16 | 28.04 | 4.04 | 12.00 | 12.00 | 38 | 23.72 | 5.72 | 9.00 | 9.00 | 60 | 9.58 | 9.58 | \ |
| 17 | 27.93 | 12.00 | 12.00 | 3.93 | 39 | 23.40 | 9.00 | 9.00 | 5.40 | 61 | 6.89 | 6.89 | \ |
| 18 | 27.82 | 3.82 | 12.00 | 12.00 | 40 | 23.07 | 5.07 | 9.00 | 9.00 | ||||
| 19 | 27.7 | 12.00 | 12.00 | 3.70 | 41 | 22.72 | 9.00 | 9.00 | 4.72 | ||||
| 20 | 27.57 | 3.57 | 12.00 | 12.00 | 42 | 22.36 | 4.36 | 9.00 | 9.00 | ||||
| 21 | 27.43 | 9.00 | 12.00 | 6.43 | 43 | 21.98 | 9.00 | 9.00 | 3.98 | ||||
| 22 | 27.29 | 6.29 | 12.00 | 9.00 | 44 | 21.58 | 3.58 | 9.00 | 9.00 |
| Required Length | Usage Count | Usage Count | Required Quantity | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| … | … | ||||||||||||
| … | … | ||||||||||||
| … | … | ||||||||||||
| … | … | ||||||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| … | … | ||||||||||||
| Scraps | … | … | |||||||||||
| Length (m) | ID | Number of Each Part Cut | Number of Cuts | |||
|---|---|---|---|---|---|---|
| 5.56 m | 3.12 m | 3.37 m | 2.78 m | |||
| 9 | 1 | 0 | 0 | 0 | 3 | 0 |
| 2 | 0 | 0 | 1 | 2 | 0 | |
| 3 | 0 | 1 | 0 | 2 | 0 | |
| 4 | 1 | 0 | 0 | 1 | 7 | |
| 5 | 0 | 0 | 2 | 0 | 0 | |
| 6 | 0 | 1 | 1 | 0 | 1 | |
| 7 | 1 | 0 | 1 | 0 | 14 | |
| 8 | 0 | 2 | 0 | 0 | 0 | |
| 9 | 1 | 1 | 0 | 0 | 10 | |
| 12 | 10 | 0 | 0 | 0 | 4 | 0 |
| 11 | 0 | 0 | 1 | 3 | 0 | |
| 12 | 0 | 1 | 0 | 3 | 0 | |
| 13 | 0 | 2 | 0 | 2 | 1 | |
| 14 | 1 | 0 | 0 | 2 | 0 | |
| 15 | 0 | 0 | 2 | 1 | 0 | |
| 16 | 0 | 1 | 1 | 1 | 0 | |
| 17 | 1 | 0 | 1 | 1 | 3 | |
| 18 | 1 | 1 | 0 | 1 | 0 | |
| 19 | 0 | 0 | 3 | 0 | 0 | |
| 20 | 0 | 1 | 2 | 0 | 1 | |
| 21 | 0 | 2 | 1 | 0 | 1 | |
| 22 | 0 | 3 | 0 | 0 | 0 | |
| 23 | 1 | 2 | 0 | 0 | 1 | |
| 24 | 2 | 0 | 0 | 0 | 15 | |
| Total | 65 | 18 | 21 | 12 | ||
| Length (m) | ID | Number of Each Part Cut | Number of Cuts | |||
|---|---|---|---|---|---|---|
| 2.45 m | 3.75 m | 4.35 m | 4.7 m | |||
| 9 | 1 | 0 | 1 | 0 | 1 | 143 |
| 2 | 1 | 0 | 0 | 1 | 11 | |
| 3 | 0 | 0 | 0 | 1 | 4 | |
| 4 | 0 | 0 | 2 | 0 | 123 | |
| 5 | 0 | 1 | 1 | 0 | 55 | |
| 6 | 1 | 0 | 1 | 0 | 31 | |
| 7 | 0 | 0 | 1 | 0 | 12 | |
| 8 | 0 | 2 | 0 | 0 | 0 | |
| 9 | 2 | 1 | 0 | 0 | 5 | |
| 10 | 1 | 1 | 0 | 0 | 1 | |
| 11 | 3 | 0 | 0 | 0 | 2 | |
| 12 | 2 | 0 | 0 | 0 | 0 | |
| 12 | 13 | 1 | 0 | 0 | 2 | 113 |
| 14 | 0 | 0 | 0 | 2 | 72 | |
| 15 | 1 | 0 | 1 | 1 | 94 | |
| 16 | 0 | 0 | 1 | 1 | 90 | |
| 17 | 1 | 1 | 0 | 1 | 3 | |
| 18 | 0 | 1 | 0 | 1 | 36 | |
| 19 | 2 | 0 | 0 | 1 | 6 | |
| 20 | 1 | 0 | 2 | 0 | 15 | |
| 21 | 0 | 0 | 2 | 0 | 64 | |
| 22 | 0 | 2 | 1 | 0 | 19 | |
| 23 | 1 | 1 | 1 | 0 | 35 | |
| 24 | 0 | 1 | 1 | 0 | 14 | |
| 25 | 3 | 0 | 1 | 0 | 1 | |
| 26 | 2 | 0 | 1 | 0 | 1 | |
| 27 | 0 | 3 | 0 | 0 | 3 | |
| 28 | 1 | 2 | 0 | 0 | 20 | |
| 29 | 0 | 2 | 0 | 0 | 0 | |
| 30 | 3 | 1 | 0 | 0 | 0 | |
| 31 | 2 | 1 | 0 | 0 | 0 | |
| 32 | 4 | 0 | 0 | 0 | 4 | |
| 33 | 3 | 0 | 0 | 0 | 2 | |
| Total | 378 | 379 | 756 | 757 | ||
| Code | Bend Length 1 (m) | Bend Length 1 (m) | Start Coordinate (m) | End Coordinate (m) | Distance to Center (m) |
|---|---|---|---|---|---|
| 010301 | 2.35 | 2.35 | −12.05 | 12.05 | 0 |
| 010302 | 2.35 | 2.35 | −12.05 | 12.05 | −0.2 |
| 010303 | 2.35 | 2.35 | −12.045 | 12.045 | −0.4 |
| 010404 | 2.35 | 1.93 | −12.035 | 3.74 | −0.6 |
| 010405 | 2.35 | 1.93 | −12.025 | 3.74 | −0.8 |
| Code | Quantity | Host Element | Start Elevation (m) | Distribution Span (m) | Radius (m) |
|---|---|---|---|---|---|
| 010200 | 11 | bottom slab | 368.95 | 2 | 12.05 |
| 020100 | 106 | Sidewall | 371.25 | 21 | 10.05 |
| 020200 | 106 | Sidewall | 371.25 | 21 | 9.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Ji, K.; Zhang, Y.; Xie, Q.; Huang, J. Intelligent Optimization Method for Rebar Cutting in Pump Stations Based on Genetic Algorithm and BIM. Buildings 2025, 15, 1790. https://doi.org/10.3390/buildings15111790
Fu X, Ji K, Zhang Y, Xie Q, Huang J. Intelligent Optimization Method for Rebar Cutting in Pump Stations Based on Genetic Algorithm and BIM. Buildings. 2025; 15(11):1790. https://doi.org/10.3390/buildings15111790
Chicago/Turabian StyleFu, Xiang, Kecheng Ji, Yali Zhang, Qiang Xie, and Jiayu Huang. 2025. "Intelligent Optimization Method for Rebar Cutting in Pump Stations Based on Genetic Algorithm and BIM" Buildings 15, no. 11: 1790. https://doi.org/10.3390/buildings15111790
APA StyleFu, X., Ji, K., Zhang, Y., Xie, Q., & Huang, J. (2025). Intelligent Optimization Method for Rebar Cutting in Pump Stations Based on Genetic Algorithm and BIM. Buildings, 15(11), 1790. https://doi.org/10.3390/buildings15111790







