Abstract
The influence of foundation pit excavation on the bearing behavior of concrete tubular piles at the pit bottom remains unclear. Based on the Vesic cavity expansion theory, this paper proposes a method for calculating pile driving resistance, which takes into account the residual effect of vertical pressure changes on earth pressure during excavation. Furthermore, relying on the statistical regularity between Qu/Pu (ratio of ultimate bearing capacity to ultimate cavity expansion pressure) and L/d (length-to-diameter ratio), theoretical formulas for calculating the ultimate bearing capacity of tubular piles before and after foundation pit excavation are established, with their reliability and influencing factors analyzed. This method only requires determining the L/d of the tubular piles and the theoretical value of pile driving resistance. With its simple parameter requirements, it is suitable for estimating the ultimate bearing capacity of tubular piles affected by excavation. By comparing the computed penetration resistance, earth pressure, and driving resistance of tubular piles with field measurements, the computed results show good agreement with field measurements, and the accuracy of the proposed method meets the requirements of engineering design, verifying its feasibility as an empirical method. The fitting results of the Qu/Pu ratios indicate that the deviations between the measured and computed values are 4.17% and 5.64% before and after excavation, respectively. Additionally, L/d and L/H (ratio of pile length to excavation depth) significantly affect the earth pressure, driving resistance, and vertical bearing capacity of monopoles. Smaller L/d and L/H ratios lead to greater earth pressure on the pile and more pronounced effects on driving resistance and vertical bearing capacity. The development of this method offers an approach for estimating the ultimate bearing capacity of tubular piles before and after foundation pit excavation during preliminary design, thereby holding substantial engineering significance.
1. Introduction
Rapid urbanization has led to numerous foundation pit projects for high-rise buildings with pile foundations. The pile foundations at the pit bottom are typically constructed using in situ cast concrete piles, precast concrete piles, and steel pipe piles. As a prevalent type of precast concrete pile, concrete tubular piles are extensively used in China due to their advantages such as high construction efficiency, energy conservation, and environmental friendliness. To construct pile foundations in deep foundation pits, piles are usually installed after excavation. However, in clayey soils with low bearing capacity or shallow foundation pits, concrete tubular piles are often installed before excavation [1,2,3], as shown in Figure 1.

Figure 1.
Concrete tubular piles before excavation.
Many studies have investigated soil unloading and ground movement using empirical approaches [4,5,6,7]. The bearing behavior of cast-in-place piles due to excavation has also attracted increasing attention [8,9,10]. Excavation reduces the vertical pressure at the pit bottom, affecting the earth pressure, skin friction, and vertical bearing capacity of piles [11,12]. In some cases, excavation causes severe engineering accidents, such as pile breakage or inclination [13], as illustrated in Figure 2.

Figure 2.
Engineering accidents of tubular piles due to excavation.
However, existing research has focused primarily on cast-in-place piles at foundation pit bottoms. Although many methods for calculating driving resistance of tubular piles and studies on vertical/horizontal soil displacements around tubular piles have been proposed [9,14,15], the mechanical response of tubular piles during foundation pit excavation, such as vertical bearing capacity, soil displacement around the pile, and earth pressure on the pile, remains uninvestigated [1,16]. Moreover, studies have shown that the construction of tubular piles induces a significant soil squeezing effect [14]. However, foundation pit excavation alters the stress state of the soil surrounding the piles, which in turn impacts the soil squeezing effect and consequently leads to an overestimation of the ultimate bearing capacity of the tubular piles. Current research on this issue is predominantly confined to case reports [13] and laboratory experimental research [17], with a notable lack of theoretical studies. This inadequacy has severely compromised engineering safety and hindered the practical application of tubular piles in engineering projects.
To clarify the mechanism of tubular pile behavior during foundation pit excavation, this study proposes an analytical approach considering the effect of soil unloading on bottom earth pressure. Firstly, based on Vesic’s cavity expansion theory [18] and the skin friction distribution model by Zhang and Deng (2003) [14], a method to calculate tubular pile driving resistance is developed. Taking into account the residual effect of unloading on the soil squeezing effect during excavation, a modified approach for driving resistance calculation is proposed. An empirical method for evaluating the vertical bearing capacity of tubular piles is then derived from the modified driving resistance approach. Secondly, two field tests and a laboratory creep test verify the accuracy of the empirical method for ultimate vertical bearing capacity. Using well-documented field static load test data from 189 tubular piles before excavation and 153 after excavation, fitting formulas for the ratio of ultimate bearing capacity to ultimate driving resistance (Qu/Pu) and pile length-to-diameter ratio (L/d) are proposed. Finally, a parametric analysis of vertical bearing behavior during excavation is conducted, focusing on the pile length-to-diameter ratio (L/d) and pile length-to-excavation depth ratio (L/H).
2. Driving Resistance of Tubular Piles Before Excavation
A mechanical model of the tubular pile driving is shown in Figure 3. The soil is homogeneous and follows the M-C yield criterion as an ideal elastoplastic material. During the driving process of a tubular pile, as the pile tip penetrates into the soil, it squeezes the surrounding soil radially outward. This mechanical behavior is highly consistent with the cavity expansion theory proposed by Vesic [18]. Therefore, ignoring the effect of pore water pressure on the tubular pile, the differential equation of cavity expansion based on Vesic’s theory [18] is as follows:
where r is the expansion radius of the tubular pile.
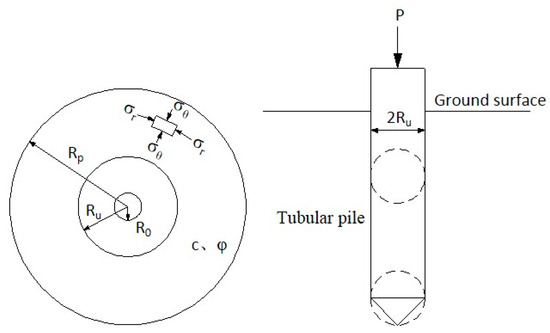
Figure 3.
Mechanical model of tubular pile.
According to the M-C yield criterion,
Combining Equations (1) and (2), the stresses and can be expressed by Equation (3):
where Pu is the ultimate expansion pressure when the expansion radius equals Ru.
If the initial pore pressure equals the at-rest earth pressure, it can be expressed as follows:
Combining Equations (3) and (4), the ultimate expansion pressure for pile driving at depth z is as follows:
Based on research on the elastic effect radius Rp [14,16], the equation for Rp is as follows:
where pa is the standard atmospheric pressure, h and t are dimensionless parameters from soil triaxial tests, and G is the soil shear modulus.
Combining Equations (3) and (6), Rp can be calculated using an iterative method, with Ru as the initial value for iteration.
Figure 4.
Load carried on pile tip.
According to Zhang and Deng (2003) [14] (see Figure 5) and Chandler (1968) [8], the skin friction of the soil–pile interface can be given as follows:
where K0 is Jaky’s at-rest earth pressure coefficient, which equals [19].
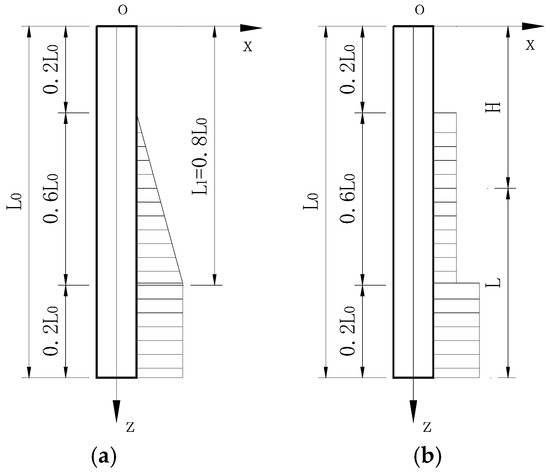
Figure 5.
Skin friction distribution at soil–pile interface: (a) before simplification; (b) after simplification [14].
As shown in Figure 6a,c, if the embedded depth of the tubular pile is L0 and the pile length is L, the virtual pile length H equals the excavation depth L0−L.
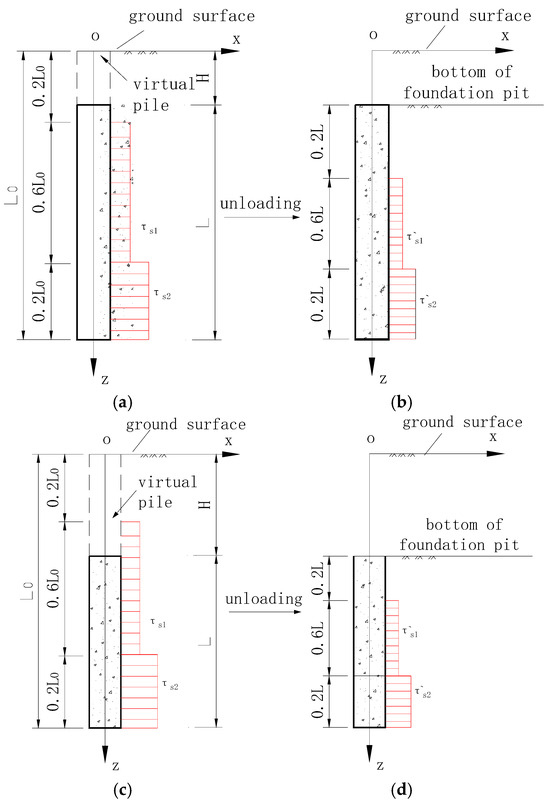
Figure 6.
Skin friction distribution of tubular piles: (a) H ≤ 0.2L0, before excavation; (b) H ≤ 0.2L0, after excavation; (c) H > 0.2L0, before excavation; (d) H > 0.2L0, after excavation.
Considering the virtual pile effect, and combining Equations (7) and (8), the driving resistance of the tubular pile at depth z before excavation is calculated as follows:
where Pubef is the ultimate driving resistance before excavation, and puL0 is the ultimate expansion pressure at depth L0.
3. Effect of Excavation on Driving Resistance
3.1. Unloading Effect at Pit Bottom
The variation in earth pressure due to bottom unloading is typically expressed as follows:
where konc is the at-rest earth pressure coefficient for normally consolidated soil, and is the unloading pressure due to excavation.
For soil excavation, the normal consolidated soil at the pit bottom changes to over-consolidated soil. However, the investigation [20] illustrates that the earth pressure on the pile due to unloading does not disappear completely (see Figure 7). Thus, the at-rest earth pressure coefficient considering residual earth pressure due to excavation is calculated as follows:
where OCRr = 1 − ln0.05/k, and and k are fitting coefficients from a molecular model based on over-consolidated soil stress release tests.
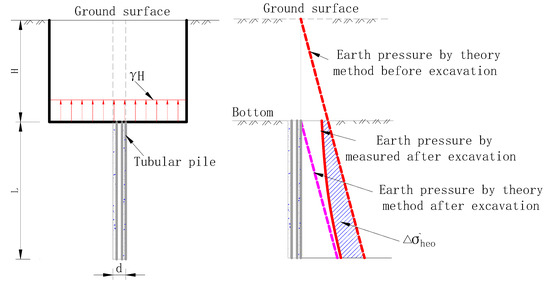
Figure 7.
Calculation model of earth pressure on pile.
Therefore, the variation in earth pressure on the pile due to excavation is calculated as follows:
3.2. Driving Resistance and Vertical Bearing Capacity of Tubular Piles During Excavation
From Equation (8), considering soil unloading effect during excavation, the skin friction of a tubular pile can be expressed as follows:
where is the expansion pressure at driving depth L1, is the variation in earth pressure on the pile surface at depth z due to excavation, and L1 is equal to 0.8L0.
Thus, the driving resistance of the tubular pile during excavation is derived from Equation (13) as follows:
where is the expansion pressure at embedded depth L0, and is the variation in earth pressure on the pile at embedded depth L0 due to excavation.
Existing studies [16,21] show a strong statistical relationship between Qu/Pu ratios and L/d ratios of tubular piles. Thus, based on the fitted Qu/Pu-L/d formula and the results of and computed by Equations (9) and (14), the ultimate vertical bearing capacities of tubular piles before and after excavation can be expressed as follows:
where and are the ratios of the vertical ultimate bearing capacity to the ultimate driving resistance before and after excavation, obtained via fitting field test measurements.
4. Test Results and Discussion
4.1. Case Analysis
To verify the feasibility of the method proposed in this paper, both laboratory and field tests were conducted. Laboratory tests included 18 unloading creep tests, while field tests comprised two static load tests on tubular piles before and after excavation in Zhuzhou, China.
4.1.1. Unloading Creep Test
According to the geotechnical engineering investigation report, the soil around the tubular piles is silty clay. The unloading creep test schemes are listed in Table 1.

Table 1.
Schemes of unloading creep test.
The scatter diagram of η which is the ratio of residual consolidation pressure to preconsolidation pressure is shown in Figure 8. The test results are fitted by the following equation:
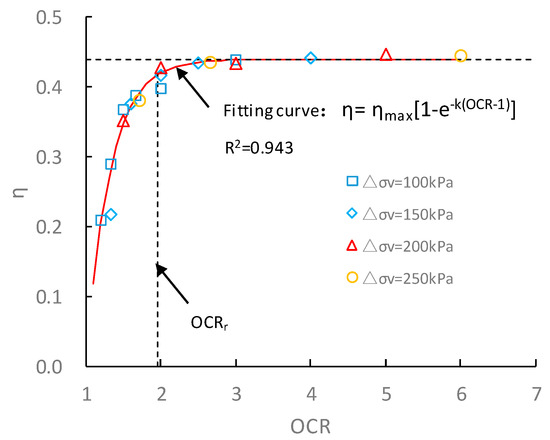
Figure 8.
Curve of OCR and η.
From the fitting curve, ηmax = 0.4396, k = 3.1358, and the critical preconsolidation ratio OCRr = 1.953.
4.1.2. Field Test
A foundation pit project with tubular piles was selected to study the effect of unloading on the vertical bearing behavior of tubular piles. Concrete tubular piles with a diameter of 50 cm and a length of 11.4 m (N16 and N17) and 12 m (N58 and N59) were driven into a 4.5 m deep foundation pit before excavation, with the pile top 4 m below the ground surface. Table 2 gives the parameters of the soil layer in this case.

Table 2.
Parameters of soil layers.
To investigate the influence of unloading on the mechanical response of tubular piles, the tubular piles (N16 and N58) before excavation and piles (N17 and N59) after excavation were selected. Meanwhile, to compare the earth pressure on the pile surface and the resistance on the pile tip after excavation with those before excavation, TD-LY350 stress sensors were used to measure the earth pressure and pipe tip resistance of N58 as shown in Figure 9.
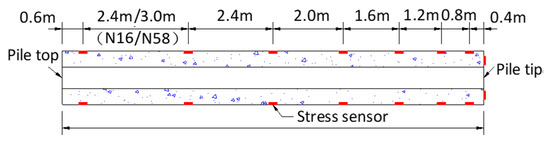
Figure 9.
Stress sensors on tubular piles N16 and N58.
- Pile Tip Resistance
Figure 10 presents a comparison between the computed and measured tip resistances of N16 and N58 piles at various driving depths. It is evident that the computed tip resistances of both piles align well with the measured values across the depth profile. Additionally, despite the fluctuations in the curves induced by soil heterogeneity, the computed values generally agree with the field measurements.
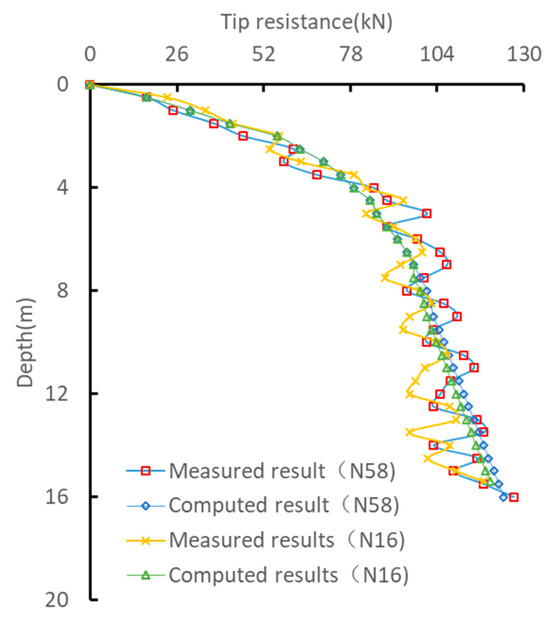
Figure 10.
Tip resistance of tubular pile before excavation.
- 2.
- Earth Pressure on Pile
Figure 11 shows the earth pressure at different depths on piles N16 and N58, which increases with driving depth but decreases due to soil disturbance from pile driving at the same depth. However, at a given depth, soil disturbance caused by pile installation leads to a reduction in lateral stress. For instance, at a driving depth of 13.5 m, the earth pressure measured by gauge N2 on pile N58 exhibits a 15.10% decrease compared to gauge N1. Conversely, the reduction in earth pressure from gauge N2 to N3 at the same depth is only 8.29%.
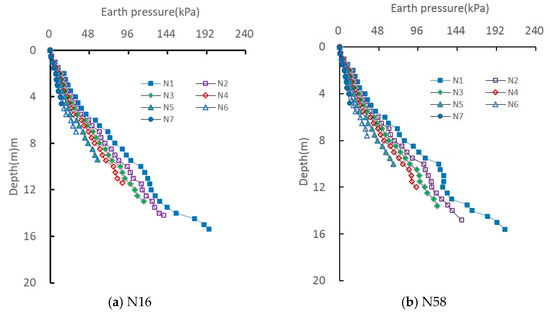
Figure 11.
Earth pressure on pile.
The earth pressure distribution along the pile shaft of N16 and N58 subjected to vertical load in static load tests is shown in Figure 12. The results indicate that for both piles, the earth pressure increases significantly with embedded depth. Moreover, both the computed and measured data reveal a consistent reduction in earth pressure after excavation.
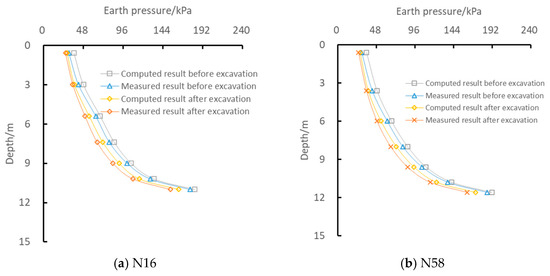
Figure 12.
Earth pressure on pile in static load test.
Taking pile N58 as an example, the maximum discrepancies between the measured and computed earth pressures at 4.0 m below the pile top are 8.16% (before excavation) and 9.59% (after excavation). These results demonstrate that the accuracy of the proposed method meets the requirements of engineering design.
- 3.
- Vertical Bearing Capacity
Figure 13 illustrates the settlements of piles N16 and N58 under varying loads before excavation and those of piles N17 and N59 after excavation. As can be observed from the figure, the load–displacement curves of the two pairs of piles (before and after excavation) are quite close due to the minimal difference in pile length (only 0.6 m). Additionally, taking piles N58 and N59 with a length of 12 m as an example, their vertical bearing capacities are initially similar but diverge significantly when the load exceeds 600 kN. The ultimate bearing capacities of N58 and N59 are 900 kN and 700 kN, respectively, indicating a reduction of 200 kN after excavation. This confirms the significant impact of unloading on the vertical bearing capacity of concrete tubular piles.
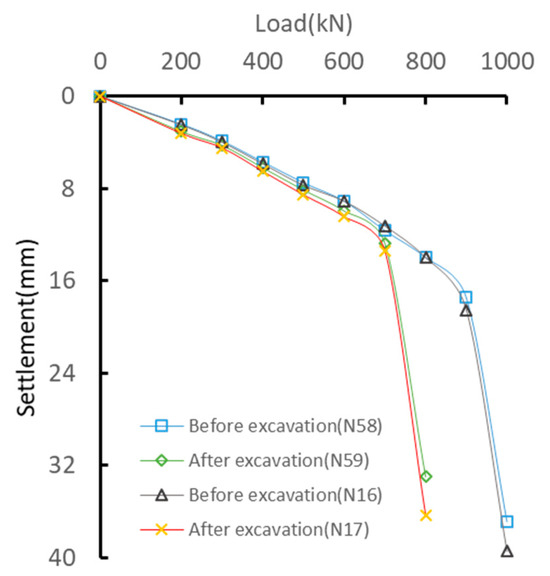
Figure 13.
Static load test curves of tubular pile.
- 4.
- Statistical Law of Qu/Pu Ratios
Case histories show that Qu/Pu ratios are associated with multiple factors, but L/d ratios have the most pronounced effect [16,20]. Figure 14 shows 189 Qu/Pu ratios before excavation and 153 Qu/Pu ratios after excavation for tubular piles in Zhuzhou with different L/d ratios.
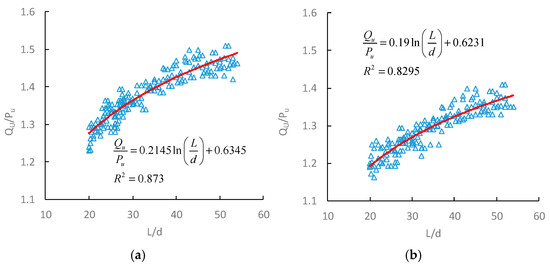
Figure 14.
Distribution of Qu/Pu ratios: (a) before excavation; (b) after excavation.
The Qu/Pu-L/d relationships before and after excavation are fitted as shown in Figure 14. Using Equations (9) and (14), the driving resistances of N58 and N59 are 751.2 kN and 624.1 kN, respectively. Moreover, for L/d = 24, the ultimate vertical bearing capacities calculated by Equation (15) are 937.5 kN (before excavation) and 739.5 kN (after excavation). It is noted that there are only 4.17% and 5.64% differences between the measured dates before and after excavation in the field tests, which verify the feasibility of the empirical method in this paper.
4.2. Parametric Studies
Parametric analyses of length-to-diameter ratio (L/d) and length-to-depth ratio (L/H) were conducted to investigate soil unloading effects on tubular pile vertical bearing behavior during excavation.
4.2.1. Effect of L/d Ratio
An assumed case with excavation depth H = 4 m, pile length L = 12 m, and diameters d = 300 mm, 400 mm, and 600 mm (L/d = 20, 30, 40) was analyzed. Figure 15 shows that smaller L/d ratios lead to more significant driving effects and higher earth pressure on the pile. Earth pressure before excavation is higher than after excavation at the same depth, with more pronounced effects as embedded depth and L/d decrease. Figure 16 shows that ultimate bearing capacity (Qu) and driving resistance (Pu) before excavation exceed those after excavation. Also, Figure 13 indicates that the effects on Qu and Pu are more significant with the decrease in L/d.
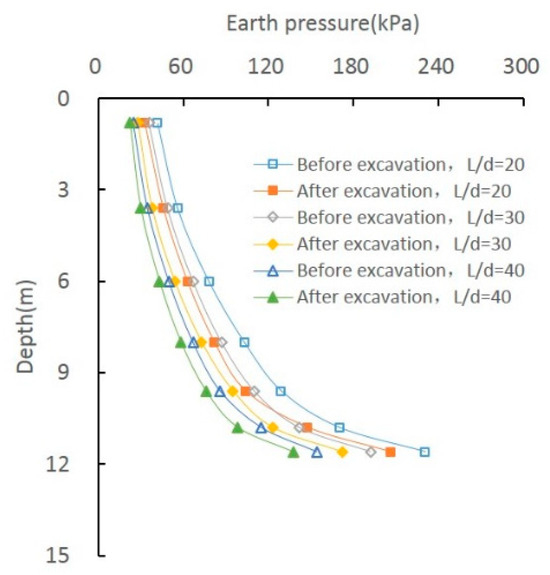
Figure 15.
Effect on earth pressure of L/d.
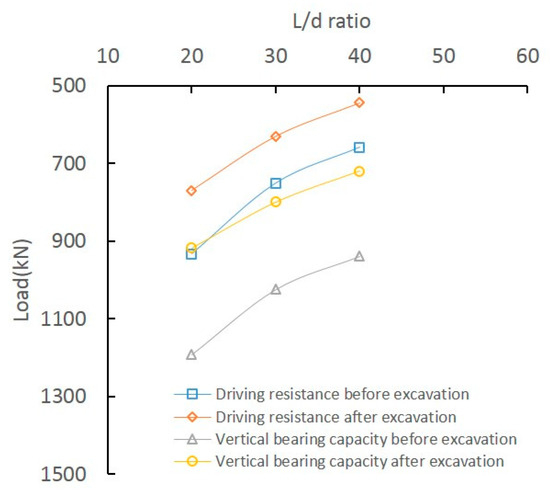
Figure 16.
Effect on Qu and Pu of L/d.
4.2.2. Effect of L/H Ratio
To analyze the effect of L/H on the vertical bearing behavior of tubular piles, another case with diameter D = 400 mm, excavation depths H = 4 m, 6 m, and 8 m, and pile length L = 12 m (L/H = 3, 2, 1.5) was analyzed. Figure 17 shows that smaller L/H ratios increase earth pressure due to greater pile sinking effects. Earth pressure before excavation is higher than after excavation, with more significant effects as depth and L/H decrease. Moreover, it is also illustrated that the earth pressure on the pile before excavation is greater than that after excavation at the same depth, and the effect on earth pressure will be more significant with the decrease in depth and the L/H ratio during excavation. Figure 18 shows the ultimate bearing capacity Qu and the driving resistance Pu with different L/H ratios. It is noted that both Qu and Pu before excavation are higher than after excavation. Also, Figure 18 shows that the effects on Qu and Pu are more significant with the decrease in the L/H ratio.
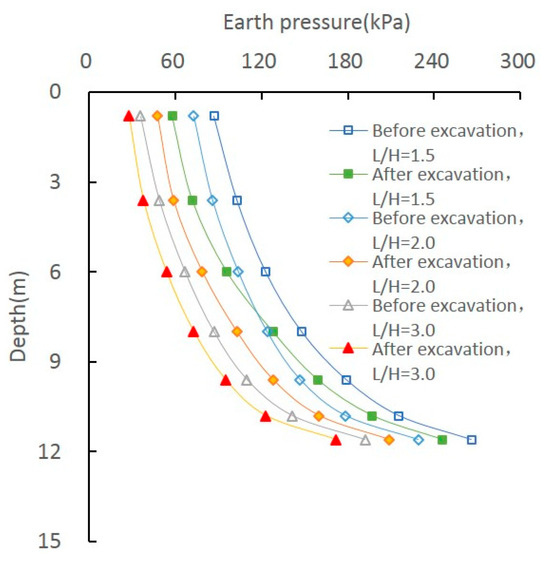
Figure 17.
Effect on earth pressure of L/H.
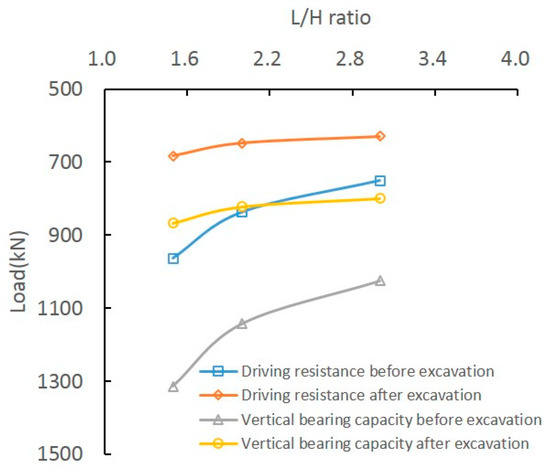
Figure 18.
Effect on Qu and Pu of L/H.
5. Conclusions
This study extends the driving resistance theory for concrete tubular piles [14] and the bearing mechanics of piles during foundation pit excavation [12,13]. An empirical method for calculating the ultimate vertical bearing capacity of tubular piles in foundation pits is proposed based on fitted Qu/Pu ratios and computed driving resistances before and after excavation. Key conclusions include the following:
- (1)
- An approach to calculating the penetration resistance of the pile tip has been adopted for the driving resistance of tubular piles in foundation pits during excavation, and the results computed by using the theory method presented in this document match well with the results obtained in the field test.
- (2)
- Excavation disturbs the earth pressure acting on the pile, which significantly affects the ultimate vertical bearing capacity of the tubular pile. This confirms the adverse impact of excavation on the soil squeezing effect of tubular piles and the parameters related to pile driving resistance. Therefore, the influence of excavation on the earth pressure of tubular piles should not be ignored in design.
- (3)
- The proposed empirical method shows only 4.17% and 5.64% deviations from field test results before and after excavation. So, the proposed empirical method here is suitable for engineering design, which makes it easy to achieve the ultimate vertical bearing ability of the tubular pile as opposed to conducting tests in the field which usually cost a lot in some engineering projects.
- (4)
- Parametric analysis shows that L/d and L/H ratios significantly affect driving resistance, earth pressure, and ultimate vertical bearing capacity. Smaller L/d and L/H ratios during excavation lead to higher earth pressure and more pronounced effects on bearing capacity. Therefore, relatively large values of L/d and L/H are essential for mitigating the impact of excavation on the ultimate bearing capacity of tubular piles.
- (5)
- In this study, the parametric analysis focused exclusively on the influence of the L/d ratio and the L/H ratio on earth pressure, Qu, and Pu. Additional factors that could affect the load-bearing performance of concrete tubular piles, such as soil stratification and groundwater level, were not incorporated into the analysis. In future research, a more refined soil constitutive model will be employed, soil layering characteristics will be explicitly considered, and time-dependent effects on pile bearing behavior during excavation will be investigated to comprehensively evaluate their impacts on the load-bearing characteristics of tubular piles.
Author Contributions
Methodology, Q.Y.; resources, H.Z.; writing—original draft preparation, S.H. and S.X.; writing—review and editing, Q.Y.; visualization, Q.S.; funding acquisition, Q.Y. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hunan Province (Project No. 2024JJ7152, 2024JJ8368) and the Scientific Research Fund of Hunan Provincial Education Department (Project No. 23A0424).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhou, X.L.; Xiao, F.; Liao, H. Analysis and disposal of construction quality accidents for prestressed concrete tubular piles in soft soil areas. Ind. Constr. 2015, 45, 191–195. [Google Scholar]
- Zhang, G.; Diao, Y.; Wu, H.W. Finite element analysis on mechanism of effect of extra-deep excavation on vertical load transfer and settlement of a monopile. Chin. J. Geotech. Eng. 2009, 31, 837–845. [Google Scholar]
- Chen, J.J.; Wang, J.H.; Fan, W. Behavior of up-lift pile foundation during large-scale deep excavation. Chin. J. Geotech. Eng. 2009, 31, 402–407. [Google Scholar]
- Clough, G.W.; O’Rourke, T.D. Construction induced movements of in situ wall. Geotech. Spec. Publ. 1990, 25, 439–470. [Google Scholar]
- Hsieh, P.G.; Ou, C.Y. Shape of ground surface settlement profiles caused by excavation. Can. Geotech. J. 1998, 35, 1004–1017. [Google Scholar] [CrossRef]
- Moormann, C. Analysis of wall and ground movements due to deep excavations in soft soil based on a new worldwide database. J. Jpn. Geotech. Soc. 2008, 44, 87–98. [Google Scholar] [CrossRef]
- Leung, E.; Ng, C. Wall and ground movements associated with deep Excavations supported by cast in situ wall in mixed ground conditions. J. Geotech. Geoenviron. Eng. 2007, 133, 129–143. [Google Scholar] [CrossRef]
- Chandler, R.J. The shaft reaction of piles in cohesive soils in terms of effective stresses. Civ. Eng. Public Work. Rev. 1968, 63, 48–51. [Google Scholar]
- Mangushev, R.A.; Kolesnik, D.S. Analysis of horizontal pile displacement caused by pit excavation. J. Phys. Conf. Series 2021, 1928, 012042. [Google Scholar] [CrossRef]
- Soomro, M.A.; Mangnejo, D.A.; Bhanbhro, R.; Memon, N.A.; Memon, M.A. 3D finite element analysis of pile responses to adjacent excavation in soft ground: Effects of different excavation depths systems relative to a floating pile. Tunneling Undergr. Space Technol. 2019, 86, 138–155. [Google Scholar] [CrossRef]
- Huang, M.S.; Ren, Q.; Wang, W.D. Analysis for ultimate uplift capacity of tension piles under deep excavation. Chin. J. Geotech. Eng. 2007, 29, 1689–1695. [Google Scholar] [CrossRef]
- Zheng, G.; Diao, Y.; Ng, C.W.W. Parametric analysis of the effects of stress relief on the performance and capacity of piles in nonrelative soils. Can Geotech. J. 2011, 48, 1354–1363. [Google Scholar] [CrossRef]
- Zheng, G.; Wang, Q.; Zhang, L.M. Parametric analysis on the influence of foundation pit excavation on the performance of pit bottom piles. Build. Struct. 2015, 45, 68–74. [Google Scholar]
- Zhang, M.Y.; Deng, A.F. A spherical cavity expansion-sliding friction calculation model on the penetration of pressed-in piles. Rock Soil Mech. 2003, 24, 701–709. [Google Scholar]
- Jiang, T.; Li, B.; Yang, X.Y. Experimental study on the influence of pile driving by static pressure pile on soil near the existing pile using PIV technique. Chin. J. Undergr. Space Eng. 2018, 14, 1185–1194. [Google Scholar]
- Yang, S.C.; Zhang, M.Y.; Guan, J.P. Experimental study on the influence of excavation unloading on existing static pressure piles in silt soil. J. Shandong Agric. Univ. (Nat. Sci. Ed.) 2021, 52, 98–104. [Google Scholar]
- Yang, Q.G.; Xiao, S.; Liu, F.; Liu, X. Research on the Influence of Foundation Pit Excavation on the Vertical Bearing Characteristics of Pipe Piles. J. Hunan Univ. Technol. 2025, 39, 19–25, 78. [Google Scholar] [CrossRef]
- Vesic, A.S. Expansion of cavity in infinite soil mass. J. Soil Mech. Found. Div. Am. Soc. Civ. Eng. 1972, 98, 265–289. [Google Scholar] [CrossRef]
- Jaky, J. Pressure in soils. In Proceedings of the 2nd International conference on Soil Mechanics and Foundation Engineering, Rotterdam, The Netherlands, 21–30 June 1948. [Google Scholar]
- Chen, S.F.; Kong, L.W.; Luo, T. Lateral stress release characteristics of overconsolidated silty clay and calculation method for lateral earth pressure coefficient at rest. Rock Soil Mech. 2022, 43, 160–168. [Google Scholar] [CrossRef]
- Lin, B.H.; Wang, L. Research on bearing capacity mechanism of statically pressed precast concrete piles. J. Build. Struct. 2004, 25, 120–124. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).