Machine Learning-Based Methods for the Seismic Damage Classification of RC Buildings †
Abstract
1. Introduction
| Authors | Type | Best ML Algorithm | Input Parameters |
|---|---|---|---|
| Giovanis et al. [24] | Regression | Artificial Neural Network | Six parameters of backbone curves |
| Morfidis and Kostinakis [25] | Regression and classification | Artificial Neural Network | 4 structural and 14 ground motion parameters |
| Hwang et al. [32] | Regression and classification | XGBoost | 15 structural modeling-related parameters (e.g., plastic rotations, post-yield strength ratio, energy dissipation capacity) 1 parameter for intensity measure (Sa(T1)) |
| Dabiri et al. [26] | Regression | Decision Tree | 7 structural parameters (construction materials, plan area, height, lateral resisting system, location, damage state, and period) 1 soil parameter |
| Bhatta and Dang [33] | Classification | Random Forest | 10 structural parameters (no. of stories, height, period, age of buildings, etc.) 7 earthquake parameters (PGA, PGV, PGD, seismic intensity, spectral acceleration, etc.) |
| Demertzis et al. [27] | Regression | LightGBM | 4 structural parameters (height, ratio of the base shear received by walls in two directions, and eccentricity) 14 seismic parameters |
| Mahmoudi et al. [34] | Classification | K-Nearest Neighbor | Arias intensity, cumulative absolute velocity, modified cumulative absolute velocity, spectral acceleration, energy ratio, drift, and correlation |
| Kostinakis et al. [36] | Classification | SVM–Gaussian kernel | 4 structural parameters (height, ratio of the base shear received by walls in two directions, and eccentricity) 14 seismic parameters |
| Zhang et al. [35] | Classification | Active Machine Learning | 8 structural parameters (e.g., no. of stories, story height, no. of bays in both directions, length of bay on both directions, constructed period, seismic design intensity) 14 ground motion parameters (e.g., peak ground acceleration, effective peak acceleration, peak ground velocity, spectrum intensity, and spectral acceleration) |
| Shahnazaryan and Reilly [28] | Regression | XGBoost Decision Trees | 6 structural parameters for describing backbone curves of SDOF systems |
| Demir et al. [29] | Regression | Random Forest | 20 ground motion parameters 1 spectral acceleration |
| Işık et al. [30] | Regression | Artificial Neural Network | Floor number PGA |
| Payán-Serrano et al. [31] | Regression | Artificial Neural Network | For RC buildings: spectral acceleration and intensity measure For SDOF buildings: fundamental period, seismic coefficient, and intensity measure |
| Wei et al. [37] | Classification | CNN + Stacking Method | Structural acceleration response signals |
Research Scope
- Datasets for RC buildings without seismic design considerations are created for ML model development. Accurate ML models are developed for rapidly assessing the damage class of buildings during earthquakes. These are valuable for locations with similar design considerations.
- A comprehensive investigation is conducted to study the effectiveness of different ML algorithms, such as basic models, ensemble methods, and ANN models, for classifying the damage class of buildings. Efficient methods are identified.
- Neural network models combined with ensemble methods (stacking and boosting) are used to improve the performance of ANN models to handle tabular data.
- The importance of input features is examined to identify significant earthquake and structural parameters for refining ML models.
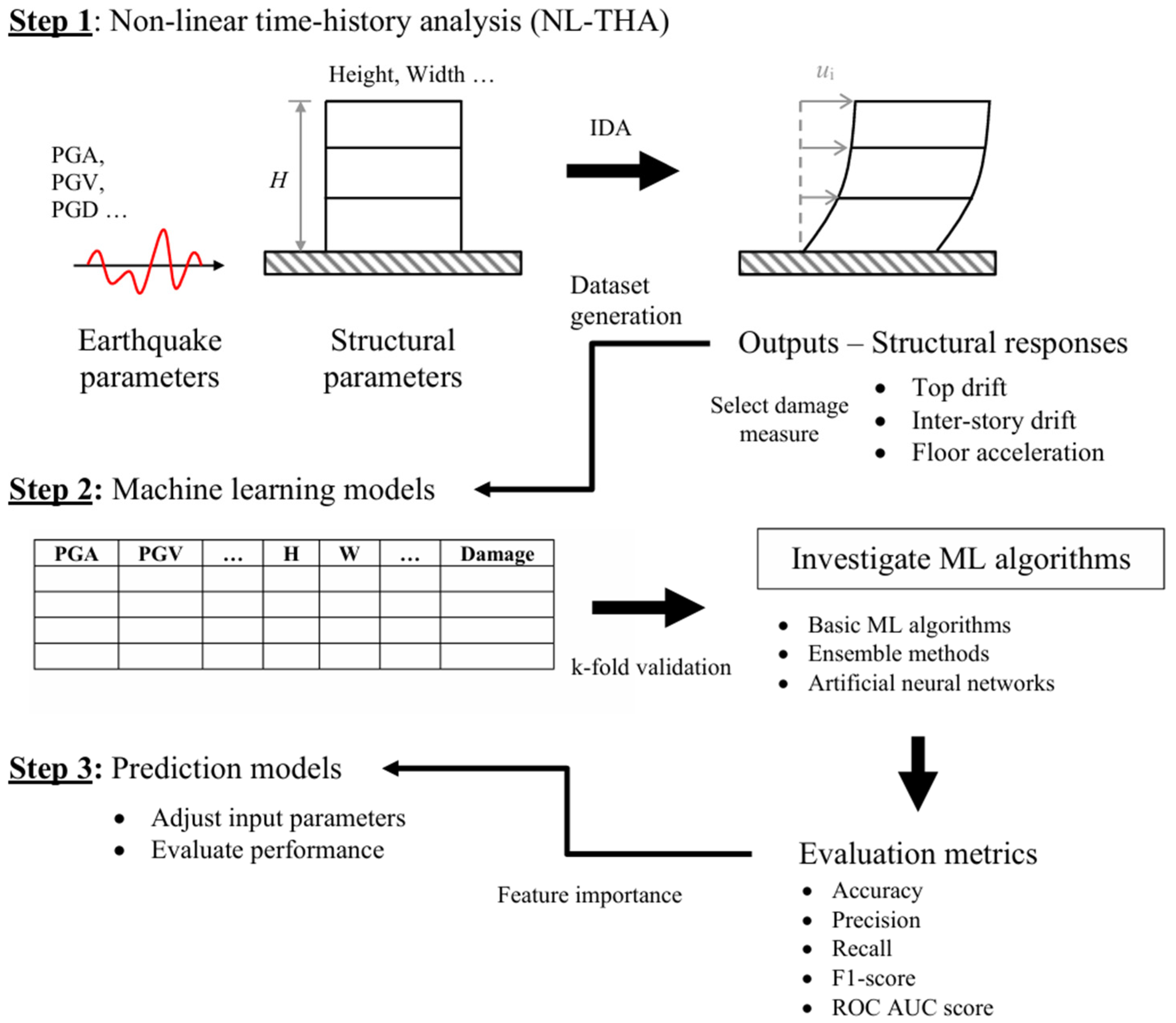
2. Methodology
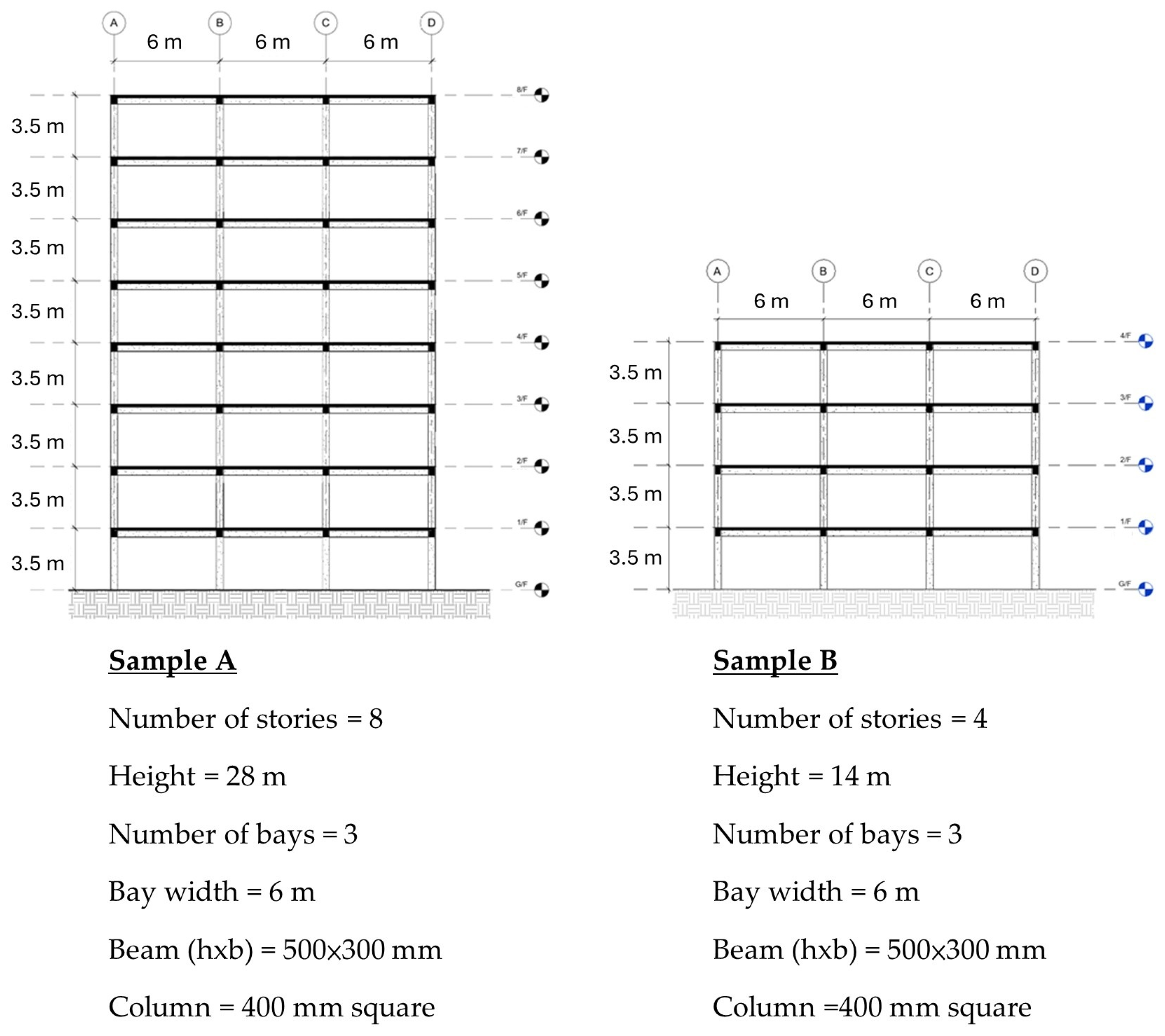
2.1. Building Models and Incremental Dynamic Analysis (IDA)
2.2. Damage Class
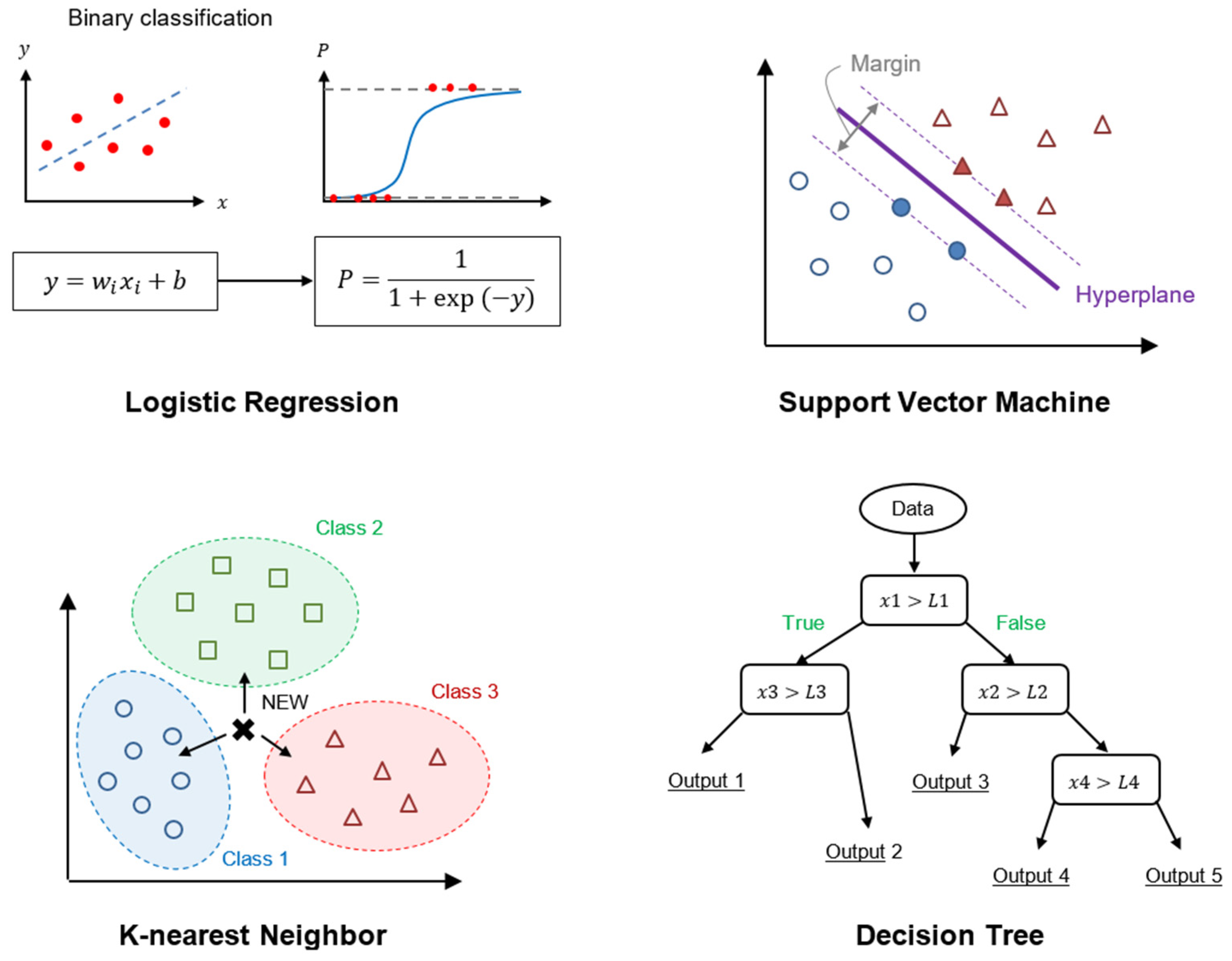
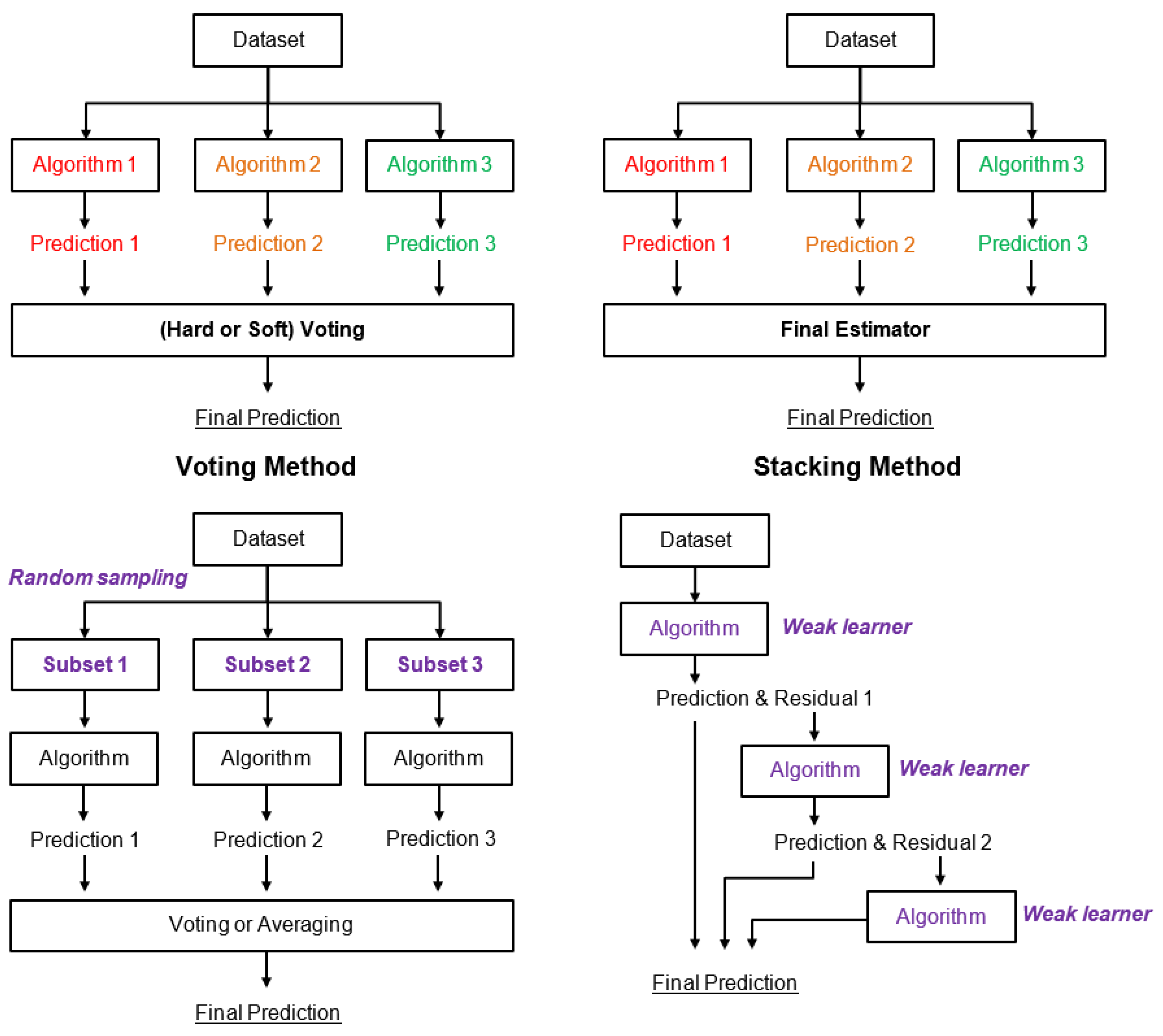
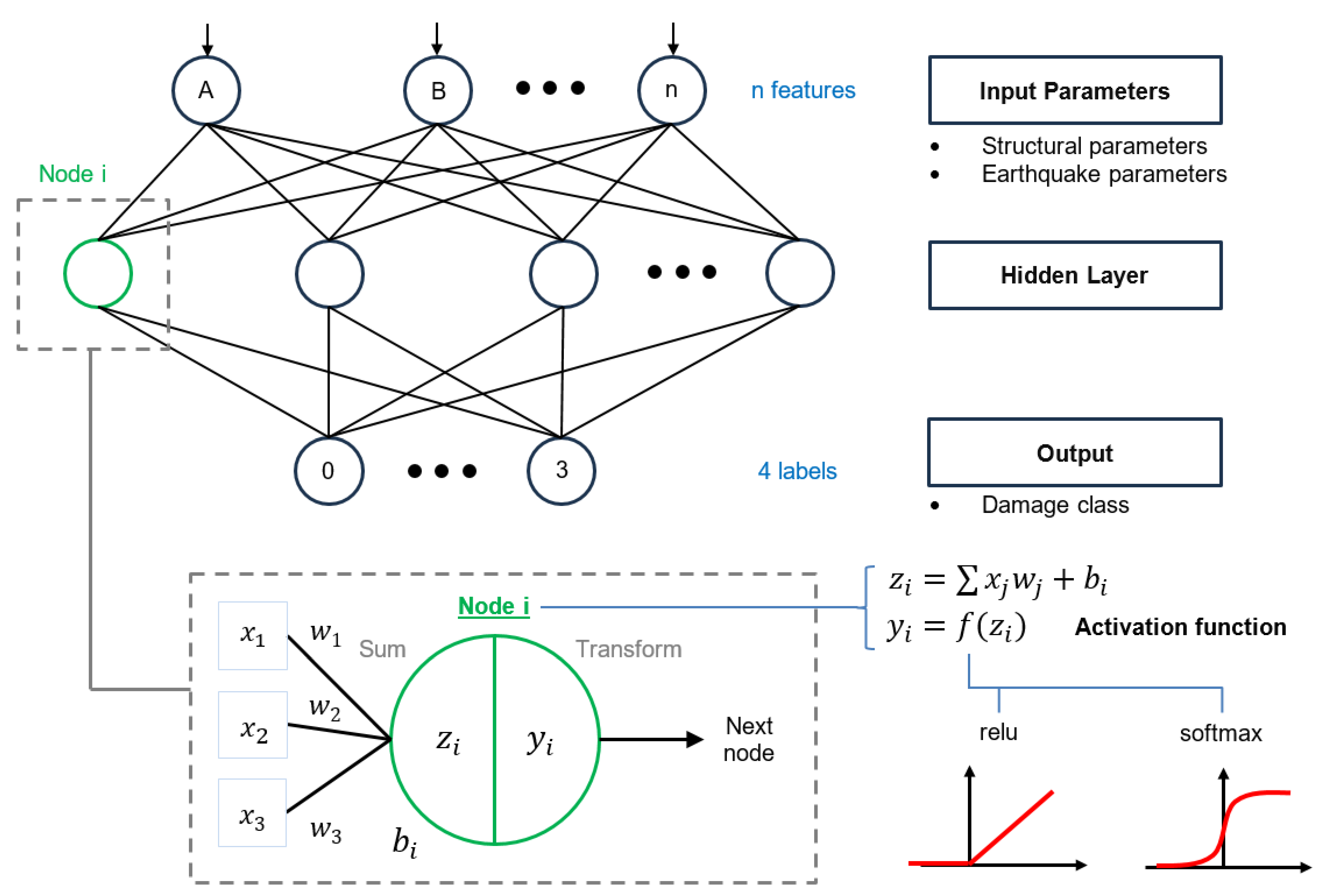
2.3. Machine Learning Algorithms
2.3.1. Basic Machine Learning Algorithms
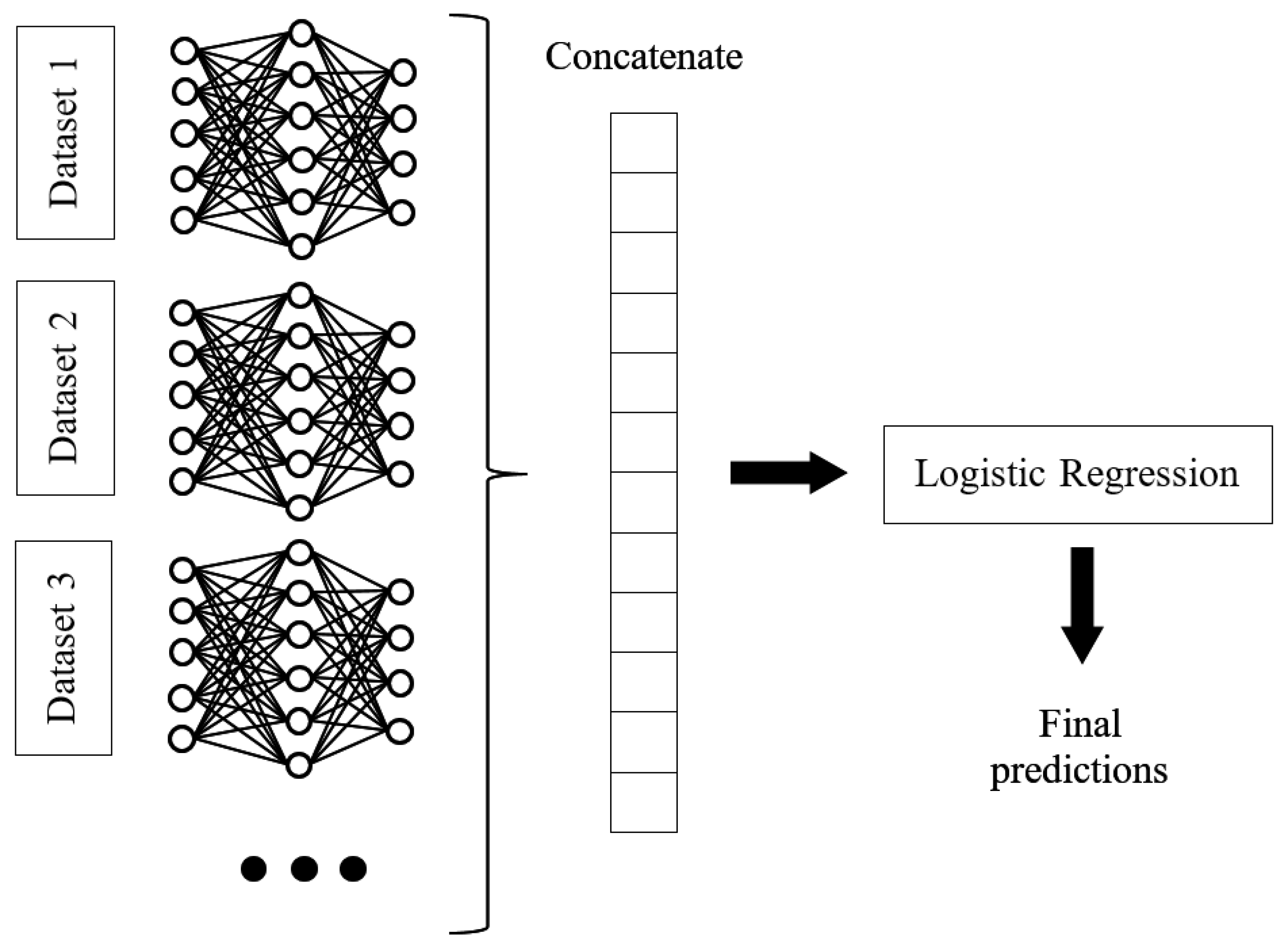
2.3.2. Ensemble Methods
2.3.3. Artificial Neural Networks (ANNs)
2.4. Data Consolidation
2.5. Data Preprocessing
2.6. Training and Testing
3. Data Analysis and Discussion
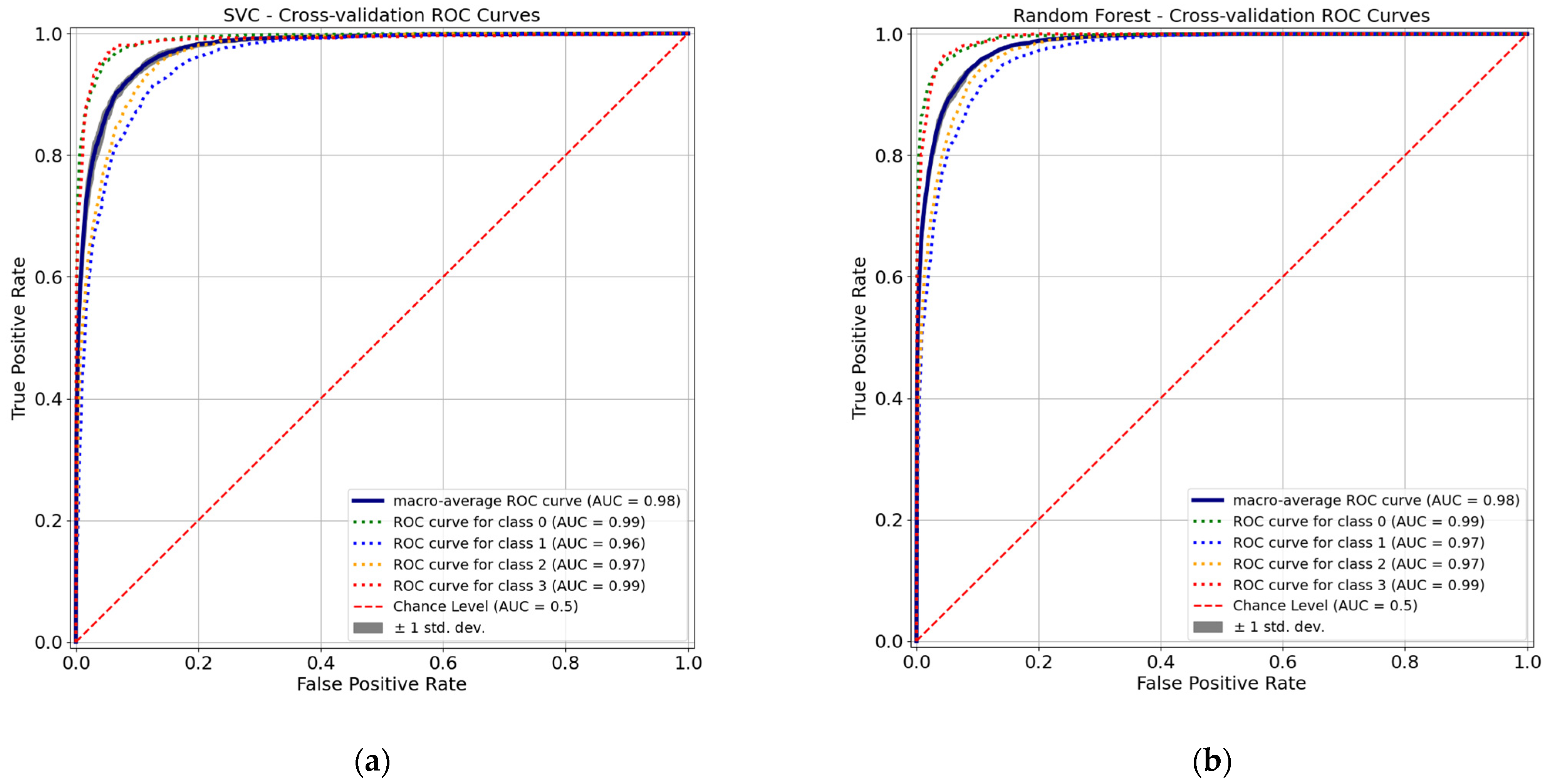
3.1. Performance of ML Models for Damage Classification
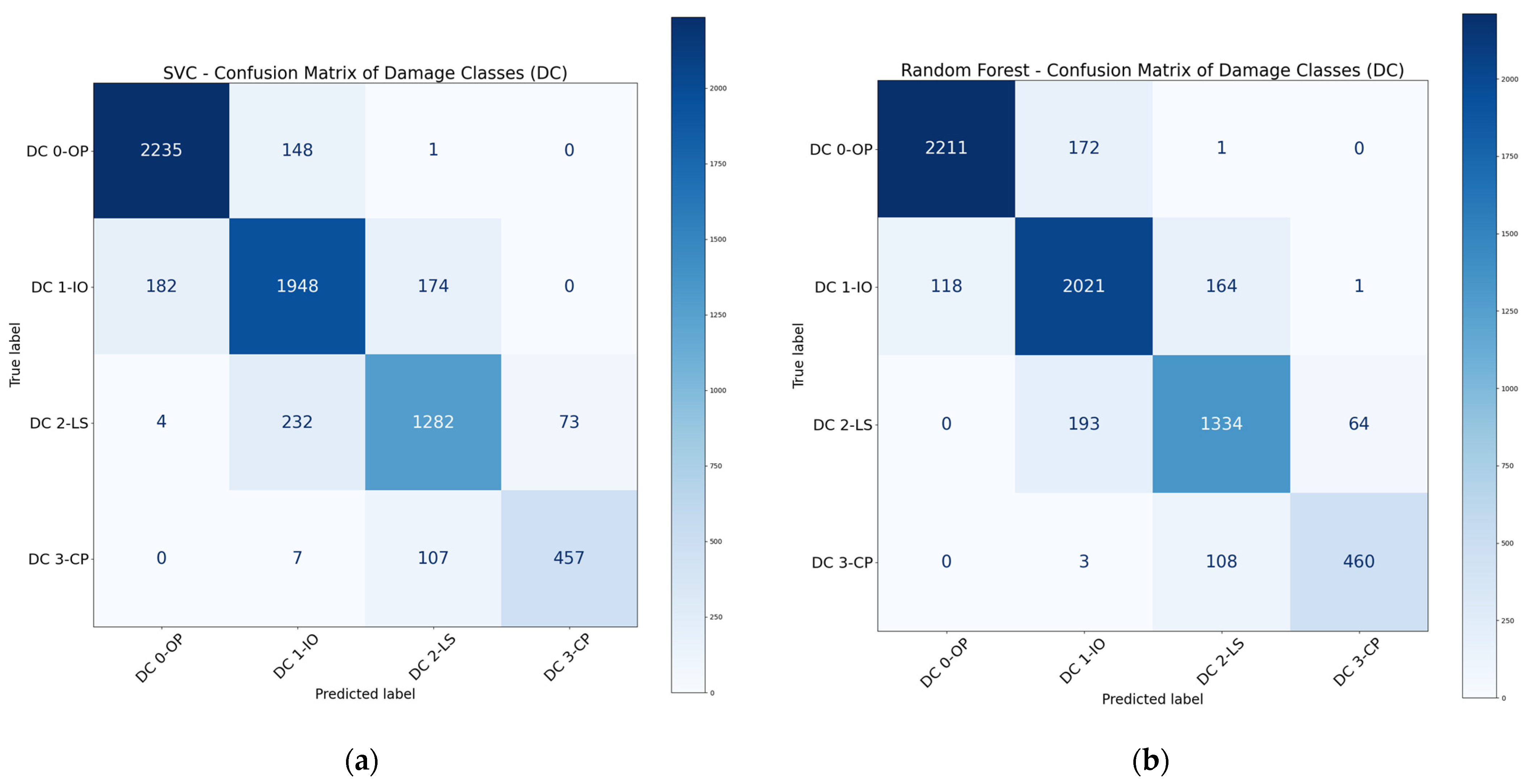
3.1.1. Performance of Basic Models
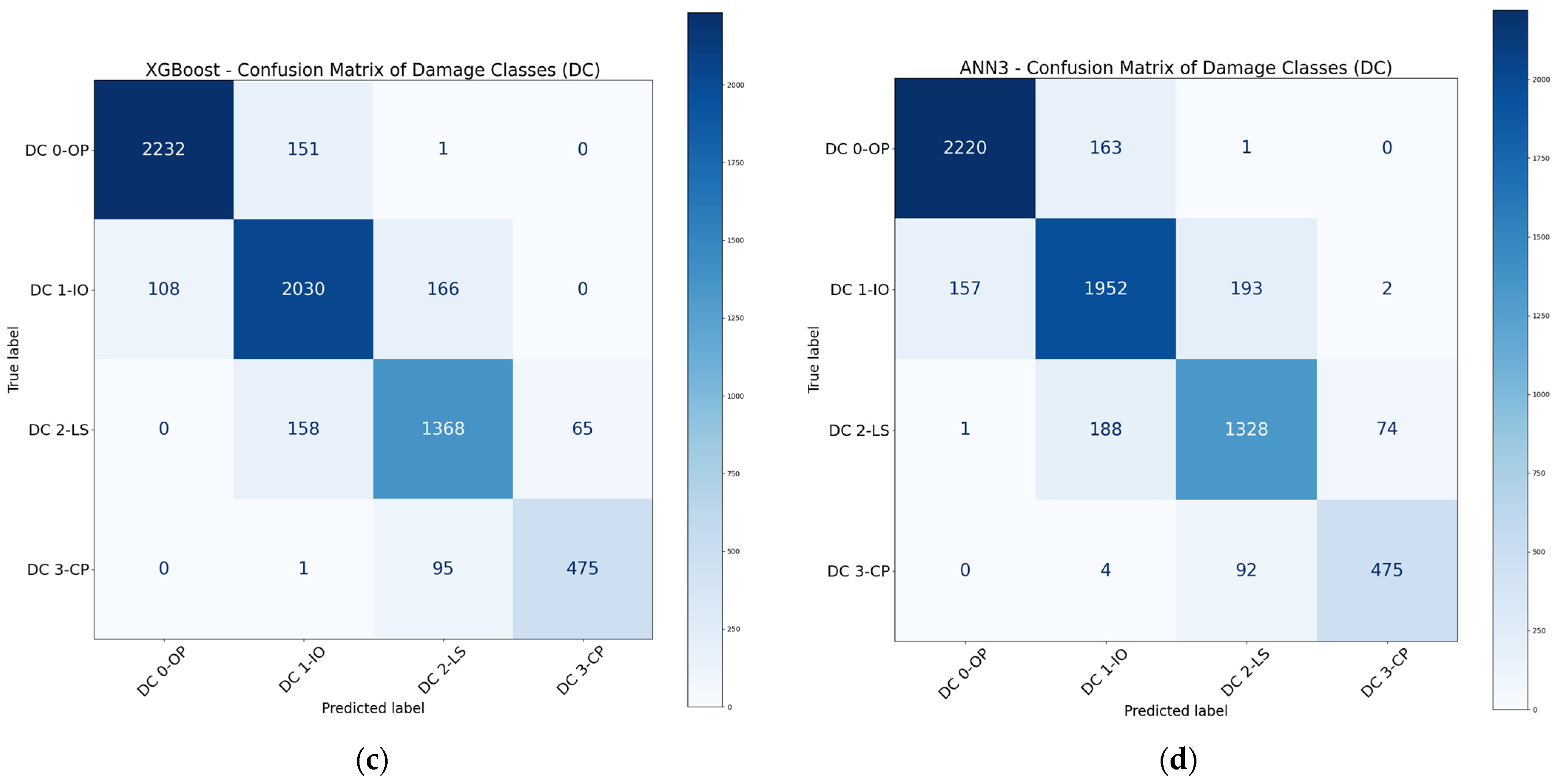
3.1.2. Performance of Ensemble Models
3.1.3. Performance of ANN Models
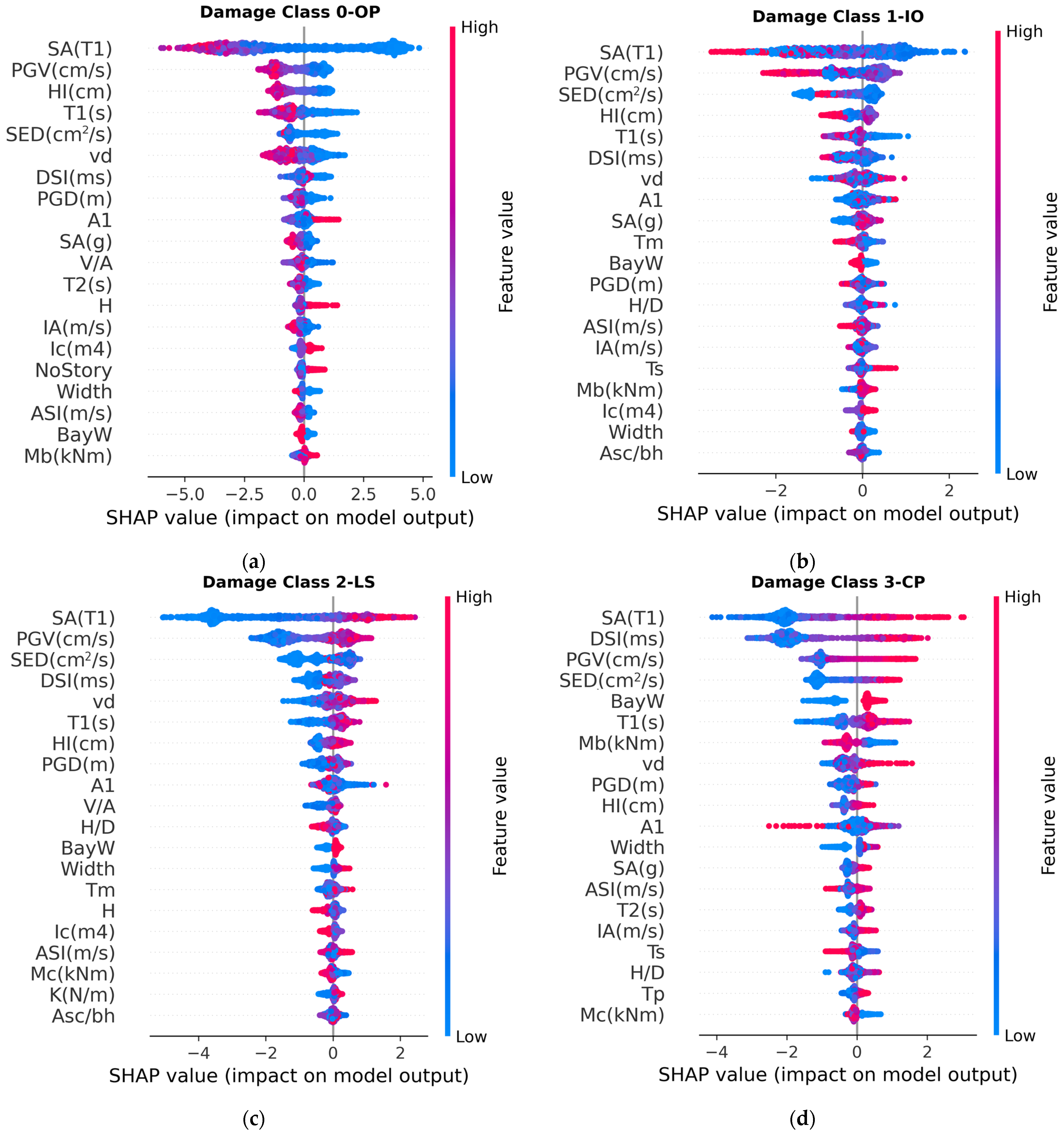
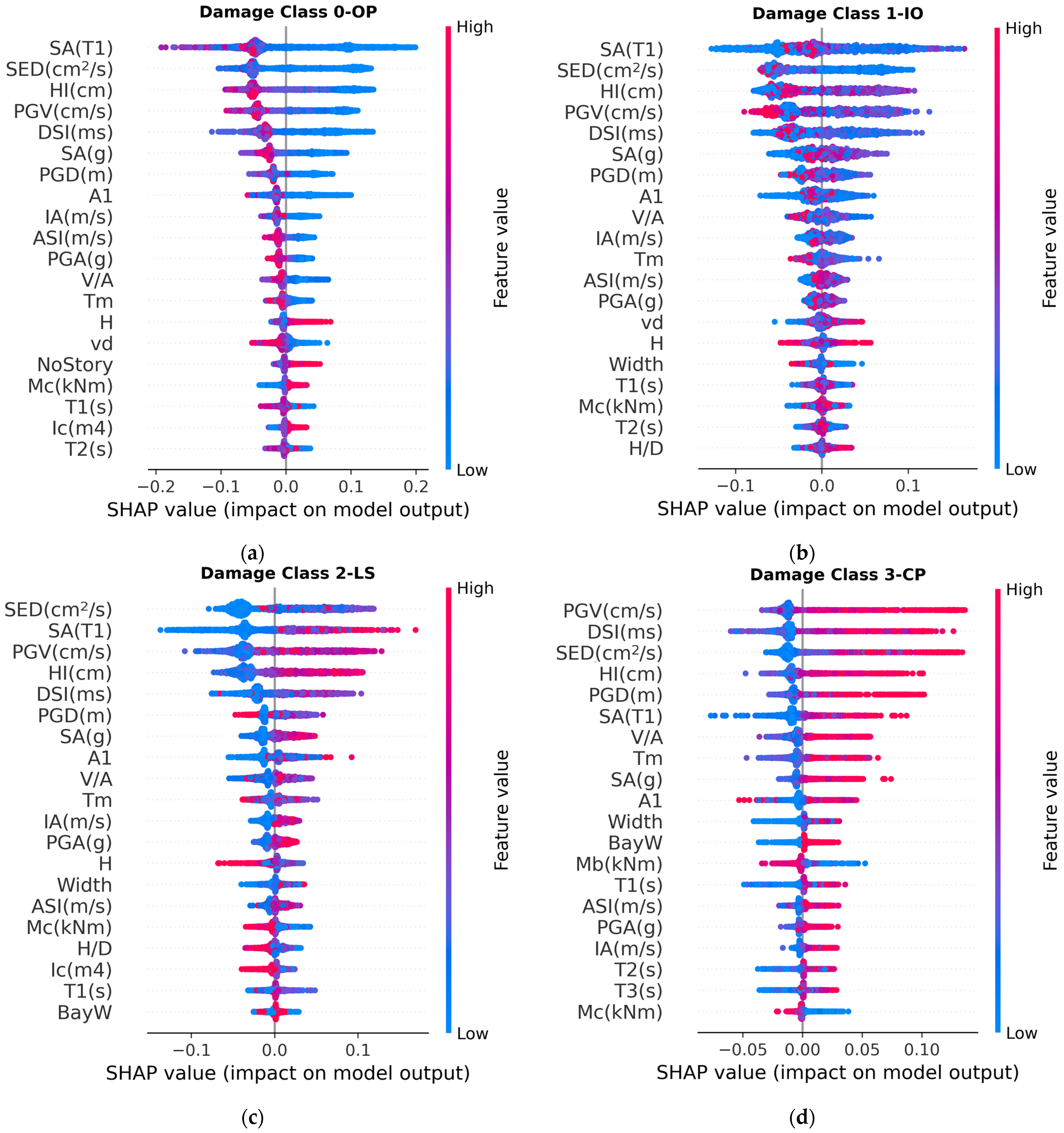
3.2. Feature Importance
3.3. Prediction Models with Reduced Parameters
4. Conclusions
- Among the five basic ML algorithms under consideration, SVM outperformed the other four basic algorithms in damage level classification. The performance of SVM is generally lower than that of the ensemble methods.
- The performance of ensemble methods was generally better than that of the basic ML algorithms. Boosting and bagging methods, particularly XGBoost and RF, were the two most effective ML algorithms and could achieve high evaluation metrics in classification tasks. On the other hand, voting and stacking methods could not always enhance the overall performance of ML models.
- ANN models were suitable for damage classification, with their performance comparable to many ensemble models. In this study, ANN models with two to three hidden layers were generally sufficient to achieve a good balance between accuracy and computation effort for classification. Further increasing the number of hidden layers cannot improve the models’ accuracy. The overall performance of ANN models could be enhanced by using stacking and boosting methods.
- The feature importance study based on impurity-based feature importance and SHAP values revealed that earthquake parameters, such as velocity-related parameters and spectral acceleration in the fundamental period, generally have large impacts on the outputs. Moreover, the geometry of buildings, maximum axial load level, first-mode vibration period, and column properties were important structural parameters that affect the outputs. The results provide valuable insights for selecting input features for future ML model development.
- ML models with optimized numbers of input features for preliminary damage classification were developed for practical applications. The studies indicated that most of the ML models could reach adequate accuracy even though the number of input features decreased. In this case, XGBoost performed the best among the other ML models under consideration. The performance of AdaBoost and RF was slightly lower than that of XGBoost. On the other hand, the performance of ANN models was satisfactory but lower than that of most of the ensemble methods.
- The ML models developed in this study are suitable for estimating the damage class of RC frames that are designed without considering seismic effects, and as such, they are suitable for buildings located in non-seismically active regions. In addition, the models were trained using far-field earthquakes. Under the conditions of near-field earthquakes, models may fail to account for the pulse-like characteristics of seismic waves.
Future Work
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| ASI | Acceleration Spectrum Intensity |
| AdaBoost | Adaptive Boosting |
| CNN | Convolutional Neural Network |
| DT | Decision Tree |
| DSI | Displacement Spectrum Intensity |
| ET | Extra Tree |
| FRP | Fiber-Reinforced Polymer |
| GBDT | Gradient Boosting Decision Tree |
| GFRP | Glass Fiber-Reinforced Polymer |
| IDA | Incremental Dynamic Analysis |
| IM | Intensity Measure |
| KNN | K-Nearest Neighbor |
| LightGBM | Light Gradient Boosting Machine |
| LR | Logistic Regression |
| MIDR | Maximum Inter-story Drift Ratio |
| ML | Machine Learning |
| NB | Naïve Bayes |
| NLTHA | Non-Linear Time–History Analysis |
| PGA | Peak Ground Acceleration |
| PGD | Peak Ground Displacement |
| PGV | Peak Ground Velocity |
| RF | Random Forest |
| ROC | Receiver Operating Characteristic |
| SED | Specific Energy Density |
| SHAP | SHapley Additive exPlanations |
| SVM | Support Vector Machine |
| XGBoost | eXtreme Gradient Boosting |
Appendix A
| Index | Name |
|---|---|
| A | 1940 Elcentro |
| B | 1995 Kobe |
| C | 1999 Chichi |
| D | 1994 Northridge |
| E | 1980 Campano Lucano |
| F | 1979 Imperial Valley |
| G | 1989 Loma Prieta |
| H | 1999 Duzce |
| I | 1999 Kocaeli |
| J | 1971 San Fernando |
| K | 1976 Friuli |
| L | 1999 Hector Mine |
| M | 1992 Landers |
| N | 1990 Manjil |
| O | 1987 Superstition Hills |
| P | 1992 Cape Mendocino |
Appendix B
| Model | Hyper-Parameter |
|---|---|
| Logistic regression (LR) | ‘C’: [0.1, 30.0] ‘solver’: [‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘saga’] |
| Support vector machine (SVM) | ‘C’: [1, 50] ‘kernel’: [‘linear’, ‘poly’, ‘rbf’] |
| Decision tree (DT) | ‘criterion’: [‘gini’, ‘entropy’, ‘log_loss’] ‘max_depth’: [5, 50] |
| K-nearest neighbor (KNN) | ‘algorithm’: [‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’] ‘n_neighbors’: [5, 20] |
| Bagging (SVM) | ‘n_estimators’: [10, 200] |
| Random forest (RF) | ‘n_estimators’: [100, 500] |
| Bagging (extra trees) | ‘n_estimators’: [100, 500] |
| Gradient boosting DT (GBDT) | ‘n_estimators’: [100, 500] |
| AdaBoost (ADA) | ‘n_estimators’: [50, 200] |
| XGBoost | ‘n_estimators’: [100, 500] ‘alpha’: [0.001, 1.0] ‘subsample’: [0.2, 1.0] |
| LightGBM | ‘num_leaves’: [10, 200] ‘max_depth’: [10, 200] |
References
- Nazari, Y.R.; Saatcioglu, M. Seismic vulnerability assessment of concrete wall buildings through fragility analysis. J. Build. Eng. 2017, 12, 202–209. [Google Scholar] [CrossRef]
- Saleemuddin, M.Z.M.; Sangle, K.K. Seismic damage assessment of reinforced concrete structure using non-linear static analysis. KSCE J. Civ. Eng. 2017, 21, 1319–1330. [Google Scholar] [CrossRef]
- Bektas, N.; Kegyes-Brassai, O. Enhancing seismic assessment and risk management of buildings: A neural network-based rapid visual screening method development. Eng. Struct. 2024, 304, 117606. [Google Scholar] [CrossRef]
- EN1998-1:2004; Eurocode 8: Design of Structures for Earthquake Resistance. European Committee for Standardization: Brussels, Belgium, 2004.
- FEMA356; Prestandard and Commentary for the Seismic Rehabilitation of Buildings. American Society of Civil Engineers: Reston, VA, USA, 2000.
- ASCE41-17; Seismic Evaluation and Retrofit of Existing Buildings. American Society of Civil Engineers: Reston, VA, USA, 2017.
- Kuria, K.K.; Kegyes-Brassai, O.K. Pushover analysis in seismic engineering: A detailed chronology and review of techniques for structural assessment. Appl. Sci. 2024, 14, 151. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2001, 31, 561–582. [Google Scholar] [CrossRef]
- Kreslin, M.; Fajfar, P. The extended N2 method considering higher mode effects in both plan and elevation. Bull. Earthq. Eng. 2012, 10, 695–715. [Google Scholar] [CrossRef]
- Xu, W.X.; Zhao, Y.S.; Yang, W.S.; Yu, D.H.; Zhao, Y.D. Seismic fragility analysis of RC frame structures based on IDA analysis and machine learning. Structures 2024, 65, 106774. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Cardone, D.; Rossino, M.; Cesualdi, G. Estimating fragility curves of pre-70 RC frame buildings considering different performance limit states. Soil Dyn. Earthq. Eng. 2018, 115, 868–881. [Google Scholar] [CrossRef]
- Pandikkadavath, M.S.; Shaijal, K.M.; Mangalathu, S.; Davis, R. Seismic robustness assessment of steel moment resisting frames employing material uncertainty incorporated incremental dynamic analysis. J. Constr. Steel Res. 2022, 191, 107200. [Google Scholar] [CrossRef]
- Peng, W.J.; Li, Z.A.; Tao, M.X. Evaluation of performance and storey drift ratio limits of high-rise structural systems with separated gravity and lateral load resisting systems using time history analysis and incremental dynamic analysis. Structures 2023, 56, 104961. [Google Scholar] [CrossRef]
- Pizarro, P.N.; Massone, L.M.; Rojas, F.R.; Ruiz, R.O. Use of convolutional networks in the conceptual structural design of shear wall buildings layout. Eng. Struct. 2021, 239, 1–19. [Google Scholar] [CrossRef]
- di Stefano, A.G.; Ruta, M.; Masera, G.; Hoque, S. Leveraging machine learning to forecast neighborhood energy use in early design stages: A preliminary application. Buildings 2024, 14, 3866. [Google Scholar] [CrossRef]
- Hosamo, H.; Mazzetto, S. Performance evaluation of machine learning models for predicting energy consumption and occupant dissatisfaction in buildings. Buildings 2025, 15, 39. [Google Scholar] [CrossRef]
- Salehi, H.; Burgueno, R. Emerging artificial intelligence methods in structural engineering. Eng. Struct. 2018, 171, 170–189. [Google Scholar] [CrossRef]
- Xie, Y.; Sichani, M.E.; Padgett, J.E.; DesRoches, R. The promise of implementing machine learning in earthquake engineering: A state-of-the-art review. Earthq. Spectra 2020, 36, 1769–1801. [Google Scholar] [CrossRef]
- Sun, H.; Burton, H.V.; Huang, H. Machine learning applications for building structural design and performance assessment: State-of-the-art review. J. Build. Eng. 2021, 33, 101816. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L. Roles of artificial intelligence in construction engineering and management: A critical review and future trends. Autom. Constr. 2021, 122, 103517. [Google Scholar] [CrossRef]
- Thai, H.T. Machine learning for structural engineering: A state-of-the-art review. Structures 2022, 38, 448–491. [Google Scholar] [CrossRef]
- Raschka, S.; Mirjalili, V. Python Machine Learning, Machine Learning and Deep Learning with Python, Scikit-Learn and TensorFlow 2, 3rd ed.; Packt Publishing Ltd.: Birmingham, UK, 2019. [Google Scholar]
- Giovanis, D.G.; Fragiadakis, M.; Papadopoulos, V. Epistemic uncertainty assessment using incremental dynamic analysis and neural networks. Bull. Earthq. Eng. 2015, 14, 529–547. [Google Scholar] [CrossRef]
- Morfidis, K.; Kostinakis, K. Approaches to the rapid seismic damage prediction of r/c buildings using artificial neural networks. Eng. Struct. 2018, 165, 120–141. [Google Scholar] [CrossRef]
- Dabiri, H.; Faramarzi, A.; Dall’Asta, A.; Tondi, E.; Fabio, M. A machine learning-based analysis for predicting fragility curve parameters of buildings. J. Build. Eng. 2022, 62, 105367. [Google Scholar] [CrossRef]
- Demertzis, K.; Kostinakis, K.; Morfidis, K.; Iliadis, L. An interpretable machine learning method for the prediction of R/C buildings’ seismic response. J. Build. Eng. 2023, 63, 105493. [Google Scholar] [CrossRef]
- Shahnazaryan, D.; O’Reilly, G.J. Next-generation non-linear and collapse prediction models for short-to-long-period systems via machine learning methods. Eng. Struct. 2024, 306, 117801. [Google Scholar] [CrossRef]
- Demir, A.; Sahin, E.K.; Demir, S. Advanced tree-based machine learning methods for predicting the seismic response of regular and irregular RC frames. Structures 2024, 64, 106524. [Google Scholar] [CrossRef]
- Işık, M.F.; Avcil, F.; Harirchian, E.; Bülbül, M.A.; Hadzima-Nyarko, M.; Işık, E.; İzol, R.; Radu, D. A hybrid artificial neural network—Particle swarm optimization algorithm model for the determination of target displacements in mid-rise regular reinforced-concrete buildings. Sustainability 2023, 15, 9715. [Google Scholar] [CrossRef]
- Payán-Serrano, O.; Bojórquez, E.; Carrillo, J.; Bojórquez, J.; Leyva, H.; Rodríguez-Castellanos, A.; Carvajal, J.; Torres, J. Seismic performance prediction of RC, BRB and SDOF structures using deep learning and the intensity measure INp. AI 2024, 5, 1496–1516. [Google Scholar] [CrossRef]
- Hwang, S.H.; Mangalathu, S.; Shin, J.; Jeon, J.S. Machine learning-based approaches for seismic demand and collapse of ductile reinforced concrete building frame. J. Build. Eng. 2021, 34, 101905. [Google Scholar] [CrossRef]
- Bhatta, S.; Dang, J. Seismic damage prediction of RC buildings using machine learning. Earthq. Eng. Struct. Dyn. 2023, 52, 3504–3527. [Google Scholar] [CrossRef]
- Mahmoudi, H.; Bitaraf, M.; Salkhordeh, M.; Soroushian, S. A rapid machine learning-based damage detection algorithm for identifying the extent of damage in concrete shear-wall buildings. Structures 2023, 47, 482–499. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Cheng, X.W.; Li, Y.; He, D.J.; Du, X.L. Rapid seismic damage state assessment of RC frames using machine learning methods. J. Build. Eng. 2023, 65, 105797. [Google Scholar] [CrossRef]
- Kostinakis, K.; Morfidis, K.; Demertzis, K.; Iliadis, L. Classification of buildings’ potential for seismic damage using a machine learning model with auto hyperparameter tuning. Eng. Struct. 2023, 290, 116359. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, X.; Fan, B.; Shahzad, M.M. A stacking ensemble-based multi-channel CNN strategy for high-accuracy damage assessment in mega-sub controlled structures. Buildings 2025, 15, 1775. [Google Scholar] [CrossRef]
- Imam, M.H.; Mohiuddin, M.; Shuman, N.M.; Oyshi, T.I.; Debnath, B.; Liham, M.I.M.H. Prediction of seismic performance of steel frame structures: A machine learning approach. Structures 2024, 69, 107547. [Google Scholar] [CrossRef]
- Asgarkhani, N.; Kazemi, F.; Jakubczyk-Galczynska, A.; Mohebi, B.; Jankowski, R. Seismic response and performance prediction of steel buckling-restrained braced frames using machine-learning methods. Eng. Appl. Artif. Intell. 2024, 128, 107388. [Google Scholar] [CrossRef]
- Kazemi, P.; Ghisi, A.; Mariani, S. Classification of the structural behavior of tall buildings with a diagrid structure: A machine learning-based approach. Algorithms 2022, 15, 349. [Google Scholar] [CrossRef]
- To, Q.B.; Lee, K.; Cuong, N.H.; Shin, J. Development of machine learning based seismic retrofit scheme for AFRP retrofitted RC column. Structures 2024, 69, 107279. [Google Scholar] [CrossRef]
- Babiker, A.; Abbas, Y.M.; Khan, M.I.; Ismail, F.I. From robust deep-learning regression to refined design formulas for punching shear strength of internal GFRP-reinforced flat slab-column connections. Eng. Struct. 2025, 326, 119534. [Google Scholar] [CrossRef]
- Wu, C.; Ma, G.; Zhu, D.; Qu, H.; Zhuang, H. Seismic retrofitting of GFRP-reinforced concrete columns using precast UHPC plates. Soil Dyn. Earthq. Eng. 2024, 187, 109024. [Google Scholar] [CrossRef]
- Junda, E.; Malaga-Chuquitaype, C.; Chawgien, K. Interpretable machine learning models for the estimation of seismic drifts in CLT buildings. J. Build. Eng. 2023, 70, 106365. [Google Scholar] [CrossRef]
- Zong, C.; Zhai, J.; Sun, X.; Liu, X.; Cheng, X.; Wang, S. Analysis of seismic responses and vibration serviceability in a high-rise timber-concrete hybrid building. Buildings 2024, 14, 2614. [Google Scholar] [CrossRef]
- Buildings Department. The Hong Kong Code of Practice for Structural Use of Concrete 2013; Hong Kong Special Administrative Region (HKSAR): Hong Kong, China, 2020. [Google Scholar]
- Luk, S.H.; Wong, H.F. Fragility curves for buildings in Hong Kong. In Proceedings of the 2019 World Congress on Advances in Structural Engineering and Mechanics (ASEM19), Jeju Island, Republic of Korea, 17–21 September 2019. [Google Scholar]
- Luk, S.H. Damage Class Prediction using Machine Learning Algorithm. In Proceedings of the 2023 World Congress on Advances in Structural Engineering and Mechanics (ASEM23), Seoul National University, Seoul, Republic of Korea, 16–18 August 2023. [Google Scholar]
- Park, Y.J.; Ang, A.H. Mechanistic seismic model for reinforced concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Kappos, A.J. Seismic damage indices for RC buildings. Prog. Struct. Eng. Mater. 1997, 1, 78–87. [Google Scholar] [CrossRef]
- Banon, H.; Biggs, J.M.; Irvine, H.M. Seismic damage in reinforced concrete frames. J. Struct. Eng. 1981, 107, 1713–1729. [Google Scholar] [CrossRef]
- Di Pasquale, E.; Cakmak, A.S. Identification of the Serviceability Limit State and Detection of Seismic Structural Damage; Technical Report NCEER-87-0022; State University of New York: Buffalo, NY, USA, 1988. [Google Scholar]
- FEMA. Hazus Earthquake Model Technical Manual; Hazus 5.1; Federal Emergency Management Agency: Washington, DC, USA, 2022.
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. A next-generation hyperparameter optimization framework. In Proceedings of the 25th SIGKDD Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression, 2nd ed.; John Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Goldberger, J.; Roweis, S.; Hinton, G.; Salakhutdinov, R. Neighborhood components analysis. In Advances in Neural Information Processing Systems 17; MIT Press: Cambridge, MA, USA, 2005; pp. 513–520. [Google Scholar]
- Breiman, L.; Friedman, J.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 1984. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995. [Google Scholar] [CrossRef]
- Freund, Y.; Schapiren, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient gradient boosting decision tree. Advances in Neural Information Processing Systems. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Red Hook, NY, USA, 4–9 December 2017. [Google Scholar]
- Atienza, R. Advanced Deep Learning with TensorFlow 2 and Keras, 2nd ed.; Packt Publishing Ltd.: Birmingham, UK, 2020. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Emami, S.; Martínez-Muñoz, G. Sequential training of neural networks with gradient boosting. IEEE Access 2023, 11, 42738–42750. [Google Scholar] [CrossRef]
- Oh, B.K.; Glisic, B.; Park, S.W.; Park, H.S. Neural network-based seismic response prediction model for building structures using artificial earthquakes. J. Sound Vib. 2020, 468, 115109. [Google Scholar] [CrossRef]
- Stafford Smith, B.; Coull, A. Tall Building Structures: Analysis and Design; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]
- FEMA P-695. Quantification of Building Seismic Performance Factors; Federal Emergency Management Agency: Washington, DC, USA, 2009.


| Name | Definition | Proposed by |
|---|---|---|
| Flexural damage ratio (stiffness-based) | Banon et al. [51] | |
| Park and Ang damage index (combined) | Park and Ang [49] | |
| Period-based damage | DiPasquale and Cakmak [52] | |
| Max. inter-story drift ratio | - |
| Damage Level/Label | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Performance 1 | OP | IO | LS | CP |
| MIDR | <1.0% | >1.0% | >2.0% | >4.0% |
| ML Model | Hyper-Parameters |
|---|---|
| Logistic regression (LR) | C = 25, solver = lbfgs |
| Support vector machine (SVM) | C = 45, kernel = poly |
| Decision tree (DT) | max_depth = 20, criterion = gini |
| K-nearest neighbor (KNN) | n_neighbors = 10, weights = distance |
| Gaussian Naïve Bayes (NB) | - |
| Bagging (SVM) | n_estimators = 100 |
| Random forest (RF) | n_estimators = 300, criterion = log_loss |
| Bagging (extra trees) | n_estimators = 210, criterion = log_loss |
| Gradient boosting DT (GBDT) | n_estimators = 240, learning_rate = 0.5 |
| AdaBoost (ADA) | estimator = DT (max_depth = 10), n_estimators = 180, learning_rate = 1.0 |
| XGBoost | booster = gbtree, eta = 0.1, n_estimators = 450, lambda = 1.0, alpha = 0.01, subsample = 0.7 |
| LightGBM | max_depth = 100, num_leaves = 200, num_iterations = 200 |
| Voting (basic) | estimator = (LR, SVM, DT, KNN) |
| Voting (ensemble) | estimator = (RF, XGB, GBDT) |
| Stacking (basic) | estimator = (LR, SVM, DT, KNN), final estimator = LR (C = 20) |
| Stacking (ensemble) | estimator = (RF, XGB, GBDT), final estimator = LR (C = 20) |
| ANN-1 | 1 hidden layer: 128 |
| ANN-2 | 1 hidden layer: 256 |
| ANN-3 | 2 hidden layers: 128, 128 |
| ANN-4 | 2 hidden layers: 256, 256 |
| ANN-5 | 3 hidden layers: 128, 128, 128 |
| ANN-6 | 3 hidden layers: 256, 256, 256 |
| Stacking ANN | 5 ANN models (2 hidden layers: 128, 128), meta-learner = LR (C = 3.0) |
| Boosting ANN | N = 25, eta = 0.2, weak learner = ANN (2 hidden layers: 128, 128) |
| Earthquake Parameter | Name | Definition | Mean | Standard Deviation (S.D.) |
|---|---|---|---|---|
| PGA (g) | Peak ground acceleration | 0.55 | 0.29 | |
| PGV (cm/s) | Peak ground velocity | 64.31 | 44.33 | |
| PGD (m) | Peak ground displacement | 0.37 | 0.34 | |
| Sa1 | Spectrum acceleration at T = 1.0 s | 0.64 | 0.40 | |
| Sa(T1) | Spectrum acceleration at T1 | 0.27 | 0.31 | |
| ASI (m/s) | Acceleration spectrum intensity | 0.47 | 0.25 | |
| HI (cm) | Housner intensity | 203.18 | 127.49 | |
| DSI (m-s) | Displacement spectrum intensity | 1.29 | 1.29 | |
| V/A | Ratio between PGV and PGA | 0.12 | 0.05 | |
| Ia (m/s) | Arias intensity | 4.98 | 4.76 | |
| Tm (s) | Mean period | where is the Fourier amplitude at frequency | 0.67 | 0.29 |
| Tp (s) | Predominant period | Time to reach max | 0.30 | 0.17 |
| Ts (s) | Significant duration | Time between 5% and 95% of | 14.91 | 7.47 |
| SED (cm2/s) | Specific energy density | 9856.81 | 16,053.95 | |
| A1 [69] | Resonance area | FFT area of a seismic wave at a frequency range near the natural frequency of the building | 112.73 | 158.19 |
| Name | Mean | Standard Deviation (S.D.) |
|---|---|---|
| Number of stories | 10.1 | 5.38 |
| Height, H (m) | 37.7 | 20.39 |
| Number of bays | 3.3 | 0.57 |
| Bay width (m) | 5.6 | 0.49 |
| Width of building, W (m) | 18.3 | 3.86 |
| Aspect ratio, H/W | 2.0 | 1.23 |
| Max axial load ratio, vd = N/fcuAc | 1.11 | 0.12 |
| Moment of inertia of beam, Ib = bh3/12 (m4) | 2.83 × 10−3 | 2.44 × 10−3 |
| Moment of inertia of column, Ic = bh3/12 (m4) | 2.59 × 10−3 | 4.97 × 10−3 |
| Moment resistance of beam, Mb (kNm) | 426.8 | 488.2 |
| Moment resistance of column, Mc (kNm) | 265.7 | 529.01 |
| First-mode period, T1 (s) | 2.65 | 1.23 |
| Second-mode period, T2 (s) | 0.86 | 0.41 |
| Third-mode period, T3 (s) | 0.50 | 0.24 |
| Fourth-mode period, T4 (s) | 0.35 | 0.17 |
| Steel ratio of beam, Asb/bh | 1.47% | 0.35% |
| Steel ratio of column, Asc/bh | 2.91% | 0.65% |
| Story stiffness, K (N/m) [70] | 21,811.1 | 23,277.4 |
| ML Model | Accuracy | Precision | Recall | F1-Score | ROC AUC Score |
|---|---|---|---|---|---|
| 1. Basic models | |||||
| Logistic regression (LR) | 0.801 | 0.792 | 0.771 | 0.780 | 0.951 |
| Support vector machine (SVM) | 0.865 | 0.860 | 0.847 | 0.853 | 0.976 |
| Decision tree (DT) | 0.820 | 0.804 | 0.808 | 0.806 | 0.873 |
| K-nearest neighbor (KNN) | 0.804 | 0.810 | 0.782 | 0.794 | 0.954 |
| Gaussian Naïve Bayes | 0.697 | 0.673 | 0.677 | 0.673 | 0.904 |
| 2. Ensemble models | |||||
| Bagging (SVM) | 0.868 | 0.881 | 0.836 | 0.853 | 0.978 |
| Random forest (RF) | 0.880 | 0.876 | 0.863 | 0.869 | 0.981 |
| Bagging (Extra trees, ET) | 0.874 | 0.868 | 0.856 | 0.861 | 0.980 |
| Gradient Boosting DT (GBDT) | 0.877 | 0.869 | 0.857 | 0.862 | 0.978 |
| AdaBoost (AdaBoost) | 0.886 | 0.886 | 0.865 | 0.874 | 0.982 |
| XGBoost (XGBoost) | 0.891 | 0.885 | 0.877 | 0.880 | 0.984 |
| LightGBM | 0.881 | 0.876 | 0.865 | 0.870 | 0.980 |
| Voting (LR, KNN, DT, SVM) | 0.861 | 0.862 | 0.842 | 0.851 | 0.976 |
| Voting (RF, XGB, ADA) | 0.883 | 0.878 | 0.868 | 0.872 | 0.982 |
| Stacking (KNN, DT, SVM, LR) | 0.862 | 0.864 | 0.841 | 0.851 | 0.964 |
| Stacking (RF, XGB, ADA) | 0.888 | 0.884 | 0.871 | 0.877 | 0.964 |
| 3. Artificial neural networks | |||||
| ANN-1 (1 layer: 128) | 0.866 | 0.864 | 0.849 | 0.854 | 0.977 |
| ANN-2 (1 layer: 256) | 0.868 | 0.866 | 0.850 | 0.856 | 0.979 |
| ANN-3 (2 layers: 128, 128) | 0.871 | 0.867 | 0.858 | 0.861 | 0.980 |
| ANN-4 (2 layers: 256, 256) | 0.868 | 0.861 | 0.862 | 0.860 | 0.979 |
| ANN-5 (3 layers: 128, 128, 128) | 0.872 | 0.868 | 0.862 | 0.864 | 0.980 |
| ANN-6 (3 layers: 256, 256, 256) | 0.867 | 0.857 | 0.858 | 0.856 | 0.978 |
| Stacking ANN | 0.882 | 0.879 | 0.869 | 0.874 | 0.983 |
| Gradient boosting ANN | 0.885 | 0.885 | 0.869 | 0.876 | 0.982 |
| ML Model | Accuracy | Precision | Recall | F1-Score | ROC AUC Score |
|---|---|---|---|---|---|
| 1. Basic model | |||||
| Support vector machine (SVM) | 0.866 | 0.863 | 0.840 | 0.850 | 0.975 |
| 2. Ensemble models | |||||
| Random forest (RF) | 0.875 | 0.866 | 0.854 | 0.859 | 0.980 |
| Bagging (extra trees, ET) | 0.868 | 0.862 | 0.848 | 0.854 | 0.978 |
| Gradient boosting DT (GBDT) | 0.860 | 0.848 | 0.835 | 0.841 | 0.971 |
| AdaBoost (AdaBoost) | 0.878 | 0.875 | 0.856 | 0.864 | 0.980 |
| XGBoost (XGBoost) | 0.882 | 0.874 | 0.863 | 0.868 | 0.982 |
| LightGBM | 0.873 | 0.862 | 0.852 | 0.856 | 0.978 |
| 3. Artificial neural networks | |||||
| ANN-1 (2 layers: 128, 128) | 0.864 | 0.855 | 0.837 | 0.844 | 0.976 |
| ANN-2 (2 layers: 256, 256) | 0.868 | 0.859 | 0.847 | 0.852 | 0.977 |
| ANN-3 (3 layers: 128, 128, 128) | 0.864 | 0.857 | 0.843 | 0.848 | 0.976 |
| ANN-4 (3 layers: 256, 256, 256) | 0.856 | 0.841 | 0.843 | 0.841 | 0.976 |
| Stacking ANN | 0.870 | 0.863 | 0.848 | 0.854 | 0.977 |
| Gradient boosting ANN | 0.873 | 0.866 | 0.852 | 0.858 | 0.979 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luk, S.H. Machine Learning-Based Methods for the Seismic Damage Classification of RC Buildings. Buildings 2025, 15, 2395. https://doi.org/10.3390/buildings15142395
Luk SH. Machine Learning-Based Methods for the Seismic Damage Classification of RC Buildings. Buildings. 2025; 15(14):2395. https://doi.org/10.3390/buildings15142395
Chicago/Turabian StyleLuk, Sung Hei. 2025. "Machine Learning-Based Methods for the Seismic Damage Classification of RC Buildings" Buildings 15, no. 14: 2395. https://doi.org/10.3390/buildings15142395
APA StyleLuk, S. H. (2025). Machine Learning-Based Methods for the Seismic Damage Classification of RC Buildings. Buildings, 15(14), 2395. https://doi.org/10.3390/buildings15142395






