Abstract
Lecture halls are characterized by large spatial dimensions, deep floor plans, and high occupant densities. Lectures are typically conducted using multimedia and blackboard-based teaching, placing higher demands on the indoor light and thermal environment compared to standard classrooms. This study aims to simulate the interrelationships between multiple building envelope parameters and building performance, in order to improve visual and thermal comfort while reducing energy consumption in cold-region lecture halls. Based on seven key envelope parameters—including openable window area ratio, west-facing window-to-wall ratio, exterior insulation thickness, shading element spacing, angle and width, and window glass type—a multi-objective optimization framework was established. The optimization process targeted three key performance indicators—useful daylight illuminance (UDI), energy use intensity (EUI), and thermal comfort percentage (TCP)—in the context of a stepped classroom. The results show that increasing the thickness of exterior insulation and reducing the width of shading components contribute positively to photothermal comfort without compromising thermal and visual performance. Compared with the baseline design, optimized schemes that incorporate appropriate west-facing window-to-wall ratios, openable window areas, insulation thicknesses, and external shading designs can reduce annual energy consumption by up to 10.82%, and increase UDI and TCP by 12.79% and 36.41%, respectively. These improvements are also found to be economically viable.
1. Introduction
Under the dual background of climate change mitigation and sustainable development, China’s growing building energy consumption has gradually become an urgent topic for research and policy [1,2]. In 2021, China’s building energy consumption in the operation phase reached 1.15 billion tons of standard coal, accounting for 21.9% of the country’s total energy consumption, of which the energy intensity per unit area of public buildings is 26.3 kgce/m2, accounting for the highest and rising trend. With high potential for energy saving, end-use energy demand such as air conditioning, equipment, etc., is the main cause of the growth of energy intensity [3,4,5,6,7]. Campus buildings are an important type of public building. In recent years, in terms of new building areas, their proportion also continues to rise; in 2022, China’s colleges and universities accounted for 9.7% of the total building area of public buildings [8]. At the same time, the proposed strategy of “Healthy China” focuses more attention on educational buildings; the development of energy efficiency in educational spaces and the focus of creating a healthy indoor environment depend largely on whether the environmental quality of the classroom is up to standard [9,10,11]. Therefore, the study of energy saving and optimization for teaching spaces in higher education is not only related to achieving the ultimate goal of energy saving in buildings, but also to improving the comfort and sustainable development of classroom users [12,13].
However, in the actual optimization process of teaching space in colleges and universities, energy consumption cannot be used as a single indicator as the basis for judging optimization, and it is also necessary to pay attention to performance indicators such as indoor lighting as well as thermal engineering [14,15]. In campus buildings, the tiered classroom is one of the typical space types in teaching with a high degree of representativeness. Lecture hall spaces are characterized by large depths, wide openings, high density of personnel, and high frequency of use, which determine more complex challenges in terms of lighting, thermal insulation, and ventilation [16]. Sadeghi et al. found that students spend approximately 30% of their school time in classrooms [17], and that the indoor thermal environment, light environment, and air quality can directly affect learning efficiency [18,19,20,21,22]. Specifically, Graça et al. suggested that thermal discomfort problems can affect mood, with behavioral responses such as reduced executive ability and reduced learning efficiency [23,24,25]. Maksoud et al. found that reasonable lighting design in educational buildings can ensure the visual comfort of classroom users, and the effective introduction of natural light can regulate the classroom student’s circadian rhythms [26,27], as well as reducing the level of student fatigue and helping them memorize information [28,29,30]. Wargocki et al. proved that improving indoor air quality can increase learning speed by 8–14% [31,32]; indoor thermal environment, light environment and air quality can even directly affect students’ health. When the human body’s tactile organs are stimulated, body heat is exacerbated, leading to muscle weakness, dizziness, and physical and mental fatigue [33,34,35,36,37,38,39].
For instance, in countries like Italy and Poland, the prolonged low-temperature environment in winter places higher demands on the insulation performance of building envelope structures [40,41]. The use of rational envelope design and shading design in classrooms is a key factor in reducing energy consumption and improving comfort [42,43]. First, for the design of the exterior envelope, existing studies have found that key parameters of the building envelope (e.g., window-to-wall ratio, insulation thickness, glazing type, etc.) have a significant impact on the quality of lighting, indoor thermal stability, and energy consumption levels [44]. For example, higher window-to-wall ratios increase the heat transfer load while enhancing the level of daylighting, resulting in increased heat loss in winter and overheating in summer [45]; Ricardo et al. proposed a method to optimize the thickness of the thermal insulation of the exterior envelope in the renovation of campus buildings to minimize the annual heating load and the thermal discomfort time [46]. Lakhdari et al. optimized the classroom glazing type and other design variables by effectively improving the three performance indicators of UDI, ACP and EUI [47]. Secondly, the shading system is an important regulating element of the enclosure; the construction form, angle, spacing and other parameters of the shading components will directly affect the solar radiation entry and glare control effect [48]. In addition, Thalfeldt and Zhao et al. showed that under cold climate conditions, building shading, the heat transfer coefficient of external windows, and the window-to-wall ratio are key factors in determining building energy consumption [49,50], and the above elements can be included in the optimization study as design variables.
There exists an interaction between solar thermal performance indicators and energy consumption indicators [51], and most of the existing studies have improved these building performance indicators by multi-objective optimization. Although the existing studies have made great progress in the methodology, there are still significant deficiencies in the setting of research objects and design variables. First of all, most of the existing multi-objective building optimization studies focus on office buildings or residential buildings, among others. Wu et al. studied the envelope parameters of open office spaces and proposed a multi-objective framework (MOO) to improve indoor thermal and optical comfort and reduce energy consumption [51]. Fesanghary et al. propose a multi-objective optimization model for residential buildings, which is aimed at reducing the life cycle cost (LCC) and carbon dioxide emissions (CO2-eq) [52]. However, educational buildings differ from office or residential buildings in terms of light and heat comfort, especially in terms of heat demand. Zomorodian et al. pointed out that classrooms differ from office and residential buildings in terms of time periods, personnel activities/clothing, behavioral freedom, and temperature setting points, and specialized research on thermal comfort is required [29]. There are relatively few studies on the optimization of teaching spaces in colleges and universities, especially lecture halls. Most of the current studies are still limited to the dual-objective optimization of energy consumption and lighting or energy consumption and thermal comfort, and there is a lack of systematic studies that incorporate visual comfort, thermal environmental comfort and energy efficiency synergy into a unified framework [53,54,55,56]. In addition, the design variable settings are mostly focused on conventional parameters such as window-to-wall ratio and insulation thickness, while the openable window area ratio, as an important variable to measure the potential of natural ventilation, has been given insufficient attention in existing studies, which makes it more difficult to reflect the positive guiding effect of natural ventilation strategies on energy efficiency and comfort [51]. Finally, studies on cold climate regions are generally insufficient, and most of the current optimization models are constructed based on temperate or subtropical climatic conditions, and there are limitations in the adaptability of their findings [57,58,59].
Based on the above problems, this study takes classroom 117 (a tiered classroom) of the second public teaching building of Hebei University of Engineering as an example, focusing on tiered classrooms in colleges and universities in cold regions, and carries out a multi-objective optimization study on the design parameters of the enclosure structure. By constructing a parametric model and selecting seven design variables, including the angle, spacing and width of sunshading elements, the west side window-to-wall ratio, the openable window area ratio, the type of external window glass and the thickness of thermal insulation, the simulation analysis is carried out by using plug-ins such as Ladybug, Honeybee, EnergyPlus, etc., and the optimization objective function is established by introducing three performance indexes, namely UDI, TCP, and EUI, and the optimization objective function is established by using the SPEA2 algorithm in the Octopus plug-in to generate the Pareto frontier solution set, combining the performance optimization scheme with the life cycle cost (LCC) to evaluate the economy, and finally forming a systematic optimization proposal for the parameters of the college tiered classroom enclosure. The study aims to improve the research on the optimization of light and heat comfort and energy consumption in tiered college classrooms in cold regions, to construct a performance optimization system adapted to the climate and spatial functional characteristics of cold regions, and to provide theoretical support and a basis for design and renovation for the construction of green campuses.
2. Methodology
This study employs a comprehensive methodology comprising field surveys, questionnaire collection, parametric modeling, performance simulation, economic and sensitivity analyses, and multi-criteria decision-making. User feedback and environmental data were first collected to assess thermal and visual comfort. A parametric model was then built on the Grasshopper platform, using Ladybug and Honeybee for daylighting, thermal, and energy simulations. Life cycle cost (LCC) and sensitivity analyses were conducted to evaluate economic feasibility and key influencing factors. Finally, the Pareto-optimal solutions were ranked using MCDM methods (TOPSIS, VIKOR, RSR) to identify the most balanced design in terms of performance and cost.
2.1. Research Approach
2.1.1. Survey Method
A questionnaire was distributed to investigate students’ subjective satisfaction with the lighting and thermal environment of the tiered classroom in the range of 300–360 people. The questionnaire involves a typical winter-season questionnaire survey, including respondents’ basic personal information, clothing thermal resistance, humidity and wind speed, causes of eyestrain, lighting comfort, etc.; data on the temperature and humidity and light levels of the tiered classroom under natural ventilation were measured to objectively quantify the indoor space in terms of the light and heat comfort level, combining subjective questionnaire research with measured data to assess the potential to optimize the light and heat comfort in the tiered classroom.
2.1.2. Simulation and Analysis Method
The research tools selected included the Ladybug and Honeybee [60,61] plug-ins of the Grasshopper [62] platform in Rhinoceros [63], articulated with Radiance [64] and EnergyPlus [65] for light, heat and energy simulation. Their better interactivity alongside data coupling can avoid repetitive modeling, making them the preferred platforms for integrated simulation.
The physical environment of a building contains light and heat environments. Within this, light and thermal metrics can be quantified and have the feasibility of being optimized. This study needs to obtain trade-offs between light, thermal comfort and building energy consumption and establish a multi-objective optimization framework to evaluate the effective daily illumination (UDI), thermal comfort percentage (TCP), and energy use intensity (EUI) to determine the quality of the indoor environment and the degree of energy saving.
The overall optimization simulation process is shown in Figure 1, which is divided into three main links. Firstly, the seven relevant parameters of sunshading panel spacing, angle, and width, openable window area ratio, external insulation thickness, and external window glass type are selected as the optimization design variables, and a parametric model is established; in the second step, the model is linked with the above plug-in to simulate the light and thermal comfort and energy consumption, and the parameters of each index are derived before optimization; finally, the value interval of the optimization variables is determined and the seven design variables and three evaluation indexes are linked with the Octopus plug-in, and the Pareto-optimal solution set is derived through the intensity Pareto evolution algorithm and the hypervolume estimation algorithm [66]. And each optimization parameter exists independently without mutual interference; the evaluation metrics are dependent variables, which change due to the change in optimization parameters. The optimization process is carried out simultaneously with the multi-objective performance simulation of each generation, and the function increases the chance in convergence with the increase in the number of algorithmic generations, gradually approaching the optimal solution, and finally arriving at the Pareto frontier solution, and then filtering out the preferred solution according to the solution set.
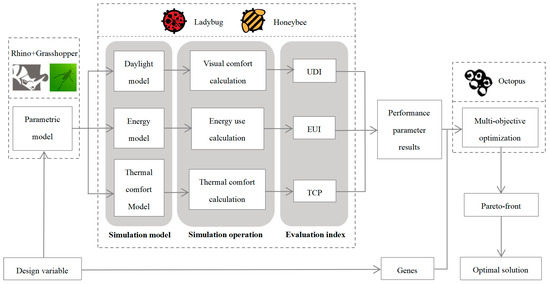
Figure 1.
Optimization of the simulation flow.
After completing the simulation of building daylighting, thermal environment, and energy performance, this study further conducted economic analysis and sensitivity analysis. The economic analysis, based on life cycle cost (LCC), evaluates the economic feasibility of different optimized designs during building operation, aiming to determine whether performance improvements are accompanied by reasonable investment returns. The sensitivity analysis quantifies the influence of each design variable on performance indicators by systematically comparing simulation results, thereby identifying the key parameters affecting daylighting, thermal comfort, and energy consumption. This provides a data-driven foundation for subsequent optimization and decision-making.
In addition, to select the most well-rounded design solution from the Pareto front, a multi-criteria decision-making (MCDM) approach was introduced to rank each solution by weighted evaluation. This method comprehensively considers four performance aspects: energy consumption, visual comfort, thermal comfort, and economic performance. Based on the integrated scores, the optimal and several sub-optimal solutions are identified, offering reliable references for practical building design and retrofit.
2.2. Case Study Construction and Questionnaire Research
According to the “Architectural Design Sourcebook” (3rd edition), the research will utilize data on three sizes of tiered classroom, holding a range of 300–360 people, including the classroom depth and volume, its surface area in contact with air, and the window opening area. The latter value is larger than the first two, resulting in lower light and thermal comfort and higher energy consumption; the optimization of the largest space can be upgraded. Therefore, in this study, the 300–360-person stepped classroom was selected to establish a typical stepped classroom model.
Classroom 117 (Figure 2) in the second public teaching building of Hebei University of Engineering was selected as the research object. The classroom is located on the southwest side of the west building of the second public teaching building facing south, with windows on the west and east sides, and the window-to-wall ratio on the west side is 0.45, which makes the users suffer from western sunlight in summer, while the east side is adjacent to the patio. The southeast and west sides are in contact with the exterior and are prone to large temperature loss in winter. The stepped classroom is 26 m long and 17.3 m wide, with a floor height of 5.4 m, and the side windows have no shading elements.

Figure 2.
Classroom 117’s district and floor plan. (a) Location map of the classroom; (b) floor plan of the classroom, a tiered lecture hall.
Since classroom 117 does not have shading elements, this provides a basis for retrofitting to optimize building performance. The east- and west-side shading elements are generally set in a vertical manner; in addition to the openable area of the window, the thickness of the external insulation layer is also closely related to indoor comfort, which will be included in the study considerations. As shown in Figure 3, the time period of this study excludes the influence of summer and winter vacations and includes the normal school hours of 8:30–12:00 and 13:30–17:00, as well as other specific parameters as shown in Table 1. Since classroom 117 only has windows on the east and west sides, and the east-side windows are adjacent to the narrow 2.6 m wide patio that separates the indoor space, it is not necessary to set up shading apparatus outside the east-side window openings, and this study takes the shading apparatus set up outside the windows on the west side of the tiered classroom as the design variables, and the members are rotated clockwise for negative values and counterclockwise for positive values (Figure 4). In addition, the possible effects of differences in the heat transfer coefficient K, shading coefficient SC, and visible light transmission ratio Tvis on the optimization results were considered when the type of external window glass was the design variable.
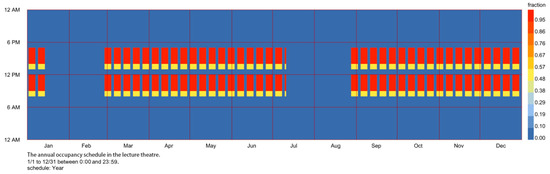
Figure 3.
Personnel attendance sheet.

Table 1.
Personnel and equipment parameterization.
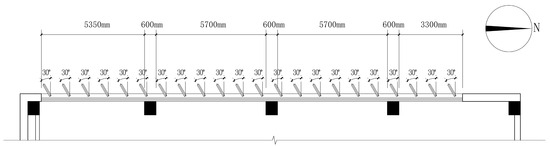
Figure 4.
Schematic diagram of west window shading elements.
The questionnaires for the tiered classrooms were distributed from 8 January 2024 to 1 March 2024 (except for the winter holidays) and were divided into two forms: offline distribution and online links. A total of 519 valid questionnaires were collected and 11 invalid questionnaires were excluded. In the end, 289 offline questionnaires and 219 online questionnaires were included, and a total of 508 valid questionnaires were recovered. The questionnaires covered both undergraduate and postgraduate academic levels. Among them, undergraduates accounted for 69.88% (355), and postgraduates accounted for 30.12% (153), so the sample had a wide range in age structure. In terms of gender ratio, there were 276 males (54.33%) and 232 females (45.67%), a relatively balanced distribution. The health condition of the respondents was generally good, with 86.02% (437 respondents) rating themselves as “good”, 9.06% (46 respondents) as “fair”, and 4.92% (25 respondents) indicating that they were suffering from a cold at the time of the survey. In terms of the choice of permanent seating during the study period, the highest percentage of students chose the window seat, 56.69% (288), followed by other seats (20.08%, 102), by the door (14.76%, 75) and near the heated area (8.46%, 43). This distribution reflects the actual preference of students for different seating areas in terms of perceived light and heat environment.
The final sample includes 289 offline questionnaires and 219 online questionnaires. The results of the light and heat environment questionnaire are shown in Figure 5; 50.39% of the respondents thought that the tiered classroom was of moderate light comfort, while another 20.47% thought that the environment was bright or too bright, and 3.15% thought that the environment was dark or too dark, and the proportion of respondents who thought that it was too bright was higher than the proportion of those who thought that it was too dark; 48.03% of the respondents thought that the heat comfort in this classroom was moderate, which means that nearly half of the respondents to the questionnaire were thermo-neutral in this classroom during the winter; another 18.9% thought the environment was warm or too hot, while 7.09% thought the environment was cool or too cold, and the percentage of respondents who thought it was too hot was higher than the percentage of respondents who thought it was too cold. Overall, the tiered classroom has some potential for optimization of light and heat comfort.
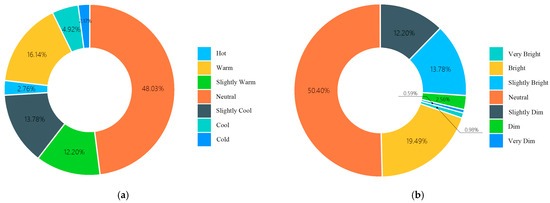
Figure 5.
Pie chart of subjective evaluation of winter solar thermal comfort. (a) Subjective evaluation map of thermal comfort in winter; (b) subjective evaluation map of light comfort in winter.
2.3. Performance Simulation
2.3.1. Light Comfort Simulation
UDI (useful daylight illuminance), also known as effective daylight illuminance, refers to the proportion of time that natural light is effectively illuminating a certain range of indoor work surfaces throughout the year. A study on light environment by Mardaljevic et al. in 2006 categorized UDI into three ranges, in which the illuminance interval of 100–2000 lx can maintain an indoor illuminance level that is neither too dark nor too bright [67], and thus can effectively avoid the occurrence of indoor illuminance overload and indoor glare. According to the different materials of each component of the room, the corresponding reflectance and transmittance were measured (Table 2); the vertical projection surface of the stepped classroom was divided into a number of equal-area test points, and sensors were set up in a grid of 0.75 m above the elevation of each part of the floor (i.e., the simulated measurement point plane was set at a horizontal height of 0.75 m. The UDI100–2000 values of all sensors in the room are calculated through simulation, and when the value of the attendance table at a certain hour is ≥0.1, the system determines that the classroom is occupied at this point in time. Finally, all UDI100–2000 data are averaged and the overall value sought is the average UDI100–2000. In the optimization simulation process, the higher the value, the better the indoor lighting environment of the tiered classroom.

Table 2.
Optical parameter settings for stepped classroom.
2.3.2. Thermal Comfort Simulation
Handan area is a cold IIB area based on heating degree days (HDD18 < 3800 °C-d) and air-conditioning degree days (CDD26 ≤ 90 °C-d), and according to China’s Uniform Standard for Civil Building Design (GB 50352-2019) [68], buildings in cold IIB areas need to satisfy the requirements of heat preservation in winter and heat protection in summer, so the study is conducted to simulate the indoor environment throughout the year.
The predicted mean thermal sensation index PMV (Predicted Mean Vote) proposed by Danish scholar Per Olaf Fanger in 1960 is the most comprehensive indoor thermal comfort evaluation index with a wide range of use, high recognition, and the most comprehensive consideration [69]. The thermal comfort model takes six factors affecting human thermal comfort (air temperature, humidity, ambient radiant temperature, clothing thermal resistance, and human activity) as independent variables and human thermal sensation as the dependent variable. The PMV index is able to effectively predict human thermal sensation and quantitatively evaluate the average level of hot and cold sensation of the majority of the people in a certain environment.
The PMV evaluation index is recognized by the American Society of Heating and Air Conditioning (ASHRAE Standard 55) [70] and the International Organization for Standardization standard (ISO7730) [71]. The correspondence between the PMV value and the thermal sensation is shown in Table 3, in which the comfort interval recommended by ISO7730 is from −0.5 to +0.5, and the comfort interval recommended by our country is from −1 to +1 [72].

Table 3.
Predicted thermal sensory factor (PMV).
Based on the construction drawings of the second public teaching building of Hebei University of Engineering, classroom 117, the thermal performance parameters of the enclosure structure were input (Table 4), and the Ladybug plug-in of the Grasshopper platform was used to read the CSWD webpage and obtain the EPW meteorological file for thermal environment simulation. By removing the summer and winter holidays of the annual thermal environment simulation analysis and screening out −1.0 ≤ PMV ≤ 1.0 in line with the thermal comfort standard interval statistics, we obtain the annual thermal comfort hours; this divided by the number of hours in the whole year obtains the ratio of annual thermal comfort hours (TCP). TCP can intuitively reflect the proportion of thermal comfort time in a year; in the optimization of the simulation process, the larger the proportion of annual thermal comfort hours, the better.

Table 4.
Thermal performance parameters of the enclosed structure of the stepped classroom.
2.3.3. Energy Consumption Simulation
In the energy simulation, the use of natural light as well as shading components is considered to reduce the building’s energy consumption, and the air-conditioning setpoints are set to relatively energy-efficient temperatures according to the Chinese Building Code Level 2 standard [73]: 26 °C for cooling and 18 °C for heating.
18 °C ≤ outdoor dry bulb temperature ≤ 26 °C
18.5 °C ≤ indoor dry bulb temperature ≤ 25.5 °C
Outdoor dry bulb temperature—Indoor dry bulb temperature ≥ 0.5 °C
When conditions (1), (2), and (3) are satisfied, natural ventilation will be enabled. The main cooling equipment for the stepped classroom is an air conditioner in the summer and a ground-source heat pump in the winter. The equipment loads remain constant in all building design variables and can therefore be ignored in the optimization process.
In the process of building performance analysis, energy use intensity (EUI) has been increasingly used in recent years [74]. Since building energy consumption is affected by a variety of internal and external factors (climatic conditions, heating and cooling loads, time–activity patterns of occupants, etc.), EUI, as an evaluation index that integrates a number of energy consumption parameters such as heating, cooling and artificial lighting loads throughout the year, is more appropriate to be used as an energy consumption evaluation index in this study. The energy use intensity (EUI) is calculated by dividing the total annual energy load (the sum of heating, cooling and electric lighting loads) by the floor area [75].
2.4. Economic Analysis
For the renovation of stepped classrooms, there is a need to avoid pursuing indoor comfort and energy efficiency at the expense of their economic investment costs. Due to the different purchasing power in different periods, it is necessary to compare the costs in different future periods with the initial investment at the time of installation and discount the future costs or benefits to present value through discounting based on time value. Therefore, this study uses the full life cycle cost (LCC) for economic analysis. The full life cycle cost method is a method that analyzes the sum of the present value of the investment and operating costs of a project over its entire life cycle by systematically analyzing the present value of the investment and operating costs of the project. The increment of the whole life cycle cost of the building after the optimized design, i.e., the difference between the whole life cycle cost of the optimized scenario (LCCpost) and the whole life cycle cost of the base scenario (LCCbase), dLCC, can intuitively respond to the benefits brought by the optimized design [76]. This study uses a 30-year analysis period, whereas insulation, windows, and shading devices typically have lifetimes of 30 years or longer [77]; therefore, replacement costs were not considered in this study. Based on the unit floor area, Equations (4)–(8) were used. If dLCC < 0, it indicates that the project is economically feasible, and if the value of dLCC is smaller, its economy is better.
where dLCC denotes the full life cycle cost increment after classroom optimization and retrofit, CNY/m2; dIC denotes the initial investment cost of the project for classroom optimization and retrofit, CNY/m2; dOC denotes the present value of the difference between the baseline state of the full-life-cycle project and the difference in the project’s energy cost after retrofit and optimization, CNY/m2; Ci denotes the initial investment cost of the ith optimization measure, CNY; A denotes the building area, m2; PWF represents the present value factor; ECC represents the annual energy consumption cost of the building, CNY/m2; I* represents the discount rate, %; N represents the number of years of the life cycle of the invested object, taken as 30 years; I represents the bank interest rate, taken as 2.57%; g represents the inflation rate, taken as 2%.
In this study, the main energy costs of the stepped classroom are focused on the ground-source heat pump heating as well as the cooling of the central air conditioning, in addition to lighting energy, fan energy, and other electrical equipment energy, calculated using Equation (9).
where QH represents the annual heating load of the classroom, kW-h /m2; QC represents the annual cooling load of the classroom, kW-h /m2; ηH represents the efficiency of the heating system, i.e., the efficiency of the ground-source heat pump, which is taken to be 0.9; ηC represents the efficiency of the refrigeration system, which is taken to be 3.0; PE represents the price of electricity, which is taken to be 0.62 CNY/kW-h; and Eo represents the loss of other energy.
2.5. Multi-Objective Optimization and Fitness Functions
In this study, we need to simultaneously optimize the three objectives of EUI, UDI and TCP to obtain the Pareto frontier solution set to find the optimal solutions for each of the three objectives. The parameters of elasticity, mutation probability, mutation rate, and crossover rate in Octopus are set to 0.5, 0.1, 0.9, and 0.8, respectively. The population size is set to 50. Since Octopus uses SPEA-2 automatic control design variables with hyper-mutation, it will continuously search for the minimum value of the three objectives, so the targets to be maximized, effective daily illuminance, UDI, and thermal comfort percentage (TCP), will both be multiplied by −1.
The multi-optimization results are affected by the range of values of the design variables. Table 5 demonstrates the specific ranges of the seven design variables including the building envelope, shading components, etc. Selection of reasonable values for the design variables can be effective in improving the building performance metrics. This study selected several different types of glass (Table 6); the construction practice of inserting rare gases into the middle of glass and the addition of low-E glass with low emissivity characteristics can improve the thermal insulation capacity of a building in cold regions. In addition, regarding the addition of vertical shading components, the spacing, angle and depth of the shading components were adequately selected as three indicators, which are more conducive to controlling the entry of solar radiation.

Table 5.
Optimization variables and parameter setting range.

Table 6.
Glass specifications and performance parameters.
3. Results and Discussion
3.1. Model Validation
According to the room area and layout of classroom 117 of Hebei University of Engineering, a rectangular grid is used to evenly distribute 32 measurement points, with the north–south measurement point being 1.625 m from the wall and the east–west measurement point being 2.15 m from the wall. The horizontal spacing of the measurement points is about 4.3 m, and the vertical spacing is 3.25 m. The sensor is placed on the ground at 0.75 m to measure the illuminance level, and the temperature and humidity measurement instrument is used to measure the temperature 1.2 m from the ground according to the measurement points at intervals of one hour in the measurement time period. The temperature and humidity measurement instrument was used to measure the temperature 1.2 m above the ground according to the measurement point every hour during the actual measurement period. During the measurement period, the artificial lighting and air conditioning were turned off and the exterior windows were kept half open.
The main deployment points were set up according to Figure 6. Measuring instruments included the “testo635 Portable Thermo-Hygrometer” (temperature accuracy: ±0.2 °C (−25 ~ +74.9 °C); manufactured by Testo SE & Co. KGaA, Titisee-Neustadt, Germany) and the “MW18-JTG01 Illuminance Meter” (dynamic range: 0.1–100,000 lx; illuminance accuracy: better than ±4%; manufactured by Beijing Century Jiantong Environmental Technology Co., Ltd., Fengtai District, Beijing, China). The temperature, humidity and illuminance measurements were recorded on 10 June 2024, from 8:30 A.M. to 17:30 P.M. The weather was cloudy, and a total of 10 sets of actual temperature, humidity and illuminance level data were measured at each measurement point.

Figure 6.
Diagram of the actual classroom, measuring points and measuring instruments: (a) classroom 117; (b) MW18-JTG01 Illuminance Meter; (c) testo635 portable temperature and humidity meter; (d) distribution of classroom test points.
The measured values of classroom 117, the second tiered classroom of Hebei University of Engineering, were compared with the simulated values for the same weather condition on the same day, so as to verify the reliability of the simulation model. In order to quantify the differences, the mean bias error (MBE) and the root mean square error coefficient variation (CV (RMSE)) were calculated according to the ASHRAE standard using Equations (10) and (11):
where Mi and Si are the measured and simulated data for instance i; n is the total number of data values used for the calculation; and M is the average of the measured data.
Initial organization of the data yielded similar distribution patterns for the measured and simulated illuminance data, indicating that the model is capable of generating realistic data. In order to quantify the differences, the variance was calculated using the mean bias error (MBE) and the root mean square error coefficient (CV (RMSE)), which are statistics that characterize the similarity/difference between two data series. MBE indicates that one data series is larger or smaller than the other. RMSE indicates the degree to which one data series “fluctuates” with respect to the other data series [78]. Acceptable limits for thermal model calibration are defined according to ASHRAE Guide 14-2014: a thermal model is considered calibrated if the calculated MBE is within ±10% and the CV (RMSE) is within ±30% when analyzing hourly data [79]. Figure 7 shows the measured versus simulated indoor temperatures at 1 h intervals from 8:30 A.M. to 17:30 P.M. on 10 June 2024. Substituting the measured and simulated values of temperature into Equations (10) and (11) yields MBE and CV (RMSE) of −0.73% and 3.9%, respectively. Therefore, the error of the thermal model is within acceptable limits.
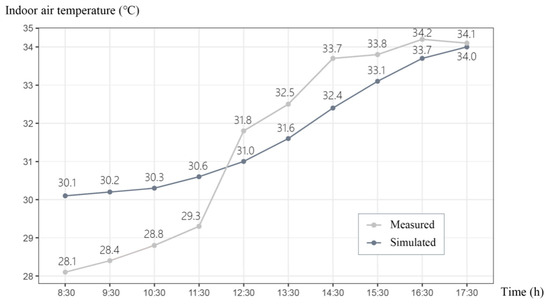
Figure 7.
Comparison of temperature simulation results with measured results.
Figure 8 shows a visualization of the simulated light levels compared to the actual light levels on 10 June 2024 at 12:00 P.M. The red diagonal cross markers in the figure represent each measurement point. Reinhart et al. [78] concluded that an error of no more than 20% in the daylighting simulation results is acceptable. A study by McNeil et al. [80] also showed that the level of error is in the acceptable range for practical applications. Merghani et al. [81] in their illuminance simulation study stated that a mean bias error (MBE) of 20% and a root mean square error (RMSE) of 32% are also considered to meet acceptable accuracy criteria for daylighting performance assessment.
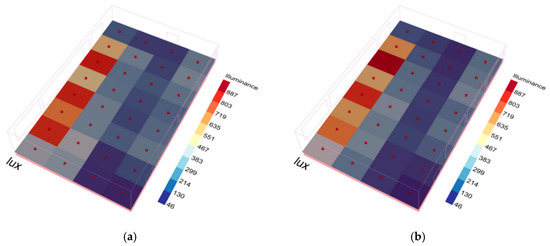
Figure 8.
Comparison of simulated light level and actual light level. (a) View of simulated light levels at 12:00 on 10 June 2024; (b) view of measured light levels at 12:00 on 10 June 2024.
The illumination level was measured and yielded MBE and CV (RMSE) of −5.5% and 24.6%. Therefore, the error of the optical model is within the acceptable range.
Although the energy consumption model in the study has not been fully validated, the energy consumption calculation is based on the validated daylighting model and thermal model [51]. In addition, the energy consumption index in this study is mainly used for the comparison and evaluation between different design options, so it is regarded as a relative index rather than an absolute value. In summary, the model developed in this study can generate reliable thermal and light environment simulation results and provide relative energy consumption data with reference value in optimization analysis.
3.2. Sensitivity Analysis
In order to assess the degree of influence of each input parameter on the building energy consumption and thermal and light comfort performance, this paper adopts the sensitivity factor method for quantitative analysis [29], which is calculated as shown in Equation (12):
where
Si is the sensitivity factor;
∆Pi is the difference between before and after the input parameters, ∆Pi = Pi − Pi,n;
Pi is the input parameter of the influencing factor;
Pi,n is the raw value corresponding to the influence factor;
∆L is the difference between before and after the output parameter, ∆L = Li − Ln;
Ln is the original value corresponding to the output parameter;
Li is the value of the output parameter.
In order to measure the combined impact weight of each input parameter on the output indicator, the sensitivity weight coefficient Wi is introduced, which is defined as shown in Equation (13):
For the sensitivity analysis of the performance indicators, the input parameters include seven envelope parameters, namely, openable window area ratio, west window-to-wall ratio, external insulation thickness, shading member spacing, angle, and width, and external window glass type, and the output parameters are three evaluation indicators, namely effective daylight intensity (UDI), energy use intensity (EUI), and thermal comfort time percentage (TCP).
The above analysis can be carried out based on the parameters of the design variables, the final energy consumption values, and the light and heat comfort time ratios under the preferred scenario, but it is not possible to break down the degree of influence of the different design variables on the simulated energy consumption as well as the light and heat comfort, so sensitivity coefficients are introduced in this study. Figure 9 shows the sensitivity study of the impact of different design variables on energy consumption as well as light and heat comfort for stepped classrooms in cold regions. Table 7, on the other hand, demonstrates the relative contribution weights of each design variable to the three performance objectives, i.e., EUI, TCP and UDI. The results show that the external window glass type occupies the highest weight in all three objectives, contributing 32.76%, 44.26%, and 53.82% to EUI, TCP, and UDI, respectively, which highlights the key role of glass photothermal performance in the optimization of overall performance. In contrast, the depth and angle of the shading elements and the ratio of the openable area of the window have a smaller overall impact, with a contribution of less than 5% in the three indicators.
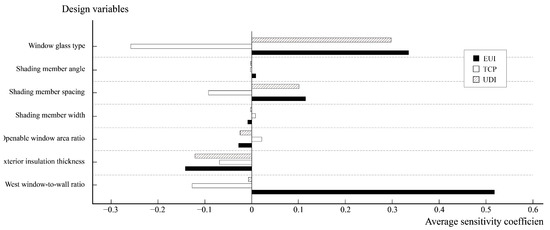
Figure 9.
Average sensitivity factors of design variables for EUI, TCP, and UDI.

Table 7.
Sensitivity weight coefficients of design variables.
In the sensitivity analysis of the energy consumption of the tiered classroom, the sensitivity of the thickness of the external insulation and the openable area ratio of the windows to the energy consumption is negative, which means that with the increase in the thickness of the external insulation and the openable area ratio of the wall and the enhancement of the natural ventilation, the energy consumption can be gradually reduced. On the other hand, the enhancement of the ratio of the west-side windows to the wall and the spacing of shading elements, as well as the values of the window K and SC and the visible light transmittance ratio Tvis, have a positive impact on the energy consumption, which means that increasing the west-facing window/wall ratio and decreasing the window performance increases the energy consumption of the stepped classroom. This may be due to the fact that increasing the ratio of west-facing windows will greatly increase the solar heat gain of the building. In addition, the increase in the spacing of shading elements and the values of glass K, SC, and visible light transmission ratio Tvis will also increase the solar heat gain into the room, thus exacerbating the energy consumption. The depth and angle of shading elements have little impact on the energy consumption, and their sensitivities to the energy consumption are negative and positive, respectively; in the analyses of the light comfort of the lecture theater, the thickness of the external insulation has a positive impact on the light comfort. In the analysis of light comfort in the tiered classroom, the effect of the thickness of the external insulation on light comfort is negative, which may be due to the fact that thicker insulation layers increase the depth of the window openings, which shades the lateral introduction of natural light, leading to insufficient illumination in some areas of the room, which leads to a decrease in UDI. The spacing of the shading elements and the type of windows, especially the visible light transmission ratio Tvis, have a positive effect on the UDI. The higher the Tvis, the stronger the light transmission rate, the higher the indoor natural light illuminance, and the easier it is to reach the effective illuminance range of 100–2000 lx; in addition, the ratio of the openable area of the windows, the ratio of the windows and walls on the west side, and the depth and angle of the shading elements do not have a great impact on the UDI. In the tiered classroom, the depth and angle of the shading elements are not significant; the UDI is reduced because of the increased depth of window apertures by thicker thermal insulation. In the analyses of thermal comfort in the stepped classroom, increasing the shading element spacing and window type (especially the SC value and visible light transmission ratio Tvis), the thickness of the external insulation, and the west side window/wall ratio have a negative impact on the TCP. Specifically, the larger shading spacing and higher SC and Tvis values make more solar radiation enter the room, which is especially significant in summer, and is easy to cause the problem of overheating. However, increasing the thickness of the insulation layer, even in the winter, is more effective in achieving the effective illuminance range of 100–2000 lx. Increased insulation thickness, although favorable in terms of thermal insulation in winter, inhibits indoor heat release in summer in the absence of a heat dissipation mechanism, thus aggravating thermal discomfort. In addition, the increase in the window-to-wall ratio on the west side significantly increased the heat gain from the west sun in the afternoon hours, further reducing comfort. The remaining indicators had little effect on TCP.
3.3. Multi-Criteria Decision-Making
Each scatter point in the scatter plot derived from the simulation represents a tiered classroom design scheme, in which the dark red scatter points represent the Pareto-optimal solution set derived from the genetic algorithm, the transparent red scatter points represent the dominant solution of the elite solution, and the yellow scatter points represent the optimal solution set of the previous generation, and the lower the number of generations is, the higher the transparency of the scatter points is. After 89 generations of the genetic algorithm, the function has basically converged, and the simulation visualization results are shown in Figure 10. Each set of data of the Pareto frontier solution set contains the values of the three indicators of EUI, TCP and UDI.
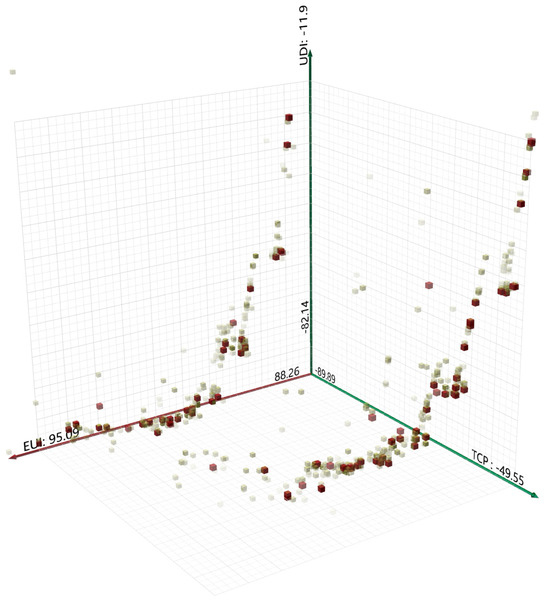
Figure 10.
Results of the 89th generation of genetic algorithm operations.
Since the overall optimal solution is to maximize the effective daylight illuminance (UDI) and thermal comfort percentage (TCP) as well as to minimize the energy use intensity (EUI) and the value-added total life cycle cost (dLCC), in order to objectively determine the relative importance of each performance indicator and to reduce the influence of artificial weighting on the results, this study adopts the entropy weight method (EWM) to assign the weights to the four indicators, including building energy intensity (EUI), thermal comfort percentage (TCP), effective daylight illuminance (UDI), and full life cycle cost (dLCC). The method is weighted based on the degree of dispersion of the indicators in the solution set, and the greater the fluctuation of the indicators, the greater the amount of information they provide, and the more significant the impact on the ranking. After obtaining the objective weights, three classical multi-criteria decision-making methods, i.e., multi-criteria optimization and compromise ranking (VIKOR), approximate ideal solution ranking (TOPSIS), and rank-sum ratio (RSR), are introduced to select the preferred solution by comprehensively ranking the Pareto-optimal solution set. Finally, the trade-off solution with optimal overall performance is determined by comparing and integrating the ranking results of the three methods.
In order to eliminate the effects of differences in the units and orders of magnitude of the indicators, the raw data are first normalized. For the indicators with larger and better values (e.g., TCP, UDI), standard forward normalization (Equation (14)) is adopted; for the indicators with smaller and better values (e.g., EUI, dLCC), reverse normalization (Equation (15)) is adopted, so as to ensure that all the indicators have the same “larger and better” characteristics in numerical significance. The formulas are shown in Equations (14) and (15).
where denotes the original value of the ith program under the jth indicator; denotes the normalized (standardized) value of the ith program under the jth indicator; denotes the minimum value of the jth indicator among all programs; denotes the maximum value of the jth indicator among all programs.
After completing the normalization process, the ratio value of each evaluation scheme under each indicator is calculated, and the information entropy of each indicator is obtained accordingly. The information entropy reflects the degree of dispersion of the indicator data; the greater the dispersion, the more information it provides, and the smaller the entropy value, the higher its importance to the comprehensive evaluation. The formulas are shown in Equations (16) and (17).
where denotes the information entropy of the jth indicator, for which a smaller value represents higher differentiation of the indicator; denotes the normalized weight of the ith scheme under the jth indicator; n denotes the number of schemes, i.e., the number of Pareto-optimal solution sets.
Finally, the objective weight of each indicator is determined by information entropy. This method ensures that in multi-objective decision-making, the assignment of indicator weights is based on the distributional characteristics of the data itself, the formula for which is given in Equation (18).
where denotes the information entropy of the jth indicator; denotes the weight of the jth indicator calculated by the entropy weight method; m denotes the number of evaluation indicators and is taken as four in this study.
Table 8 is derived from the above equation.

Table 8.
Entropy weights of optimization indicators.
In order to objectively determine the relative importance of each performance indicator in multi-objective decision-making, this paper adopts the entropy weight method to process 77 groups of optimal solution samples and calculates the information entropy and redundancy of each indicator based on the normalization matrix, so as to determine their weights. The final results are shown in Table 8. The weight of UDI, the proportion of available daylight illumination, is the largest, 0.4864, reflecting that it is the most informative in the sample distribution and has the highest differentiation of the solutions; the weights of TCP, the thermal comfort indicator, and EUI, the building energy consumption indicator, are 0.1876 and 0.1649, respectively, indicating a mid-level weight. The weight of dLCC, the economy indicator, is the smallest, 0.1611, indicating its low degree of fluctuation in the set of optimal solutions. The above weights have been normalized and directly used in subsequent multi-indicator ranking methods such as TOPSIS, VIKOR and RSR as the basis for weighting calculation.
The VIKOR method is a compromise ranking method for multi-criteria optimization, which aims to balance the overall utility and the individual minimum regret, and is suitable for multi-objective problems with conflicts between objectives. In this study, based on the weighted normalization matrix and the ideal and negative ideal values of each index, the group utility value S, the maximum regret value R, and the comprehensive evaluation index Q are calculated for each scheme. The smaller the value of Q, the closer the scheme is to the optimal compromise solution in terms of comprehensive performance. We use Equations (19)–(21) for calculation.
where denotes the weight of the jth indicator calculated by entropy weighting method; represents the value of the jth indicator for the ith alternative; denotes the optimal value (maximum value) of the jth indicator; denotes the worst value (minimum value) of the jth indicator; denotes the total value of weighted distance of the ith program (overall disadvantage); denotes the maximum single disadvantage of the ith program; and denote the minimum value and maximum value of Si, respectively; v denotes the trade-off factor, which denotes the VIKOR comprehensive evaluation index of the ith program, and the more the program is evaluated, the more the VIKOR is evaluated, and the smaller the better. and denote the minimum and maximum values of all S(i); denotes the minimum and maximum values of all Ri.
The Approximate Ideal Solution Ranking Method (TOPSIS) is a classical multi-criteria decision-making method, whose basic idea is to evaluate the advantages and disadvantages of each solution by calculating the Euclidean distance between each evaluated solution and the positive and negative ideal solutions. In this study, a weighted normalized decision matrix is first constructed based on entropy weights, followed by calculating the distance between each solution and the positive and negative ideal solutions, and ranking all the solutions by the closeness coefficient. The larger the closeness, the better the solution is represented. We use Equations (22)–(25) for calculation.
where denotes the weighted normalized value of the ith solution under the jth indicator; denotes the ideal value of the jth indicator (the maximum value); denotes the negative ideal value of the jth indicator (the minimum value); denotes the distance of the ith solution to the positive ideal solution; denotes the distance of the ith solution to the negative ideal solution; denotes the integrated closeness of the ith solution (the larger the better).
The rank-sum ratio (RSR) method is a comprehensive evaluation method based on ordinal statistics, which derives the relative degree of superiority or inferiority of each solution by normalizing and summing the ranking results of each solution under each indicator. In this study, the RSR method, as a concise and intuitive ranking method, corroborates the TOPSIS and VIKOR methods to provide a multidimensional reference for the selection of the optimal solution, which is calculated using Equation (26).
where denotes the rank-sum ratio of the ith program, the larger the better; denotes the rank order (sorting value) of the ith program under the jth indicator; denotes the weight of the jth indicator calculated by entropy weighting method; m denotes the number of evaluation indicators, which is four in this study.
Eventually, the optimization scheme with the most comprehensive advantages was determined by comparing the ranking results of the three methods and calculating their average rankings, and the top five schemes are shown in Table 9.

Table 9.
Indicators for the top five preferred options.
The research objective solution set and its optimization rate are shown in Table 10, and the minimum building energy consumption (EUImin), the minimum value-added full life cycle cost (dLCCmin), the maximum light comfort time ratio (UDImax), and the thermal comfort time ratio (TCPmax) are 91.08 kWh/m2/y, −38.71 USD/m2, 81.12%, and 86.69%, respectively; EUI, UDI, and TCP are 10.82%, 12.79%, and 36.41%, respectively, and dLCC can reach −38.71 USD/m2 (86.69%). Using a multi-criteria decision-making (MCDM) method to comprehensively evaluate the performance of each scheme, the optimization rates of EUI and TCP among the three selected superior solutions are close to the respective single maximum optimization rates, and they demonstrate better economic performance as well. The UDI value also shows improvement, reaching approximately 10%. Figure 11 illustrates the position of the optimal solution within the Pareto solution set.

Table 10.
Research objective solution set and its optimization rate.
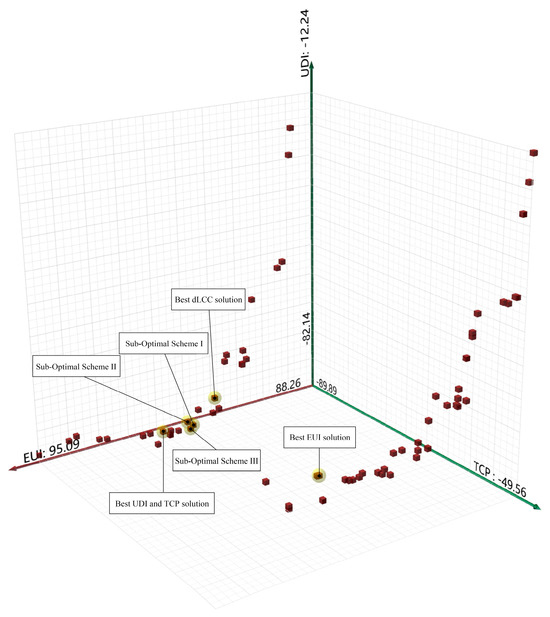
Figure 11.
Optimization scheme at Pareto solution set location.
Overall, the energy efficiency of the building is relatively small, which may be due to the fact that the building has adopted the energy utilization of the ground-source heat pump to make the energy efficiency of this classroom higher. The glass type of all the optimal solutions is vacuum-composite insulating single low-E glass, which indicates that under the economic constraints, this type of glass has the conditions to improve the light and heat energy consumption indicators to a certain extent; at the same time, the correlation between the width of the components and the value of the light comfort time ratio of the UDI is relatively high, and when the width of the components is greater than 0.2 m, the value of the UDI is usually below 75%, which indicates that the smaller width of the components is more suitable for improving the light comfort performance of the classroom. The west window/wall ratio in the scheme with a higher comprehensive ranking of the adaptability function is always in the interval of 0.3~0.6; in addition, when the thermal comfort time ratio TCP ≥ 80% for any scheme, the thickness of the thermal insulation layer is always 0.1 m. Finally, the comparison analysis of the initial scheme with the optimal thermal comfort scheme and the better scheme shows that in the case of a similar window/wall ratio on the west side, the setting of shading components, a smaller openable window area ratio, and larger thickness of the thermal insulation layer can greatly improve the value of the thermal comfort time ratio, which indicates that increasing the thickness of the thermal insulation layer in the process of designing or retrofitting is an effective means of improving the thermal comfort in cold areas under the premise of ensuring the economicity.
4. Conclusions
In this study, the indoor physical environment and energy consumption of the tiered classroom are optimized, and the simulation of light, heat, and energy consumption is carried out based on the Ladybug and Honeybee plug-ins of the Grasshopper platform. A multi-objective evaluation system is established, with the goal of reducing building energy consumption and improving the light and thermal comfort time ratio throughout the year. Shading components are added and the parameters of the original classroom envelope are optimized, and genetic algorithms are employed through the Octopus plug-in to obtain the Pareto frontier solution set for building performance. Subsequently, by incorporating economic indicators, a multi-criteria decision-making (MCDM) approach is adopted to rank and select the preferred solution from the Pareto set.
(1) Compared with the initial scheme, based on the addition of vertical sunshading components and the the optimization of its openable window area ratio, west window/wall ratio, and external insulation thickness, we use the genetic algorithm to obtain the following solution set of Pareto front screening and sorting: the final energy optimal scheme classroom EUI value is 91.08 kWh/m2/y; the optimization rate of energy consumption is 10.82%; the optimal scheme classroom light comfort UDI value is 81.12%; the light comfort time ratio optimization rate is 12.79%; the optimal thermal comfort scheme’s classroom TCP value is 86.69%; the thermal comfort time ratio optimization rate is 36.41%. The UDI value of the optimal solution for light comfort is 81.12%, and the optimization rate of light comfort time ratio is 12.79%; the TCP value of the optimal solution for thermal comfort is 86.69%, and the optimization rate of thermal comfort time ratio is 36.41%; and the value added of the most economic solution, i.e., the minimum whole life cycle cost, dLCC, is −38.71 CNY/m2.
(2) The optimized scheme is compared horizontally, and when the window-to-wall ratio on the west side of the classroom is 0.3~0.6, the spacing of shading panels is 0.9~1 m, the angle is −50~90°, the shading panel width is smaller, and the area ratio of openable windows and the thickness of the external insulation are larger, the UDI, TCP, and EUI are optimized, simultaneously ensuring economic feasibility.
(3) In cold regions, priority should be given to choosing reasonable types of external window glass for the stepped classroom, which has a greater impact on the three indicators of EUI, UDI and TCP. If priority is given to EUI, in addition to the type of external window glass, consideration should be given to controlling the reasonable west window-to-wall ratio, the thickness of external insulation and the reasonable spacing of sunshading panels, and the rest of the indicators are considered second; if priority is given to UDI, the main consideration should be maintaining the reasonable spacing of sunshading components and the thickness of external insulation, and the rest of the indicators have a lesser impact on UDI; if priority is given to TCP, the main consideration should be choosing a reasonable west window-to-wall ratio, thickness of external insulation and spacing of sunshading components, with the final consideration being influence of the three indicators, including EUI and TCP.
Given that this study focuses on a specific case of a lecture hall in a university located in northern China, future research can be extended in the following directions:
(1) Expanding the optimization framework to teaching buildings with different orientations and in different climatic regions, such as south-facing, north-facing, or classrooms with mixed daylighting conditions;
(2) Further integrating intelligent building control systems to enable dynamic regulation of shading, natural ventilation, and lighting, thereby improving the adaptive performance of the building;
(3) Incorporating indoor air quality (IAQ) indicators, such as CO2 concentration and PM2.5 levels, into the performance evaluation system. These factors have a significant impact on occupant health, cognitive performance, and overall comfort, especially in high-density usage spaces like lecture halls. Considering IAQ alongside thermal and visual comfort, as well as energy performance, will contribute to the development of a more comprehensive indoor environmental quality (IEQ) assessment framework, ultimately promoting building design strategies that synergize health and low energy consumption.
Author Contributions
Writing—review & editing, Supervision, Resources, H.X.; Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing—Original draft, Writing—review & editing, Visualization, S.G.; Writing—review & editing, Supervision, Resources, W.H.; Conceptualization, Methodology, Resources, B.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are included within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Guo, Y.-Y. Revisiting the building energy consumption in China: Insights from a large-scale national survey. Energy Sustain. Dev. 2022, 68, 76–93. [Google Scholar] [CrossRef]
- Mischke, P.; Karlsson, K.B. Modelling tools to evaluate China’s future energy system—A review of the Chinese perspective. Energy 2014, 69, 132–143. [Google Scholar] [CrossRef]
- China Association of Building Energy Efficiency, Institute of Urban and Rural Construction and Development, Chongqing University. Research report on building energy consumption and carbon emissions in China (2023). Constr. Archit. 2024, 2, 46–59. (In Chinese) [Google Scholar]
- Shan, G.; Youling, X.; Weihui, L. Investigation and analysis on current situation of energy consumption status and application of building technology in public buildings. Heat. Vent. Air Cond. 2024, 54, 30–37. (In Chinese) [Google Scholar]
- Yugen, W.; Tong, W.; Qi, M.; Liu, Y.; Chen, M.; Lou, Y. Analysis of China’s Energy Consumption Situation and Construction of Energy Security System. Coal Geol. China 2024, 36, 38–42. (In Chinese) [Google Scholar]
- Li, P.; Li, Y.; Luo, J.; Liu, B.; Liu, W.; Shi, H. Energy consumption test and energy saving optimization of newly built farm house in cold area. Buil. Energy Effic. 2024, 52, 30–35. [Google Scholar]
- Chua, K.; Chou, S.; Yang, W.; Yan, J. Achieving better energy-efficient air conditioning—A review of technologies and strategies. Appl. Energy 2013, 104, 87–104. [Google Scholar] [CrossRef]
- Ma, D.; Sun, Y.; Ma, S.; Ma, H. Energy consumption characteristics and evaluation of public buildings in Tianjin, China. Energy Built Environ. 2024, in press. [CrossRef]
- Building Energy Efficiency Research Center, Tsinghua University. China Building Energy Efficiency Annual Development Research Report 2022 (Public Buildings Topic) M1; China Building Industry Press: Beijing, China, 2022; Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=172u0t60cv3a06x0q20q06s0t3059838&site=xueshu_se (accessed on 25 April 2025).
- Wang, Q.; Dang, Y.; Li, G.; Meng, C.; Xie, L.; Liu, M.; Zeng, L. Current situation and prospect of healthy building development in China. Sci. Bull. 2020, 65, 246–255. Available online: https://www.cnki.com.cn/Article/CJFDTotal-FCYY202204027.htm (accessed on 25 April 2025). (In Chinese).
- Kuang, W.; Liu, J.; Dong, J.; Chi, W.; Zhang, C. The rapid and massive urban and industrial land expansions in China between 1990 and 2010: A CLUD-based analysis of their trajectories, patterns, and drivers. Landsc. Urban Plan. 2016, 145, 21–33. [Google Scholar] [CrossRef]
- Chou, J.-S.; Nguyen, H.-M. Simulating long-term energy consumption prediction in campus buildings through enhanced data augmentation and metaheuristic-optimized artificial intelligence. Energy Build. 2024, 312, 114191. [Google Scholar] [CrossRef]
- Afzal, S.; Shokri, A.; Ziapour, B.M.; Shakibi, H.; Sobhani, B. Building energy consumption prediction and optimization using different neural network-assisted models; comparison of different networks and optimization algorithms. Eng. Appl. Artif. Intell. 2024, 127, 107356. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Wang, R.; Lu, S.; Feng, W. A three-stage optimization methodology for envelope design of passive house considering energy demand, thermal comfort and cost. Energy 2020, 192, 116723. [Google Scholar] [CrossRef]
- Wu, C. Research on the Daylighting Environment Design of Auditoriums in Tianjin Area Based on Multi-Objective Optimization. Master’s Thesis, Tianjin University, Tianjin, China, 2020. Available online: https://link.cnki.net/doi/10.27356/d.cnki.gtjdu.2020.003645 (accessed on 25 April 2025). (In Chinese).
- Sadeghi, S.A.; Karava, P.; Konstantzos, I.; Tzempelikos, A. Occupant interactions with shading and lighting systems using different control interfaces: A pilot field study. Build. Environ. 2016, 97, 177–195. [Google Scholar] [CrossRef]
- Xiong, J.; Awalgaonkar, N.M.; Tzempelikos, A.; Bilionis, I.; Karava, P. Efficient learning of personalized visual preferences in daylit offices: An online elicitation framework. Build. Environ. 2020, 181, 107013. [Google Scholar] [CrossRef]
- Lee, M.; Mui, K.; Wong, L.; Chan, W.; Lee, E.; Cheung, C. Student learning performance and indoor environmental quality (IEQ) in air-conditioned university teaching rooms. Build. Environ. 2012, 49, 238–244. [Google Scholar] [CrossRef]
- Makaremi, N.; Schiavoni, S.; Pisello, A.L.; Asdrubali, F.; Cotana, F. Quantifying the effects of interior surface reflectance on indoor lighting. Energy Procedia 2017, 134, 306–316. [Google Scholar] [CrossRef]
- Elliott, M.; Quintino, V. The estuarine quality paradox concept. Encycl. Ecol. 2018, 1, 78–85. [Google Scholar] [CrossRef]
- Lan, L.; Lian, Z. Use of neurobehavioral tests to evaluate the effects of indoor environment quality on productivity. Build. Environ. 2009, 44, 2208–2217. [Google Scholar] [CrossRef]
- da Graça, V.A.C.; Kowaltowski, D.C.C.K.; Petreche, J.R.D. An evaluation method for school building design at the preliminary phase with optimisation of aspects of environmental comfort for the school system of the State São Paulo in Brazil. Build. Environ. 2007, 42, 984–999. [Google Scholar] [CrossRef]
- Amaral, A.R.; Rodrigues, E.; Gaspar, A.R.; Gomes, Á. A thermal performance parametric study of window type, orientation, size and shadowing effect. Sustain. Cities Soc. 2016, 26, 456–465. [Google Scholar] [CrossRef]
- Lee, J.W.; Jung, H.J.; Park, J.Y.; Lee, J.B.; Yoon, Y. Optimization of building window system in Asian regions by analyzing solar heat gain and daylighting elements. Renew. Energy 2013, 50, 522–531. [Google Scholar] [CrossRef]
- Maksoud, A.; Mushtaha, E.; Chouman, L.; Al Jawad, E.; Samra, S.A.; Sukkar, A.; Yahia, M.W. Study on Daylighting Performance in the CFAD Studios at the University of Sharjah. Civ. Eng. Arch. 2022, 10, 2134–2143. [Google Scholar] [CrossRef]
- Acosta, I.; Campano, M.Á.; Leslie, R.; Radetsky, L. Daylighting design for healthy environments: Analysis of educational spaces for optimal circadian stimulus. Sol. Energy 2019, 193, 584–596. [Google Scholar] [CrossRef]
- Puteh, M.; Ibrahim, M.H.; Adnan, M.; Che’aHmad, C.N.; Noh, N.M. Thermal comfort in classroom: Constraints and issues. Procedia—Soc. Behav. Sci. 2012, 46, 1834–1838. [Google Scholar] [CrossRef]
- Zomorodian, Z.S.; Tahsildoost, M.; Hafezi, M. Thermal comfort in educational buildings: A review article. Renew. Sustain. Energy Rev. 2016, 59, 895–906. [Google Scholar] [CrossRef]
- Zeiler, W.; Boxem, G. Effects of thermal activated building systems in schools on thermal comfort in winter. Build. Environ. 2009, 44, 2308–2317. [Google Scholar] [CrossRef]
- Wargocki, P.; Wyon, D.P. The effects of outdoor air supply rate and supply air filter condition in classrooms on the performance of schoolwork by children: ASHRAE 1257-RP. HVAC&R Res. 2007, 13, 165–191. [Google Scholar] [CrossRef]
- Wargocki, P.; Wyon, D.P. The effects of moderately raised classroom temperatures and classroom ventilation rate on the performance of schoolwork by children: ASHRAE 1257-RP. HVAC&R Res. 2007, 13, 193–220. [Google Scholar] [CrossRef]
- Yang, W.; Moon, H.J. Combined effects of acoustic, thermal, and illumination conditions on the comfort of discrete senses and overall indoor environment. Build. Environ. 2019, 148, 623–633. [Google Scholar] [CrossRef]
- Wang, D.; Xu, Y.; Liu, Y.; Wang, Y.; Jiang, J.; Wang, X.; Liu, J. Experimental investigation of the effect of indoor air temperature on students’ learning performance under the summer conditions in China. Build. Environ. 2018, 140, 140–152. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, F.; Wang, J.; Doyle, J.K.; Hancock, P.A.; Mak, C.M.; Liu, S. How indoor environmental quality affects occupants’ cognitive functions: A systematic review. Build. Environ. 2021, 193, 107647. [Google Scholar] [CrossRef]
- Liu, C.; Sun, L.; Jing, X.; Zhang, Y.; Meng, X.; Jia, C.; Gao, W. How correlated color temperature (CCT) affects undergraduates: A psychological and physiological evaluation. J. Build. Eng. 2022, 45, 103573. [Google Scholar] [CrossRef]
- Working Memory. Available online: https://www.taylorfrancis.com/chapters/edit/10.4324/9780429449642-4/working-memory-alan-baddeley (accessed on 25 April 2025).
- Critchley, H.D. Psychophysiology of neural, cognitive and affective integration: FMRI and autonomic indicants. Int. J. Psychophysiol. Off. J. Int. Organ. Psychophysiol. 2009, 73, 88–94. [Google Scholar] [CrossRef]
- Leech, J.A.; Burnett, R.; Nelson, W.; Aaron, S.D.; Raizenne, M. Outdoor Air Pollution Epidemiologic Studies. 2000. Available online: https://www.researchgate.net/publication/306151715_Outdoor_air_pollution_epidemiologic_studies (accessed on 26 April 2025).
- Pisello, A.L.; Cotana, F.; Nicolini, A.; Buratti, C. Effect of dynamic characteristics of building envelope on thermal-energy performance in winter conditions: In field experiment. Energy Build. 2014, 80, 218–230. [Google Scholar] [CrossRef]
- Chwieduk, D.A. Some aspects of energy efficient building envelope in high latitude countries. Sol. Energy 2016, 133, 194–206. [Google Scholar] [CrossRef]
- Amasuomo, T.T.; Amasuomo, J.O. Perceived thermal discomfort and stress behaviours affecting students’ learning in lecture theatres in the humid tropics. Buildings 2016, 6, 18. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, W.; Wang, Q. Multi-objective parametric optimization of the composite external shading for the classroom based on lighting, energy consumption, and visual comfort. Energy Build. 2022, 275, 112441. [Google Scholar] [CrossRef]
- Altun, A.F. Determination of Optimum Building Envelope Parameters of a Room concerning Window-to-Wall Ratio, Orientation, Insulation Thickness and Window Type. Buildings 2022, 12, 383. [Google Scholar] [CrossRef]
- Yao, R.; Short, A. Energy efficient building design. In Design and Management of Sustainable Built Environments; Yao, R., Ed.; Springer: London, UK, 2013; pp. 179–202. [Google Scholar] [CrossRef]
- Almeida, R.M.S.F.; De Freitas, V.P. An insulation thickness optimization methodology for school buildings rehabilitation combining artificial neural networks and life cycle cost. Statyba 2016, 22, 915–923. [Google Scholar] [CrossRef]
- Lakhdari, K.; Sriti, L.; Painter, B. Parametric optimization of daylight, thermal and energy performance of middle school classrooms, case of hot and dry regions. Build. Environ. 2021, 204, 108173. [Google Scholar] [CrossRef]
- Dokhanian, F.; Mohajerani, M.; Nikravan, E.M. Shading design optimization in a semi-arid region: Considering energy consumption, greenhouse gas emissions, and cost. J. Clean. Prod. 2023, 428, 139293.1–139293.19. [Google Scholar] [CrossRef]
- Thalfeldt, M.; Pikas, E.; Kurnitski, J.; Voll, H. Facade design principles for nearly zero energy buildings in a cold climate. Energy Build. 2013, 67, 309–321. [Google Scholar] [CrossRef]
- Zhao, M.; Künzel, H.M.; Antretter, F. Parameters influencing the energy performance of residential buildings in different Chinese climate zones. Energy Build. 2015, 96, 64–75. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, T. Multi-objective optimization of energy, visual, and thermal performance for building envelopes in China’s hot summer and cold winter climate zone. J. Build. Eng. 2022, 59, 105034. [Google Scholar] [CrossRef]
- Fesanghary, M.; Asadi, S.; Geem, Z.W. Design of low-emission and energy-efficient residential buildings using a multi-objective optimization algorithm. Build. Environ. 2012, 49, 245–250. [Google Scholar] [CrossRef]
- Yuan, F.; Yao, R.; Sadrizadeh, S.; Li, B.; Cao, G.; Zhang, S.; Zhou, S.; Liu, H.; Bogdan, A.; Croitoru, C.; et al. Thermal comfort in hospital buildings—A literature review. J. Build. Eng. 2022, 45, 103463. [Google Scholar] [CrossRef]
- Ma, N.; Aviv, D.; Guo, H.; Braham, W.W. Measuring the right factors: A review of variables and models for thermal comfort and indoor air quality. Renew. Sustain. Energy Rev. 2021, 135, 110436. [Google Scholar] [CrossRef]
- Sharma, A.; Kumar, A.; Kulkarni, K.S. Thermal comfort studies for the naturally ventilated built environments in Indian subcontinent: A review. J. Build. Eng. 2021, 44, 103242. [Google Scholar] [CrossRef]
- Yüksel, A.; Arıcı, M.; Krajčík, M.; Civan, M.; Karabay, H. A review on thermal comfort, indoor air quality and energy consumption in temples. J. Build. Eng. 2021, 35, 102013. [Google Scholar] [CrossRef]
- Zou, Y.; Lou, S.; Xia, D.; Lun, I.Y.; Yin, J. Multi-objective building design optimization considering the effects of long-term climate change. J. Build. Eng. 2021, 44, 102904. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E.; Natarajan, S. Multi-objective Building Design Optimization under Operational Uncertainties Using the NSGA II Algorithm. Buildings 2020, 10, 88. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Tang, R. Robust optimal design of zero/low energy buildings considering uncertainties and the impacts of objective functions. Appl. Energy 2019, 254, 113683. [Google Scholar] [CrossRef]
- Ladybugtools. 2025. Available online: https://www.ladybug.tools/ (accessed on 15 May 2025).
- Roudsari, M.S.; Pak, M.; Smith, A. Ladybug: A parametric environmental plugin for grasshopper to help designers create an environmentally-conscious design. In Proceedings of the 13th International IBPSA Conference, Chambery, France, 25–28 August 2013; pp. 3128–3135. Available online: https://publications.ibpsa.org/conference/paper/?id=bs2013_2499 (accessed on 26 April 2025).
- Grasshopper. 2025. Available online: https://www.grasshopper3d.com/ (accessed on 15 May 2025).
- Rhinoceros. 2025. Available online: https://www.rhino3d.com (accessed on 15 May 2025).
- Radiance. 2025. Available online: http://radsite.lbl.gov/radiance/ (accessed on 15 May 2025).
- EnergyPlus. 2025. Available online: https://energyplus.net (accessed on 15 May 2025).
- Luo, Z.; Lu, Y.; Cang, Y.; Yang, L. Study on dual-objective optimization method of life cycle energy consumption and economy of office building based on HypE genetic algorithm. Energy Build. 2022, 256, 111749. [Google Scholar] [CrossRef]
- Nabil, A.; Mardaljevic, J. Useful daylight illuminances: A replacement for daylight factors. Energy Build. 2006, 38, 905–913. [Google Scholar] [CrossRef]
- GB 50352–2019; Uniform Standard for Design of Civil Buildings. National Standard of the People’s Republic of China. China Architecture & Building Press: Beijing, China, 2019.
- van Hoof, J. Forty years of Fanger’s model of thermal comfort: Comfort for all? Indoor Air 2008, 18, 182–201. [Google Scholar] [CrossRef]
- ANSI/ASHRAE Standard 55-2023; Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2023.
- ISO 7730; Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria. International Standard Organization: Genève, Switzerland, 2005.
- Liu, N.; Qin, Y. Building Thermal Environment; Tsinghua University Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- GB50736-2012; Design Code for Heating, Ventilation and Air Conditioning of Civil Buildings. Ministry of Housing and Urban-Rural Development (MOHURD): Beijing, China, 2012.
- Borgstein, E.; Lamberts, R.; Hensen, J. Evaluating energy performance in non-domestic buildings: A review. Energy Build. 2016, 128, 734–755. [Google Scholar] [CrossRef]
- Star, E. Energy Star®. Program Requirements for Residential. 2010. Available online: https://www.responsibilityreports.co.uk/HostedData/ResponsibilityReportArchive/k/NYSE_KRC_2016.pdf (accessed on 26 April 2025).
- Shao, T.; Zhang, N.; Zhang, K.; Zheng, W.; Wang, J. Multi-objective collaborative optimization design for rural residential buildings in Xi’an using SVM and NSGA-II algorithms. Build. Sci. 2024, 10, 0232–0243. (In Chinese) [Google Scholar]
- Xue, Q.; Wang, Z.; Chen, Q. Multi-objective optimization of building design for life cycle cost and CO2 emissions: A case study of a low-energy residential building in a severe cold climate. Build. Simul. 2022, 15, 83–98. [Google Scholar] [CrossRef]
- Reinhart, C.F.; Andersen, M. Development and validation of a Radiance model for a translucent panel. Energy Build. 2006, 38, 890–904. [Google Scholar] [CrossRef]
- Guideline, A. Measurement of energy, demand, and water savings. ASHRAE Guidel. 2014, 4, 1–150. [Google Scholar]
- McNeil, A.; Lee, E. A validation of the Radiance three-phase simulation method for modelling annual daylight performance of optically complex fenestration systems. J. Build. Perform. Simul. 2013, 6, 24–37. [Google Scholar] [CrossRef]
- Merghani, A.H.; Bahloul, S.A. Comparison between radiance daylight simulation software results and Measured on-site data. J. Build. Road Res. 2016, 20, 48–69. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).