Integrated Wavelet-Grey-Neural Network Model for Heritage Structure Settlement Prediction
Abstract
1. Introduction
2. Principles and Methods
2.1. Wavelet Multiscale Decomposition
2.2. Grey Model
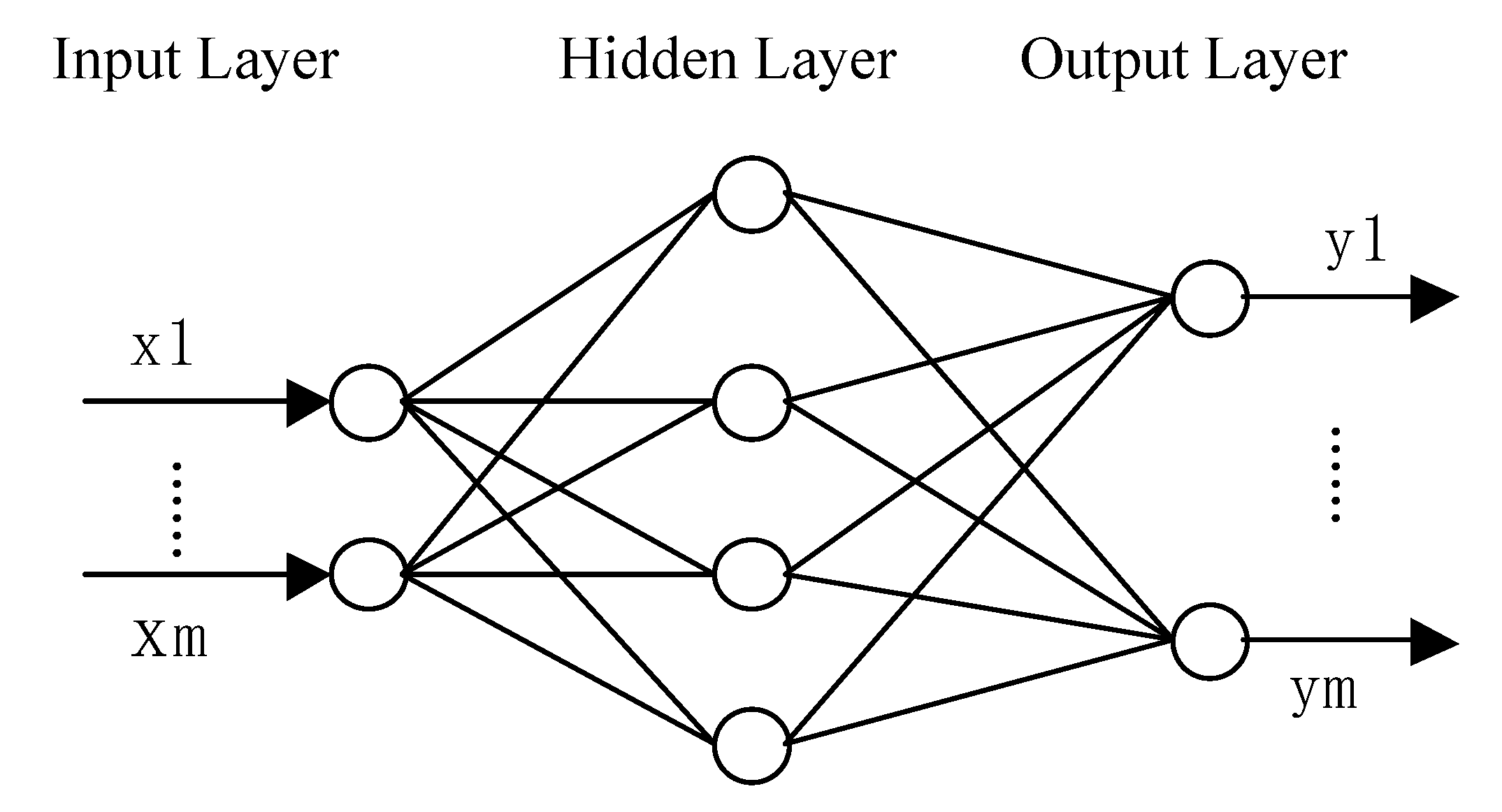
2.3. BP Neural Network Model
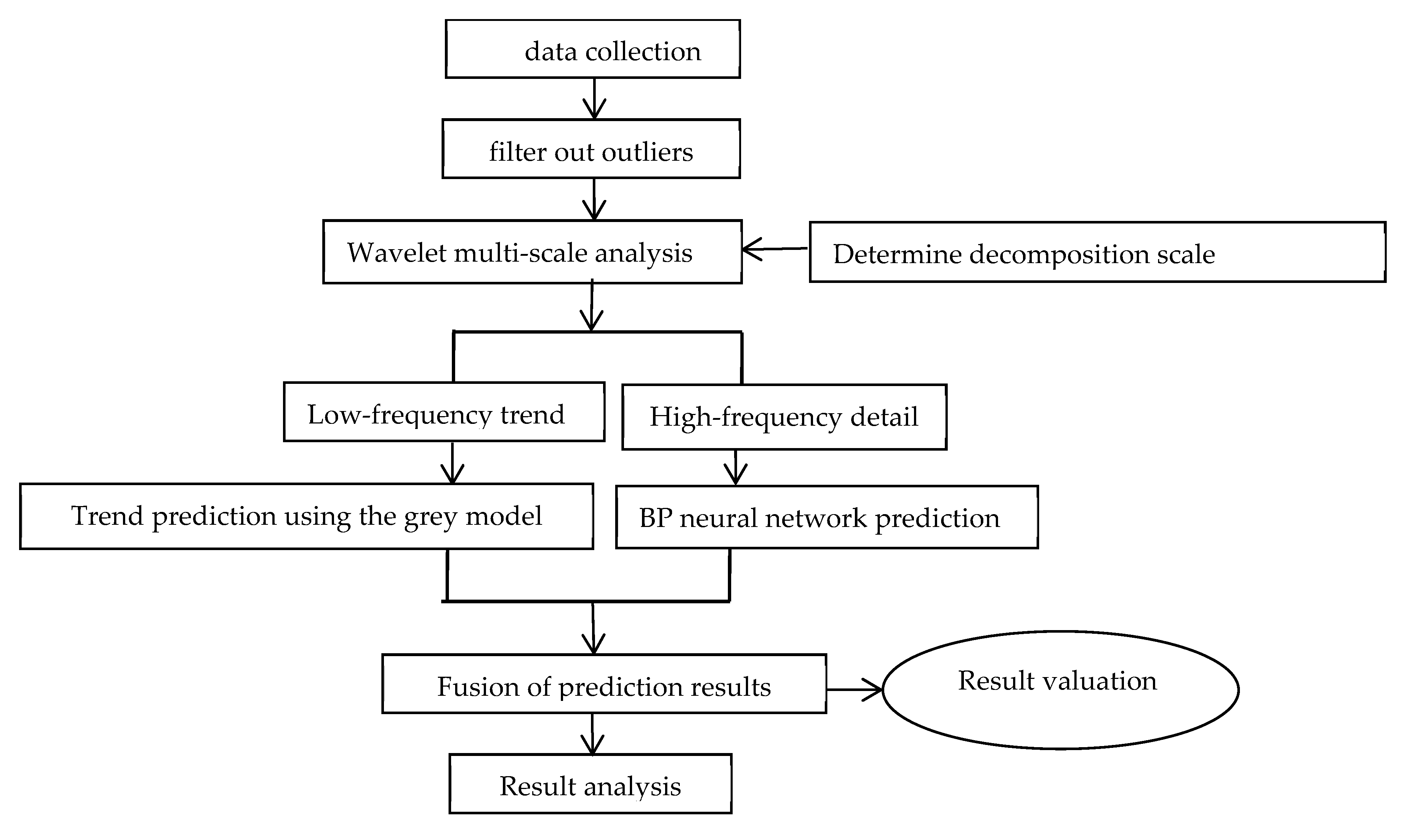
2.4. Improved Model
- (1)
- Time-frequency feature decoupling: The Mallat algorithm is used to perform wavelet decomposition on the original monitoring sequence [24]. By setting the optimal number of decomposition layers , the low-frequency approximate component representing the long-term trend and the high-frequency detail component containing the environmental disturbance features are obtained.
- (2)
- Trend extrapolation modeling: A GM(1,1) model is established for the low-frequency component and prediction is carried out. The equation is expressed as:In the equation, the parameter reflects the system development coefficient, and is the grey action quantity.
- (3)
- Detail feature learning: An adaptive BP neural network is constructed for the high-frequency component . The gradient descent algorithm is used to update the network weights. The hyperbolic tangent function is used in the hidden layer to enhance the nonlinear expression ability.
- (4)
- Dynamic fusion reconstruction: A fusion function that takes into account the trend information and detail information is established, and the time-domain reconstruction is realized through the inverse wavelet transform:
2.5. Model Accuracy Test
3. Experimental Results and Analysis
3.1. Overview of the Case
3.2. Data Processing Procedure
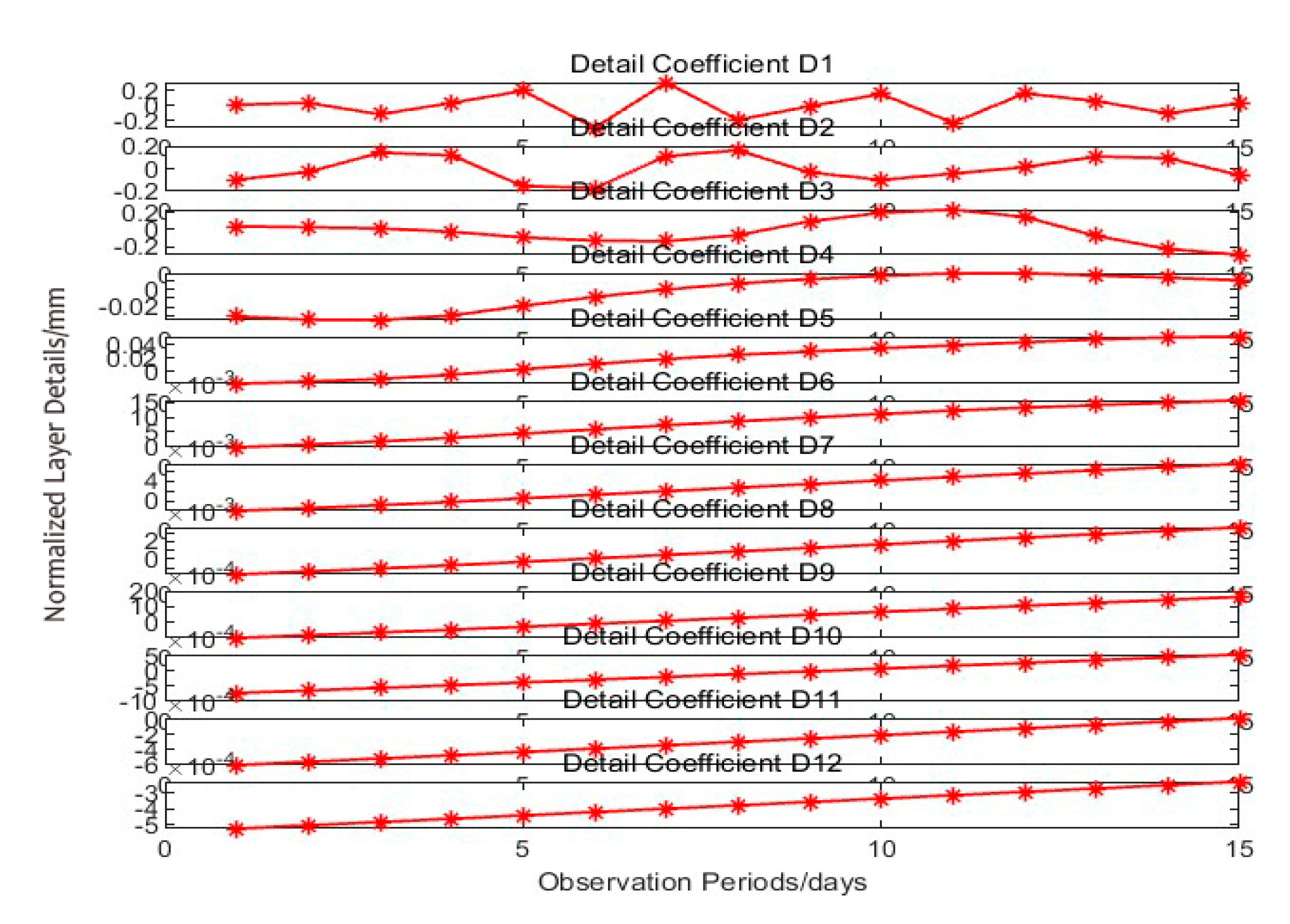
3.2.1. Data Preprocessing Process
3.2.2. Processing Processes of the Grey Model and the BP Neural Network
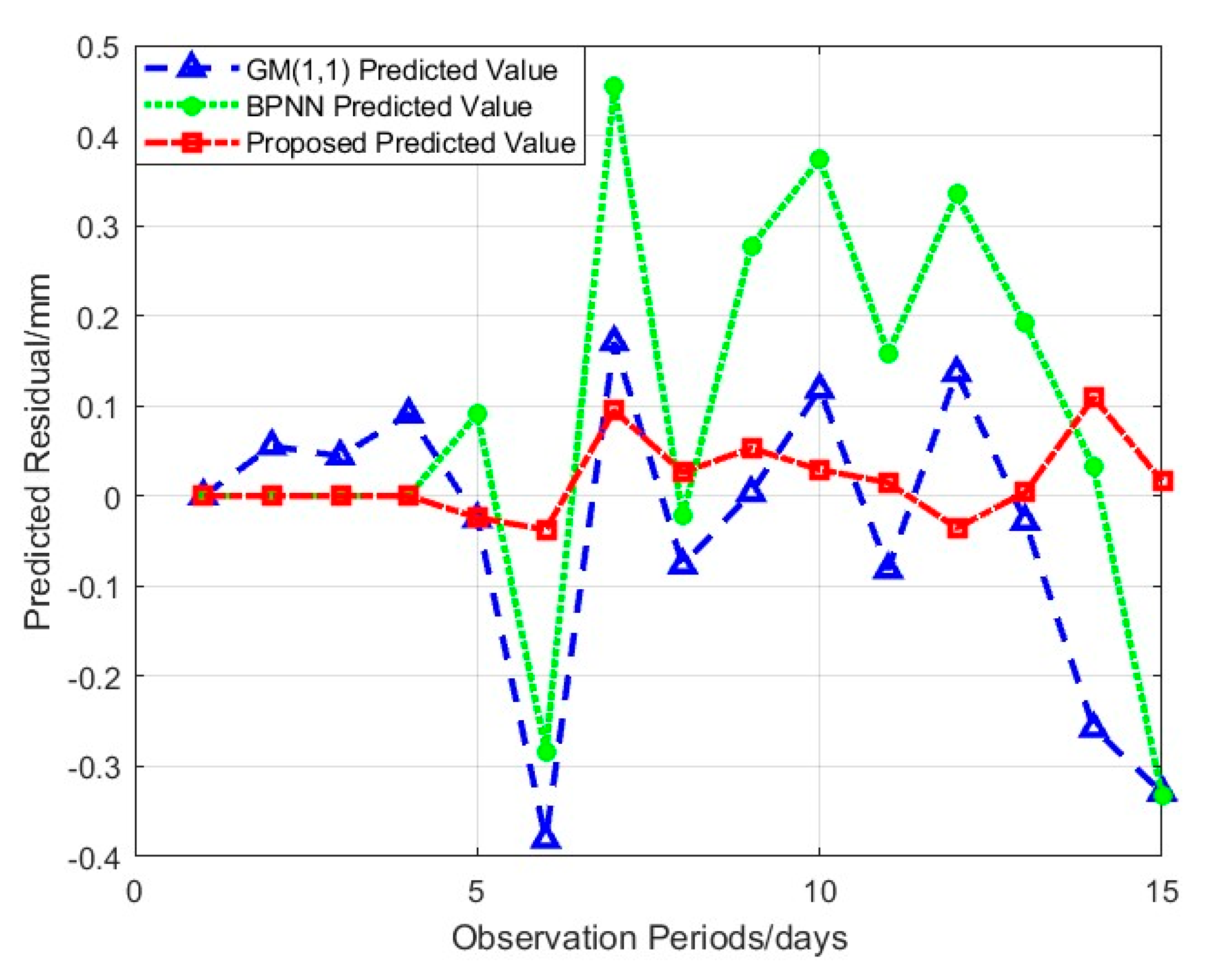
3.3. Results Analysis
4. Conclusions
- (1)
- Substantial Enhancement in Model Performance
- (2)
- Multi-scale Synergistic Mechanism
- (3)
- Deficiencies and Improvement Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hou, J.; Zhou, J.; He, Y.; Hou, B.; Li, J. Automatic reconstruction of semantic façade model of architectural heritage. Heritage Sci. 2024, 12, 400. [Google Scholar] [CrossRef]
- Delcea, C.; Javed, S.A.; Florescu, M.-S.; Ioanas, C.; Cotfas, L.-A. 35 years of grey system theory in economics and education. Kybernetes 2025, 54, 649–683. [Google Scholar] [CrossRef]
- Jiang, J.; Liu, C.; Yao, Y.; Lu, Y.; Xie, W.; Liu, C.; Li, Q. An Improved Grey Model with Time Power and Its Application. Complexity 2022, 2022, 6910865. [Google Scholar] [CrossRef]
- Huang, C.; Cao, Y.; Zhou, L. Application of optimized GM (1,1) model based on EMD in landslide deformation prediction. Comput. Appl. Math. 2021, 40, 261. [Google Scholar] [CrossRef]
- Kankanamge, Y.; Hu, Y.; Shao, X. Application of wavelet transform in structural health monitoring. Earthq. Eng. Eng. Vib. 2020, 19, 515–532. [Google Scholar] [CrossRef]
- Comert, G.; Begashaw, N.; Medhin, N.G. Bayesian parameter estimations for grey system models in online traffic speed predictions. arXiv 2021. [Google Scholar] [CrossRef]
- Wang, X.; Li, W.; Ma, M.; Yang, F.; Song, S. Bridge damage identification based on encoded images and convolutional neural network. Buildings 2024, 14, 3104. [Google Scholar] [CrossRef]
- Yun, D.Y.; Shim, H.B.; Park, H.S. SSI-LSTM network for adaptive operational modal analysis of building structures. Mech. Syst. Signal Process. 2023, 195, 110306. [Google Scholar] [CrossRef]
- Yessoufou, F.; Zhu, J. Classification and regression-based convolutional neural network and long short-term memory configuration for bridge damage identification using long-term monitoring vibration data. Struct. Health Monit. 2023, 22, 4027–4054. [Google Scholar] [CrossRef]
- Chaiyasarn, K. Crack detection in historical structures based on convolutional neural network. Int. J. Geomate 2018, 15, 240–251. [Google Scholar] [CrossRef]
- Xiao, F.; Yan, Y.; Meng, X.; Xu, L.; Chen, G.S. Parameter identification of beam bridges based on stiffness separation method. Structures 2024, 67, 107001. [Google Scholar] [CrossRef]
- Li, Z.; Li, D.; Shen, W. Methods for Visualizing Deep Learning to Elucidate Contributions of Various Signal Features in Structural Health Monitoring. J. Comput. Civ. Eng. 2025, 39, 04025042. [Google Scholar] [CrossRef]
- Sun, X.; Xin, Y.; Wang, Z.; Yuan, M.; Chen, H. Damage detection of steel truss bridges based on gaussian bayesian networks. Buildings 2022, 12, 1463. [Google Scholar] [CrossRef]
- Saadatmorad, M.; Jafari-Talookolaei, R.-A.; Khatir, S.; Fantuzzi, N.; Cuong-Le, T. Frugal wavelet transform for damage detection of laminated composite beams. Comput. Struct. 2025, 314, 107765. [Google Scholar] [CrossRef]
- Mousavi, V.; Rashidi, M.; Ghazimoghadam, S.; Mohammadi, M.; Samali, B.; Devitt, J. Transformer-based time-series GAN for data augmentation in bridge digital twins. Autom. Constr. 2025, 175, 106208. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing. The Sparse Way, 3rd ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar] [CrossRef]
- Ma, Q.; Xu, J.; Gao, X.; Liu, M. Structural damage localization based on wavelet packet analysis under varying environment effects. J. Civ. Struct. Health Monit. 2025, 1–21. [Google Scholar] [CrossRef]
- Li, Q.; Xie, J. Bridge Alignment Prediction Based on Combination of Grey Model and BP Neural Network. Appl. Sci. 2024, 14, 7955. [Google Scholar] [CrossRef]
- Hao, W.; Yin, H.; Liu, J.; Ma, R.; Zhao, D.; Lu, S. Seismic response prediction of soil tunnel structure based on CNN-LSTM model. Structures 2025, 73, 108381. [Google Scholar] [CrossRef]
- Dejamkhooy, A.; Dastfan, A.; Ahmadyfard, A. Modeling and Forecasting Nonstationary Voltage Fluctuation Based on Grey System Theory. IEEE Trans. Power Deliv. 2017, 32, 1212–1219. [Google Scholar] [CrossRef]
- Xiao, Y.T.; Fan, S.J.; Zang, J.F.; Mu, C.L.; Diao, J. Application research on improved GM(1,1) model in foundation pit settlement prediction of urban rail transit engineering. Geomat. Eng. 2024, 33, 62–67. [Google Scholar]
- Deng, J. Grey System Theory Tutorial; Huazhong University of Science and Technology Press: Wuhan, China, 2013. [Google Scholar]
- Wilamowski, B.M.; Yu, H. Neural network learning without backpropagation. IEEE Trans. Neural Netw. 2010, 21, 1793–1803. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Hu, W.S.; Wu, J.; Li, H.F.; Qiao, Y. Extracting vibration information of Runyang Bridge based on wavelet threshold denoising and EMD decomposition method. J. Vib. Shock. 2019, 38, 264–270. [Google Scholar]
- DB11/T 1473—2017; Code for Safety Monitoring of Cultural Relic Buildings [Local Standard]. Beijing Municipal Bureau of Cultural Heritage: Beijing, China, 2017.
- Chen, J. Exploration of Settlement Observation and Analysis Methods for Cultural Relic Buildings. Henan Build. Mater. 2020, 3–4. [Google Scholar]
- Yuan, B. Deformation monitoring analysis method of ancient buildings. Geomat. Technol. Equip. 2023, 25, 1–5. [Google Scholar]
- He, Y.; Jin, P.; Jiang, C. An airborne dual PolInSAR orbit error removal method based on multi-scale correlation analysis. J. Geo-Inf. Sci. 2021, 23, 670–679. [Google Scholar] [CrossRef]




| Grade | Posterior Variance Ratio C | Probability of Small Error p | Model Evaluation |
|---|---|---|---|
| First Grade | Excellent (High Precision) | ||
| Second Grade | Good | ||
| Third Grade | Qualified | ||
| Fourth Grade | Unqualified |
| Models | RMSE | MAE | Maximum Positive Residual | Maximum Negative Residual | Peak-to-Peak Value of the Residual |
|---|---|---|---|---|---|
| GM(1,1) | 0.1651 | 0.12 | 0.1708 | −0.3808 | 0.5516 |
| BPNN | 0.2305 | 0.17 | 0.4540 | −0.3327 | 0.7867 |
| Improved model | 0.0440 | 0.0296 | 0.1093 | −0.0373 | 0.1466 |
| Settlement Value | GM (1,1) | BPNN | Improved Model | |
|---|---|---|---|---|
| Number of Prediction Periods | Predicted Value | Predicted Value | Predicted Value | |
| The 11th period | 6.823 | 6.9655 | 6.7264 | 6.8691 |
| The 12th period | 6.92 | 6.9853 | 6.7869 | 7.1573 |
| The 13th period | 6.854 | 7.0050 | 6.7855 | 6.9731 |
| The 14th period | 6.846 | 7.0249 | 6.7341 | 6.6577 |
| The 15th period | 6.794 | 7.0447 | 7.04870 | 6.6999 |
| RMSE | 0.1651 | 0.2305 | 0.0440 | |
| MAE | 0.1200 | 0.1700 | 0.0296 | |
| Models | Accuracy Level | Posterior Variance Ratio C | Probability of Small Error p |
|---|---|---|---|
| GM(1,1) | The fourth level | 1.0592 | 0.5333 |
| BPNN | The fourth level | 1.4113 | 0.4667 |
| Improved model | The first level | 0.2681 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Jin, P.; Wang, X.; Shen, S.; Ma, J. Integrated Wavelet-Grey-Neural Network Model for Heritage Structure Settlement Prediction. Buildings 2025, 15, 2240. https://doi.org/10.3390/buildings15132240
He Y, Jin P, Wang X, Shen S, Ma J. Integrated Wavelet-Grey-Neural Network Model for Heritage Structure Settlement Prediction. Buildings. 2025; 15(13):2240. https://doi.org/10.3390/buildings15132240
Chicago/Turabian StyleHe, Yonghong, Pengwei Jin, Xin Wang, Shaoluo Shen, and Jun Ma. 2025. "Integrated Wavelet-Grey-Neural Network Model for Heritage Structure Settlement Prediction" Buildings 15, no. 13: 2240. https://doi.org/10.3390/buildings15132240
APA StyleHe, Y., Jin, P., Wang, X., Shen, S., & Ma, J. (2025). Integrated Wavelet-Grey-Neural Network Model for Heritage Structure Settlement Prediction. Buildings, 15(13), 2240. https://doi.org/10.3390/buildings15132240







