Shaking Table Test of a Subway Station–Soil–Aboveground Structures Interaction System: Structural Impact on the Field
Abstract
1. Introduction
- Can the test solve the boundary problem effectively?
- For the free field, what is the effect of long-period earthquakes on the field response?
- For the free field, what is the effect of a subway station with joints on the field response?
- For the free field, what is the effect of aboveground structures on the field response?
- For the free field, what is the effect of structures on the field response spectra?
2. USSI Experimental Equipment and Design
2.1. Model Soil Container
2.2. Similitude Theory
- Uniform similitude ratios for the structures and soil should be considered;
- The loss of gravity was allowed, and no additional weight was added to the soil owing to the complications of adding artificial mass to the soil;
- The similitude ratio design should be based on the size and bearing capacity of the shaking table and the size of the soil container.
2.3. Material and Designation of the Model
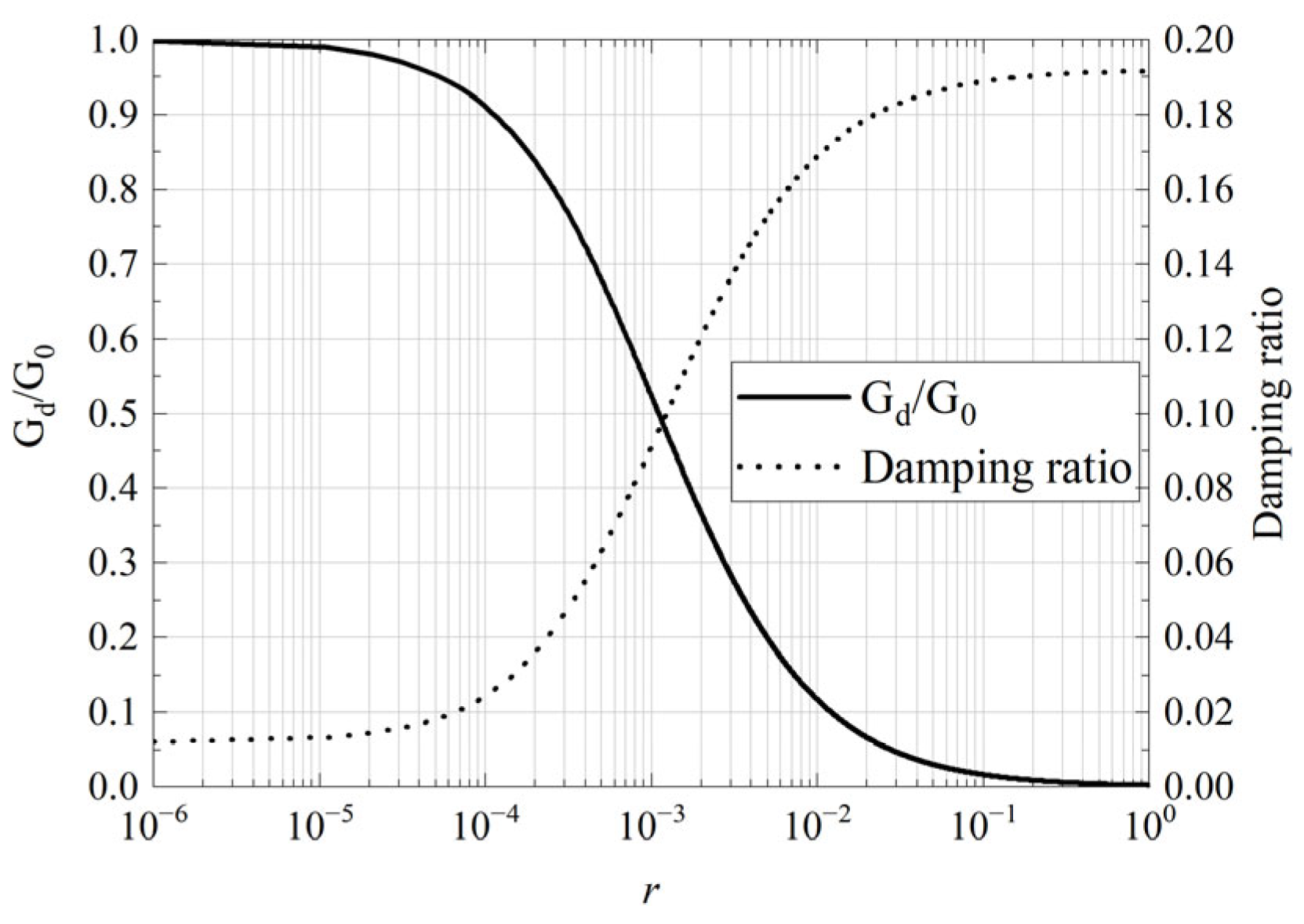
2.3.1. Model Soil
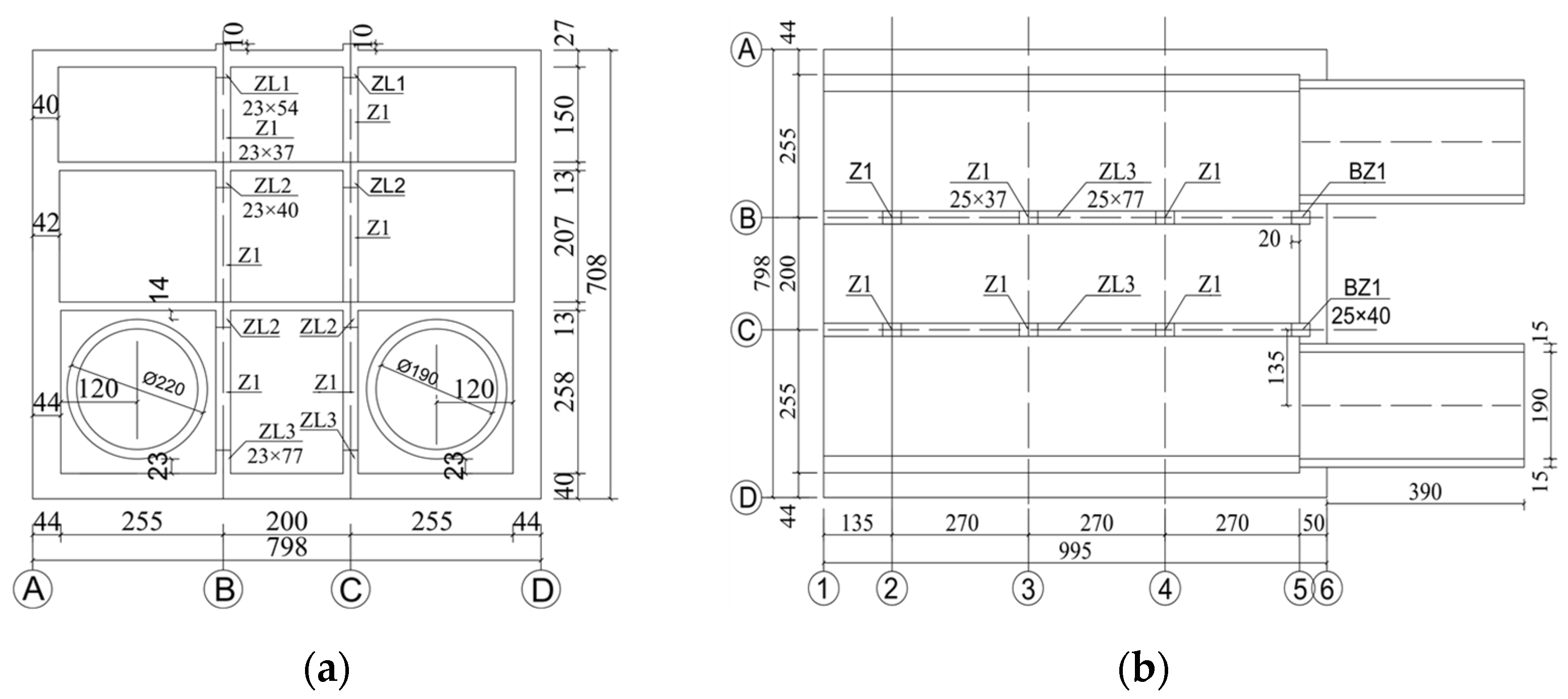
2.3.2. Model Subway Station Structure with Tunnel Connecting Joints
2.3.3. Model Aboveground Structures
3. USSI Test Configuration and Instruments
3.1. Loading Method
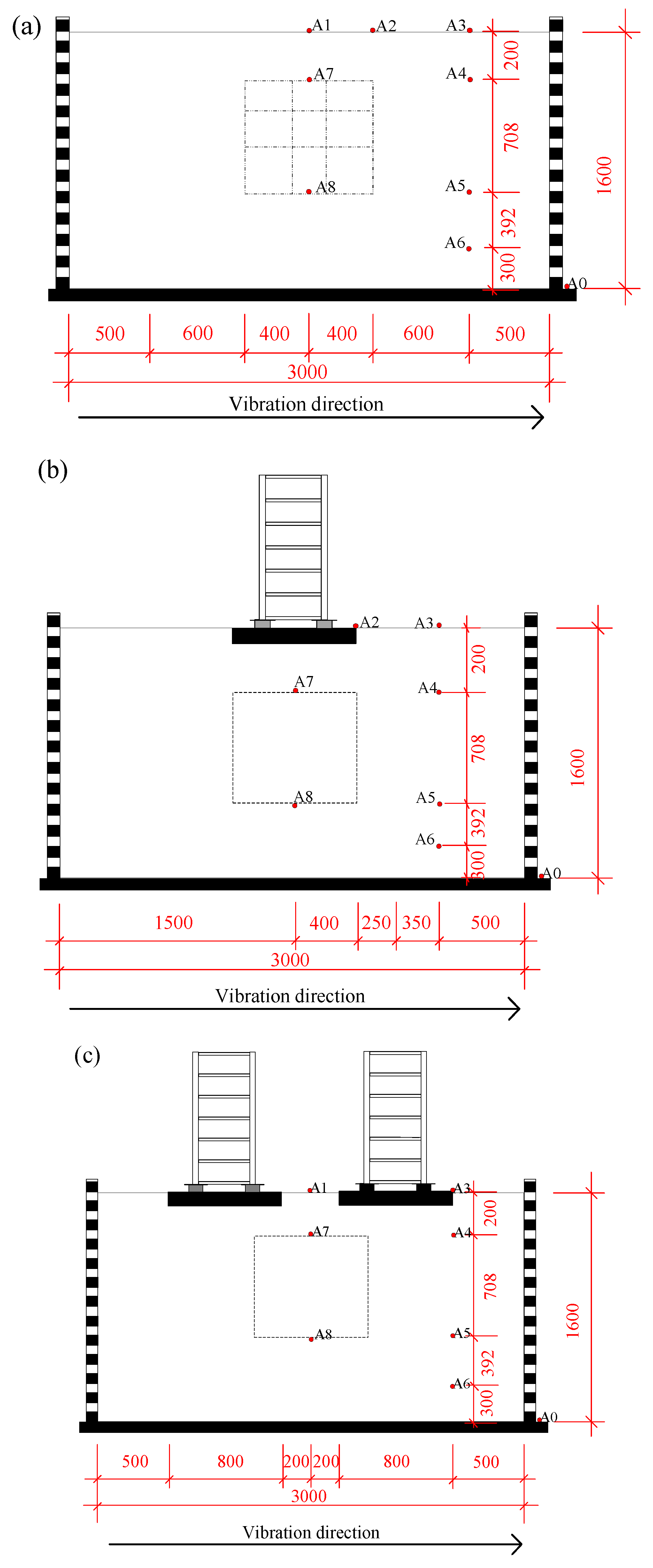
3.2. Test Configuration
3.3. Boundary Effect
4. Structural Impact on the Field and Discussion
4.1. Dynamic Characteristics
4.1.1. Dynamic Characteristics of the Model Soil
4.1.2. Dynamic Characteristics of Six Systems
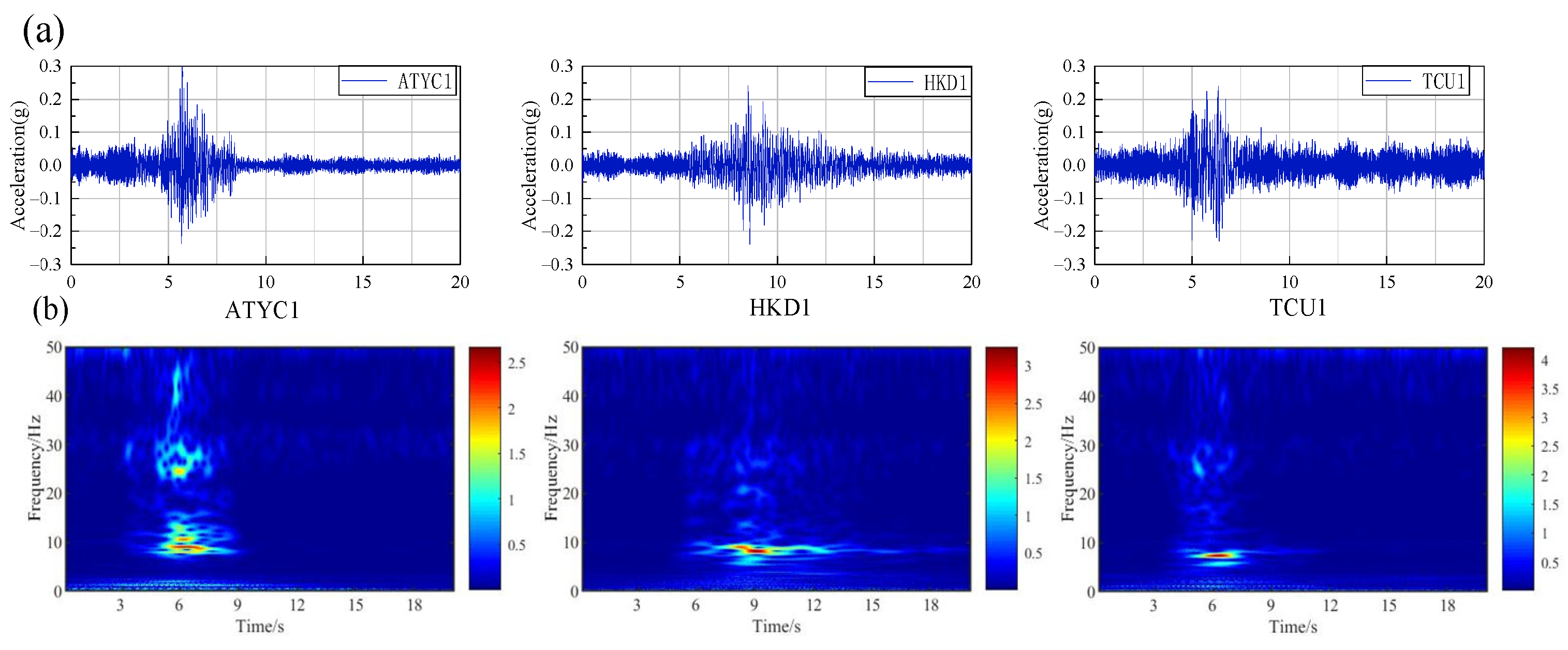
4.2. Response of Benchmark Model (FF) to Earthquake Ground Motion
4.3. Field Response in Terms of Acceleration
4.3.1. PGA Analysis
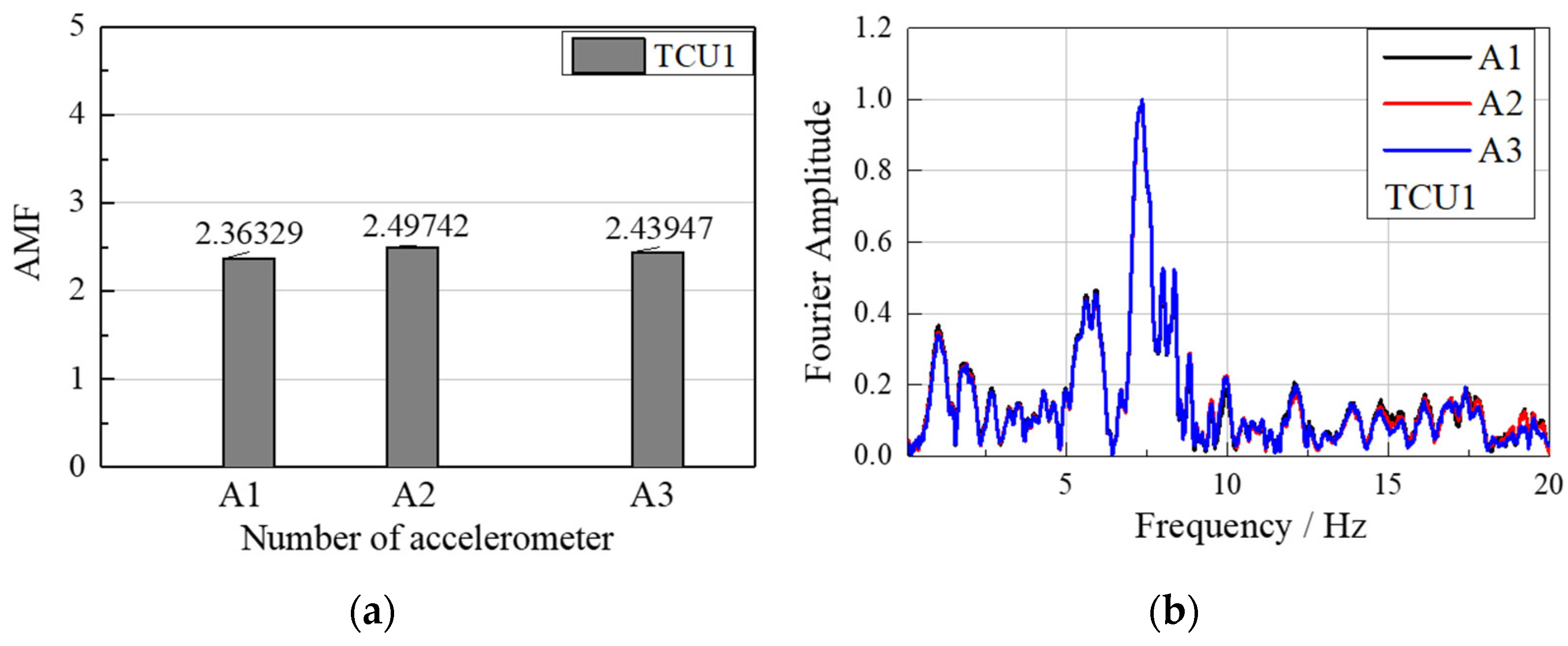
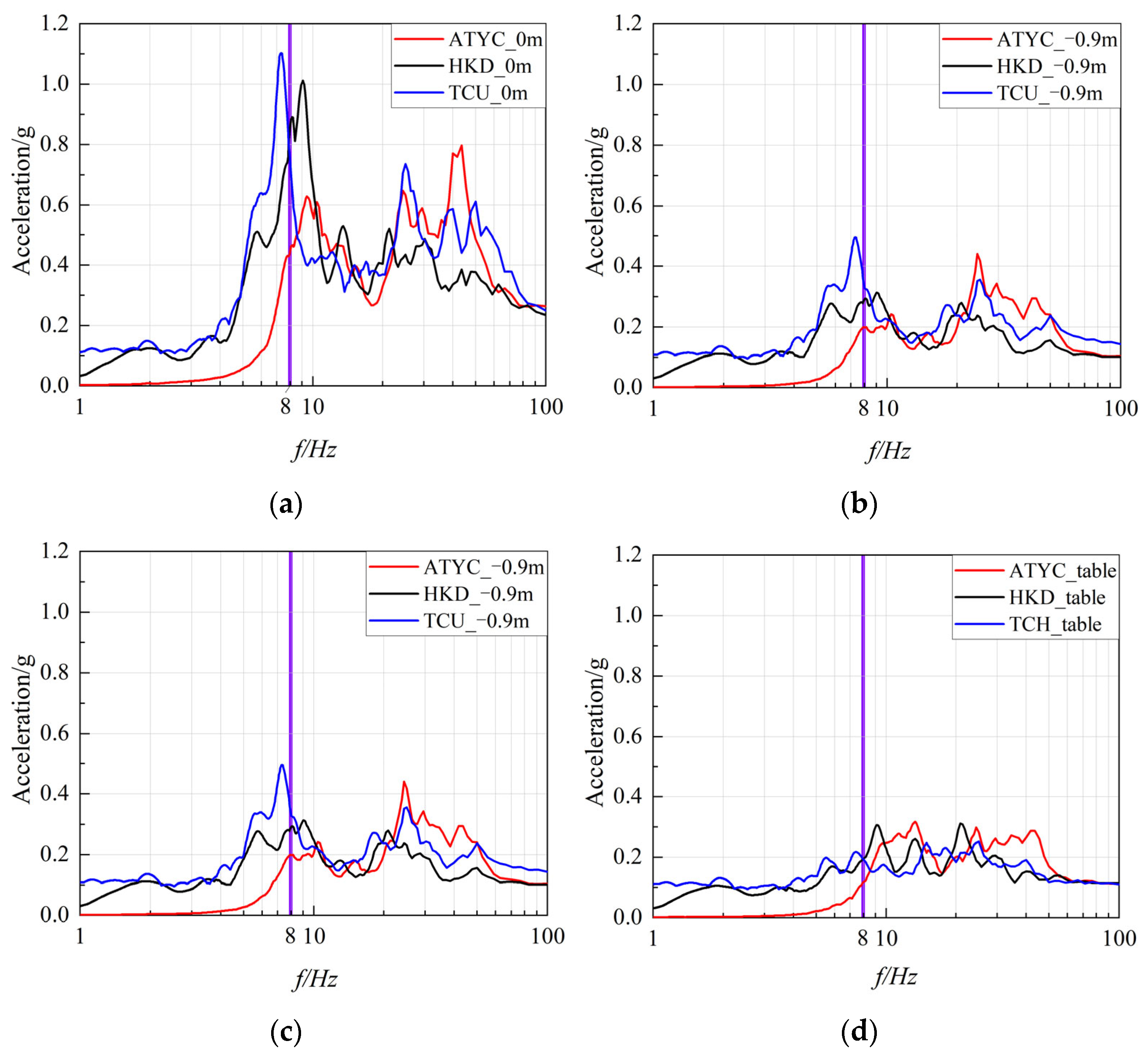
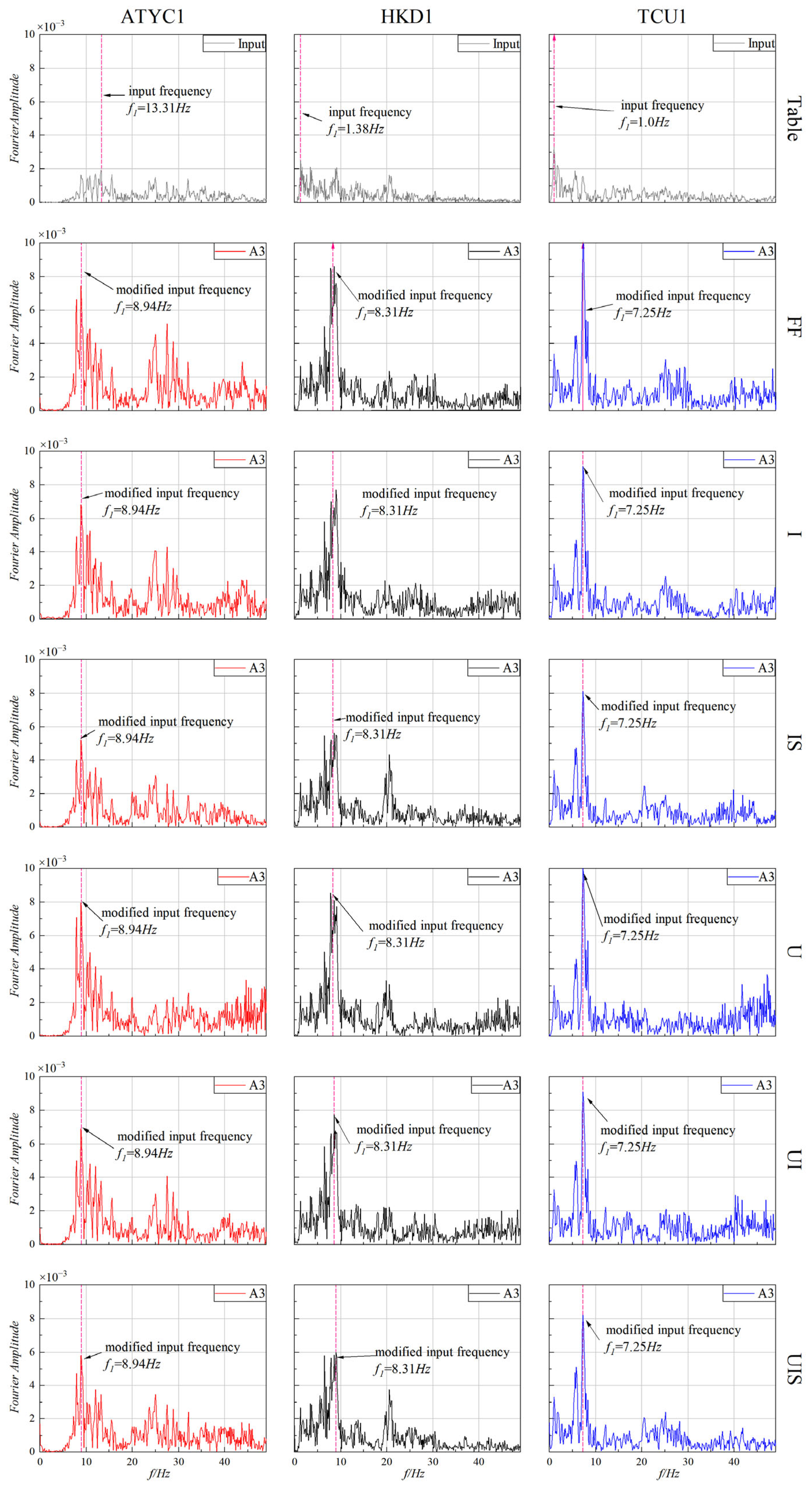
4.3.2. Frequency Analysis
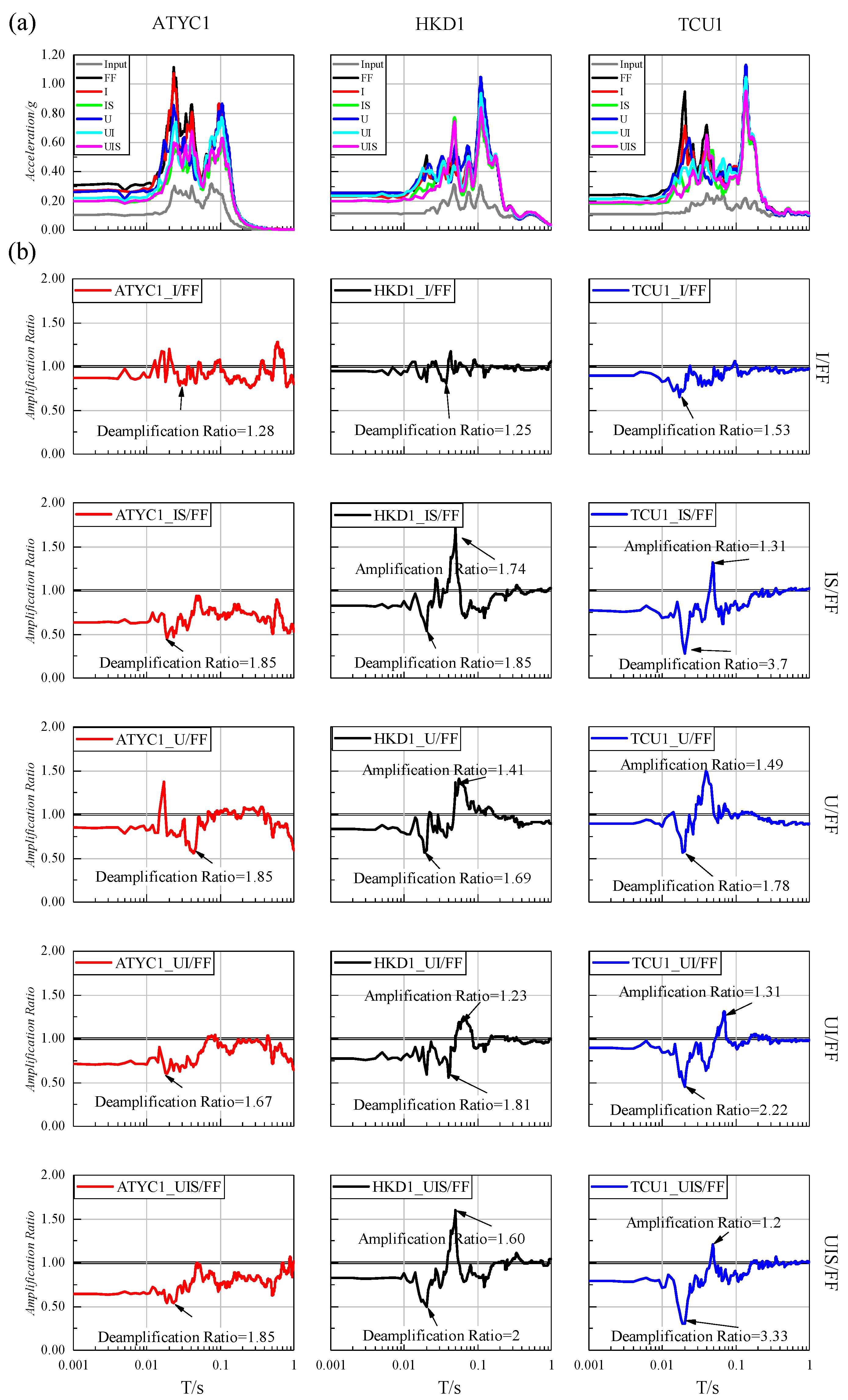
4.3.3. Response Spectra Analysis
5. Conclusions
- The boundary effect was effectively minimized under the test conditions and found to have a negligible influence on the overall results.
- The seismic response of the soil was significantly amplified, particularly under strong ground motions enriched with low-frequency components. Increased peak ground acceleration (PGA) led to enhanced hysteretic energy dissipation in the model soil. A clear pattern of high-frequency attenuation and low-frequency amplification was observed from the shaking table to the soil surface.
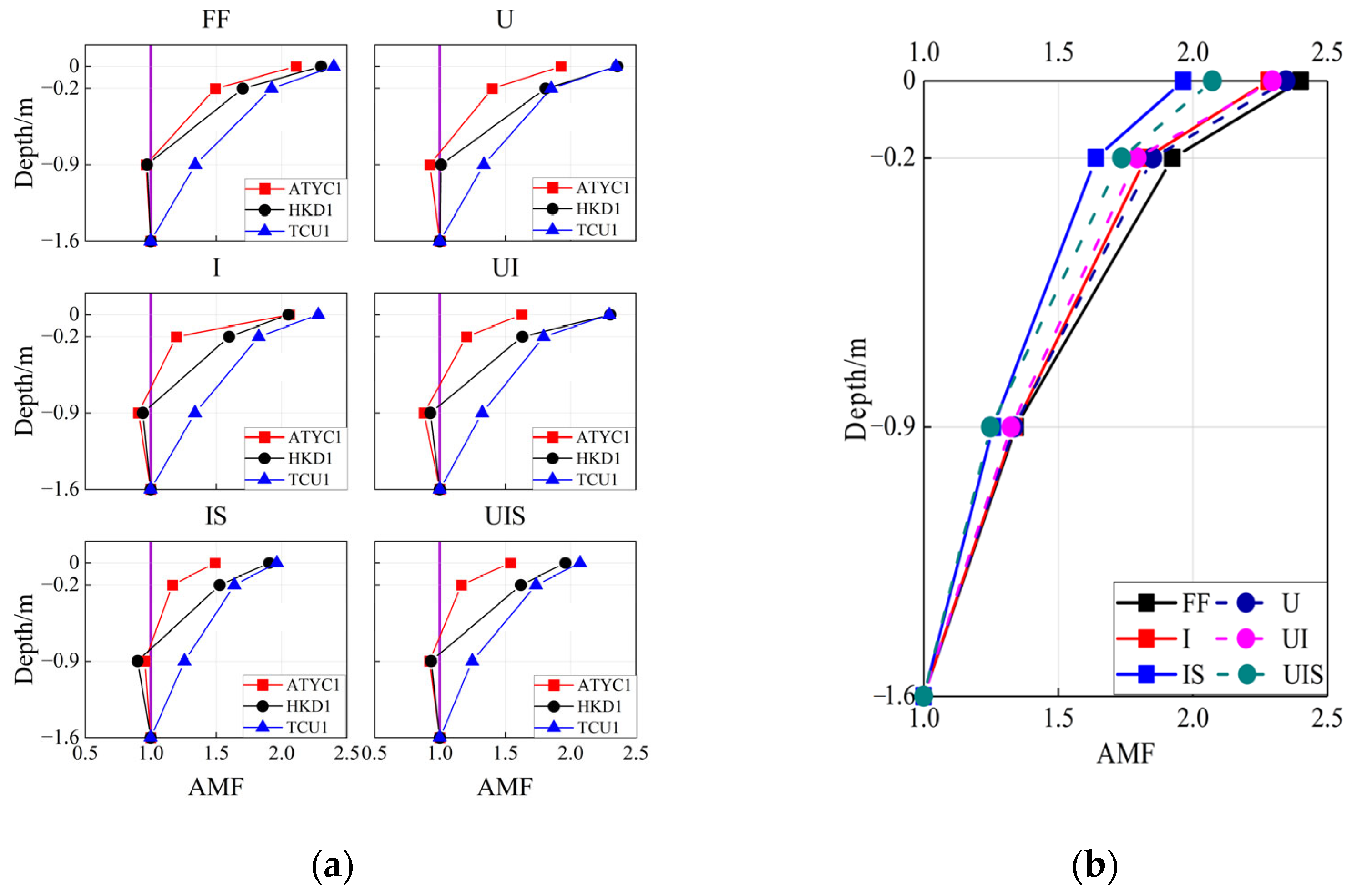
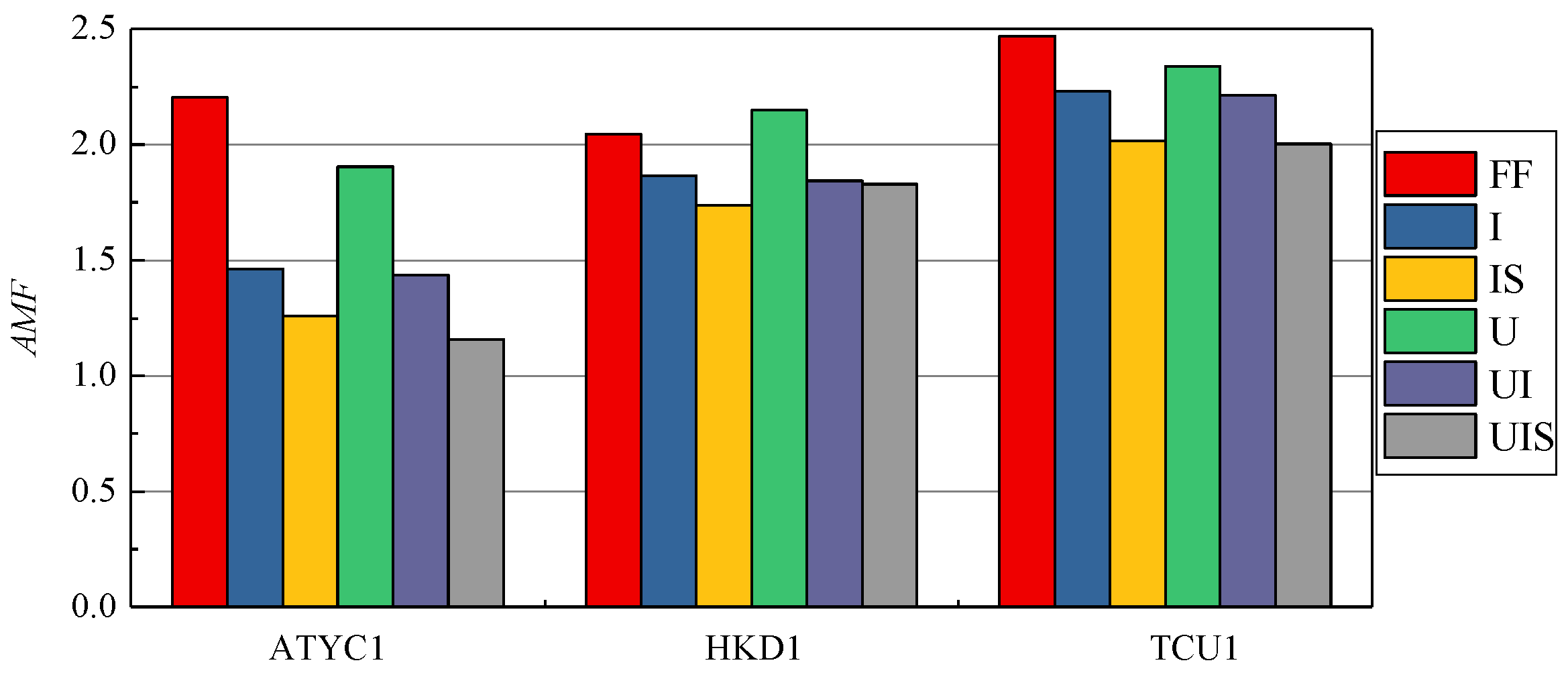
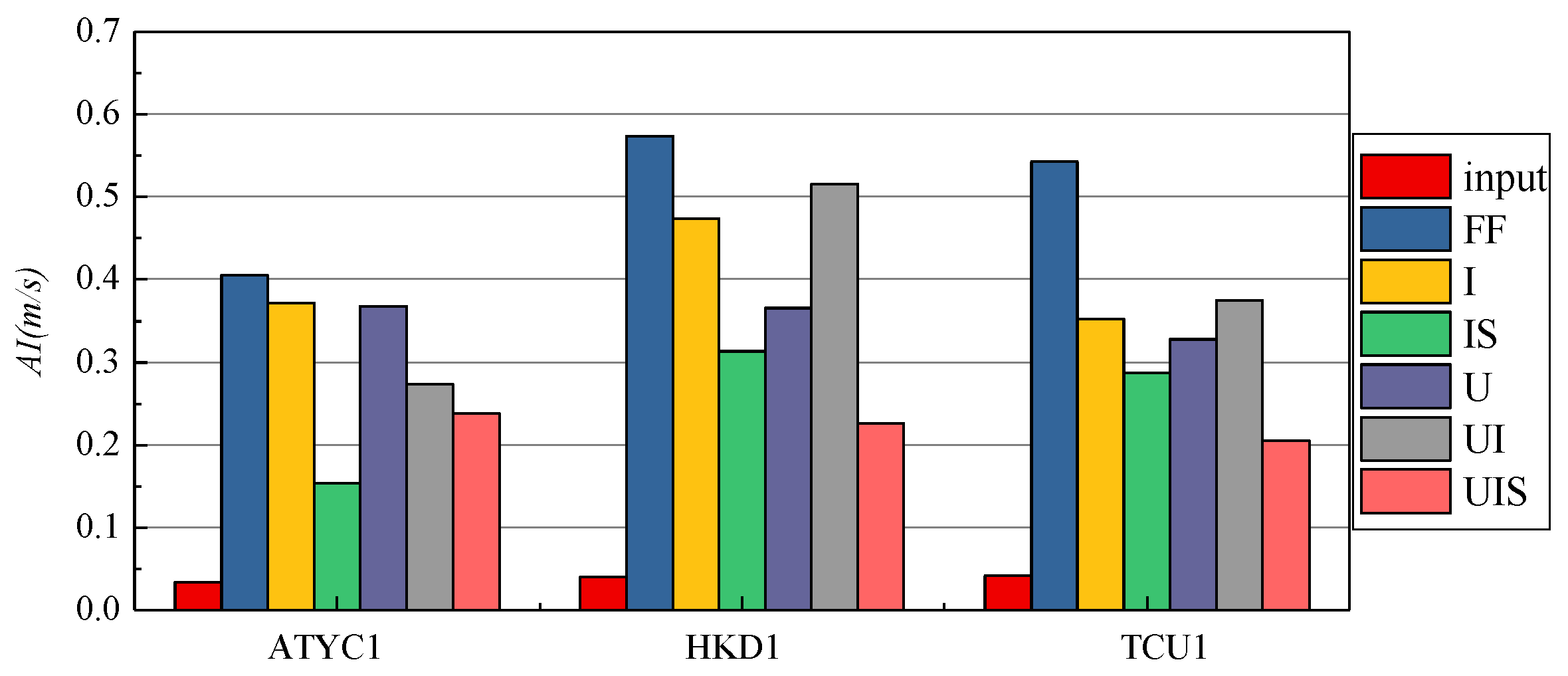
- The presence of a subway station increases the first-order frequency of the field. It amplifies the AMF of the field response with aboveground structures at a certain distance from the subway station and de-amplifies the AMF with that directly above the station. Additionally, it altered the frequency characteristics of input motions and reduced the Arias intensity compared to the benchmark case. Overall, the subway station exerted a protective influence on nearby urban areas while potentially increasing seismic risk for more distant regions.
- The presence of aboveground buildings reduces the first-order frequency of soil. Increasing the number of aboveground structures further reduces the first-order frequency. In addition, it reduces the AMF of the field, and the effect is greater with the addition of the number of buildings, at least as far as the case analyzed here is concerned. The input motions’ frequency characteristics change, and the Arias intensity is also reduced.
- The presence of a subway station and/or aboveground buildings causes de-amplification of the acceleration response spectra with high-frequency excitation and de-amplification for short periods and amplification for long periods with low-frequency excitation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghergu, M.; Ionescu, I.R. Structure–soil–structure coupling in seismic excitation and “city effect”. Int. J. Eng. Sci. 2009, 47, 342–354. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, X.; Huang, W. Simulation Method of Soil Boundary Condition in Shaking Table Tests of Soil-Structure Interaction. Struct. Eng. 2000, 3, 25–30. [Google Scholar]
- Wang, F.; Sett, K. Time domain stochastic finite element simulation towards probabilistic seismic soil-structure interaction analysis. Soil Dyn. Earthq. Eng. 2019, 116, 460–475. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, M.; Fan, Z.; Yuan, Y.; Sun, Q. Shaking table test on shaft-tunnel junction in liquefiable sand site. Tunn. Undergr. Space Technol. 2024, 154, 106097. [Google Scholar] [CrossRef]
- Tao, L.; Shi, C.; Ding, P.; Yang, X.; Bao, Y.; Wang, Z. Shaking table test of the effect of an enclosure structure on the seismic performance of a prefabricated subway station. Tunn. Undergr. Space Technol. 2022, 125, 104533. [Google Scholar] [CrossRef]
- Yue, F.; Liu, B.; Zhu, B.; Jiang, X.; Chen, L.; Liao, K. Shaking table test and numerical simulation on seismic performance of prefabricated corrugated steel utility tunnels on liquefiable ground. Soil Dyn. Earthq. Eng. 2021, 141, 106527. [Google Scholar] [CrossRef]
- Xu, C.; Jiang, Z.; Du, X.; Shen, Y.; Chen, S. 1-g shaking table tests of precast horseshoe segmental tunnel: Experimental design, dynamic properties, deformation mode and damage pattern. Tunn. Undergr. Space Technol. 2021, 113, 103976. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, Y.; Wu, Q.; Chen, Z.; Wang, C. Shaking table tests on the seismic responses of underground structures in coral sand. Tunn. Undergr. Space Technol. 2021, 109, 103775. [Google Scholar] [CrossRef]
- Zhu, T.; Hu, J.; Zhang, Z.; Zhang, J.-M.; Wang, R. Centrifuge Shaking Table Tests on Precast Underground Structure-Superstructure System in Liquefiable Ground. J. Geotech. Geoenviron. Eng. 2021, 147, 106756. [Google Scholar] [CrossRef]
- Wu, W.; Ge, S.; Yuan, Y.; Ding, W.; Anastasopoulos, I. Seismic response of subway station in soft soil: Shaking table testing versus numerical analysis. Tunn. Undergr. Space Technol. 2020, 100, 103389. [Google Scholar] [CrossRef]
- Tao, L.; Ding, P.; Yang, X.; Lin, P.; Shi, C.; Bao, Y.; Wei, P.; Zhao, J. Comparative study of the seismic performance of prefabricated and cast-in-place subway station structures by shaking table test. Tunn. Undergr. Space Technol. 2020, 105, 103583. [Google Scholar] [CrossRef]
- Ding, X.; Feng, L.; Wang, C.; Chen, Z.; Han, L. Shaking table tests of the seismic response of a utility tunnel with a joint connection. Soil Dyn. Earthq. Eng. 2020, 133, 106133. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, Y.; Bao, Z.; Yu, H.; Bilotta, E. Shaking table tests on shaft-tunnel junction under longitudinal excitations. Soil Dyn. Earthq. Eng. 2020, 132, 106055. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, D.; Li, X.; Li, J. Seismic response of underground structure–soil–aboveground structure coupling system: Current status and future prospects. Tunn. Undergr. Space Technol. 2022, 122, 104372. [Google Scholar] [CrossRef]
- Smerzini, C.; Pitilakis, K.; Hashemi, K. Evaluation of earthquake ground motion and site effects in the Thessaloniki urban area by 3D finite-fault numerical simulations. Bull. Earthq. Eng. 2017, 15, 787–812. [Google Scholar] [CrossRef]
- Moghadam, M.R.; Baziar, M.H. Seismic ground motion amplification pattern induced by a subway tunnel: Shaking table testing and numerical simulation. Soil Dyn. Earthq. Eng. 2016, 83, 81–97. [Google Scholar] [CrossRef]
- Alielahi, H.; Kamalian, M.; Adampira, M. Seismic ground amplification by unlined tunnels subjected to vertically propagating SV and P waves using BEM. Soil Dyn. Earthq. Eng. 2015, 71, 63–79. [Google Scholar] [CrossRef]
- Chen, G.; Chen, S.; Qi, C.; Du, X.; Wang, Z.; Chen, W. Shaking table tests on a three-arch type subway station structure in a liquefiable soil. Bull. Earthq. Eng. 2015, 13, 1675–1701. [Google Scholar] [CrossRef]
- Baziar, M.H.; Moghadam, M.R.; Kim, D.; Choo, Y.W. Effect of underground tunnel on the ground surface acceleration. Tunn. Undergr. Space Technol. 2014, 44, 10–22. [Google Scholar] [CrossRef]
- Clouteau, D.; Broc, D.; Devésa, G.; Guyonvarh, V.; Massin, P. Calculation methods of Structure–Soil–Structure Interaction (3SI) for embedded buildings: Application to NUPEC tests. Soil Dyn. Earthq. Eng. 2012, 32, 129–142. [Google Scholar] [CrossRef]
- Smerzini, C.; Avilés, J.; Paolucci, R.; Sánchez-Sesma, F.J. Effect of underground cavities on surface earthquake ground motion under SH wave propagation. Earthq. Eng. Struct. Dyn. 2009, 38, 1441–1460. [Google Scholar] [CrossRef]
- Yiouta, P.; Kouretzis, G.; Bouckovalas, G.; Sofianos, A. Effect of underground structures in earthquake resistant design of surface structures. In Dynamic Response and Soil Properties. 2007. Available online: https://ascelibrary.org/doi/abs/10.1061/40904(223)16 (accessed on 17 June 2025).
- Nam, S.H.; Song, H.W.; Byun, K.J.; Maekawa, K. Seismic analysis of underground reinforced concrete structures considering elasto-plastic interface element with thickness. Eng. Struct. 2006, 28, 1122–1131. [Google Scholar] [CrossRef]
- Pitilakis, K.; Tsinidis, G.; Leanza, A.; Maugeri, M. Seismic behaviour of circular tunnels accounting for above ground structures interaction effects. Soil Dyn. Earthq. Eng. 2014, 67, 1–15. [Google Scholar] [CrossRef]
- Rizos, D.C.; Wang, Z. Coupled BEM–FEM solutions for direct time domain soil–structure interaction analysis. Eng. Anal. Bound. Elem. 2002, 26, 877–888. [Google Scholar] [CrossRef]
- Mroueh, H.; Shahrour, I. A full 3-D finite element analysis of tunneling–adjacent structures interaction. Comput. Geotech. 2003, 30, 245–253. [Google Scholar] [CrossRef]
- Azadi, M.; Hosseini, S.M.M.M. The Impact of Underground Tunnel Excavation on Adjacent Buildings During Earthquake Case Study: Shiraz Underground, Iran. Electron. J. Geotech. Eng. 2007, 12, 1–10. [Google Scholar]
- Tzarmados, D. Dynamic Interaction of Shallow Metro Tunnels with Aboveground Structures at the Surface. Master’s Thesis, Civil Engineering Department, Aristotle University of Thessaloniki, Thessaloniki, Greece, 2011. [Google Scholar]
- Guo, J.; Chen, J.; Bobet, A. Influence of a subway station on the inter-story drift ratio of adjacent surface structures. Tunn. Undergr. Space Technol. 2013, 35, 8–19. [Google Scholar] [CrossRef]
- Abate, G.; Massimino, M.R. Numerical modelling of the seismic response of a tunnel–soil–aboveground building system in Catania (Italy). Bull. Earthq. Eng. 2017, 15, 469–491. [Google Scholar] [CrossRef]
- Abate, G.; Massimino, M.R. Parametric analysis of the seismic response of coupled tunnel-soil-aboveground building systems by numerical modelling. Bull. Earthq. Eng. 2017, 15, 443–467. [Google Scholar] [CrossRef]
- Wang, G.; Yuan, M.; Miao, Y.; Wu, J.; Wang, Y. Experimental study on seismic response of underground tunnel-soil-surface structure interaction system. Tunn. Undergr. Space Technol. 2018, 76, 145–159. [Google Scholar] [CrossRef]
- Wang, G.; Yuan, M.; Ma, X.; Wu, J. Numerical study on the seismic response of the underground subway station-surrounding soil mass-ground adjacent building system. Front. Struct. Civ. Eng. 2017, 11, 424–435. [Google Scholar] [CrossRef]
- Meymand, P.J. Shaking Table Scale Model Tests of Nonlinear Soil-Pile-Superstructure Interaction in Soft Clay. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1998. [Google Scholar]
- Moss, R.E.S.; Crosariol, V.A. Scale model shake table testing of an underground tunnel cross section in soft clay. Earthq. Spectra 2013, 29, 1413–1440. [Google Scholar] [CrossRef]
- Li, P.; Yang, J.; Lu, Z. Shaking table test and theoretical analysis of the pile-soil-structure interaction at a liquefiable site. Struct. Des. Tall Spec. Build. 2018, 27, e1513. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, W.; Li, Y.; Yuan, Y. Shaking table test of a multi-story subway station under pulse-like ground motions. Soil Dyn. Earthq. Eng. 2016, 82, 111–122. [Google Scholar] [CrossRef]
- Moncarz, P.D.; Krawinkler, H. Theory and Application of Experimental Model Analysis in Earthquake Engineering (Report No. 50); John A. Blume Earthquake Engineering Center, Department of Civil Engineering, Stanford University: Stanford, CA, USA, 1981. [Google Scholar]
- Shang, S.; Liu, F.; Lu, H. Design and experimental study of a model soil used for shaking table test. Earthq. Eng. Eng. Vib. 2006, 4, 199–204. [Google Scholar]
- Blaney, G.M.W. Synthetic clay soil for dynamic model pile tests. In Dynamic Response of Pile Foundations—Experiment, Analysis and Observation; ASCE: New York, NY, USA, 1987. [Google Scholar]
- Tavenas, F.R.M.L. An Artificial Material for Simulating Champlain Clays. Can. Geotech. J. 1973, 3, 489–503. [Google Scholar] [CrossRef]
- Yan, X.; Yu, H.; Yuan, Y. Multi-point shaking table test of the free field under non-uniform earthquake excitation. Soils Found. 2015, 55, 985–1000. [Google Scholar] [CrossRef]
- Martin, P.P.; Seed, H.B. One-dimensional dynamic ground response analyses. J. Geotech. Eng. Div. ASCE 1982, 108, 935–952. [Google Scholar] [CrossRef]
- Jinping, Y. Shaking Table Test on Energy Dissipating Structures Considering Soil-Structure Dynamic Interaction. Ph.D. Thesis, Tongji University, Shanghai, China, 2018. [Google Scholar]
- Arias, A. A Measure of Earthquake Intensity. In Seismic Design for Nuclear Power Plants; Hansen, R.J., Ed.; MIT Press: Cambridge, MA, USA, 1970. [Google Scholar]









| Platform size | 4 m × 4 m |
| Maximum capacity | 25 t |
| Shaking direction | X, Y, Z six degrees of freedom |
| Peak accelerations | X: 1.2 g~0.8 g |
| Y: 0.8 g~0.6 g | |
| Z: 0.7 g~0.5 g | |
| Maximum velocities | X/Y: ±1000 mm/s |
| Maximum displacements | X/Y: ±500 mm |
| Frequency range | 0.1 Hz~50 Hz |
| Types | Physical Quantities | Similitude Relation | Similarity Ratio |
|---|---|---|---|
| Geometry properties | Length (l) | 1/30 | |
| Displacement (r) | 1/30 | ||
| Material properties | Elastic modulus (E) | 2.6/30 = 0.0867 | |
| Stress (σ) | 0.0867 | ||
| Strain (ε) | 1.0 | ||
| Equivalent density (ρ) | 1.3 | ||
| Poisson’s ratio (μ) | 1.0 | ||
| Load properties | Line load (P) | 0.00289 | |
| Surface load (q) | 0.0867 | ||
| Dynamic properties | Mass (m) | 0.000048148 | |
| Stiffness (k) | 0.00289 | ||
| Time (t) | 0.1291 | ||
| Frequency (f) | 7.7460 | ||
| Acceleration (a) | 2.0 |
| (MPa) | A | B | ||||
|---|---|---|---|---|---|---|
| 6.30 | 9.09 × 10−4 | 1.14 | 0.45 | 1.21 × 10−2 | 0.18 | 1.11 |
| Number of Tests | Load No. | Name of Input Wave | PGA (g) |
|---|---|---|---|
| 1 | WN1 | White noise | 0.05 |
| 2 | ATYC1 | Mexican | 0.1 |
| 3 | TCU1 | Chi-Chi | 0.1 |
| 4 | HKD1 | Tokachi | 0.1 |
| 5 | WN2 | White noise | 0.05 |
| 6 | ATYC2 | Mexican | 0.2 |
| 7 | TCU2 | Chi-Chi | 0.2 |
| 8 | HKD1 | Tokachi | 0.2 |
| 9 | WN3 | White noise | 0.05 |
| 10 | ATYC3 | Mexican | 0.3 |
| 11 | TCU3 | Chi-Chi | 0.3 |
| 12 | HKD3 | Tokachi | 0.3 |
| 13 | WN4 | White noise | 0.05 |
| First Order | Second Order | |||
|---|---|---|---|---|
| Loading Case | Frequency (Hz) | Damping Ratio | Frequency (Hz) | Damping Ratio |
| Wn1 | 8.023068564 | 0.067142735 | 26.84408251 | 0.049318623 |
| Wn2 | 7.938435657 | 0.071101806 | 26.49870362 | 0.048931665 |
| Wn3 | 7.865083823 | 0.071152032 | 26.55452582 | 0.047449223 |
| Wn4 | 7.783742241 | 0.075354539 | 25.84688735 | 0.043373584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, N.; Ling, Y.; Yang, Z.; Ha, X.; Xu, B. Shaking Table Test of a Subway Station–Soil–Aboveground Structures Interaction System: Structural Impact on the Field. Buildings 2025, 15, 2223. https://doi.org/10.3390/buildings15132223
Hong N, Ling Y, Yang Z, Ha X, Xu B. Shaking Table Test of a Subway Station–Soil–Aboveground Structures Interaction System: Structural Impact on the Field. Buildings. 2025; 15(13):2223. https://doi.org/10.3390/buildings15132223
Chicago/Turabian StyleHong, Na, Yan Ling, Zixiong Yang, Xiaochun Ha, and Bin Xu. 2025. "Shaking Table Test of a Subway Station–Soil–Aboveground Structures Interaction System: Structural Impact on the Field" Buildings 15, no. 13: 2223. https://doi.org/10.3390/buildings15132223
APA StyleHong, N., Ling, Y., Yang, Z., Ha, X., & Xu, B. (2025). Shaking Table Test of a Subway Station–Soil–Aboveground Structures Interaction System: Structural Impact on the Field. Buildings, 15(13), 2223. https://doi.org/10.3390/buildings15132223





