Structural Damage Identification Using PID-Based Search Algorithm: A Control-Theory Inspired Application
Abstract
1. Introduction
2. Theoretical Background
2.1. Damage Indentification Problem
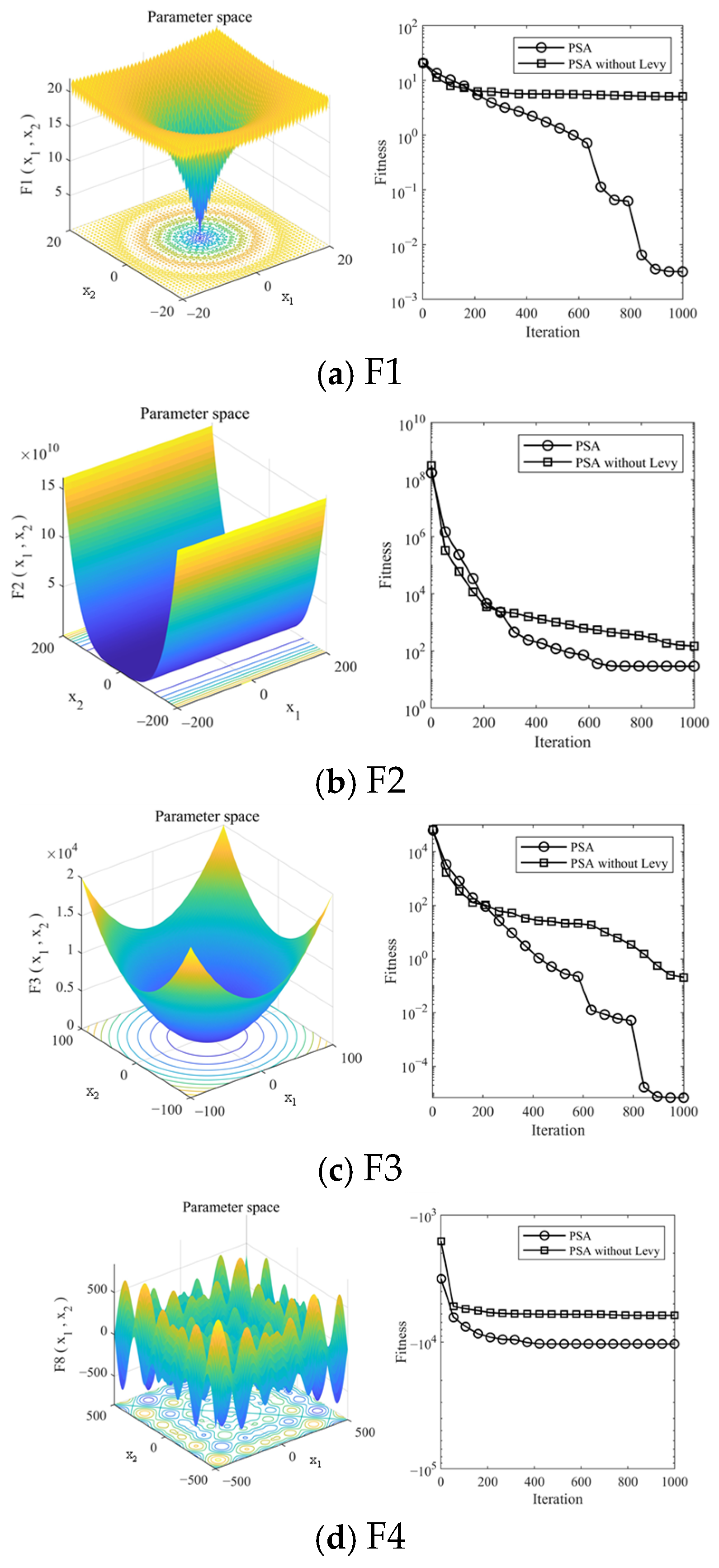
2.2. PID-Based Search Algorithm
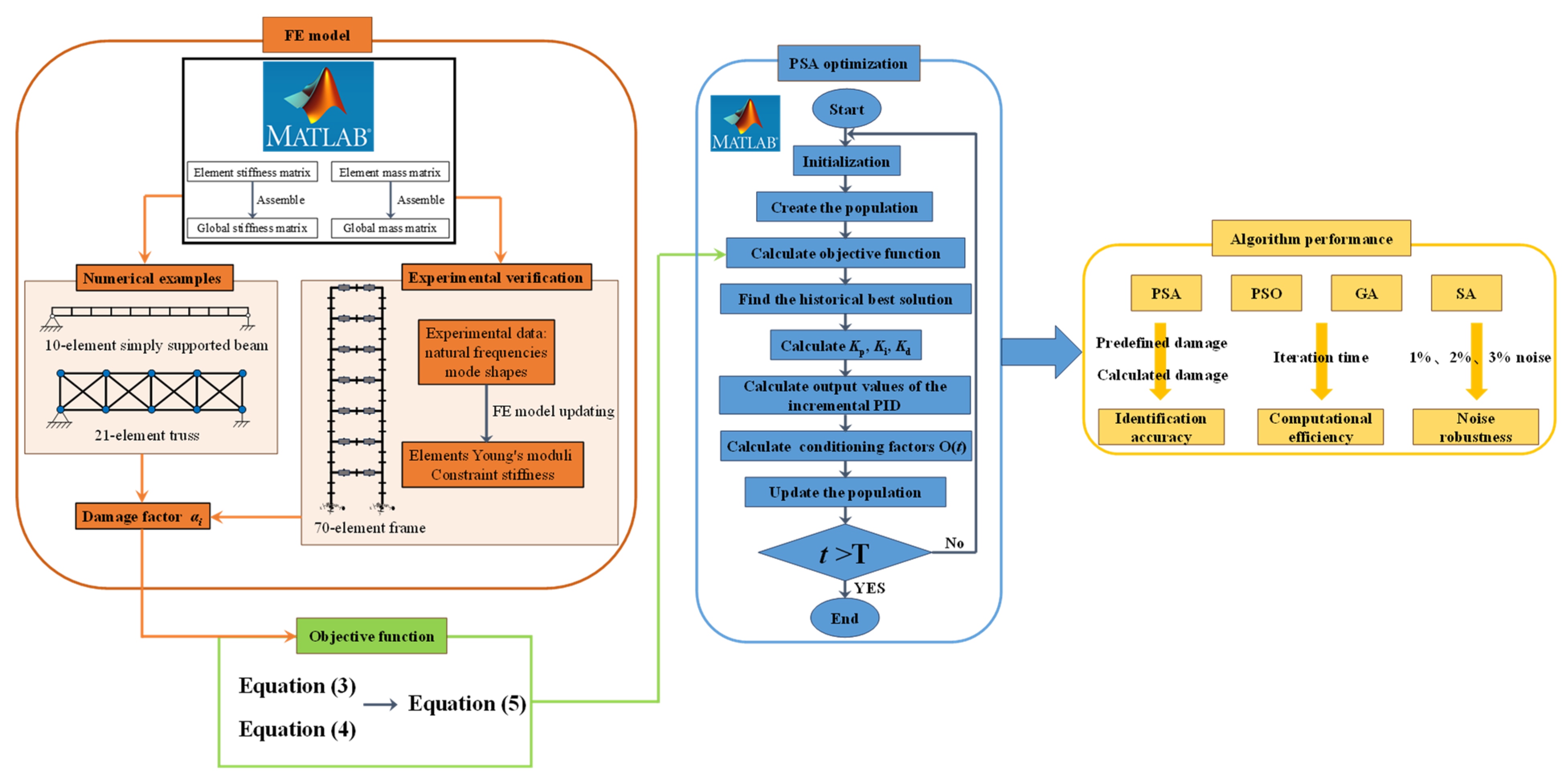
2.3. Workflow
3. Simulation Examples
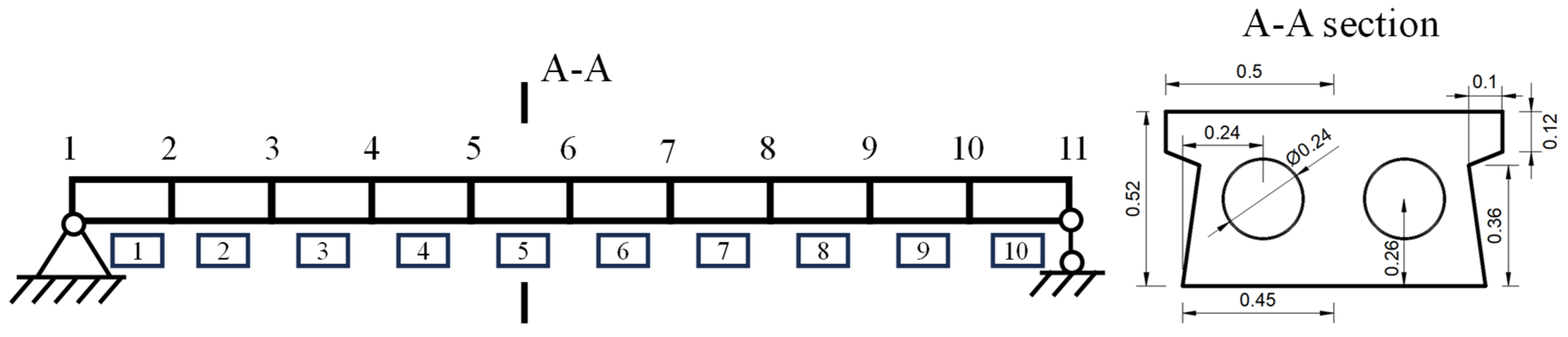
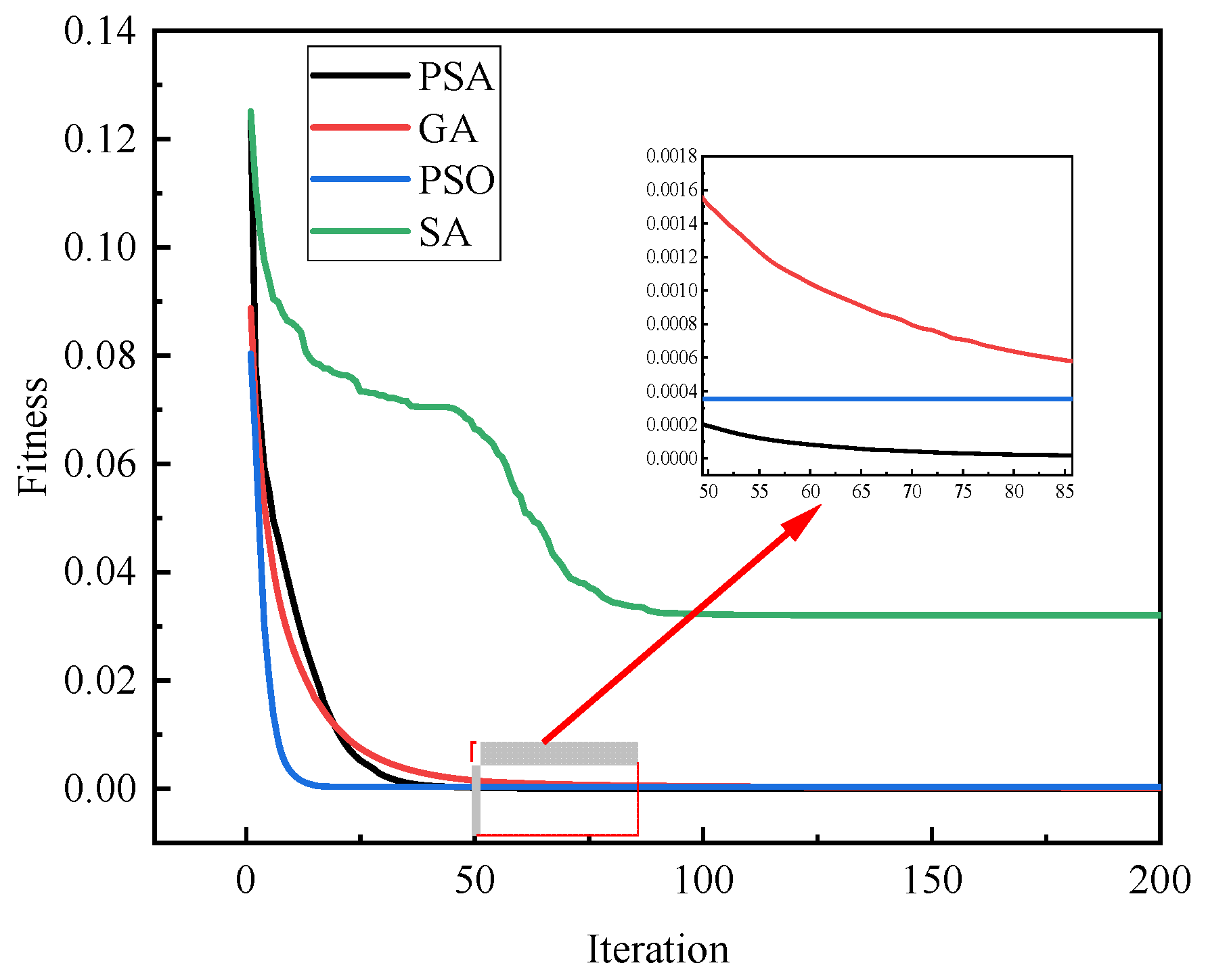
3.1. Simply Supported Beam
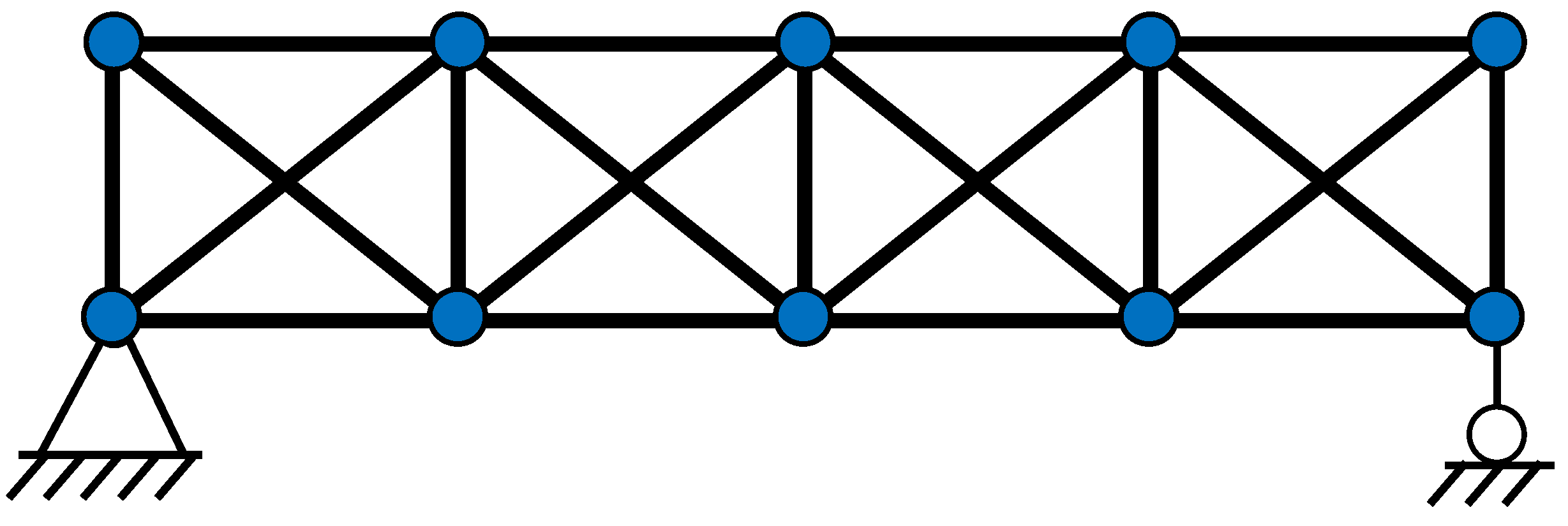
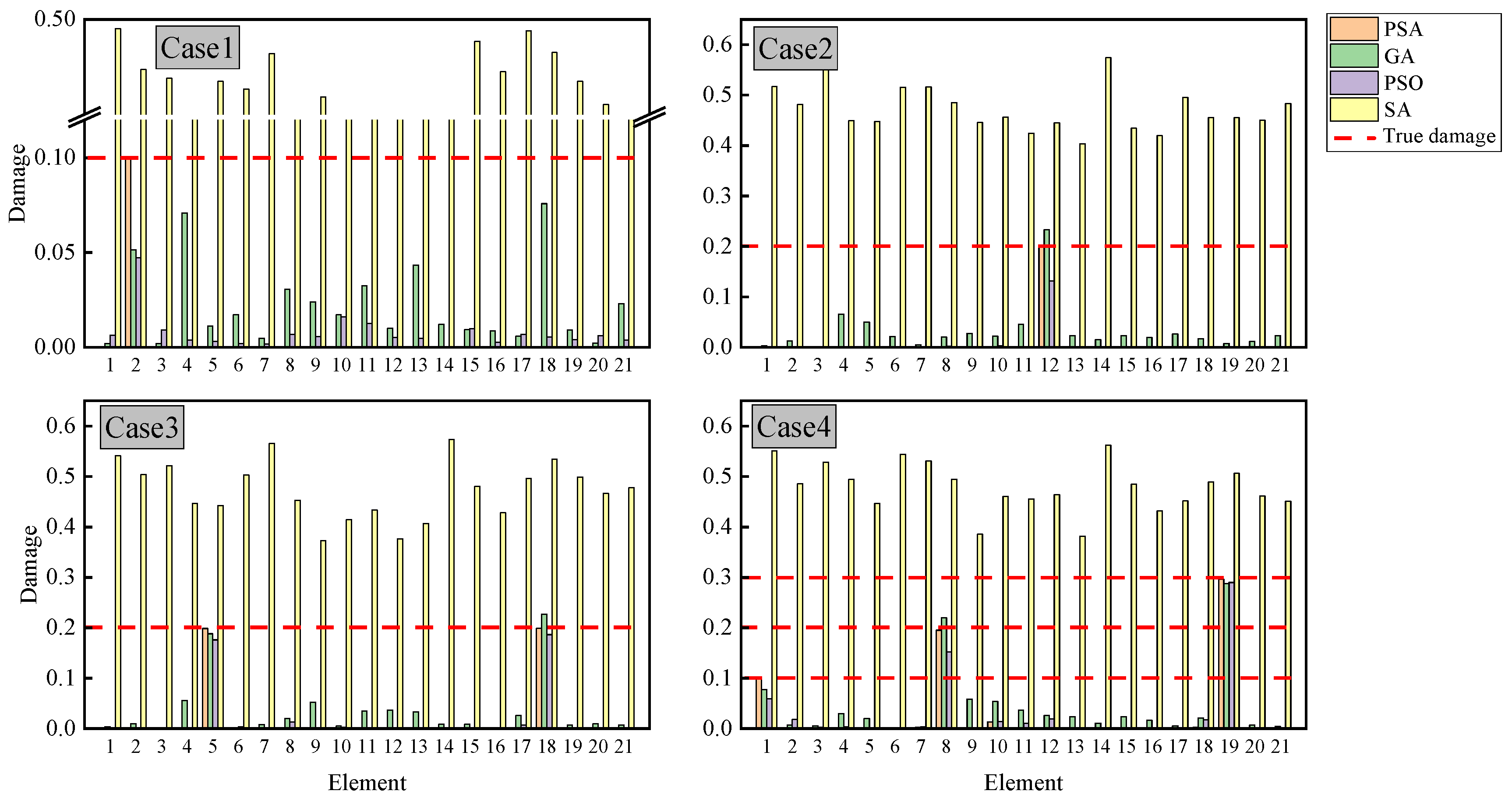
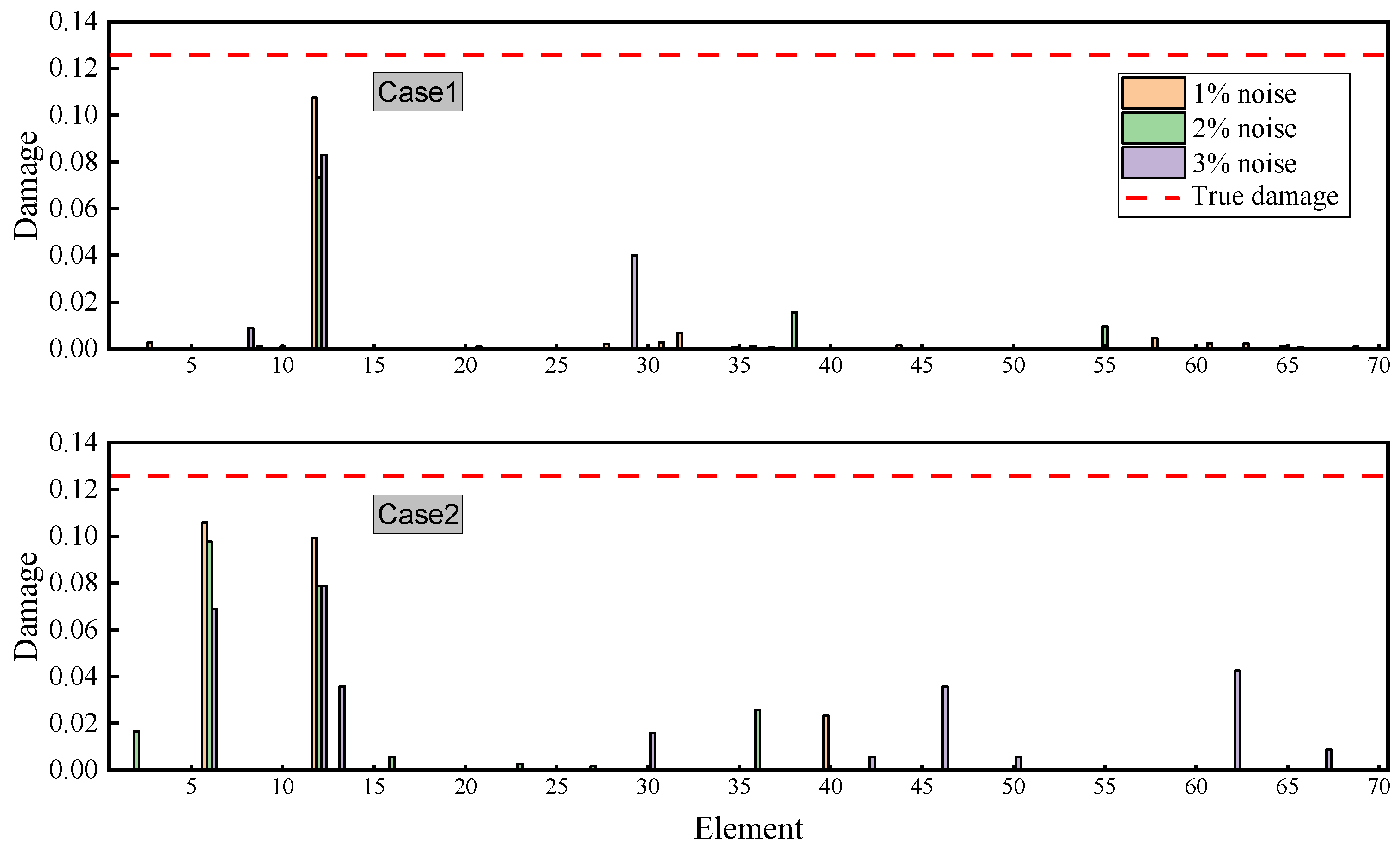
3.2. 21-Bar Truss
4. Experimental Verification
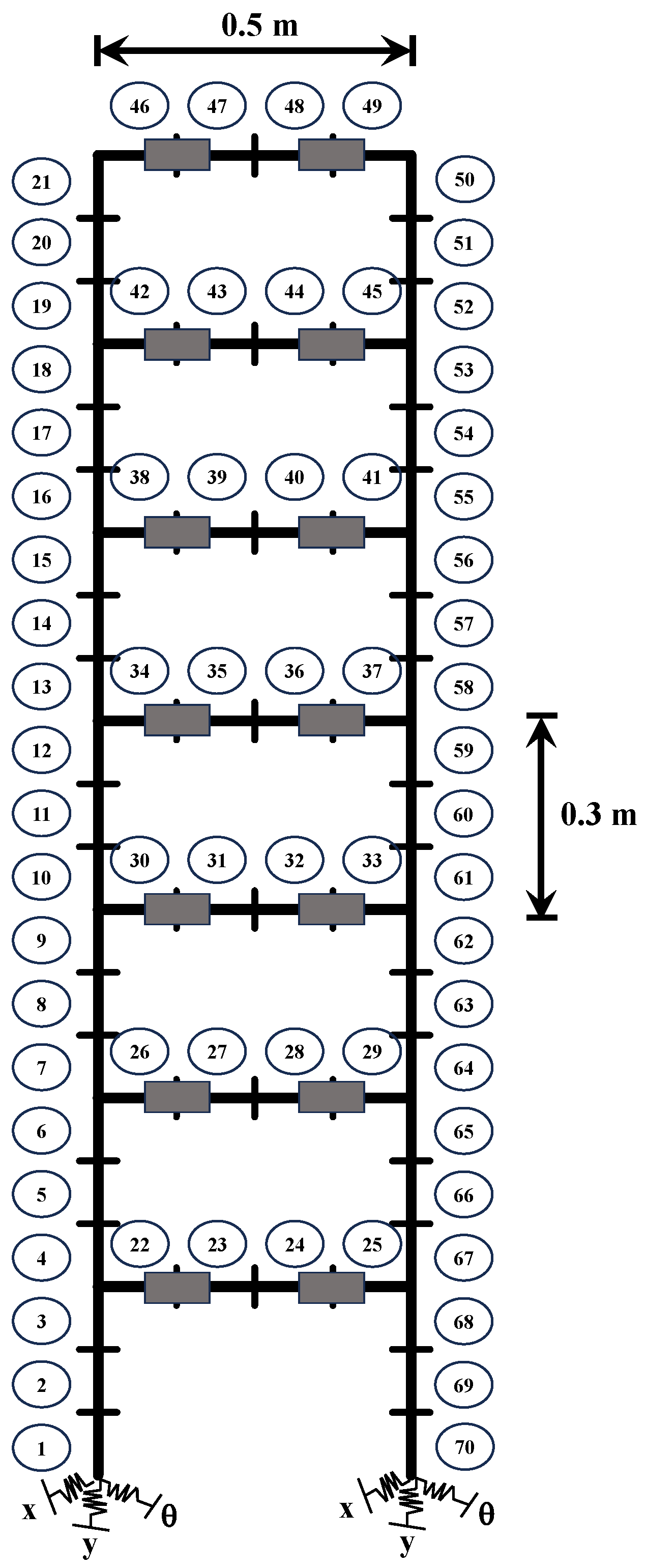
4.1. Experimental Setup
4.2. FE Model Updating
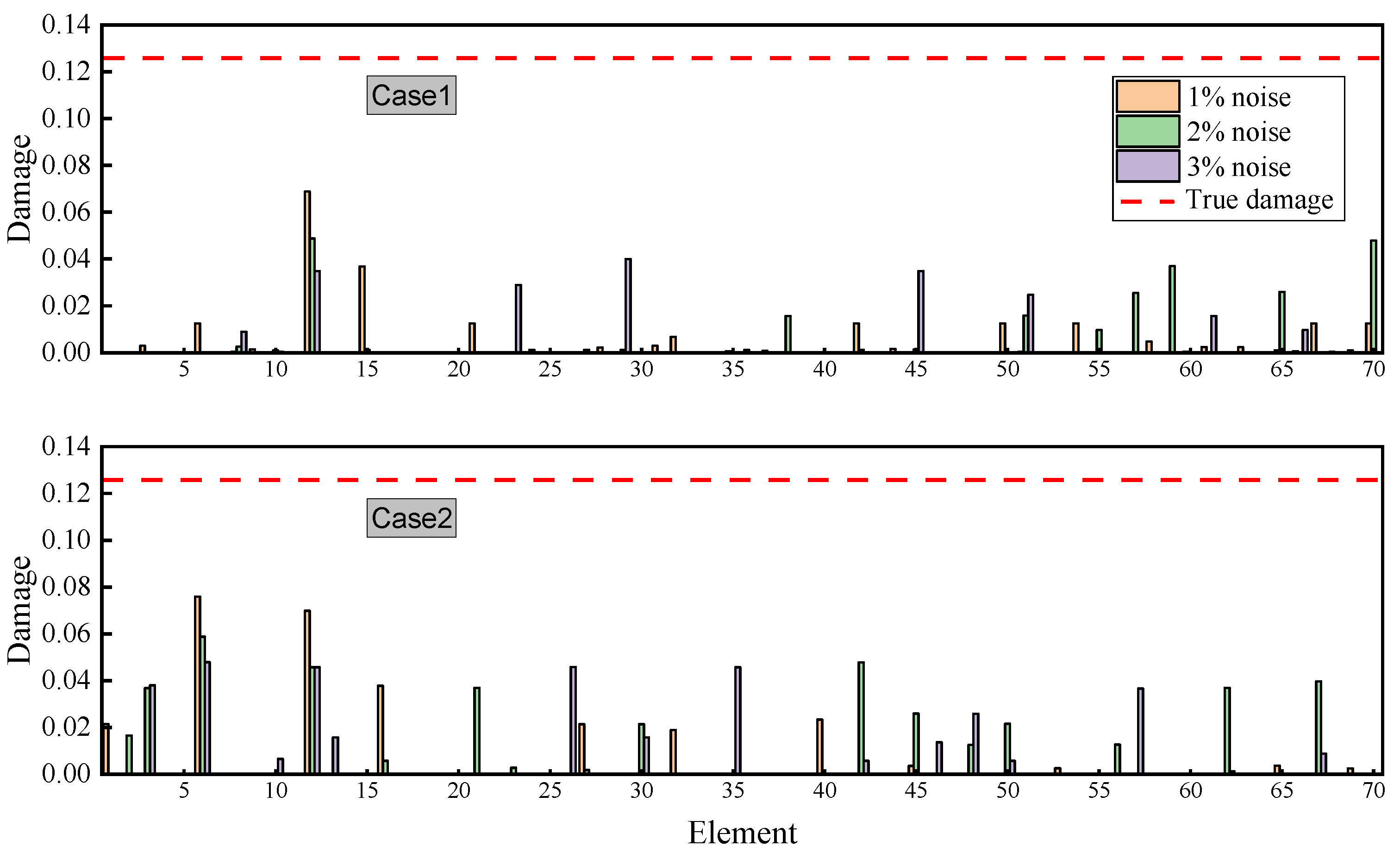
4.3. SDI Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cantero, D.; Sarwar, Z.; Malekjafarian, A.; Corbally, R.; Alamdari, M.M.; Cheema, P.; Aggarwal, J.; Noh, H.Y.; Liu, J.X. Numerical benchmark for road bridge damage detection from passing vehicles responses applied to four data-driven methods. Arch. Civ. Mech. Eng. 2024, 24, 190. [Google Scholar] [CrossRef]
- Wang, Q.A.; Dai, Y.; Ma, Z.G.; Ni, Y.Q.; Tang, J.Q.; Xu, X.Q.; Wu, Z.Y. Towards probabilistic data-driven damage detection in SHM using sparse Bayesian learning scheme. Struct. Control. Health Monit. 2022, 29, e3070. [Google Scholar] [CrossRef]
- Tavares, A.; Di Lorenzo, E.; Cornelis, B.; Peeters, B.; Desmet, W.; Gryllias, K. Machine Learning approaches to damage detection in composite structures combining experimental and simulation domains. Mech. Syst. Signal Process. 2024, 215, 111412. [Google Scholar] [CrossRef]
- Lazaridis, P.C.; Kavvadias, I.E.; Demertzis, K.; Iliadis, L.; Vasiliadis, L.K. Structural damage prediction of a reinforced concrete frame under single and multiple seismic events using machine learning algorithms. Appl. Sci. 2022, 12, 3845. [Google Scholar] [CrossRef]
- Chen, Z.P.; Di, Z.; Zhou, C.; Wenxue, W.X. Structural damage detection based on modal feature extraction and multi-objective optimization method for steel structures. Front. Mater. 2022, 9, 1015322. [Google Scholar] [CrossRef]
- Chen, Z.P.; Liu, Q.T.; Pan, C.D. Structural damage detection based on modal strain energy assurance criterion using adaptive region shrinkage assisted IGOA. Structures 2023, 58, 105458. [Google Scholar] [CrossRef]
- Corbally, R.; Malekjafarian, A. Bridge damage detection using operating deflection shape ratios obtained from a passing vehicle. J. Sound Vib. 2022, 537, 117225. [Google Scholar] [CrossRef]
- Mostafaei, H. Modal Identification Techniques for Concrete Dams: A Comprehensive Review and Application. Science 2024, 6, 40. [Google Scholar] [CrossRef]
- Gulgec, N.S.; Takáč, M.; Pakzad, S.N. Convolutional neural network approach for robust structural damage detection and localization. J. Comput. Civ. Eng. 2019, 33, 04019005. [Google Scholar] [CrossRef]
- Lee, K.; Chung, M.; Kim, S.; Shin, D.H. Damage detection of catenary mooring line based on recurrent neural networks. Ocean. Eng. 2021, 227, 108898. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Wahab, M.A. Damage detection in slab structures based on two-dimensional curvature mode shape method and Faster R-CNN. Adv. Eng. Softw. 2023, 176, 103371. [Google Scholar] [CrossRef]
- Choe, D.E.; Kim, H.C.; Kim, M.H. Sequence-based modeling of deep learning with LSTM and GRU networks for structural damage detection of floating offshore wind turbine blades. Renew. Energy 2021, 174, 218–235. [Google Scholar] [CrossRef]
- Huang, L.W.; Hong, X.B.; Yang, Z.J.; Liu, Y.; Zhang, B. CNN-LSTM network-based damage detection approach for copper pipeline using laser ultrasonic scanning. Ultrasonics 2022, 121, 106685. [Google Scholar] [CrossRef]
- Ge, Q.Y.; Li, C.M.; Yang, F.L. Research on the Application of Deep Learning Algorithm in the Damage Detection of Steel Structures. IEEE Access 2025, 13, 76732–76746. [Google Scholar] [CrossRef]
- Hassani, S.; Shadan, F. Using incomplete FRF measurements for damage detection of structures with closely-spaced eigenvalues. Measurement 2022, 188, 110388. [Google Scholar] [CrossRef]
- Yang, Y.; Lu, H.C.; Tan, X.K.; Wang, R.Q.; Zhang, Y. Mode shape identification and damage detection of bridge by movable sensory system. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1299–1313. [Google Scholar] [CrossRef]
- Zhang, F.L.; Kim, C.W.; Goi, Y. Efficient Bayesian FFT method for damage detection using ambient vibration data with consideration of uncertainty. Struct. Control. Health Monit. 2021, 28, e2659. [Google Scholar] [CrossRef]
- Duarte, H.V.; Donadon, L.V. Frequency-based damage detection method for excitation signals above work frequencies: Theoretical aspects and experimental results. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–11. [Google Scholar] [CrossRef]
- Xu, Y.F.; Huang, G.L. Modal sensitivity analysis of acoustic metamaterials for structural damage detection. Int. J. Mech. Sci. 2023, 259, 108571. [Google Scholar] [CrossRef]
- Lee, Y.; Kim, H.; Min, S.; Yoon, H. Structural damage detection using deep learning and FE model updating techniques. Sci. Rep. 2023, 13, 18694. [Google Scholar] [CrossRef]
- Huang, M.S.; Zhang, J.W.; Li, J.; Deng, Z.H.; Luo, J. Damage identification of steel bridge based on data augmentation and adaptive optimization neural network. Struct. Health Monit. 2025, 24, 1674–1699. [Google Scholar] [CrossRef]
- Ding, Z.H.; Hou, R.R.; Xia, Y. Structural damage identification considering uncertainties based on a Jaya algorithm with a local pattern search strategy and L0. 5 sparse regularization. Eng. Struct. 2022, 261, 114312. [Google Scholar] [CrossRef]
- Ghannadi, P.; Kourehli, S.S. Model updating and damage detection in multi-story shear frames using Salp Swarm Algorithm. Earthq. Struct. 2019, 17, 63–73. [Google Scholar] [CrossRef]
- Firouzi, B.; Abbasi, A.; Sendur, P. Improvement of the computational efficiency of metaheuristic algorithms for the crack detection of cantilever beams using hybrid methods. Eng. Optim. 2022, 54, 1236–1257. [Google Scholar] [CrossRef]
- Ereiz, S.; Duvnjak, I.; Jiménez-Alonso, J.F. Review of finite element model updating methods for structural applications. Structures 2022, 41, 684–723. [Google Scholar] [CrossRef]
- Alkayem, N.F.; Shen, L.; Al-hababi, T.; Qian, X.D.; Cao, M.S. Inverse analysis of structural damage based on the modal kinetic and strain energies with the novel oppositional unified particle swarm gradient-based optimizer. Appl. Sci. 2022, 12, 11689. [Google Scholar] [CrossRef]
- Tiachacht, S.; Khatir, S.; Thanh, C.L.; Rao, R.V.; Mirjalili, S.; Wahab, M.A. Inverse problem for dynamic structural health monitoring based on slime mould algorithm. Eng. Comput. 2022, 38, 2205–2228. [Google Scholar] [CrossRef]
- Gara, F.; Nicoletti, V.; Arezzo, D.; Cipriani, L.; Leoni, G. Model updating of cultural heritage buildings through swarm intelligence algorithms. Int. J. Archit. Herit. 2025, 19, 259–275. [Google Scholar] [CrossRef]
- Wang, X.G.; Liang, P.; Ma, M.; Zhou, Z.W.; Wu, G.; Song, S. Finite element model updating and response prediction of a frame structure based on optimal sensor placement. Adv. Struct. Eng. 2025, 28, 55–67. [Google Scholar] [CrossRef]
- Ramezani, M.; Bahar, O. Structural damage identification for elements and connections using an improved genetic algorithm. Smart Struct. Syst. 2021, 28, 643–660. [Google Scholar] [CrossRef]
- Wang, N.G.; Jiang, Y.Y.; Zhong, Y.T.; Shao, L. An adaptive damage detection method based on differential evolutionary algorithm for beam structures. Measurement 2021, 178, 109227. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, L. A new structural damage detection strategy of hybrid PSO with Monte Carlo simulations and experimental verifications. Measurement 2018, 122, 658–669. [Google Scholar] [CrossRef]
- Majumdar, A.; Nanda, B. A comparative study on inverse vibration based damage assessment techniques in beam structure using ant colony optimization and particle swarm optimization. Adv. Sci. Eng. Med. 2020, 12, 918–923. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Zhang, K.; Chan, T.H.; Wang, Z.Z. Damage detection and location using a simulated annealing-artificial hummingbird algorithm with an improved objective function. Struct. Health Monit. 2025, 24, 129–147. [Google Scholar] [CrossRef]
- Fallahian, S.; Seyedpoor, S.M.; Norouzi, E.; Ghasemi, S. Structural Damage Identification Using a Multi-stage Gravitational Search Algorithm. J. Civ. Eng. Res. 2024, 6, 33–48. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Pawar, S.N. A review of PID control, tuning methods and applications. Int. J. Dyn. Control. 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Feng, H.; Ma, W.; Yin, C.B.; Cao, D.H. Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller. Autom. Constr. 2021, 127, 103722. [Google Scholar] [CrossRef]
- Jian, M.L.; Zhu, S.; Du, W.Y.; Yang, L.Q.; Zhang, J.H. Design of a temperature control system for transient thermal measurement utilizing the backpropagation PID algorithm. Int. J. Therm. Sci. 2025, 210, 109654. [Google Scholar] [CrossRef]
- Zhang, J.Q.; Yang, X.; Wang, W.; Brilakis, I.; Davletshina, D.; Wang, H.N. Robust ELM-PID tracing control on autonomous mobile robot via transformer-based pavement crack segmentation. Measurement 2025, 242, 116045. [Google Scholar] [CrossRef]
- Gao, Y.S. PID-based search algorithm: A novel metaheuristic algorithm based on PID algorithm. Expert Syst. Appl. 2023, 232, 120886. [Google Scholar] [CrossRef]
- Wang, X.; Palka, R.; Wardach, M. Nonlinear digital simulation models of switched reluctance motor drive. Energies 2020, 13, 6715. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Huang, S.C. Using the extended finite element method to integrate the level-set method to simulate the stress con-centration factor at the circular holes near the material boundary of a functionally-graded material plate. J. Mater. Res. Technol. 2022, 21, 4658–4673. [Google Scholar] [CrossRef]
- Li, J.; Law, S.S.; Ding, Y. Substructure damage identification based on response reconstruction in frequency domain and model updating. Eng. Struct. 2012, 41, 270–284. [Google Scholar] [CrossRef]



| Algorithm | Parameters |
|---|---|
| GA | crossover_rate = 0.8, mutation_rate = 0.1, tournament_size = 5, Pop = 30 |
| PSO | w = 0.729, c1 = 1.5, c2 = 1.5, Pop = 30 |
| SA | initial_temp = 200, cooling_rate = 0.95 |
| PSA | Kp = 1, Ki = 0.5, Kd = 1.2, Pop = 30 |
| Damage Scenarios | Damage Location and Severity |
|---|---|
| Case 1 | Element 5, 10% |
| Case 2 | Element 3, 20% |
| Case 3 | Element 9, 30% |
| Case 4 | Element 4, 15%&Element 7 15% |
| Case 5 | Element 2, 10%&Element 6, 30% |
| Case 6 | Element 1, 10%&Element 5, 20%&Element 7, 30% |
| Case | Time/s | |||
|---|---|---|---|---|
| PSA | GA | PSO | SA | |
| Case 1 | 0.494 | 1.843 | 0.534 | 0.018 |
| Case 2 | 0.500 | 1.837 | 0.527 | 0.019 |
| Case 3 | 0.509 | 1.875 | 0.568 | 0.019 |
| Case 4 | 0.529 | 1.916 | 0.545 | 0.018 |
| Case 5 | 0.529 | 1.825 | 0.532 | 0.019 |
| Case 6 | 0.526 | 1.828 | 0.533 | 0.019 |
| Damage Scenarios | Damage Location and Severity |
|---|---|
| Case 1 | Element 2, 10% |
| Case 2 | Element 12, 20% |
| Case 3 | Element 5, 20%&Element 18 20% |
| Case 4 | Element 1, 10% &Element 8, 20% &Element 19, 30% |
| Case | Time/s | |||
|---|---|---|---|---|
| PSA | GA | PSO | SA | |
| Case1 | 2.328 | 5.813 | 3.533 | 0.063 |
| Case2 | 2.132 | 5.643 | 3.499 | 0.062 |
| Case3 | 2.547 | 5.635 | 3.873 | 0.065 |
| Case4 | 2.910 | 6.418 | 3.933 | 0.062 |
| Mode | Measured | Initial FE Model | Updated FE Model | ||
|---|---|---|---|---|---|
| Caculated | Error (%) | Caculated | Error (%) | ||
| 1 | 2.54 | 2.49 | 1.97 | 2.54 | 0.00 |
| 2 | 7.66 | 7.52 | 1.83 | 7.63 | 0.39 |
| 3 | 12.86 | 12.51 | 2.72 | 12.85 | 0.08 |
| 4 | 18.03 | 17.64 | 2.16 | 17.99 | 0.22 |
| 5 | 22.96 | 22.37 | 2.57 | 22.91 | 0.22 |
| 6 | 26.99 | 25.92 | 3.96 | 26.94 | 0.19 |
| 7 | 29.91 | 28.82 | 3.64 | 29.87 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Sun, T. Structural Damage Identification Using PID-Based Search Algorithm: A Control-Theory Inspired Application. Buildings 2025, 15, 2216. https://doi.org/10.3390/buildings15132216
Shi K, Sun T. Structural Damage Identification Using PID-Based Search Algorithm: A Control-Theory Inspired Application. Buildings. 2025; 15(13):2216. https://doi.org/10.3390/buildings15132216
Chicago/Turabian StyleShi, Kuang, and Tingting Sun. 2025. "Structural Damage Identification Using PID-Based Search Algorithm: A Control-Theory Inspired Application" Buildings 15, no. 13: 2216. https://doi.org/10.3390/buildings15132216
APA StyleShi, K., & Sun, T. (2025). Structural Damage Identification Using PID-Based Search Algorithm: A Control-Theory Inspired Application. Buildings, 15(13), 2216. https://doi.org/10.3390/buildings15132216






