Optimizing the Food–Energy–Water Nexus: A Multi-Objective Spatial Configuration Framework for High-Density Communities

Abstract

Global urbanization and climate change are intensifying challenges in the sustainable management of the Food–Energy–Water (FEW) system. This study introduces a multi-objective optimization framework that redefines urban spaces through a dual rooftop-ground hierarchy, interlinkage nodes for mapping material and energy flows, and the application of NSGA-II optimization to balance food production, energy output, and costs. The framework was applied to a case study area, generating non-dominated solutions with diverse resource-cost configurations. The findings revealed that optimal scenarios could meet 40.6% of local energy demands and exceed 102.9% of local grain demands, while maintaining economic viability. This approach bridges resource systems theory and spatial planning practice, providing economically viable pathways for high-density cities to transform into hybrid production-consumption spaces, effectively addressing the dual pressures of urbanization and climate change.

1. Introduction

The climate crisis and rapid urbanization are driving unprecedented global challenges. By 2050, urban populations are projected to reach 68%, resulting in a 70% increase in food demand, a doubling of energy demand, and a 30% rise in water usage [1,2,3]. High-density urban residential areas, which occupy over one-third of urban space, face critical imbalances within Food–Energy–Water (FEW) systems [4,5]. While traditional urban planning has tended to address these challenges in isolation, recent evidence highlights the potential of productive retrofitting—integrating food production, energy generation, and water recycling—which offers a more effective c pathway to enhance self-sufficiency, urban sustainability, and resilience [6].

Current approaches to urban spatial resource optimization can be categorized into four distinct streams, each with specific advantages and limitations. The first focuses on single-resource optimization models, such as photovoltaic (PV) layouts for energy production, rooftop farming for food production, or rainwater harvesting to alleviate water scarcity [7,8]. While these models have advanced spatial allocation techniques, they typically operate at building or site scale and overlook critical interactions between resource systems [9]. The second approach utilizes urban metabolism models to optimize resource efficiency by analyzing material flows at urban or regional scales [10]. Although these models address the entire process of energy transfer, they lack explicit spatial guidance for implementation at the neighborhood level. The third and emerging approach is the FEW-Nexus model, which integrates food, energy, and water systems to explore synergies and coupling relationships [11,12]. Yet, most FEW-Nexus studies remain conceptual, focus on regional scales, and offer limited spatial specificity for urban planning applications.

These limitations reveal three critical research gaps. First, most studies address source systems in isolation, neglecting the complex interactions among them [13] note, systematic research on spatial optimization for efficient FEW system integration at the residential scale remains underexplored. Second, a central challenge in applying FEW-Nexus research to urban design lies in cross-scale integration—aligning macro-level resource flow efficiency with micro-level spatial configurations. The absence of a theoretical and methodological framework for cross-scale coordination constitutes a key bottleneck in advancing this field [14]. Third, there is a notable lack of multi-objective optimization studies on FEW systems in high-density urban residential areas [15]. While multi-objective optimization methods have been employed to balance social, economic, and environmental benefits in urban resource management, insufficient consideration of cost constraints often limits their practical application [16,17].

To address these gaps, this study proposes a multi-objective coordinated optimization framework tailored to the FEW system in high-density urban residential contexts. The specific aims are (1) to develop a green retrofitting strategy that integrates food, energy, and water resources, overcoming the limitations of single-system approaches; (2) to explore coupling patterns between resource transformation processes and spatial configurations, bridging the gap between abstract resource flow models and concrete spatial planning; and (3) to maximize resource production potential through multi-objective optimization, while ensuring both economic feasibility and practical operability.

2. Conceptual Framework and Research Hypotheses

The FEW system within residential communities comprises three interlinked subsystems—food, energy, and water—and the dynamic interactions among them. Unlike conventional siloed approaches, our framework conceptualizes these components as spatially and materially integrated, forming closed or semi-closed loops of resource metabolism [18,19]. The food subsystem utilizes ground-level green spaces, rooftop areas, greenhouses, and indoor environments to support vegetable and fruit cultivation, hydroponics, and small-scale processing. Water for these processes is supplied through rainwater harvesting and water reclamation systems, while energy is primarily derived from distributed PV installations and, in part, from systems converting organic waste into usable energy. The energy subsystem is predominantly composed of PV arrays installed on flat rooftops, greenhouse roofs, or sloped surfaces, complemented by biogas systems and waste processing infrastructure. The water subsystem is structured through rainwater collection, storage, and distribution, as well as domestic wastewater recovery and treatment, providing water for irrigation and non-potable purposes. Purification and reuse processes are energy-driven, and a portion of the treated water is reintegrated into the food production cycle, enabling bidirectional flows of materials and energy.

Building upon this integrated framework, this study introduces a dual spatial hierarchy—“rooftop–ground level”—to reorganize the spatial structure of residential communities. Unlike conventional urban planning, our model transforms rooftops and ground surfaces from recreational space into multifunctional micro-production units combining resource generation, waste management, and renewable energy production. Through the coordinated planning of key interventions—such as rooftop farming, rainwater capture, solar energy generation, and organic waste recycling—the strategy simultaneously increases resource availability and reduces consumption, minimizing external resource dependency while enhancing local self-sufficiency and spatial efficiency.

Moreover, the study introduces the concept of “coupling nodes” to elucidate material and energy transformation pathways among subsystems (Figure 1). The water–energy coupling is reflected in the electricity demand for rainwater treatment and wastewater reuse. The food–energy coupling manifests in the energy required for crop cultivation and processing, as well as in energy recovered from organic waste. The food–water interconnection primarily involves rainwater and reclaimed water for irrigation, and the recovery of water and nutrients during waste treatment. Unlike previous conceptual models that identify but rarely quantify these relationships [20,21,22]. Our approach provides measurable indicators for system optimization. These interwoven pathways constitute the core resource flow routes within the community-scale FEW system, offering theoretical underpinnings for systemic optimization during micro-scale urban renewal.

Building on the above conceptual framework, this study proposes the following research hypotheses:

H1. 

Within the FEW system, the food, energy, and water subsystems exhibit significant synergistic interactions, whereby integrated system optimization outperforms the optimization of individual subsystems.

H2. 

Resource production efficiency and economic cost vary markedly across different spatial configuration scenarios, and an optimal configuration exists that simultaneously maximizes local resource self-sufficiency while minimizing economic expenditure.

H3. 

In high-density residential areas, optimizing the spatial allocation ratio between rooftop and ground-level resource production strategies can substantially enhance the local production capacity of the FEW system, thereby facilitating sustainable and circular development at the community scale.

3. Methods

3.1. Definition of System Boundaries

This study aimed to develop a broadly applicable decision-making framework and methodological process. To ensure scientific rigor and operational feasibility, the system boundaries were defined as follows: Spatial boundaries encompassed three types of areas—rooftops, ground-level green spaces, and hardscaped surfaces. While building façades offer integration potential, they were excluded from the current model due to limitations in technological adaptability. Additionally, building-induced shading effects, which are closely tied to site-specific spatial morphologies, were not considered in this study. Temporal boundaries were established based on annual average values. Technological boundaries were restricted to mature and widely implemented technologies. The PV system was assumed to utilize monocrystalline silicon modules, and vegetable cultivation was designated as the default planting type. Economic boundaries encompassed both the initial capital investment—covering materials, equipment, and installation—and the average annual operation and maintenance (O&M) costs associated with each facility. To ensure comparability across subsystems, a uniform 20-year lifecycle was applied. All construction and O&M costs were annualized and incorporated into the optimization model. Although external benefits—such as environmental and educational value—were acknowledged as important, they were not included in the current optimization objective function.

3.2. Data Collection and Spatial Survey

This study selected Xuefu Subdistrict in Nankai District, Tianjin Municipality, as the research site (Figure 2). Located in a solar-rich region, Nankai District offers favorable conditions for both agricultural production and photovoltaic energy generation. Xuefu Subdistrict spans approximately 0.848 square kilometers and has a population of about 34,470, indicating high population density and substantial food and energy demand. According to statistical yearbooks, the annual per capita electricity consumption is 1169 kWh. Notably, some residents have already undertaken self-initiated retrofitting activities to repurpose available spaces for productive uses, such as small-scale cultivation or renewable energy applications.

The three-dimensional data of objects within the site were rapidly acquired using low-altitude unmanned aerial vehicle (UAV) information technology. A point cloud model was subsequently generated with the Context Capture software, serving as a reference for constructing a three-dimensional site model. Based on this model and findings from on-site investigations, areas available for production and utilization within the residential zone were identified and quantified (

Table 1. Spatial inventory of residential area.

Spatial Category	Subtype	Area Available for Productive Use
Green Space	Community Parks	85,125 m2
	Inter-building Landscaped Areas
	Courtyards	Excluded due to high privacy
Transportation	Road Space	47,200 m2
	Parking Areas
Idle Land	Vacant Land	23,845 m2
Rooftop Space	Flat Roofs	196,815 m2
	Sloped Roofs	26,535 m2

). Statistical analysis revealed that the total flat roof area suitable for production and utilization amounts to 196,815 square meters, while the green space area totals 85,125 square meters.

The data selection process for this study followed three principles: contextual relevance, technical validity, and implementation feasibility. Climate and resource data were prioritized from official statistical sources, technical parameters were derived from field-validated studies rather than theoretical maximums, and economic parameters incorporated market surveys and industry reports, using conservative estimates to ensure practical applicability. Specific parameter selections and validation methods will be detailed within their respective models.

3.3. Assessment Model for Resource Production Potential

This study developed mathematical models to assess the resource potential of the food, energy, and water subsystems, with the land area allocated to each type of resource production serving as the independent variable.

The energy subsystem incorporates two widely adopted and mature technologies: PV power generation and biogas-based electricity generation. To ensure computational feasibility, the model calculates annual energy output as the total of each technology’s unit-area energy yield multiplied by its corresponding allocated area:

$$E=\sum _{i=1}^m{b}_i·y_i$$

(1)

In this equation, E represents the total annual energy output (kWh/year). yᵢ denotes the area or volume allocated to the ith type of energy production, such as flat roof PV area (y₁), greenhouse surface area (y₂), and sloped roof PV area (y₃). The energy yield parameters (bi) were carefully selected to represent realistic performance under Tianjin’s specific conditions: 178.39 kWh/m² for PV systems and 5.8 kWh/m³ for biogas systems.

The PV energy yield was determined through PVSyst 7.4 software simulation using monocrystalline silicon panels—currently the predominant commercial technology—with Tianjin’s solar radiation data from the China Meteorological Administration. This approach provides more realistic estimates than laboratory efficiency ratings or theoretical calculations and ensures the validity of the data. Biogas yields were estimated based on calorific value and power station conversion efficiency, referencing the Comprehensive Methods for Biogas Production Calculation and Calorific Value Conversion [23] and the Renewable Energy Statistical Yearbook [24]. According to the calorific value of biogas, 1 m³ of biogas is equivalent to 0.714 kg of standard coal and 5.8 kWh of electricity production.

The annual vegetable production potential was calculated as the sum of the products of unit-area yields and the corresponding areas for each food production type:

$$F=\sum _{j=1}{a}_j·x_j$$

(2)

In this equation, F denotes the total annual food output (kg/year). aⱼ represents the average annual yield per unit area (kg/m²) of the jth food production type. xⱼ refers to the cultivable area (m²) available for the jth method, which includes ground cultivation (x₁), rooftop cultivation (x₂), PV greenhouse cultivation (x₃), and indoor hydroponic systems (x₄).

The food yield parameters (a_j) were established based on experimental data from the Facility Agriculture Experimental [25] Base of Beijing Academy of Agriculture and Forestry Sciences, rather than idealized agricultural models. The yield of lettuce grown on land is approximately 14 plants per square meter, with two harvests per year, resulting in an annual yield of about 28 plants per square meter. Taking hydroponic cultivation in three layers as an example, the annual yield is approximately 480 plants per square meter. For large plants, the weight per plant ranges from 200 to 300 g, while for small plants, it ranges from 100 to 200 g. Therefore, unit yields were set at 5.6 kg/m² for ground and rooftop cultivation and 40 kg/m² for controlled-environment agriculture, such as PV greenhouses and hydroponics.

For the water subsystem, this analysis focused on the collection and utilization of rainwater:

$$W=\sum _{k=1}^t{R·c}_k·z_k$$

(3)

In this equation, W represents the total annual volume of rainwater collected (m³). zₖ is the area (m²) of the kth rainwater-harvestable surface type, such as flat roof collection areas (z₁) and newly added hardscape surfaces (z₂). cₖ represents the surface runoff coefficient, set at 0.9 for flat roofs and 0.6 for hardscapes, based on the Tianjin local standard DB/T 29-236-2016: Technical Specifications for Urban Rainwater Utilization [26]. R is the annual precipitation (m), with a long-term average of 0.6186 m (618.6 mm) for Tianjin’s central urban area, as reported in the Tianjin Statistical Yearbook 2023 [27]. All outputs were standardized to cubic meters.

A critical interaction within the FEW-Nexus lies in the water demand associated with food production. For newly developed cultivation spaces, the total irrigation demand was calculated as follows:

$$G=\sum _{p=1}^q{d}_p·s_p$$

(4)

In this equation, G represents the total annual irrigation water demand for the food subsystem (L/year). sₚ is the irrigated area (m²) for the pth cultivation type, including open-field cultivation (s₁), greenhouse drip irrigation (s₂), and hydroponic drip irrigation (s₃). dₚ denotes the unit irrigation demand, set at 142.5 L/m² for open-field cultivation and 180.0 L/m² for both greenhouse and hydroponic systems. These values are based on the standard DB11/T 1764.2-2021: Water Use Quotas for Irrigating Leafy Vegetables [28] in both open-field and protected environments and are adjusted according to practical water allocation strategies in the Tianjin Plain region. The water parameters were selected from local established engineering standards, ensuring the model reflects realistic efficiency factors rather than ideal-case scenarios.

3.4. Cost Assessment Method

The total economic cost was calculated as the combined expenditure of four subsystems (

Table 2. Cost calculation indicators.

System Type	Cost Components	Parameter
Photovoltaic Power Generation	A: Construction cost of PV modules	525 CNY/m2
	B: Operation and maintenance cost	6.45 CNY/m2
	C: Revenue from electricity generation	57.8 CNY/m2
Open-field Cultivation	D: Land preparation and cultivation cost	2.5 CNY/m2
	E: Fertilizer cost	3 CNY/m2
	F: Pesticide cost	1.5 CNY/m2
	G: Labor cost	4.29 CNY/m2
	H: Irrigation cost	1 CNY/m3
Greenhouse Cultivation/ Indoor Hydroponics	I: Greenhouse construction cost	350 CNY/m2
	J: production input cost	6.28 CNY/m2
	K: Operation and maintenance cost	20 CNY/m2
	L: Fertilizer cost	0.17 CNY/m2
	M: Pesticide cost	0.11 CNY/m2
	N: Waste management cost	10 CNY/m2
	O: Irrigation cost	1.59 CNY/m3
Rainwater Harvesting	P: Construction cost of rainwater collection facilities	30 CNY/m2
	Q: Operation and maintenance cost	2 CNY/m2
	R: Water quality treatment cost	0.5 CNY/m3
	S: Economic benefit from water savings	0.5 CNY/m3

): PV power generation, open-field cultivation, greenhouse and hydroponic cultivation, and rainwater harvesting, as shown in Equation (5). Each subsystem’s cost includes its respective capital investment, O&M expenses, production input costs, and resource consumption, with deductions made for revenue generated, such as income from electricity production.

Since the biogas yield is treated as a fixed parameter, independent of spatial configuration, its associated cost does not vary with decision variables and is, therefore, excluded from the cost component of the objective function. However, it is included in the total energy output calculation.

$${C_{total}=C_{pv}+C_{openfield}+C_{greenhouse}+C}_{rainwater}$$

(5)

The cost evaluation of PV systems includes module installation costs and annual O&M expenses, net of revenue generated from electricity production. Key parameters were sourced from the China Photovoltaic Industry Development Roadmap (2022–2023), market quotations, and O&M standards issued by the China Photovoltaic Industry Association. These parameters were further calibrated using 2024 mainstream PV module specifications and local commercial electricity prices to ensure an accurate, contemporary, and context-specific economic evaluation. We computed the comprehensive expenditure for solar power production as the sum of the PV module installation cost (A) and system O&M cost (B), minus the electricity revenue (C):

$$C_{pv}=A+B-C$$

(6)

The cost assessment of open-field cultivation was based on the Compilation of Costs and Returns of Agricultural Products in China 2024, which disaggregates cost components for vegetable production in urban settings, including land preparation, fertilizers, pesticides, labor, and irrigation. To ensure conservative and operationally feasible evaluations, the lowest estimated values were adopted. The total cost of open-field cultivation consists of land preparation and tillage cost (D), fertilizer cost (E), pesticide cost (F), labor cost (G), and irrigation cost (H):

$$C_{openfield}=D+E+F+G+H$$

(7)

The construction, operation, and resource input costs of greenhouse and indoor hydroponic systems were derived from the empirical study by Zhen et al. (2020) on lifecycle costs of community-supported agriculture (CSA) in peri-urban Beijing [29]. These values were further adjusted based on current greenhouse configurations and management practices to ensure data representativeness and practical applicability. The total cost of greenhouse cultivation and indoor hydroponics includes construction cost (I), production input cost (J), O&M cost (K), fertilizer cost (L), pesticide cost (M), waste management cost (N), and irrigation cost (O):

$$C_{greenhouse}=I+J+K+L+M+N+O$$

(8)

For the rainwater harvesting system, the cost was assessed in terms of construction expenses, O&M costs, and water quality treatment fees. These estimates were based on market surveys of leading commercial suppliers and calibrated against municipal water pricing systems in representative Chinese cities. This provides a robust framework for evaluating the cost–benefit potential of rainwater harvesting. The total cost of rainwater utilization comprises construction cost (P), O&M cost (Q), and water treatment cost (R), offset by the economic benefit of conserved water resources (S). The rainwater catchment area was optimized to precisely match the irrigation demand:

$$C_{rainwater}=P+Q+R-S$$

(9)

3.5. Multi-Objective Optimization Model Construction

To enable system-level optimization within the FEW-Nexus framework, this study developed a multi-objective optimization model that simultaneously seeks to maximize annual food production (F_max), maximize annual energy production (E_max), and minimize total system cost (C_min). These objectives inherently involve structural trade-offs and potential synergies: food and energy systems often compete for limited spatial resources (e.g., rooftops), and increasing outputs generally requires higher capital investment, thereby elevating system costs. However, through integrated system design and coordinated resource utilization—such as leveraging shared infrastructure or reclaiming water resources—these conflicts can be mitigated, and overall efficiency can be enhanced. The Non-dominated Sorting Genetic Algorithm II (NSGA-II) was employed to derive a Pareto-optimal set of solutions from a wide range of potential resource allocation configurations. To ensure the model’s reliability and robustness, its outcomes were further validated through local sensitivity analysis, assessing the impact of parameter variations on optimization results.

3.6. Decision Variables and Constraint Settings

To ensure that optimization results were both practically feasible and implementable, this study established two primary types of constraints: resource system constraints and spatial area constraints. The resource system constraints focus on achieving internal resource circularity and self-sufficiency, while the spatial constraints define realistic bounds based on the physical availability and accessibility of space.

At the resource system level, two key constraints were applied. First, the annual rainwater harvesting volume (W) must meet or exceed the total annual irrigation water demand (G) required for controlled-environment agriculture, i.e., W ≥ G, thereby supporting water recycling and ensuring irrigation stability (

Table 3. Overview of key constraints in multi-objective optimization.

Category	Constraint Expression	Description
Food Subsystem	≤85,125	Ground agriculture area limit
	≤59,044.5	Rooftop cultivation area limit
	X4 ≤ X3	Indoor hydroponic ≤ rooftop greenhouse
Energy Subsystem	y1 + y2 ≤ 78,726	Flat-roof PV and PV on greenhouse roofs area limit
Water Resource System	W ≥ 26,535	Annual rainwater harvesting ≥ annual irrigation water demand

). Second, the cost objective function is minimized, and the objective functions of food production and energy production are maximized while satisfying the above physical constraints, ensuring sustainable resource system operations alongside economic feasibility and practical applicability.

In terms of spatial constraints, this study defined clear upper limits for the developable areas of various productive facilities based on field investigations and remote sensing classification results, combined with the actual conditions of building layouts, green space types, road systems, and rooftop structures within the study area. The upper limit of the ground-level agricultural area was estimated based on the internal green space resources of the residential district. Excluding buildings, roads, and courtyards unsuitable for productive development, this study identified relatively open and contiguous public green spaces and landscaped areas as potential locations for ground-based agriculture. These include residential parks and squares, public green spaces, and inter-building landscaped green spaces, totaling a developable green area of 85,125 m², which is taken as the upper limit for the ground-level agricultural system. Although private courtyards have some greening potential, they are generally enclosed and reserved for private use by residents and are, therefore, excluded from the calculation of developable areas.

To account for practical factors such as building structural load capacity, shading from facilities, and access requirements for equipment maintenance, feasible utilization rates were further defined (Table 3). Based on the three-dimensional model, field surveys of 30 buildings of varying ages within the study area, and references to global and domestic urban agriculture and green roof retrofit practices [30,31], the upper limit of the utilization area for flat roof photovoltaic (PV) installation was set at 40%, corresponding to a developable area of 78,726 m². Further, the upper limit of rooftop cultivation utilization area was set at 50%, corresponding to a developable area of 59,044.5 m². For sloped rooftops, factors such as orientation, slope angle, drainage system interference, and the load-bearing capacity of older buildings result in a utilization rate of 20%, corresponding to a developable area of 5307 m². Studies indicate that actual rooftop utilization rates in high-density cities typically range between 30% and 50%, with an upper limit of rooftop utilization around 75%, making these estimates conservative yet realistic.

In configuring the energy system, additional parameters were established for rooftop areas available for PV installations. For PV greenhouse roofs (y₂), considering the impact of panel shading on plant growth and the requirements for light and thermal regulation in facility agriculture, this study references modern PV greenhouse practices [32] and set the usable area as 70% of the total greenhouse roof area (y₂ = 0.7X₃). For sloped rooftop PV (y₃), the usable area was defined as 20% of the developable sloped rooftop area (y₃ = 0.2S_slope), prioritizing deployment on unobstructed south-facing roofs while accounting for slope, drainage, and structural stability. To simplify the model structure and reduce variable dimensions, certain variables with minimal impact on the objective function were assigned their maximum feasible values.

In the production scenario comparisons, although PV greenhouses are advantageous for enhancing residential self-sufficiency, their high construction and operational costs, coupled with their impact on rainwater harvesting, make them unsuitable for immediate large-scale deployment. Therefore, to ensure the practical feasibility and data consistency of the energy system configuration, annual biogas production (primarily derived from residential sewage and organic household waste, approximately 845,822 m³) is treated as a fixed constraint in the optimization model (

Table 4. Annual waste output of the residential community. Data source: Tianjin Statistical Yearbook 2023 and World Health Organization.

Waste Output Type	Domestic Wastewater	Household Waste	Organic Household Waste	Feces	Urine
Per Capita Output	Domestic Water Use × 85%	0.62 kg/(person·day)	Household Waste × 60%	0.2 kg/(person·day)	1.15 kg/(person·day)
Annual Output (Community)	1,313,369.136 t	7800.561 t	4680.337 t	2516.31 t	14,468.7825 t

and

Table 5. Biogas yield potential of organic waste and total solid (TS) content.

Waste Type	Organic Household Waste	Human Feces
Biogas Yield Potential (m3/kg TS)	0.389	0.49
Total Solids (TS) Content (%)	10.2	20

).

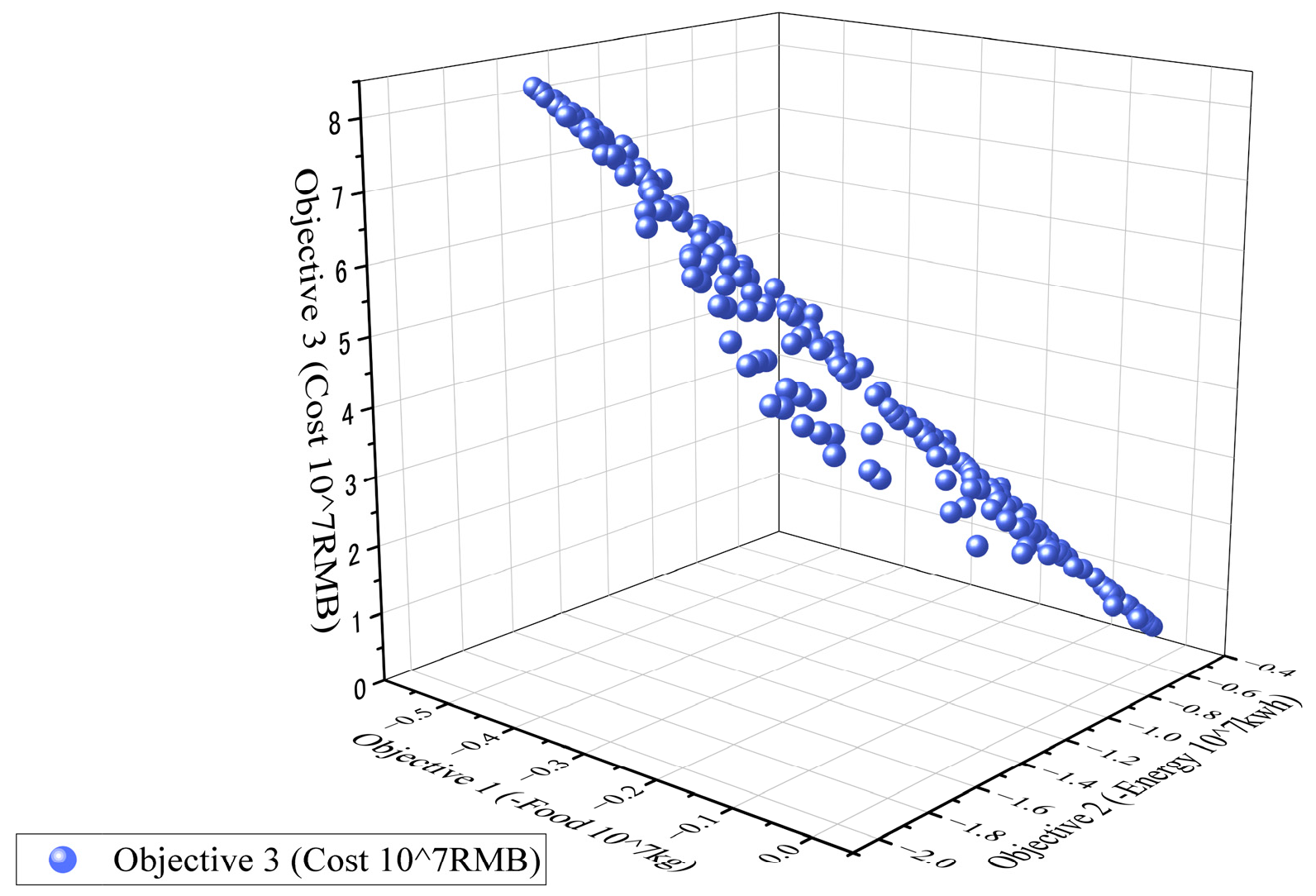
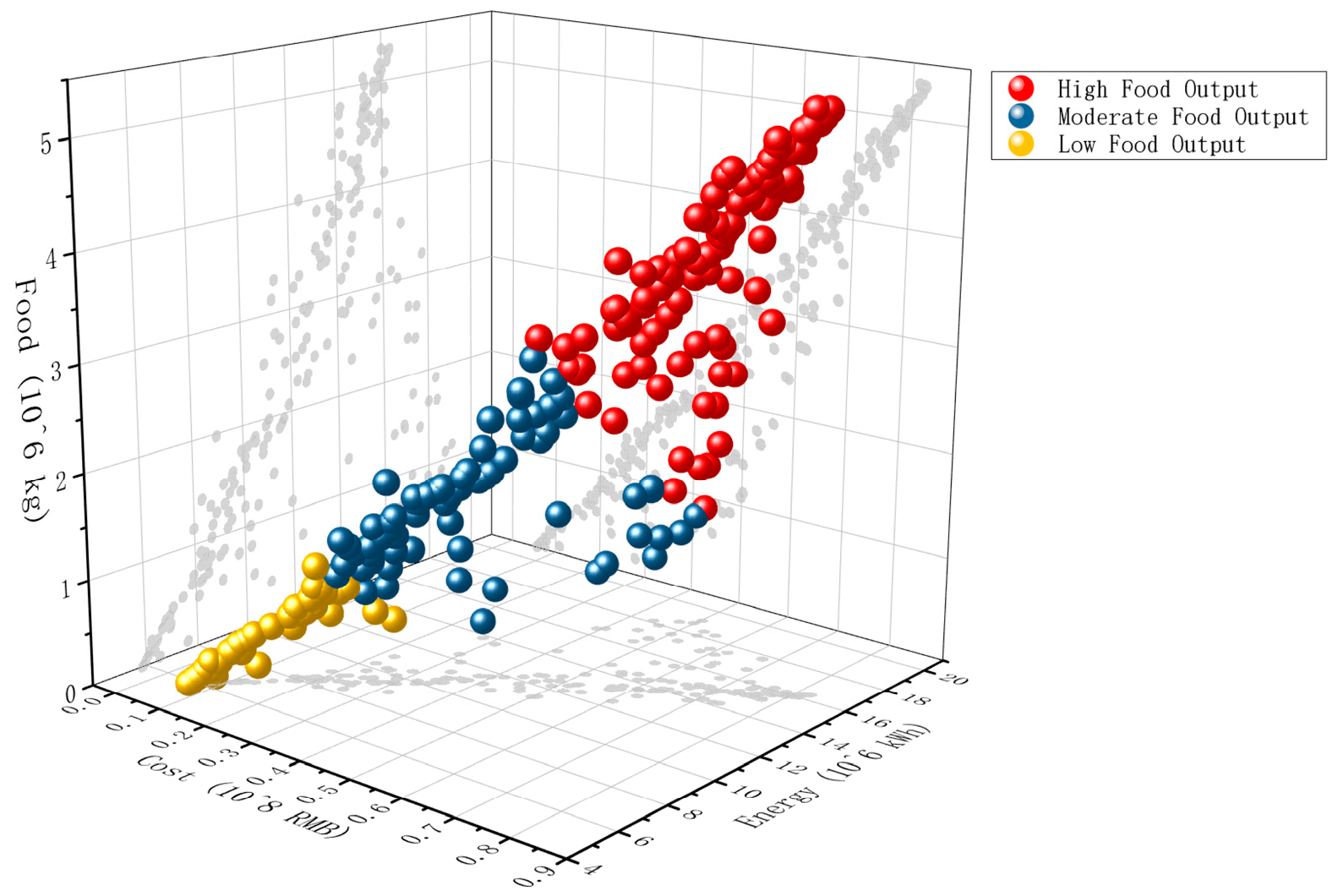
Following the generation of a Pareto-optimal solution set through the multi-objective optimization model, this study employed a standardized scoring method with equal weighting to comprehensively evaluate all candidate solutions. The solution achieving the highest composite score was identified as the compromise optimal solution for subsequent spatial configuration analysis. By normalizing the three objective functions—maximizing food production, maximizing energy output, and minimizing total system cost—and assigning equal importance to each, this approach ensures a balanced optimization outcome. It enables effective cost control without significantly compromising resource productivity, thus enhancing both the feasibility and contextual adaptability of the solution.

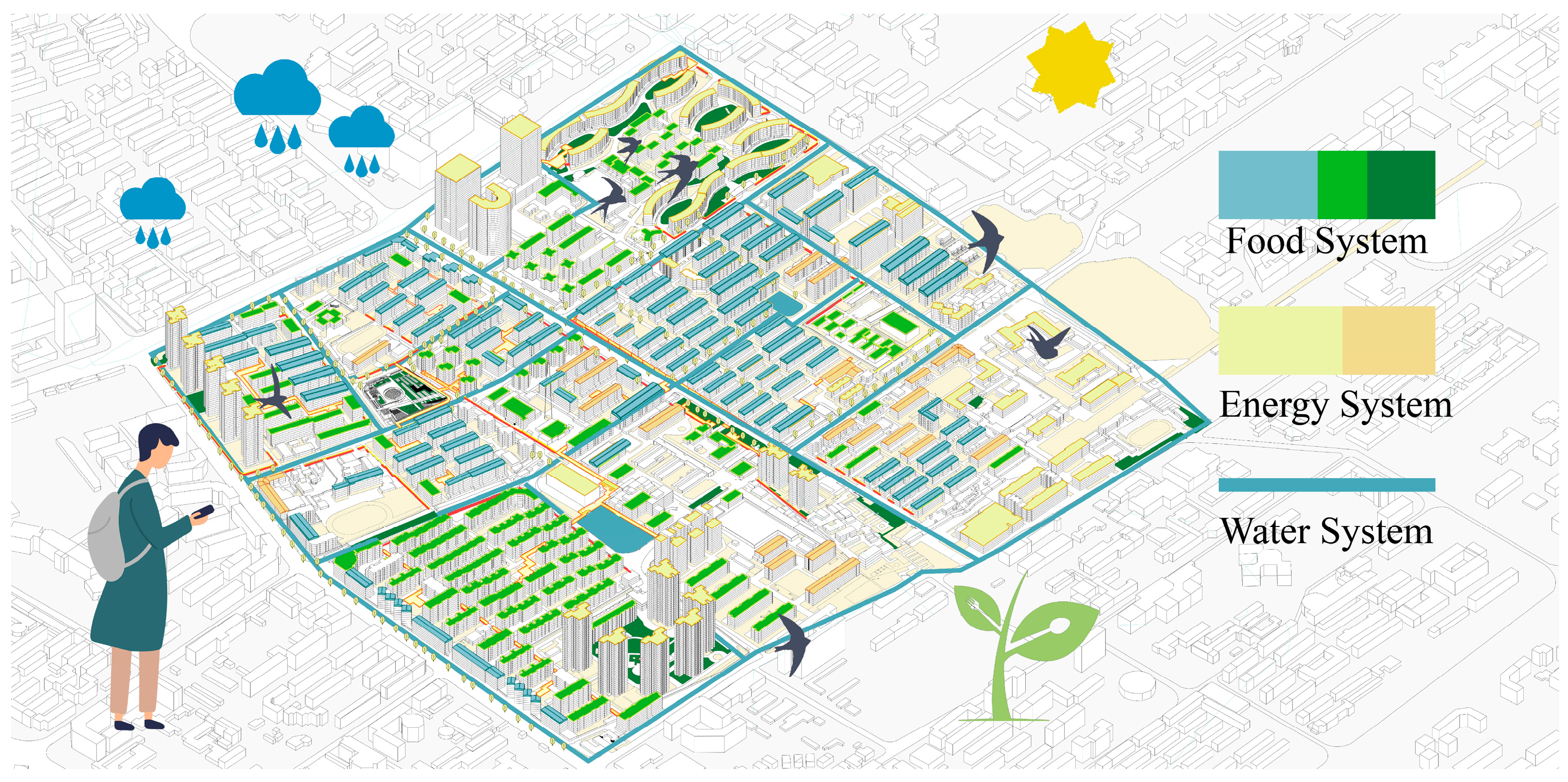
However, while the optimization model provides the area allocation among food, energy, and water systems, it does not specify methods for their spatial integration within the built environment. To address this, we summarized a series of practical typologies for integrating these systems within high-density urban residential areas, providing actionable implementation pathways. These typologies include ground-level elements (e.g., rain gardens, community gardens), roof-level elements (e.g., photovoltaic panels, photovoltaic greenhouses), and building-integrated components (e.g., photovoltaic, photovoltaic curtain walls, canopies), etc. Each typology supports multi-functional land use and resource efficiency.

Building on these typologies, master planning strategies must account for the broader spatial structure and systemic interactions within the study area. At the master planning level, functional zones should be delineated based on the site’s existing spatial structure. and tailored retrofitting strategies should be developed for each subsystem according to spatial suitability. For example, flat rooftops are optimal for agricultural production, whereas the rooftops of high-rise buildings—due to heightened wind loads and thermal variation—are better suited for photovoltaic (PV) installations. Roofs of industrial buildings or those with pollution risks should prioritize PV deployment, whereas public buildings offer opportunities for multifunctional use, integrating agriculture with recreation and commercial services. Sloped rooftops are best suited for PV panel installation. For idle or underutilized land parcels, lightweight and mobile planting systems are recommended to minimize initial capital investment and facilitate site restoration after use.

In this case study, specific typologies were applied to various spatial contexts: roof-tops were utilized for photovoltaic panels, photovoltaic greenhouses, and open-air planting. All ground-level green spaces were designated for open-air planting, while rainwater collection and utilization systems were integrated across both ground and roof areas. Implementation required context-specific decisions based on building types, roof forms, spatial accessibility, and infrastructure compatibility. This demonstrates how abstract optimization results can be translated into concrete spatial arrangements tailored to specific environmental conditions.

4. Result

4.1. Optimization Results and Validation

In the FEW three-objective optimization model constructed in this study, in order to improve the computational efficiency and model operability, five key variables were selected as optimization objects, including ground-level cultivation area (X₁), rooftop cultivation area (X₂), PV greenhouse area (X₃), indoor hydroponics area (X₄), and flat-roof PV installation area (y₁). The genetic algorithm utilized specific operational parameters: 500 individuals per generation running through 800 evolutionary cycles, with solution retention set at 0.7 to ensure a balanced trade-off between convergence and solution diversity. This process generated a set of 210 Pareto-optimal, non-dominated solutions, providing a diverse and robust basis for guiding residential regeneration and integrated resource allocation strategies.

To assess the robustness of the selected compromise solution, a local sensitivity analysis was conducted (

Table 6. Sensitivity analysis results of decision variables (±5% perturbation).

Variable	Food (%)	Energy (%)	Cost (%)
X1 Ground Planting Area	0.14%	0.00%	0.02%
X2 Rooftop Planting Area	0.18%	0.00%	0.02%
X3 PV Greenhouse Area	2.45%	2.48%	2.84%
X4 Indoor Hydroponics Area	2.23%	0.00%	1.39%
y1 Flat Roof PV Area	0.00%	0.74%	0.39%

). The compromise optimal solution was subjected to a ±5% disturbance test to observe the impact of changes in the five decision variables on the three objective functions. By increasing and decreasing each variable by 5%, the objective function value was recalculated and compared with the original optimal solution to obtain the maximum relative change percentage of each indicator to determine the sensitivity of the model to the variable. The analysis results show that the change amplitude of all objective functions did not exceed 3%, and the overall robustness was good. This result shows that the current optimization solution exhibits stable performance under local disturbance conditions, and small adjustments to key variables will not cause drastic fluctuations in system performance. It has strong practical feasibility and anti-interference ability, and provides solid model support for subsequent actual deployment and strategy implementation.

The 3D scatter plot in Figure 3 directly illustrates the original value distribution of the objective functions. Since the algorithm employs a minimization strategy, the two objectives intended for maximization (Food and Energy) are transformed into negative values, resulting in a Pareto front extending from the lower left to the upper right. The plot reveals that while Cost (Objective 3) is relatively concentrated across most solutions, a significant nonlinear coupling persists between Food (Objective 1) and Energy (Objective 2). This gradually inclined solution set suggests that increases in food or energy production do not correspond to linear cost increases, reflecting the classic pattern of diminishing marginal returns in resource allocation.

Figure 3 reconstructs the solution set, which is further classified into three categories based on food output: high food output type (red), medium output type (blue), and low output type (yellow), enhancing the readability of the Pareto frontier. It can be clearly observed that in the high-yield area (upper right), the cost of the solution set increases significantly, reflecting the high investment required for the construction, operation, and maintenance of the system under conditions of extreme resource output. In contrast, the low-yield section achieves low-cost operation, but with limited production capacity. The cone-shaped distribution presented in the figure further illustrates the inherent trade-off structure of the solution set between the three objectives.

Collectively, Figure 3 and Figure 4 demonstrate that no single solution achieves optimal performance across all three objectives. Trade-offs are intrinsic to the system, and selecting an appropriate compromise requires balancing available resources, policy constraints, and fiscal capacity. In practical terms, urban renewal strategies should prioritize the selection of a compromise solution of “moderate cost-reliable output” from the Pareto frontier that is both financially viable and operationally scalable. It is also worth noting that the medium-low cost area in Figure 4 contains more solution points, and the distribution density between solutions is high, which means that the solution space is more flexible and suitable for flexible strategy design, while the extremely high-yield-high-cost area is sparsely distributed, and it is recommended to carefully evaluate the economic boundaries during implementation.

4.2. Selection of the Compromise Solution and Parameter Description

From the tri-objective optimization results, the model produced a diverse set of Pareto-optimal solutions, all satisfying the non-dominance condition and reflecting the inherent trade-offs between food production, energy generation, and total system cost. To identify a balanced and practical solution, this study employed an equal-weight normalized scoring method, resulting in the following compromise-optimal configuration:

As shown in

Table 7. Decision variables in the compromise-optimal solution.

System	Variable	Description	Value	Utilization Rate of Upper Bound
Food	X1	Ground-level cultivation area (m2)	23,763.4	27.9% (≤85,125)
	X2	Rooftop cultivation area (m2)	12,164.2	20.6% (X2 ≤ 59,044.5)
	X3	PV greenhouse area (m2)	66,778.9	99.6% (X3 + y1 ≤ 78,726)
	X4	Indoor hydroponic area (m2)	60,507.5	X4 ≤ X3
Energy	y1	Flat-roof PV area (m2)	11,636.7	99.6% (X3 + y1 ≤ 78,726)
	y2	PV on greenhouse roofs = 0.7 × X3 (m2)	46,745.2	–
	y3	PV on sloped roofs = 0.2 × S_slope (m2)	5307	–
	y4	Biogas production (m3)	845,822	–
Water	W	Annual rainwater harvest (m3)	127,093.5	–
	G	Annual irrigation demand (m3)	26,535	478.96% (W ≥ G)

Note: “–“ indicates either a fixed parameter or one not constrained by an upper limit.

, the selected compromise solution satisfies all constraint conditions. For instance, the ground-level cultivation area is 23,763.4 m², remaining well below the maximum threshold of 85,125 m². The roof planting area (X₂) is 12,164.2 m², accounting for 20.6% of its upper limit of 59,044.5 m². The flat roof area shared by the greenhouse and photovoltaic system (X₃ + y₁) totals 78,415.6 m², which is approximately 99.6% of the upper limit of 78,726 m², indicating that this constraint is close to saturation. In terms of the energy system, the power generation area provided by the photovoltaic greenhouse roof is 46,745.2 m² (0.7X₃), while the photovoltaic area of the sloped roof is 5307 m². The photovoltaic area of the flat roof (y₁) reaches 11,636.7 m². The coordinated utilization of multiple roof types ensures a stable and sustainable source of clean energy for the system. Regarding water resources, the annual rainfall is 127,093.5 m³, which far exceeds the annual irrigation demand of 26,535 m³ required by facility agriculture. This indicates that the water system has significant redundancy, meaning this constraint does not pose a restrictive bottleneck and supports the safe and reliable operation of the system.

From the perspective of space utilization, flat roofs are predominantly used for energy system configurations, such as photovoltaic modules, while the roof planting area remains relatively small. In contrast, greenhouses and indoor hydroponic facilities are deployed on a larger scale, reinforcing the dominant role of facility agriculture in overall output. The indoor hydroponic area totals 60,507.5 m², and its configuration adheres to the spatial nesting constraint of the photovoltaic greenhouse area (X₄ ≤ X₃).

As shown in

Table 8. Objective values of the compromise solution.

Objective	Value
Food Output (F)	5,223,462 kg/year
Energy Output (E)	16,267,235 kWh/year
Total Cost (C)	82,902,144.01 RMB

, the compromise solution uses an algorithm to automatically search for a configuration combination that balances output benefits and investment costs without presetting preference weights. This configuration achieves an annual food output of 5,292,649 kg, an annual energy output of 16,267,235 kWh, and a total system cost of 82,902,144.01 yuan. Although the energy output does not fully cover the preset annual electricity demand of 40.03 GWh, it has reached about 40.6%, laying the foundation for the linkage of multiple energy systems. The current compromise solution takes into account both output efficiency and investment controllability, provides a high level of food and energy supply under the premise of controlling costs, and demonstrates a strong system cost-effectiveness and promotion value.

4.3. Spatial Configuration and System Distribution Characteristics

The compromise solution generated by the optimization algorithm not only achieves a mathematical balance among the three objective functions but also provides a spatially feasible and implementable configuration. Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the schematic spatial layouts of the residential district based on this optimal solution.

As shown in the overall layout (Figure 5), the differences in the morphological characteristics of building roof spaces determine the preferred renovation methods. For agricultural systems, open-air cultivation is more suitable for mid- to high-rise public buildings, commercial complexes, and structurally robust residential towers with lower building densities. Conversely, rooftop greenhouses are better suited for residential building areas with higher building densities, as centralized rooftop greenhouses facilitate coordinated management, stabilized output, and seasonal production control.

PV systems are deployed based on factors such as building orientation, solar exposure, and structural load-bearing capacity. High-rise buildings and industrial buildings are particularly suitable for PV installations. The roofs of these buildings—whether flat or sloped—experience minimal shading, thereby optimizing solar access and enhancing photovoltaic power generation output. Water systems are spatially organized with a focus on rainwater harvesting, storage, and reuse, ensuring efficient water resource management.

Ground-level agricultural areas are primarily located in open zones within the residential district that are flat, well-lit, and free from shading. These areas are also selected for their low foot traffic, ensuring good ventilation and operational convenience, making them ideal for open-field cultivation and community farming initiatives. The design of ground-level agriculture is carefully integrated with road networks, drainage systems, and rainwater harvesting infrastructure, enabling cost-effective and minimally invasive deployment of agricultural land use.

Overall, the spatial configuration derived from the optimization ensures the synergistic operation of the integrated FEW system while accommodating the diversity of existing spatial structures and architectural forms. The design achieves a high degree of spatial coupling between ground-level and rooftop resources, maximizing land-use efficiency within the constraints of urban density.

4.4. System Outputs and Resource Balance Validation

To evaluate the applicability and resource allocation effectiveness of the optimal compromise solution at the scale of an actual residential district, this study integrated annual resource consumption data for urban communities in Tianjin. Drawing from the 2024 Tianjin Statistical Yearbook [33], the 2022 Urban and Rural Construction Statistical Yearbook [34], and field-based survey data, the annual resource demand and supply for the target district were estimated and compared against the model’s output. This comparison assesses the degree of supply–demand alignment and identifies system redundancies.

For the food system, based on the annual per capita consumption of fresh vegetables and fruits (110.6 kg and 75.7 kg, respectively), the total annual demand for produce within the district is approximately 2609 tons (

Table 9. Annual fresh fruit and vegetable consumption in the residential community.

Food Type	Fresh Fruit	Fresh Vegetables
Annual Per Capita Consumption (kg)	75.7	110.6
Total Annual Community Consumption (kg)	2,609,379	8372.42

). The compromise solution incorporates ground-level cultivation, rooftop farming, and protected agriculture units, collectively producing 5293 tons annually. This output not only ensures full self-sufficiency but also generates surplus capacity for external distribution, highlighting the potential for enhancing urban agricultural productivity in high-density contexts.

Regarding the energy system, the annual per capita energy demand, expressed in electricity consumption and converted to standard coal equivalent (SCE), is 1196 kWh per person (

Table 10. Annual energy consumption in the residential community.

Energy Type	Electricity (Annual)	Household Energy Consumption (Annual)
Per Capita Consumption	1196 kWh/person (146.95 kg of standard coal)	959 kg of standard coal/person
Total Annual Community Consumption	40,030,120 kWh (4,744,700 kg of standard coal)	33,056,730 kg of standard coal

), resulting in a total demand of approximately 40.03 GWh for the residential community. The optimized configuration supplies 16.27 GWh of clean energy, meeting 40.64% of the demand. This surplus enhances system resilience against uncertainties such as climatic fluctuations or grid instability. Importantly, the configuration avoids spatial conflicts between rooftop PV and agriculture by prioritizing energy generation on greenhouse rooftops and sloped roofs, thereby maximizing both spatial and energy efficiencies.

Regarding the water system, per capita domestic water use averages 122.81 kg per day, totaling 1.545 million tons annually, with approximately 1.313 million tons of wastewater requiring treatment (

Table 11. Annual water consumption in the residential community.

Water Metric	Daily Per Capita Water Use	Annual Per Capita Water Resource
Per Capita Consumption	122.81 kg/(person·day)	121.71 m3/person
Total Annual Community Consumption	1,545,140.16 t	4,195,343.7 m3

). The integrated system includes rainwater harvesting infrastructure with an annual yield of 127,093.5 m³, meeting nearly all of the 26,535 m³ irrigation demand for protected agriculture. Additionally, treated wastewater is reused for green space maintenance and supplemental agricultural irrigation, significantly reducing freshwater demand and supporting the development of a water-efficient residential community.

In conclusion, the selected compromise solution not only meets the multi-objective optimization criteria at the modeling level but also demonstrates strong alignment with real-world consumption patterns, robust redundancy across subsystems, and scientifically rational spatial configurations. These outcomes validate the model’s practical feasibility and scalability, offering a robust framework for advancing the productive renewal of urban residential districts.

5. Discussion

The tri-objective optimization model developed in this study generated 210 non-dominated solutions, revealing nonlinear trade-offs among food production, energy output, and total cost. The Pareto front exhibits a conical distribution, highlighting diminishing marginal returns on resource inputs, particularly when energy output exceeds 60 million kWh, beyond which costs rise sharply. Sensitivity analysis confirmed the model’s robustness: under ±5% perturbations in key decision variables, all objective functions varied by less than 3%. The selected compromise solution achieved high performance, delivering an annual output of 5293 tons of food and 16.27 GWh of energy at a total cost of 83 million CNY—exceeding residential food demand by 102.9% and meeting 40.6% of the energy demand. These results not only validated the three core hypotheses but also significantly enhanced community-level resource self-sufficiency while introducing system redundancy, providing critical buffering capacity against uncertainties such as climate variability and unstable energy supply.

The spatial configuration automatically identified by the optimization algorithm reveals a differentiated land-use pattern: ground cultivation occupies 23,763.4 m² (27.9%), rooftop cultivation 12,164.2 m² (20.6%), the combined area of PV greenhouses and Flat-roof PV occupies 78,415.6 m² (99.6%), and indoor hydroponics reaches 60,507.5 m². Energy generation primarily relies on flat-roof PV and greenhouse rooftop installations, with output meeting 40.6% of energy demand. The water system achieved a complete closed-loop cycle, exceeding irrigation demand by approximately 379%. These findings extend the work of Toboso-Chavero, et al. [35] on multifunctional urban rooftop use, offering more precise and quantifiable spatial configuration indicators. The energy self-sufficiency rate obtained in this study is close to the conclusion of Jianli Sun et al. [36] in the central urban area of Wuhan (the maximum annual PV power generation potential could satisfy 31.83% of local energy consumption). In addition, the empirical research conducted by Gao et al. [37] in eastern Chinese cities, it was also found that it is feasible to combine the agricultural production recycling process with the urban ecosystem to form a closed ecological cycle system through technical means.

This study advances the FEW-Nexus framework by translating it into a quantifiable spatial optimization model, introducing several theoretical and methodological innovations. The novel concept of “coupling nodes” enables the mapping of material and energy flows across subsystems. The model integrates isolated resource solutions—such as PV deployment, rooftop farming, and rainwater harvesting—into a cohesive and computable composite system. By applying the NSGA-II algorithm to the spatial FEW system optimization, the model transcends the limitations of single-objective approaches and simplistic scenario analyses. The results demonstrate that coordinated spatial planning can generate synergistic benefits exceeding the aggregate effect of individually optimized subsystems, echoing the conclusions of Hachaichi and Egieya [38] on the advantages of integrated resource systems. These findings align with empirical observations from pilot FEW-Nexus projects in Thammasat University Rangsit Campus, which utilizes approximately 22,000 square meters of idle rooftop space [39] to incorporate sustainable food production, renewable energy, organic waste, water management and public space.

Importantly, this study incorporated spatial dimensions into the resource optimization framework, bridging the gap between macro-level resource flows and micro-scale spatial configurations [15]. It reconceptualizes urban residential areas as hybrid micro-production units, offering practical solutions to urban external dependency challenges highlighted by Zhang, Zhang, Chang, Xu, Hao, Liang, Liu, Yang and Wang [14]. In doing so, the research moves beyond theoretical modeling to provide actionable guidance for urban planning and policy development applicable across diverse urban contexts globally.

The implementation of the FEW system in a real urban environment universally faces significant governance and social challenges that extend beyond technical feasibility. Urban resource production is often regarded as irregular land use: current building regulations in most cities worldwide, including Tianjin, lack explicit provisions for productive spaces, leading to legal ambiguities regarding liability, safety standards, and permissible activities. Empirical evidence from New York City (urban agriculture) and Berlin (photovoltaics) demonstrates the critical role of regulatory frameworks in successful implementation. However, no jurisdiction has yet established comprehensive legal frameworks specifically tailored to FEW systems. Furthermore, institutional structures typically treat food, energy, and water as separate domains governed by distinct regulatory frameworks, exacerbating governance challenges and raising unresolved questions about the equitable distribution of benefits among stakeholders.

Based on these identified worldwide challenges,, we propose the following policy recommendations: (1) reform building codes to formally recognize productive building surfaces with clear technical standards and safety requirements, reducing legal uncertainty that currently deters investment; (2) establish interdepartmental coordination mechanisms to overcome fragmented resource governance; and (3) develop inclusive economic frameworks to equitably distribute costs and benefits, supported by financial incentives that reflect the public benefits of urban resource systems. These interventions address key institutional barriers while ensuring sustainability and community acceptance.

This study has several methodological and analytical limitations. First, the model’s parameter selection lacks empirical validation, particularly for crop yields in urban environments and energy conversion efficiencies under varying conditions. Second, the spatial analysis excludes building façades and detailed shading effects, potentially overestimating production capacities in high-density contexts. Third, externalities such as urban heat island effects and biodiversity impacts are not fully addressed, though their outcomes may be positive or negative depending on system design. Fourth, the mechanisms driving optimization outcomes remain insufficiently explored. Finally, the model prioritizes technical optimization, with limited consideration of social factors like stakeholder preferences, management complexity, and community acceptance.

Future research should expand the model to incorporate carbon emissions targets, seasonal variability, regional climate adaptability, and cross-scale system integration. The framework could also be extended to diverse urban typologies beyond the Tianjin case study, enhancing its generalizability and applicability in varied socioeconomic and climatic contexts. Despite these limitations, this study offers a novel pathway for transforming high-density cities from consumption-driven to integrated production–consumption spaces. These findings affirm the critical role of FEW-Nexus optimization in enhancing urban resilience and sustainability.

6. Conclusions

This study developed a multi-objective optimization framework for the integrated transformation of the FEW system in high-density urban residential areas, successfully validating three core hypotheses. First, significant synergies exist among food, energy, and water subsystems, with joint optimization yielding superior outcomes compared to isolated subsystem optimization. Second, balanced optimal solutions can be identified between resource production and economic cost within different retrofitting scenarios. Third, rational spatial configuration can substantially enhance the system’s overall resource production potential.

The Pareto-optimal solutions generated by the NSGA-II algorithm reveal nonlinear trade-offs between resource outputs and total cost. The selected compromise solution achieves high levels of self-sufficiency, producing 5293 tons of food and 16.27 GWh of energy annually at a total cost of CNY 83 million, exceeding residential food demand by 102.9% and meeting 40.6% of the energy demand. The central innovation of this study lies in transforming the FEW-Nexus conceptual framework into an actionable spatial optimization model with broad applicability, bridging the long-standing gap between macro-scale resource flows and micro-scale spatial configurations.

While limitations remain—such as insufficient empirical validation of key parameters, exclusion of building façades in spatial analysis, limited consideration of externalities, and primary focus on technical rather than social dimensions—this study demonstrated the pivotal role of FEW system co-optimization in enhancing urban resilience and sustainability across diverse geographical and governance contexts. The framework’s adaptability to different urban typologies suggests its potential for implementation beyond the specific conditions of Tianjin. Looking ahead, we envision a future urban landscape composed of interconnected “productive residential communities”, linked through decentralized energy microgrids, shared food networks, and closed-loop water systems. This transformation represents not merely a technological or spatial shift, but a fundamental reconfiguration of urban logic: from linear consumption to circular regeneration. Within this vision, urban residents evolve from passive resource consumers to active participants in production, reestablishing a harmonious relationship between humans and nature and between production and everyday life.

This study takes a concrete step toward realizing that vision, demonstrating that resource self-sufficiency and economic viability can be simultaneously achieved, even in densely populated urban contexts. In light of escalating global resource constraints and intensifying climate challenges, this integrated, multifunctional approach to urban spatial planning offers a compelling and scalable pathway toward sustainable urban development. It presents a replicable solution to the pressing resource challenges faced by rapidly urbanizing regions worldwide.