Outdoor Environment Design Optimization of an Office Building Based on Indoor Thermal Conditions and Building Energy Performance
Abstract
1. Introduction
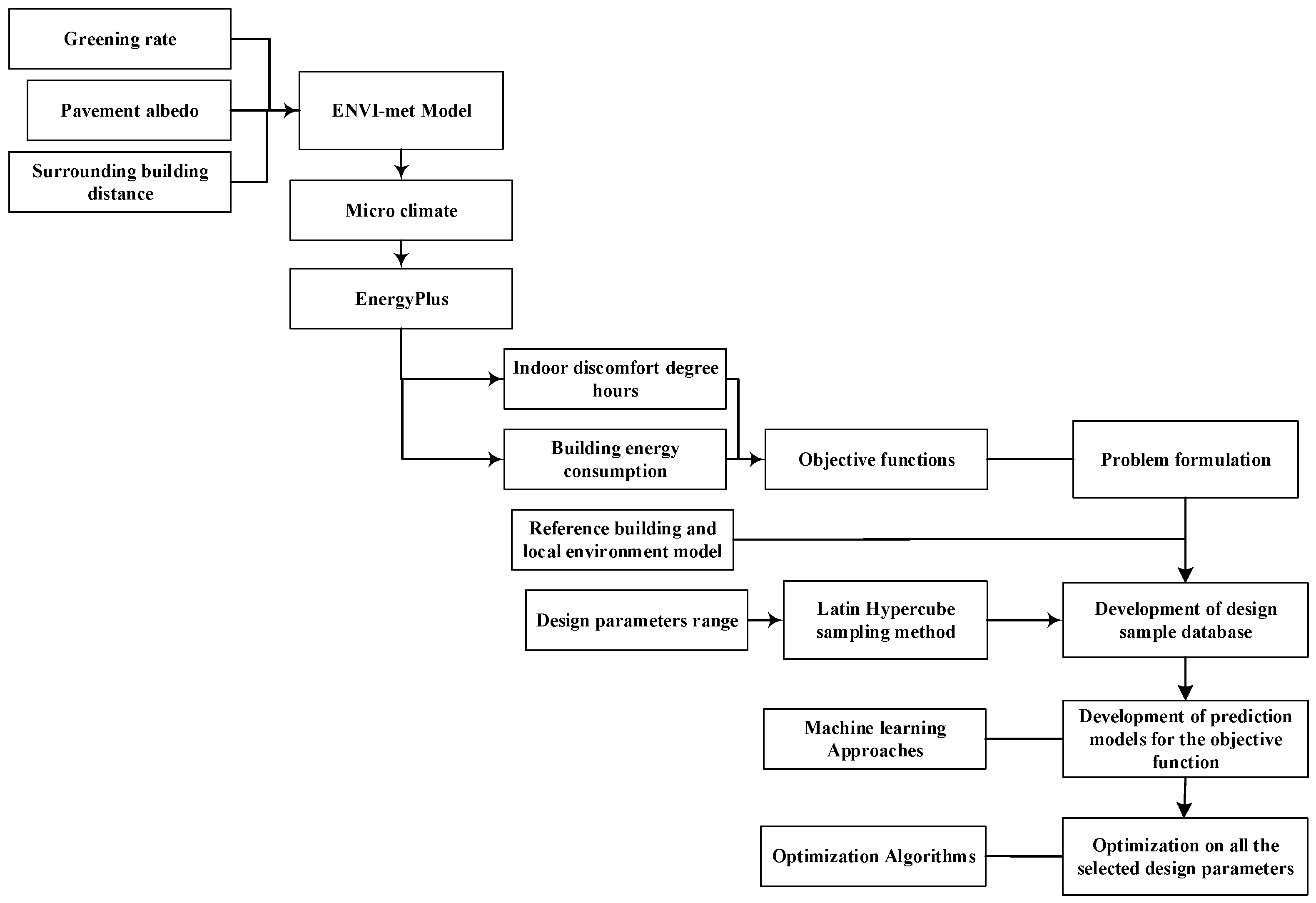
2. Method
2.1. Objective Functions
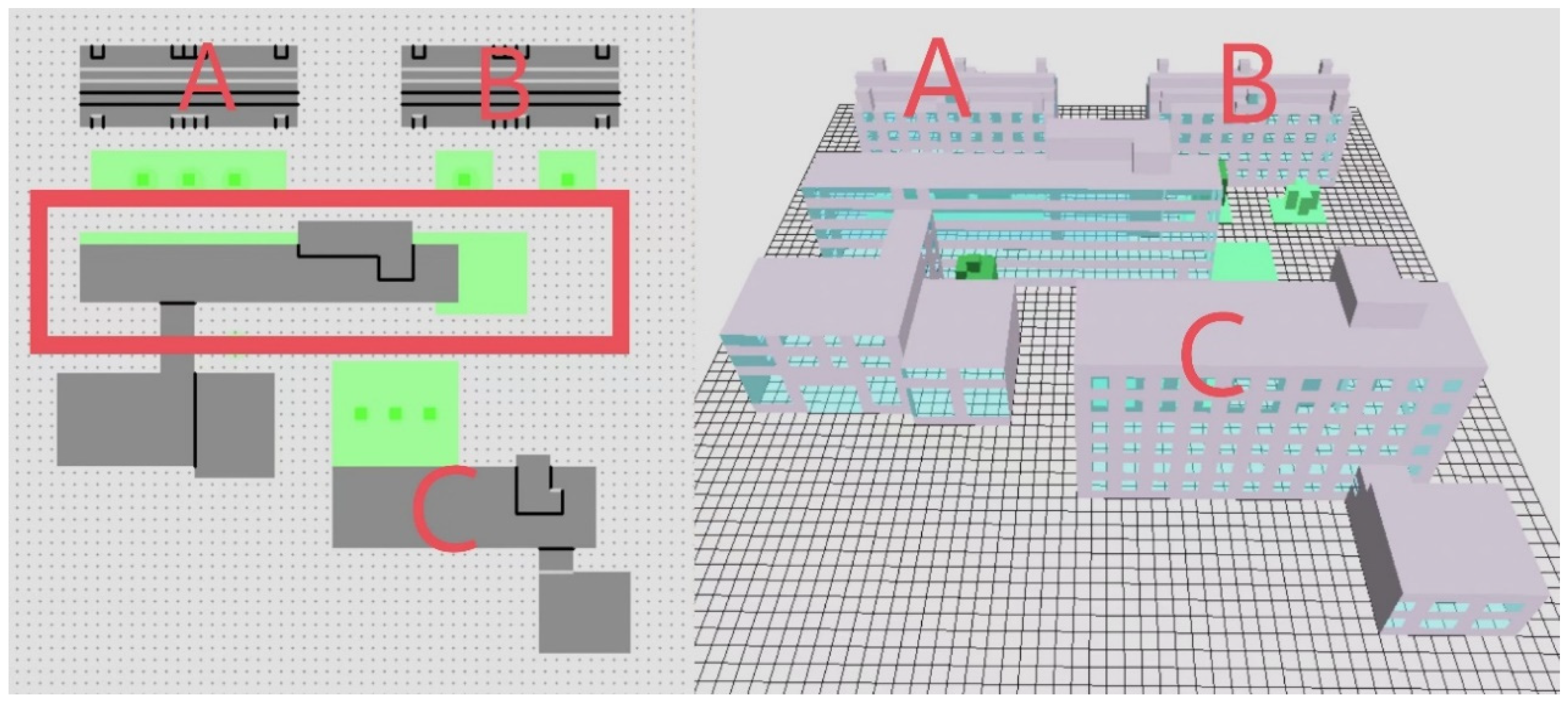
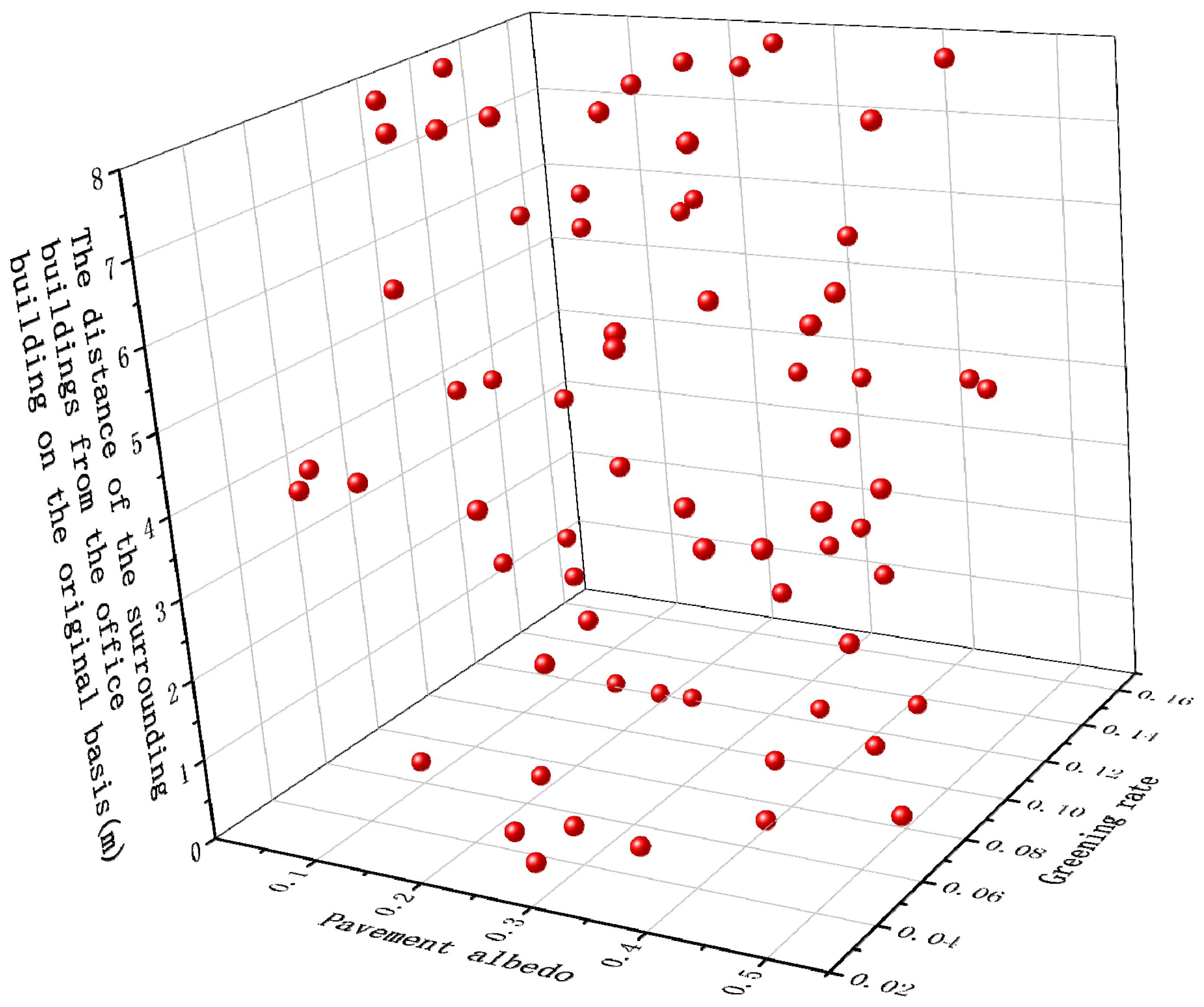
2.2. Design Parameters and Ranges
2.3. Prediction Model
2.3.1. Sample Database Generation
2.3.2. Prediction Model Development
- Artificial neural network model
- Locally Weighted Regression
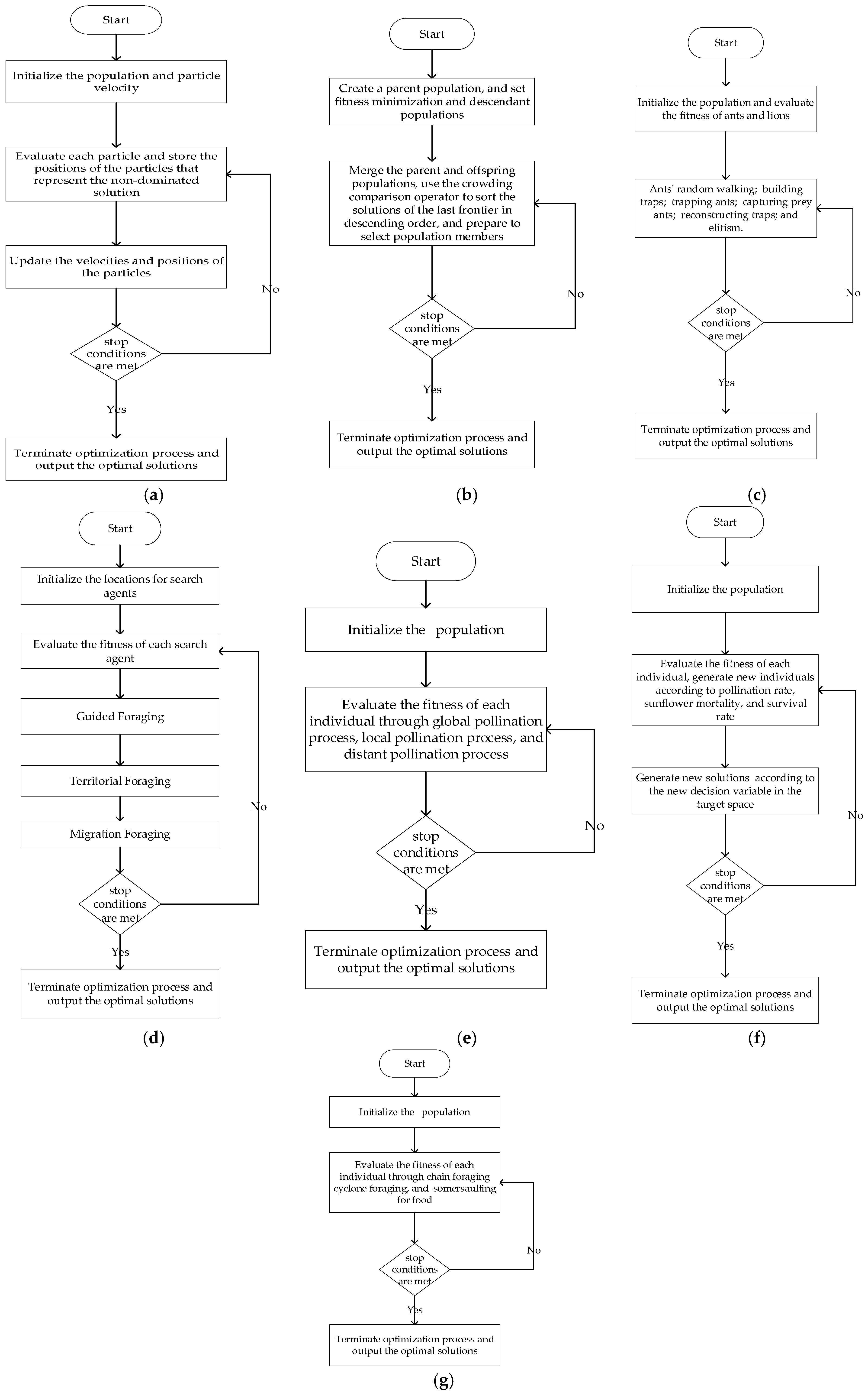
2.4. Optimization Algorithm
2.4.1. MOPSO
2.4.2. NSGA-II
2.4.3. MOALO
2.4.4. MOAHA
2.4.5. MOFPA
2.4.6. MOSFO
- (1)
- Firstly, the first population of sunflowers is generated in a random order in the search space, which is divided into a grid hypercube. One solution is generated for each decision variable in the search space. The non-dominated solutions are filtered and retained, and the dominated solutions are removed;
- (2)
- Secondly, according to the pollination rate, sunflower mortality, and survival rate, new individuals can be generated randomly and orderly. In each iteration, the cross-pollination proportion of individuals is determined by the pollination rate;
- (3)
- Thirdly, new solutions are generated according to the new decision variable in the target space. The newly generated solution is merged with the non-dominated solution that was initially saved, and the new non-dominated solutions are retained, with a restricted number of non-dominated solutions to save the computational cost.
2.4.7. MOMRFO
2.4.8. Parameter Settings
3. Results and Discussion
3.1. Results of Model Validation
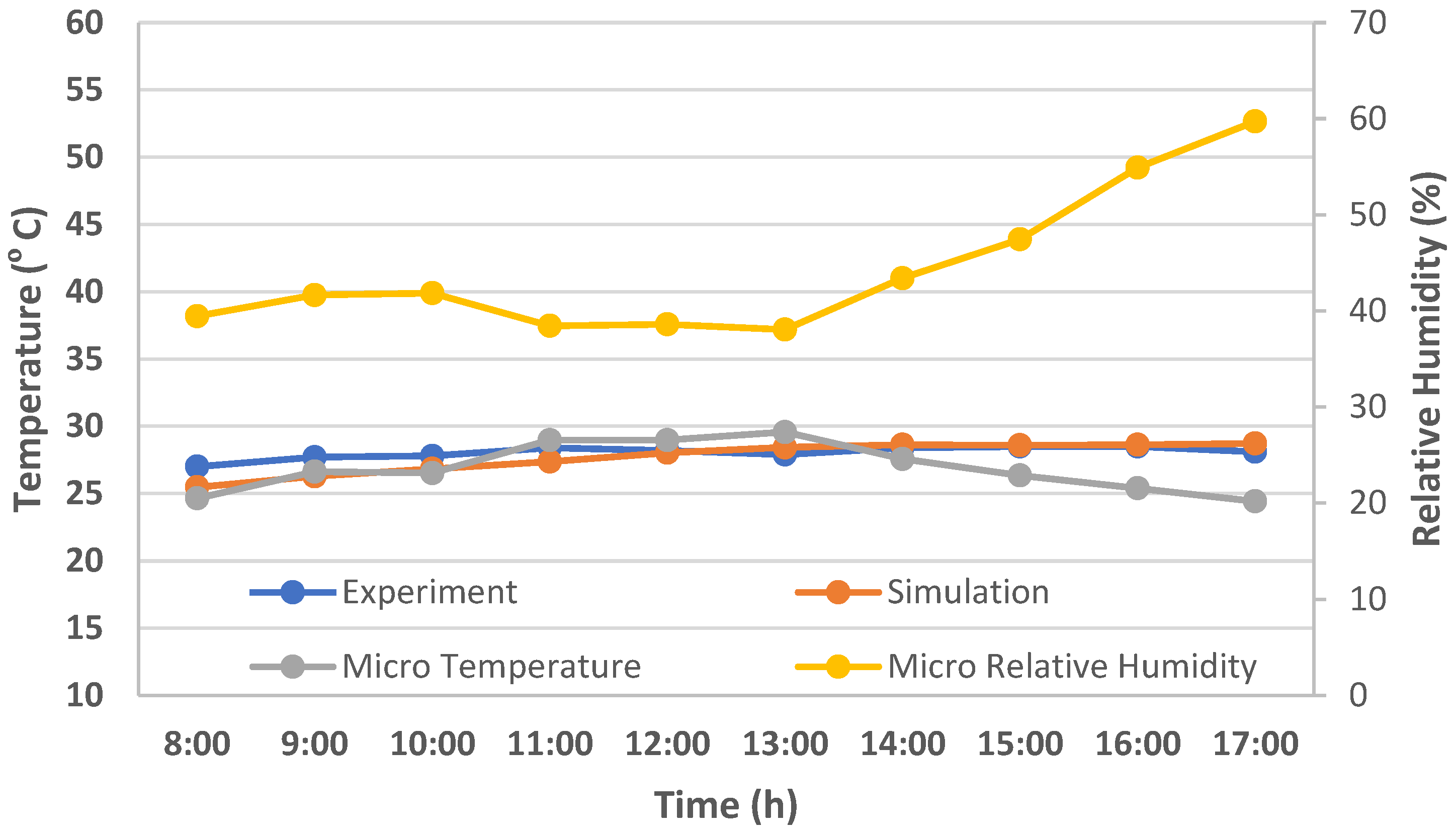
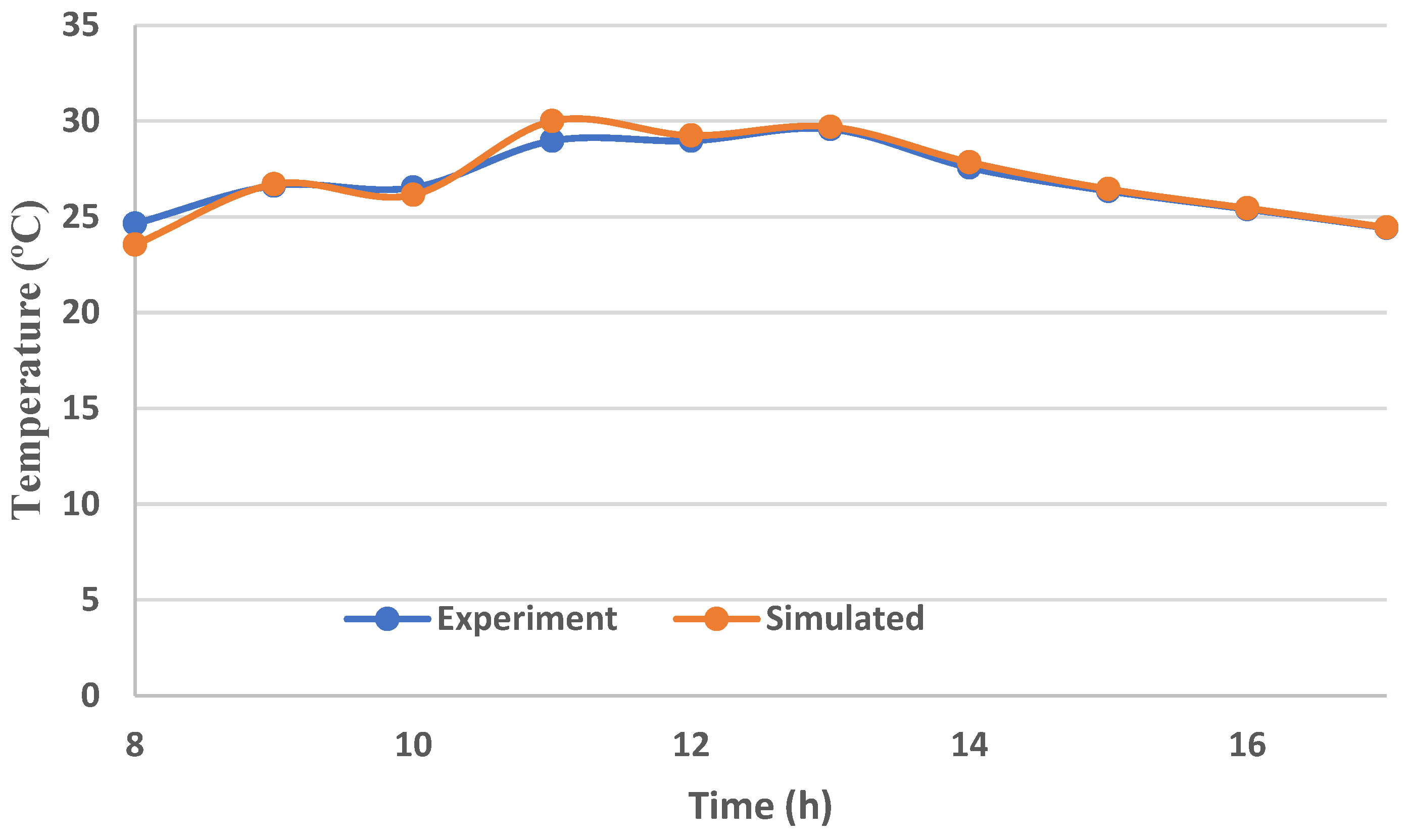
3.1.1. Results of EnergyPlus Model Validation
3.1.2. Results of ENVI-met Model Validation
3.1.3. Results of k-Fold Cross-Validation on BPNN Model
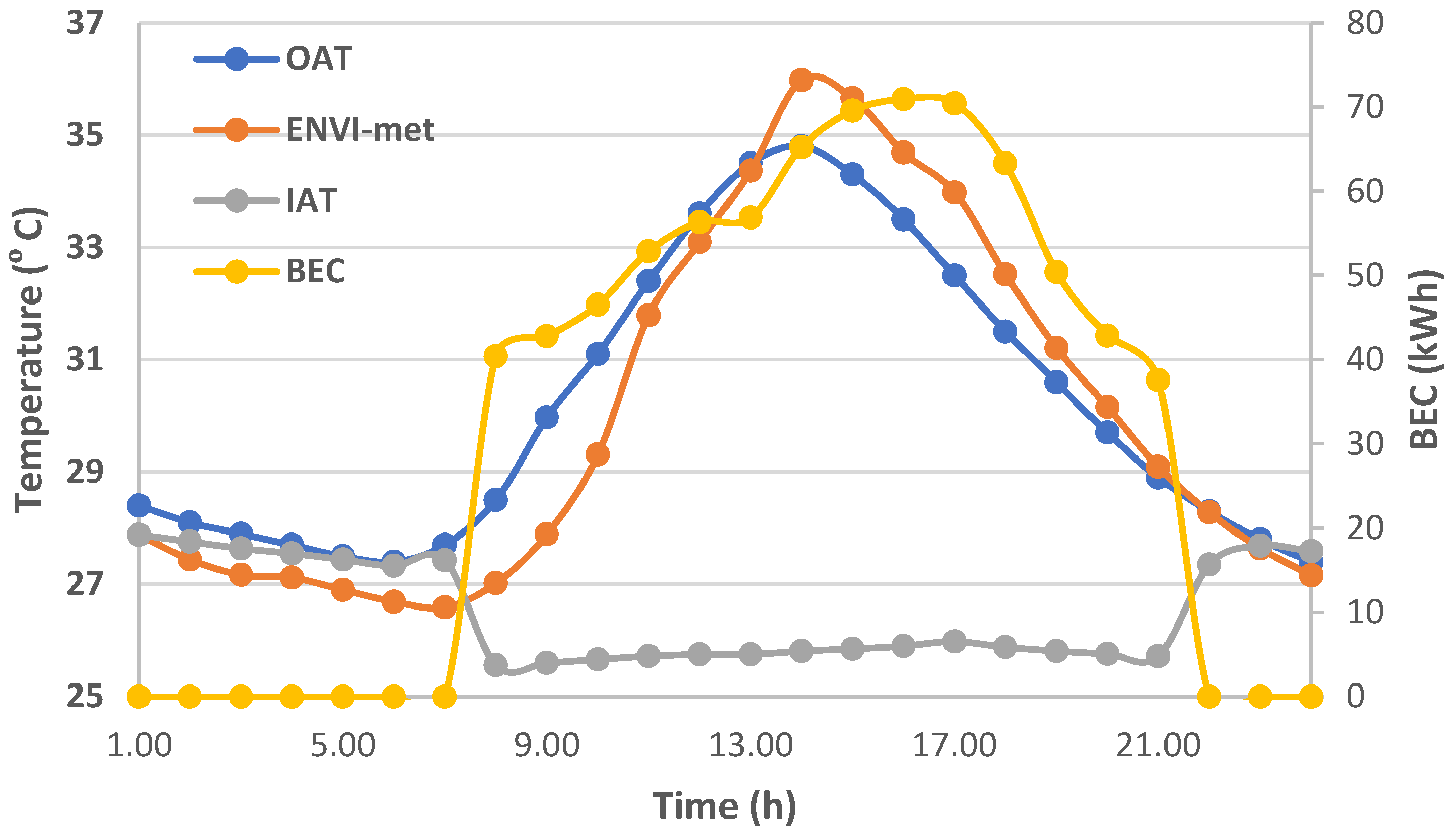
3.2. Results of ENVI-Met and EnergyPlus
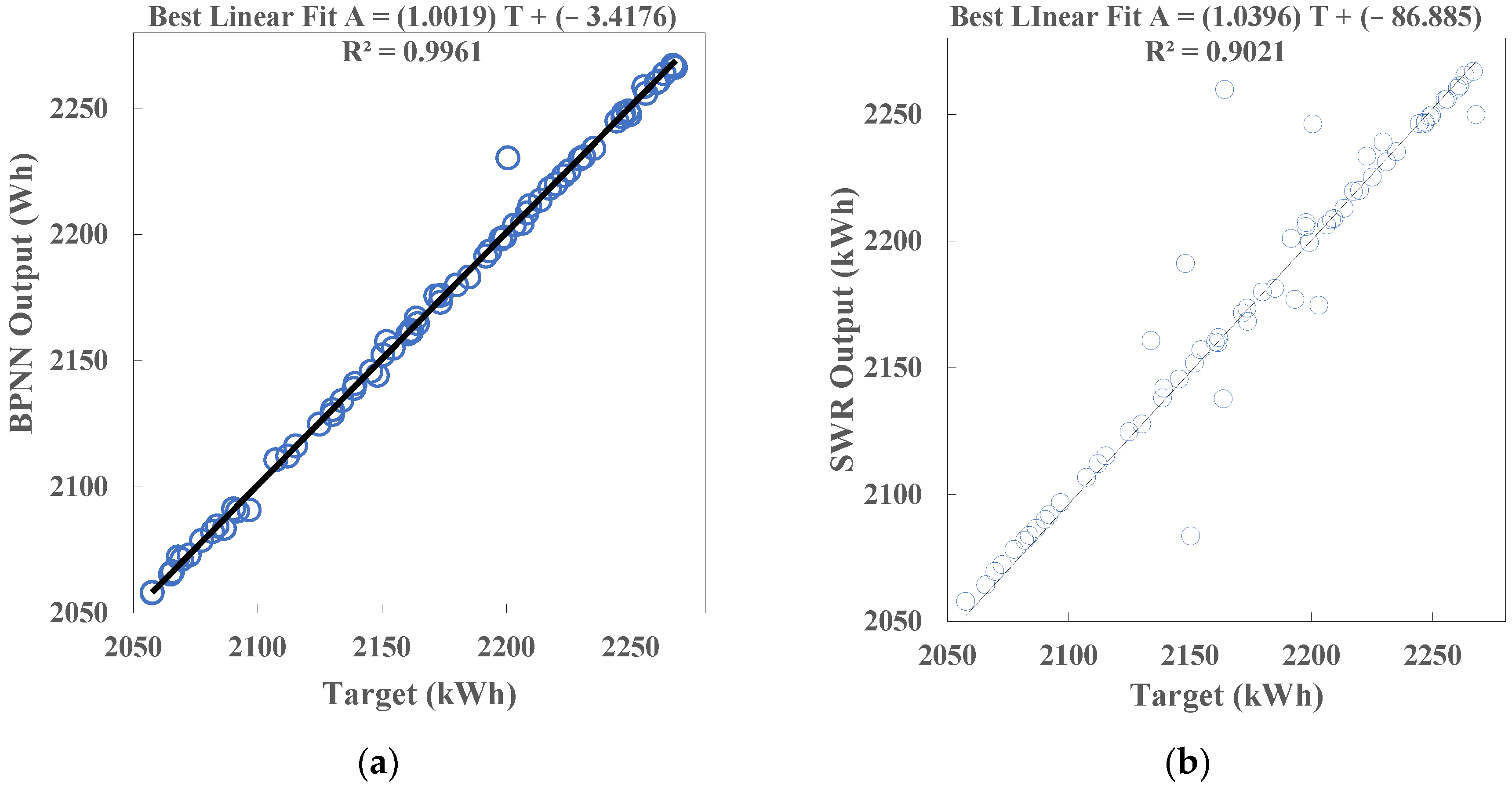
3.3. Prediction Model Performance Comparision
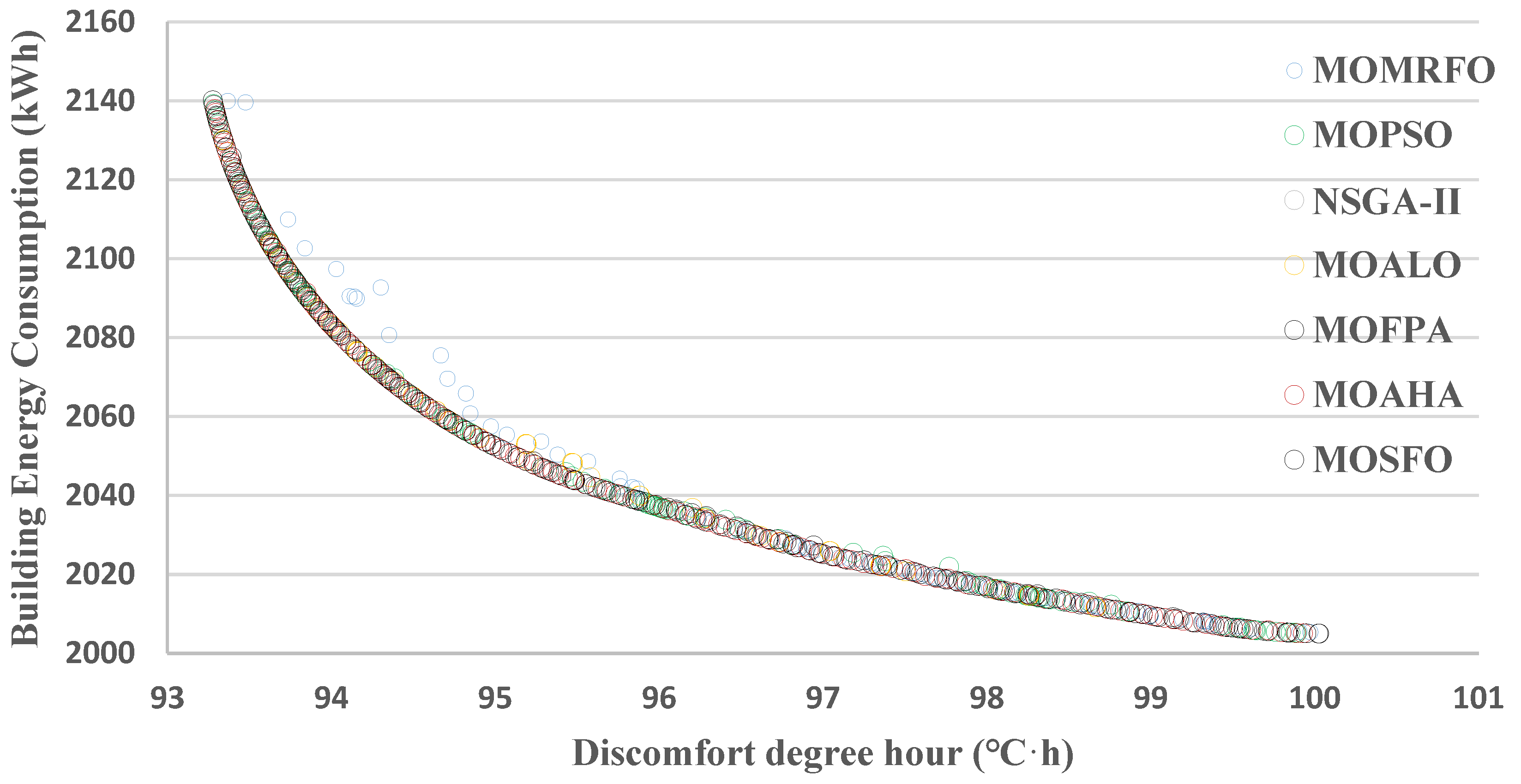
3.4. Optimization Algorithm Performance Comparision
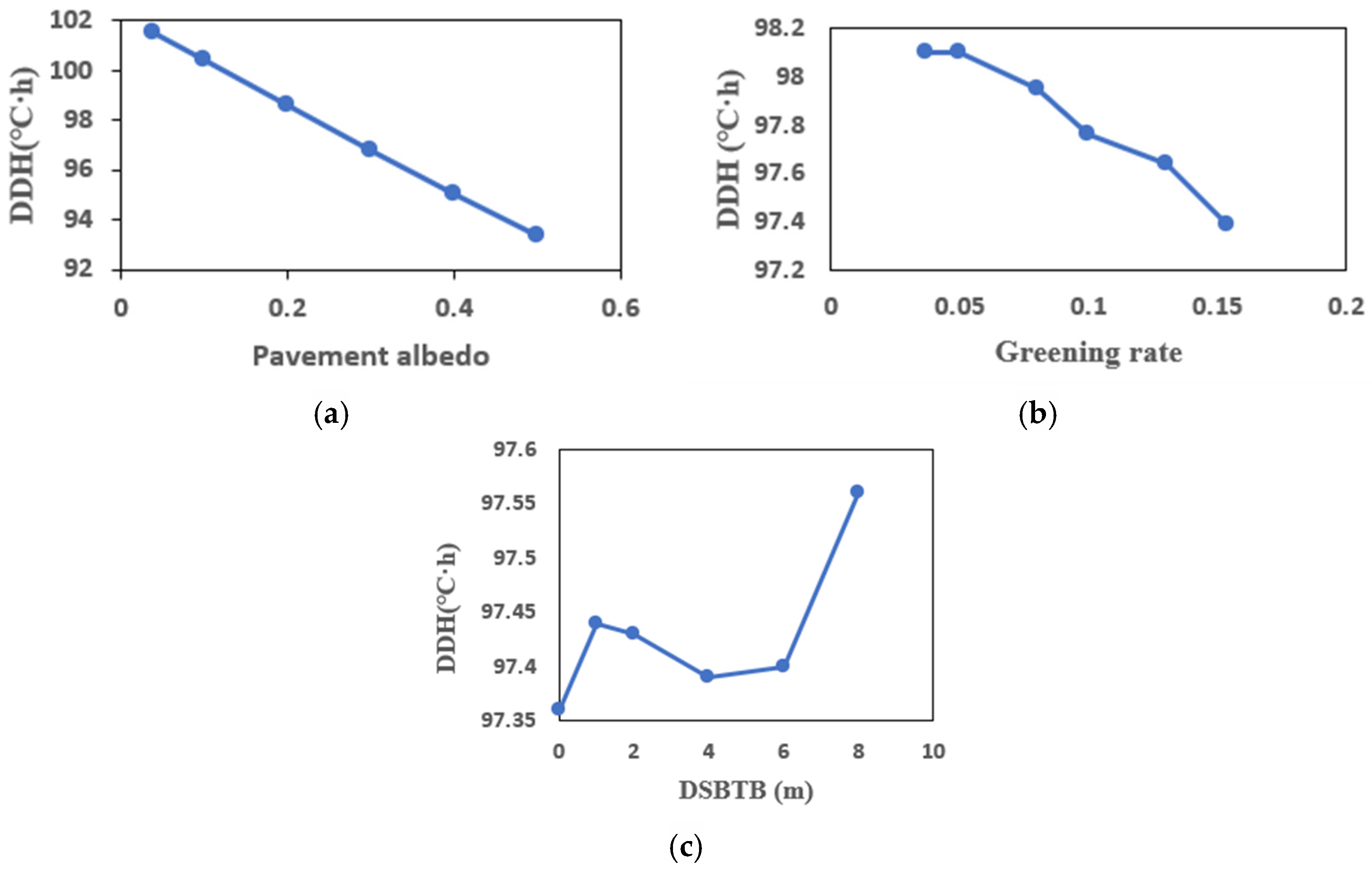
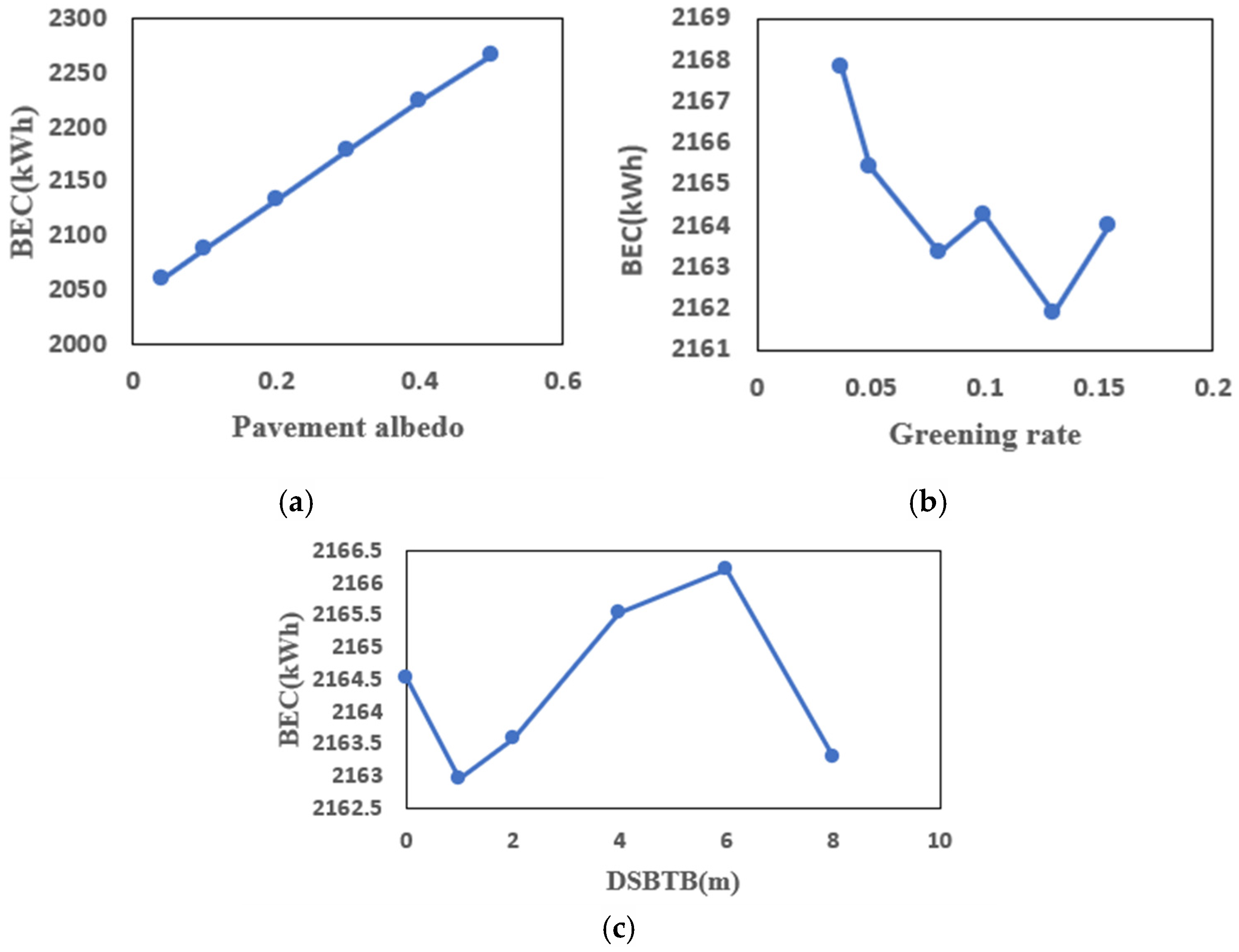
3.5. Optimal Solutions Analysis
4. Conclusions
- (1)
- The R-squares of the BPNN models for predicting IDDHs and BEC are 0.9942 and 0.996, respectively, with maximum absolute relative errors less than 2%, indicating the BPNN models outperform the LWR models;
- (2)
- It can be found from the outcomes of the Pareto solutions of all the optimization algorithms that the reduction rate in IDDHs is greater than that in BEC;
- (3)
- The MOAHA algorithm outperforms other optimization algorithms in terms of solution quality, speed (109 s), and convergence (reaching convergence at 151 generations) and achieves maximum reductions in IDDHs and BEC of 7.45% and 4.12%, respectively. The average reduction in IDDHs and BEC is 4.99% and 1.70%, respectively;
- (4)
- The Pareto solutions indicate that for a climate with hot summers and cold winters, setting the road surface albedo to the lowest value and the greening rate to the highest value can achieve the best indoor thermal environment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACSEC | Air-conditioning system energy consumption |
| AHOA | Artificial hummingbird optimization algorithm |
| ALO | Antlion Optimizer |
| ANN | Artificial Neural Network |
| BEC | Building energy consumption |
| BPNN | Backpropagation neural network |
| CDDH | Cooling discomfort degree hour |
| DSBTB | Distance between surrounding buildings and targeted building |
| H/W | Height to street wide (H/W) |
| HDDH | Heating discomfort degree hour |
| HSCW | Hot summer and cold winter |
| IAT | Indoor air temperature |
| IDDHs | Indoor discomfort degree hours |
| LHS | Latin Hypercube Sampling |
| LWR | Locally weighted regression |
| ML | Machine learning |
| MLR | Multiple Linear Regression |
| MOAHA | Multi-Objective Artificial Hummingbird Algorithm |
| MOFPA | Multi-objective Flower Pollination Algorithm |
| MOMRFO | Multi-objective Manta Ray Foraging Optimizer |
| MOPSO | Multi-Objective Particle Swarm Optimization |
| MOSFO | Multi-objective Sunflower Optimization |
| NSGA-II | Nondominated Sorting Genetic Algorithm version II |
| PSO | Particle Swarm Optimization |
| SVR | Support Vector Regression |
| f1 | IDDHs, °C∙h |
| f2 | BEC, kWh |
| IC | CDDHs, °C∙h |
| IH | HDDHs, °C∙h |
| IAT at time i, °C | |
| tH | The higher thermal comfort temperature limits, taken as 26 °C |
| tL | The lower thermal comfort temperature limits, taken as 18 °C |
| m | the numbers of nodes of input layer |
| a | the numbers of nodes of input variables |
| b | the numbers of nodes of output variables |
| c | a constant, 0~10 |
| W | the Gaussian kernel function |
| k | the rate at which the weight changes with distance |
| X | the independent variable |
| Y | the dependent variable |
| Umax | the maximum reduction rates in IDDHs |
| the average reduction rates in IDDHs | |
| the maximum reduction rates on BEC | |
| the average reduction rates on BEC | |
| the maximum reduction rates in air-conditioning system energy consumption | |
| the average reduction rates in air-conditioning system energy consumption | |
| Tr | the IDDHs of the reference building, °C·h |
| Tmin | the minimum IDDHs among the optimal solutions, °C·h |
| Ti | the IDDHs of the ith solution, °C·h |
| Er | the BEC of the reference building, kWh |
| Emin | the minimum BEC among the optimal solutions, °C·h |
| n | the number of optimal solutions |
| the ACSEC of the reference building, kWh | |
| the minimum ACSEC among the optimal solutions, kWh | |
| El | the lighting energy consumption, kWh |
| Ee | the electrical equipment energy consumption, kWh |
| the ACSEC of the ith solution, kWh |
References
- Lin, Y.; Huang, T.; Yang, W.; Hu, X.; Li, C. A Review on the Impact of Outdoor Environment on Indoor Thermal Environment. Buildings 2023, 13, 2600. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Yang, Y.; Huang, Z. Evaluating the impact of shading from surrounding buildings on heating/ cooling energy demands of different community forms. Build. Environ. 2021, 206, 108322. [Google Scholar] [CrossRef]
- Strømann-Andersen, J.; Sattrup, P.A. The urban canyon and building energy use: Urban density versus daylight and passive solar gains. Energy Build. 2011, 43, 2011–2020. [Google Scholar] [CrossRef]
- Yaghoobian, N.; Kleissl, J. Effect of reflective pavements on building energy use. Urban. Clim. 2012, 2, 25–42. [Google Scholar] [CrossRef]
- Ichinose, T.; Lei, L.; Lin, Y. Impacts of shading effect from nearby buildings on heating and cooling energy consumption in hot summer and cold winter zone of China. Energy Build. 2017, 136, 199–210. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, G.; Wang, Y.; Zhou, H.; Ma, L. A quantitative analysis of the impact of residential cluster layout on building heating energy consumption in cold IIB regions of China. Energy Build. 2021, 253, 111515. [Google Scholar] [CrossRef]
- Morakinyo, T.E.; Dahanayake, K.W.D.K.C.; Adegun, O.B.; Balogun, A.A. Modelling the effect of tree-shading on summer indoor and outdoor thermal condition of two similar buildings in a Nigerian university. Energy Build. 2016, 130, 721–732. [Google Scholar] [CrossRef]
- Taleghani, M.; Marshall, A.; Fitton, R.; Swan, W. Renaturing a microclimate: The impact of greening a neighbourhood on indoor thermal comfort during a heatwave in Manchester, UK. Sol. Energy 2019, 182, 245–255. [Google Scholar] [CrossRef]
- Simpson, J.R.; McPherson, E.G. Simulation of tree shade impacts on residential energy use for space conditioning in Sacramento. Atmos. Environ. 1998, 32, 69–74. [Google Scholar] [CrossRef]
- Darvish, A.; Eghbali, G.; Eghbali, S.R. Tree-configuration and species effects on the indoor and outdoor thermal condition and energy performance of courtyard buildings. Urban. Clim. 2021, 37, 100861. [Google Scholar] [CrossRef]
- Akbari, H.; Kurn, D.M.; Bretz, S.E.; Hanford, J.W. Peak power and cooling energy savings of shade trees. Energy Build. 1997, 25, 139–148. [Google Scholar] [CrossRef]
- Li, Z.; Chow, D.H.C.; Yao, J.; Zheng, X.; Zhao, W. The effectiveness of adding horizontal greening and vertical greening to courtyard areas of existing buildings in the hot summer cold winter region of China: A case study for Ningbo. Energy Build. 2019, 196, 227–239. [Google Scholar] [CrossRef]
- Synnefa, A.; Karlessi, T.; Gaitani, N.; Santamouris, M.; Assimakopoulos, D.N.; Papakatsikas, C. Experimental testing of cool colored thin layer asphalt and estimation of its potential to improve the urban microclimate. Build. Environ. 2011, 46, 38–44. [Google Scholar] [CrossRef]
- Carnielo, E.; Zinzi, M. Optical and thermal characterisation of cool asphalts to mitigate urban temperatures and building cooling demand. Build. Environ. 2013, 60, 56–65. [Google Scholar] [CrossRef]
- Aboelata, A. Reducing outdoor air temperature, improving thermal comfort, and saving buildings’ cooling energy demand in arid cities—Cool paving utilization. Sustain. Cities Soc. 2021, 68, 102762. [Google Scholar] [CrossRef]
- Salvati, A.; Kolokotroni, M.; Kotopouleas, A.; Watkins, R.; Giridharan, R.; Nikolopoulou, M. Impact of reflective materials on urban canyon albedo, outdoor and indoor microclimates. Build. Environ. 2022, 207, 108459. [Google Scholar] [CrossRef]
- Jandaghian, Z.; Berardi, U. Analysis of the cooling effects of higher albedo surfaces during heat waves coupling the Weather Research and Forecasting model with building energy models. Energy Build. 2020, 207, 109627. [Google Scholar] [CrossRef]
- Santamouris, M.; Haddad, S.; Saliari, M.; Vasilakopoulou, K.; Synnefa, A.; Paolini, R.; Ulpiani, G.; Garshasbi, S.; Fiorito, F. On the energy impact of urban heat island in Sydney: Climate and energy potential of mitigation technologies. Energy Build. 2018, 166, 154–164. [Google Scholar] [CrossRef]
- Xu, X.; AzariJafari, H.; Gregory, J.; Norford, L.; Kirchain, R. An integrated model for quantifying the impacts of pavement albedo and urban morphology on building energy demand. Energy Build. 2020, 211, 109759. [Google Scholar] [CrossRef]
- Kleissl, J.; Yaghoobian, N.; Krayenhoff, E.S. Modeling the Thermal Effects of Artificial Turf on the Urban Environment. J. Appl. Meteorol. Climatol. 2010, 49, 332–345. [Google Scholar]
- Qin, Y. Urban canyon albedo and its implication on the use of reflective cool pavements. Energy Build. 2015, 96, 86–94. [Google Scholar] [CrossRef]
- Li, H.; Harvey, J.; Kendall, A. Field measurement of albedo for different land cover materials and effects on thermal performance. Build. Environ. 2013, 59, 536–546. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, L. Influence of subway entrance layout on indoor and outdoor environments in street canyons with different geometric form. J. Clean. Prod. 2023, 425, 138784. [Google Scholar] [CrossRef]
- Du, L.; Wang, H.; Bian, C.; Chen, X. Impact of block form on building energy consumption, urban microclimate and solar potential: A case study of Wuhan, China. Energy Build. 2025, 328, 115224. [Google Scholar] [CrossRef]
- Gonçalves, E.L.S.; Braga, J.L.; de Oliveira Sampaio, A.; dos Santos Batista, V.; da Rocha Menezes, L.J.; Eli, L.G.; Barata, M.S.; da Silva Ventura Neto, R.; Zemero, B.R. Multiscale modeling to optimize thermal performance design for urban social housing: A case study. Appl. Therm. Eng. 2024, 236, 121379. [Google Scholar] [CrossRef]
- Wu, C.; Pan, H.; Luo, Z.; Liu, C.; Huang, H. Multi-objective optimization of residential building energy consumption, daylighting, and thermal comfort based on BO-XGBoost-NSGA-II. Build. Environ. 2024, 254, 111386. [Google Scholar] [CrossRef]
- Chen, Z.; Cui, Y.; Zheng, H.; Ning, Q.; Wang, Y.; Hu, L.; Hou, L.; Cai, W.; Wang, L.; He, Y. Study on energy consumption, thermal comfort and economy of passive buildings based on multi-objective optimization algorithm for existing passive buildings. J. Clean. Prod. 2023, 425, 138760. [Google Scholar]
- Ismail, N.; Ouahrani, D. A comprehensive optimization study of personal cooling radiant desks integrated to HVAC system for energy efficiency and thermal comfort in office buildings. Int. J. Refrig. 2023, 156, 54–71. [Google Scholar] [CrossRef]
- Hosamo, H.H.; Tingstveit, M.S.; Nielsen, H.K.; Svennevig, P.R.; Svidt, K. Multiobjective optimization of building energy consumption and thermal comfort based on integrated BIM framework with machine learning-NSGA II. Energy Build. 2022, 277, 112479. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, K.; Zhang, Q.; Di, H. Ideal thermophysical properties for free-cooling (or heating) buildings with constant thermal physical property material. Energy Build. 2006, 38, 1164–1170. [Google Scholar] [CrossRef]
- JGJ 134-2010; Design Standard for Energy Efficiency of Residential Buildings in Hot Summer and Cold Winter Zone. China Construction Industry Press: Beijing, China, 2010.
- GB55015-2021; General Code for Energy Efficiency and Renewable Energyapplication in Buildings. China Construction Industry Press: Beijing, China, 2021.
- Yang, X.; Zhao, L.; Bruse, M.; Meng, Q. An integrated simulation method for building energy performance assessment in urban environments. Energy Build. 2012, 54, 243–251. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Lin, Y.; Zhou, S.; Yang, W.; Li, C.-Q. Design Optimization Considering Variable Thermal Mass, Insulation, Absorptance of Solar Radiation, and Glazing Ratio Using a Prediction Model and Genetic Algorithm. Sustainability 2018, 10, 336. [Google Scholar] [CrossRef]
- Mihalakakou, G.; Santamouris, M.; Tsangrassoulis, A. On the energy consumption in residential buildings. Energy Build. 2002, 34, 727–736. [Google Scholar] [CrossRef]
- Ruano, A.E.; Crispim, E.M.; Conceição, E.Z.E.; Lúcio, M.M.J.R. Prediction of building’s temperature using neural networks models. Energy Build. 2006, 38, 682–694. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Olsthoorn, D.; Torjan, M.; Haghighat, F. Urban neighborhood characteristics influence on a building indoor environment. Sustain. Cities Soc. 2015, 19, 403–413. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation CEC’02 (Cat No. 02TH8600), Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Mirjalili, S.; Jangir, P.; Saremi, S. Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems. Appl. Intell. 2016, 46, 79–95. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Software 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Khodadadi, N.; Mirjalili, S.M.; Zhao, W.; Zhang, Z.; Wang, L.; Mirjalili, S. Multi-Objective Artificial Hummingbird Algorithm. In Advances in Swarm Intelligence; Kacprzyk, J., Ed.; Springer: Gewerbestrasse, Switzerland, 2023; Volume 1054, pp. 407–419. [Google Scholar]
- Yang, X.-S.; Karamanoglu, M.; He, X. Flower pollination algorithm: A novel approach for multiobjective optimization. Eng. Optim. 2013, 46, 1222–1237. [Google Scholar] [CrossRef]
- Yang, X.-S. Flower pollination algorithm for global optimization. In Proceedings of the International Conference on Unconventional Computing and Natural Computation, Orléan, France, 3–7 September 2012. [Google Scholar]
- Pereira, J.L.J.; Gomes, G.F. Multi-objective sunflower optimization: A new hypercubic meta-heuristic for constrained engineering problems. Expert Syst. 2023, 40, 13331. [Google Scholar] [CrossRef]
- Got, A.; Zouache, D.; Moussaoui, A. MOMRFO: Multi-objective Manta ray foraging optimizer for handling engineering design problems. Knowl.-Based Syst. 2022, 237, 107880. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, J.; Yang, W.; Chan, M.; Hu, X. A Case Study of Multi-objective Design Optimization of a Healthy Building in Shanghai, China. J. Build. Eng. 2024, 96, 110581. [Google Scholar] [CrossRef]


| Parameter | Value | Range |
|---|---|---|
| Road pavement albedo (−) | 0.04 | 0.04–0.5 |
| Greening rate (%) | 10.9 | 3.7–15.4 |
| DSBTB (m) | 4 | 0–8 |
| Parameter | Value |
|---|---|
| Air-conditioned area (m2) | 1850 |
| Building height (m) | 18 |
| Exterior wall heat transfer coefficient (HTC) (W/m2·K) | 0.483 |
| Roof HTC (W/m2·K) | 0.23 |
| External window HTC (W/m2·K) | 3.9 |
| East-facing window-to-wall ratio (WWR) (%) | 45 |
| South-facing WWR (%) | 7 |
| West-facing WWR (%) | 7 |
| North-facing WWR (%) | 45 |
| Location | Shanghai |
|---|---|
| Date/time | From 9:00 to 24:00 a.m., 20 January, to 24:00 a.m., 21 January From 9:00 to 24:00 a.m., 20 July, to 24:00 a.m., 21 July |
| Model domain | 60 × 70 × 35 grids Δx = Δy = Δz = 2 m |
| Meteorological inputs | Chinese Standard Weather Data (CSWD) |
| Optimal Number of Nodes of Hidden Layer | Learning Rate | Maximum Number of Iteration | Maximum Error | Training vs. Testing |
|---|---|---|---|---|
| 9 | 0.01 | 1000 | 1 × 10−5 | 80:20 |
| Parameter | MOPSO | NSGA-II | MOALO | MOAHA | MOFPA | MOSFO | MOMRFO |
|---|---|---|---|---|---|---|---|
| Maximum number of generations | 200 | 200 | 200 | 200 | 200 | 200 | 200 |
| Population size | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Crossover rate | 0.9 | ||||||
| Mutation rate | 0.1 | ||||||
| Proximity probability | 0.8 | ||||||
| Pollination rate | 0.1 | ||||||
| Personal learning coefficient | 1 | ||||||
| Global learning coefficient | 2 | ||||||
| Archive size | 100 | 150 | 150 | 150 | 150 | 150 | 150 |
| Inertia weight | 0.5 | ||||||
| Death rate | 0.1 | ||||||
| Grid size | 7 | 25 | |||||
| Inflation rate | 1 | ||||||
| Leader selection pressure | 2 | ||||||
| Deletion selection pressure | 2 | ||||||
| Survival rate | 0.8 |
| 1st Fold 0–20% | 2nd Fold 20–40% | 3rd Fold 40–60% | 4th Fold 60–80% | 5th Fold 80–100% | Average | ||
|---|---|---|---|---|---|---|---|
| IDDHs (°C·h) | R-square | 0.983 | 0.945 | 0.991 | 0.990 | 0.985 | 0.979 |
| MSE | 0.129 | 0.282 | 0.048 | 0.060 | 0.112 | 0.126 | |
| RMSE | 0.359 | 0.531 | 0.219 | 0.246 | 0.335 | 0.338 | |
| MAE | 0.259 | 0.320 | 0.200 | 0.166 | 0.238 | 0.237 | |
| MAPE | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | |
| BEC (kWh) | R-square | 0.998 | 0.968 | 0.992 | 0.996 | 0.992 | 0.989 |
| MSE | 7.379 | 120.138 | 27.977 | 14.549 | 29.192 | 39.847 | |
| RMSE | 2.716 | 10.961 | 5.289 | 3.814 | 5.403 | 5.637 | |
| MAE | 2.198 | 6.426 | 4.253 | 3.190 | 4.765 | 4.166 | |
| MAPE | 0.001 | 0.003 | 0.002 | 0.001 | 0.002 | 0.002 |
| Range | BPNN | LWR | Range | BPNN |
|---|---|---|---|---|
| IDDHs (°C·h) | BEC (kWh) | IDDHs (°C·h) | ||
| <0.5% | 85.71% | 92.86% | <0.5% | 85.71% |
| <1% | 100% | 92.86% | <1% | 100% |
| <2% | 100% | 100% | 95% | 95% |
| <3% | 100% | 100% | 95% | 95% |
| <4% | 100% | 100% | 100% | 100% |
| <5% | 100% | 100% | 100% | 100% |
| Average | 0.27% | 0.23% | 0.53% | 0.50% |
| Parameter | MOPSO | NSGA-II | MOALO | MOAHA | MOFPA | MOSFO | MOMRFO |
|---|---|---|---|---|---|---|---|
| Number of generations when converged | 184 | 176 | 185 | 151 | 163 | 179 | 157 |
| Computation time (s) | 131 | 125 | 155 | 109 | 152 | 135 | 149 |
| Algorithm | ||||||
|---|---|---|---|---|---|---|
| MOPSO | 7.45% | 5.02% | 4.12% | 1.58% | 5.80% | 2.22% |
| NSGA-II | 7.45% | 4.98% | 4.08% | 1.67% | 5.73% | 2.34% |
| MOALO | 7.39% | 6.00% | 3.81% | 0.90% | 5.36% | 1.26% |
| MOAHA | 7.45% | 4.99% | 4.12% | 1.70% | 5.80% | 2.40% |
| MOFPA | 7.45% | 4.82% | 4.13% | 1.82% | 5.80% | 2.56% |
| MOSFO | 7.45% | 4.96% | 4.13% | 1.69% | 5.80% | 2.38% |
| MOMRFO | 7.36% | 3.69% | 4.11% | 2.75% | 5.78% | 3.87% |
| Pavement Albedo | Greening Rate | Offsets of Surrounding Building from the Original Position (m) | IDDHs (°C·h) | BEC (kWh) |
|---|---|---|---|---|
| 0.049 | 0.148 | 1.274 | 98.25 | 2014.83 |
| 0.040 | 0.154 | 0.544 | 94.01 | 2082.88 |
| 0.040 | 0.154 | 0.194 | 93.40 | 2123.13 |
| 0.040 | 0.154 | 0.354 | 93.60 | 2105.72 |
| 0.045 | 0.154 | 1.01 | 96.02 | 2036.74 |
| 0.040 | 0.154 | 0 | 93.28 | 2140.07 |
| 0.040 | 0.142 | 1.344 | 99.39 | 2007.05 |
| 0.040 | 0.154 | 0.948 | 95.73 | 2040.42 |
| 0.048 | 0.154 | 1.102 | 96.47 | 2031.15 |
| 0.040 | 0.154 | 0.3 | 93.52 | 2112.00 |
| 0.054 | 0.150 | 1.26 | 97.76 | 2018.91 |
| 0.040 | 0.154 | 0.328 | 93.56 | 2108.77 |
| 0.051 | 0.150 | 1.316 | 98.09 | 2015.76 |
| 0.040 | 0.154 | 0.826 | 95.08 | 2050.72 |
| 0.051 | 0.154 | 1.188 | 96.82 | 2027.26 |
| 0.040 | 0.154 | 0.416 | 93.71 | 2098.58 |
| 0.053 | 0.154 | 1.162 | 96.68 | 2028.65 |
| 0.040 | 0.154 | 0.382 | 93.65 | 2102.61 |
| 0.040 | 0.154 | 0.796 | 94.94 | 2053.65 |
| 0.049 | 0.148 | 1.288 | 98.29 | 2014.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Huang, T.; Yang, W.; Chan, M.; Li, C.-Q.; Dai, M.; Chen, P. Outdoor Environment Design Optimization of an Office Building Based on Indoor Thermal Conditions and Building Energy Performance. Buildings 2025, 15, 2190. https://doi.org/10.3390/buildings15132190
Lin Y, Huang T, Yang W, Chan M, Li C-Q, Dai M, Chen P. Outdoor Environment Design Optimization of an Office Building Based on Indoor Thermal Conditions and Building Energy Performance. Buildings. 2025; 15(13):2190. https://doi.org/10.3390/buildings15132190
Chicago/Turabian StyleLin, Yaolin, Tao Huang, Wei Yang, Melissa Chan, Chun-Qing Li, Mingqi Dai, and Pengju Chen. 2025. "Outdoor Environment Design Optimization of an Office Building Based on Indoor Thermal Conditions and Building Energy Performance" Buildings 15, no. 13: 2190. https://doi.org/10.3390/buildings15132190
APA StyleLin, Y., Huang, T., Yang, W., Chan, M., Li, C.-Q., Dai, M., & Chen, P. (2025). Outdoor Environment Design Optimization of an Office Building Based on Indoor Thermal Conditions and Building Energy Performance. Buildings, 15(13), 2190. https://doi.org/10.3390/buildings15132190









