Construction Concrete Price Prediction Based on a Double-Branch Physics-Informed Neural Network
Abstract
1. Introduction
2. Literature Review
3. Methodology
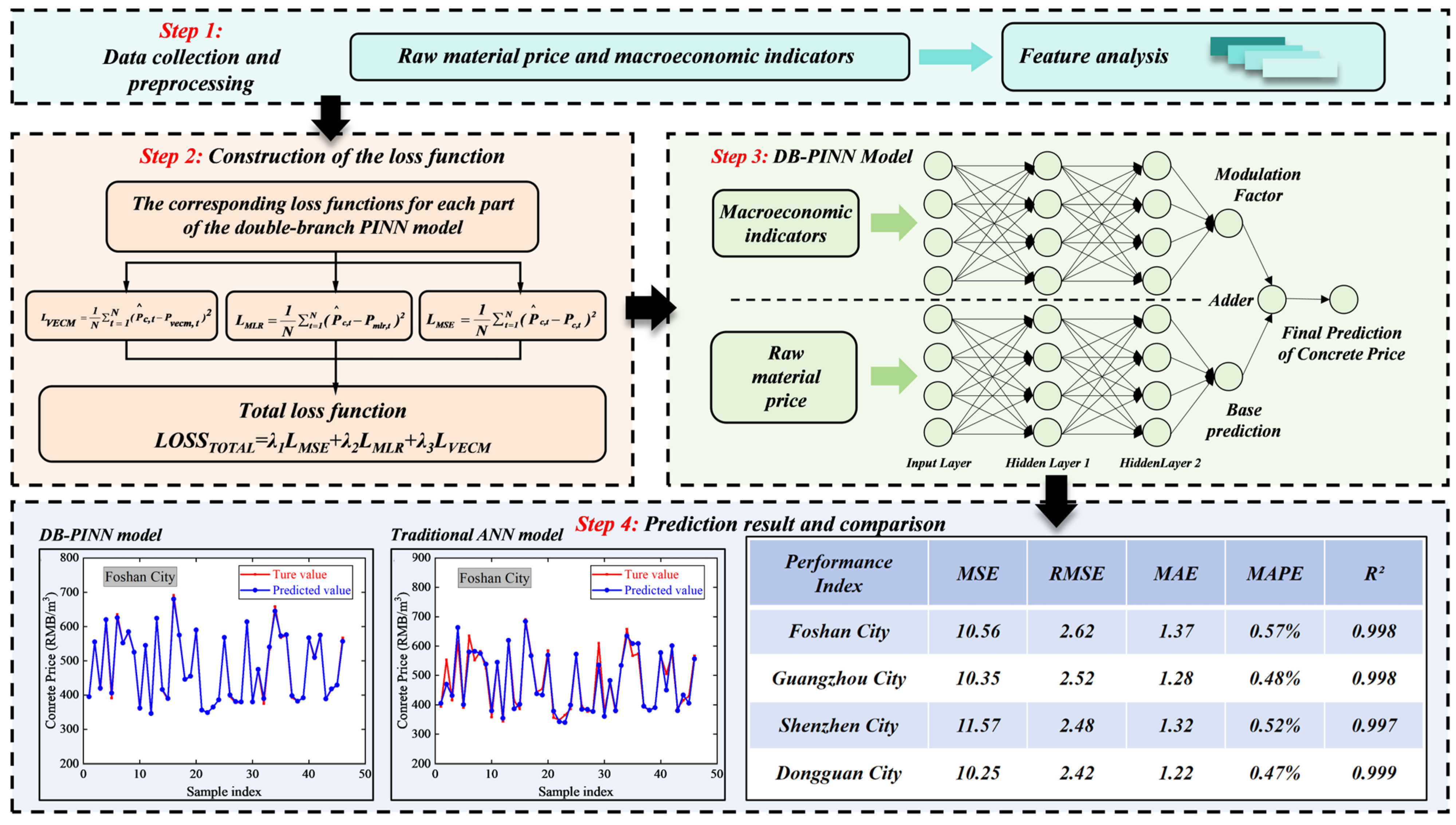
3.1. DB-PINN Prediction Model
3.2. Research Procedure
- Data collection
- Data preprocessing
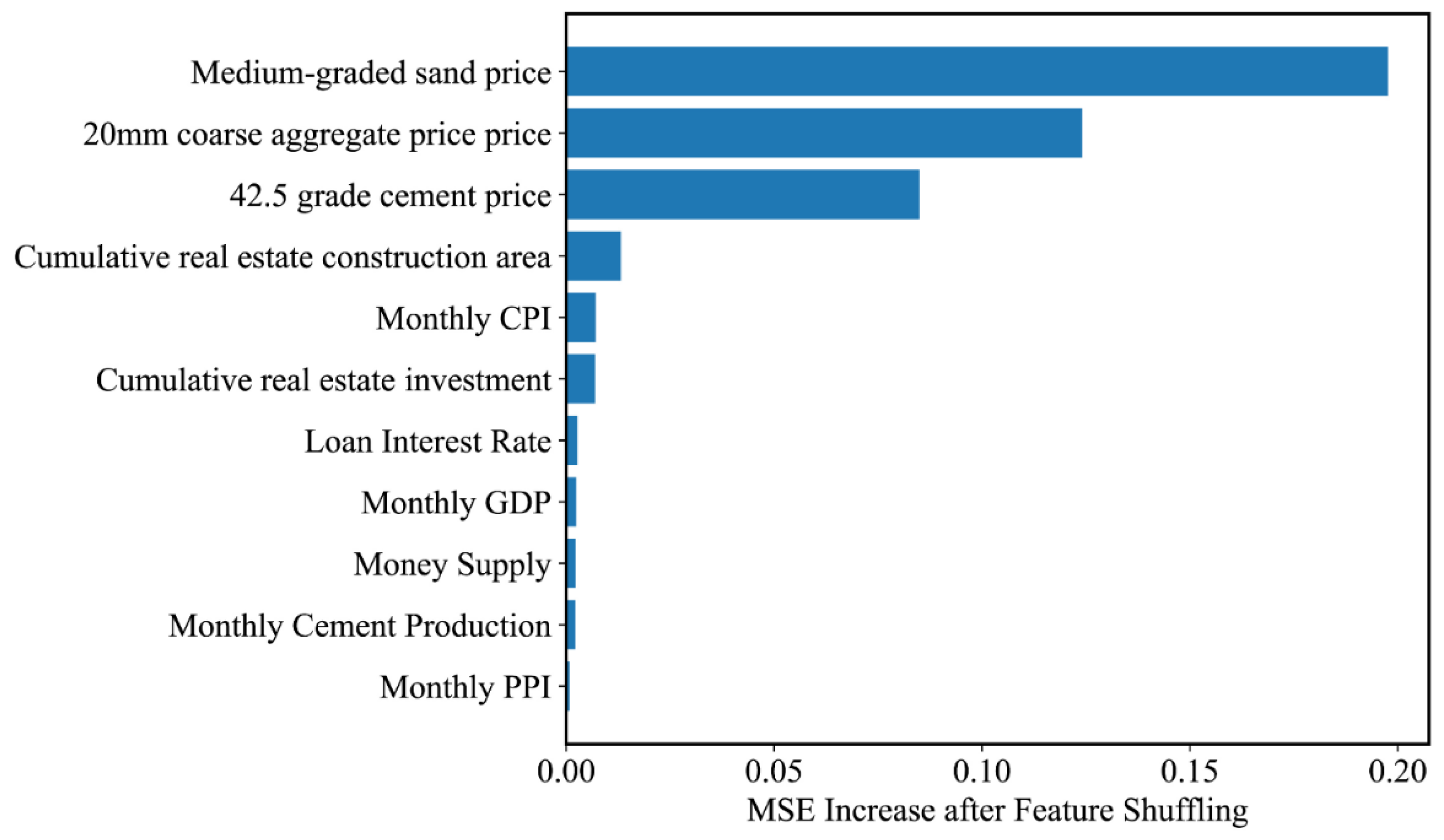
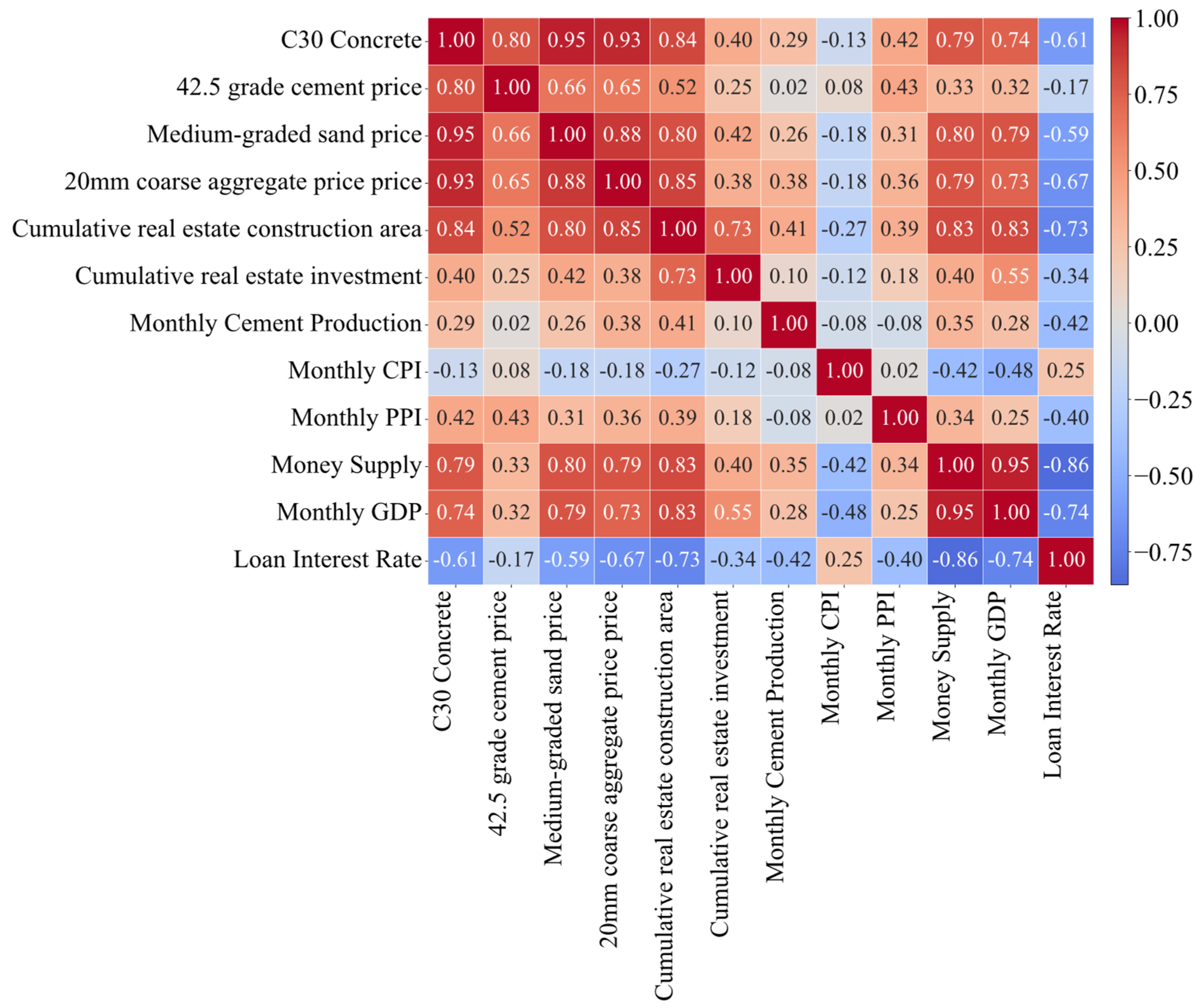
- Feature Analysis
- Marginal Effect Analysis
- Comparison Analysis
- Parameter Sensitivity Analysis
4. Results and Discussion
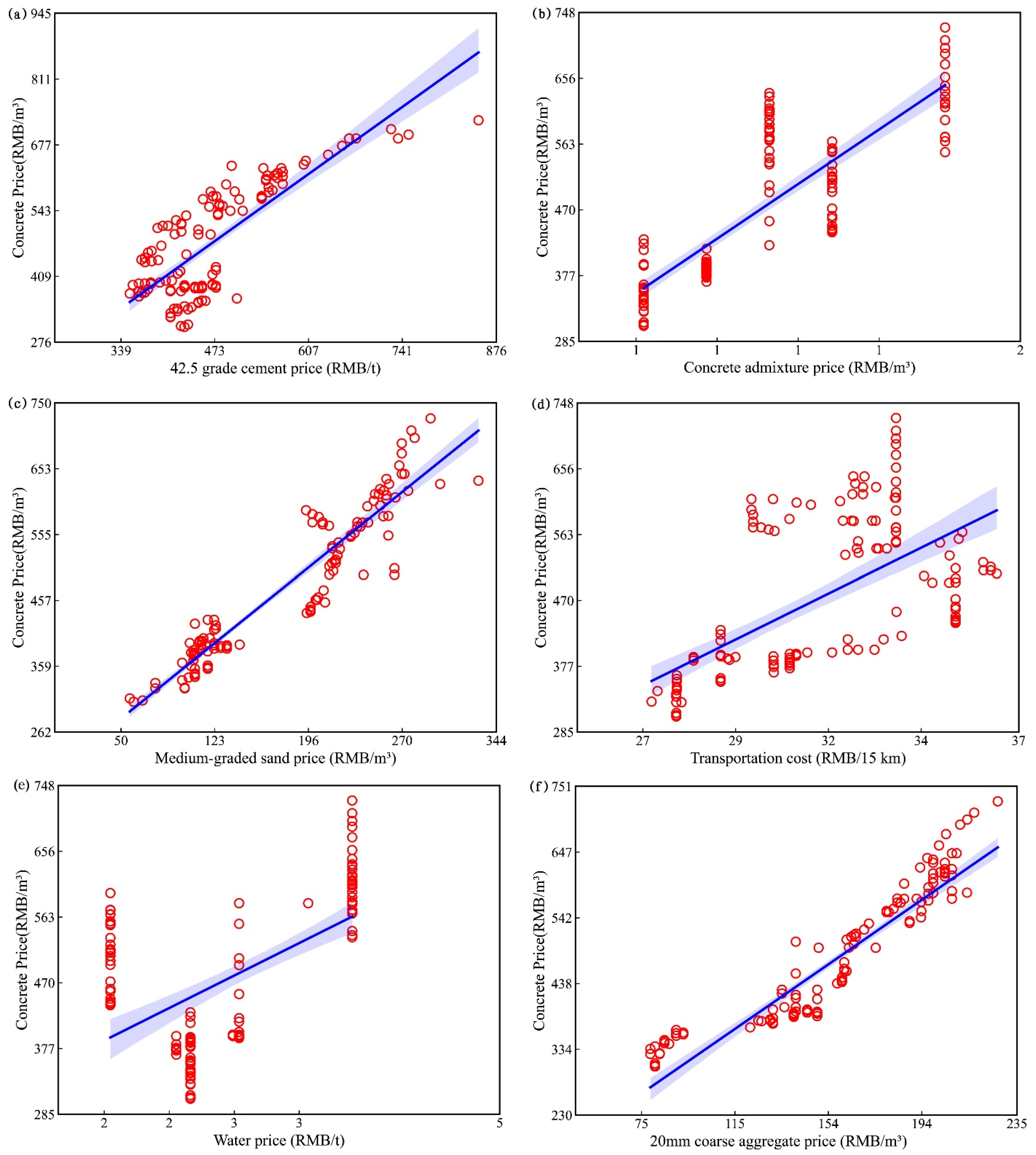
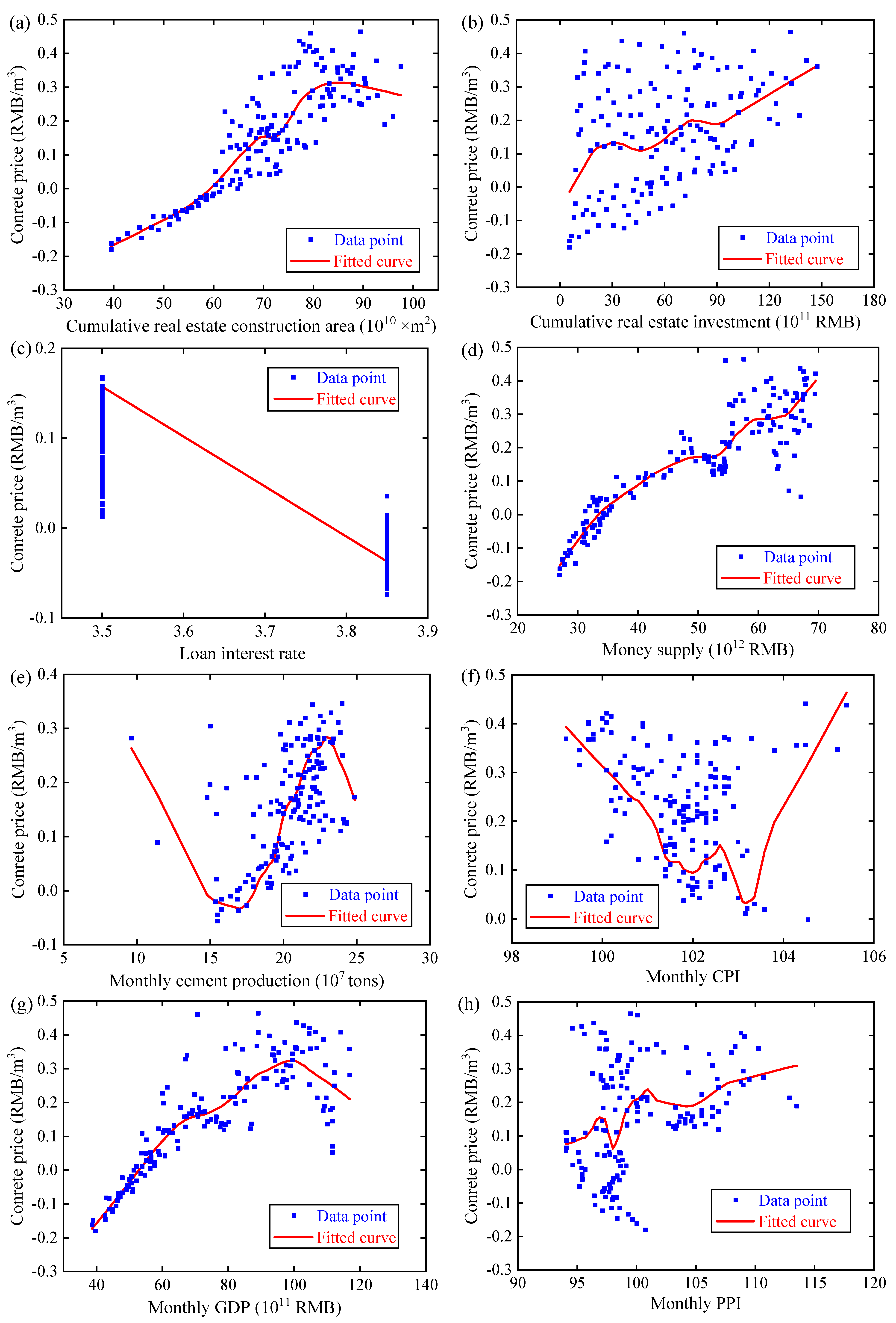
4.1. Result of Feature Analysis
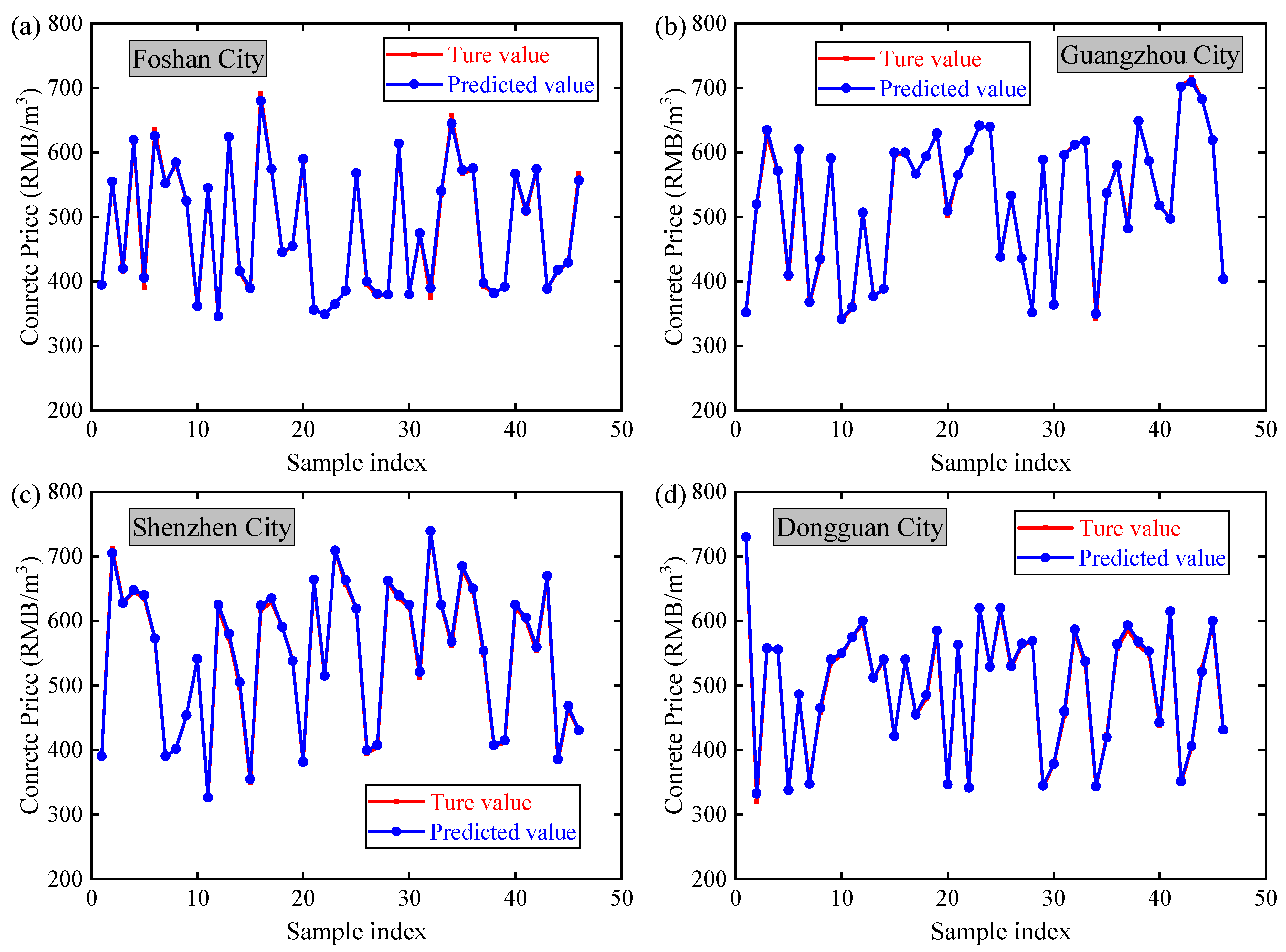
4.2. Prediction Results
4.3. Result of Marginal Effect Analysis
4.4. Result of Comparison Analysis
4.5. Result of Parameter Sensitivity Analysis
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Description of Macroeconomic Indicators
| Macroeconomic Indicators | Impact on Prices of Construction Materials |
|---|---|
| CPI | The CPI measures the general level of inflation for consumer goods and services. In an inflationary environment, manufacturers may raise material prices to maintain profits [15,21,23]. |
| PPI | PPI tracks price changes from the perspective of product manufacturers. When PPI rises, it indicates that manufacturers are charging higher fees for raw materials and processed materials [15,21]. |
| Money supply | The money supply (usually measured by M2) represents the liquidity available in the economy. Expansionary monetary policy tends to lead to lower interest rates and more available credit, stimulating investment in RE and construction [16]. |
| GDP | GDP represents the total amount and growth of the economy. Higher GDP growth usually indicates more construction spending and higher demand for construction materials [15,21,23]. |
| Industrial production volume | The volume of industrial production such as cement, steel, and aggregates is an important factor in determining the price of construction materials. This relationship follows the basic supply and demand principle [16]. |
| Loan interest rate | Many construction projects are usually financed through loans; lower interest rates reduce borrowing costs for developers and homebuyers. When the supply side is under pressure from additional demand, it may lead to rising material prices [15,21]. |
| Number of new construction projects | The number of new construction projects can reflect changes in the demand for construction materials. New construction projects often require a large quantity of construction materials, so construction material manufacturers will adjust their product prices based on changes in supply and demand [21,23,41,42]. |
| Market size of the construction industry | The market size of the construction industry refers to the overall scale of construction business in an economy. A larger construction industry scale means a higher baseline demand for construction materials, which causes inflationary pressure in the material market and in turn pushes up the prices of construction materials [41,42]. |
References
- Statista. Urbanization Rate in China 1980–2024. Available online: https://www.statista.com/statistics/270162/urbanization-in-china/ (accessed on 19 February 2025).
- Statista. China: Real Estate Sales Revenue Monthly 2024. Available online: https://www.statista.com/statistics/1459232/monthly-sales-revenue-of-real-estate-in-china/ (accessed on 19 February 2025).
- Statista. China: Real Estate Construction Started Monthly 2024. Available online: https://www.statista.com/statistics/1459210/monthly-construction-of-real-estate-in-china/ (accessed on 19 February 2025).
- Holm, L.; Schaufelberger, J.E. Construction Cost Estimating; Routledge: London, UK, 2021; ISBN 978-1-003-02349-4. [Google Scholar]
- Ekung, S.; Lashinde, A.; Adu, E. Critical Risks to Construction Cost Estimation. J. Eng. Proj. Prod. Manag. 2021, 11, 19–29. [Google Scholar]
- Potts, K.; Ankrah, N. Construction Cost Management: Learning from Case Studies; Routledge: London, UK, 2014; ISBN 978-0-203-75294-4. [Google Scholar]
- Trackunit. Construction Project Cost Breakdown: Estimate the Total Cost. Available online: https://trackunit.com/articles/construction-project-breakdown/ (accessed on 12 March 2025).
- Tigranyan, H. Detailed Construction Project Cost Breakdown [Examples Included]. Available online: https://buildern.com/resources/blog/construction-project-cost-breakdown/ (accessed on 20 April 2025).
- Zhang, J.; Peng, L.; Wen, S.; Huang, S. A review on concrete structural properties and damage evolution monitoring techniques. Sensors 2024, 24, 620. [Google Scholar] [CrossRef] [PubMed]
- JGJ 55-2011; Specification for Mix Proportion Design of Ordinary Concrete. MOHURD: Beijing, China, 2011.
- Samuel, E.; Snapp, S. Cost model for unit rate pricing of concrete in construction projects. Int. J. Constr. Eng. Manag. 2015, 4, 149–158. [Google Scholar]
- Elmousalami, H.H. Artificial intelligence and parametric construction cost estimate modeling: State-of-the-art review. J. Constr. Eng. Manag. 2020, 146, 03119008. [Google Scholar] [CrossRef]
- Igwe, U.S.; Mohamed, S.F.; Azwarie, M.B.M.D. Recent Technologies in Construction; A Novel Search for Total Cost Management of Construction Projects. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020; Volume 884, p. 012041. [Google Scholar]
- Matel, E.; Vahdatikhaki, F.; Hosseinyalamdary, S.; Evers, T.; Voordijk, H. An artificial neural network approach for cost estimation of engineering services. Int. J. Constr. Manag. 2022, 22, 1274–1287. [Google Scholar] [CrossRef]
- Liu, Q.; He, P.; Peng, S.; Wang, T.; Ma, J. A Survey of Data-Driven Construction Materials Price Forecasting. Buildings 2024, 14, 3156. [Google Scholar] [CrossRef]
- Peško, I.; Mučenski, V.; Šešlija, M.; Radović, N.; Vujkov, A.; Bibić, D.; Krklješ, M. Estimation of Costs and Durations of Construction of Urban Roads Using ANN and SVM. Complexity 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Juszczyk, M.; Leśniak, A.; Zima, K. ANN based approach for estimation of construction costs of sports fields. Complexity 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Chandanshive, V.; Kambekar, A.R. Estimation of building construction cost using artificial neural networks. J. Soft Comput. Civ. Eng. 2019, 3, 91–107. [Google Scholar]
- Ahmadu, H.; Ibrahim, Y.; Abdulrahman, R.; Jibril, U.; Yamusa, M. Developing Machine Learning Prediction Models for Construction Material Prices in Nigeria. ATBU J. Environ. Technol. 2023, 16, 22–42. [Google Scholar]
- Bassioni, H.A.; Elmasry, M.I.; Ragheb, A.M.; Youssef, A.A. Time series analysis for the prediction of RC material components prices in Egypt. In Proceedings of the 28th Annual ARCOM Conference, Edinburgh, UK, 3–5 September 2012; pp. 381–390. [Google Scholar]
- Shiha, A.; Dorra, E.M.; Nassar, K. Neural networks model for prediction of construction material prices in Egypt using macroeconomic indicators. J. Constr. Eng. Manag. 2020, 146, 04020010. [Google Scholar] [CrossRef]
- Hosny, S.; Elsaid, E.; Hosny, H. Prediction of construction material prices using ARIMA and multiple regression models. Asian J. Civ. Eng. 2023, 24, 1697–1710. [Google Scholar] [CrossRef]
- Mir, M.; Kabir, H.D.; Nasirzadeh, F.; Khosravi, A. Neural network-based interval forecasting of construction material prices. J. Build. Eng. 2021, 39, 102288. [Google Scholar] [CrossRef]
- Rešetar, Z.; Rešetar, N.P.; Lukić, F. The impact of the increase in raw material prices on costs in the construction sector in the city of Osijek. In Proceedings of the International Scientific Conference on Economy, Management and Information Technologies, Blace, Serbia, 21–23 September 2023; Volume 1, pp. 257–268. [Google Scholar]
- Abdul Nabi, M.; Chammout, B.; El-adaway, I.H.; Assaad, R.H.; Assaf, G. Investigating price fluctuation transmission among construction materials. In Proceedings of the Construction Research Congress, Des Moines, Iowa, 20–23 March 2024; pp. 339–349. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-Driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Numerical Gaussian processes for time-dependent and nonlinear partial differential equations. SIAM J. Sci. Comput. 2018, 40, A172–A198. [Google Scholar] [CrossRef]
- Guo, M.; Haghighat, E. Energy-based error bound of physics-informed neural network solutions in elasticity. J. Eng. Mech. 2022, 148, 04022038. [Google Scholar] [CrossRef]
- Reyes, B.; Howard, A.A.; Perdikaris, P.; Tartakovsky, A.M. Learning unknown physics of non-Newtonian fluids. Phys. Rev. Fluids 2021, 6, 073301. [Google Scholar] [CrossRef]
- Aliakbari, M.; Mahmoudi, M.; Vadasz, P.; Arzani, A. Predicting high-fidelity multiphysics data from low-fidelity fluid flow and transport solvers using physics-informed neural networks. Int. J. Heat Fluid Flow 2022, 96, 109002. [Google Scholar] [CrossRef]
- Ahmed, B.; Howard, A.A.; Perdikaris, P.; Tartakovsky, A.M. Physics-informed deep operator networks with stiffness-based loss functions for structural response prediction. Eng. Appl. Artif. Intell. 2025, 144, 110097. [Google Scholar] [CrossRef]
- Aliyu, S.U. Oil price shocks and the macroeconomy of Nigeria: A non-linear approach. J. Int. Bus. Entrepren. Dev. 2011, 5, 179–198. [Google Scholar] [CrossRef]
- Fernandez, V. Linear and non-linear causality between price indices and commodity prices. Resour. Policy 2014, 41, 40–51. [Google Scholar] [CrossRef]
- Gupta, M.; Varshney, S. Non-linear Effect of Real Exchange Rate Variability with Macroeconomic Variable on Non-Petroleum Commodities of India–US Trade. Foreign Tr. Rev. 2023, 58, 289–328. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; ISBN 978-1-107-07599-3. [Google Scholar]
- Engle, R.F.; Granger, C.W. Co-integration and error correction: Representation, estimation, and testing. Econom. J. Econom. Soc. 1987, 55, 251–276. [Google Scholar] [CrossRef]
- Hauzenberger, N.; Pfarrhofer, M.; Rossini, L. Sparse time-varying parameter VECMs with an application to modeling electricity prices. Int. J. Forecast. 2025, 41, 361–376. [Google Scholar] [CrossRef]
- Perez-Rosero, D.A.; Álvarez-Meza, A.M.; Castellanos-Dominguez, C.G. A regularized physics-informed neural network to support data-driven nonlinear constrained optimization. Computers 2024, 13, 176. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Shakantu, W.; Tookey, J.E.; Bowen, P.A. The hidden cost of transportation of construction materials: An overview. J. Eng. Des. Technol. 2003, 1, 103–118. [Google Scholar] [CrossRef]
- Skitmore, M. Construction Prices: The Market Effect; University of Salford Environmental Resources Unit: Salford, UK, 1987; ISBN 0-901025-10-0. [Google Scholar]
- Tajani, F.; Morano, P.; Saez-Perez, M.P.; Di Liddo, F.; Locurcio, M. Multivariate dynamic analysis and forecasting models of future property bubbles: Empirical applications to the housing markets of Spanish metropolitan cities. Sustainability 2019, 11, 3575. [Google Scholar] [CrossRef]
- Han, L.; Liu, C.; Ren, Z.; Zhang, X.; Yang, H. Research on project cost management under the mode of bill of quantities valuation. Int. J. Front. Eng. Technol. 2022, 4, 63–69. [Google Scholar] [CrossRef]
- NSBC. Consultation Disclosure—National Bureau of Statistics. Available online: https://www.stats.gov.cn/hd/lyzx/zxgk/202405/t20240524_1954065.html (accessed on 5 April 2025).
- Imtiaz, S.A.; Shah, S.L. Treatment of missing values in process data analysis. Can. J. Chem. Eng. 2008, 86, 838–858. [Google Scholar] [CrossRef]
- Lepot, M.; Aubin, J.-B.; Clemens, F. Interpolation in time series: An introductive overview of existing methods, their performance criteria and uncertainty assessment. Water 2017, 9, 796. [Google Scholar] [CrossRef]
- Santos, N.P. The expansion of data science: Dataset standardization. Standards 2023, 3, 400–410. [Google Scholar] [CrossRef]
- Cheadle, C.; Vawter, M.P.; Freed, W.J.; Becker, K.G. Analysis of microarray data using Z score transformation. J. Mol. Diagn. 2003, 5, 73–81. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable; Independently Published; 2020. ISBN 978-0-244-76852-2.
- Data MasterClub. Applying Artificial Neural Networks (ANNs) for Linear Regression: Yay or Nay? Available online: https://datamastersclub.com/applying-artificial-neural-networks-anns-for-linear-regression-yay-or-nay/ (accessed on 7 June 2025).
- Raja, M.N.A.; Abdoun, T.; El-Sekelly, W. Smart prediction of liquefaction-induced lateral spreading. J. Rock Mech. Geotech. Eng. 2024, 16, 2310–2325. [Google Scholar] [CrossRef]
- De Veaux, R.D.; Ungar, L.H. Multicollinearity: A tale of two nonparametric regressions. In Selecting Models from Data; Cheeseman, P., Oldford, R.W., Eds.; Lecture Notes in Statistics; Springer: New York, NY, USA, 1994; Volume 89, pp. 393–402. [Google Scholar]

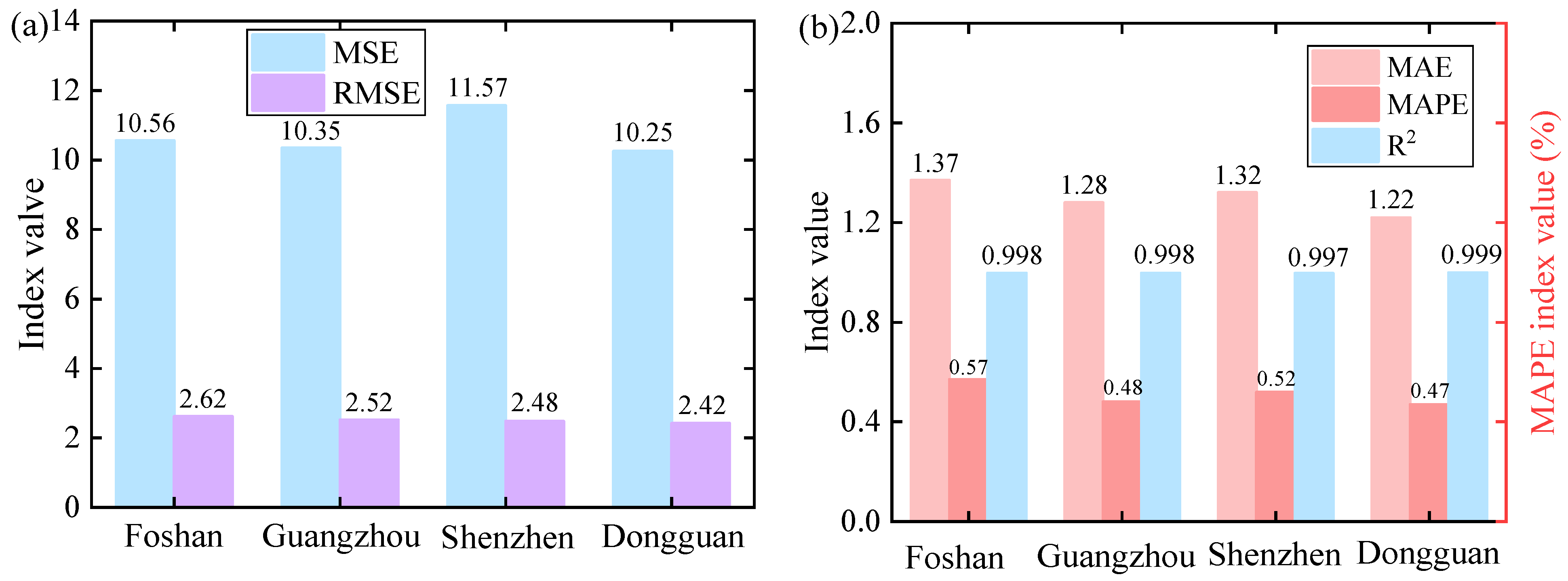
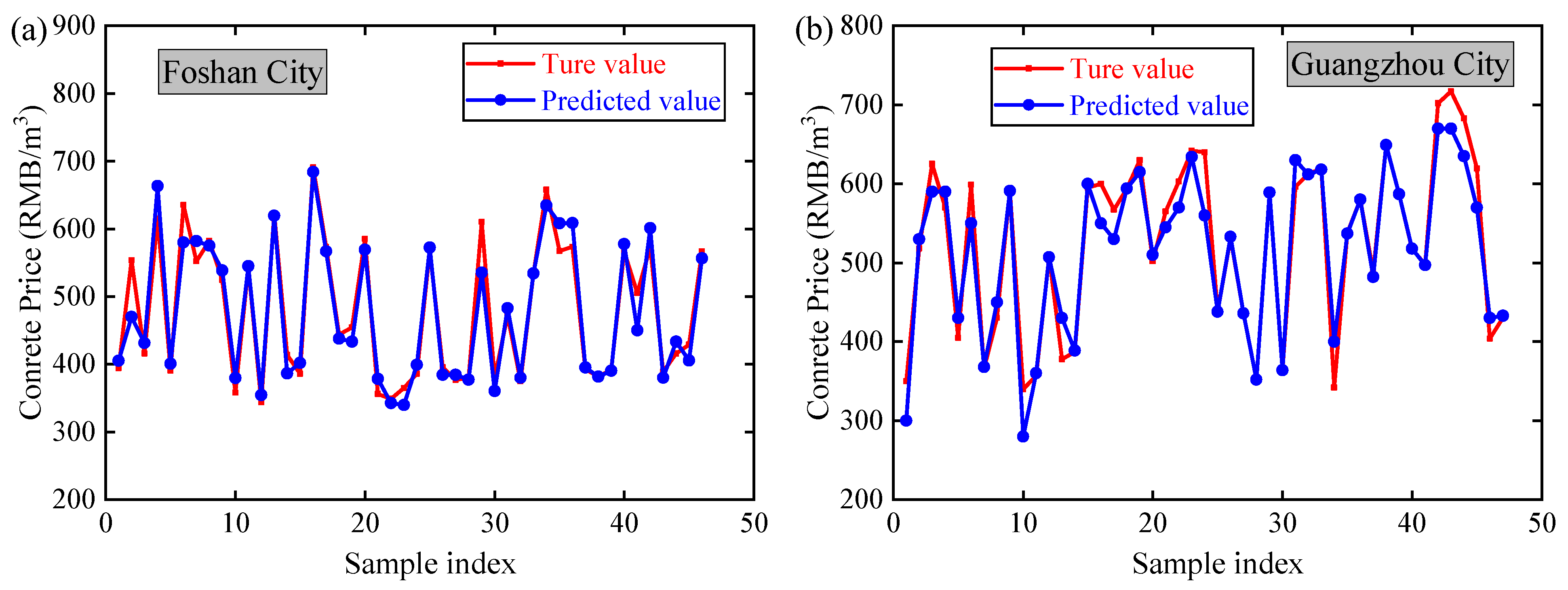
| Performance Index | Foshan City | Guangzhou City | Shenzhen City | Dongguan City |
|---|---|---|---|---|
| MSE | 10.56 | 10.35 | 11.57 | 10.25 |
| RMSE | 2.62 | 2.52 | 2.48 | 2.42 |
| MAE | 1.37 | 1.28 | 1.32 | 1.22 |
| MAPE | 0.57% | 0.48% | 0.52% | 0.47% |
| R2 | 0.998 | 0.998 | 0.997 | 0.999 |
| Performance Index | DB-PINN Model | Traditional ANN Model |
|---|---|---|
| MSE | 10.56 | 1115.21 |
| RMSE | 2.62 | 33.39 |
| MAE | 1.37 | 21.82 |
| MAPE | 0.57% | 2.34% |
| R2 | 0.998 | 0.892 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, K.; Han, R.; Li, Z.; Guo, P. Construction Concrete Price Prediction Based on a Double-Branch Physics-Informed Neural Network. Buildings 2025, 15, 2171. https://doi.org/10.3390/buildings15132171
Shi K, Han R, Li Z, Guo P. Construction Concrete Price Prediction Based on a Double-Branch Physics-Informed Neural Network. Buildings. 2025; 15(13):2171. https://doi.org/10.3390/buildings15132171
Chicago/Turabian StyleShi, Kaier, Ruiqing Han, Zhipeng Li, and Pan Guo. 2025. "Construction Concrete Price Prediction Based on a Double-Branch Physics-Informed Neural Network" Buildings 15, no. 13: 2171. https://doi.org/10.3390/buildings15132171
APA StyleShi, K., Han, R., Li, Z., & Guo, P. (2025). Construction Concrete Price Prediction Based on a Double-Branch Physics-Informed Neural Network. Buildings, 15(13), 2171. https://doi.org/10.3390/buildings15132171






