A Generalized Span–Depth Ratio Model for Minimum Thickness Design of Flat Plate Slabs Incorporating ACI Deflection Criteria

Abstract

This study proposes a unified span–depth ratio model aimed at optimizing the minimum thickness of reinforced concrete flat plate slabs, addressing the limitations of the simplified span-to-depth ratio provisions in ACI 318. The existing code does not fully consider critical parameters such as panel aspect ratio, reinforcement ratio, support conditions, concrete strength, and long-term deflections due to creep and shrinkage. To overcome these shortcomings, a generalized analytical model is developed based on fundamental deflection theory, incorporating both immediate and time-dependent behaviors. The model is validated through numerical simulations applied to interior, edge, and corner slab panels subjected to various geometric configurations, loading scenarios, and reinforcement levels. Results from the parametric study indicate that deflection control improves significantly with higher reinforcement ratios and lower aspect ratios, leading to more efficient slab designs. Comparisons with ACI 318 guidelines reveal that the proposed model provides enhanced accuracy, particularly for irregular slab geometries and stringent deflection limits (e.g., L/480). The findings highlight that conventional code-based thickness limits may underestimate slab depth requirements in many practical scenarios. The study advocates for integrating deflection-based considerations into the preliminary design stage, offering structural engineers a more robust and practical tool to ensure serviceability while optimizing material use.

1. Introduction

Deflection control in different building codes and standards are determined using two approaches; (indirect method), by assuming suitable upper limits on the depth–span ratio which is satisfactory for many cases of spans, load distribution, member size and properties, and (direct method) by calculating the deflection for the actual case and compare the results with the specific limitations that permitted by the codes and standards.

Generally, the deflection is determined when the member is loaded by the normal full-service load to ensure that stresses in the stream fiber in both steel and concrete remain in elastic range, i.e., the un-cracked section properties are used to calculate the immediate deflection [1,2,3,4,5,6,7,8,9,10,11].

Deflection is a function of the load which on the member, span length, cross section property (moment of inertia), material property (modulus of elasticity) and boundary conditions. The elastic deflection can be expressed in the following form:

$${\delta }_{max}={\displaystyle \frac{f(load, span, support condition)}{EI}}$$

(1)

ACI-code [1] provides the minimum depth for one-way slabs and beams, for non-prestressed members, normal concrete weight (γc = 145 pcf or 2320 kg/m³) and steel yielding strength (fy = 60,000 psi or 414 MPa).

Correction factor of (1.65–0.005 γc) ≥ 1.09 is used for light weight concrete with density in the range (90–115 pcf or 1440–1840 kg/m³), and (0.4 + fy/100,000) is used for steel yielding strength other than (60,000 psi).

Table 1. Minimum thickness of one-way slab as per ACI 318-25.

Support Condition	Minimum Thickness
Simply Supported	l/20
One–end continuous	l/24
Both ends continuous	l/28
Cantilever	l/10

shows the minimum thickness of one-way slab.

ACI-code [1] established minimum thickness for two-way slabs designed by the equivalent frame method or the direct design method; simplified criteria are included for slabs without interior beam, i.e., flat slab and flat plates slabs, while more complicated limit equations are applied for slabs with beams between supports on all sides.

The calculated deflection must be less than the specified code limits shown in Table 3.

Table 2. Minimum thickness of slabs without interior beams, ACI-code [1].

fy MPa	Without Drop Panels			With Drop Panels
	Exterior Panels		Interior Panels	Exterior Panels		Interior Panels
	Without Edge Beams	With Edge Beams		Without Edge Beams	With Edge Beams
280	Ln/33	Ln/36	Ln/36	Ln/36	Ln/40	Ln/40
420	Ln/30	Ln/33	Ln/33	Ln/33	Ln/36	Ln/36
520	Ln/28	Ln/31	Ln/31	Ln/31	Ln/34	Ln/34

shows the minimum thicknesses of slabs without interior beams (flat slabs and flat plate slabs with and without edge beams for slabs with and without drop panels); as shown there is no indication to the slab panel aspect ratio, dead and live load subjected on the slab, concrete compressive strength, support rotation and amount of reinforcement, also there is no attention to time (long term deflection). The beams were referenced to establish the theoretical foundation of span–depth ratio development in structural elements.

In this research, the general equation of the minimum thickness (span–depth ratio) is derived to determine minimum thickness of flat plate slab on the basis of controlling the maximum central deflection within the specified maximum permissible deflection given by ACI–code,

Table 3. Maximum permissible calculated deflections.

Member	Condition		Deflection to Be Considered	Deflection Limitation
Flat roofs	Not supporting or attached to nonstructural elements likely to be damaged by large deflections		Immediate deflection due to maximum of Lr, S, and R	L/180
Floors			Immediate deflection due to L	L/360
Roof or floors	Supporting or attached to nonstructural elements	Likely to be damaged by large deflections	That part of the total deflection occurring after attachment of nonstructural elements, which is the sum of the time-dependent deflection due to all sustained loads and the immediate deflection due to any additional live load	L/480
		Not likely to be damaged by large deflections		L/240

. The model’s equation includes the effect of slab panel aspect ratio, amount of steel reinforcement, concrete compressive strength, support rotation, live and dead loads applied on the slab, and effect of long-term deflection.

Lee et al. [12] compared the deflection and minimum thickness that obtained by different codes and standards, they concluded that the CSA and ACI provisions have limited application, and they recommended an equation for calculating the minimum thickness. Read and Thomoson [13] presented an approximate depth–span ratio for the preliminary design specification in terms of (${\displaystyle \frac{M}{b{d}^2}}$) rather than (${\displaystyle \frac{Ms}{bd}}$) to include the effect of steel stress. Shehata et al. [14] presented a theoretical study for the minimum steel ratio that is required for bending shear and torsion for beams with different concrete strengths. Ho et al. [15] developed a simplified method for providing minimum flexural ductility and evaluation of maximum values of tension steel ratio and neutral axis depth corresponding to the proposed minimum curvature ductility factor for various concrete grades and steel yielding strengths. Akmaluddin [16] presented an improvement model of the effective moment of inertia to predict the short-term deflection of reinforced light weight concert beam. The proposed model is verified and compared with the experimental results and in some cases have similar trends to the ACI and SNI provisions. Orvin and Anik [17] determined the minimum thickness of reinforced concrete slabs to resist undesirable vibration, and compare the results with other study.

Zahid and Khan, Ghalla et al. and Elsamak et al. [18,19,20,21] conclude that ACI minimum thickness limits is not satisfactory for vibration. Three-dimensional finite element modeling is carried out to study the natural floor vibration and the results are verified by ANSYS 18.1 model and ETABS modeling. Several parameters such as slab thickness, span length and floor panel aspect ratio are taken into consideration. Islamkhan et al. [22,23] investigated reinforced concrete building analysis using three-dimensional finite element modeling to determine the minimum slab thickness to prevent undesirable vibration. The developed finite element model is applied on post experiments which validated the applicability of the model for further parametric study. Different slab thickness, span length and floor aspect ratio are studied. An empirical equation is suggested which provides minimum slab thickness of a short–span reinforced concrete building. Sarkawt and Bahman and Lee et al. [24,25] examine how aspect ratio, concrete strength grade, and live load affect the long-term deflection of corner flat plate floor panels without edge beams. It highlights the oversight of aspect ratio in five national codes when determining minimum slab thickness and aims to identify a “slab reference span” for calculating deflection. Using finite element analysis with varying parameters according to ACI 318 recommendations, including long span length, aspect ratio, thickness, concrete grade and live load, deflection calculations were performed. Findings reveal that the aspect ratio parameter has the most significant impact on long-term deflection, yet it is disregarded by all five codes. While ACI 318 provisions generally meet L/360 and L/240 deflection limits for typical spans and concrete grades, they often fail to satisfy the L/480 limit.

Elgohary and El Zareef [26] conducted a study to assess the validation of long-term deflection limitations outlined in the ACI 318-25 [1] Code across a broad spectrum of span lengths for two-way flat slabs, both with and without drop panels. The first phase of their investigation involved nonlinear finite element analysis of 63 flat slabs without drop panels and 63 flat slabs with drop panels using the SAFE 2000 commercial software. In the second phase, the researchers proposed adjustments to the minimum slab thickness to ensure compliance with permissible deflection criteria. They recommended minimum thickness limits for flat slabs ranging from Ln/30 to Ln/19.9 for those without drop panels and from Ln/33 to Ln/21.2 for those with drop panels. This research identifies these deficiencies and proposes a generalized model that predicts the required minimum thickness of flat plate slabs while satisfying deflection limits prescribed by the ACI code. The model is developed through theoretical analysis and validated using numerical examples for various slab configurations.

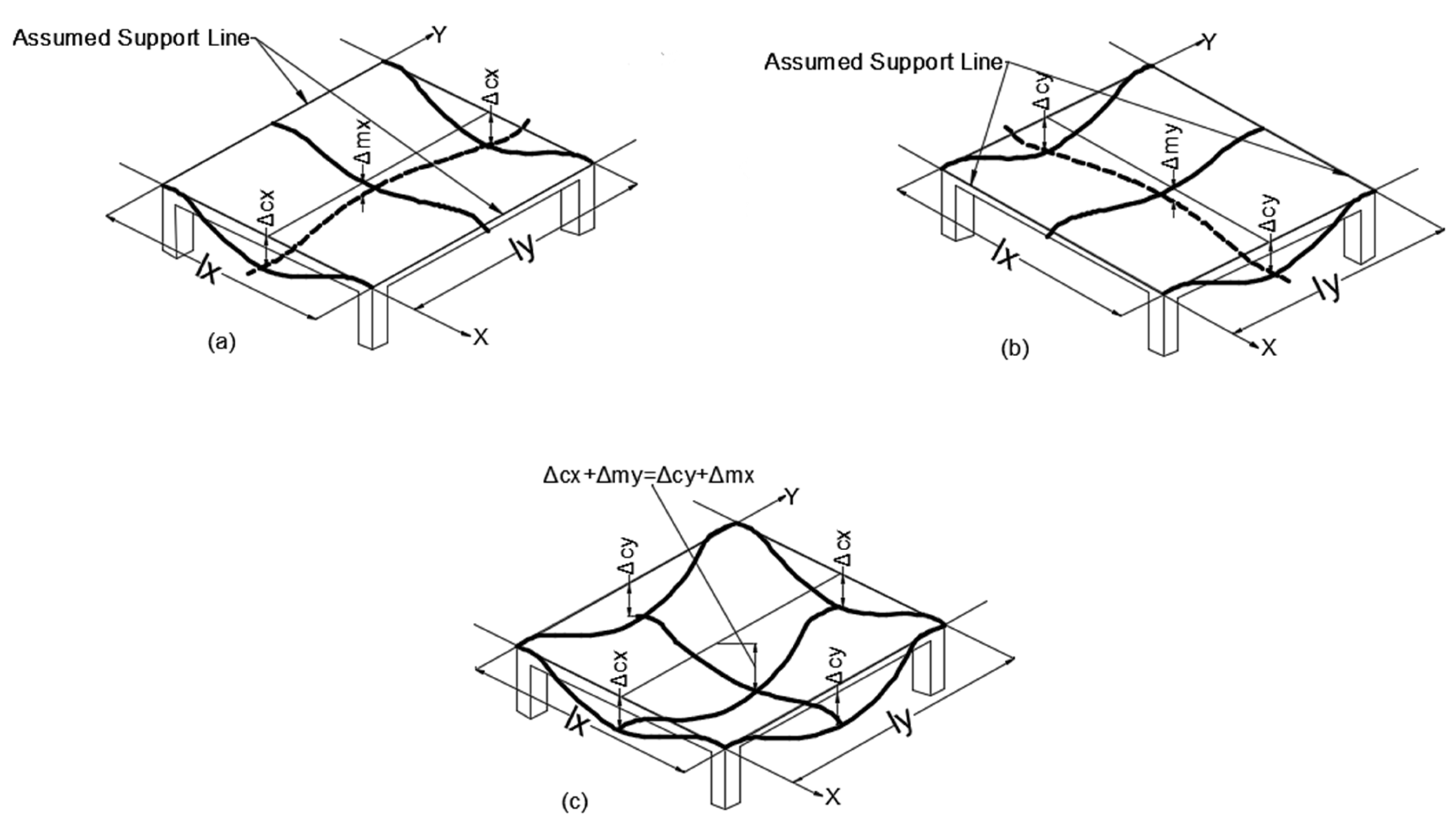
2. Theoretical Background

The deflection of flat plate slabs can be evaluated using either the Direct Design Method or the Equivalent Frame Method. In this approach, the slab panel is subdivided into column strips and middle strips, and the longitudinal and transverse moment distribution coefficients are provided in

Table 4. Distribution factors for static moment Mo based on slab edge conditions and support configurations [1].

	(a)	(b)	(c)	(d)	(e)
	Exterior Edge Unrestrained	Slab with Beams Between All Supports	Slab Without Beams Between Interior Supports		Exterior Edge Fully Restrained
			Without Edge Beam	With Edge Beam
Interior negative moment	0.75	0.70	0.70	0.70	0.65
Positive moment	0.63	0.57	0.52	0.50	0.35
Exterior negative moment	0	0.16	0.26	0.30	0.65

Mo: total factored static moment, N-mm.

and

Table 5. Distribution factors for static moment Mo based on span aspect ratio (L2/L1) and support conditions [1].

		L2/L1
		0.50	1.0	2.0
Interior negative moment
αf1 L2/L1 = 0		75	75	75
αf1 L2/L1 ≥ 1.0		90	75	45
Exterior negative moment
αf1 L2/L1 = 0	βt = 0	100	100	100
	βt ≥ 0	75	75	75
αf1 L2/L1 ≥ 1.0	βt = 0	100	100	100
	βt ≥ 0	90	75	45
Positive moment
αf1 L2/L1 = 0		60	60	60
αf1 L2/L1 ≥ 1.0		90	75	45

α_f1: ratio of flexural stiffness of beam section to flexural stiffness of a width of slab bounded laterally by centerlines of adjacent panels. L₁: length of span in direction that moments are being determined, measured center-to-center of supports. L₂: length of span in direction perpendicular to L₁, measured center-to-center of supports. β_t: ratio of torsional stiffness of edge beam section to flexural stiffness of a width of slab equal to span length of beam, center-to-center of supports. Mo: total factored static moment, N-mm.

.

The deflection calculations consider the deformation of each typical region in one direction at a time, after which the contributions from each direction are added to obtain the total deflection at any point. The total deflection at mid-span deflection of the column strip in one direction and that of the middle strip in the other direction [27,28], as shown in Figure 1 [2].

The following Equations (2)–(32), as mentioned in [2], are used to calculate the deflection analysis:

Δ_max = Δ_cx + Δ_my

(2)

or = Δcy+ Δmx

(3)

whichever is greater. The reference deflection for fully fixed supports can be determined as:

$${\Delta }_f ref.={\displaystyle \frac{W{L}^4}{384E_c{I}_{frame}}}$$

(4)

where

• W: is the load on the slab per unit area;
• I_frame: is the moment of inertia of the full width panel.

The deflection of column and middle strip are determined by multiplying the reference deflection by the ratio of the moment of inertia and ratio of moment distribution.

$$\Delta col. strip={\Delta }_{f}ref.{\phi }_c{\displaystyle \frac{E{I}_{frame}}{E{I}_{col.}}}$$

(5)

$${\Delta }_{f}col. strip=\left({\displaystyle \frac{(W{L_2)L_1}^4}{384E_c{I}_{frame}}}\right){\phi }_c{\displaystyle \frac{E{I}_{frame}}{E{I}_{col.}}}$$

(6)

$${\Delta }_{f}col. strip={\displaystyle \frac{(W{L_2)L_1}^4}{384E_c{I}_{col.}}}{\phi }_c$$

(7)

$$\Delta mid. strip={\Delta }_{f}ref.{\phi }_m{\displaystyle \frac{E{I}_{frame}}{E{I}_{mid.}}}$$

(8)

$${\Delta }_{f}mid. strip=\left({\displaystyle \frac{(W{L_2)L_1}^4}{384E_c{I}_{frame}}}\right){\phi }_m{\displaystyle \frac{E{I}_{frame}}{E{I}_{mid.}}}$$

(9)

$${\Delta }_{f}mid. strip={\displaystyle \frac{(W{L_2)L_1}^4}{384E_c{I}_{mid}}}{\phi }_m$$

(10)

where φ_c and φ_m are the average transverse moment coefficient of column and middle strip, which are shown in Table 5.

Including the rotation of supports, the deflection due to the support rotation can be determined by the moment–area method; the mid-span deflection of the equivalent frame can be determined as the following:

$${\Delta }_{\theta }={\displaystyle \frac{\theta L}{8}}$$

(11)

where

$$\theta ={\displaystyle \frac{M_{net}}{k_{ec}}}$$

θ = support rotation (rad.);

K_ec = Stiffness of equivalent column;

M_net = net moment difference at the support between left and right of column.

For external support,

M_net = 0.16M_o

where

$$M_0={\displaystyle \frac{\left(W{L}_2\right){L_{n1}}^2}{8}}$$

Stiffness of equivalent column is determined using equivalent frame method as following:

$${\displaystyle \frac{1}{K_{ec}}}={\displaystyle \frac{1}{\sum K_c}}+{\displaystyle \frac{1}{\sum K_t}}$$

(12)

where

• K_c = stiffness of the column = (4EI/L);
• K_t = torsional stiffness of the edge beam.

$$K_t=\sum {\displaystyle \frac{9E_{c}C}{L_2{(1-\frac{C_2}{L_2})}^2}}$$

(13)

where

• E_c = modulus of elasticity of the concrete;
• C₂ = column size in direction L₂.

$$\mathrm{C}=\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{s}\mathrm{s} \mathrm{s}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}=\sum (1-0.63{\displaystyle \frac{x}{y}}){\displaystyle \frac{x^{3}y}{3}}$$

(14)

where

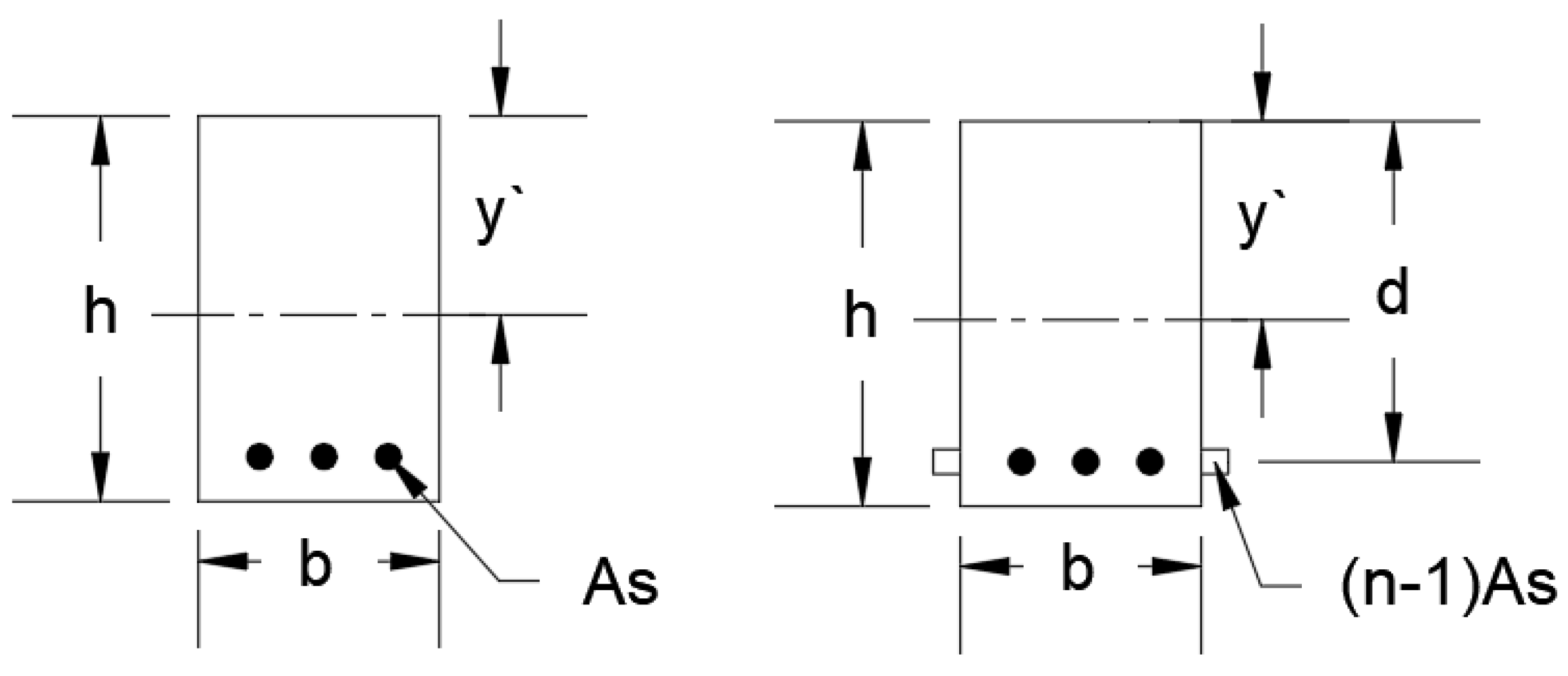
• x = is the smaller dimension of the cross section;
• y = is the larger dimension of the cross section.

The total deflection at mid-span of the column and middle strip is the sum of the deflection due to the load and the rotation of the support at the left and right ends of the span.

$${\Delta }_{col.}={\Delta }_{f}col.+{\Delta }_{\theta }l+{\Delta }_{\theta }r$$

(15)

where (r) refers to right and $l$ refers to left of the support.

The rotation at the interior column, i.e., right end of the support, may be considered negligible, while the rotation at the left exterior column cannot be negligible and must be included; in this case the deflection of the column and middle strip becomes the following:

$${\Delta }_{col.}={\displaystyle \frac{W{L}_2{L_1}^4}{384E{I}_{col.}}}{\phi }_c+{\left({\displaystyle \frac{\theta L}{8}}\right)}_l$$

(16)

$${\Delta }_{mid.}={\displaystyle \frac{W{L}_2{L_1}^4}{384E{I}_{mid.}}}{\phi }_m+{\left({\displaystyle \frac{\theta L}{8}}\right)}_l$$

(17)

To include the effect of reinforcement, a transformed uncracked section is used to determine the depth of neutral axis and moment of inertia of the slab cross section.

For a rectangular cross section with steel reinforcement (As) shown in Figure 2, As = ρbd, Let d = 0.85 h, Neutral axis depth:

y′ = φ_y h

where

$${\phi }_y={\displaystyle \frac{0.5+0.7225 (n-1)\rho }{1+0.85(n-1)\rho }}$$

(18)

$$\mathrm{M}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{a}I={\lambda }_R{\displaystyle \frac{b{h}^3}{12}}$$

(19)

where

λ_R = 1+ 12(φ_y − 0.5)² + 10.2 (n − 1) ρ (0.85 − φ_y)²

(20)

For a flat plate slab panel with dimensions (L₁ and L₂), the width of column strips = L₂/2 and width of middle strip = L₂/2; h = depth of the slab.

The long-term deflection resulting from the combined effects of creep and shrinkage can be estimated by multiplying the immediate (short-term) deflection by a time-dependent factor, as specified in ACI 318-25 (Clause 24.2.4.1.1). This codified approach is widely adopted in design practice due to its simplicity and its consideration of the reinforcement ratio through the use of the following factor:

$${\lambda }_t={\displaystyle \frac{\xi }{1+50{\rho }^{\prime }}}$$

(21)

where

• ξ: is a time dependent coefficient shown in Figure 3,

  $${\rho }^{\prime }={\displaystyle \frac{{As}^{\prime }}{bd}}$$
• As′: is steel reinforcement in compression zone;

For a slab without compression zone reinforcement, $\mathsf{\rho }$′ = 0, thus λ_t = ξ.

For long duration, beyond (5 years), ξ = 2, the long-term coefficient factor is λ_t = 2, which is used with sustained or dead load, while the deflection due to live load is immediate or short-term deflection.

The immediate deflection for column and middle strips due to live and dead loads are determined using Equations (15) and (16), then the total deflection using equation (1 or 2).

$$\mathrm{T}\mathrm{h}\mathrm{e} \mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\text{-}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m} \mathrm{d}\mathrm{e}\mathrm{f}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n} {\Delta }_{max t}=3{\Delta }_{max d.l}+{\Delta }_{max L.L}$$

(22)

Equation (22) assumes linear superposition of short-term and long-term deflections as per ACI 318 guidance. While nonlinear creep effects may influence deflection over time, especially in high-stress or humidity-variable environments, this study adopts the simplified multiplier method (λt = 3) for sustained loads in accordance with standard design practices.

The long-term deflection (Δmax t) is compared with the permissible ACI-Code maximum deflection shown in Table 3 [1,2]. In this study the derivation is based on the maximum limit L/360 and L/480.

Taking deflection of the column strip in x-direction (L₁), and the middle strip in y-direction (L₂):

$${\phi }_y={\displaystyle \frac{0.5+0.7225 (n-1)\rho }{1+0.85(n-1)\rho }}$$

(23)

$$\mathrm{M}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{a} I={\lambda }_R{\displaystyle \frac{b{h}^3}{12}}$$

(24)

where

λ_R = 1+ 12(φ_y − 0.5)² + 10.2 (n − 1) ρ (0.85 − φ_y)²

(25)

$$E_c=4730\sqrt{f{c}^{\prime }}\left(\mathrm{M}\mathrm{P}\mathrm{a}\right)$$

where fc′ is in MPa.

Subsisting Equations (23) and (24) in (25):

$${\displaystyle \frac{W{L}_2{L_1}^4}{384E{I}_{col.}}}{\phi }_{cx}+{\displaystyle \frac{W{L}_1{L_2}^4}{384E{I}_{mid.}}}{\phi }_{my}+{\displaystyle \frac{{\theta }_x{L}_1}{8}}+{\displaystyle \frac{{\theta }_y{L}_2}{8}}={\displaystyle \frac{L_2}{480}}$$

(26)

For column and middle strips of width (L₂/2), the moment of inertia $I={\lambda }_R\left({\displaystyle \frac{L_2}{2}}\right){\displaystyle \frac{h^3}{12}}={\lambda }_R{\displaystyle \frac{L_2{h}^3}{24}}$.

Substituting I_col. and I_mid. into Equation (21), and after some procedures of simplification and re-arrangements, to determine the minimum slab thickness satisfying the deflection criteria, Equation (26) is reformulated by substituting expressions for load-induced and rotational deflections in terms of geometric and material properties. Grouping the terms appropriately and isolating the span-to-depth ratio L1h, a generalized form is obtained, expressed as Equation (27), where the coefficient N is defined by Equation (28). This formulation accounts for concrete properties, load magnitude, moment distribution factors φcx and φmy, as well as support rotation effects. The maximum thickness of the flat plates can be determined as the following:

$$h={\displaystyle \frac{L_1}{N}}$$

(27)

where

$$N={\displaystyle \frac{5.4\beta {{\lambda }_R}^{\frac{1}{3}}{(fc\prime )}^{1/6}{[1-60({\theta }_x\beta +{\theta }_y\left)\right]}^{1/3}}{{\left[{\phi }_t{W}_{d.L}\left({\beta }^4{\phi }_{cx}+\beta {\phi }_{my}\right)\right]}^{1/3}}}$$

(28)

where

• β = aspect ratio of the slab (L₁/L₂);
• WDL = dead load of the slab (N/mm²);
• φt = long term deflection factor = 3 + (W_LL/W_d.L);
• λ_R = Effect of the steel reinforcement;
• θx = rotation of the exterior support in x-direction (rad);
• θy = rotation of the exterior support in x-direction (rad).

When the maximum deflection limit is taken as (L₂/360), Equation (24) changed to the following equation:

$$N={\displaystyle \frac{5.95\beta {{\lambda }_R}^{\frac{1}{3}}{(fc\prime )}^{1/6}{[1-45({\theta }_x\beta +{\theta }_y\left)\right]}^{1/3}}{{\left[{\phi }_t{W}_{d.L}\left({\beta }^4{\phi }_{cx}+\beta {\phi }_{my}\right)\right]}^{1/3}}}$$

(29)

Equation (29) can be written in the following general form:

$$N={\displaystyle \frac{{\alpha }_1\beta {{\lambda }_R}^{\frac{1}{3}}{(fc\prime )}^{1/6}{[1-{\alpha }_2({\theta }_x\beta +{\theta }_y\left)\right]}^{1/3}}{{\left[{\phi }_t{W}_{d.L}\left({\beta }^4{\phi }_{cx}+\beta {\phi }_{my}\right)\right]}^{1/3}}}$$

(30)

$$N={\alpha }_1\beta {{\lambda }_R}^{{\displaystyle \frac{1}{3}}}{\left(fc\prime \right)}^{{\displaystyle \frac{1}{6}}}{\left({\displaystyle \frac{1-{\alpha }_2\left({\theta }_x\beta +{\theta }_y\right)}{{\phi }_t{W}_{d.L}\left({\beta }^4{\phi }_{cx}+\beta {\phi }_{my}\right)}}\right)}^{1/3}$$

(31)

α1 and α2 are coefficients depending on the maximum deflection limit given in Table 3 and determined from the following

Table 6. Value of the coefficient α₁ and α₂ in Equations (30) and (31).

Maximum Deflection Limit	α1	α2
L/180	7.50	22.50
L/360	5.95	45.00
L/480	5.40	60.00
L/240	6.80	30.00

.

Value of the column strip moment coefficient (Φc) and middle strip moment (Φm) are determined for external, internal and edge panel, based on

• − For external panel without edge beam:

αL₂/L₁ = 0 & for all values of L₂/L₁

Case	φc
Interior negative moment −MI	75%
Exterior negative moment −ME	100%
Positive moment +M	60%

Avg. ${\phi }_c={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{75+100}{2}}+60\right]=73.75\mathrm{\%}=0.7375$, ${\phi }_m=1-{\phi }_c=26.25\mathrm{\%}=0.2625$.

• − For an internal panel without an edge beam

αL₂/L₁ = 0

case	φc
−MI	75%
+M	60%

Avg. ${\phi }_c={\displaystyle \frac{75+60}{2}}=67.5\mathrm{\%}=0.675$, ${\phi }_m=1-{\phi }_c=32.5\mathrm{\%}=0.325$.

• − Edge panel without an edge beam

X-direction

case	φc
−MI	75%
−ME	10%
+M	60%

Avg. ${\phi }_{cx}={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{75+60}{2}}+60\right]=73.75\mathrm{\%}=0.7375$, ${\phi }_{mx}=1-{\phi }_c=26.25\mathrm{\%}=0.2625$.

Y-direction

case	φc
−M	75%
+M	60%

Avg. ${\phi }_c={\displaystyle \frac{75+60}{2}}=67.5\mathrm{\%}=0.675$, ${\phi }_{my}=1-{\phi }_c=32.5\mathrm{\%}=0.325$.

For an external panel with an edge beam, following the same procedures of derivation, and taking the parameter (α) as the ratio between moment of inertia of column and middle strip.

$$\alpha ={\displaystyle \frac{I_{cx}}{I_{my}}}$$

The following general equation is obtained to predict the span thickness ratio of an external panel flat slab with edge beams.

$$N={\displaystyle \frac{{\mathsf{\alpha }}_1\beta {{\lambda }_R}^{\frac{1}{3}}{(fc\prime )}^{1/6}{{(2\mathsf{\beta }-1)}^{1/3}[1-{\mathsf{\alpha }}_2({\theta }_x\beta +{\theta }_y\left)\right]}^{1/3}}{{\left[{\lambda }_R\right(3+\frac{W_{LL}}{W_{dL}}\left)\left(\frac{{\beta }^4{\phi }_{cx}}{\alpha }+\beta {\phi }_{my}\right)\right]}^{1/3}}}$$

(32)

α₁ and α₂ are coefficients depend on the ACI maximum deflection limit as shown in the

Table 7. Value of the coefficient α₁ and α₂ in Equation (27).

Maximum Deflection Limit	α1	α2
L/180	5.06	22.50
L/360	4.00	45.00
L/480	3.65	60.00
L/240	4.60	30.00

Table A1. Minimum span/thickness ratio (N) for external panel slab and maximum deflection limit (Ln/480), N = L/h.

WDL (N/mm) =	0.01
WLL (N/mm) =	0.02
β = L1/L2	1
fc′ (Mpa) =	28
Ψc =	0.7375
Ψm =	0.2625
β = L1/L2	1		θ = 0	θ = 0.0005	θ = 0.001	θ = 0.0015	θ = 0.002
θ =			0	0.0005	0.001	0.0015	0.002
ρ	ρ/ρb	λR	N	N	N	N	N
0	0	1	25.5425	25.0211	24.4770	23.9075	23.3096
0.5ρb	0.5	1.11426	26.4805	25.9399	25.3758	24.7855	24.1656
ρt	0.63	1.1426	26.7031	26.1580	25.5891	24.9938	24.3687
ρmax	0.72	1.1617	26.8511	26.3029	25.7309	25.1323	24.5038
ρb	1	1.212	27.2331	26.6772	26.0971	25.4899	24.8524
β = L1/L2	1.5
ρ	ρ/ρb	λR	N	N	N	N	N
0	0	1	23.8853	23.2726	22.6258	21.9398	21.2079
0.5ρb	0.5	1.11426	24.7624	24.1272	23.4567	22.7454	21.9867
ρt	0.63	1.1426	24.9706	24.3301	23.6539	22.9366	22.1715
ρmax	0.72	1.1617	25.1090	24.4649	23.7849	23.0637	22.2944
ρb	1	1.212	25.4663	24.8130	24.1234	23.3919	22.6116
β = L1/L2	2
ρ	ρ/ρb	λR	N	N	N	N	N
0	0	1	22.1156	21.4311	20.6999	19.9131	19.0586
0.5ρb	0.5	1.11426	22.9277	22.2181	21.4601	20.6443	19.7585
ρt	0.63	1.1426	23.1204	22.4049	21.6405	20.8179	19.9246
ρmax	0.72	1.1617	23.2485	22.5291	21.7604	20.9333	20.0350
ρb	1	1.212	23.5794	22.8496	22.0700	21.2311	20.3201

shows the results of (N = L_n/h_f) obtained from Equation (32) for concrete compressive strength (fc′ = 28 MPa), steel yielding strength (fy = 420 MPa), for slab aspect, α = 3, ratio (β = 1.0, 1.5 and 2.0) and different reinforcement ratio (ρ/ρb).

3. Validation and Results

Equation (31) is applied for exterior, interior and edge flat slab panels for different values of slab aspect ratio (β), support rotation (θ) and different reinforcement ration (ρ/ρb).

• Table A1,

  Table A2. Minimum span/thickness ratio (N) for Internal panel slab and maximum deflection limit (L_n/480), N = L/h.

  WDL (N/mm) =	0.01
  WLL (N/mm) =	0.02
  β = L1/L2	1
  fc′ (Mpa) =	28
  Ψc =	0.675
  Ψm =	0.325
  			θ = 0	θ = 0.0005	θ = 0.001	θ = 0.0015	θ = 0.002
  θ =			0	0.0005	0.001	0.0015	0.002
  ρ	ρ/ρb	λR	N	N	N	N	N
  0	0	1	25.5425	25.0211	24.4770	23.9075	23.3096
  0.5ρb	0.5	1.11426	26.4805	25.9399	25.3758	24.7855	24.1656
  ρt	0.63	1.1426	26.7031	26.1580	25.5891	24.9938	24.3687
  ρmax	0.72	1.1617	26.8511	26.3029	25.7309	25.1323	24.5038
  ρb	1	1.212	27.2331	26.6772	26.0971	25.4899	24.8524
  β = L1/L2	1.5
  ρ	ρ/ρb	λR	N	N	N	N	N
  0	0	1	24.3310	23.7068	23.0479	22.3491	21.6036
  0.5ρb	0.5	1.11426	25.2244	24.5774	23.8943	23.1698	22.3969
  ρt	0.63	1.1426	25.4365	24.7840	24.0952	23.3646	22.5852
  ρmax	0.72	1.1617	25.5775	24.9213	24.2287	23.4940	22.7103
  ρb	1	1.212	25.9414	25.2759	24.5735	23.8284	23.0335
  β = L1/L2	2
  ρ	ρ/ρb	λR	N	N	N	N	N
  0	0	1	22.6651	21.9637	21.2143	20.4079	19.5322
  0.5ρb	0.5	1.11426	23.4974	22.7702	21.9934	21.1574	20.2495
  ρt	0.63	1.1426	23.6950	22.9617	22.1783	21.3352	20.4197
  ρmax	0.72	1.1617	23.8263	23.0889	22.3012	21.4535	20.5329
  ρb	1	1.212	24.1653	23.4174	22.6185	21.7587	20.8250

  and

  Table A3. Minimum span/thickness ratio (N) for edge panel slab and maximum deflection limit (Ln/480), N = L/h.

  WDL (N/mm) =	0.01
  WLL (N/mm) =	0.02
  β = L1/L2	1
  fc′ (Mpa) =	28
  Ψc =	0.7375
  Ψm =	0.325
  			θ = 0	θ = 0.0005	θ = 0.001	θ = 0.0015	θ = 0.002
  θ =			0	0.0005	0.001	0.0015	0.002
  ρ	ρ/ρb	λR	N	N	N	N	N
  0	0	1	25.0315	24.5205	23.9873	23.4293	22.8433
  0.5ρb	0.5	1.11426	25.9507	25.4210	24.8682	24.2896	23.6821
  ρt	0.63	1.1426	26.1689	25.6347	25.0772	24.4938	23.8812
  ρmax	0.72	1.1617	26.3139	25.7767	25.2162	24.6295	24.0135
  ρb	1	1.212	26.6883	26.1435	25.5750	24.9800	24.3552
  β = L1/L2	1.5
  ρ	ρ/ρb	λR	N	N	N	N	N
  0	0	1	23.7072	23.0990	22.4570	21.7761	21.0497
  0.5ρb	0.5	1.11426	24.5777	23.9473	23.2817	22.5758	21.8227
  ρt	0.63	1.1426	24.7844	24.1486	23.4774	22.7656	22.0061
  ρmax	0.72	1.1617	24.9217	24.2824	23.6075	22.8917	22.1281
  ρb	1	1.212	25.2763	24.6279	23.9435	23.2174	22.4429
  β = L1/L2	2
  ρ	ρ/ρb	λR	N	N	N	N	N
  0	0	1	22.0413	21.3592	20.6304	19.8462	18.9946
  0.5ρb	0.5	1.11426	22.8507	22.1435	21.3880	20.5750	19.6921
  ρt	0.63	1.1426	23.0428	22.3297	21.5678	20.7480	19.8577
  ρmax	0.72	1.1617	23.1705	22.4534	21.6873	20.8630	19.9677
  ρb	1	1.212	23.5002	22.7729	21.9959	21.1598	20.2518

  show the results of the slab thickness ratio (N = L/h) for exterior, interior and edge slab panels, respectively, for concrete compressive strength (fc′ = 28 MPa) and steel reinforcement yielding strength (fy = 420 MPa).
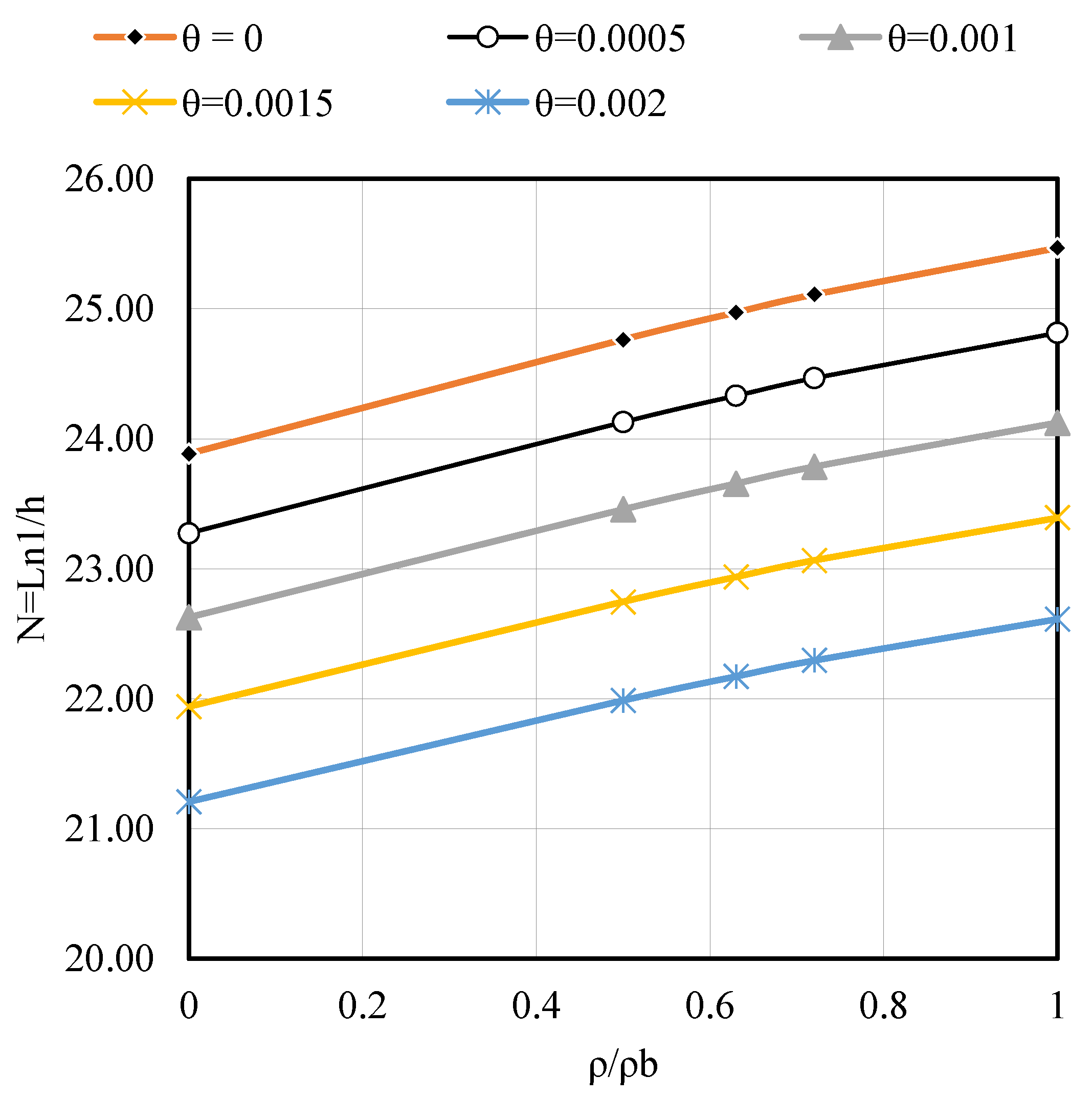
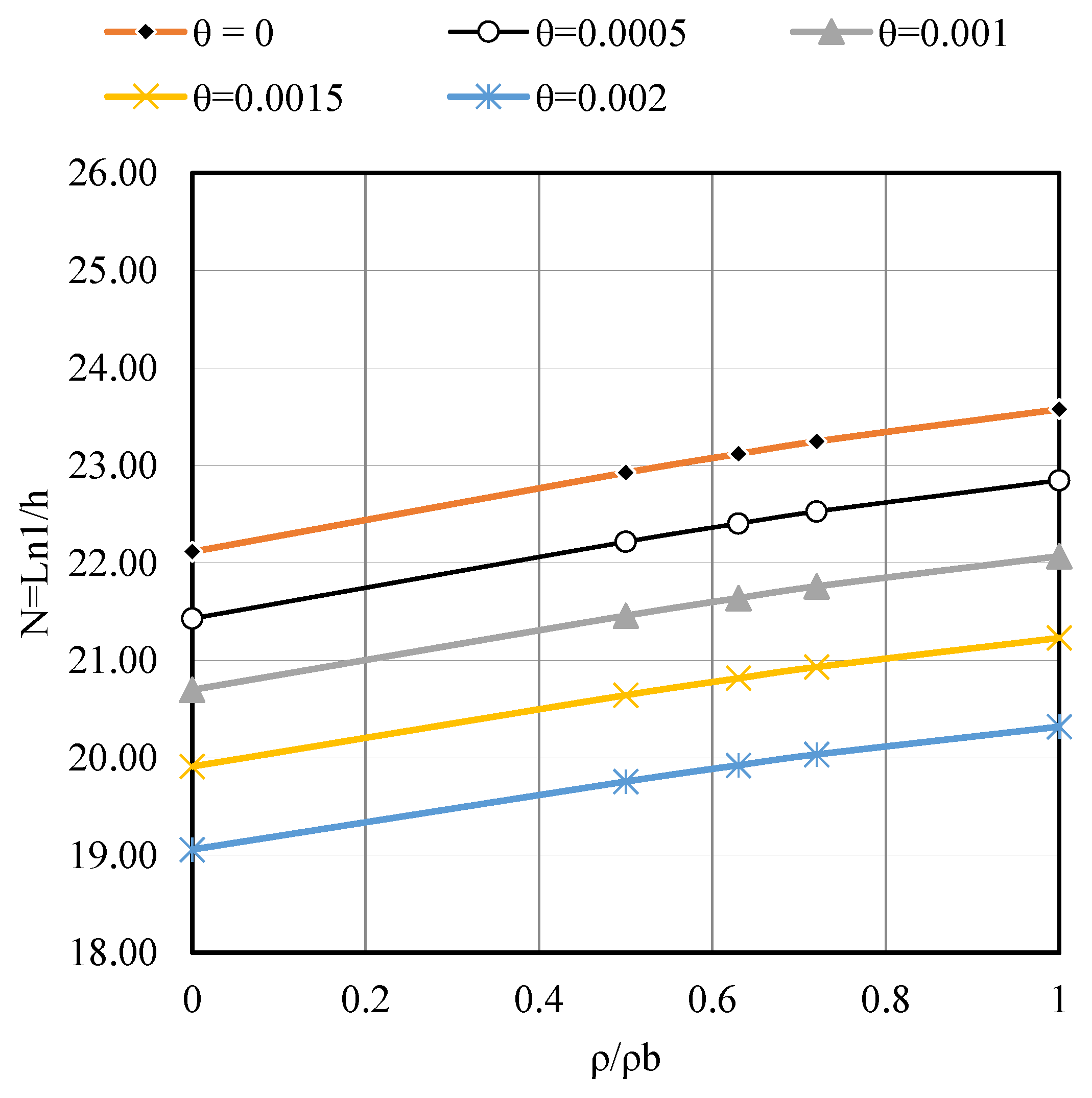
• Figure A3, Figure A4 and Figure A5 clearly illustrate the impact of the reinforcement ratio on the required span–depth ratio (N = L/h) for external slab panels with different aspect ratios β = 1.0, 1.5, and 2.0). As reinforcement increases from β = 0 to 1.0, the required slab thickness consistently decreases, demonstrating the effectiveness of higher steel content in reducing deflection. Notably, for B = 2.0, the effect is more pronounced, indicating greater sensitivity of slender slabs to reinforcement changes.
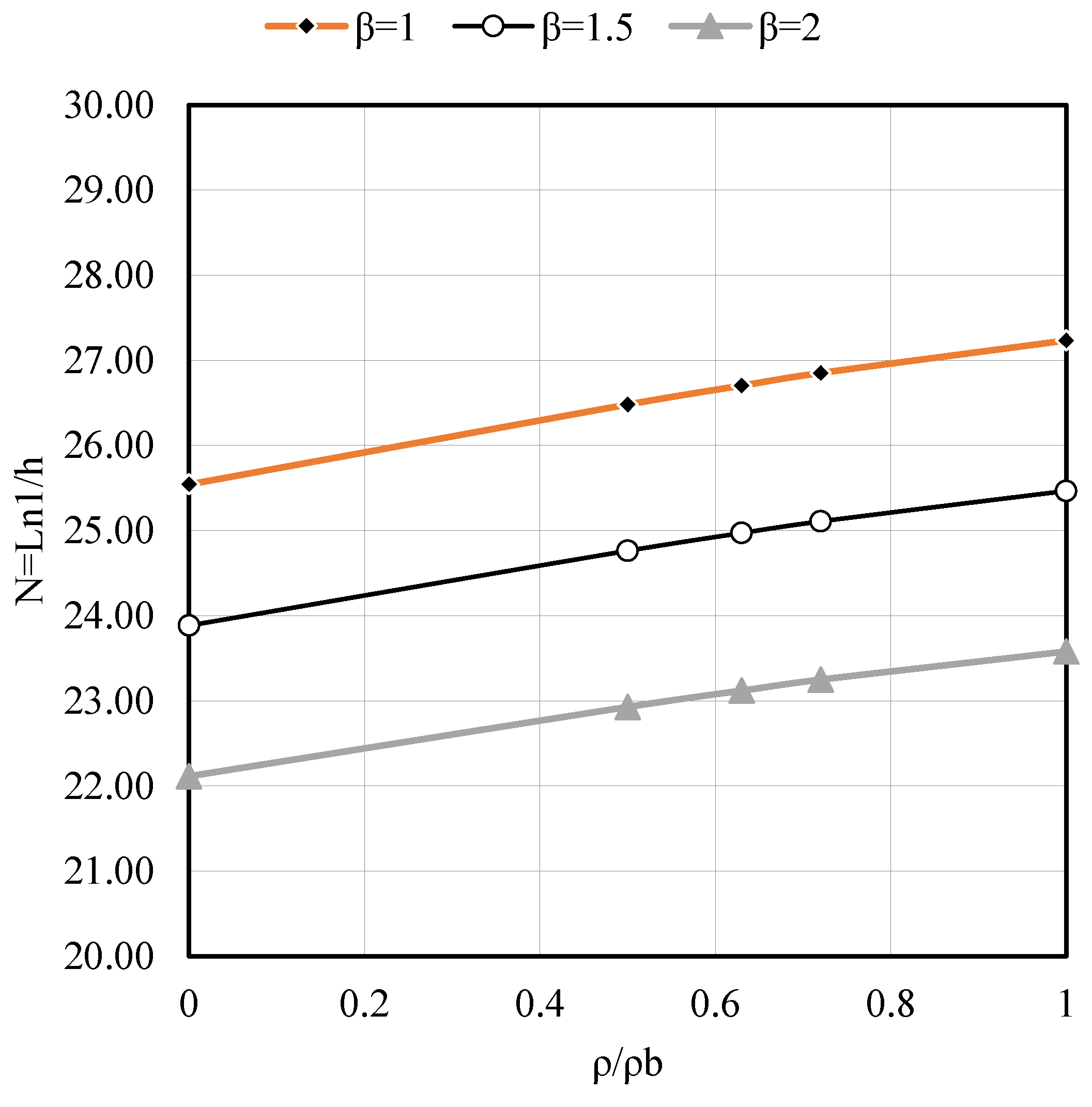
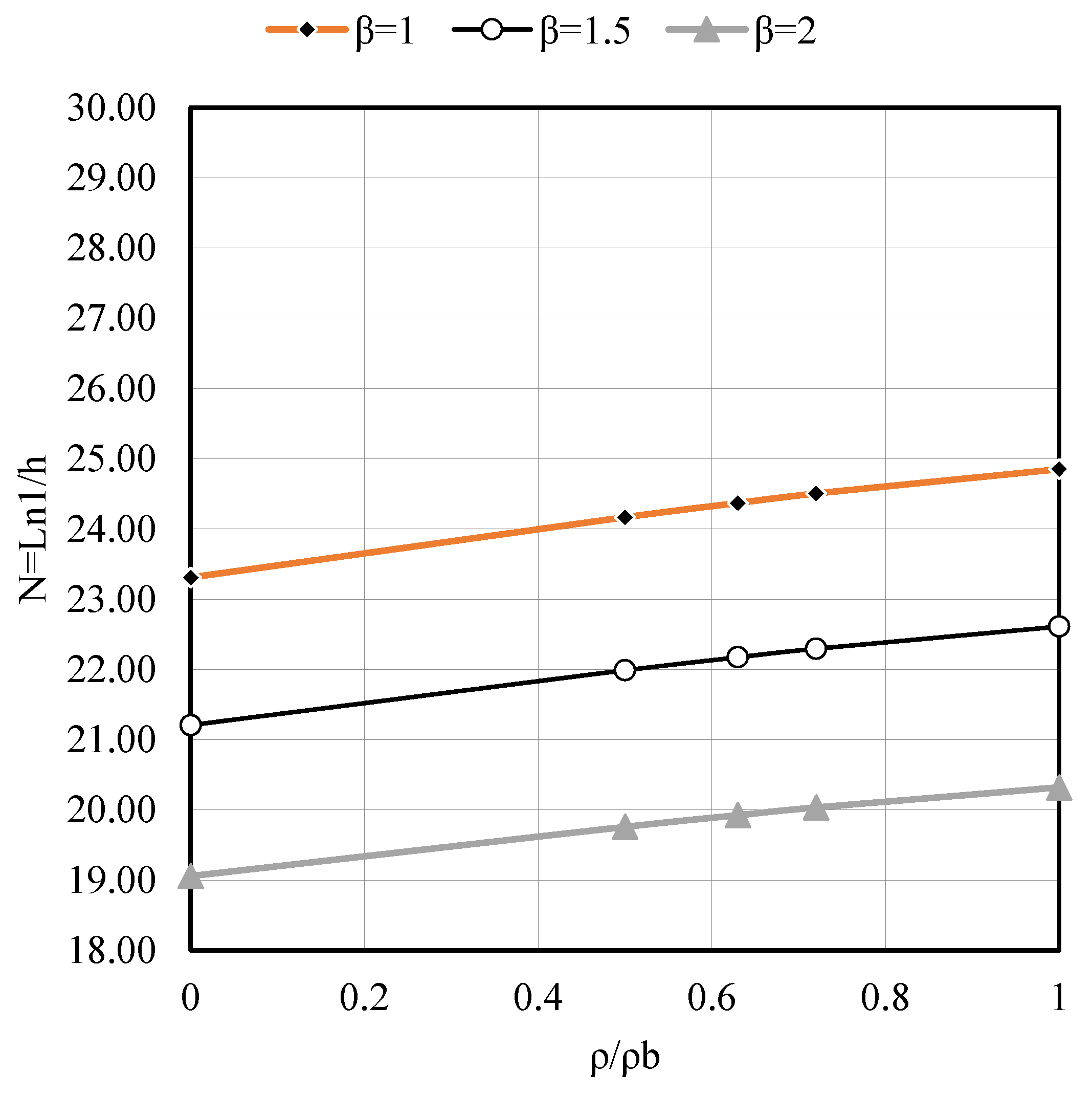
• Figure A6, Figure A7 and Figure A8 highlight that the span–depth ratio decreased with increasing the aspect ratio of the slab (β), i.e., greater thickness is required when the aspect ratio (β) increased from 1 to 2, or in other words, a rectangular slab with (β = 2) required greater thickness than a square slab (β = 1.0); the same conclusion is obtained at support rotation (θ = 0, 0.001 and 0.002).
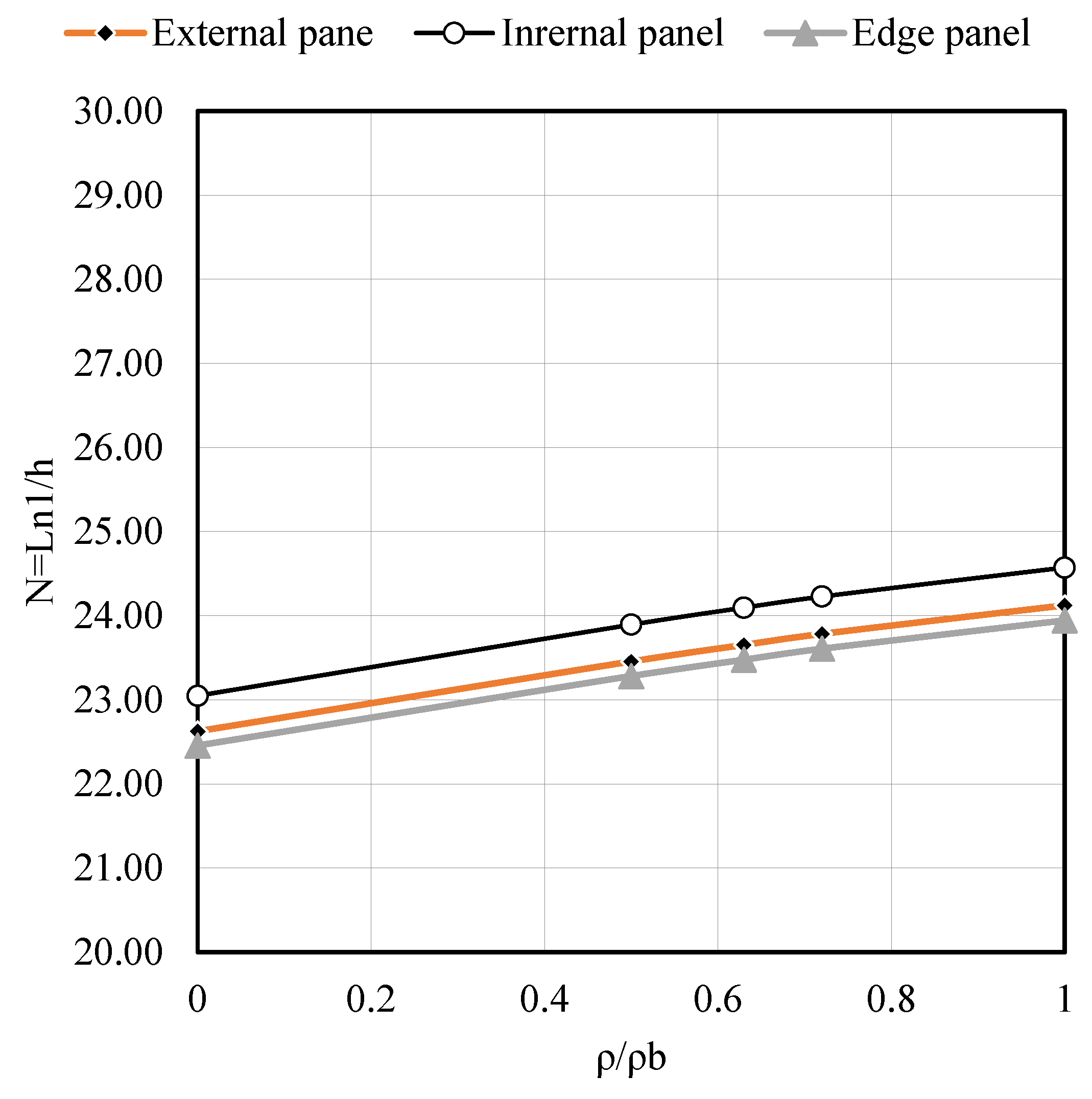
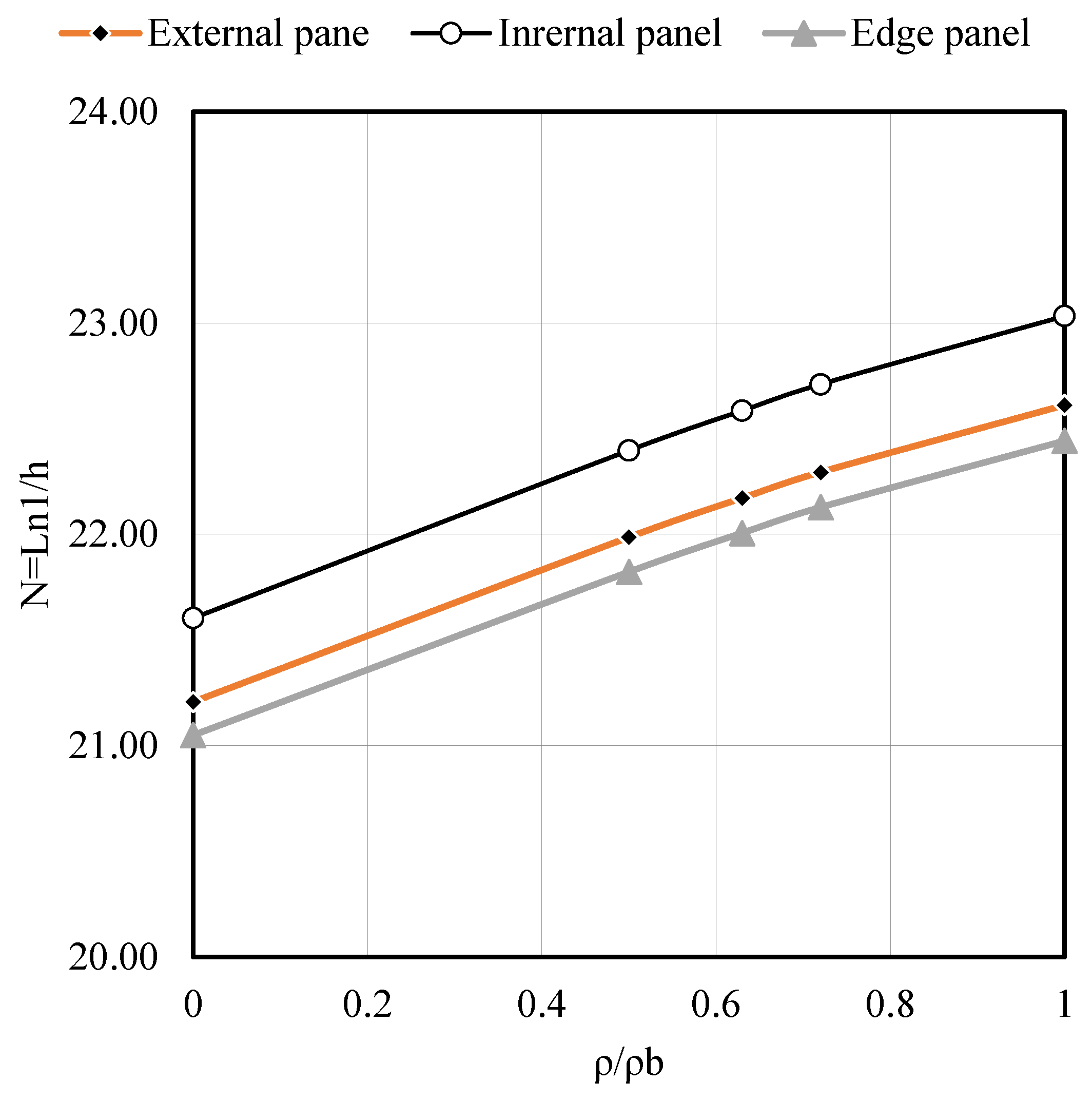
• Figure A9 and Figure A10 show that the span–depth ratio (N) in an interior slab panel is greater than exterior (corner) and edge panels, i.e., exterior (corner) and edge panels required greater thickness than an interior panel, as expected. This behavior is true for any value of the slab aspect ratio (β) and support rotation (θ).

4. Numerical Examples

The following numerical examples are solved to verify and check the result of the span/depth ratio (N) equation

4.1. Example 1

For a corner panel with central dimensions (L₁ = 9.0 m (x-direction) and L₂ = 6.0 m (y-direction) subjected to dead load of (10 kN/m²) and live load of (20 kN/m²), the slab is reinforced with steel reinforcement ratio (ρ/ρb = 0.5). Concrete compressive strength (fc′ = 28 MPa and steel yield strength fy = 420 MPa), find the minimum thickness required to control the maximum central deflection within the maximum deflection limit (L_n/480), column dimensions (500 × 500) mm.

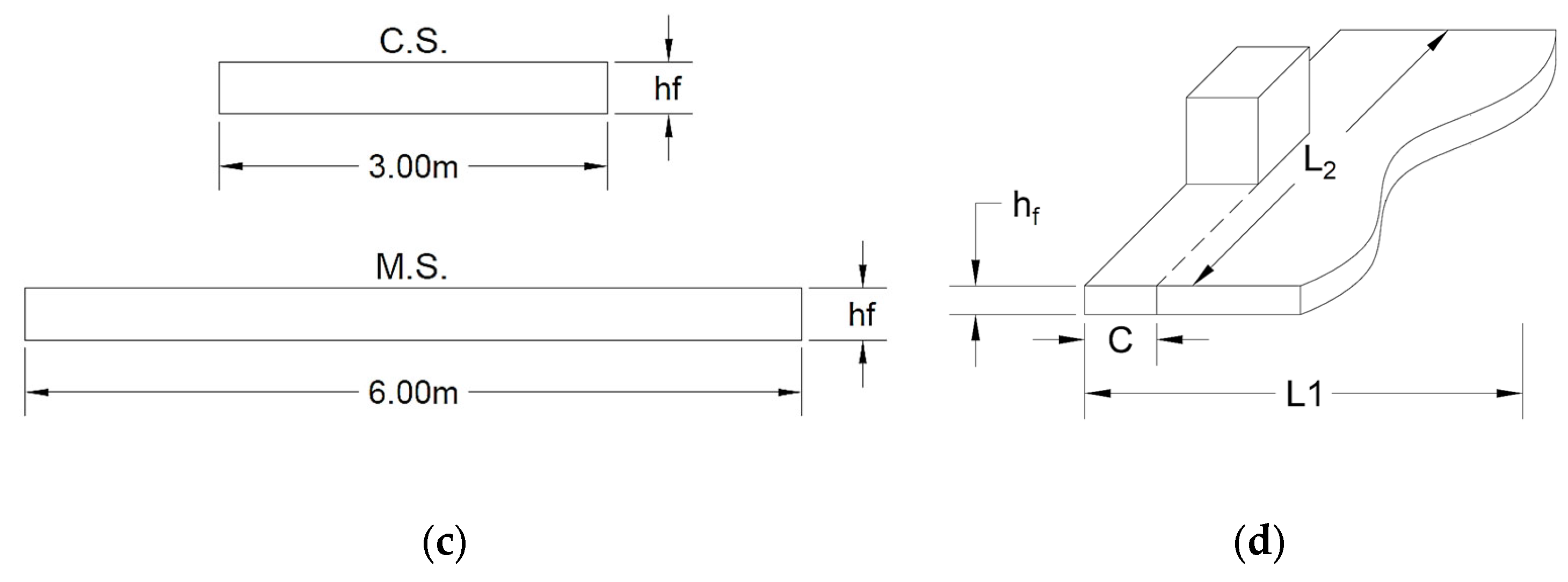
• Solution:

The minimum thickness of flat slabs given in ACI-Code [1] are shown in Table 4. As shown the limits are (L_n/30) for an exterior panel without edge beams and (Ln/33) for interior panels for steel yield strength (fy = 420 MPa); there is no indication to the aspect ratio of the panel, rotation of supports and the steel reinforcement ratio—that is the reason for this study. The general equation of the span–depth ratio (N) is derived on the bases to control the maximum deflection within the maximum ACI-Code deflection limits given in Table 3.

The span–depth ratio (N) determined in Table 4, Table 5 and Table 6 are less than ACI code value (300 and 33); this means that ACI–minimum thickness is not adequate for maximum deflection, and a greater thickness of slab is required to control the deflection within the maximum ACI-Code limit. In this example, the effect of torsional stiffness from adjacent slab panels was not included, assuming a free-edge condition. This conservative assumption is representative of edge and corner slab behavior without adjacent continuity. In practice, torsional contributions from surrounding slabs or beams could further reduce deflection, especially when edge beams or orthogonal slab spans provide rotational restraint. The detailed layout of the corner slab panel is presented in Figure 4.

fc′ = 28 MPa fy = 420 MPa β = 9/6 = 1.5 ρ/ρb = 0.5 Wd.l = 10 kN/m2 = 0.01 N/mm2 WL.L = 20 kN/m2 = 0.02 N/mm2 $E_c=4700\sqrt{28}=\mathrm{25,028.8} \mathrm{M}\mathrm{P}\mathrm{a}$ Assume θx = θy = 0.002 This value reflects an upper-bound estimate based on typical flat slab behavior without edge beams, as observed in validated analytical studies [24,25], and ensures conservative thickness design with respect to ACI deflection limits. From Table A1; hmin = L1/21.9867 = 8500/21.9867 = 386.60 mm ≈ 400 mm - Y-direction: Figure 4b $I_{cx}=I_{mx}={\displaystyle \frac{3000{\left(400\right)}^3}{12}}$ =1.6 × 1010 mm4 - X-direction: Figure 4c $I_{cy}={\displaystyle \frac{3000{\left(400\right)}^3}{12}}$ =1.6 × 1010 mm4 $I_{my}={\displaystyle \frac{6000{\left(400\right)}^3}{12}}$ =3.2 × 1010 mm4 $E_c=4730\sqrt{28}$ = 25,028.8 MPa ${\Delta }_{cx}={\displaystyle \frac{0.01\times 6000\times {8500}^4}{384\times \mathrm{25,028.8}\times 1.6\times {10}^{10}}}=2.037 \mathrm{m}\mathrm{m}$ ${\Delta }_{cy}={\displaystyle \frac{0.01\times 9000\times {5500}^4}{384\times \mathrm{25,028.8}\times 3.2\times {10}^{10}}}=0.268 \mathrm{m}\mathrm{m}$ For a symmetric external panel; φc = 0.7375; ${\Delta }_{cx}=0.3775\left(2.037\right)=1.502 \mathrm{m}\mathrm{m}$ φm = 0.2625; ${\Delta }_{cy}=0.2625\left(2.68\right)=0.070 \mathrm{m}\mathrm{m}$ Y-direction           ${\Delta }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\Delta }_{cx}+{\Delta }_{\mathrm{m}\mathrm{y}}=1.572 \mathrm{m}\mathrm{m}$ For a symmetric external panel; φc = 0.7375; ${\Delta }_{cy}=0.536\left(0.7375\right)=0.395 \mathrm{m}\mathrm{m}$ φm = 0.2625; ${\Delta }_{mx}=2.0367\left(0.2625\right)=0.535 \mathrm{m}\mathrm{m}$ ${\Delta }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\Delta }_{cy}+{\Delta }_{\mathrm{m}\mathrm{x}}=0.93 \mathrm{m}\mathrm{m}$ Thuds: Δmax = 1.572 mm Using $\theta ={\displaystyle \frac{M_{net}}{K_{ec}}}$ X-direction: For column (500 × 500) mm & height = 4.0 m Ic = 500 × 5004/12 = 5.2083 × 109 mm4 Kc = 4EI/L = 4 × (5.2083 × 109) (25,028.8)/4000 = 1.3036 × 1011 mm4 C = (1 − 0.63(400/500)) 4003 × 500/3 = 5.29 × 109 mm4 ${\mathrm{K}}_{\mathrm{t}}=\sum {\displaystyle \frac{9E_{c}C}{L_2{(1-\frac{C_2}{L_2})}^2}}$ $K_t=\sum {\displaystyle \frac{9\left(\mathrm{25,028.8}\right)(5.29\times {10}^9)}{6000{(1-\frac{500}{6000})}^2}}$ = 2.579 × 1011 N.mm ${\displaystyle \frac{1}{K_{ec}}}={\displaystyle \frac{1}{\sum K_c}}+{\displaystyle \frac{1}{\sum K_t}}={\displaystyle \frac{1}{2(2.579\times {10}^{11})}}+{\displaystyle \frac{1}{2(1.3036\times {10}^{11})}}$ $K_{ec}=1.73176\times {10}^{11} \mathrm{N}.\mathrm{m}\mathrm{m}$ $\mathsf{\theta }={\displaystyle \frac{M_{net}}{K_{ec}}}$ $M_{net}$ = 0.16 Mo $=0.16\left[{\displaystyle \frac{0.01\times 6000\times {8500}^2}{8}}\right]=8.67\times {10}^7 \mathrm{N}.\mathrm{m}\mathrm{m}$ $\mathsf{\theta }={\displaystyle \frac{8.67\times {10}^7}{1.73176\times {10}^{11}}}=0.0005 \mathrm{r}\mathrm{a}\mathrm{d}.$ ${\displaystyle \frac{\theta L}{8}}={\displaystyle \frac{0.0005\left(8500\right)}{8}}$ = 0.532 mm - In y-direction $K_t=\sum {\displaystyle \frac{9\left(\mathrm{25,028.8}\right)(5.29\times {10}^9)}{9000{(1-\frac{500}{9000})}^2}}$ =1.5717 × 1011 N.mm ${\displaystyle \frac{1}{K_{ec}}}={\displaystyle \frac{1}{2(1.5717\times {10}^{11})}}+{\displaystyle \frac{1}{2(1.3036\times {10}^{11})}}$ $K_{ec}=1.425\times {10}^{11} \mathrm{N}.\mathrm{m}\mathrm{m}$ $M_{net}$ = 0.16Mo $=0.16\left[{\displaystyle \frac{0.01\times 9000\times {5500}^2}{8}}\right]=5.445\times {10}^7 \mathrm{N}.\mathrm{m}\mathrm{m}$ ${\displaystyle \frac{\theta L}{8}}={\displaystyle \frac{0.000385\left(5500\right)}{8}}$ = 0.2626 mm ${\Delta }_{max}=1.572+0.532+0.2626=2.3666 \mathrm{m}\mathrm{m}$ Short term deflection Or     = 0.93 + 0.532 + 0.2626 = 1.7246 mm Short term deflection ${\Delta }_{max long}={\Delta }_{dl}{\lambda }_{dl}+{\Delta }_{dl}({\displaystyle \frac{W_{LL}}{W_{dL}}}$)${\lambda }_{LL}$ ${\lambda }_{dl}$ = 3.0, ${\lambda }_{LL}=1.0$ For ${\displaystyle \frac{W_{LL}}{W_{dL}}}=2$; ${\Delta }_{max long}={5\Delta }_{dl}$           ${\Delta }_{max long}=5\left(2.3666\right)=11.833 \mathrm{m}\mathrm{m}$ Or     = 5(1.7246) = 8.623 mm [Ln2/480 = 5500/480 = 11.458 mm] 11.833 ≈ 11.458 o.k.

To verify the results of the equation slabs with edge beams, the previous example is solved again with an external edge beam.

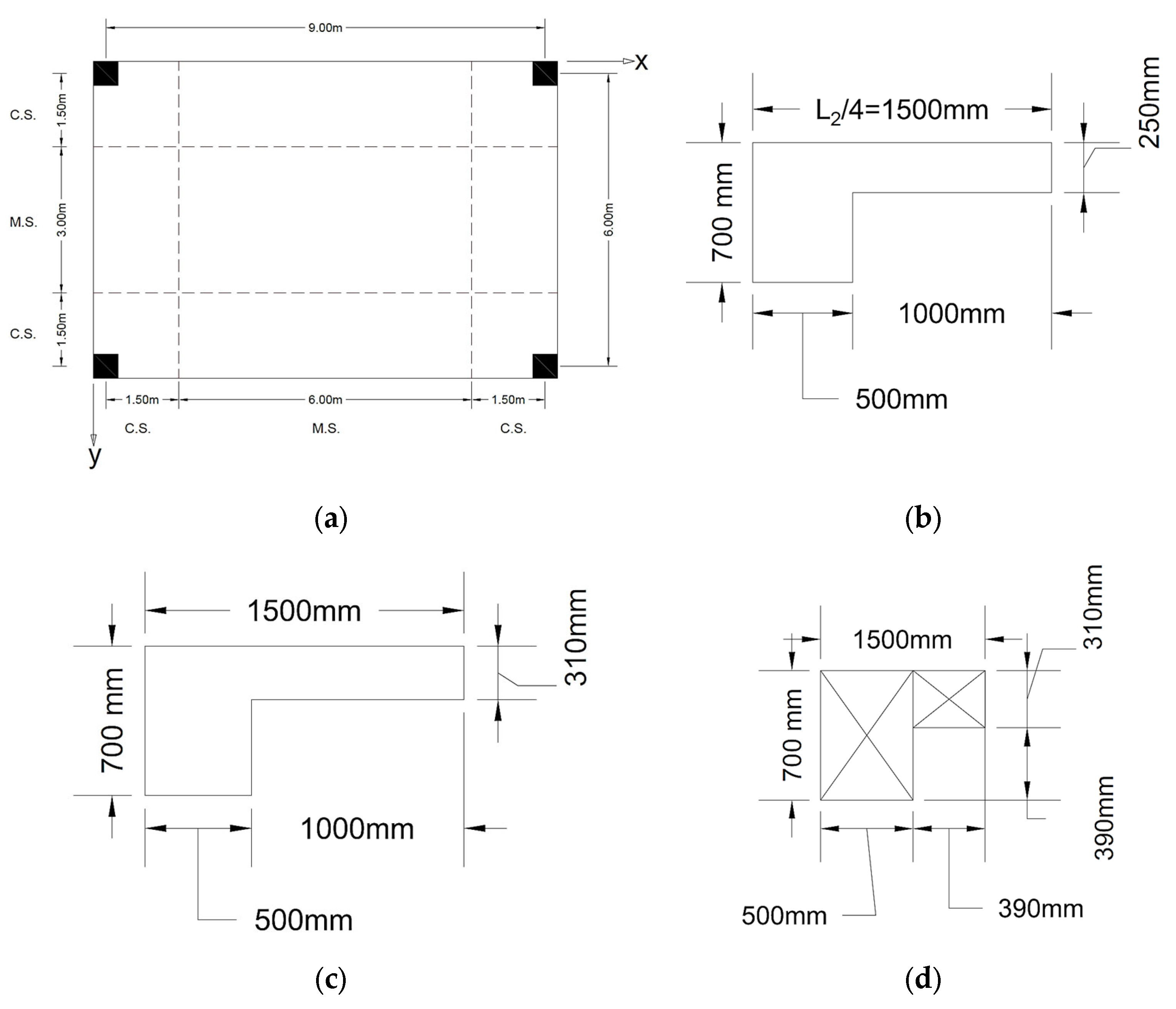
4.2. Example 2

For an external (corner) panel, as in the previous example 1, the edge beam dimensions (500 × 700) mm, slab dimension (h_f = 250 mm) was tried for calculation of (α), for the column strip shown in the Figure 5.

• y′ = 256.25 mm
• Icx = 2.303 × 1010 mm⁴

For the middle strips in y-direction (width = 6.0 m), the moment of inertia Imy = 7.8125 × 109 mm4 $\mathsf{\alpha }={\displaystyle \frac{I_{cx}}{I_{my}}}$ = 2.944 say 3.0 For the slab with reinforcement ρ/ρb = 0.5 and taking θx = θy = 0.0005 for 1st estimation of the span–depth ratio. φy = 0.52718 and λR = 1.11415       $N={\displaystyle \frac{3.65\left(1.5\right){\left(1.11415\right)}^{1/3}{\left(28\right)}^{1/6}{{(2\times 1.5-1)}^{1/3}[1-60(0.0005)+(1.5+1\left)\right]}^{1/3}}{{\left[0.01\right(3+\frac{20}{10}\left)\left(\frac{{1.5}^4}{3}0.7375+1.5\ast 0.2625\right)\right]}^{1/3}}}$ N = 27.957 ≈ 28 hf = Ln/28 = 8500/28 = 303.57 mm ~310 mm Take hf = 310 mm Checking the maximum deflection $E_c=4730\sqrt{28}$= 25,028.8 MPa x-direction: for column strip (L2/4 = 1.5 m) and with edge beam (500 × 700 mm) y′ = 256.25 mm Icx = 2.303 × 1010 mm4 For middle strip width (6.0 m) Imy = 1.49 × 1010 mm4 ${\Delta }_{\mathrm{c}\mathrm{x}}={\displaystyle \frac{\mathrm{W}{\mathrm{L}}^4}{384EI}}=\left[{\displaystyle \frac{0.01\times 6000\times {8500}^4}{384\times \mathrm{25,028.8}\times 2.303\times {10}^{10}}}\right]0.7375=1.044 \mathrm{m}\mathrm{m}$ ${\Delta }_{\mathrm{m}\mathrm{y}}=\left[{\displaystyle \frac{0.01\times 9000\times {5500}^4}{384\times \mathrm{25,028.8}\times 1.49\times {10}^{10}}}\right]0.2625=0.151 \mathrm{m}\mathrm{m}$ ${\Delta }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{x}}=1.195 \mathrm{m}\mathrm{m}$ Y-direction: For same edge beams & column strip width, Icy = 2.303$\times$1010 mm4. ${\Delta }_{\mathrm{c}\mathrm{x}}=\left[{\displaystyle \frac{0.01\times 9000\times {5500}^4}{384\times \mathrm{25,028.8}\times 2.303\times {10}^{10}}}\right]0.7375=0.274 \mathrm{m}\mathrm{m}$ ${\Delta }_{\mathrm{m}\mathrm{x}}=\left[{\displaystyle \frac{0.01\times 6000\times {8500}^4}{384\times \mathrm{25,028.8}\times 7.448\times {10}^9}}\right]0.2625=1.148 \mathrm{m}\mathrm{m}$ ${\Delta }_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{y}}=1.422 \mathrm{m}\mathrm{m}$ Calculation of the end rotations X-direction For the edge beam, the section is divided in a manner to maximize the torsional constant (C), as the following C = (1 − 0.63(x/y))x3y/3 C1 = (1 − 0.63(500/700))5003(700)/3 = 1.604 × 109 mm4 C2 = (1 − 0.63(310/390))3103(390)/3 = 1.933 × 109 mm4 C = C1+ C2 = 1.797 × 1010 mm4 Or $K_t=\sum {\displaystyle \frac{9\left(\mathrm{25,028.8}\right)(1.797\times {10}^{10})}{6000{(1-\frac{500}{6000})}^2}}$ =8.759 × 1011 N.mm ${\displaystyle \frac{1}{K_{ec}}}={\displaystyle \frac{1}{\sum K_c}}+{\displaystyle \frac{1}{\sum K_t}}$ Taking column size (500 × 500) mm and height (4.0 m) Ic =5.208 × 109 mm4, Kc = 4EI/L = 1.3036 × 1011 mm4 ${\displaystyle \frac{1}{K_{ec}}}={\displaystyle \frac{1}{\sum K_c}}+{\displaystyle \frac{1}{\sum K_t}}={\displaystyle \frac{1}{2(8.759\times {10}^{11})}}+{\displaystyle \frac{1}{2(1.3036\times {10}^{11})}}$ $K_{ec}=2.277\times {10}^{11} \mathrm{N}.\mathrm{m}\mathrm{m}$ $\mathsf{\theta }={\displaystyle \frac{M_{net}}{K_{ec}}}$ $M_{net}$ = 0.16Mo $=0.16\left[{\displaystyle \frac{0.01\times 6000\times {8500}^2}{8}}\right]=8.67\times {10}^7 \mathrm{N}.\mathrm{m}\mathrm{m}$ $\mathsf{\theta }={\displaystyle \frac{8.67\times {10}^7}{2.277\times {10}^{11}}}=0.0003808 \mathrm{r}\mathrm{a}\mathrm{d}.$ ${\displaystyle \frac{\theta L}{8}}={\displaystyle \frac{0.0003808\left(8500\right)}{8}}$ = 0.405 mm - in y-direction $K_t=\sum {\displaystyle \frac{9\left(\mathrm{25,028.8}\right)(1.747\times {10}^{10})}{9000{(1-\frac{500}{9000})}^2}}$ = 5.339 × 1011 N.mm $K_{ec}=2.0955\times {10}^{11} \mathrm{N}.\mathrm{m}\mathrm{m}$ $M_{net}$ = 0.16Mo $=0.16\left[{\displaystyle \frac{0.01\times 9000\times {5500}^2}{8}}\right]=5.445\times {10}^7 \mathrm{N}.\mathrm{m}\mathrm{m}$ $\mathsf{\theta }={\displaystyle \frac{M_{net}}{K_{ec}}}=0.00026 \mathrm{r}\mathrm{a}\mathrm{d}$ ${\displaystyle \frac{\theta L}{8}}={\displaystyle \frac{0.00026\left(5500\right)}{8}}$ = 0.179 mm        ${\Delta }_{x total}=1.195+0.405+0.179=1.779 \mathrm{m}\mathrm{m}$        ${\Delta }_{y total}=1.422+0.405+0.179=2.005 \mathrm{m}\mathrm{m}$ Taking the maximum value in both directions           ${\Delta }_{max}=2.005 \mathrm{m}\mathrm{m} (short term)$ Taking the effect of long term of d.L after (5 years) and adding the effect of live load ${\Delta }_{max long}=2.005\left(3+{\displaystyle \frac{W_{LL}}{W_{dL}}}\right)=2.005\left(3+{\displaystyle \frac{20}{10}}\right)=10.03 \mathrm{m}\mathrm{m}$ The ACI-Code maximum limit = Ln2/480 = 5500/480 = 11.458 mm ${\Delta }_{max}\le {\displaystyle \frac{L_{n2}}{480}}o.k.$ (The thickness (310 mm) satisfy the deflection control limit of ACI-Code.

5. Conclusions

In this research, a comprehensive and unified span–depth ratio equation has been successfully derived to accurately determine the minimum thickness for flat plate slabs, addressing the limitations inherent in existing ACI-Code provisions. Unlike traditional methodologies, the proposed equation incorporates crucial parameters such as slab panel aspect ratio, steel reinforcement ratio, concrete compressive strength, applied loads, and long-term deflection effects, thereby enhancing the precision of deflection control. Through extensive analysis and numerical validation, it was demonstrated that the required slab thickness increases notably with larger aspect ratios and support rotations, underscoring their critical influence on slab design. This study focuses solely on deflection-based serviceability criteria and does not address strength limit states such as punching shear. Designers are advised to verify punching shear capacity separately in accordance with ACI 318 requirements.

Conversely, higher reinforcement ratios consistently allowed for reduced slab thickness, highlighting the structural efficiency achieved by optimal reinforcement. Comparative analyses revealed that interior slab panels generally require thinner sections compared to exterior and edge panels, emphasizing the importance of localized design considerations. Ultimately, this study provides engineers with a robust, versatile equation, facilitating more accurate design decisions that conform to the permissible deflection limits prescribed by ACI standards. Although the proposed model demonstrates strong numerical consistency with ACI limits and previous literature, future research will incorporate experimental or field validation to further establish its accuracy under real-world conditions. This paper focuses on serviceability behavior (i.e., deflection) rather than failure modes. As such, flexural failure, punching shear, and other strength-related mechanisms are not explicitly addressed. Future extensions of this work may integrate boundary condition modeling with structural failure analysis for a more comprehensive design framework. This innovative approach not only improves structural performance but also ensures economic efficiency and sustainability in modern concrete slab construction practices.