Local Scour Around Marine Structures: A Comprehensive Review of Influencing Factors, Prediction Methods, and Future Directions
Abstract
1. Introduction
2. Main Factors Affecting Local Scour
2.1. Hydrodynamic Factor
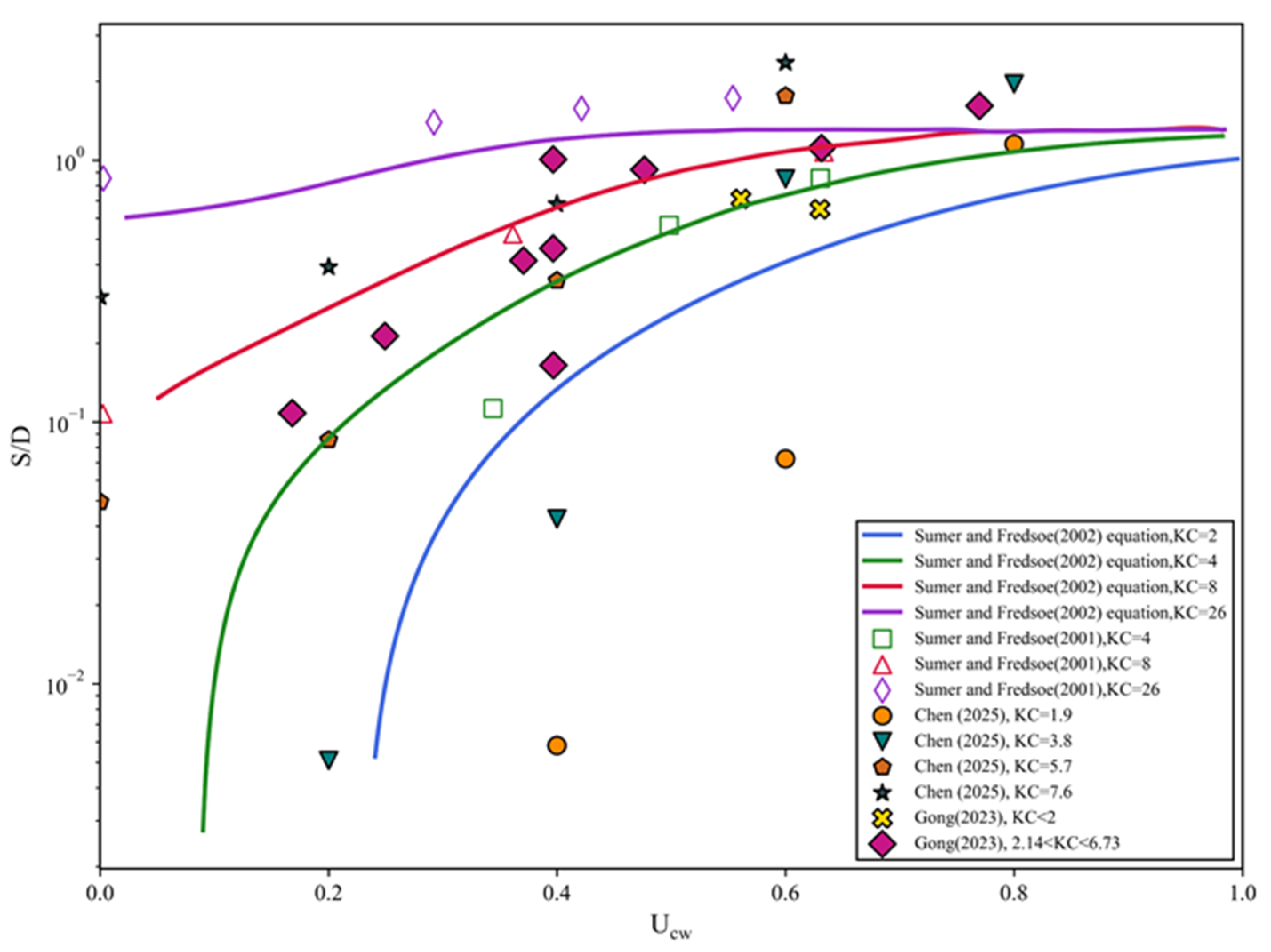
2.1.1. Flow Velocities, Waves, and Wave–Current Interactions
2.1.2. Turbulence
2.2. Influence of Structural Properties and Spatial Layout on Scour Behavior
2.2.1. Structural Size and Shape
2.2.2. Spatial Arrangement of Structures
2.3. Influence of Seabed Sediment Properties on Local Scour
2.4. Other Factors
2.4.1. Tides
2.4.2. Climate Change
2.5. Scour Protection and Mitigation Measures
3. Local Scour Prediction Methods
3.1. Numerical Modeling of Local Scour
3.1.1. CFD-Based Single-Phase Model
3.1.2. Two-Phase Model
3.1.3. SPH Method
3.2. Local Scour Prediction Equation
| Formula/Model | Advantages | Limitations | Applicable Conditions |
|---|---|---|---|
| HEC-18 Equation [153] | 1. Performs well for laboratory data prediction results; | 1. Prediction of field data often tends to overestimate scour depth; | 1. Suitable for bridge piers of simple geometry; |
| 2. Data support: fitted based on a large amount of laboratory data. | 2. The accuracy of scour depth prediction for complex piles is low. | 2. Mainly suitable for clear water scour conditions. | |
| FDOT Equation [154] | 1. Considers sediment properties; | 1. The prediction accuracy is relatively low and often overestimated; | 1. Suitable for bridge piers of simple geometry; |
| 2. Applicable to various shapes. | 2. Theoretical limitations in dealing with complex piers. | 2. Mainly suitable for clear water scour conditions. | |
| 65-1R and 65-2 [145] | 1. Performs well in field data (especially in live-bed conditions); | 1. Underestimation of scour depth for laboratory data (especially for clear water conditions); | 1. Equation 65-2 generally performs better than 65-1R; |
| 2. Considers the effect of sediment grain size. | 2. Overestimation of scour depth for large diameter abutments and large abutment–sediment ratios. | 2. Equation 65-2 is recommended for medium-diameter piers (5–15 m) or moderate D/D50 ratios. | |
| Amini Baghbadorani Equation [147] | 1. Higher accuracy and lower absolute error in scour depth prediction; | 1. Comprehensive data on geometric parameters of bridge piers and water flow conditions are needed; | Complex bridge pier structures with different geometric parameters. |
| 2. Considers complex pier structures. | 2. Relatively complex calculation. | ||
| Hamidifar Equation [150] | 1. Demonstrates high accuracy under multiple statistical indicators; | 1. May slightly overestimate scour depths in practical applications; | 1. Cylindrical piers in clear water; |
| 2. Low sensitivity to critical flow rates and less affected by errors in critical flow rate estimates. | 2. Needs to be used in conjunction with specific critical flow equations. | 2. Applicable to both lab and field. | |
| Sui Equation [20] | 1. Avoids scale effects; | Limited sediment type. | 1. Single piles in a sandy environment; |
| 2. Considers the Reynolds number effect. | 2. Specific Reynolds number range. | ||
| Crowley Equation [149] | 1. Turbulent energy spectrum attenuation is considered with a theoretical basis; | 1. A deeper understanding of turbulent diffusivity is needed; | 1. For relatively well-defined particle and structure sizes; |
| 2. More explicit consideration of particle size characteristics. | 2. Needs improvement at low b/D50 values. | 2. Supported by turbulent diffusivity data. | |
| Tang Equation [151] | 1. Avoids dependence on the concept of equilibrium scour depth; | 1. The applicability to fine-grained sand needs further verification; | 1. Clean water scour conditions; |
| 2. Provides better flexibility and fault tolerance. | 2. Accuracy at low flow intensities needs to be improved. | 2. Non-uniform sand beds. |
3.3. Machine Learning
| Machine Learning Models | Advantages | Limitations | Applicable Conditions |
|---|---|---|---|
| Neural Networks [156,160]: ANN, ANFIS, etc. | 1. Powerful nonlinear mapping capability; | 1. “Black box” problem; | Scenarios where the dataset is large and the signal-to-noise ratio is high, and where extreme prediction accuracy is sought. |
| 2. Good prediction performance; | 2. Strong data dependency; | ||
| 3. Can be enhanced by optimization algorithms or integration methods. | 3. Risk of overfitting. | ||
| Support Vector Machines [22,163]: SVM, SVR, etc. | 1. Capable of being applied to different scour types and conditions; | 1. Requires parameter tuning; | Small to medium-sized datasets with high feature dimensions. |
| 2. Suitable for dealing with complex nonlinear relationships. | 2. Certain “black box” characteristics; | ||
| 3. Data-dependent. | |||
| Tree-Based Models [22,161,168,170]: DT, M5Tree, M5MT, GTB, REPTree, etc. | 1. Intuitive and interpretable; | 1. Possible overfitting; | Scenarios where physical interpretation or decision analysis of prediction results is required. |
| 2. Able to handle nonlinear relationships; | 2. Performance is affected by the range of data; | ||
| 3. Does not require extensive data preprocessing; | 3. Limited interpretability. | ||
| 4. Good predictive performance. | |||
| Boosting/Ensemble Methods [22,168,171]: RF, Boosting Model (AdaBoost, XGBoost, CatBoost, LightGBM), BRT, SGB, etc. | 1. Superior predictive performance; | 1. Parameter optimization requirements; | Various scour prediction tasks with extremely high requirements for prediction accuracy. |
| 2. Capable of handling complex nonlinear relationships and variable interactions; | 2. Potential risk of overfitting; | ||
| 3. Wide range of applications. | 3. Performance may vary with specific conditions. | ||
| Genetic Algorithm Models [156,161,163,169]: GEP, GP, EPR, MGGP, etc. | 1. Generates explicit prediction formulas; | 1. Complex and computationally expensive parameter optimization; | Exploratory research aims to discover new, concise physical laws or empirical formulas from data. |
| 2. Dealing with complex nonlinear problems; | 2. Highly dependent on data. | ||
| 3. Superior prediction performance; | |||
| 4. Applicable to a wide range of scour conditions and structure types. | |||
| Enhanced Models Based on Optimization Algorithms [21,160,172]: ANN-PSO; ANFIS-GA; NF-GMDH-PSO; PSO-XGBoost; RFO-XGBoost; RPSO-XGBoost; RS-REPTree, etc. | 1. Significantly improved prediction accuracy; | 1. Higher demand for data; | When the performance of existing single models fails to meet requirements for specific issues, seek breakthroughs in performance. |
| 2. Excels in dealing with complex nonlinear relationships; | 2. Requires parameter tuning; | ||
| 3. Broader scope of application. | 3. Risk of overfitting. |
3.4. Probabilistic Prediction Methods
4. Conclusions and Future Work
- Research on scour mechanisms in complex real marine environments
- 2.
- Development and validation of high-efficiency numerical models for engineering applications
- 3.
- Intelligent prediction methods integrating data-driven and physical mechanisms
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Zhang, J.; Zhang, P.; Guo, Y.; Ji, Y.; Fu, R. Large Eddy Simulation of the Flow Field Characteristics around a Jacket Foundation under Unidirectional Flow Actions. Ocean Eng. 2025, 317, 120057. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, S.; Li, B.; Huang, W. Local Scour around the Monopile Based on the CFD-DEM Method: Experimental and Numerical Study. Comput. Geotech. 2024, 168, 106117. [Google Scholar] [CrossRef]
- Yang, Y.; Qi, M.; Li, J.; Ma, X. Evolution of Hydrodynamic Characteristics with Scour Hole Developing around a Pile Group. Water 2018, 10, 1632. [Google Scholar] [CrossRef]
- Liang, F.; Wang, C.; Huang, M.; Wang, Y. Experimental Observations and Evaluations of Formulae for Local Scour at Pile Groups in Steady Currents. Mar. Georesour. Geotechnol. 2017, 35, 245–255. [Google Scholar] [CrossRef]
- Liu, H.; Tao, Z.; Zhang, R.; Zhang, C.; Sun, X.; Fan, S.; Zhu, R. A Study on Local Scour of Large-Diameter Monopile under Combined Waves and Current. Sustainability 2023, 15, 5746. [Google Scholar] [CrossRef]
- Li, A.; Melville, B.; Yang, Y.; Zhou, S.; He, F.; Shamseldin, A.; Zhang, G. The Semi-Empirical Model for Critical Bed Shear Stress in the Local Scour Hole Downstream of a Submerged Structure Based on Turbulent Velocity Distribution. Appl. Ocean Res. 2024, 153, 104238. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Y.P. Full-Scale Tsunami-Induced Scour around a Circular Pile with Three-Dimensional Seepage. Coast. Eng. 2025, 197, 104676. [Google Scholar] [CrossRef]
- Wang, W.; Wei, S.; Zhu, D.; Wang, J.; Duan, H. Characteristics and Mechanism of Downflow in Front of a Cylindrical Pier with Clear-Water Local Scour. Water 2024, 16, 1863. [Google Scholar] [CrossRef]
- Adnan, M.; Zhao, M.; Wu, H.; Dhamelia, V. Experimental Study of Local Scour around a Compound Pile under Steady Current. Ocean Eng. 2025, 318, 120151. [Google Scholar] [CrossRef]
- Ghodsi, H.; Najafzadeh, M.; Khanjani, M.; Beheshti, A. Effects of Different Geometric Parameters of Complex Bridge Piers on Maximum Scour Depth: Experimental Study. J. Waterw. Port Coast. Ocean Eng. 2021, 147, 04021021. [Google Scholar] [CrossRef]
- Cheng, N.-S.; Wei, M.; Lu, Y.; Chiew, Y.-M. Evaluation of Sediment Gradation Effects on Clear-Water Pier Scour with Densimetric Froude Number. J. Eng. Mech. 2020, 146, 04020133. [Google Scholar] [CrossRef]
- Chenxi, Q.; Lunliang, D.; Duoyin, W.; Jianting, Z.; Bingchuan, D.; Hao, F. Experimental Study on Silty Seabed Scour around the Single Pile Induced by the Current. Ocean Eng. 2024, 293, 116680. [Google Scholar] [CrossRef]
- Chibana, T.; Quiocho, R.; Watanabe, K. Role of Grain Size Distribution and Pier Aspect Ratio in Scouring and Sorting around Bridge Piers. Water 2022, 14, 2066. [Google Scholar] [CrossRef]
- Li, Z.; Lin, W.; Chu, D.; Liu, F.; Sun, Z.; Yang, W.; Huang, H.; Xu, D. Prediction of Pier Scour Depth under Extreme Typhoon Storm Tide. J. Mar. Sci. Eng. 2024, 12, 1244. [Google Scholar] [CrossRef]
- Wang, C.; Yang, G.; Li, C.; Zhao, C.; Zhu, J.; Ma, X. The Response of Sediment Transport and Morphological Evolution to Storms with Different Characteristics. Sci. Total Environ. 2024, 946, 173987. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsøe, J.; Michelsen, J. Numerical and Experimental Investigation of Flow and Scour around a Circular Pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.; Zhang, N.; Zhao, H.; Liu, L.; Huang, K.; Chen, X. Local Scour Mechanism of Offshore Wind Power Pile Foundation Based on CFD-DEM. J. Mar. Sci. Eng. 2022, 10, 1724. [Google Scholar] [CrossRef]
- Fraga, V.; Yin, G.; Ong, M.; Myrhaug, D. CFD Investigation on Scour beneath Different Configurations of Piggyback Pipelines under Steady Current Flow. Coast. Eng. 2022, 172, 104060. [Google Scholar] [CrossRef]
- Yan, S.; Wang, D.; Li, Y.; Gao, Y.; Lin, J.; Shi, Y. Incompressible Smoothed Particle Hydrodynamics Simulation of Sediment Erosion around Submarine Pipelines. Water 2024, 16, 1445. [Google Scholar] [CrossRef]
- Sui, S.; Zhao, X.; Chen, X.; Deng, W.; Shen, K. Full-Scale Numerical Simulation of the Local Scour Under Combined Current and Wave Conditions Based on Field Data. China Ocean Eng. 2023, 37, 1032–1043. [Google Scholar] [CrossRef]
- Eini, N.; Bateni, S.M.; Jun, C.; Heggy, E.; Band, S.S. Estimation and Interpretation of Equilibrium Scour Depth around Circular Bridge Piers by Using Optimized XGBoost and SHAP. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2244558. [Google Scholar] [CrossRef]
- Nandi, B.; Patel, G.; Das, S. Prediction of Maximum Scour Depth at Clear Water Conditions: Multivariate and Robust Comparative Analysis between Empirical Equations and Machine Learning Approaches Using Extensive Reference Metadata. J. Environ. Manage. 2024, 354, 120349. [Google Scholar] [CrossRef] [PubMed]
- Jafari-Asl, J.; Ben Seghier, M.E.A.; Ohadi, S.; Dong, Y.; Plevris, V. A Comparative Study on the Efficiency of Reliability Methods for the Probabilistic Analysis of Local Scour at a Bridge Pier in Clay-Sand-Mixed Sediments. Modelling 2021, 2, 63–77. [Google Scholar] [CrossRef]
- Pähtz, T.; Clark, A.H.; Valyrakis, M.; Durán, O. The Physics of Sediment Transport Initiation, Cessation, and Entrainment Across Aeolian and Fluvial Environments. Rev. Geophys. 2020, 58, e2019RG000679. [Google Scholar] [CrossRef]
- Ratul, D. Influence of Sediment Mobility on Universal von Kármán Coefficient k and Traversing Length of Eddy in Fluvial Streams. Water Resour. 2020, 47, 222–230. [Google Scholar] [CrossRef]
- Salinas, J.S.; Shringarpure, M.; Cantero, M.I.; Balachandar, S. Mixing at a Sediment Concentration Interface in Turbulent Open Channel Flow. Environ. Fluid Mech. 2018, 18, 173–200. [Google Scholar] [CrossRef]
- Uruba, V. Reynolds Number in Laminar Flows and in Turbulence. AIP Conf. Proc. 2019, 2118, 020003. [Google Scholar]
- Chekmarev, S.F. Tendency to Occupy a Statistically Dominant Spatial State of the Flow as a Driving Force for Turbulent Transition. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 013144. [Google Scholar] [CrossRef]
- Tan, W.; Yuan, J. Experimental Study of Sheet-Flow Sediment Transport under Nonlinear Oscillatory Flow over a Sloping Bed. Coast. Eng. 2019, 147, 1–11. [Google Scholar] [CrossRef]
- Zhou, Y.; Linyun, S. A Criterion for the Initiation of Sediment Movement in Oscillatory Waves. In Asian and Pacific Coasts 2003: (With CD-ROM); World Scientific: Singapore, 2004; pp. 1–7. [Google Scholar]
- Kassem, H.; Thompson, C.E.; Amos, C.L.; Townend, I.H. Wave-Induced Coherent Turbulence Structures and Sediment Resuspension in the Nearshore of a Prototype-Scale Sandy Barrier Beach. Cont. Shelf Res. 2015, 109, 78–94. [Google Scholar] [CrossRef]
- Lyu, X.; Cheng, Y.; Wang, W.; An, H.; Li, Y. Experimental Study on Local Scour around Submerged Monopile under Combined Waves and Current. Ocean Eng. 2021, 240, 109929. [Google Scholar] [CrossRef]
- Yang, Y.; Melville, B.W.; Macky, G.H.; Shamseldin, A.Y. Experimental Study on Local Scour at Complex Bridge Pier under Combined Waves and Current. Coast. Eng. 2020, 160, 103730. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, J.; Guo, Y.; Cui, L.; Guan, D.; Jiang, L. Laboratory Modeling Study on the Scour Characteristics around a Jacket Foundation Subjected to Combined Wave-Current Loading. Renew. Energy 2025, 242, 122443. [Google Scholar] [CrossRef]
- Gong, E.; Chen, S.; Chen, X.; Guan, D.; Zheng, J. Large-Scale Experimental Study on Scour around Offshore Monopile under Combined Wave and Current Condition. Ocean Eng. 2023, 283, 115186. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour around Pile in Combined Waves and Current. J. Hydraul. Eng. 2001, 127, 403–411. [Google Scholar] [CrossRef]
- Fredsøe, J.; Sumer, B.M. The Mechanics of Scour in the Marine Environment; World Scientific Publishing Company: Singapore, 2002; Volume 17, ISBN 981-310-595-X. [Google Scholar]
- Kawata, Y.; Tsuchiya, Y. Local Scour around Cylindrical Piles Due to Waves and Currents Combined. In Proceedings of the 21st International Conference on Coastal Engineering, Malaga, Spain, 20–25 June 1988; pp. 1310–1322. [Google Scholar]
- Deng, X.; Law, A.W.-K.; Zhang, J.; Lin, X. Two Phase Fluid-Actuator Line-Immersed Boundary Coupling for Tidal Stream Turbine Modeling with Scouring Morphology under Wave-Current Loading. Energy 2025, 329, 136757. [Google Scholar] [CrossRef]
- Afzal, M.S.; Holmedal, L.E.; Myrhaug, D. Effect of Wave Skewness and Sediment Particle Size on Sediment Transport Due to Combined Wave–Current Seabed Boundary Layer Streaming. J. Hydraul. Eng. 2022, 148, 06022011. [Google Scholar] [CrossRef]
- Misuriya, G.; Eldho, T.; Mazumder, B. Turbulent Flow Field and Scour Characteristics around Bridge Pier in Combined Wave and Current Conditions. J. Waterw. Port Coast. Ocean Eng. 2024, 150, 04024010. [Google Scholar] [CrossRef]
- Cheng, Y.; Cheng, H.; Wang, X.; Huang, X.; Lyu, X. Experimental Study on Local Scour Characteristics around an Upstream Inclined Pile under Combined Wave and Current Action. Adv. Water Sci. 2022, 33, 306–315. [Google Scholar]
- Du, S.; Wu, G.; Zhu, D.; Wang, R.; Lu, Y.; Liang, B. Experimental Study of Local Scour around Submerged Square Piles in Combined Waves and Current. Ocean Eng. 2022, 266, 113176. [Google Scholar] [CrossRef]
- Bentkamp, L.; Wilczek, M. Temporal Large-Scale Intermittency and Its Impact on the Statistics of Turbulence. J. Fluid Mech. 2025, 1004, A12. [Google Scholar] [CrossRef]
- Hofland, B.; Battjes, J.A. Probability Density Function of Instantaneous Drag Forces and Shear Stresses on a Bed. J. Hydraul. Eng. 2006, 132, 1169–1175. [Google Scholar] [CrossRef]
- Cheng, Z.; Chauchat, J.; Hsu, T.-J.; Calantoni, J. Eddy Interaction Model for Turbulent Suspension in Reynolds-Averaged Euler–Lagrange Simulations of Steady Sheet Flow. Adv. Water Resour. 2018, 111, 435–451. [Google Scholar] [CrossRef]
- Chen, B.; Li, S. Experimental Study of Local Scour around a Vertical Cylinder under Wave-Only and Combined Wave-Current Conditions in a Large-Scale Flume. J. Hydraul. Eng. 2018, 144, 04018058. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, J.; Guo, A. On Wave–Current Interaction with a Horizontal Cylinder: Load Characteristics and Vortex Pattern. Phys. Fluids 2023, 35, 017101. [Google Scholar] [CrossRef]
- Liang, D.; Jia, H.; Xiao, Y.; Yuan, S. Experimental Investigation of Turbulent Flows around High-Rise Structure Foundations and Implications on Scour. Water Sci. Eng. 2022, 15, 47–56. [Google Scholar] [CrossRef]
- Shringarpure, M.; Cantero, M.I.; Balachandar, S. Dynamics of Complete Turbulence Suppression in Turbidity Currents Driven by Monodisperse Suspensions of Sediment. J. Fluid Mech. 2012, 712, 384–417. [Google Scholar] [CrossRef]
- Voßkuhle, M.; Pumir, A.; Lévêque, E.; Wilkinson, M. Prevalence of the Sling Effect for Enhancing Collision Rates in Turbulent Suspensions. J. Fluid Mech. 2014, 749, 841–852. [Google Scholar] [CrossRef]
- Singh, U.K.; Ahmad, Z.; Kumar, A. Turbulence Characteristics of Flow over the Degraded Cohesive Bed of Clay–Silt–Sand Mixture. ISH J. Hydraul. Eng. 2017, 23, 308–318. [Google Scholar] [CrossRef]
- Misuriya, G.; Eldho, T.; Mazumder, B. Turbulent Flow Field around a Cylindrical Pier on a Gravel Bed. J. Hydraul. Eng. 2023, 149, 04023040. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Yang, Z. Influence of Scour Development on Turbulent Flow Field in Front of a Bridge Pier. Water 2020, 12, 2370. [Google Scholar] [CrossRef]
- Jenssen, U.; Manhart, M. Flow around a Scoured Bridge Pier: A Stereoscopic PIV Analysis. Exp. Fluids 2020, 61, 1–18. [Google Scholar] [CrossRef]
- Bordbar, A.; Sharifi, S.; Hemida, H. Investigation of the Flow Behaviour and Local Scour around Single Square-Shaped Cylinders at Different Positions in Live-Bed. Ocean Eng. 2021, 238, 109772. [Google Scholar] [CrossRef]
- Tariq, M.; Khan, A.; Khan, M. Experimental Study of Scour Hole Depth around Bridge Pile Using Efficient Cross-Section. Appl. Sci. 2022, 12, 5205. [Google Scholar] [CrossRef]
- Yao, W.; An, H.; Draper, S.; Cheng, L.; Harris, J.M. Experimental Investigation of Local Scour around Submerged Piles in Steady Current. Coast. Eng. 2018, 142, 27–41. [Google Scholar] [CrossRef]
- Tafarojnoruz, A.; Lauria, A. Large Eddy Simulation of the Turbulent Flow Field around a Submerged Pile within a Scour Hole under Current Condition. Coast. Eng. J. 2020, 62, 489–503. [Google Scholar] [CrossRef]
- Yao, W.; Draper, S.; An, H.; Cheng, L.; Harris, J.M.; Whitehouse, R.J.S. Experimental Study of Local Scour around Submerged Compound Piles in Steady Current. Coast. Eng. 2021, 165, 103831. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Z.; Hu, Z.; Ma, H. Microscopic Investigation of Shape Effect on Local Scour around the Monopile Using CFD-DEM. Comput. Geotech. 2025, 177, 106872. [Google Scholar] [CrossRef]
- Jalal, H.K.; Hassan, W.H. Effect of Bridge Pier Shape on Depth of Scour. IOP Conf. Ser. Mater. Sci. Eng. 2020, 671, 012001. [Google Scholar] [CrossRef]
- Khan, K.A.; Waseem, M.; Alam, M.; Khan, M.; Leta, M.K. Experimental Investigation of Pier Scour Depth and Its Scour Hole Pattern for Different Shapes. J. Infrastruct. Policy Dev. 2024, 8, 3096. [Google Scholar] [CrossRef]
- Yang, Q.; Yu, P.; Liu, Y.; Liu, H.; Zhang, P.; Wang, Q. Scour Characteristics of an Offshore Umbrella Suction Anchor Foundation under the Combined Actions of Waves and Currents. Ocean Eng. 2020, 202, 106701. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, X.; Sui, S.; Deng, W.; Shen, K. Experimental Study of Local Scour around Bucket Foundation in Sand. Ocean Eng. 2023, 286, 115482. [Google Scholar] [CrossRef]
- Sarmiento, J.; Guanche, R.; Losada, I.J.; Rosendo, E.M.; Guindo, A.; Guevara, J.L. de Scour Processes around Pile Clusters of Jacket Foundations under Steady Currents. Ocean Eng. 2024, 313, 119502. [Google Scholar] [CrossRef]
- Devi, G.; Kumar, M. Characteristics Assessment of Local Scour Encircling Twin Bridge Piers Positioned Side by Side (SbS). Sadhana-Acad. Proc. Eng. Sci. 2022, 47, 109. [Google Scholar] [CrossRef]
- Pasupuleti, L.N.; Timbadiya, P.V.; Patel, P.L. Space–Time Dynamics of Local Scour around Submerged Tandem and Staggered Piers in Sand Beds. Curr. Sci. 2023, 125, 1227. [Google Scholar] [CrossRef]
- Tang, J.-H.; Puspasari, A.D. Numerical Simulation of Local Scour around Three Cylindrical Piles in a Tandem Arrangement. Water 2021, 13, 3623. [Google Scholar] [CrossRef]
- Gong, M.; Pan, X.; Du, S.; Wu, G.; Lv, Y.; Sun, Y.; Ding, G.; Liang, B. Laboratory Study of Local Scour Around an Array of Pile Groups in Clear-Water Scour Conditions. J. Mar. Sci. Eng. 2025, 13, 137. [Google Scholar] [CrossRef]
- Lian, J.; Li, J.; Guo, Y.; Wang, H.; Yang, X. Numerical Study on Local Scour Characteristics of Multi-Bucket Jacket Foundation Considering Exposed Height. Appl. Ocean Res. 2022, 121, 103092. [Google Scholar] [CrossRef]
- Puspasari, A.; Tang, J. Numerical Simulation of Scouring around Groups of Six Cylinders with Different Flow Directions. J. Chin. Inst. Eng. 2023, 46, 420–430. [Google Scholar] [CrossRef]
- Mamoon, A.-A.; Zhao, M.; Wu, H.; Keshavarzi, A. Experimental Investigation of Local Scour around Two Submerged Short Square Piles under Tandem, Side-by-Side and Staggered Arrangements in Steady Current. Ocean Eng. 2022, 261, 112156. [Google Scholar] [CrossRef]
- Welzel, M.; Schendel, A.; Satari, R.; Neuweiler, I.; Schlurmann, T. Spatio-Temporal Analysis of Scour around Complex Offshore Foundations under Clear Water and Live Bed Conditions. Ocean Eng. 2024, 298, 117042. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, W.; Zhou, P.; Du, F.; Wang, L. Experimental Investigation on Scour Development and Scour Protection for Offshore Converter Platform. Mar. Struct. 2023, 90, 103440. [Google Scholar] [CrossRef]
- Zhou, K.; Duan, J.; Bombardelli, F. Experimental and Theoretical Study of Local Scour around Three-Pier Group. J. Hydraul. Eng. 2020, 146, 04020069. [Google Scholar] [CrossRef]
- Kadono, T.; Okazaki, S.; Kabeyama, Y.; Matsui, T. Effect of Angle between Pier and Center of River Flow on Local Scouring around the Bridge Pier. Water 2020, 12, 3192. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, M. Study of Local Scour around Rectangular and Square Subsea Caissons under Steady Current Condition. Coast. Eng. 2024, 190, 104513. [Google Scholar] [CrossRef]
- Qi, W.; Li, Y.; Xu, K.; Gao, F. Physical Modelling of Local Scour at Twin Piles under Combined Waves and Current. Coast. Eng. 2019, 143, 63–75. [Google Scholar] [CrossRef]
- Liu, M.; Tang, G.; Jin, X.; Geng, S. Experimental Study of Local Scour Around Four Piles Under Different Attack Angles and Gap Ratios. China Ocean Eng. 2024, 38, 612–624. [Google Scholar] [CrossRef]
- Ma, L.; Wang, L.; Guo, Z.; Jiang, H.; Gao, Y. Time Development of Scour around Pile Groups in Tidal Currents. Ocean Eng. 2018, 163, 400–418. [Google Scholar] [CrossRef]
- Sonia Devi, Y.; Barbhuiya, A.K. Bridge Pier Scour in Cohesive Soil: A Review. Sādhanā 2017, 42, 1803–1819. [Google Scholar] [CrossRef]
- Wang, C.; Yuan, Y.; Liang, F.; Yu, X. Investigating the Effect of Grain Composition on the Erosion around Deepwater Foundations with a New Simplified Scour Resistance Test. Transp. Geotech. 2021, 28, 100527. [Google Scholar] [CrossRef]
- Shields, A. Application of Similitude Mechanics and Research on Turbulence to Bed Load Movement; California Institute of Technology: Pasadena, CA, USA, 1936; Volume 26. [Google Scholar]
- Chen, X.; Zhang, X.; Liu, X.; Zhang, F.; Yan, J.; Wang, H. Experimental Study of Scour Characteristics and Scour Hole Dimensions in Consolidated Silt Sediment under a Current. Ocean Eng. 2022, 266, 112801. [Google Scholar] [CrossRef]
- Mahalder, B.; Schwartz, J.S.; Palomino, A.M.; Zirkle, J. Influence of Cumulative Effective Stream Power on Scour Depth Prediction Around Bridge Piers in Cohesive Bed Sediments. Transp. Res. Rec. J. Transp. Res. Board 2024, 2678, 710–723. [Google Scholar] [CrossRef]
- Qin, C.; Duan, L.; Wang, D.; Duan, B.; Liu, W. A Local Scour Model for Single Pile on Silty Seabed Considering Soil Cohesion (SedCohFOAM): Model and Validation. Phys. Fluids 2024, 36, 053340. [Google Scholar] [CrossRef]
- Zaidan, J.; Bennabi, A.; Poupardin, A.; Benamar, A.; Marin, F. Spatio-Temporal Characterisation of Local Scour around a Circular Bridge Pier in Cohesive Soil with Different Clay/Silt Ratio. Eur. J. Environ. Civ. Eng. 2024, 28, 3328–3347. [Google Scholar] [CrossRef]
- Tan, G.; Wang, J.; Shu, C.; Lai, Y. Effects of Consolidation Time and Particle Size on Scour Rates of Cohesive Sediment. J. Hydrodyn. 2007, 19, 160–164. [Google Scholar] [CrossRef]
- Mohr, H.; Draper, S.; White, D.J.; Cheng, L. The Influence of Permeability on the Erosion Rate of Fine-Grained Marine Sediments. Coast. Eng. 2018, 140, 124–135. [Google Scholar] [CrossRef]
- Wang, C.; Yuan, Y.; Liang, F.; Tao, J. Experimental Investigation of Local Scour around Cylindrical Pile Foundations in a Double-Layered Sediment under Current Flow. Ocean Eng. 2022, 251, 111084. [Google Scholar] [CrossRef]
- Yu, P.; Chen, J.; Zhou, J.; Li, J.; Yu, L. Experimental Investigation of Local Scour around Complex Bridge Pier of Sea-Crossing Bridge under Tidal Currents. Ocean Eng. 2023, 290, 116374. [Google Scholar] [CrossRef]
- Wei, Y.; Ma, A.; Deng, Y.; Hu, Y.; Liu, M.; Cao, M. Scour Pit Characteristics and Safety Operation Index of Riprap Spur Dikes under Runoff and Tidal Current. Water 2024, 16, 438. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, S.; Guo, Y.; Yang, Y.; Zeng, J.; Sui, T.; Wei, R.; Li, Z. Field Study of Local Scour around Bridge Foundations on Silty Seabed under Irregular Tidal Flow. Coast. Eng. 2023, 185, 104382. [Google Scholar] [CrossRef]
- Jeon, B.J.; Jeong, S.W.; Jeon, I.; Ha, H.K. Influence of Tidal Asymmetry on Local Scour near the Offshore Platform. Reg. Stud. Mar. Sci. 2024, 80, 103891. [Google Scholar] [CrossRef]
- Schendel, A.; Hildebrandt, A.; Goseberg, N.; Schlurmann, T. Processes and Evolution of Scour around a Monopile Induced by Tidal Currents. Coast. Eng. 2018, 139, 65–84. [Google Scholar] [CrossRef]
- Nasr, A.; Björnsson, I.; Johansson, J. National-Level Analysis of the Impact of Climate Change on Local Scour under Bridge Piers in Sweden. J. Infrastruct. Syst. 2023, 29, 05023001. [Google Scholar] [CrossRef]
- Li, J.; Kong, X.; Yang, Y.; Deng, L.; Xiong, W. CFD Investigations of Tsunami-Induced Scour around Bridge Piers. Ocean Eng. 2022, 244, 110373. [Google Scholar] [CrossRef]
- Chen, J.; Qu, Y.; Sun, Z. Protection Mechanisms, Countermeasures, Assessments and Prospects of Local Scour for Cross-Sea Bridge Foundation: A Review. Ocean Eng. 2023, 288, 116145. [Google Scholar] [CrossRef]
- Tang, Z.; Melville, B.; Singhal, N.; Shamseldin, A.; Zheng, J.; Guan, D.; Cheng, L. Countermeasures for Local Scour at Offshore Wind Turbine Monopile Foundations: A Review. Water Sci. Eng. 2022, 15, 15–28. [Google Scholar] [CrossRef]
- Gaudio, R.; Tafarojnoruz, A.; Calomino, F. Combined Flow-Altering Countermeasures against Bridge Pier Scour. J. Hydraul. Res. 2012, 50, 35–43. [Google Scholar] [CrossRef]
- Wang, G.; Xu, S.; Zhang, Q.; Zhang, J. An Experimental Study of the Local Scour Protection Methods around the Monopile Foundation of Offshore Wind Turbines. Ocean Eng. 2023, 273, 113957. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Z.; Wang, L.; Yang, H.; Li, Y.; Zhu, J. An Innovative Eco-Friendly Method for Scour Protection around Monopile Foundation. Appl. Ocean Res. 2022, 123, 103177. [Google Scholar] [CrossRef]
- Wang, C.; Jin, L.; Qian, Y.; Wu, Y.; Liang, F. Investigation of the Protection Mechanism and Failure Modes of Solidified Soil Utilized for Scour Mitigation. Constr. Build. Mater. 2025, 472, 140858. [Google Scholar] [CrossRef]
- Wu, X.; Li, R.; Shu, J.; Tang, C.; Chen, J.; Wang, H.; Jiang, H.; Wang, X. Experimental Study on Engineering Behavior of Solidified Soil for Scour Repair and Protection. China Ocean Eng. 2024, 38, 625–635. [Google Scholar] [CrossRef]
- Xie, A.; Chen, X.; Liu, X.; Li, K.; Chen, S.; Zhang, F. New Methods for the Scour Protection around the Pile Foundation Based on Oyster Reef Cover. Ocean Eng. 2025, 335, 121682. [Google Scholar] [CrossRef]
- Tang, Z.; Melville, B.; Shamseldin, A.; Guan, D.; Singhal, N.; Yao, Z. Experimental Study of Collar Protection for Local Scour Reduction around Offshore Wind Turbine Monopile Foundations. Coast. Eng. 2023, 183, 104324. [Google Scholar] [CrossRef]
- Khan, Z.U.; Ahmed, A.; Valyrakis, M.; Pasha, G.A.; Farooq, R.; Murtaza, N.; Khan, D. Effectiveness of Collars and Hooked-Collars in Mitigating Scour around Different Abutment Shapes. Water 2024, 16, 2550. [Google Scholar] [CrossRef]
- Zheng, Z.; Hu, Z.; Ma, H.; Huang, W. Role of Sacrificial Pile in Scour Mitigation around the Monopile: A Multiscale Perspective Using CFD-DEM. Ocean Eng. 2025, 327, 120979. [Google Scholar] [CrossRef]
- Li, H.; Qiu, X.; Yan, S.; Zhao, H.; Ma, W. Numerical Investigation on the Influence of a Spoiler Structure for Local Scour Protection. Appl. Ocean Res. 2023, 138, 103675. [Google Scholar] [CrossRef]
- Zhu, C.; Li, Q.; Zheng, J.; Liu, H.; Yu, P. Experimental and Numerical Investigation on the Impact of MS2AF on Local Scour Protection Performance. Ocean Eng. 2024, 293, 116613. [Google Scholar] [CrossRef]
- Heravi, Z.; Moghaddam, M.A.; Esmaili, K.; Givehchi, M.; Bahrpeyma, A. Impact of Installing New Scour Prevention Countermeasure (F-Jacks) around Bridge Pier on Flow Pattern and Scour Control. Ocean Eng. 2024, 313, 119326. [Google Scholar] [CrossRef]
- Bharadwaj, M.R.; Gupta, L.K.; Pandey, M.; Valyrakis, M. Countermeasures for Local Scour around the Bridge Pier: A Review. Acta Geophys. 2025, 73, 701–728. [Google Scholar] [CrossRef]
- Lai, Y.G.; Liu, X.; Bombardelli, F.A.; Song, Y. Three-Dimensional Numerical Modeling of Local Scour: A State-of-the-Art Review and Perspective. J. Hydraul. Eng. 2022, 148, 03122002. [Google Scholar] [CrossRef]
- Zhao, M. A Review on Recent Development of Numerical Modelling of Local Scour around Hydraulic and Marine Structures. J. Mar. Sci. Eng. 2022, 10, 1139. [Google Scholar] [CrossRef]
- Dutta, D.; Afzal, M.S. Scour around Twin-Piles under Combined Wave-Current Flows. Coast. Eng. 2024, 189, 104477. [Google Scholar] [CrossRef]
- Song, Y.; Xu, Y.; Liu, X. Physically Based Sand Slide Method in Scour Models Based on Slope-Limited Diffusion. J. Hydraul. Eng. 2020, 146, 04020074. [Google Scholar] [CrossRef]
- Okhravi, S.; Gohari, S.; Alemi, M.; Maia, R. Numerical Modeling of Local Scour of Non-Uniform Graded Sediment for Two Arrangements of Pile Groups. Int. J. Sediment Res. 2023, 38, 597–614. [Google Scholar] [CrossRef]
- Yu, P.; Liu, J.; Yu, L.; Zhu, L. Numerical Investigation of Local Scour around Tandem Piers Using Proposed Self-Sustaining Inlet Turbulent Boundary Conditions. Ocean Eng. 2023, 274, 113987. [Google Scholar] [CrossRef]
- Song, Y.; Xu, Y.; Ismail, H.; Liu, X. Scour Modeling Based on Immersed Boundary Method: A Pathway to Practical Use of Three-Dimensional Scour Models. Coast. Eng. 2022, 171, 104037. [Google Scholar] [CrossRef]
- Lee, C.-H.; Low, Y.M.; Chiew, Y.-M. Multi-Dimensional Rheology-Based Two-Phase Model for Sediment Transport and Applications to Sheet Flow and Pipeline Scour. Phys. Fluids 2016, 28, 053305. [Google Scholar] [CrossRef]
- Xiong, H.; Xiao, J.; Jin, Y.; Sun, X.; Chen, X. Numerical Investigation of Scour Development around Offshore Tensioners under Steady Current. Ocean Eng. 2024, 313, 119373. [Google Scholar] [CrossRef]
- Li, J.; Tao, J. CFD-DEM Two-Way Coupled Numerical Simulation of Bridge Local Scour Behavior under Clear-Water Conditions. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 107–117. [Google Scholar] [CrossRef]
- Hu, D.; Tang, W.; Sun, L.; Li, F.; Ji, X.; Duan, Z. Numerical Simulation of Local Scour around Two Pipelines in Tandem Using CFD-DEM Method. Appl. Ocean Res. 2019, 93, 101968. [Google Scholar] [CrossRef]
- Deng, Q.; Chen, N.; Stechmann, S.N.; Hu, J. LEMDA: A Lagrangian-Eulerian Multiscale Data Assimilation Framework. J. Adv. Model. Earth Syst. 2025, 17, e2024MS004259. [Google Scholar] [CrossRef]
- Yang, J.; Low, Y.M.; Lee, C.-H.; Chiew, Y.-M. Numerical Simulation of Scour around a Submarine Pipeline Using Computational Fluid Dynamics and Discrete Element Method. Appl. Math. Model. 2018, 55, 400–416. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, S.; Li, B. Numerical Investigation of Local Scour around Twin Piles under Steady Current Using CFD-DEM Coupling Method. Comput. Geotech. 2023, 164, 105805. [Google Scholar] [CrossRef]
- Zhang, S.; Li, B.; Ma, H. Numerical Investigation of Scour around the Monopile Using CFD-DEM Coupling Method. Coast. Eng. 2023, 183, 104334. [Google Scholar] [CrossRef]
- Ma, H.; Li, B. CFD-CGDEM Coupling Model for Scour Process Simulation of Submarine Pipelines. Ocean Eng. 2023, 271, 113789. [Google Scholar] [CrossRef]
- Ma, H.; Li, B.; Zhang, S. Scour Mechanism around a Pipeline under Different Current-Wave Conditions Using the CFD-DEM Coupling Model. Comput. Geotech. 2024, 170, 106304. [Google Scholar] [CrossRef]
- Tofany, N.; Wirahman, T. Numerical Simulation of Early Stages of Scour around a Submarine Pipeline Using a Two-Phase Flow Model. Ocean Eng. 2022, 264, 112503. [Google Scholar] [CrossRef]
- Nagel, T.; Chauchat, J.; Bonamy, C.; Liu, X.; Cheng, Z.; Hsu, T. Three-Dimensional Scour Simulations with a Two-Phase Flow Model. Adv. Water Resour. 2020, 138, 103544. [Google Scholar] [CrossRef]
- Bakhtyar, R.; Yeganeh-Bakhtiary, A.; Barry, D.A.; Ghaheri, A. Two-Phase Hydrodynamic and Sediment Transport Modeling of Wave-Generated Sheet Flow. Adv. Water Resour. 2009, 32, 1267–1283. [Google Scholar] [CrossRef]
- Hu, J.; Xu, J.; Xie, J.; Pan, D. Numerical Investigation on Settling Process of Bi-Disperse Cohesive Particle Clouds. Powder Technol. 2025, 457, 120912. [Google Scholar] [CrossRef]
- Peng, Y.; Yin, Z.-Y. Micromechanical Analysis of Local Scour Behaviors around Circular Piles in Granular Soil under Steady Flows with SPH-DEM. Ocean Eng. 2025, 328, 121061. [Google Scholar] [CrossRef]
- Zhang, R.; Xiong, W.; Gao, Y. A Meshless Model for Three-Dimensional Direct Numerical Simulation of Local Scour around Cylinder Bridge Foundation. Ocean Eng. 2024, 312, 119220. [Google Scholar] [CrossRef]
- Zhu, G.; Cui, Y.; Khoo, B.C.; Zheng, S.; Yu, Z.; Gao, Y. A Parallel Multi-Resolution Smoothed Particle Hydrodynamics Model with Local Time Stepping. J. Comput. Phys. 2024, 508, 113039. [Google Scholar] [CrossRef]
- Burmistrova, O.A.; Markelova, T.V.; Arendarenko, M.S.; Stoyanovskaya, O.P. A New Method for Approximating of First Derivatives in Smoothed Particle Hydrodynamics: Theory and Practice for Linear Transport Equation. Lobachevskii J. Math. 2025, 46, 43–54. [Google Scholar] [CrossRef]
- Cabezón, R.M.; García-Senz, D.; Simsek, O.S.; Keller, S.; Sanz, A.; Zhu, Y.; Mayer, L.; Klessen, R.; Ciorba, F.M. Modelling Subsonic Turbulence with SPH-EXA. arXiv 2025, arXiv:250310273. [Google Scholar]
- Zhang, S.; Fan, Y.; Ren, Y.; Qian, B.; Hu, X. Generalized and High-Efficiency Arbitrary-Positioned Buffer for Smoothed Particle Hydrodynamics. Phys. Fluids 2024, 36, 127107. [Google Scholar] [CrossRef]
- Lirong, T.; Shenglong, G.; Songdong, S.; Yushuai, W. Turbulent Models of Shallow-Water Equations-Based Smoothed Particle Hydrodynamics. Phys. Fluids 2024, 36, 107164. [Google Scholar] [CrossRef]
- Li, S.; Peng, M.; Gao, L.; Xia, C.; Zhu, Y. A 3D SPH Framework for Simulating Landslide Dam Breaches by Coupling Erosion and Side Slope Failure. Comput. Geotech. 2024, 175, 106699. [Google Scholar] [CrossRef]
- Al-Obaidi, K.; Valyrakis, M. A Sensory Instrumented Particle for Environmental Monitoring Applications: Development and Calibration. IEEE Sens. J. 2021, 21, 10153–10166. [Google Scholar] [CrossRef]
- Nandi, B.; Das, S. A Novel Formula to Determine the Time to Achieve Quasi-Equilibrium Scour around a Circular Pier. ISH J. Hydraul. Eng. 2025, 1–16. [Google Scholar] [CrossRef]
- Qi, M.; Li, J.; Chen, Q. Comparison of Existing Equations for Local Scour at Bridge Piers: Parameter Influence and Validation. Nat. Hazards 2016, 82, 2089–2105. [Google Scholar] [CrossRef]
- Vonkeman, J.; Basson, G. Evaluation of Empirical Equations to Predict Bridge Pier Scour in a Non-Cohesive Bed under Clear Water Conditions. J. S. Afr. Inst. Civ. Eng. 2019, 61, 2–20. [Google Scholar] [CrossRef]
- Amini Baghbadorani, D.; Ataie-Ashtiani, B.; Beheshti, A.; Hadjzaman, M.; Jamali, M. Prediction of Current-Induced Local Scour around Complex Piers: Review, Revisit, and Integration. Coast. Eng. 2018, 133, 43–58. [Google Scholar] [CrossRef]
- Jazaeri, S.A.; Nistor, I.; Mohammadian, A.; Liu, X. A Critical Review on the Tsunami-Induced Scour around Structures. Coast. Eng. J. 2024, 66, 563–590. [Google Scholar] [CrossRef]
- Crowley, R.; Cottrell, W.; Singleton, A. An Examination of the Dependency between Maximum Equilibrium Local Scour Depth and the Grain Size/Structure Size Ratio. Water 2020, 12, 3117. [Google Scholar] [CrossRef]
- Hamidifar, H.; Zanganeh-Inaloo, F.; Carnacina, I. Hybrid Scour Depth Prediction Equations for Reliable Design of Bridge Piers. Water 2021, 13, 2019. [Google Scholar] [CrossRef]
- Tang, H.; Liu, Q.; Zhou, J.; Guan, D.; Yuan, S.; Tang, L.; Zhang, H. Process-Based Design Method for Pier Local Scour Depth under Clear-Water Condition. J. Hydraul. Eng. 2023, 149, 06023009. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Cao, Z.; Zhang, D. Prediction of Contraction Channel Scour Depth: Based on Interpretability Analysis and PCA-Enhanced SVR. J. Hydroinform. 2024, 26, 3287–3305. [Google Scholar] [CrossRef]
- Arneson, L.A.; Zevenbergen, L.W.; Lagasse, P.F.; Clopper, P.E. Evaluating Scour at Bridges; National Highway Institute: Washington, DC, USA, 2012.
- Sheppard, D.M.; Renna, R. Bridge Scour Manual; Florida Department of Transportation: Tallahassee, FL, USA, 2005.
- Devi, K.; Khuntia, J.; Mumtaz, M.; Elgamal, M.; Das, B. Advancements in Predicting Scour Depth Induced by Turbulent Wall Jets: A Comparative Analysis of Mathematical Formulations and Machine Learning Models. AIP Adv. 2024, 14, 055008. [Google Scholar] [CrossRef]
- Abd El-Hady Rady, R. Prediction of Local Scour around Bridge Piers: Artificial-Intelligence-Based Modeling versus Conventional Regression Methods. Appl. Water Sci. 2020, 10, 57. [Google Scholar] [CrossRef]
- Baranwal, A.; Das, B. Live-Bed Scour Depth Modelling Around the Bridge Pier Using ANN-PSO, ANFIS, MARS, and M5Tree. Water Resour. Manag. 2024, 38, 4555–4587. [Google Scholar] [CrossRef]
- Sharafati, A.; Tafarojnoruz, A.; Motta, D.; Yaseen, Z.M. Application of Nature-Inspired Optimization Algorithms to ANFIS Model to Predict Wave-Induced Scour Depth around Pipelines. J. Hydroinform. 2020, 22, 1425–1451. [Google Scholar] [CrossRef]
- Sharafati, A.; Tafarojnoruz, A.; Yaseen, Z.M. New Stochastic Modeling Strategy on the Prediction Enhancement of Pier Scour Depth in Cohesive Bed Materials. J. Hydroinform. 2020, 22, 457–472. [Google Scholar] [CrossRef]
- Dang, N.; Anh, D.; Dang, T. ANN Optimized by PSO and Firefly Algorithms for Predicting Scour Depths around Bridge Piers. Eng. Comput. 2021, 37, 293–303. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Oliveto, G. More Reliable Predictions of Clear-Water Scour Depth at Pile Groups by Robust Artificial Intelligence Techniques While Preserving Physical Consistency. Soft Comput. 2021, 25, 5723–5746. [Google Scholar] [CrossRef]
- Kim, T.; Shahriar, A.R.; Lee, W.-D.; Choi, Y.; Kwon, S.; Gabr, M.A. Field Data-Based Prediction of Local Scour Depth around Bridge Piers Using Interpretable Machine Learning. Transp. Geotech. 2025, 52, 101567. [Google Scholar] [CrossRef]
- Choi, S.; Choi, S. Prediction of Local Scour around Bridge Piers in the Cohesive Bed Using Support Vector Machines. KSCE J. Civ. Eng. 2022, 26, 2174–2182. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mosavi, A.; Rabczuk, T. Particle Swarm Optimization Model to Predict Scour Depth around a Bridge Pier. Front. Struct. Civ. Eng. 2020, 14, 855–866. [Google Scholar] [CrossRef]
- Valyrakis, M.; Diplas, P.; Dancey, C.L. Prediction of Coarse Particle Movement with Adaptive Neuro-fuzzy Inference Systems. Hydrol. Process. 2011, 25, 3513–3524. [Google Scholar] [CrossRef]
- Jiang, L.; Cheng, Y.; Luo, K.; Fan, J. PT-PINNs: A Parametric Engineering Turbulence Solver Based on Physics-Informed Neural Networks. arXiv 2025, arXiv:250317704. [Google Scholar]
- Naderibeni, M.; Reinders, M.J.; Wu, L.; Tax, D.M. Learning Solutions of Parametric Navier-Stokes with Physics-Informed Neural Networks. arXiv 2024, arXiv:240203153. [Google Scholar]
- Wang, C.; Wu, Q.; Liang, J.; Liang, F.; Yu, X. (Bill) Establishment and Implementation of an Artificial Intelligent Flume for Investigating Local Scour around Underwater Foundations. Transp. Geotech. 2024, 49, 101433. [Google Scholar] [CrossRef]
- Zhang, W.; Rennie, C.D.; Nistor, I. A New Model Developed by Multigene Genetic Programming for the Temporal Evolution of Bridge Pier Scour. Can. J. Civ. Eng. 2023, 50, 549–559. [Google Scholar] [CrossRef]
- Sreedhara, B.; Patil, A.; Pushparaj, J.; Kuntoji, G.; Naganna, S. Application of Gradient Tree Boosting Regressor for the Prediction of Scour Depth around Bridge Piers. J. Hydroinform. 2021, 23, 849–863. [Google Scholar] [CrossRef]
- Kumar, L.; Afzal, M. Estimating Pier Scour Depth under Combined Waves and Current Using Boosting Machine-Learning Models. Acta Geophys. 2024, 72, 1895–1911. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shirzadi, A.; Amini, A.; Shahabi, H.; Al-Ansari, N.; Hamidi, S.; Singh, S.K.; Thai Pham, B.; Ahmad, B.B.; Ghazvinei, P.T. A Hybrid Intelligence Approach to Enhance the Prediction Accuracy of Local Scour Depth at Complex Bridge Piers. Sustainability 2020, 12, 1063. [Google Scholar] [CrossRef]
- Tubaldi, E.; Macorini, L.; Izzuddin, B.A.; Manes, C.; Laio, F. A Framework for Probabilistic Assessment of Clear-Water Scour around Bridge Piers. Struct. Saf. 2017, 69, 11–22. [Google Scholar] [CrossRef]
- Vatani, A.; Jafari-Asl, J.; Ohadi, S.; Safaeian Hamzehkolaei, N.; Afzali Ahmadabadi, S.; Correia, J.A.F.O. An Efficient Surrogate Model for Reliability Analysis of the Marine Structure Piles. Proc. Inst. Civ. Eng. Marit. Eng. 2023, 176, 176–192. [Google Scholar] [CrossRef]
- Lu, B.; Zuo, J.; Shahhosseini, M.; Wang, H.; Liu, H.; Zhang, M.; Yu, G. Visual Deep Learning with Physics Constraints for Local Scour Evolution Prediction at Monopiles. J. Ocean Eng. Sci. 2024, 10, 342–352. [Google Scholar] [CrossRef]
- Chen, X.; Yu, Y.; Wang, L. Assessing Scour Prediction Models for Monopiles in Sand from the Perspective of Design Robustness. Mar. Struct. 2024, 93, 103532. [Google Scholar] [CrossRef]
- Homaei, F.; Najafzadeh, M. Failure Analysis of Scouring at Pile Groups Exposed to Steady-State Flow: On the Assessment of Reliability-Based Probabilistic Methodology. Ocean Eng. 2022, 266, 112707. [Google Scholar] [CrossRef]
- Yu, T.; Tong, X.; Chen, X.; Song, H.; Zhao, X.; Wang, Y. Prediction of Scour Depth around Monopiles in Combined Waves and Current: A Probabilistic Assessment of M5’-MCS. Appl. Ocean Res. 2024, 153, 104271. [Google Scholar] [CrossRef]
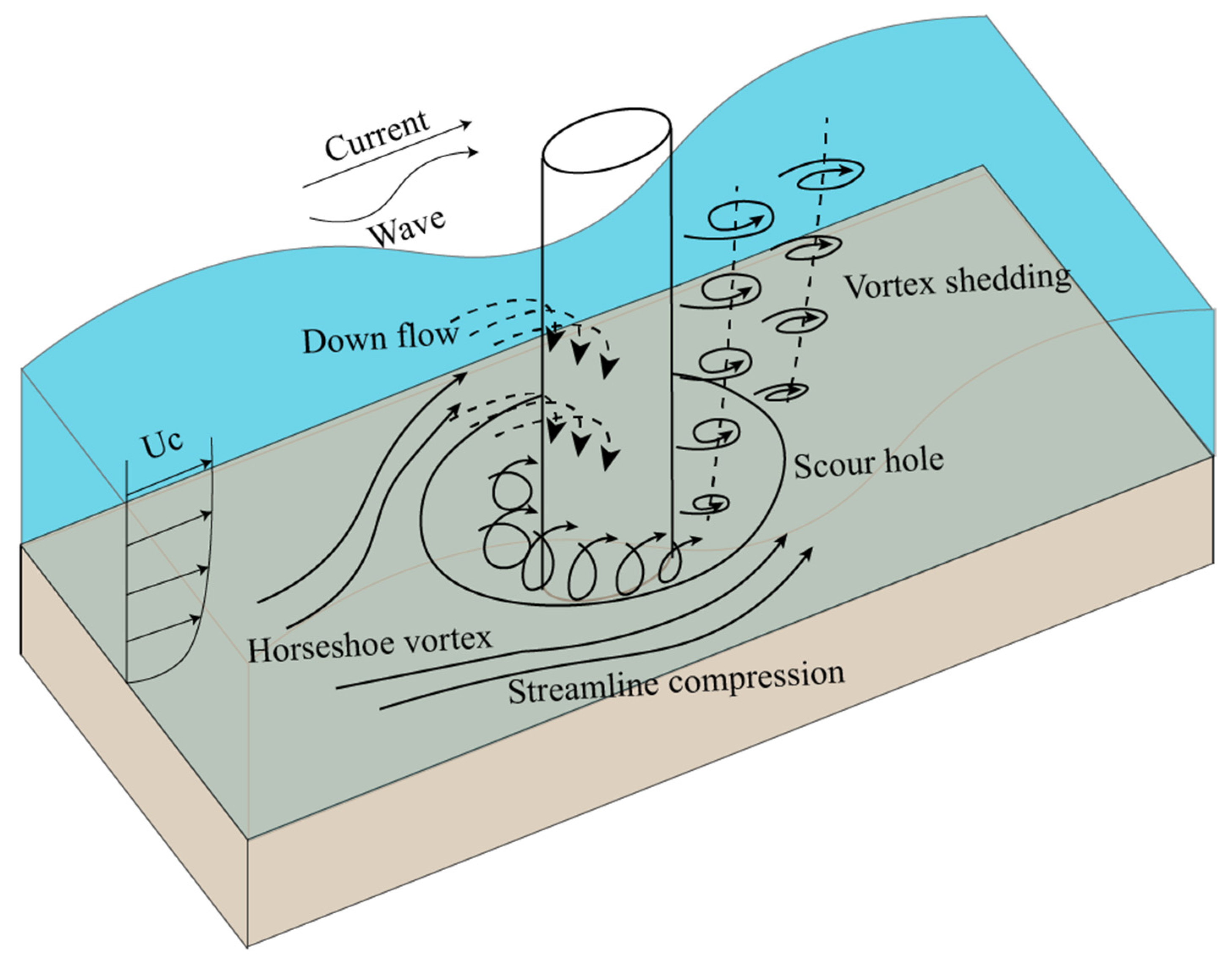

| Modeling Approach | Advantages | Limitations | Applicable Conditions |
|---|---|---|---|
| CFD-based single-phase model | 1. Relatively low computational costs; | 1. Inability to capture microscopic mechanisms; | 1. Macroscopic prediction and engineering design; |
| 2. Simulates macroscopic scour phenomena; | 2. Reliance on empirical formulas and parameters. | 2. Parametric studies and alternative comparison. | |
| 3. Mature technology and flexible framework. | |||
| The Eulerian–Lagrangian two-phase model | 1. Models microscopic mechanisms; | 1. Extremely high computational cost; | 1. Mechanism investigation; |
| 2. Captures particle kinematics; | 2. Scenarios requiring detailed interactions; | ||
| 3. Considers true fluid–particle coupling; | 2. Limited number of particles. | 3. Low to medium sediment transport conditions. | |
| 4. Includes inter-particle contact. | |||
| The Eulerian–Eulerian two-phase model | 1. Capable of modeling the interaction of two phases, fluid and sediment, as a continuous medium; | 1. Ignores the discrete nature of particles; | Suitable for high-concentration sediment transport conditions. |
| 2. Computational efficiency is superior to DEM for scenarios with high sediment concentrations. | 2. Relies on constitutive relationships; | ||
| 3. High computational costs. | |||
| SPH method | 1. Excellent at handling large deformations; | 1. Higher computational costs; | Flows with complex interfaces. |
| 2. Avoids mesh-related issues. | 2. More complex realization of boundary conditions. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, B.; Wang, D.; Qin, C.; Duan, L. Local Scour Around Marine Structures: A Comprehensive Review of Influencing Factors, Prediction Methods, and Future Directions. Buildings 2025, 15, 2125. https://doi.org/10.3390/buildings15122125
Duan B, Wang D, Qin C, Duan L. Local Scour Around Marine Structures: A Comprehensive Review of Influencing Factors, Prediction Methods, and Future Directions. Buildings. 2025; 15(12):2125. https://doi.org/10.3390/buildings15122125
Chicago/Turabian StyleDuan, Bingchuan, Duoyin Wang, Chenxi Qin, and Lunliang Duan. 2025. "Local Scour Around Marine Structures: A Comprehensive Review of Influencing Factors, Prediction Methods, and Future Directions" Buildings 15, no. 12: 2125. https://doi.org/10.3390/buildings15122125
APA StyleDuan, B., Wang, D., Qin, C., & Duan, L. (2025). Local Scour Around Marine Structures: A Comprehensive Review of Influencing Factors, Prediction Methods, and Future Directions. Buildings, 15(12), 2125. https://doi.org/10.3390/buildings15122125






