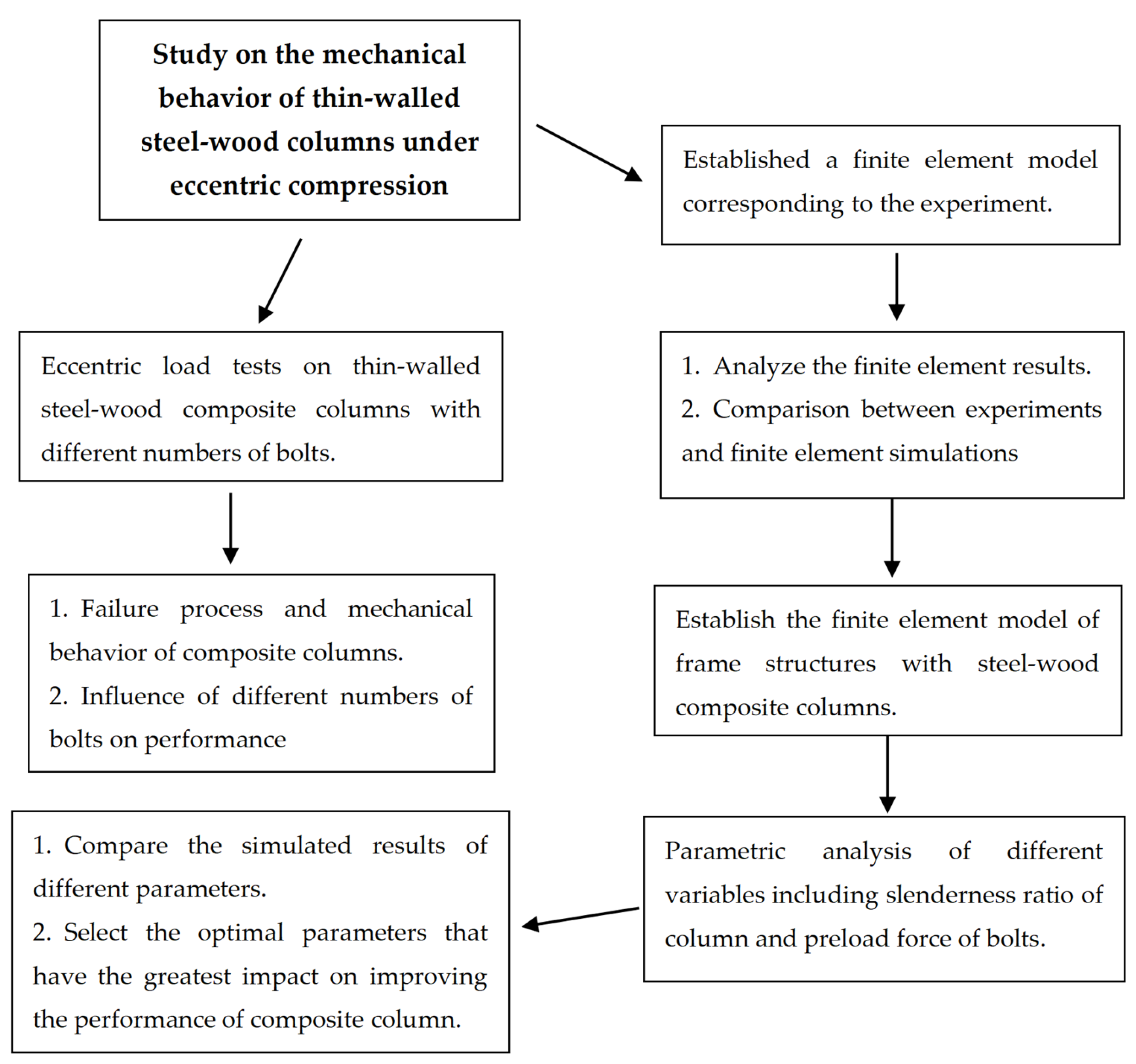
Experiment and Finite Element Research on Mechanical Performance of Thin-Walled Steel–Wood Composite Columns Under Eccentric Compression
Abstract
1. Introduction
2. Experimental Setup and Design of Test Specimens
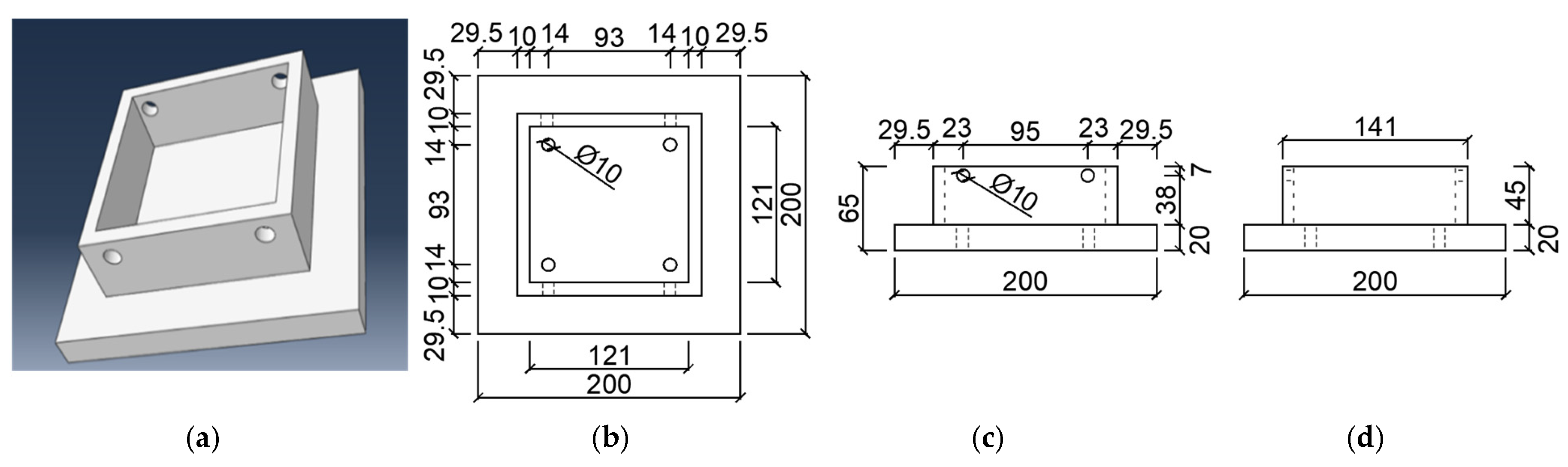
2.1. Specimen Size
2.2. Loading Device and Test Material
2.3. Arrangement of Strain Gauges and Displacement Meters
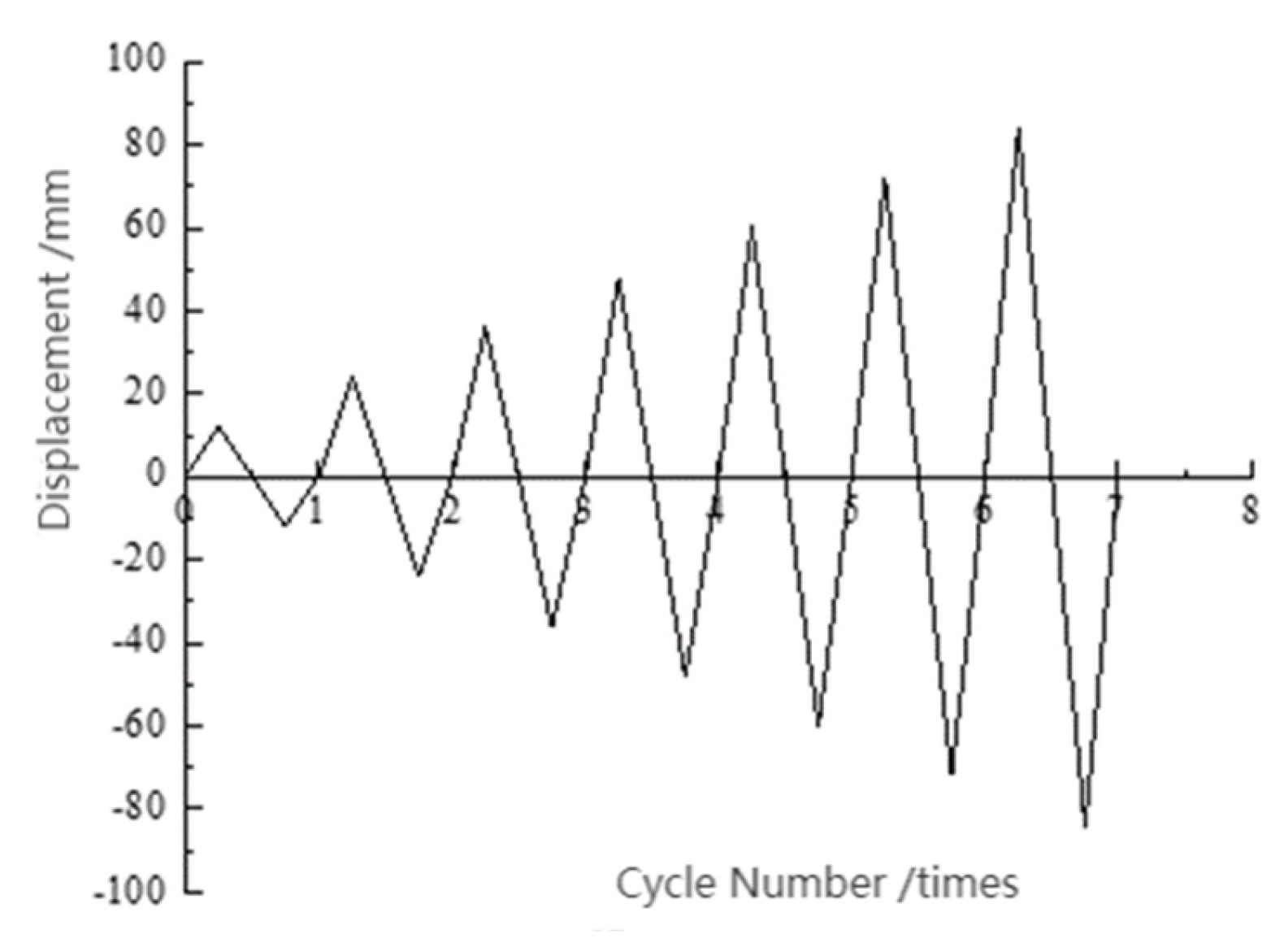
2.4. Loading Program
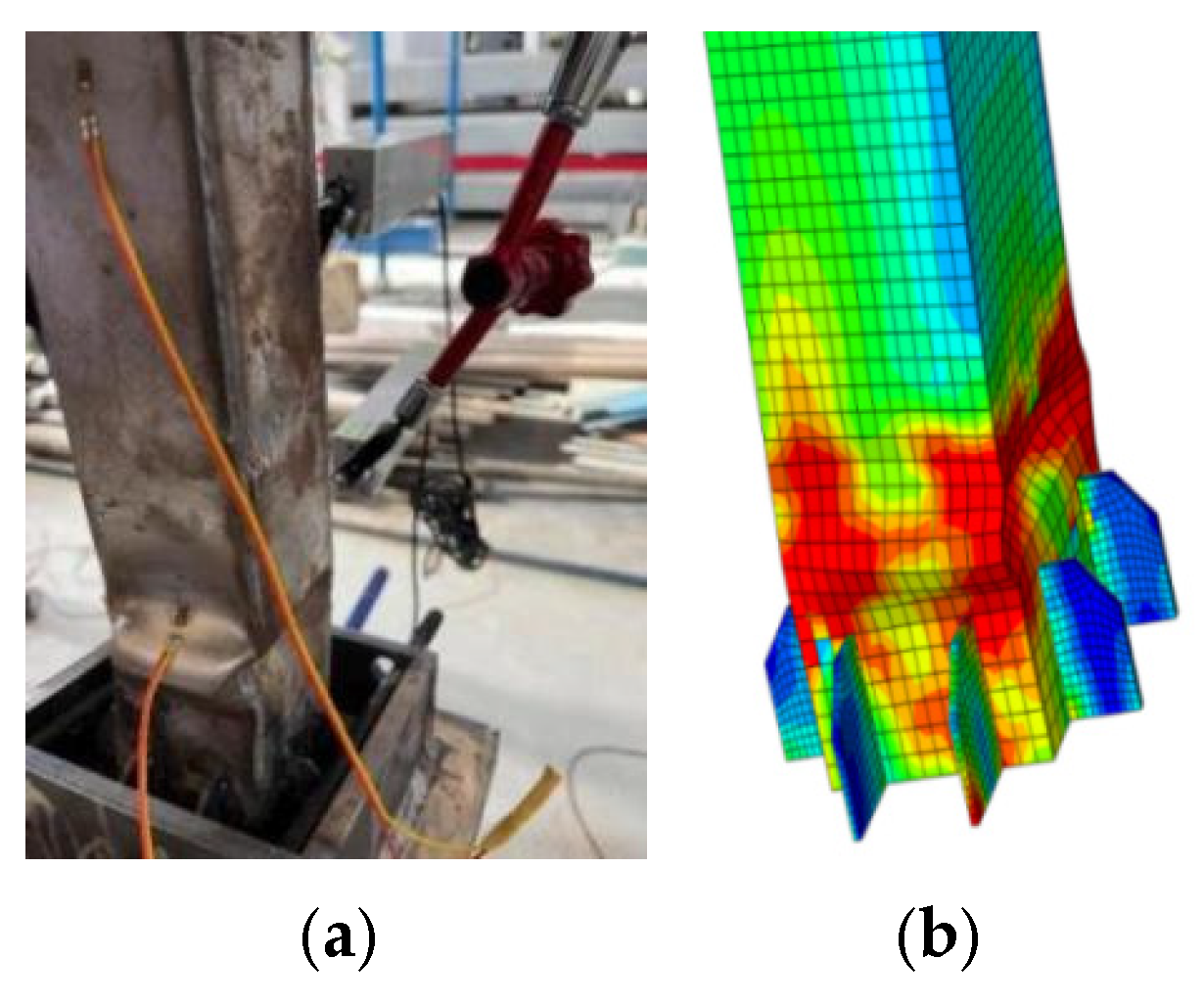
2.5. Test Phenomenon and Damage Pattern
- (1)
- Eccentric compression test of specimen G1
- (2)
- Eccentric compression test of G2 specimen
- (3)
- Eccentric compression test of specimen G3
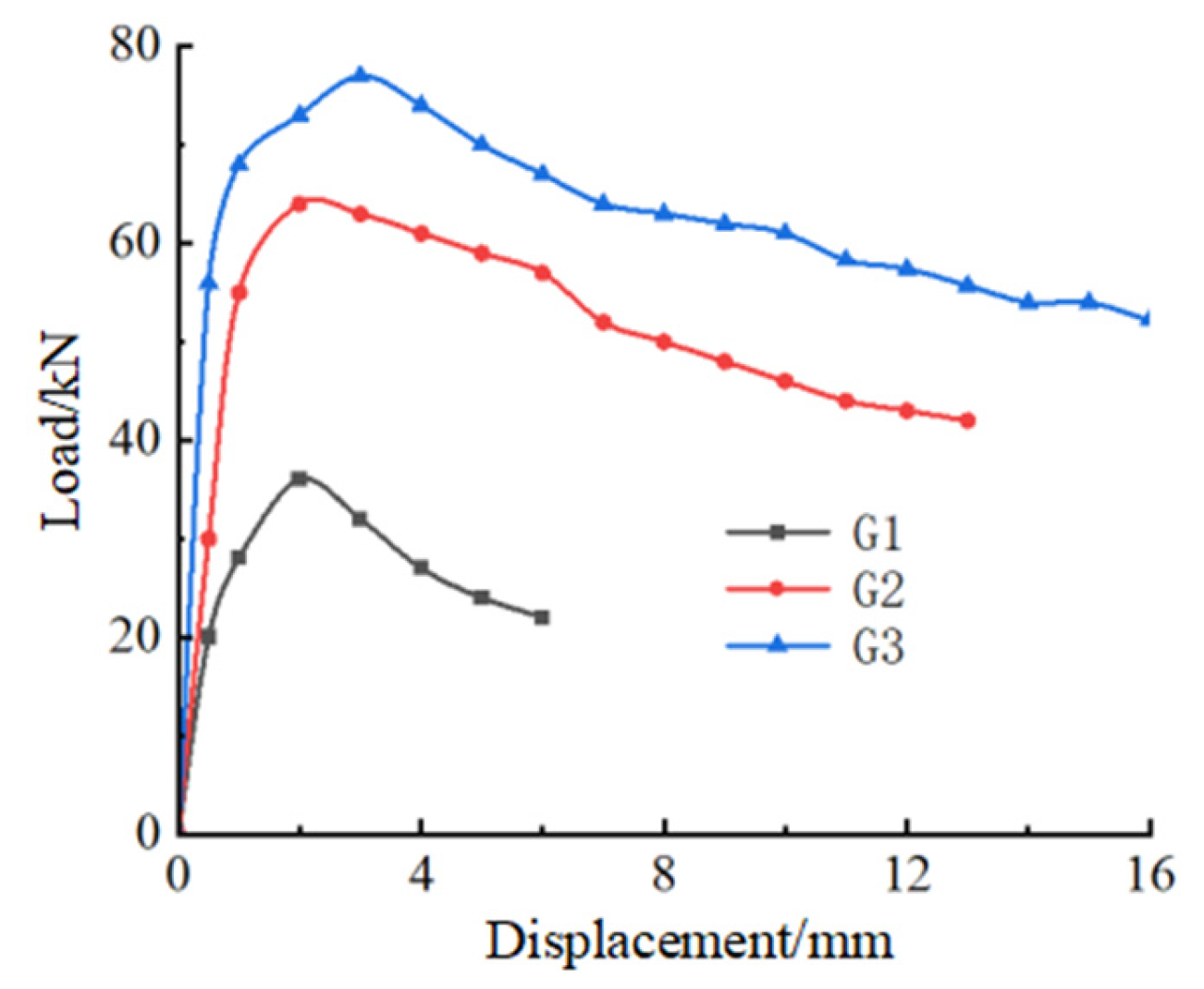
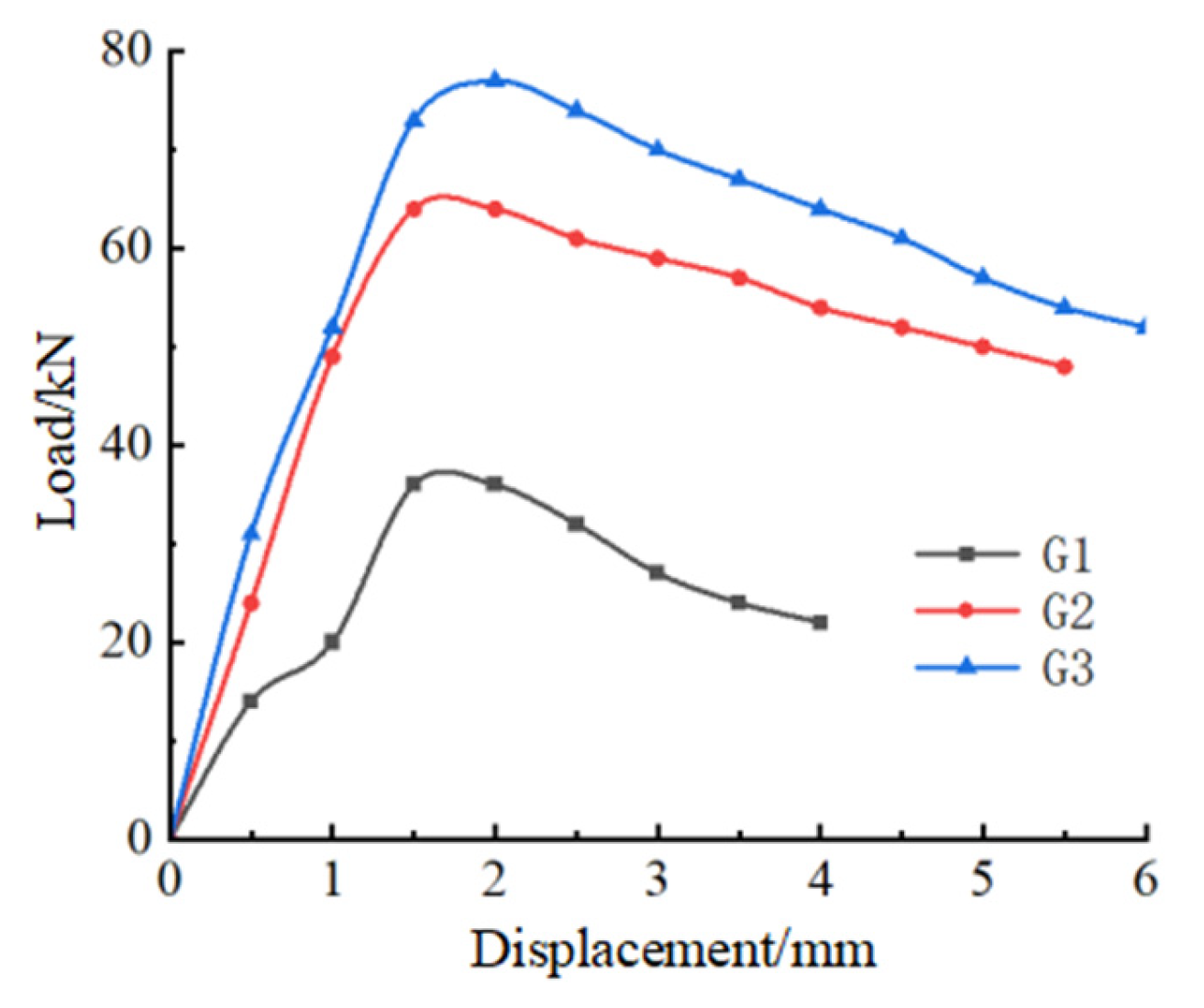
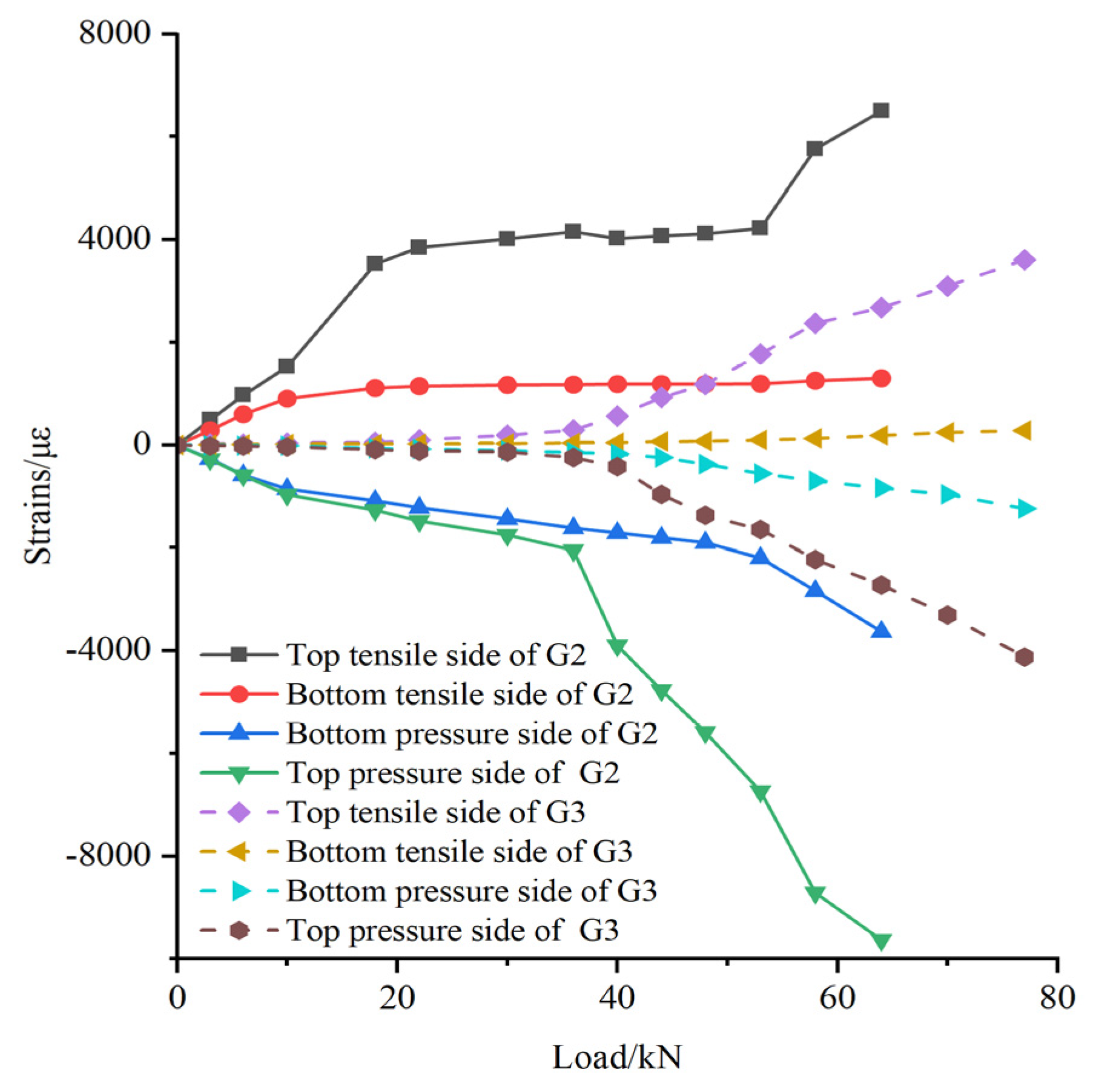
2.6. Analysis of Test Results
- (1)
- Load–vertical displacement curves of specimens
- (2)
- Load–lateral deflection curves of specimens
- (3)
- Load–strain curves of specimens
3. Finite Element Analysis of Thin-Walled Steel–Wood Composite Column
3.1. Definition of Material Properties of Finite Element Model
- Fij (i = 1, 2, 3) and Nij (i ≠ j = 1, 2, 3) are constants; 1—longitudinal, 2—radial, 3—tangential; Rij—yield ratio; σii—normal yield stress; σij—tangential yield stress; σ0—custom yield stress.
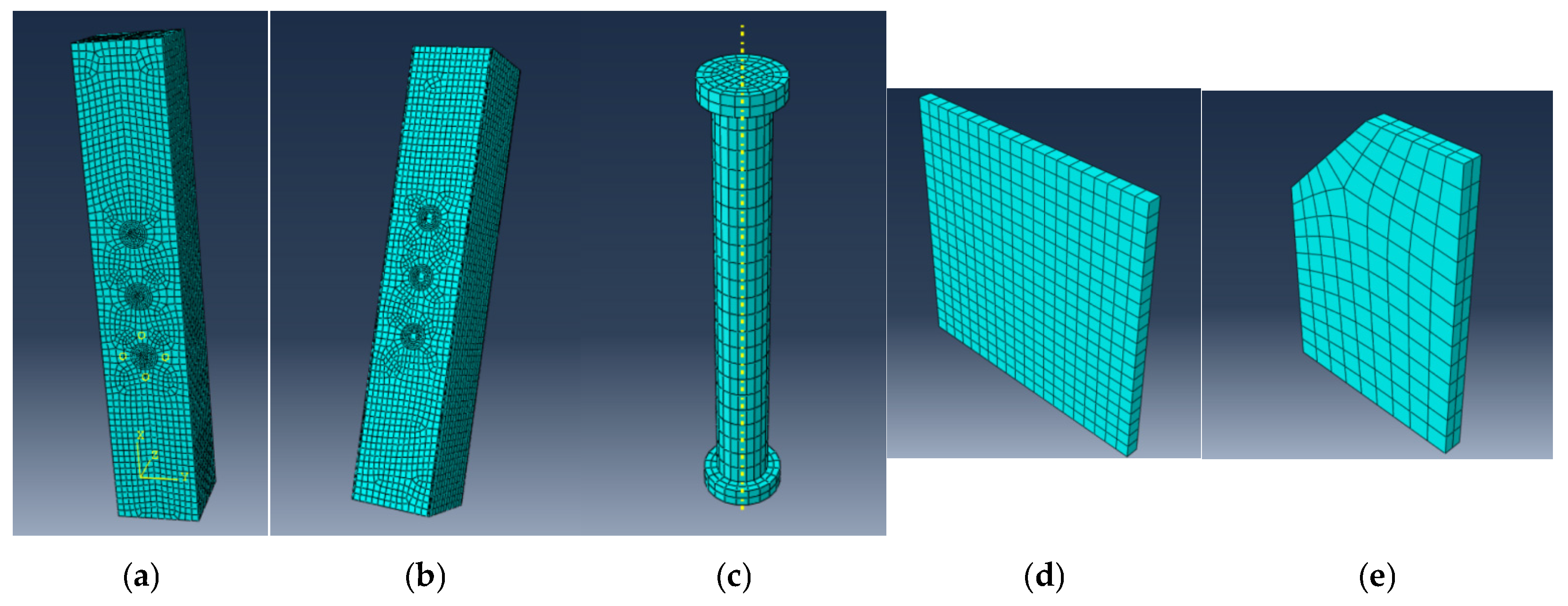
3.2. Establishment of the Finite Element Model
3.2.1. Component Meshing
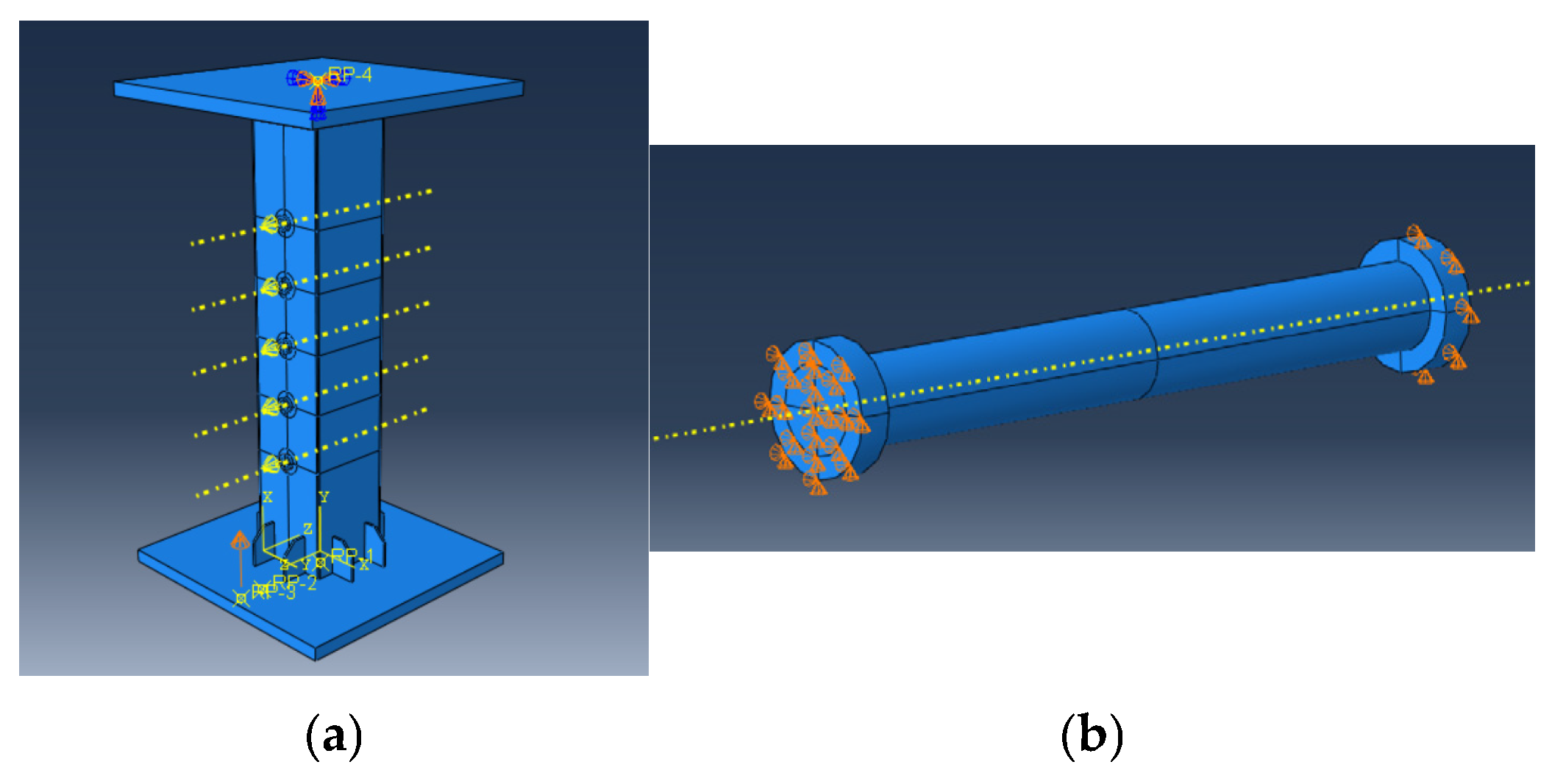
3.2.2. Contact Relationships and Boundary Conditions
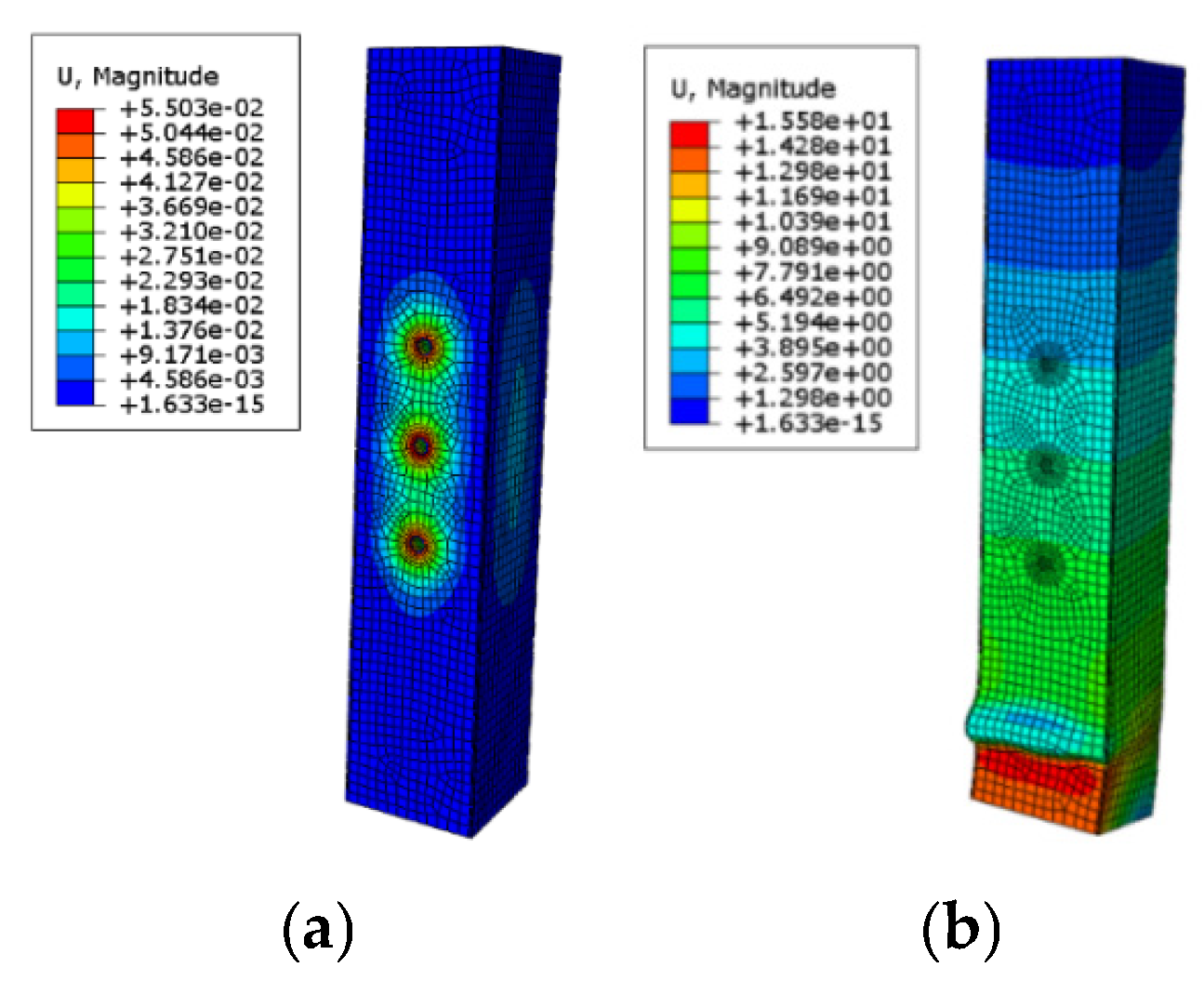
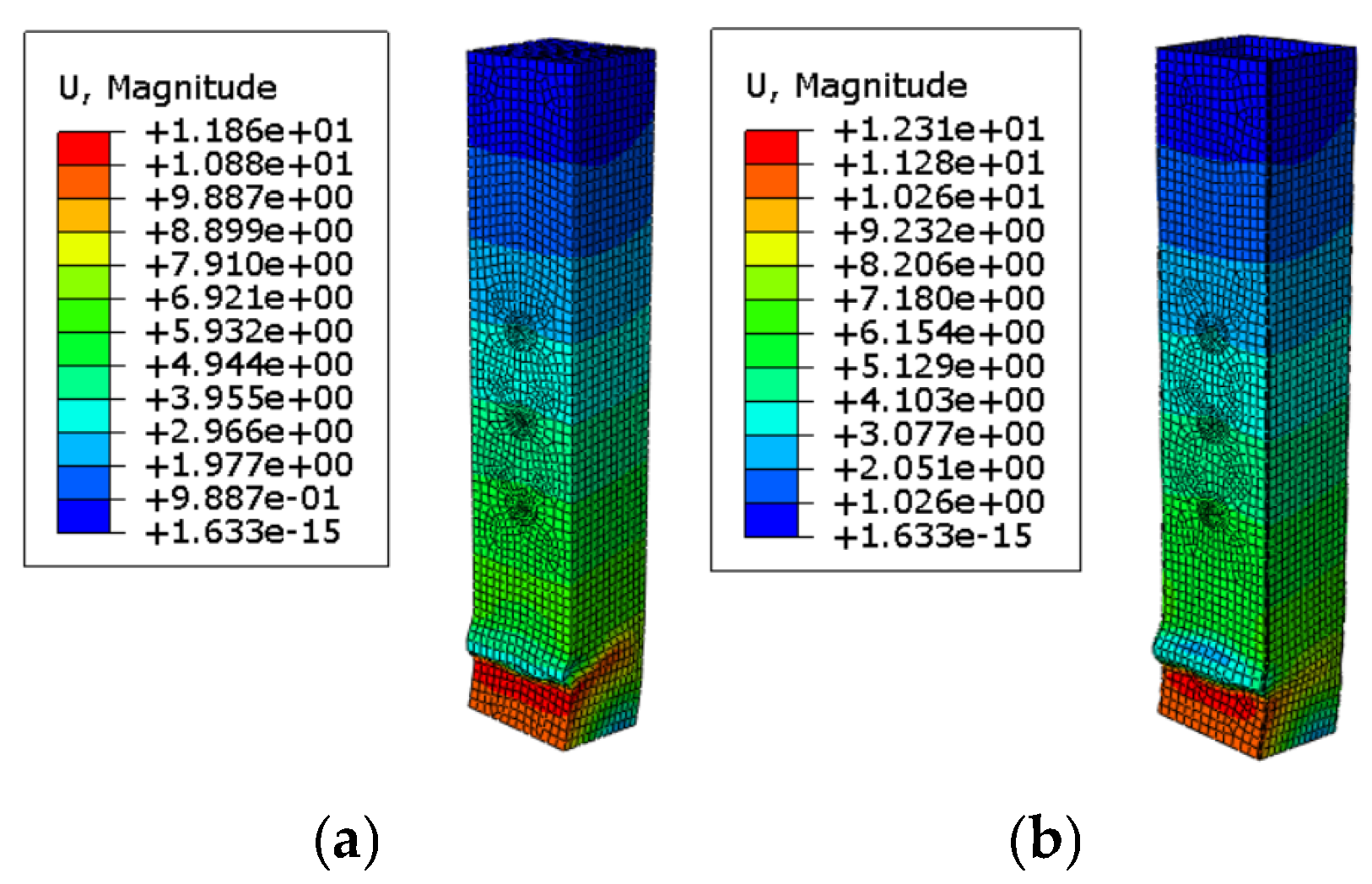
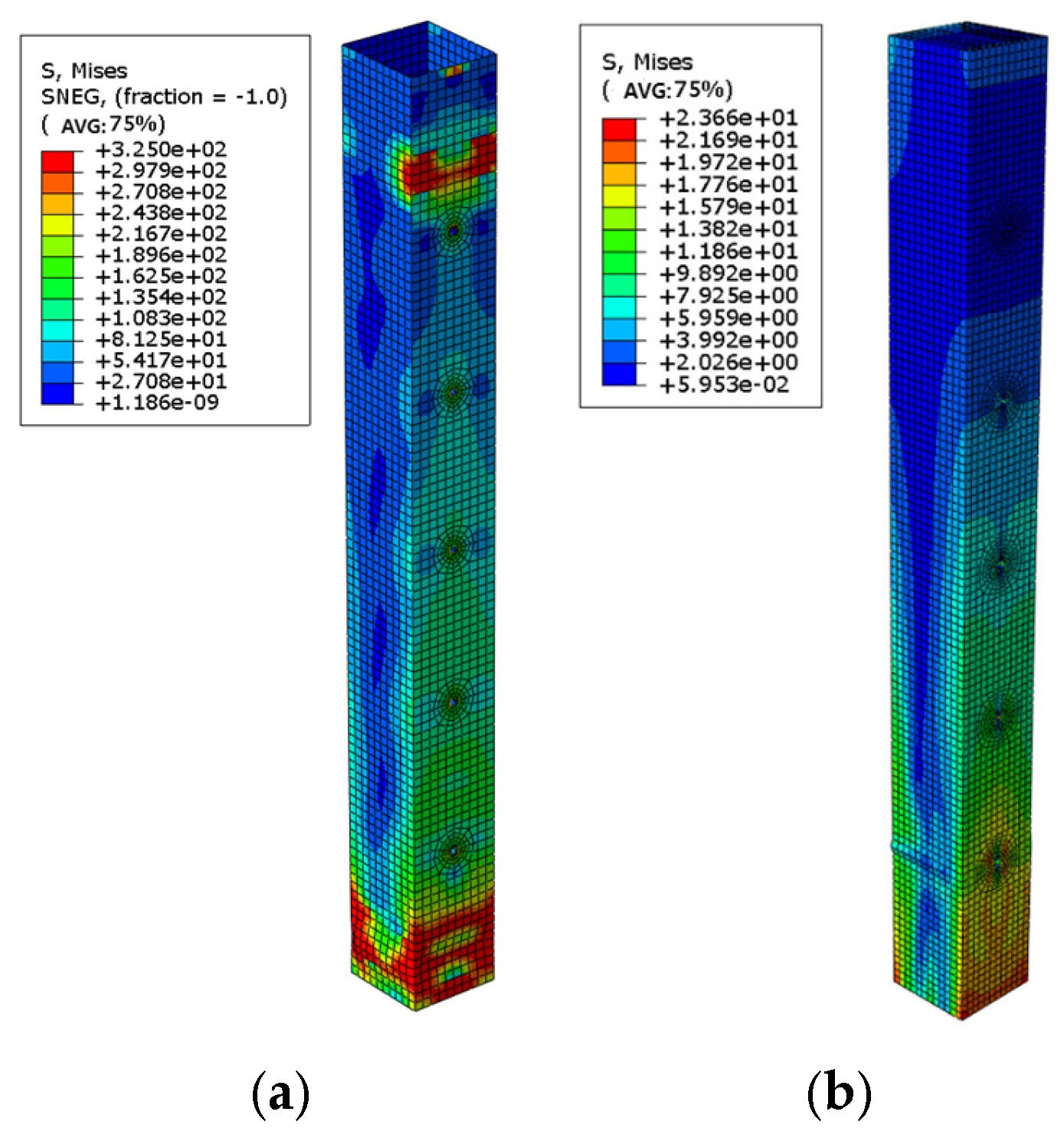
3.3. Comparison of Simulation Results
- (1)
- Model analysis of specimen G1
- (2)
- Model analysis of specimen G2
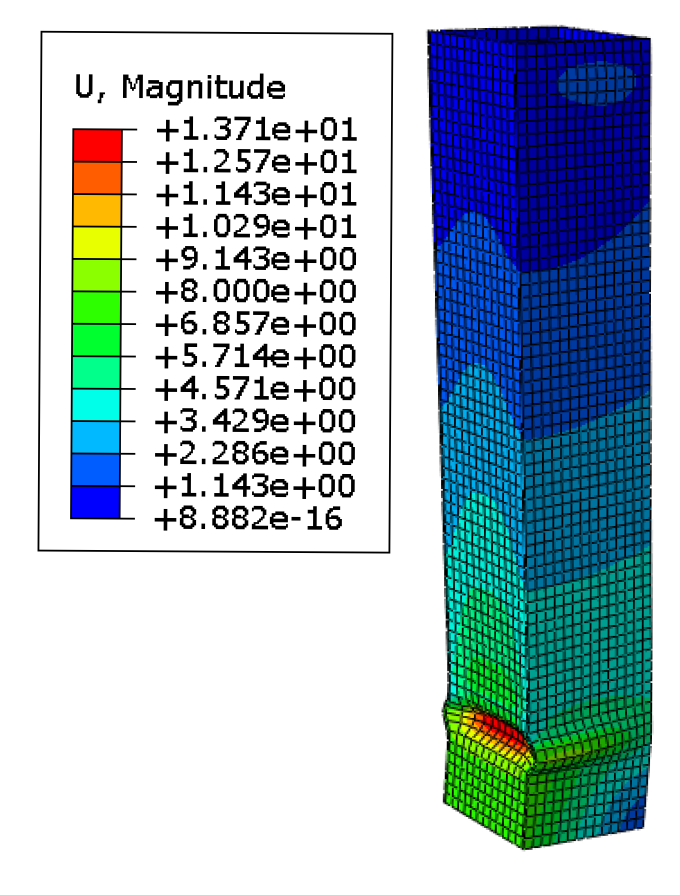
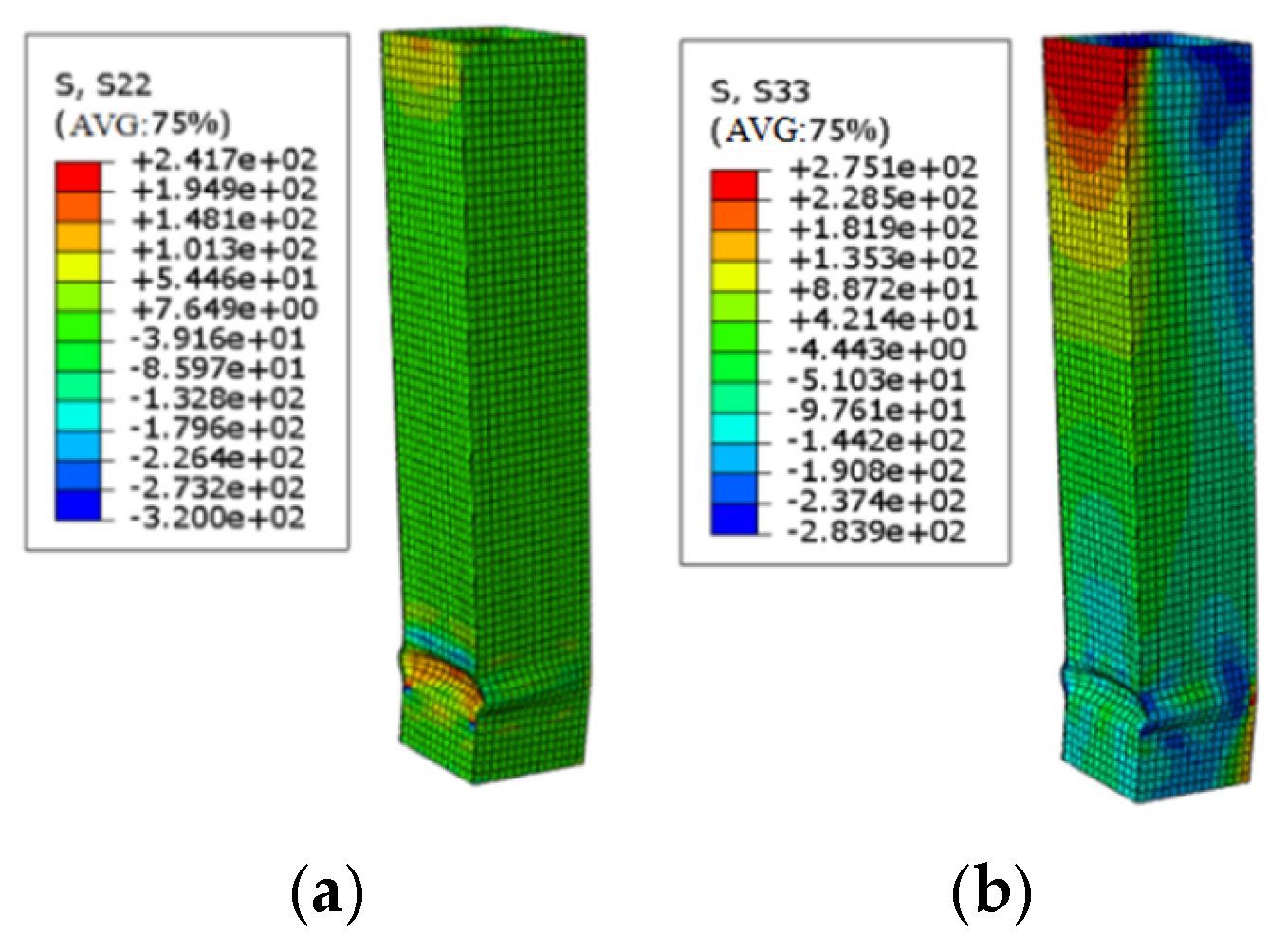
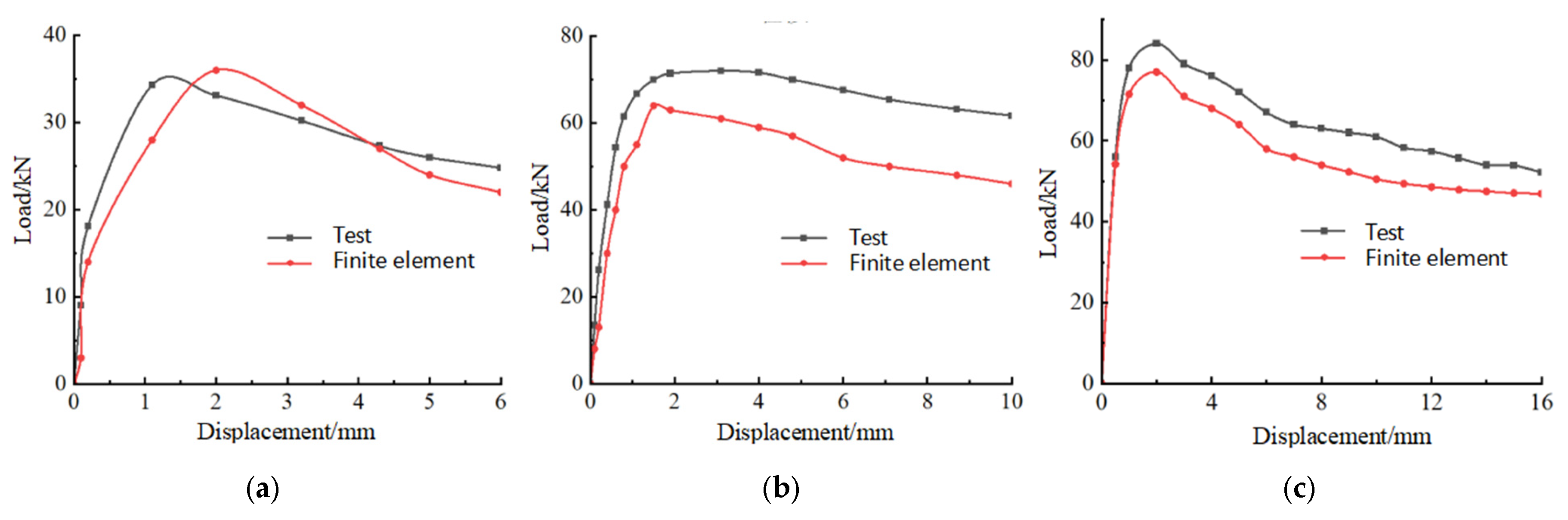
3.4. Finite Element Result Analysis
- (1)
- Comparative analysis of simulated and tested load–displacement curves
- (2)
- Comparative Analysis of Finite Element Simulation and Test Ultimate Load
4. Parametric Analysis of Thin-Walled Steel–Wood Composite Columns
4.1. Selection of Frame Parameters and Model Design
4.1.1. Selection of Frame Parameters
4.1.2. Model Design
4.2. Structural Calculation Results
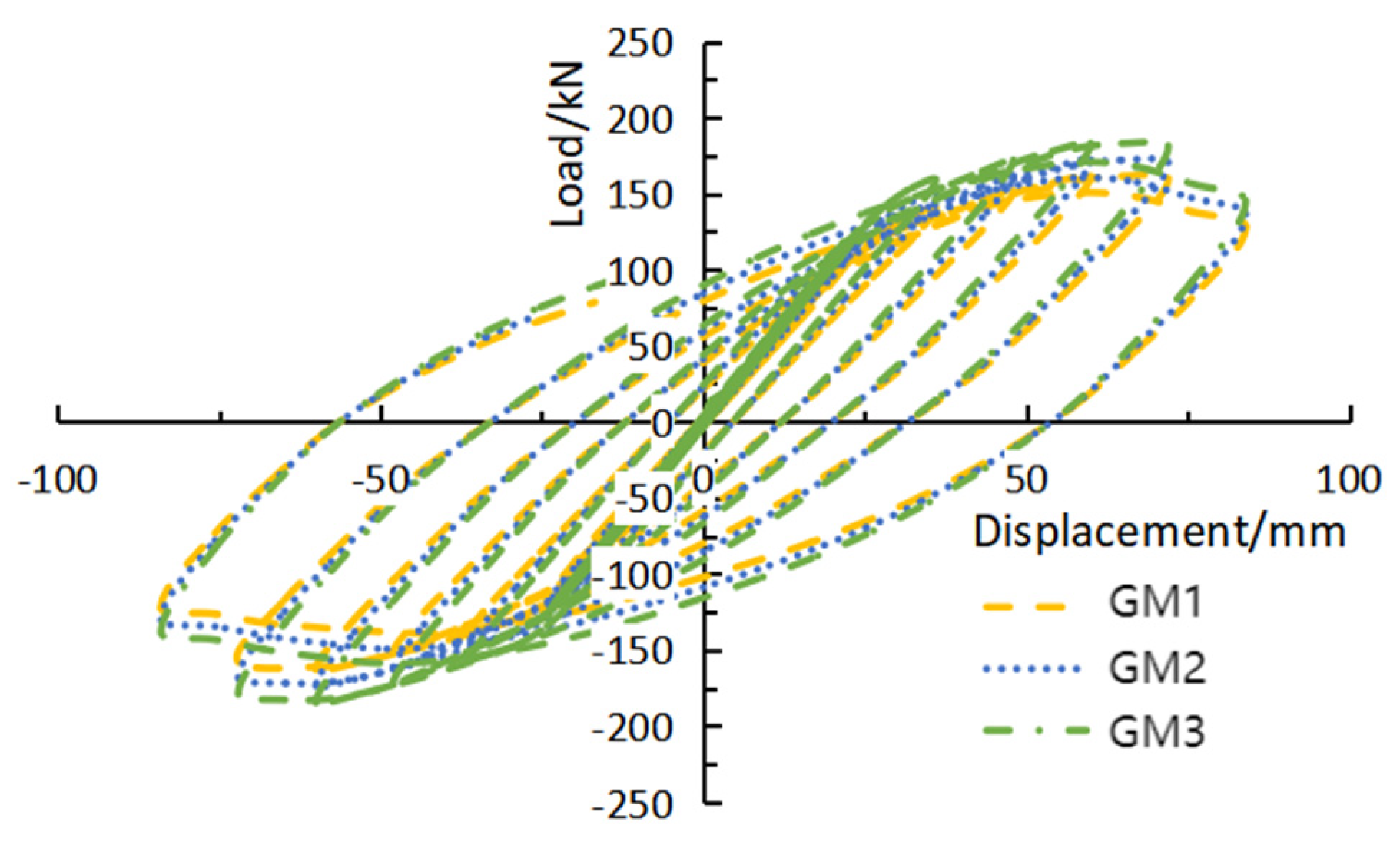
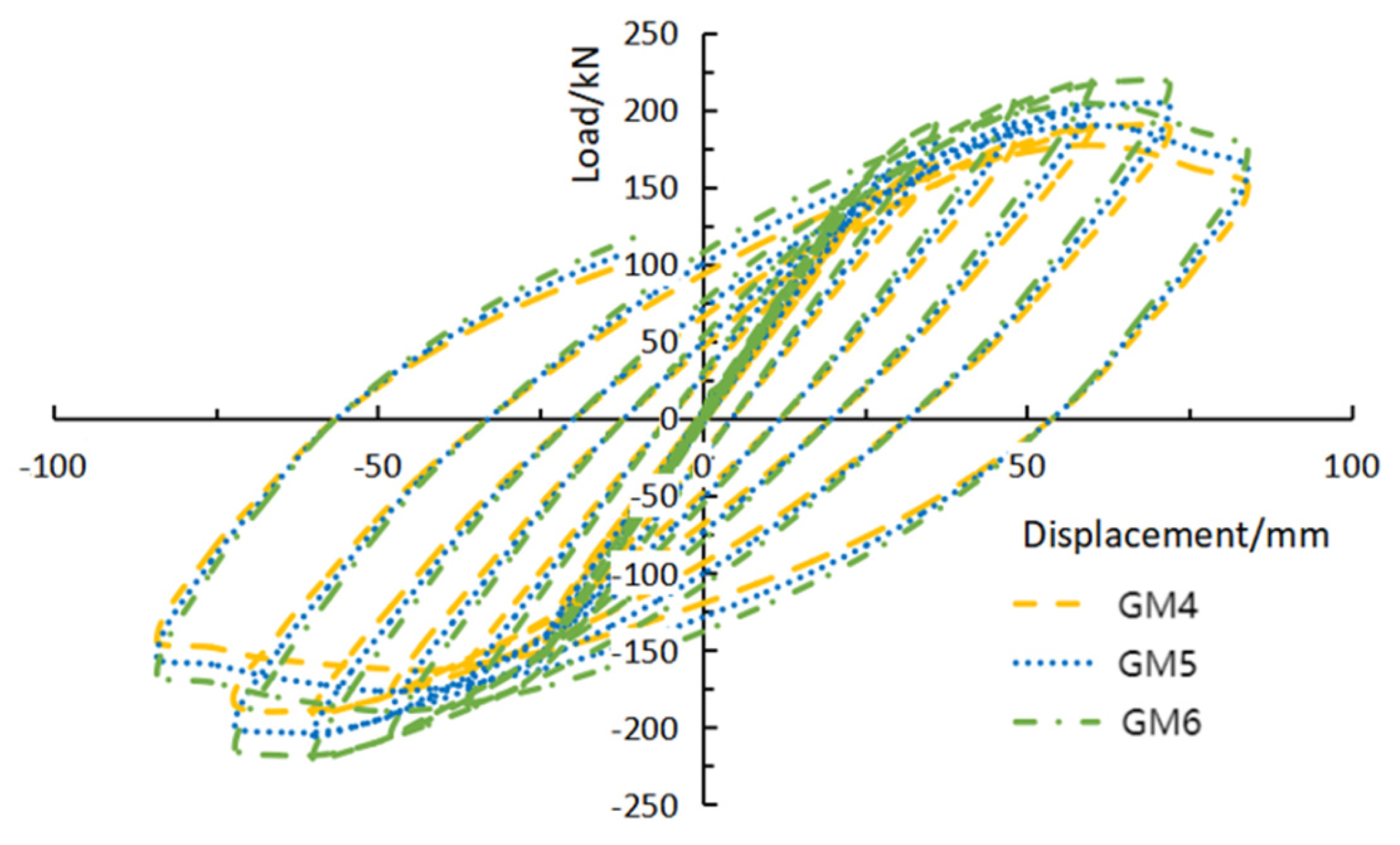
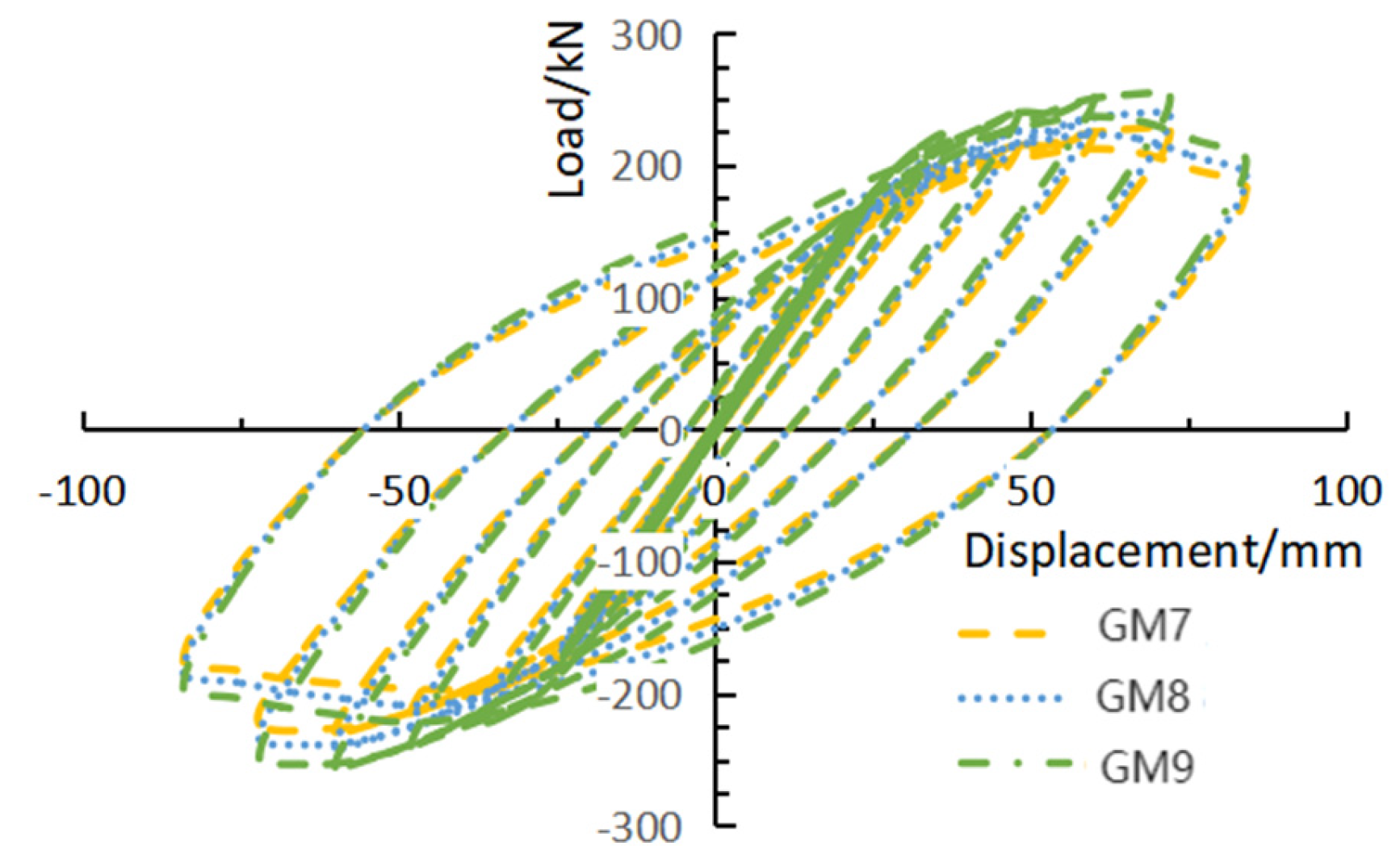
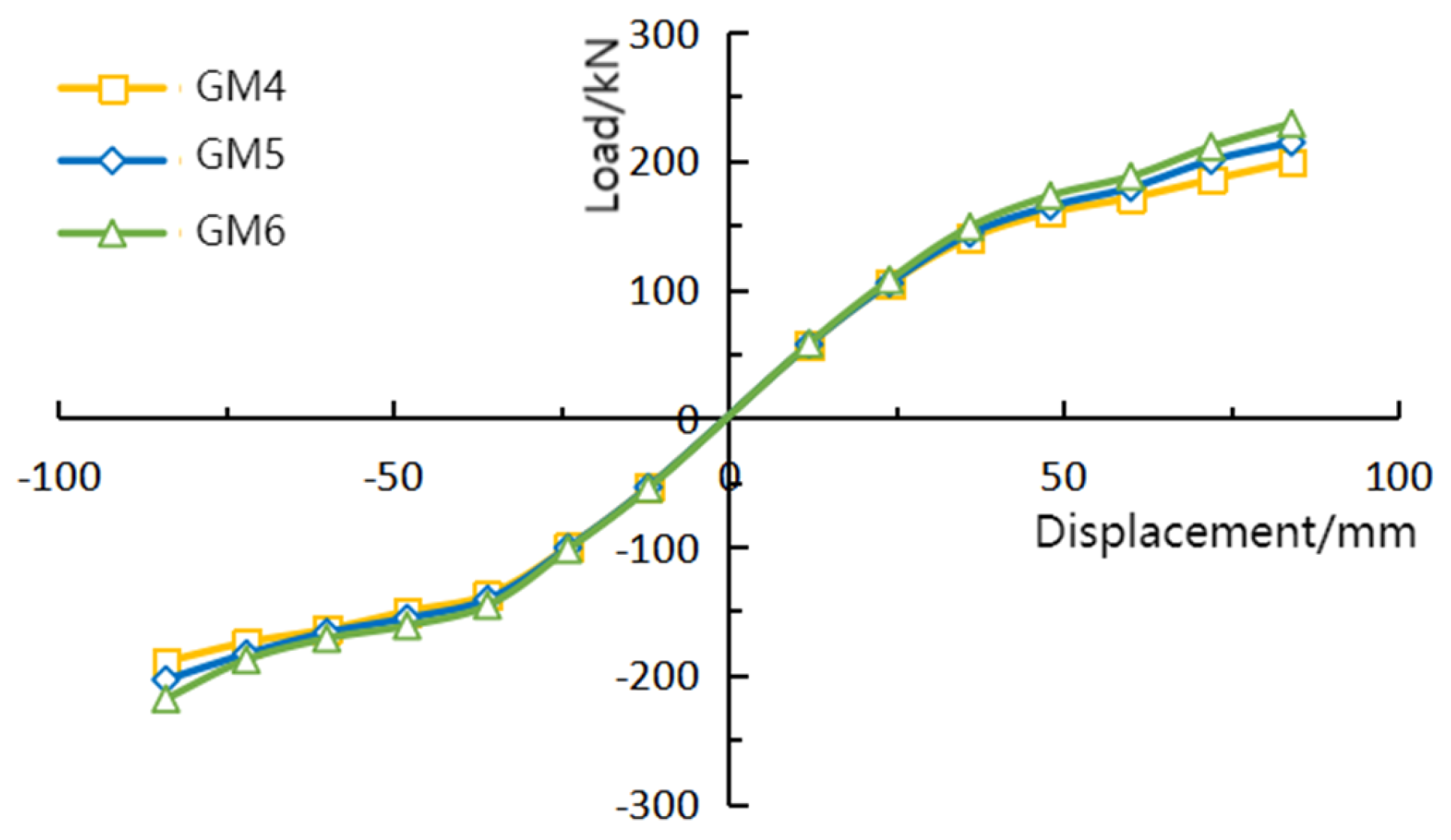
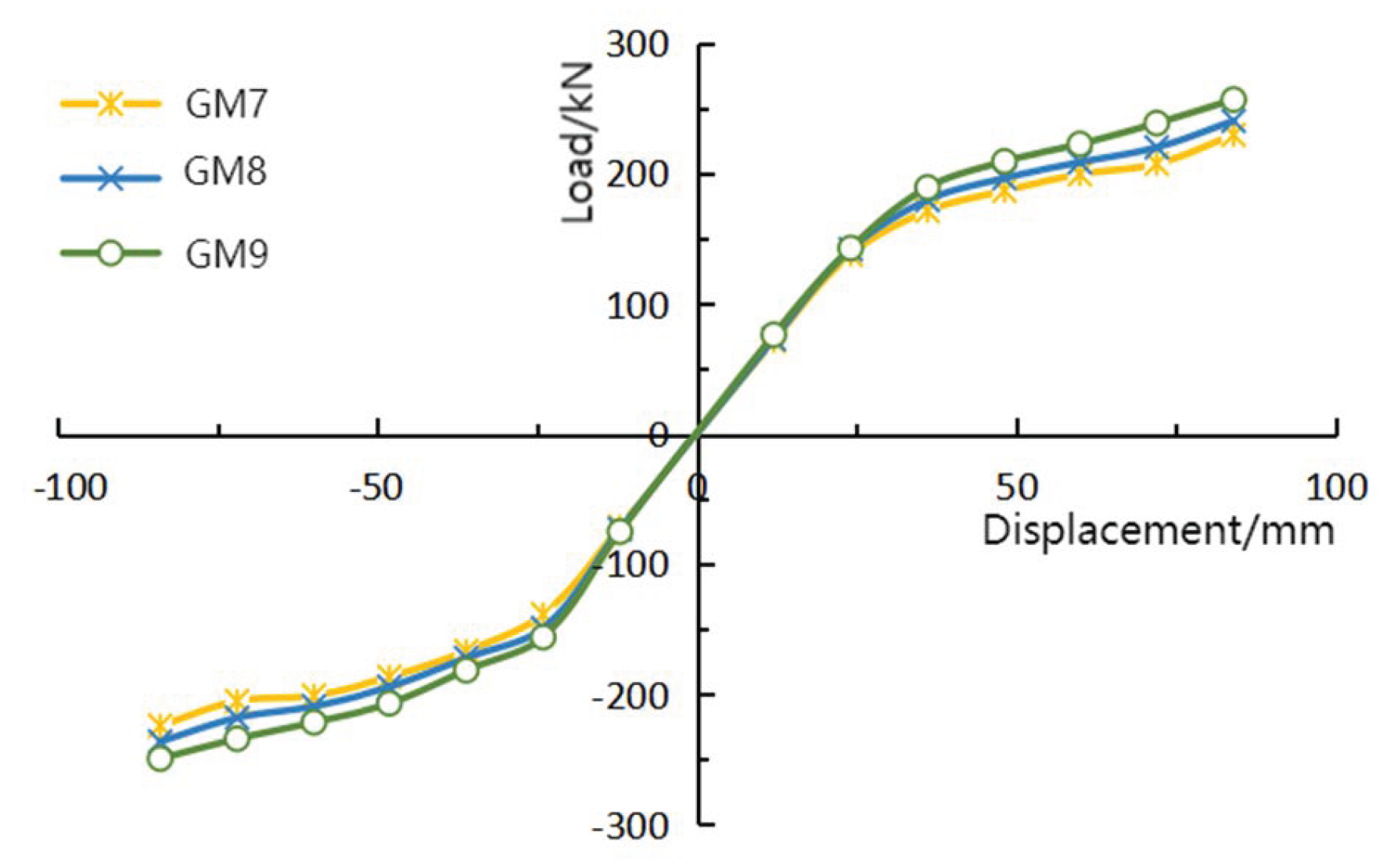
4.2.1. Comparison of Hysteresis Curves
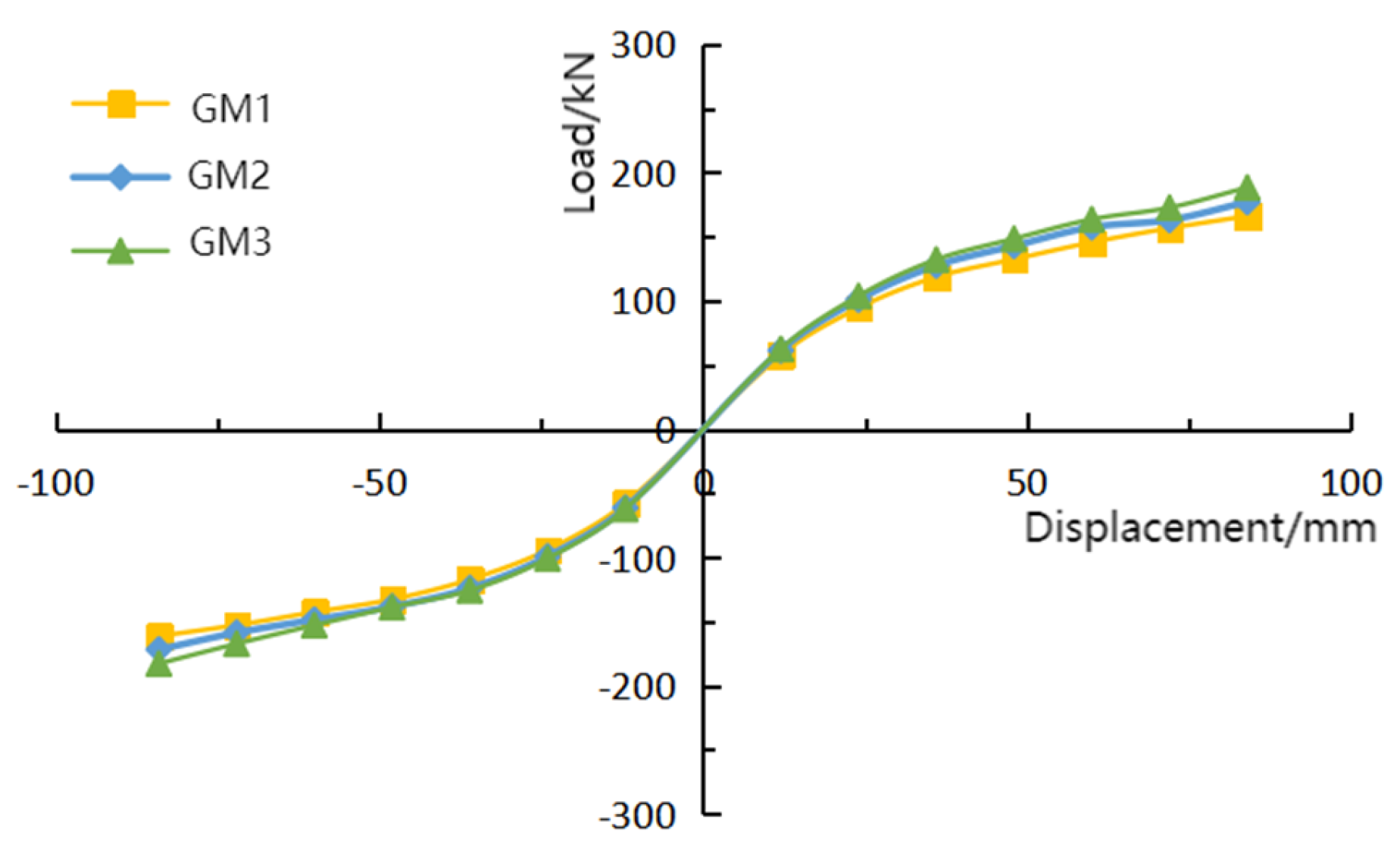
4.2.2. Comparison of Skeleton Curves
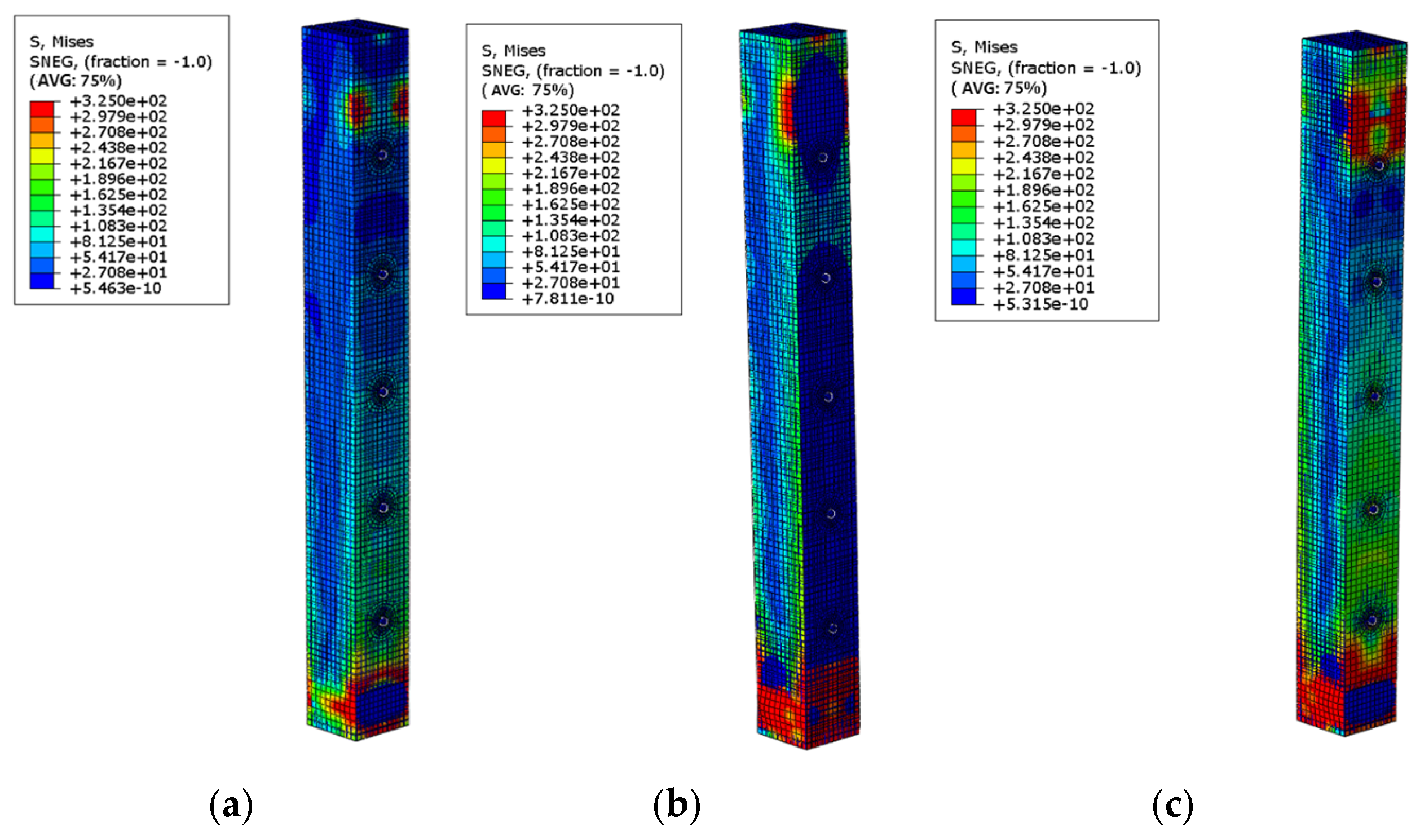
4.2.3. Comparison of Stress Nephograms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Zhou, J. Study on the mechanical properties and application prospects of the traditional and modern connection of wood structure. IOP Conf. Ser. Earth Environ. Sci. 2021, 638, 012085. [Google Scholar] [CrossRef]
- Octavia, S.; Raubaba, H.S.; Simorangkir, Y.V. Wood and steel as a material alternative of concrete replacement in house structure in Merauke city. IOP Conf. Ser. Earth Environ. Sci. 2019, 343, 012231. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Feng, X.; Zhao, Y.; Li, Z. Mechanical properties and probabilistic models of wood and engineered wood products: A review of green construction materials. Case Stud. Constr. Mater. 2024, 21, 3796. [Google Scholar] [CrossRef]
- Song, X.B.; Zhang, Y.; Lu, Y.; Peng, Y.Q.; Zhou, H. Experimental study on fire resistance of traditional timber mortise-tenon joints with damages. Fire Saf. J. 2023, 138, 103780. [Google Scholar] [CrossRef]
- Abdelrahman, M.; Khaloian-Sarnaghi, A.; van de Kuilen, J.W. Fire performance of wood-steel hybrid elements: Finite element analysis and experimental validation. Wood Sci. Technol. 2025, 59, 23. [Google Scholar] [CrossRef]
- Liu, K.; Shao, J.; Tang, B.; Wu, Q.; Wang, Z. Seismic performance of low-yield-point steel plate shear walls under horizontal cyclic load. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 3739–3752. [Google Scholar] [CrossRef]
- Shao, J.; Wang, K.; Kaewunruen, S.; Cai, W.; Wang, Z. Experimental investigations into earthquake resistance of steel frame retrofitted by low-yield-point steel energy absorbers. Appl. Sci. 2019, 9, 3299. [Google Scholar] [CrossRef]
- Wang, T.; Shao, J.; Xu, T.; Wang, Z. Study on axial compression properties of aluminum foam-filled steel tube members after high temperature. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 883900. [Google Scholar] [CrossRef]
- Wang, Z.; Shao, J. Study on quasi-static axial compression performance and energy absorption of aluminum foam-filled steel tubes. Materials 2023, 16, 4485. [Google Scholar] [CrossRef]
- Wang, T.; Shao, J.; Zhao, C.; Liu, W.; Wang, Z. Shaking table test for evaluating the seismic performance of steel frame retrofitted by buckling-restrained braces. Shock Vib. 2021, 1–17. [Google Scholar] [CrossRef]
- Xu, T.; Shao, J.; Zhang, J.; Kaewunruen, S. Experimental performance evaluation of multi-storey steel plate shear walls designed by different methods. Int. J. Civ. Eng. 2019, 17, 1145–1154. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Fang, H.; Liu, W.; Hong, J.; Hui, D.; Gaff, M. Compressive behaviour of wood-filled GFRP square columns with latticeweb reinforcements. Constr. Build. Mater. 2021, 310, 125129. [Google Scholar] [CrossRef]
- Navaratnam, S.; Thamboo, J.; Poologanathan, K.; Roy, K.; Gatheeshgar, P. Finite element modelling of timber infilled steel tubular shortcolumns under axial compression. Structures 2021, 30, 910–924. [Google Scholar] [CrossRef]
- Hu, Q.; Gao, Y.; Meng, X.; Diao, Y. Axial compression of steel-timber composite column consisting of H-shaped-steel and glulam. Eng. Struct. 2020, 216, 110561. [Google Scholar] [CrossRef]
- Yang, R.; Li, H.; Lorenzo, R.; Ashraf, M.; Sun, Y.; Yuan, Q. Mechanical behaviour of steel timber composite shear connections. Constr. Build. Mater. 2020, 258, 119605. [Google Scholar] [CrossRef]
- Qiao, Q.; Yang, Z.; Mou, B. Experimental study on axial compressive behavior of CFRP confined square timber filled steel tube stub columns. Structures 2020, 24, 823–834. [Google Scholar] [CrossRef]
- Ghazijahani, G.T.; Jiao, H.; Holloway, D. Timber filled CFRP jacketed circular steel tubes under axial compression. Constr. Build. Mater. 2015, 94, 791–799. [Google Scholar] [CrossRef]
- Heinisuo, M.; Mela, K.; Pajunen, S.; Malaska, M. New steel-timber composite beam, Nordic system. Ce/Papers 2019, 3, 193–202. [Google Scholar] [CrossRef]
- Wu, C.; Duan, J.; Yang, Z.; Zhao, Z.; Xu, Y. A Novel Rectangular Section Combined Beam of Welded Thin-Walled H-Shape Steel/Camphor Pine Wood: The Bending Performance Study. Sustainability 2023, 15, 7450. [Google Scholar] [CrossRef]
- Zhang, F.; Lu, Z.; Wang, D.; Fang, H. Mechanical properties of the composite sandwich structures with cold formed profiled steel plate and balsa wood core. Eng. Struct. 2024, 300, 117256. [Google Scholar] [CrossRef]
- Vogiatzis, T.; Efthymiou, E.; Tsalkatidis, T. Investigation of Wood-Steel Composite Shear Walls Behavioural Parameters. Ce/Papers 2023, 6, 243–247. [Google Scholar] [CrossRef]
- Sadat, S.I.; Ding, F.-X.; Lyu, F.; Wang, E.; Sun, H.; Akhunzada, K.; Lessani, N. Axial compression behavior and reliable design approach of rectangular dune sand concrete-filled steel tube stub columns. Dev. Built Environ. 2024, 18, 100437. [Google Scholar] [CrossRef]
- Sadat, S.I.; Ding, F.-X.; Wang, M.; Lyu, F.; Akhunzada, K.; Xu, H.; Hui, B. Behavior and Reliable Design Methods of Axial Compressed Dune Sand Concrete-Filled Circular Steel Tube Columns. Appl. Sci. 2024, 14, 6939. [Google Scholar] [CrossRef]
- Zhang, C.-C.; Ding, F.-X.; Sadat, S.I.; Lyu, F.; Huang, X.-Y.; Gao, R.; Yu, T.; Liu, Y.-L. Flexural Behavior of Desert Sand Concrete-Filled Steel Tube: Experimental Validation, FEM Analysis, and Design Formulas. Materials 2025, 18, 2371. [Google Scholar] [CrossRef]
- Wang, Y.; Gu, Y.; Liu, J. A domain-decomposition generalized finite difference method for stress analysis in three-dimensional composite materials. Appl. Math. Lett. 2020, 104, 106226. [Google Scholar] [CrossRef]
- Kabir, H.; Aghdam, M.M. A generalized 2D Bézier-based solution for stress analysis of notched epoxy resin plates reinforced with graphene nanoplatelets. Thin-Walled Struct. 2021, 169, 108484. [Google Scholar] [CrossRef]
- Kaushal, M.; Joshi, Y.M. Three-dimensional yielding in anisotropic materials: Validation of Hill’s criterion. Soft Matter 2019, 15, 4915–4920. [Google Scholar] [CrossRef]

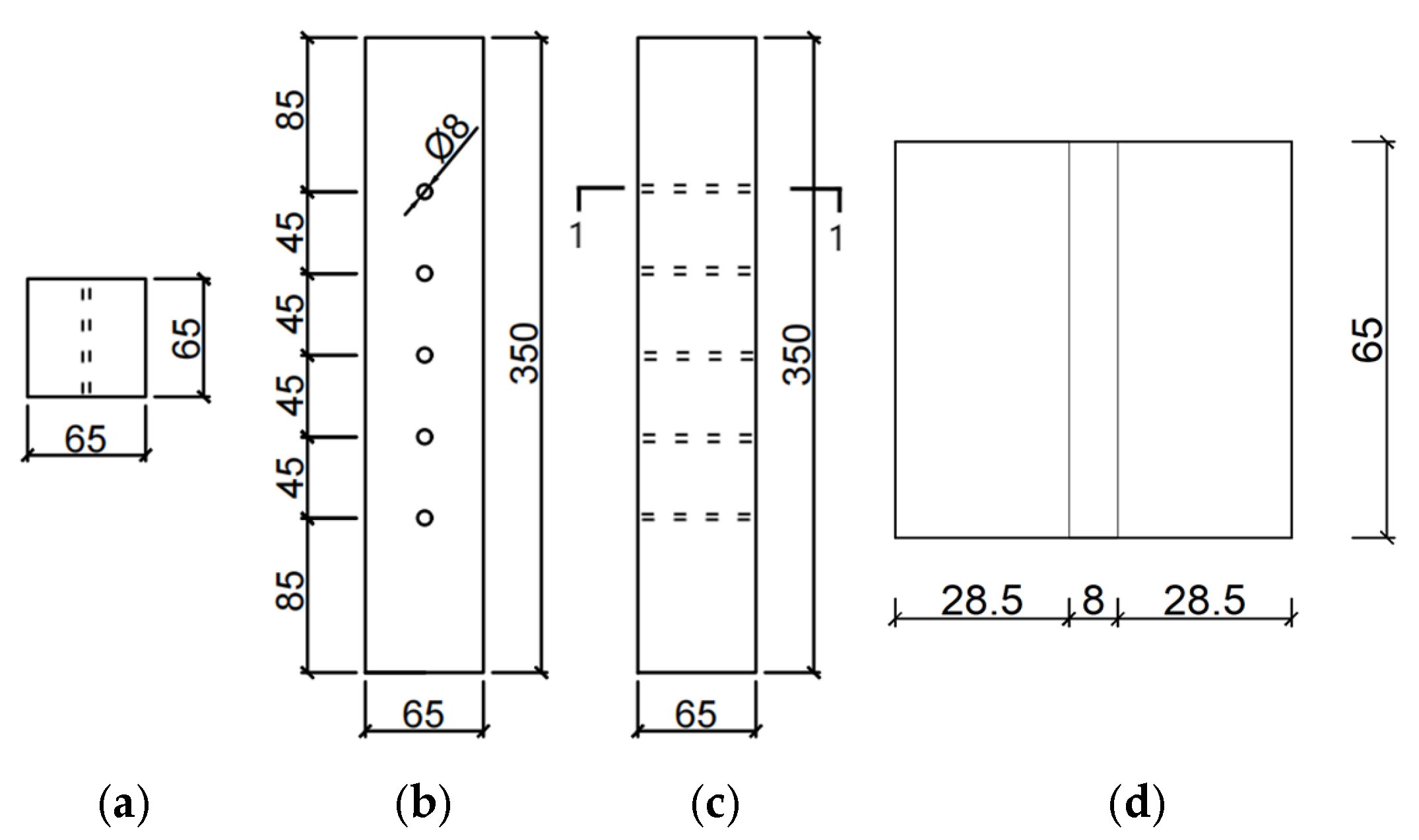
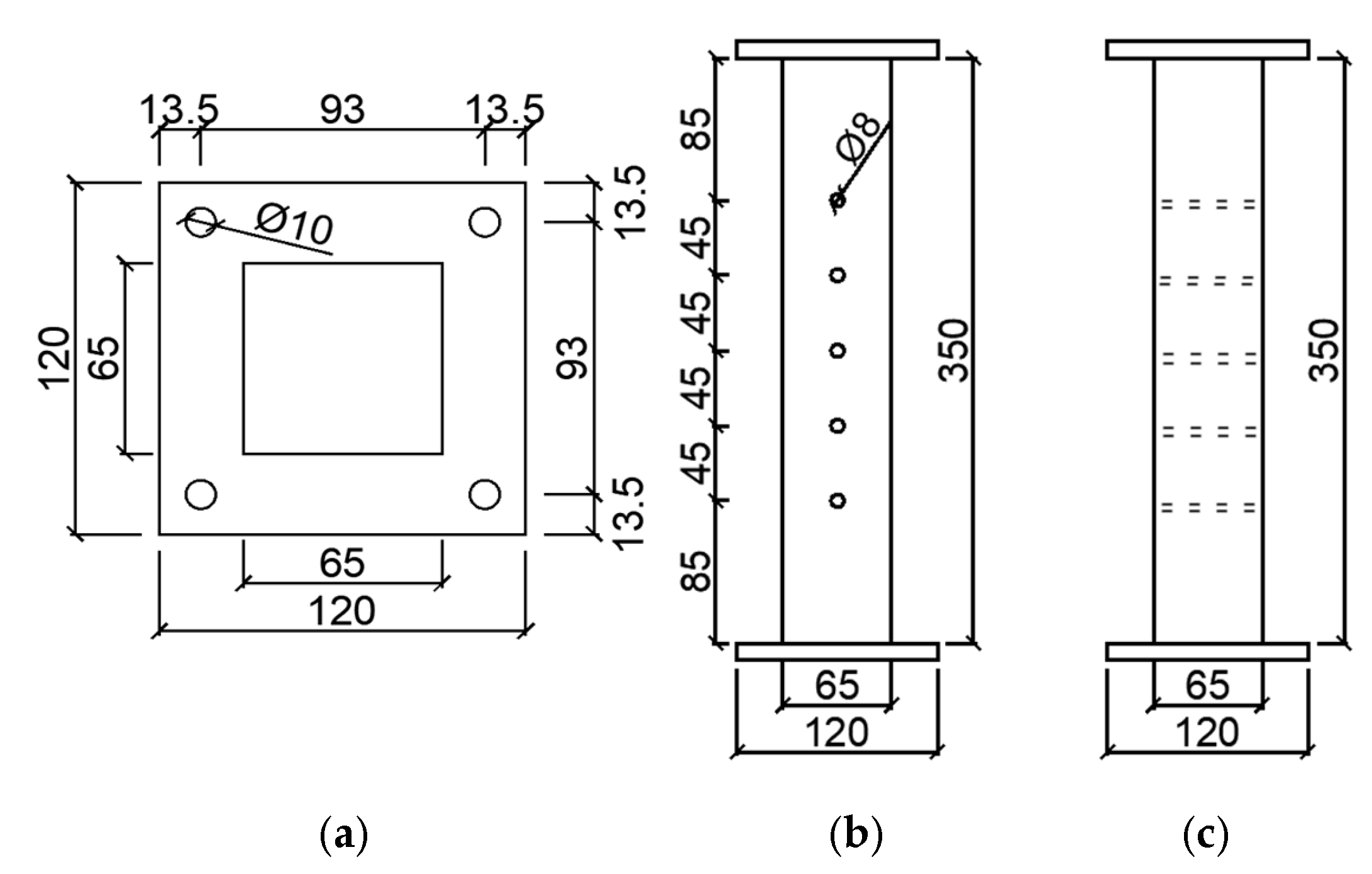












| Numbering of Specimens | Lengths/mm | Section Size/mm | Filled Wood | Number of Bolts | Distance of Bolts/mm |
|---|---|---|---|---|---|
| G1 | 350 | 65 × 65 | No | 0 | / |
| G2 | 350 | 65 × 65 | Yes | 3 | 45 |
| G3 | 350 | 65 × 65 | Yes | 5 | 45 |
| Load/kN | Lateral Deflection of Specimen/mm | Reduction Rate of Lateral Deflection | ||||
|---|---|---|---|---|---|---|
| G1 | G2 | G3 | G2 Than G1 | G3 Than G1 | G3 Than G2 | |
| 36 | 1.50 | 0.73 | 0.60 | 51.33% | 60.00% | 17.81% |
| 64 | / | 1.49 | 1.25 | / | / | 16.11% |
| E1/MPa | E2/MPa | E3/MPa | μ1 | μ2 | μ3 | G12/MPa | G23/MPa | G13/MPa |
|---|---|---|---|---|---|---|---|---|
| 11059 | 242.7 | 217.1 | 0.5 | 0.5 | 0.4 | 829.4 | 663.5 | 199.1 |
| σ11/MPa | σ22/MPa | σ33/MPa | σ12/MPa | σ13/MPa | σ23/MPa | R11 | R22 | R33 | R12 | R13 | R23 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 1.5 | 1.5 | 3 | 3 | 3 | 1 | 0.06 | 0.06 | 0.12 | 0.12 | 0.12 |
| Numbering of Specimens | G1 | G2 | G3 |
|---|---|---|---|
| Tested values for ultimate loads/kN | 36 | 64 | 77 |
| Simulated values for extreme loads/kN | 34.3 | 72 | 84 |
| Ultimate bearing capacity error | +4.9% | −11.1% | 8.3% |
| Elastic stiffness of the test/(kN/mm) | 17.54 | 60.95 | 109.13 |
| Elastic stiffness in finite element/(kN/mm) | 18.41 | 58.06 | 112.01 |
| Elastic stiffness error | −4.7% | −5.0% | 2.6% |
| Specimen Numbering | The Cross-Sectional Dimensions of Wooden Columns (mm) | Bolt Pretension (N) |
|---|---|---|
| GM1 | 200 × 200 | 2000 |
| GM2 | 200 × 200 | 4000 |
| GM3 | 200 × 200 | 6000 |
| GM4 | 250 × 250 | 2000 |
| GM5 | 250 × 250 | 4000 |
| GM6 | 250 × 250 | 6000 |
| GM7 | 300 × 300 | 2000 |
| GM8 | 300 × 300 | 4000 |
| GM9 | 300 × 300 | 6000 |
| Bolt Pretension (N) | 2000 | 4000 | 6000 | |
|---|---|---|---|---|
| Cross-Sectional Dimensions of Wooden Columns (mm) | ||||
| 200 × 200 | 163.66 | 174.38 | 185.54 | |
| 250 × 250 | 194.23 | 208.86 | 223.54 | |
| 300 × 300 | 226.85 | 238.28 | 252.96 | |
| Bolt Pretension (N) | 2000 | 4000 | 6000 | |
|---|---|---|---|---|
| Cross-Sectional Dimensions of Wooden Columns (mm) | ||||
| 200 × 200 | 0% | 6.55% | 13.37% | |
| 250 × 250 | 18.68% | 27.62% | 36.59% | |
| 300 × 300 | 38.61% | 45.59% | 54.56% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Shao, J.; Feng, A.; Li, X.; Wang, Z.; Xu, H.; Gao, J.; Ma, B. Experiment and Finite Element Research on Mechanical Performance of Thin-Walled Steel–Wood Composite Columns Under Eccentric Compression. Buildings 2025, 15, 2114. https://doi.org/10.3390/buildings15122114
Zhu Y, Shao J, Feng A, Li X, Wang Z, Xu H, Gao J, Ma B. Experiment and Finite Element Research on Mechanical Performance of Thin-Walled Steel–Wood Composite Columns Under Eccentric Compression. Buildings. 2025; 15(12):2114. https://doi.org/10.3390/buildings15122114
Chicago/Turabian StyleZhu, Yangfa, Jianhua Shao, Anxiang Feng, Xianglan Li, Zhanguang Wang, Hongxuan Xu, Jiajun Gao, and Boshi Ma. 2025. "Experiment and Finite Element Research on Mechanical Performance of Thin-Walled Steel–Wood Composite Columns Under Eccentric Compression" Buildings 15, no. 12: 2114. https://doi.org/10.3390/buildings15122114
APA StyleZhu, Y., Shao, J., Feng, A., Li, X., Wang, Z., Xu, H., Gao, J., & Ma, B. (2025). Experiment and Finite Element Research on Mechanical Performance of Thin-Walled Steel–Wood Composite Columns Under Eccentric Compression. Buildings, 15(12), 2114. https://doi.org/10.3390/buildings15122114







