A Review: The Application of Path Optimization Algorithms in Building Mechanical, Electrical, and Plumbing Pipe Design

Abstract

This review systematically integrates recent advancements in path optimization algorithms for the automated layout of mechanical, electrical, and plumbing (MEP) systems within complex building environments. A hybrid optimization framework is introduced, combining the global search capability of Ant Colony Optimization (ACO) with the local refinement efficiency of the A* algorithm, enhanced by dynamic weight adjustment and context-aware mechanisms. Simulation experiments based on a hospital BIM model demonstrate that the proposed approach improves design efficiency by approximately 25–35% and reduces conflict incidence by around 40%. The framework further incorporates Building Information Modeling (BIM) and real-time clash detection enabled by IoT devices to enable scalable, multi-objective optimization in high-density spatial configurations. The potential of generative artificial intelligence—such as Generative Adversarial Networks (GANs) and diffusion models—is also explored for generating initial pipeline layouts and enhancing spatial adaptability. To support low-carbon building initiatives, the framework is adaptable to LEED-compliant sustainable MEP design practices. Despite notable progress, challenges remain in algorithmic scalability, dynamic constraint modeling, and multi-objective trade-offs. This review identifies research gaps in diameter-aware layout optimization and BIM-driven multi-scale generative modeling, and outlines future directions toward intelligent, high-performance MEP system design in future sustainable buildings.

1. Introduction

The design and implementation of mechanical, electrical, and plumbing (MEP) systems are critical across all phases of the building life cycle. Well-optimized pipeline layouts can significantly reduce material consumption, minimize energy loss, and lower carbon emissions, meeting sustainability goals and certification standards such as LEED. As the demand for intelligent and sustainable design increases, path optimization algorithms have emerged as key tools in improving the efficiency and quality of MEP systems’ layouts.

Existing research has mainly focused on enhancing the performance of individual algorithms. However, in complex and dynamic building environments, single algorithms often struggle to accommodate multidimensional constraints. Building Information Modeling (BIM), though widely adopted, is still predominantly used during the static design phase and lacks real-time responsiveness during construction.

Several widely used optimization methods, including Ant Colony Optimization (ACO), Genetic Algorithms (GAs), and A*, have demonstrated specific advantages. Existing methods such as ACO and A* offer complementary capabilities in global searches and local refinement. However, studies that explore their collaborative use within dynamic BIM contexts remain limited. Furthermore, recent advances in digital twin systems and the Internet of Things (IoT) have introduced promising opportunities for real-time MEP layout optimization. By dynamically updating the BIM environment based on on-site sensor data, these technologies enable path reconfiguration and adaptive planning throughout the construction phase [1,2,3].

The primary objectives and contributions of this review are as follows.

This review systematically examined the application of path optimization algorithms in BIM-supported MEP design. It evaluates algorithmic categories, integration strategies, and implementation techniques to summarize research trends and identify key challenges. The main contributions are as follows.

(1) It establishes a structured classification of optimization algorithms based on their suitability for BIM-integrated MEP applications.

(2) It introduces a multi-algorithm collaboration framework combining global (ACO) and local (A*) optimization strategies, with potential extensions to IoT and digital twin environments.

(3) It categorizes future research challenges into five thematic areas, offering a reference for advancing intelligent, adaptive, and sustainable MEP design.

By providing a structured synthesis of recent developments, this paper contributes a comprehensive foundation for understanding and improving BIM-based MEP path optimization. It also highlights future directions in areas such as dynamic adaptability, component-level intelligence, and integration with emerging computational technologies [4].

2. Review of Path Optimization Algorithms for MEP Systems

By integrating intelligent search and optimization strategies, path optimization algorithms can automatically generate pipeline layouts, thereby reducing the workload during the early design phase and minimizing the risk of rework during construction [5]. For example, in a specific engineering case, the application of the A* algorithm resulted in a 33.8% reduction in design time and a 14.8% reduction in user interactions during adjustment compared with traditional BIM tools [6]. In addition, path optimization algorithms can effectively reduce pipeline length and the number of elbows, thereby optimizing spatial utilization, lowering energy consumption, and reducing operational costs [7]. Moreover, path optimization algorithms can proactively identify and mitigate conflicts among different MEP systems, preventing design flaws and additional issues during construction, which helps improve both design quality and construction efficiency.

Currently, the path optimization algorithms commonly applied in architectural MEP design are primarily categorized into deterministic, stochastic, and heuristic algorithms [8]. Different path optimization algorithms are suited to distinct application scenarios, each with their own advantages and limitations.

Table 1. Comparison of the functionalities of path optimization algorithms.

Algorithm	Ant Colony Optimization	Genetic Algorithm	Simulated Annealing Algorithm	Particle Swarm Optimization	A* Algorithm
Advantage	Strong combinatorial optimization	Handles nonlinear spaces	Avoids local optima	Fast global convergence	Efficient path searching
Disadvantage	Slow convergence	Prone to local optima	Slow convergence	Susceptible to local optima	Resource-intensive
Application	Cable routing in high-rise buildings	MEP modular partitioning	BIM-integrated clash resolution	Electrical conduit routing	3D MEP layout

summarizes the advantages and disadvantages of various path optimization algorithms [9,10,11].

At the technological frontier, several studies have begun exploring the potential of quantum heuristic algorithms for MEP design. Owing to their high parallelism and global search capabilities in solving nonlinear and multi-objective problems, these algorithms have been preliminarily applied to address node conflict issues in high-density pipeline layouts and have initially demonstrated superior performance compared with traditional metaheuristic algorithms. However, this line of research remains in its infancy and lacks empirical validation within the context of building MEP systems. Further research is required to assess aspects such as robustness, interpretability, and compatibility with BIM systems.

Moreover, path optimization of MEP systems in BIM is a critical component for ensuring the effective operation and maintenance of MEP systems in complex buildings. The integration of data and technology within BIM facilitates more effective management and optimization, thereby significantly improving operational efficiency and reliability while reducing both time and cost [12,13]. In the field of architecture, scholars have actively explored automated MEP pipeline design using BIM models, achieving notable progress that has significantly enhanced design efficiency as well as construction and installation accuracy.

2.1. Ant Colony Optimization (ACO)

In the optimization of gravity sewer systems, Villiers et al. incorporated a hydraulic design and validated the effectiveness of a node and edge-based selection strategy [14]. Yuan Bao et al. developed an improved ACO-based method for electrical pre-embedding wiring in high-rise buildings. By calculating electrical loads and incorporating parallel wiring, wall-mounted wiring, and stress acceleration strategies, this method was applied to engineering projects. The results showed that the proposed approach reduced the total wiring length by 37% [15]. These research outcomes demonstrate the potential of Ant Colony Optimization (ACO) algorithms in practical engineering applications.

In recent years, the Ant Colony Optimization (ACO) algorithm has undergone significant advancements, particularly in the domain of adaptive pheromone updating. By incorporating machine learning techniques, researchers have proposed adaptive pheromone update mechanisms capable of dynamically adjusting pheromone levels in response to environmental variations, thereby enhancing the algorithm’s adaptability and computational efficiency. These innovations have substantially improved the flexibility and effectiveness of ACO when addressing complex optimization problems. For example, recent studies in the electronics domain have investigated the integration of machine learning with ACO to optimize pheromone update strategies, resulting in improved performance in path planning tasks. The incorporation of machine learning allows ACO to autonomously modify its pheromone updating process on the basis of historical search patterns, thereby increasing its suitability for solving a broader range of problem types and application scenarios.

The ACO algorithm proposed by Pemarathne et al. demonstrated strong feasibility and practical effectiveness in solving the cable routing problem. However, it lacks a detailed discussion on the performance differences under specific conditions, particularly the insufficient explanation of the algorithm’s parameter selection, which limits its adaptability in various circuit routing scenarios [14,15,16]. In summary, Ant Colony Optimization (ACO) can adapt to multi-objective optimization problems, meeting the optimization requirements for multiple objectives such as pipeline length, cost, and space utilization. In the future, maintaining a certain proportion of “elite ants” during the ACO process, which consistently perform well across iterations, will ensure that high-quality solutions are retained and passed on, thereby enhancing overall stability. This will broaden the application prospects of ACO in building engineering.

2.2. Genetic Algorithm (GA)

Iida et al. proposed a hierarchical Genetic Algorithm that enhances crossover and mutation strategies through hierarchical chromosome encoding [17]. Du Ke et al. employed a Genetic Algorithm to automatically generate pipeline paths by evaluating path length, the number of bends, obstacle avoidance, and compactness. The algorithm was applied to a large commercial complex project, and the results showed a 15% improvement in pipeline layout efficiency and a 10% reduction in construction time [18]. In another study, Zhao Xuefeng et al. proposed an optimization method integrating a Genetic Algorithm with Building Information Modeling (BIM) [19]. The study demonstrated that the optimized partitioning scheme effectively avoids critical pipe fittings, reduces rework and adjustments during installation, and enhances installation efficiency. Liu Xinnan et al. developed and validated a multi-objective optimization tool based on the Non-dominated Sorting Genetic Algorithm II (NSGA-II) to assist in the conceptual design phase of building structures [20]. By providing multiple optimized solutions, this approach enhances the flexibility and sustainability of the design process, thereby improving design efficiency.

Genetic Algorithms, by simulating the biological evolution process and performing operations such as crossover and mutation, have significant advantages in handling nonlinear and discontinuous solution spaces. However, the algorithm proposed by Du Ke neglected the influence of pipe diameter and insulation layer size during the encoding process, and it did not comprehensively simulate the complexity of real-world project conditions.

The Genetic Algorithm (GA) demonstrates considerable potential for optimization in the layout design of MEP (mechanical, electrical, and plumbing) pipelines [21]. However, existing studies on chromosome encoding schemes exhibit limited expressive capacity, making it challenging to address the highly variable spatial requirements encountered during the early stages of architectural design. To overcome these limitations, future research could explore the integration of generative artificial intelligence models, such as Transformer networks or diffusion-based models, to enhance the chromosome encoding and path generation process. By training on large-scale datasets of building pipeline configurations, generative models can enable the construction of semantically informed initial solutions. Such mechanisms are expected to improve encoding quality, accelerate convergence rates, and ultimately advance the practical implementation of intelligent MEP routing optimization.

2.3. Simulated Annealing Algorithm (SA)

In recent years, simulated annealing (SA) has been extensively applied to the automatic layout of MEP (mechanical, electrical, and plumbing) systems within Building Information Modeling (BIM) environments. Its popularity stems from its inherent capability to escape local optima in high-dimensional and non-convex solution spaces, making it particularly suitable for solving complex spatial arrangement problems encountered in modern building design. Hsu et al. proposed a layout optimization system integrating the BIM software programming interface with the simulated annealing algorithm, which was validated in an electrical circuit assembly plant. The BIM model had a moderate level of complexity, comprising 400 components and 200 conflict points. The algorithm’s parameters were configured with an initial temperature of 1000, a cooling rate of 0.95, and a minimum temperature of 1. Data analysis revealed that the design iteration cycle was shortened from 30 to 20 days, and the number of errors decreased from 50 to 5. Before optimization, the total pipeline length was 3000 m, the number of elbows was 100, and there were 30 conflict points. After optimization, the pipeline length was reduced to 2700 m, the number of elbows was reduced to 80, and the conflict points were eliminated [22]. Xiaotong Sun et al. proposed an innovative approach involving algorithm fusion, developing an adaptive simulated annealing particle swarm optimization algorithm. This algorithm combines adaptive adjustment of evolutionary parameters with strategies for optimizing particle positions. Through simulation experiments, it was compared with the particle swarm optimization algorithm. The results demonstrated that the proposed algorithm achieved high-quality solutions and significantly improved the optimization performance of pipeline layout [23]. Cheng and Singh applied the A* algorithm for single pipeline layout optimization and integrated the simulated annealing algorithm to achieve approximate global optimization for composite pipeline layouts in large-scale search spaces. Simulation was conducted on an indoor space of a building containing nine pipelines. The results showed that this method reduced the total pipeline length by 10% and decreased the number of pipeline intersections by 34% [24].

Table 2. Summary of applying SA to MEP system design in buildings.

Researcher	Research Method	Research Steps	Experimental Method
H.C. Hsu	Proposed a BIM-based method utilizing Adaptive Simulated Annealing Particle Swarm Optimization (ASA-PSO) to automate and optimize single and multiple pipeline layouts in 3D building environments.	1. Established a 3D building environment and the corresponding pipeline models. 2. Employed Genetic Algorithms and particle swarm optimization to optimize pipeline layouts. 3. Proposed an ASA-PSO algorithm to enhance optimization performance. 4. Investigated multi-pipeline systems in buildings by improving the penalty function model and the initial population initialization strategy.	Compared the simulation outcomes of the standard particle swarm optimization algorithm and the ASA-PSO algorithm.
Xiaotong Sun	A BIM-integrated simulated annealing (SA) algorithm was employed, utilizing the BIM software’s API to identify layout adjustments aimed at minimizing design clashes.	1. Development of a computer programming system. 2. Utilization of the BIM software’s API to control building components. 3. Implementation of an iterative learning process using the SA algorithm to simulate coordination cycles.	A case study was conducted on the MEP system of the cleanroom located on the first floor of an integrated circuit assembly facility, in which design clashes were identified and corrected.
Jack C.P. Cheng	This study proposed an automated layout design approach for multiple pipeline systems by integrating BIM with heuristic search methods. To achieve global optimization of the pipe routing configuration, the SA algorithm was utilized.	1. Conducted BIM modeling to extract both geometric and semantic information. 2. Performed spatial and constraint modeling to generate a navigational graph. 3. Defined a fitness function to evaluate layout performance. 4. Implemented and compared optimization algorithms, including Dijkstra, Fruit Fly Optimization Algorithm (FOA), and the SA algorithm.	A room within a water treatment facility was selected as a case study. BIM data were extracted using Dynamo to capture both geometric and semantic information, upon which, the proposed algorithm was applied to optimize the pipeline layout.

summarizes existing approaches that employ the simulated annealing algorithm for the design and optimization of mechanical, electrical, and plumbing (MEP) systems in building projects.

To enhance the adaptability of traditional simulated annealing (SA) algorithms in path search tasks, Fuat Kosanoglu et al. proposed a hybrid optimization framework integrating Deep Reinforcement Learning (DRL), coupling a dual-deep network with SA to solve optimal strategies for complex maintenance scheduling problems [25]. Unlike conventional SA, which relies solely on random neighborhood selection, this method employs a DRL module to autonomously learn the preferred neighborhood structures. Through iterative interaction and mutual refinement of the initial solutions across optimization cycles, the hybrid approach significantly improves the global search capability and convergence performance. Experimental results demonstrate that the proposed hybrid algorithm outperforms various metaheuristic approaches, including Genetic Algorithms (GA), in resource scheduling tasks. Furthermore, its learned strategies exhibit transferability to multi-objective trade-offs and constraint-heavy scenarios, such as MEP routing in complex building systems.

In addition, another study further extended the application scope of SA to model structure optimization by incorporating the “Reversible Jump” mechanism. This approach applied SA to non-convex structural optimization of deep neural networks, enabling posterior sampling and structural compression of the model’s parameters, including the number of layers and neuron widths [26]. Compared with Bayesian Optimization and Genetic Algorithms, this method yielded smaller model sizes and superior prediction accuracy in tasks such as image recognition and time-series forecasting. This structurally aware optimization paradigm offers valuable insights into the structural search capabilities of SA within building information systems. It holds significant potential for applications such as automated routing rule generation, support and hanger configuration, and subsystem coupling modeling in BIM-based MEP design.

In summary, simulated annealing retains strong adaptability for the automated design of BIM-MEP systems due to its global optimization capabilities. Its integration with deep learning and structural optimization techniques offers promising directions for advancing intelligent design within increasingly complex building information environments.

2.4. Particle Swarm Optimization (PSO)

Wang Changtao et al. proposed a new method for rapidly generating orthogonal paths and combined it with PSO to optimize pipeline routing. The algorithm parameters were configured as follows: a particle size of 30, a path encoding length of 21, a maximum velocity of 5, and a maximum iteration count of 100, with an inertia weight of 1.1. Simulation results using these parameters in MATLAB 8.5 showed a 20% reduction in the optimized pipeline length and a 25% decrease in the number of elbows [27]. Chen Min proposed an improved PSO-based optimization method for electrical conduit routing in super-tall buildings, based on an improved PSO algorithm [28]. In practical application tests, using a Grade A office building as the background project, the method was validated through comparative testing, demonstrating high applicability and superior performance. Specific experimental data show that the improved Particle Swarm Optimization algorithm achieved an average fitness of 64.31 in five-fold cross-validation experiments, significantly higher than the traditional PSO algorithm (50.18) and the Genetic Algorithm (36.85).

Although Particle Swarm Optimization (PSO) is known for its simple structure and rapid convergence, it remains susceptible to premature convergence when applied to high-dimensional or multi-objective search spaces. This vulnerability often leads the algorithm to become trapped in local optima, thereby limiting its effectiveness in complex optimization tasks. While existing studies have attempted to address this issue by incorporating mutation operators to enhance the global search capability [29], these heuristic-based approaches are inherently reliant on randomness and generally lack the adaptive mechanisms required to navigate complex and dynamic problem domains. Consequently, their generalization and adaptability remain constrained.

To overcome these limitations, recent research has explored the integration of Reinforcement Learning (RL) techniques into the PSO framework, enabling adaptive parameter tuning and dynamic search optimization. For instance, a variant known as Reinforcement Learning Layered PSO (RLLPSO) introduces a hierarchical population structure along with a layer control mechanism based on reward feedback. This design improves population diversity and has demonstrated superior performance over conventional optimization algorithms in several large-scale benchmark scenarios [30]. Moreover, hybrid algorithms that combine RL with enhanced PSO variants have been successfully applied to intelligent path planning. In such frameworks, cumulative rewards from the RL module are utilized to dynamically adjust the fitness evaluations of both local best and global best particles, effectively improving path planning accuracy while reducing the computational overhead associated with ineffective particles [31].

The application of Deep Reinforcement Learning (DRL) and neural network-based surrogate models presents promising avenues for achieving intelligent parameter tuning within PSO. These advancements are expected to further mitigate the issue of local optima, while enhancing the algorithm’s global search capabilities, adaptability, and efficiency, particularly in the context of optimizing complex pipeline layouts within three-dimensional Building Information Modeling (BIM) environments.

2.5. A* Algorithm

In recent years, Algorithm A has made significant advancements in enhancing the layout efficiency and robustness of MEP pipelines within complex built environments. Zhao Xinyu et al. proposed an adaptive A* algorithm, which can more effectively select predefined routing points based on the surrounding environment and conditions. Simulation experiments in simple 2D, 3D, and complex 3D spaces showed that the adaptive A* algorithm exhibited superior robustness compared with the classical A* algorithm [32]. Singh combined the 3D A* algorithm with the simulated annealing algorithm to optimize the MEP (mechanical, electrical, and plumbing) system layout [33]. By adjusting the parameters, the 3D A* algorithm was benchmarked against the Fruit Fly Optimization Algorithm (FOA). The results showed that the proposed framework had a lower total cost compared with FOA, saving 50% of the time and reducing the number of iterations by 25%.

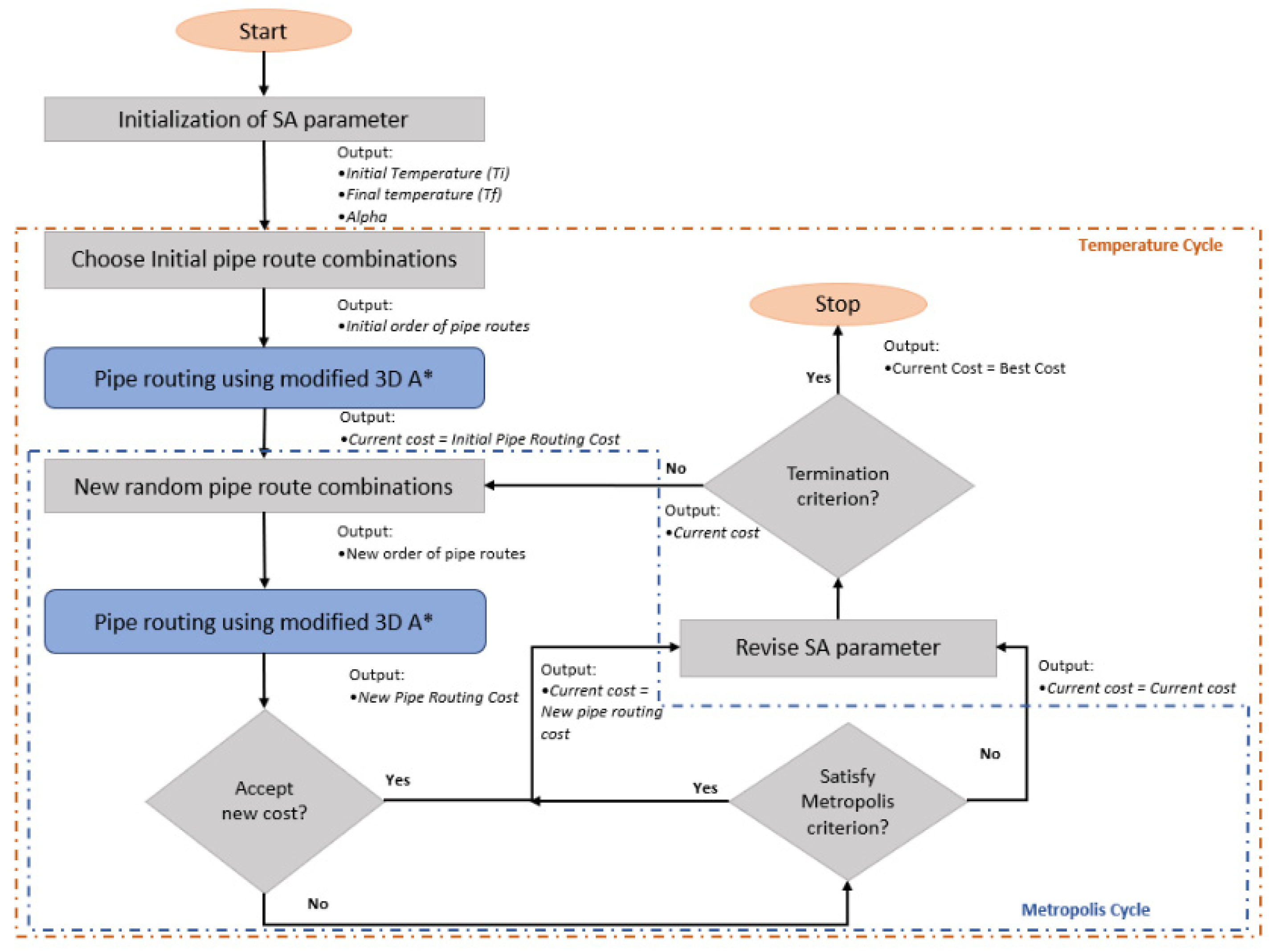
To better illustrate the optimization logic and workflow of this integrated approach, Figure 1 presents the developed framework combining the 3D A* algorithm with SA. The framework introduces an iterative temperature-based cycle and the Metropolis criterion to evaluate new routing solutions, systematically balancing exploration and exploitation. This hybrid mechanism significantly enhances routing efficiency and solution quality, making it particularly suitable for multi-pipe layout optimization under complex spatial constraints.

WonjunChoi et al. proposed an improved A* algorithm framework for path generation. This framework modifies the node selection and post-processing steps, utilizing temporarily created grids to calculate avoidance paths when collisions occur with other elements [6]. When applied to seven example structures, the algorithm demonstrated superior performance compared with existing manual modeling methods and the path design functions in traditional commercial BIM tools. Wu Tong developed a key-plane-based MEP path optimization framework using the A* algorithm [34]. By redesigning the cost function of the A* algorithm and conducting an analysis based on actual engineering projects, this method was compared with traditional pipeline path design approaches. The results further demonstrated the soundness and practicality of the three-dimensional pipeline integrated path optimization method based on the A* algorithm.

The A* algorithm exhibits significant advantages in path optimality and heuristic search efficiency. However, the A* algorithm, as proposed by Wu Tong, which is based on the grid method, considers only horizontal and vertical directions. When extended to multi-directional path layouts, this approach substantially increases the computational resource requirements. With the continuous development of large-scale data processing technologies, the computational difficulty associated with such tasks will be significantly reduced. As a result, the A* algorithm will realize its full potential in pipeline optimization design for large-scale construction projects.

To further enhance the adaptability of the A* algorithm in dynamic scenarios, future research could explore the integration of “digital twin” technology into the A* path planning framework. By dynamically linking real-time environmental data from Building Information Modeling (BIM) models or Internet of Things (IoT) sensors with the algorithm, it would be possible to adaptively update path planning in response to the construction conditions or spatial changes. Future studies could focus on developing a digital twin-driven A* optimization closed-loop system that facilitates continuous feedback and automatic adjustments, thereby advancing the transition from static path planning to real-time, dynamic, and intelligent layout of building MEP systems [35,36,37].

3. Proposed Framework for BIM-Integrated Multi-Algorithm Collaborative Optimization

The single-path optimization algorithm is often constrained by the limited global search capability and susceptibility to local optima in MEP pipeline design. However, complex architectural scenarios, such as hospitals and commercial complexes, present higher demands for dynamic adaptability and multi-objective optimization, encompassing factors such as length, conflicts, and costs, in the pipeline layout. To overcome the limitations of single-path optimization algorithms, such as limited global search capacity and susceptibility to local optima, in MEP pipeline layout design, this study proposes a BIM-integrated multi-algorithm collaborative optimization framework. The framework integrates the strengths of multiple intelligent algorithms to support efficient, adaptive, and real-time optimization in complex architectural environments. It comprises four primary functional modules, as outlined below.

3.1. Architecture of the Framework

This module integrates the global search capability of Ant Colony Optimization (ACO) with the local refinement efficiency of the A* algorithm. Algorithmic priorities are dynamically adjusted on the basis of the spatial complexity and the specific phase of the design process. For instance, ACO is employed during the conceptual design stage to explore multiple potential pipeline routes, while A* is utilized during the construction documentation phase to perform detailed local refinements. This adaptive mechanism ensures a balance between global exploration and local precision through dynamic weight switching between the two algorithms.

The specific code is selected as follows:

# Initialize the BIM model and algorithm parameters

def initialize_bim_and_params():

bim_model = load_bim_model()

aco_params = init_aco_params()

astar_params = init_astar_params()

return bim_model, aco_params, astar_params, []

# Multi-algorithm collaborative optimization

def optimize_mep_paths(mep_network, threshold):

bim_model, aco_params, astar_params, path_set = initialize_bim_and_params()

for pipe in mep_network:

# Adjust the weights according to the complexity of the pipeline

if pipe.complexity > threshold:

aco_weight, astar_weight = 0.8, 0.2

# Prioritize the global search of ACO

else:

aco_weight, astar_weight = 0.2, 0.8

# Priority A* Local optimization

# Iterative optimization

while not end_condition():

aco_path = aco_search(pipe, aco_params, aco_weight)

astar_path = astar_search(pipe, astar_params, astar_weight)

best_path = evaluate_paths(aco_path, astar_path, [’length’, ’conflict’, ’cost’])

aco_weight, astar_weight = update_weights(bim_model.feedback)

path_set.append(best_path)

return path_set

3.2. Real-Time Adaptation via IoT and Digital Twins

To ensure responsiveness to dynamic spatial changes during construction, such as equipment displacement or obstacle addition, this module integrates Internet of Things (IoT) sensors and digital twin technology [38]. Real-time data collected from the physical environment are fused into the BIM platform, allowing continuous updates of both geometric and semantic information. On the basis of this input, the pheromone matrix in ACO or the cost function in A* is dynamically adjusted. For example, the integration of the YOLOv7 deep learning model enables the system to detect spatial disturbances and automatically trigger re-optimization procedures. Simulation results indicate that this mechanism can reduce layout adjustment response times by approximately 50%, thereby significantly enhancing the adaptability of the system [39].

The specific code is selected as follows:

# Initialize the digital twin system and sensor network

def initialize_system():

sensor_network = init_sensor_network()

bim_model = load_bim_model()

digital_twin = link_digital_twin_to_bim(bim_model)

return sensor_network, digital_twin

# Update the BIM model in real time based on sensor data

def update_bim_model(sensor_network, digital_twin):

realtime_data = collect_sensor_data(sensor_network)

updated_bim = update_digital_twin(digital_twin, realtime_data)

return updated_bim

# Detect the changed areas and trigger the optimization process

def optimize_affected_pipes(updated_bim, affected_zone):

for pipe in affected_zone:

# The marking needs to be re-planned

pipe.recalculate_path = True

# Update the algorithm parameters

adjust_cost_functions(pipe)

update_pheromone_matrix(pipe)

update_astar_heuristics(pipe)

# Start the collaborative optimization of multiple algorithms

optimized_path = hybrid_path_planning(pipe)

pipe.update_path(optimized_path)

# Main execution process

def main():

sensor_network, digital_twin = initialize_system()

while project_is_active():

updated_bim = update_bim_model(sensor_network, digital_twin)

if detect_significant_change(updated_bim):

affected_zone = locate_affected_zone(updated_bim)

optimize_affected_pipes(updated_bim, affected_zone)

3.3. Multi-Objective Optimization and Pareto Frontier

With the assistance of the fitness function in the Genetic Algorithm (GA), the following objectives are simultaneously optimized: minimizing pipeline length, controlling the number of elbows, improving space utilization, and managing construction costs. The optimal solution set is derived through a Pareto frontier search, offering multiple alternative paths for designers to select and adjust according to the project’s specific requirements.

Moreover, this study is the first to propose a BIM-driven multi-scale optimization framework, which achieves seamless integration of optimization algorithms within BIM through the following steps:

(1) Data Interaction Layer: Based on the automated rule-checking system developed by Xie Xuanfeng [40], and in conjunction with the Revit API and Navisworks interface, semantic enhancement and automatic extraction of model information are realized. This includes geometric attributes (such as the pipes’ diameter, material, and spatial position), which are mapped to the input of the path optimization model. Any real-time parameter changes are subsequently sent back to the optimization algorithm, supporting dynamic recalculation.

(2) Multi-Scale Modeling: The path optimization strategy is divided into different stages of the project life cycle. During the conceptual design stage, a global path layout is developed, focusing on space occupation and the primary pipeline routes. In the construction coordination stage, conflict resolution and path fine-tuning are performed at the module or zone level. In the operation and maintenance stage, the strategy supports the optimization of maintenance paths and simulates potential transformations.

(3) Visual feedback layer: The dynamic display of optimization results and the interface for manual intervention are implemented through the BIM platform and the digital twin platform, enabling the following functions: switching and comparing multi-objective path solution sets, spatial view linkage, construction simulation, and the incorporation of user feedback into the optimization feedback loop.

3.4. Parallel Computing and Performance Improvement

To address the high computational complexity of large-scale architectural scenarios, this paper further integrates a cloud computing platform to support parallel processing. Cloud-based parallel scheduling is employed to accelerate population evolution in Ant Colony Optimization (ACO) and the Genetic Algorithm (GA) [41]. In large-scale MEP model tests, computational efficiency is improved by an average of 30% to 40%. Additionally, the system also supports remote model access and data uploads from edge devices, enhancing scalability and adaptability.

The specific code is selected as follows:

# Initialize the parallel task distribution system

def initialize_cloud_environment(mep_tasks):

cloud_nodes = allocate_cloud_nodes(len(mep_tasks))

distributed_tasks = distribute_tasks_to_nodes(mep_tasks, cloud_nodes)

return distributed_tasks, cloud_nodes

# The optimization algorithm module for performing a single task

def execute_algorithm_module(subtask):

result = run_optimization_algorithm(subtask)

return result

# MEP tasks are executed in parallel in the cloud

def parallel_mep_optimization(distributed_tasks):

intermediate_results = []

# Execute each sub-task in parallel

for subtask in distributed_tasks:

result = execute_algorithm_module(subtask)

intermediate_results.append(result)

return intermediate_results

# Aggregate and output the final optimization result

def aggregate_results(intermediate_results):

optimized_design = merge_optimized_outputs(intermediate_results)

return optimized_design

# Main process entry

def main():

mep_tasks = load_mep_tasks_from_bim()

distributed_tasks, cloud_nodes = initialize_cloud_environment(mep_tasks)

# Cloud parallel computing

intermediate_results = parallel_mep_optimization(distributed_tasks)

# Aggregate and generate the final design

optimized_design = aggregate_results(intermediate_results)

return optimized_design

4. Challenges and Future Directions

Advanced path optimization algorithms have played a critical role in optimizing MEP systems’ routing in BIM environments. These algorithms assist in determining the optimal pipeline paths and avoiding conflicts with structural elements and other facilities. However, existing path optimization algorithms, such as Particle Swarm Optimization (PSO), the A* algorithm, and simulated annealing, still exhibit certain limitations and require further enhancement.

4.1. Selection of Supply and Demand Points for Pipeline Layout

In traditional pipeline system layout design, the positions of supply and demand points are typically predefined according to industry norms and the designer’s experience. However, in complex architectural environments, adjusting the direction of equipment and the positions of these points often leads to more efficient layouts. Most existing methods assume fixed positions for supply and demand points, neglecting scenarios where the positions are unclear or the layout is suboptimal, thus limiting design flexibility and optimization potential.

To address this limitation, future research could explore the integration of an artificial intelligence-driven decision-making framework that enables dynamic adjustment of supply and demand point positions. The Generative Adversarial Network (GAN) has demonstrated potential in generating spatially adaptive point layouts under complex geometric and functional constraints. Specifically, Generative Adversarial Networks (GANs) can utilize encoded spatial features of buildings (e.g., geometric boundaries, obstacle distributions, and equipment demand density maps) as inputs to generate candidate layout points using the generator. The discriminator evaluates the feasibility of the generated points and guides the generator through adversarial feedback based on predefined spatial constraints, such as spatial overlap and service coverage. This iterative adversarial training process progressively enhances the spatial rationality and adaptability of the layout solutions [42].

Furthermore, combining GAN-based point generation with multi-objective optimization algorithms could simultaneously consider critical factors such as pipeline length, space utilization efficiency, energy consumption, and construction feasibility. This hybrid approach is expected to enhance the flexibility, stability, and overall performance of pipeline systems in dynamic building environments.

4.2. Layout of Pipelines and Their Sub-Components

Recent research on the design of building MEPsystems has primarily focused on optimizing pipeline paths, while relatively less attention has been given to the layout of key sub-components such as supports and hangers, joints, and valves. However, these sub-components are critical to ensuring the structural integrity, installation feasibility, and overall stability of the system. Future research should integrate the detailed parameter data of these components into the BIM workflow and embed them within path optimization algorithms to enable rule-based automatic deployment and configuration.

In response to this challenge, future research could explore the integration of the Non-dominated Sorting Genetic Algorithm II (NSGA-II) into the component layout decision-making framework. NSGA-II demonstrates strong convergence characteristics and solution diversity in multi-objective optimization problems, making it well-suited for identifying Pareto-optimal solutions among competing objectives, including layout cost, structural stability, and spatial utilization. This approach can incorporate parameters such as the quantity, positioning, and spacing of supports and hangers as decision variables, while leveraging spatial data from the BIM platform and relevant construction specifications to enable constraint-driven automatic layout optimization. By integration with parametric modeling tools (e.g., the Revit API), the optimized results can be directly incorporated into the BIM model, thereby enhancing data consistency and traceability between the design and construction phases [43].

Furthermore, decision-making frameworks that incorporate methods such as expert scoring, the Continuous Weighted Average (COWA) operator, game theory, and the Ideal Solution Similarity Ranking Method (TOPSIS) have proven effective in identifying the optimal design schemes within the Pareto solution set. These methods, which fully consider technical constraints and stakeholder preferences, are well suited to the parametric layout of components in complex BIM environments. Research has demonstrated that factors such as the spacing of supports and hangers, the height of the web, and subjective weightings significantly influence the selection of optimal section schemes. These findings provide a feasible guiding path for future intelligent MEP sub-component layout strategies.

4.3. The Setting of Pipeline Dimensions

Pipe diameter optimization is a crucial aspect of building MEP design, as it directly impacts the fluid dynamic performance, energy consumption, and operational efficiency of the system. Research from submarine pipeline engineering demonstrates that appropriate selection of pipeline diameters can significantly reduce frictional pressure losses by 14.76% in vertical pipelines and by 3.5% in horizontal pipelines [44]. These findings underscore the clear advantages of optimizing pipe diameter in terms of both technical performance and economic feasibility. Such results emphasize the importance of incorporating fluid mechanics principles into the pipe diameter selection process during the early stages of design.

In building MEP system design, most existing path optimization models regard pipe diameter as a fixed input variable, overlooking its dynamic impact on hydraulic performance, pressure drop characteristics, and operational costs. Current research lacks a mechanism for incorporating pipe diameter as a coupled decision variable within the optimization framework, which constrains the feasibility and robustness of design solutions under real-world operating conditions. To address this challenge, future research may introduce Computational Fluid Dynamics (CFD) tools into the co-optimization process of path planning and pipe sizing, serving as the simulation backbone for evaluating systems’ performance. CFD platforms such as Fluent and OpenFOAM are capable of simulating three-dimensional flow fields under various pipe diameters and path configurations, and generate key indicators such as velocity profiles, pressure drops, and turbulence intensity, thereby providing accurate feedback for optimization algorithms. In practice, the optimization model can produce a series of candidate path–pipe diameter configurations, assess their hydraulic performance, and iteratively refine the solutions under the integrated constraints of structural feasibility, energy efficiency, and cost-effectiveness. While this approach has seen preliminary applications in petroleum engineering and aerospace thermal management, it remains underexplored in the context of MEP systems. The integration of CFD simulations with multi-objective algorithms such as Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) is expected to enable dynamic and coupled optimization of path layouts and pipe sizing in complex built environments.

4.4. Computational Complexity of Path Optimization Algorithms

With the growing emphasis on spatial aesthetics and functional integration in architectural design, the density of mechanical and electrical systems (MEP) components within buildings has increased rapidly. This has made the efficient arrangement of these components within the limited ceiling and shaft spaces a highly complex computational task. The growing complexity significantly elevates the computational demands of pipeline layout design, particularly in large-scale Building Information Modeling (BIM) models, which pose the dual challenges of requiring both high real-time performance and advanced data processing capabilities for path optimization algorithms.

To address these challenges, future research should prioritize the development and deployment of parallel computing frameworks to decompose and parallelize sub-problems within the MEP path optimization process. As demonstrated in the integration framework proposed by Ehmke et al., parallel computing merges algorithmic structures with distributed computing resources, enabling scalable path optimization in heterogeneous data environments [45]. By implementing meta-heuristic or hybrid optimization strategies for parallel execution on GPU-accelerated cloud platforms or high-performance computing clusters, researchers can significantly reduce algorithm execution times while maintaining the solutions’ quality.

Moreover, parallel optimization not only enhances the computational feasibility of algorithms but also facilitates the trade-offs among multiple objectives such as space efficiency, construction feasibility, and energy consumption performance. When such parallel frameworks are integrated into the BIM design process, they can support real-time adaptive layout generation and dynamic re-optimization during iterative design phases. This approach would provide robust support for the design of high-performance, computationally efficient MEP systems in future intelligent buildings.

4.5. Standardized Evaluation Indicators

Future research on the optimization of MEP systems should focus on developing a standardized multi-index evaluation system to objectively assess the performance of optimization algorithms across different project contexts. This assessment framework should encompass quantifiable core indicators such as energy consumption per unit of area (e.g., kWh/m²), collision and conflict resolution rates, calculation duration, and life cycle cost savings. Such a system will enable comprehensive comparative evaluations of pipeline optimization outcomes from both the technical and economic perspectives.

Regarding the development of specific indicator systems, future research on MEP system optimization may draw upon energy efficiency benchmarks established by green building standards such as LEED and ASHRAE. By defining operationally feasible and quantifiable performance targets, the practicality and comparability of the evaluation framework can be significantly enhanced. For instance, energy consumption per unit of area can be limited to ≤100 kWh/m²/year, representing a critical parameter in assessing the operational sustainability of built environments. The resolution rate of spatial conflicts is recommended to be ≥95% to satisfy the reliability requirements of layout schemes during actual construction. In complex BIM models, to support real-time design iterations, the average convergence time of the path planning algorithm should be maintained within 5 min. Furthermore, the life cycle cost savings ratio is suggested to range between 10% and 25%, on the basis of empirical engineering cases, and should be flexibly adjusted according to building types and system functions.

Furthermore, to more comprehensively evaluate the stability and adaptability of optimization algorithms in complex design environments, the assessment framework should incorporate additional performance dimensions, including path robustness, convergence stability, and dynamic responsiveness. Drawing inspiration from methodologies in robot performance evaluation [46], path robustness can be assessed by the variance of results under different initial layout configurations, with a recommended threshold of ≤10%. Convergence stability should be defined by maintaining the difference between the worst and average solutions below 5%. In BIM systems operating within dynamic construction environments, the response time for path updates should not exceed 30 s to ensure the real-time adaptability of the optimization scheme to changes in the construction scene.

By incorporating interdisciplinary evaluation dimensions such as energy management, computer science, and systems engineering, this framework is expected to overcome the fragmented nature of existing MEP optimization evaluation systems. It will provide context-adaptive, performance-oriented criteria for algorithm selection, thereby offering a solid foundation for intelligent building design.

5. Conclusions and Outlook

Path optimization algorithms have demonstrated significant potential in improving the efficiency, accuracy, and intelligence of MEP (mechanical, electrical, and plumbing) systems’ layout in building design. By incorporating optimization theory and considering architectural constraints, these algorithms can automatically generate conflict-free routing schemes, minimize manual intervention, reduce material waste, and enhance space and energy utilization. Despite their advantages, the current applications remain limited, particularly in addressing complex environments and real-time constraints.

5.1. Conclusion

Currently, the application of path optimization algorithms in the automated layout of building MEP systems remains in its early stages, despite its considerable potential to address the complexity and high conflict rate inherent in traditional MEP design processes. Traditional design approaches often rely on manual experience, leading to lengthy, repetitive processes that are prone to conflicts, which can adversely affect both the functionality and safety of the building systems. In contrast, path optimization algorithms, grounded in operational research optimization theory, can efficiently generate multiple feasible layout schemes, systematically avoid potential conflicts, and significantly enhance design automation.

According to research by Tang et al., an automation framework based on path optimization can reduce MEP-related construction costs by approximately 10% to 15%, with energy consumption reductions of up to 20%. This reduction is primarily attributed to the shortening of pipeline lengths, the reduction in material waste, and the optimization of the system’s performance. These algorithms can dynamically adapt to the constraints of building space and functional area requirements, improving the space utilization of equipment concentration areas, ensuring reasonable zoning, and preventing interference between various systems. Additionally, by optimizing both path and equipment selection, these algorithms help minimize system pressure drops and heat losses, thereby significantly improving the operational efficiency of HVAC systems and enhancing the Building Energy Efficiency Index (EPI).

The applicability of path optimization algorithms is particularly notable in highly complex building environments, such as hospitals, industrial plants, and data centers, where demands for reliability, redundancy, and operational safety are extremely high. These algorithms support integrated collision detection in complex BIM models, meet the requirements for system redundancy, and allow rapid iteration of design schemes, thereby significantly improving the integration of design and construction. Consequently, path optimization algorithms are increasingly recognized as a key technology in promoting intelligent, performance-oriented MEP system design in complex building projects.

5.2. Future Prospects

Future research should focus on integrating Deep Reinforcement Learning (DRL) technologies to enable the dynamic and adaptive adjustment of path optimization algorithms’ parameters. Such an integration would allow for real-time optimization, effectively addressing the complex architectural space constraints and multi-objective design requirements inherent in modern building systems.

Furthermore, the advancement of generative AI technologies, particularly the successful application of Generative Adversarial Networks (GANs), Variational Autoencoders (VAEs), and Diffusion Probability Models (DDPMs), has introduced a novel intelligent approach to the layout of electromechanical systems [47,48]. In contrast to traditional rule-based or heuristic methods, generative AI has the capability to simultaneously accommodate multiple constraints, such as building structure, safety redundancy, and equipment compatibility, and generate layout schemes that are not only high-performance but also innovative. This is especially critical in high-demand environments, such as hospitals and data centers, where the goals of security, reliability, and ease of maintenance must be met in a balanced and efficient manner.

To facilitate the widespread application of these technologies in engineering practices, it is essential to establish a standardized evaluation system encompassing key performance indicators (KPIs), such as energy consumption (e.g., energy consumption per unit area, kWh/m²), life cycle cost savings, and the success rate of collision resolution. Additionally, pilot studies should be conducted in real-world projects, particularly in medical, industrial, and large-scale building environments, to assess the scalability, robustness, and generalizability of these technologies. These empirical findings will provide valuable data for subsequent optimization efforts and contribute to the advancement of industry standards, ultimately fostering the broader adoption of AI-driven optimization systems within the construction industry.