Blast Performance of Multi-Layer Composite Door Panel with Energy Absorption Connectors
Abstract
1. Introduction
2. Methodology
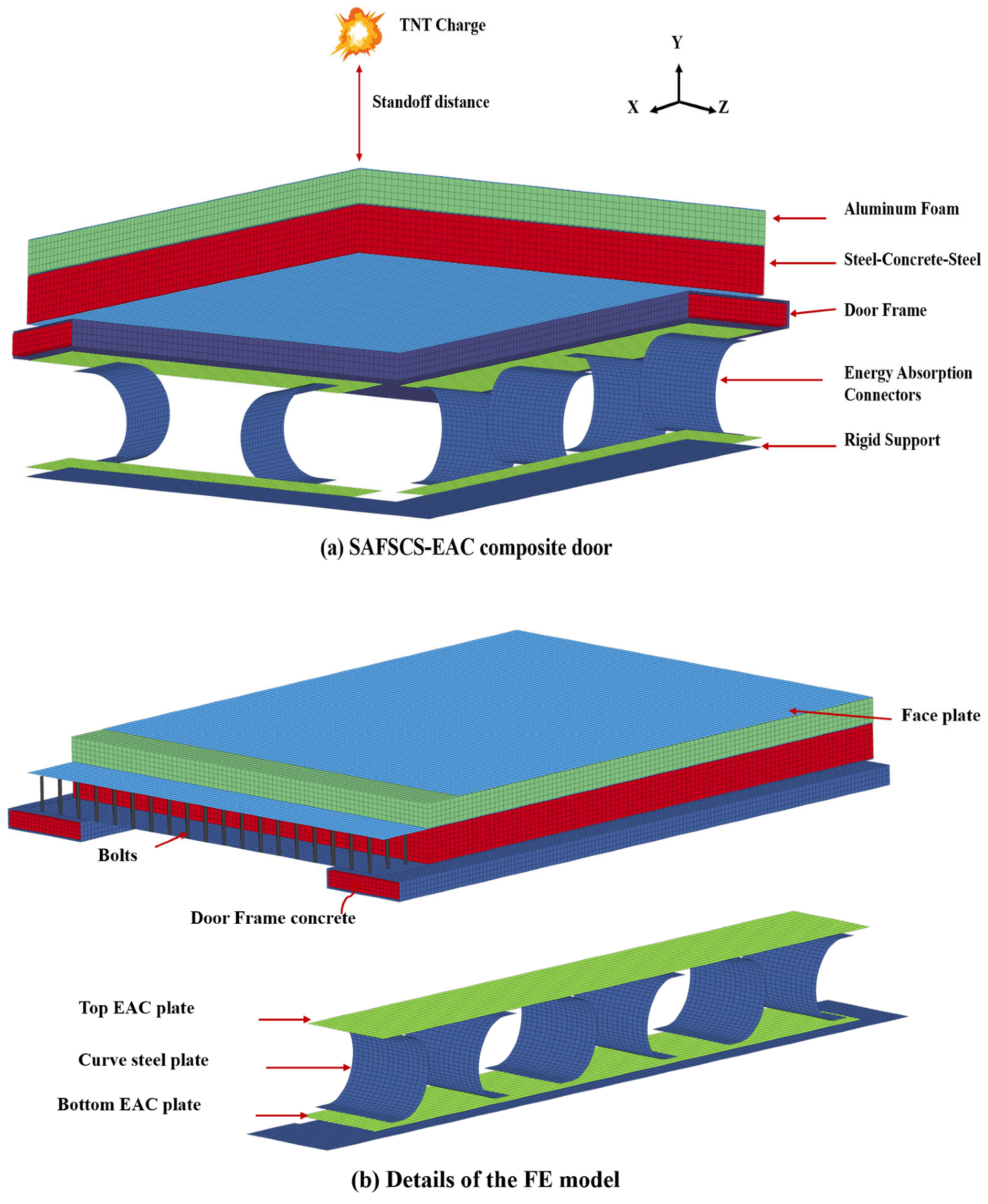
2.1. Design of the Blast-Resistant Door
2.2. FE Model Description
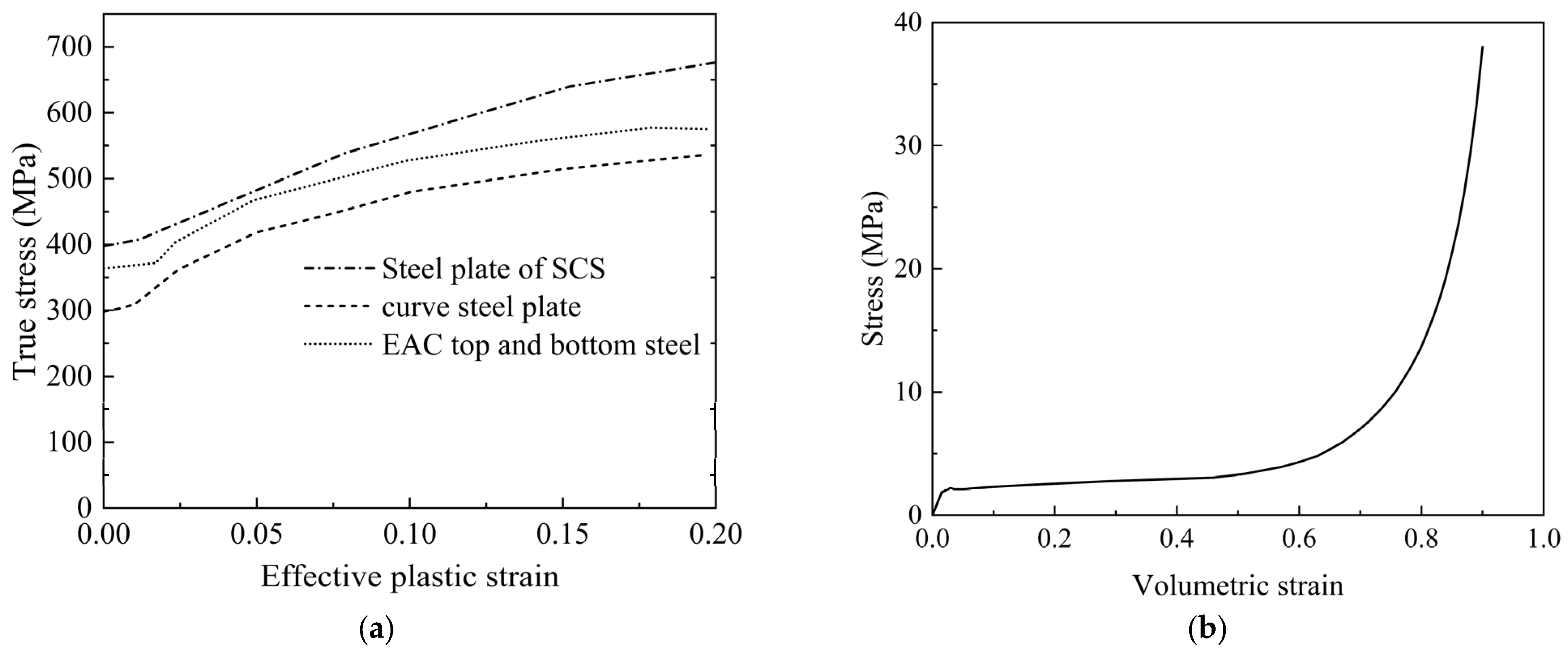
2.3. Material Model
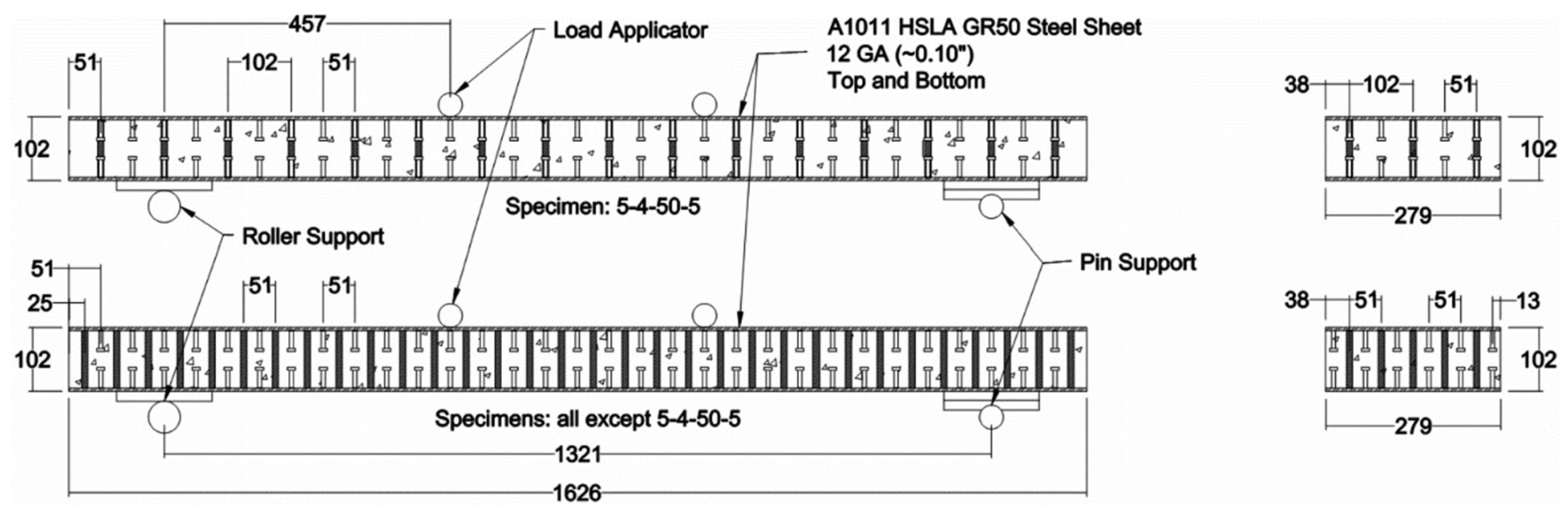
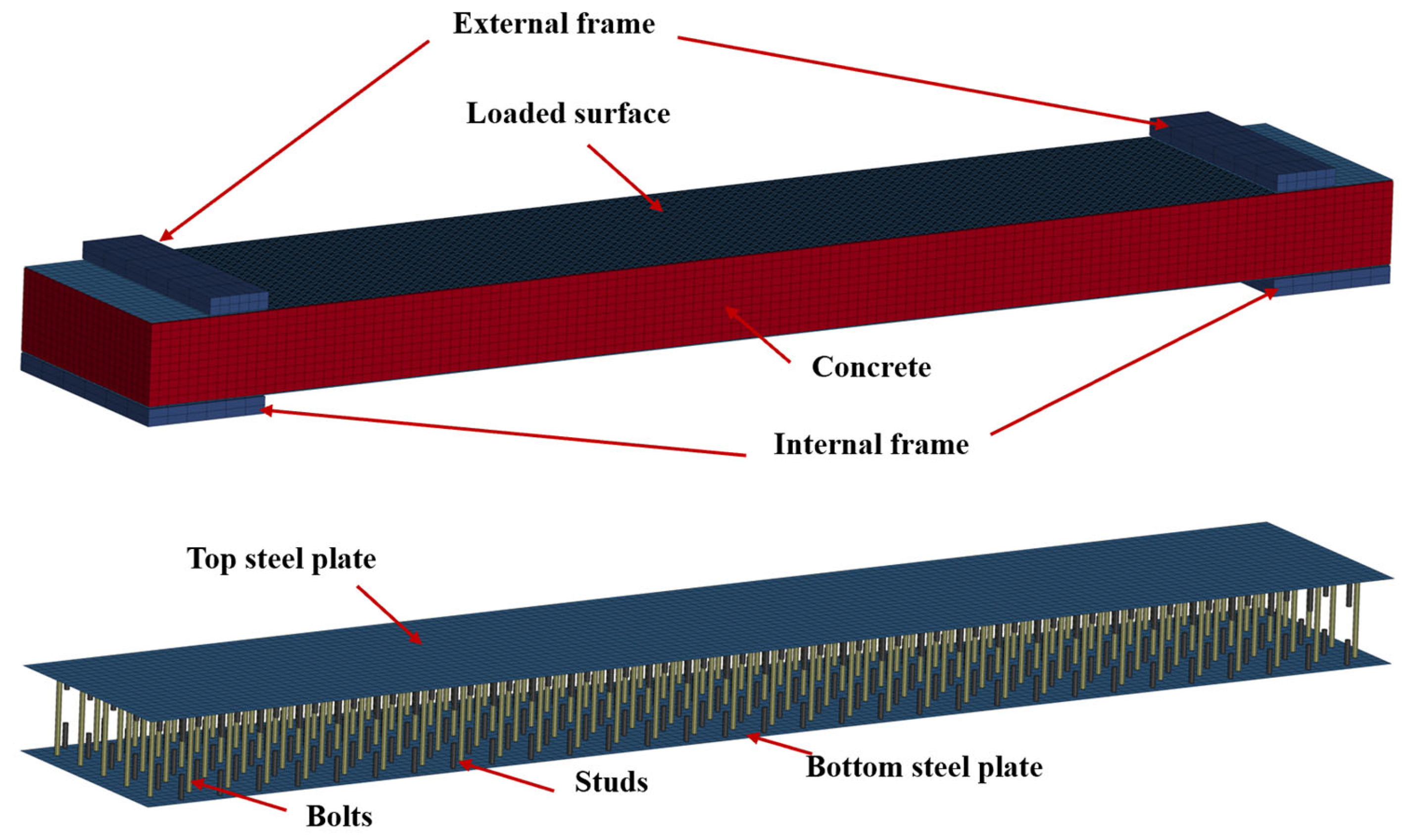
2.4. Validation of FE Model
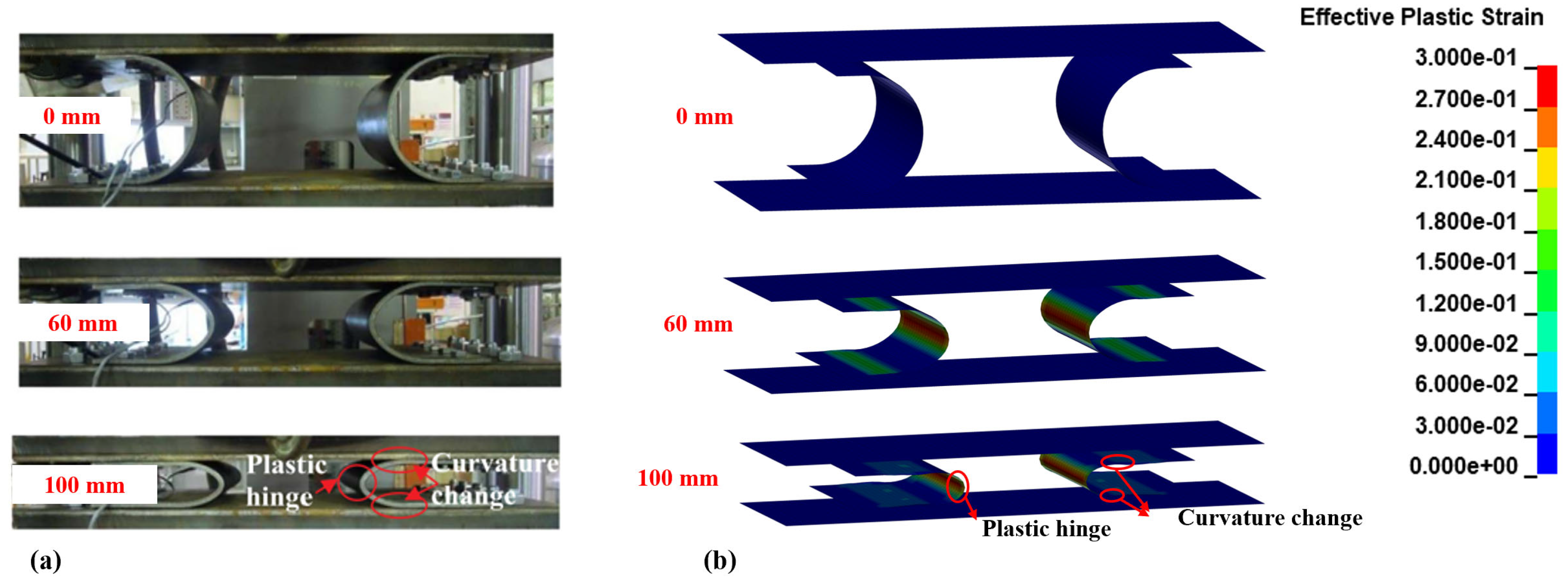
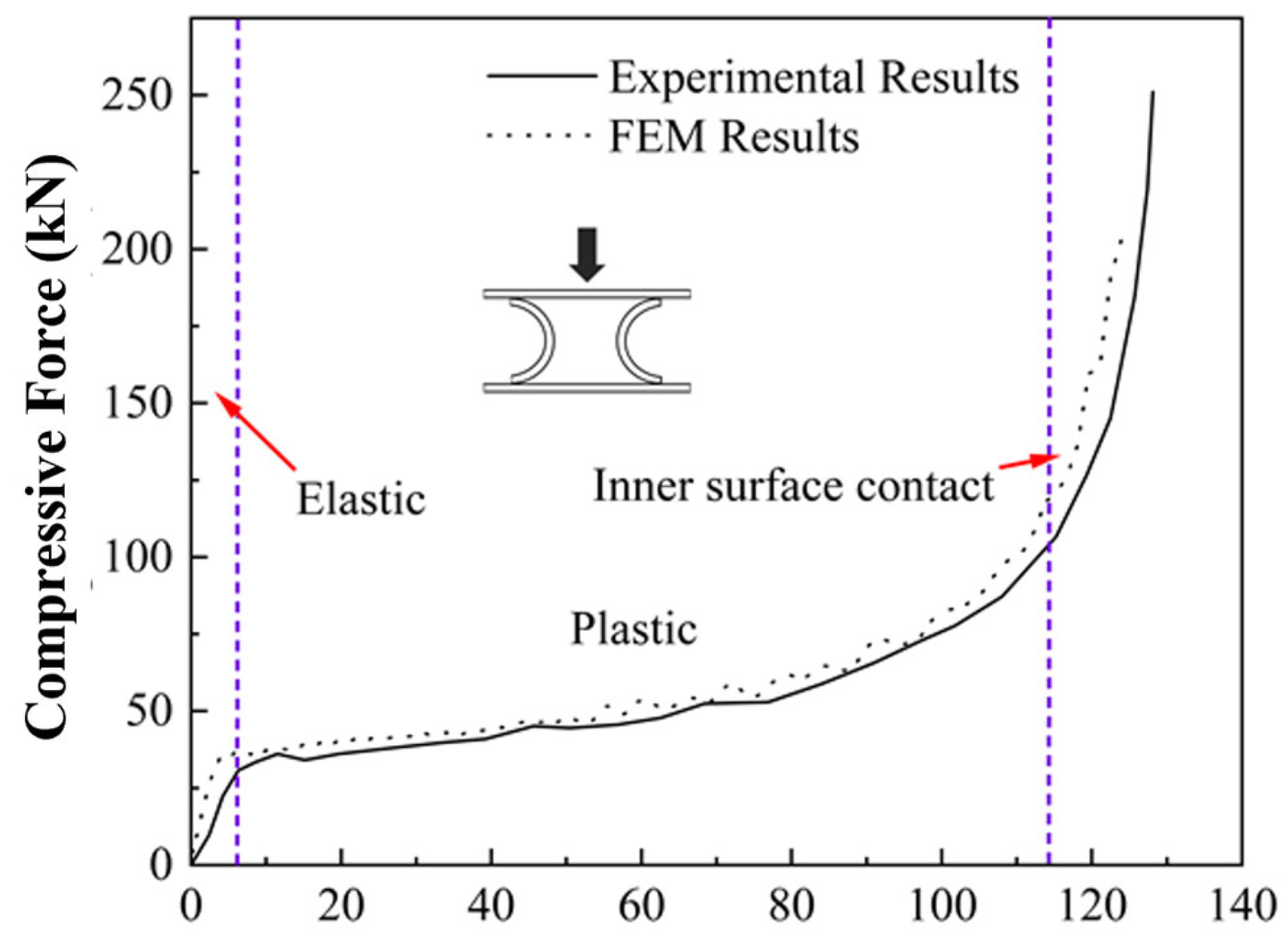
2.4.1. Part 1
2.4.2. Part 2
3. Results
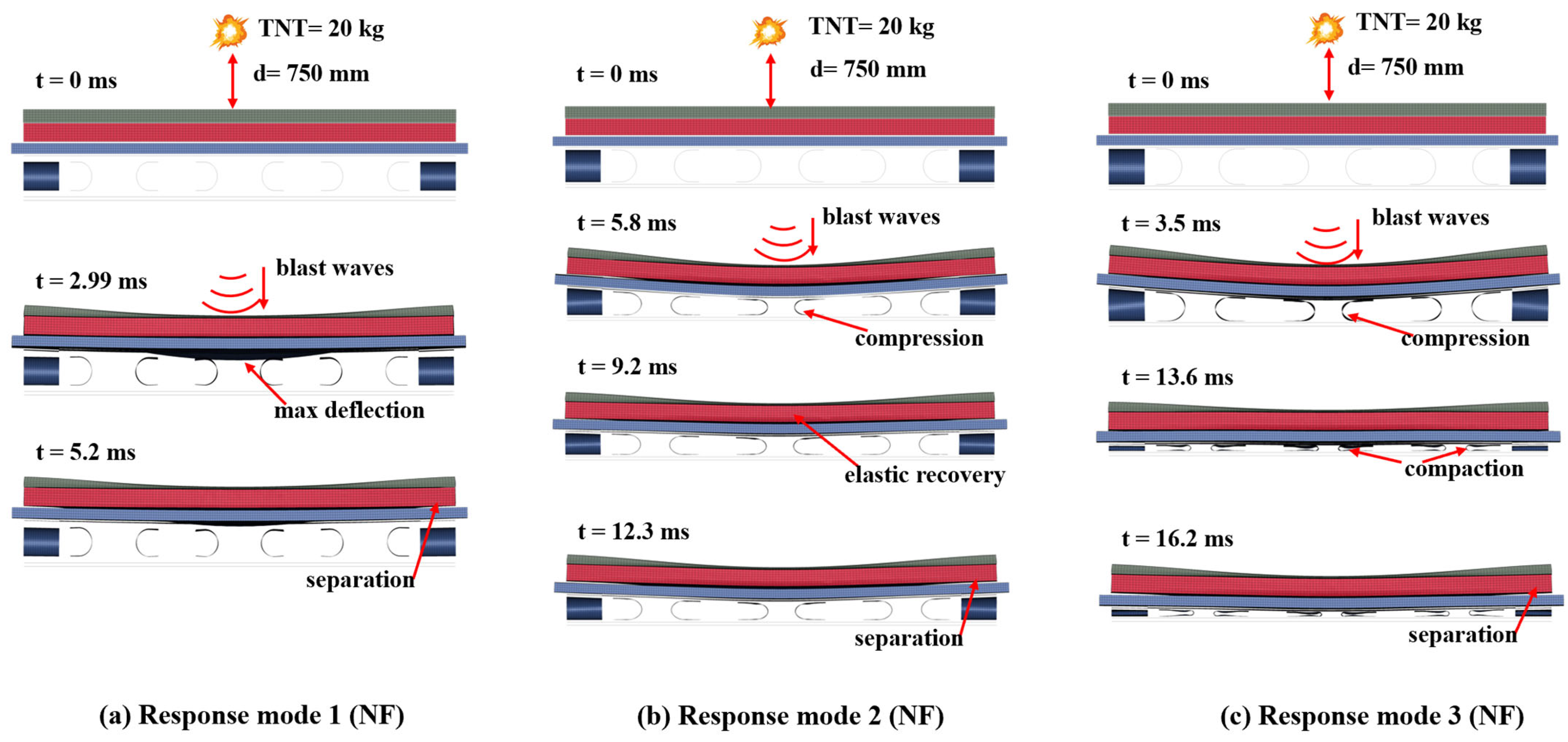
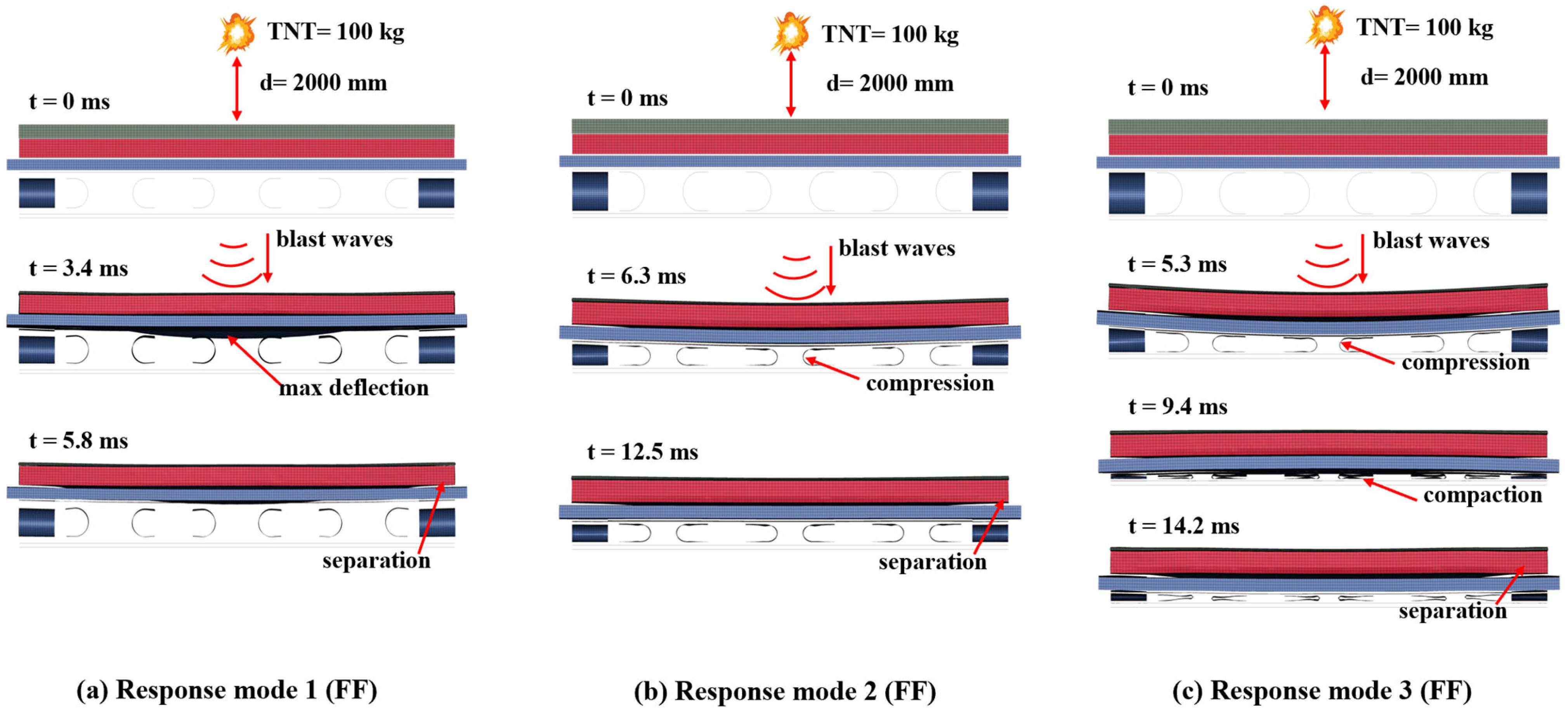
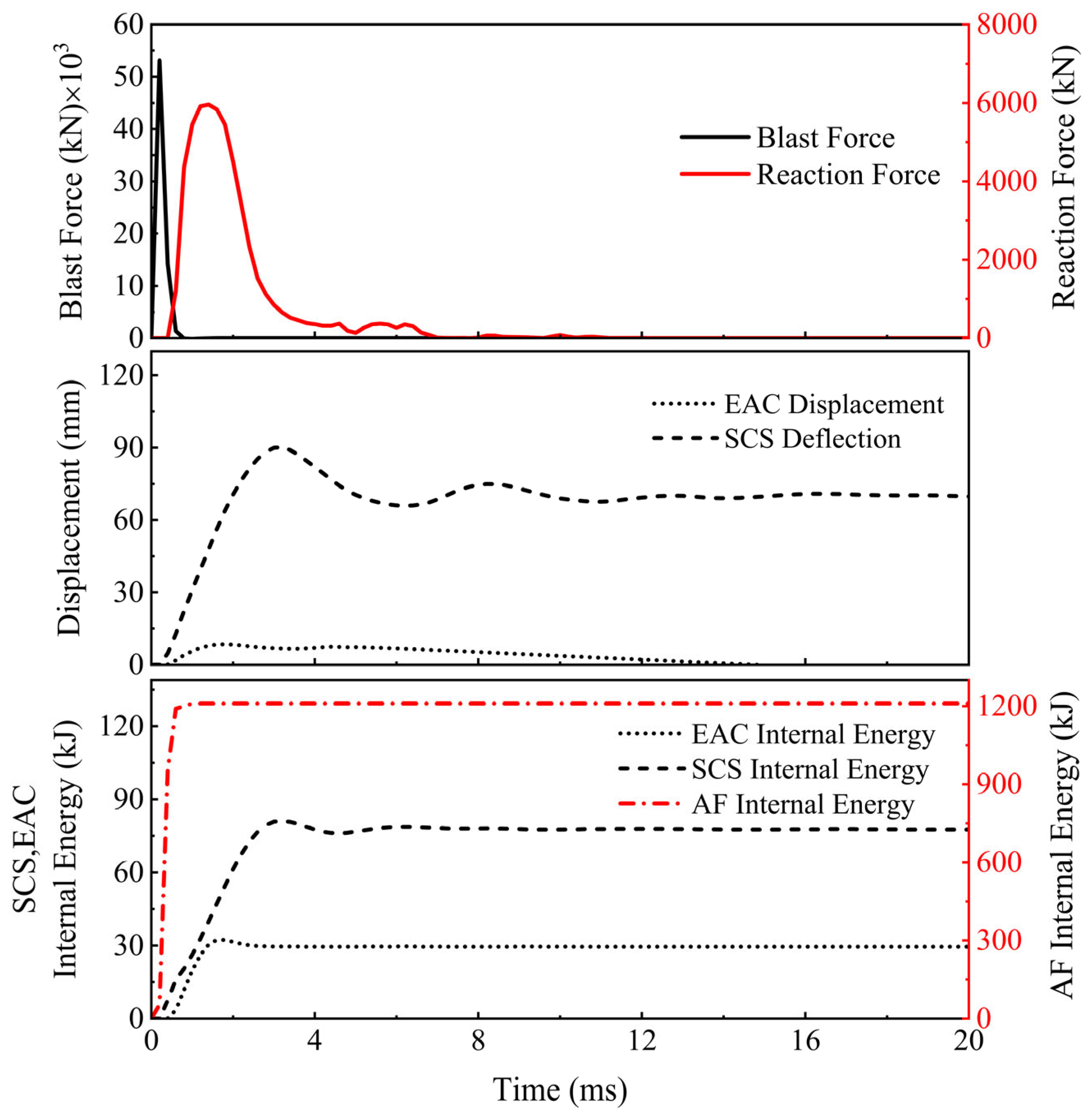
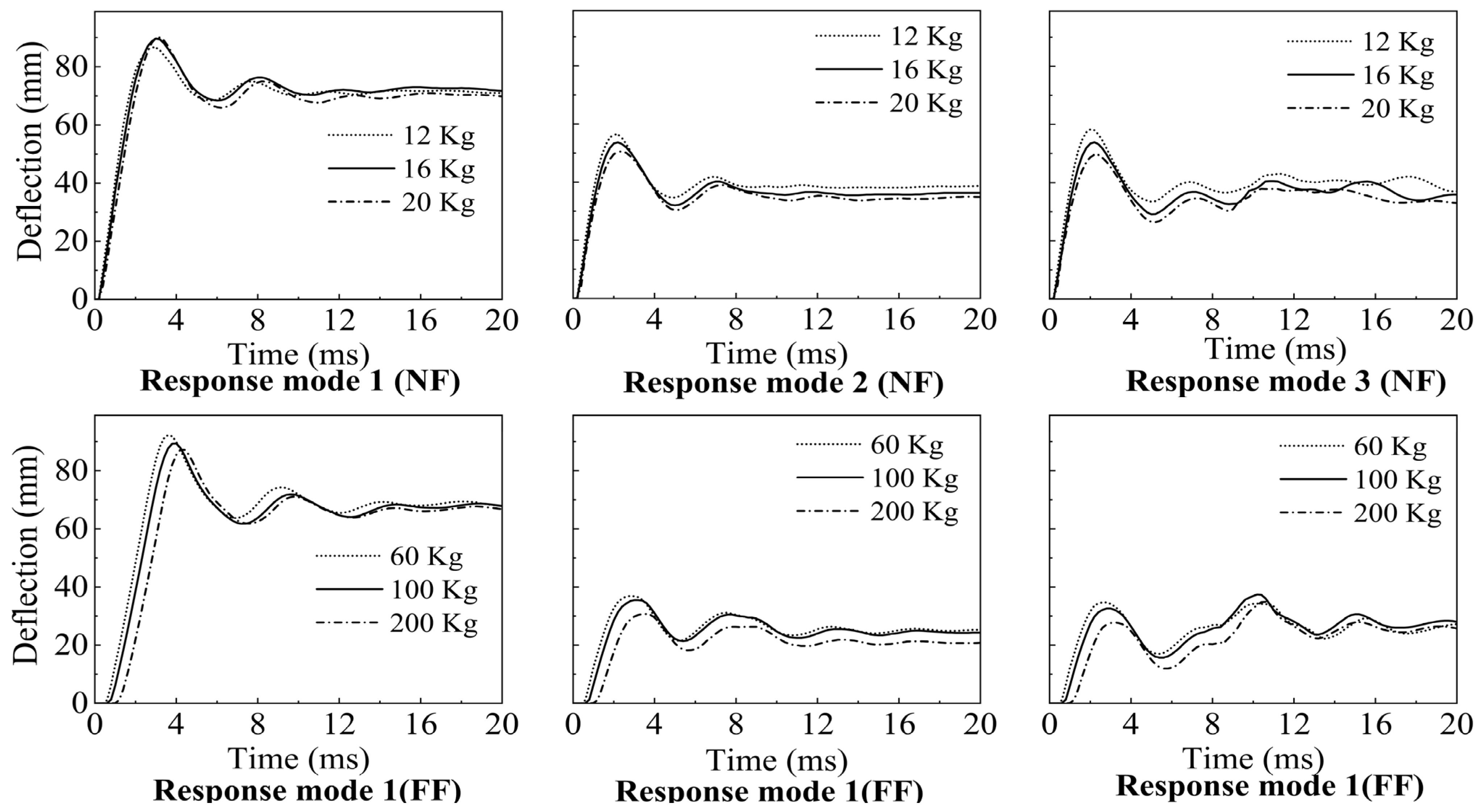
3.1. Response Mode 1
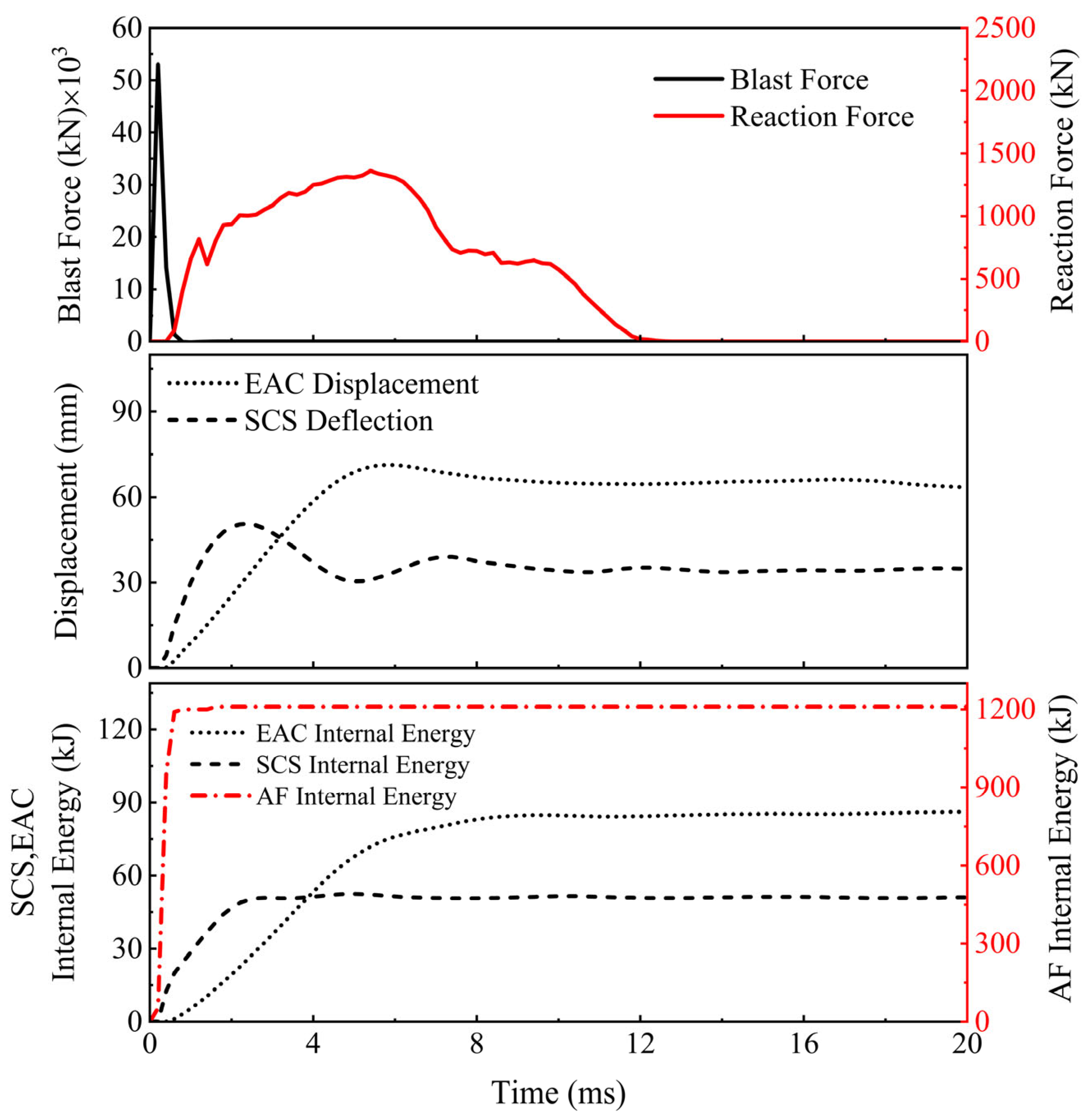
3.2. Response Mode 2
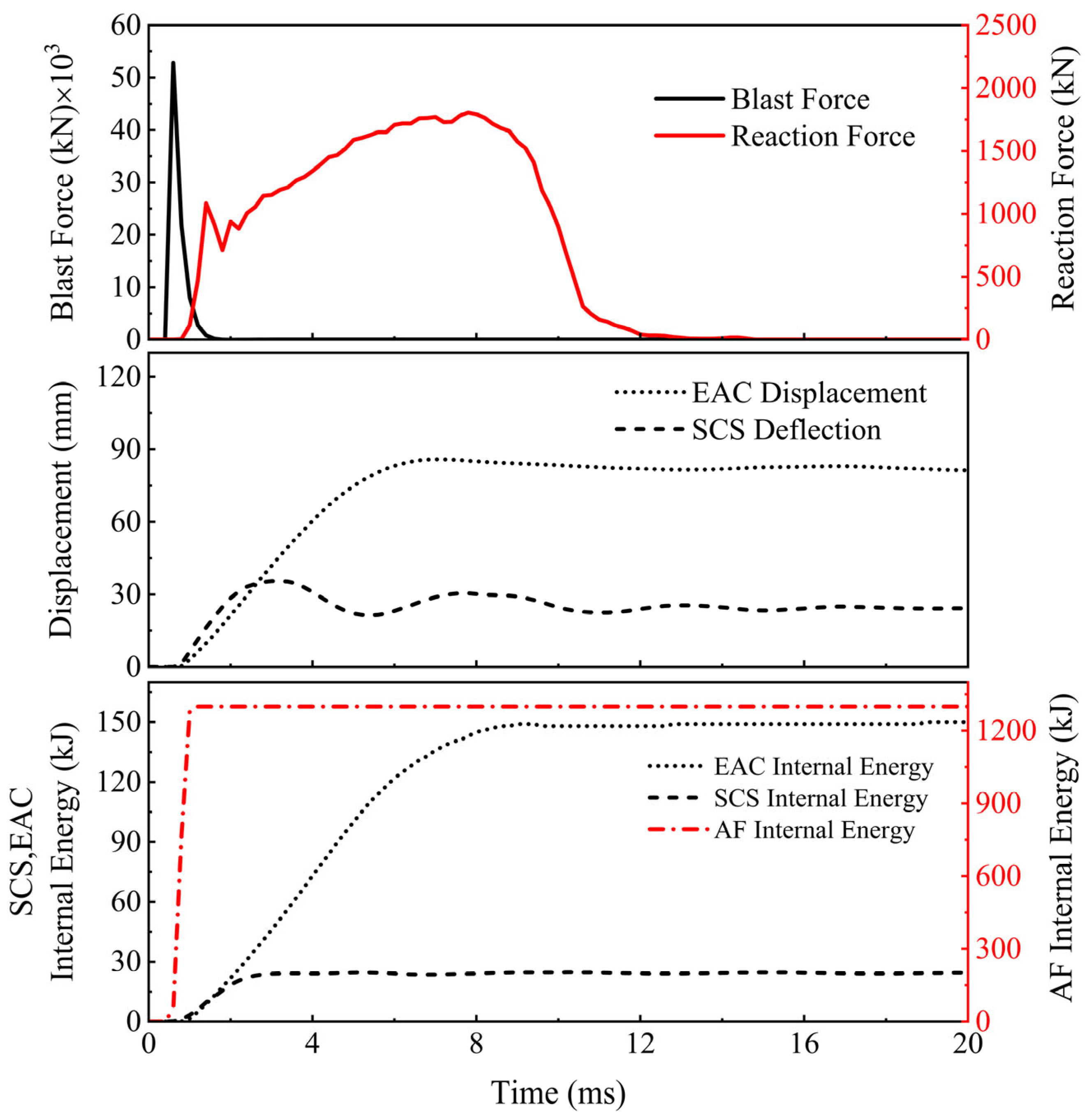
3.3. Response Mode 3
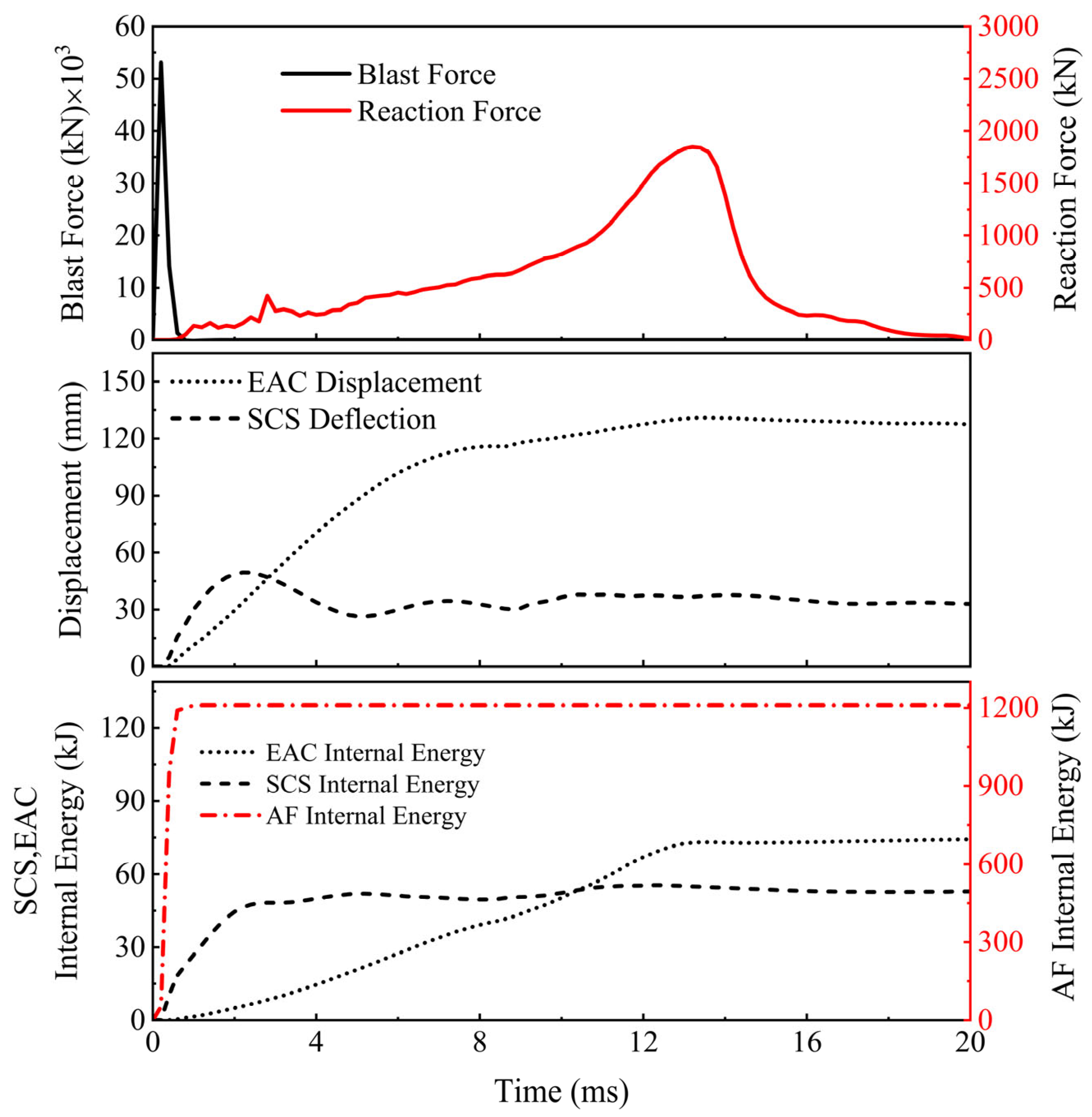
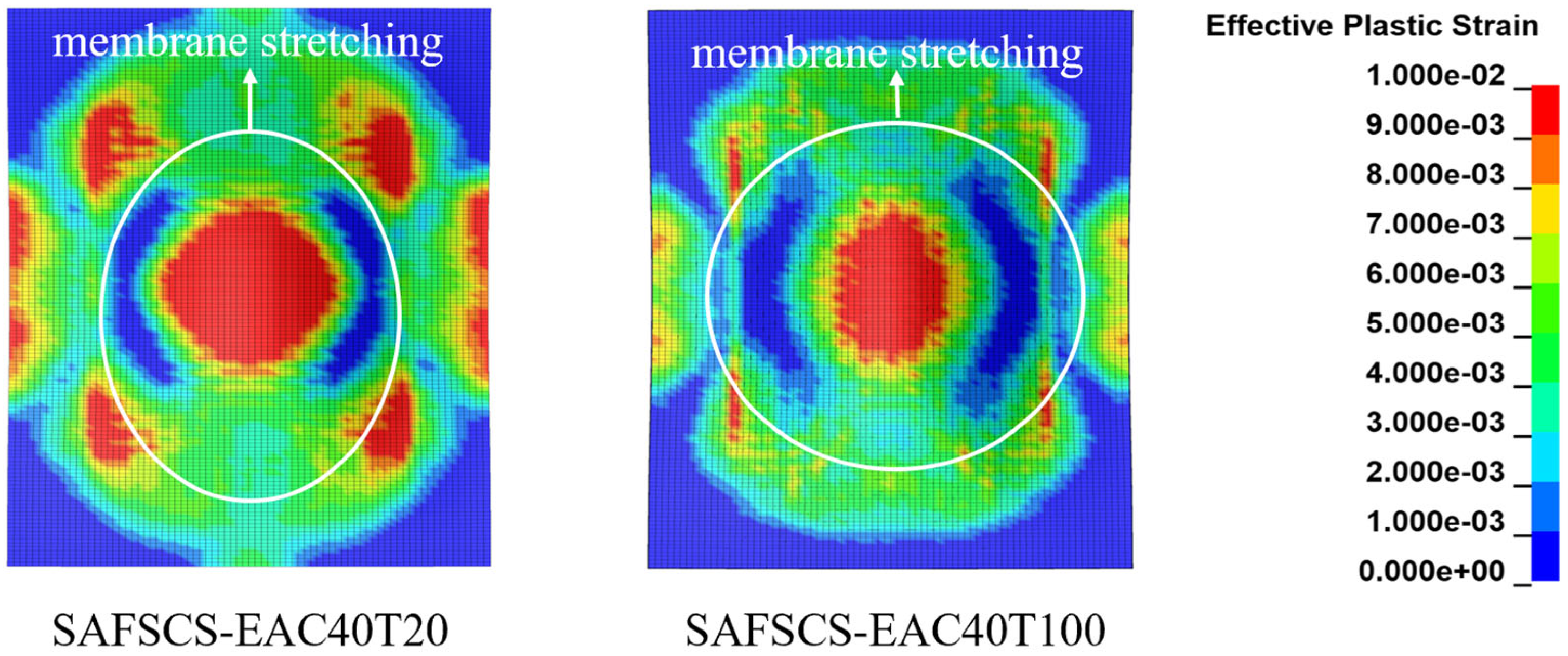
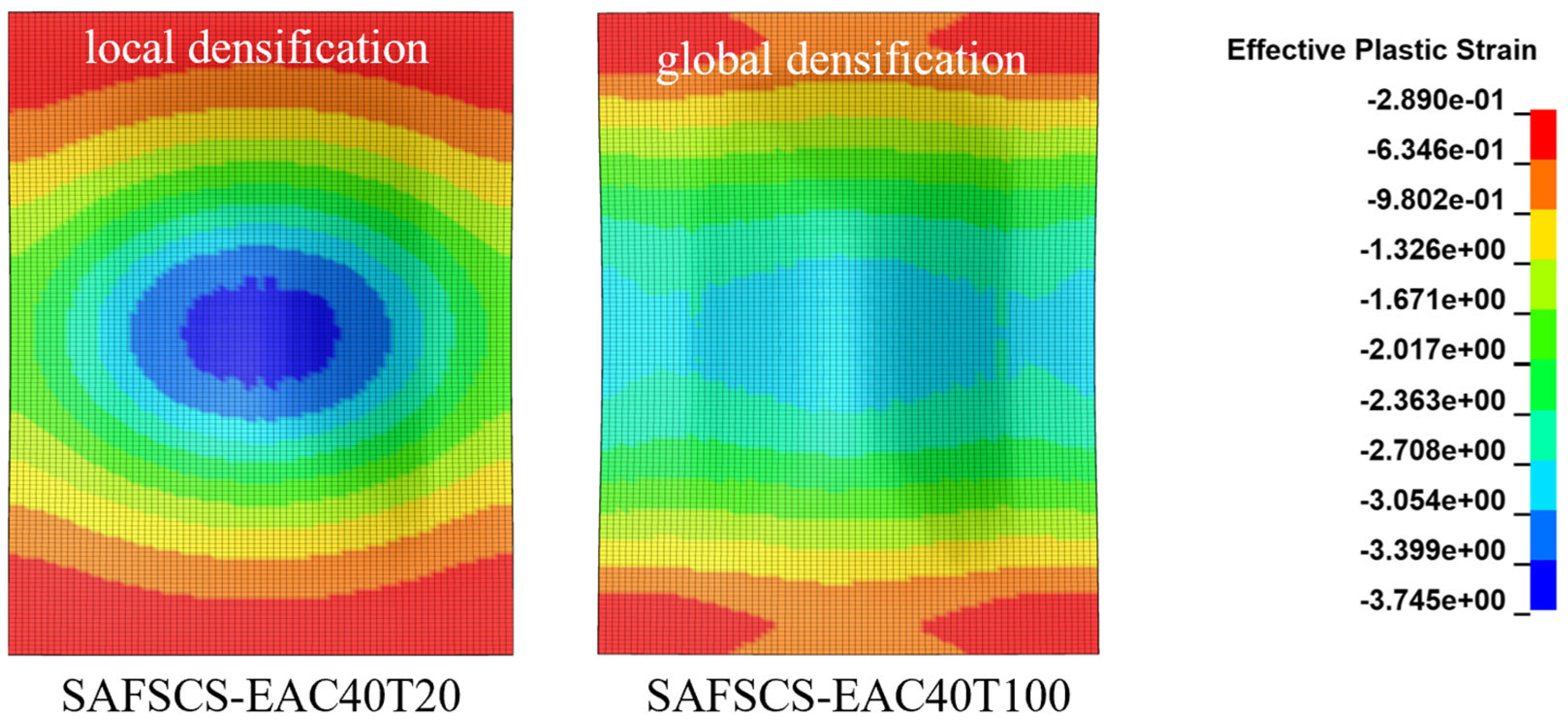
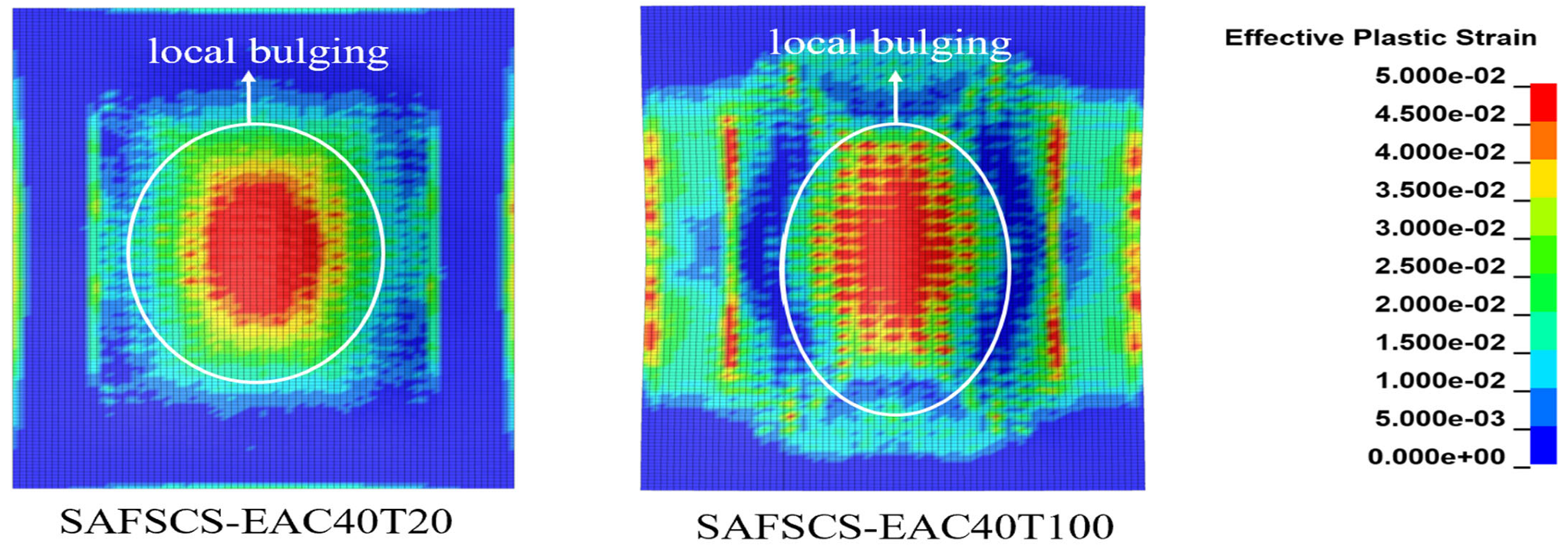
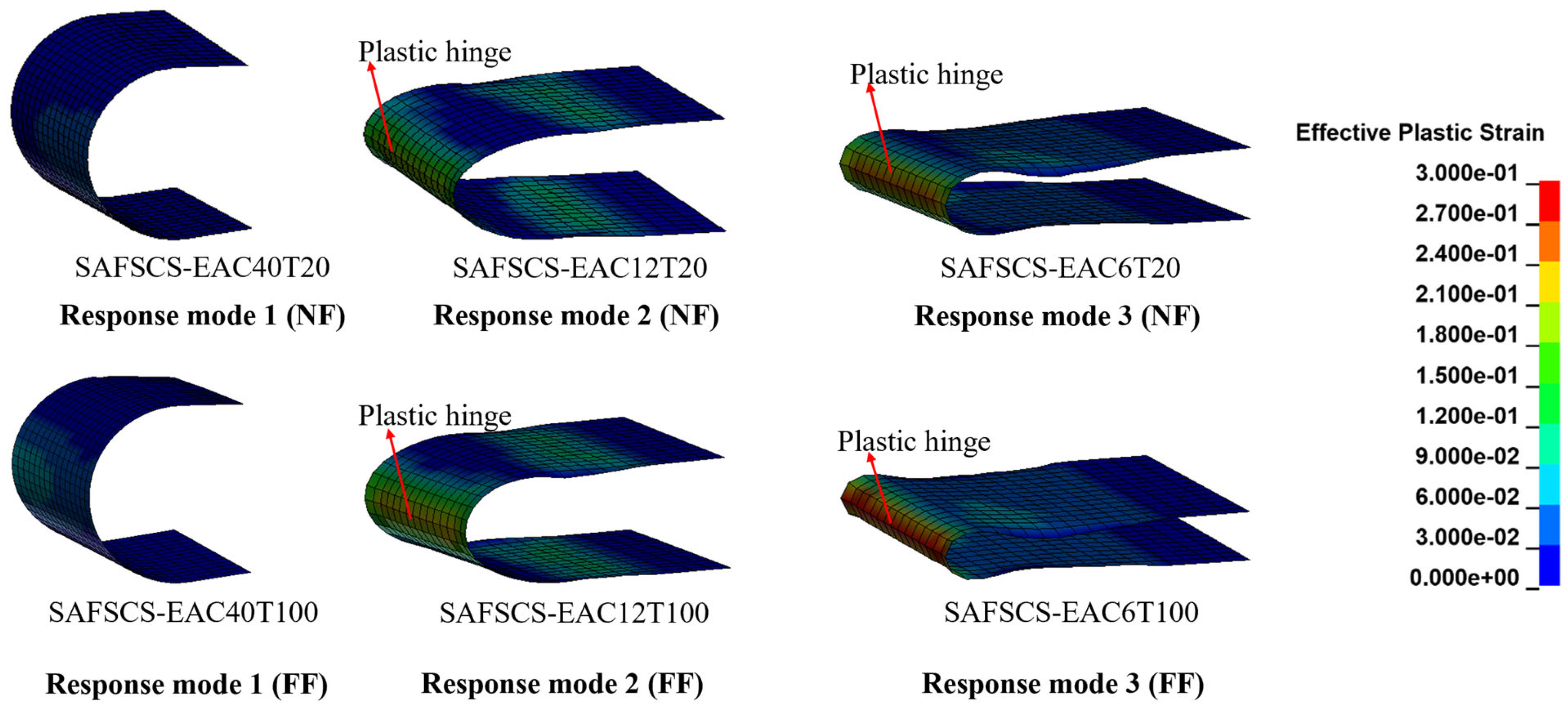
3.4. Failure Modes
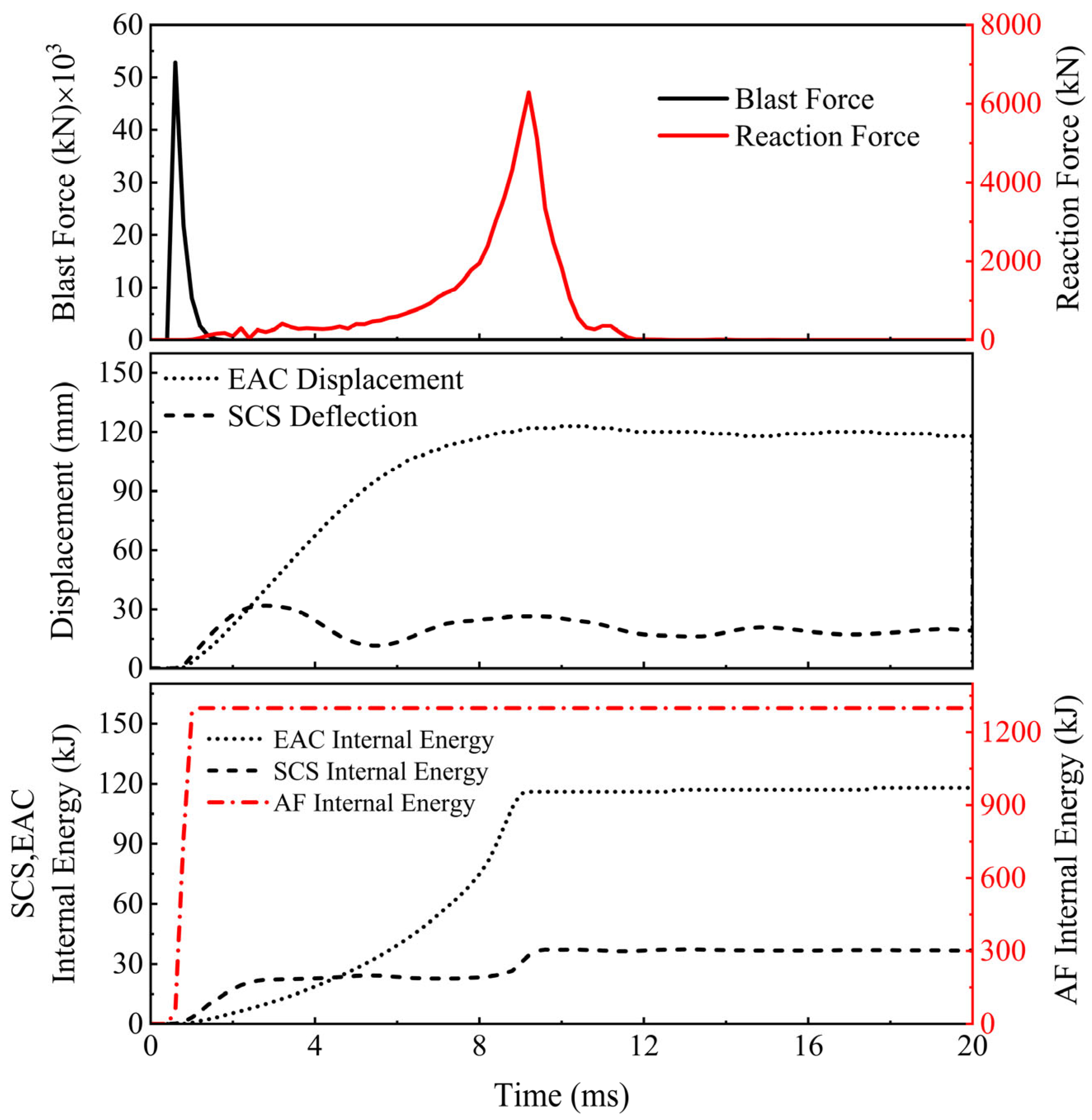
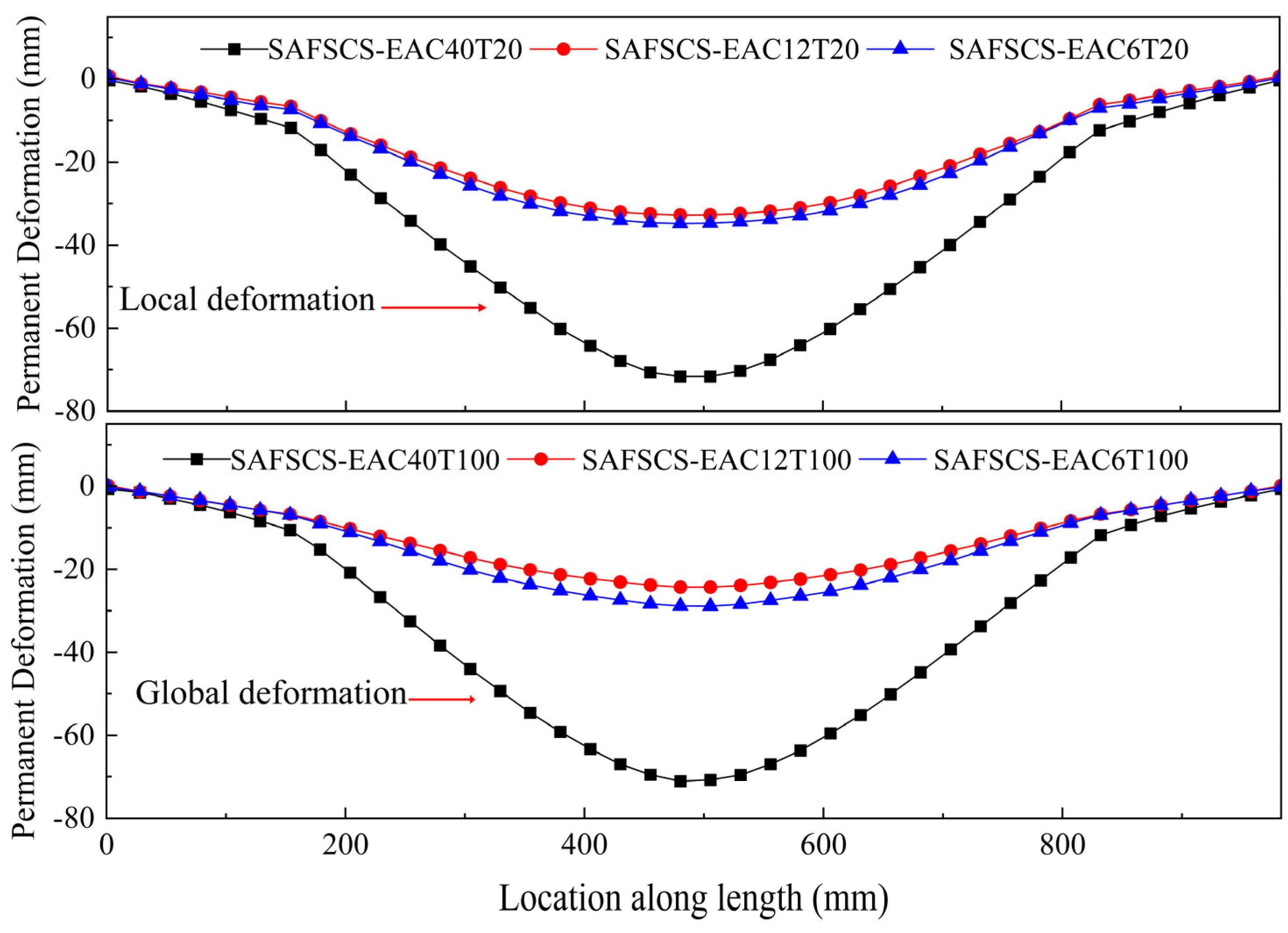
3.5. Displacement and Energy Absorption Responses
3.6. Parametric Study
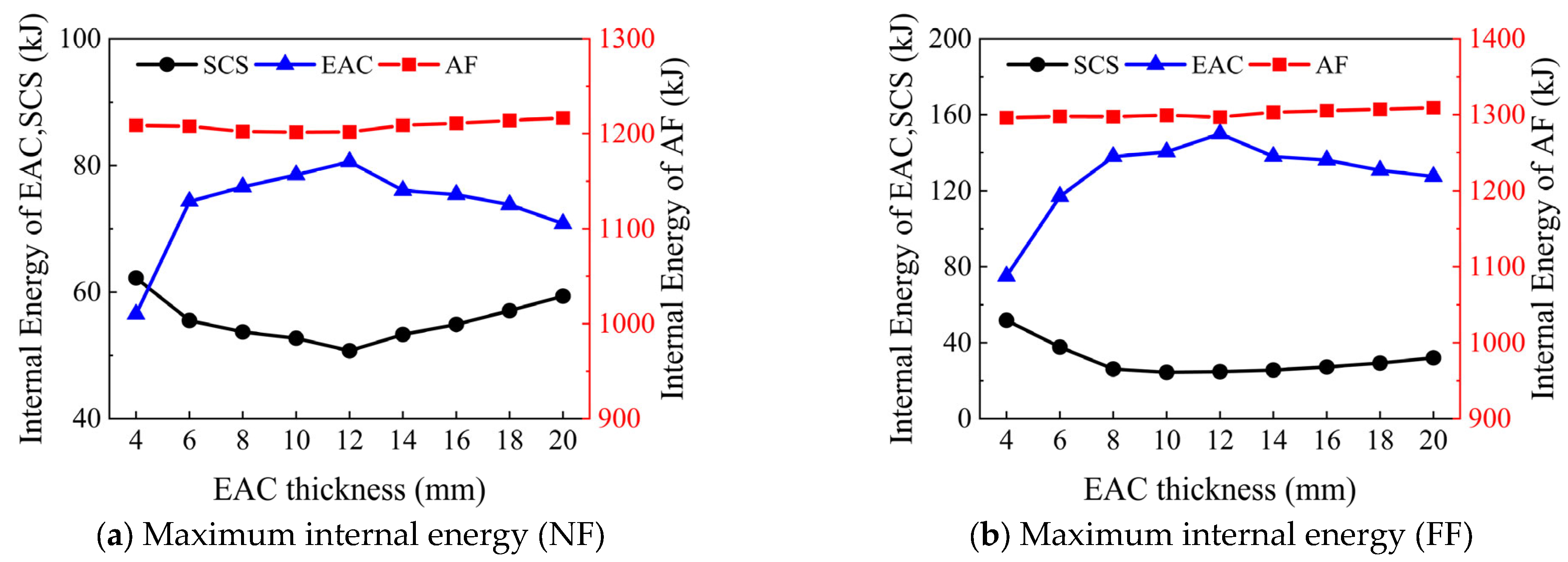
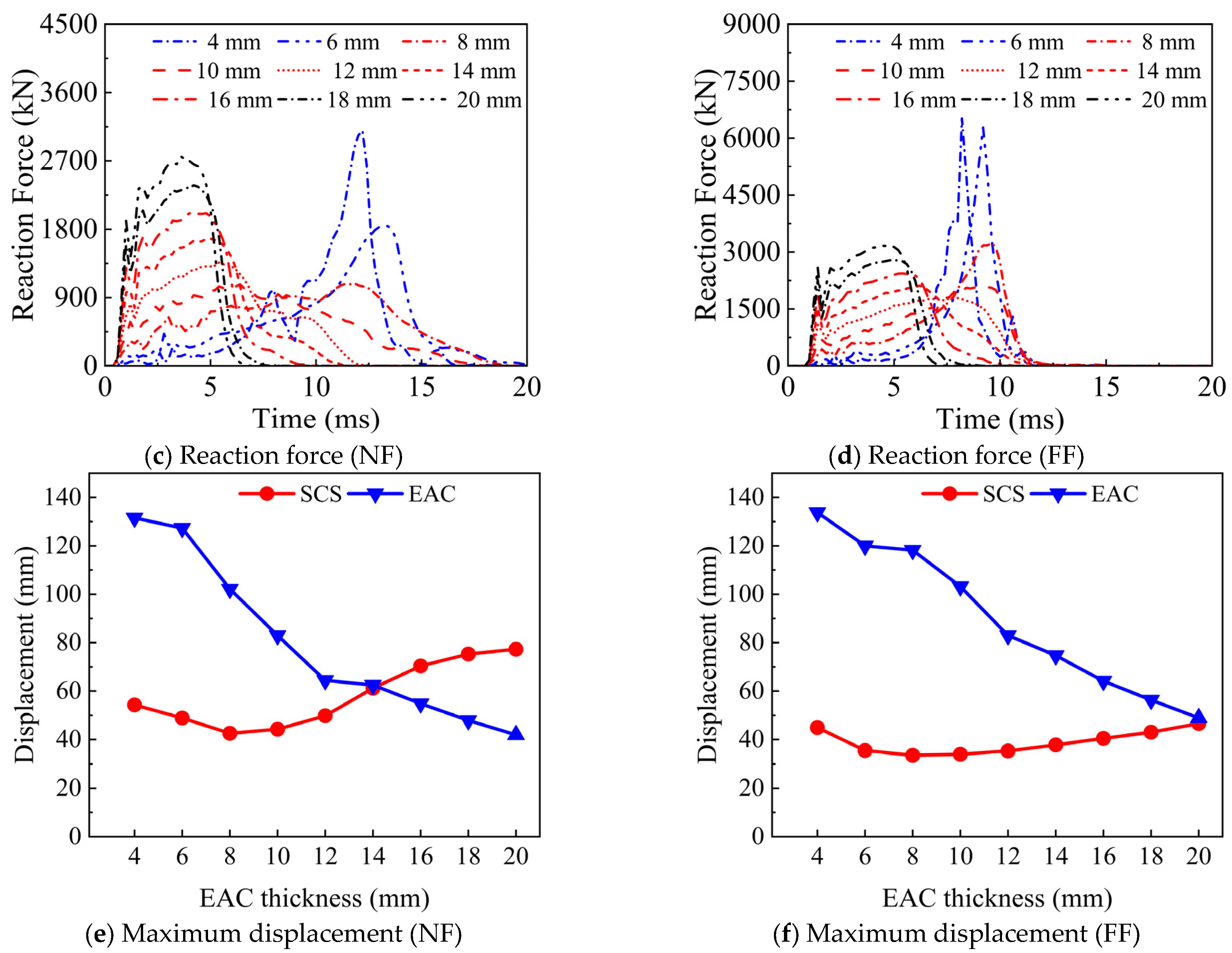
3.6.1. Effect of EAC Thickness
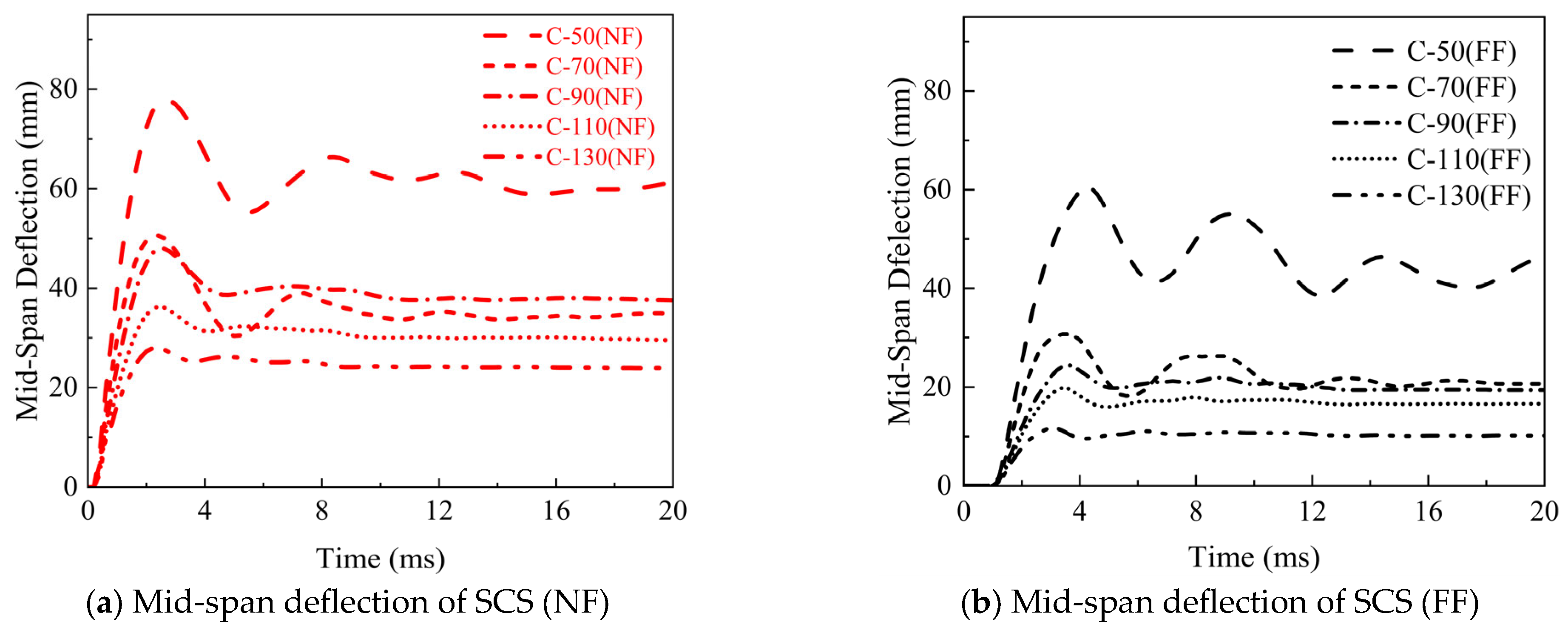
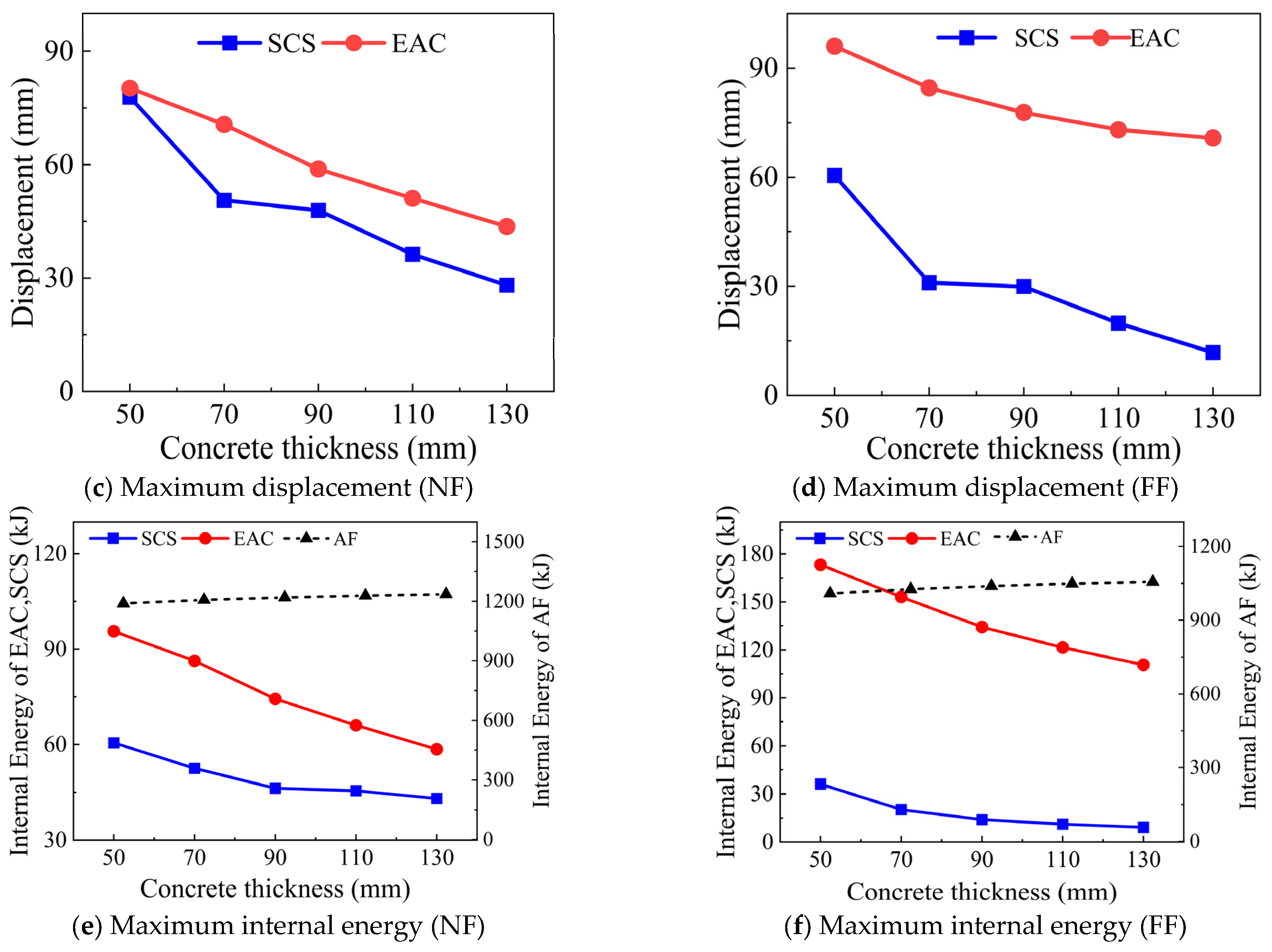
3.6.2. Effect of Concrete Thickness
4. Conclusions
5. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, M.; Dover, D. Lightweight, Blast-Resistant Doors for Retrofit Protection against the Terrorist Threat. In Proceedings of the 2nd International Conference on Innovation in Architecture, Engineering and Construction, Loughborough, UK, 25–27 June 2003; pp. 23–33. [Google Scholar]
- Goel, M.D.; Matsagar, V.A.; Marburg, S.; Gupta, A.K. Comparative Performance of Stiffened Sandwich Foam Panels under Impulsive Loading. J. Perform. Constr. Facil. 2013, 27, 540–549. [Google Scholar] [CrossRef]
- Salomoni, V.A.; Mazzucco, G.; Xotta, G.; Fincato, R.; Majorana, C.E.; Schiavon, M. Nonlinear Modelling, Design, and Test of Steel Blast-Resistant Doors. Adv. Mech. Eng. 2013, 5, 908373. [Google Scholar] [CrossRef]
- Veeredhi, L.S.B.; Ramana Rao, N.V. Studies on the Impact of Explosion on Blast Resistant Stiffened Door Structures. J. Inst. Eng. India Ser. A 2015, 96, 11–20. [Google Scholar] [CrossRef]
- Choi, Y.; Lee, J.; Yoo, Y.-H.; Yun, K.-J. A Study on the Behavior of Blast Proof Door under Blast Load. Int. J. Precis. Eng. Manuf. 2016, 17, 119–124. [Google Scholar] [CrossRef]
- Chen, L.; Fang, Q.; Zhang, Y.-D.; Zhang, Y.; Fan, J.-Y. Numerical and Experimental Investigations on the Blast-Resistant Properties of Arched RC Blast Doors. Int. J. Prot. Struct. 2010, 1, 425–441. [Google Scholar] [CrossRef]
- Yan, Q.; Guo, D. Elastic Rebound of a Blast Door Under Explosion Loadings. Int. J. Str. Stab. Dyn. 2018, 18, 1871011. [Google Scholar] [CrossRef]
- Dong, S.; Tian, Z.; Cao, X.; Tian, C.; Wang, Z. Analysis of the Ultimate Load-Bearing Capacity of Steel-Clad Concrete-Filled Steel Tube Arched Protective Doors under Blast Shock Waves. Buildings 2023, 13, 1424. [Google Scholar] [CrossRef]
- Thimmesh, T.; Shirbhate, P.A.; Mandal, J.; Sandhu, I.S.; Goel, M.D. Numerical Investigation on the Blast Resistance of a Door Panel. Mater. Today Proc. 2021, 44, 659–666. [Google Scholar] [CrossRef]
- Hsieh, M.-W.; Hung, J.-P.; Chen, D.-J. Investigation on the Blast Resistance of a Stiffened Door Structure. J. Mar. Sci. Technol. 2008, 16, 7. [Google Scholar] [CrossRef]
- Chen, H.; Li, F. Design of Quadrilateral Zero-Poisson’s Ratio Metamaterial and Its Application in Ship Explosion-Proof Hatch Door. Ocean. Eng. 2022, 266, 112667. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, B.; Zhou, J.; Chen, H.; Wang, B.; Zhou, Y.; Xu, Y.; Jin, F.; Fan, H. Quasi-Far-Field Blast Responses of Hierarchical Orthogrid-Stiffened Sheet Molding Compound (SMC) Protective Door Structures. Eng. Struct. 2018, 168, 431–446. [Google Scholar] [CrossRef]
- Meng, F.; Zhang, B.; Zhao, Z.; Xu, Y.; Fan, H.; Jin, F. A Novel All-Composite Blast-Resistant Door Structure with Hierarchical Stiffeners. Compos. Struct. 2016, 148, 113–126. [Google Scholar] [CrossRef]
- Guo, H.; Yuan, H.; Zhang, J.; Ruan, D. Review of Sandwich Structures under Impact Loadings: Experimental, Numerical and Theoretical Analysis. Thin-Walled Struct. 2024, 196, 111541. [Google Scholar] [CrossRef]
- Li, J.; Qin, Q.; Zhang, J. Internal Blast Resistance of Sandwich Cylinder with Lattice Cores. Int. J. Mech. Sci. 2021, 191, 106107. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, R.; Wang, M.; Qin, Q.; Ye, Y.; Wang, T.J. Dynamic Response of Double-Layer Rectangular Sandwich Plates with Metal Foam Cores Subjected to Blast Loading. Int. J. Impact Eng. 2018, 122, 265–275. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, Q.; Wang, T.J. Compressive Strengths and Dynamic Response of Corrugated Metal Sandwich Plates with Unfilled and Foam-Filled Sinusoidal Plate Cores. Acta Mech 2013, 224, 759–775. [Google Scholar] [CrossRef]
- Wang, Y.; Zhai, X.; Lee, S.C.; Wang, W. Responses of Curved Steel-Concrete-Steel Sandwich Shells Subjected to Blast Loading. Thin-Walled Struct. 2016, 108, 185–192. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, J.; Liu, S.; Zhai, X.; Zhi, X.; Yan, J.-B. Behaviour of a Novel Stiffener-Enhanced Steel–Concrete–Steel Sandwich Beam Subjected to Impact Loading. Thin-Walled Struct. 2021, 165, 107989. [Google Scholar] [CrossRef]
- Meng, L.; Wang, Y.; Zhai, X. Modeling and Dynamic Response of Curved Steel–Concrete–Steel Sandwich Shells Under Blast Loading. Int. J. Steel Struct. 2020, 20, 1663–1681. [Google Scholar] [CrossRef]
- Lan, S.; Lok, T.-S.; Heng, L. Composite Structural Panels Subjected to Explosive Loading. Constr. Build. Mater. 2005, 19, 387–395. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, Y.; Jin, Q.; Wang, J.; Li, X. Blast Resistance of Single Steel-concrete Composite Slabs under Contact Explosion. Struct. Concr. 2023, 24, 6025–6048. [Google Scholar] [CrossRef]
- Zhao, C.; He, K.; Zhi, L.; Lu, X.; Pan, R.; Gautam, A.; Wang, J.; Li, X. Blast Behavior of Steel-Concrete-Steel Sandwich Panel: Experiment and Numerical Simulation. Eng. Struct. 2021, 246, 112998. [Google Scholar] [CrossRef]
- Yu, J.; Liang, S.-L.; Ren, Z.-P.; Deng, Y.-J.; Fang, Q. Structural Behavior of Steel-Concrete-Steel and Steel-Ultra-High-Performance-Concrete-Steel Composite Panels Subjected to near-Field Blast Load. J. Constr. Steel Res. 2023, 210, 108108. [Google Scholar] [CrossRef]
- Roberts, T.M.; Edwards, D.N.; Narayanan, R. Testing and Analysis of Steel-Concrete-Steel Sandwich Beams. J. Constr. Steel Res. 1996, 38, 257–279. [Google Scholar] [CrossRef]
- Schlaseman, C.; Russell, J. Application of Advanced Construction Technologies to New Nuclear Power Plants; US Department of Energy: Washington, DC, USA, 2004.
- Farhan, J.A.; Hussain, H.M. Development of Three-Layer Composite Steel-Concrete-Steel Beam Element with Applications. Eng. Technol. J. 2010, 28, 6970–6985. [Google Scholar] [CrossRef]
- Koh, C.G.; Ang, K.K.; Chan, P.F. Dynamic Analysis of Shell Structures with Application to Blast Resistant Doors. Shock Vib. 2003, 10, 269–279. [Google Scholar] [CrossRef]
- Chen, D.; Gao, K.; Yang, J.; Zhang, L. Functionally Graded Porous Structures: Analyses, Performances, and Applications—A Review. Thin-Walled Struct. 2023, 191, 111046. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.; Zheng, Z.; Chen, H.; Yu, J. Crashworthiness Design and Impact Tests of Aluminum Foam-Filled Crash Boxes. Thin-Walled Struct. 2022, 180, 109937. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Pei, W.; Yu, F.; Jiang, Y. Energy-Absorbing Mechanism and Crashworthiness Performance of Thin-Walled Tubes Diagonally Filled with Rib-Reinforced Foam Blocks under Axial Crushing. Compos. Struct. 2022, 299, 116149. [Google Scholar] [CrossRef]
- Chakravarty, U.K. An Investigation on the Dynamic Response of Polymeric, Metallic, and Biomaterial Foams. Compos. Struct. 2010, 92, 2339–2344. [Google Scholar] [CrossRef]
- Yun, N.-R.; Shin, D.-H.; Ji, S.-W.; Shim, C.-S. Experiments on Blast Protective Systems Using Aluminum Foam Panels. KSCE J. Civ. Eng. 2014, 18, 2153–2161. [Google Scholar] [CrossRef]
- Ganorkar, K.; Goel, M.D.; Chakraborty, T. Numerical Analysis of Double-Leaf Composite Stiffened Door Subjected to Blast Loading. J. Perform. Constr. Facil. 2023, 37, 04022067. [Google Scholar] [CrossRef]
- Wang, Y.; Liew, J.R.; Lee, S.C. Experimental and Numerical Studies of Non-Composite Steel–Concrete–Steel Sandwich Panels under Impulsive Loading. Mater. Des. 2015, 81, 104–112. [Google Scholar] [CrossRef]
- Wang, Y.; Pokharel, R.; Lu, J.; Zhai, X. Experimental, Numerical, and Analytical Studies on Polyurethane Foam-Filled Energy Absorption Connectors under Quasi-Static Loading. Thin-Walled Struct. 2019, 144, 106257. [Google Scholar] [CrossRef]
- Harris, J.A.; McShane, G.J. Impact Response of Metallic Stacked Origami Cellular Materials. Int. J. Impact Eng. 2021, 147, 103730. [Google Scholar] [CrossRef]
- Baroutaji, A.; Gilchrist, M.D.; Olabi, A.-G. Quasi-Static, Impact and Energy Absorption of Internally Nested Tubes Subjected to Lateral Loading. Thin-Walled Struct. 2016, 98, 337–350. [Google Scholar] [CrossRef]
- Meng, L.; Wang, Y.; Zhai, X. Experimental and Numerical Studies on Steel-Polyurethane Foam-Steel–Concrete-Steel Panel under Impact Loading by a Hemispherical Head. Eng. Struct. 2021, 247, 113201. [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation. LS-DYNA Keyword User’s Manual; LSTC Co.: Livermore, CA, USA, 2007. [Google Scholar]
- Abramowicz, W.; Jones, N. Dynamic Progressive Buckling of Circular and Square Tubes. Int. J. Impact Eng. 1986, 4, 243–270. [Google Scholar] [CrossRef]
- Murray, Y.D. Users Manual for LS-DYNA Concrete Material Model 159; US Department of Transportation, Federal Highway Administration: McLean, VA, USA, 2007.
- Castedo, R.; Santos, A.P.; Alañón, A.; Reifarth, C.; Chiquito, M.; López, L.M.; Martínez-Almajano, S.; Pérez-Caldentey, A. Numerical Study and Experimental Tests on Full-Scale RC Slabs under Close-in Explosions. Eng. Struct. 2021, 231, 111774. [Google Scholar] [CrossRef]
- Bruhl, J.C. Behavior and Design of Steel-Plate Composite (SC) Walls for Blast Loads. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2015. [Google Scholar]
- Wang, Y.; Liew, J.R.; Lee, S.C.; Wang, W. Experimental and Analytical Studies of a Novel Aluminum Foam Filled Energy Absorption Connector under Quasi-Static Compression Loading. Eng. Struct. 2017, 131, 136–147. [Google Scholar] [CrossRef]
- Wang, Y.; Zhai, X.; Wang, W. Numerical Studies of Aluminum Foam Filled Energy Absorption Connectors under Quasi-Static Compression Loading. Thin-Walled Struct. 2017, 116, 225–233. [Google Scholar] [CrossRef]
- Momeni, M.; Hadianfard, M.A.; Bedon, C.; Baghlani, A. Damage Evaluation of H-Section Steel Columns under Impulsive Blast Loads via Gene Expression Programming. Eng. Struct. 2020, 219, 110909. [Google Scholar] [CrossRef]






| Blast Type | Model | Blast Load TNT (kg) | Standoff Distance (mm) | Concrete (mm) | Scale Distance (m/kg1/3) |
|---|---|---|---|---|---|
| Near field blast | SAFSCS-EAC-6 | 12 16 20 | 550 650 750 | 70 70 70 | 0.24 0.26 0.28 |
| SAFSCS-EAC-12 | 12 16 20 | 550 650 750 | 70 70 70 | 0.24 0.26 0.28 | |
| SAFSCS-EAC-40 | 12 16 20 | 1500 2000 3000 | 70 70 70 | 0.24 0.26 0.28 | |
| Far field blast | SAFSCS-EAC-6 | 60 100 200 | 1500 2000 3000 | 70 70 70 | 0.39 0.44 0.52 |
| SAFSCS-EAC-12 | 60 100 200 | 1500 2000 3000 | 70 70 70 | 0.39 0.44 0.52 | |
| SAFSCS-EAC-40 | 60 100 200 | 1500 2000 3000 | 70 70 70 | 0.39 0.44 0.52 |
| Components | Material Model | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|---|
| Steel plate of SCS | PIECWISE_LINEAR_PLASTICITY (MAT_024) | 398 | 472 | 200 |
| Curved steel plate | 298 | 536 | 204.6 | |
| EAC top and bottom steel plate | 363 | 577 | 217.7 | |
| Bolt | 410 | 496 | 144.8 | |
| Concrete | CSCM (MAT_159) | Compressive strength (MPa) 42.7 | Elastic modulus (GPa) 24.3 | Poisson’s ratio 0.2 |
| Aluminum foam | CRUSHABLE_FOAM (MAT_063) | Young’s modulus (MPa) 120 | Plateau stress (MPa) 2.69 | Density (g/cm3) 0.286 |
| Panel | Shot | Bruhal Experimental | Bruhal FEM | FEM Results | Difference |
|---|---|---|---|---|---|
| XM | XM | XM | |||
| (mm) | (mm) | (mm) | (%) | ||
| 3-2-50-5(1) | 1 | 4.6228 | 4.1656 | 4.12098 | 12.18 |
| 5-2b-50-5(1) | 3 | 2.4384 | 2.4384 | 2.34528 | 3.97 |
| 5-2b-50-5(1) | 4 | 13.3858 | 13.4366 | 13.2383 | 1.11 |
| 5-2-50-5(2) | 6 | 13.9954 | 11.6078 | 13.1314 | 6.58 |
| Experimental Results Mean Force (kN) | FEM Results Mean Force (kN) | Difference (%) | |
|---|---|---|---|
| Mean force | 47.4 | 48.9 | 3.16 |
| Specimen | TNT Charge (kg) | Response Mode | Internal Energy (kJ) | δSCS (mm) | ΔEAC (mm) | ||
|---|---|---|---|---|---|---|---|
| AF | SCS | EAC | |||||
| 12 | 1 | 927.3 | 68.5 | 18.2 | 86.7 | ||
| SAFSCS-EAC-40 | 16 | 1 | 1100.9 | 84.4 | 25.8 | 89.4 | |
| 20 | 1 | 1240.4 | 81.2 | 32.3 | 89.2 | 11.2 | |
| 12 | 2 | 925.5 | 67.4 | 54.8 | 56.4 | ||
| SAFSCS-EAC-12 | 16 | 2 | 1098.8 | 61.1 | 72.8 | 53.7 | |
| 20 | 2 | 1206.7 | 52.5 | 86.3 | 56 | 71 | |
| 12 | 3 | 927.9 | 65.5 | 49.9 | 58.3 | ||
| SAFSCS-EAC-6 | 16 | 3 | 1100.7 | 62.1 | 63.9 | 53.9 | |
| 20 | 3 | 1208.5 | 55.5 | 74.3 | 50 | 130 | |
| Specimen | TNT Charge (kg) | Response Mode | Internal Energy (kJ) | δSCS (mm) | ΔEAC (mm) | ||
|---|---|---|---|---|---|---|---|
| AF | SCS | EAC | |||||
| 60 | 1 | 1359.7 | 71.552 | 59.4 | 92.3 | ||
| SAFSCS-EAC-40 | 100 | 1 | 1300 | 69 | 68 | 90.2 | 11.2 |
| 200 | 1 | 1030.8 | 66.5 | 68.3 | 87.2 | ||
| 60 | 2 | 1358.3 | 27.7 | 133.7 | 36.9 | ||
| SAFSCS-EAC-12 | 100 | 2 | 1297 | 24.7 | 150 | 35.5 | 83 |
| 200 | 2 | 1026.4 | 20.3 | 153.1 | 30.7 | ||
| 60 | 3 | 1359.1 | 35.5 | 113.5 | 34.7 | ||
| SAFSCS-EAC-6 | 100 | 3 | 1298 | 37.7 | 117 | 32.6 | 120 |
| 200 | 3 | 1027.3 | 35.1 | 120.5 | 27.8 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, S.; Zeb, S.; Wang, Y.; Umair, M. Blast Performance of Multi-Layer Composite Door Panel with Energy Absorption Connectors. Buildings 2025, 15, 2073. https://doi.org/10.3390/buildings15122073
Ahmad S, Zeb S, Wang Y, Umair M. Blast Performance of Multi-Layer Composite Door Panel with Energy Absorption Connectors. Buildings. 2025; 15(12):2073. https://doi.org/10.3390/buildings15122073
Chicago/Turabian StyleAhmad, Shahab, Shayan Zeb, Yonghui Wang, and Muhammad Umair. 2025. "Blast Performance of Multi-Layer Composite Door Panel with Energy Absorption Connectors" Buildings 15, no. 12: 2073. https://doi.org/10.3390/buildings15122073
APA StyleAhmad, S., Zeb, S., Wang, Y., & Umair, M. (2025). Blast Performance of Multi-Layer Composite Door Panel with Energy Absorption Connectors. Buildings, 15(12), 2073. https://doi.org/10.3390/buildings15122073







