Numerical Simulation of Freezing-Induced Crack Propagation in Fractured Rock Masses Under Water–Ice Phase Change Using Discrete Element Method
Abstract
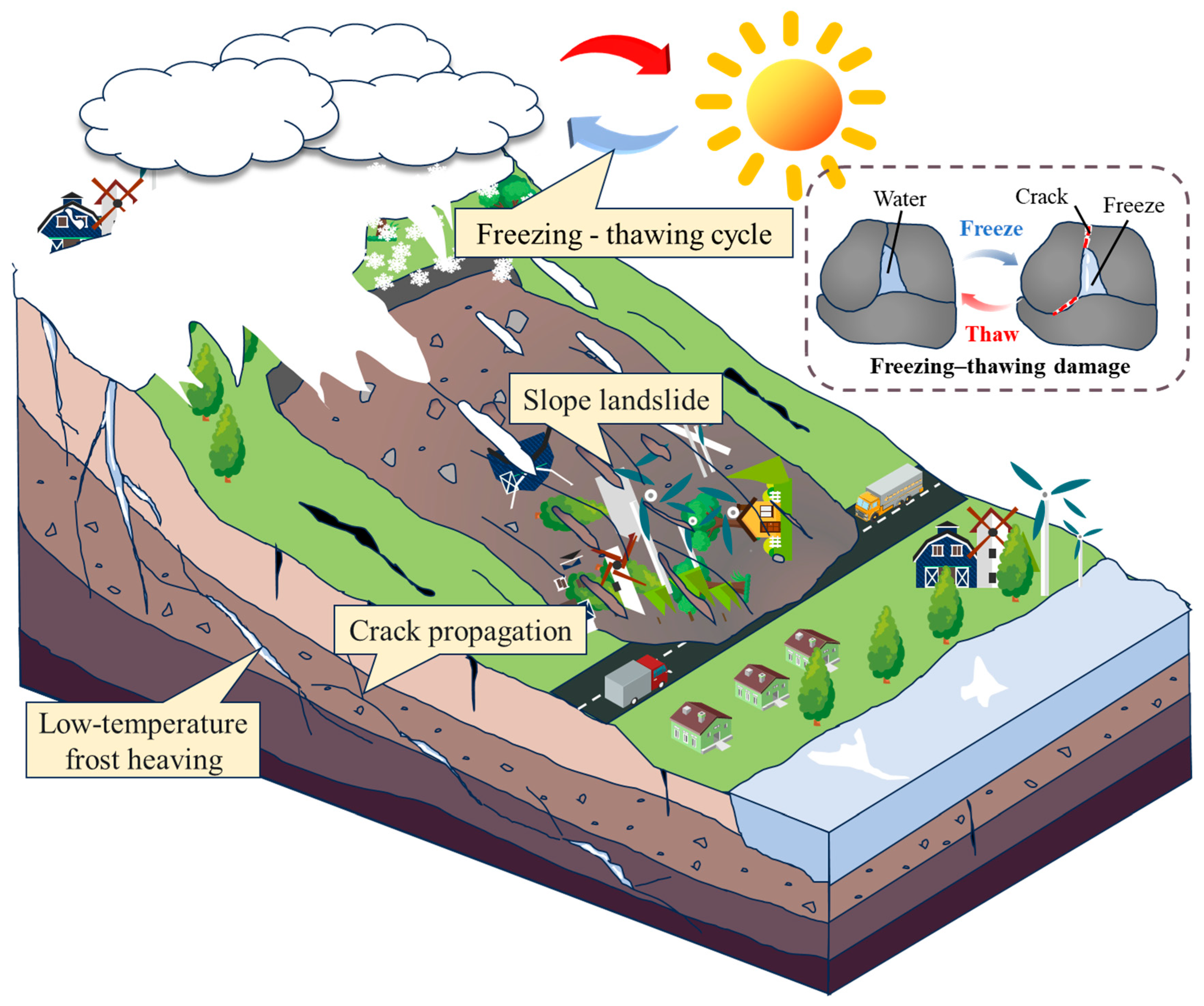
1. Introduction
2. Numerical Simulation Based on PFC2D
2.1. Numerical Simulation Scheme
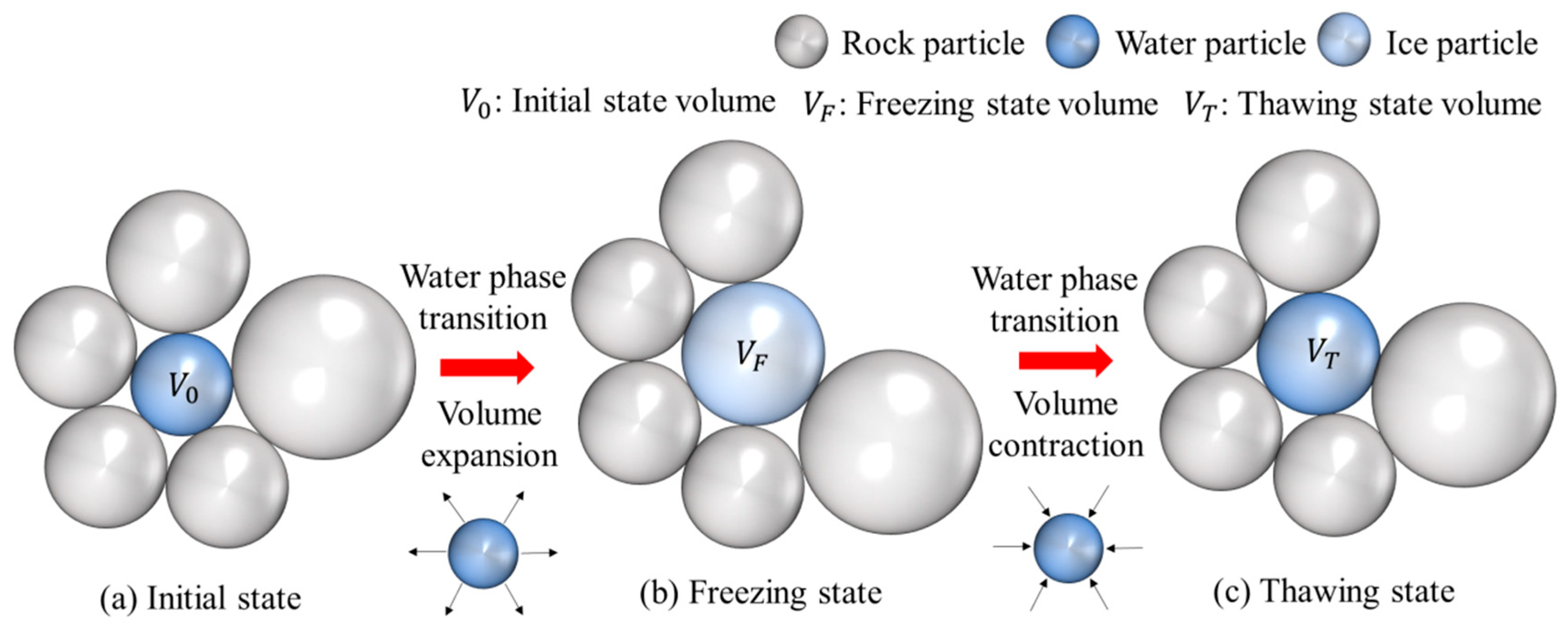
2.2. Freeze–Thaw Cycle Implementation Method
2.3. Contact Model Selection in PFC2D
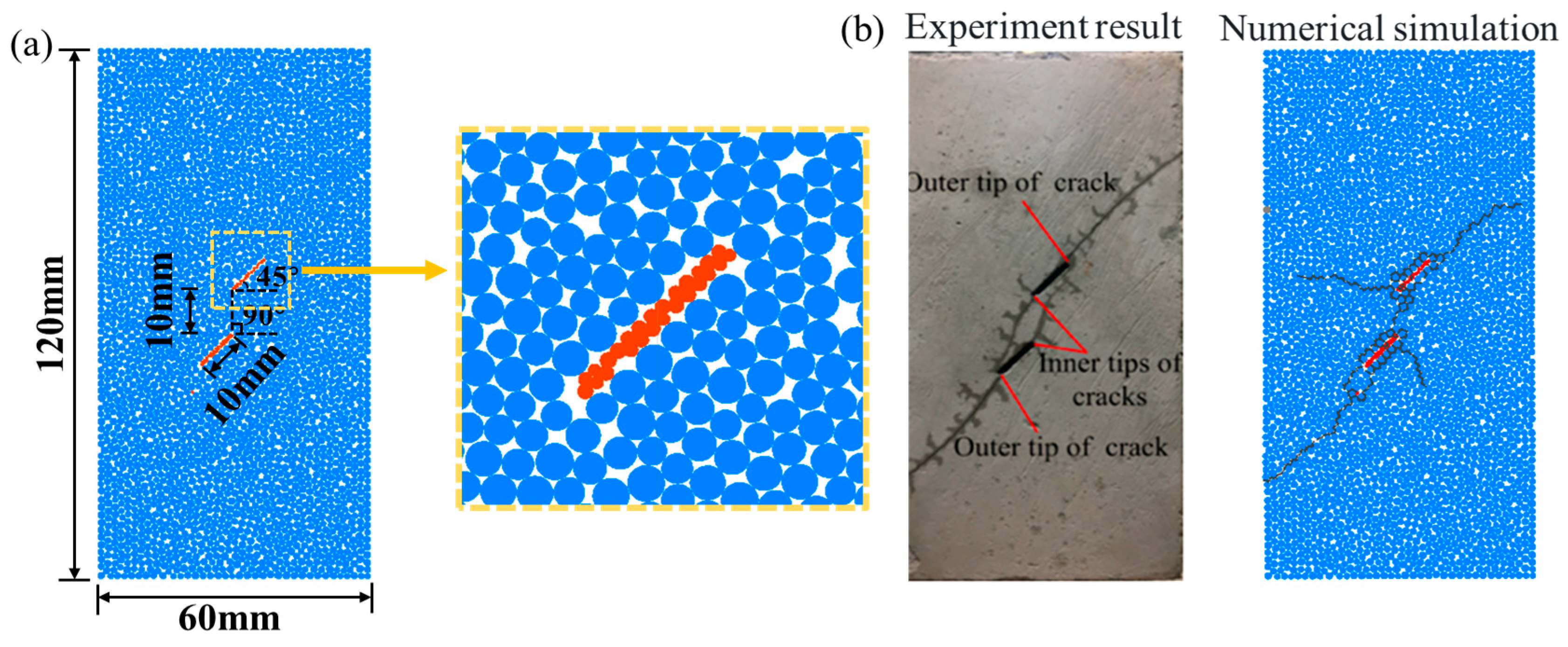
3. Freeze–Thaw Cycle Validation Case for Double-Fractured Rock Specimens
4. Numerical Simulation Results of Crack Propagation
5. Discussion
5.1. Effect of Rock Bridge Distance on Freeze–Thaw Damage of Rock Slopes
5.2. Effect of Rock Bridge Angle on Freeze–Thaw Damage of Rock Slopes
5.3. Effect of Fissure Angle on Freeze–Thaw Damage of Rock Slopes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, M.; Wang, Z.; Xu, Y.; Chang, Y.; Wang, L.; Zhu, Y. The failure behavior of prefabricated fractured sandstone with different rock bridge inclination angles under freeze-thaw cycles. Unconv. Resour. 2025, 6, 100152. [Google Scholar] [CrossRef]
- Zhang, S.; Song, Y.; Wang, X.; Ren, J. Multi-dimensional real-time data-driven identification for progressive fracturing characteristics of sandstone under freeze-thaw cycles and seepage-stress coupling. Eng. Appl. Artif. Intell. 2025, 152, 110803. [Google Scholar] [CrossRef]
- Xiao, J.; Shuai, J.; Deng, W.; Liu, L.; Wang, P.; Li, L. Low-Carbon and Green Materials in Construction: Latest Advances and Prospects. Buildings 2025, 15, 1508. [Google Scholar] [CrossRef]
- Zhu, T.; Zhu, H.; Li, A.; Zong, X.; Zeng, B.; He, X. Physical properties and anisotropy of sandstone during freeze-thaw cycle under unidirectional constraint. Cold Reg. Sci. Technol. 2024, 228, 104324. [Google Scholar] [CrossRef]
- Qiu, P.; Tang, L.; Zheng, J.; Wang, W.; Li, Y.; Li, G.; Jin, L.; Yu, Y.; Duan, X. Experimental investigations on the shear strength and creep properties of soil-rock mixture under freeze-thaw cycles. Cold Reg. Sci. Technol. 2024, 217, 104037. [Google Scholar] [CrossRef]
- Li, B.; Zhu, Z.; Zhang, F.; Chunyu, Z.; Li, T. Impact mechanical properties of frozen soil after experiencing freeze–thaw cycles: Experimental and numerical study. Cold Reg. Sci. Technol. 2023, 213, 103914. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, K.; Ren, J.; Liu, Q.; Wang, L.; Liu, Z. Estimating rock fracture characteristics based on determined mechanical properties and simulation parameters calibration methodology. Theor. Appl. Fract. Mech. 2025, 139, 104984. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, Y.; Chen, J. Macro-meso crack propagation characteristics and safety performance assessment of flawed rock mass. Theor. Appl. Fract. Mech. 2025, 137, 104867. [Google Scholar] [CrossRef]
- Shi, S.; Wang, G.; Zhu, F.; Feng, D.; Zhang, F. Investigation on fracture mechanism of rock containing pre-existing fissures subjected to freeze–thaw cycles under different stress conditions. Theor. Appl. Fract. Mech. 2025, 138, 104948. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, W.; Tan, X.; Chen, W.; Yang, D.; Su, Z.; Zhang, X.; Xu, F. Numerical simulation of fracture propagation in freezing rocks using the extended finite element method (XFEM). Int. J. Rock Mech. Min. Sci. 2021, 148, 104963. [Google Scholar] [CrossRef]
- Ali, M.; Zubair, A.; Farooq, Z.; Farooq, K.; Masoud, Z. Prediction of small-strain elastic stiffness of natural and artificial soft rocks subjected to freeze-thaw cycles. J. Rock Mech. Geotech. Eng. 2025, 17, 104963. [Google Scholar] [CrossRef]
- Yahaghi, J.; Liu, H.; Chan, A.; Fukuda, D. Experimental and numerical studies on failure behaviours of sandstones subject to freeze-thaw cycles. Transp. Geotech. 2021, 31, 100655. [Google Scholar] [CrossRef]
- Sun, K.; Jia, J.; Xiong, Z.; Wu, J.; Liu, Y.; Wei, Y. Investigation of hydro-thermal variations and mechanical properties in cold region tunnels under long-term freeze–thaw cycles. Tunn. Undergr. Space Technol. 2024, 143, 105469. [Google Scholar] [CrossRef]
- Tang, X.; Tao, S.; Li, P.; Rutqvist, J.; Hu, M.; Sun, L. The propagation and interaction of cracks under freeze-thaw cycling in rock-like material. Int. J. Rock Mech. Min. Sci. 2022, 154, 105112. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Mu, W.; Yang, T.; Du, Y.; Lu, J. Damage characteristics and mechanisms of shear strength at the interface between fiber-reinforced concrete and rock under freeze-thaw cycles. J. Build. Eng. 2024, 98, 111191. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, Q.; Jia, C.; Lei, M.; Zhao, C.; Pang, R.; Li, Z.; Zeng, T. Experimental and DEM simulations of the mechanical properties of rock under freeze–thaw cycles. Cold Reg. Sci. Technol. 2023, 211, 103866. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, E.; Wei, X.; Yin, X.; Xiao, W.; Yu, D.; He, C. Experimental study and numerical modeling of the thermo-hydro-mechanical process in unsaturated soil under freeze-thaw cycles. Cold Reg. Sci. Technol. 2024, 218, 104063. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, Z.; Duan, X.; Wu, J. Mesoscopic Mechanism of Deterioration of Silty Mudstone under Freeze-Thaw Cycles with Different Freezing Temperatures. J. Chang. Univ. Sci. Technol. (Nat. Sci. Ed.) 2025, 1–11. [Google Scholar]
- Zhang, Z. Study on the Mechanical Properties and Damage Mechanism of Basalt in Highway Cutting Slope under Wet-Dry and Freeze-Thaw Cycles. Highway 2025, 70, 41–49. [Google Scholar]
- Hou, Z.; Liu, X.; Wang, T.; Zhang, J.; Yuan, S.; Hu, J. Mechanical Properties and Damage Constitutive Model of Quartzite with Freeze-Thaw Damage. J. Yangtze River Sci. Res. Inst. 2025, 42, 177–185. [Google Scholar]
- Liang, B.; Yang, G.; Feng, W.; Pan, Z.; Sun, J.; Liu, H.; Chen, Q. Model Test Study on the Instability of Rock Slopes with Planar Slip Induced by Freeze-Thaw. J. Xi’an Univ. Sci. Technol. 2024, 44, 1118–1126. [Google Scholar]
- Zhang, H.; Hao, L.; Chen, S.; Cheng, R. Anisotropic Analysis of Mesoscopic Damage Evolution of Freeze-Thaw Sandstone. Min. Res. Dev. 2024, 44, 99–106. [Google Scholar]
- Yin, F.; Li, Y.; Li, K.; Zhang, S.; Wang, C.; Dai, F.; Wang, K. Mechanical behaviors and failure mechanism of flawed sandstone containing infillings under freeze-thaw cycles and uniaxial compression. Theor. Appl. Fract. Mech. 2023, 126, 103979. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Liang, L. Freeze-thaw failure characteristics and strength loss of non-penetrating fractured rock mass with different fracture densities. Theor. Appl. Fract. Mech. 2023, 124, 103792. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Y.; Guo, Y.; Zhang, Z.; Cai, Y. Strength and failure characteristics of rock-like material containing single crack under freeze-thaw and uniaxial compression. Cold Reg. Sci. Technol. 2019, 162, 1–10. [Google Scholar] [CrossRef]
- Li, J.; Kaunda, R.B.; Zhou, K. Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structure deterioration of sandstone. Cold Reg. Sci. Technol. 2018, 154, 133–141. [Google Scholar] [CrossRef]
- Gou, D.; Li, Y.; Hu, Y.; Zhou, Z.; Zhang, S.; Li, K.; Wang, K. Investigations on mechanical behaviors and failure mechanisms of rock-concrete composite specimens with different interface inclinations subjected to freeze-thaw cycles and uniaxial compression. Eng. Fract. Mech. 2025, 322, 111196. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Y.; Du, R.; Zhao, X.; Wu, J. Macroscopic and microscopic mechanical characteristics and crack propagation behavior of sandstone-like samples with single cracks under freeze–thaw cycles: Experimental and numerical simulation. Theor. Appl. Fract. Mech. 2024, 129, 104201. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Zhou, K.; Jiang, C.; Shen, Y.; Jia, H. Fracture mechanical properties of sandstone with pre-fabricated cracks under freeze–thaw cycles. Theor. Appl. Fract. Mech. 2024, 131, 104444. [Google Scholar] [CrossRef]
- Li, T.; Zhang, L.; Gong, W.; Tang, H.; Jiang, R. Initiation mechanism of landslides in cold regions: Role of freeze-thaw cycles. Int. J. Rock Mech. Min. Sci. 2024, 183, 105906. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Y.; Du, R.; Huang, Z.; Zhao, X. Experimental study and numerical simulation verification of the macro- and micromechanical properties of the sandstone–concrete interface under freeze–thaw cycles. Constr. Build. Mater. 2024, 432, 136584. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.; Yin, F.; Dai, F.; Wang, C.; Zhang, S.; Wang, K. Mechanical properties and failure mechanism of rock-like specimens with arc-shaped flaws under freeze–thaw cycles. Theor. Appl. Fract. Mech. 2024, 130, 104275. [Google Scholar] [CrossRef]
- Sun, C.; Pu, Y.; Ao, Y.; Tao, Q. Study on Mechanical Properties and Mesoscopic Fracture Evolution Characteristics of Frozen-Thawed Saturated Fractured Sandstone. Rock Soil Mech. 2025, 8, 1–14. [Google Scholar]
- Li, H.; Yao, Z.; Zeng, Z.; Li, L. Study on Deformation and Failure Characteristics of Sandstone with Unequal-Length Intersecting Fractures under Uniaxial Compression during Freeze-Thaw Cycles. J. China Three Gorges Univ. (Nat. Sci.) 2024, 46, 65–72. [Google Scholar]
- Sun, L.; Grasselli, G.; Liu, Q.; Aboayanah, K.R.; Huang, S.; Tang, X. Investigating the frost cracking mechanism and the related shallow alpine rockfall initiation process using three-dimensional FDEM. Eng. Geol. 2025, 348, 107960. [Google Scholar] [CrossRef]
- Shi, Z.; Li, J.; Wang, J.; Chen, J.; Lin, H.; Cao, P. Experimental and numerical study on fracture characteristics and constitutive model of sandstone under freeze-thaw-fatigue. Int. J. Fatigue 2023, 166, 107236. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, B.; Zhao, J.; Wang, Y.; Jia, C.; Zhang, Q. An improved model for discrete element method simulation of spatial gradient distributions of freeze-thaw-induced damage to sandstone. Comput. Geotech. 2024, 171, 106412. [Google Scholar] [CrossRef]
- Huang, S.; Xu, L.; Ye, Y.; Musonda, K. Evaluation of the frost resistance of sandstones from the aspect of frost deformation. Bull. Eng. Geol. Environ. 2025, 84, 25. [Google Scholar] [CrossRef]
- Yu, S.; Ren, X.; Zhang, J. Modeling the rock frost cracking processes using an improved ice-Stress-Damage coupling method. Theor. Appl. Fract. Mech. 2024, 131, 104421. [Google Scholar] [CrossRef]
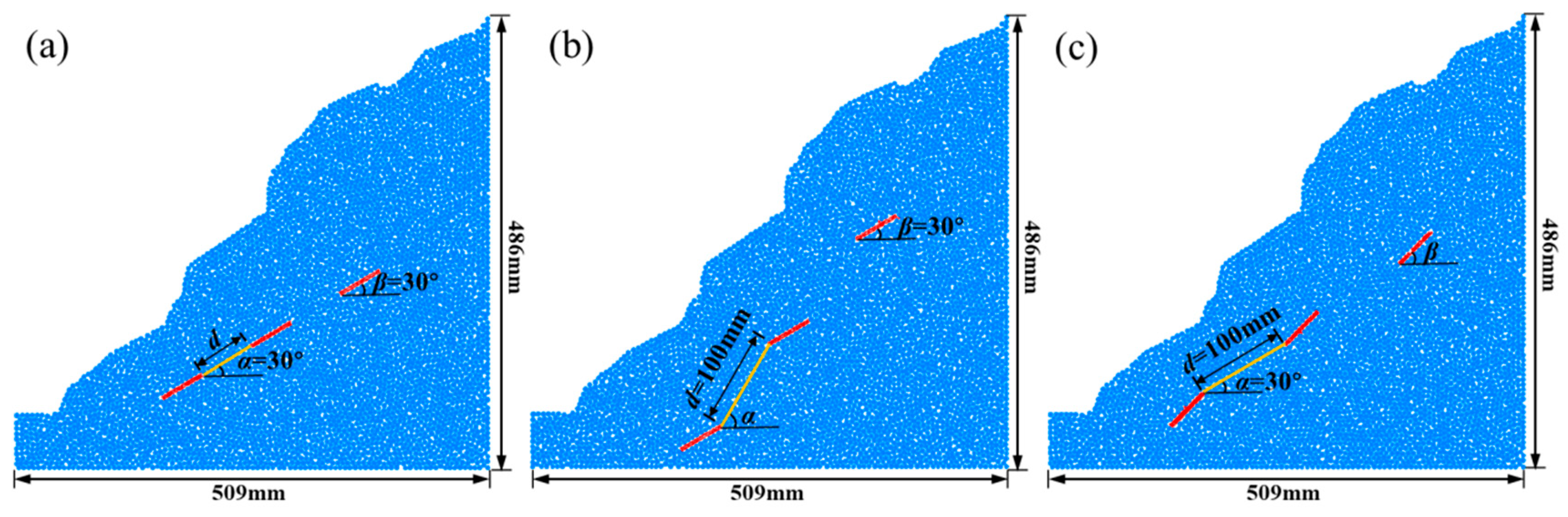



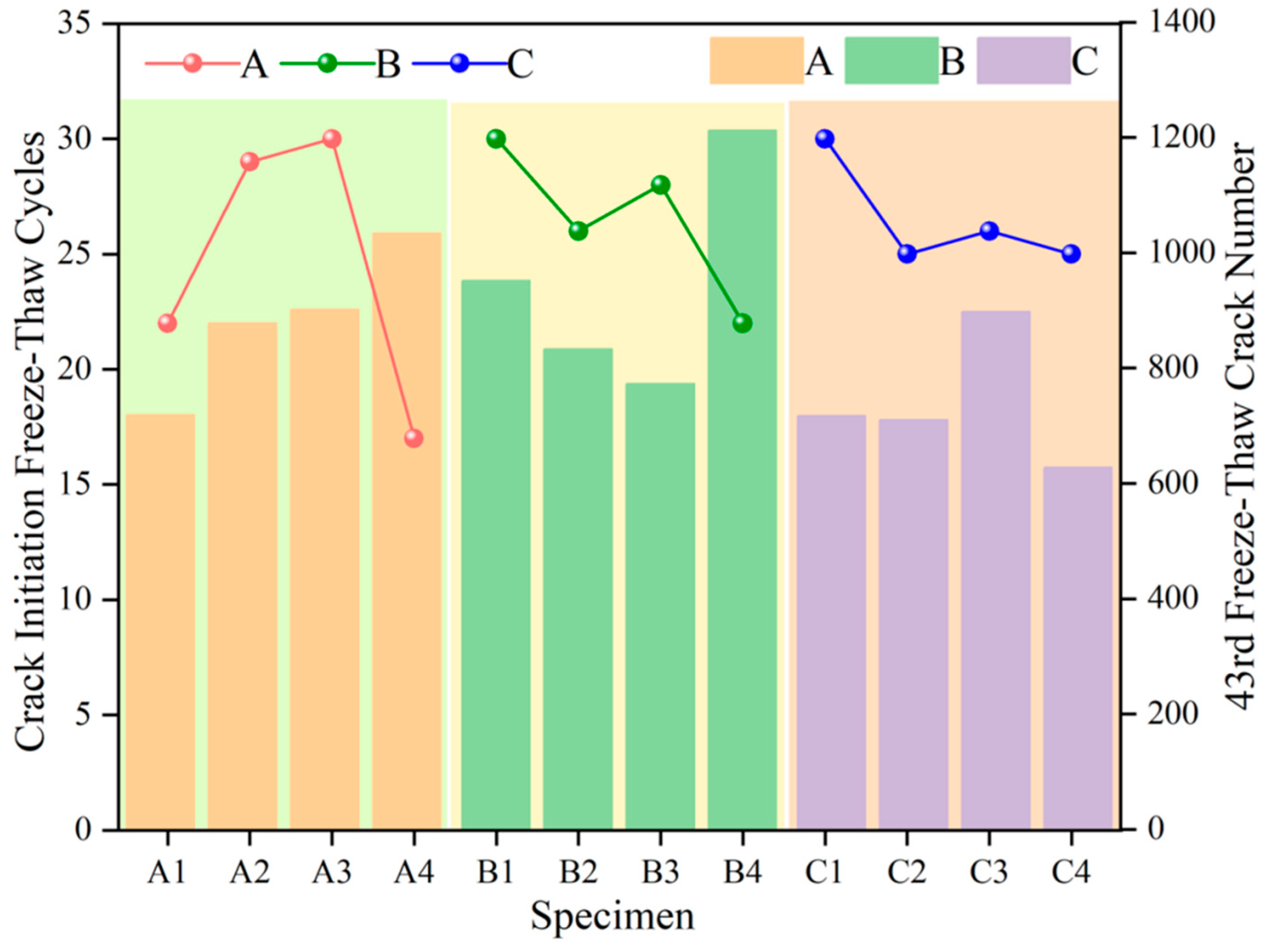

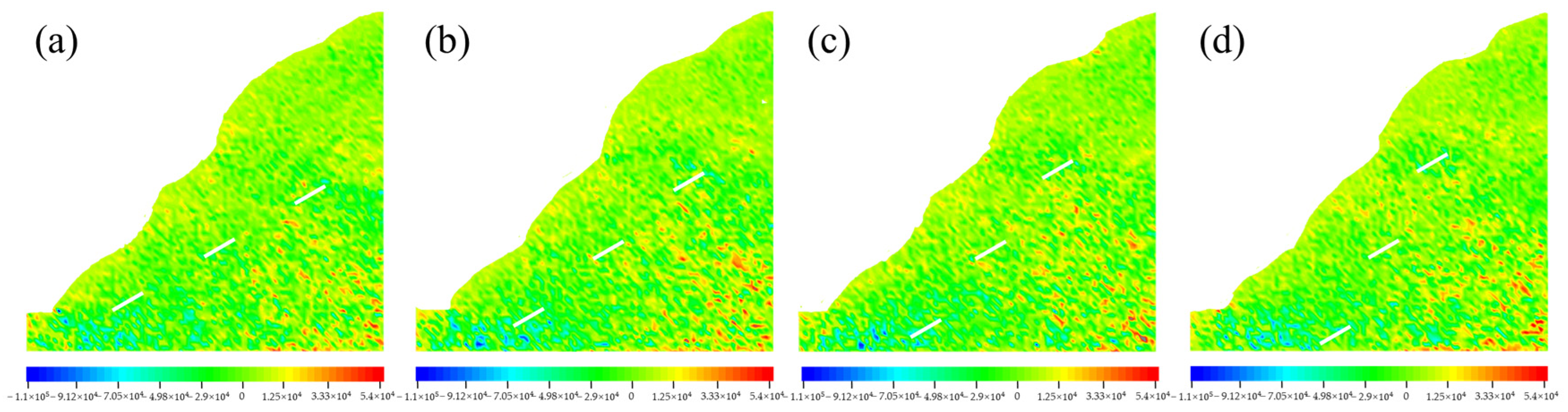
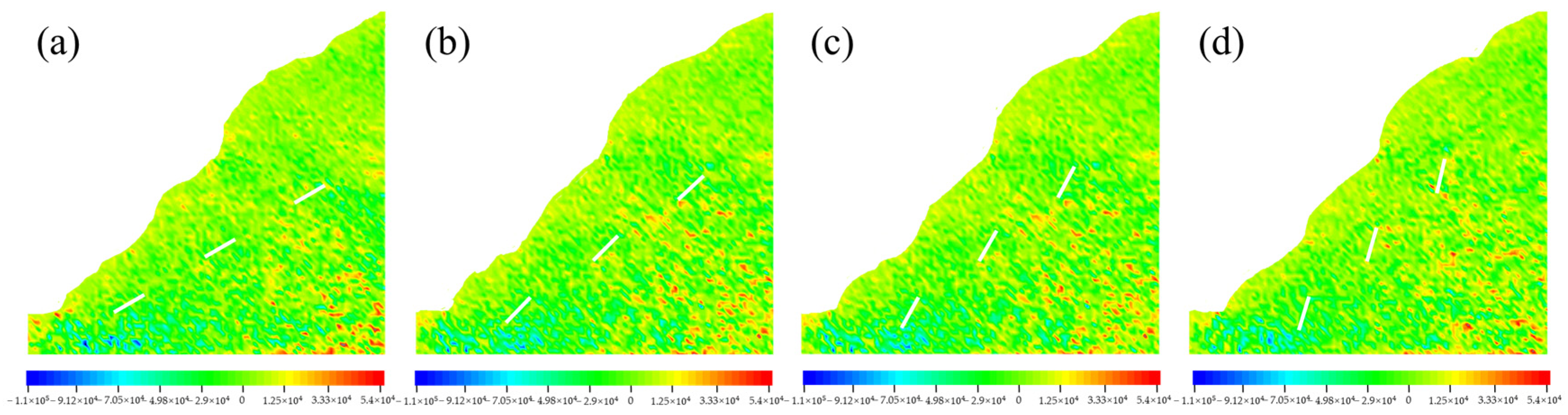
| Specimen Number | Specimen Scheme | Specimen Number | Specimen Scheme |
|---|---|---|---|
| A1 | d = 60 | B3 | α = 60° |
| A2 | d = 80 | B4 | α = 75° |
| A3 | d = 100 | C1 | β = 30° |
| A4 | d = 120 | C2 | β = 45° |
| B1 | α = 30° | C3 | β = 60° |
| B2 | α = 45° | C4 | β = 75° |
| Micro-Parameters | Value | Ball-Parameters | Value |
|---|---|---|---|
| Emod(Pa) | 2.8 × 109 | Yanshi_Rmax(m) | 0.9 × 10−3 |
| Yanshi_pb_emod(Pa) | 2.8 × 109 | Yanshi_Rmin(m) | 0.7 × 10−3 |
| Yanshi_pb_ten(Pa) | 3.03 × 105 | Yanshi_density | 2600 |
| Yanshi_pb_coh(Pa) | 5.06 × 104 | Shui_Rmax(m) | 0.4 × 10−3 |
| Yanshi_Pb_fa(°) | 30 | Shui_Rmin(m) | 0.3 × 10−3 |
| Shui_pb_emod(Pa) | 2.8 × 109 | Shui_density | 2600 |
| Shui_pb_ten(Pa) | 1.5 × 108 | Shui_zhanbi | 0.05 |
| Shui_pb_coh(Pa) | 1.5 × 108 | fric | 0.5 |
| Shui_Pb_fa(°) | 0 | damp | 0.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Putsikai, B.; Yu, S.; Yu, J.; Li, Y.; Gu, P. Numerical Simulation of Freezing-Induced Crack Propagation in Fractured Rock Masses Under Water–Ice Phase Change Using Discrete Element Method. Buildings 2025, 15, 2055. https://doi.org/10.3390/buildings15122055
Xu H, Putsikai B, Yu S, Yu J, Li Y, Gu P. Numerical Simulation of Freezing-Induced Crack Propagation in Fractured Rock Masses Under Water–Ice Phase Change Using Discrete Element Method. Buildings. 2025; 15(12):2055. https://doi.org/10.3390/buildings15122055
Chicago/Turabian StyleXu, Hesi, Brian Putsikai, Shuyang Yu, Jun Yu, Yifei Li, and Pingping Gu. 2025. "Numerical Simulation of Freezing-Induced Crack Propagation in Fractured Rock Masses Under Water–Ice Phase Change Using Discrete Element Method" Buildings 15, no. 12: 2055. https://doi.org/10.3390/buildings15122055
APA StyleXu, H., Putsikai, B., Yu, S., Yu, J., Li, Y., & Gu, P. (2025). Numerical Simulation of Freezing-Induced Crack Propagation in Fractured Rock Masses Under Water–Ice Phase Change Using Discrete Element Method. Buildings, 15(12), 2055. https://doi.org/10.3390/buildings15122055







