Abstract
Solar exposure and shading critically influence outdoor thermal comfort in residential areas, yet quantitative links between spatial morphology and microclimate remain insufficiently explored in cold-region cities. This study proposes a novel morphological indicator, the Insolation Shadow Ratio (ISR), to quantify sunlight–shade dynamics and investigates its correlation with outdoor thermal comfort (UTCI) in Xi’an, China. Combining field observations, microclimate simulations, and statistical analysis, we quantified ISR and UTCI across three representative outdoor spaces in a residential area. Photographic analysis and spatial parameterization were employed to calculate hourly ISR values. Significant correlations were observed between ISR and UTCI values. The measured data showed the strongest correlation at summer solstice at site C (Spearman’s r = 0.883, p < 0.01). GAM analysis of seasonal peak correlation data revealed that an optimal UTCI comfort range of 9 °C to 26 °C, corresponding to ISR thresholds of 0.0202–0.8384, achieved the highest autumn correlation at site C (r = 0.686, p < 0.01), while effectively balancing shade cooling effects and solar accessibility. The ISR framework provides a quantifiable tool for designers to optimize outdoor thermal environments and, when enhanced by parametric modeling tools, enables them to proactively optimize thermal performance during early-stage residential planning, offering a data-driven pathway for climate-resilient outdoor space design.
1. Introduction
The rapid densification of urban residential areas in cold-region cities like Xi’an has significantly altered solar exposure patterns, exacerbating seasonal thermal stress in outdoor spaces [1]. While sunlight enhances winter comfort, excessive solar radiation in summer intensifies urban heat island effects, reducing space usability. Effective management of sunlight–shadow dynamics is thus critical for climate-responsive design. Some studies highlighted significant correlations between solar exposure [2], shadow coverage [3], and thermal comfort in urban spaces [4,5], emphasizing the importance of balancing sunlight and shading management [6,7,8]. Compagnon demonstrated the significant impact of solar and shadow movement on outdoor thermal comfort through software simulations [9,10]. Acero et al. investigated seasonal variations in urban sunlight and shadows, revealing their profound impact on thermal comfort across different seasons [11]. Advanced modeling techniques, such as Structural Equation Modeling (SEM), have quantified the impacts of sunlight and shading on thermal comfort, offering valuable insights for urban planning [12]. Numerous studies have explored strategies to improve urban outdoor thermal conditions [13]. Modification of solar irradiation conditions through shading, with higher levels of shade in summer, improve thermal comfort [7,14,15]. Thermal comfort indices such as the Physiological Equivalent Temperature (PET) and the Universal Thermal Climate Index (UTCI) have been widely used to evaluate outdoor thermal environments [16]. These indices consider factors like solar exposure and shading to provide comprehensive assessments of thermal conditions [17,18,19].
Urban morphology governs the distribution of solar access and shade, both of which critically shape outdoor thermal comfort. Current studies on morphological indicators and thermal comfort have widely adopted the Sky View Factor (SVF) and Floor Area Ratio (FAR) as core metrics to quantify the relationship between urban morphology and thermal environments [20]. SVF, calculated as the proportion of visible sky at a given point, reflects the openness of urban canyons and has demonstrated significant impacts on outdoor thermal comfort. For instance, higher SVF values correlate with elevated UTCI in unshaded areas due to increased solar exposure [21,22]. FAR, defined as the ratio of total building volume to site area, controls urban density and indirectly influences shadow coverage. While increasing FAR enhances summer shadow coverage [23], it may exacerbate insufficient daylight penetration in winter, thereby compromising seasonal thermal balance [24,25]. Morphological indicators like the SVF and FAR optimize thermal comfort by controlling solar access and enhancing airflow [16]. Together, these interdependent factors—form, shade, and microclimate—underscore the need for a dynamic, geometry-driven indicator that links spatial configuration directly to thermal comfort performance.
Considering other morphological indicators and thermal comfort studies, Song et al. [15] found that building orientation and height play critical roles in optimizing solar exposure and shadow projection. Yi et al. [23] explored the relationship between urban density and sunlight/shadow patterns, noting that denser areas typically reduce sunlight exposure while increasing shading, thereby influencing outdoor comfort.
However, current urban planning practices often rely on generic metrics like the SVF and FAR, which inadequately capture time-varying solar–shadow interactions at human scales [18,21,26]. Prior studies have demonstrated strong links among solar exposure, shadow coverage, and thermal comfort—highlighting the role of factors such as vegetation density [2], building aspect ratio [15], and material albedo [27]—yet common morphological metrics like the SVF and FAR remain static and cannot capture diurnal and seasonal solar trajectories. This gap motivates the development of ISR, a time-sensitive indicator that dynamically integrates solar azimuth and altitude to quantify hourly sunlit fractions, providing a continuous, geometry-driven proxy for outdoor thermal comfort. Furthermore, while parametric tools like ENVI-met enable detailed microclimate simulations, their complexity limits integration into early-stage design workflows. Crucially, no study has proposed a time-sensitive morphological indicator that balances solar accessibility and shading requirements across seasons while remaining operable for architects and planners. To address these limitations, this study proposes the Insolation Shadow Ratio (ISR), defined as the hourly ratio of sunlit area to total site area. Unlike the SVF or FAR, ISR dynamically quantifies solar–shadow interplay by explicitly incorporating hourly variations in solar position, including azimuth and altitude, across different seasons. This dynamic consideration enables ISR to capture temporal patterns of solar exposure and shading that are overlooked by static indicators such as the SVF. Conceptually, while SVF is a static ratio representing the proportion of visible sky dome regardless of time, ISR is defined as the ratio of sunlit area to total site area at a specific hour, which allows for continuous assessment of solar access and shading dynamics throughout the diurnal and seasonal cycles, thereby enhancing its applicability in thermal comfort-oriented urban design. The dynamic trajectory of solar position across seasonal and diurnal cycles (with hourly variations) serves to quantify the spatiotemporal patterns of solar exposure and shadowing at multiple temporal scales (e.g., summer solstice, winter solstice, and equinoxes), thereby enabling precise characterization of the dynamic impacts of architectural morphology on outdoor thermal environments. Ground-level shadow patterns are shaped by building morphology, with radiative heat exchange mechanisms demonstrating a measurable correlation between these patterns and UTCI. This evidence establishes the critical role of shadow dynamics in urban thermal regulation.
The influence of building shadows on urban microclimates has been widely explored in recent years. Lindberg et al. [28] demonstrated that shading can significantly reduce mean radiant temperature (T_MRT) in residential areas, thereby improving outdoor thermal comfort. Prior research in diverse climatic regions has employed simulation-based models such as SOLWEIG and ENVI-met to assess the thermal effects of solar access and shadow distribution. For instance, studies in the Phoenix–Tempe metropolitan area used SOLWEIG to generate high-resolution shadow and T_MRT maps to support summer heat mitigation and urban cooling strategies. In China, the Building Shadow Generation Ratio (BSGR) was proposed as a dynamic alternative to the Sky View Factor (SVF), offering improved evaluation of microscale thermal conditions in residential environments [16].
However, most existing studies are constrained by two key limitations. First, they typically focus on single-season optimization—primarily summer—without addressing the seasonal contradictions in temperate regions where summer shading needs to be balanced against winter solar access. Second, morphological–climatic interactions are often modeled using static indicators or rule-based parameters, lacking a temporally explicit, quantitative framework for analyzing shadow dynamics across seasons.
The present study addresses these gaps through three novel contributions. First, by selecting Xi’an—a representative temperate monsoon city with four distinct seasons—the study investigates solar–shadow interactions across solstices and equinoxes, enabling a seasonally balanced analysis of thermal comfort. Second, the proposed Insolation Shadow Ratio (ISR) offers a time-sensitive morphological indicator that captures diurnal and seasonal variations in solar altitude and azimuth. Its correlation with thermal comfort (UTCI) is quantified using both field measurements and generalized additive modeling (GAM), providing improved temporal resolution over static metrics such as SVF and BSGR. Third, the derived thresholds offer a quantifiable link between spatial form and environmental performance, supporting climate-responsive urban design beyond the capabilities of existing models.
This study aims to establish ISR as a novel morphological indicator for solar–shadow management and quantify correlations between ISR and UTCI across diverse residential layouts. Therefore, the research contents of this study corresponding to the above-raised limitations are: (1) serving as a design-friendly metric for real-time shadow optimization using parametric tools (Grasshopper + Ladybug), (2) analyzing the relationship between ISR and UTCI to validate ISR as an indicator for managing outdoor thermal comfort, and (3) providing ISR thresholds for a climate-specific area. By resolving the above research questions, ISR advances practical design workflows.
2. Methodology
2.1. Research Framework
Focusing on three high-activity hotspots (western, north-central, and southeastern zones) on a mixed-use residential campus (prioritizing residential over academic areas), we defined “high-activity” areas as those exhibiting pedestrian flows above 30 persons/hour during peak periods, corroborated by semi-structured interviews with residents. At each hotspot, we then integrated field measurements, parametric modeling (Grasshopper + Ladybug), and statistical analysis to assess dynamic solar–shadow interactions and outdoor thermal comfort. Hourly ISR values were derived from spatial geometry parameterization and time-series solar radiation simulations, while UTCI was calculated using localized meteorological data. The research framework (Figure 1) consists of several steps: ① Field Observations and Interviews: Site surveys and resident interviews were conducted to identify frequently used outdoor spaces of residential area. Key environmental features, such as building enclosure form, shading patterns, and vegetation, were documented. ② Data Collection: Climatic variables including air temperature, relative humidity, wind speed, and mean radiant temperature were measured. Meanwhile, photographic analysis and simulation tools, such as Ladybug and Honeybee in Grasshopper, were used to calculate solar exposure and shading patterns. ③ Calculation of Insolation Shadow Ratio (ISR): Calculation of the ISR was divided into two parts: the measured ISR was calculated based on the projected area of insolation shadows of the actual site, and the simulated ISR was obtained based on the established settlement models. ④ Access to ISR and UTCI Simulated Data: Calculation of ISR and UTCI simulated data by Ladybug and Honeybee. ⑤ Correlation Analysis: Statistical correlation analysis was performed to evaluate the relationship between ISR and UTCI. A combination of measured and simulated data was used to ensure accuracy and reliability. ⑥ Find the ISR Threshold: The seasons with high correlation are filtered out, and the comfort intervals of ISR and UTCI are fitted by the GAM model to obtain the corresponding ISR thresholds.
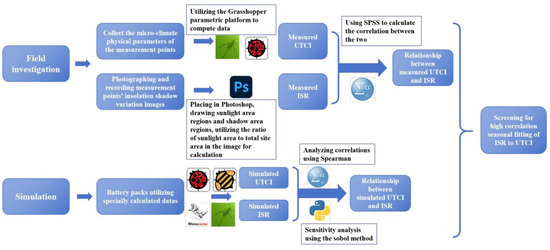
Figure 1.
Research framework diagram.
2.2. Sites
Preliminary investigations identified three key areas within the neighborhood—the western region, the north-central region, and the southeastern region—as hotspots of resident activity. These areas were selected as representative observation sites. The neighborhood comprises both residential and teaching areas, and the study focused exclusively on the residential areas (Figure 2a,b).
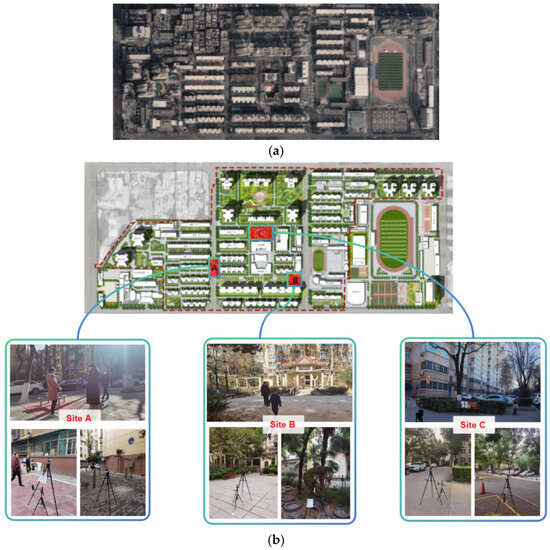
Figure 2.
(a) Photo of the survey area (source: Baidu web map). (b) General plan of the survey area (source: Authors’ record of residential area).
Site A is situated in the western part of the residential neighborhood and occupies a rectangular area approximately 17 m in width and 72 m in depth, covering a total area of about 1224 m2. The site is surrounded by buildings five to seven stories high on its eastern and western sides, with scattered vegetation distributed across the area.
Site B is situated in the south-central part of the neighborhood and covers a rectangular area approximately 26 m in width and 40 m in depth, with a total area of about 1040 m2. A 12-story residential building is located to the south of the site, with residential and office buildings. To the east, it is adjacent to a school campus. The site is surrounded by a mix mid- to high-rise buildings, public structures, and landscaped vegetation. Additionally, it is equipped with seating areas for pedestrians to rest.
Site C is situated within a street garden in the residential neighborhood. It is rectangular, measuring approximately 55 m in width and 32 m in depth, covering a total area of about 1760 square meters. To the west, it is bordered by six-story residential buildings, while the north side features an 18-story high-rise residential building. The east and south sides are adjacent to public buildings. The site is surrounded by trees and dense vegetation. Nearby, there is an affiliated kindergarten, contributing to an active pedestrian zone primarily frequented by elderly individuals engaging in exercise and parents accompanying their children.
2.3. Field Investigation
2.3.1. Objectives
The field investigation targeted two primary aspects. The first focused on outdoor climatic factors influencing residents’ activities, such as air temperature, relative humidity, wind speed, solar radiation, and variations in sunlight and shadow. The aim was to understand how changes in these factors affect thermal comfort in real-life outdoor residential areas. The second aspect examined the surrounding building forms and their basic configurations to analyze how they shape outdoor environments.
2.3.2. Content and Methods
Using an existing residential neighborhood in Xi’an as a case, the study explored changes in sunlight and shadows areas in outdoor spaces under varying building configurations and how these changes impact thermal comfort of the space. Field measurements were conducted on key seasonal days—the winter solstice, the spring equinox, and the summer solstice. The winter solstice and the summer solstice represent extremes in solar radiation: minimal sunlight during the winter solstice and maximum sunlight during the summer solstice. These data provide insights into the influence of sunlight variations on outdoor spaces and environments. Due to the COVID-19 pandemic restrictions in 2022, autumn equinox measurements were unavailable. Instead, the spring equinox was included to bridge the seasonal gap between the solstices, offering a balanced perspective on seasonal sunlight conditions. The nearly 12 h daylight period during the spring equinox, similar to the autumn equinox, provided complementary data for analyzing ISR’s influence on outdoor thermal comfort across seasons.
Observations were conducted between sunrise and sunset (8:00 a.m. to 6:00 p.m.), capturing sunlight–shadow patterns at two-hour intervals. Images documenting shadow distribution and residents’ activities were recorded, alongside climatic variables such as air temperature, Wet Bulb Globe Temperature (WBGT), relative humidity, and wind velocity, at one-minute intervals. Behavioral observations complemented environmental measurements to provide insights into how residents interacted with the environment.
2.4. Selection of Outdoor Thermal Comfort Indicators
Since the mid-20th century, outdoor thermal comfort evaluation methods have evolved significantly—from simplified heat balance models to more physiologically accurate indices. Early research identified key environmental variables such as air temperature, relative humidity, wind speed, and mean radiant temperature, alongside physiological factors like clothing insulation and metabolic rate, as fundamental determinants of human thermal comfort [29,30,31]. When exploring the relationship between outdoor thermal comfort and solar–shadow conditions, it is essential to select appropriate indicators for evaluation [32,33]. These foundational insights led to the development of steady-state indices, including the Physiological Equivalent Temperature (PET) [34,35], Standard Effective Temperature (SET) [36,37,38], and Universal Thermal Climate Index (UTCI) [39,40,41,42].
More recently, the Universal Thermal Climate Index (UTCI) was introduced, based on a dynamic multi-node thermoregulation model that accounts for human physiological responses under fluctuating outdoor conditions [39,40]. Compared to steady-state indices, UTCI provides improved accuracy in capturing the transient effects of solar radiation and wind, making it particularly suitable for outdoor environments [40,43,44].
In China, researchers such as Jin Hong [45], Nie Ting [46], and Wu Jinkui [47] have studied the applicability of the UTCI across different regions. Wu Zhifeng [48] demonstrated its relevance in analyzing thermal conditions under four greening retrofit scenarios in residential areas during typical summers. Wereski Sylwester [42] analyzed the spatial and temporal variations of the UTCI during 21st century winters in Poland, indicating that the UTCI can also be used to assess large-scale thermal comfort. Park Sookuk [49] argued that the UTCI is a widely accepted and easily determined thermal index, making it a valuable tool for analyzing outdoor thermal effects on humans in urban and landscape planning and design.
In summary, the UTCI is not only suitable for evaluating outdoor thermal comfort, but also capable of revealing human thermal sensations under varying environmental conditions [50]. Given its dynamic modeling framework and strong empirical support, UTCI is adopted in this study as the core indicator for assessing outdoor thermal comfort. It integrates key climatic variables—air temperature, humidity, wind speed, and mean radiant temperature—to provide a comprehensive representation of human thermal sensation. In this research, UTCI was computed through parametric simulations using Grasshopper, enabling spatially and temporally refined analysis of thermal comfort conditions in relation to the ISR [25].
2.4.1. Method for Calculating the UTCI Based on Field Measurements
To obtain the Universal Thermal Climate Index (UTCI) for the measured residential area, the “LB UTCI Comfort” component in Ladybug was used to calculate the UTCI. The simulation assumed a standing posture (1.2 met) docs.ladybug.tools (accessed on 21 June 2024), with seasonal clothing insulation set to 0.5 clo for summer and 1.0 clo for winter, based on typical ensemble values recommended by ASHRAE 55. The input data include the measured values for air temperature, mean radiant temperature (MRT), relative humidity, and wind velocity at various measurement points to calculate the UTCI for the residential area (as shown in Figure 3).
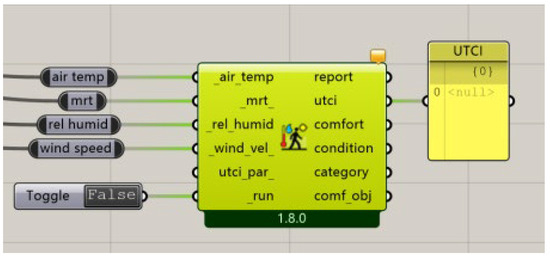
Figure 3.
Ladybug UTCI computing battery.
2.4.2. Method for Calculating the UTCI Based on Simulation
Based on the building types and enclosure characteristics of site A, site B, and site C in the measured residential area, 3D models of the three sites were created. To explore the relationship between UTCI data and the ISR under ideal model conditions, Ladybug components were used to acquire and analyze site data. The constructed building models of the sites are input as the analysis objects. The corresponding weather files for the simulation’s climate zone are selected, and the weather data is input into the “LB Solar Outdoor MRT” component to calculate the mean radiant temperature (MRT). The obtained MRT, along with other weather data, is then input into the component for calculating the UTCI. Finally, through simulation analysis of the building models, the average, minimum, and maximum UTCI values for the study period are obtained on an hourly basis. Establishing a 5 × 5 m grid based on the site area facilitates picking up variation of the UTCI in the area, so that the maximum, minimum, and average values of UTCI for the site can be obtained through battery calculations.
2.5. Concept and Calculation Method of the ISR Index
This study introduces a new morphological index, the Insolation Shadow Ratio (ISR), to quantify the variation between sunlight and shadow in outdoor residential areas. It is defined as the ratio of the sunlit area to the total area of the site. In this study, the shadow area is primarily composed of the shadows cast by buildings onto the ground area of the outdoor site under solar radiation. As shown in Figure 4, “As” represents the shadow area, “Ai” represents the sunlit area, and the green squares represent the building. The calculation formula is as follows:
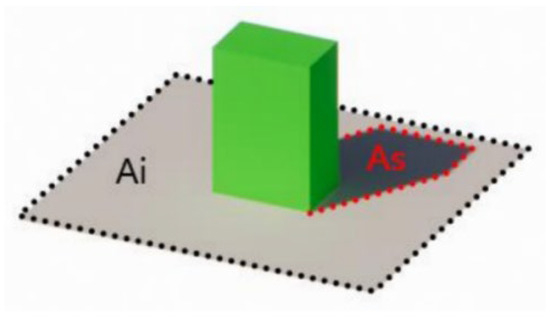
Figure 4.
Schematic diagram of the ISR (illustration by the author).
By explicitly aggregating overlapping shadows into As, ISR remains robust in complex urban settings where multiple structures cast intersecting shadow patterns. Figure 5 provides a schematic comparison of ISR calculations for single-building and multi-building configurations, clearly illustrating how group shadow masking is accounted for.
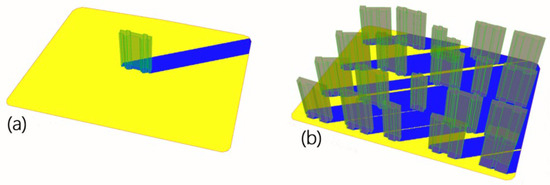
Figure 5.
(a) ISR calculation for a single building. (b) ISR calculation for a group of buildings (illustration by the author).
2.5.1. Method for Obtaining ISR Values Through Field Measurements
The method for obtaining ISR values through field measurements involved observing variation in sunlight and shadow on the site. This was done by using panoramic photographs and image recognition techniques to record changes in sunlight and shadow. The contrast images of sunlight and shadow were extracted according to time periods, allowing calculation of the ratio of the sunlit area to the total site area. The typical solar terms were selected as the representative days of the seasons. Therefore, field data were collected on 22 December 2022 (the winter solstice), 21 March 2023 (the spring equinox), and 22 June 2023 (the summer solstice).
2.5.2. Method for Obtaining ISR Values Through Simulation
Grasshopper is a tool that integrates visual programming and building environmental performance analysis. It is typically used in conjunction with Rhino 3D to create parametric designs and perform various computational tasks. By utilizing built-in components in Grasshopper, such as solar trajectory and sunlight angle functions, the ratio of ground area receiving sunlight to the total site area can be calculated.
The geometric shapes to be analyzed, such as buildings, sites, or other structures requiring sunlight and shadow ratio simulations, were first input into Grasshopper. Subsequently, Grasshopper was configured, and a new definition for the ISR was created. The parameters necessary for the simulation, including location data (latitude, longitude, date, and time), solar attributes (solar position and radiation data), and other relevant information (e.g., terrain, site, and buildings), were then defined. Using the solar analysis components of the Honeybee tool, calculations were performed to determine sunlight exposure, shadow ratios, and other solar-related data, such as solar radiation and shadow analysis. Finally, visualizations of the ISR were generated, presenting this information graphically through Grasshopper components.
2.6. Validation of the Relationship Between Outdoor Thermal Comfort and the ISR
This study aims to conduct a quantitative accuracy assessment between field-measured data and simulated outputs. Correlation and sensitivity analyses between ISR and UTCI need to be performed. However, given the inherent environmental dynamics (e.g., spatiotemporal heterogeneity of meteorological variables) and persistent anthropogenic disturbances (e.g., land-use alterations and infrastructure interventions) observed in field conditions, coupled with data availability constraints, the sensitivity analysis is confined to evaluating seasonal variations within the modeling framework. This targeted approach allows systematic exploration of model robustness under controlled temporal parameters while acknowledging limitations in empirical data acquisition. Therefore, the sensitivity analysis was performed only for the simulated data.
2.6.1. Spearman Correlation
The correlation analysis framework adopts a hypothesis-agnostic approach to statistically identify key covariates exhibiting coordinated variation patterns. By systematically quantifying bivariate associations (Spearman’s |r| > 0.5, p < 0.01), this methodology simultaneously addresses two operational objectives: (a) revealing latent variable co-dependencies through dimension-reduced projection, and (b) establishing empirically grounded variable screening criteria for subsequent mechanistic modeling [51,52,53].
The aim of this study is to explore whether there is a correlation between outdoor thermal comfort and ISR in residential areas of Xi’an. To validate the correlation and determine the strength of the relationship, normality tests and correlation analysis were conducted on both the field measurement data and simulation data using SPSS 26. For the correlation between the variables, Spearman’s method was selected.
2.6.2. Sobol Sensitivity Analysis
The sensitivity analysis protocol was strategically designed to elucidate causal mechanisms and facilitate model optimization by systematically addressing a pivotal question: how can parametric adjustments enhance system performance [54,55,56]? By leveraging the Sobol variance decomposition method—a globally convergent sensitivity analysis technique—this study quantitatively evaluates both individual parameter effects (first-order indices, Si) and higher-order interaction impacts (total-order indices, ST) through variance-based importance metrics. Implemented via the SALib Python (3.12) package, this approach overcomes the limitations of local sensitivity analysis (LSA) through quasi-Monte Carlo sampling (Saltelli sequence, N = 1000 iterations), with parameter importance rankings validated via convergence diagnostics (Anderson-Darling test, p > 0.1) [57]. From the point of view of the amount of data, as well as the questions explored, this study conducted a sensitivity analysis only for the simulated data.
3. Results
3.1. Field Measurement Results
3.1.1. Measured Results of the Insolation Shadow Ratio for Different Types of Spaces
The data obtained from field measurements were calculated, and the ISR data are detailed in Table 1. Panoramic photographs documenting changes in sunshine and shadow at the site were collected during the field survey. Examples of the field recordings for the insolation shadow variation at site A are shown in Appendix A Table A1, Table A2 and Table A3.

Table 1.
Changes in the insolation shadow ratio during different seasons at site A.
3.1.2. Measured UTCI Results for Different Types of Spaces
- (1)
- Comparison of measured UTCI data
During the winter solstice, the average UTCI for site A was 9.95 °C, significantly higher than site B’s 7.30 °C and site C’s 6.71 °C. The higher UTCI value for site A indicates that, although there was more sunlight in winter, the thermal comfort level remained relatively low, likely due to lower temperatures. Site C had the lowest UTCI, reflecting the limited sunlight conditions and thermal environment in winter.
During the summer solstice, site C had the highest average UTCI, at 39.71 °C, indicating the worst thermal comfort, possibly due to stronger solar radiation or insufficient shading. Site A followed, with an average UTCI of 38.89 °C, while site B had the lowest UTCI value of 37.42 °C, suggesting that site B may have better shading or architectural forms that contribute to microclimate regulation.
During the spring equinox, the UTCI values for site A (20.82 °C) and site C (20.72 °C) were similar, indicating comparable thermal comfort in spring. Site B’s UTCI value was slightly lower, at 19.47 °C, possibly due to site layout or shading coverage.
- (2)
- Analysis of UTCI Differences Between Sunlit and Shaded Areas
The measured data were visualized through graphical representation, as shown in the figures below. These figures illustrate the variations in sunlit and shaded areas for different sites across typical solar terms, including the summer solstice, the winter solstice, and the spring equinox. Specifically, they depicted the sunlit and shaded distributions for site A during the summer solstice (SSA-Sunlit, SSA-Shaded), the winter solstice (WSA-Sunlit, WSA-Shaded), and the spring equinox (SEA-Sunlit, SEA-Shaded); for site B under the same solar terms (SSB-Sunlit, SSB-Shaded, WSB-Sunlit, WSB-Shaded, SEB-Sunlit, SEB-Shaded); and for site C under identical conditions (SSC-Sunlit, SSC-Shaded, WSC-Sunlit, WSC-Shaded, SEC-Sunlit, SEC-Shaded). These visualizations clearly depicted seasonal variations in solar exposure across different sites and served as foundational data for further analysis of the correlation between ISR and outdoor thermal comfort.
During the winter solstice, the UTCI for the sunlit area of site A was significantly higher than that for the shaded area, with the positive effect of sunlight on thermal comfort being particularly evident. During the summer solstice, the UTCI for the sunlit area was also significantly higher than for the shaded area, indicating that sunlight exposure has a significant impact on thermal comfort. In contrast, the UTCI difference between sunlit and shaded areas during the spring equinox was smaller, likely due to weaker solar radiation and moderate temperatures in spring (Figure 6a).
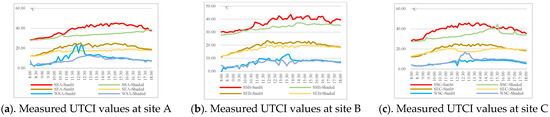
Figure 6.
Measured UTCI changes.
For site B during the winter solstice, the UTCI for the sunlit area was significantly higher than for the shaded area, but the overall values were lower than those for site A, indicating more limited sunlight conditions in winter. During the summer solstice, the UTCI for the sunlit area was higher than for the shaded area, though the difference was smaller than for site A, suggesting that site layout has a relatively smaller impact on thermal comfort. During the spring equinox, the UTCI for the sunlit area was still slightly higher than for the shaded area, but the difference was not significant (Figure 6b).
For site C during the winter solstice, the UTCI for the sunlit area was slightly lower than for the shaded area, which may be due to the shading and insulation effects of nearby trees. During the summer solstice, the UTCI for the sunlit area was the highest, much higher than for the shaded area, and was overall the highest among the three sites. The UTCI difference between the sunlit and shaded areas was smallest during the spring equinox, reflecting a more balanced distribution of sunlight and shadow (Figure 6c). However, the UTCI for the sunlit area during the winter solstice was slightly lower than for the shaded area, which could be related to the tree canopy in site C and the dense vegetation surrounding the site. Previous studies have shown that trees not only have a cooling effect [24], but also contribute to insulation during winter through various mechanisms. Thus, multiple uncertain factors may interfere with the site conditions during field surveys.
- (3)
- Results and Analysis
First, the field measurement results confirmed the regulatory role of shadow on thermal comfort. The differences in UTCI values for shaded areas across different sites highlight the critical importance of site layout and shading design in optimizing thermal comfort.
Additionally, a clear correlation between UTCI differences and seasonal changes was observed. The gap in UTCI values between sunlit and shaded areas varied significantly with the seasons, being most pronounced during the summer and winter solstices and relatively balanced during the spring equinox.
During the summer solstice, the UTCI in sunlit areas was substantially higher than in shaded areas across all sites, demonstrating the direct impact of solar intensity on thermal comfort. Notably, site C recorded the highest UTCI values, likely due to inadequate shadow coverage provided by surrounding buildings. Similarly, during the winter solstice, the UTCI in sunlit areas was significantly higher than in shaded areas, particularly at site A and site B, highlighting the critical role of sunlight in improving thermal comfort during colder seasons.
3.2. Correlation Analysis Between Measured ISR and UTCI
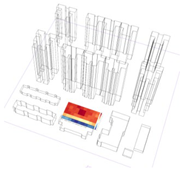
The sunlight and shadow conditions recorded in the surveyed images were converted into hourly ISR data. This conversion facilitated subsequent discussions regarding the relationship between outdoor thermal comfort and ISR (Figure 7). Additionally, over 600 valid datasets were collected from both sunlit and shaded areas at each of the three measurement sites. Spearman’s method was used for the correlation analysis.
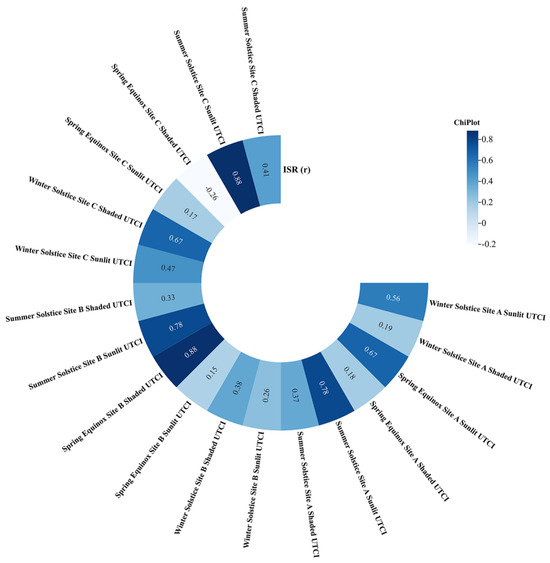
Figure 7.
Correlation between ISR and seasonal comfort across three sites (source: calculated using SPSS).
A correlation analysis between the ISR and the UTCI was conducted for site A based on the measured data. The results showed that the UTCI in the sunlit areas exhibited a generally high degree of positive correlation with the ISR during the winter solstice, the spring equinox, and the summer solstice (Spearman’s |r| > 0.5, p < 0.01). In contrast, the UTCI in the shaded areas showed a generally lower degree of positive correlation with the ISR. The analysis results for both sunlit and shaded areas indicated statistical significance.
For site B, the correlation analysis revealed a low degree of positive correlation between the UTCI and the ISR in the sunlit areas during the winter solstice and the spring equinox, while a higher degree of positive correlation was observed in the sunlit area during the summer solstice. In the shaded areas, the UTCI showed a high degree of positive correlation with ISR during the spring equinox.
For site C, the analysis indicated a moderate degree of positive correlation between the UTCI and the ISR in the sunlit areas during the winter solstice, a high degree of positive correlation during the summer solstice, and a low degree of positive correlation during the spring equinox. In the shaded areas, the UTCI exhibited a high degree of positive correlation with the ISR during the winter solstice, a moderate degree of positive correlation during the summer solstice, and a low degree of negative correlation during the spring equinox. Notably, site C was the only site where a negative correlation was observed.
3.3. Simulation Results
In traditional Chinese meteorology, the start of each season is marked by specific solar terms: Lichun (Beginning of Spring, 4 or 5 February), Lixia (Beginning of Summer, 5 or 6 May), Liqiu (Beginning of Autumn, 7 or 8 August), and Lidong (Beginning of Winter, 7 or 8 November). Following this seasonal division, the simulation periods in this study were defined as follows: spring (5 February to 5 May), summer (6 May to 7 August), autumn (8 August to 7 November), and winter (8 November to 4 February).This study primarily investigates the influence of solar shadow variations on outdoor thermal comfort. Therefore, the research period was set between 8:00 and 18:00, corresponding to daytime hours with direct solar exposure. The detailed simulation results are summarized in Table 2.

Table 2.
Average simulated ISR values for the three sites across seasonal reference days.
3.3.1. Simulated ISR
Simulation of the ISR was conducted using 3D models of sites A, B, and C, representing different architectural typologies and spatial enclosures. The models were analyzed in Grasshopper with the Ladybug plugin to compute the hourly ISR values for each site during the defined seasonal periods.
Local geographic and climatic data, including latitude, longitude, solar angles, and weather files specific to Xi’an, were incorporated into the simulation. For each season, the insolation–shadow variation was calculated under clear sky conditions from 8:00 to 18:00. The simulated ISR values provided insights into the spatial and temporal distribution of sunlight and shadow across the study sites, which were subsequently analyzed for their effects on outdoor thermal comfort.
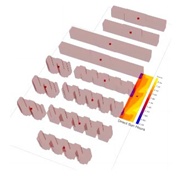
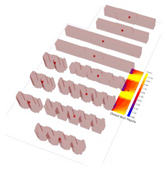
Through simulated calculations of the ISR for sites A, B, and C during the four typical solar terms, distinct seasonal trends and site-specific differences were observed. The specific changes in ISR trends are illustrated in Figure 8. At site A, ISR remained consistently high from 8:00 to 12:00 during all four seasons, showing minimal variation. However, a significant decrease was observed after 12:00, with a pronounced decline in magnitude. At site B, the ISR exhibited a rapid decrease from 8:00 to 13:00 during the winter solstice, spring equinox, and autumnal equinox, followed by a relatively stable trend after 13:00, with minimal differences between time intervals. Conversely, during the summer solstice, the ISR at site B demonstrated a unique pattern, characterized by an initial decrease, a subsequent increase, and another decline, differing markedly from other seasonal trends. At site C, the ISR displayed a parabolic pattern, reaching its lowest values at 8:00 in the morning and 18:00 in the evening, exhibiting a symmetrical distribution.
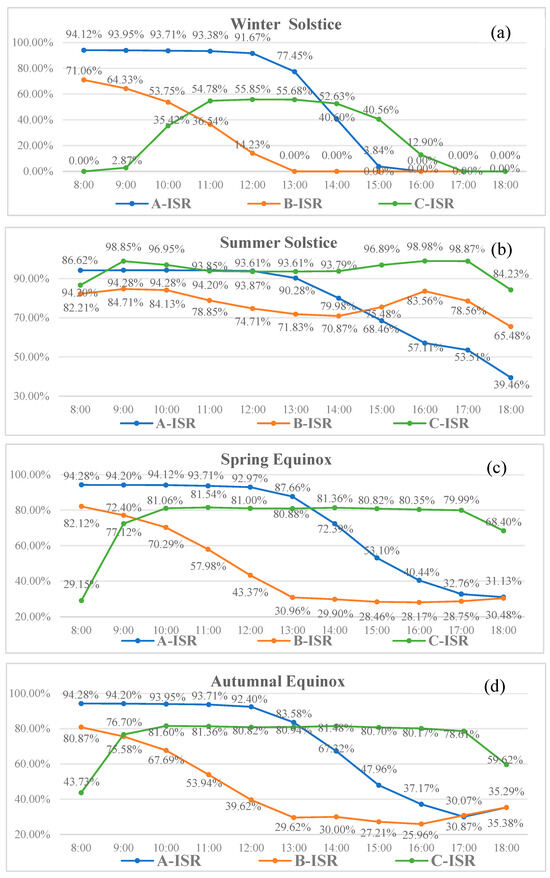
Figure 8.
Simulated ISR dynamics for different sites. (a) Winter solstice; (b) Summer solstice; (c) Autumnal equinox; (d) Spring equinox.
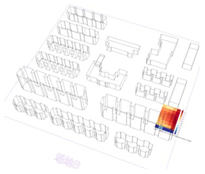
3.3.2. Simulated UTCI
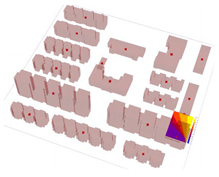
In the simulation process for the three sites, the shading effects of surrounding buildings and the variations in climatic conditions at different time points were considered. Illustrations of the simulation models for the three sites are presented in Table 3.

Table 3.
Average simulated UTCI for the three sites during the simulated periods.
- (1)
- Comparison of simulated UTCI data
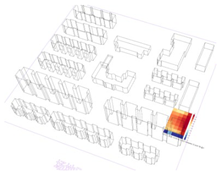
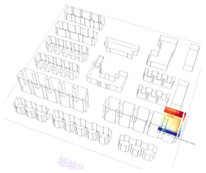
For the winter solstice, the simulated UTCI data for the three sites showed a trend of increasing followed by a decrease, peaking at 14:00 before declining. Site A exhibited the largest fluctuations between the minimum and maximum UTCI values. At 14:00, the minimum UTCI for site A rose to 3.1 °C, while the maximum reached 7.14 °C, demonstrating a significant increase in temperature difference. Site B’s UTCI displayed a minimum of 3.1 °C and a maximum of 6.66 °C, slightly lower than site A’s corresponding values. Site C’s UTCI ranged from a minimum of 4.39 °C to a maximum of 5.65 °C, indicating less fluctuation in the thermal environment during the winter solstice.
For the summer solstice, the UTCI results for the three sites exhibited a steady increase, peaking at 14:00, after which they began to decline. At 14:00, the minimum UTCI for site A rose to 28.32 °C, with a maximum value of 34.19 °C, showing the largest difference between minimum and maximum values among the three sites. Site B followed a similar trend to site A, but during the peak high-temperature period (around 14:00), the maximum value was lower, reaching 33.88 °C. Site C displayed a similar trend in UTCI to sites A and B, but with overall lower temperature levels. At 14:00, site C’s maximum UTCI was 33.2 °C, significantly lower than site A (34.19 °C) and site B (33.88 °C), indicating that its thermal environment performed better overall.
For both the spring equinox and the autumn equinox, the UTCI trend at site A was similar, with temperatures reaching their highest values around midday and a small day–night temperature difference, reflecting relatively stable thermal comfort during the transitional periods of the seasons. At site B, the UTCI also reached a high value around midday, with a small day–night temperature difference, but there was some divergence from site A, likely due to differences in shading layout and microclimate effects. At site C, the UTCI exhibited a characteristic midday high and a small day–night temperature difference. The values at different time points showed certain differences compared to sites A and B, reflecting the unique local conditions that affected the site.
- (2)
- Results and Analysis
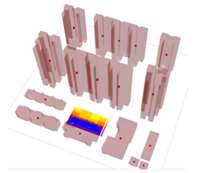
Based on the simulated UTCI data and visual analysis of the three sites during the four representative solar terms (Figure 9), it was observed that site A exhibited the largest threshold range between UTCI-Max and UTCI-Min. This indicates that site A experienced the most significant thermal environment fluctuations, primarily influenced by the shading effect of buildings on the western side of the site, which created considerable differences in solar and shaded areas and subsequently impacted thermal comfort.
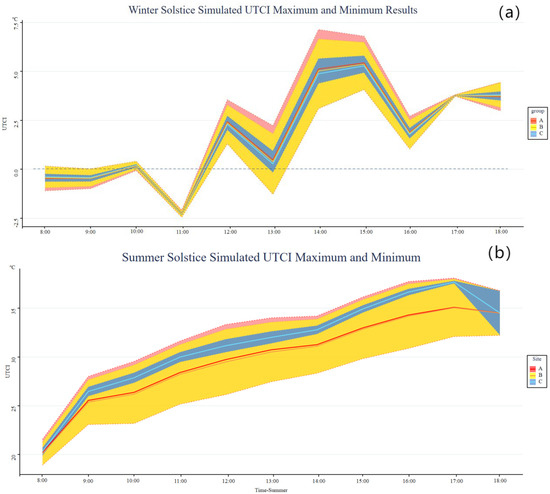
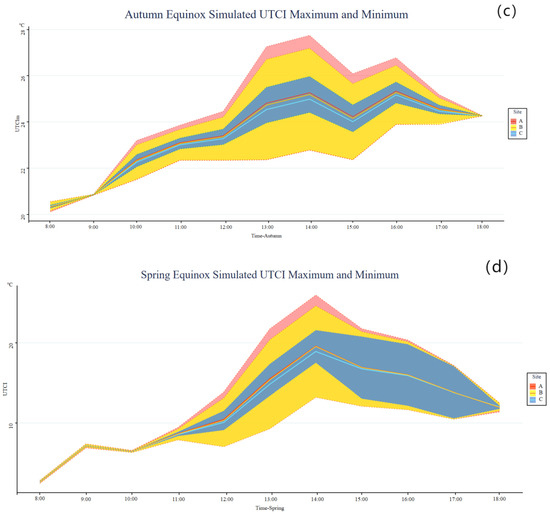
Figure 9.
Simulated maximum and minimum UTCI values for different sites. (a) Winter solstice; (b) Summer solstice; (c) Autumnal equinox; (d) Spring equinox.
Site B showed a moderate range of UTCI differences, with shading effects from buildings on the northern and southern sides exerting a balanced impact on the thermal environment. Consequently, temperature variations within site B are less intense compared to site A but still exhibited a degree of unevenness.
Site C demonstrated the smallest range of UTCI differences. The layout of buildings on its southern and northern sides ensured a relatively stable distribution of ISR across the site, resulting in more consistent thermal environment conditions.
3.4. Workflow Efficiency Comparison
Comparative analysis shows that, for a typical 100 m × 100 m block, the ISR workflow (Grasshopper + Ladybug) completes geometry import and sun–shade setup in 2 min and computes seasonal hourly ISR in under 10 min on a standard desktop (Intel i7, 16 GB RAM). By contrast, an equivalent ENVI-met simulation requires approximately 1 h for setup and 3–4 h for runtime. Implementing ISR demands only intermediate parametric-design skills, whereas full microclimate modeling requires advanced CFD expertise. Overall, ISR reduces total project time from 6 h to under 30 min (over 90% time savings), decreases computational load by an order of magnitude, and lowers the technical barrier to thermal–environment optimization for practitioners.
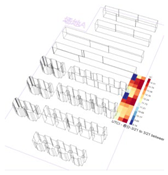
3.5. Correlation Analysis Between Simulated ISR and UTCI
Using a simulation platform and locally available meteorological data, simulations were conducted with an hourly time step for ISR and UTCI during all four seasons. The simulation periods spanned from 8:00 to 18:00 daily, generating 900 to over 1000 datasets per site per season. After conducting normality tests on the data, it was observed that the data did not follow a normal distribution. Consequently, the Spearman algorithm was applied to analyze the correlation between the ISR and UTCI simulation results (Figure 10).
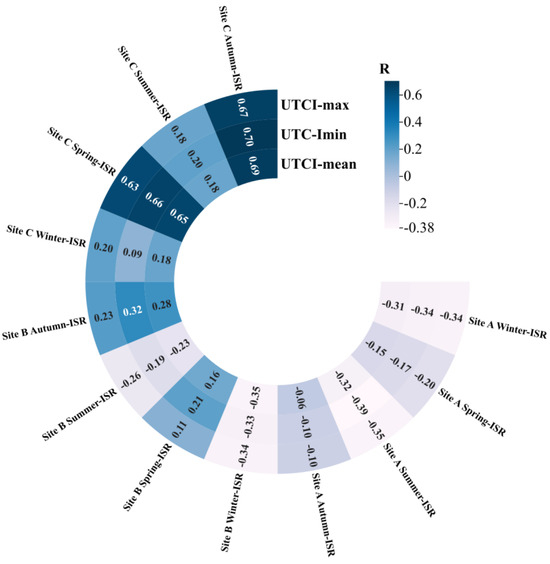
Figure 10.
Correlation between simulated ISR and UTCI values across the three sites.
The relationship between the ISR and UTCI was examined during the simulation stage. An analysis of the simulation data for the three sites revealed that ISR plays a significant role in influencing UTCI, exerting both positive and negative effects under different conditions.
First, for site A, ISR showed varying degrees of negative correlation with the maximum, minimum, and mean UTCI values in all four seasons, with p < 0.01 indicating significance between ISR and UTCI. Second, for site B, ISR was correlated with the UTCI metrics for all four seasons. Finally, for site C, ISR was strongly positively correlated with UTCI metrics for the spring and fall seasons.
3.6. Sensitivity Analysis Between Simulated ISR and UTCI Values
The Sobol variance decomposition framework revealed ISR as the principal deterministic factor governing UTCI variations across all observational stations and seasonal cycles. Quantitative sensitivity metrics demonstrated exceptional dominance (Table 4). The sensitivity indices (Si and ST) of the ISR to the UTCI were close to or slightly above 1 for all sites and seasons, indicating that ISR is the most critical influence on UTCI, and its independent contribution covers almost the entire output variance. The values of Si and ST for all seasons and sites are almost equal (difference < 0.001), indicating that the effect of the ISR on the UTCI is dominated by independent effects, and the interaction effect is negligible; thus, it can be stated that the ISR has a dominant effect on the UTCI.

Table 4.
Sensitivity analysis of different seasons between simulated ISR and UTCI values.
4. Discussion
4.1. Effect of ISR Variation on the UTCI
In different seasons, the interaction between the ISR and solar radiation intensity produces varying impacts on thermal comfort. Specifically, an increase in the ISR leads to greater solar radiation exposure in outdoor spaces, resulting in higher temperatures. While this effect improves thermal comfort in winter by warming the environment, it can cause overheating during summer, negatively affecting outdoor comfort.
Comparing the simulated results of the ISR and the UTCI across the three sites during four seasons, site A exhibited the largest ISR fluctuations from morning to evening. Correspondingly, site A also demonstrated the greatest difference between UTCI maximum and minimum values among the three sites. Site B followed, with moderate ISR variation and UTCI fluctuations. By contrast, site C showed a parabolic trend in ISR variation throughout the day, with smaller differences between morning and evening ISR values. Consequently, the difference in UTCI maximum and minimum values for site C was the smallest among the three sites.
Larger ISR variation indicates significant changes in solar exposure conditions, which results in pronounced surface temperature fluctuations and, subsequently, substantial UTCI changes. Conversely, smaller ISR variations signify more stable shadowing conditions, leading to relatively steady surface temperatures and smaller UTCI fluctuations. The strong influence of the ISR on the UTCI underscores the role of solar radiation in altering surface radiation intensity, which in turn affects human-perceived thermal loads.
The three study sites presented distinct ISR–UTCI patterns due to differences in morphological layout and environmental context. Site A, characterized by a relatively open layout, experienced the highest diurnal variation in ISR and the widest UTCI range, indicating strong sensitivity to temporal solar exposure. In contrast, site C, with higher vegetation density and enclosed spatial form, exhibited limited ISR fluctuation and the most stable UTCI values. Site B represented an intermediate case, where the correlation was seasonally variable and spatially balanced.
These variations suggest that the effectiveness of shading and solar exposure on outdoor thermal comfort is not uniform but influenced by microclimatic modifiers such as vegetation, enclosure ratio, and surface material. The results underline the need for localized design strategies that account for morphological context when applying ISR-based thresholds.
4.2. Reasons for Differences Between Measured Data and Simulated Data
Comparison between measured and simulated data revealed discrepancies in correlation trends across the three sites. For site A, the measured correlation was the opposite of the simulated results. For site B, the measured data for the spring and autumn equinoxes aligned with the simulation, while the measured results for the winter and summer solstices exhibited opposite correlations. For site C, the measured and simulated correlations showed consistent trends overall. The higher correlation observed in the field measurements (r = 0.883) versus the parametric simulations (r = 0.686) can be attributed to several factors. First, the datasets differ in temporal coverage and resolution: the measured ISR and UTCI values were recorded over a single day at one-minute intervals, capturing fine-scale fluctuations, whereas simulated values span an entire season at one-hour intervals, yielding smoother, aggregated profiles. Second, the empirical data incorporate real-world perturbations—shading from mature vegetation, heterogeneous ground-surface emissivity, and transient wind gusts—that enhance momentary ISR–UTCI coupling but are not fully represented in the idealized simulation environment. Third, simulation boundary conditions (e.g., uniform sky models, steady wind fields) and assumptions about surface albedo and canopy structure necessarily simplify complex urban microclimates, which can attenuate modeled correlation strength. Nonetheless, both Spearman coefficients exceed 0.6, indicating robust, statistically significant relationships between the ISR and the UTCI in both contexts.
These inconsistencies between the measured and simulated data may be attributed to several factors:
- (1)
- Nonlinear relationships: The relationship between ISR and thermal comfort is not strictly linear. For instance, excessive solar exposure can increase discomfort in high-temperature seasons, while enhancing comfort in colder seasons. This suggests that the relationship between thermal comfort and ISR is complex, influenced by multiple factors such as season, wind speed, and humidity.
- (2)
- Localized microclimate effects: Factors such as the built environment, vegetation coverage, and surface materials can alter local microclimatic conditions, affecting thermal comfort. Even with the same ISR, variations in material thermal properties (e.g., absorption and reflectivity) can lead to differing surface temperatures, causing deviations in measured results.
- (3)
- Real-world complexity vs. idealized models: Real-world sites often involve numerous interacting factors not accounted for in idealized models. While the simulation primarily considers building-induced shadowing effects, real environments introduce additional uncertainties and overlapping variables, leading to deviations from predicted outcomes.
4.3. Data-Driven ISR Threshold Determination
A multi-dimensional analytical framework (field measurements, simulation validation, and sensitivity tests) systematically identified seasons with significant ISR–UTCI correlations (|r| > 0.5). We subsequently employed generalized additive models (GAMs) to characterize their nonlinear relationships, aiming to (1) quantify the complex influence of solar–shade dynamics (ISR) on outdoor thermal comfort (UTCI) and (2) determine critical ISR thresholds corresponding to the UTCI comfort range (18–26 °C), providing actionable parameters for daylight regulation in outdoor design.
GAMs were selected for their capacity to model nonlinear responses through thin-plate regression splines (Figure 11), outperforming conventional linear regression in detecting threshold inflection points. This flexibility proves critical when analyzing the dynamic equilibrium between ISR-mediated shade cooling and solar accessibility effects on the UTCI. To guard against overfitting, all smooth terms in the GAM were fitted using penalized thin-plate regression splines with a restricted basis dimension (k = 4) and smoothing parameters selected via REML (as implemented in the mgcv package). This penalization framework automatically balances model flexibility against parsimony.
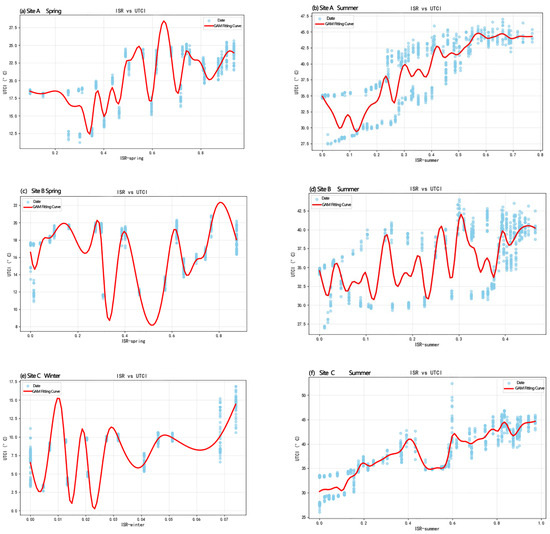
Figure 11.
GAM model fitting based on measured data.
- (1)
- Measured ISR Threshold Patterns
The results revealed pronounced seasonal variations in ISR comfort thresholds across sites: site A required 0.3423–0.6303 ISR during the vernal equinox, but ISR < 0.1243 at the summer solstice, while site B showed higher vernal thresholds (ISR: 0.5383–0.8030) with similar summer constraints (ISR < 0.1172). Site C necessitated winter ISR > 0.0554 to mitigate cold stress, contrasting sharply with near-zero ISR requirements (approaching 0) for summer thermal comfort attainment.
- (2)
- Simulated ISR Threshold Patterns
Simulated data predictions further demonstrated(Figure 12) broader transitional season ISR thresholds (spring: 0.6465–0.8687; autumn: 0.0202–0.8384), a pattern fundamentally stemming from Xi’an’s temperate monsoon climate.
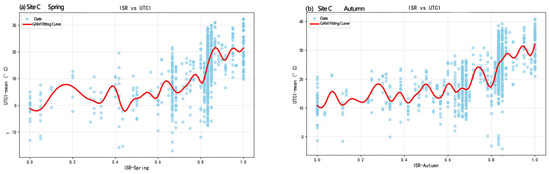
Figure 12.
GAM model fitting based on simulated data.
The region’s extreme thermal conditions—winter temperatures below −10 °C and summer peaks exceeding 40 °C—create significant deviations from the UTCI comfort range (9–26 °C). In contrast, spring or autumn mean temperatures (10–22 °C) align closely with UTCI criteria, enabling stable characterization of ISR–thermal comfort nonlinear relationships during these periods. Crucially, the findings demonstrate that extreme climates demand opposing design strategies: maximal shade coverage (ISR → 0) to counter summer heat stress versus minimal shading (ISR > 0.05) for winter solar gain optimization. While these results provide quantitative guidelines for seasonal dynamic shading design in transitional seasons, they simultaneously highlight limitations in winter–summer optimization frameworks, suggesting the need for auxiliary climate adaptation measures beyond ISR adjustments in extreme thermal scenarios.
4.4. Practical Implementation of ISR Thresholds
The Insolation Shadow Ratio (ISR) framework, while novel, is readily implementable through existing modeling platforms and simple guidelines. In the Xi’an residential case study, ISR thresholds (e.g., maintaining an hourly sunlit-area ratio ≥ 0.70 during 10 a.m.–2 p.m. at summer solstice) were derived via field measurements and Grasshopper + Ladybug simulations. Practitioners can replicate this workflow as follows.
Using Grasshopper, the LB_Sunlight Hourly and LB_ShadeAnalysis components can be combined to compute the ISR in real time, allowing building massing to be adjusted interactively until the model’s hourly ISR meets the target threshold.
5. Conclusions
5.1. Limitations
This study exhibits three principal limitations requiring scholarly attention:
- (a)
- Data Acquisition Constraints in Complex Urban Environments
Dense tree coverage in residential areas obstructed aerial views, preventing top-down capture of solar–shadow variations. Consequently, panoramic images from fixed ground vantage points were used, which may have constrained the spatial completeness and accuracy of ISR measurements. Future studies could employ drone-based photogrammetry or terrestrial LiDAR scanning to obtain high-resolution, three-dimensional shadow data. Additionally, resident activity diversity introduced variability into field observations, and differences in building orientation and height among the three hotspots limited direct comparability.
- (b)
- Geographic Impact ISR Thresholds
The ISR metric exhibits strong spatial dependency, requiring new calculations in distinct geographical contexts due to its limited universal applicability.
- (c)
- Mono-Variable Model Simplification
While the ISR-focused framework effectively reduces design complexity, it inherently neglects critical microclimate interactions. Future studies should integrate morphological and microclimatic parameters (e.g., humidity ratios, wind velocity) to better capture the multifactorial influences on UTCI. As this study represents the first systematic exploration of ISR as a morphological indicator, the thresholds reported herein reflect only the preliminary variability derived from UTCI. To enhance precision and establish more convergent, design-ready threshold ranges, future work will extend the GAM framework by incorporating covariates such as wind speed, relative humidity, air temperature, and solar radiation intensity.
- (d)
- Lag Effects between Shading and Thermal Comfort Perception
While the ISR and the UTCI were synchronized at an hourly temporal resolution in this initial investigation, future research will include time-lagged cross-correlation analyses and higher-frequency simulations to capture any delayed thermal responses and improve the temporal robustness of the ISR–UTCI relationship.
Field measurements were conducted in late 2022 and early 2023, corresponding to the post-pandemic period in China. Although no lockdown measures were in place, and public activity had largely normalized, residual behavioral patterns may still have influenced outdoor space usage and thermal comfort responses. Future studies are encouraged to collect data under fully stabilized social conditions to further validate the representativeness of ISR–UTCI relationships. Although the ISR proved reproducible and highly correlated with the UTCI, a detailed sensitivity analysis was not undertaken. Our workflow relies on precise building and vegetation geometry to ensure repeatability but has yet to assess ISR’s response to variations in height, aspect ratio, or canopy density. In addition, panoramic imagery—used solely for validation—introduces uncertainty through thresholding and spatial parameterization. Future work will (1) perform systematic parametric sweeps of urban form, (2) run perturbation tests to quantify imaging errors, and (3) develop robustness metrics (e.g., confidence intervals) to refine ISR thresholds across diverse morphologies.
5.2. Key Findings
This study introduces a novel morphological indicator, the Insolation Shadow Ratio (ISR), of outdoor spaces in residential areas. The relationship between the ISR and outdoor thermal comfort (UTCI) was explored, revealing the following findings:
- (1)
- Analytical results of the measured data:
- ➀
- A correlation between the ISR and the UTCI was observed across different sites, and it was validated using SPSS based on measured ISR and UTCI data from the actual residential area. The degree of correlation varied among the three sites. Site A and site B exhibited stronger positive correlations, while site C demonstrated a weaker correlation. An exception was observed during the vernal equinox at site C, where the measured ISR and UTCI data showed a negative correlation. Site C exhibited outliers during the vernal equinox. However, this anomaly is likely influenced by complex environmental factors, making it difficult to attribute the phenomenon to a single cause.
- ➁
- The strength of the correlation between the ISR and the UTCI of site A and site C was significantly higher in the sunlit areas than in the shaded areas; however, at site B, it was higher in the shaded areas than in the sunlit areas. The stronger correlation between ISR and UTCI in shaded areas compared to sunlit areas can be explained by two main factors: environmental factors and measurement point distribution. Shaded areas are more influenced by factors like building layout, vegetation, wind speed, and humidity. For example, vegetation in shaded areas can further cool the environment through transpiration, enhancing the ISR–UTCI correlation. Sunlit areas, less affected by these factors, show a weaker correlation. The placement of measurement points and surrounding shading from buildings or vegetation can amplify the impact of ISR on UTCI in shaded areas, especially when these areas are heavily obstructed or influenced by microclimatic conditions. Therefore, this demonstrates that shaded areas are more sensitive to environmental and microclimatic interactions than sunlit areas.
- (2)
- Analytical results of the simulation date:
The three sites all demonstrated a correlation between the ISR and the UTCI, but with varying degrees and trends (positive or negative).
- ➀
- The ISRs of site A on the four typical solar term days showed negative correlations with the UTCI, of different degrees.
- ➁
- The ISRs of site B showed positive correlations with the UTCI on the spring and autumn equinoxes and negative correlations on the winter and summer solstices.
- ➂
- The ISRs of site C on the four typical solar term days showed positive correlations with the UTCI, of different degrees.
- ➃
- The magnitude of the ISR variations had a direct impact on the range of outdoor thermal comfort fluctuations. As the ISR differences increased, the UTCI fluctuations became more pronounced, suggesting ISR as a potentially key factor in shaping the thermal environment of outdoor spaces.
Through this study path and the seasonal fitting results of the GAM (generalized additive model), spring and autumn can better find ISR threshold ranges, possibly because the UTCI corresponding comfort range is 9–26 °C. Xi’an is located in a temperate monsoon climate in the alpine region of the Chinese Plateau, with distinct seasons. The average temperature in cold and dry winters is 1 to −1 °C, and the minimum is below −10 °C; the highest temperature in summer heat is more than 40 °C. Therefore, the comfort range is obviously different from the actual temperature in winter and summer in Xi’an.
Although the ISR is unprecedented, the strong positive correlations we observe between higher sunlit fractions and improved UTCI values echo similar patterns reported for static sky view metrics [22], where increased sky exposure corresponded to elevated PET and UTCI in cold-season conditions. Likewise, our finding of inverted relationships under dense canopy at site C parallels Morganti et al.’s [2] demonstration that vegetation density can reverse expected comfort trends by prolonging low-angle shading. By situating ISR’s dynamic radiative insights alongside these established static and vegetative studies, we underscore both its continuity with—and advancement beyond—prior morphological analyses.
Overall, the analytical results of both the measured and simulated data revealed a correlation between the ISR and the UTCI in some seasons (primary outcome at site C in spring and autumn) and patterns of the influence of ISR variations on UTCI fluctuations. Therefore, the ISR indicator could potentially be used as a tool in outdoor space design for improving the outdoor thermal environment in specific areas. Future research can be conducted to further clarify and validate the correlation between the ISR and the outdoor thermal environment under different climatic conditions, so as to develop a more comprehensive understanding of the ISR–thermal comfort relationship.
5.3. Contributions
This study makes three seminal contributions to climate-responsive urban design:
- (1)
- Theoretical Innovation: We propose the ISR as a novel morphometric index that quantifies solar shade dynamics and their nonlinear coupling with UTCI-based thermal comfort. This metric establishes an intuitive visualization framework linking shadow coverage (0–1 normalized) to physiological heat stress thresholds (9–26 °C UTCI).
- (2)
- Design Praxis Transformation: The ISR enables direct conversion of thermal comfort requirements into implementable shade design parameters and reduces the technical threshold of thermal environment optimization.
- (3)
- Build A New Research Pathway: We establish a dynamic solar exposure analysis framework that integrates field microclimate measurements and simulated data with GAM-based threshold modeling. Although the present study focuses on Xi’an, the ISR computation protocol—grounded in local solar trajectories and parametric solar–shadow modeling—is directly transferable to other cold-region contexts.
Author Contributions
Conceptualization, J.S. and Y.L.; Methodology, J.S., Y.L. and S.C.; Software, J.S. and B.L.; Validation, J.S. and B.L.; Formal analysis, J.S., D.H.C.C. and S.C.; Investigation, J.S. and B.L.; Resources, Y.L. and D.H.C.C.; Data curation, D.H.C.C.; Writing—original draft, J.S. and Y.L.; Writing—review & editing, Y.L. and D.H.C.C.; Visualization, J.S.; Supervision, Y.L.; Funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (Project No. 52078422). This work was also funded by the Royal Society Funding Number: IEC\NSFC\233170-International Exchanges 2023 Cost Share (NSFC)-Research on key technical pathways for low-carbon construction of urban residential areas based on climate change assessment and vernacular examples.
Data Availability Statement
No new data were created for this study, if there is a request for data please contact the authors to provide it.
Acknowledgments
Declaration of generative AI and AI-assisted technologies in the writing process: during the preparation of this work, the authors used AI only for language polishing. The authors reviewed and edited the content as needed and take full responsibility for the content of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Records of variations in sunshine and shadow at site A during the winter solstice.
Table A1.
Records of variations in sunshine and shadow at site A during the winter solstice.
| 22 December 2022 | Panoramic Picture |
|---|---|
| 8:00–10:00 |  |
| 12:00–14:00 |  |
| 16:00–18:00 |  |

Table A2.
Records of variations in sunshine and shadow at site A during the spring equinox.
Table A2.
Records of variations in sunshine and shadow at site A during the spring equinox.
| 21 March 2023 | Panoramic Picture |
|---|---|
| 8:00–10:00 |  |
| 12:00–14:00 |  |
| 16:00–18:00 |  |

Table A3.
Records of variations in sunshine and shadow at site A during the summer solstice.
Table A3.
Records of variations in sunshine and shadow at site A during the summer solstice.
| 22 June 2023 | Panoramic Picture |
|---|---|
| 8:00–10:00 |  |
| 12:00–14:00 |  |
| 16:00–18:00 |  |

Table A4.
Time-wise ISR simulation of the three sites.
Table A4.
Time-wise ISR simulation of the three sites.
| Time | Winter Solstice | Spring Equinox | Summer Solstice | Autumnal Equinox | |
|---|---|---|---|---|---|
| Site A | 8:00 | 0.941 | 0.943 | 0.942 | 0.943 |
| 9:00 | 0.940 | 0.942 | 0.943 | 0.942 | |
| 10:00 | 0.937 | 0.941 | 0.943 | 0.940 | |
| 11:00 | 0.934 | 0.937 | 0.942 | 0.937 | |
| 12:00 | 0.917 | 0.930 | 0.939 | 0.924 | |
| 13:00 | 0.775 | 0.877 | 0.903 | 0.836 | |
| 14:00 | 0.406 | 0.724 | 0.800 | 0.673 | |
| 15:00 | 0.038 | 0.531 | 0.685 | 0.480 | |
| 16:00 | 0.000 | 0.404 | 0.571 | 0.372 | |
| 17:00 | 0.000 | 0.328 | 0.535 | 0.301 | |
| 18:00 | 0.000 | 0.311 | 0.395 | 0.353 | |
| Site B | 8:00 | 0.711 | 0.821 | 0.822 | 0.809 |
| 9:00 | 0.643 | 0.771 | 0.847 | 0.756 | |
| 10:00 | 0.538 | 0.703 | 0.841 | 0.677 | |
| 11:00 | 0.365 | 0.580 | 0.788 | 0.539 | |
| 12:00 | 0.142 | 0.434 | 0.747 | 0.396 | |
| 13:00 | 0.000 | 0.310 | 0.718 | 0.296 | |
| 14:00 | 0.000 | 0.299 | 0.709 | 0.300 | |
| 15:00 | 0.000 | 0.285 | 0.755 | 0.272 | |
| 16:00 | 0.000 | 0.282 | 0.836 | 0.260 | |
| 17:00 | 0.000 | 0.288 | 0.786 | 0.309 | |
| 18:00 | 0.000 | 0.305 | 0.655 | 0.354 | |
| Site C | 8:00 | 0.000 | 0.292 | 0.866 | 0.437 |
| 9:00 | 0.029 | 0.724 | 0.988 | 0.767 | |
| 10:00 | 0.354 | 0.811 | 0.970 | 0.816 | |
| 11:00 | 0.548 | 0.815 | 0.938 | 0.814 | |
| 12:00 | 0.559 | 0.810 | 0.936 | 0.808 | |
| 13:00 | 0.557 | 0.809 | 0.936 | 0.809 | |
| 14:00 | 0.526 | 0.814 | 0.938 | 0.815 | |
| 15:00 | 0.406 | 0.808 | 0.969 | 0.807 | |
| 16:00 | 0.129 | 0.803 | 0.990 | 0.802 |

Table A5.
UTCI simulation at site A.
Table A5.
UTCI simulation at site A.
| Time | Winter Solstice | Spring Equinox | Summer Solstice | Autumnal Equinox | ||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | |
| 8:00 | −1.1 | 0.16 | 2.43 | 2.81 | 18.92 | 21.57 | 20.1 | 20.55 |
| 9:00 | −0.99 | 0.02 | 6.87 | 7.38 | 23.08 | 28 | 20.83 | 20.87 |
| 10:00 | −0.07 | 0.41 | 6.29 | 6.56 | 23.19 | 29.54 | 21.51 | 23.2 |
| 11:00 | −2.45 | −2.09 | 7.87 | 9.43 | 25.16 | 31.62 | 22.34 | 23.86 |
| 12:00 | 1.3 | 3.55 | 7.02 | 13.88 | 26.12 | 33.32 | 22.34 | 24.46 |
| 13:00 | −1.28 | 2.23 | 9.27 | 21.77 | 27.45 | 34.01 | 22.36 | 27.26 |
| 14:00 | 3.1 | 7.14 | 13.21 | 26.01 | 28.32 | 34.19 | 22.78 | 27.75 |
| 15:00 | 4.07 | 6.8 | 12.09 | 21.79 | 29.81 | 36.14 | 22.36 | 26.09 |
| 16:00 | 1.04 | 2.71 | 11.65 | 20.38 | 30.87 | 37.73 | 23.89 | 26.78 |
| 17:00 | 3.73 | 3.81 | 10.46 | 17.19 | 32.09 | 38.09 | 23.95 | 25.18 |
| 18:00 | 2.98 | 4.44 | 11.38 | 12.49 | 32.21 | 36.79 | 24.26 | 24.27 |

Table A6.
UTCI simulation at site B.
Table A6.
UTCI simulation at site B.
| Time | Winter Solstice | Spring Equinox | Summer Solstice | Autumnal Equinox | ||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | |
| 8:00 | −0.95 | 0.16 | 2.48 | 2.81 | 18.92 | 21.3 | 20.15 | 20.55 |
| 9:00 | −0.88 | 0.02 | 6.93 | 7.38 | 23.08 | 27.66 | 20.83 | 20.87 |
| 10:00 | −0.02 | 0.41 | 6.29 | 6.53 | 23.19 | 29.18 | 21.51 | 23.01 |
| 11:00 | −2.45 | −2.13 | 7.87 | 9.25 | 25.16 | 31.26 | 22.34 | 23.68 |
| 12:00 | 1.3 | 3.29 | 7.02 | 13.13 | 26.12 | 32.84 | 22.34 | 24.21 |
| 13:00 | −1.28 | 1.82 | 9.27 | 20.41 | 27.45 | 33.57 | 22.36 | 26.71 |
| 14:00 | 3.1 | 6.66 | 13.21 | 24.66 | 28.32 | 33.88 | 22.78 | 27.19 |
| 15:00 | 4.07 | 6.49 | 12.09 | 21.42 | 29.81 | 35.87 | 22.36 | 25.66 |
| 16:00 | 1.04 | 2.52 | 11.65 | 20.17 | 30.87 | 37.49 | 23.89 | 26.45 |
| 17:00 | 3.73 | 3.8 | 10.46 | 17.14 | 32.09 | 38 | 23.89 | 25.04 |
| 18:00 | 3.15 | 4.44 | 11.51 | 12.49 | 32.21 | 36.78 | 24.26 | 24.27 |

Table A7.
UTCI simulation at site C.
Table A7.
UTCI simulation at site C.
| Time | Winter Solstice | Spring Equinox | Summer Solstice | Autumnal Equinox | ||||
|---|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max | |
| 8:00 | −0.63 | −0.24 | 2.57 | 2.69 | 19.94 | 20.7 | 20.27 | 20.4 |
| 9:00 | −0.62 | −0.31 | 7.06 | 7.21 | 25.99 | 26.92 | 20.84 | 20.85 |
| 10:00 | 0.1 | 0.25 | 6.38 | 6.46 | 27.36 | 28.37 | 22.06 | 22.59 |
| 11:00 | −2.34 | −2.22 | 8.37 | 8.86 | 29.48 | 30.47 | 22.83 | 23.3 |
| 12:00 | 2.02 | 2.72 | 9.12 | 11.51 | 30.49 | 31.8 | 23.02 | 23.69 |
| 13:00 | −0.16 | 0.93 | 13.41 | 17.36 | 31.4 | 32.61 | 23.96 | 25.5 |
| 14:00 | 4.39 | 5.65 | 17.54 | 21.59 | 32.36 | 33.2 | 24.41 | 25.97 |
| 15:00 | 4.94 | 5.8 | 13.05 | 20.79 | 34.55 | 35.28 | 23.57 | 24.74 |
| 16:00 | 1.58 | 2.1 | 12.17 | 19.83 | 36.33 | 36.97 | 24.82 | 25.73 |
| 17:00 | 3.75 | 3.78 | 10.58 | 17.06 | 37.55 | 37.8 | 24.35 | 24.73 |
| 18:00 | 3.52 | 3.97 | 11.78 | 12.13 | 32.27 | 36.75 | 24.26 | 24.27 |
References
- Huo, K.; Qin, R.; Zhao, J.; Ma, X. Long-Term Tracking of Urban Structure and Analysis of Its Impact on Urban Heat Stress: A Case Study of Xi’an, China. Ecol. Indic. 2025, 174, 113418. [Google Scholar] [CrossRef]
- Morganti, M.; Salvati, A.; Coch, H.; Cecere, C. Urban Morphology Indicators for Solar Energy Analysis. Energy Procedia 2017, 134, 807–814. [Google Scholar] [CrossRef]
- Open Knowledge Maps. Knowledge Map for Research on Outdoor Thermal Comfort in Shaded Areas. 11 June 2024. Available online: https://openknowledgemaps.org/map/b898def6d0ee7b3ff345d7fdfa13fb5c (accessed on 4 June 2024).
- Lai, D.; Liu, W.; Gan, T.; Liu, K.; Chen, Q. A Review of Mitigating Strategies to Improve the Thermal Environment and Thermal Comfort in Urban Outdoor Spaces. Sci. Total Environ. 2019, 661, 337–353. [Google Scholar] [CrossRef]
- Elnabawi, M.H.; Jamei, E. The thermal perception of outdoor urban spaces in a hot arid climate: A structural equation modelling (SEM) approach. Urban Clim. 2024, 55, 101969. [Google Scholar] [CrossRef]
- Jänicke, B.; Milošević, D.; Manavvi, S. Review of User-Friendly Models to Improve the Urban Micro-Climate. Atmosphere 2021, 12, 1291. [Google Scholar] [CrossRef]
- Lau, K.K.-L.; Lindberg, F.; Rayner, D.; Thorsson, S. The Effect of Urban Geometry on Mean Radiant Temperature under Future Climate Change: A Study of Three European Cities. Int. J. Biometeorol. 2015, 59, 799–814. [Google Scholar] [CrossRef]
- Li, J. A Theory and Method of Solar Adaptive Urban Design. Ph.D. Thesis, Southeast University, Nanjing, China, 2019. Available online: https://kns.cnki.net/kcms2/article/abstract (accessed on 8 June 2024).
- Compagnon, R. Solar and Daylight Availability in the Urban Fabric. Energy Build. 2004, 36, 321–328. [Google Scholar] [CrossRef]
- Salata, F.; Golasi, I.; de Lieto Vollaro, R.; de Lieto Vollaro, A. Urban Microclimate and Outdoor Thermal Comfort. A Proper Procedure to Fit ENVI-Met Simulation Outputs to Experimental Data. Sustain. Cities Soc. 2016, 26, 318–343. [Google Scholar] [CrossRef]
- Acero, J.A.; Koh, E.J.Y.; Tan, Y.S.; Leslie; Norford, K. Quantifying the Effect of Building Shadowing and Cloudiness on Mean Radiant Temperature in Singapore. Atmosphere 2021, 12, 1012. [Google Scholar] [CrossRef]
- Wang, M.; Gou, Z. Gaussian Mixture Model Based Classification for Analyzing Longitudinal Outdoor Thermal Environment Data to Evaluate Comfort Conditions in Urban Open Spaces. Urban Clim. 2024, 53, 101792. [Google Scholar] [CrossRef]
- Huang, T.; Li, J.; Xie, Y.; Niu, J.; Mak, C.M. Simultaneous Environmental Parameter Monitoring and Human Subject Survey Regarding Outdoor Thermal Comfort and Its Modelling. Build. Environ. 2017, 125, 502–514. [Google Scholar] [CrossRef]
- Johansson, E.; Emmanuel, R. The Influence of Urban Design on Outdoor Thermal Comfort in the Hot, Humid City of Colombo, Sri Lanka. Int. J. Biometeorol. 2006, 51, 119–133. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Wang, Y.; Li, J.; Liu, T.; Li, Y. How Building Arrangements Can Improve Outdoor Thermal Comfort and Indoor Sunlight? Proc. Inst. Civ. Eng.—Munic. Eng. 2024, 177, 111–129. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Xi, T. A Review of Thermal Comfort Evaluation and Improvement in Urban Outdoor Spaces. Buildings 2023, 13, 3050. [Google Scholar] [CrossRef]
- Costa, I.T.; Wollmann, C.A.; Writzl, L.; Iensse, A.C.; da Silva, A.N.; de Freitas Baumhardt, O.; Gobo, J.P.A.; Shooshtarian, S.; Matzarakis, A. A Systematic Review on Human Thermal Comfort and Methodologies for Evaluating Urban Morphology in Outdoor Spaces. Climate 2024, 12, 30. [Google Scholar] [CrossRef]
- Han, Y.; Jo, Y.; Kim, E.J. Influence of Landscape Interventions on Thermal Comfort under Time-Varying Building Shadow; New Gwanghwamun Square Case, Seoul, South Korea. Heliyon 2023, 9, e19436. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.; Cho, S.; Chow, D.H.C. Urban Morphology Indicators and Solar Radiation Acquisition: 2011–2022 Review. Renew. Sustain. Energy Rev. 2024, 199, 114548. [Google Scholar] [CrossRef]
- Nouri, A.S.; Costa, J.P.; Matzarakis, A. Examining Default Urban-Aspect-Ratios and Sky-View-Factors to Identify Priorities for Thermal-Sensitive Public Space Design in Hot-Summer Mediterranean Climates: The Lisbon Case. Build. Environ. 2017, 126, 442–456. [Google Scholar] [CrossRef]
- Miao, C.; Yu, S.; Hu, Y.; Zhang, H.; He, X.; Chen, W. Review of Methods Used to Estimate the Sky View Factor in Urban Street Canyons. Build. Environ. 2020, 168, 106497. [Google Scholar] [CrossRef]
- Watson, I.D.; Johnson, G.T. Graphical Estimation of Sky View-Factors in Urban Environments. J. Climatol. 1987, 7, 193–197. [Google Scholar] [CrossRef]
- Yi, P.; Liu, L.; Huang, Y.; Zhang, M.; Liu, H.; Bedra, K.B. Study on the Coupling Relationship between Thermal Comfort and Urban Center Spatial Morphology in Summer. Sustainability 2023, 15, 5084. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, L.; Ding, X.; Zhang, Z.; Qi, Z.; Jiang, L.; Bu, D. Multi-Objective Optimization of Outdoor Thermal Comfort and Sunlight Hours in Elderly Residential Areas: A Case Study of Beijing, China. Buildings 2024, 14, 3770. [Google Scholar] [CrossRef]
- Zhang, M.; You, W.; Qin, Q.; Peng, D.; Hu, Y.; Gao, Z.; Buccolieri, R. Investigation of Typical Residential Block Typologies and Their Impact on Pedestrian-Level Microclimate in Summers in Nanjing, China. Front. Archit. Res. 2022, 11, 278–296. [Google Scholar] [CrossRef]
- Salgado-Conrado, L.; Lopez-Montelongo, A.; Alvarez-Macias, C.; Hernadez-Jaquez, J. Review of Heliodon Developments and Computational Tools for Building Shadow Analysis. Buildings 2022, 12, 627. [Google Scholar] [CrossRef]
- Lin, T.-P.; Matzarakis, A.; Hwang, R.-L. Shading Effect on Long-Term Outdoor Thermal Comfort. Build. Environ. 2010, 45, 213–221. [Google Scholar] [CrossRef]
- Lindberg, F.; Grimmond, C.S.B. Nature of vegetation and building morphology characteristics across a city: Influence on shadow patterns and mean radiant temperatures in London. Urban Ecosyst. 2011, 14, 617–634. [Google Scholar] [CrossRef]
- Memon, R.A.; Chirarattananon, S.; Vangtook, P. Thermal Comfort Assessment and Application of Radiant Cooling: A Case Study. Build. Environ. 2008, 43, 1185–1196. [Google Scholar] [CrossRef]
- de Dear, R.J.; Brager, G.S. Thermal Comfort in Naturally Ventilated Buildings: Revisions to ASHRAE Standard 55. Energy Build. 2002, 34, 549–561. [Google Scholar] [CrossRef]
- Shaw, E.W. Thermal Comfort: Analysis and Applications in Environmental Engineering, by P. O. Fanger. 244 Pp. DANISH TECHNICAL PRESS. Copenhagen, Denmark, 1970. Danish Kr. 76, 50. R. Soc. Health J. 1972, 92, 164. [Google Scholar] [CrossRef]
- Das, S.; Subudhi, S. A Review on Different Methodologies to Study Thermal Comfort. Int. J. Environ. Sci. Technol. 2022, 19, 2155–2171. [Google Scholar] [CrossRef]
- Lai, D.; Chen, B.; Liu, K. Quantification of the Influence of Thermal Comfort and Life Patterns on Outdoor Space Activities. Build. Simul. 2020, 13, 113–125. [Google Scholar] [CrossRef]
- Höppe, P. The Physiological Equivalent Temperature—A Universal Index for the Biometeorological Assessment of the Thermal Environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef]
- Matzarakis, A.; Mayer, H.; Iziomon, M.G. Applications of a Universal Thermal Index: Physiological Equivalent Temperature. Int. J. Biometeorol. 1999, 43, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Ji, W.; Zhu, Y.; Du, H.; Cao, B.; Lian, Z.; Geng, Y.; Liu, S.; Xiong, J.; Yang, C. Interpretation of Standard Effective Temperature (SET) and Explorations on Its Modification and Development. Build. Environ. 2022, 210, 108714. [Google Scholar] [CrossRef]
- Jia, X.; Li, S.; Zhu, Y.; Du, Z.; Cao, B. Development of the Universal Standard Effective Temperature for Evaluating Thermal Comfort across Different Metabolic Rates. Build. Environ. 2024, 250, 111149. [Google Scholar] [CrossRef]
- Zhao, Q.; Lian, Z.; Lai, D. Thermal Comfort Models and Their Developments: A Review. Energy Built Environ. 2021, 2, 21–33. [Google Scholar] [CrossRef]
- Bröde, P.; Krüger, E.; Fiala, D. UTCI: Validation and Practical Application to the Assessment of Urban Outdoor Thermal Comfort. Geogr. Pol. 2013, 86, 11–20. [Google Scholar] [CrossRef]
- Fiala, D.; Havenith, G.; Broede, P.; Kampmann, B.; Jendritzky, G. UTCI-Fiala Multi-Node Model of Human Heat Transfer and Temperature Regulation. Int. J. Biometeorol. 2012, 56, 429–441. [Google Scholar] [CrossRef]
- Mahdavinejad, M.; Shaeri, J.; Nezami, A.; Goharian, A. Comparing Universal Thermal Climate Index (UTCI) with Selected Thermal Indices to Evaluate Outdoor Thermal Comfort in Traditional Courtyards with BWh Climate. Urban Clim. 2024, 54, 101839. [Google Scholar] [CrossRef]
- Wereski, S.; Krzyżewska, A.; Dobek, M. Winter UTCI Variability in Poland in the 21st Century. Misc. Geogr. 2020, 24, 128–137. [Google Scholar] [CrossRef]
- Blazejczyk, K.; Epstein, Y.; Jendritzky, G.; Staiger, H.; Tinz, B. Comparison of UTCI to Selected Thermal Indices. Int. J. Biometeorol. 2012, 56, 515–535. [Google Scholar] [CrossRef] [PubMed]
- Zare, S.; Hasheminejad, N.; Shirvan, H.E.; Hemmatjo, R.; Sarebanzadeh, K.; Ahmadi, S. Comparing Universal Thermal Climate Index (UTCI) with Selected Thermal Indices/Environmental Parameters during 12 Months of the Year. Weather. Clim. Extrem. 2018, 19, 49–57. [Google Scholar] [CrossRef]
- Jin, H.; Liu, S.; Kang, J. Thermal Comfort Range and Influence Factor of Urban Pedestrian Streets in Severe Cold Regions. Energy Build. 2019, 198, 197–206. [Google Scholar] [CrossRef]
- Nie, T.; Lai, D.; Liu, K.; Lian, Z.; Yuan, Y.; Sun, L. Discussion on Inapplicability of Universal Thermal Climate Index (UTCI) for Outdoor Thermal Comfort in Cold Region. Urban Clim. 2022, 46, 101304. [Google Scholar] [CrossRef]
- Wu, J.; Jin, T.; Wu, Y.; Ding, Y.; Mu, Y.; Zeng, D. The Variation of UTCI with the Background of Climate Change and Its Implications for Tourism in a Complicated Climate Region in Western China. Sustainability 2022, 14, 15047. [Google Scholar] [CrossRef]
- Wu, Z.; Kong, F.; Wang, Y.; Sun, R.; Chen, L. The Impact of Greenspace on Thermal Comfort in a Residential Quarter of Beijing, China. Int. J. Environ. Res. Public Health 2016, 13, 1217. [Google Scholar] [CrossRef]
- Park, S.; Stanton; Tuller, E.; Jo, M. Application of Universal Thermal Climate Index (UTCI) for Microclimatic Analysis in Urban Thermal Environments. Landsc. Urban Plan. 2014, 125, 146–155. [Google Scholar] [CrossRef]
- Ning, S.; Jing, W.; Ge, Z. Sunlight Perception and Outdoor Thermal Comfort in College Campuses: A New Perspective. Sci. Rep. 2023, 13, 16112. [Google Scholar] [CrossRef]
- Cohen, J.; Cohen, P.; Stephen; West, G.; Aiken, L. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed.; Routledge: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Jebli, I.; Belouadha, F.-Z.; Kabbaj, M.I.; Tilioua, A. Prediction of Solar Energy Guided by Pearson Correlation Using Machine Learning. Energy 2021, 224, 120109. [Google Scholar] [CrossRef]
- de Winter, J.C.F.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol. Methods 2016, 21, 273–290. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ Sensitivity Analysis of a Complex Environmental Model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Tian, W. A Review of Sensitivity Analysis Methods in Building Energy Analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- Tortorelli, D.A.; Michaleris, P. Design Sensitivity Analysis: Overview and Review. Inverse Probl. Eng. 1994, 1, 71–105. [Google Scholar] [CrossRef]
- Zhou, Y.; Tam, V.W.Y.; Le, K.N. Sensitivity Analysis of Design Variables in Life-Cycle Environmental Impacts of Buildings. J. Build. Eng. 2023, 65, 105749. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).