Learning-Enhanced Differential Evolution for Multi-Mode Resource-Constrained Multi-Project Scheduling Problem in Industrial Prefabrication

Abstract

Efficient scheduling in industrial prefabrication environments—such as Prefabricated Bathroom Unit (PBU) production—faces increasing challenges due to resource limitations, overlapping projects, and complex task dependencies. To address these challenges, this paper presents a Learning-Enhanced Differential Evolution (LEDE) framework for solving the Multi-Mode Resource-Constrained Multi-Project Scheduling Problem (MRCMPSP). The MRCMPSP models the operational difficulty of coordinating interdependent activities across multiple PBU projects under limited resource availability. To address the computational intractability of this NP-hard problem, we first formulate a mixed-integer linear programming (MILP) model, and then develop an adaptive DE-based metaheuristic. The proposed LEDE method co-evolves activity sequencing and mode assignment using floating-point encodings, incorporating strategy switching, parameter adaptation, elitism, stagnation handling, and rank-based crossover control. Evaluated on real-world production data from the PBU industry, the algorithm produces high-quality solutions with strong scalability. These results demonstrate its practical potential as a decision-support tool for dynamic, resource-constrained industrial scheduling.

1. Introduction

Offsite construction has gained significant momentum in recent years due to its advantages in productivity, quality control, and sustainability [1]. Within this domain, Prefabricated Bathroom Units (PBUs)—a form of 3D modular construction—have become increasingly popular, particularly in large-scale residential projects [2]. In Singapore, the use of PBUs has been mandatory for all residential developments on government land sales sites since 2014, underscoring their role in modern construction practices [3].

The PBU fit-out process involves a series of interdependent tasks carried out under fixed-position assembly. In practice, manufacturers often manage multiple projects simultaneously, all competing for limited production resources [4,5,6]. This situation gives rise to a resource-constrained multi-project scheduling problem (RCMPSP) [7]. When tasks can be executed in different modes, each with varying durations and resource requirements, the problem becomes more complex-known as the multi-mode resource-constrained multi-project scheduling problem (MRCMPSP). Each mode represents a trade-off between resource allocation and execution time, making mode selection a critical part of scheduling efficiency [8].

The MRCMPSP is NP-hard, and as problem size and complexity grow, exact methods become computationally impractical [9,10]. To tackle such problems, researchers have explored heuristics, metaheuristics, and hybrid optimization strategies. Metaheuristics such as genetic algorithms (GA) and particle swarm optimization (PSO) offer global search capabilities [11,12], while priority-rule (PR) heuristics are valued for their computational speed [10]. Hybrid methods aim to combine these strengths to achieve better performance [13,14].

This paper proposes a novel optimization framework based on a co-evolved, Learning-Enhanced Differential Evolution (LEDE) algorithm to solve MRCMPSP in the context of Prefabricated Bathroom Unit (PBU) production. The key components of the proposed method are:

■

A Differential Evolution-based metaheuristic is employed to simultaneously determine the activity sequence and execution mode for each job across multiple projects.

■

Both activity sequencing and mode assignment are co-evolved using continuous representations, with activity priorities derived from sorted float values and modes selected via an argmax operator over learned mode score vectors.

■

The LEDE algorithm incorporates adaptive parameter control, strategy switching, elitism, crossover adaptation, and stagnation handling, allowing it to balance exploration and exploitation dynamically throughout the optimization process.

Computational experiments were conducted on benchmark datasets derived from real-world PBU production scenarios to evaluate the performance of the proposed method. The results demonstrate that the LEDE approach achieves high solution quality, stable convergence behaviour, and strong robustness across complex scheduling environments. The algorithm also exhibits adaptability to varying resource availability conditions, making it suitable for diverse and dynamic production settings.

The aim of this study is to develop a scalable and adaptive optimization framework for solving the MRCMPSP in industrial prefabrication settings, with a focus on Prefabricated Bathroom Unit (PBU) production. The main objectives are as follows: (1) to formulate the MRCMPSP under realistic multi-project and multi-mode constraints observed in prefabrication processes; and (2) to co-optimize activity sequencing and mode assignment through a continuous representation within a Differential Evolution (DE) framework. The novelty of this study lies in the integration of multiple enhancement strategies—including adaptive parameter control, strategy switching, elitism, crossover adaptation, and stagnation handling—within a unified DE-based approach that improves flexibility, robustness, and applicability in complex, resource-constrained scheduling environments.

2. Literature Review

This section reviews existing research on the Multi-Mode Resource-Constrained Multi-Project Scheduling Problem (MRCMPSP), focusing on the application of metaheuristic optimization techniques. The MRCMPSP extends classical scheduling problems by introducing multiple execution modes and complex inter-project dependencies, making it particularly challenging to solve using exact methods alone. In response, metaheuristic algorithms—such as genetic algorithms, particle swarm optimization, and differential evolution—have been widely adopted due to their flexibility and ability to handle large, nonlinear search spaces. These approaches have proven especially relevant in practical manufacturing scenarios, including prefabricated bathroom unit (PBU) production, where dynamic constraints and resource limitations are common.

2.1. Multi-Mode Resource-Constrained Multi-Project Scheduling (MRCMPSP)

The MRCMPSP extends classical scheduling problems by addressing multiple concurrent projects, each with activities that can be executed in different modes (varying in duration and resource demand), while sharing constrained renewable resources. It builds on the resource-constrained multi-project scheduling problem (RCMPSP) and the multi-mode resource-constrained project scheduling problem (MRCPSP), which originated from operations research and project management domains in the 1980s and 1990s [7,15].

To stimulate progress, the MISTA 2013 Challenge [8] provided benchmark instances and invited researchers to develop heuristic and metaheuristic solutions under strict computational budgets. Most submissions used activity-mode list representations combined with serial schedule generation schemes (SGS) and single-mode-change neighbourhood structures.

Asta et al. [16] introduced the winning algorithm, a hybrid of Monte Carlo Tree Search (MCTS) and Genetic Algorithm (GA). Projects were grouped using partial ordering; MCTS determined their positions, and GA optimized activity sequences. A dedicated local search was applied to further improve the GA’s solutions.

Common objectives in MRCMPSP include minimizing total project delay (TPD) and total makespan (TMS), where objectives that are often conflicting and handled via Pareto-based multi-objective optimization [17]. TPD-oriented solutions tend to be more dispersed in the search space, requiring broad exploration strategies.

Voß and Witt [12] addressed MRCMPSP with batching constraints, introducing a priority-rule-based heuristic tailored for parallel machines. Their approach grouped jobs by production stages, and their modified R&M rule focused on local cost minimization. Their findings revealed that local evaluations of scheduling decisions (based only on the current job) outperformed global strategies (which account for downstream impact).

It is also well-recognized that schedules optimized for one performance criterion may not generalize well to others. Consequently, hybrid metaheuristic methods that offer flexible exploration and objective-driven adaptability are of increasing interest in the field.

2.2. Learning Metaheuristics

Metaheuristics such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Differential Evolution (DE) have been extensively applied to solve the NP-hard multi-mode resource-constrained multi-project scheduling problem (MRCMPSP), owing to their capacity to balance global exploration and local exploitation [9,18]. These methods are particularly useful when exact methods become computationally infeasible in large and complex instances.

However, traditional metaheuristics often rely on fixed algorithmic parameters and static operator strategies, which may limit adaptability in dynamic or heterogeneous problem environments. To address this, recent literature has increasingly focused on adaptive and hybrid variants that incorporate learning-inspired mechanisms. For instance, self-adaptive DE variants such as $jDE$ [19] and strategy-adaptive DE (SaDE) [20] have been shown to improve convergence speed and robustness by adjusting parameters like the scaling factor ($F$) and crossover rate ($CR$) over time.

Elitism and feedback-driven mechanisms have also been introduced to improve search stability and escape local optima. Zhang et al. [21] proposed an adaptive DE with rank-based crossover adjustment, allowing poor-performing individuals to explore more aggressively, while preserving strong solutions. Stagnation-handling techniques such as population reinitialization and solution perturbation further promote diversity in prolonged search processes [22].

While these strategies have demonstrated promising results in classical DE contexts, their application in multi-mode, multi-project scheduling remains limited. Existing MRCMPSP studies rarely integrate such adaptive mechanisms into co-evolution frameworks for sequence and mode decisions. This research addresses this gap by incorporating multiple adaptive enhancements into a unified DE-based metaheuristic tailored for realistic prefabrication scheduling environments.

While some studies integrate reinforcement learning (e.g., Q-learning) with metaheuristics [23], others demonstrate that adaptive metaheuristics alone can capture similar learning behaviour. For example, Qin et al. [20] showed that mutation strategy switching based on historical performance enhances search efficiency in complex optimization landscapes.

2.3. Other Methods

In addition to metaheuristics, prior studies on the Multi-Mode Resource-Constrained Multi-Project Scheduling Problem (MRCMPSP) and its variants have also investigated exact, heuristic, and simulation-based approaches. Exact methods, such as branch-and-bound and mixed-integer linear programming (MILP) formulations, guarantee optimality but are limited to small or medium problem sizes due to exponential complexity. For instance, Bold and Goerigk (2022) [24] proposed a robust MILP formulation for the MRCPSP with uncertain activity durations, demonstrating improved computational efficiency over previous methods. Similarly, Mirnezami et al. [25] developed a MILP model for multi-project scheduling with multiple resource constraints in ship repair, addressing practical considerations in industrial settings.

Heuristic methods, including priority-rule-based scheduling (e.g., minimum slack, most successors), are fast and interpretable but often suffer from poor scalability and limited flexibility under dynamic constraints. Peng et al. [26] introduced a hybrid approach combining priority rules with metaheuristics to enhance solution quality for the MRCMPSP. Additionally, Najafi et al. [27] proposed composite priority rules for scheduling multi-mode resource-constrained projects under dynamic conditions, highlighting the adaptability of heuristic methods in complex environments.

Simulation-based techniques, such as discrete event simulation (DES), are used to evaluate schedule robustness or explore probabilistic disruptions, though they typically require external optimization loops and do not offer embedded decision-making. Alvarez-Campana et al. (2024) [28] presented a simulation-based approach for multi-project scheduling that integrates composite priority rules, demonstrating improved performance in handling uncertainty and resource constraints.

Further, Pinha et al. (2016) [29] proposed a simulation-based approach for the combinatorial MRCMPSP that generates multiple feasible schedules, allowing project managers to select solutions under changing practical constraints such as shifting resource availability or project priorities. This flexible decision-support model emphasizes robustness over single-point optimality, which is critical in dynamic industrial environments.

Kannimuthu et al. (2019) [30] compared two modelling strategies—single-project (portfolio) optimization versus multi-project decomposition—using both benchmark and real-world data. Their findings highlighted that portfolio-level optimization generally yields superior time–cost–quality trade-offs, though at increased computational expense, reinforcing the need for scalable yet high-quality scheduling strategies.

Sadeghloo et al. (2024) [31] introduced a multi-objective MILP model for the MRCMPSP with contractor heterogeneity and duration uncertainty. The model incorporates cost, satisfaction, and earliness/tardiness penalties, and applies Benders decomposition for tractability. This study exemplifies how uncertainty-aware, multi-criteria formulations can support more realistic planning in engineering consulting contexts.

In contrast, our proposed Learning-Enhanced Differential Evolution (LEDE) framework provides a computationally scalable, directly optimizable, and learning-enhanced approach that combines the strengths of metaheuristics with embedded learning mechanisms. This integration addresses the limitations of both exact and heuristic methods, offering a robust solution for complex, real-world production environments [32].

3. PBU Fit-Out Process

This section describes the current practice of PBU fit-out and the problems faced by manufacturers in managing project schedules under resource and time constraints. In particular, it highlights the challenges related to coordinating multiple prefabricated units simultaneously, allocating limited resources efficiently, and meeting stringent project deadlines. These practical difficulties motivate the need for advanced scheduling models that can optimize production workflows and improve overall project performance.

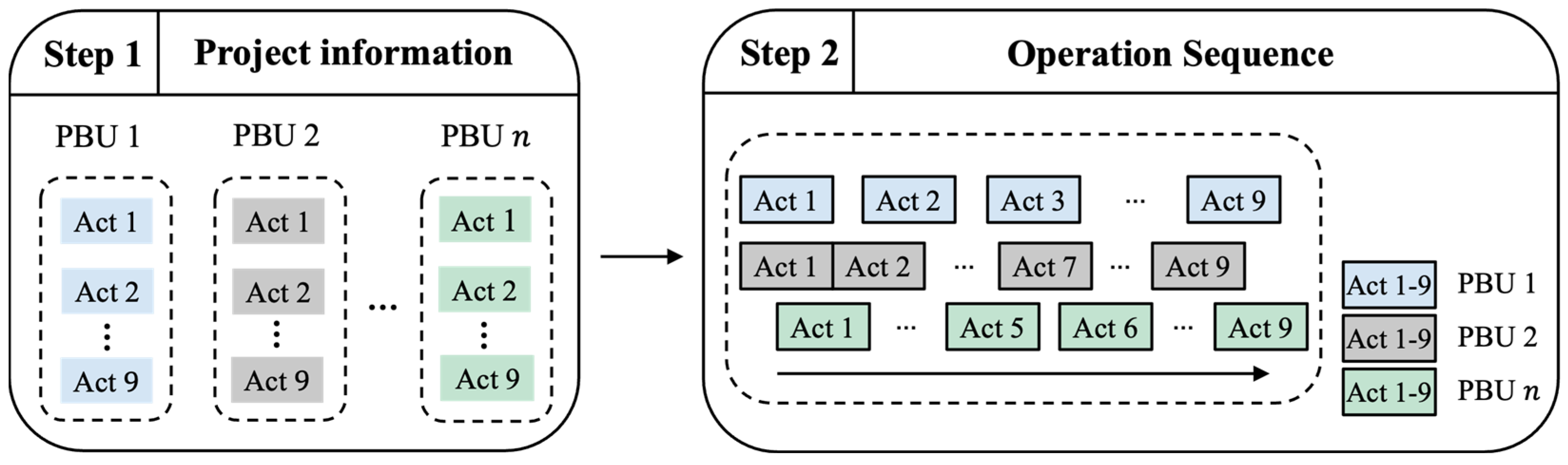
Figure 1 presents the proposed optimization framework for PBU production scheduling. In Step 1, each PBU is conceptualized as an independent project comprising nine sequential activities. In Step 2, the operation sequence is established, wherein activities from different PBUs are arranged across the timeline. While the initiation of Activity 1 for each PBU may occur either concurrently or at staggered times, the internal sequence of activities within each PBU must strictly adhere to the order from Activity 1 to Activity 9. Furthermore, the commencement of each subsequent activity may either immediately follow the completion of the preceding activity or incorporate a buffer time to accommodate resource availability and operational flexibility.

In Singapore, PBU products are mainly bathrooms and kitchens for residential developments, particularly in high-rise public and private housing projects [33]. These units are fully pre-fitted with finishes, sanitary wares, plumbing, and electrical services before being transported to construction sites for installation. The use of PBUs significantly reduces on-site labour requirements, shortens construction timelines, and improves overall workmanship quality [33].

The typical fit-out process for a bathroom PBU can be divided into nine sequential operational stages, as summarized in Figure 2. Each activity may be executed in different modes, where different resource allocations result in varying durations. Based on the processing times listed in

Table 1. List of activities for PBU with duration and resource needed for each mode.

Sequence	Activity	Mode	Duration (Days)	Resource (People)
1	The production of raw materials for the frame: cement and steel bars	1	1	6
		2	2	4
		3	4	2
2	The pouring and manufacturing of the frame	1	3	8
		2	4	6
		3	6	4
3	Assembly of the frame: welding	1	2	6
		2	3	4
		3	4	3
4	The installation of HVAC pipes	1	1	3
		2	3	2
5	Interior decoration: wall painting, furniture installation, floor finishing	1	2	3
		2	3	2
6	Exterior decoration: installation of windows and doors	1	2	3
		2	3	2
7	Installation of lighting and sanitation accessories	1	2	3
		2	3	2
8	Quality control and testing	1	1	4
		2	2	2
		3	4	1
9	Packaging and preparation for delivery	1	1	2

, the estimated total throughput time required to complete one PBU is approximately fourteen days.

When a batch of PBUs is ordered—typically consisting of multiple identical units—it becomes critical to determine an efficient scheduling plan that enables simultaneous delivery. Although each PBU follows the same sequential fit-out process, constraints such as limited resources, varying execution modes, and workspace availability complicate the scheduling task. Therefore, the key challenge lies in assigning activity sequences and resource allocations in such a way that all PBUs in the batch can be completed within the desired time frame. Optimizing this schedule is essential to minimize production time, balance resource usage, and meet project deadlines effectively.

4. Mathematical Model of MRCMPSP

This section formulates the MRCMPSP as a mixed-integer linear programming (MILP) model. All relevant notations and parameters used in the formulation are summarized in

Table 2. Notation lists.

Indices
$i$	$\mathrm{PBU} \mathrm{index}, i=1,\dots ,n$$. \mathrm{Usually}, \mathrm{PBUs} \mathrm{come} \mathrm{in} \mathrm{batches} \mathrm{of} \mathrm{units}, \mathrm{e}.\mathrm{g}., n=5, n=10$.
$j,j^{\prime }$	$\mathrm{activity} \mathrm{index}, j,j\prime =1,\dots ,J$$. \mathrm{In} \mathrm{our} \mathrm{real}-\mathrm{life} \mathrm{scenario}, J=9$.
$r$	$\mathrm{resource} \mathrm{type}, r=1,\dots ,R$$. \mathrm{In} \mathrm{our} \mathrm{case} r=1$, only human resource, which is renewable after usage.
$m$	$\mathrm{mode} \mathrm{index}, m=1,\dots ,{\mathit{M}}_{i,j}$$, \mathrm{where} {\mathit{M}}_{i,j}$ $\mathrm{is} \mathrm{the} \mathrm{number} \mathrm{of} \mathrm{modes} \mathrm{for} \mathrm{activity} j$ $\mathrm{of} \mathrm{project} i$. Dummy activity only has one mode, requiring no resources.
$t$	$\mathrm{execution} \mathrm{time} \mathrm{index}, t=1,\dots ,T$.
Parameters
$a_{i,j}$	$j$-th activity in project $i,$0 denotes a “start” dummy activity and $J+1$ denotes a “finish” dummy activity.
$d_{i,j,m}$	duration of $a_{i,j}$ in mode $m$.
$U_{i,j,m,r}$	amount of type $r$ resource required by activity $a_{i,j}$ executed in mode $m$.
$P_{r,t}$	$\mathrm{available} \mathrm{amount} \mathrm{of} \mathrm{resource} r$$\mathrm{at} \mathrm{time} t$.
${EF}_{i,j}$	$\mathrm{earliest} \mathrm{possible} \mathrm{finish} \mathrm{time} \mathrm{of} \mathrm{activity} a_{i,j}$.
${LF}_{i,j}$	$\mathrm{latest} \mathrm{possible} \mathrm{finish} \mathrm{time} \mathrm{of} \mathrm{activity} a_{i,j}$.
Decision variables
$x_{i,j,m,t}$	1 if $a_{i,j}$ is executed in mode m and finishes at time t; 0, otherwise.
$y_{i,j,m}$	1 if $a_{i,j}$ is executed in mode $m$; 0, otherwise.
$\mathit{P}\mathit{O}\mathit{R}$	project set
${\mathit{A}\mathit{C}\mathit{T}}_{\mathit{i}}$	activity set of project $i$
${\mathit{S}\mathit{U}\mathit{C}}_{\mathit{i},\mathit{j}}$	succession activities of activity $j$ in project $i$
$\mathit{R}\mathit{E}\mathit{S}$	resource type set
$\mathit{T}\mathit{I}\mathit{M}$	possible time space

.

Minimize:

$$\underset{i\in \mathit{POR}}{\max }\left\{{\sum }_{t={EF}_{i,J+1}}^{{LF}_{i,J+1}}t·x_{i,J+\mathrm{1,1},t}\right\}$$

(1)

Subject to:

$${\sum }_{m=1}^{M_{i,j}}{\sum }_{t={EF}_{i,j}}^{{LF}_{i,j}}{x}_{i,j,m,t}=1, \forall i\in \mathit{P}\mathit{O}\mathit{R}, \forall j\in {\mathit{A}\mathit{C}\mathit{T}}_{\mathit{i}}$$

(2)

$${\sum }_{m=1}^{M_{i,j}}{y}_{i,j,m}=1, \forall i\in \mathit{P}\mathit{O}\mathit{R}, \forall j\in {\mathit{A}\mathit{C}\mathit{T}}_{\mathit{i}}$$

(3)

$${\sum }_{t={EF}_{i,j}}^{{LF}_{i,j}}{x}_{i,j,m,t}=y_{i,j,m}, \forall i\in \mathit{P}\mathit{O}\mathit{R}, \forall j\in {\mathit{A}\mathit{C}\mathit{T}}_{\mathit{i}}, \forall m\in {\mathit{M}}_{\mathit{i},\mathit{j}}$$

(4)

$$\begin{gathered} {\sum }_{m=1}^{M_{i,j^{\prime }}}{\sum }_{t={EF}_{i,j^{\prime }}}^{{LF}_{i,j^{\prime }}}\left(t-d_{i,j^{\prime },m}\right)·x_{i,j^{\prime },m,t}\ge {\sum }_{m=1}^{M_{i,j}}{\sum }_{t={EF}_{i,j}}^{{LF}_{i,j}}t·x_{i,j,m,t} \\ \forall i\in \mathit{P}\mathit{O}\mathit{R},\forall j\in {\mathit{A}\mathit{C}\mathit{T}}_{\mathit{i}}, \forall j^{\prime }\in {\mathit{S}\mathit{U}\mathit{C}}_{\mathit{i},\mathit{j}} \end{gathered}$$

(5)

$$\begin{gathered} {\sum }_{i=1}^n{\sum }_{j=1}^J{\sum }_{m=1}^{M_{i,j}}{U}_{i,j,m,r}·{\sum }_{q=t}^{t+d_{i,j,m}-1}{x}_{i,j,m,q}\le P_{r,t} \\ \forall i\in \mathit{P}\mathit{O}\mathit{R},\forall j\in {\mathit{A}\mathit{C}\mathit{T}}_{\mathit{i}},\forall r\in \mathit{R}\mathit{E}\mathit{S},\forall t\in \mathit{T}\mathit{I}\mathit{M}, \end{gathered}$$

(6)

The objective function (1) minimizes the maximum completion time among all PBUs in the portfolio. This is achieved by evaluating the finishing time of the dummy “finish” activity $J+1$ in each project $i\in \mathit{P}\mathit{O}\mathit{R}$. The variables $x_{i,J+\mathrm{1,1},t}$ capture the execution mode and finish time of this terminal dummy activity. ${EF}_{i,j}$ and ${LF}_{i,j}$ can be calculated by performing a traditional forward-backward pass.

Constraint (2) ensures that each activity $a_{i,j}$ is scheduled exactly once across all modes and feasible finish times. Constraint (3) enforces that only one mode is selected for each activity. Constraint (4) links the binary variable $y_{i,j,m}$ to the execution variable $x_{i,j,m,t}$, ensuring that the activity is only executed in the selected mode. Constraint (5) encodes the precedence relationships: for any activity $a_{i,j}$ all its successors $j^{\prime }\in {\mathit{S}\mathit{U}\mathit{C}}_{i,j}$ can only start after the current activity has completed. This is enforced using the activity’s duration and finish time. Constraint (6) ensures the availability of resources at any time $t$. For each renewable resource type $r$, the sum of resource usage across all activities that are active at time $t$ must not exceed the available amount $P_{r,t}$.

5. Differential Evolution Algorithms for MRCMPSP

5.1. Standard Differential Evolution Algorithm

Differential Evolution (DE) is a population-based evolutionary algorithm widely used for global optimization problems with continuous variables. It evolves a population of candidate solutions by applying three primary operators: mutation, crossover, and selection. Its simplicity and strong global search capability make it a popular choice for solving complex scheduling and combinatorial problems when suitably adapted.

Each individual in the DE population is represented as a real-valued vector. Let ${\overrightarrow{x}}_l{\mathbb{R}}^D$ denote the solution vector of individual $l$ in a population of size $N$, where $D$ is the dimensionality of the problem. DE initializes this population randomly within the feasible bounds of each variable.

In each generation, a mutant vector ${\overrightarrow{v}}_l$ is generated for each individual $l$ by adding the weighted difference of two randomly selected population vectors to a third:

$${\overrightarrow{v}}_l={\overrightarrow{x}}_a+F·({\overrightarrow{x}}_b-{\overrightarrow{x}}_c)$$

(7)

Here, ${\overrightarrow{x}}_a$, ${\overrightarrow{x}}_b$, ${\overrightarrow{x}}_c$ are distinct individuals randomly selected from the current population and $F\in [0.4, 1.0]$ is a scaling factor controlling the amplification of the differential variation.

DE applies binomial crossover to generate a trial vector ${\overrightarrow{u}}_l$ by mixing the mutant vector ${\overrightarrow{v}}_l$ with the current individual ${\overrightarrow{x}}_l$. Each dimension $j$ of the trial vector is selected according to the rule:

$${\overrightarrow{u}}_{l,j}\left\{\begin{array}{c}{\overrightarrow{v}}_{l,j}\\ {\overrightarrow{x}}_{l,j} \end{array}{\displaystyle \genfrac{}{}{0pt}{}{ \mathrm{i}\mathrm{f} {rand}_j<CR \mathrm{o}\mathrm{r} j=j_{rand}}{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}}\right.$$

(8)

where ${rand}_j~U(0, 1)$ is a uniformly distributed random number and $j_{rand}$ is a randomly selected dimension to ensure that at least one component is inherited from the mutant vector. $CR\in [0.1, 0.95]$ is the crossover probability.

After crossover, DE evaluates the fitness of the trial vector. If it is better (lower, in minimization problems) than the current individual, the trial vector replaces it in the next generation:

$${\overrightarrow{x}}_l^{(t+1)}\left\{\begin{array}{c}{\overrightarrow{u}}_l\\ {\overrightarrow{x}}_l \end{array}{\displaystyle \genfrac{}{}{0pt}{}{ \mathrm{i}\mathrm{f} f\left({\overrightarrow{u}}_l\right)<f\left({\overrightarrow{x}}_l\right) }{\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}}}\right.$$

(9)

Here, $f\left(·\right)$ is the fitness function that evaluates the quality of the generated schedule. The fitness is computed based on the decoded sequence and mode assignment using the Parallel Schedule Generation Scheme described in Section 5.3. This greedy selection mechanism ensures that the population either improves or retains the best solutions over time.

5.2. Learning-Enhanced Differential Evolution (LEDE) Algorithm

To address the complexities of the MRCMPSP in industrial prefabrication settings, this study proposes a Learning-Enhanced Differential Evolution (LEDE) algorithm that incorporates several adaptive mechanisms and co-evolution strategies. Unlike the standard DE algorithm, which evolves flat solution vectors using fixed strategies and parameters, the LEDE framework integrates domain-specific problem representations, dynamic strategy selection, adaptive parameter control, and self-diversification techniques to improve flexibility and robustness across diverse scheduling scenarios.

5.2.1. Problem Representation

The solution is encoded using two key components: the activity sequence and the mode assignment for each activity, both represented in continuous (floating-point) form (Figure 3). This co-evolutionary encoding enables DE to optimize both execution order and mode decisions simultaneously.

Sequence Encoding: The activity sequence is represented as a real-valued vector, with each element corresponding to an activity. Sorting the values in ascending order yields the activity execution order while naturally respecting intra-project precedence constraints.

Mode Encoding: Mode selection is encoded via mode score vectors. For each activity $a_{i,j}$ with $M_{i,j}$ feasible modes, a sub-vector of length $M_{i,j}$ stores continuous mode scores ${ms}_{i,j,m}$. The selected mode $m_{i,j}$ is determined using the argmax rule:

$$m_{i,j}=\underset{m\in \{1,\dots ,M_{i,j}\}}{\mathit{argmax}}{ms}_{i,j,m}$$

(10)

This approach allows smooth optimization over discrete mode choices without explicit enumeration, improving scalability and stability.

A parallel generation scheme (SGS) is used to construct a feasible schedule from the decoded sequence and mode assignment, ensuring constraint satisfaction during fitness evaluation.

5.2.2. Search Enhancements

To improve search effectiveness, LEDE incorporates several enhancement mechanisms into the standard DE process:

Adaptive Parameter Control: The scaling factor $F$ and crossover rate $CR$ are dynamically adjusted based on the generation stage. Early stages use higher diversity (larger $F$, smaller $CR$), while later stages adopt more exploitative settings to refine solutions.

Strategy Switching: Rather than relying on a single mutation strategy, LEDE switches among multiple strategies throughout the optimization process. It begins with DE/rand/1 for exploration and gradually transitions to exploitative strategies such as DE/best/1, DE/rand-to-best/1, and DE/current-to-best/1, depending on the search phase and performance trends.

Elitism: To prevent loss of high-quality solutions, LEDE retains a subset of top-performing individuals across generations, ensuring that the search process remains guided by strong candidates.

Stagnation Handling: If the best fitness value does not improve over a predefined number of generations, LEDE introduces a controlled perturbation to the best solution and reinitializes a portion of the population. This encourages escape from local optima without full randomization.

Rank-Based Crossover Adaptation: LEDE adjusts the crossover probability $CR$ for each individual based on its relative fitness rank. Poorer-performing individuals receive higher $CR$ values to encourage exploration, while top individuals are evolved more conservatively to maintain stability.

These mechanisms collectively allow LEDE to maintain diversity, adapt to search conditions, and avoid premature convergence, making it more robust than the classical DE algorithm for complex, real-world scheduling problems like the MRCMPSP.

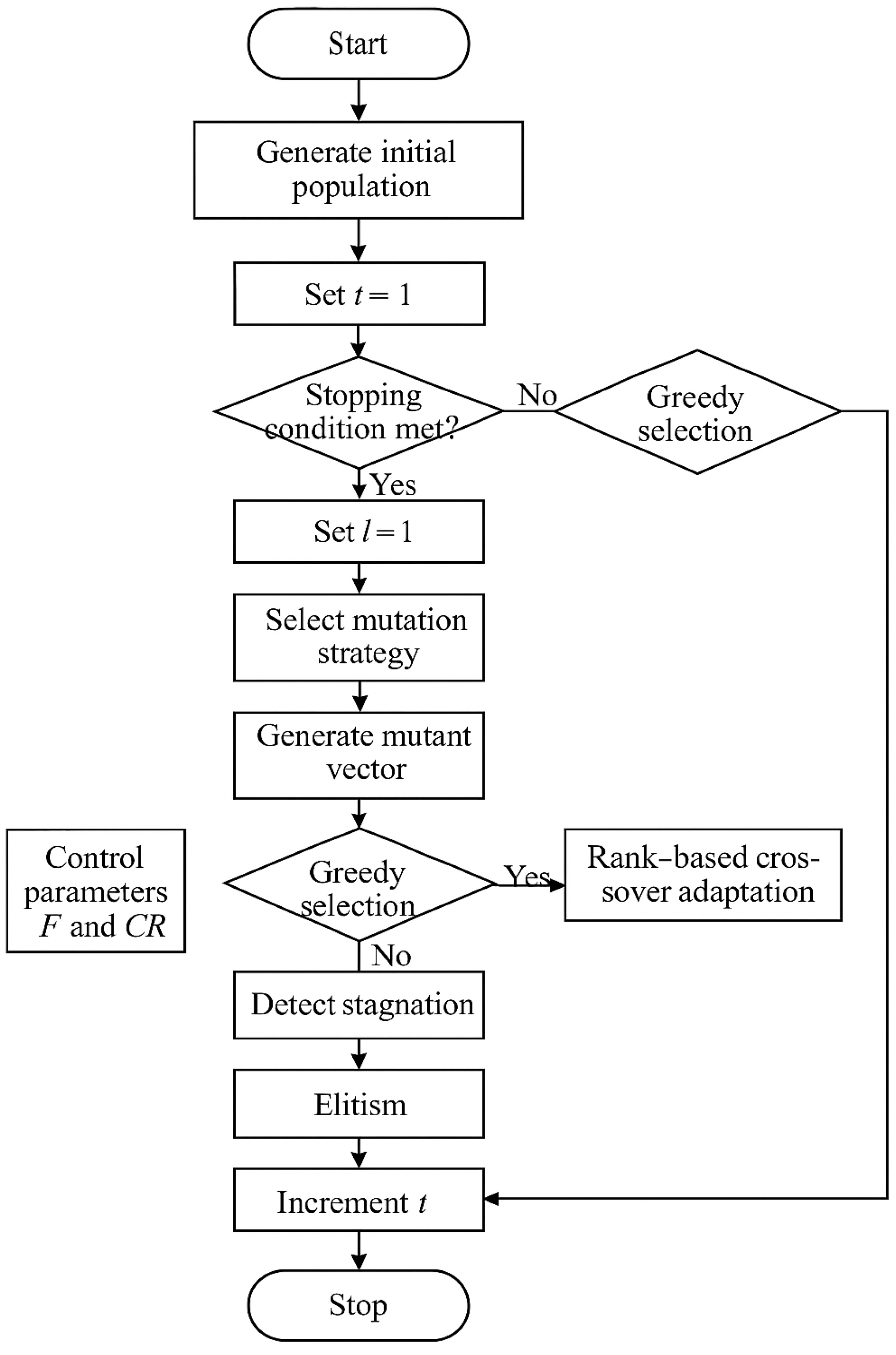
The entire LEDE process, including co-evolution of sequence and mode vectors, adaptive parameter control, strategy switching, elitism, stagnation handling, and rank-based crossover adaptation, is summarized in the flowchart presented in Figure 4. This figure illustrates the iterative update cycle for each individual and highlights the decision points that distinguish LEDE from standard DE.

5.2.3. Initial Population

In metaheuristic optimization, the initial population significantly influences early convergence behaviour. In this study, the initial population is partially generated using a diverse set of priority rules (PRs) such as minimum slack, shortest processing time, and most successors. These rules create heuristically informed initial individuals that provide a strong foundation for exploration. The remaining individuals in the population are initialized randomly to ensure diversity and prevent premature convergence [34].

5.2.4. Local Improvement: Backward–Forward Adjustment

To enhance the quality and robustness of generated schedules, a backward-forward heuristic is employed during the fitness evaluation phase. This two-phase local improvement strategy begins with a backward pass, which schedules each activity as late as possible within its feasible time window without violating precedence or resource constraints. This delay allows for greater flexibility in absorbing disruptions and optimizing makespan robustness. Subsequently, a forward pass is executed, rescheduling the activities based on their updated start times to improve resource utilization and minimize idle time. By smoothing the resource profiles and tightening the schedule structure, this heuristic effectively refines the overall solution, particularly in large-scale multi-project settings where shared resource contention is significant. This method has been shown to improve schedule stability and is well-supported in the literature [22,23].

5.3. Parallel Schedule Generation Scheme (SGS)

The parallel SGS operates by incrementing time and iteratively scheduling the first feasible activity based on precedence and resources, following the defined activity sequence order. When there are no activities that can be scheduled at that time, the time is incremented, and the procedure repeats until all activities are scheduled.

5.4. Pseudo Codes for the LEDE

The pseudo codes for the proposed algorithm are given as follows. Algorithm 1 is for the LEDE and Algorithm 2 is for back-forward heuristics.

Algorithm 1. LEDE

Input:  – Activity durations  – Precedence constraints between activities  – Resource availability Output:  – Best activity sequence  – Best mode selection Define the maximum number of iterations ${Max}_{iter}$ (a) Initialize mode selection probability (b) Initialize the population of individuals ${\stackrel{⃑}{x}}_l$ for $l$ = $1,2,\dots ,n$ (c) Initialize mode score vectors for each individual (d) Initialize best solution ${\stackrel{⃑}{x}}^{*}$, best fitness = $\infty$ While $t<{Max}_{iter}$ do: For each individual $l=1 to n$ (a) Adapt $F$ and $CR$ based on iteration $t$ (b) Select mutation strategy based on phase - Early: DE/rand/1 - Mid: DE/best/1 or DE/rand-to-best/1 - Late: DE/current-to-best/1 (c) Generate mutant vector ${\overrightarrow{v}}_l$ using the selected strategy (d) Apply binomial crossover with adaptive $CR$ based on fitness rank (e) Form trial vector ${\overrightarrow{u}}_l$ convert to sequence and modes (f) Evaluate fitness of ${\overrightarrow{u}}_l$ (g) Apply greedy selection: $\mathrm{i}\mathrm{f}f\left({\overrightarrow{u}}_l\right)<f\left({\overrightarrow{x}}_l\right)$, then ${\overrightarrow{x}}_l={\overrightarrow{u}}_l$ (h) Update best solution if improved If stagnation is detected (no improvement for $k$ iterations): (a) Slightly perturb the best individual (b) Re-evaluate and update if improved (c) If prolonged stagnation, reinitialize 30% of worst individuals Apply elitism: retain top-performing individuals Construct final schedule using parallel schedule generation scheme (SGS) Increment iteration counter $t=t+1$ Return the best individual ${\stackrel{⃑}{x}}^{*}$ as the optimal schedule with associated activity sequence and mode assignments.

Algorithm 2. Backward–forward heuristic

Input:  – Activity durations $d_{i,j,m}$  – Precedence constraints between activities $a_{i,j}$  – Resource availability $P_{r,t}$  – Project deadline $T_{i,J}$ Output:  – Optimized schedule with start and finish times Initialize Parameters For each activity $(i,j)$, initialize:  (a) Earliest Start Time (EST): ${ES}_{i,j}$  (b) Earliest Finish Time (EFT): ${EF}_{i,j}$  (c) Latest Start Time (LST): ${LS}_{i,j}$  (d) Latest Finish Time (LFT): ${LF}_{i,j}$ 2. Backward Pass (Calculate LST and LFT) (a) Set the LFT of the final activity to the project deadline: ${LF}_{i,J}=T_{i,J}$ (b) Process activities in reverse order (from last to first) Compute ${LS}_{i,j}={LF}_{i,j}-d_{i,j,m}$ Update LFT of predecessor tasks: ${LF}_{i,j^{\prime }}$ = min $\left({LS}_{i,j}\right)$ for all successors ($i,j$) 3. Forward Pass (Calculate EST and EFT with Resource Constraints) (a) Set the EST of the first activity to 0: ${EF}_{i,0}$ = 0 (b) Process activities in order (from first to last): Compute: ${EF}_{i,j}={ES}_{i,j}+d_{i,j,m}$ If required resources $U_{i,j,m,r}$ exceed available $P_{r,t}$ at ${ES}_{i,j}$, delay the activity Adjust ${ES}_{i,j}$ based on predecessor constraints and resource limits

6. Experimental Cases

This section describes the computational experiments conducted to evaluate the performance of the proposed co-evolved multi-strategy Differential Evolution (DE) algorithm. The DE framework incorporates adaptive parameter control, strategy switching, elitism, stagnation handling, and rank-based crossover adaptation to address the complexity of the Multi-Mode Resource-Constrained Multi-Project Scheduling Problem (MRCMPSP). The mathematical formulation and all DE-based procedures, including serial schedule generation and backward-forward improvement, were implemented in Python 3.9. Experiments were executed on a machine equipped with an Apple MacBook Pro featuring an M4 Pro 14-core processor and 64 GB of RAM. The implementation leverages vectorized operations and efficient data structures to ensure computational scalability across varied scheduling instances.

6.1. Test Instances

The dataset used in this study was compiled through interviews with PBU manufacturers in Singapore. To reflect real-world production scenarios, scheduling instances were generated in batch sizes of 3, 6, 9, 12, and 15 PBUs. For each batch, multiple instances were created by replicating activity structures and adjusting precedence relationships accordingly.

To evaluate scalability, additional large-scale instances with 50 and 100 PBUs were tested, simulating workloads typical of full-floor or multi-floor modular projects. These larger batches were evaluated under a fixed workforce of 25 workers to reflect resource-constrained conditions.

The experiments also assessed resource adaptability by varying labour availability from 20 to 40 workers across selected batch sizes.

This test design supports a comprehensive evaluation of the algorithm’s effectiveness under diverse batch sizes and resource conditions.

6.2. Parameter Tuning

The proposed algorithm involves several hyperparameters that must be properly tuned to achieve optimal performance. To calibrate these parameters, a preliminary experiment was conducted. Exhaustively evaluating all possible parameter combinations would result in an impractically large number of experiments. Therefore, the Taguchi method was employed to efficiently identify suitable parameter settings. For a detailed explanation of the Taguchi method, readers are referred to Sharifi et al. [35].

The Taguchi approach enables a significant reduction in the number of experiments while still yielding robust conclusions. To assess the performance of each parameter configuration, the signal-to-noise (S/N) ratio is used as the evaluation criterion. In this study, the S/N ratio for the “smaller-the-better” objective (i.e., minimizing project completion time) is computed using the following formula:

$${\displaystyle \frac{S}{N}}=-10·{\log }_{10}\left[{\displaystyle \frac{1}{n_{exp}}}{\sum }_{i=1}^n{y}_i^2\right]$$

(11)

where $n_{exp}$ represents the number of experiments and $y_i$ is the final fitness value (i.e., the total project completion time) obtained in the $i$-th run. A higher S/N ratio indicates a more stable and preferable parameter setting, as it reflects both high performance and low variability.

Datasets containing 3, 6, 9, 12, and 15 PBUs were evaluated under a fixed workforce of 25 workers.

Table 3. Levels of parameters.

Parameter	Description	Levels
		1	2	3
𝒜	DE population size	10	20	30
$F$	DE scaling factor	0.5	0.6	0.7
$CR$	DE Crossover rate	0.3	0.6	0.9

summarizes the levels tested for each parameter. Three parameters were considered, each with three levels, leading to 27 possible combinations. However, by applying the Taguchi orthogonal array design, the number of required experiments was reduced to 9.

The results of these experiments are presented in

Table 4. Results of Taguchi experimental arrays.

Experiment	𝒜	$\mathit{F}$	$\mathit{C}\mathit{R}$	S/N
1	10	0.5	0.3	−32.30
2	10	0.6	0.6	−31.70
3	10	0.7	0.9	−31.41
4	20	0.5	0.6	−31.18
5	20	0.6	0.9	−30.89
6	20	0.7	0.3	−32.57
7	30	0.5	0.9	−30.85
8	30	0.6	0.3	−32.19
9	30	0.7	0.6	−31.09
Maximum	30	0.5	0.9	−30.85

. Based on the analysis, with a population size of 30, DE scaling factor $F=0.5$, and DE crossover rate parameter $CR=0.9$, demonstrated the best performance. Consequently, these settings were adopted for all subsequent experiments.

6.3. Comparative Evaluation

To evaluate the effectiveness and robustness of the proposed Learning-Enhanced Differential Evolution (LEDE) algorithm, a comparative study was conducted against two baseline methods: a standard Differential Evolution (DE) algorithm and a Genetic Algorithm (GA), both of which are commonly employed in resource-constrained project scheduling literature.

The comparison was conducted using three PBU projects and a fixed labour resource of 25 workers. All algorithms—LEDE, standard DE, and GA—were run for 100 iterations with population size of 30 and schedule evaluation performed using the parallel schedule generation scheme (SGS).

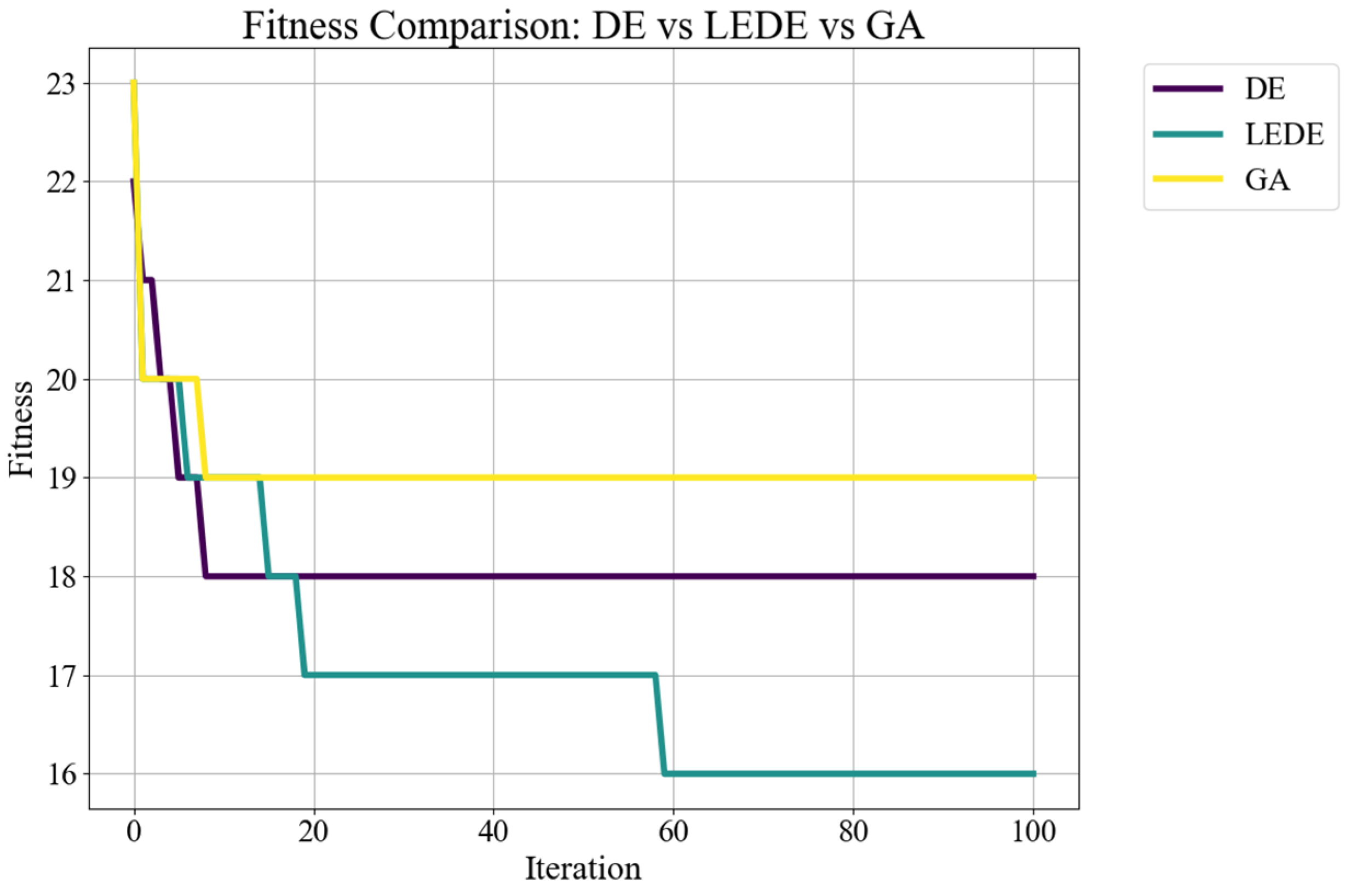
Figure 5 presents the fitness convergence curves of DE, LEDE, and GA over the 100-iteration horizon. As shown, the LEDE algorithm consistently outperforms both DE and GA in terms of final solution quality. LEDE achieves a lower final fitness value and converges faster toward high-quality solutions.

Genetic Algorithm (GA) stagnates early and fails to escape local optima, yielding the highest makespan among the three.

Standard DE shows moderate performance, improving over GA but exhibiting limited refinement capacity due to the absence of adaptive search control.

LEDE demonstrates superior performance by achieving the lowest final fitness among all methods. This advantage is driven by its adaptive parameter control, dynamic strategy switching, and selective reinitialization, which collectively enhance search effectiveness while maintaining a balance between exploration and exploitation.

These results confirm the robustness and effectiveness of the proposed LEDE framework in handling complex, multi-mode, multi-project scheduling challenges. The comparative performance supports the value of integrating learning-inspired enhancements within metaheuristic scheduling solutions.

6.4. Computational Experiments

6.4.1. Convergence Tests

To investigate the convergence characteristics of the proposed co-evolved DE-based multi-strategy algorithm, a series of experiments were performed using datasets comprising different batch sizes of prefabricated bathroom units (PBUs): specifically, batches of 3, 6, 9, 12, and 15 units. Each configuration was evaluated under a consistent parameter setting: a population size of 30, scaling factor $F=0.5$, and crossover rate $CR=0.9$, as determined in the previous tuning section. The convergence curves are shown in Figure 5.

As illustrated in Figure 6, the fitness values exhibit a steep decline in the early iterations for all batch sizes, indicating rapid initial convergence. This is followed by a gradual stabilization phase, where improvements taper off, suggesting that the algorithm quickly locates a near-optimal region in the solution space.

It is evident that smaller batches (e.g., copies = 3 and copies = 6) achieve lower objective function values and faster convergence. In contrast, larger batches (e.g., copies = 12 and copies = 15) exhibit higher final fitness values and slower convergence, reflecting the increased complexity and computational challenge associated with scaling up the problem size.

Despite this, the proposed algorithm maintains consistent convergence behaviour across all batch sizes, underscoring its robustness and adaptability to varying problem scales.

6.4.2. Scalability Under Different Resource Quantities

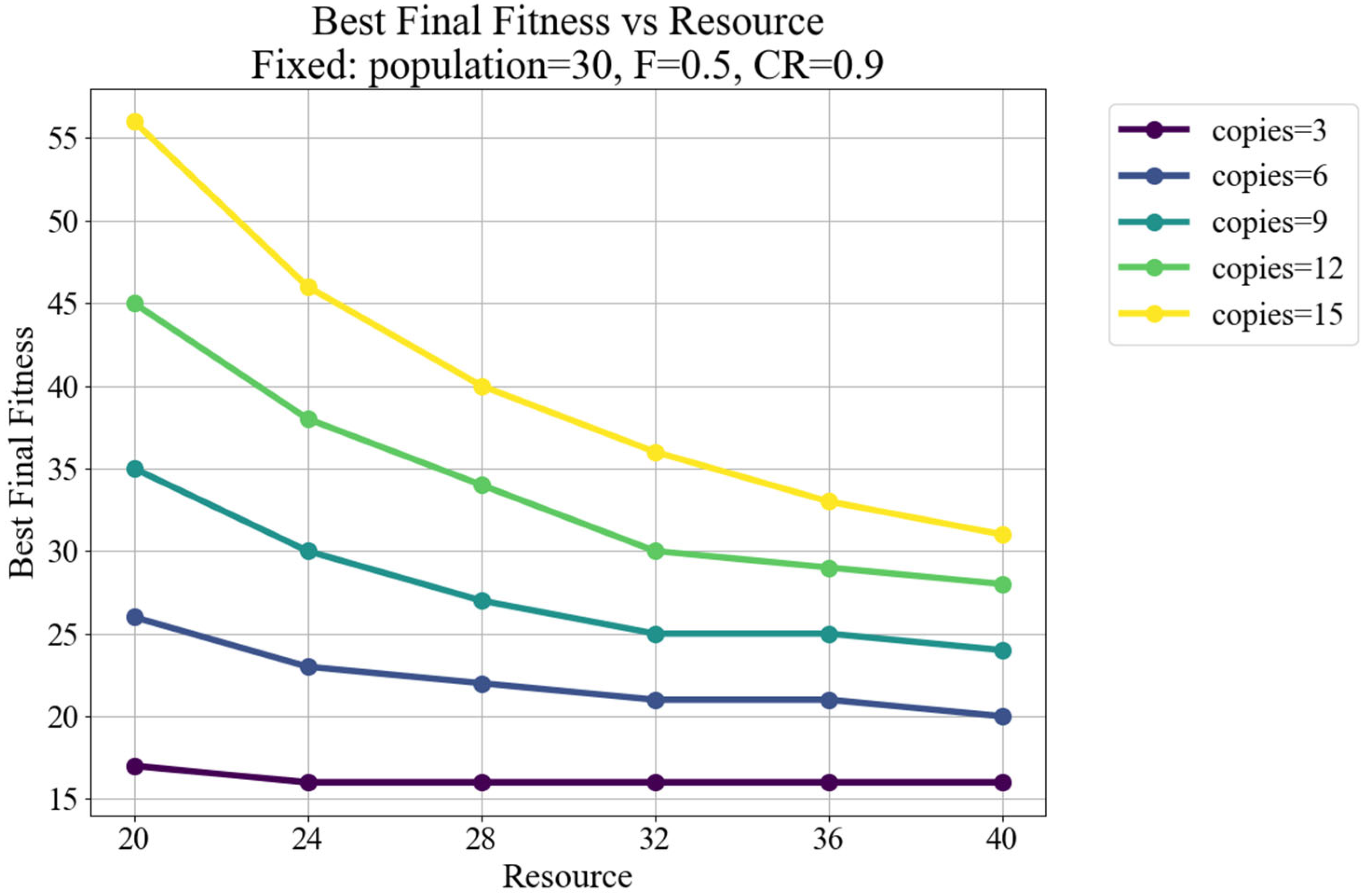
To further evaluate the scalability and adaptability of the proposed algorithm, additional experiments were conducted to investigate the impact of resource availability on scheduling performance. Figure 7 illustrates the best final fitness values obtained under varying resource levels, ranging from 20 to 40 units, across different batch sizes of PBUs (copies = 3, 6, 9, 12, 15), while keeping other parameters fixed (population = 30, $F=0.5$, $CR=0.9$).

As expected, increasing the available resources consistently led to improved (lower) final fitness values across all scenarios. This reflects the fact that higher resource availability reduces competition among activities, thereby facilitating more efficient scheduling and enabling the algorithm to find better solutions.

The benefit of resource increase is more pronounced in larger batch sizes (e.g., copies = 12 and 15). In these cases, the final fitness shows a steep decline as resources increase from 20 to 30, followed by a plateau beyond 30, indicating diminishing returns. This behaviour suggests that while initial resource increases alleviate critical constraints, the marginal utility of additional resources decreases once a certain threshold is reached.

Conversely, for smaller batch sizes (e.g., copies = 3 and 6), the final fitness values are already low, and the performance remains relatively stable with increasing resources. This indicates that smaller instances are less resource-intensive and can be efficiently handled even under constrained conditions.

Overall, the results demonstrate that the algorithm is sensitive to resource constraints and can leverage additional resources effectively, particularly in more complex, larger-scale scheduling scenarios. This highlights its suitability for dynamic production environments where resource availability and incoming workloads may fluctuate unpredictably.

In such settings, the ability to adjust scheduling plans in response to resource variations becomes critical. The algorithm’s consistent performance across different batch sizes and resource levels indicates a strong capacity to adapt to changing operational conditions. Moreover, the observed diminishing returns beyond a certain resource threshold suggest that the method can support decision-making for optimal resource allocation—enabling manufacturers to strike a balance between resource investment and scheduling efficiency. These findings reinforce the algorithm’s practical value for real-world prefabricated construction applications, where constrained capacity and delivery precision are common challenges.

6.4.3. Scalability to Bigger Batch Size

To further assess the scalability of the proposed LEDE algorithm under realistic industrial workloads, additional experiments were conducted using batch sizes of 50 and 100 PBUs. These larger scenarios represent production scales typical of full-floor or multi-floor modular projects in prefabricated construction. A constant workforce of 25 workers was maintained across both cases to simulate resource-constrained conditions.

The results, summarized in

Table 5. Results for optimization on large batch sizes.

Batch Size	Resource (Workers)	Fitness
50	25	146
100	25	291

, demonstrate that the LEDE algorithm remains effective and computationally tractable even as problem size increases significantly. Both experiments were completed within 1 h on the test machine (Apple M4 Pro, 64 GB RAM). These findings confirm the algorithm’s capacity to handle large, resource-constrained scheduling instances while maintaining practical runtime and solution quality.

7. Conclusions

This study presents a Learning-Enhanced Differential Evolution (LEDE) framework to solve the Multi-Mode Resource-Constrained Multi-Project Scheduling Problem (MRCMPSP) in the context of Prefabricated Bathroom Unit (PBU) production. By co-evolving activity sequencing and mode selection within a unified continuous representation, the proposed method integrates adaptive parameter control, strategy switching, and selective reinitialization to improve scheduling performance under resource constraints.

Experimental results on real-world-inspired datasets demonstrated the LEDE algorithm’s strong performance across varying batch sizes and resource levels. Compared to standard DE and GA baselines, LEDE consistently achieved superior solution quality and convergence behaviour. Scalability tests further confirmed the method’s ability to handle industrial-scale instances (up to 100 PBUs) within acceptable runtime limits while maintaining high-quality scheduling outcomes. Additionally, sensitivity analysis revealed a diminishing return in performance beyond a specific resource threshold, underscoring LEDE’s utility for informed resource allocation.

Despite these strengths, the current framework is limited to deterministic, single-objective scheduling and assumes complete knowledge of project parameters and resource availability. It is also tailored to a single production environment and does not currently address stochastic disruptions, learning under uncertainty, or coordination across multiple production sites.

Future research may explore several promising directions. These include extending the model to stochastic or fuzzy scheduling frameworks, incorporating real-time feedback for adaptive control, and integrating multi-objective optimization to jointly minimize duration, cost, and disruption. In addition, coupling the LEDE engine with digital construction platforms such as Building Information Modelling (BIM) could improve implementation in real-world settings.

Moreover, the integration of vision-based monitoring tools can further enhance schedule validation and adaptive rescheduling. Advanced deep learning models such as DeepLab [36]—a semantic segmentation network for precise activity recognition—and EfficientNet [37]—a scalable and efficient convolutional neural network—offer potential for real-time progress tracking and resource monitoring on-site. Embedding these tools into a scheduling feedback loop may significantly enhance responsiveness and robustness in dynamic prefabrication environments.