Prediction of Shear Capacity of Fiber-Reinforced Polymer-Reinforced Concrete Beams Based on Machine Learning
Abstract
1. Introduction
2. Methodology
- (1)
- ANN
- (2)
- Extreme Gradient Boosting (XGBoost)
3. Dataset Description
3.1. Input and Output Variables
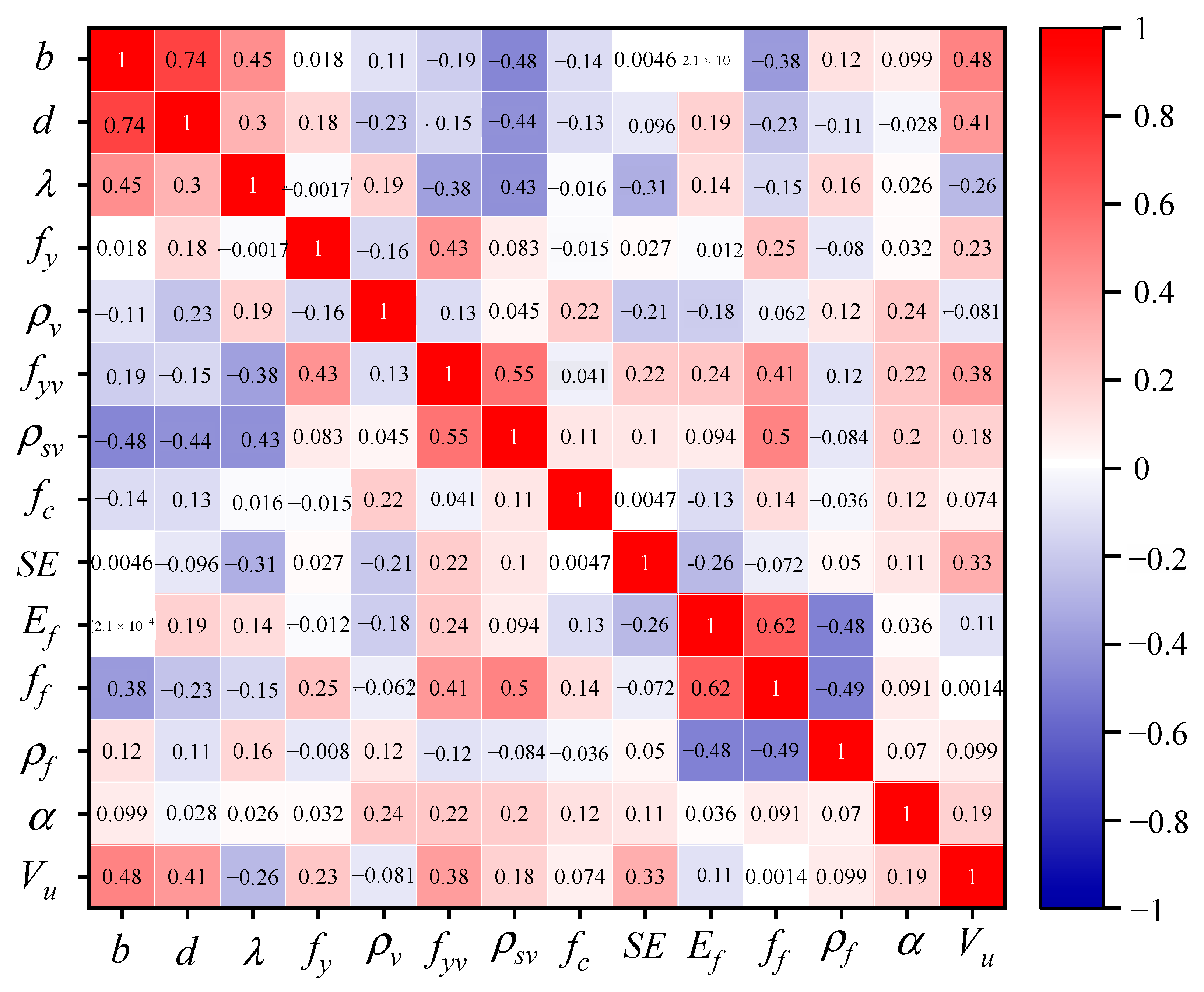
3.2. Correlation Analysis
3.3. Model Training Process
3.4. Evaluation Indicators
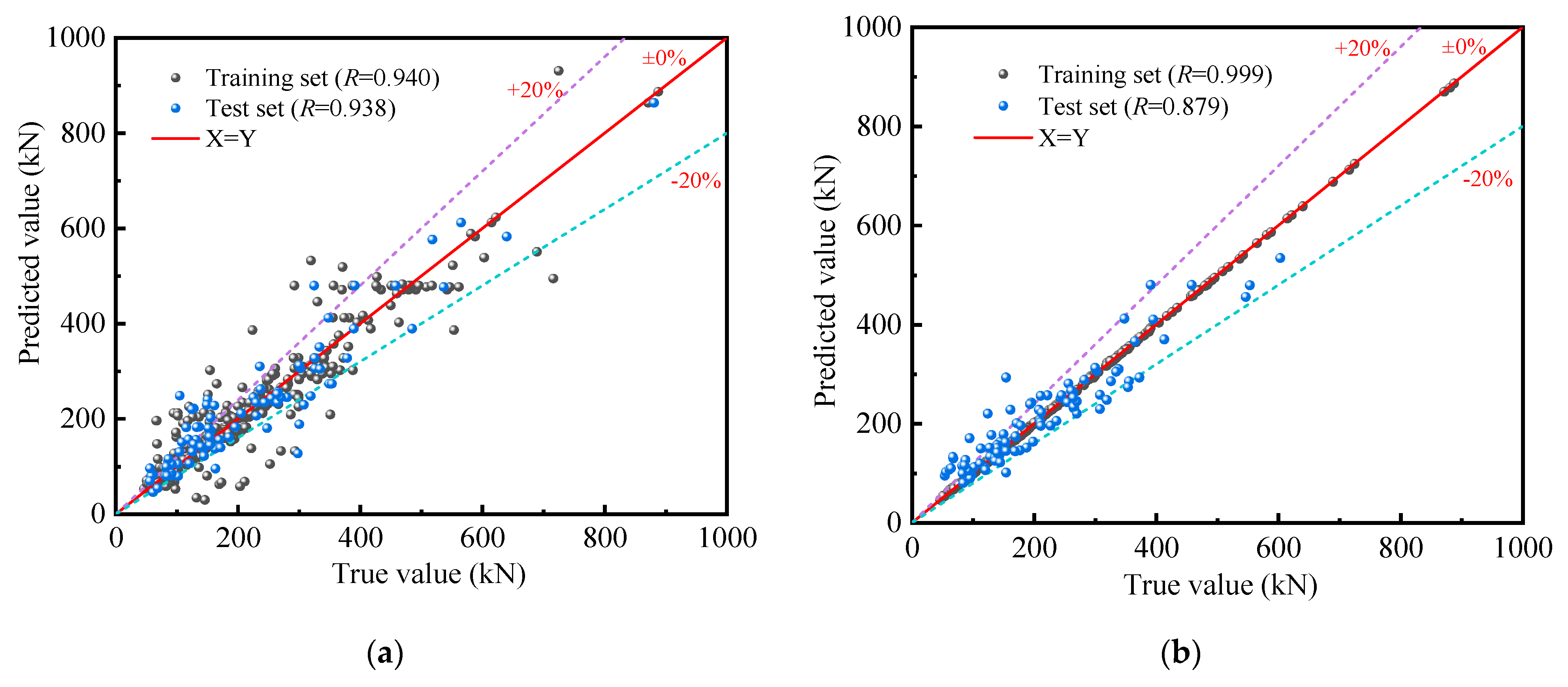
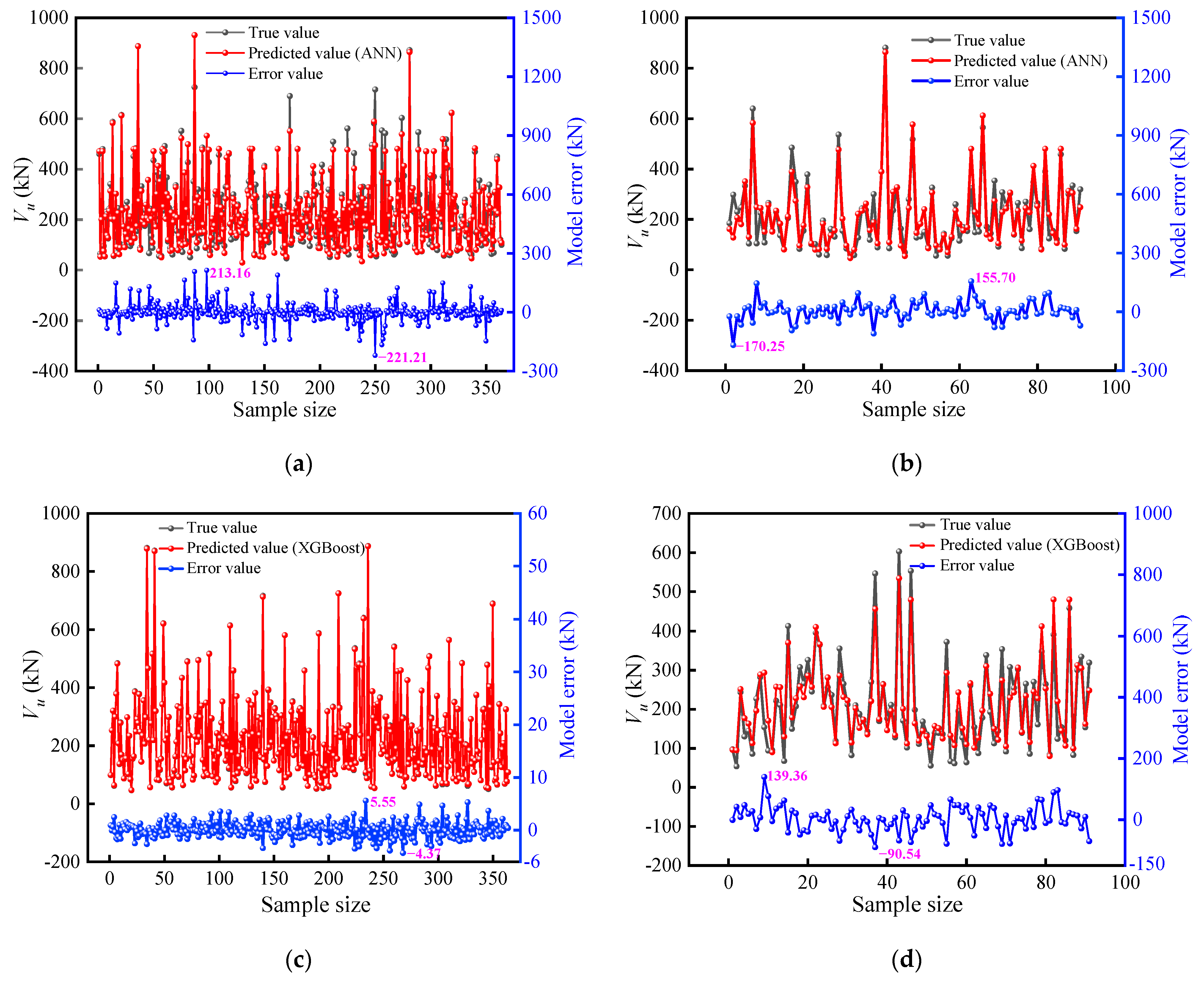
4. Model Performance
5. Comparative Analysis with Existing Design Codes
5.1. Overview of Design Code Models
| Specifications | Vcs | Vf |
|---|---|---|
| Chinese code GB 50010-2010 [95] | Without web reinforcement With web reinforcement | |
| American code ACI 318-19 [96] | ||
| European code EN 1992-1-1:2004 [97] | Without web reinforcement With web reinforcement | |
| Notation: Shear capacity coefficient of concrete. For the component under uniform load, 0.7 is taken; and for the independent beam under concentrated load, . When , 1.5 is taken; when , 3.0 is taken. The influence coefficient of cross-sectional height, . When , 800 is taken; when , 2000 is taken. The influence coefficient of longitudinal tensile steel reinforcement ratio, . is the longitudinal tensile steel reinforcement ratio. Design value of concrete axial tensile strength. Design value of stirrup tensile strength. Stirrup area configured in the same section. s Stirrup spacing along the member length direction. The reduction coefficient of shear capacity is calculated according to Table 4. When the shear span ratio is in the middle, it is calculated according to the internal interpolation method. The vertical distance from the upper end of FRP to the center of the longitudinal bar. Compressive strength of concrete cylinder. Size effect correction factor. The reduction factor related to the pasting form. For side pasting and U-pasting form, ; For the full-pasting form, . The angle between FRP and beam axis. The effective stress of FRP. The effective strain of FRP. The ultimate tensile strain of FRP. The correction factor, which is related to concrete strength, FRP bonding scheme, FRP-concrete interface bonding and FRP effective bonding length. Design value of yield strength of shear reinforcement. The strength reduction factor of shear-fractured concrete, which is calculated by . The angle between the concrete pressure bar and the longitudinal pressure bar. Considering the stress state coefficient in the compression chord. In the case of no prestress, the specification is recommended . Design value of concrete compressive strength. z The internal force arm of the cross-section, which can be approximated as . | ||
| Strip Anchoring Method | Shear Span Ra-tio | Uniform Load or Shear Span Ratio |
|---|---|---|
| Ring hoop or self-locking U-shaped hoop | 0.68 | 1 |
| Rubber anchor or steel anchor U-shaped hoop | 0.6 | 0.88 |
| General U-shaped hoop with fabric laminates | 0.5 | 0.75 |
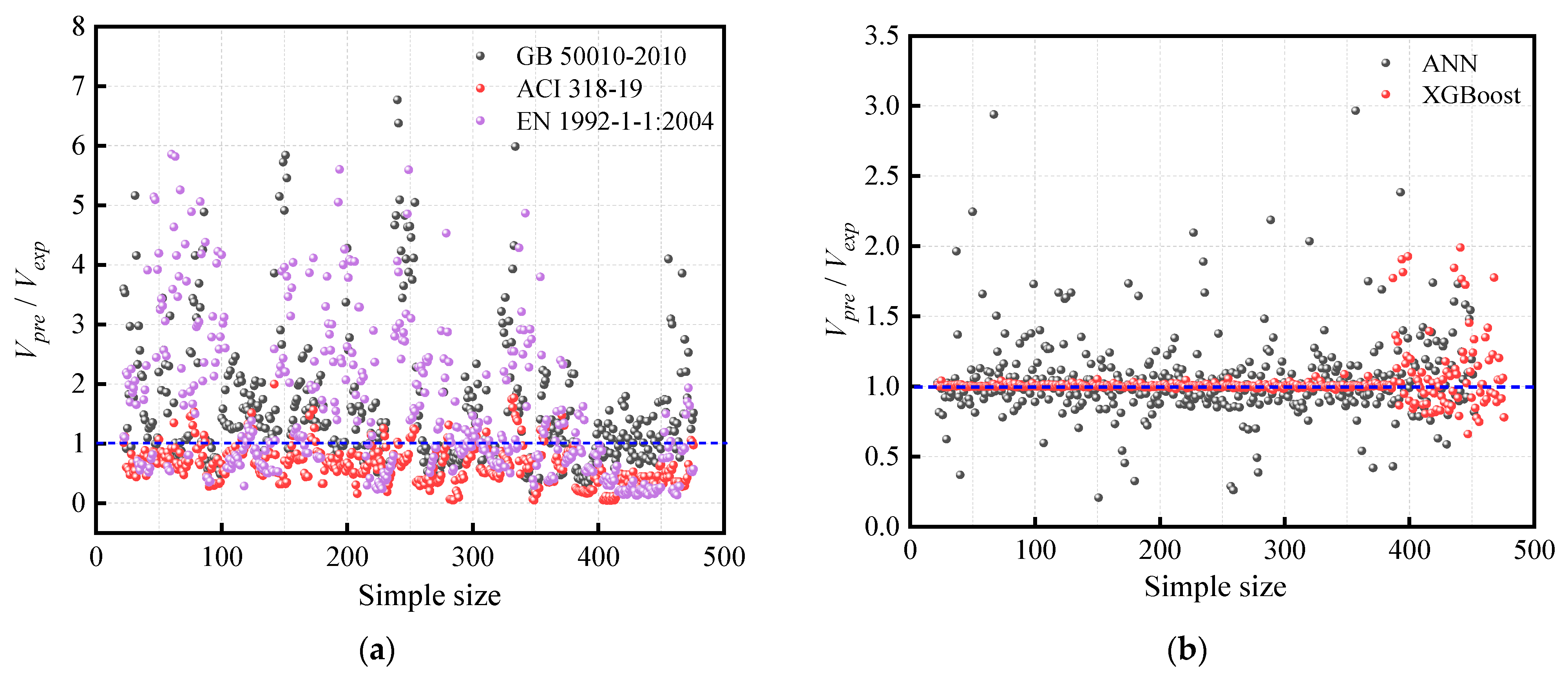
5.2. Comparison of Calculation Results of Different Design Codes
6. Conclusions
- (1)
- Pearson correlation analysis shows that the shear capacity Vu of FRP-SRCB has a relatively high positive correlation with the beam width b and the beam effective height d (correlation coefficients are 0.48 and 0.41), while the correlation coefficients with the other variables are low.
- (2)
- The intelligent prediction model for FRP-SRCB shear capacity was established by using the database to train the ML algorithm. The results show that the two ML models established perform well in shear capacity prediction. In general, the performance of the integrated model (XGBoost) is better than that of the single model (ANN), showing favorable accuracy.
- (3)
- The prediction results of three national standard formulas are compared with the ANN and XGBoost algorithms. The results reveal that the accuracy of the standard formula is limited and the variability is large. On the contrary, ML models greatly improve the prediction precision compared with traditional standard formulas. The variation coefficients of the ratio of the predicted value the actual value the ANN model and the XGBoost model are 27% and 13%, respectively, while the coefficient of variation in the standard model is more than 50%.
- (4)
- Future research should incorporate additional experimental data under extreme conditions (such as ultra-high-strength concrete components or specimens with large shear/span ratio) to enhance the generalization ability of the model. Moreover, integrating mechanism models (such as modified compression field theory) with ML algorithms to develop hybrid models that combine high accuracy with strong interpretability should be considered. This approach not only expands the application boundaries of ML in the engineering field but also provides an innovative solution for the intelligent evaluation of structural performance.
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hassam, M.; Guo, L.H.; Haq, M.A.U.; Tahir, M. Strengthening schemes of special-shaped concrete-filled steel tubes: A review. Structures 2024, 63, 106417. [Google Scholar] [CrossRef]
- Li, Y.; Yao, Z.A.; Dong, W.Y.; Ying, D.H. Study on flexural behavior of concrete slabs strengthened with externally prestressed recycled bead wires. Case Stud. Constr. Mater. 2024, 21, e03456. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.R.; Gao, Y.B.; Wang, W.T.; Wang, Z.M. Influence of macadamia nutshell particles on the apparent density and mechanical behavior of cement-based mortars. Constr. Build. Mater. 2024, 411, 134600. [Google Scholar] [CrossRef]
- Siddika, A.; Mamun, M.A.A.; Alyousef, R.; Amran, Y.H.M. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review. J. Build. Eng. 2019, 25, 100798. [Google Scholar] [CrossRef]
- Zheng, F.; Gao, L.; Wu, Y.F.; Liu, J.Y. Flexural design of reinforced concrete structures strengthened with hybrid bonded FRP. Compos. Struct. 2021, 269, 113996. [Google Scholar] [CrossRef]
- Siddika, A.; Mamun, M.A.A.; Ferdous, W.; Alyousef, R. Performances, challenges and opportunities in strengthening reinforced concrete structures by using FRPs—A state-of-the-art review. Eng. Fail. Anal. 2020, 111, 104480. [Google Scholar] [CrossRef]
- Mohammadi, A.; Barros, J.A.O.; Sena-Cruz, J. A new model for predicting the shear strength of RC beams strengthened with externally bonded FRP sheets. Compos. Struct. 2023, 319, 117081. [Google Scholar] [CrossRef]
- Bocciarelli, M.; Pisani, M.A. Survey on the interface behaviour in reinforced concrete beams strengthened with externally bonded FRP reinforcement. Compos. Part B 2017, 118, 169–176. [Google Scholar] [CrossRef]
- Lee, D.H.; Han, S.J.; Kim, K.S.; LaFave, J.M. Shear strength of reinforced concrete beams strengthened in shear using externally-bonded FRP composites. Compos. Struct. 2017, 173, 177–187. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Chen, X.L.; Fan, Z.H.; Sui, L.L.; Li, D.W.; Xing, F. Bond behaviors of FRP-to-concrete interface under the control of a novel end-anchorage system. Compos. Struct. 2017, 168, 130–142. [Google Scholar] [CrossRef]
- Ababneh, A.N.; Al-Rousan, R.Z.; Ghaith, I.M.N. Experimental study on anchoring of FRP-strengthened concrete beams. Structures 2020, 23, 26–33. [Google Scholar] [CrossRef]
- Azevedo, A.S.; Firmo, J.P.; Correia, J.R. Bond behaviour at high temperatures between concrete and CFRP or steel strengthening bars applied according to the embedded through-section (ETS) technique. Cem. Concr. Comp. 2024, 151, 105580. [Google Scholar] [CrossRef]
- D’Antino, T.; Pisani, M.A. General analytical model for the bond capacity of NSM FRP-concrete joints. J. Compos. Constr. 2020, 24, 04020065. [Google Scholar] [CrossRef]
- Amran, Y.H.M.; Alyousef, R.; Rashid, R.S.M.; Alabduljabbar, H.; Hung, C.C. Properties and applications of FRP in strengthening RC structures: A review. Structures 2018, 16, 208–238. [Google Scholar] [CrossRef]
- Sengun, K.; Arslan, G. Parameters affecting the behaviour of RC beams strengthened in shear and flexure with various FRP systems. Structures 2022, 40, 202–212. [Google Scholar] [CrossRef]
- Ji, C.Y.; Li, W.W.; Hu, C.Y.; Xing, F. Data analysis on fiber-reinforced polymer shear contribution of reinforced concrete beam shear strengthened with U-jacketing fiber-reinforced polymer composites. J. Reinf. Plast. Compos. 2017, 36, 98–120. [Google Scholar] [CrossRef]
- Ombres, L.; Aiello, M.A.; Cascardi, A.; Verre, S. Modeling of Steel-Reinforced Grout Composite System-To-Concrete Bond Capacity Using Artificial Neural Networks. J. Compos. Constr. 2024, 28, 04024034. [Google Scholar] [CrossRef]
- Marani, A.; Nehdi, M.L. Predicting shear strength of FRP-reinforced concrete beams using novel synthetic data driven deep learning. Eng. Struct. 2022, 257, 114083. [Google Scholar] [CrossRef]
- Ke, Y.; Zhang, S.S.; Jedrzejko, M.J.; Lin, G.; Li, W.G.; Nie, X.F. Strength models of near-surface mounted (NSM) fibre-reinforced polymer (FRP) shear-strengthened RC beams based on machine learning approaches. Compos. Struct. 2024, 337, 118045. [Google Scholar] [CrossRef]
- Anvari, T.A.; Babanajad, S.; Gandomi, A.H. Data-driven prediction models for total shear strength of reinforced concrete beams with fiber reinforced polymers using an evolutionary machine learning approach. Eng. Struct. 2023, 276, 115292. [Google Scholar] [CrossRef]
- Liu, Y.; He, J.T.; Liang, J.; Wang, W.T.; Wang, Z.M. A new improved particle swarm algorithm for optimization of anchor lattice beam support structures. Nat. Hazards 2024, 121, 225–243. [Google Scholar] [CrossRef]
- Perera, R.; Barchín, M.; Arteaga, A.; De Diego, A. Prediction of the ultimate strength of reinforced concrete beams FRP-strengthened in shear using neural networks. Compos. Part B 2010, 41, 287–298. [Google Scholar] [CrossRef]
- Tanarslan, H.M.; Secer, M.; Kumanlioglu, A. An approach for estimating the capacity of RC beams strengthened in shear with FRP reinforcements using artificial neural networks. Constr. Build. Mater. 2012, 30, 556–568. [Google Scholar] [CrossRef]
- Tanarslan, H.M.; Kumanlioglu, A.; Sakar, G. An anticipated shear design method for reinforced concrete beams strengthened with anchoraged carbon fiber-reinforced polymer by using neural network. Struct. Des. Tall Spec. Build. 2015, 24, 19–39. [Google Scholar] [CrossRef]
- Yavuz, G.; Arslan, M.H.; Baykan, O.K. Shear strength predicting of FRP-strengthened RC beams by using artificial neural networks. Sci. Eng. Compos. Mater. 2014, 21, 239–255. [Google Scholar] [CrossRef]
- Naderpour, H.; Alavi, S.A. A proposed model to estimate shear contribution of FRP in strengthened RC beams in terms of Adaptive Neuro-Fuzzy Inference System. Compos. Struct. 2017, 170, 215–227. [Google Scholar] [CrossRef]
- Abuodeh, O.R.; Abdalla, J.A.; Hawileh, R.A. Prediction of shear strength and behavior of RC beams strengthened with externally bonded FRP sheets using machine learning techniques. Compos. Struct. 2020, 234, 111698. [Google Scholar] [CrossRef]
- Wang, C.X.; Zou, X.X.; Snee, L.H.; Zhang, F.; Zheng, K.Q.; Xu, H.; Li, G.F. Shear strength prediction of FRP-strengthened concrete beams using interpretable machine learning. Constr. Build. Mater. 2023, 407, 133553. [Google Scholar] [CrossRef]
- Rahman, J.; Arafin, P.; Muntasir Billah, A.H.M. Machine learning models for predicting concrete beams shear strength externally bonded with FRP. Structures 2023, 53, 514–536. [Google Scholar] [CrossRef]
- Sung, W.; Potnuru, N.; Alfaris, S.; Sideris, P.; Paal, S.; Koliou, M.; Birely, A.; Hueste, M.B.; Hurlebaus, S. Shear capacity prediction model for prestressed concrete beams via data-driven methods. Structures 2025, 71, 108122. [Google Scholar] [CrossRef]
- Dong, Y.H.; Fu, Z.T.; Peng, Y.Q.; Zheng, Y.J.; Yan, H.J.; Li, X.X. Precision fertilization method of field crops based on the Wavelet-BP neural network in China. J. Clean. Prod. 2020, 246, 118735. [Google Scholar] [CrossRef]
- Khalifa, A.; Nanni, A. Rehabilitation of rectangular simply supported RC beams with shear deficiencies using CFRP composites. Constr. Build. Mater. 2002, 16, 135–146. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. Fiber reinforced polymer shear strengthening of reinforced concrete beams with transverse steel reinforcement. J. Compos. Constr. 2002, 6, 104–111. [Google Scholar] [CrossRef]
- Diagana, C.; Li, A.; Gedalia, B.; Delmas, Y. Shear strengthening effectiveness with CFF strips. Eng. Struct. 2003, 25, 507–516. [Google Scholar] [CrossRef]
- Täljsten, B. Strengthening concrete beams for shear with CFRP sheets. Constr. Build. Mater. 2003, 17, 15–26. [Google Scholar] [CrossRef]
- Adhikary, B.B.; Mutsuyoshi, H. Behavior of concrete beams strengthened in shear with carbon-fiber sheets. J. Compos. Constr. 2004, 8, 258–264. [Google Scholar] [CrossRef]
- Ianniruberto, U.; Imbimbo, M. Role of fiber reinforced plastic sheets in shear response of reinforced concrete beams: Experimental and analytical results. J. Compos. Constr. 2004, 8, 415–424. [Google Scholar] [CrossRef]
- Carolin, A.; Täljsten, B. Experimental study of strengthening for increased shear bearing capacity. J. Compos. Constr. 2005, 9, 488–496. [Google Scholar] [CrossRef]
- Monti, G.; Liotta, M. Tests and design equations for FRP-strengthening in shear. Constr. Build. Mater. 2006, 21, 799–809. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Hsu, C.T. Shear strengthening of reinforced concrete beams using carbon-fiber-reinforced polymer laminates. J. Compos. Constr. 2005, 9, 158–169. [Google Scholar] [CrossRef]
- Cao, S.Y.; Chen, J.F.; Teng, J.G.; Hao, Z.; Chen, J. Debonding in RC beams shear strengthened with complete FRP wraps. J. Compos. Constr. 2005, 9, 417–428. [Google Scholar] [CrossRef]
- Barros, J.A.O.; Dias, S.J.E.; Lima, J.L.T. Efficacy of CFRP-based techniques for the flexural and shear strengthening of concrete beams. Cem. Concr. Comp. 2006, 29, 203–217. [Google Scholar] [CrossRef]
- Pellegrino, C.; Modena, C. Fiber-reinforced polymer shear strengthening of reinforced concrete beams: Experimental study and analytical modeling. Aci Struct. J. 2006, 103, 720–728. [Google Scholar]
- Grande, E.; Imbimbo, M.; Rasulo, A. Effect of transverse steel on the response of RC beams strengthened in shear by FRP: Experimental study. J. Compos. Constr. 2009, 13, 405–414. [Google Scholar] [CrossRef]
- Alzate, A.; Arteaga, A.; Diego, A.D.; Perera, R. Shear strengthening of reinforced concrete beams using fibre reinforced polymers (FRP). Eur. J. Env. Civ. Eng. 2009, 13, 1051–1060. [Google Scholar] [CrossRef]
- Leung, C.K.Y.; Chen, Z.F.; Lee, S.; Ng, M.; Xu, M.; Tang, J.M. Effect of size on the failure of geometrically similar concrete beams strengthened in shear with FRP strips. J. Compos. Constr. 2007, 11, 487–496. [Google Scholar] [CrossRef]
- Kim, G.; Sim, J.S.; Oh, H. Shear strength of strengthened RC beams with FRPs in shear. Constr. Build. Mater. 2007, 22, 1261–1270. [Google Scholar] [CrossRef]
- Bae, S.W.; Tann, B.D.; Belarbi, A. Size effect of reinforced concrete beams strengthened in shear with externally bonded CFRP sheets. In Proceedings of the 6th International Conference on FRP Composites in Civil Engineering (CICE 2012), Rome, Italy, 13–15 June 2012. [Google Scholar]
- Allam, S.M.; Ebeido, T.I. Retrofitting of RC beams predamaged in shear using CFRP sheets. Alex. Eng. J. 2003, 42, 87–101. [Google Scholar]
- Adhikary, B.B.; Mutsuyoshi, H.; Ashraf, M. Shear strengthening of reinforced concrete beams using fiber-reinforced polymer sheets with bonded anchorage. Aci Struct. J. 2004, 101, 660–668. [Google Scholar]
- Pellegrino, C.; Modena, C. An experimentally based analytical model for the shear capacity of FRP-strengthened reinforced concrete beams. Mech. Compos. Mater. 2008, 44, 231–244. [Google Scholar] [CrossRef]
- Godat, A.; Qu, Z.; Lu, X.Z.; Labossière, P.; Ye, L.P.; Neale, K.W. Size effects for reinforced concrete beams strengthened in shear with CFRP strips. J. Compos. Constr. 2010, 14, 260–271. [Google Scholar] [CrossRef]
- Jayaprakash, J.; Samad, A.A.A.; Abbasovich, A.A.; Ali, A.A.A. Shear capacity of precracked and non-precracked reinforced concrete shear beams with externally bonded bi-directional CFRP strips. Constr. Build. Mater. 2007, 22, 1148–1165. [Google Scholar] [CrossRef]
- Beber, A.J.; Filho, A.C. CFRP composites on shear strengthening of reinforced concrete beams. Ibracon Struct. J. 2005, 1, 127–143. [Google Scholar]
- Abdel-Jaber, M.S.; Walker, P.R.; Hutchinson, A.R. Shear strengthening of reinforced concrete beams using different configurations of externally bonded carbon fibre reinforced plates. Mater. Struct. 2003, 36, 291–301. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Hsu, C.T.; Moren, J. Shear strengthening of reinforced concrete deep beams using carbon fiber reinforced polymer laminates. J. Compos. Constr. 2004, 8, 403–414. [Google Scholar] [CrossRef]
- Donatone, G.; Oliva, A.; Sollazzo, A.; Trentadue, F. Rinforzi strutturali con uso di compositi a matrice polimerica. Indag. Sper. 2003, 12, 3–8. [Google Scholar]
- Teng, J.G.; Chen, G.M.; Chen, J.F.; Rosenboom, O.A.; Lam, L. Behavior of RC beams shear Strengthened with bonded or unbonded FRP wraps. J. Compos. Constr. 2009, 13, 394–404. [Google Scholar] [CrossRef]
- Colalillo, M.A.; Sheikh, S.A. Seismic retrofit of shear-critical reinforced concrete beams using CFRP. Constr. Build. Mater. 2012, 32, 99–109. [Google Scholar] [CrossRef]
- Lee, J.Y.; Hwang, H.B.; Doh, J.H. Effective strain of RC beams strengthened in shear with FRP. Compos. Part B 2012, 43, 754–765. [Google Scholar] [CrossRef]
- Li, W.W.; Leung, C.K.Y. Shear span-depth ratio effect on behavior of RC beam shear strengthened with full-wrapping FRP strip. J. Compos. Constr. 2015, 20, 04015067. [Google Scholar] [CrossRef]
- Ebead, U.; Saeed, H. Hybrid shear strengthening system for reinforced concrete beams: An experimental study. Eng. Struct. 2013, 49, 421–433. [Google Scholar] [CrossRef]
- Bukhari, I.A.; Vollum, R.; Ahmad, S.; Sagaseta, J. Shear strengthening of short span reinforced concrete beams with CFRP sheets. Arab. J. Sci. Eng. 2013, 38, 523–536. [Google Scholar] [CrossRef]
- Li, W.W.; Leung, C.K.Y. Effect of shear span-depth ratio on mechanical performance of RC beams strengthened in shear with U-wrapping FRP strips. Compos. Struct. 2017, 177, 141–157. [Google Scholar] [CrossRef]
- Al-Lebban, Y.F.; Mackie, K.R. Polyurethane-FRP external strengthening of RC beams with no steel stirrups. J. Compos. Constr. 2019, 23, 04018074. [Google Scholar] [CrossRef]
- Javed, M.A.; Irfan, M.; Khalid, S.; Chen, Y.; Ahmed, S. An experimental study on the shear strengthening of reinforced concrete deep beams with carbon fiber reinforced polymers. KSCE J. Civ. Eng. 2016, 20, 2802–2810. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z.; Issa, M.A. The effect of beam depth on the shear behavior of reinforced concrete beams externally strengthened with carbon fiber-reinforced polymer composites. Adv. Struct. Eng. 2016, 19, 1769–1779. [Google Scholar] [CrossRef]
- Ahlam, M.; Kaiss, S.; Nabeel, A.B. Shear strength enhancement of lightweight aggregate reinforced concrete deep beams by using CFRP strips. MATEC Web Conf. 2018, 162, 04011. [Google Scholar]
- Ernesto, G.; Maura, I.; Rasulo, A. Experimental response of RC beams strengthened in shear by FRP sheets. Open Civ. Eng. J. 2013, 7, 127–135. [Google Scholar]
- Jirawattanasomkul, T.; Dai, J.G.; Zhang, D.W.; Senda, M.; Ueda, T. Experimental study on shear behavior of reinforced-concrete members fully wrapped with large rupture-strain FRP composites. J. Compos. Constr. 2013, 18, A4013009. [Google Scholar] [CrossRef]
- Hu, Z.H.; Zhou, X.Q.; Guo, M.H.; Huang, X.X.; Hu, B. Enhancing the performance of CFRP shear-strengthened RC beams using “ductile” anchoring devices. Front. Mater. 2020, 7, 292. [Google Scholar] [CrossRef]
- Saribiyik, A.; Abodan, B.; Balci, M.T. Experimental study on shear strengthening of RC beams with basalt FRP strips using different wrapping methods. Eng. Sci. Technol. 2020, 24, 192–204. [Google Scholar] [CrossRef]
- Bukhari, I.A.; Vollum, R.L.; Ahmad, S.; Sagaseta, J. Shear strengthening of reinforced concrete beams with CFRP. Arab. J. Sci. Eng. 2010, 62, 65–77. [Google Scholar] [CrossRef]
- Dias, S.J.; Barros, J.A. Experimental research of a new CFRP-based shear strengthening technique for rein forced concrete beams. Ibracon Struct. J. 2005, 1, 104–113. [Google Scholar]
- Kar, S.; Biswal, K.C. External shear strengthening of RC beams with basalt fiber sheets: An experimental study. Structures 2021, 31, 305–315. [Google Scholar] [CrossRef]
- Yu, F.; Guo, S.Q.; Wang, S.L.; Fang, Y. Experimental study on high pre-cracked RC beams shear-strengthened with CFRP strips. Compos. Struct. 2019, 225, 111163. [Google Scholar] [CrossRef]
- Karzad, A.S.; Leblouba, M.; Toubat, S.A.; Maalej, M. Repair and strengthening of shear-deficient reinforced concrete beams using carbon fiber reinforced polymer. Compos. Struct. 2019, 223, 110963. [Google Scholar] [CrossRef]
- Alam, M.A.; Riyami, K.A. Shear strengthening of reinforced concrete beam using natural fibre reinforced polymer laminates. Constr. Build. Mater. 2018, 162, 683–696. [Google Scholar] [CrossRef]
- Samad, A.A.A.; Ali, N.; Mohamad, N.; Jayaprakash, J.; Tee, K.F.; Mendis, P. Shear strengthening and shear repair of 2-span continuous RC beams with CFRP strips. J. Compos. Constr. 2016, 21, 04016099. [Google Scholar] [CrossRef]
- Manos, G.C.; Theofanous, M.; Katakalos, K. Numerical simulation of the shear behaviour of reinforced concrete rectangular beam specimens with or without FRP-strip shear reinforcement. Adv. Eng. Softw. 2014, 67, 47–56. [Google Scholar] [CrossRef]
- Gonzalez-Libreros, J.H.; Sneed, L.H.; D’Antino, T.; Pellegrino, C. Behavior of RC beams strengthened in shear with FRP and FRCM composites. Eng. Struct. 2017, 150, 830–842. [Google Scholar] [CrossRef]
- Mostofinejad, D.; Hosseini, S.A.; Razavi, S.B. Influence of different bonding and wrapping techniques on performance of beams strengthened in shear using CFRP reinforcement. Constr. Build. Mater. 2016, 116, 310–320. [Google Scholar] [CrossRef]
- Mei, S.J.; Bai, Y.L.; Dai, J.G. Shear strengthening of reinforced concrete beams completely wrapped by large rupture strain (LRS) FRP. Eng. Struct. 2024, 314, 118361. [Google Scholar] [CrossRef]
- Akkaya, H.C.; Aydemir, C.; Arslan, G. Investigation on shear behavior of reinforced concrete deep beams without shear reinforcement strengthened with fiber reinforced polymers. Case Stud. Constr. Mater. 2022, 17, e01392. [Google Scholar] [CrossRef]
- Akkaya, H.C.; Aydemir, C.; Arslan, G. An experimental research on reinforced concrete deep beams fully wrapped with fiber reinforced polymers against shear. Case Stud. Constr. Mater. 2022, 17, e01198. [Google Scholar] [CrossRef]
- Akkaya, H.C.; Aydemir, C.; Arslan, G. Evaluation of shear behavior of short-span reinforced concrete deep beams strengthened with fiber reinforced polymer strips. Eng. Struct. 2024, 299, 117145. [Google Scholar] [CrossRef]
- SENGUN, K.; ARSLAN, G. Investigation of the parameters affecting the behavior of RC beams strengthened with FRP. Front. Struct. Civ. Eng. 2022, 16, 729–743. [Google Scholar] [CrossRef]
- Sengun, K.; Arslan, G. Performance of RC beams strengthened in flexure and shear with CFRP and GFRP. Iran. J. Sci. Tech-Trans. Civ. Eng. 2023, 48, 117–130. [Google Scholar] [CrossRef]
- Moradi, E.; Naderpour, H.; Kheyroddin, A. An experimental approach for shear strengthening of RC beams using a proposed technique by embedded through-section FRP sheets. Compos. Struct. 2020, 238, 111988. [Google Scholar] [CrossRef]
- Javed, M.F.; Fawad, M.; Lodhi, R.; Najeh, T.; Gamil, Y. Forecasting the strength of preplaced aggregate concrete using interpretable machine learning approaches. Sci. Rep. 2024, 14, 8381. [Google Scholar] [CrossRef]
- Khan, M.; Javed, M.F. Towards sustainable construction: Machine learning based predictive models for strength and durability characteristics of blended cement concrete. Mater. Today Commun. 2023, 37, 107428. [Google Scholar] [CrossRef]
- Liu, K.H.; Dai, Z.H.; Zhang, R.B.; Zheng, J.K.; Zhu, J.; Yang, X.C. Prediction of the sulfate resistance for recycled aggregate concrete based on ensemble learning algorithms. Constr. Build. Mater. 2022, 317, 125917. [Google Scholar] [CrossRef]
- Huang, T.; Liu, T.B.; Ai, Y.; Ren, Z.X.; Ou, J.X.; Li, Y.X.; Xu, N. Modelling the interface bond strength of corroded reinforced concrete using hybrid machine learning algorithms. J. Build. Eng. 2023, 74, 106862. [Google Scholar] [CrossRef]
- Umer, K.; Bilal, A.; Abbas, K.Z.; Ahsen, M.; Irshad, Q.M. Integrated support vector regressor and hybrid neural network techniques for earthquake prediction along Chaman fault, Baluchistan. Arab. J. Geosci. 2021, 14, 2192. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. 2015th ed. Architecture & Building Press: Beijing, China, 2016.
- ACI 318-14; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2014.
- EN 1992-1-1:2004; Eurocede2: Design of Concrete Structures. Comité Européen de Normalisation: Brussels, Belgium, 2004.
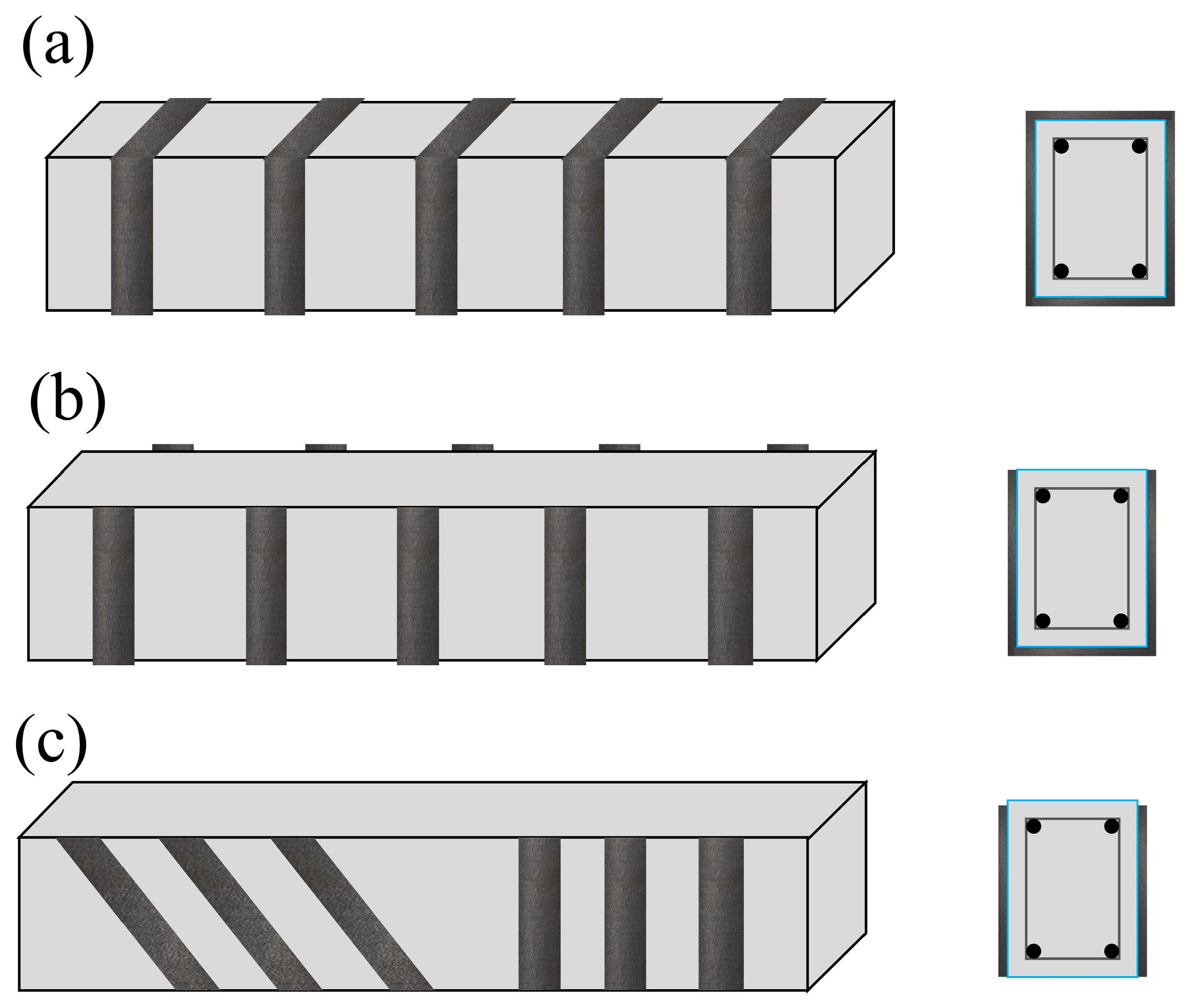

| Classification | Parameter | Minimum | Maximum | Median | Mean | Standard Deviation |
|---|---|---|---|---|---|---|
| Input parameter | b (mm) | 75.00 | 406.00 | 150.00 | 173.34 | 56.15 |
| d (mm) | 123.00 | 660.00 | 260.00 | 273.53 | 91.33 | |
| 0.94 | 4.88 | 2.80 | 2.61 | 0.77 | ||
| fy (MPa) | 311.22 | 625.10 | 500.00 | 494.11 | 61.40 | |
| (%) | 0.75 | 7.54 | 2.50 | 2.91 | 1.50 | |
| fyv (MPa) | 240.00 | 740.00 | 363.30 | 429.64 | 152.83 | |
| (%) | 0 | 0.84 | 0.11 | 0.16 | 0.18 | |
| fc (MPa) | 13.30 | 71.00 | 34.70 | 35.47 | 11.03 | |
| Ef (GPa) | 5.30 | 392.00 | 233.60 | 210.38 | 96.56 | |
| ff (MPa) | 110.00 | 4900.00 | 3450.00 | 3064.34 | 1352.38 | |
| (%) | 0.02 | 2.80 | 0.18 | 0.37 | 0.51 | |
| (°) | 45.00 | 90.00 | 90.00 | 84.76 | 14.45 | |
| Output parameter | Vu (kN) | 45.90 | 888.00 | 187.50 | 224.25 | 141.49 |
| Dataset | Model | R2 | MAE | RMSE |
|---|---|---|---|---|
| Training set | ANN | 0.880 | 29.433 | 48.635 |
| XGBoost | 0.999 | 1.096 | 1.438 | |
| Test set | ANN | 0.877 | 36.337 | 50.741 |
| XGBoost | 0.879 | 31.872 | 40.898 |
| Models/Specifications | AVE | SD | COV |
|---|---|---|---|
| ANN Model | 1.05 | 0.29 | 0.27 |
| XGB Model | 1.02 | 0.14 | 0.13 |
| GB 50010-2010 | 1.57 | 1.13 | 0.72 |
| ACI 318-19 | 0.64 | 0.33 | 0.51 |
| EN 1992-1-1:2004 | 1.56 | 1.26 | 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhu, M.; Xu, L.; Chen, M.; Shi, M. Prediction of Shear Capacity of Fiber-Reinforced Polymer-Reinforced Concrete Beams Based on Machine Learning. Buildings 2025, 15, 1908. https://doi.org/10.3390/buildings15111908
Zhao J, Zhu M, Xu L, Chen M, Shi M. Prediction of Shear Capacity of Fiber-Reinforced Polymer-Reinforced Concrete Beams Based on Machine Learning. Buildings. 2025; 15(11):1908. https://doi.org/10.3390/buildings15111908
Chicago/Turabian StyleZhao, Jitao, Miaomiao Zhu, Lidan Xu, Ming Chen, and Mingfang Shi. 2025. "Prediction of Shear Capacity of Fiber-Reinforced Polymer-Reinforced Concrete Beams Based on Machine Learning" Buildings 15, no. 11: 1908. https://doi.org/10.3390/buildings15111908
APA StyleZhao, J., Zhu, M., Xu, L., Chen, M., & Shi, M. (2025). Prediction of Shear Capacity of Fiber-Reinforced Polymer-Reinforced Concrete Beams Based on Machine Learning. Buildings, 15(11), 1908. https://doi.org/10.3390/buildings15111908





