DSS-MobileNetV3: An Efficient Dynamic-State-Space- Enhanced Network for Concrete Crack Segmentation

Abstract

Crack segmentation is crucial for health monitoring and preventive maintenance of concrete structures. However, the complex morphologies of cracks and the limited resources of mobile devices pose challenges for accurate and efficient segmentation. To address this, we propose an efficient dynamic-state-space-enhanced network termed DSS-MobileNetV3 for crack segmentation. The DSS-MobileNetV3 adopts a U-shaped encoder–decoder architecture, and a dynamic-state-space (DSS) block is designed into the encoder to improve the MobileNetV3 bottleneck module in modeling global dependencies. The DSS block improves the MobileNetV3 model in structural perception and global dependency modeling for complex crack morphologies by integrating dynamic snake convolution and a state space model. The decoder utilizes the upsampling and depthwise separable convolution to progressively decode and efficiently restore the spatial resolution. In addition, to suppress complex noise in the image background and highlight crack textures, the strip pooling module is introduced into the skip connection between the encoder and decoder for performance enhancement. Extensive experiments are conducted on three public crack datasets, and the proposed DSS-MobileNetV3 achieves SOTA performance in both accuracy and efficiency.

1. Introduction

Cracks are prevalent defects in concrete structures, typically exhibiting complex structural patterns such as irregular linear, mesh-like, or branching forms. These cracks not only compromise the mechanical performance of infrastructure but also precipitate further deterioration [1]. Consequently, efficient crack segmentation holds significant importance for preventive maintenance [2]. However, in real-world scenarios, uneven illumination, obstructions by debris, and background interference impede accurate crack segmentation. Additionally, the limited memory and computational resources of mobile devices pose challenges in efficient crack segmentation.

To address the above challenges, traditional methods utilize crack morphology, contrast with background pixels, and spatial clustering algorithms to extract cracks. For example, Landstrom et al. [3] develop an automatic crack detection system based on crack morphology and logistic regression statistical classification, which successfully extract 80% of the crack length. A pavement crack segmentation method based on grayscale histograms and the Otsu thresholding method is proposed in [4]. This method searches for cracks based on the ratio between the Otsu threshold of the image and the maximum histogram value and is capable of efficiently extracting various types of cracks from different pavement images. These traditional methods can efficiently extract prominent cracks. However, for crack images with complex backgrounds, traditional methods struggle to accurately identify fine-grained cracks. Furthermore, the repeated parameter tuning process can easily cause the algorithm to become trapped in local optimality.

With the emergence of deep learning technologies, CNN-based methods have alleviated the limitations of traditional algorithms in efficient crack segmentation, significantly improving accuracy. For instance, Xu et al. [5] propose an innovative deep learning framework, YOLO-DL, for detecting cracks in concrete. This method builds upon DeepLabv3+ [6] and incorporates attention mechanisms and calibration modules to achieve accurate crack segmentation. Guo et al. [7] incorporate the proposed Instance Normalization Wavelet (INW) layer into a deep model for crack segmentation. This model leverages prior knowledge from wavelets to capture crack features while simultaneously filtering out high-frequency noise. Liu et al. [8] propose an efficient deep learning model based on stereo vision for crack segmentation. By integrating the Semi-Global Block Matching (SGBM) algorithm, this method effectively segments the crack structures, laying a foundation for the subsequent quantitative analysis of crack length, width, and orientation angle. To improve the efficiency of CNNs, MobileNetV3 [9] builds upon MobileNetV1 [10] and MobileNetV2 [11] by introducing the Squeeze-and-Excitation module [12] and neural architecture search, enabling efficient and accurate semantic segmentation. These CNN-based methods have significant advantages in extracting cracks with localized variations. However, the limited receptive field of CNNs cannot accurately model the global dependencies of complex and long-spanned cracks, which are prone to fragmentation.

With the introduction of Vision Transformer (ViT) [13] in the Computer Vision (CV) field, a series of Transformer-based crack segmentation models have been proposed. Liu et al. [14] leverage the merit of Transformers in global relationship modeling and design a Crackformer for accurate crack detection. Shan et al. [15] designed a novel DCUFormer to address the bottleneck of existing Transformer-based methods in boundary delineation. By introducing a dual-cross attention module and an up-sampling attention module, the proposed DCUFormer effectively integrates low-level and high-level features, enabling it to refine boundary pixels. To improve accuracy, a new tunnel crack segmentation network, CGV-Net, has been proposed in [16]. This method integrates the advantages of CNN, Graph Neural Networks (GNNs) and ViT. By exchanging information between local features, CGV-Net effectively models the global structural patterns of cracks and achieves SOTA performance. However, as the core component of the Transformer-based methods, the self-attention mechanism requires significant computational resources, which poses a challenge for efficient segmentation tasks.

Recently, Mamba [17] has emerged as a competitor to Transformers due to its global modeling capability and computational efficiency. The core of Mamba is the state space model, which can linearly model global dependencies. Inspired by this, we propose an improved MobileNetV3 based on the state space model and attention mechanism for efficient crack segmentation. Specifically, the proposed model adopts a U-shaped encoder–decoder architecture. For the encoder, we use the improved MobileNetV3 to extract hierarchical features by replacing the Squeeze-and-Excitation (SE) attention module with the proposed Dynamic State Space (DSS) block. The DSS block improves the inaccurate limitation of SE attention module in crack feature activation by combining dynamic snake convolution with state space model, thereby achieving more accurate representation for elongated and slender cracks. For the decoder, we use upsampling and depthwise separable convolutions to progressively restore spatial resolution. Considering the complex background in images captured by real-time devices, we introduce the strip pooling module to highlight cracks and suppress noise.

In summary, our contributions are as follows:

• We propose an improved MobileNetV3 based on the state space model and attention mechanism for efficient crack segmentation, which efficiently integrates both local and global features of cracks.
• The DSS block is designed based on dynamic snake convolution and state space model to effectively model the global dependence of crack curves and boost encoding performance.
• Depthwise separable convolution and upsampling are utilized to progressively decode local textures, and the strip pooling module is incorporated to effectively fuse fine-grained crack features and filter out background-related noise.
• Extensive experiments are conducted and the results show that our proposed model achieves the SOTA performance with fewer parameters and FLOPs.

2. Related Work

2.1. Crack Segmentation Algorithms

We classify existing crack segmentation algorithms into traditional methods and deep learning-based methods. Traditional methods primarily rely on morphological operations, edge detection, and adaptive thresholding for crack segmentation. For example, Abdel-Qader et al. [18] demonstrated the effectiveness and superiority of the fast Haar transform edge detection algorithm in segmenting bridge cracks, while traditional methods efficiently extract prominent cracks, they struggle to capture key textures in cracks with complex backgrounds.

Deep learning-based crack segmentation methods are mainly divided into models based on CNN and Transformer architectures. The CNN-based methods primarily extend variants on the FCN [19] framework. For example, Lee et al. [20] proposed an FCN-based variant integrated with an autoencoder structure for pavement surface detection. Di Benedetto et al. [21] introduced the ResNet-50 encoder [22] into U-Net, achieving impressive performance on the Crack500 dataset. In [23], a hybrid network termed CrackNet has been proposed to accurately segment cracks by harnessing the strengths of both CNNs and Transformers. A CNN-based model termed CrackNet-V [24] is designed for asphalt pavement crack segmentation, showcasing the efficacy of deep learning methods in the realm of automated crack segmentation systems.

These CNN-based methods are more accurate in extracting local crack structures, but they may encounter breaks in the segmentation of long-spanned and elongate cracks. Liu et al. [14] leverage the strengths of Transformers in modeling global relationships and design a Crackformer for accurate crack detection. However, the computational complexity of Transformers limits their deployment on real-time devices.

2.2. Segmentation Methods Based on MobileNetV3

MobileNetV3 [9] has been widely applied to various segmentation tasks due to its efficient segmentation performance. In the medical imaging field, Alsenan et al. [25] integrated the advantages of the U-Net architecture and MobileNetV3, proposing MobileUNetV3 for the segmentation of spinal cord gray matter. In agricultural engineering, MobileNetV3 has been used to efficiently encode deep features, and combined with an attention mechanism to improve the accuracy of rice disease detection [26]. For lane lines in traffic scenarios, Deng et al. [27] employed MobileNetV3 to enhance the encoding capability and real-time performance of vehicle and lane line features. These MobileNetV3-based variants have achieved SOTA performance across various downstream tasks. However, due to the inherent limitations of CNNs, they struggle to model global features of diverse cracks.

Recently, Mamba [17] has achieved great success in the field of NLP. Its core is the state space model, which is capable of modeling long-range dependencies with linear complexity. Motivated by this, we combine the strengths of both Mamba and MobilenetV3 and propose a novel state space-based MobilenetV3 bottleneck module for efficient crack segmentation.

3. Method

3.1. Overall Architecture

The proposed model adopts a U-shaped encoder–decoder architecture for efficient crack segmentation, as shown in Figure 1. The U-shaped encoder–decoder architecture was proposed by Ronneberger et al. [28]. Its main advantage is combining multi-scale features efficiently, which improves crack segmentation performance, especially for recovering fine-grained crack textures. For the encoder, we use MobileNetV3 [9] to extract features. The core of MobileNetV3 is the bottleneck module, which uses an inverted residual design combined with Squeeze-and-Excitation (SE) attention module [12] to encode features efficiently. However, the SE attention module highlights crack semantics by compressing channels, which cannot effectively solve the mismatch between local receptive fields of CNNs and complex crack global morphologies. Thus, we introduce the dynamic state space (DSS) block into the MobileNetV3 bottleneck module and propose the state space-based MobileNetV3 bottleneck module to extract hierarchical features. For the decoder, we primarily use upsampling operation and depthwise separable convolution to progressively restore and integrate features. Considering the complex background and uneven lighting in images captured by mobile devices, we embed the strip pooling module between the encoder and decoder to highlight cracks and suppress background-related noise. Additionally, we jointly use cross-entropy loss and boundary loss as the objective functions to optimize the classification of crack pixels and the accuracy of boundary pixels.

3.2. State-Space-Based MobileNetV3 Bottleneck Module

The bottleneck module in MobileNetV3 [9] achieves a good balance between accuracy and efficiency. This module is mainly composed of depthwise separable convolution, inverted residual structure, SE attention module, and hard-swish activation function. It efficiently models local dependencies and encodes features. However, it still cannot escape the inherent limitations of convolution, as it is unable to model global dependencies for diverse types of cracks.

To address this, we propose a state-space-based bottleneck module, which improves the performance of the original bottleneck module by incorporating the dynamic state space block. Specifically, given the input feature $x_{in}$, the state-space-based bottleneck module first uses a $1\times 1$ convolution to expand the number of channels, enhancing the representation capability. Then, it utilizes depthwise separable convolution $DSConv(·)$ to efficiently extract local features and outputs $x_{dw}$, which can be reformulated as

$$\begin{array}{cc}\hfill x_{dw}& =DSConv\left(Expand\left(x_{in}\right)\right),\hfill \end{array}$$

(1)

where $Expand(·)$ is the $1\times 1$ convolution. Different from the bottleneck module in MobileNetV3, we replace the SE attention module with a DSS block to model global dependencies in deep features. This effectively addresses the limitations of convolution operations in terms of receptive field size. Finally, $1\times 1$ convolution and a residual connection are used to compress the channels and prevent gradient vanishing, respectively. Moreover, the output is $x_{out}$, which can be reformulated as

$$\begin{array}{cc}\hfill x_{out}& =Conv\left(DSS\left(x_{dw}\right)\right)+x_{in},\hfill \end{array}$$

(2)

3.3. Dynamic State Space Block

Due to the uncertainty in the shape and distribution of crack curves, we design a dynamic state space block to bridge the gap between state space models and 2D crack images, as shown in Figure 2. Inspired by [29], the DSS block consists of a linear layer for feature expansion, a set of dynamic snake convolutions (DSCs) [30] in both horizontal and vertical directions, a SiLU function for local representation enhancement, the SS2D module for modeling contextual relationships for 2D images with linear complexity, and the layer normalization for standardizing deep features.

In contrast to the 1D sequence-based selective scan algorithm in Mamba [17], the SS2D block involves three steps, including crossing scan, selective scan and crossing merge. Specifically, it first scans the slices in four different directions, and then flattens them into sequences. The scanning directions are represented by the following matrix. Next, the S6 block in Mamba is applied to simultaneously process the sequences derived from the four scanning directions. In the final crossing merge step, the processed sequences are integrated and reshaped to generate the output. Based on the above process, the workflow of the DSS block can be reformulated as

$$x_{DSS}=(Linear\ast DSC\ast SiLU\ast SS2D\ast LN)\left(x_{dw}\right),$$

(3)

where $LN$ represents the layer normalization, ‘*’ is the cascaded operation, $Linear$ is the linear layer, and $DSC$ is the dynamic snake convolution. The dynamic snake convolution is a deformable convolution that is more suitable for cracks. We take the accumulation process of DSC in the x-axis as an example, as shown in Figure 3.

The central coordinate of DSC is defined as $K_i$, and the point coordinate $K_{i\pm c}=(x_{i\pm c},y_{i\pm c})$ (where $c\in [0,4]$) in the DSC under $3\times 3$ receptive field. The position of $K_{i\pm c}$ is the result of dynamic accumulation. Starting from the center point $K_i$, $K_{i\pm 1}$ is determined by $K_i$ and offset $\Delta$ (where $\Delta =\{\delta \mid \delta \in [-1,1\left]\right\}$. The accumulation process of DSC in x-axes can be formalized as follows:

$$K_{i\pm c}=\left\{\begin{array}{cc}(x_{i+c},y_{i+c})\hfill & =(x_i+c,y_i+\sum _i^{i+c}\Delta y)\hfill \\ (x_{i-c},y_{i-c})\hfill & =(x_i-c,y_i+\sum _i^{i-c}\Delta y)\hfill \end{array}\right.$$

(4)

The accumulation process of DSC in y-axes is similar to the above process, which can be formalized as

$$K_{j\pm c}=\left\{\begin{array}{cc}(x_{j+c},y_{j+c})\hfill & =(x_j+c,y_j+\sum _j^{j+c}\Delta y)\hfill \\ (x_{j-c},y_{j-c})\hfill & =(x_j-c,y_j+\sum _j^{j-c}\Delta y)\hfill \end{array}\right.$$

(5)

where ∑ is the dynamic accumulation process.

3.4. Strip Pooling Module

Directly using skip connections to fuse deep and shallow features may introduce background-related noise and disrupt the structured representation of cracks. Images captured by mobile devices contain various types of objects, and uneven lighting can reduce the distinction between crack and background pixels. To highlight crack features and suppress noise, we embed the strip pooling module [31] in the skip connections between the encoder and decoder.

As shown in Figure 4, the strip pooling module consists of the strip pooling branch and the skip connection branch. Given the features from the encoder $x_e$, it first undergoes horizontal and vertical strip pooling to extract band-like features in different directions in a parallel manner. Next, 1D convolution and interpolation are used to integrate the strip-like features and restore the spatial resolution. Through $1\times 1$ convolution and the sigmoid function, features from different directions are fused, and the output is $x_e^{\prime }$, as follows:

$$\begin{array}{c}\hfill x_e^{\prime }=Sigmoid\left(Conv\left(F\left({Conv}_{1D}\left(S{P}_h\left(x_e\right)\right)\right)\right)\right)+F\left({Conv}_{1D}\left(S{P}_v\left(x_e\right)\right)\right),\end{array}$$

(6)

where $S{P}_h$ and $S{P}_v$ represent horizontal and vertical strip pooling, respectively. The $F(·)$ is the interpolation operation. Finally, by multiplying the output with the original input, cracks are highlighted, and background noise is suppressed, which can be represented as

$$\begin{array}{c}\hfill x_{out}=x^{\prime }\odot x,\end{array}$$

(7)

where ‘⊙’ is the Hadamard product.

3.5. Loss Function

To accurately segment crack pixels, we utilize the cross-entropy loss and boundary loss as the objective functions. The cross-entropy loss effectively measures the discrepancy between the predictions and the labels, while the boundary loss focuses on the inference of the crack boundaries. Therefore, the total loss can be expressed as

$$\begin{array}{cc}\hfill Los{s}_{total}& =\lambda ·Los{s}_{CE}+(1-\lambda )·Los{s}_{Bo},\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill Los{s}_{CE}& =-[GT·log(Pred)+(1-GT)·log(1-Pred\left)\right],\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill Los{s}_{Bo}& =\left|DT\right(Pred)-DT(GT\left)\right|,\hfill \end{array}$$

(10)

where $\lambda$ is the hyperparameter that balances the contributions of each loss term. $Pred$ and $GT$ are the prediction and ground truth, respectively. The $DT(·)$ is the distance transformation operation.

4. Experiments

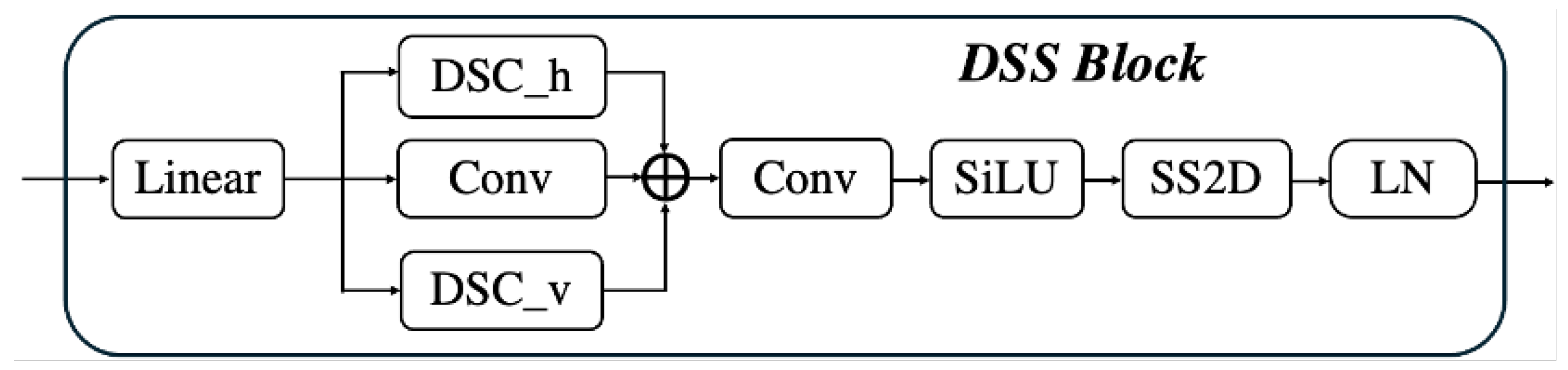
4.1. Datasets

DeepCrack. The DeepCrack dataset [32] is a publicly available dataset specifically designed for crack segmentation, comprising 537 RGB images along with manually annotated mask images. As shown in the first row of Figure 5, each image and its corresponding mask have a resolution of 544 × 284 pixels. In this paper, we follow the original setup and divide DeepCrack into training and testing sets, containing 300 and 237 image/mask pairs, respectively.

Crack500. The public Crack500 dataset [33] is collected using mobile phones on the main campus of Temple University, as shown in the second row of Figure 5. Each image and its corresponding annotated mask contain pavement cracks, with a resolution of approximately 2000 × 1500 pixels. In the original dataset, the training, validation, and testing sets are divided into 250, 50, and 200 images, respectively. To balance the high resolution of the images and limited computational resources, these high-resolution images are cropped into 16 non-overlapping sub-regions, and only slices containing more than 1000 crack pixels are retained. Based on this approach, the training, validation, and testing data consist of 1896, 348, and 1124 image patches, respectively.

CFD. The CFD dataset [34] is collected using an iPhone 5 on urban road surfaces in Beijing. As shown in the last row of Figure 5, the challenges of the CFD dataset include complex backgrounds, uneven illumination, and interference from various obstructions, such as water stains, oil spots, and lane lines. The dataset consists of 118 images with a resolution of $480\times 320$, along with manually annotated masks. In our experiments, the dataset is split into training and testing sets in a 6:4 ratio, respectively.

4.2. Performance Metrics

To quantitatively evaluate the segmentation performance of the models, we selected six evaluation metrics: intersection over union ($IoU$), dice similarity coefficient ($Dice$), precision ($Pre$), accuracy ($Acc$), and centerline dice ($clDice$). The first five metrics primarily assess the accuracy performance at the pixel level, while $clDice$ evaluates the discrepancy between the predicted values and the ground truth based on the connectivity of the curve. The calculation principles of these metrics are as follows:

$$\begin{array}{cc}\hfill IoU& ={\displaystyle \frac{TP}{TP+FP+FN}},\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill Dice& ={\displaystyle \frac{2TP}{2TP+FP+FN}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill Pre& ={\displaystyle \frac{TP}{TP+FP}},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill Acc& ={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}},\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill clDice& ={\displaystyle \frac{2|Pred\cap Ground|}{\left|Pred\right|+\left|Ground\right|}},\hfill \end{array}$$

(15)

where $TP$, $FP$, $FN$ and $TN$ are true positives, false positives, false negatives and true negatives.

4.3. Implementation Details

All the experiments in this study were conducted on a server equipped with the Ubuntu 18.04 operating system and a GeForce RTX 3070 8GB GPU. For the software environment, we chose the PyTorch 2.0 framework and set up the necessary dependencies using Anaconda version 23.5.2. During model training, we meticulously configured the hyperparameters: the batch size was set as 4, and the initial learning rate and training iterations were 0.0001 and 80,000, respectively. The AdamW optimizer was utilized to optimize deep learning models. In addition, to effectively prevent overfitting, we employed data augmentation techniques, including random flipping, random cropping, and random deformation, as well as rotation, color jittering, and scaling operations. All the images were resized to $256\times 256$. The hyperparameter $\lambda$ in the loss function was set to 0.6.

4.4. Comparison Experiments

We compared the proposed method with fifteen different segmentation methods, including FCN [19], U-Net [28], MobileNetV1 [10], MobileNetV2 [11], MobileNetV3 (small version) [9], DeepLabv3+ [6] (Resnet-50 as backbone), Swin Transformer (tiny version) [35], SegFormer (b0 version) [36], CrackSegNet [37], CrackW-Net [38], TEED [39], CrackFormer [40], DECSNet [41] (Resnet-50 as backbone), RHACrackNet [2] and CarNet [42] (MobileNetV3-small as backbone) on three public datasets. Note that the methods without marking the backbone network keep the same configuration as the original methods. These methods can be divided into specialized real-time crack segmentation methods and general segmentation models. Moreover, all the methods were loaded with pre-trained weights on the ImageNet-1K dataset [43].

We quantified the performance of all methods on the DeepCrack dataset and recorded the results in

Table 1. Comparison performance (%) between our proposed DSS-MobileNetV3 and SOTA methods on the DeepCrack dataset [32].

Method	Year	IoU	Dice	Recall	Acc	clDice
FCN [19]	2015	68.81	81.79	74.55	98.37	86.79
Unet [28]	2015	69.03	81.83	74.96	98.40	86.92
MobilenetV1 [10]	2017	69.28	81.94	75.20	98.49	87.13
MobilenetV2 [11]	2018	70.81	82.11	78.14	98.52	87.36
MobileNetV3 [9]	2019	72.59	82.29	79.62	98.57	88.09
Deeplabv3+ [6]	2018	71.34	82.22	78.87	98.54	87.61
Swin Transformer [35]	2021	73.04	82.58	83.11	98.51	88.42
SegFormer [36]	2021	73.39	83.01	83.49	98.61	88.84
CrackSegNet [37]	2020	73.28	83.07	83.41	98.68	88.61
CrackW-Net [38]	2021	73.17	82.92	83.25	98.62	88.34
TEED [39]	2023	70.50	82.14	78.42	98.53	87.39
CrackFormer [40]	2023	73.37	82.95	83.43	98.58	88.80
DECSNet [41]	2024	71.67	82.18	78.95	98.54	87.60
RHACrackNet [2]	2024	73.43	83.06	83.57	98.67	88.91
CarNet [42]	2024	73.73	83.27	83.86	98.71	89.10
Ours	−	74.21	84.36	84.93	98.87	89.20

. Upon observation, we found that the proposed model achieved the highest scores across all metrics. Compared to the general-purpose Unet, our proposed method outperformed in $IoU$, $Dice$, $Recall$, $Acc$, and $clDice$ scores by 5.18%, 2.53%, 9.97%, 0.47% and 2.28%, respectively. Additionally, the proposed method surpassed the CarNet model, which is specifically designed for crack segmentation, by 0.48% in $IoU$, 1.09% in $Dice$, 1.07% in $Recall$, 0.16% in $Acc$, and 0.1% in $clDice$. 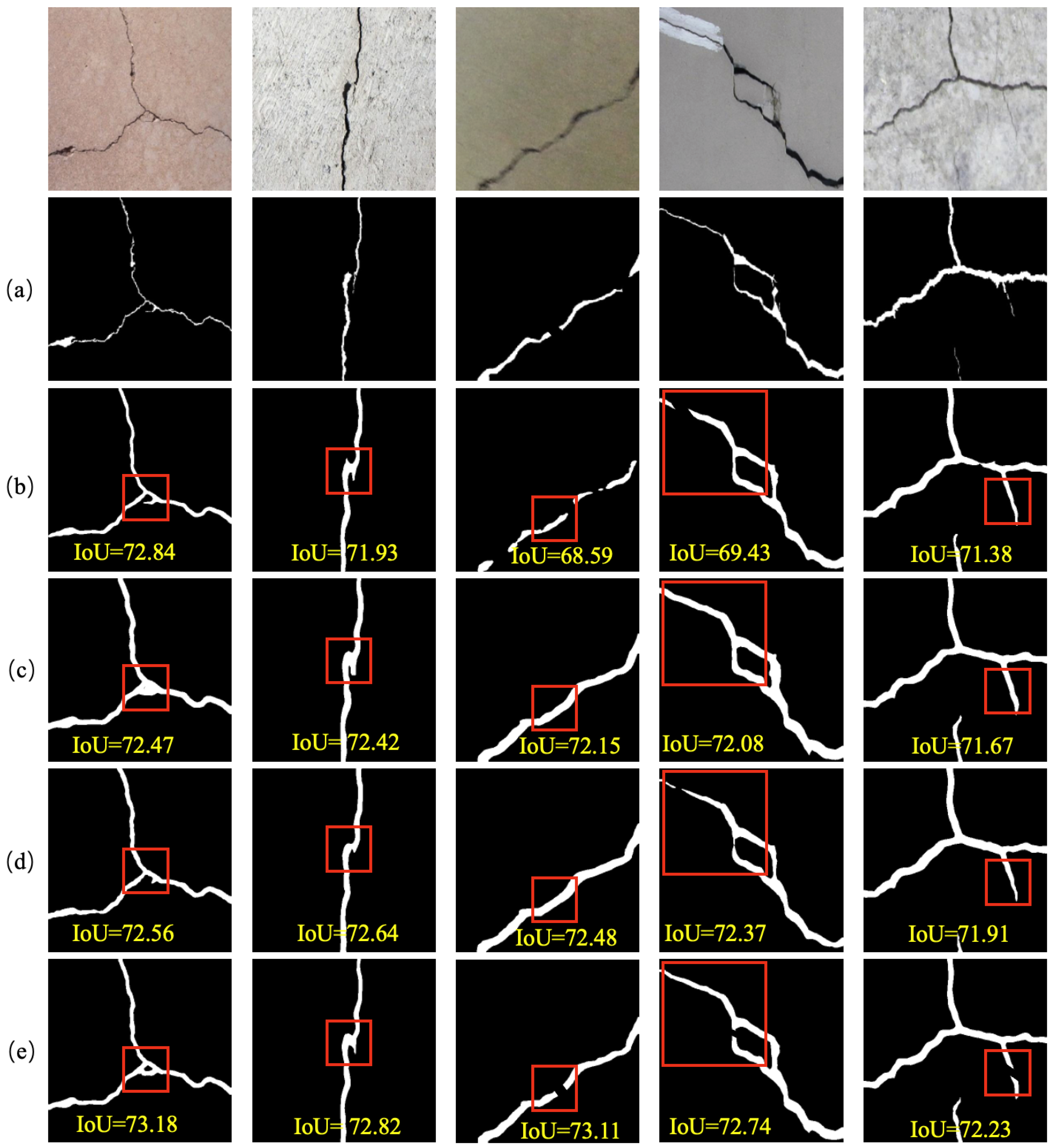For an intuitive comparison, we visualized the top performance models including Unet, RHACrackNet and CarNet methods in Figure 6. We observed that the segmentation results from U-Net and RHACrackNet contained more false positive pixels, while CarNet exhibited discontinuities in its segmentation of slender cracks. In contrast, the proposed method demonstrated superior accuracy in detecting cracks from the DeepCrack images, particularly in regions where cracks are discontinuous. In addition, the proposed method is not sensitive enough to cracks and artifacts in blurred image areas, making the segmentation results prone to fragmentation.

As shown in

Table 2. Comparison performance (%) between our proposed DSS-MobileNetV3 and SOTA methods on the Crack500 dataset [33].

Method	Year	IoU	Dice	Recall	Acc	clDice
FCN [19]	2015	53.11	69.70	67.95	96.68	74.80
Unet [28]	2015	53.25	69.91	68.14	96.70	74.88
MobilenetV1 [10]	2017	53.87	70.01	69.38	96.79	74.94
MobilenetV2 [11]	2018	54.10	70.23	69.75	96.87	75.10
MobileNetV3 [9]	2019	54.88	70.57	72.17	96.95	75.39
DeepLabv3+ [6]	2018	54.57	70.14	70.39	96.88	74.95
Swin Transformer [35]	2021	55.81	71.07	75.27	96.66	75.14
SegFormer [36]	2021	56.02	71.06	75.82	97.07	75.40
CrackSegNet [37]	2020	55.21	71.07	73.84	97.04	75.96
CrackW-Net [38]	2021	54.97	70.65	73.72	97.10	75.71
TEED [39]	2023	53.46	70.04	69.60	97.12	75.78
CrackFormer [40]	2023	56.03	71.12	75.49	96.71	76.20
DECSNet [41]	2024	54.58	70.41	71.75	96.89	75.18
RHACrackNet [2]	2024	56.06	71.19	76.12	96.68	75.23
CarNet [42]	2024	56.16	71.39	77.28	96.75	74.92
Ours	−	56.68	71.72	77.67	97.29	76.69

, our proposed model consistently outperformed all others across all evaluation metrics. Specifically, it achieved improvements of 3.43%, 1.81%, 9.53%, 0.59%, and 1.81% over the Unet model in terms of $IoU$, $Dice$, $Recall$, $Acc$, and $clDice$, respectively. Furthermore, the proposed method also outperformed the CarNet model, which is specialized for crack segmentation, with gains of 0.52% in $IoU$, 0.33% in $Dice$, 0.39% in $Recall$, 0.54% in $Acc$, and 1.77% in $clDice$. To provide a clearer comparison of the segmentation performance, we visualized the results for Unet and CarNet in Figure 7. We observed that the proposed model demonstrated more precise segmentation performance on Crack500 images, with significantly fewer false positive pixels and fracture points. For the mesh-like structures formed by interconnected annular cracks, the proposed method demonstrates superior capability in capturing pixel-level correlations. Moreover, it successfully identifies crack textures that were overlooked in the ground truth images. However, the accuracy of the proposed method in segmenting boundary pixels of thick cracks needs further enhancement.

We quantified the performance of all methods on the CFD dataset, and the results are recorded in

Table 3. Comparison performance (%) between our proposed DSS-MobileNetV3 and SOTA methods on the CFD dataset [34].

Method	Year	IoU	Dice	Recall	Acc	clDice
FCN [19]	2015	51.44	72.56	75.29	93.99	78.29
Unet [28]	2015	51.53	72.77	75.39	94.01	78.50
MobilenetV1 [10]	2017	51.64	72.90	75.61	94.22	78.71
MobilenetV2 [11]	2018	52.38	73.08	76.31	94.72	79.22
MobileNetV3 [9]	2019	54.92	73.40	78.54	95.05	79.56
DeepLabv3+ [6]	2018	53.63	73.22	77.56	94.89	79.30
Swin Transformer [35]	2021	56.36	73.51	79.67	95.35	79.44
SegFormer [36]	2021	56.96	73.80	79.94	95.66	79.82
CrackSegNet [37]	2020	55.85	73.84	78.89	95.43	79.70
CrackW-Net [38]	2021	55.51	73.27	79.12	95.58	79.51
TEED [39]	2023	52.39	72.95	76.41	94.50	78.53
CrackFormer [40]	2023	56.98	73.77	79.83	95.53	79.78
DECSNet [41]	2024	53.65	73.21	77.80	94.94	79.38
RHACrackNet [2]	2024	57.05	73.94	80.62	95.51	79.35
CarNet [42]	2024	57.23	74.02	80.88	95.60	79.75
Ours	−	58.37	74.29	81.36	95.83	80.08

. We found that the proposed model achieved the highest scores across all metrics. Compared to the Unet model, the proposed method outperformed it by 6.84%, 1.52%, 5.97%, 1.82%, and 1.58% in $IoU$, $Dice$, $Recall$, $Acc$, and $clDice$ metrics, respectively. Moreover, the proposed model surpassed the CarNet model, which is specifically designed for crack segmentation, by 1.14% in $IoU$, 0.27% in $Dice$, 0.48% in $Recall$, 0.23% in $Acc$, and 0.33% in $clDice$. To provide a clear comparison of the segmentation performance, we visualized the Unet and CarNet methods in Figure 8. We found that U-Net and RHACrackNet exhibited suboptimal performance in segmenting complex annular crack networks, failing to accurately capture pixel-level connectivity relationships. In contrast, the proposed model demonstrated superior accuracy and continuity in segmenting both long-span and intricately meshed crack structures. Additionally, the proposed method achieved more precise identification of crack junctions. However, the proposed method is not precise in capturing local textures of jagged cracks. This suggests that the proposed model should incorporate edge-related features, which will be our future research focus.

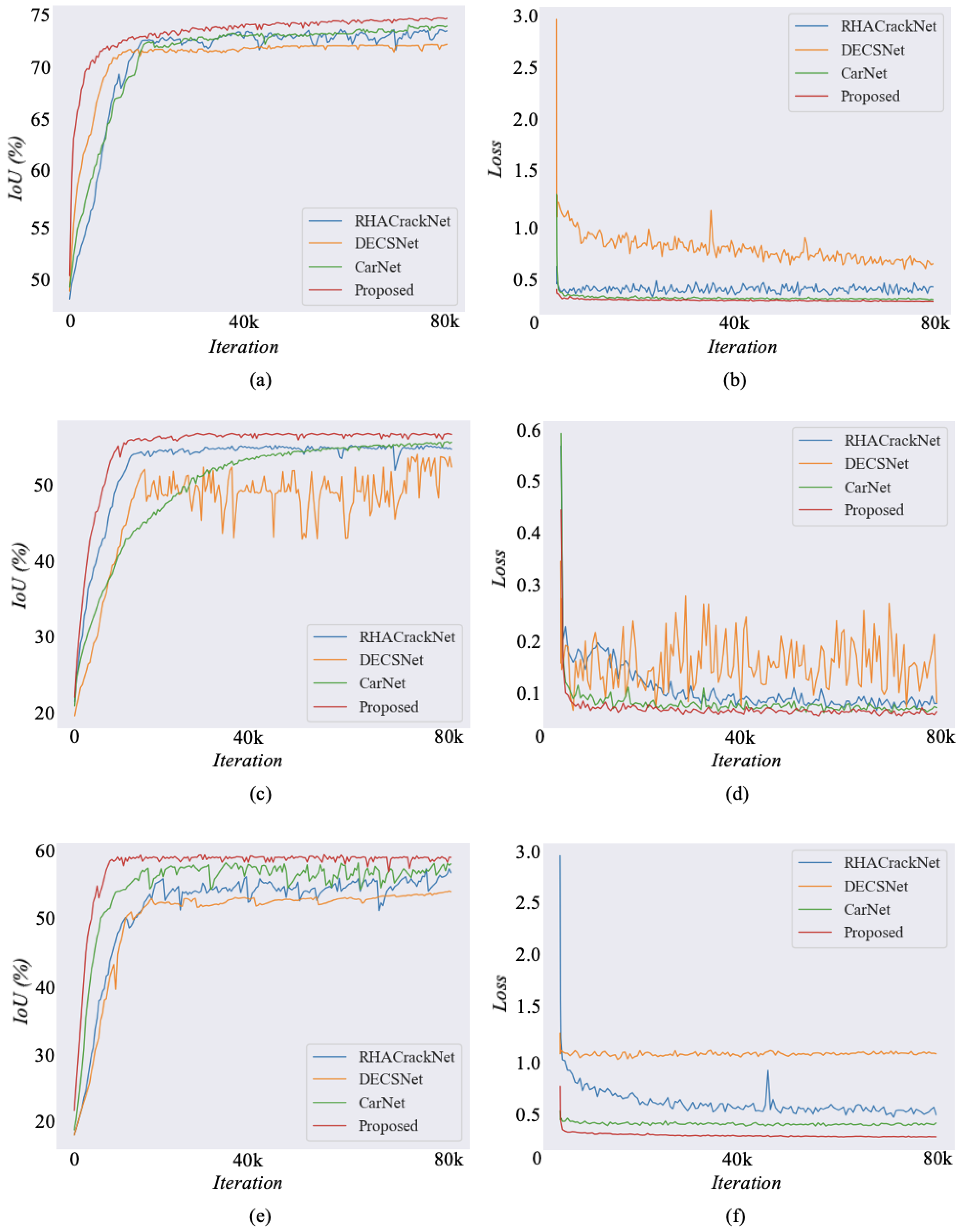
We present the training process of our proposed method and recent SOTA models on three public datasets. As shown in the first row of Figure 9, compared to the three SOTA methods, including RHACrackNet, DECSNet and CarNet, the proposed method converges faster and achieves a lower loss on the DeepCrack dataset. On the challenging Crack500 dataset, DECSNet exhibits severe oscillations and does not converge stably. In contrast, our proposed method demonstrates stable convergence. On the CFD dataset, the IoU curve and loss curve of the proposed method also converge quickly and achieve higher accuracy, which effectively validates the superiority of the proposed method. Consequently, the proposed method demonstrates stable segmentation performance and achieves rapid convergence to optimal values across three public datasets, which also proves its superiority.

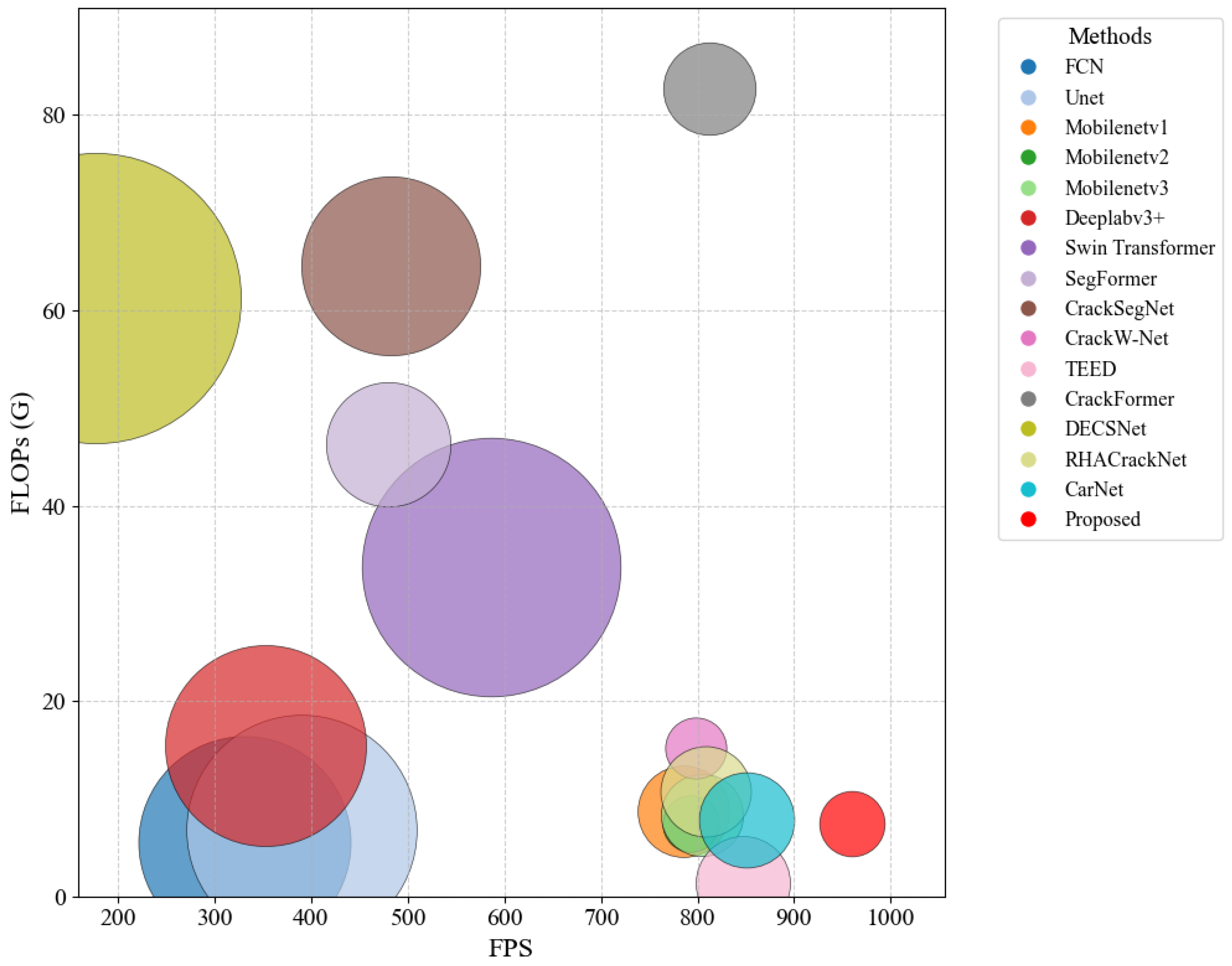
To evaluate the comprehensive performance of the model, we report the number of parameters, FLOPs and FPS values for all methods. As shown in

Table 4. The parameter counts, FLOPs and FPS of the methods.

Method	Year	# Param (M)	FLOPs (G)	FPS
FCN [19]	2015	25.3	5.6	331.4
Unet [28]	2015	29.8	6.8	389.7
MobilenetV1 [10]	2017	4.7	8.7	785.6
MobilenetV2 [11]	2018	1.8	7.4	792.4
MobileNetV3 [9]	2019	3.8	8.3	804.9
DeepLabv3+ [6]	2018	22.7	15.4	352.9
Swin Transformer [35]	2021	37.6	33.7	586.2
SegFormer [36]	2021	8.7	46.3	479.1
CrackSegNet [37]	2020	18.0	64.6	482.3
CrackW-Net [38]	2021	2.1	15.2	798.2
TEED [39]	2023	5.0	1.3	846.8
CrackFormer [40]	2023	4.8	82.7	812.7
DECSNet [41]	2024	47.4	61.3	176.5
RHACrackNet [2]	2024	4.6	10.8	808.4
CarNet [42]	2024	5.1	7.8	851.1
Ours	−	2.4	7.5	960.1

, compared to general-purpose methods, the proposed model has significantly fewer parameters. Additionally, compared to real-time segmentation models, our proposed method has a lower FLOP value and faster FPS. To visually assess the efficiency of all models, we have visualized their performance in terms of parameter count, FLOPs and FPS. As shown in Figure 10, the proposed method is located in the bottom-right corner and has the smallest radius, indicating lower parameter count, fewer FLOPs, and faster FPS. Thus, our method is competitive in efficient crack segmentation tasks.

4.5. Ablation Experiments

To evaluate the contribution of each module in the proposed model, we conducted corresponding ablation experiments. As shown in

Table 5. Ablation study for the proposed method. Note that all the values are the IoU performance (%) of the corresponding methods.

Method	DeepCrack	Crack500	CFD
Backbone	72.36	54.64	54.89
Backbone + decoder	72.84	55.31	55.74
Backbone + decoder + SE attention module	73.18	55.52	56.83
Backbone + decoder + DSS block (Middle)	73.59	56.20	57.75
Backbone + decoder + DSS block (Head)	73.21	55.78	56.71
Backbone + decoder + DSS block (Tail)	73.07	55.62	56.34
Proposed	74.21	56.68	58.37

, we used MobileNetV3 (small version) as the backbone network, and by incorporating a progressive decoder, we found that the proposed method achieved an 0.48% increase in the IoU metric. Furthermore, we observed that the DSS block contributed the most to the model, boosting the IoU score by 0.75%, which also suggests that the proposed DSS block has great potential for crack segmentation. As shown in the fourth and fifth rows of Table 5, our proposed DSS module surpasses the original SE attention module by 0.41% in IoU metric across the DeepCrack dataset, which proves the superiority of our proposed DSS module. To validate the impact of embedding the DSS block at different positions within the MobileNetV3 module, we integrated the DSS block into three distinct locations. As observed in Table 5, embedding the DSS block in the middle position of the MobileNetV3 module yields the most significant improvement for the crack segmentation task, which proves the effectiveness of the proposed method. Finally, we conducted an ablation of the strip pooling module and found that it improved the IoU score by 0.62%. Therefore, based on the above analysis, we have demonstrated the effectiveness of each module in our method.

To investigate the impact of different input image resolutions on the proposed method, we conducted corresponding ablation experiments. As shown in

Table 6. Ablation study for the resolution of input images on the DeepCrack dataset [32]. Note that ‘⋆’ represents the proposed method.

Resolution	IoU (%)	Dice (%)	Recall (%)	Acc (%)	clDice (%)
$128\times 128$	73.97	83.85	84.33	98.37	88.62
$224\times 224$	74.04	83.97	84.46	98.50	88.79
$256\times 256$ $(\star )$	74.21	84.36	84.93	98.87	89.20
$448\times 448$	74.26	84.41	84.83	98.70	88.61

, when using input images with resolutions of $128\times 128$ and $224\times 224$, the proposed method performed suboptimally. We believe this is because the images were resized too small, resulting in the loss of fine-grained features. When we increased the input image resolution to $448\times 448$, we found that the proposed method achieved lower scores in recall, accuracy, and clDice indicators. This suggests that increasing the input image resolution may lead to noise interference and disrupt the structural features of cracks. In contrast, the proposed method achieved SOTA performance by resizing the input images to $256\times 256$.

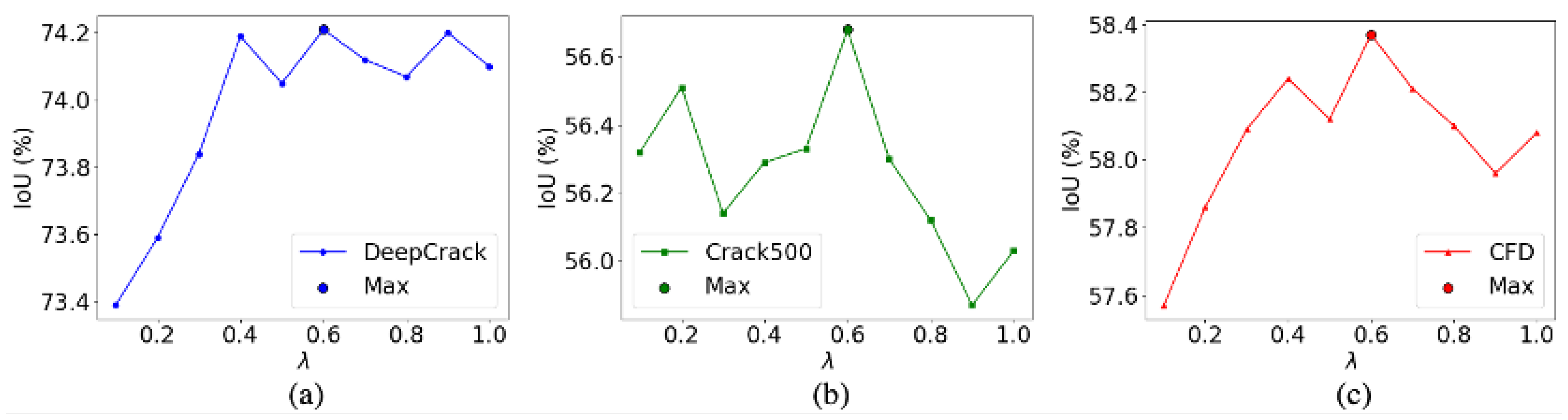
Moreover, we evaluated the hyperparameters which controlled the fusion of the cross-entropy loss and boundary loss across three public datasets, as shown in Figure 11. We found that when $\lambda =0.6$, the proposed method achieves the highest IoU scores on all three datasets. Furthermore, we also conducted corresponding ablation experiments on other hyperparameters, including the learning rate, architecture depth, and batch size. As shown in

Table 7. Ablation study for the hyperparameters including the learning rate, architecture depth, and batch size on the DeepCrack dataset [32]. Note that ‘⋆’ represents the proposed method.

Hyperparameter	Setting	IoU (%)	Acc (%)	clDice (%)
Learning Rate	0.01	73.95	98.47	88.37
	0.001	74.04	98.51	88.64
	0.0001 (⋆)	74.21	98.87	89.20
Architecture Depth	7	73.98	98.66	89.02
	5 (⋆)	74.21	98.87	89.20
	4	74.05	98.77	89.14
Batch Size	1	74.13	98.78	89.08
	2	74.15	98.81	89.13
	4 (⋆)	74.21	98.87	89.20

, we find that initializing with a smaller learning rate facilitates model convergence to the optimal solution. Furthermore, deepening the encoder architecture unexpectedly degrades segmentation accuracy, suggesting that excessive model depth may impair the decoder’s capacity to recover crack semantics. Notably, batch size adjustments demonstrate a negligible impact on overall model performance.

To evaluate the impact of the offset range $\Delta$ in dynamic snake convolution on model performance, we conducted targeted ablation experiments. As shown in

Table 8. Ablation study for the offset range $\Delta$ of dynamic snake convolution on the DeepCrack dataset.

Offset Range $\mathbf{\Delta }$	IoU (%)	Dice (%)	Recall (%)	Acc (%)	clDice (%)
$\Delta \in [-5,5]$	73.78	83.95	84.41	98.30	88.78
$\Delta \in [-3,3]$	73.87	84.06	84.54	98.42	88.83
$\Delta \in [-2,2]$	74.05	84.12	84.69	98.59	89.04
$\Delta \in [-1,1]$	74.21	84.36	84.93	98.87	89.20

, four distinct offset ranges were configured. We observed a moderate decline in performance across all three datasets when expanding the offset range $\Delta$, which may be attributed to the mismatch between the receptive fields generated by dynamic snake convolution and the inherent crack morphology. Specifically, a larger offset range compromises the model’s ability to focus on the curvilinear and continuous nature of cracks. Furthermore, when the offset range $\Delta$ was constrained to [−1, 1], the model achieved state-of-the-art (SOTA) performance, validating the efficacy of our parameter configuration in aligning with the structural characteristics of cracks.

4.6. Cross-Dataset Transfer Experiments

To test the sensitivity and robustness of the proposed method, we conducted cross-dataset transfer experiments. Specifically, we loaded the model’s weight trained on one dataset and used them to test two other datasets. As shown in

Table 9. Cross-dataset transfer experiments. Note that all the values are the dice performance (%) of the proposed method.

Transfer Dataset	DeepCrack	Crack500	CFD
DeepCrack	84.36	52.58	51.94
Crack500	55.88	71.72	53.42
CFD	55.64	56.26	74.29

, the first column represents the dataset from which the model weights were loaded, while the first row represents the test datasets. By observing the results, we found that the proposed method achieved stable segmentation performance across all cross-dataset transfer experiments. These results also indicate that the proposed model is highly robust and not significantly affected by external factors, like background or environmental changes.

4.7. Conclusions

In this paper, we propose an efficient dynamic-state-space-enhanced network to accurately and efficiently segment concrete cracks. We embed a dynamic state space (DSS) block into the encoder to improve the global dependencies modeling capability of MobileNetV3 bottleneck modules. Specifically, we replace the SE module in the original MobileNetV3 bottleneck module with our proposed DSS block for power representation. For the decoding stage, we utilize the upsampling and depthwise separable convolution to progressively restore the spatial resolution. Moreover, to highlight the crack textures and suppress the background-related noise, we embed the strip pooling module into the skip connection between the encoder and decoder. Extensive experiments are conducted on three public datasets, and the results show the superiority of our proposed method in accuracy and efficiency.

Although our method achieves good results on crack segmentation, it still has some limitations. Firstly, it struggles to detect cracks in blurred image areas, leading to fragmented segmentation results. Secondly, the accuracy of segmenting thick crack boundaries needs improvement, as the model often misses clear edges. Thirdly, the method cannot precisely capture the fine textures of jagged cracks, which suggests that edge-related features should be strengthened in future work.