Study on the Wind Pressure Distribution in Complicated Spatial Structure Based on k-ε Turbulence Models
Abstract
1. Introduction
2. Wind Tunnel Test
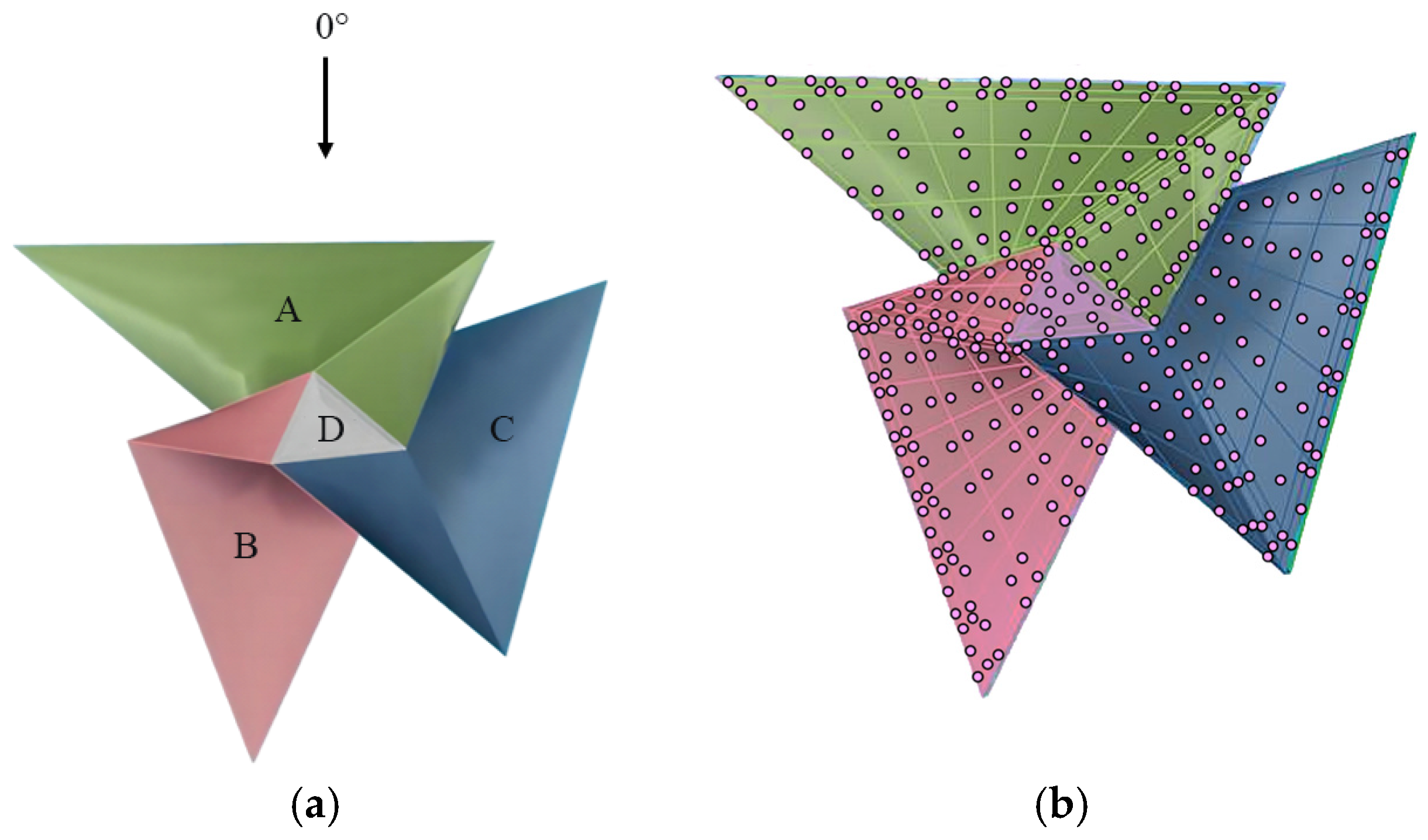
2.1. Test Model
2.2. Wind Tunnel Test Results
3. Numerical Simulation in CFD
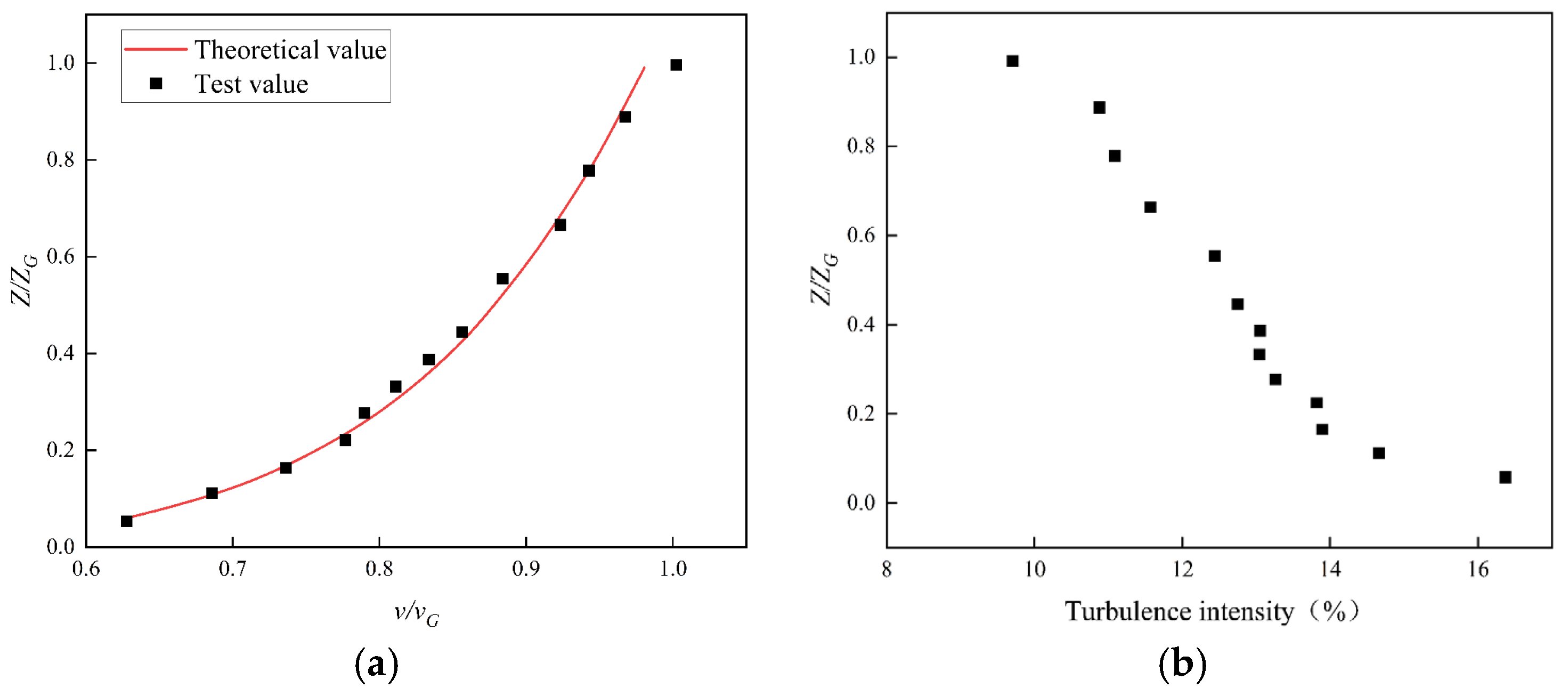
3.1. Determination of Turbulence Models and Treatment of Wall-Adherent Surfaces
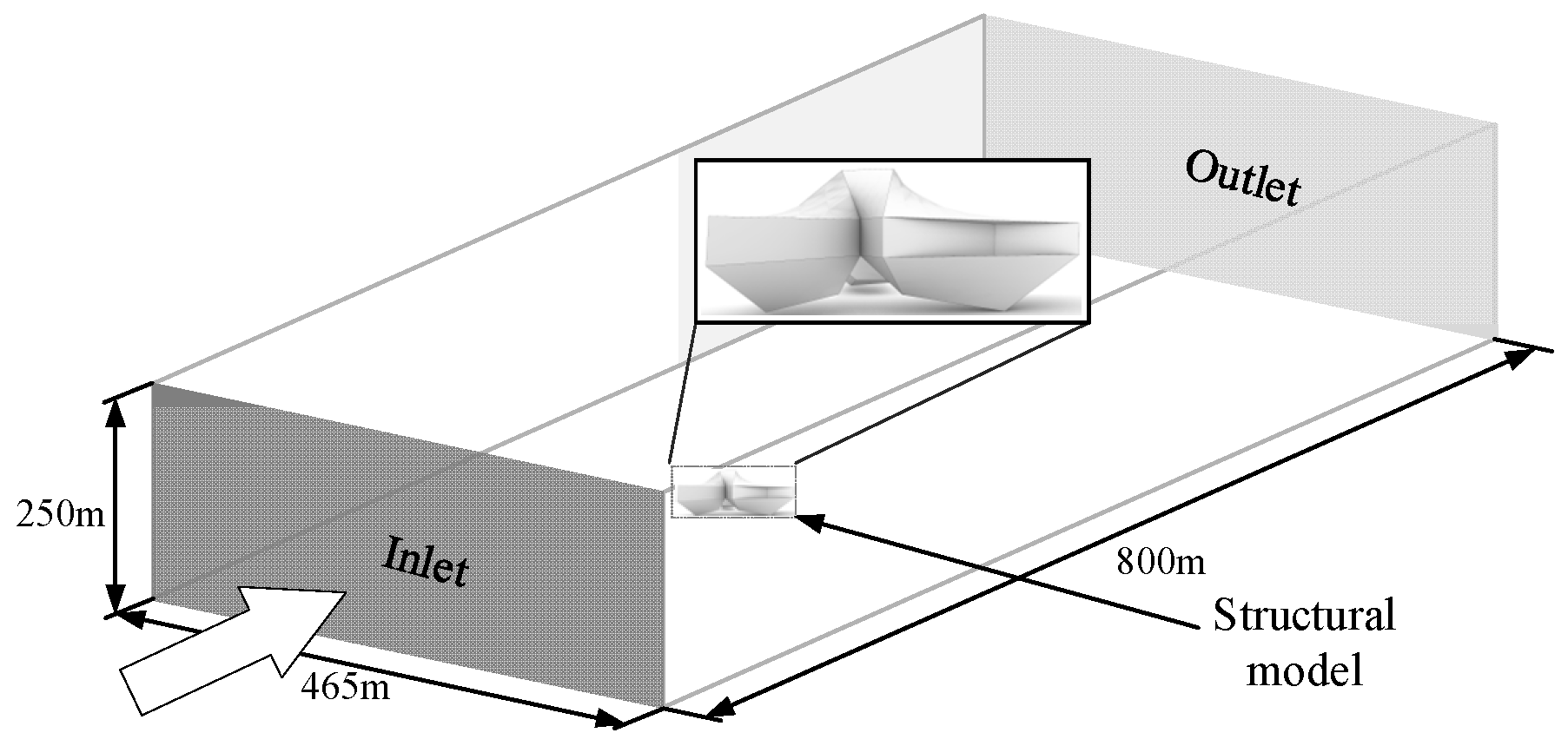
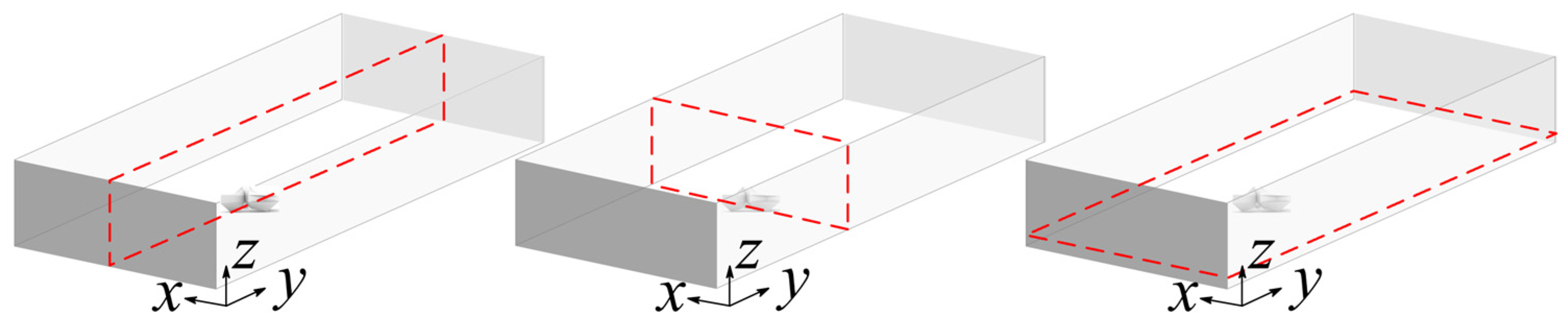
3.2. Computational Domain and Boundary Conditions
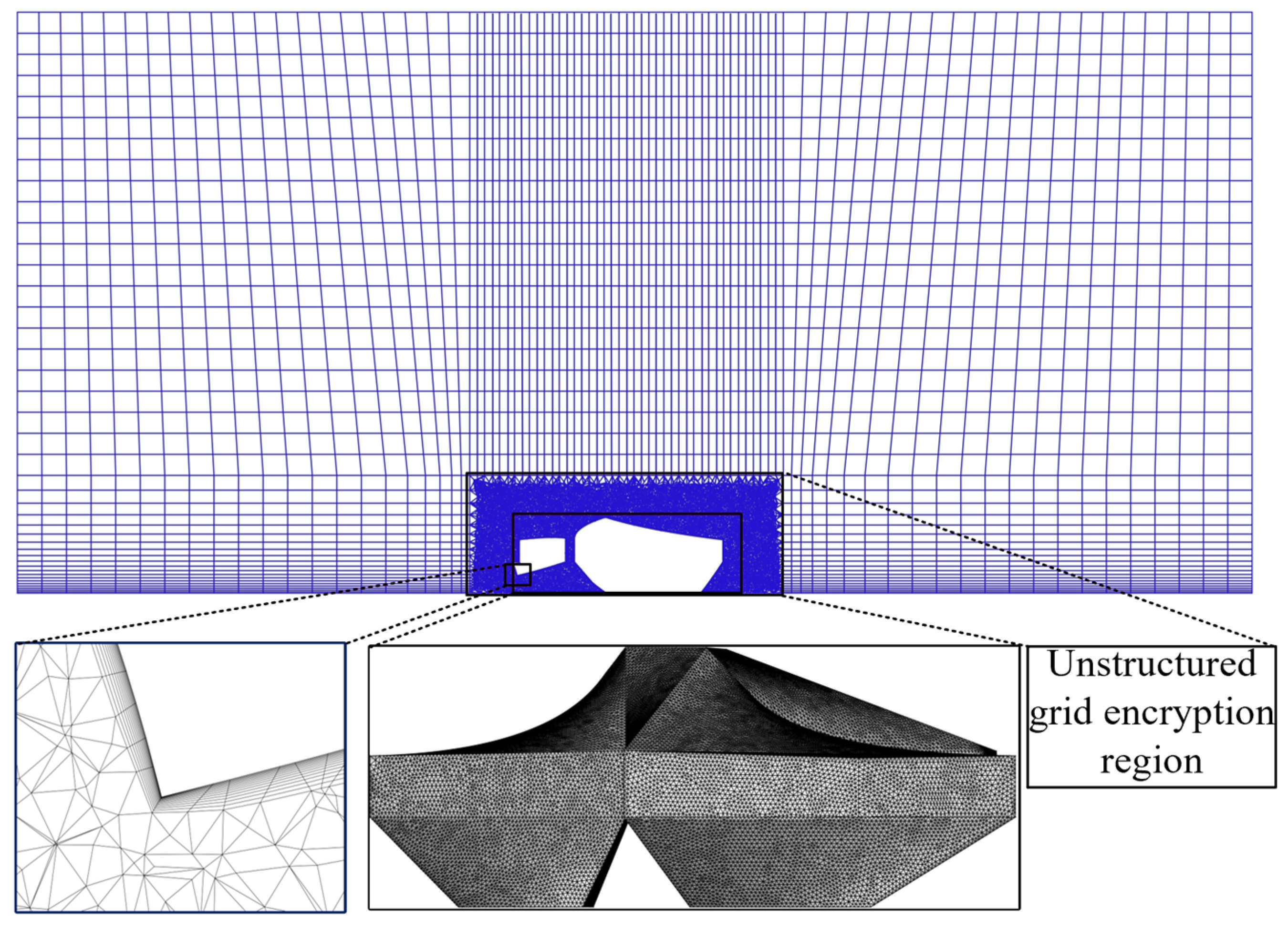
3.3. Mesh Partition
4. Analysis of the Calculation Results
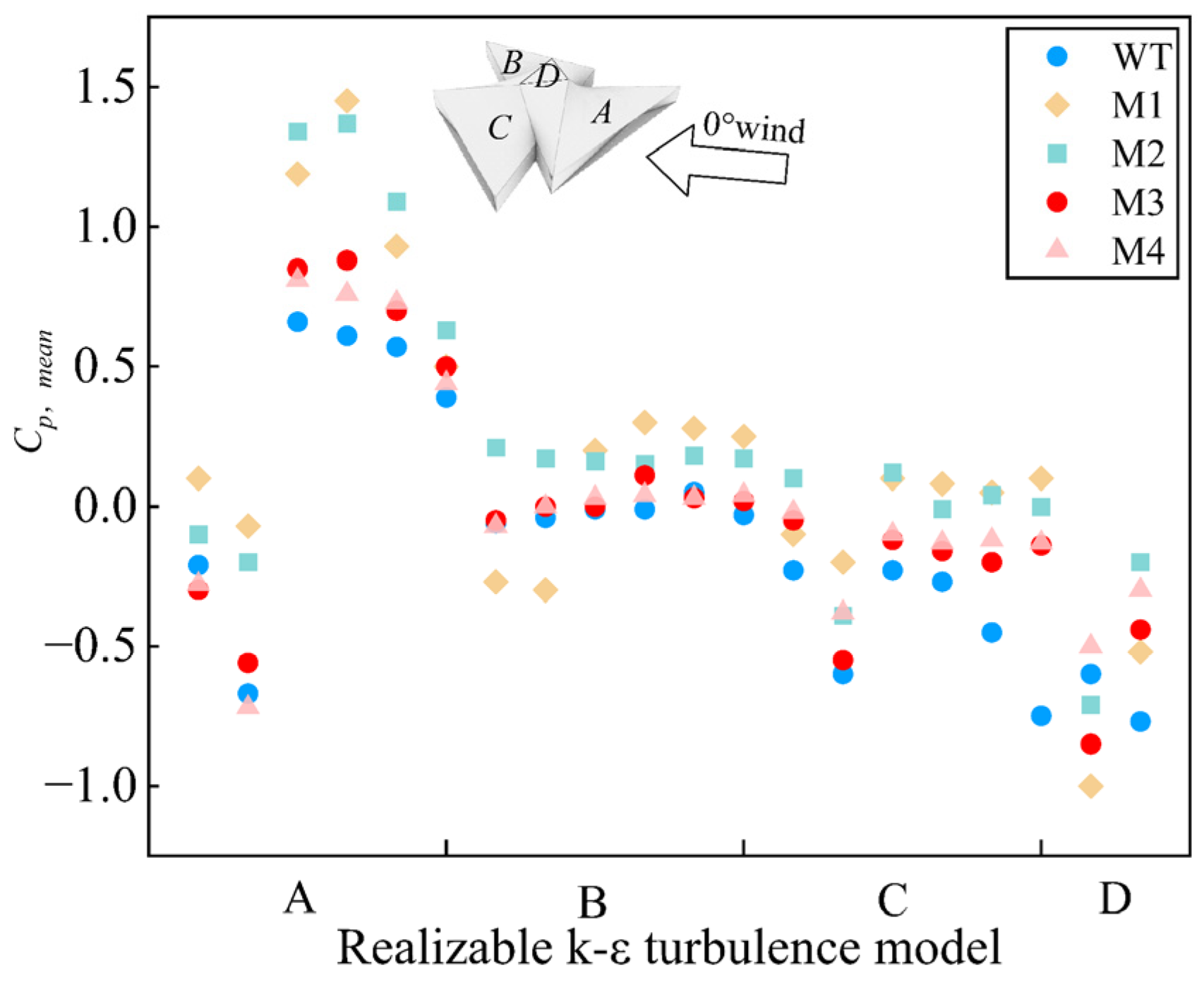
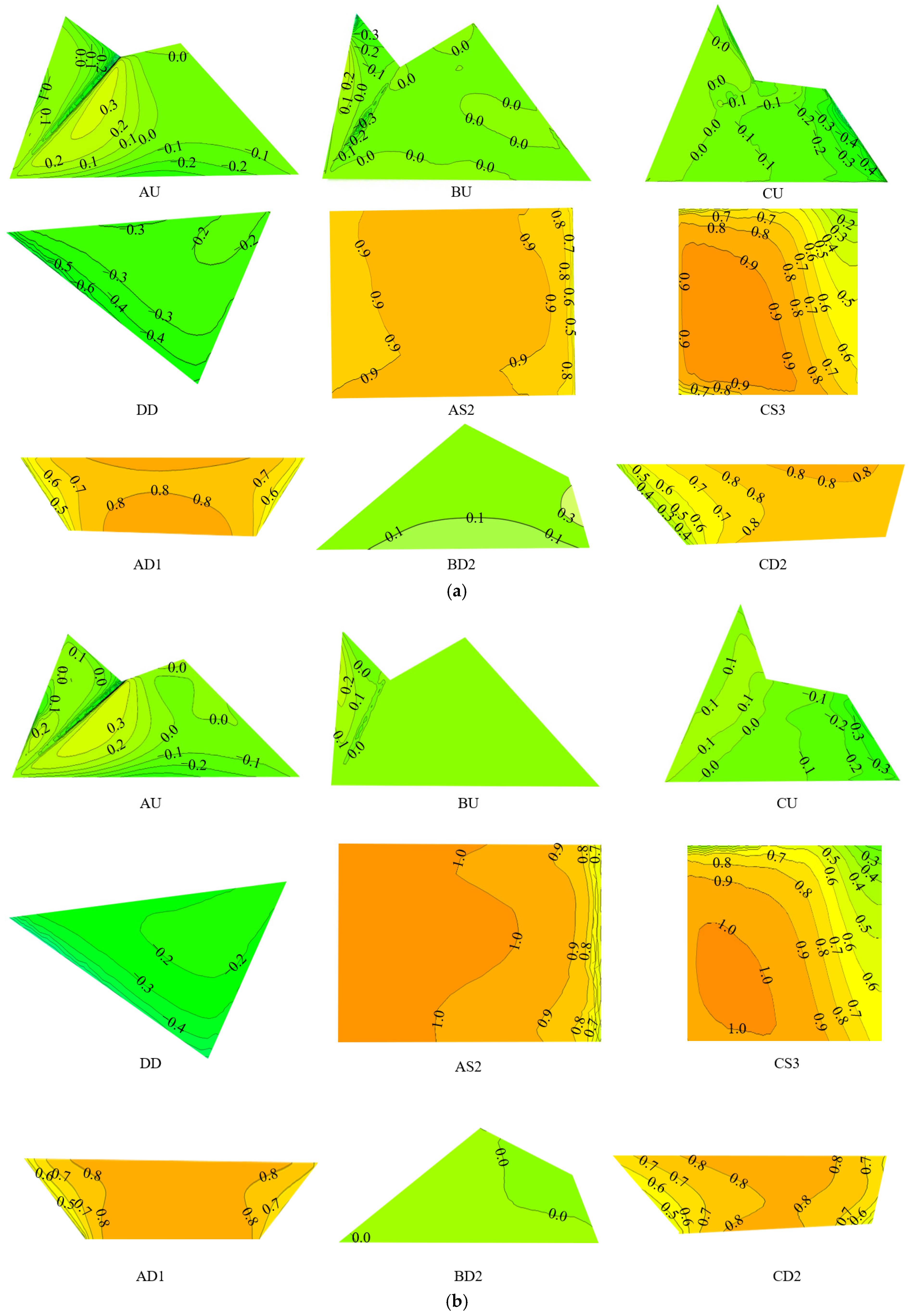
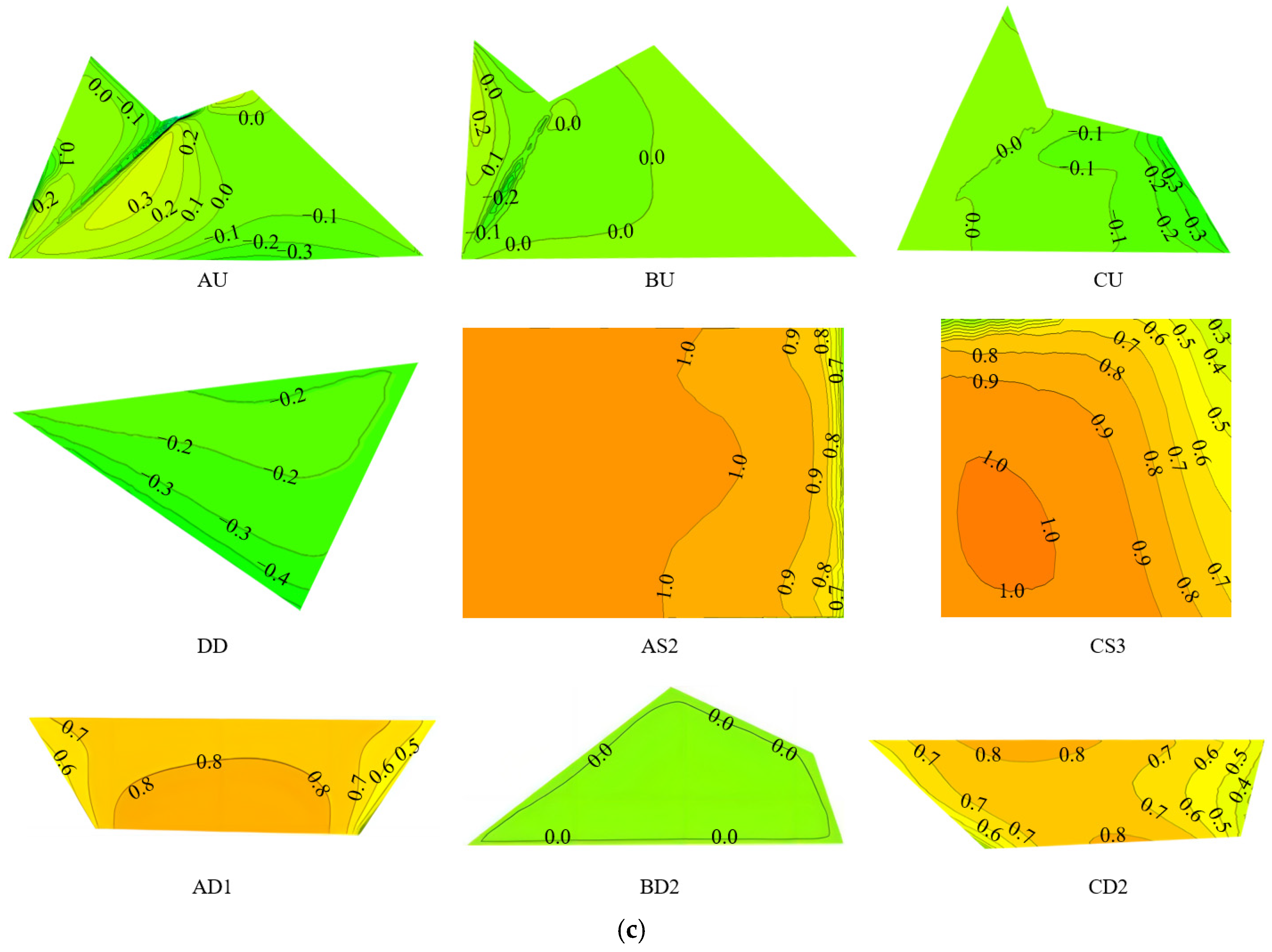
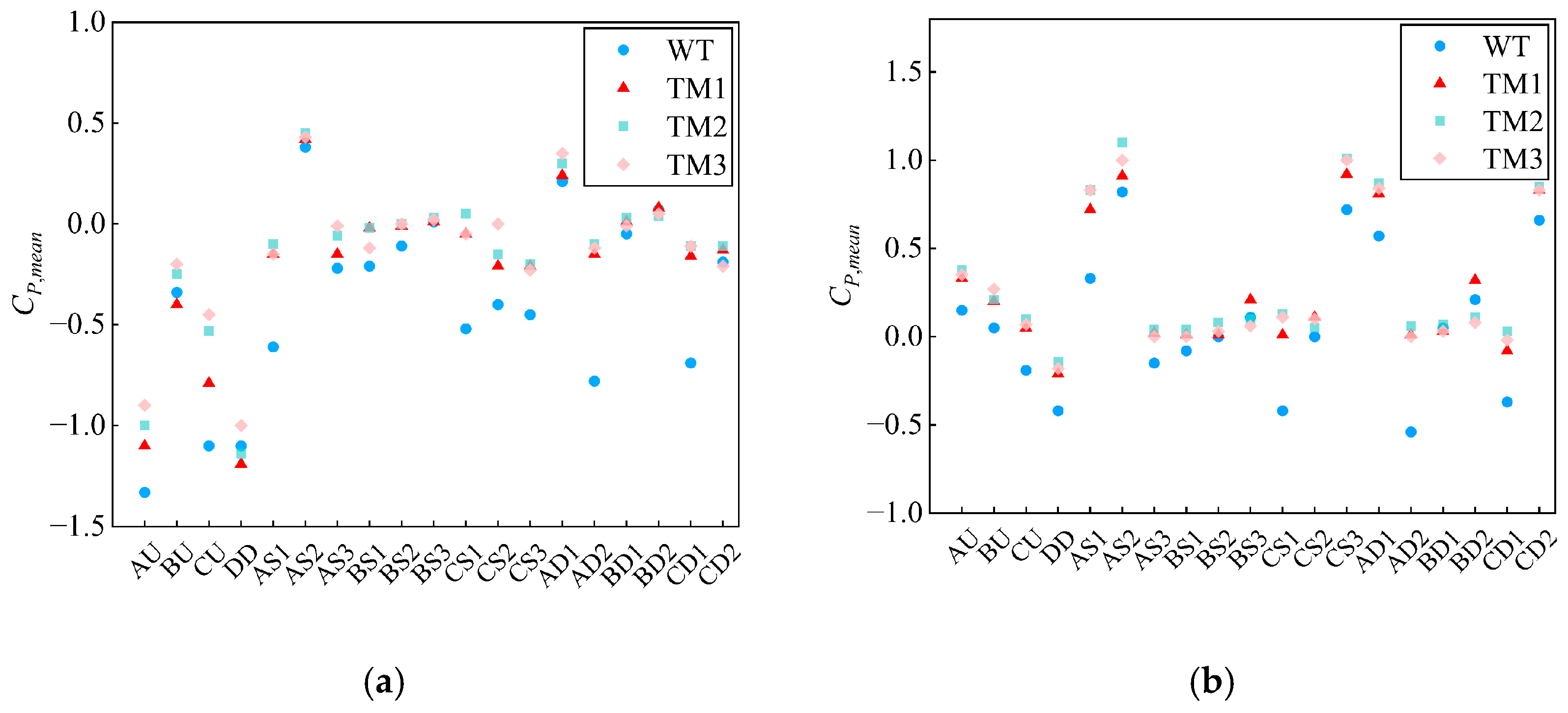
4.1. Comparison of Various Turbulence Models
4.2. Wind Pressure Distribution at the Structure Surface
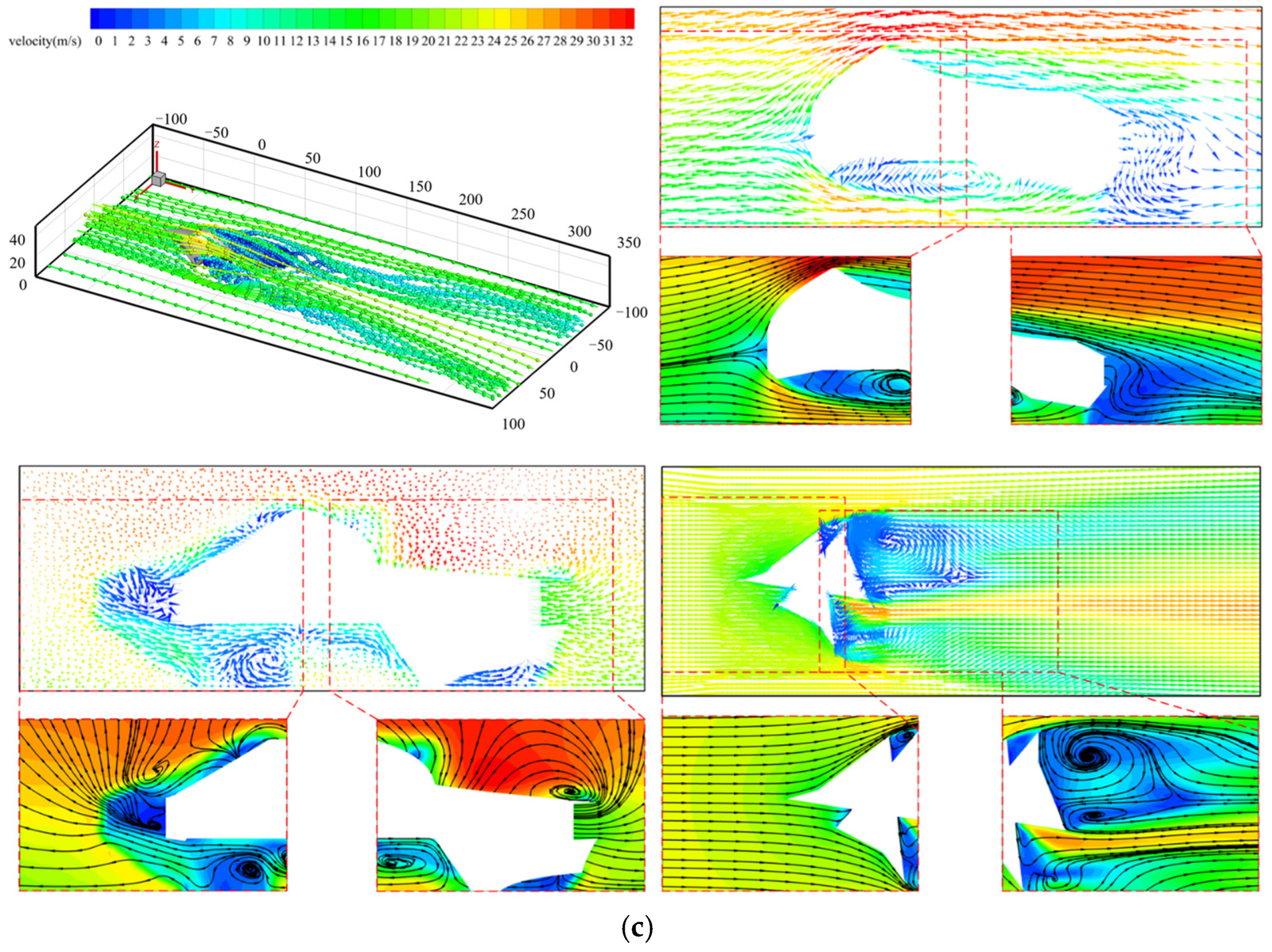
4.3. Airflow Field Around Structure
5. Conclusions
- (1)
- The wind pressure distribution of complex spatial structures is analyzed using RANS method with k-ε turbulence models, a scalable wall function, and a hybrid meshing strategy. Compared to wind tunnel tests, the RANS method slightly overestimates the positive wind pressure distribution range and the extreme positive mean wind pressure coefficient due to inherent limitations of the k-ε models, while underestimating the negative wind pressure distribution range and the absolute value of the extreme mean negative wind pressure coefficient. Although some flow prediction discrepancies occur at specific locations due to structural complexity, the RANS method effectively captures the overall flow characteristics of intricate structures and aligns closely with the distribution patterns in wind tunnel tests, demonstrating its suitability for such analyses.
- (2)
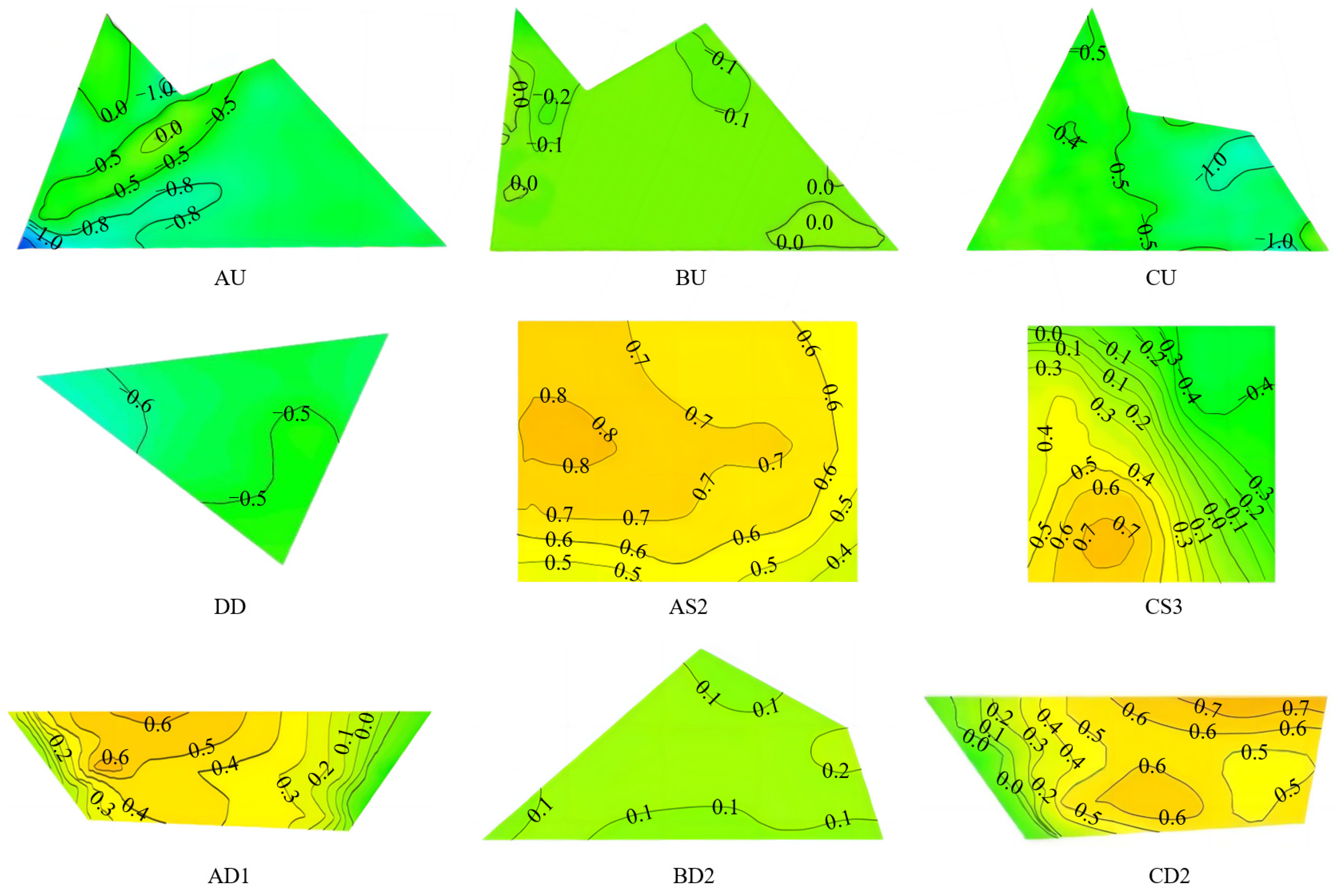
- Simulation results using the RANS method with k-ε turbulence models are affected by the shape of complex structures in wind pressure distribution analysis. Accuracy is highest in smooth, flat areas, especially in the middle and lower sections. However, it decreases in regions with pronounced surface changes, such as large curved roofs, where complexity increases. Significant errors in mean wind pressure coefficients can occur at sharp corners due to insufficient modeling of complex flow separation.
- (3)
- The sharp corners, curved surfaces, ridges, and large internal concave features of the complex structure cause multiple flow separations at the edges and re-attachments on the roof. This results in a larger negative pressure zone and a steeper gradient of the unfavorable wind pressure coefficient. The leading edge blocks incoming flow, creating maximum positive pressures on the windward side, despite a minimal change in the pressure coefficient’s gradient. Additionally, the inward shape of the rear generates positive pressures on the lower part of the leeward side. Consequently, the intricate design creates a highly complex wind pressure distribution.
- (4)
- Wind pressure distribution on complex structures varies significantly with wind angles. Sharp corners and ridges cause flow separation at multiple points. Analysis shows the most severe negative wind pressure coefficients of −1.10 at 0° and −1.80 at 60°, with the latter being about 1.6 times greater. Furthermore, at 60°, the wind pressure coefficient contours are denser and the change gradient is steeper. Thus, wind pressure distribution is highly sensitive to wind direction for complex-shaped structures.
- (5)
- The numerical simulation method illustrates how the flow field around complex structures varies with different wind angles, highlighting the bypassing phenomenon. Flow separation occurs at gables, sharp corners, and ridges on the windward side, resulting in vortex shedding and multiple reattachments that create significant turbulence. As the wind angle changes, the wake flow adopts distinct forms, leading to considerable alterations in the surrounding flow field due to the structure’s intricate spatial profiles.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, Y.J.; Guan, H.W.; Shao, S.; Yang, Q.S. Provisions and Comparison of Chinese Wind Load Standard for Roof Components and Cladding. Structures 2021, 33, 2587–2598. [Google Scholar] [CrossRef]
- Shen, G.H.; Que, L.H.; Wan, H.P. Experimental Study on the Aerodynamic Characteristics of Combined Angle Transmission Tower Subject to Skew Wind. Adv. Struct. Eng. 2024, 27, 1016–1030. [Google Scholar] [CrossRef]
- Bandi, E.K.; Tamura, Y.; Yoshida, A.; Chul Kim, Y.; Yang, Q. Experimental Investigation on Aerodynamic Characteristics of Various Triangular-section High-rise Buildings. J. Wind Eng. Ind. Aerod. 2013, 122, 60–68. [Google Scholar] [CrossRef]
- Gu, M.; Wang, X.R.; Quan, Y. Wind Tunnel Test Study on Effects of Chamfered Corners on the Aerodynamic Characteristics of 2D Rectangular Prisms. J. Wind Eng. Ind. Aerod. 2020, 204, 104305. [Google Scholar] [CrossRef]
- Uematsu, Y.; Tsuruishi, R. Wind Load Evaluation System for the Design of Roof Cladding of Spherical Domes. J. Wind Eng. Ind. Aerod. 2008, 96, 2054–2066. [Google Scholar] [CrossRef]
- Chen, F.B.; Wang, W.J.; Zhou, J.F.; Shou, Z.R.; Li, Q.S. Experimental Investigation of Wind Pressure Characteristics and Aerodynamic Optimization of a Large-span Cantilevered Roof. Structures 2021, 34, 303–313. [Google Scholar] [CrossRef]
- Frontini, G.; Argentini, T.; Rosa, L.; Rocchi, D. Advances in the Application of the Principal Static Wind Loads:A large-span Roof Case. Eng. Struct. 2022, 262, 114314. [Google Scholar] [CrossRef]
- Rizzo, F.; D’asdia, P.; Ricciardelli, F.; Bartoli, G. Characterization of Pressure Coefficients on Hyperbolic Paraboloid Roofs. J. Wind Eng. Ind. Aerod. 2012, 102, 61–71. [Google Scholar] [CrossRef]
- Xin, L.G.; Zhou, X.Y.; Gu, M. Wind Tunnel Test and CFD Simulation of the Near-roof Wind Speed and Friction Velocity on Gable Roofs. J. Wind Eng. Ind. Aerod. 2022, 225, 105009. [Google Scholar] [CrossRef]
- Peren, J.I.; Van Hooff, T.; Ramponi, R.; Blocken, B.; Leite, B.C.C. Impact of Roof Geometry of an Isolated Leeward Sawtooth Roof Building on Cross-ventilation: Straight, Concave, Hybrid or Convex? J. Wind Eng. Ind. Aerod. 2015, 145, 102–114. [Google Scholar] [CrossRef]
- Durbin, P.A. Some Recent Developments in Turbulence Closure Modeling. Annu. Rev. Fluid Mech. 2015, 50, 77–103. [Google Scholar] [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences. NASA Rep. 2014, NASA/CR-2014-218178. [Google Scholar]
- Rajasekarababu, K.B.; Vinayagamurthy, G.; Ajay Kumar, T.M.; Selvirajan, S. Experimental and Computational Investigation of Wind Flow Field on a Span Roof Structure. Int. J. High-Rise Build. 2022, 11, 287–300. [Google Scholar]
- Yang, Q.S.; Chen, F.X.; Tamura, Y.; Li, T.; Yan, B.W. Fluid-structure Interaction Behaviors of Tension Membrane Roofs by Fully-coupled Numerical Simulation. J. Wind Eng. Ind. Aerod. 2024, 244, 1056092. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.S.; Huang, S.H.; Fu, J.Y.; Xiao, Y.Q. Large Eddy Simulation of Wind Loads on a Long-span Spatial Lattice Roof. Wind Struct. 2010, 13, 57–83. [Google Scholar] [CrossRef]
- Liu, M.; Li, Q.S.; Huang, S.H.; Shi, F.; Chen, F.B. Evaluation of Wind Effects on a Large Span Retractable Roof Stadium by Wind Tunnel Experiment and Numerical Simulation. J. Wind Eng. Ind. Aerod. 2018, 179, 39–57. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in Building Simulation for Outdoor and Indoor Applications: A Foregone Conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Han, Y.; Stoellinger, M.K.; Peng, H.W.; Zhang, L.H.; Liu, W. Large Eddy Simulation of Atmospheric Boundary Layer Flow over Complex Terrain in Comparison with RANS Simulation and On-site Measurements under Neutral Stability Condition. J. Renew. Sustain. Ener. 2023, 15, 023301. [Google Scholar] [CrossRef]
- Hanjalic, K. Will RANS Survive LES? A View of Perspectives. J. Fluid. Eng. Asme 2005, 127, 831–839. [Google Scholar] [CrossRef]
- Cecora, R.; Radespiel, R.; Eisfeld, B.; Probst, A. Differential Reynolds-stress Modeling for Aeronautics. AIAA J. 2015, 53, 739–755. [Google Scholar] [CrossRef]
- Peralta, C.; Navarro, J.; Cruz, I.; Toja-Silva, F.; Lopez-Garcia, O. Roof Region Dependent Wind Potential Assessment with Different RANS Turbulence Models. J. Wind Eng. Ind. Aerod. 2015, 142, 258–271. [Google Scholar]
- Potsis, T.; Tominaga, Y.; Stathopoulos, T. Computational Wind Engineering: 30 Years of Research Progress in Building Structures and Environment. J. Wind Eng. Ind. Aerod. 2023, 234, 105346. [Google Scholar] [CrossRef]
- Yang, Q.; Chen, F.; Yan, B.; Li, T.; Yan, J. A Transport Model of Convective Flow on Self-excited Vibrating Flat Flexible Roofs Using LES. J. Wind. Eng. Ind. Aerod. J. Int. Assoc. Wind. Eng. 2023, 238, 105426. [Google Scholar] [CrossRef]
- Liu, J.N.; Wang, D.X.; Huang, X.Q. Investigation of Turbulence Models for Aerodynamic Analysis of a High-pressure-ratio Centrifugal Compressor. Phys. Fluids. 2023, 35, 21. [Google Scholar] [CrossRef]
- Quaresma, A.L.; Romão, F.; Pinheiro, A.N. A Comparative Assessment of Reynolds Averaged Navier–Stokes and Large-Eddy Simulation Models: Choosing the Best for Pool-Type Fishway Flow Simulations. Water 2025, 17, 686. [Google Scholar] [CrossRef]
- Pool Blanco, S.J.; Hincz, K. Computational Wind Engineering of a Mast-supported Tensile Structure. Period. Polytech. Civ. Eng. 2022, 66, 210–219. [Google Scholar] [CrossRef]
- Rumsey, C.L. Apparent Transition Behavior of Widely-used Turbulence Models. Int. J. Heat Fluid Flow 2007, 28, 1460–1471. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, Z.J. CPR High-order Discretization of the RANS Equations with the SA Model. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; AIAA: Reston, VI, USA, 2015. [Google Scholar]
- Schoenawa, S.; Hartmann, R. Discontinuous Galerkin discretization of the Reynolds-averaged Navier-Stokes equations with the shear-stress transport model. J. Comput. Phys. 2014, 262, 194–216. [Google Scholar] [CrossRef]
- Karvelis, A.C.; Dimas, A.A.; Gantes, C.J. Unsteady Numerical Simulation of Two-dimensional Airflow over a Square Cross-section at High Reynolds Numbers as a Reduced Model of Wind Actions on Buildings. Buildings 2024, 14, 561. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1993. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Model of Turbulence; Academic Press: Cambridge, MA, USA, 1974; Volume 3, pp. 269–289. [Google Scholar]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.G.; Zhu, J. A New k-ε Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Murakami, S. Overview of Turbulence Models Applied in CWE-1997. J. Wind Eng. Ind. Aerod. 1998, 74–76, 1–24. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ Guidelines for Practical Applications of CFD to Pedestrian Wind Environment around Buildings. J. Wind Eng. Ind. Aerod. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Mani, M.; Dorgan, A.J. A Perspective on the State of Aerospace Computational Fluid Dynamics Technology. Annu. Rev. Fluid Mech. 2023, 55, 431–457. [Google Scholar] [CrossRef]
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Development: Beijing, China, 2012.
- AIJRLB-2004; AIJ Recommendations for Loads on Buildings. Architectural Institute of Japan: Tokyo, Japan, 2004.
- Baum, J.D.; Loehner, R.; Luo, H. High-Reynolds Number Viscous Flow Computations Using an Unstructured-grid Method. J. Aircr. 2005, 42, 483–492. [Google Scholar]
- Mohotti, D.; Wijesooriya, K.; Dias-da-Costa, D. Comparison of Reynolds Averaging Navier-Stokes (RANS) Turbulent Models in Predicting Wind Pressure on Tall Buildings. J. Build. Eng. 2019, 21, 1–17. [Google Scholar] [CrossRef]


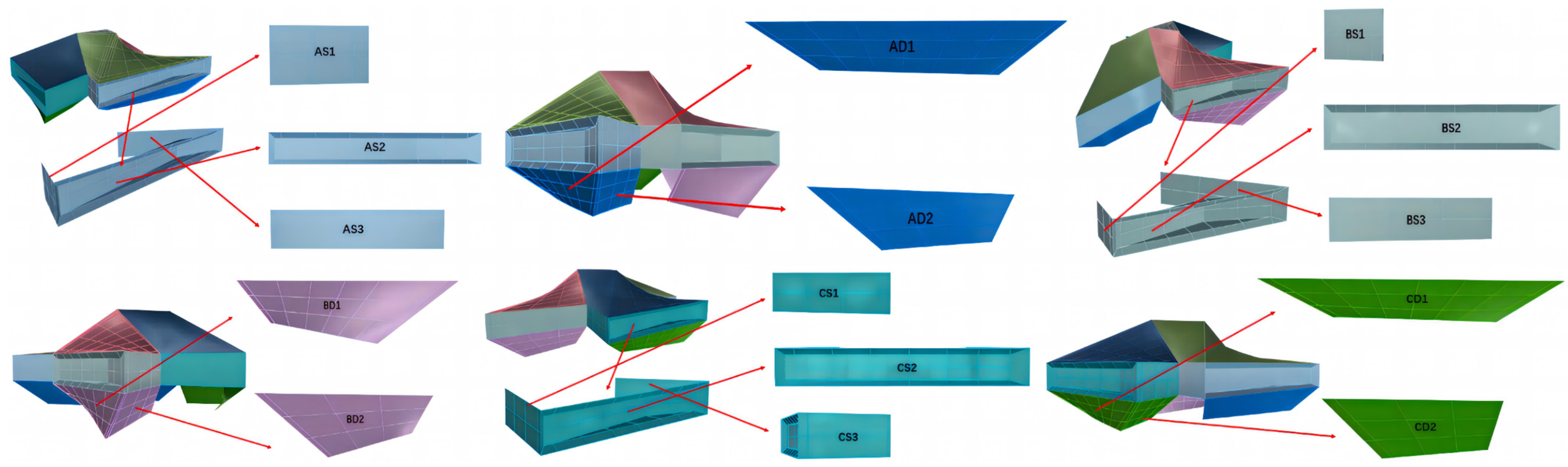
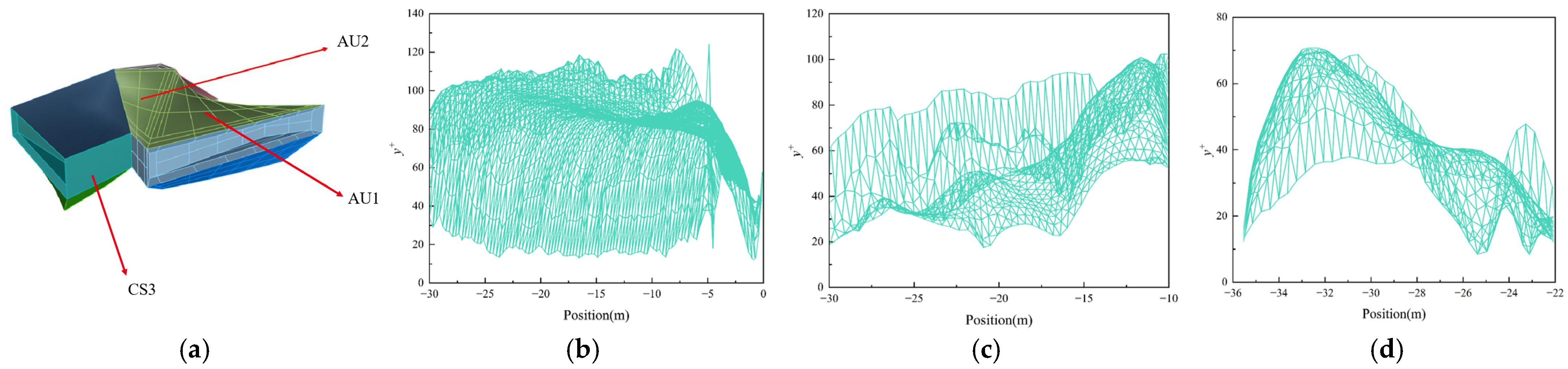

| Structural Main Zones | Structural Subregions | Quantity of Subzones |
|---|---|---|
| A | AU | 59 |
| AS | 28 | |
| AD | 36 | |
| B | BU | 59 |
| BS | 28 | |
| BD | 36 | |
| C | CU | 54 |
| CS | 30 | |
| CD | 36 | |
| D | DD | 7 |
| Meshing Scheme | M1 | M2 | M3 | M4 |
|---|---|---|---|---|
| Size of surface grid/m | 1 | 0.8 | 0.5 | 0.3 |
| Size of unstructured grid/m | 2 | 1.5 | 1 | 0.8 |
| Height of the first layer of the grid m | 0.005 | 0.005 | 0.003 | 0.003 |
| Number of mesh cell | 1,121,514 | 1,896,425 | 3,002,519 | 5,804,584 |
| Meshing Scheme | M1 | M2 | M3 | M4 |
|---|---|---|---|---|
| A | 47.95% | 38.02% | 25.06% | 27.03% |
| B | 30.99% | 25.01% | 16.96% | 13.06% |
| C | 34.07% | 37.97% | 28.96% | 25.06% |
| D | 25.93% | 31.91% | 23.03% | 17.98% |
| Subregions | WT | TM1 | TM2 | TM3 | |||
|---|---|---|---|---|---|---|---|
| Extreme Value | Extreme Value | Deviation | Extreme Value | Deviation | Extreme Value | Deviation | |
| AU | −1.33 | −1.10 | 17.3% | −1.00 | 24.8% | −0.90 | 32.3% |
| BU | −0.34 | −0.40 | 17.6% | −0.25 | 26.5% | −0.20 | 41.2% |
| CU | −1.10 | −0.79 | 28.2% | −0.53 | 51.8% | −0.45 | 59.1% |
| DD | −1.10 | −1.19 | 8.2% | −1.14 | 3.6% | −1.00 | 9.1% |
| AS2 | 0.82 | 0.91 | 10.9% | 1.10 | 34.1% | 1.00 | 22.0% |
| CS3 | 0.72 | 0.92 | 27.8% | 1.01 | 40.3% | 1.00 | 38.9% |
| AD1 | 0.57 | 0.81 | 42.1% | 0.87 | 52.6% | 0.84 | 47.4% |
| BD2 | 0.21 | 0.32 | 52.4% | 0.11 | 47.1% | 0.08 | 61.9% |
| CD2 | 0.66 | 0.83 | 25.8% | 0.85 | 28.8% | 0.83 | 25.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhou, S.; Liu, H.; Zhao, S.; He, F.; Zhao, L. Study on the Wind Pressure Distribution in Complicated Spatial Structure Based on k-ε Turbulence Models. Buildings 2025, 15, 1877. https://doi.org/10.3390/buildings15111877
Wang J, Zhou S, Liu H, Zhao S, He F, Zhao L. Study on the Wind Pressure Distribution in Complicated Spatial Structure Based on k-ε Turbulence Models. Buildings. 2025; 15(11):1877. https://doi.org/10.3390/buildings15111877
Chicago/Turabian StyleWang, Jing, Shixiong Zhou, Hui Liu, Shixing Zhao, Fei He, and Lei Zhao. 2025. "Study on the Wind Pressure Distribution in Complicated Spatial Structure Based on k-ε Turbulence Models" Buildings 15, no. 11: 1877. https://doi.org/10.3390/buildings15111877
APA StyleWang, J., Zhou, S., Liu, H., Zhao, S., He, F., & Zhao, L. (2025). Study on the Wind Pressure Distribution in Complicated Spatial Structure Based on k-ε Turbulence Models. Buildings, 15(11), 1877. https://doi.org/10.3390/buildings15111877






