Research on a Damage Assessment Method for Concrete Components Based on Material Damage
Abstract
1. Introduction
2. Constitutive Relationship of Concrete
3. Damage Assessment Method for Concrete Components
4. Numerical Simulation
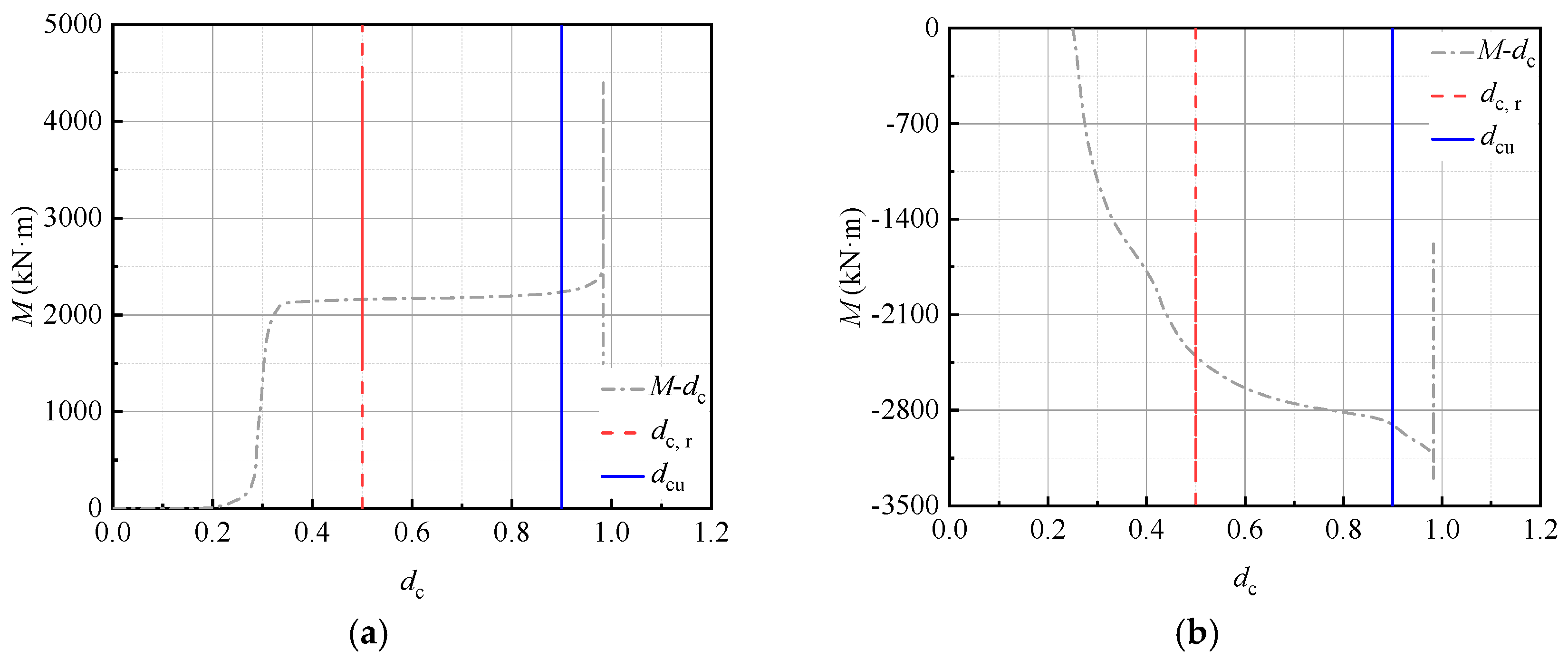
4.1. Application of Uniaxial Damage Evolution Parameter of Concrete dc(t) in ABAQUS
4.2. Test Results
4.3. Development of FE Model
4.4. Verification of FE Model
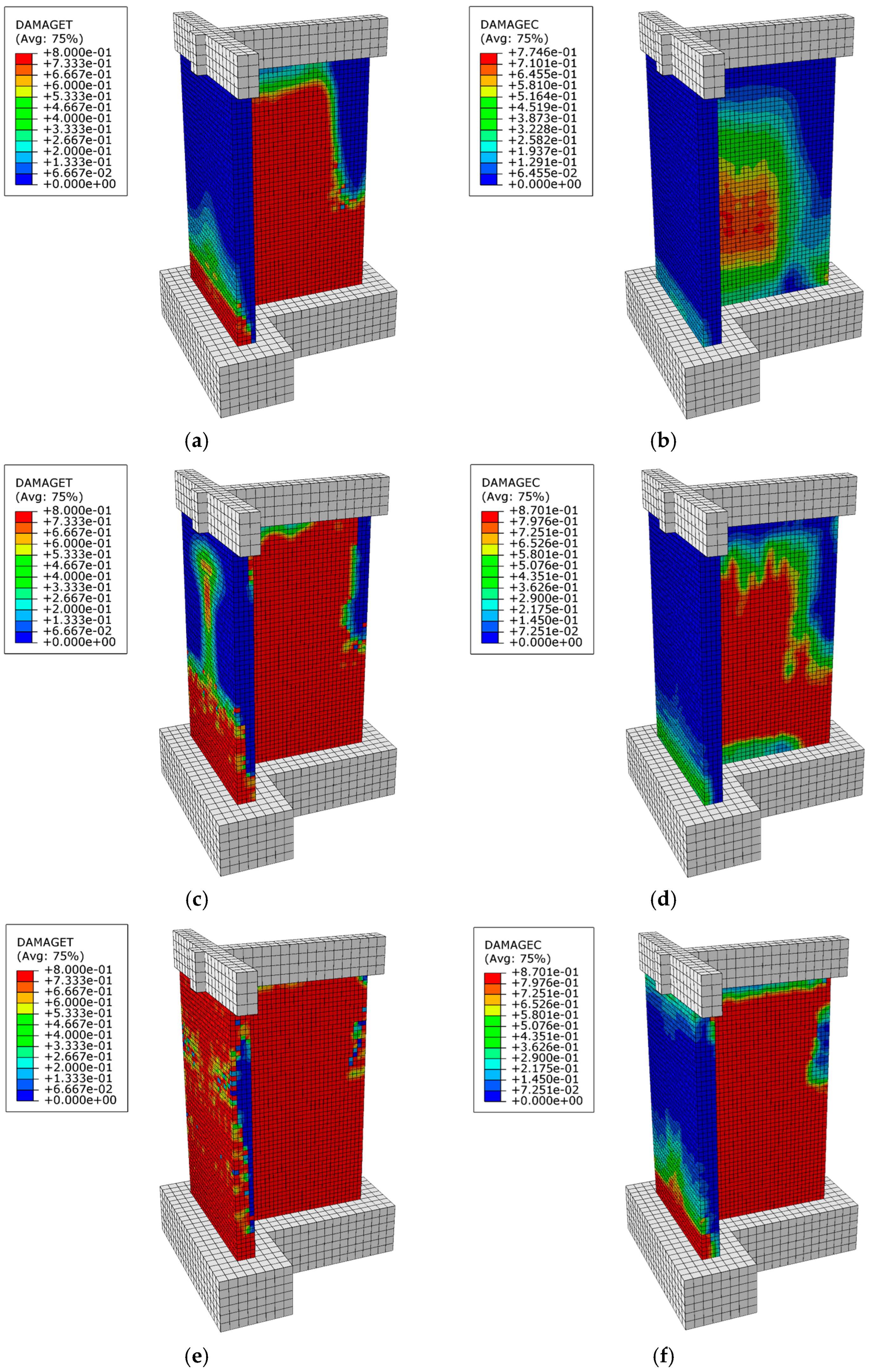
4.5. Damage Analysis
4.6. Damage Assessment
5. Conclusions
- (1)
- The damage assessment method for concrete components proposed in this study can well represent the damage grades of concrete shear wall components. Due to the poor tensile performance of concrete and the early development of cracks, the tensile plastic damage factor Dt reaches the peak value quickly; it is more scientific and reasonable to define the damage grade of concrete shear wall components using the value of dc than using the value of dt, as it can more accurately reflect the actual damage status of the components.
- (2)
- Using dc and the compressive damage index of concrete Dc0 to define the damage grade of the concrete shear wall component, the evaluation results are basically consistent.
- (3)
- From a macroscopic perspective, the damage assessment method for concrete components based on dc(t) is more in line with actual expectations and has a higher safety factor compared with the damage assessment method for concrete components based on concrete compressive strain εc mentioned in the Chinese association standard T/CECA 20024-2022.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shan, J.; Wang, L.; Loong, C.N.; Zhang, H.; Huang, P. Damage tracking and hysteresis-based evaluation of seismic-excited RC shear wall using monitoring data. Struct. Des. Tall Spec. Build. 2024, 33, e2087. [Google Scholar] [CrossRef]
- Shan, J.; Zhuang, C.; Loong, C.N. Parametric identification of Timoshenko-beam model for shear-wall structures using monitoring data. Mech. Syst. Signal Process. 2023, 189, 110100. [Google Scholar] [CrossRef]
- Hernandez, E.M.; May, G. Dissipated energy ratio as a feature for earthquake-induced damage detection of instrumented structures. J. Eng. Mech. 2013, 139, 1521–1529. [Google Scholar] [CrossRef]
- Xiong, C.; Lu, X.; Lin, X. Damage assessment of shear wall components for RC frame–shear wall buildings using story curvature as engineering demand parameter. Eng. Struct. 2019, 189, 77–88. [Google Scholar] [CrossRef]
- SEAOC Vision 2000 Committee. Performance-Based Seismic Engineering of Building; Structural Engineers Association of California: Sacramento, CA, USA, 1995. [Google Scholar]
- Xu, R.F.; Dai, G.Y. Performance-based seismic design of tall building structures beyond the code-specification. China Civ. Eng. J. 2005, 1, 1–10. (In Chinese) [Google Scholar]
- Park, Y.J.; Ang, A.H.S. Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Wu, J.Y.; Li, J.; Faria, R. An energy release rate-based plastic-damage model for concrete. Int. J. Solids Struct. 2006, 43, 583–612. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef]
- Li, J.; Ren, X. Stochastic damage model for concrete based on energy equivalent strain. Int. J. Solids Struct. 2009, 46, 2407–2419. [Google Scholar] [CrossRef]
- Cicekli, U.; Voyiadjis, G.Z.; Al-Rub, R.K.A. A plasticity and anisotropic damage model for plain concrete. Int. J. Plast. 2007, 23, 1874–1900. [Google Scholar] [CrossRef]
- Nie, J.G.; Wang, Y.H. Comparison study of constitutive model of concrete in ABAQUS for static analysis of structures. Eng. Mech. 2013, 30, 59–67. (In Chinese) [Google Scholar]
- Scientists of the US Geological Survey and the Southern California Earthquake Center. The magnitude 6.7 Northridge, California, earthquake of 17 January 1994. Science 1994, 266, 389–397. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, N.; Yamazaki, F. Estimation of strong motion distribution in the 1995 Kobe earthquake based on building damage data. Earthq. Eng. Struct. Dyn. 2001, 30, 787–801. [Google Scholar] [CrossRef]
- Durukal, E.; Erdik, M. Physical and economic losses sustained by the industry in the 1999 Kocaeli, Turkey earthquake. Nat. Hazards 2008, 46, 153–178. [Google Scholar] [CrossRef]
- Zhao, B.; Taucer, F.; Rossetto, T. Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China. Eng. Struct. 2009, 31, 1707–1723. [Google Scholar] [CrossRef]
- Jünemann, R.; de La Llera, J.C.; Hube, M.A.; Cifuentes, L.A.; Kausel, E. A statistical analysis of reinforced concrete wall buildings damaged during the 2010, Chile earthquake. Eng. Struct. 2015, 82, 168–185. [Google Scholar] [CrossRef]
- Goda, K.; Pomonis, A.; Chian, S.C.; Offord, M.; Saito, K.; Sammonds, P.; Fraser, S.; Raby, A.; Macabuag, J. Ground motion characteristics and shaking damage of the 11th March 2011 Mw9.0 Great East Japan earthquake. Bull. Earthq. Eng. 2013, 11, 141–170. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Zhou, Y.; Lin, X.; Wang, X.; Shang, Q. Preliminary investigation of building damage in Hatay under February 6, 2023 Turkey earthquakes. Earthq. Eng. Eng. Vib. 2023, 22, 853–866. [Google Scholar] [CrossRef]
- Xu, G.; Guo, T.; Li, A.Q. Seismic resilient shear wall structures: A state-of-the-art review. Sci. China Technol. Sci. 2023, 66, 1640–1661. [Google Scholar] [CrossRef]
- T/CECA 20024–2022; Standard for Performance-Based Seismic Design of Building Structures. China Building Materials Industry Press: Beijing, China, 2022. (In Chinese)
- Dougill, J.W. On stable progressively fracturing solids. J. Appl. Math. Phys. 1976, 27, 423–437. [Google Scholar] [CrossRef]
- Lemaitre, J.; Desmorat, R. Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures; Springer: Berlin/Heidelberg, Germany, 2006. (In Chinese) [Google Scholar]
- GB/T 50010–2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2024. (In Chinese)
- Ren, X.D.; Li, J. Calculation of concrete damage and plastic deformation. Build. Struct. 2015, 45, 29–31. (In Chinese) [Google Scholar]
- JGJ 3–2010; Technical Specification for Concrete Structures of Tall Building. China Architecture & Building Press: Beijing, China, 2010. (In Chinese)
- Ou, J.P.; He, Z.; Wu, B.; Qiu, F.W. Seismic damage performance-based design of reinforced concrete structures. Earthq. Eng. Eng. Dyn. 1999, 1, 21–30. (In Chinese) [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Lei, B.; Qi, T.; Li, Y.; Jin, Z.; Qian, W. An enhanced damaged plasticity model for concrete under cyclic and monotonic triaxial compression. Eur. J. Mech.-A/Solids 2023, 100, 104999. [Google Scholar] [CrossRef]
- Shafaie, V.; Ghodousian, O.; Ghodousian, A.; Homayounfar, M.; Rad, M.M. Slant shear tests and fuzzy logic integration for evaluating shear bond strength in SCC and FRSCC repair applications. Case Stud. Constr. Mater. 2025, 22, e04176. [Google Scholar] [CrossRef]
- Hibbitt, Karlsson & Sorensen. ABAQUS/Standard: User’s Manual; Dassault Systèmes: Johnston, RI, USA, 1997. [Google Scholar]
- Yao, F.B.; Guan, Q.; Wang, P.D. Simulation analysis of damage factor based on ABAQUS damaged plasticity model. Struct. Eng. 2019, 35, 76–81. (In Chinese) [Google Scholar]
- Dong, G.; Gu, Q.; Tan, Y.; Tian, S.; Gao, H. Experimental analysis on the seismic performance of prefabricated double-face superposed shear walls with different horizontal connection. J. Vib. Shock. 2020, 39, 107–114. (In Chinese) [Google Scholar]
- Luo, Y.Q.; Gu, Q.; Zhao, D.F.; Tian, S.; Tan, Y. Research on a seismic performances of T-shaped double-sided composited concrete shear walls with constructional edge members. Ind. Constr. 2021, 51, 90–97. (In Chinese) [Google Scholar]
- Gu, Q.; Yu, G.; Tan, Y.; Zhao, D.-F.; Gao, H.-Y. Experimental study on seismic behavior of L-shape double-side precast composite shear walls with constructional boundary elements. J. Archit. Civ. Eng. 2021, 38, 47–55. (In Chinese) [Google Scholar]
- Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing. Bull. N. Z. Soc. Earthq. Eng. 1989, 22, 155–166. [Google Scholar] [CrossRef]
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef]
- Gu, Q.; Ji, Y.; Cheng, J.F.; Peng, Y.; Zhao, D.; Ruan, Z. Seismic Behavior of L-Shaped Precast Concrete Double-Faced Superposed Shear Wall with Steel Truss Connectors. J. Build. Eng. 2025, 106, 112658. [Google Scholar] [CrossRef]
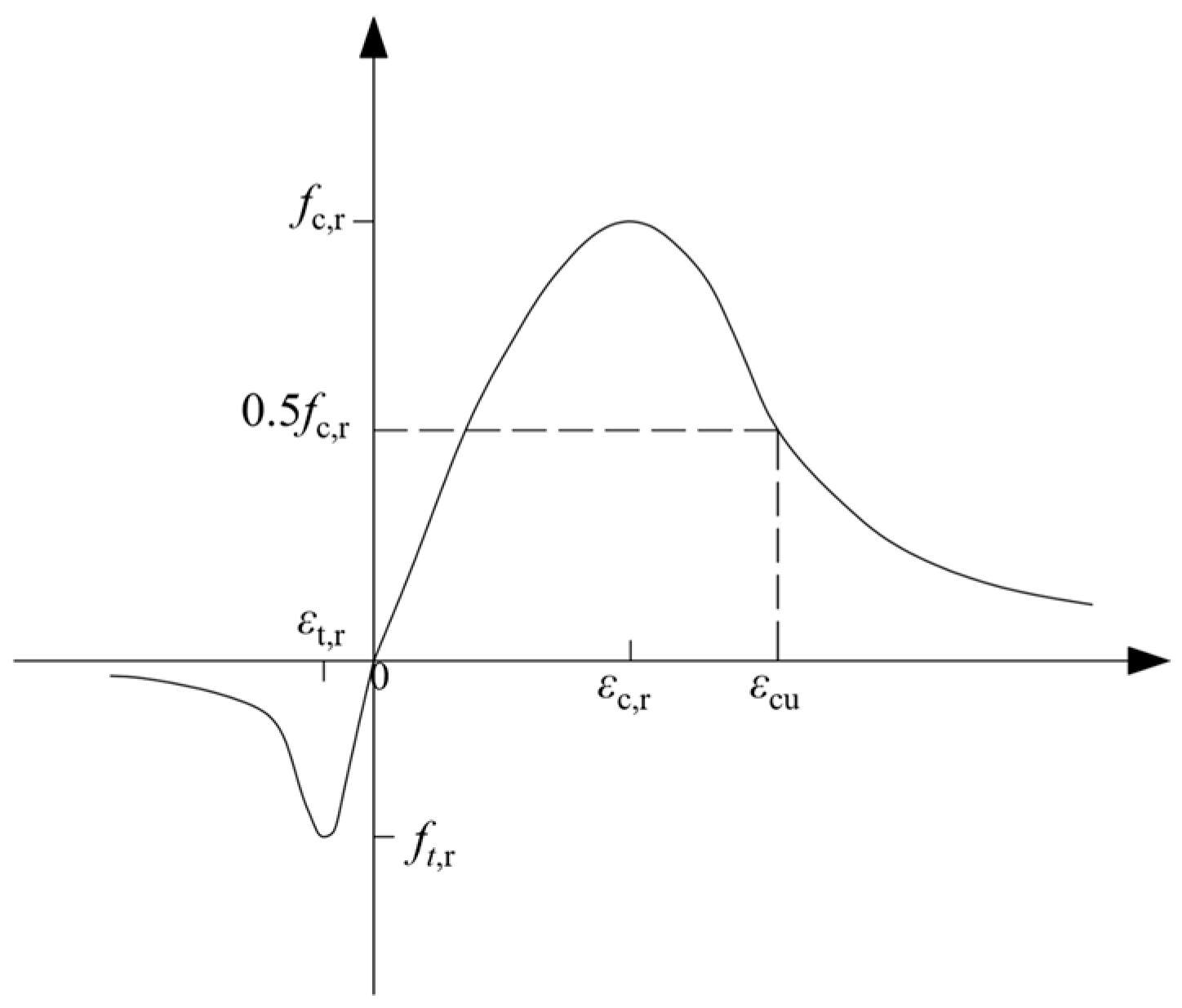

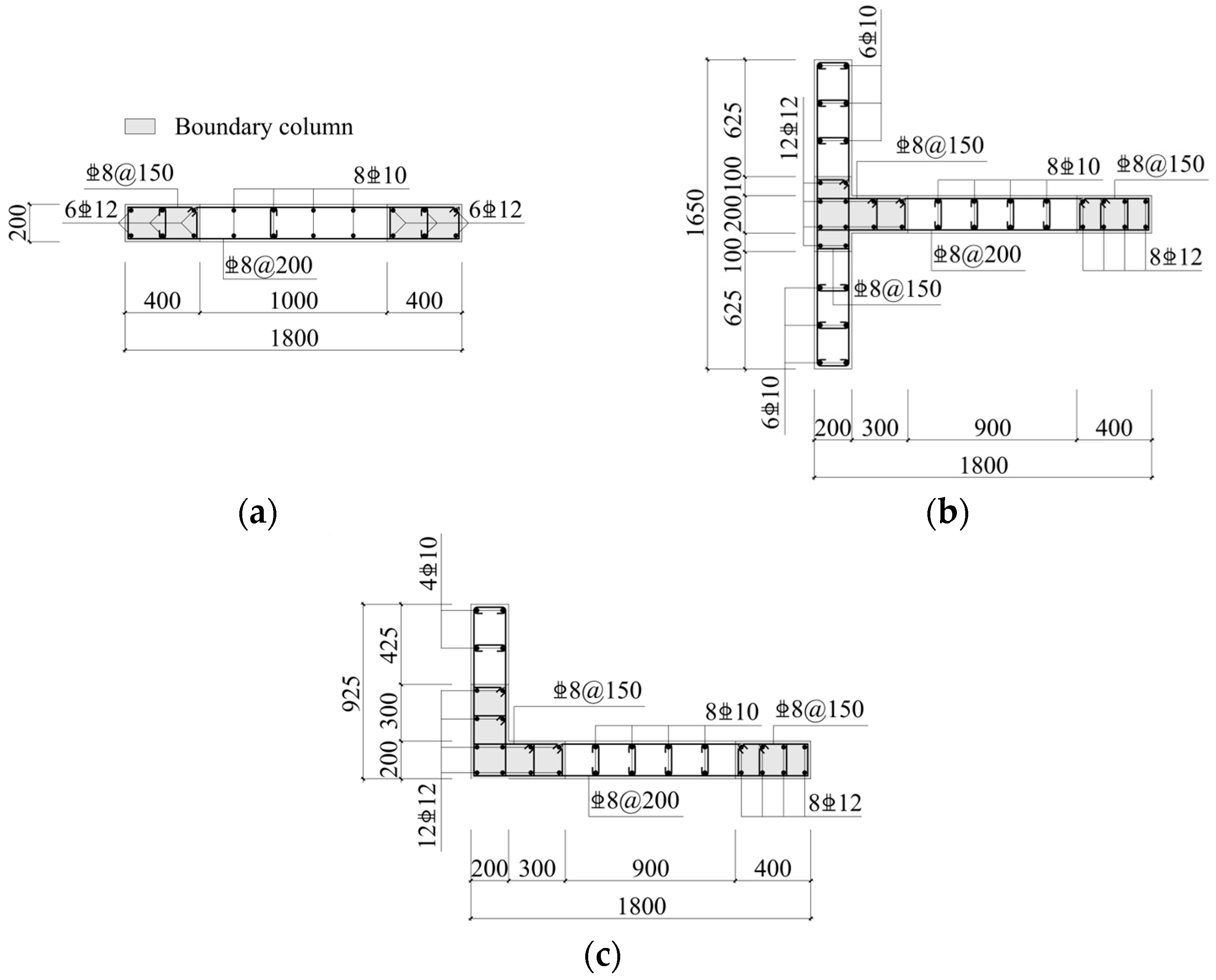
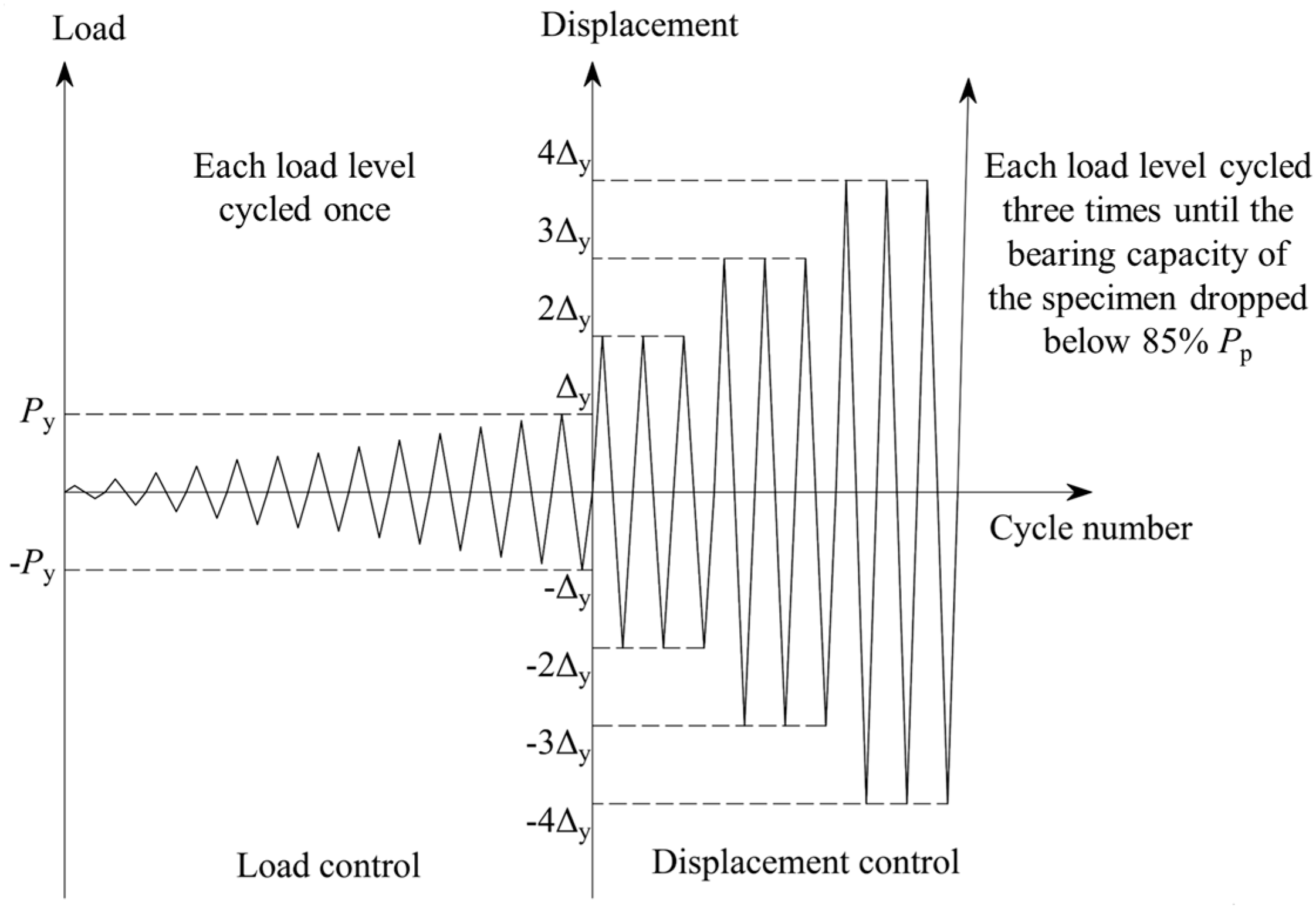
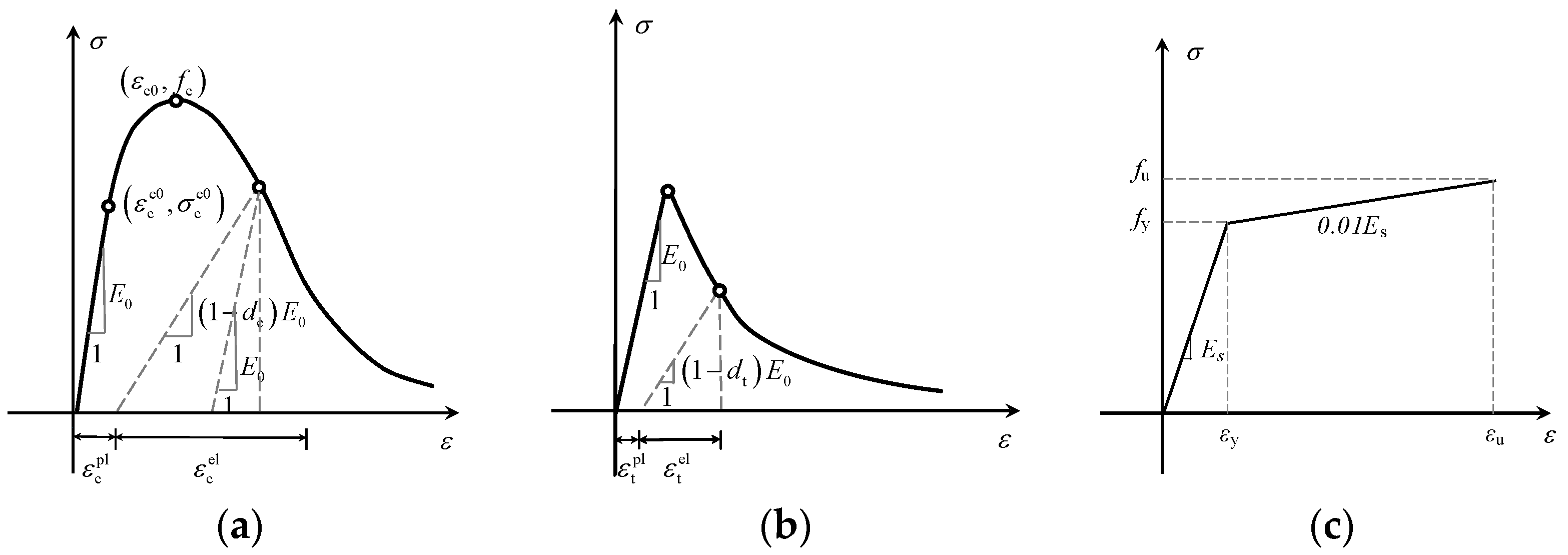





| Concrete Strength Grades | ft,r (MPa) | εt,r (10−6) | αt | εtu/εt,r | dt,r | dtu |
|---|---|---|---|---|---|---|
| C30 | 2.01 | 95 | 1.25 | 2.51 | 0.30 | 0.86 |
| C35 | 2.20 | 100 | 1.53 | 2.26 | 0.30 | 0.85 |
| C40 | 2.39 | 104 | 1.80 | 2.10 | 0.30 | 0.83 |
| C45 | 2.51 | 107 | 1.95 | 2.02 | 0.30 | 0.83 |
| C50 | 2.64 | 110 | 2.19 | 1.93 | 0.30 | 0.82 |
| C55 | 2.74 | 112 | 2.36 | 1.87 | 0.31 | 0.82 |
| C60 | 2.85 | 115 | 2.55 | 1.82 | 0.31 | 0.81 |
| C65 | 2.93 | 116 | 2.69 | 1.79 | 0.31 | 0.81 |
| C70 | 2.99 | 118 | 2.81 | 1.76 | 0.32 | 0.81 |
| C75 | 3.05 | 119 | 2.91 | 1.74 | 0.32 | 0.80 |
| C80 | 3.11 | 120 | 3.03 | 1.72 | 0.32 | 0.80 |
| Concrete Strength Grades | fc,r (MPa) | εc,r (10−6) | αc | εc,u/εc,r | dc,r | dcu |
|---|---|---|---|---|---|---|
| C30 | 20.1 | 1472 | 0.75 | 2.86 | 0.54 | 0.92 |
| C35 | 23.4 | 1531 | 0.96 | 2.73 | 0.51 | 0.91 |
| C40 | 26.8 | 1589 | 1.17 | 2.49 | 0.48 | 0.90 |
| C45 | 29.6 | 1634 | 1.34 | 2.32 | 0.46 | 0.88 |
| C50 | 32.4 | 1678 | 1.50 | 2.20 | 0.44 | 0.87 |
| C55 | 35.5 | 1727 | 1.68 | 2.09 | 0.42 | 0.86 |
| C60 | 38.5 | 1769 | 1.85 | 2.03 | 0.40 | 0.85 |
| C65 | 41.5 | 1808 | 2.02 | 1.97 | 0.37 | 0.84 |
| C70 | 44.5 | 1844 | 2.18 | 1.91 | 0.35 | 0.82 |
| C75 | 47.4 | 1884 | 2.34 | 1.90 | 0.33 | 0.82 |
| C80 | 50.2 | 1922 | 2.49 | 1.90 | 0.31 | 0.82 |
| Type | Damage Grade | |||||
|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | |
| Compressive damage variable | ≤0.01 | ≤0.2 | ≤0.5 | ≤0.65 | ≤0.8 | >0.8 |
| Compressive strain | ≤0.5εc,r | ≤1.0εc,r | ≤1.5εc,r | ≤1.0εcu | ≤1.5εcu | >1.5εcu |
| Damage Grade | Macro Description | dc | dt |
|---|---|---|---|
| L1 | Non-damaged state | ≤dc,r | ≤dt,r |
| L2 | Slightly damaged state | ≤0.25dcu + 0.75dc,r | ≤0.25dtu + 0.75dt,r |
| L3 | Mildly damaged state | ≤0.50dcu + 0.50dc,r | ≤0.50dtu + 0.50dt,r |
| L4 | Moderately damaged state | ≤0.75dcu + 0.25dc,r | ≤0.75dtu + 0.25dt,r |
| L5 | Relatively severely damaged state | ≤dcu | ≤dtu |
| L6 | Severely damaged state | >dcu | >dtu |
| Concrete Strength Grades | Damage Grade | |||||
|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | |
| C30 | ≤0.30 | ≤0.44 | ≤0.58 | ≤0.72 | ≤0.86 | >0.86 |
| C35 | ≤0.30 | ≤0.44 | ≤0.58 | ≤0.71 | ≤0.85 | >0.85 |
| C40 | ≤0.30 | ≤0.43 | ≤0.57 | ≤0.70 | ≤0.83 | >0.83 |
| C45 | ≤0.30 | ≤0.43 | ≤0.57 | ≤0.70 | ≤0.83 | >0.83 |
| C50 | ≤0.30 | ≤0.43 | ≤0.56 | ≤0.69 | ≤0.82 | >0.82 |
| C55 | ≤0.31 | ≤0.44 | ≤0.57 | ≤0.69 | ≤0.82 | >0.82 |
| C60 | ≤0.31 | ≤0.44 | ≤0.56 | ≤0.69 | ≤0.81 | >0.81 |
| C65 | ≤0.31 | ≤0.44 | ≤0.56 | ≤0.69 | ≤0.81 | >0.81 |
| C70 | ≤0.32 | ≤0.44 | ≤0.57 | ≤0.69 | ≤0.81 | >0.81 |
| C75 | ≤0.32 | ≤0.44 | ≤0.56 | ≤0.68 | ≤0.80 | >0.80 |
| C80 | ≤0.32 | ≤0.44 | ≤0.56 | ≤0.68 | ≤0.80 | >0.80 |
| Concrete Strength Grades | Damage Grade | |||||
|---|---|---|---|---|---|---|
| L1 | L2 | L3 | L4 | L5 | L6 | |
| C30 | ≤0.54 | ≤0.64 | ≤0.73 | ≤0.83 | ≤0.92 | >0.92 |
| C35 | ≤0.51 | ≤0.61 | ≤0.71 | ≤0.81 | ≤0.91 | >0.91 |
| C40 | ≤0.48 | ≤0.59 | 0.69 | ≤0.80 | ≤0.90 | >0.90 |
| C45 | ≤0.46 | ≤0.57 | ≤0.67 | ≤0.78 | ≤0.88 | >0.88 |
| C50 | ≤0.44 | ≤0.55 | ≤0.66 | ≤0.76 | ≤0.87 | >0.87 |
| C55 | ≤0.42 | ≤0.53 | ≤0.64 | ≤0.75 | ≤0.86 | >0.86 |
| C60 | ≤0.40 | ≤0.51 | ≤0.63 | ≤0.74 | ≤0.85 | >0.85 |
| C65 | ≤0.37 | ≤0.49 | ≤0.61 | ≤0.72 | ≤0.84 | >0.84 |
| C70 | ≤0.35 | ≤0.47 | ≤0.59 | ≤0.70 | ≤0.82 | >0.82 |
| C75 | ≤0.33 | ≤0.45 | ≤0.58 | ≤0.70 | ≤0.82 | >0.82 |
| C80 | ≤0.31 | ≤0.44 | ≤0.57 | ≤0.69 | ≤0.82 | >0.82 |
| Damage Grade | Macro Description | Damage Index Dc(t)0 |
|---|---|---|
| L1 | Non-damaged state | Dc(t)0 = 0 |
| L2 | Slightly damaged state | 0 < Dc(t)0 ≤ 0.2 |
| L3 | Mildly damaged state | 0.2 < Dc(t)0 ≤ 0.4 |
| L4 | Moderately damaged state | 0.4 < Dc(t)0 ≤ 0.6 |
| L5 | Relatively severely damaged state | 0.6 < Dc(t)0 ≤ 0.8 |
| L6 | Severely damaged state | Dc(t)0 > 0.8 |
| Specimen | Loading Direction | Crack | Yield | Peak | Ultimate | ||||
|---|---|---|---|---|---|---|---|---|---|
| Pcr (kN) | Δcr (mm) | Py (kN) | Δy (mm) | Pp (kN) | Δp (mm) | Pu (kN) | Δu (mm) | ||
| RCW-1 | positive | 410 | 6.58 | 573 | 14.36 | 686 | 28.86 | 650 | 45.70 |
| negative | 387 | 2.25 | 597 | 7.21 | 746 | 30.33 | 580 | 50.03 | |
| RCW-L | positive | 326 | 2.70 | 1009 | 17.58 | 1130 | 23.84 | 751 | 45.78 |
| negative | 314 | 3.05 | 862 | 13.55 | 1011 | 46.10 | 840 | 60.60 | |
| RCW-T | positive | 284 | 1.04 | 1246 | 13.68 | 1415 | 22.05 | 1010 | 31.81 |
| negative | 276 | 0.80 | 942 | 9.84 | 1072 | 29.84 | 923 | 38.88 | |
| Parameter | Value |
|---|---|
| Dilation angle ψ | 30° |
| Eccentricity e | 0.1 |
| Ratio of the initial biaxial compressive yield stress to the initial uniaxial compressive yield stress fb0/fc0 | 1.16 |
| Ratio of the second stress invariant on the tensile meridian Kc | 0.667 |
| Viscosity coefficient ν | 0.005 |
| Specimen | Loading Direction | Load | Displacement | ||||
|---|---|---|---|---|---|---|---|
| PpE (kN) | PpS (kN) | PpE/PpS | ΔuE (mm) | ΔuS (mm) | ΔuE/ΔuS | ||
| RCW-1 | positive | 686 | 737 | 1.07 | 28.86 | 25.53 | 0.88 |
| negative | 746 | 769 | 1.03 | 30.33 | 26.27 | 0.87 | |
| RCW-L | positive | 1130 | 1085 | 0.96 | 23.84 | 25.23 | 1.06 |
| negative | 1011 | 1122 | 1.11 | 46.10 | 37.82 | 0.82 | |
| RCW-T | positive | 1415 | 1521 | 1.07 | 22.05 | 24.20 | 1.10 |
| negative | 1072 | 1140 | 1.06 | 29.84 | 27.56 | 0.92 | |
| Damage Grade | εc (10−3) | dc | dt | Dc0 | ||
|---|---|---|---|---|---|---|
| RCW-1 | crack | value | 0.3 | 0.37 | 0.99 | 0 |
| damage grade | L1 | L1 | L6 | L1 | ||
| yield | value | 5.16 | 0.81 | 0.99 | 0.62 | |
| damage grade | L5 | L5 | L6 | L5 | ||
| peak | value | 90 | 0.98 | 0.99 | 0.96 | |
| damage grade | L6 | L6 | L6 | L6 | ||
| RCW-L | crack | value | 1.1/0.93 | 0.88/0.83 | 0.99 | 0.76/0.66 |
| damage grade | L2 | L5 | L6 | L5 | ||
| yield | value | 3.6/2.1 | 0.98 | 0.99 | 0.96 | |
| damage grade | L4/L3 | L6 | L6 | L6 | ||
| peak | value | 27/20 | 0.98 | 0.99 | 0.96 | |
| damage grade | L6 | L6 | L6 | L6 | ||
| RCW-T | crack | value | 0.8/0.2 | 0.82/0.43 | 0.99 | 0.64/L1 |
| damage grade | L1 | L4/L2 | L6 | L5/L3 | ||
| yield | value | 18/0.8 | 0.98/0.65 | 0.99 | 0.96/0.3 | |
| damage grade | L6/L1 | L6/L4 | L6 | L6/L3 | ||
| peak | value | 57/6 | 0.98 | 0.99 | 0.96 | |
| damage grade | L6 | L6 | L6 | L6 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Ren, X.; Li, Z.; Tang, M. Research on a Damage Assessment Method for Concrete Components Based on Material Damage. Buildings 2025, 15, 1844. https://doi.org/10.3390/buildings15111844
Wang H, Ren X, Li Z, Tang M. Research on a Damage Assessment Method for Concrete Components Based on Material Damage. Buildings. 2025; 15(11):1844. https://doi.org/10.3390/buildings15111844
Chicago/Turabian StyleWang, Hongjun, Xiaodan Ren, Zhi Li, and Mingsheng Tang. 2025. "Research on a Damage Assessment Method for Concrete Components Based on Material Damage" Buildings 15, no. 11: 1844. https://doi.org/10.3390/buildings15111844
APA StyleWang, H., Ren, X., Li, Z., & Tang, M. (2025). Research on a Damage Assessment Method for Concrete Components Based on Material Damage. Buildings, 15(11), 1844. https://doi.org/10.3390/buildings15111844




