Wind Tunnel Tests and Buffeting Response Analysis of Concrete-Filled Steel Tubular Arch Ribs During Cantilever Construction
Abstract
1. Introduction
2. Wind Tunnel Tests
2.1. Design of Section Models
2.2. Manufacturing of Section Models
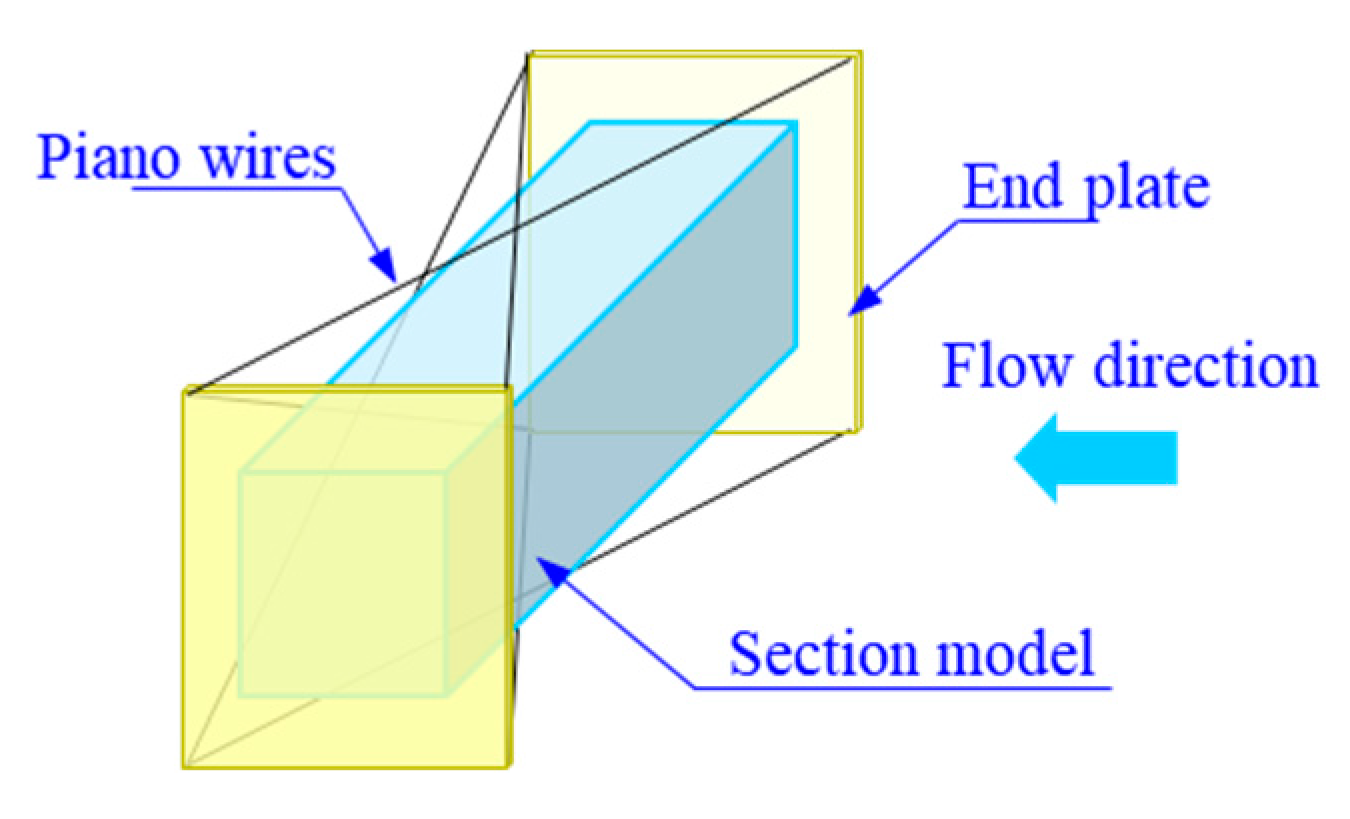
2.3. Test Setup and Measurement
2.4. Generation of Turbulent Wind Field
2.5. Measurement Process
3. Experimental Results
3.1. Aerodynamic Force Coefficient
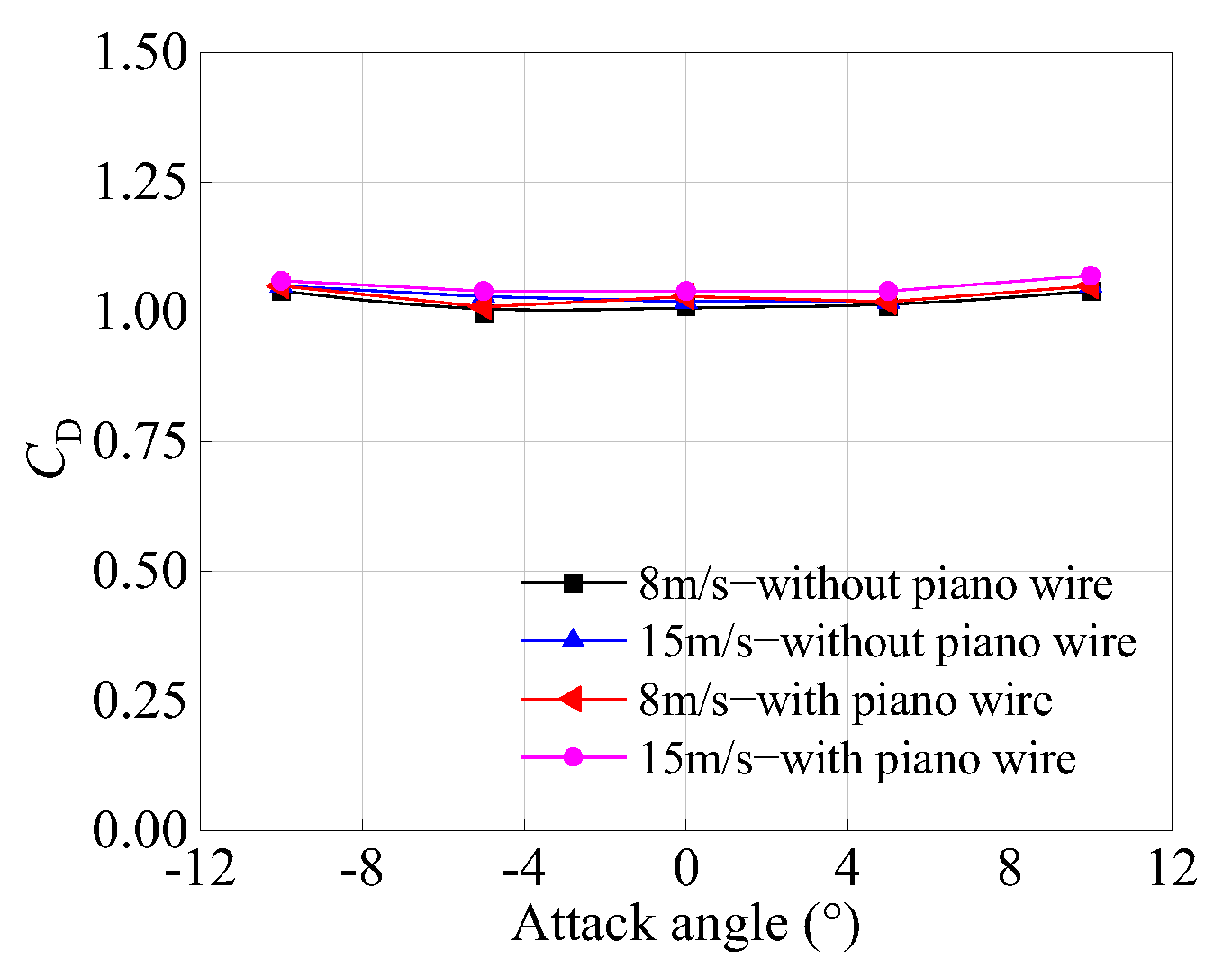
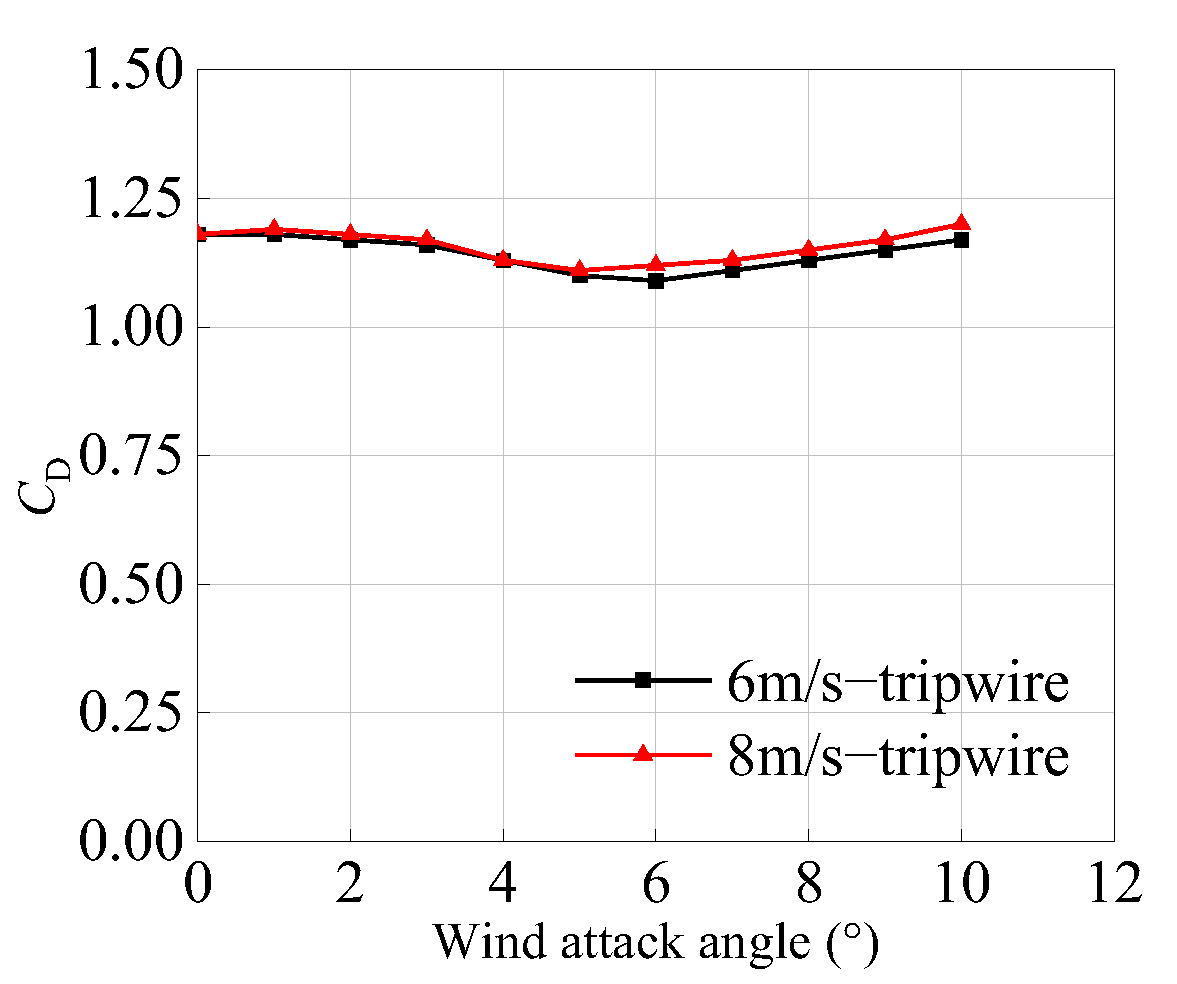
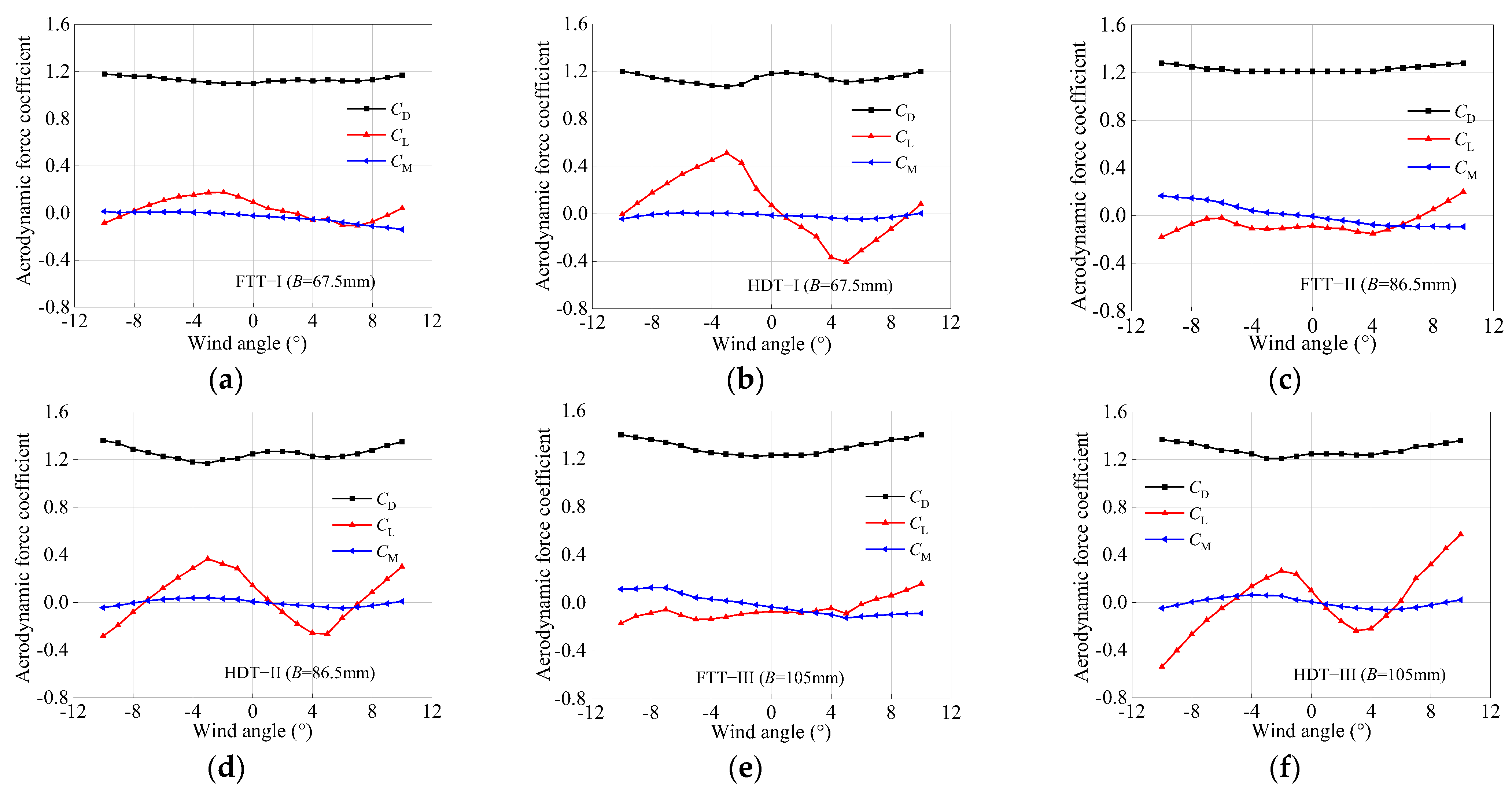
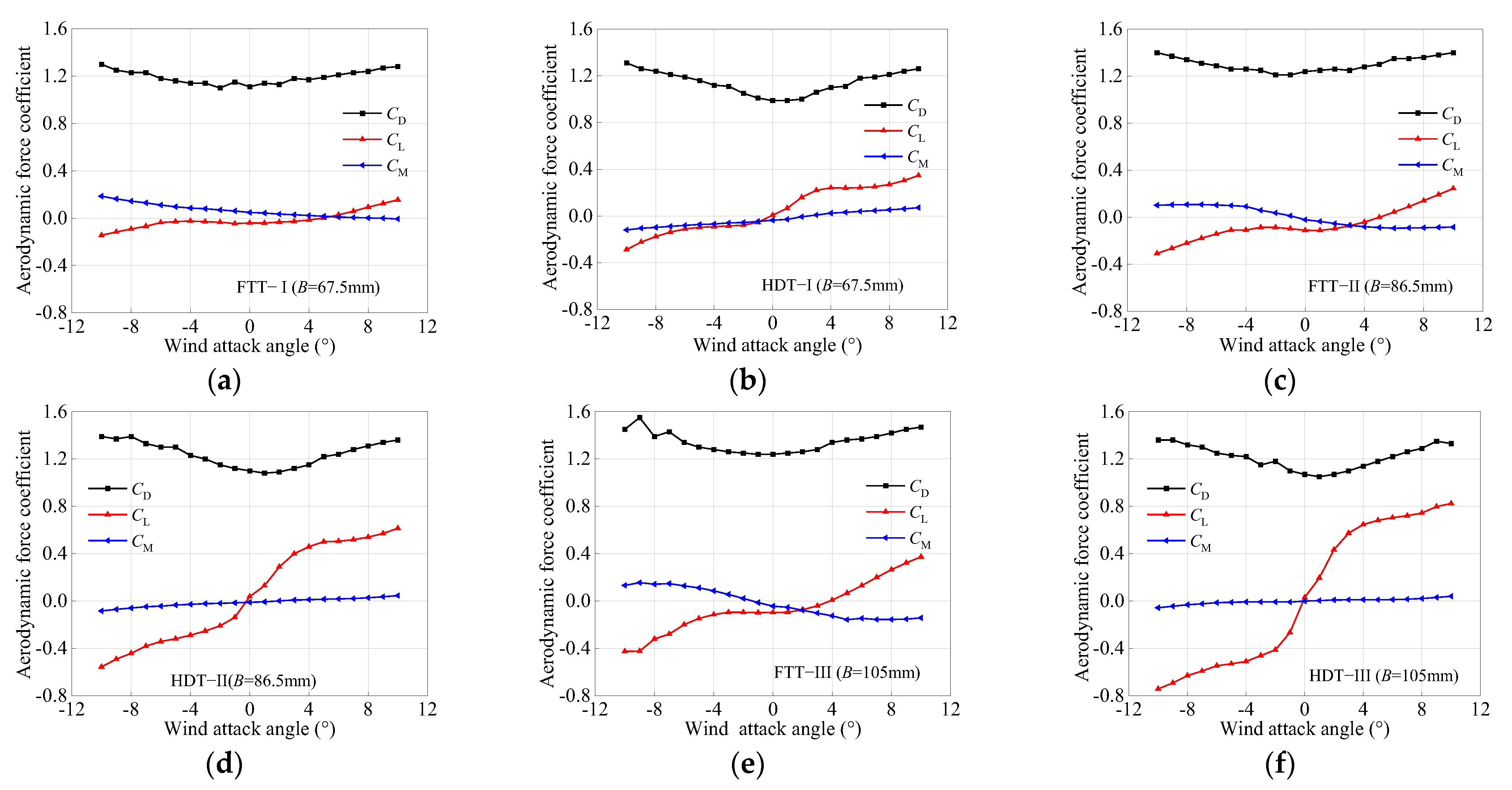
3.1.1. Aerodynamic Force Coefficients Under Laminar Flow
3.1.2. Aerodynamic Force Coefficients Under Turbulent Flow
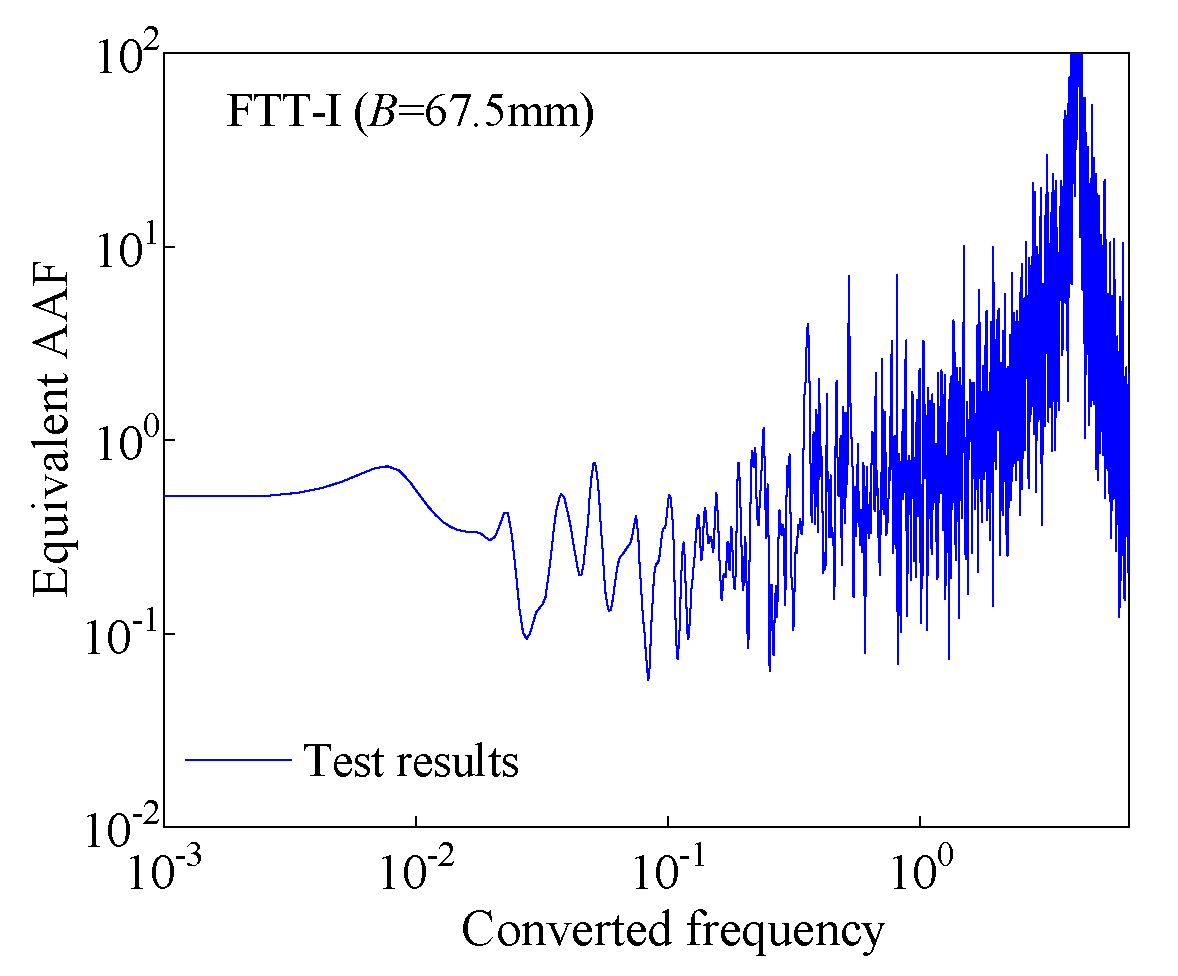
3.2. Aerodynamic Admittance Function
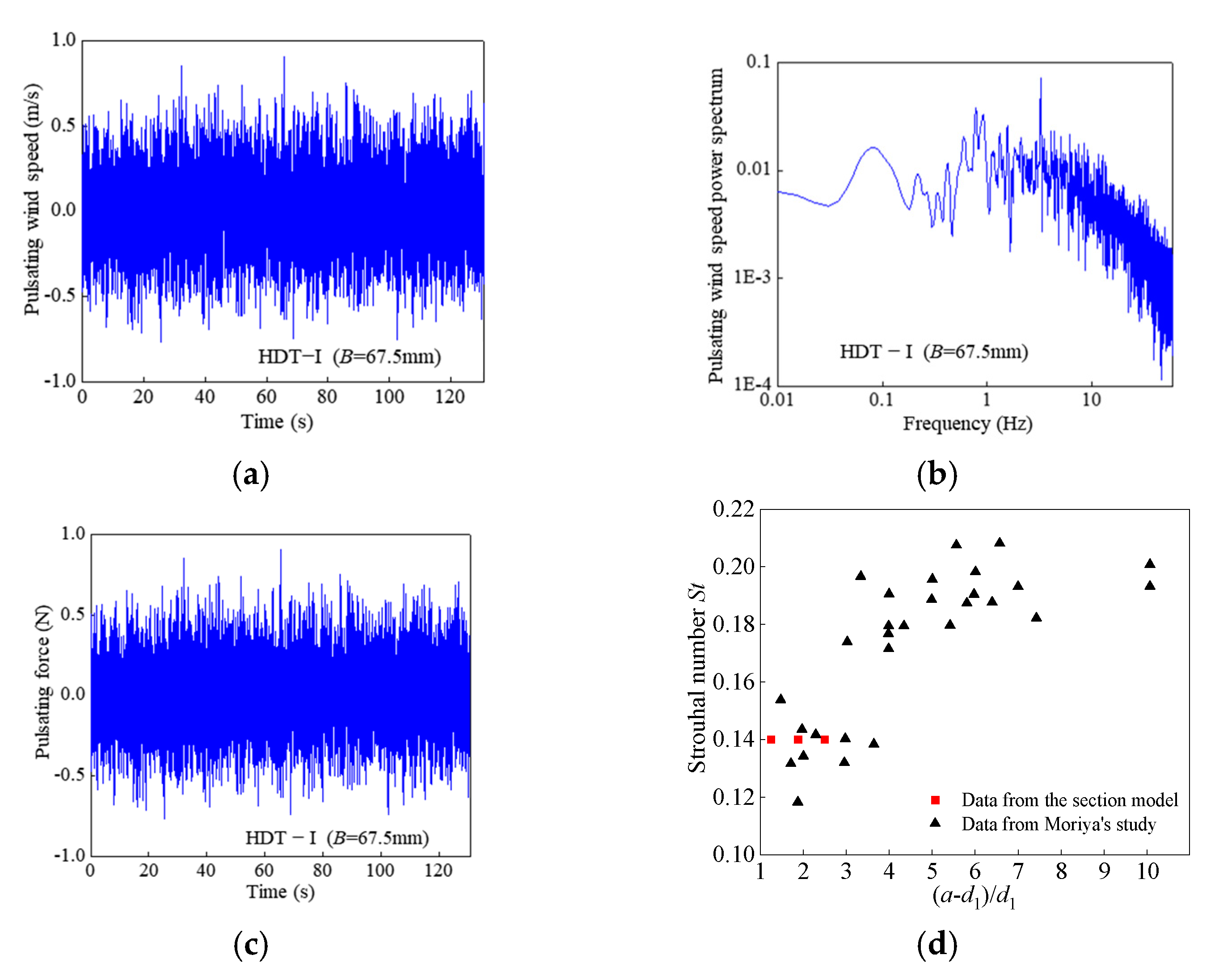
3.2.1. Power Spectrum Estimation
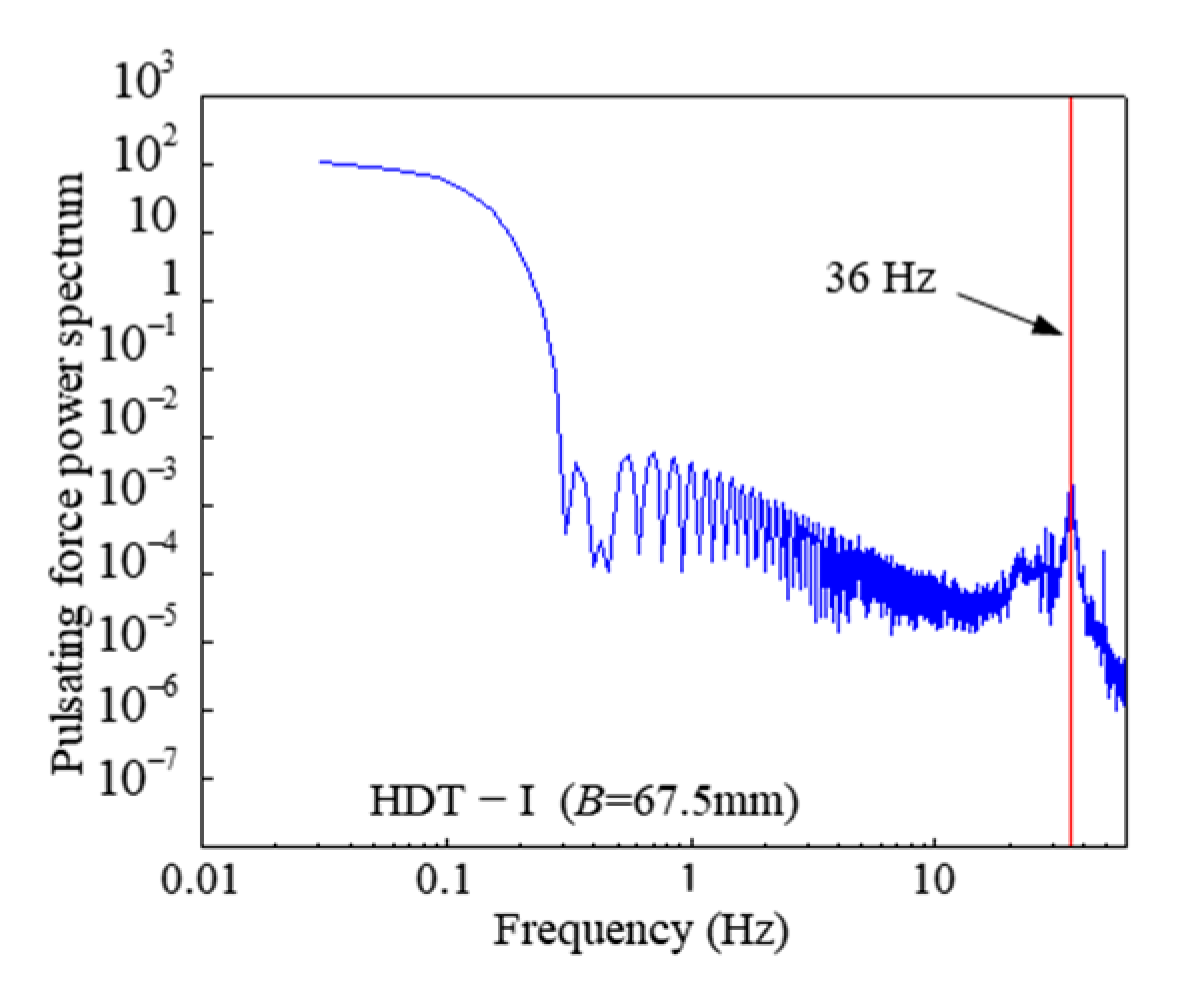
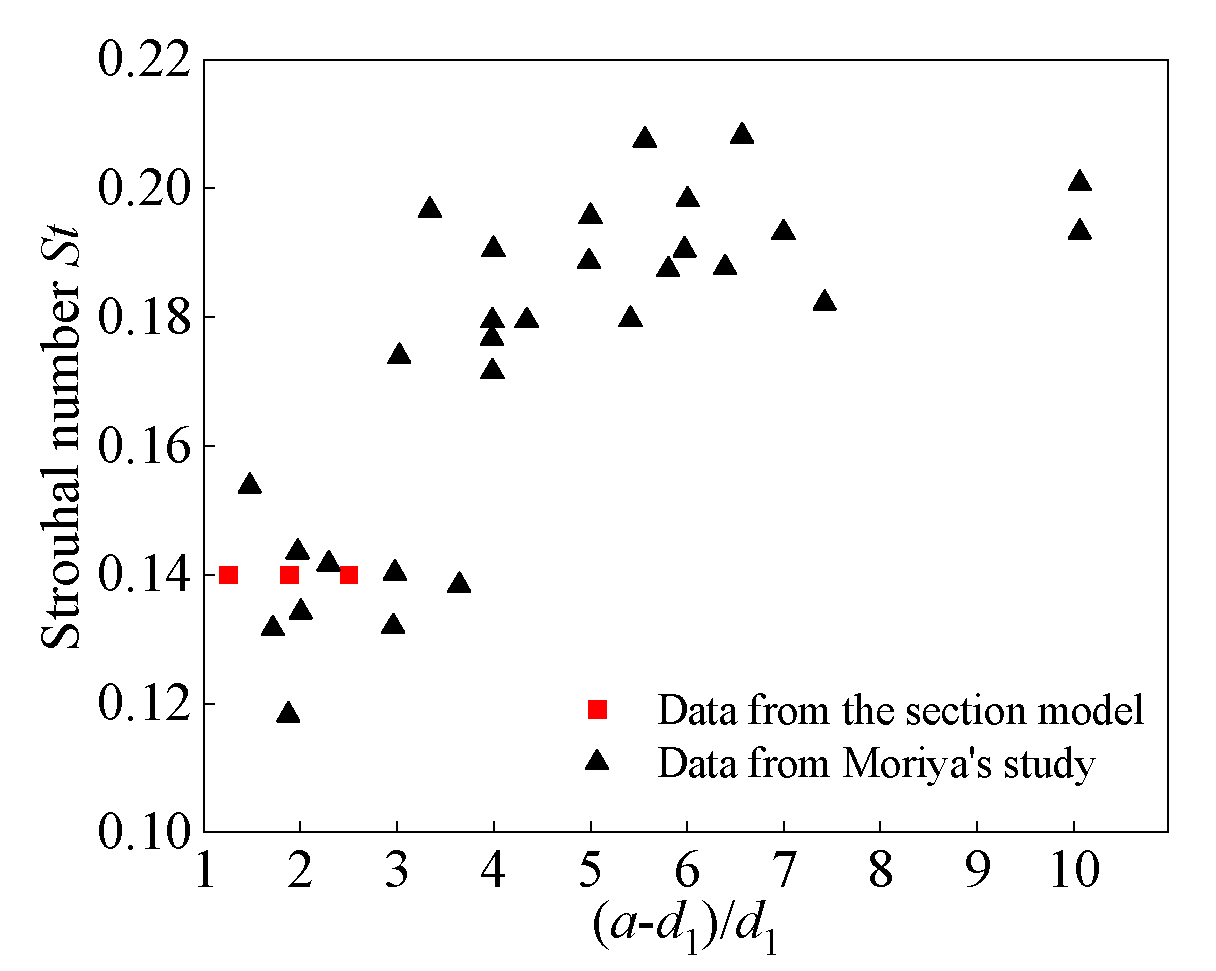
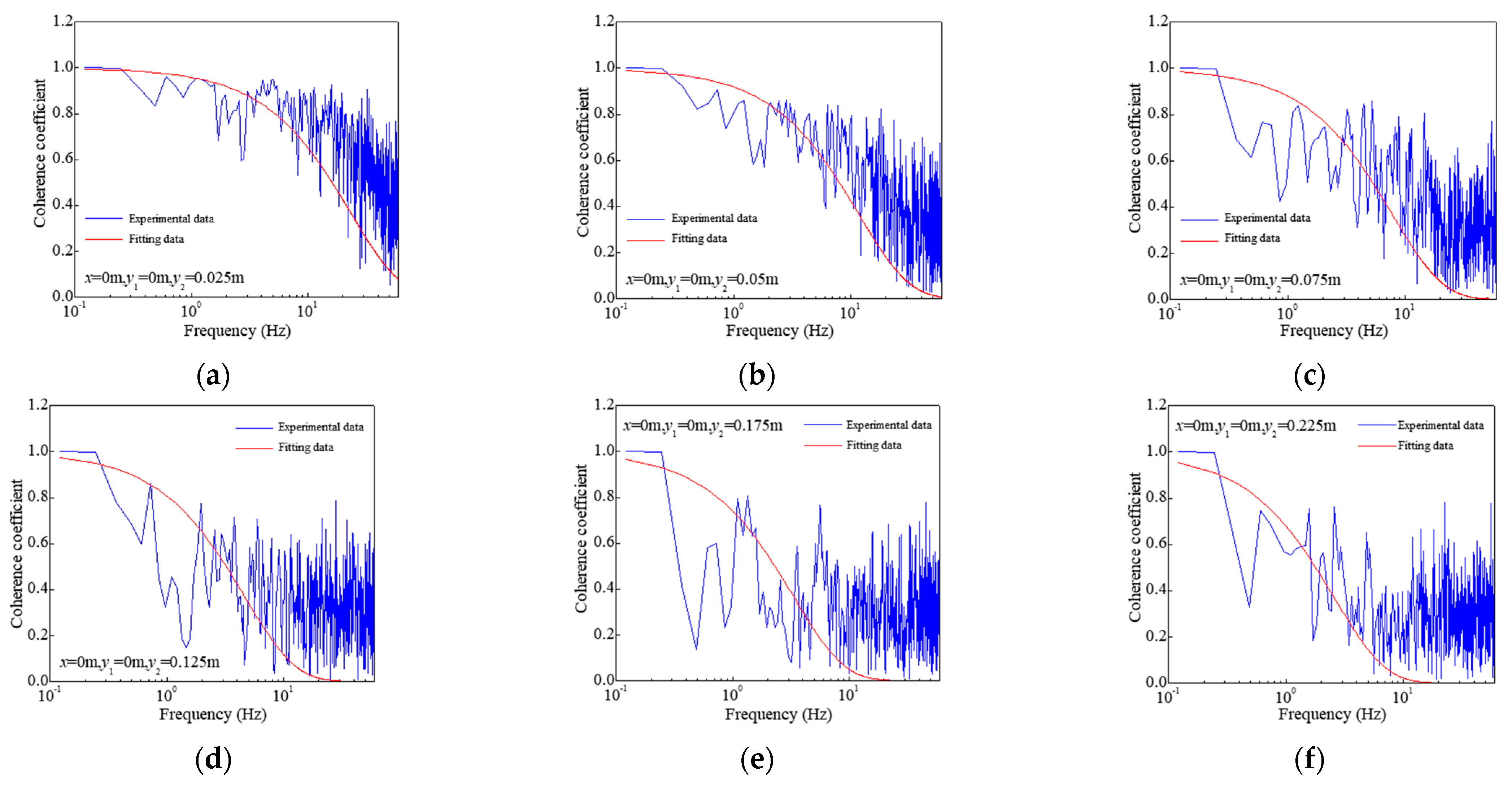
3.2.2. Decay Factor
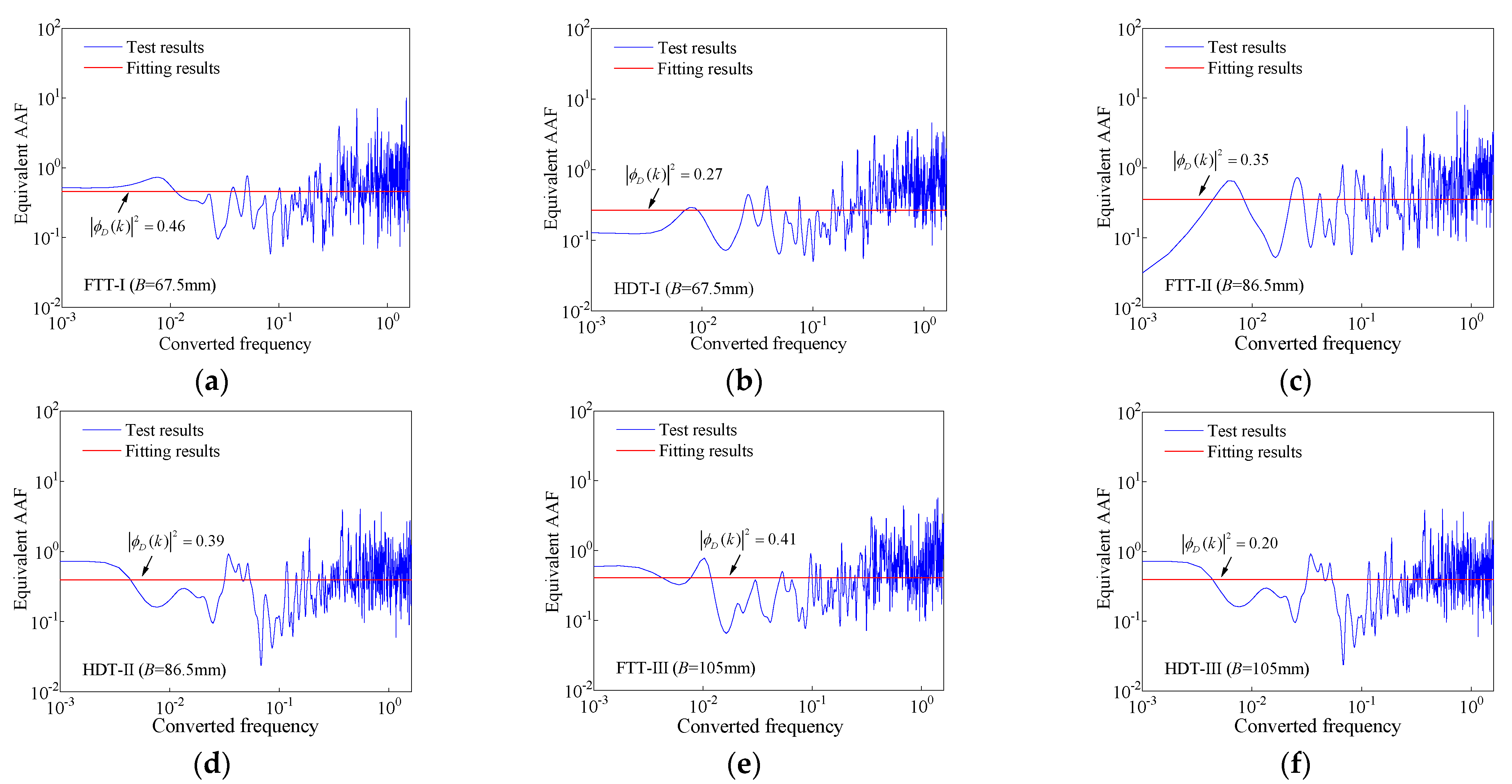
3.2.3. Equivalent Aerodynamic Admittance Function
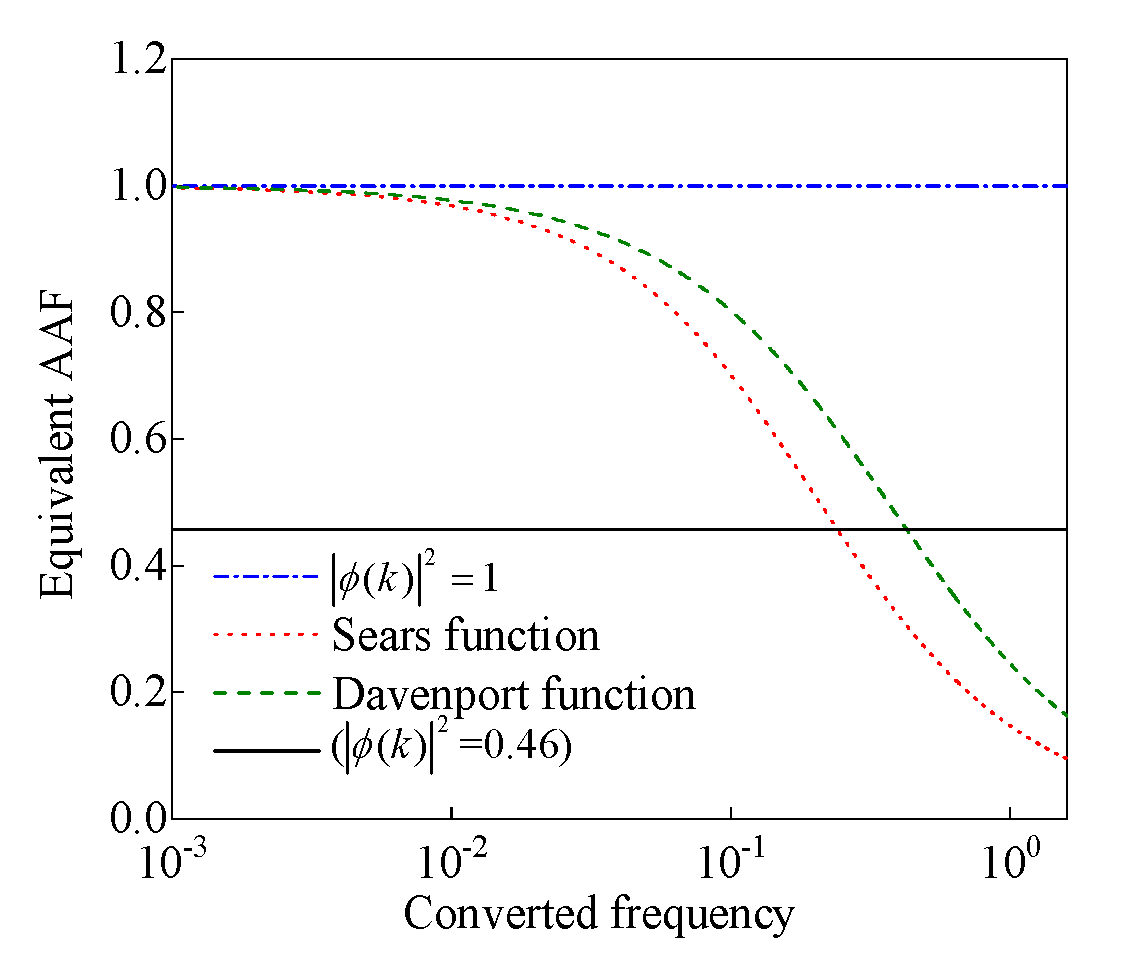
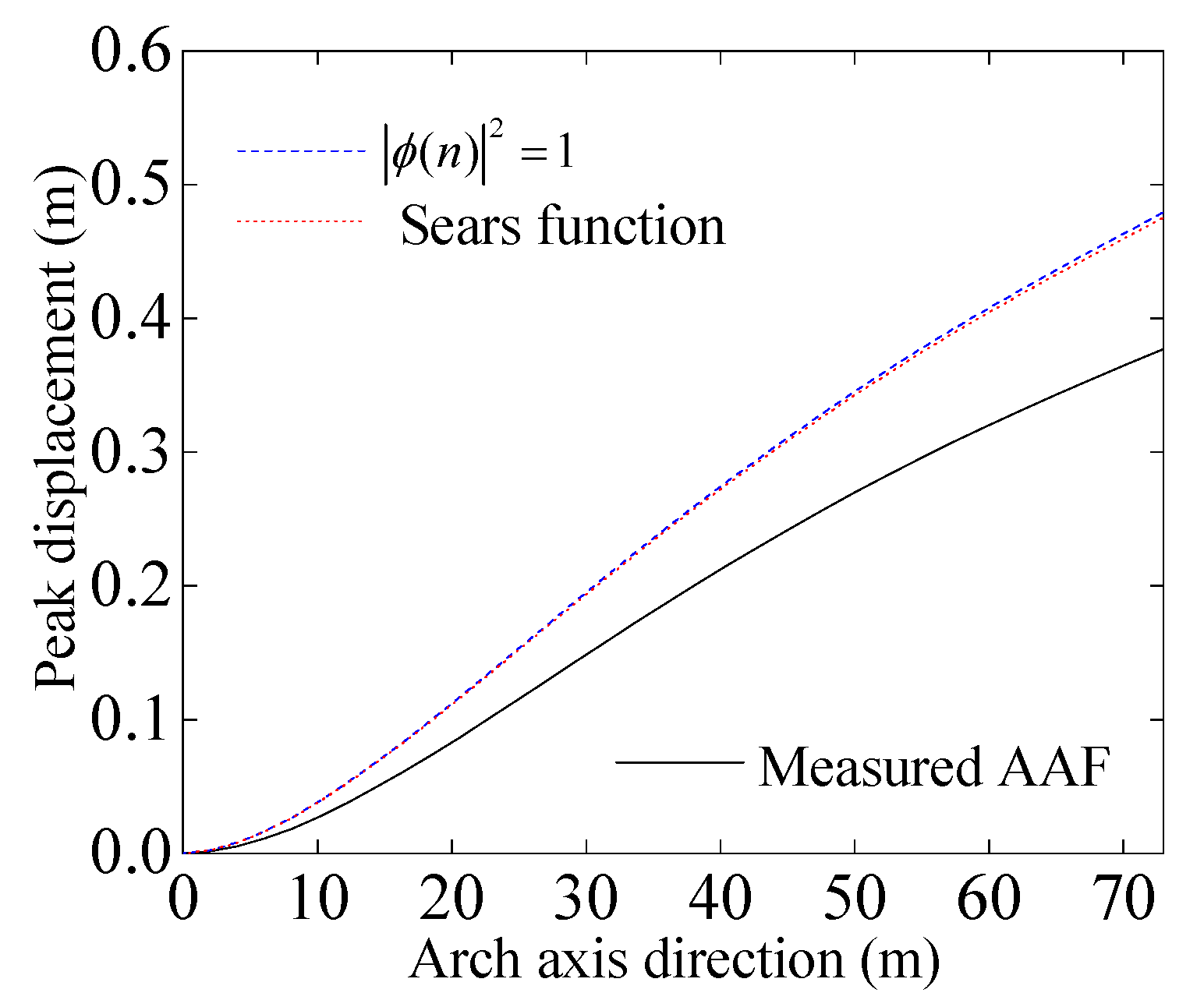
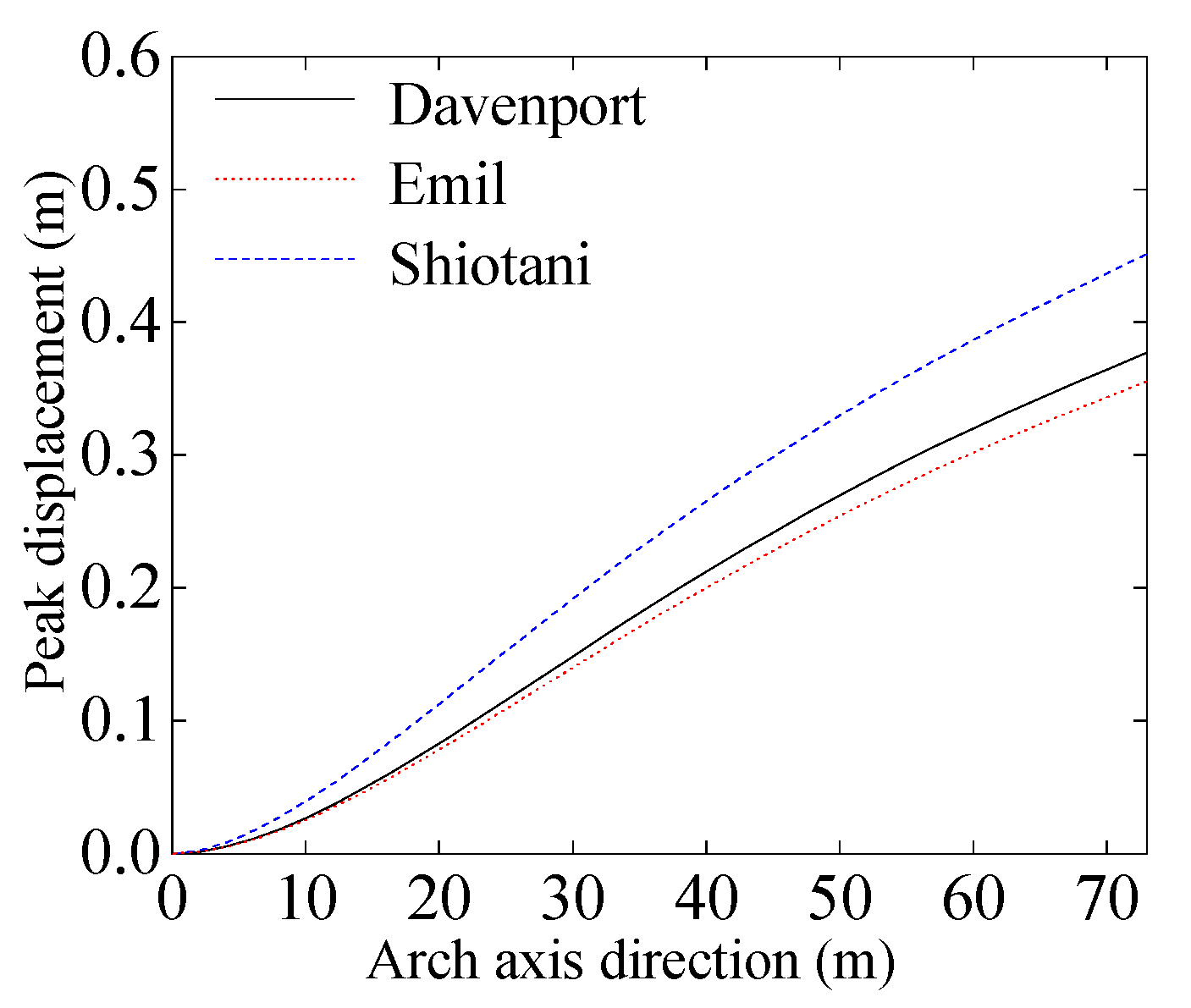
3.2.4. Comparisons of the Measured Equivalent AAFs with Other Commonly Used AAFs
4. Buffeting Response
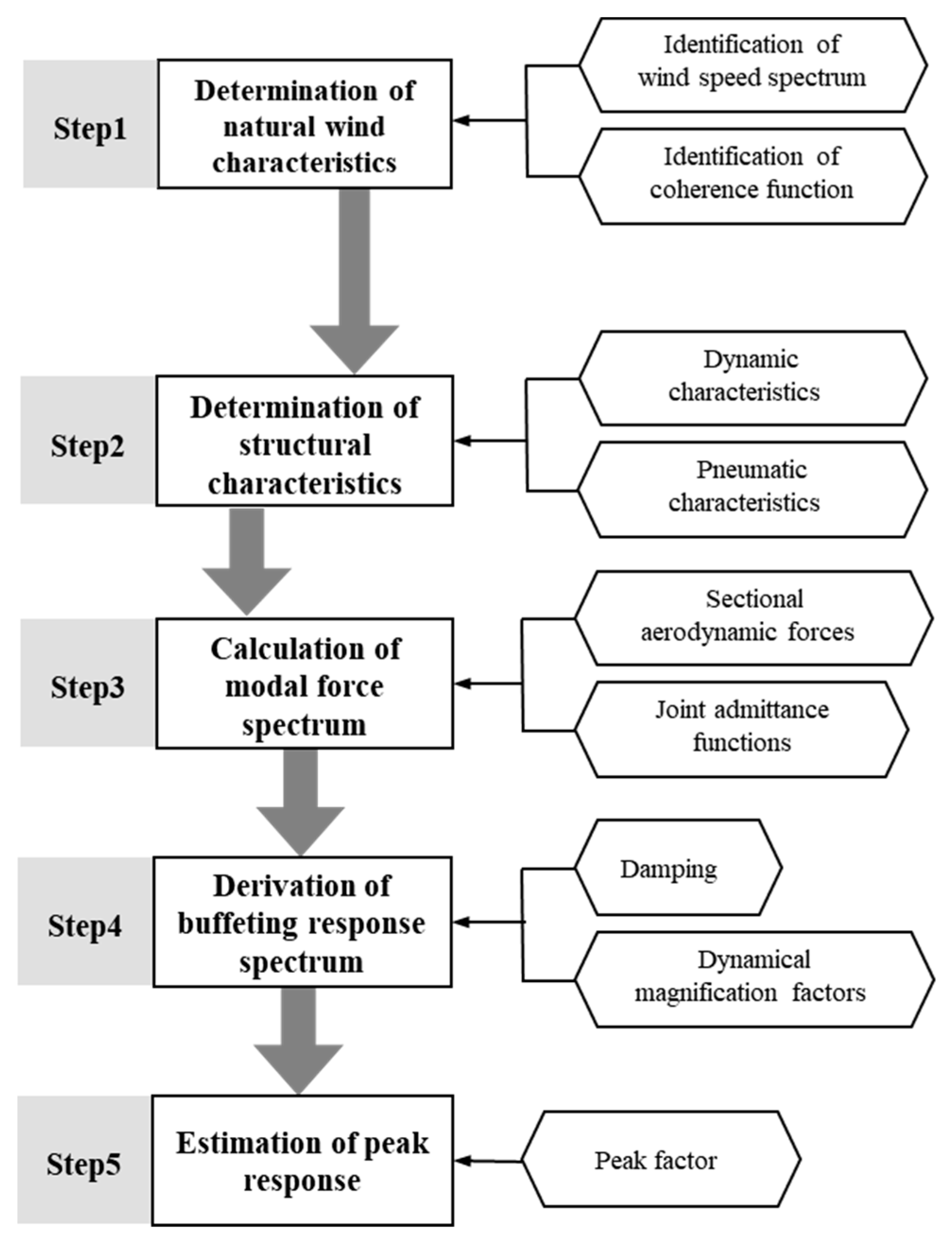
4.1. Buffeting Analysis Program
- (1)
- Determination of natural wind characteristics, including the identification of the wind speed spectrum and coherence function;
- (2)
- Determination of structural characteristics, involving the evaluation of sectional aerodynamic force coefficients, AAFs, structural frequencies, and mode shapes;
- (3)
- Calculation of modal force spectrum, including the determination of sectional aerodynamic forces and joint admittance functions;
- (4)
- Derivation of buffeting response spectrum, involving the assessment of structural damping and dynamic amplification factors;
- (5)
- Estimation of peak response, which can be determined using the peak factor method.
4.2. Verification of the Buffeting Analysis Procedure
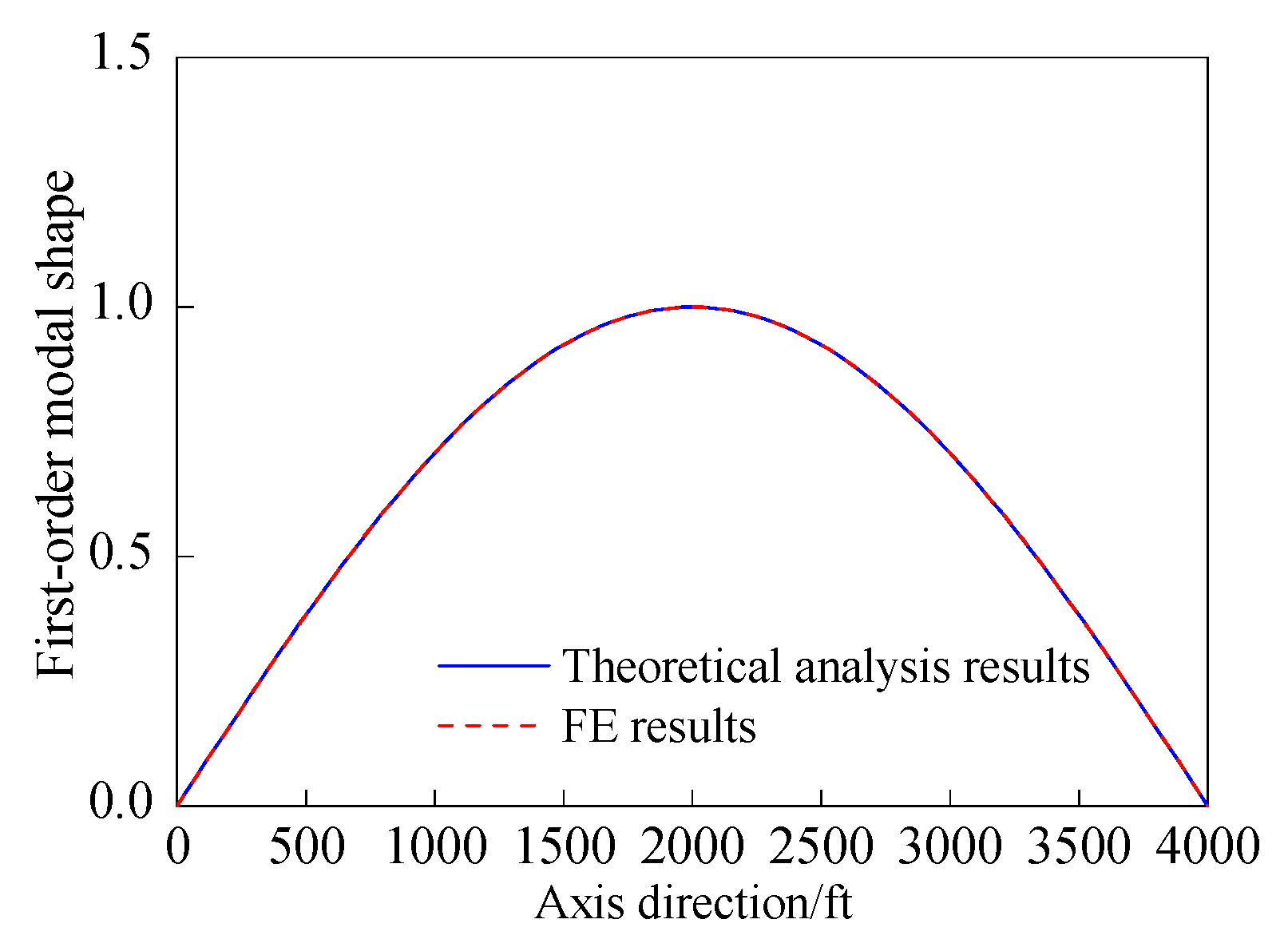
4.2.1. Buffeting Analysis of Suspension Cables
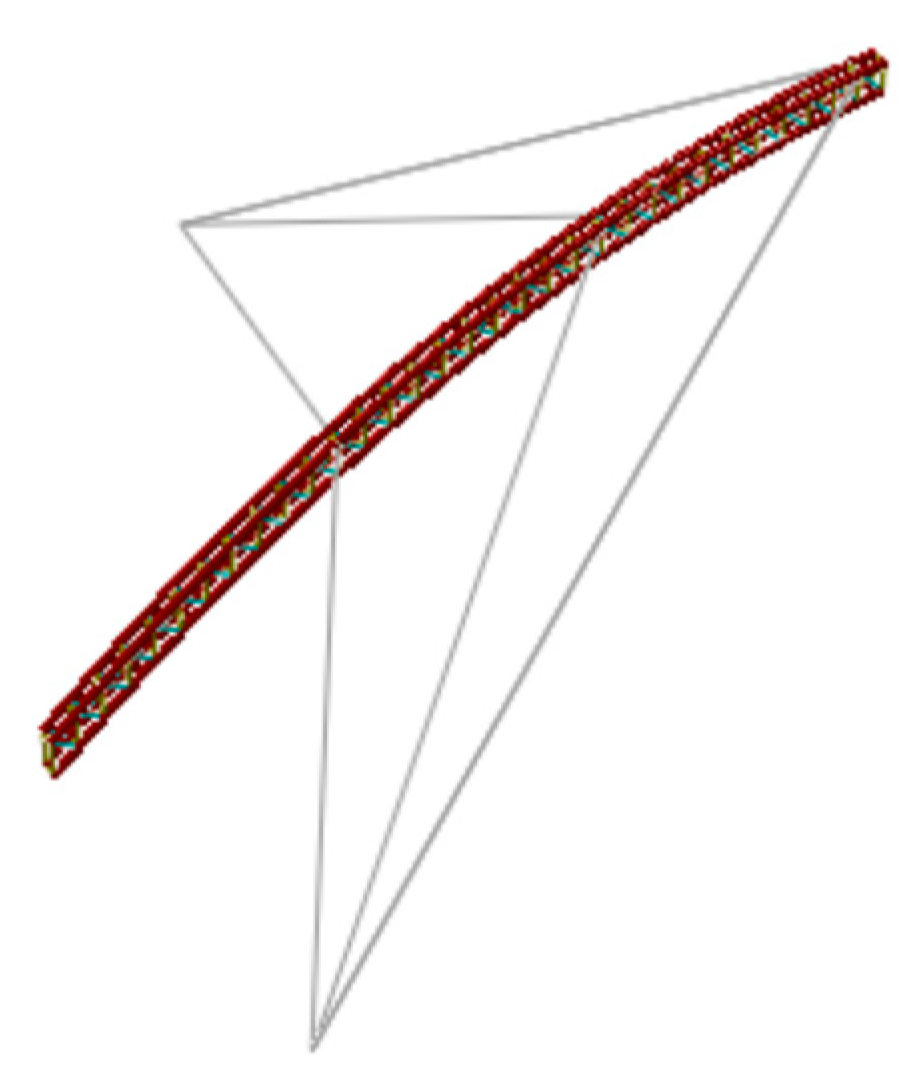
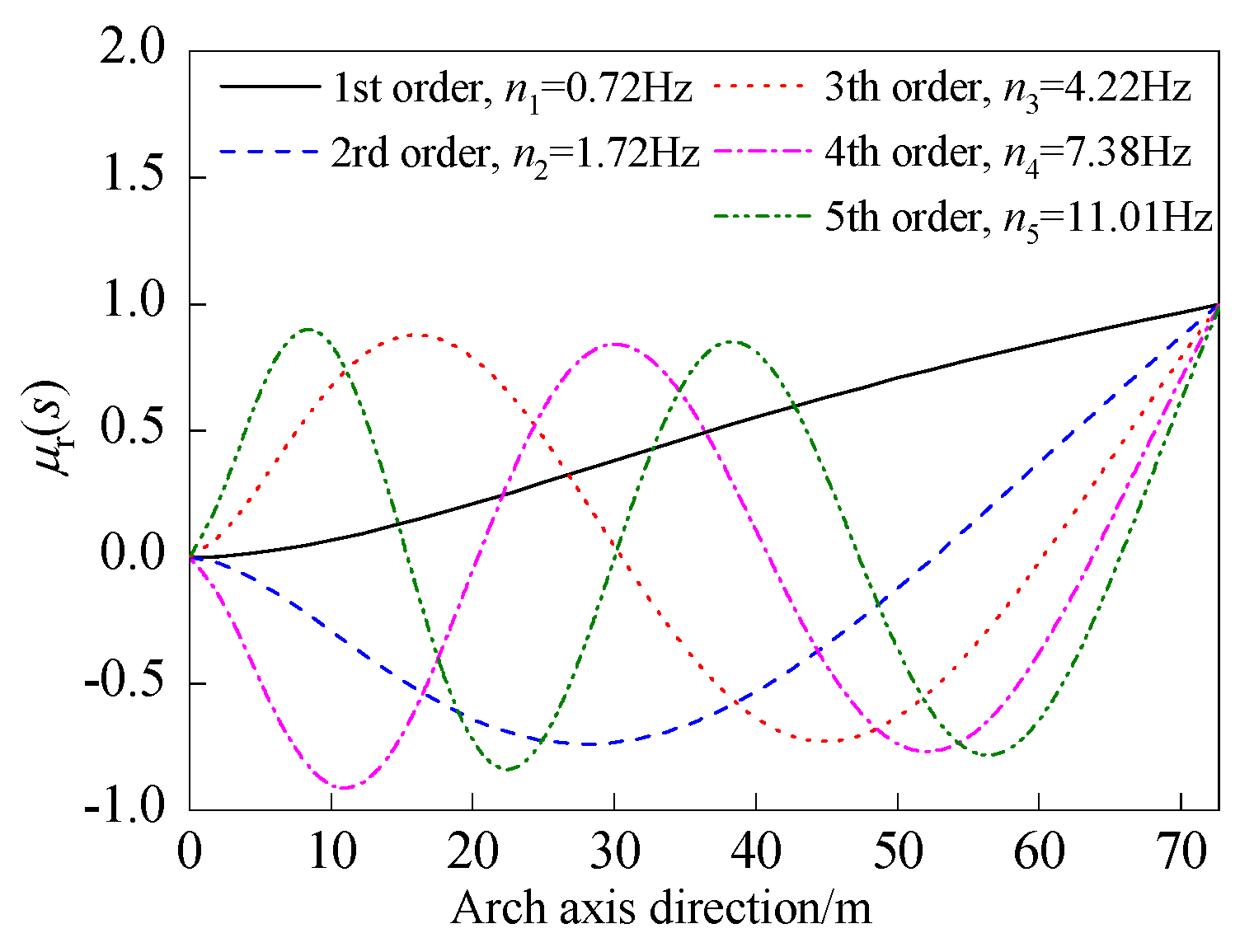
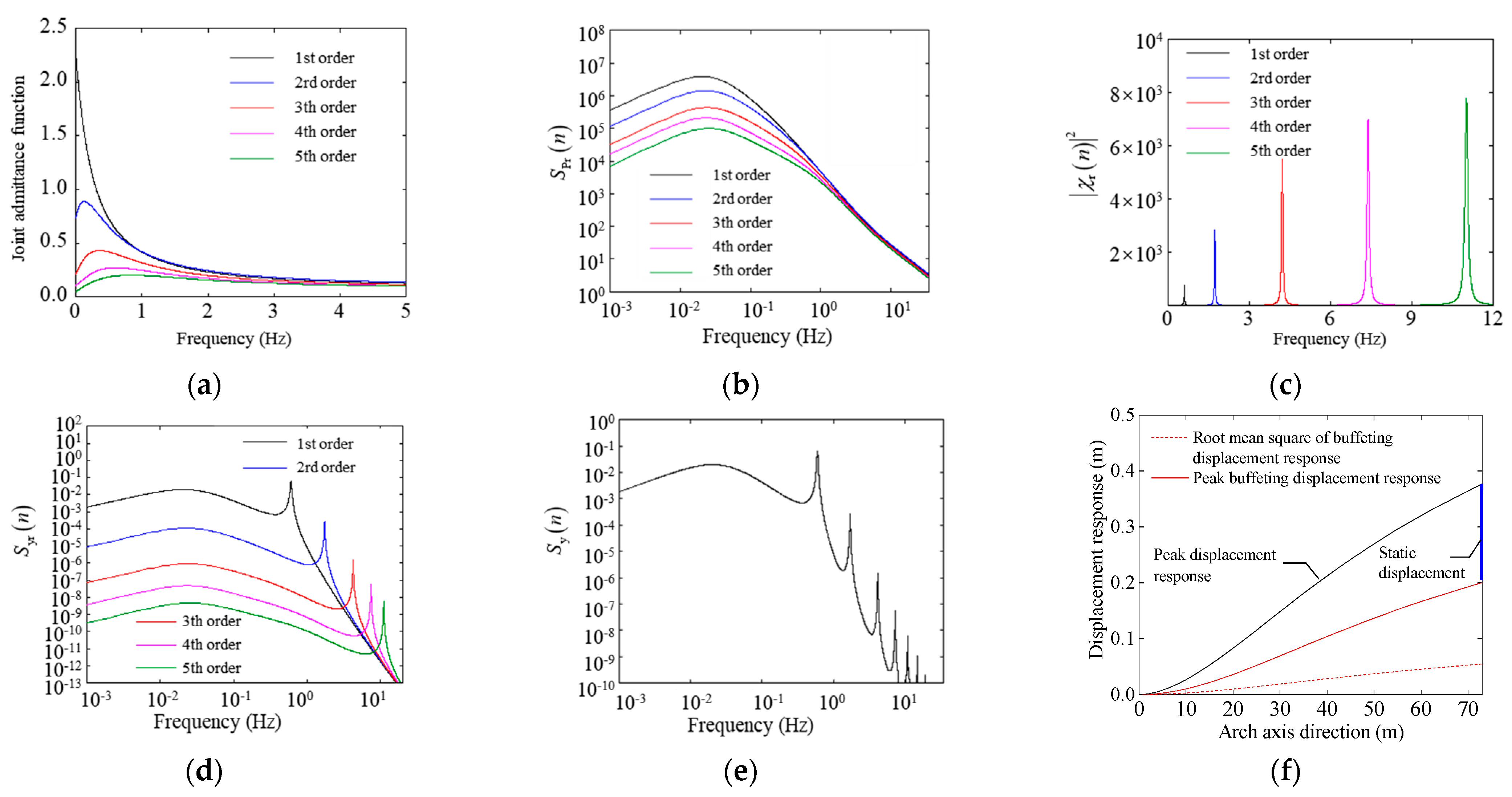
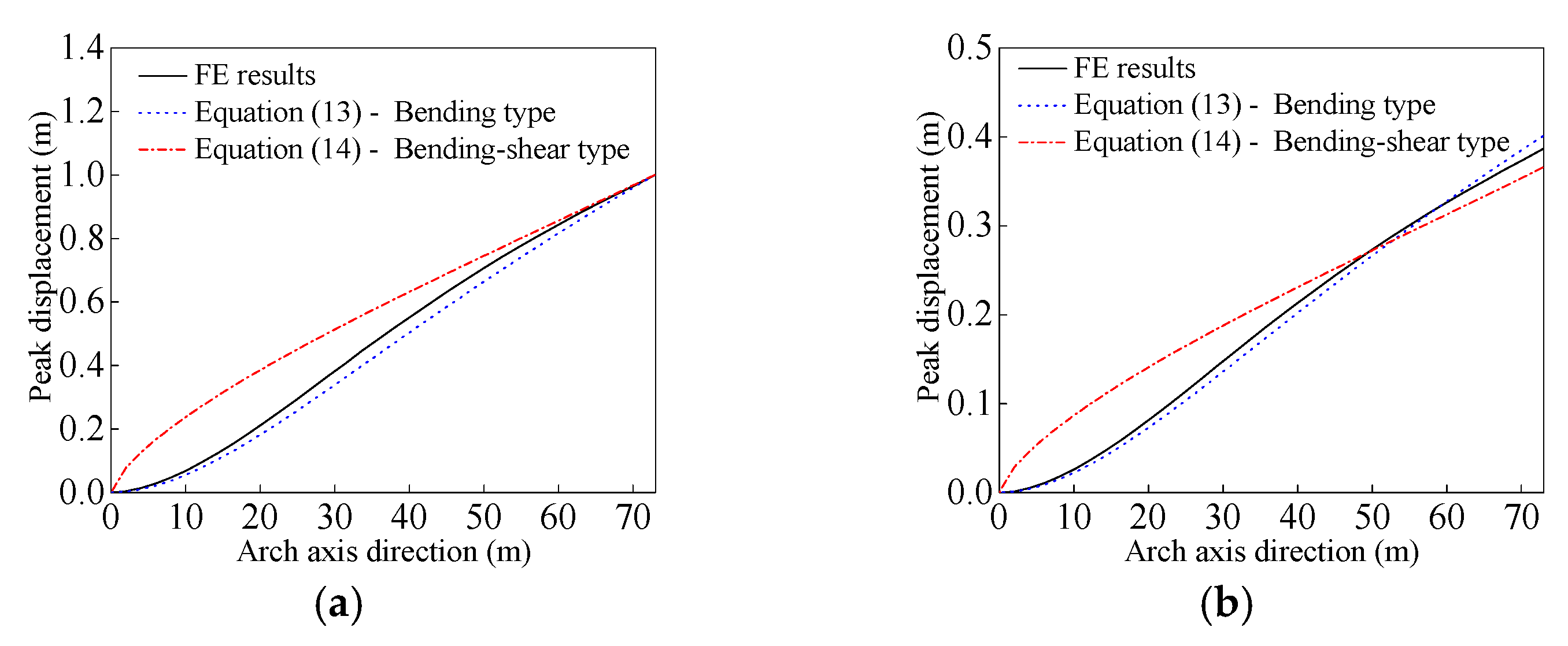
4.2.2. Buffeting Analysis of Cantilevered Arch Rib
4.3. Influence of Analysis Parameters on Wind-Induced Response in Buffeting Analysis
4.3.1. Influence of Equivalent AAF
4.3.2. Influence of Coherence Function
4.3.3. Influence of Shape Function
4.3.4. Influence of the Number of Modes
5. Conclusions
- (1)
- The aerodynamic forces acting on the section models of cantilevered CFST arch ribs are primarily governed by drag, with aerodynamic force coefficients showing minimal variation with changes in model width. Under laminar flow conditions, the aerodynamic force coefficients for the four-tube trussed section are 1.2 for drag, 0 for lift, and 0 for lift moment, while those for the horizontal dumbbell trussed section are 1.2, 0.1, and 0, respectively.
- (2)
- By measuring the fluctuating wind speeds at various points in the wind tunnel and fitting the decay factor, the equivalent AAFs for the arch rib section were determined. The equivalent AAFs for both four-tube trussed and horizontal dumbbell trussed sections can be approximated by a horizontal line and conservatively taken as 0.46.
- (3)
- Based on the measured aerodynamic force coefficients and equivalent AAFs, a buffeting analysis program for the cantilevered arch rib was developed and validated through comparisons of the classical theoretical analysis results and field measurements.
- (4)
- The influence of various parameters on the peak response in the buffeting calculation of cantilevered CFST arch ribs was analyzed, including the equivalent AAFs, coherence function, first-order mode shape, and the number of structural modes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Statistical Data on the Sectional Dimensions of CFST Truss Arch Bridges Constructed in China
| CFST Arches | B | H | B/H | d1 | d2 | d3 | d4 | d5 |
|---|---|---|---|---|---|---|---|---|
| Beijing–Hangzhou Grand Canal Bridge | 2.00 | 3.70 | 0.541 | 0.85 | 0.40 | 2.50 | 0.73 | - |
| Sanmenkou Crossing Sea Bridge | 2.40 | 5.30 | 0.453 | 0.80 | 0.40 | 4.00 | 0.40 | 2.00 |
| Shitanxi Bridge | 1.60 | 3.00 | 0.533 | 0.55 | 0.22 | 2.70 | 0.40 | 1.35 |
| Jialingjiang Bridge | 2.00 | 3.50 | 0.571 | 0.76 | 0.35 | 3.50 | 0.35 | - |
| Caihong Bridge | 2.00 | 3.00 | 0.667 | 0.75 | 0.25 | 2.00 | 0.40 | 2.00 |
| Yongjiang Bridge | 2.00 | 4.30 | 0.465 | 0.82 | 0.38 | - | 0.38 | - |
| Changqing Bridge | 1.80 | 3.40 | 0.529 | 0.70 | 0.25 | - | 0.30 | - |
| Shenxigou Bridge | 2.30 | 4.05 | 0.568 | 0.85 | 0.34 | - | 0.34 | - |
| Songao Bridge | 2.60 | 4.80 | 0.542 | 0.80 | 0.40 | - | 0.60 | - |
| Jiangwan Bridge | 2.20 | - | - | 0.70 | 0.35 | - | 0.40 | - |
| Lingfeng Bridge | 1.83 | 2.40 | 0.763 | 0.70 | 0.35 | 1.67 | 0.35 | 1.67 |
| Shawan Bridge | 1.60 | 3.00 | 0.533 | 0.61 | - | - | - | - |
| Daduhe Bridge | 1.70 | 3.30 | 0.515 | 0.70 | - | - | - | - |
| Taiping Lake Bridge | 3.00 | 7.28 | 0.412 | 1.28 | 0.61 | 8.00 | 0.81 | - |
| Maocaojie Bridge | 3.20 | 4.00 | 0.800 | 1.00 | 0.55 | 4.00 | 0.65 | 4.00 |
| Rongzhou Bridge | - | 4.00 | - | 1.02 | 0.46 | 4.00 | - | - |
| Yangtze River Bridge | 4.14 | 7.00 | 0.591 | 1.22 | 0.61 | 6.00 | 0.71 | 6.00 |
| Meixihe Bridge | 4.40 | 5.00 | 0.880 | 0.92 | 0.35 | 5.00 | 0.35 | 5.00 |
| Nanlidu Bridge | 2.10 | 4.00 | 0.525 | 0.92 | 0.34 | 4.00 | 0.34 | 4.00 |
| Jingyang River Bridge | - | 5.00 | - | 1.02 | 0.43 | 5.00 | 0.43 | 5.00 |
| Yellow River Grand Canal Bridge | 6.50 | 7.50 | 0.867 | 1.50 | - | - | - | - |
| CFST Arches | B | H | B/H | d1 | d2 | d3 | T |
|---|---|---|---|---|---|---|---|
| Nanpu Bridge | 2.55 | 5.20 | 0.490 | 0.85 | 0.61 | - | - |
| Shuidao Grand Canal Bridge | 2.50 | 5.50 | 0.455 | 1.00 | 0.60 | 5.00 | 0.70 |
| Yongjiang Grand Canal Bridge | - | - | - | 1.02 | - | 5.00 | - |
| Qiandao Lake 1# Bridge | 2.50 | 5.00 | 0.500 | 1.00 | 0.40 | 5.00 | - |
| Jiantiao Bridge | 1.90 | 4.40 | 0.432 | 0.80 | 0.40 | 5.90 | - |
| Changfeng Bridge | 2.40 | 4.50 | 0.533 | 1.00 | 0.50 | 5.00 | 0.80 |
| Beipanjiang Bridge | 2.50 | 5.40 | 0.463 | 1.00 | 0.45 | 5.50 | 0.80 |
| Shengmi Bridge | 3.00 | 5.00 | 0.600 | 0.90 | 0.30 | 3.00 | - |
| Longtanhe Bridge | 2.40 | - | - | 0.90 | 0.40 | 4.00 | 0.50 |
| Sanshan West Bridge | - | 3.50 | - | 0.70 | 0.35 | - | - |
| Wangcun Grand Canal Bridge | 2.00 | 3.8 | 0.526 | 0.75 | 0.30 | 3.25 | 0.50 |
| Wujiang Bridge | - | - | - | 0.60 | - | 5.07 | - |
| Panjiahe Bridge | 1.40 | 2.70 | 0.519 | 0.60 | 0.43 | - | - |
| Heishipu Bridge | 2.50 | 4.00 | 0.625 | 1.00 | 0.43 | 6.00 | - |
| Lijiang Bridge | 1.75 | 3.50 | 0.500 | 0.71 | 0.33 | - | - |
| Junzhou Bridge | 1.80 | 3.00 | 0.600 | 0.75 | 0.30 | 2.60 | - |
| Yuanyangjiang Bridge | 1.80 | 3.30 | 0.545 | 0.75 | 0.25 | - | - |
| Fuxing Bridge | 2.60 | 4.50 | 0.578 | 0.95 | 0.40 | 4.00 | 0.60 |
| Pubugou Bridge | 2.00 | 2.80 | 0.714 | 0.76 | 0.30 | 2.00 | 0.65 |
| Qijiadu Yellow River Bridge | 1.70 | 3.50 | 0.486 | 0.70 | 0.33 | 2.50 | 0.40 |
| Wushan New Longmen Bridge | 2.40 | 4.50 | 0.533 | 1.00 | 0.50 | 3.00 | 0.80 |
| Caoejiang Bridge | 2.25 | 4.00 | 0.563 | 0.90 | 0.40 | - | 0.50 |
| Tongde Bridge | 2.05 | 3.50 | 0.586 | 0.75 | 0.35 | - | - |
| Nanhuan Bridge | 1.80 | 3.50 | 0.514 | 0.75 | 0.40 | 3.00 | 0.52 |
| Rainbow Bridge | 2.40 | 5.50 | 0.436 | 1.00 | 0.22 | 5.00 | 0.78 |
| Zhongshan Bridge | 1.75 | 3.40 | 0.515 | 0.75 | 0.30 | 2.25 | 0.65 |
| Yesanhe Railway Bridge | 2.20 | 3.80 | 0.579 | 0.80 | 0.42 | 3.25 | 0.52 |
| Shengzhou Caoejiang Bridge | 2.00 | 3.00 | 0.667 | 0.75 | 0.35 | 3.50 | - |
| Yonghe Bridge | 3.00 | 8.00 | 0.375 | 1.22 | 0.61 | 9.20 | - |
| Baoding Bridge | - | 3.50 | - | 0.75 | 0.35 | - | - |
| Qingganhe Bridge | 2.40 | 2.40 | 1.000 | 1.00 | 0.40 | 4.00 | 0.50 |
References
- Gu, M.; Su, L.K.; Quan, Y.; Huang, J.; Fu, G. Experimental study on wind-induced vibration and aerodynamic mitigation measures of a building over 800 meters. J. Build. Eng. 2022, 46, 103681. [Google Scholar] [CrossRef]
- Wang, J.Y.; Wang, F.; Chen, X.M.; Wei, J.; Ma, J. Investigation of wind load characteristics of cantilevered scaffolding of a high-rise building based on field measurement. Energy Build. 2025, 328, 115123. [Google Scholar] [CrossRef]
- Zhou, S.H.; Liao, H.L.; Zheng, S.X.; Li, Y.L. Experimental study on wind resistance performance model of Yajisha Bridge. In Proceedings of the 13th National Bridge Academic Conference, Shanghai, China, 16–19 November 1998; pp. 566–571. (In Chinese). [Google Scholar]
- Wang, Z.G.; He, J.; Sun, B.N.; Lou, W.J.; Yu, X.M. Wind tunnel tests and calculation analysis of wind resistance stability segment model of steel-concrete arch bridge. In Proceedings of the 8th National Conference on Structural Engineering, Yunnan, China, 22–26 October 1999; pp. 208–213. (In Chinese). [Google Scholar]
- Luo, X.; Pan, Y.Y. Buffeting analysis for concrete-filled tubular arch bridge in time domain. J. Southwest Jiaotong Univ. 2000, 35, 475–479. (In Chinese) [Google Scholar]
- Lu, B.; Hu, Z.T. Study of wind resistance of long-span concrete-filled steel tube arch bridge erected by integral lifting method. World Bridges 2005, 3, 68–71. (In Chinese) [Google Scholar]
- Yan, Z.T. Study on Wind-Induced Vibration of Long Span Half-Through Arch Bridges. Ph.D. Thesis, Chongqing University, Chongqing, China, 2006. (In Chinese). [Google Scholar]
- Claudio, B.; Claudio, M. Aeroelastic Phenomena and Pedestrian-Structure Dynamic Interaction on Non-Conventional Bridges and Footbridges; Firenze University Press: Florence, Italy, 2010. [Google Scholar]
- Yu, H.G. Study on Aerodynamic Parameter Identification and Wind-Induced Responses of Long-Span Arch Bridges. Ph.D. Thesis, Tongji University, Shanghai, China, 2008. (In Chinese). [Google Scholar]
- JTG/T 3360-01-2018; Wind-Resistant Design Specification for Highway Bridges. Ministry of Transport of the People’s Republic of China: Beijing, China, 2018.
- Chen, B.C.; Liu, J.P.; Wei, J.G. Concrete-Filled Steel Tubular Arch Bridges; China Commu, Press Co. Ltd. & Springer: Beijing, China, 2023. [Google Scholar]
- Zheng, J.L.; Du, H.L.; Mu, T.M.; Liu, J.P.; Qin, D.Y.; Mei, G.X.; Tu, B. Innovations in design, construction, and management of Pingnan third bridge-the largest-span arch bridge in the world. Struct. Eng. Int. 2021, 32, 134–141. [Google Scholar] [CrossRef]
- Zheng, J.L.; Wang, J.J. Concrete-filled steel tube arch bridges in China. Engineering 2018, 4, 143–155. [Google Scholar] [CrossRef]
- Simiu, E.; Scanlan, R.H. Wind Effects on Structures: Fundamentals and Applications to Design, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996; pp. 297–298. [Google Scholar]
- Chen, Z.Q. Bridge Wind Engineering; China Communications Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Alam, M.M.; Zhou, Y.; Zhao, J.M.; Flamand, O.; Boujard, O. Classification of the tripped cylinder wake and bi-stable phenomenon. Int. J. Heat Fluid Flow 2010, 31, 545–560. [Google Scholar] [CrossRef]
- Masaru, M.; Hiroshi, S.; Masaru, K.; Mikio, A. Fluctuating force acting on two circular cylinders in series. Proc. Mech. Soc. 1983, 7, 1364–1372. (In Japanese) [Google Scholar]
- Davenport, A.G. The response of slender line-like structures to a gusty wind. Proc. Inst. Civ. Eng. 1962, 23, 389–408. [Google Scholar] [CrossRef]
- Qian, X.G. Construction and Monitoring Technique Research on Shenzhen Rainbow Bridge. Master’s Thesis, Hunan University, Changsha, China, 2002. (In Chinese). [Google Scholar]
- Chen, Z.G. Wind resistant design and practice of Shenzhen Rainbow Bridge. West-China Explor. Eng. 2004, 10, 194–196. (In Chinese) [Google Scholar]
- Qian, X.G. Wind resistant design and practice of arch rib construction for Shenzhen North Station Bridg. Highway 2001, 8, 75–78. (In Chinese) [Google Scholar]
- Davenport, A.G. The dependence of wind load upon meteorological parameters. In Proceedings of the International Research Seminar on Wind Effects on Buildings and Structures, Ottawa, ON, Canada, 11–15 September 1967; pp. 19–82. [Google Scholar]
- Shiotani, M.; Iwatani, Y. Correlations of wind velocities in relation to the gust loadings. In Proceedings of the Third International Conference on Wind Effects on Building and Structures, Tokyo, Japan, 6 September 1971; pp. 57–67. [Google Scholar]
- GB 50009-2012; Load Code for The Design of Building Structures. China Architecture & Building Press: Beijing, China, 2016.

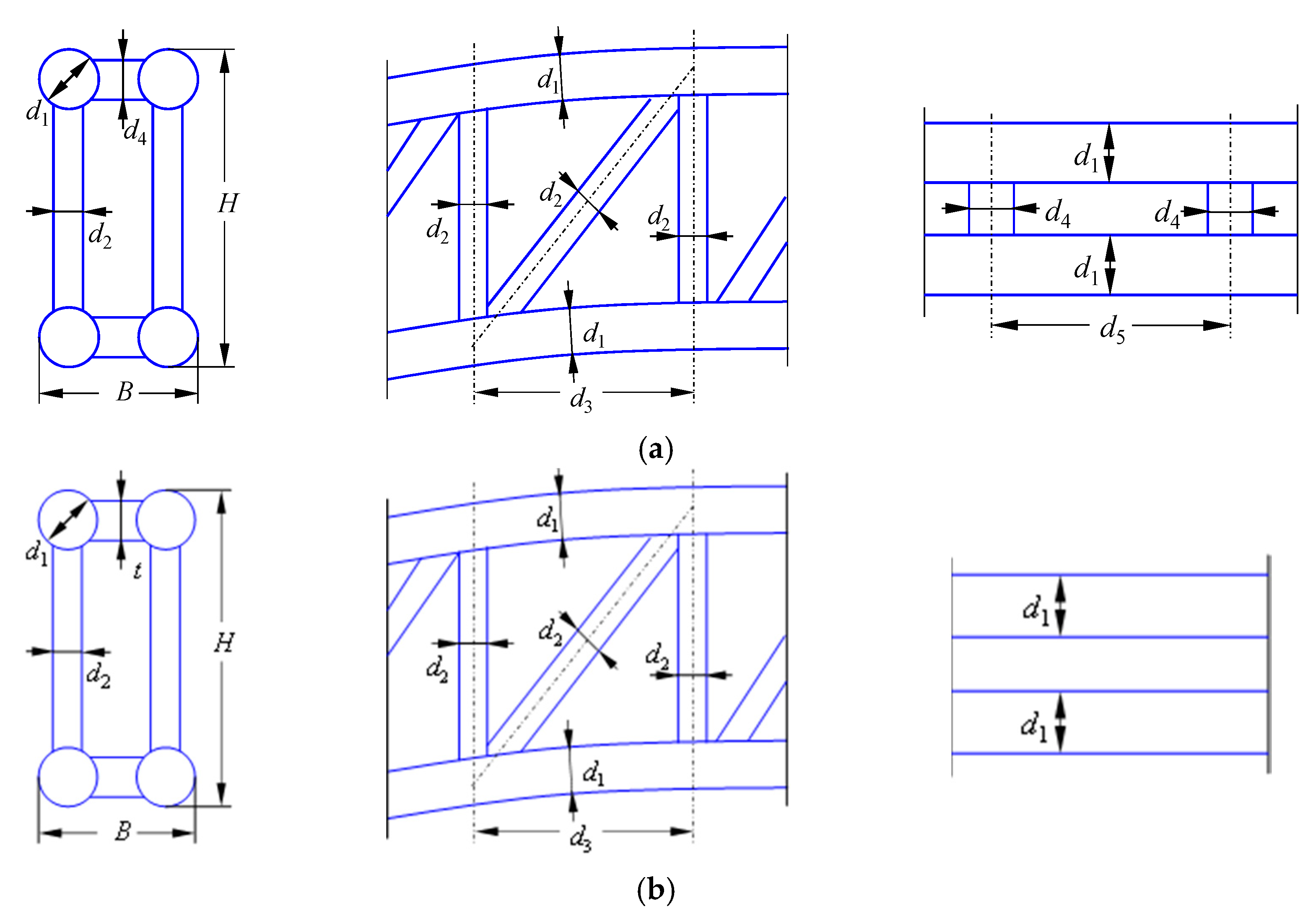

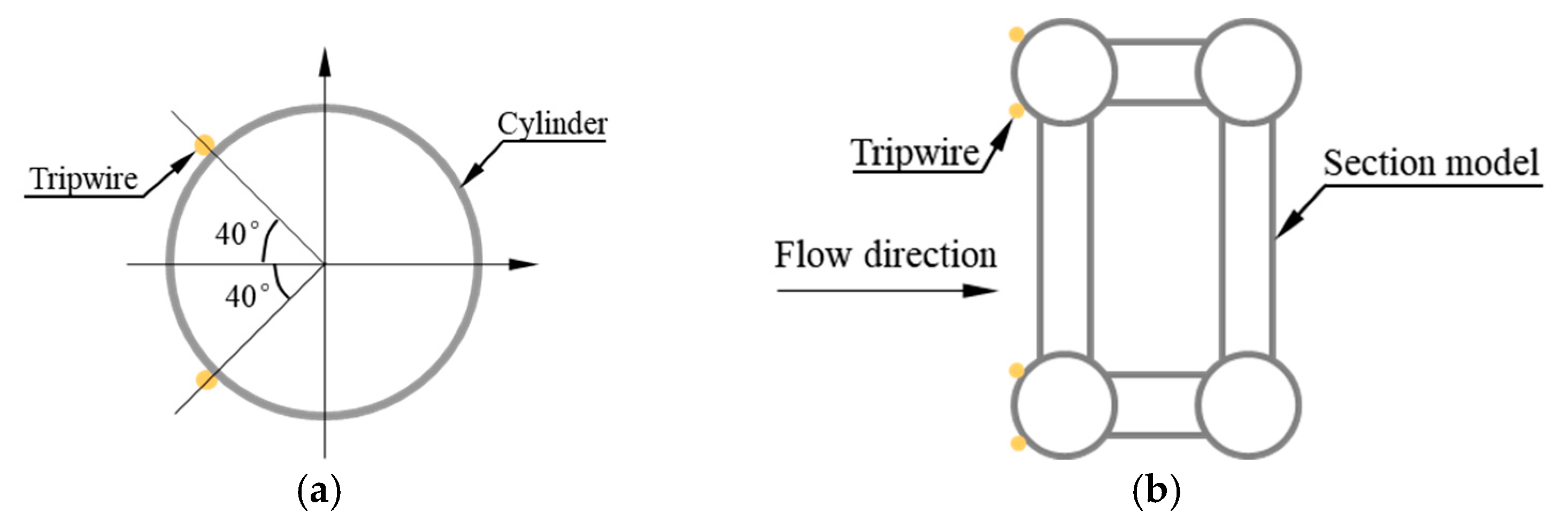



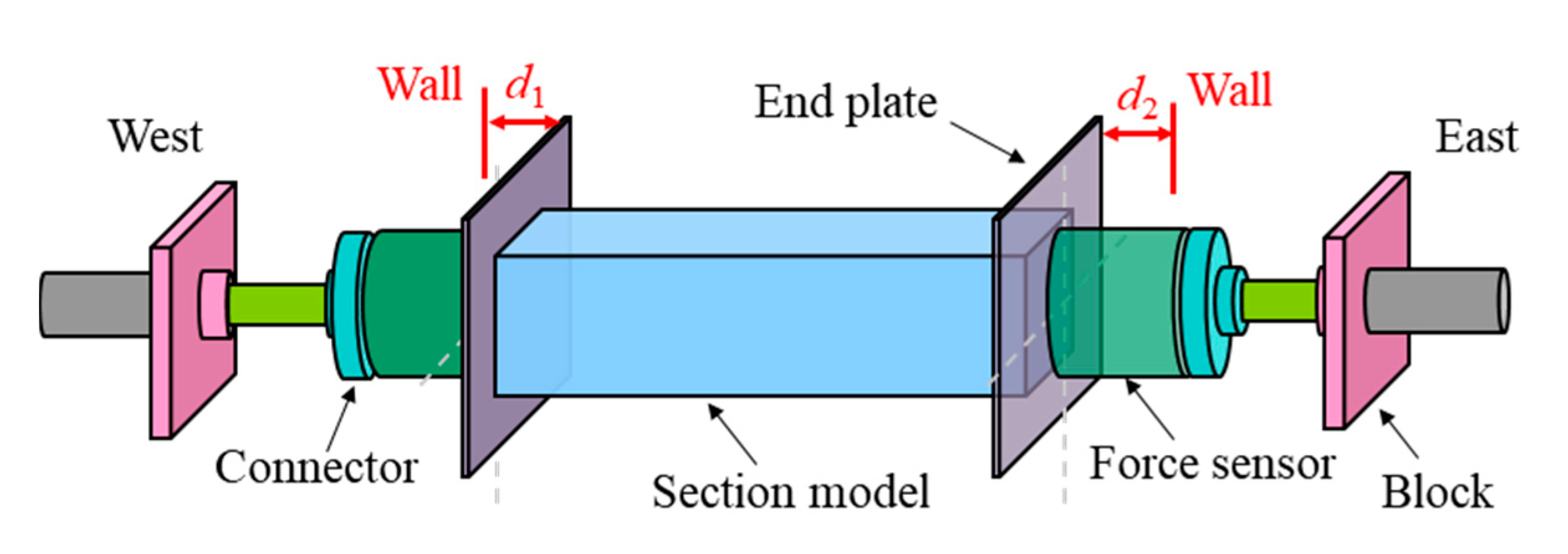


| Section Models | l | B | H | B/H | d1 | d2 | d3 | d4 | d5 | t |
|---|---|---|---|---|---|---|---|---|---|---|
| FTT-I | 900 | 67.5 | 150 | 0.45 | 30 | 15 | 150 | 15 | 150 | - |
| FTT-II | 900 | 86.5 | 150 | 0.58 | 30 | 15 | 150 | 15 | 150 | - |
| FTT-III | 900 | 105.0 | 150 | 0.7 | 30 | 15 | 150 | 15 | 150 | - |
| HDT-I | 900 | 67.5 | 150 | 0.45 | 30 | 15 | 150 | - | - | 21 |
| HDT-II | 900 | 86.5 | 150 | 0.58 | 30 | 15 | 150 | - | - | 21 |
| HDT-III | 900 | 105.0 | 150 | 0.7 | 30 | 15 | 150 | - | - | 21 |
| Section Models | B/mm | CD | CL | CM |
|---|---|---|---|---|
| FTT-I | 67.5 | 1.11 | −0.0405 | 0.0478 |
| FTT-II | 86.5 | 1.24 | −0.110 | −0.0203 |
| FTT-III | 105.0 | 1.24 | −0.0958 | −0.0435 |
| HDT-I | 67.5 | 0.99 | 0.00714 | −0.0359 |
| HDT-II | 86.5 | 1.10 | 0.0375 | −0.0112 |
| HDT-III | 105.0 | 1.07 | 0.0292 | −0.000732 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Wu, X.; Zhang, S.; Lu, D. Wind Tunnel Tests and Buffeting Response Analysis of Concrete-Filled Steel Tubular Arch Ribs During Cantilever Construction. Buildings 2025, 15, 1837. https://doi.org/10.3390/buildings15111837
Hu Q, Wu X, Zhang S, Lu D. Wind Tunnel Tests and Buffeting Response Analysis of Concrete-Filled Steel Tubular Arch Ribs During Cantilever Construction. Buildings. 2025; 15(11):1837. https://doi.org/10.3390/buildings15111837
Chicago/Turabian StyleHu, Qing, Xinrong Wu, Shilong Zhang, and Dagang Lu. 2025. "Wind Tunnel Tests and Buffeting Response Analysis of Concrete-Filled Steel Tubular Arch Ribs During Cantilever Construction" Buildings 15, no. 11: 1837. https://doi.org/10.3390/buildings15111837
APA StyleHu, Q., Wu, X., Zhang, S., & Lu, D. (2025). Wind Tunnel Tests and Buffeting Response Analysis of Concrete-Filled Steel Tubular Arch Ribs During Cantilever Construction. Buildings, 15(11), 1837. https://doi.org/10.3390/buildings15111837








