Study on the Effect of Crack Density and Micro-Cracking Block Size of In Situ Softening Semi-Rigid Base
Abstract
1. Introduction
2. Exploitation Concept for In Situ Softening of Semi-Rigid Base
2.1. Mechanical Properties of the Semi-Rigid Base During the Service Period
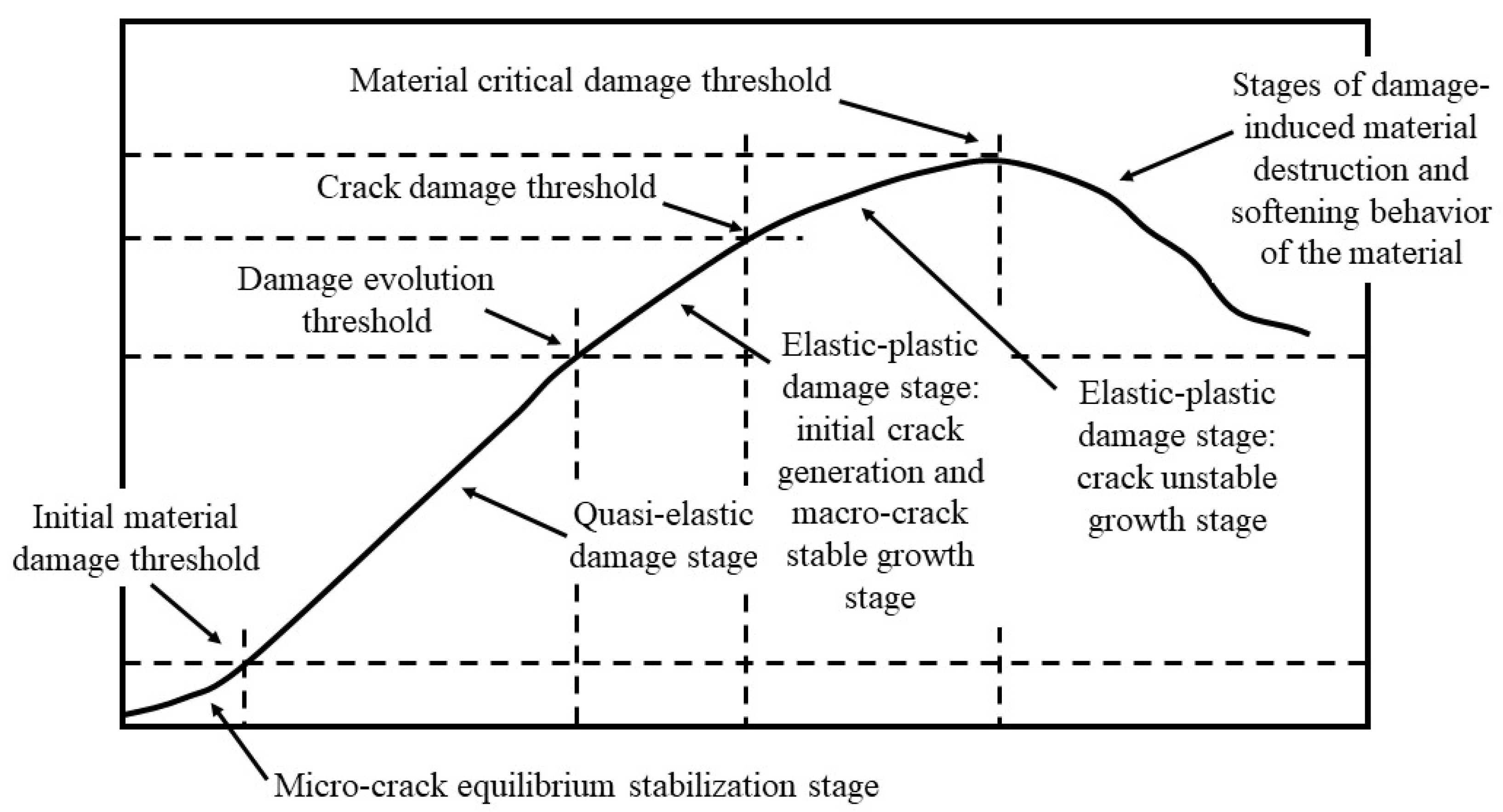
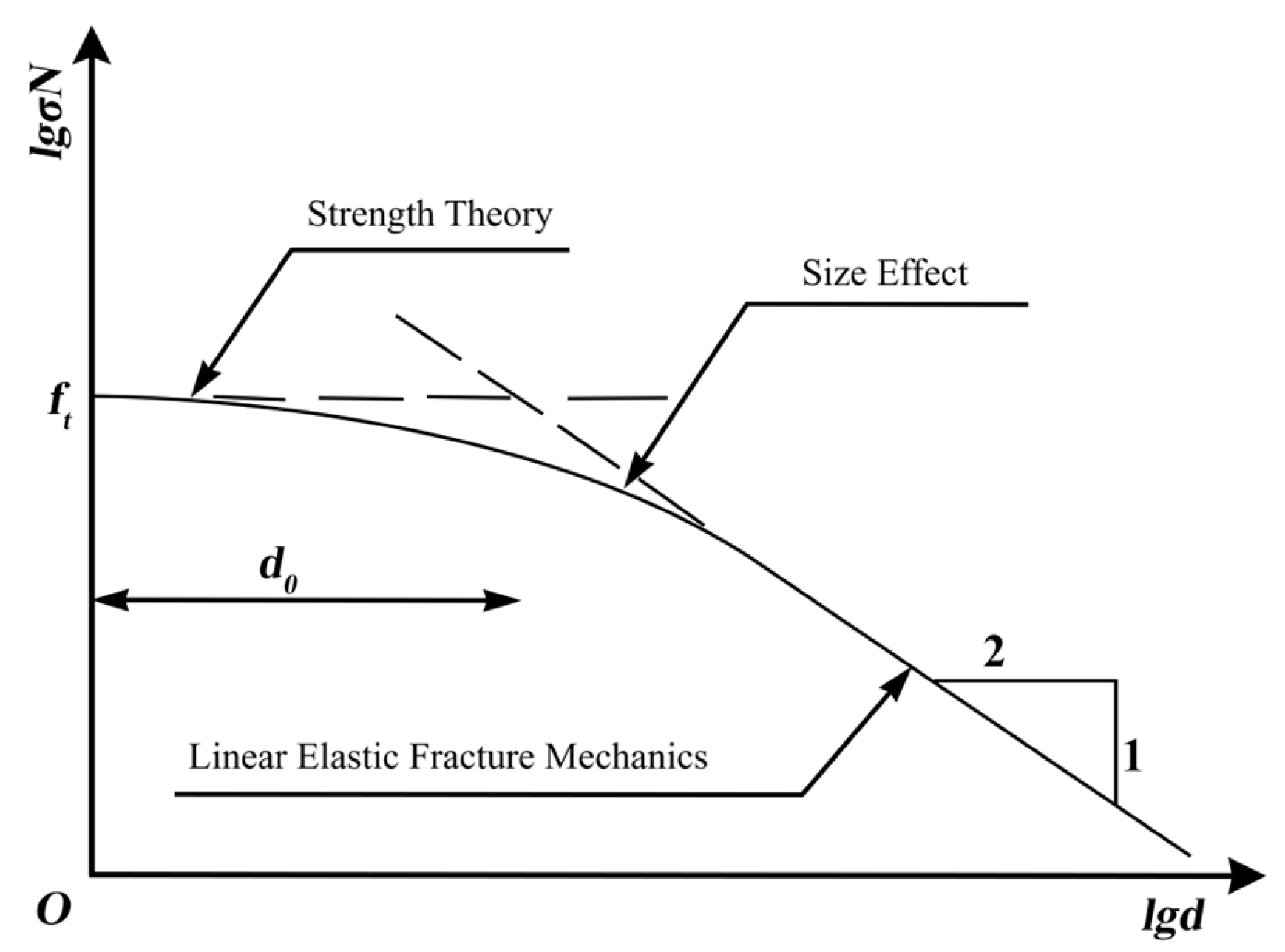
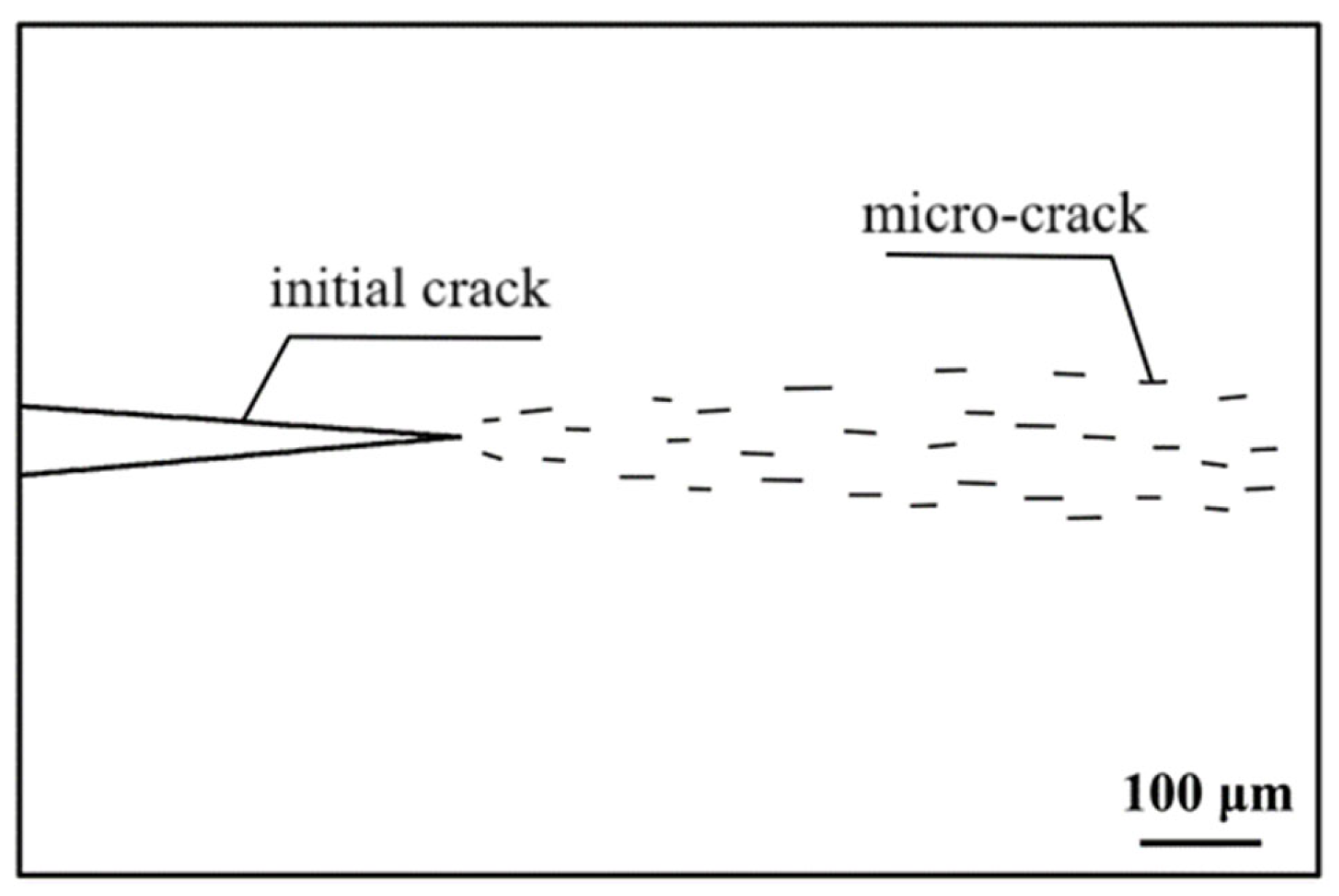
2.2. Failure Characteristics of Semi-Rigid Base Materials
2.3. Adaptive Conditions for In Situ Softening of Semi-Rigid Base
3. Numerical Model
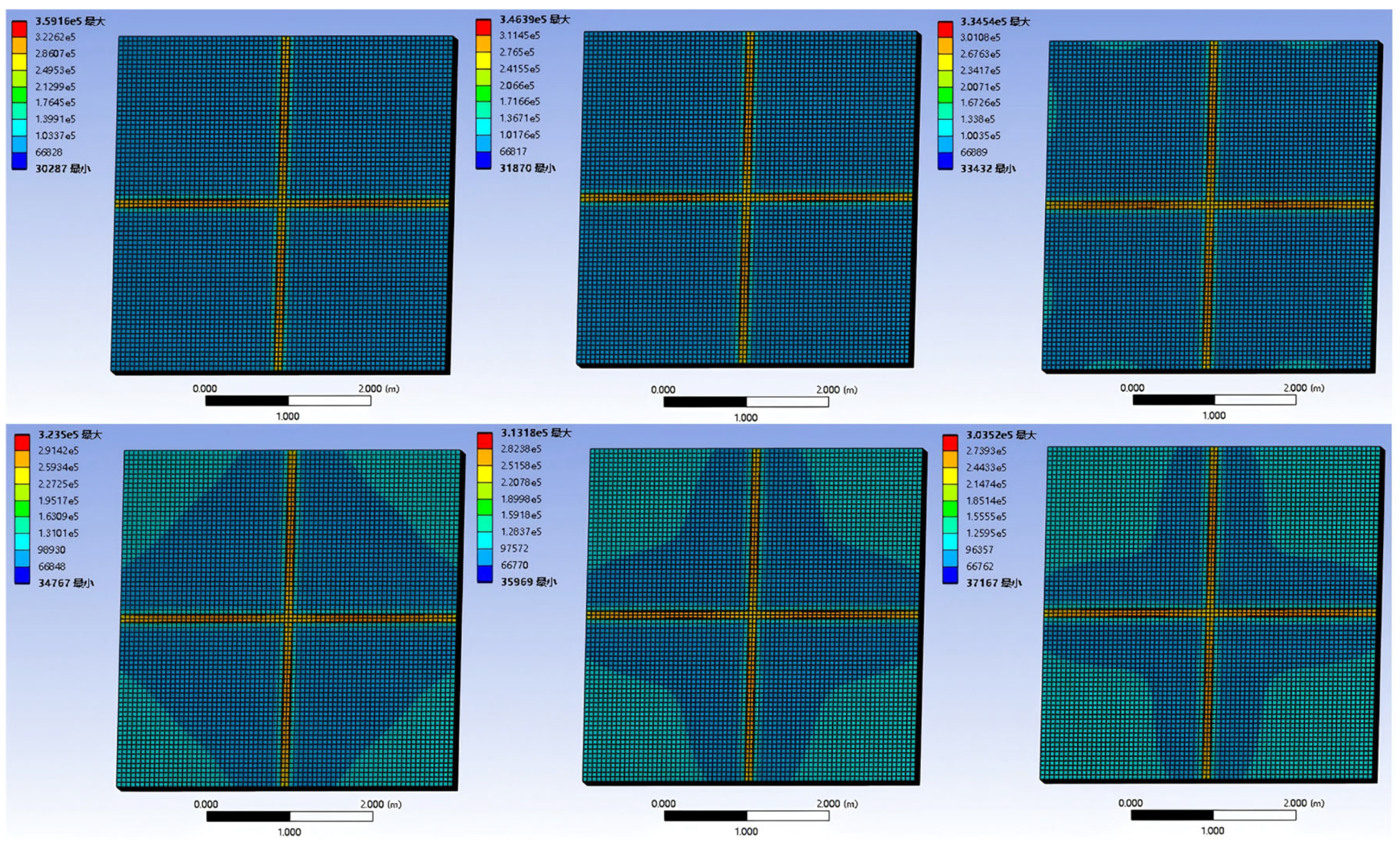
3.1. Base Cracking Density Effect Modeling
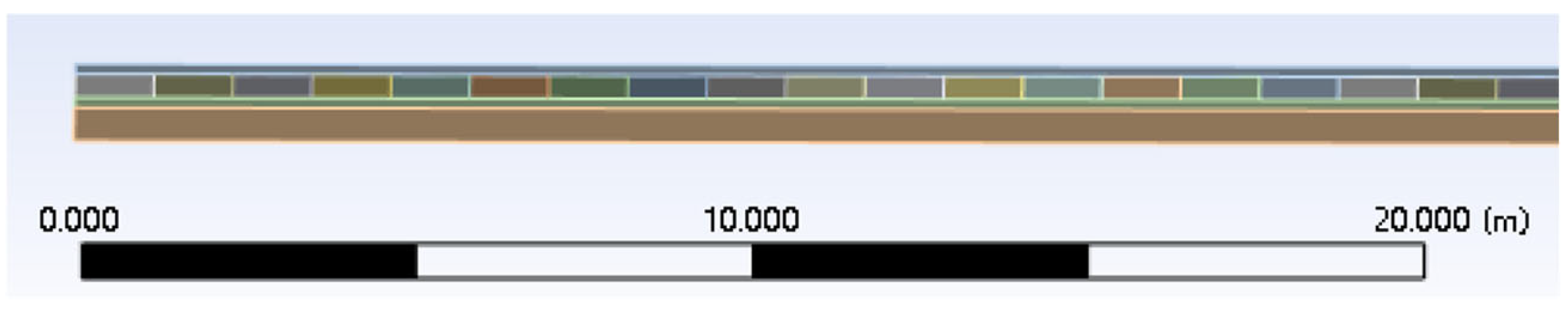
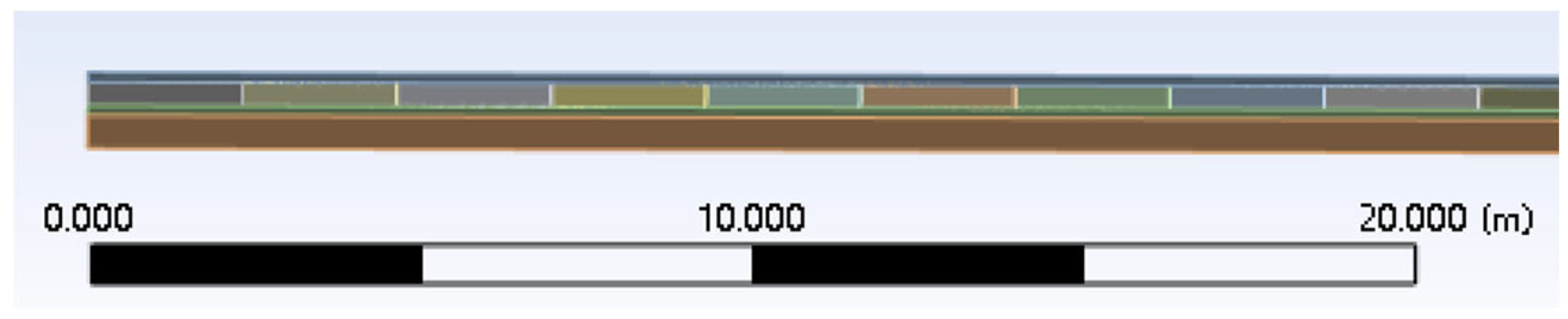
3.2. Cracking Block-Size Effect Modeling
4. Base Cracking Properties
4.1. Cracking Properties Based on Different Crack Densities
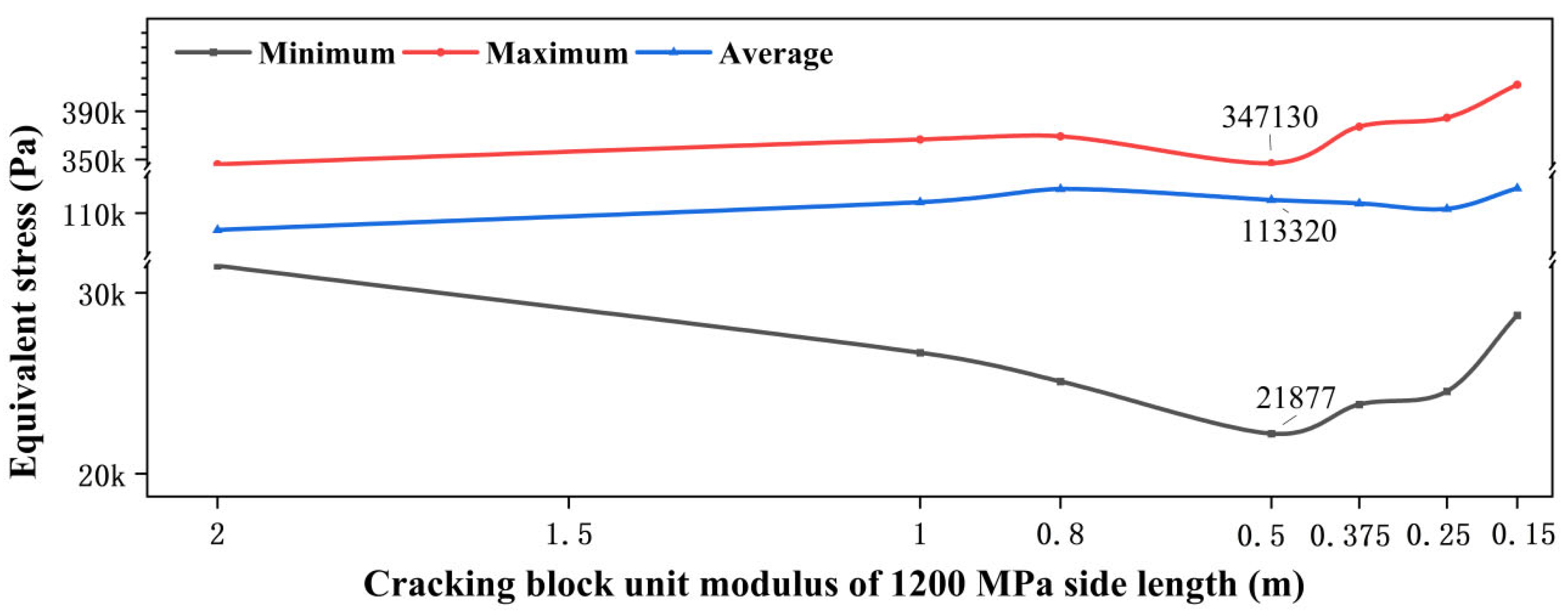
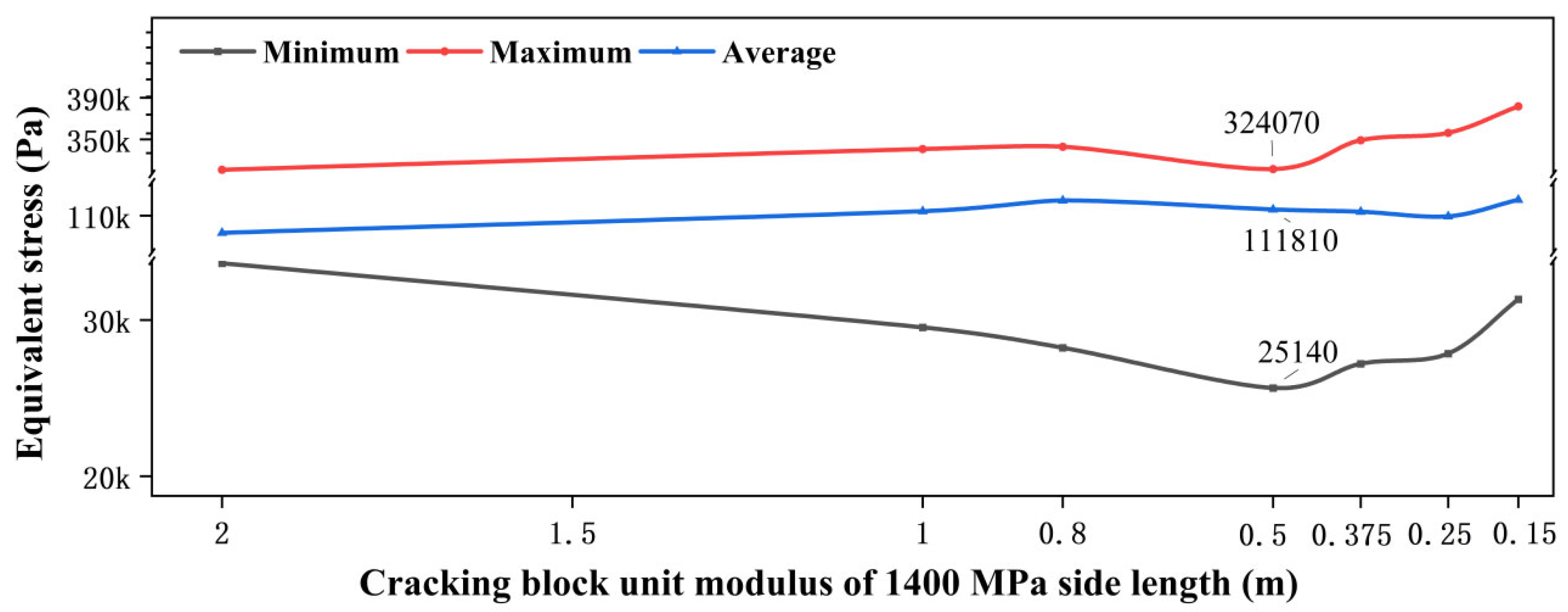
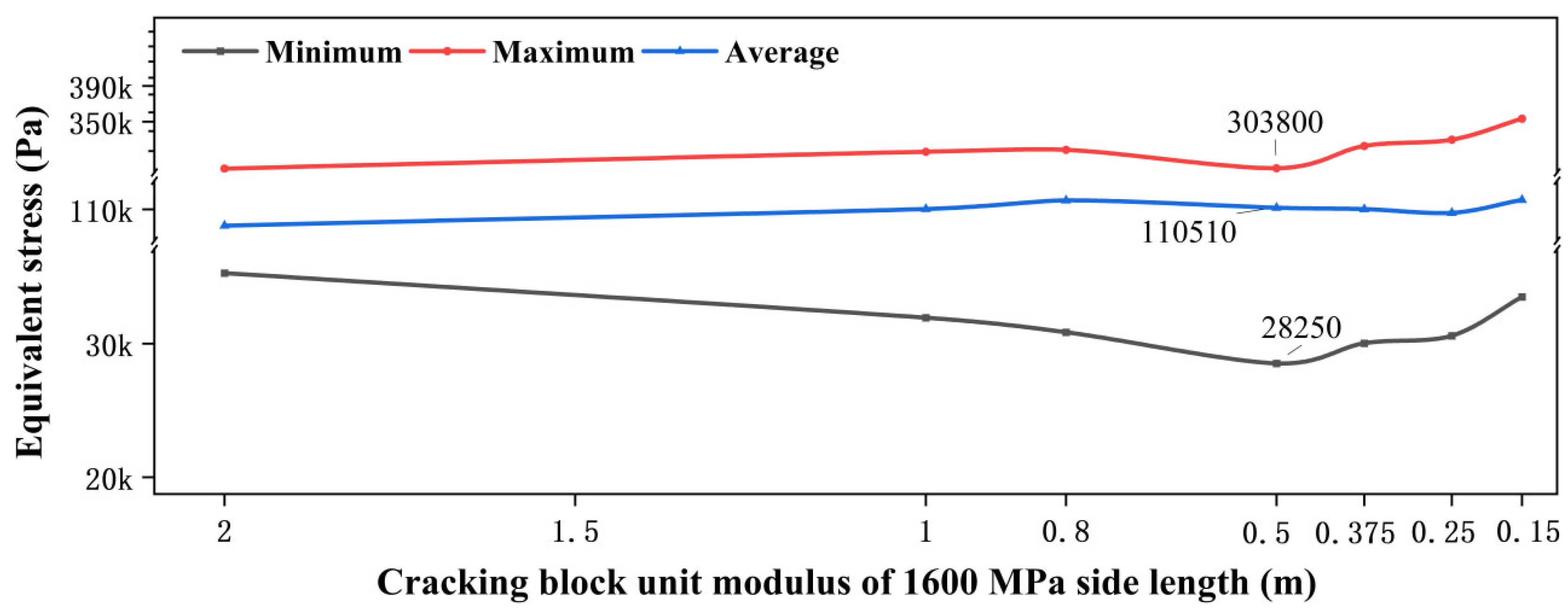
4.2. Bearing Capacity Characteristics Based on Different Cracked Block Sizes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, L.; Wu, Y.; Meng, Y.; Huang, G.; Li, R.; Pei, J. Study on fatigue crack propagation failure in semi-rigid base. Constr. Build. Mater. 2023, 409, 134007. [Google Scholar] [CrossRef]
- Botvina, L.R. Damage Evolution and Fracture in Terms of The Theory of Phase Transition. Procedia Struct. Integr. 2019, 14, 26–33. [Google Scholar] [CrossRef]
- Maurizi, M.; Berto, F. 3D Effects on Fracture Mechanics. Procedia Struct. Integr. 2020, 25, 261–268. [Google Scholar] [CrossRef]
- Shahbazpanahi, S.; Karim, H.; Abdullah, W.; Reuter, U.; Mosavi, A.H. Crack Propagation Modeling of Strengthening Reinforced Concrete Deep Beams with CFRP Plates. Mater. Res. Express 2021, 8, 095502. [Google Scholar] [CrossRef]
- Clayton, J.D. Finsler Differential Geometry in Continuum Mechanics: Fundamental Concepts, History, and Renewed Application to Ferromagnetic Solids. Math. Mech. Solids 2021, 27, 910–995. [Google Scholar] [CrossRef]
- Barras, F.; Aldam, M.; Roch, T.; Brener, E.A.; Bouchbinder, E.; Molinari, J.-F. The Emergence of Crack-like Behavior of Frictional Rupture: Edge Singularity and Energy Balance. Earth Planet. Sci. Lett. 2019, 531, 115978. [Google Scholar] [CrossRef]
- Paglialunga, F.; Passelègue, F.X.; Brantut, N.; Barras, F.; Lebihain, M.; Violay, M. On the Scale Dependence in The Dynamics of Frictional Rupture: Constant Fracture Energy Versus Size-dependent Breakdown Work. Earth Planet. Sci. Lett. 2021, 584, 117442. [Google Scholar] [CrossRef]
- Doitrand, A.; Sapora, A. Nonlinear Implementation of Finite Fracture Mechanics: A Case Study on Notched Brazilian Disk Samples. Int. J. Non-Linear Mech. 2020, 119, 103245. [Google Scholar] [CrossRef]
- Gvirtzman, S.; Fineberg, J. Nucleation Fronts Ignite the Interface Rupture That Initiates Frictional Motion. Nat. Phys. 2021, 17, 1037. [Google Scholar] [CrossRef]
- Rajbongshi, P.; Das, A. Estimation of Temperature Stress and Low-Temperature Crack Spacing in Asphalt Pavements. J. Transp. Eng. 2009, 135, 745–752. [Google Scholar] [CrossRef]
- Alavi, M.Z. Comprehensive, Methodologies for Analysis of Thermal Cracking in Asphalt Concrete Pavements. Bachelor’s Thesis, University of Nevada, Reno, NV, USA, 2013. [Google Scholar]
- Park, J.-W.; Ryu, S.; Oh, H.; Cho, Y.-H. Relationship Between Cracking Closure and Zero Stress Temperature in Concrete Pavements. Ksce J. Civ. Eng. 2019, 23, 3961–3967. [Google Scholar] [CrossRef]
- Golrokh, A.J.; Lu, Y. An Experimental Study of The Effects of Climate Conditions on Thermography and Pavement Assessment. Int. J. Pavement Eng. 2019, 22, 1030–1041. [Google Scholar] [CrossRef]
- Xie, P.; Wang, H. Analysis of Temperature Variation and Thermally-Induced Reflective Cracking Potential in Composite Pavements. Transp. Res. Rec. 2020, 2674, 177–188. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, P.; Zhang, Z.; Pan, Y. Experimental Study of The Performance of a Stress-absorbing Waterproof Layer for Use in Asphalt Pavements on Bridge Decks. Constr. Build. Mater. 2020, 254, 119290. [Google Scholar] [CrossRef]
- Adam, Q.; Englmair, G.; Levenberg, E.; Skar, A. Active Mitigation of Low-Temperature Cracking in Asphalt Pavements. In Proceedings of the RILEM International Symposium on Bituminous Materials, Lyon, France, 14–16 December 2020; Springer Publishing: Cham, Switzerland, 2020; Volume 21–23. [Google Scholar]
- Yu, B.; Lu, Q.; Yang, J. Evaluation of Anti-Reflective Cracking Measures by Laboratory Test. Int. J. Pavement Eng. 2013, 14, 553–560. [Google Scholar] [CrossRef]
- Gonzalez-Torre, I.; Calzada-Perez, M.A.; Vega-Zamanillo, A.; Castro-Fresno, D. Evaluation of Reflective Cracking in Pavements Using A New Procedure That Combines Loads with Different Frequencies. Constr. Build. Mater. 2015, 75, 368–374. [Google Scholar] [CrossRef]
- Horníček, L.; Zikmund, R. Mechanical Stabilization of Intermediate Granular Layers in Pavement Structures-Laboratory Study. Procedia Eng. 2017, 189, 174–180. [Google Scholar] [CrossRef]
- Chen, D.; Hong, F.; Zhou, F. Premature Cracking from Cement-Treated Base and Treatment to Mitigate Its Effect. J. Perform. Constr. Facil. 2011, 25, 113–120. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, L.; Zheng, J.; Wu, H. Reflective Crack Propagation and Control in Asphalt Pavement Widening. J. Test. Eval. 2016, 44, 838–846. [Google Scholar] [CrossRef]
- Golewski, G.L.; Golewski, P.; Sadowski, T. Numerical modeling crack propagation under model Ⅱ fracture in plain concretes containing siliceous fly-ash additive using XFEM method. Comput. Mater. Sci. 2012, 61, 75–78. [Google Scholar] [CrossRef]
- Gracie, R.; Wang, H.W.; Belytschko, T. Blending in the finite element method by discontinuous Galerkin and assumed strain methods. Int. J. Numer. Methods Eng. 2008, 74, 1645–1669. [Google Scholar] [CrossRef]
- Gracie, R.; Oswald, J.; Belytschko, T. On a new extended finite element method for dislocations: Core enrichments. J. Mech. Phys. Solids 2008, 56, 200–214. [Google Scholar] [CrossRef]
- Dave, E.V.; Buttlar, W.G. Thermal reflective cracking of asphalt concrete overlays. Int. J. Pavement Eng. 2010, 11, 477–488. [Google Scholar] [CrossRef]
- Zamora-Barraza, D.; Calzada-Pérez, M.A.; Castro-Fresno, D.; Vega-Zamanillo, A. Evaluation of anti-reflective cracking systems using geosynthetics in the interlayer zone. Geotextile Geomembr. 2011, 29, 130–136. [Google Scholar] [CrossRef]
- Yu, L.; Wang, L.; Pei, J.; Li, R.; Zhang, J.; Cheng, S. Structural Optimization Study Based on Crushing of Semi-rigid Base. Electron. Res. Arch. 2023, 31, 1769–1788. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, F.; Zhang, J.; Hu, D.; Minelli, M.; Pei, J.; Sangiorgi, C. Contributions of Fourier-transform infrared spectroscopy technologies to the research of asphalt materials: A comprehensive review. Fuel 2024, 371, 132078. [Google Scholar] [CrossRef]
- JTG D50-2017; Specification for Design of Highway Asphalt Pavement. China Highway Specification and Design Institute: Beijing, China, 2017.
- Pérez-Acebo, H.; Linares-Unamunzaga, A.; Rojí, E.; Gonzalo-Orden, H. IRI performance models for flexible pavements in two-lane roads until first maintenance and/or rehabilitation work. Coatings 2020, 10, 97. [Google Scholar] [CrossRef]
- Pérez-Acebo, H.; Gonzalo-Orden, H.; Findley, D.J.; Rojí, E. Modeling the international roughness index performance on semi-rigid pavements in single-carriageway roads. Constr. Build. Mater. 2021, 272, 121665. [Google Scholar] [CrossRef]
- Zu, F.; Du, C.; Han, C.; Xu, L.; Peng, Q. Applicable conditions of room-and-pillar mining goaf treatment methods under a traffic load. Appl. Sci. 2023, 13, 2024. [Google Scholar] [CrossRef]
- Yu, L.; Tang, D.; Kang, H.; He, H.; Hu, D.; Li, R.; Pei, J.; Cheng, S. Research on the Stress Characteristics of Reuse of Semi-Rigid Base. Sensors 2024, 24, 8004. [Google Scholar] [CrossRef]
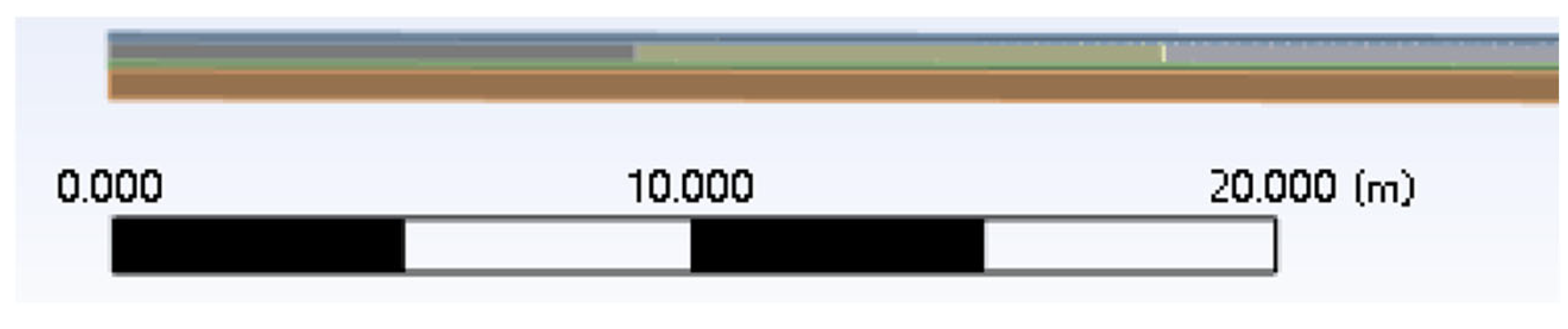
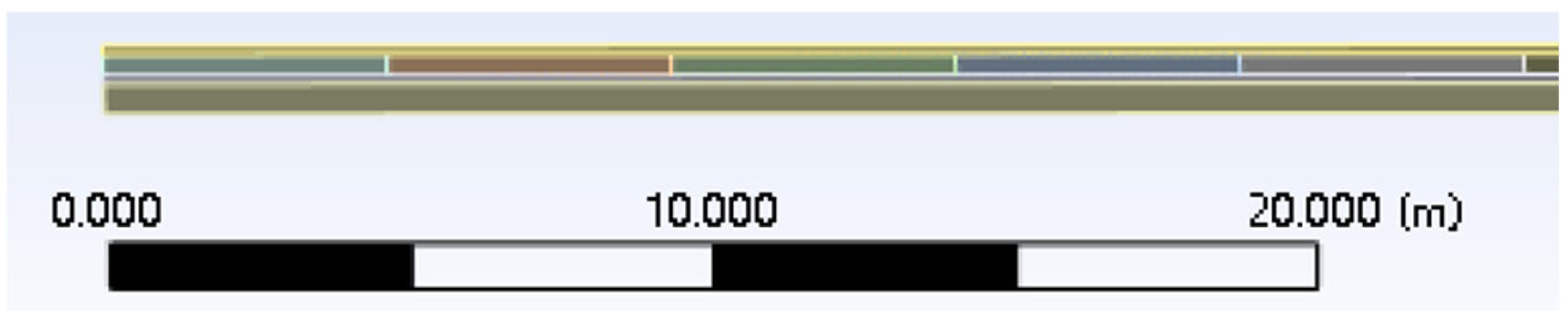









| Crack density (piece/100 m) | 5 | 10 | 20 | 40 | 80 | 150 |
| Model length (m) | 100 | 100 | 100 | 100 | 100 | 100 |
| Number of model cracks | 5 | 10 | 20 | 40 | 80 | 150 |
| Structural | Material | Modulus of Elasticity (MPa) | Poisson’s Ratio | Thickness (mm) |
|---|---|---|---|---|
| Surface | Asphalt mixture | 1400 | 0.25 | 150 |
| Base | Cement-stabilized aggregate | 2100/2200/2300/2400/ 2500/2600 | 0.25 | 350 |
| Sub-base | Gravel | 400 | 0.35 | 150 |
| subgrade | Soil | 80 | 0.4 | 500 |
| Cracking Block Unit Side Length | Number of Cracked Blocks | Rigid Connection Depth | Model Length/Width | Model Thickness |
|---|---|---|---|---|
| 2 m | 2 × 2 | 100 mm | 4.10 m | 350 mm |
| 1 m | 4 × 4 | 100 mm | 4.30 m | 350 mm |
| 0.8 m | 5 × 5 | 100 mm | 4.40 m | 350 mm |
| 0.5 m | 8 × 8 | 80 mm | 4.56 m | 350 mm |
| 0.375 m | 4 × 4 | 80 mm | 1.74 m | 350 mm |
| 0.25 m | 4 × 4 | 30 mm | 1.15 m | 250 mm |
| 0.15 m | 4 × 4 | 20 mm | 0.66 m | 150 mm |
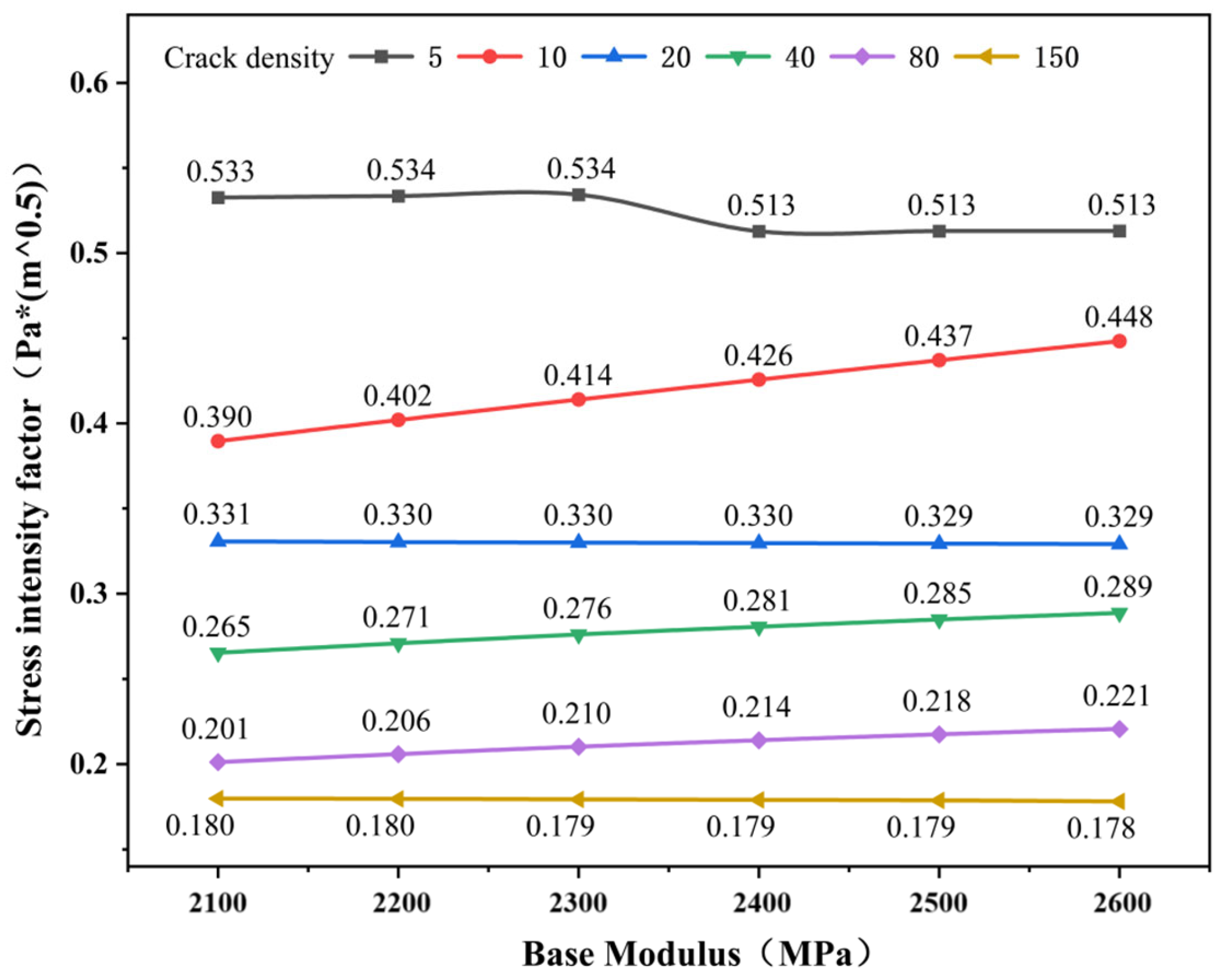
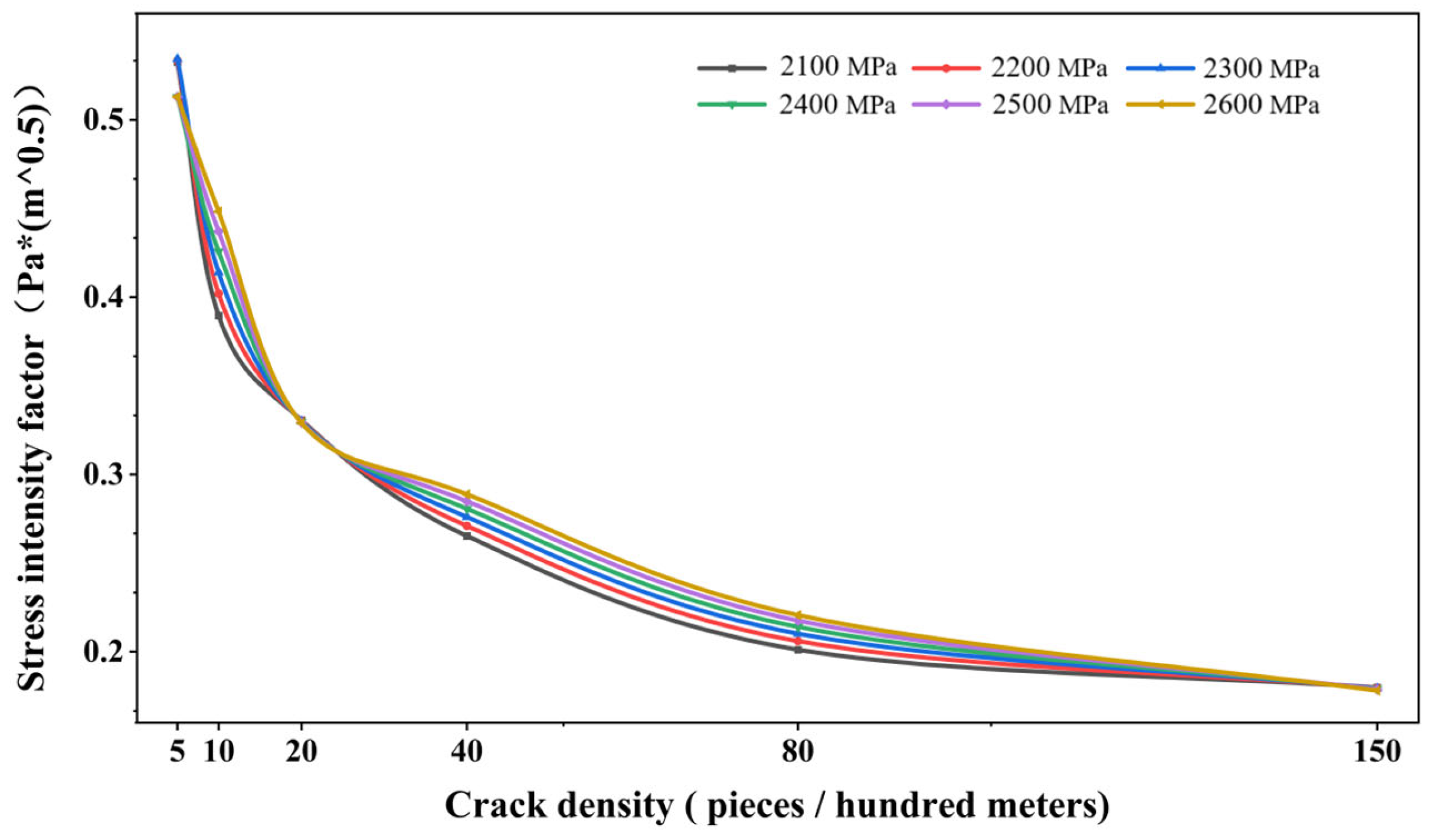
| Base Modulus | 2100 MPa | 2200 MPa | 2300 MPa | 2400 MPa | 2500 MPa | 2600 MPa | |
|---|---|---|---|---|---|---|---|
| Crack Density | |||||||
| 5 pieces | 0.5326 | 0.5335 | 0.5343 | 0.5128 | 0.5129 | 0.5130 | |
| 10 pieces | 0.3896 | 0.4020 | 0.4140 | 0.4257 | 0.4371 | 0.4483 | |
| 20 pieces | 0.3306 | 0.3302 | 0.3299 | 0.3296 | 0.3293 | 0.3290 | |
| 40 pieces | 0.2653 | 0.2709 | 0.2760 | 0.2806 | 0.2848 | 0.2887 | |
| 80 pieces | 0.2012 | 0.2059 | 0.2102 | 0.2140 | 0.2175 | 0.2206 | |
| 150 pieces | 0.1798 | 0.1796 | 0.1793 | 0.1790 | 0.1787 | 0.1781 | |
| A Hundred-Meter Crack in Base | Pavement Condition | Suggested Curing Methods |
|---|---|---|
| Less than 5 | Newly built | Surface observation |
| 5~10 pieces | The surface layer is slightly damaged | Overlay, chipping seal and overlay, etc. |
| 10~20 pieces | The surface layer is completely damaged | Milling and planing the surface course and resurfacing the surface course after reinforcing the base course as required |
| 20~40 pieces | Crack penetration of base course | Micro-cracking treatment to convert the semi-rigid base into the bottom and lower base |
| 40~80 pieces | The base course is loose | Semi-rigid base granular material-type softening regeneration |
| More than 150 pieces | Loss of overall pavement function | Overall reconstruction of pavement |
| Size of the Cracking Block (Approximate Value) | The Main Bearing Mode of External Force |
|---|---|
| 2 m | Mainly plate-type load-bearing |
| 1 m | Mainly block-type load-bearing |
| 0.8 m | Block-type bearing force as the highest point of the main mode |
| 0.5 m | The edge friction force begins to participate in the main way and bears the external force, together with the block-type bearing force |
| 0.375 m | The most effective connection stress state and the internal and edge friction of the block uniformly bear the external force |
| 0.25 m | The bearing capacity is uneven, mainly due to edge friction, and the middle part of the block has failed |
| Less than 0.25 m | Failure of edge friction and block-bearing force |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Yu, C.; He, H.; Xu, Z.; Hu, D.; Li, R.; Pei, J. Study on the Effect of Crack Density and Micro-Cracking Block Size of In Situ Softening Semi-Rigid Base. Buildings 2025, 15, 1791. https://doi.org/10.3390/buildings15111791
Yu L, Yu C, He H, Xu Z, Hu D, Li R, Pei J. Study on the Effect of Crack Density and Micro-Cracking Block Size of In Situ Softening Semi-Rigid Base. Buildings. 2025; 15(11):1791. https://doi.org/10.3390/buildings15111791
Chicago/Turabian StyleYu, Liting, Chunyang Yu, Haiqi He, Zikai Xu, Donliang Hu, Rui Li, and Jianzhong Pei. 2025. "Study on the Effect of Crack Density and Micro-Cracking Block Size of In Situ Softening Semi-Rigid Base" Buildings 15, no. 11: 1791. https://doi.org/10.3390/buildings15111791
APA StyleYu, L., Yu, C., He, H., Xu, Z., Hu, D., Li, R., & Pei, J. (2025). Study on the Effect of Crack Density and Micro-Cracking Block Size of In Situ Softening Semi-Rigid Base. Buildings, 15(11), 1791. https://doi.org/10.3390/buildings15111791






