Theoretical Research on the Shear Mechanical Properties and Size Effect of Recycled Concrete Beams Without Stirrups
Abstract
1. Introduction
2. Microscopic Numerical Analysis Model
2.1. Geometric Model
2.2. Constitutive Relationship of Microscopic Components
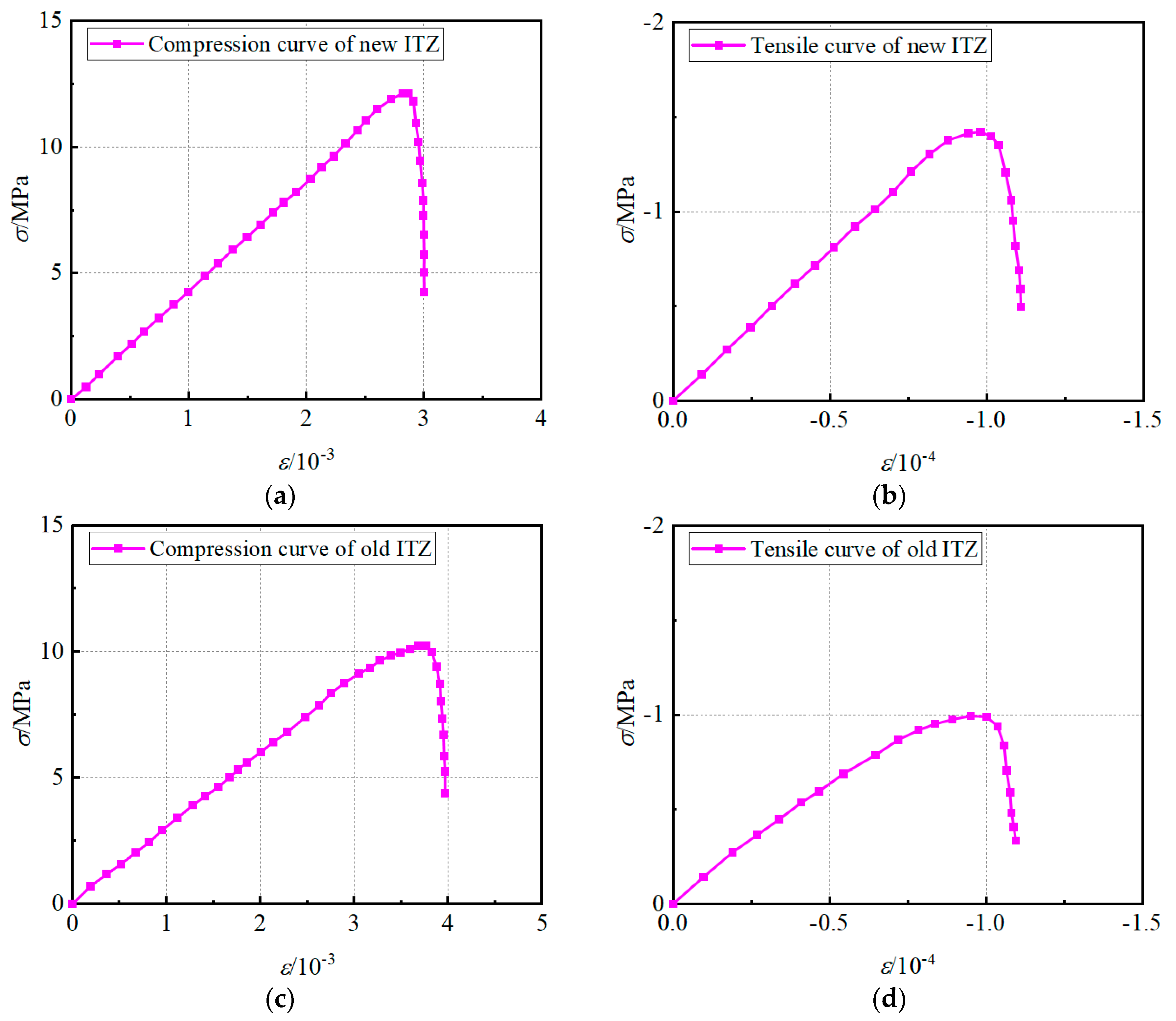
2.2.1. Constitutive Relationship of Concrete
2.2.2. Constitutive Relationship of Reinforcement Bar
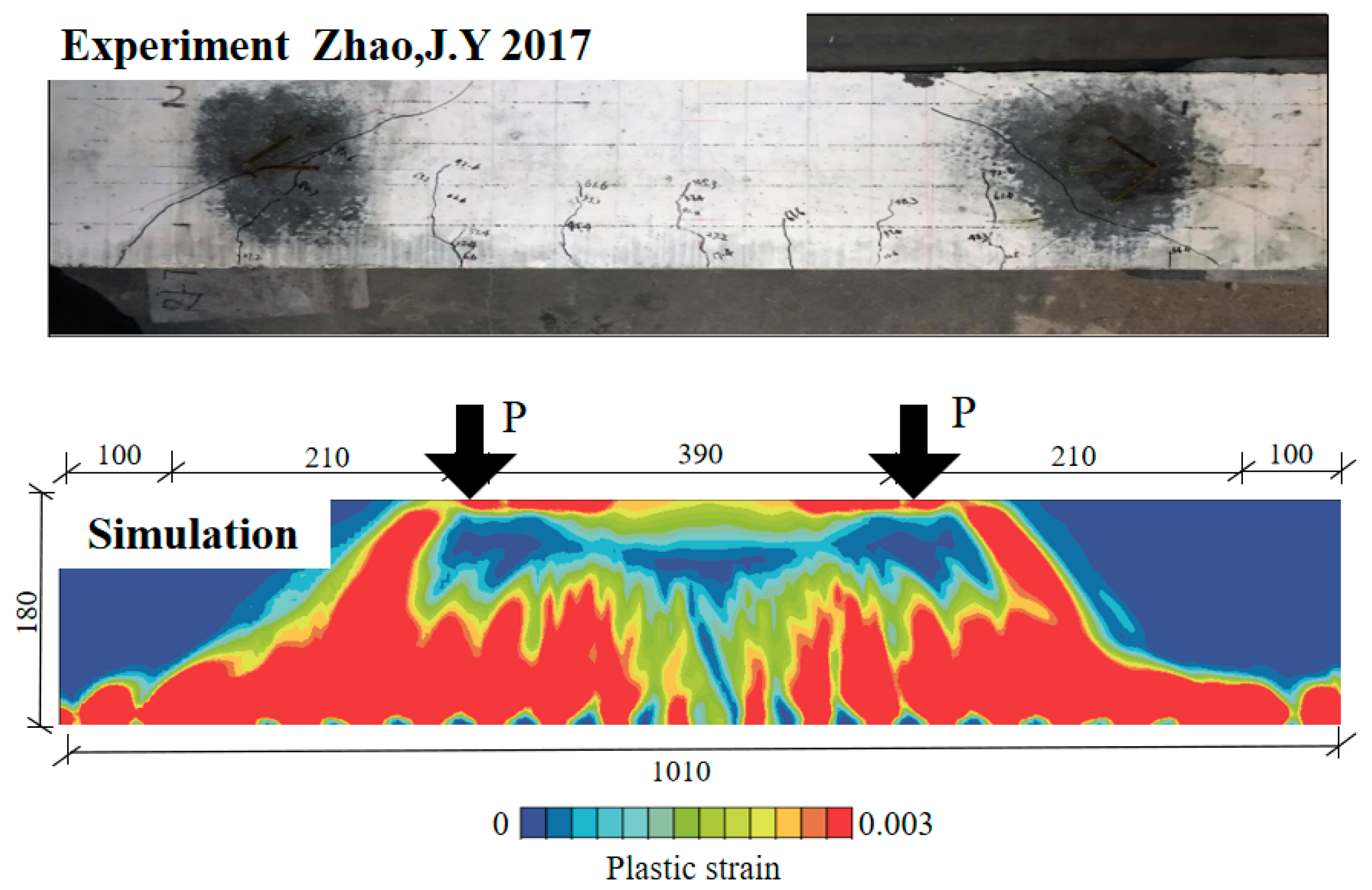
2.3. Model Verification
3. Analysis of Shear-Span Ratio on the Shear Damage and Size Effect
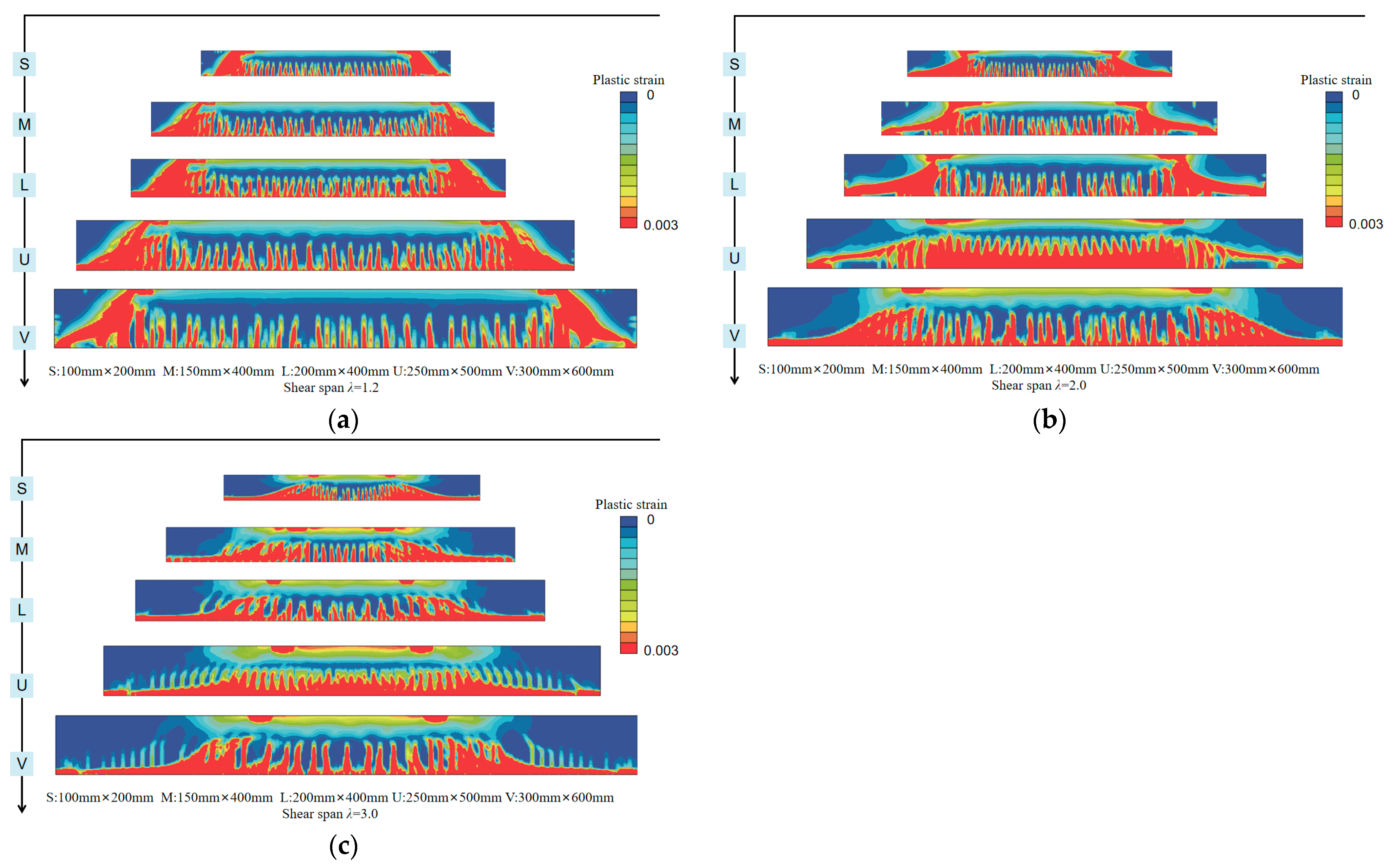
3.1. Shear Damage Mode
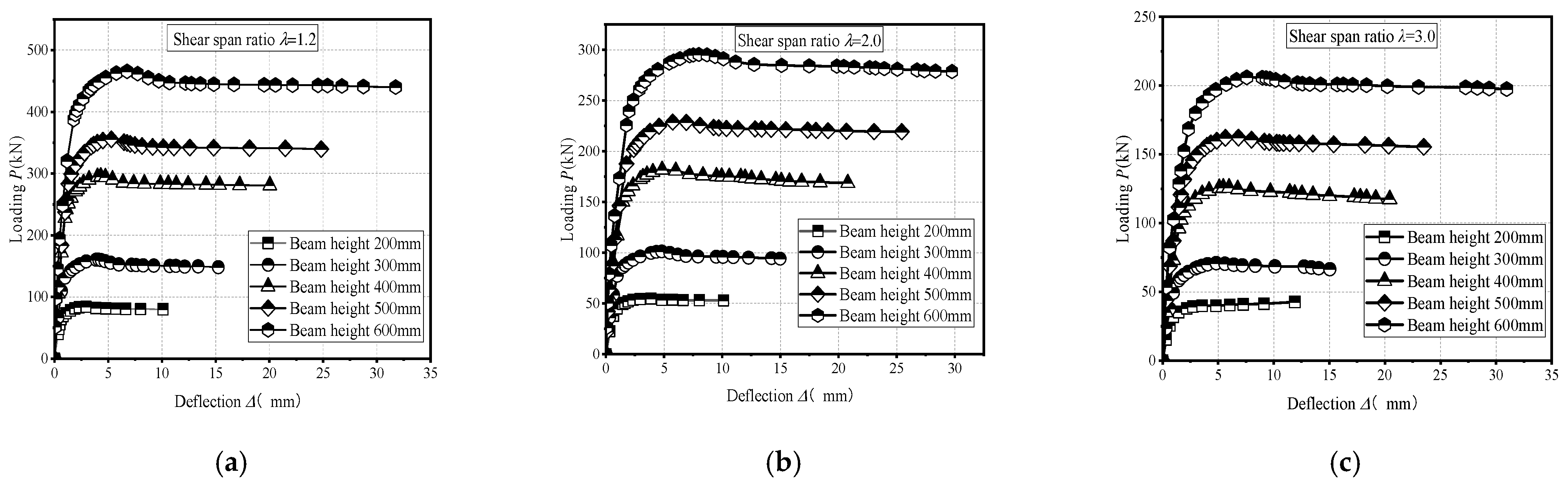
3.2. Load–Displacement Curves
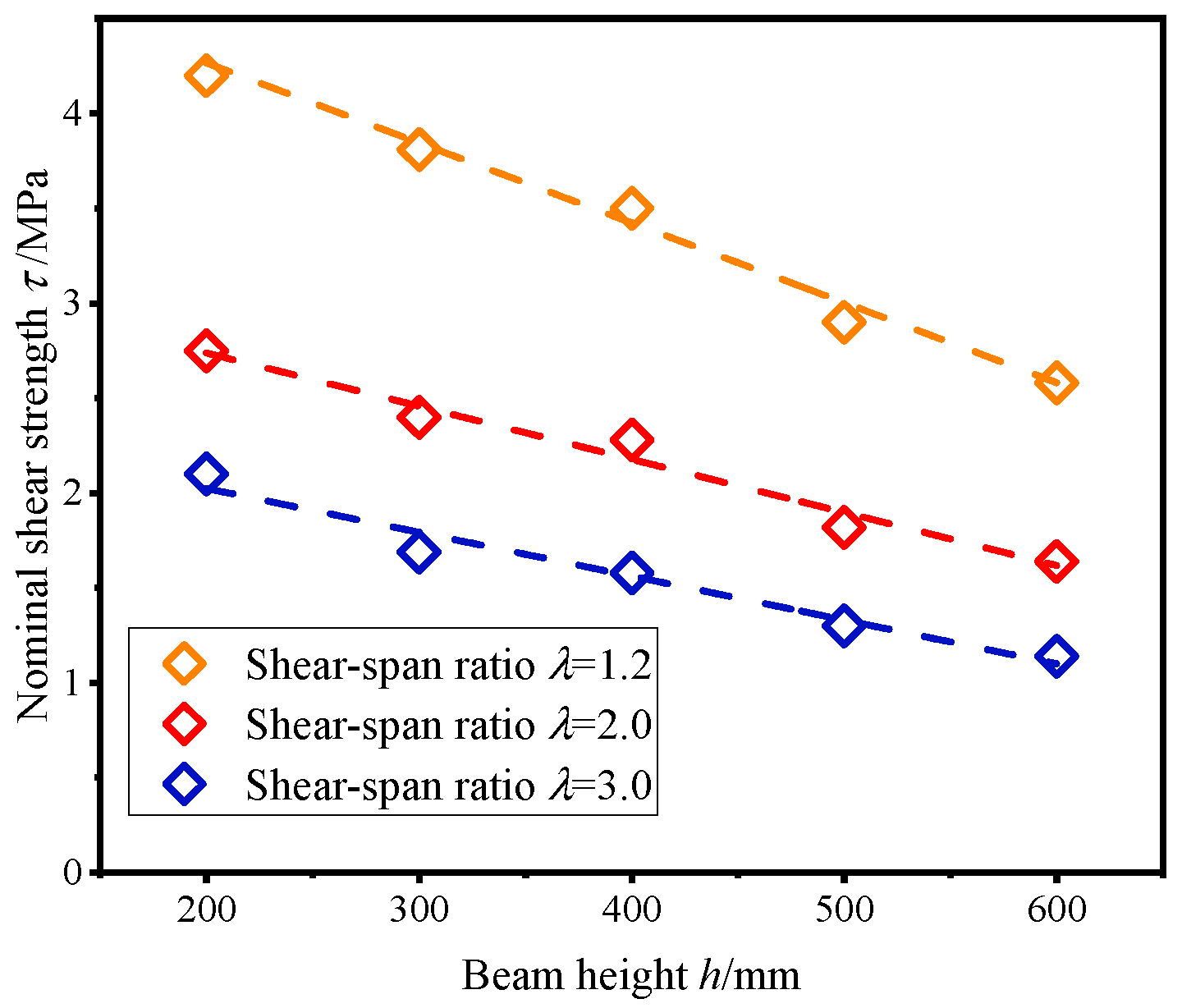
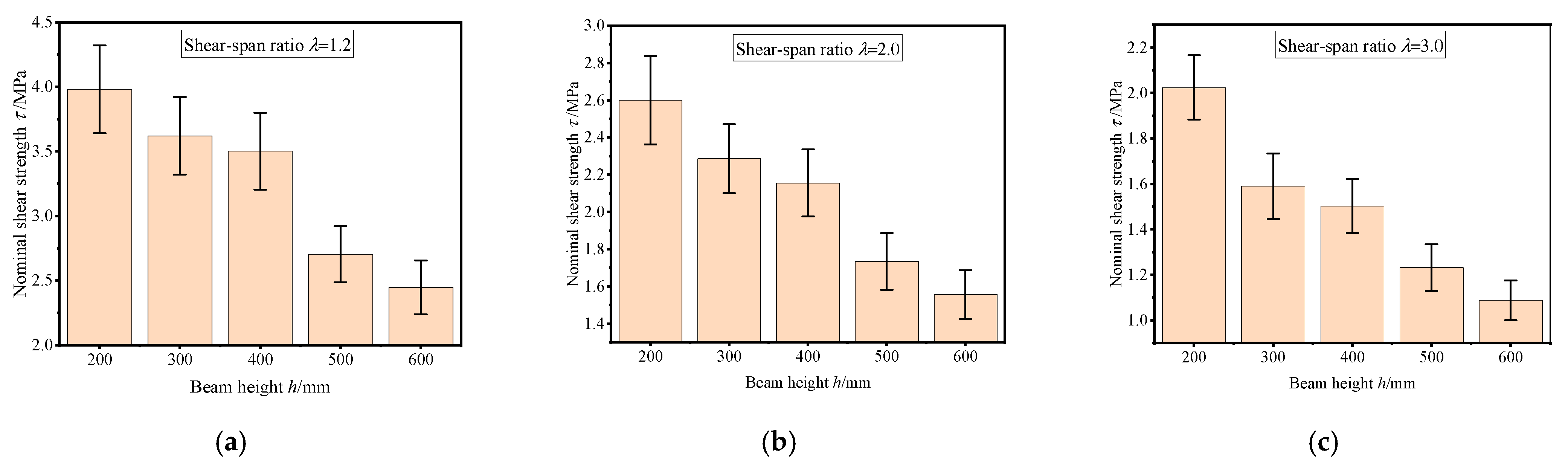
3.3. Analysis of Size Effect of Shear-Span Ratio on the Nominal Shear Strength
4. Influence of Replacement Rate on the Shear Failure and Size Effect
4.1. Shear Failure Mode
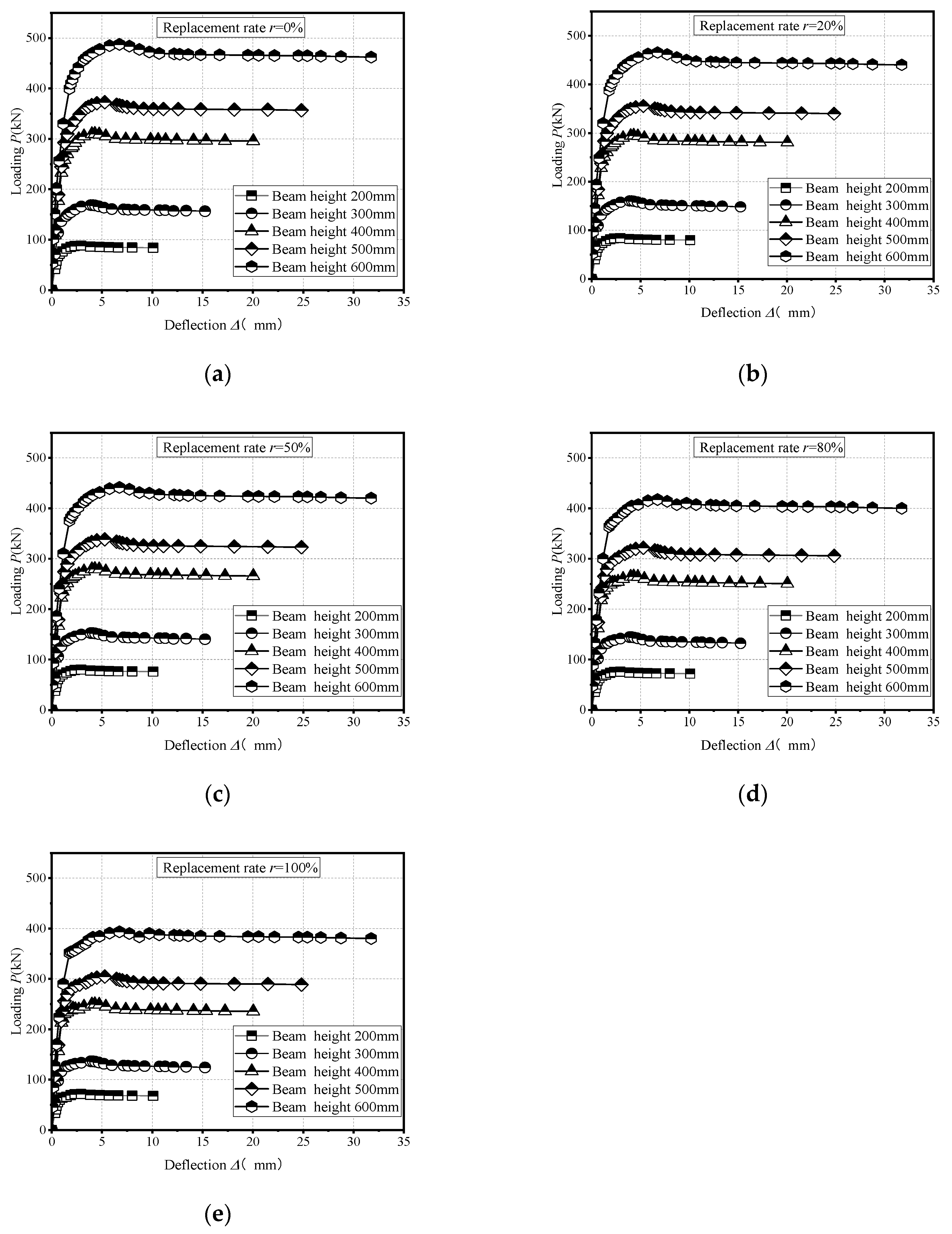
4.2. Load–Displacement Curve
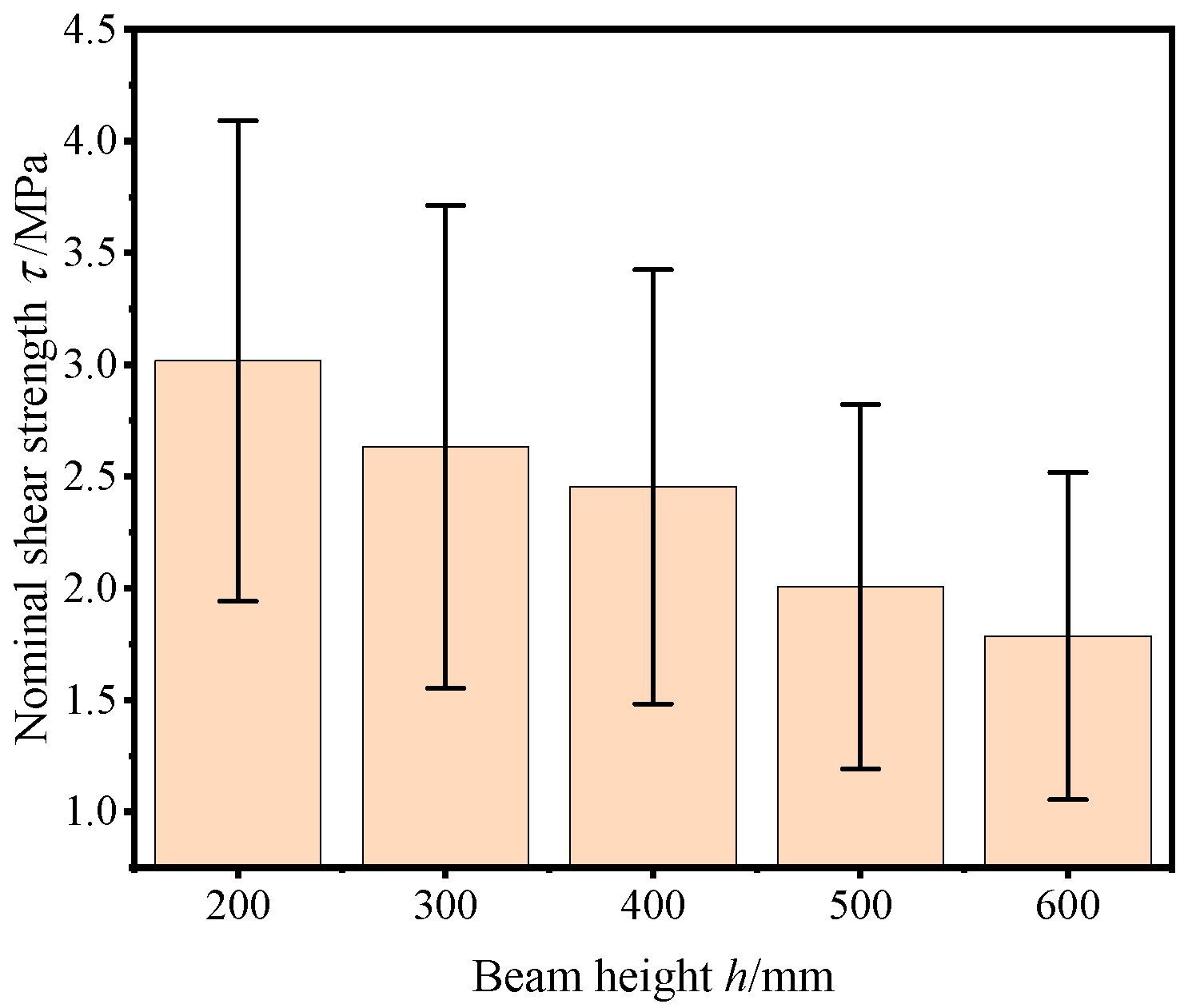
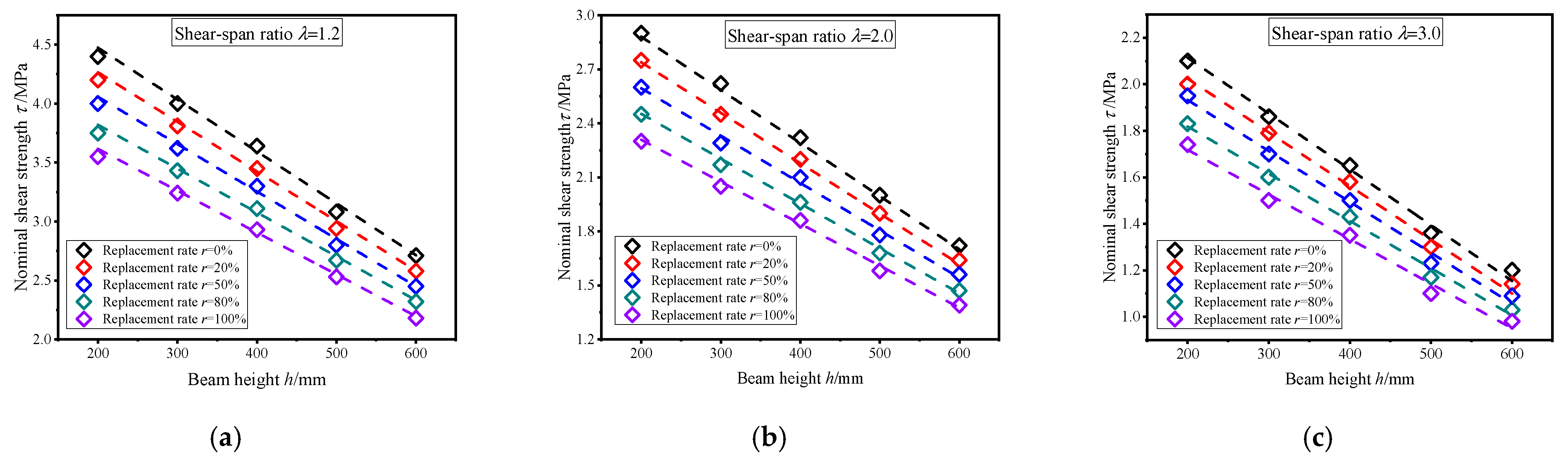
4.3. Analysis of Size Effect of Replacement Rate on the Nominal Shear Strength
5. Size-Effect Law of Shear Strength
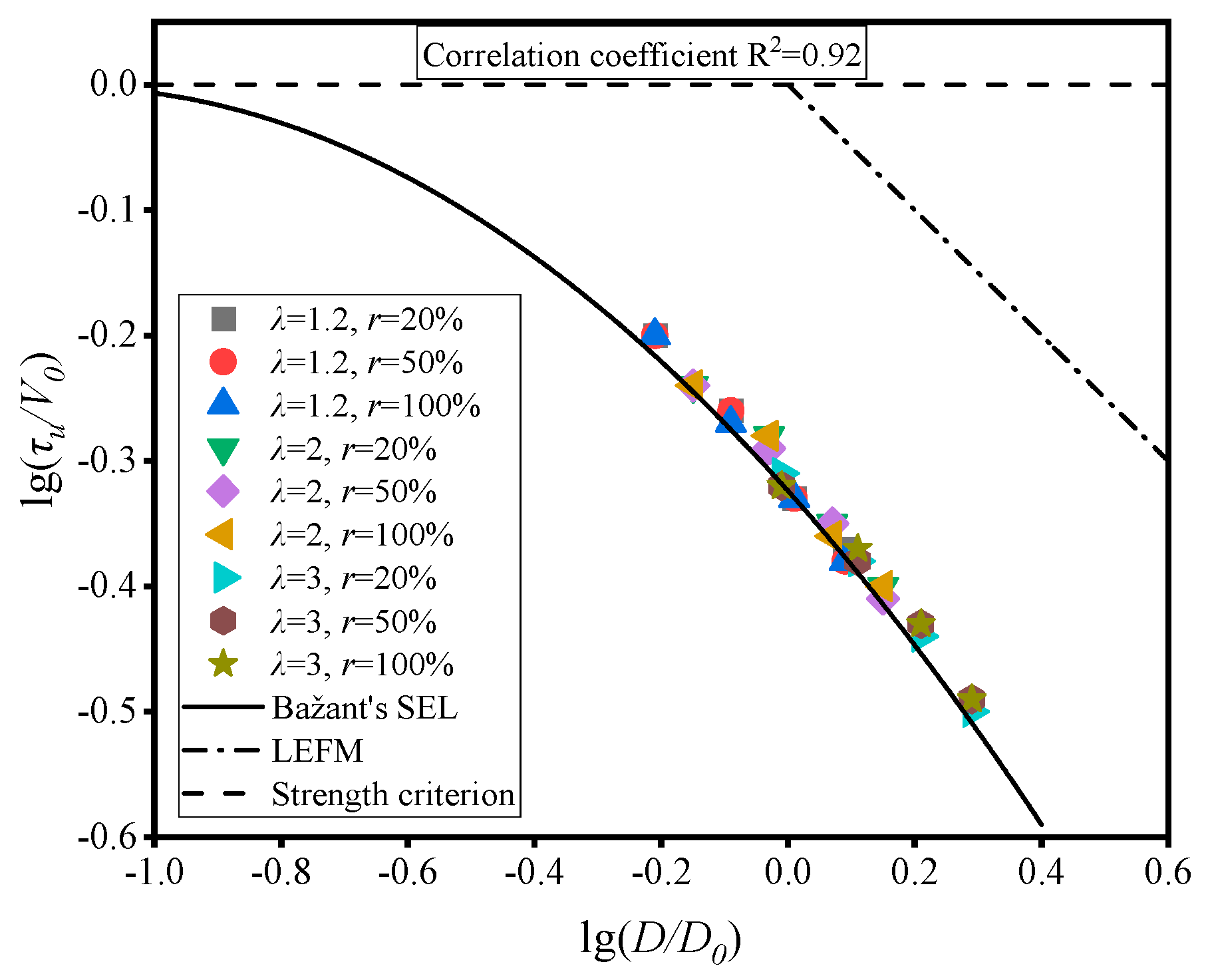
5.1. Comparison of the Simulated Results and Bažant Size-Effect Law
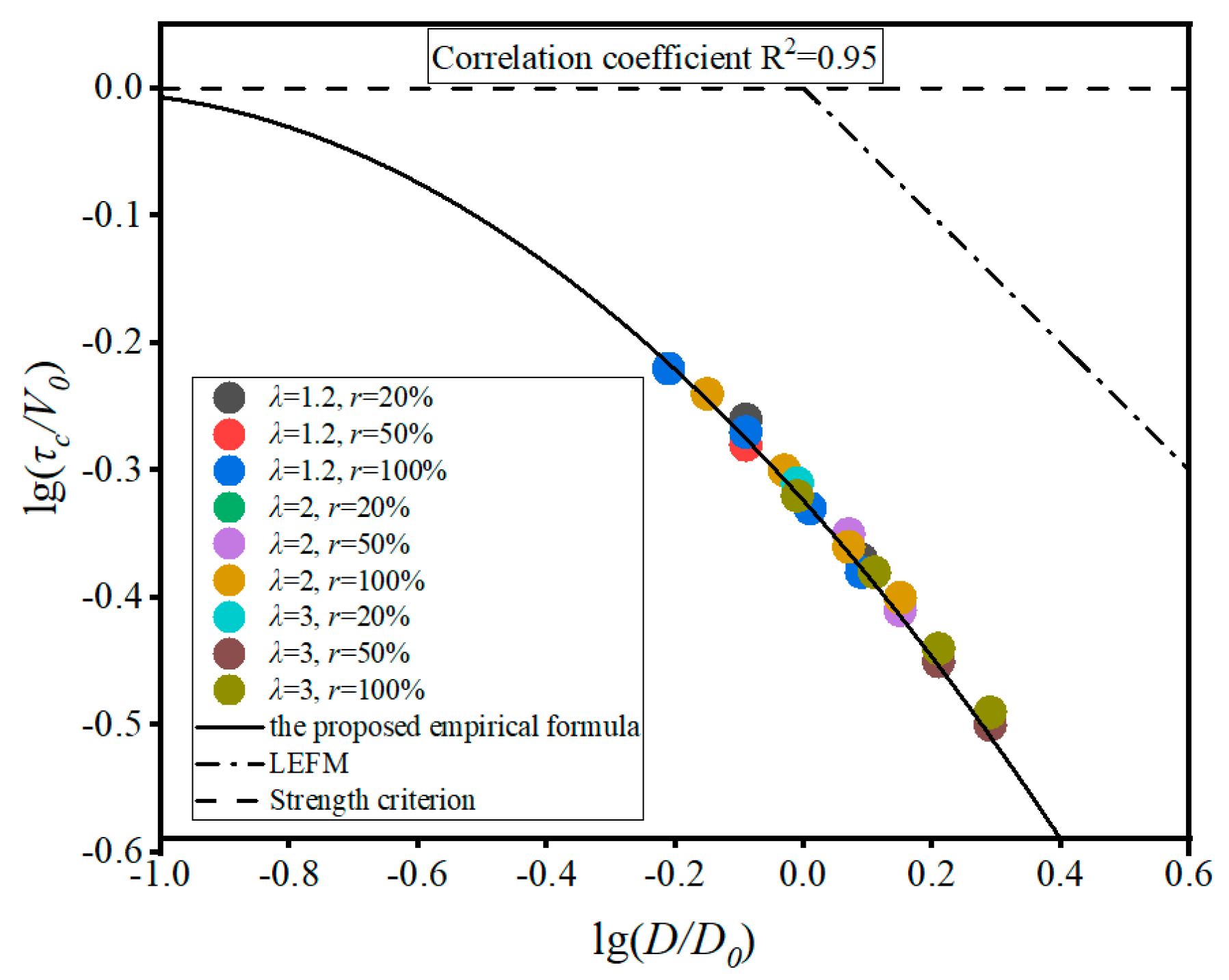
5.2. Theoretical Formula for the Dimension Effect of Nominal Shear Strength
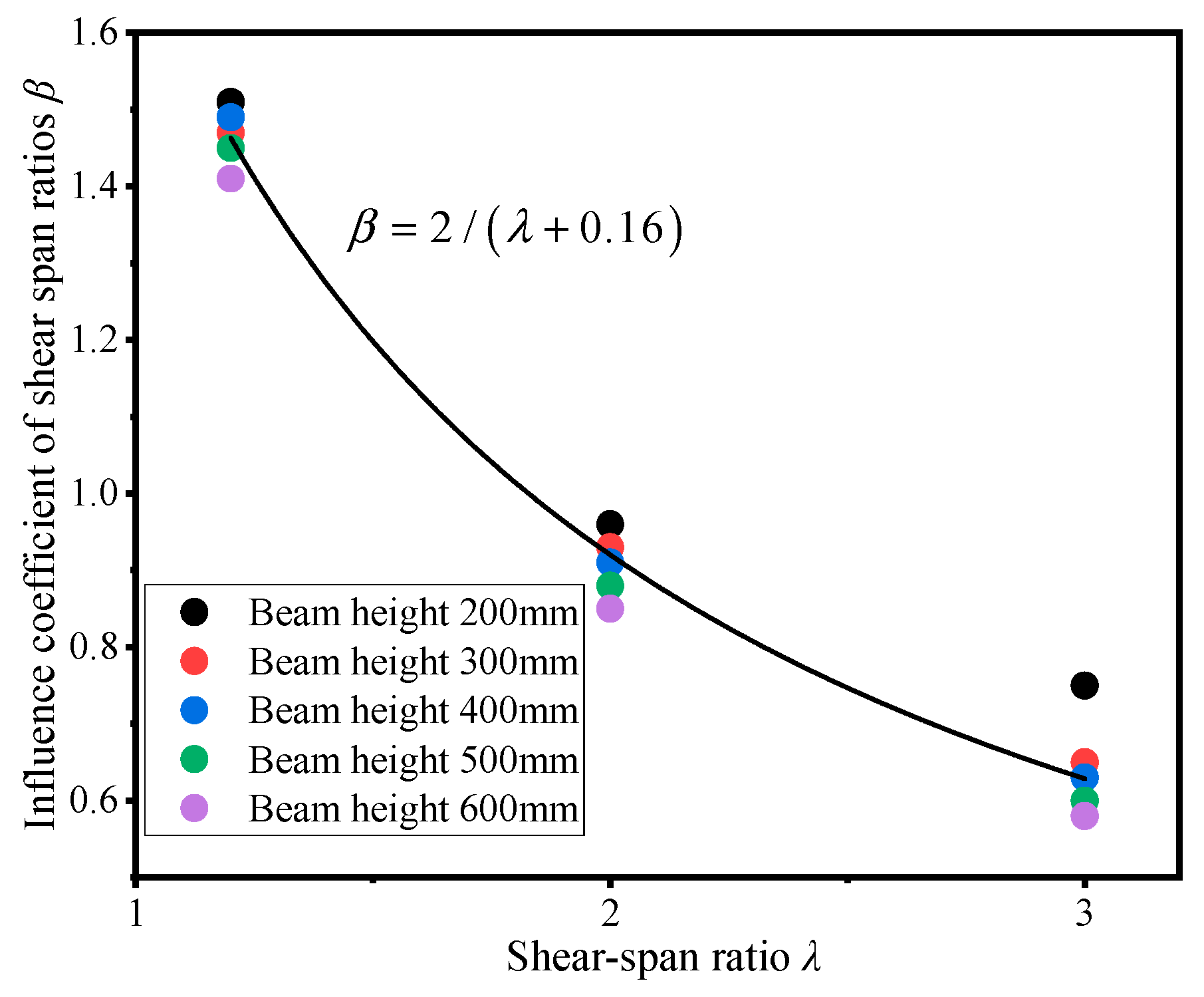
5.2.1. Determination of the Effect Coefficient of Shear-Span Ratio β
5.2.2. Determination of the Effect Coefficient of Replacement Rate γ
5.2.3. Fitting Formula for the Dimension Effect of NSS
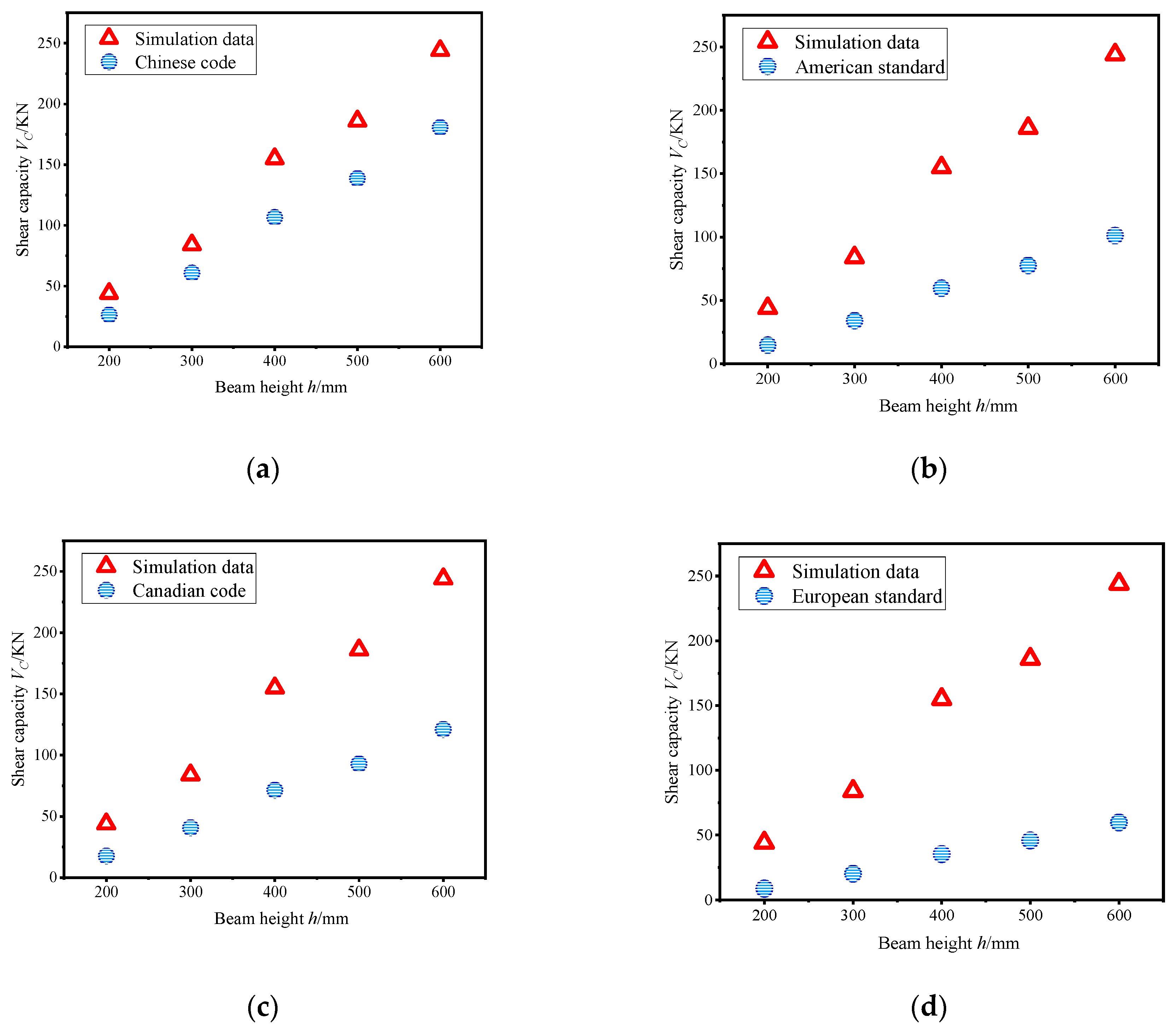
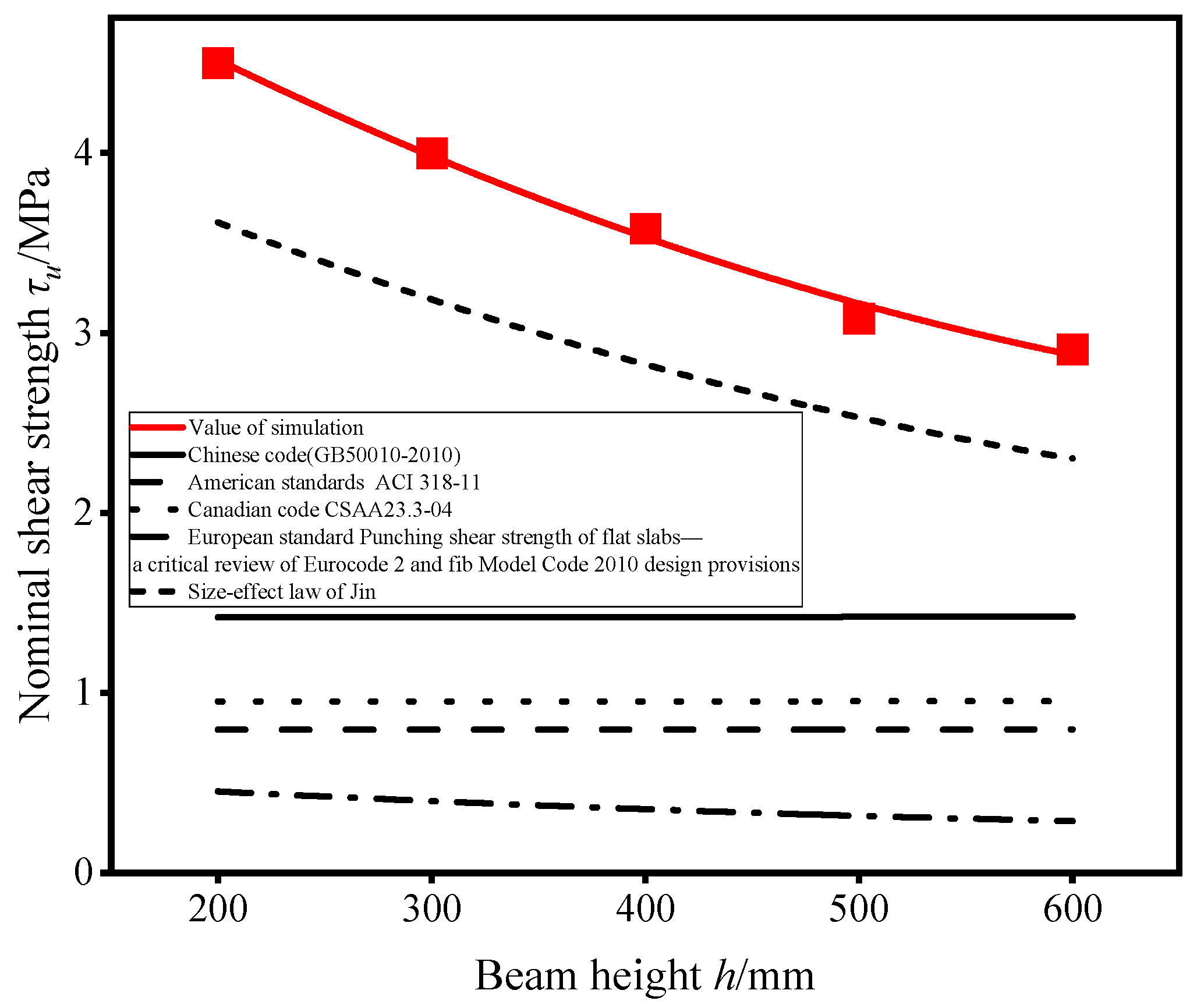
5.3. Comparison with Existing Methods for the Shear-Bearing Capacity of Beams
5.3.1. Comparison of the Simulated Results with Those Obtained from Existing Calculation Methods
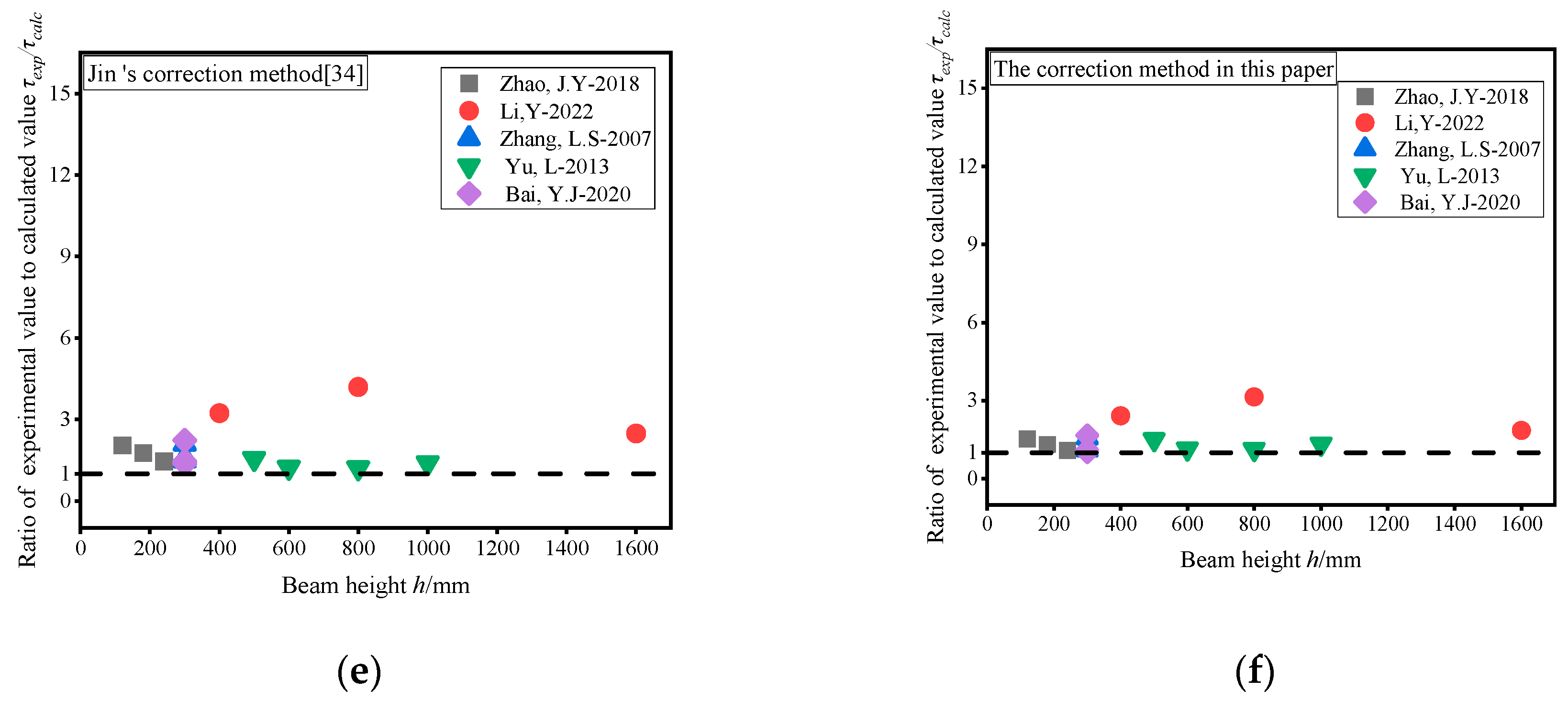
5.3.2. Comparison Between the Proposed Formula and Experimental Results
6. Conclusions
- The three-dimensional microscopic analysis model can capture the heterogeneity of concrete and describe the crack development and failure process in recycled concrete beams, showing good agreement with experimental results. The NSS of recycled concrete beams possesses a distinguished dimension effect. The NSS of the beam with a height of 600 mm is reduced by nearly 40% compared to the beam with a height of 200 mm as the shear-span ratio reaches 1.2.
- The NSS of recycled concrete beams abates as the shear-span ratio rises. Specifically, the NSS of a beam with a shear-span ratio of 3 is nearly 50% lower than that of a beam with a shear-span ratio of 1.2. As the shear-span ratio increases, the failure mode of the beam transitions from shear compression to diagonal tension. Compared with small-sized beams, large-sized beams have fewer bending cracks at failure, and the initiation point of the penetrating diagonal crack is farther away from the point of loading. This is due to the greater stiffness of large-sized beams, which reduces the likelihood of concrete near the loading point cracking under shear stresses.
- The replacement rate of recycled aggregate significantly affects the shear-bearing ability of recycled concrete beams without stirrups. As the replacement rate of recycled aggregate increases, the NSS of recycled concrete beams decreases. The shear-bearing capacity of beams with a 100% replacement rate is reduced by 18.9% compared to that with a replacement rate of 0%. In addition, the higher the replacement rate of recycled aggregate, the wider the diagonal cracks in recycled concrete beams.
- The design shear strengths of formulas of various countries’ standards and proposed formulas for the NSS are all below the experimental results. European Code (EC2010) is the most conservative, with a minimum error of 75% compared to experimental results. The calculated results of the proposed formula closely match the experimental results, with a minimum error of 9%, which demonstrates the closest agreement with experiment values. Notably, the formula proposed in this study has certain limitations, for instance, it is only applicable to static loading and rectangular cross-sections. Future work will expand to dynamic loading conditions, non-rectangular cross-sections, or other recyclable material types, to narrow the gap between research and practical application.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iguro, M.; Shioya, T.; Nojiri, Y.; Akiyama, H. Experimental studies on shear strength of large reinforced concrete beams under uniformly distributed load. Concr. Libr. JSCE 1985, 5, 137–154. [Google Scholar] [CrossRef] [PubMed]
- Shioya, T.; Iguro, M.; Nojiri, Y.; Akiyama, H.; Okada, T. Shear strength of large reinforced concrete beams. Spec. Publ. 1990, 118, 259–280. [Google Scholar] [CrossRef]
- Tan, K.H.; Lu, H.Y.; Teng, S. Size effect in large prestressed concrete deep beams. ACI Struct. J. 1999, 96, 937–946. [Google Scholar] [CrossRef]
- Yu, L.; Che, Y.; Song, Y.P. Experimental study on shear behavior of large-size reinforced concrete beams without stirrups. J. Civ. Environ. Eng. 2013, 46, 1–7. (In Chinese) [Google Scholar] [CrossRef]
- Che, Y.; Yu, L. Study on the safety of large size reinforced concrete members without stirrups under shear force. J. Build. Struct. 2014, 35, 144–151. (In Chinese) [Google Scholar] [CrossRef]
- Zararis, P.D.; Papadakis, G.C. Diagonal shear failure and size effect in RC beams without web reinforcement. J. Struct. Eng. 2001, 127, 733–742. [Google Scholar] [CrossRef]
- Sherwood, E.G.; Bentz, E.C.; Collins, M.P. Effect of aggregate size on beam-shear strength of thick slabs. ACI Struct. J. 2007, 104, 180–190. [Google Scholar] [CrossRef]
- Sneed, L.H.; Ramirez, J.A. Influence of Effective Depth on Shear Strength of Concrete Beams—Experimental Study. ACI Struct. J. 2010, 107, 554–562. [Google Scholar]
- Lee, Y.O.; Yun, H.D. Shear Performance of Full-Scale Recycled Fine Aggregate Concrete Beams without Shear Reinforcement. J. Korea Concr. Inst. 2012, 24, 225–232. [Google Scholar] [CrossRef]
- Ignjatovic, I.S.; Marinkovic, S.B.; Tosic, N. Shear behaviour of recycled aggregate concrete beams with and without shear reinforcement. Eng. Struct. 2017, 141, 386–401. [Google Scholar] [CrossRef]
- Knaack, A.M.; Kurama, Y.C. Service-load deflection behavior of reinforced concrete beams with recycled concrete aggregate. In Structures Congress 2013: Bridging Your Passion with Your Profession, Proceedings of the Structures Congress 2013, Pittsburgh, PA, USA, 2–4 May 2013; American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 2705–2716. [Google Scholar] [CrossRef]
- Gonzalez-Fonteboa, B.; Martmez-Abella, F. Shear strength of recycled concrete beams. Constr. Build. Mater. 2007, 21, 887–893. [Google Scholar] [CrossRef]
- Choi, H.B.; Yi, C.K.; Cho, H.H.; Kang, K.I. Experimental study on the shear strength of recycled aggregate concrete beams. Mag. Concr. Res. 2010, 62, 103–114. [Google Scholar] [CrossRef]
- Zhang, L.S.; Zhang, X.L.; Yan, G.X. Experimental study on shear performance of recycled concrete beams without stirrups. Ind. Constr. 2007, 57–61. (In Chinese) [Google Scholar]
- Ni, T.Y. Experimental study on the Shear Bearing Capacity of recycled Concrete Beams without Web reinforcement. Sichuan Build. Sci. Res. 2010, 36, 5–7. (In Chinese) [Google Scholar]
- Chen, Z.P.; Fan, J.; Ye, P.H.; Zheng, W. Experimental study on mechanical properties of reinforced recycled concrete beams. J. Build. Struct. 2013, 43, 92–95+9. (In Chinese) [Google Scholar] [CrossRef]
- Jin, L.; Su, X.; Xiao, H.B.; Li, D.; Du, X.L. Size effect of shear capacity of concrete beams with stirrups based on mesoscopic model. J. Civ. Environ. Eng. 2019, 41, 80–88. (In Chinese) [Google Scholar]
- Jin, L.; Jiang, X.A.; Du, X.L. Shear failure and size effect of lightweight aggregate concrete beams without stirrups: Mesoscopic simulation. Eng. Mech. 2020, 37, 57–67. (In Chinese) [Google Scholar]
- Caballero, A.; Lopez, C.M.; Carol, I. 3D meso-structural analysis of concrete specimens under uniaxial tension. Comput. Methods Appl. Mech. Eng. 2006, 195, 7182–7195. [Google Scholar] [CrossRef]
- López, C.M.; Carol, I.; Aguado, A. Meso-structural study of concrete fracture using interface elements. I: Numerical model and tensile behavior. Mater. Struct. 2008, 41, 583–599. [Google Scholar] [CrossRef]
- Jin, L.; Yu, W.X.; Du, X.L.; Zhang, S.; Li, D. Meso-scale modelling of the size effect on dynamic compressive failure of concrete under different strain rates. Int. J. Impact Eng. 2019, 125, 1–12. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, S.; Li, D.; Xu, H.; Du, X.; Li, Z. A combined experimental and numerical analysis on the seismic behavior of short reinforced concrete columns with different structural sizes and axial compression ratios. Int. J. Damage Mech. 2018, 27, 1416–1447. [Google Scholar] [CrossRef]
- Du, X.; Jin, L.; Ma, G. A meso-scale analysis method for the simulation of nonlinear damage and failure behavior of reinforced concrete members. Int. J. Damage Mech. 2013, 22, 878–904. [Google Scholar] [CrossRef]
- Yu, Q.; Bažant, Z.P. Can stirrups suppress size effect on shear strength of RC beams. J. Struct. Eng. 2011, 137, 607–617. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI J. 1986, 83, 219–231. [Google Scholar] [CrossRef]
- Xiao, J.Z.; Li, W.G.; Corr, D.J.; Shah, S.P. Effects of interfacial transition zones on the stress–strain behavior of modeled recycled aggregate concrete. Cem. Concr. Res. 2013, 52, 80–99. [Google Scholar] [CrossRef]
- GB 50011-2010; Code for Seismic Design of Buildings. China Building Industry Press: Beijing, China, 2010.
- Xiao, J.Z. Experimental study on the complete stress-strain curve of recycled concrete under uniaxial compression. J. Tongji Univ. 2007, 11, 1445–1449. (In Chinese) [Google Scholar]
- Liu, Q. The Experiment Study and Lattice Model Simulation on the Failure Mechanism of Recycled Concrete. Master’s Thesis, Tongji University, Shanghai, China, 2010. [Google Scholar]
- Yue, Q.; Wang, L.; Liu, F.S. Numerical study on the damage of recycled coagulation based on the real mesoscopic model. J. Build. Mater. 2016, 19, 221–228. (In Chinese) [Google Scholar]
- Zhao, J.Y. Strength Evaluation and Size Effect of Recycled Concrete Beams. Master’s Thesis, Shaoxing University, Shaoxing, China, 2017. (In Chinese). [Google Scholar]
- Bažant, Z.P. Size effect in blunt fracture: Concrete, rock, metal. J. Eng. Mech. 1984, 110, 518–535. [Google Scholar] [CrossRef]
- Eurocode2 1992−2; Design of Concrete Structures. British Standards Institution: London, UK, 2001.
- Jin, L.; Wang, T.; Du, X.L. Theoretical study on shear strength and size effect of RC cantilever beam without stirrups. J. Comput. Mech. 2020, 37, 396–404. (In Chinese) [Google Scholar]
- ACI 318−11; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2011.
- CSA A23.3−04; Design of Concrete Structures. Canadian Standards Association: Toronto, ON, Canada, 2004.
- Zhao, J.Y.; Yang, Q.W.; Zhang, Y.; Wang, X.H.; Lu, C.; Liang, C.F.; Sun, B.F. Experimental study on size effect of shear performance of recycled concrete beams without stirrups. Concrete 2018, 39–42. (In Chinese) [Google Scholar]
- Li, Y.; Li, Z.; Yi, W.J.; Chen, H.; Zhang, W.X. Study on the size effect of shear bearing capacity of concrete short beams without stirrups. China Civ. Eng. J. 2022, 55, 1–12. (In Chinese) [Google Scholar] [CrossRef]
- Bai, Y.J.; Liu, H.X.; Li, Q.W.; Wang, X.Z.; Peng, C.L. Shear performance of basalt fiber reinforced recycled concrete beams without stirrups. Ind. Constr. 2020, 50, 156–161+137. (In Chinese) [Google Scholar] [CrossRef]
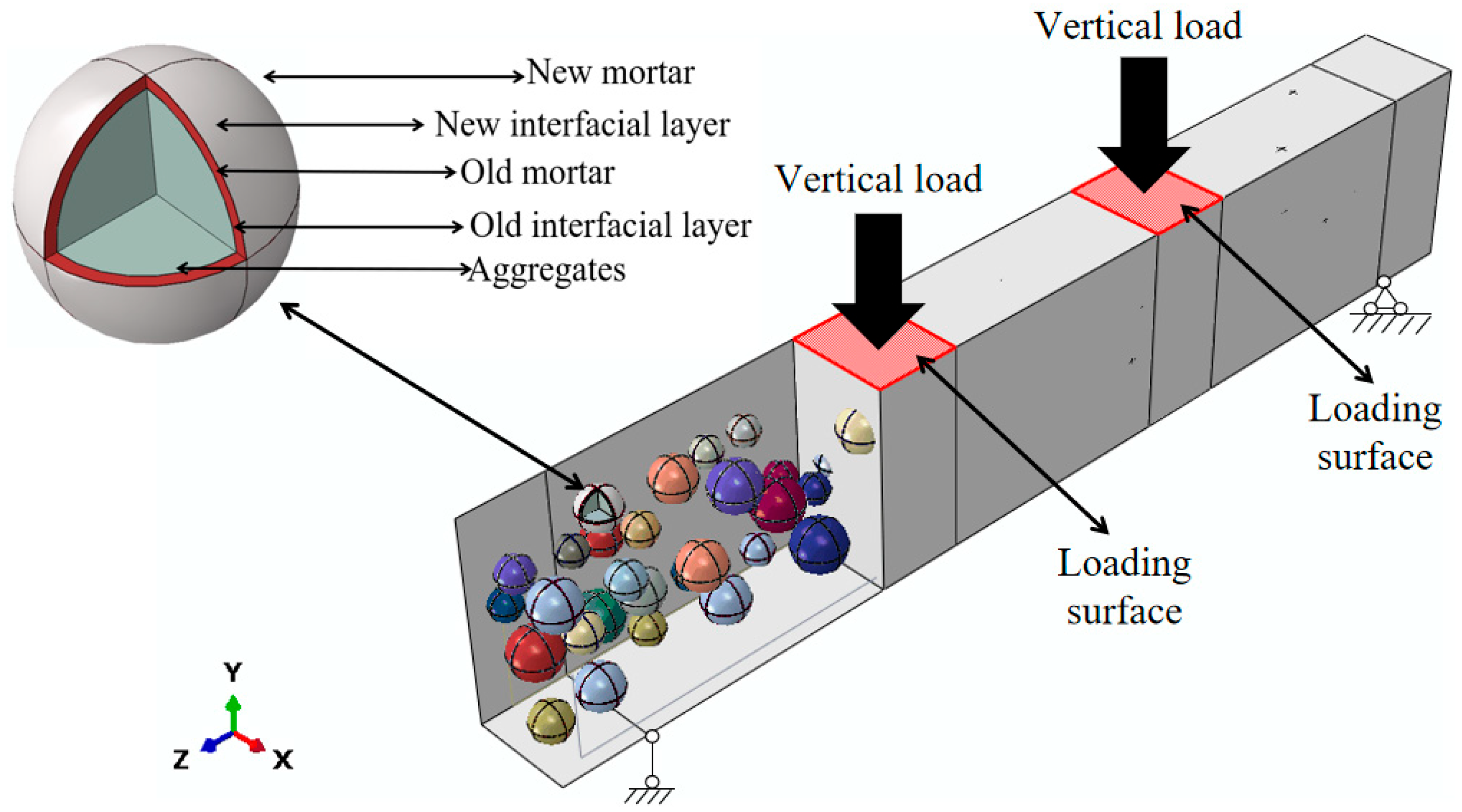





| Recycled Coarse Aggregate Replacement Percentage | 0 | 30% | 50% | 70% | 100% |
|---|---|---|---|---|---|
| d | 1.19 | 1.21 | 1.23 | 1.24 | 1.26 |
| Composition | Elastic Modulus E/GPa | Compressive Strength σc/MPa | Compressional Strain εc | Ultimate Strength σ/MPa | Ultimate Strain ε | Tensile Strength σt/MPa | Tensile Strain εt | Poisson’s Ratio ν |
|---|---|---|---|---|---|---|---|---|
| Aggregates | 80.00 | 80.00 | - | - | - | 10.00 | - | 0.16 |
| Old mortar | 19.27 | 18.17 | 3.77 × 10−3 | 6.06 | 0.010 | 1.66 | 1.0 × 10−4 | 0.22 |
| New mortar | 23.68 | 26.78 | 2.80 × 10−3 | 8.93 | 0.008 | 1.91 | 1.0 × 10−4 | 0.22 |
| OTZ | 19.27 | 10.20 | 3.77 × 10−3 | 3.40 | 0.010 | 1.02 | 1.0 × 10−4 | 0.20 |
| ITZ | 23.68 | 12.20 | 2.80 × 10−3 | 4.06 | 0.008 | 1.22 | 1.0 × 10−4 | 0.20 |
| Replacement Rate r/% | Water–Cement Ratio | Cement/(kg/m3) | Water/(kg/m3) | Sand/(kg/m3) | Recycled Coarse Aggregate/(kg/m3) |
|---|---|---|---|---|---|
| 100 | 1:0.34 | 623.3 | 211.8 | 491.4 | 1073.5 |
| Composition | Aggregates | Old Mortar | New Mortar | OTZ | ITZ | Longitudinal Reinforcement |
|---|---|---|---|---|---|---|
| Compressive strength σc/MPa | 80 | 18.17 | 26.78 | 10.20 | 12.20 | - |
| Tensile strength σt/MPa | 10 | 1.66 | 1.91 | 1.02 | 1.22 | 528 |
| Elastic modulus E/GPa | 80 | 19.27 | 23.68 | 19.27 | 23.68 | 189 |
| Poisson’s ratio ν | 0.16 | 0.22 | 0.22 | 0.2 | 0.2 | 0.3 |
| Yield stress fy/MPa | - | - | - | - | - | 459 |
| Specimens | Section Size b × h (mm) | Virtual Height h0/mm | Shear Span Ratio λ | Beam Length l/mm | Longitudinal Reinforcement Ratio ρ/% | Recycled Aggregate Replacement r/% |
|---|---|---|---|---|---|---|
| S-group | 100 × 200 | 175 | 1.2~3.0 | 2000 | 1.2 | 20 |
| M-group | 150 × 300 | 275 | 1.2~3.0 | 3000 | 1.2 | 20 |
| L-group | 200 × 400 | 370 | 1.2~3.0 | 4000 | 1.2 | 20 |
| U-group | 250 × 500 | 470 | 1.2~3.0 | 5000 | 1.2 | 20 |
| V-group | 300 × 600 | 565 | 1.2~3.0 | 6000 | 1.2 | 20 |
| Specimens | Section Size b × h (mm) | Virtual Height h0/mm | Shear Span Ratio λ | Beam Length l/mm | Longitudinal Reinforcement Ratio ρ/% | Recycled Aggregate Replacement r/% |
|---|---|---|---|---|---|---|
| S-group | 100 × 200 | 175 | 1.2~3.0 | 2000 | 1.2 | 0–100 |
| M-group | 150 × 300 | 275 | 1.2~3.0 | 3000 | 1.2 | 0–100 |
| L-group | 200 × 400 | 370 | 1.2~3.0 | 4000 | 1.2 | 0–100 |
| U-group | 250 × 500 | 470 | 1.2~3.0 | 5000 | 1.2 | 0–100 |
| V-group | 300 × 600 | 565 | 1.2~3.0 | 6000 | 1.2 | 0–100 |
| Order Number | The Existing Calculation Method | The Main Calculation Expressions and Key Parameters |
|---|---|---|
| 1 | Chinese code 6.3 Calculation of bearing capacity of the inclined section (GB 50010-2010) [27] | λ: shear-span ratio, when λ ≤ 1.5, λ = 1.5, when λ ≥ 3, λ = 3; ft: design value of axial tensile strength of concrete; b: rectangular section width; h0: effective depth of section. τc: NSS of beams; Vc: the calculated value of shear-bearing capacity; b: section width of the beam; h0: the effective height of the beam section. |
| 2 | American standards ACI 318 Punching Shear Design ACI 318-11 [35] | fc′: compressive strength of concrete cylinder; ordinary concrete γ = 1; bw: calculate the width of the cross-section; h0: effective depth of section. τc: NSS of beams; Vc: the calculated value of shear-bearing capacity; b: section width of the beam; h0: the effective height of the beam section. |
| 3 | Canadian code CSAA23.3 Punching Shear Design CSAA23.3-04 [36] | εx: longitudinal strain at the midpoint of the section height; Sz: crack spacing parameters, value with dv; dv: calculate the effective shear width of the section, taken 0.9 h0; ordinary concrete γ = 1; ag: maximum aggregate size; bw: calculate the width of the cross-section. τc: NSS of beams; Vc: the calculated value of shear-bearing capacity; b: section width of the beam; h0: the effective height of beam section. |
| 4 | European standard Punching shear strength of flat slabs—a critical review of Eurocode 2 and fib Model Code 2010 design provisions [33] | fc′: compressive strength of concrete cylinder; ρs: longitudinal reinforcement ratio; d: Beam depth; bw: calculate the width of the cross-section; h0: the effective height of beam section; C1: correlation coefficient of concrete aggregate, conventional aggregate C1 = 0.1. τc: NSS of beams; Vc: the calculated value of shear-bearing capacity; b: section width of the beam; h0: the effective height of beam section. |
| 5 | Size-effect law of Jin [34] | τc: NSS of beams; D: section height of beam; V0 and D0: empirical coefficient in Bažant size-effect law; γ: influence coefficient of shear-span ratio on nominal shear-bearing ability; β: influence coefficient of longitudinal reinforcement ratio on NSS; λ: shear-span ratio; ρ: longitudinal reinforcement ratio of beam. |
| Data Sources | Number | b (mm) | fc (MPa) | h (mm) | l (mm) | λ | r (%) | ρs (%) | Vu (KN) | τu (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| Literature [37] | 4 | 120 | 53.4 | 120~300 | 740~1550 | 1.7 | 100 | 1.4 | 86.3~177.7 | 4.72~6.54 |
| Literature [38] | 8 | 200 | 31.4~52.7 | 200~1600 | 1440~7140 | 2 | 0 | 1.74~1.85 | 394~1674 | 3.76~11.6 |
| Literature [14] | 13 | 151~154 | 28.7~38.7 | 300~309 | 1700~2100 | 1~3 | 0~100 | 2.49 | 114~530 | 2.78~4.44 |
| Literature [4] | 7 | 250~600 | 39.2~42.8 | 500~1206 | 2600~6400 | 2.6 | 0 | 0.67~1.19 | 299-1260 | 0.94~1.2 |
| Literature [39] | 12 | 200 | 40~50.2 | 300 | 2700 | 2~3.3 | 0~100 | 1.21~2.42 | 84~289.8 | 1.4~3.21 |
| Data Sources | GB 50010-2010 [27] | ACI 318-11 [35] | CSAA23.3-04 [36] | EC 2010 [33] | Jin’s Correction Method [34] | The Correction Method in This Paper | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τu Calculated Value | Error (%) | τu Calculated value | Error (%) | τu Calculated Value | Error (%) | τu Calculated Value | Error (%) | τu Calculated Value | Error (%) | τu Calculated Value | Error (%) | |
| Literature [37] | 2.11~2.15 | 54~67 | 1.19~1.2 | 74~81 | 1.41~1.44 | 69~78 | 0.69~0.7 | 85~89 | 3.17~3.23 | 32~51 | 4.25~4.33 | 9~35 |
| Literature [38] | 1.01~1.02 | 73~84 | 0.57~0.58 | 84~91 | 0.67~0.68 | 81~86 | 0.33~0.34 | 91~94 | 1.51~1.52 | 60~76 | 2.01~2.02 | 46~68 |
| Literature [14] | 1.18~1.41 | 55~68 | 0.66~0.79 | 75~82 | 0.79~0.94 | 70~79 | 0.39~0.47 | 85~89 | 1.76~2.11 | 33~52 | 2.37~2.38 | 10~35 |
| Literature [4] | 0.7~0.71 | 25~41 | 0.39~0.4 | 58~67 | 0.47~0.48 | 50~61 | 0.23~0.24 | 75~81 | 0.76~0.78 | 17~35 | 0.8~0.81 | 12~34 |
| Literature [39] | 0.68~0.96 | 51~70 | 0.37~0.53 | 72~83 | 0.46~0.64 | 69~80 | 0.22~0.32 | 84~90 | 1.02~1.44 | 27~55 | 1.37~2.02 | 9~40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Zhou, G.; Wang, H.; Wang, Y. Theoretical Research on the Shear Mechanical Properties and Size Effect of Recycled Concrete Beams Without Stirrups. Buildings 2025, 15, 1737. https://doi.org/10.3390/buildings15101737
Liu C, Zhou G, Wang H, Wang Y. Theoretical Research on the Shear Mechanical Properties and Size Effect of Recycled Concrete Beams Without Stirrups. Buildings. 2025; 15(10):1737. https://doi.org/10.3390/buildings15101737
Chicago/Turabian StyleLiu, Chunyang, Guangkai Zhou, Hao Wang, and Yilin Wang. 2025. "Theoretical Research on the Shear Mechanical Properties and Size Effect of Recycled Concrete Beams Without Stirrups" Buildings 15, no. 10: 1737. https://doi.org/10.3390/buildings15101737
APA StyleLiu, C., Zhou, G., Wang, H., & Wang, Y. (2025). Theoretical Research on the Shear Mechanical Properties and Size Effect of Recycled Concrete Beams Without Stirrups. Buildings, 15(10), 1737. https://doi.org/10.3390/buildings15101737








