Fire Resistance of Prefabricated Steel Tubular Columns with Membrane Protections
Abstract
1. Introduction
2. Experiment Program
2.1. Test Specimens
2.2. Test Setup and Specimen Installation
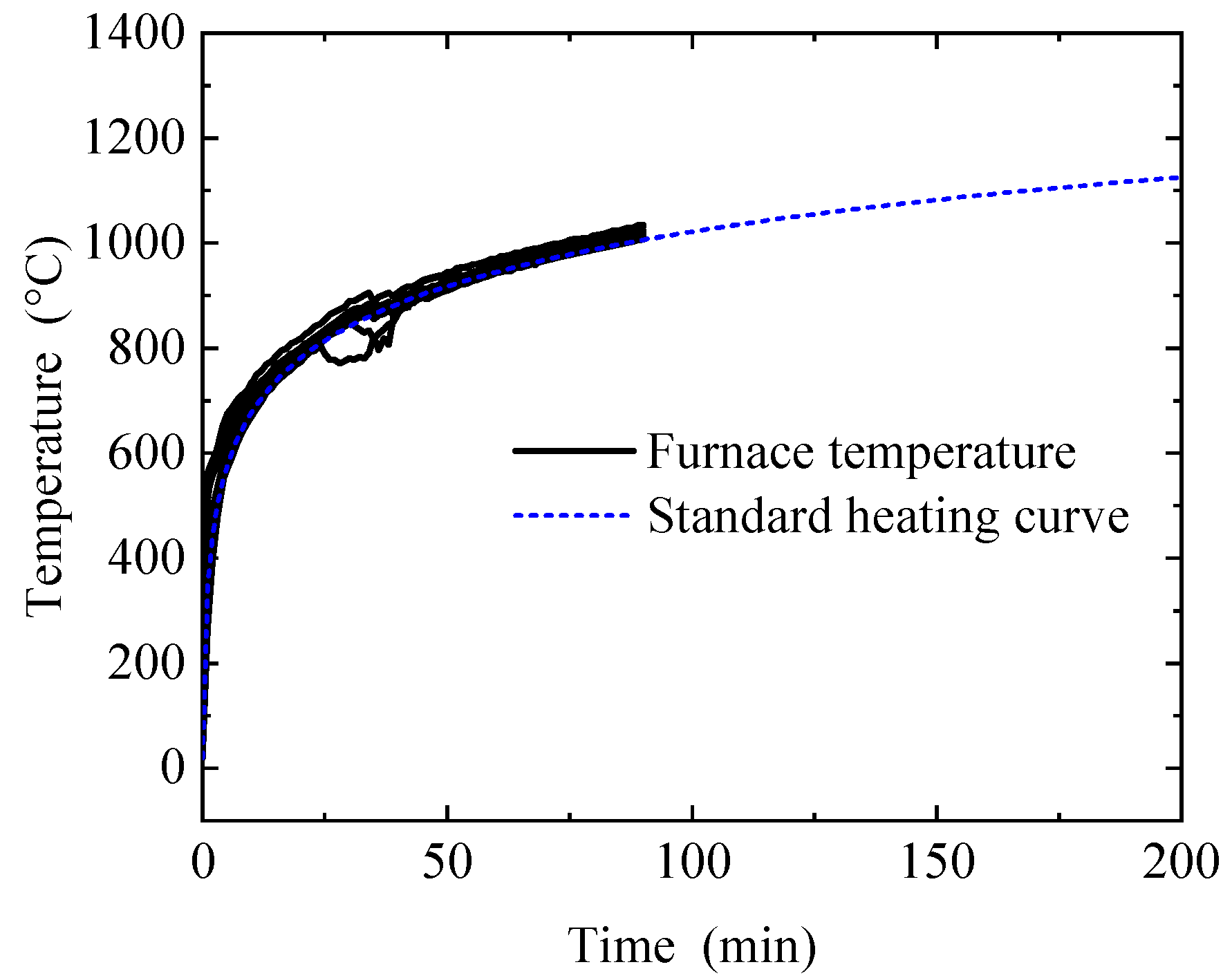
2.3. Test Procedures
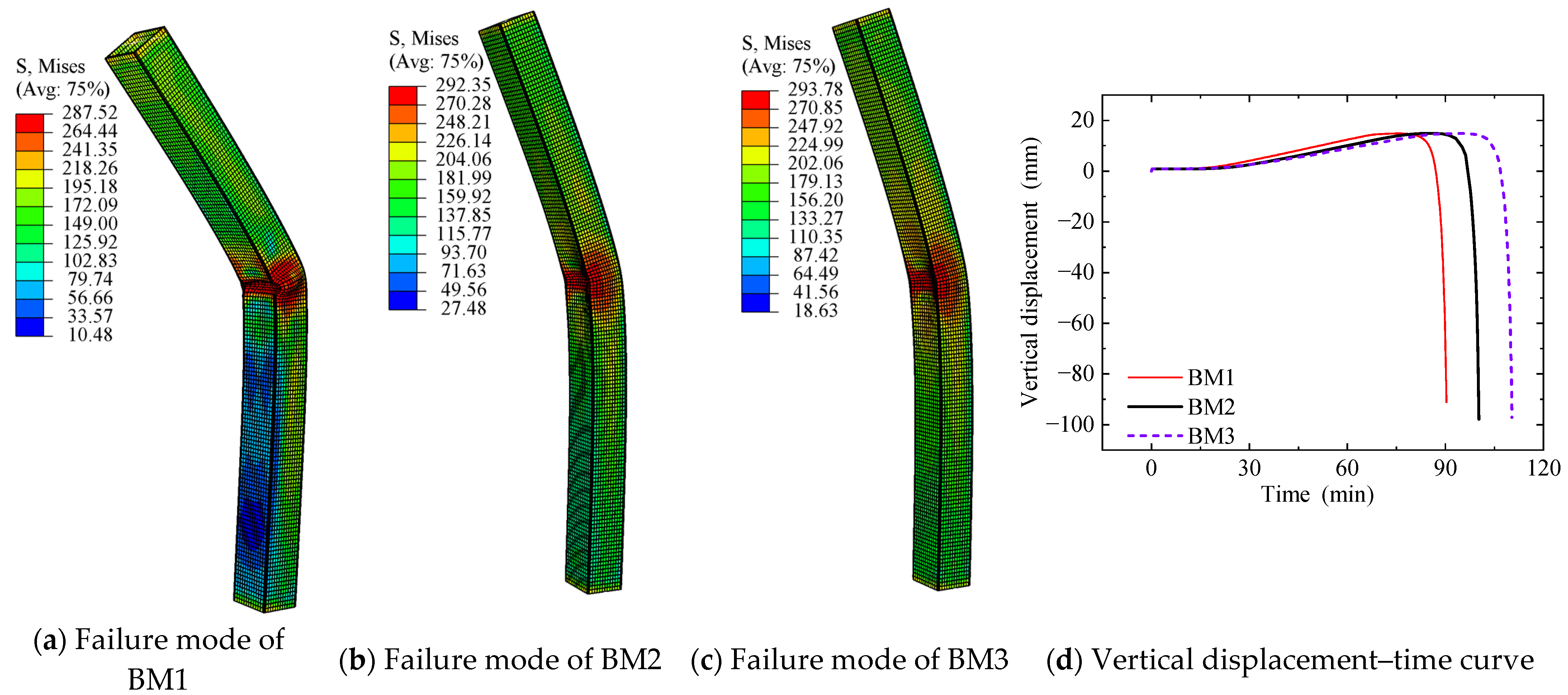
3. Test Results and Discussions
3.1. Observations
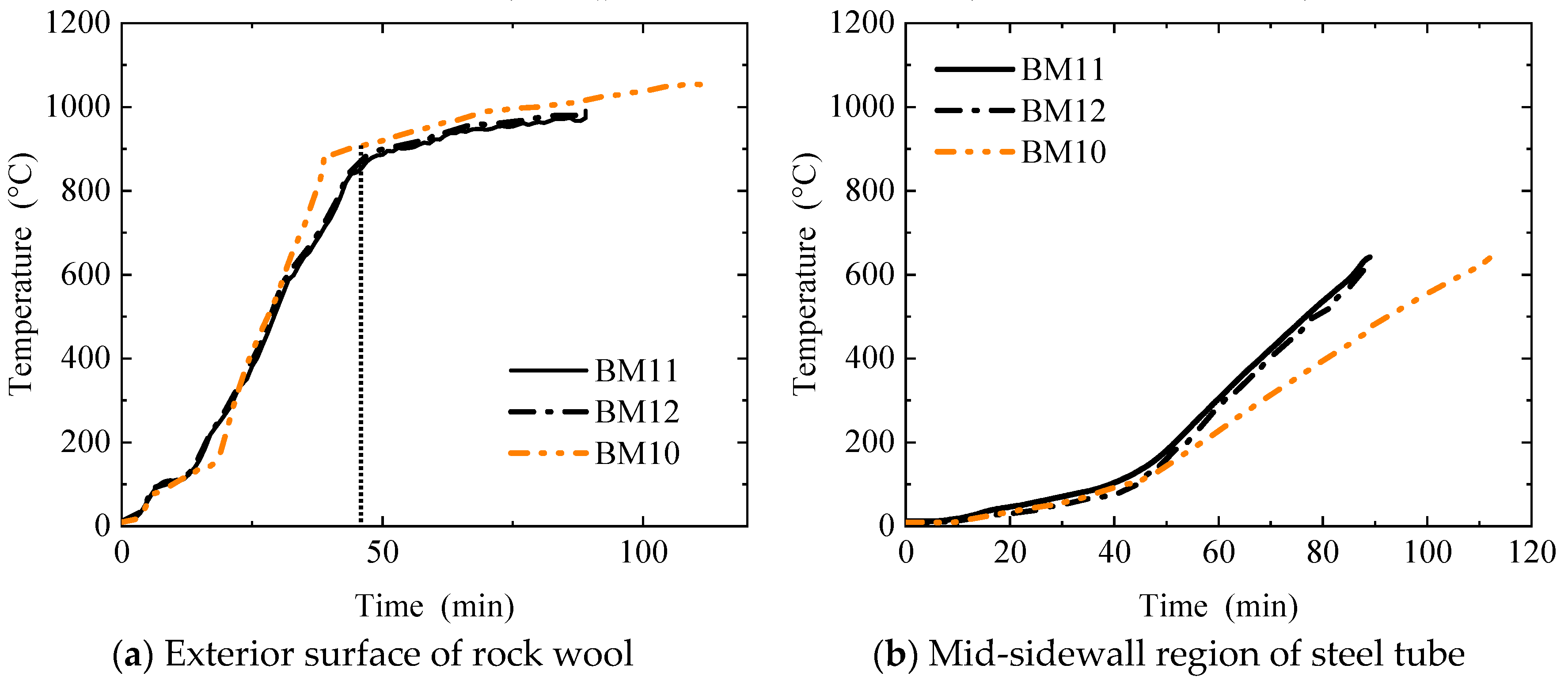
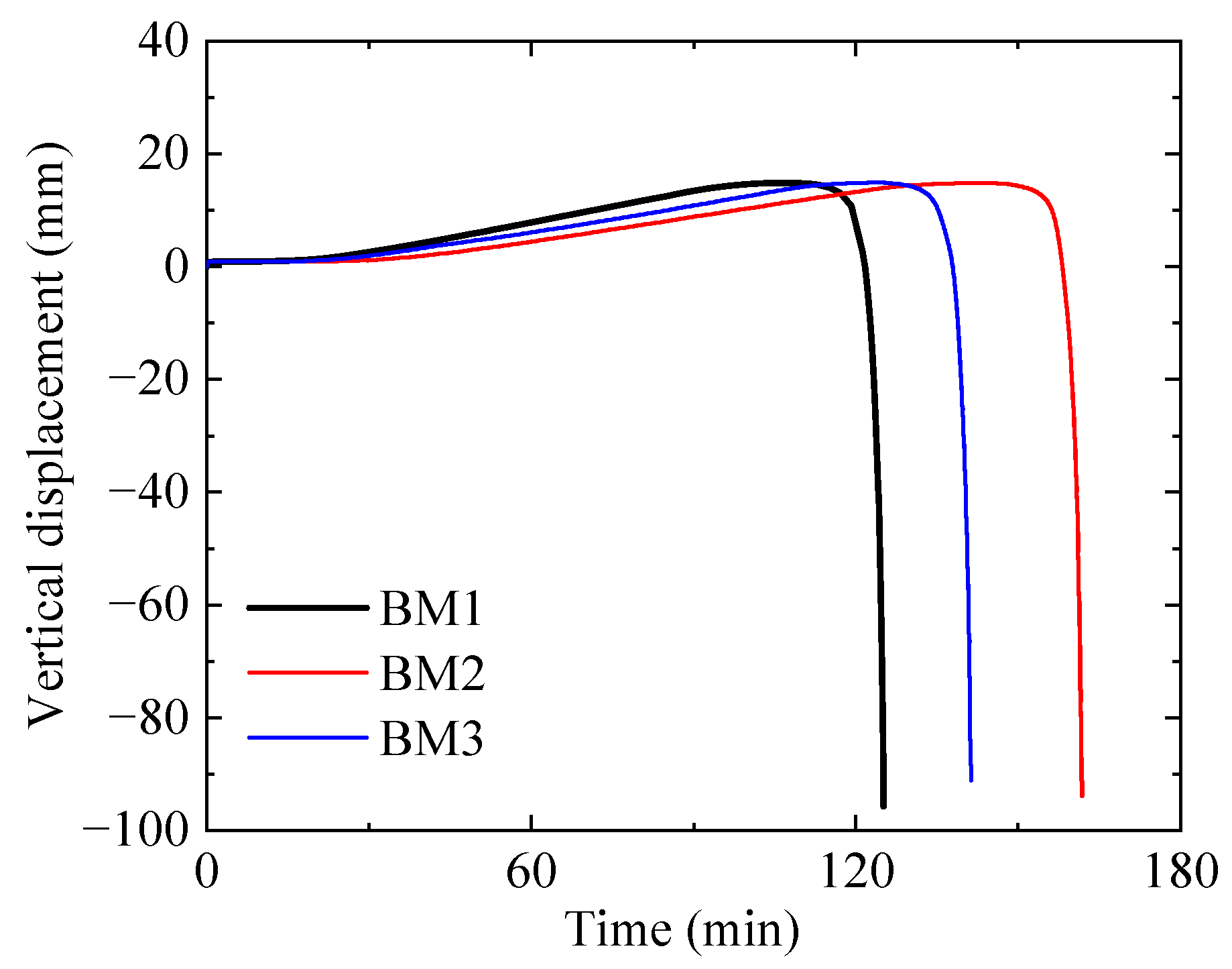
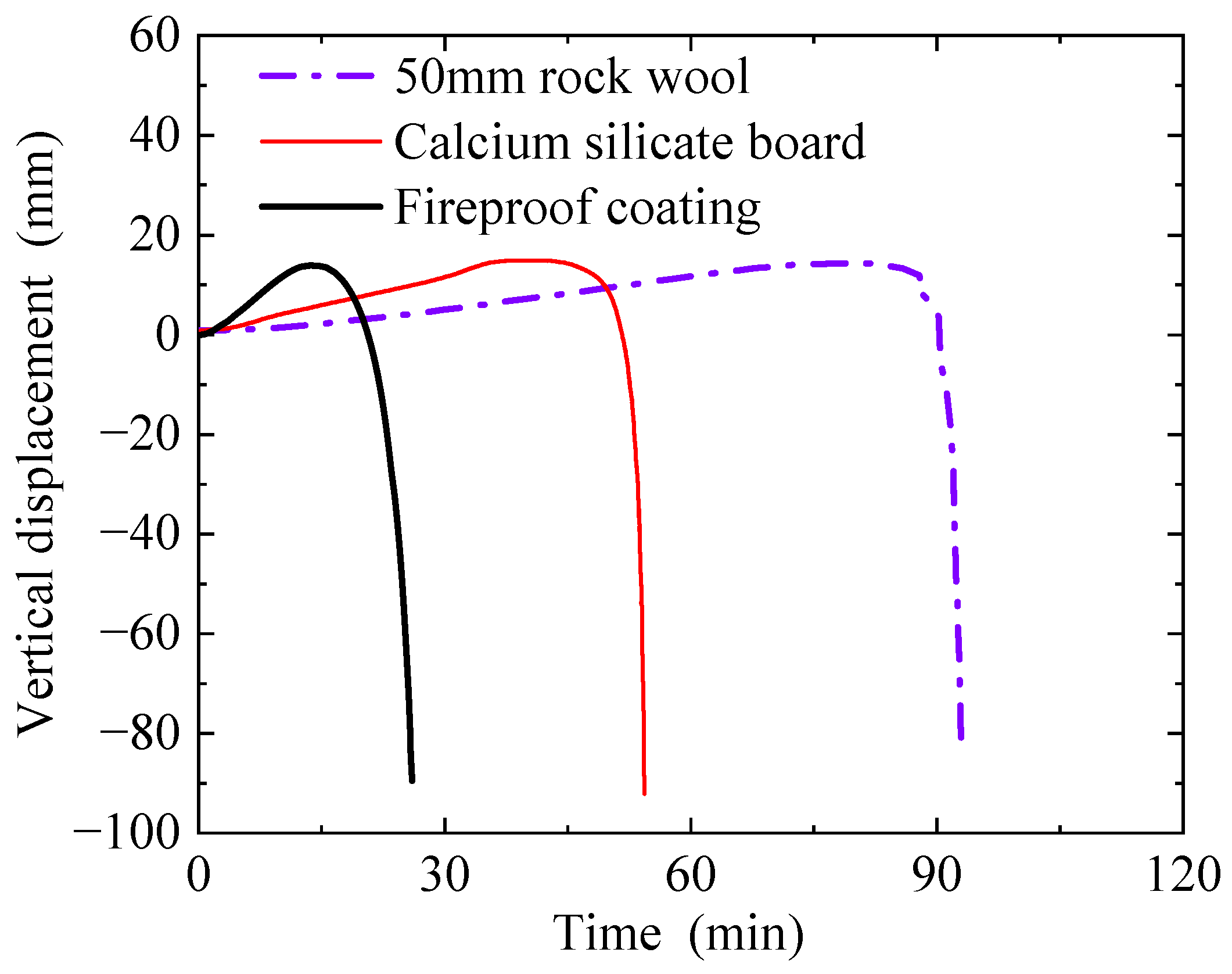
3.2. Measurements
3.3. Discussion
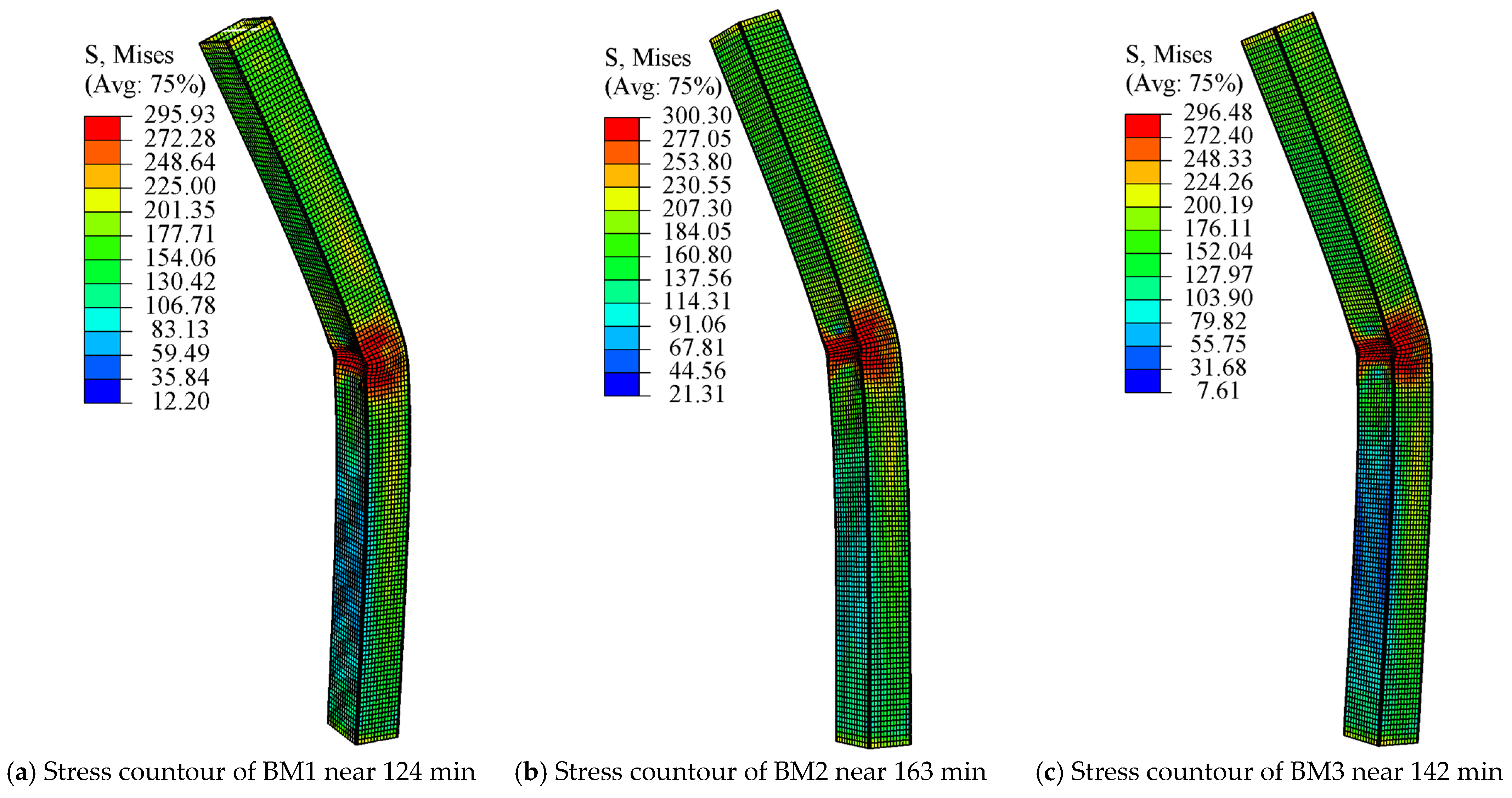
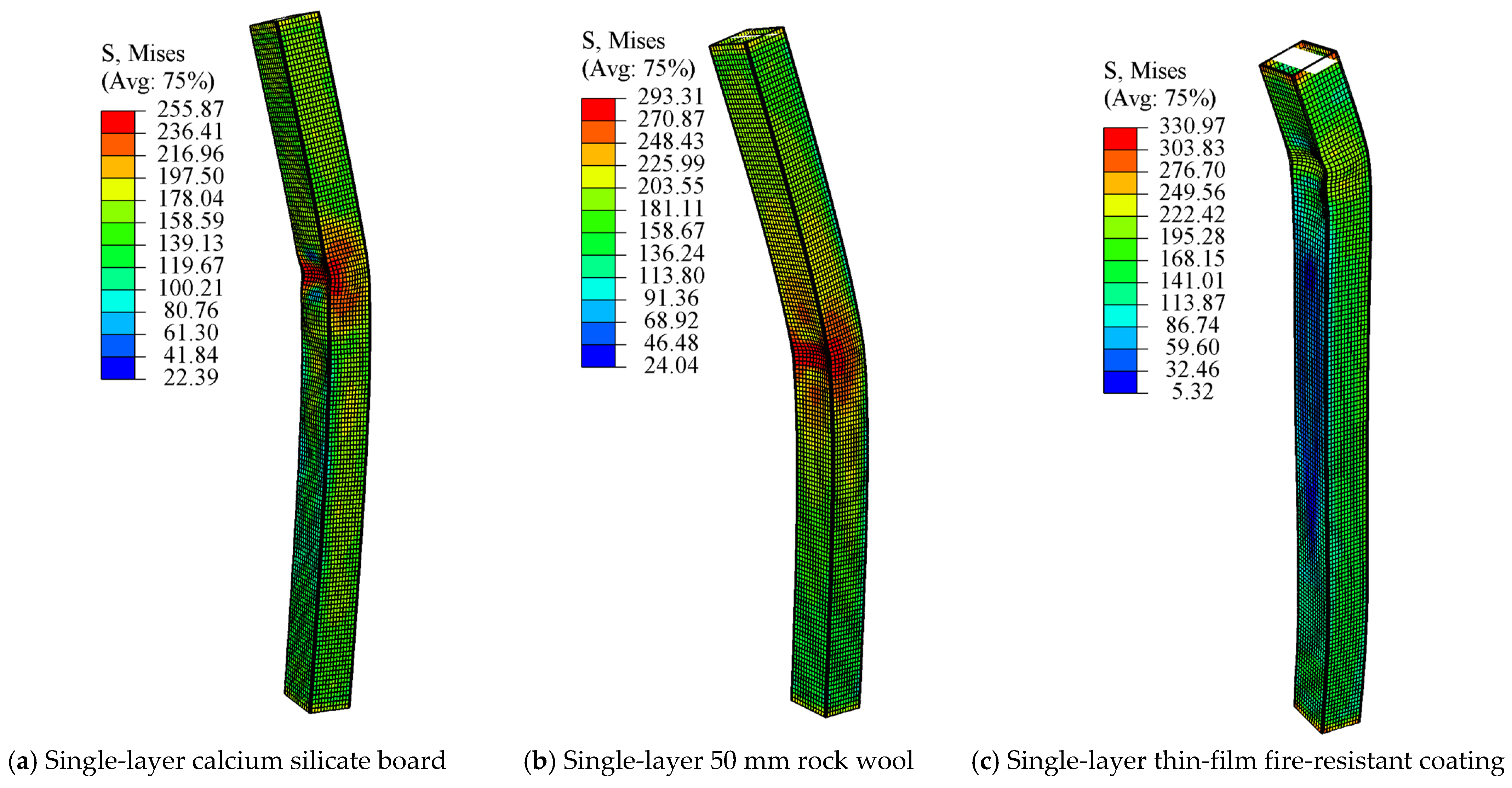
4. Finite Element Simulation and Verification
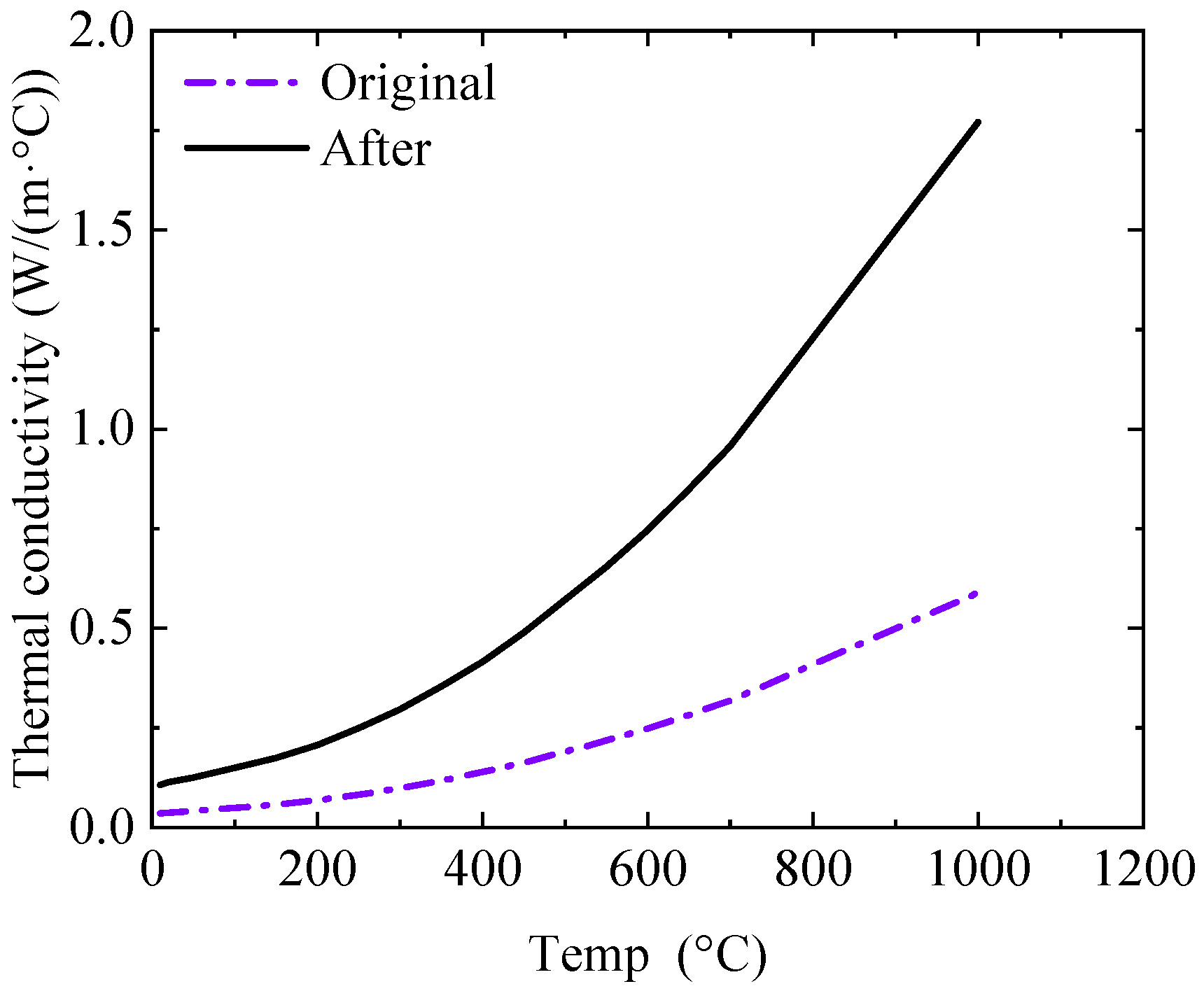
4.1. Thermal Parameters
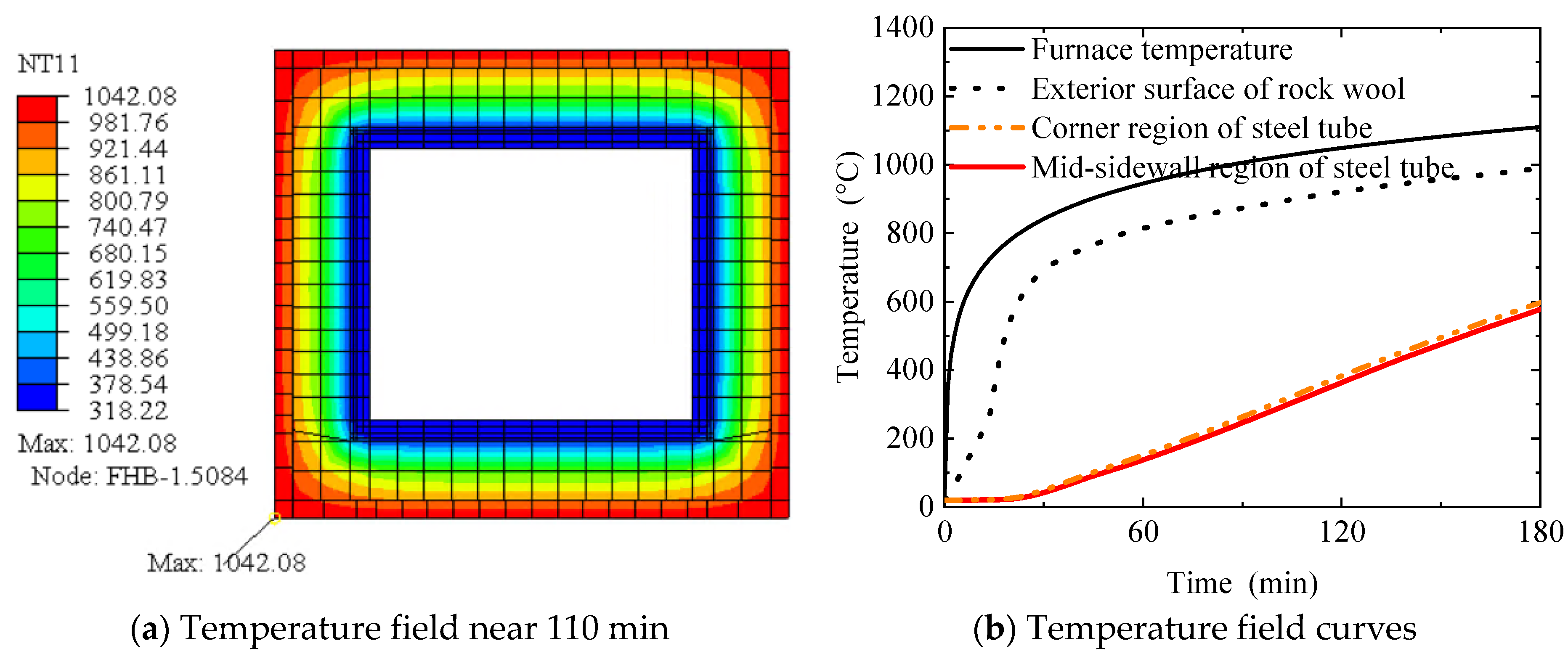
4.2. Thermal Field Model
4.3. Thermo-Mechanical Coupling Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, Y.; Deng, E.-F.; Zong, L.; Dai, X.-M.; Lou, N.; Chen, Y. Cyclic tests on corrugated steel plate shear walls with openings in modularized-constructions. J. Constr. Steel Res. 2017, 138, 675–691. [Google Scholar] [CrossRef]
- Dao, T.N.; van de Lindt, J.W. Seismic performance of an innovative light-frame cold-formed steel frame for midrise construction. J. Struct. Eng. 2013, 139, 837–848. [Google Scholar] [CrossRef]
- Zhang, A.; Liu, X. The new development of industrial assembly high-rise steel structure system in China. In Proceedings of the 10th Pacific Structural Steel Conference (PSSC’13), Singapore, 8–11 October 2013; 2013; pp. 976–981. [Google Scholar]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Review of bolted inter-module connections in modular steel buildings. J. Build. Eng. 2019, 23, 207–219. [Google Scholar] [CrossRef]
- Gatheeshgar, P.; Poologanathan, K.; Gunalan, S.; Shyha, I.; Sherlock, P.; Rajanayagam, H.; Nagaratnam, B. Development of affordable steel-framed modular buildings for emergency situations (COVID-19). Structures 2021, 31, 862–875. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Effect of inter-module connection stiffness on structural response of a modular steel building subjected to wind and earthquake load. Eng. Struct. 2020, 213, 110628. [Google Scholar] [CrossRef]
- Shan, S.; Pan, W. Collapse mechanisms of multi-story steel-framed modular structures under fire scenarios. J. Constr. Steel Res. 2022, 196, 107419. [Google Scholar] [CrossRef]
- Gomes, F.C.; Costa, P.M.P.E.; Rodrigues, J.P.C.; Neves, I.C. Buckling length of a steel column for fire design. Eng. Struct. 2007, 29, 2497–2502. [Google Scholar] [CrossRef][Green Version]
- Franssen, J.-M.; Talamona, D.; Kruppa, J.; Cajot, L. Stability of steel columns in case of fire: Experimental evaluation. J. Struct. Eng. 1998, 124, 158–163. [Google Scholar] [CrossRef]
- Agarwal, A.; Choe, L.; Varma, A.H. Fire design of steel columns: Effects of thermal gradients. J. Constr. Steel Res. 2014, 93, 107–118. [Google Scholar] [CrossRef]
- Wang, J. The protective effects and aging process of the topcoat of intumescent fire-retardant coatings applied to steel structures. J. Coat. Technol. Res. 2016, 13, 143–157. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.-H. Experimental research on the creep buckling of fire-resistant steel columns at elevated temperature. Steel Compos. Struct. 2013, 15, 163–173. [Google Scholar] [CrossRef]
- Alam, M.S.; Billah, A.M.; Quayyum, S.; Ashraf, M.; Rafi, A.; Rteil, A. Fire performance curves for unprotected HSS steel column. Steel Compos. Struct. Int. J. 2013, 15, 705–724. [Google Scholar] [CrossRef]
- Siligardi, C.; Miselli, P.; Francia, E.; Gualtieri, M.L. Temperature-induced microstructural changes of fiber-reinforced silica aerogel (FRAB) and rock wool thermal insulation materials: A comparative study. Energy Build. 2017, 138, 80–87. [Google Scholar] [CrossRef]
- Paudel, D.; Rinta-Paavola, A.; Mattila, H.-P. Multiphysics Modelling of Stone Wool Fire Resistance. Fire Technol. 2021, 57, 1283–1312. [Google Scholar] [CrossRef]
- Keerthan, P.; Mahendran, M. Thermal Performance of Composite Panels Under Fire Conditions Using Numerical Studies: Plasterboards, Rockwool, Glass Fibre and Cellulose Insulations. Fire Technol. 2013, 49, 329–356. [Google Scholar] [CrossRef]
- Steau, E.; Mahendran, M.; Poologanathan, K. Experimental study of fire resistant board configurations under standard fire conditions. Fire Saf. J. 2020, 116, 103153. [Google Scholar] [CrossRef]
- Wang, Y.; Chuang, Y.-J.; Lin, C.-Y. The Performance of Calcium Silicate Board Partition Fireproof Drywall Assembly with Junction Box under Fire. Adv. Mater. Sci. Eng. 2015, 2015, 642061. [Google Scholar] [CrossRef]
- Tsai, K.-C. Influence of substrate on fire performance of wall lining materials. Constr. Build. Mater. 2009, 23, 3258–3263. [Google Scholar] [CrossRef]
- Beh, J.H.; Yew, M.C.; Yew, M.K.; Saw, L.H. Fire Protection Performance and Thermal Behavior of Thin Film Intumescent Coating. Coatings 2019, 9, 483. [Google Scholar] [CrossRef]
- Puri, R.G.; Khanna, A.S. Intumescent coatings: A review on recent progress. J. Coat. Technol. Res. 2017, 14, 1–20. [Google Scholar] [CrossRef]
- GB/T 9978.1-2008; Fire—Resistance Tests—Elements of Building Construction—Part 1: General Requirements. Standards Press of China: Beijing, China, 2017. (In Chinese)
- GB/T 9978.7-2008; Fire—Resistance Tests—Elements of Building Construction—Part 7: Specific Requirements for Columns. Standards Press of China: Beijing, China, 2017. (In Chinese)
- GB50017-2017; Code for Design of Steel Structures. China Planning Press: Beijing, China, 2017. (In Chinese)
- GBT2614-2010; General Administration of Quality Supervision. Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2010. (In Chinese)
- Song, T.Y. Research on Post-Fire Performance of Steel-Concrete Composite Beam-Column Joints; Tsinghua University: Beijing, China, 2010. [Google Scholar]
- Lie, T. Fire resistance of circular steel columns filled with bar-reinforced concrete. J. Struct. Eng. 1994, 120, 1489–1509. [Google Scholar] [CrossRef]
- GB/T11835-2007; Rock Wool, Slag Wool and Their Products for Thermal Insulation. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2017. (In Chinese)
- Fan, G.M.; Wang, L.L.; Wang, W.H. Experimental study on insulating properties of fire-resistant plates commonly used in building under different fire conditions. J. Disaster Prev. Mitig. Eng. 2022, 42, 391–402. [Google Scholar]
- EN 1993-1-2; Eurocode 3: Design of Steel Structures—Part 1-2: General Rules—Structural Fire Design. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
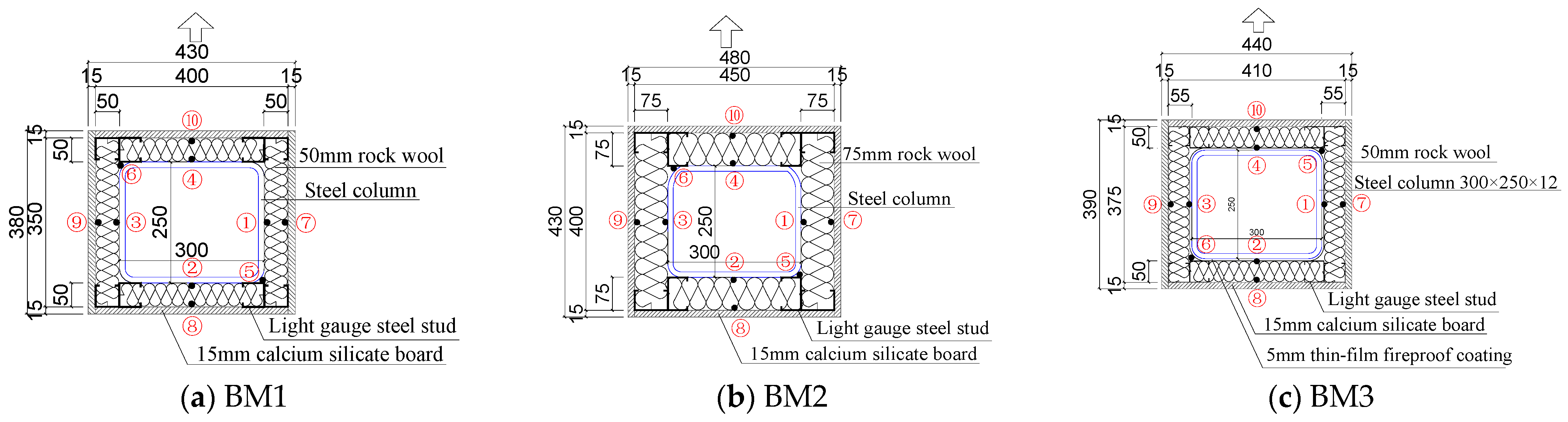









| No. | Protection Method | Hight (mm) | Section Size (mm) | Load Applied (kN) |
|---|---|---|---|---|
| BM1 | 50 mm rock wool + 15 mm calcium silicate board | 3750 | 300 × 250 × 12 | 2100 |
| BM2 | 75 mm rock wool + 15 mm calcium silicate board | 3750 | 300 × 250 × 12 | 2100 |
| BM3 | 5.86 mm thin-film fireproof coating + 50 mm rock wool + 15 mm calcium silicate board | 3750 | 300 × 250 × 12 | 2100 |
| Rock Wool | ||||||
|---|---|---|---|---|---|---|
| Density | Conductivity | Temp | Specific Heat | Temp | Expension | Temp |
| kg/m3 | ° C | ° C | ° C | |||
| 100 | 0.036 | 10 | 900.00 | 20 | 8.00 × 10−5 | 20 |
| 0.038 | 20 | 900.00 | 650 | 8.00 × 10−5 | 1000 | |
| 0.042 | 50 | 900.00 | 725 | 8.00 × 10−5 | 1200 | |
| 0.050 | 100 | 900.00 | 800 | |||
| 0.058 | 150 | 900.00 | 1200 | |||
| 0.069 | 200 | |||||
| 0.083 | 250 | |||||
| 0.099 | 300 | |||||
| 0.118 | 350 | |||||
| 0.139 | 400 | |||||
| 0.163 | 450 | |||||
| 0.218 | 550 | |||||
| 0.249 | 600 | |||||
| 0.283 | 650 | |||||
| 0.319 | 700 | |||||
| 0.590 | 1000 | |||||
| Calcium Silicate Board | ||||||
|---|---|---|---|---|---|---|
| Density | Temp | Temp | Expension | Temp | ||
| kg/m3 | ||||||
| 1050 | 0.50 | 20 | 1100 | 20 | 8.25 × 10−5 | 20 |
| 0.170 | 35 | 1100 | 1200 | 8.25 × 10−5 | 1200 | |
| 0.09 | 80 | |||||
| 0.01 | 250 | |||||
| 0.43 | 360 | |||||
| 0.04 | 385 | |||||
| 0.25 | 420 | |||||
| 0.35 | 880 | |||||
| 0.50 | 920 | |||||
| Thin-Film Fire-Resistant Coating | ||||||
|---|---|---|---|---|---|---|
| Density | Temp | Temp | Expension | Temp | ||
| kg/m3 | ||||||
| 1200 | 0.50 | 20 | 1100 | 20 | 8.25 × 10−5 | 20 |
| 0.50 | 1200 | 1100 | 1200 | 8.25 × 10−5 | 1200 | |
| No. | Experimental Fire Resistance Limit min | Simulated Fire Resistance Limit min |
|---|---|---|
| BM1 | 86 | 124 |
| BM2 | 88 | 163 |
| BM3 | 110 | 142 |
| No. | Experimental Fire Resistance Limit Min | Simulated Fire Resistance Limit min |
|---|---|---|
| BM1 | 86 | 88 |
| BM2 | 88 | 100 |
| BM3 | 110 | 110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zheng, X.Y.; Li, W. Fire Resistance of Prefabricated Steel Tubular Columns with Membrane Protections. Buildings 2025, 15, 1730. https://doi.org/10.3390/buildings15101730
Zhang X, Zheng XY, Li W. Fire Resistance of Prefabricated Steel Tubular Columns with Membrane Protections. Buildings. 2025; 15(10):1730. https://doi.org/10.3390/buildings15101730
Chicago/Turabian StyleZhang, Xinxin, Xiang Yuan Zheng, and Wentao Li. 2025. "Fire Resistance of Prefabricated Steel Tubular Columns with Membrane Protections" Buildings 15, no. 10: 1730. https://doi.org/10.3390/buildings15101730
APA StyleZhang, X., Zheng, X. Y., & Li, W. (2025). Fire Resistance of Prefabricated Steel Tubular Columns with Membrane Protections. Buildings, 15(10), 1730. https://doi.org/10.3390/buildings15101730






