Effect of Steel Fiber on First-Cracking Behavior of Ultra-High-Performance Concrete: New Insights from Digital Image Correlation Analysis
Abstract
1. Introduction
2. Experimental Program
2.1. Raw Materials and Mixture Proportions
2.2. Test Methods and Preparation of Specimens
2.2.1. Flowability
2.2.2. Compressive Testing
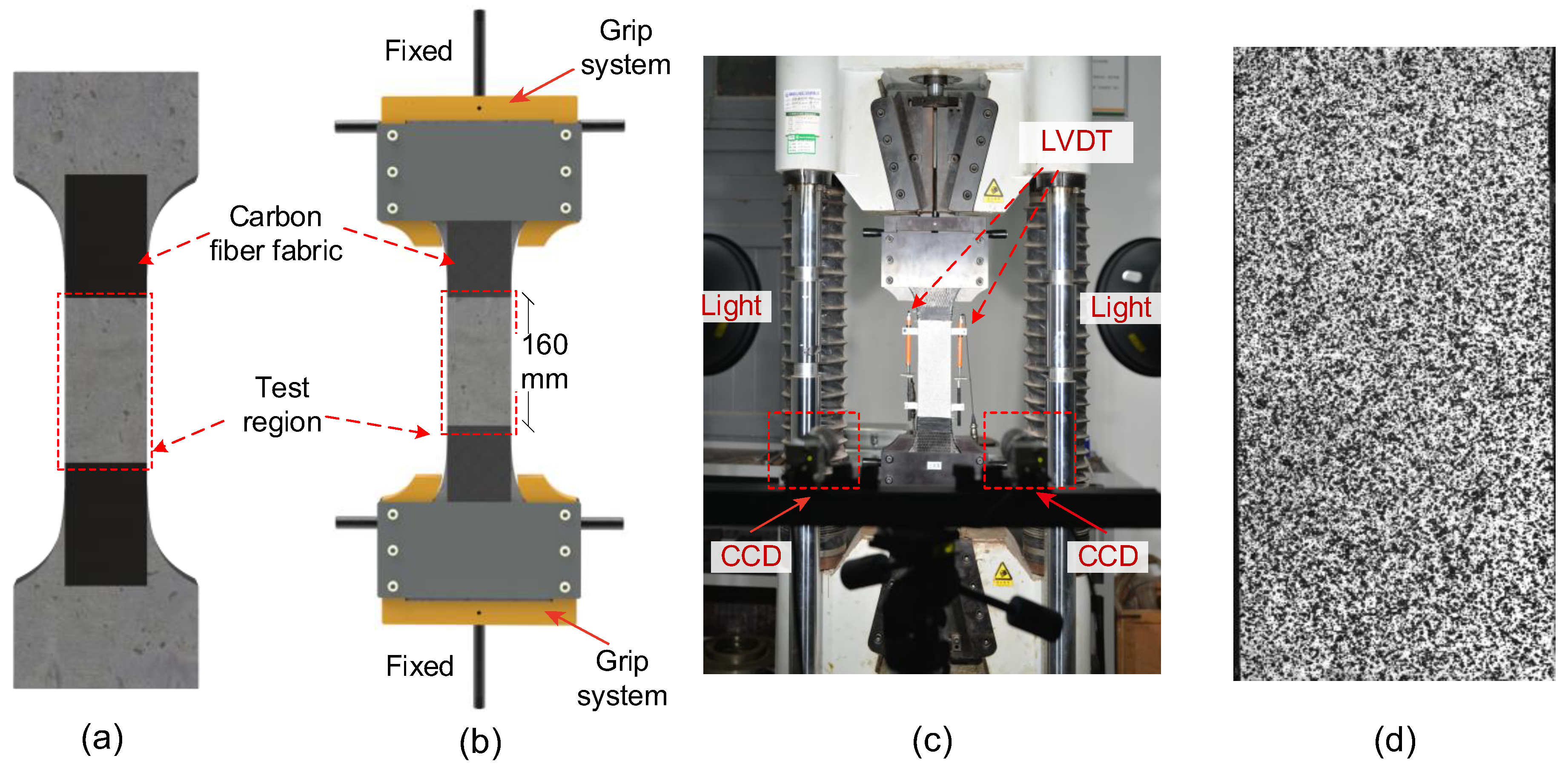
2.2.3. Direct Tensile Testing
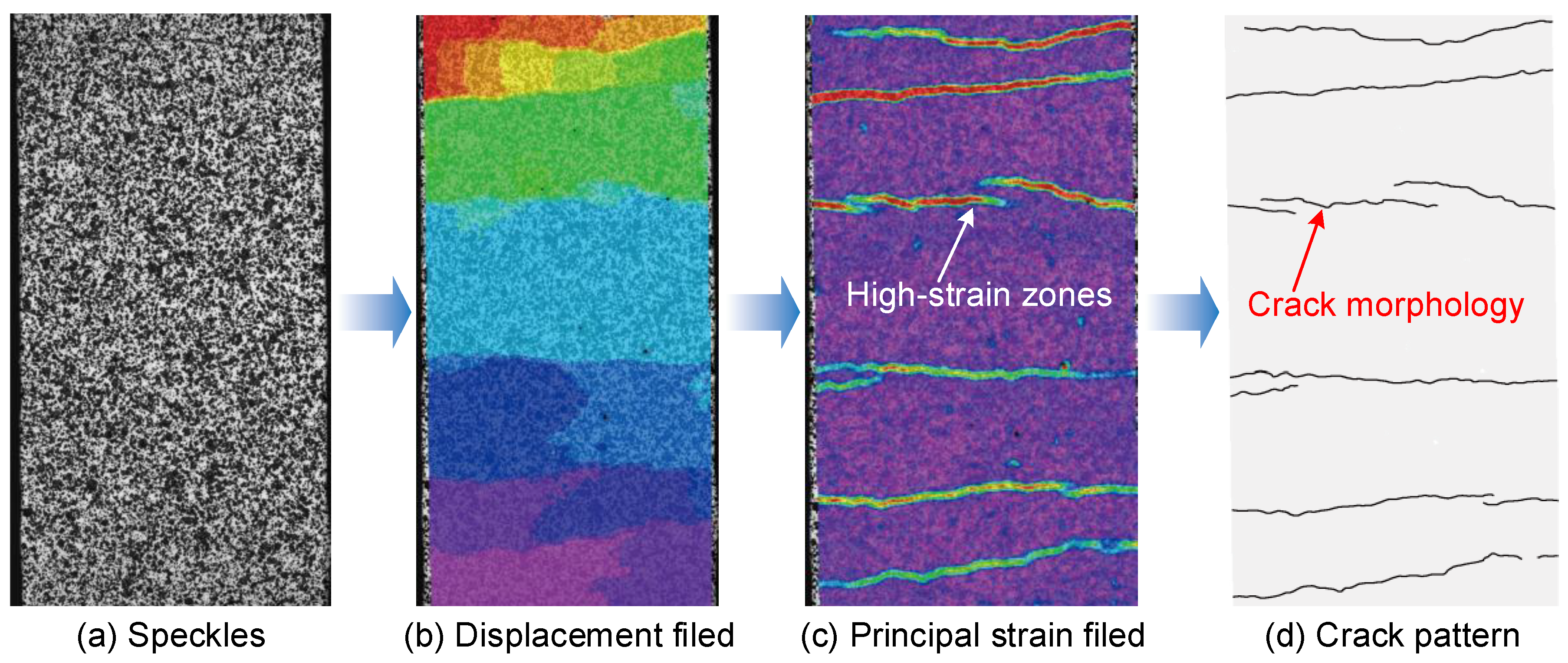
2.3. Crack Identification by Improved DIC Technology
3. Results and Discussion
3.1. Effect of Steel Fiber on Flowability of UHPC
3.2. Effect of Steel Fiber on Compressive Strength of UHPC
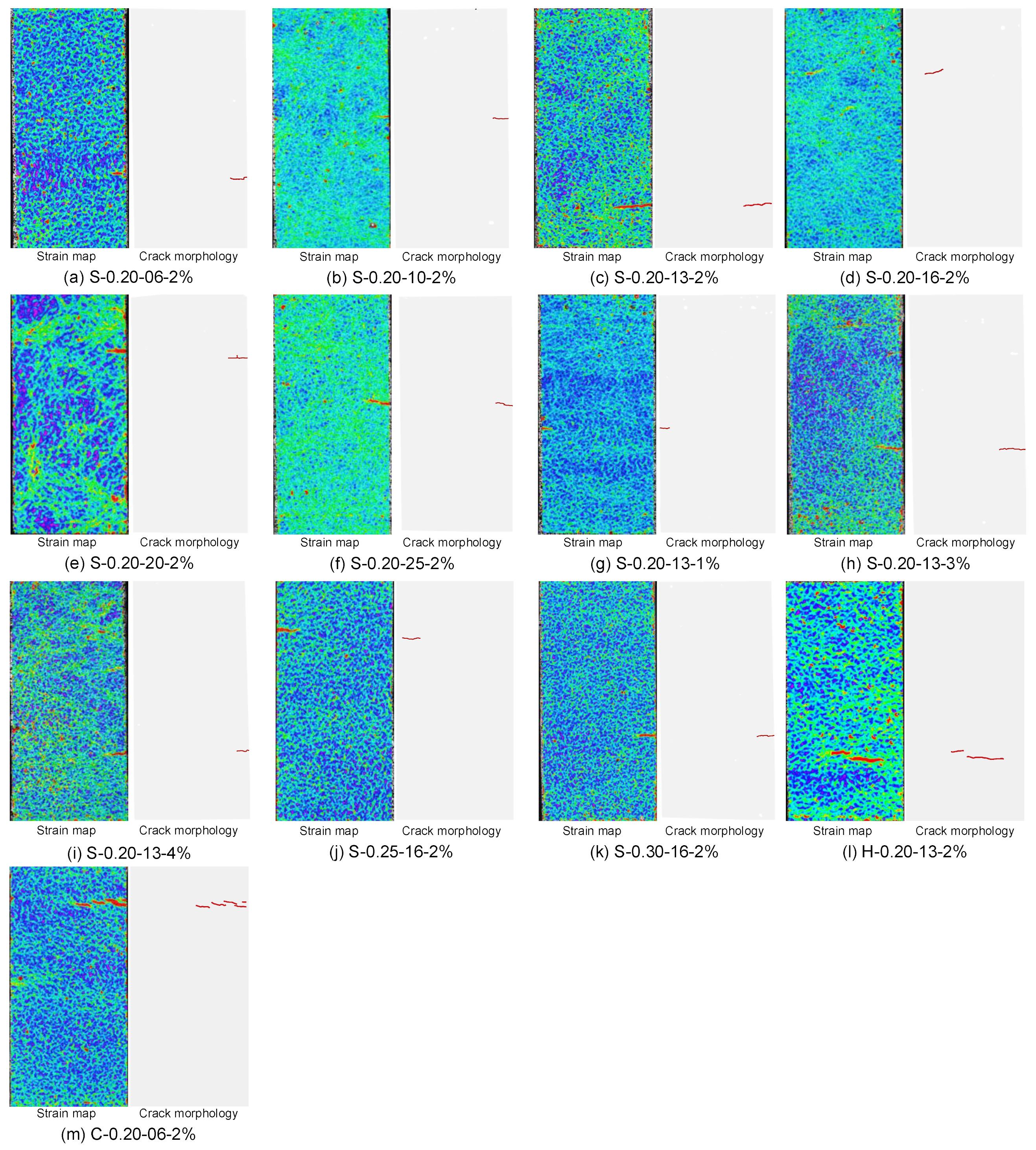
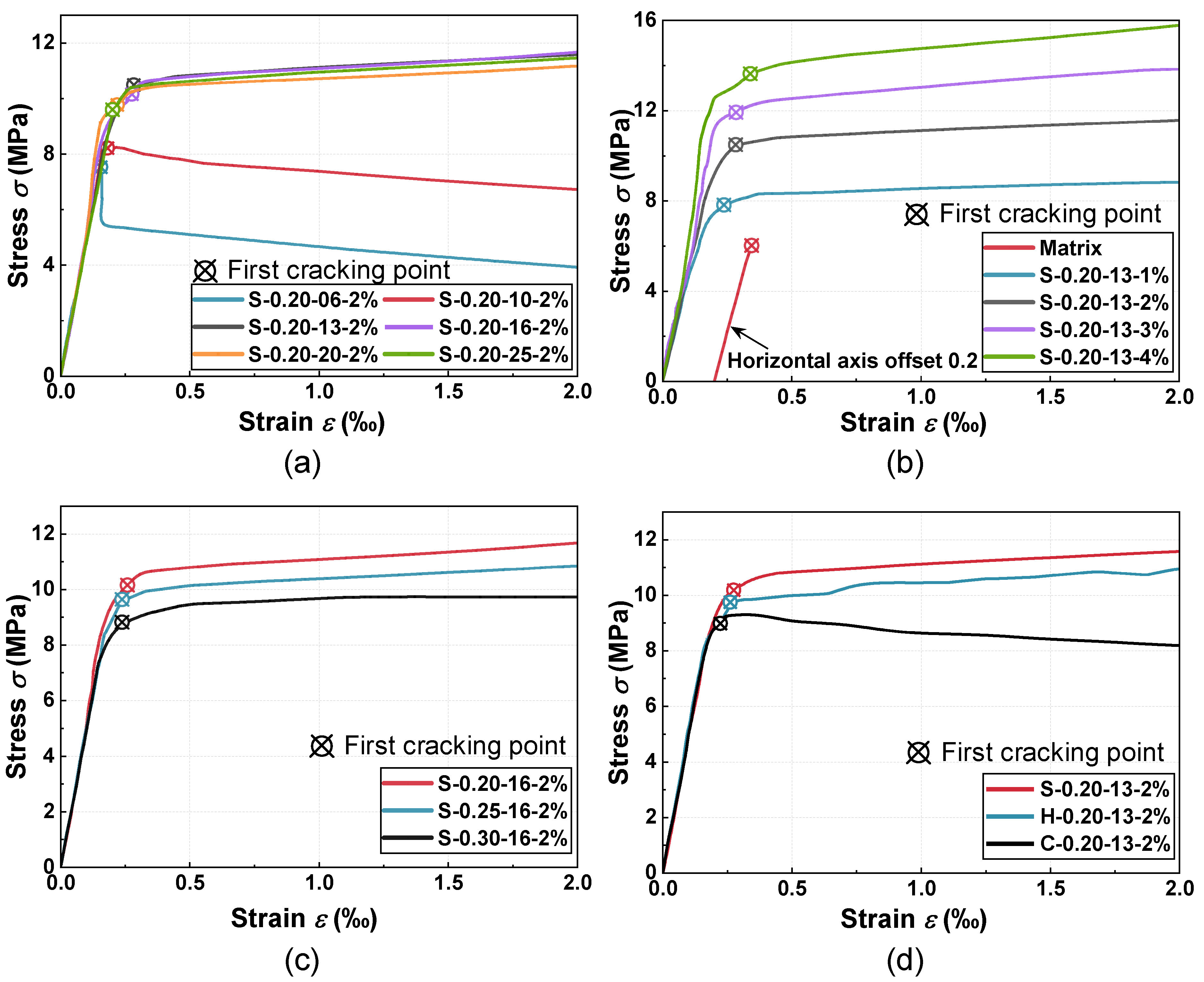
3.3. Initial Crack Pattern of UHPC
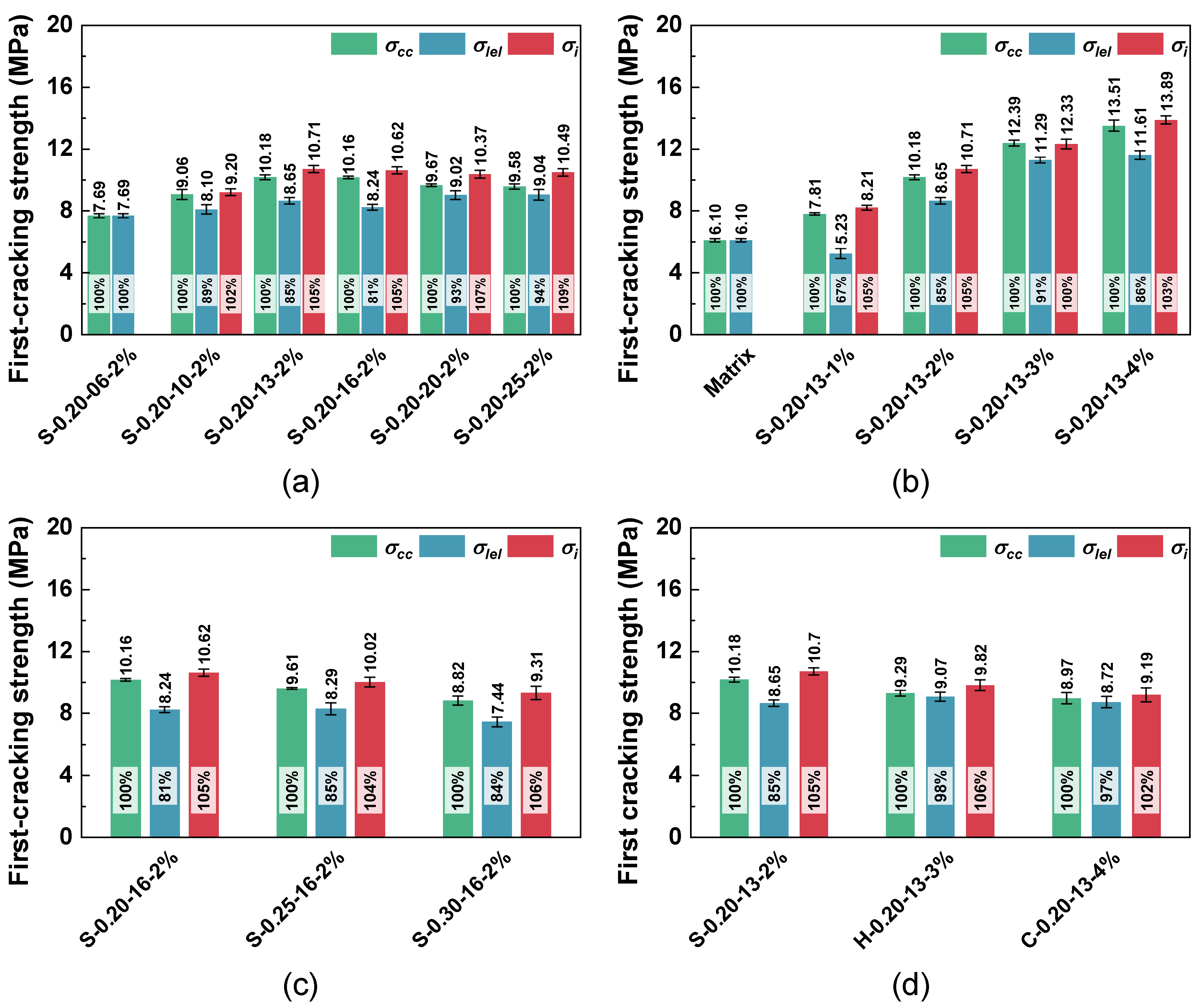
3.4. Effect of Steel Fiber on First-Cracking Behavior of UHPC
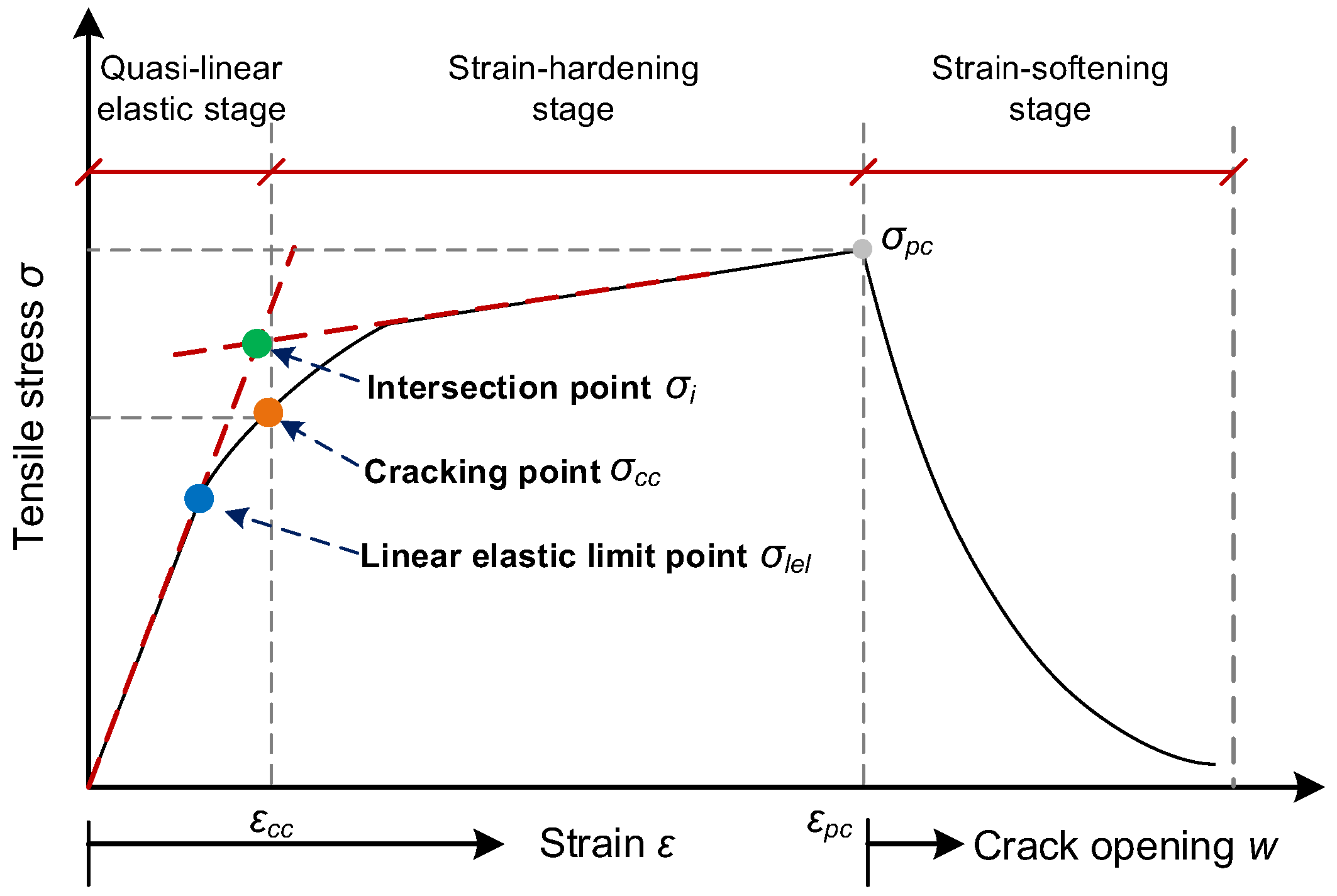
3.5. Comparison of First-Cracking Strength According to Different Methods
4. Establishment of a Model for Predicting the First-Crack Strength
4.1. Background
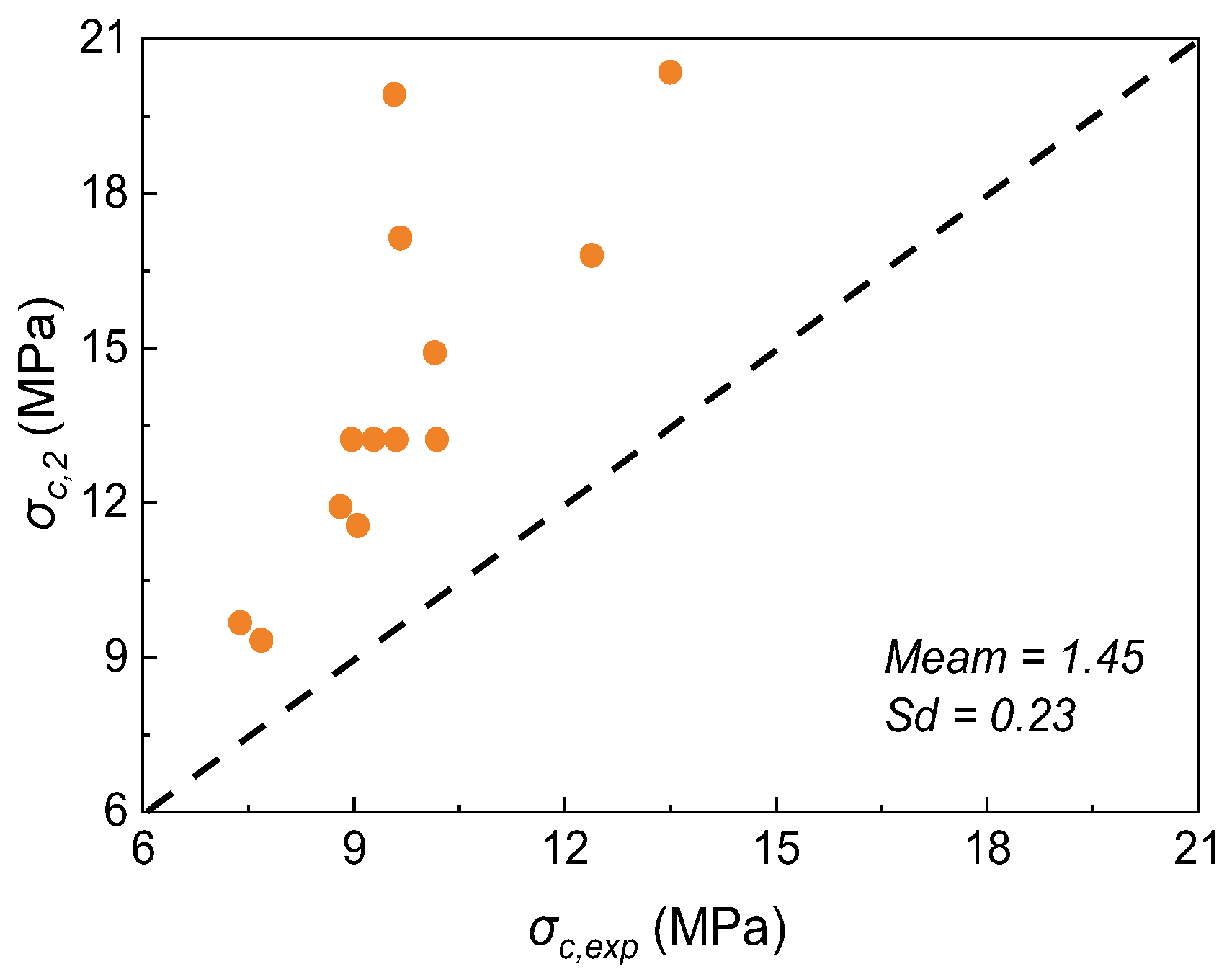
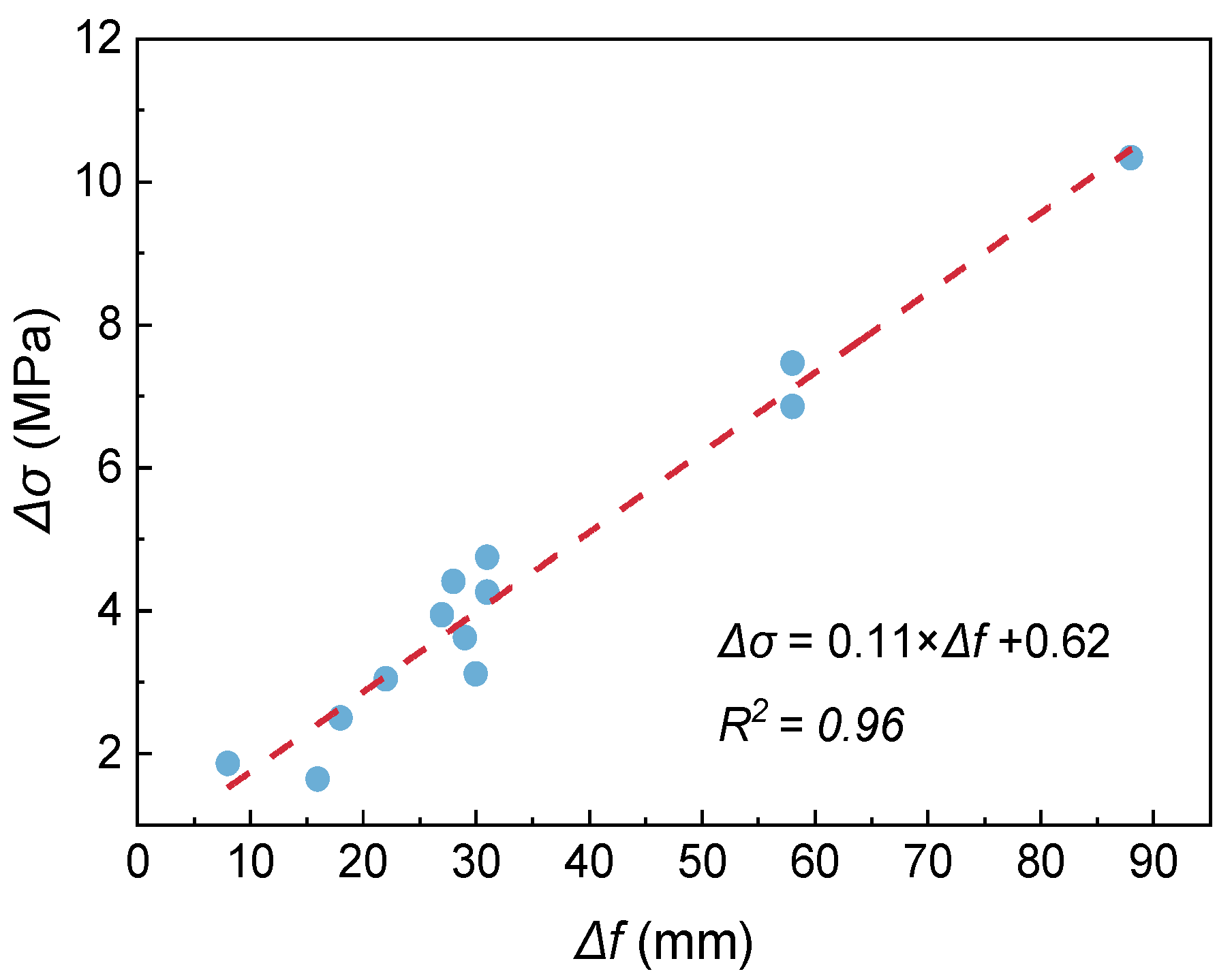
4.2. Establishment and Verification of Formula
5. Conclusions
- DIC analysis reveals distinctions between the first-cracking and linear limit points during DTT. Employing DIC technology reduces the uncertainty in manually pinpointing initial cracks or linear limit points, thus enabling objective determination of the initial cracking strength. Adopting the linear limit point as the benchmark for initial cracking leads to a more conservative design methodology for UHPC.
- The length, volume fraction, diameter, and shape of steel fibers each contribute to the enhancement of the initial cracking strength, with improvements ranging from 26.07% to 121.31%. Among these parameters, fiber length and volume fraction exhibit a more pronounced influence, while the effects of diameter and shape are relatively modest.
- Steel fibers can exert both favorable and adverse effects on the compressive and first-cracking strengths of UHPC. On the one hand, they reinforce the matrix, inhibit crack propagation, and enhance compressive strength; on the other hand, the incorporation of steel fibers also introduces air, which compromises the compactness of the packing system and reduces the matrix strength.
- Stress concentration within steel fibers (such as corrugated or hooked-end fibers) affects both the first-cracking strength and the morphology of the resulting cracks. UHPC reinforced with corrugated fibers, which have more stress concentration points compared to straight and hooked-end fibers, exhibits a discontinuous crack pattern and the lowest initial cracking strength.
- For strain-softening UHPC, the linear elastic limit point method can be used to determine the first-cracking strength. For strain-hardening UHPC, the intersection point method can serve as a simplified approach to determine the first-cracking strength, though it tends to slightly overestimate the actual cracking strength.
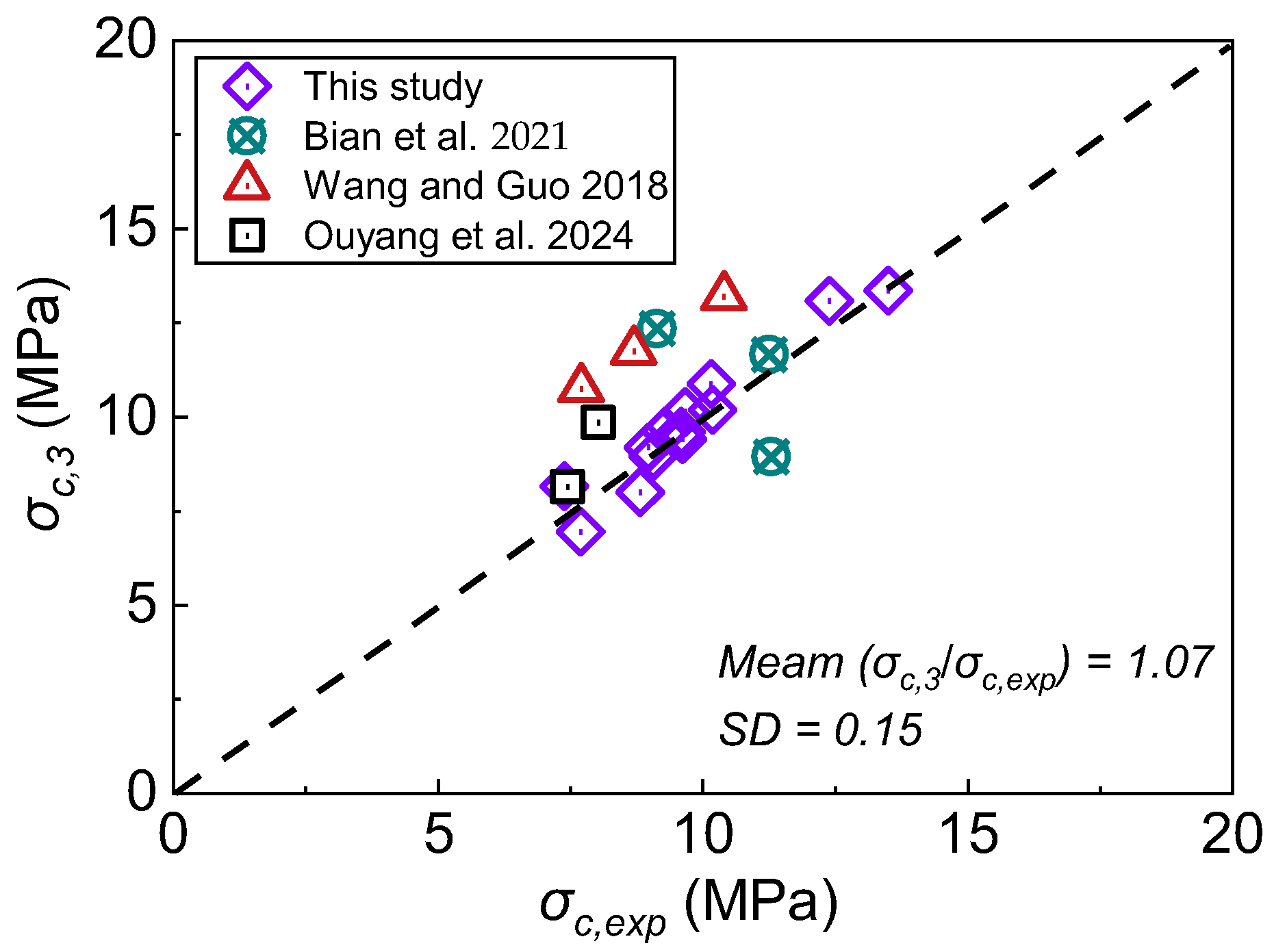
- Considering that previous studies did not account for the adverse effects of steel fibers, this research proposes an updated formula that can predict the initial cracking strength of UHPC with reasonable accuracy, evidenced by a mean ratio of 1.07 and a standard deviation of 0.15.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yoo, D.-Y.; Banthia, N.; Yoon, Y.-S. Recent development of innovative steel fibers for ultra-high-performance concrete (UHPC): A critical review. Cem. Concr. Compos. 2024, 145, 105359. [Google Scholar] [CrossRef]
- Naaman, A.E.; Shah, S.P. Strain capacity of strain-hardening ultra-high-performance concrete with steel fibers. ACI Mater. J. 2022, 119, 171–180. [Google Scholar]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Lee, J.-H.; Yoon, Y.-S. Effect of fiber content on mechanical and fracture properties of ultra high performance fiber reinforced cementitious composites. Compos. Struct. 2013, 106, 742–753. [Google Scholar] [CrossRef]
- Feng, J.; Fang, S.; Chen, M.; Fang, Z.; Liang, W. Effect of joint width on shear behaviour of wet joints using reactive powder concrete with confining stress. Eng. Struct. 2023, 293, 116566. [Google Scholar] [CrossRef]
- Kim, S.; Kim, M.-J.; Yoon, H.; Yoo, D.-Y. Effect of cryogenic temperature on the flexural and cracking behaviors of ultra-high-performance fiber-reinforced concrete. Cryogenics 2018, 93, 75–85. [Google Scholar] [CrossRef]
- Othman, H.; Sabrah, T.; Marzouk, H. Conceptual design of ultra-high performance fiber reinforced concrete nuclear waste container. Nucl. Eng. Technol. 2019, 51, 588–599. [Google Scholar] [CrossRef]
- ASTM C1018; Standard Test Method for Flexural Toughness and First-Crack Strength of Fiber Reinforced Concrete (Using Beam with Third-Point Loading). ASTM: West Conshohocken, PA, USA, 2017.
- Park, J.-J.; Yoo, D.-Y.; Park, G.-J.; Kim, S.-W. Feasibility of reducing the fiber content in ultra-high-performance fiber-reinforced concrete under flexure. Materials 2017, 10, 118. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wu, L. Effects of steel fiber content and shape on mechanical properties of ultra high performance concrete. Constr. Build. Mater. 2016, 103, 8–14. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Kim, S.-W.; Park, J.-J. Comparative flexural behavior of ultra-high-performance concrete reinforced with hybrid straight steel fibers. Constr. Build. Mater. 2017, 132, 219–229. [Google Scholar] [CrossRef]
- Kang, S.T.; Lee, B.Y.; Kim, J.-K.; Kim, Y.Y. The effect of fibre distribution characteristics on the flexural strength of steel fibre-reinforced ultra high strength concrete. Constr. Build. Mater. 2011, 25, 2450–2457. [Google Scholar] [CrossRef]
- Meng, W.; Khayat, K.H. Effect of hybrid fibers on fresh properties, mechanical properties, and autogenous shrinkage of cost-effective UHPC. J. Mater. Civ. Eng. 2018, 30, 04018030. [Google Scholar] [CrossRef]
- Mindess, S.; Chen, L.; Morgan, D. Determination of the first-crack strength and flexural toughness of steel fiber-reinforced concrete. Adv. Cem. Based Mater. 1994, 1, 201–208. [Google Scholar] [CrossRef]
- Wille, K.; El-Tawil, S.; Naaman, A.E. Properties of strain hardening ultra high performance fiber reinforced concrete (UHP-FRC) under direct tensile loading. Cem. Concr. Compos. 2014, 48, 53–66. [Google Scholar] [CrossRef]
- Donnini, J.; Lancioni, G.; Chiappini, G.; Corinaldesi, V. Uniaxial tensile behavior of ultra-high performance fiber-reinforced concrete (uhpfrc): Experiments and modeling. Compos. Struct. 2021, 258, 113433. [Google Scholar] [CrossRef]
- Shi, Z.; Su, Q.; Kavoura, F.; Veljkovic, M. Uniaxial tensile response and tensile constitutive model of ultra-high performance concrete containing coarse aggregate (CA-UHPC). Cem. Concr. Compos. 2023, 136, 104878. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, Y.; Qu, S.; Kumar, A.; Shao, X. Improvement of flexural and tensile strength of layered-casting UHPC with aligned steel fibers. Constr. Build. Mater. 2020, 251, 118893. [Google Scholar] [CrossRef]
- Pyo, S.; Kim, H.-K.; Lee, B.Y. Effects of coarser fine aggregate on tensile properties of ultra high performance concrete. Cem. Concr. Compos. 2017, 84, 28–35. [Google Scholar] [CrossRef]
- Park, S.H.; Kim, D.J.; Ryu, G.S.; Koh, K.T. Tensile behavior of ultra high performance hybrid fiber reinforced concrete. Cem. Concr. Compos. 2012, 34, 172–184. [Google Scholar] [CrossRef]
- Yang, J.; Chen, B.; Wu, X.; Xu, G. Quantitative analysis of steel fibers on UHPFRC uniaxial tensile behavior using X-CT and UTT. Constr. Build. Mater. 2023, 368, 130349. [Google Scholar] [CrossRef]
- Guo, J.-Y.; Wang, J.-Y.; Wu, K. Effects of self-healing on tensile behavior and air permeability of high strain hardening UHPC. Constr. Build. Mater. 2019, 204, 342–356. [Google Scholar] [CrossRef]
- Gehri, N.; Mata-Falcón, J.; Kaufmann, W. Refined extraction of crack characteristics in Large-scale concrete experiments based on digital image correlation. Eng. Struct. 2022, 251, 113486. [Google Scholar] [CrossRef]
- Qiu, M.; Qian, Y.; Dai, J.-G. Enhancing the flexural performance of concrete beams with 3D-printed UHP-SHCC permanent formwork via graded fiber volume fraction. Compos. Struct. 2024, 341, 118211. [Google Scholar] [CrossRef]
- Tu, L.; Zhao, H.; Qiao, D.; Hu, J.; Tan, C.; Ma, J.; Hu, Z.; Qiu, H.; Shao, X. Concept and flexural performance of non-prestressed steel plate-UHPC-NC composite girder bridge. Eng. Struct. 2024, 315, 118417. [Google Scholar] [CrossRef]
- Tu, L.; Zhao, H.; Tan, C.; Cao, J.; Yi, D.; Qiu, M. Prediction of tensile strain capacity of ultra-high performance concrete based on crack characteristics. Constr. Build. Mater. 2025, 458, 139632. [Google Scholar] [CrossRef]
- GB/T 2419-2005; Test Method for Fluidity of Cement Mortar. Standards Press of China: Beijing, China, 2005.
- GB/T 31387-2015; Reactive Powder Concrete. Standards Press of China: Beijing, China, 2015.
- Neuber, H. Der zugbeanspruchte Flachstab mit optimalem Querschnittsübergang. Forsch. Ingenieurwesen A 1969, 35, 29–30. [Google Scholar] [CrossRef]
- Kheir, J.; Klausen, A.; Hammer, T.A.; De Meyst, L.; Hilloulin, B.; Van Tittelboom, K.; Loukili, A.; De Belie, N. Early age autogenous shrinkage cracking risk of an ultra-high performance concrete (UHPC) wall: Modelling and experimental results. Eng. Fract. Mech. 2021, 257, 108024. [Google Scholar] [CrossRef]
- Liu, C.; Shen, D.; Yang, X.; Shao, H.; Tang, H.; Cai, L. Early-age properties and shrinkage induced stress of ultra-high-performance concrete under variable temperature and uniaxial restrained condition. Constr. Build. Mater. 2023, 384, 131382. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Hussein, H.H.; Liu, J.; Chen, G. Experimental study and theoretical prediction on shrinkage-induced restrained stresses in UHPC-RC composites under normal curing and steam curing. Cem. Concr. Compos. 2020, 110, 103602. [Google Scholar] [CrossRef]
- Ghorbani, R.; Matta, F.; Sutton, M.A. Full-field deformation measurement and crack mapping on confined masonry walls using digital image correlation. Exp. Mech. 2015, 55, 227–243. [Google Scholar] [CrossRef]
- Mobasher, B.; Li, A.; Yao, Y.; Arora, A.; Neithalath, N. Characterization of toughening mechanisms in uhpc through image correlation and inverse analysis of flexural results. Cem. Concr. Compos. 2021, 122, 104157. [Google Scholar] [CrossRef]
- Niu, Y.; Wei, J.; Jiao, C.; Miao, Q. A mesomechanics-based analysis on the flexural behavior of ultra-high-performance concrete (UHPC) with different steel fiber lengths. J. Mater. Res. Technol. 2022, 17, 3066–3079. [Google Scholar] [CrossRef]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Martinie, L.; Rossi, P.; Roussel, N. Rheology of fiber reinforced cementitious materials: Classification and prediction. Cem. Concr. Res. 2010, 40, 226–234. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H. Mix design and properties assessment of ultra-high performance fibre reinforced concrete (UHPFRC). Cem. Concr. Res. 2014, 56, 29–39. [Google Scholar] [CrossRef]
- Wang, R.; Gao, X. Relationship between flowability, entrapped air content and strength of UHPC mixtures containing different dosage of steel fiber. Appl. Sci. 2016, 6, 216. [Google Scholar] [CrossRef]
- Fan, D.; Rui, Y.; Liu, K.; Tan, J.; Shui, Z.; Wu, C.; Wang, S.; Guan, Z.; Hu, Z.; Su, Q. Optimized design of steel fibres reinforced ultra-high performance concrete (UHPC) composites: Towards to dense structure and efficient fibre application. Constr. Build. Mater. 2021, 273, 121698. [Google Scholar]
- Yang, J.; Chen, B.; Nuti, C. Influence of steel fiber on compressive properties of ultra-high performance fiber-reinforced concrete. Constr. Build. Mater. 2021, 302, 124104. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Chun, B.; Kim, J.-J. Bond performance of abraded arch-type steel fibers in ultra-high-performance concrete. Cem. Concr. Compos. 2020, 109, 103538. [Google Scholar] [CrossRef]
- Bian, C.; Wang, J.-Y.; Guo, J.-Y. Damage mechanism of ultra-high performance fibre reinforced concrete at different stages of direct tensile test based on acoustic emission analysis. Constr. Build. Mater. 2021, 267, 120927. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Guo, J.-Y. Damage investigation of ultra high performance concrete under direct tensile test using acoustic emission techniques. Cem. Concr. Compos. 2018, 88, 17–28. [Google Scholar] [CrossRef]
- Li, B.; Xu, L.; Shi, Y.; Chi, Y.; Liu, Q.; Li, C. Effects of fiber type, volume fraction and aspect ratio on the flexural and acoustic emission behaviors of steel fiber reinforced concrete. Constr. Build. Mater. 2018, 181, 474–486. [Google Scholar] [CrossRef]
- Banthia, N. A study of some factors affecting the fiber–matrix bond in steel fiber reinforced concrete. Can. J. Civ. Eng. 1990, 17, 610–620. [Google Scholar] [CrossRef]
- Naaman, A.E. A Statistical Theory of Strength for Fiber Reinforced Concrete; Massachusetts Institute of Technology: Cambridge, MA, USA, 1972. [Google Scholar]
- Swamy, R.; Mangat, P. A theory for the flexural strength of steel fiber reinforced concrete. Cem. Concr. Res. 1974, 4, 313–325. [Google Scholar] [CrossRef]
- Lee, Y.; Kang, S.-T.; Kim, J.-K. Pullout behavior of inclined steel fiber in an ultra-high strength cementitious matrix. Constr. Build. Mater. 2010, 24, 2030–2041. [Google Scholar] [CrossRef]
- Niu, Y.; Wei, J.; Jiao, C. Multi-scale fiber bridging constitutive law based on meso-mechanics of ultra high-performance concrete under cyclic loading. Constr. Build. Mater. 2022, 354, 129065. [Google Scholar] [CrossRef]
- Qu, S.; Zhang, Y.; Zhu, Y.; Huang, L.; Qiu, M.; Shao, X. Prediction of tensile response of UHPC with aligned and ZnPh treated steel fibers based on a spatial stochastic process. Cem. Concr. Res. 2020, 136, 106165. [Google Scholar] [CrossRef]
- Ouyang, X.; Huang, Y.; Hu, X.; Yin, J.; Shi, C. Evaluation of tensile failure behavior of ultra high performance concrete under double-edge wedge splitting and direct tension loadings. J. Build. Eng. 2024, 90, 109480. [Google Scholar] [CrossRef]



| Cement | Silica Fume | Fly Ash | Quartz Sand | Quartz Flour | Superplasticizer | Water |
|---|---|---|---|---|---|---|
| 772.1 | 154.2 | 77.1 | 848.4 | 154.2 | 20.1 | 180.5 |
| Notation | Fiber Type | Fiber Diameter (mm) | Fiber Length (mm) | Steel Fiber Volume Fraction (%) |
|---|---|---|---|---|
| Matrix | / | / | / | / |
| S-0.20-06-2% | Straight | 0.2 | 6 | 2 |
| S-0.20-10-2% | Straight | 0.2 | 10 | 2 |
| S-0.20-13-2% | Straight | 0.2 | 13 | 2 |
| S-0.20-16-2% | Straight | 0.2 | 16 | 2 |
| S-0.20-20-2% | Straight | 0.2 | 20 | 2 |
| S-0.20-25-2% | Straight | 0.2 | 25 | 2 |
| S-0.20-13-1% | Straight | 0.20 | 13 | 1 |
| S-0.20-13-3% | Straight | 0.20 | 13 | 3 |
| S-0.20-13-4% | Straight | 0.20 | 13 | 4 |
| S-0.25-16-2% | Straight | 0.25 | 16 | 2 |
| S-0.30-16-2% | Straight | 0.30 | 16 | 2 |
| H-0.20-13-2% | Hooked | 0.20 | 13 | 2 |
| C-0.20-13-2% | Corrugated | 0.20 | 13 | 2 |
| Notation | First-Crack Strength (MPa) | First-Crack Strain (με) | ||||||
|---|---|---|---|---|---|---|---|---|
| Specimen 1 | Specimen 2 | Specimen 3 | Mean (Sd) | Specimen 1 | Specimen 2 | Specimen 3 | Mean (Sd) | |
| Matrix | 5.96 | 6.12 | 6.21 | 6.10 (0.10) | 138 | 140 | 141 | 140 (1.25) |
| S-0.20-06-2% | 7.87 | 7.59 | 7.60 | 7.69 (0.13) | 202 | 215 | 216 | 211 (6.38) |
| S-0.20-10-2% | 9.39 | 9.12 | 8.67 | 9.06 (0.30) | 249 | 224 | 219 | 231 (13.12) |
| S-0.20-13-2% | 10.07 | 10.40 | 10.08 | 10.18 (0.15) | 266 | 272 | 284 | 274 (7.48) |
| S-0.20-16-2% | 10.06 | 10.25 | 10.16 | 10.16 (0.08) | 273 | 253 | 252 | 259 (9.67) |
| S-0.20-20-2% | 9.56 | 9.68 | 9.77 | 9.67 (0.09) | 262 | 247 | 240 | 250 (9.18) |
| S-0.20-25-2% | 9.84 | 9.45 | 9.46 | 9.58 (0.18) | 236 | 258 | 233 | 242 (11.15) |
| S-0.20-13-1% | 7.81 | 7.70 | 7.91 | 7.81 (0.08) | 256 | 254 | 228 | 246 (12.75) |
| S-0.20-13-2% | 10.07 | 10.40 | 10.08 | 10.18 (0.15) | 266 | 272 | 284 | 274 (7.48) |
| S-0.20-13-3% | 12.52 | 12.52 | 12.12 | 12.39 (0.19) | 278 | 284 | 276 | 279 (3.40) |
| S-0.20-13-4% | 13.02 | 13.56 | 13.90 | 13.50 (0.36) | 311 | 313 | 323 | 316 (5.25) |
| S-0.20-16-2% | 10.06 | 10.25 | 10.16 | 10.16 (0.08) | 273 | 253 | 252 | 259 (9.67) |
| S-0.25-16-2% | 9.66 | 9.52 | 9.65 | 9.61 (0.06) | 249 | 234 | 232 | 238 (7.59) |
| S-030-16-2% | 8.89 | 8.43 | 9.12 | 8.82 (0.29) | 243 | 223 | 249 | 238 (11.12) |
| S-0.20-13-2% | 10.07 | 10.40 | 10.08 | 10.18 (0.15) | 266 | 272 | 284 | 274 (7.48) |
| H-0.20-13-2% | 8.96 | 9.65 | 9.25 | 9.29 (0.28) | 247 | 236 | 252 | 245 (6.68) |
| C-0.20-13-2% | 8.59 | 9.18 | 9.15 | 8.97 (0.27) | 235 | 228 | 232 | 232 (2.87) |
| Resource | Notation | σm | df | lf | Vf | τ | Δf | σc,3 | σcc | σc,3/σcc |
|---|---|---|---|---|---|---|---|---|---|---|
| MPa | mm | mm | % | MPa | mm | MPa | MPa | |||
| This paper | S-0.20-06-2% | 6.10 | 0.20 | 6 | 2 | 6.80 | 16 | 6.94 | 7.69 | 0.90 |
| S-0.20-10-2% | 6.10 | 0.20 | 10 | 2 | 6.80 | 18 | 8.95 | 9.06 | 0.99 | |
| S-0.20-13-2% | 6.10 | 0.20 | 13 | 2 | 6.80 | 22 | 10.19 | 10.18 | 1.00 | |
| S-0.20-16-2% | 6.10 | 0.20 | 16 | 2 | 6.80 | 31 | 10.87 | 10.16 | 1.07 | |
| S-0.20-20-2% | 6.10 | 0.20 | 20 | 2 | 6.80 | 58 | 10.13 | 9.67 | 1.05 | |
| S-0.20-25-2% | 6.10 | 0.20 | 25 | 2 | 6.80 | 88 | 9.62 | 9.58 | 1.00 | |
| S-0.20-13-1% | 6.10 | 0.20 | 13 | 1 | 6.80 | 8 | 8.16 | 7.39 | 1.11 | |
| S-0.20-13-3% | 6.10 | 0.20 | 13 | 3 | 6.80 | 28 | 13.09 | 12.39 | 1.06 | |
| S-0.20-13-4% | 6.10 | 0.20 | 13 | 4 | 6.80 | 58 | 13.35 | 13.50 | 0.99 | |
| S-0.25-16-2% | 6.10 | 0.25 | 16 | 2 | 6.80 | 29 | 9.42 | 9.61 | 0.98 | |
| S-0.30-16-2% | 6.10 | 0.30 | 16 | 2 | 6.80 | 30 | 8.00 | 8.82 | 0.91 | |
| H-0.20-13-2% | 6.10 | 0.20 | 13 | 2 | 6.80 | 27 | 9.64 | 9.29 | 1.04 | |
| C-0.20-13-2% | 6.10 | 0.20 | 13 | 2 | 6.80 | 31 | 9.20 | 8.97 | 1.02 | |
| Bian [43] | High strain-hardening UHPFRC | 7.60 | 0.20 | 16 | 2 | 6.80 | 31 | 12.34 | 9.14 | 1.35 |
| Low strain-hardening UHPFRC | 7.60 | 0.20 | 13 | 2 | 6.80 | 22 | 11.66 | 11.25 | 1.04 | |
| Strain-softening UHPFRC | 7.60 | 0.20 | 16 | 1 | 6.80 | 22 | 8.94 | 11.29 | 0.79 | |
| Wang [44] | High strain-hardening UHPFRC | 7.70 | 0.20 | 13 | 2.5 | 6.80 | 25 | 13.20 | 10.40 | 1.27 |
| Low strain-hardening UHPFRC | 7.70 | 0.20 | 13 | 2 | 6.80 | 22 | 11.75 | 8.70 | 1.35 | |
| Strain-softening UHPFRC | 7.70 | 0.20 | 13 | 1.5 | 6.80 | 15 | 10.75 | 7.70 | 1.40 | |
| Ouyang [52] | S-1-0.16 | 6.42 | 0.22 | 13 | 1 | 6.80 | 8 | 8.15 | 7.44 | 1.10 |
| S-2-0.16 | 6.42 | 0.22 | 13 | 2 | 6.80 | 22 | 9.84 | 8.02 | 1.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Tu, L.; Tan, C.; Zhao, H. Effect of Steel Fiber on First-Cracking Behavior of Ultra-High-Performance Concrete: New Insights from Digital Image Correlation Analysis. Buildings 2025, 15, 1727. https://doi.org/10.3390/buildings15101727
Lu X, Tu L, Tan C, Zhao H. Effect of Steel Fiber on First-Cracking Behavior of Ultra-High-Performance Concrete: New Insights from Digital Image Correlation Analysis. Buildings. 2025; 15(10):1727. https://doi.org/10.3390/buildings15101727
Chicago/Turabian StyleLu, Xing, Lei Tu, Chengjun Tan, and Hua Zhao. 2025. "Effect of Steel Fiber on First-Cracking Behavior of Ultra-High-Performance Concrete: New Insights from Digital Image Correlation Analysis" Buildings 15, no. 10: 1727. https://doi.org/10.3390/buildings15101727
APA StyleLu, X., Tu, L., Tan, C., & Zhao, H. (2025). Effect of Steel Fiber on First-Cracking Behavior of Ultra-High-Performance Concrete: New Insights from Digital Image Correlation Analysis. Buildings, 15(10), 1727. https://doi.org/10.3390/buildings15101727






