Abstract
High energy consumption in residential buildings poses significant challenges, prompting governments to regulate this sector through comprehensive energy assessments and classification strategies. This study introduces a multi-layer perceptron artificial neural network (ANN) model to grade and predict energy consumption levels in residential buildings in Tabriz, Iran, based on their geometric and functional characteristics. This study uses the K-Nearest Neighbors (KNN) algorithm to classify energy consumption grades based on energy ratio (R-value). Six sample buildings were modeled using Rhinoceros 3D version 7 and Grasshopper version 1.0.0007 software to extract key energy-influencing factors. A parametric geometric model was developed for rapid data generation and validated against reference buildings to ensure reliability. Building classifications spanned areas of 40 to 300 square meters and heights of up to six stories, with energy evaluations conducted using EnergyPlus. The collected data informed the ANN model, enabling accurate predictions for existing and future constructions. The results demonstrate that the model achieves a remarkable prediction error of just 0.001, facilitating efficient energy assessments without requiring extensive modeling expertise. This research emphasizes the role of geometric features and natural lighting in energy consumption prediction, highlighting the model’s practicality for early design evaluations and architectural validations.
1. Introduction
Currently, building energy use is higher in less developed countries compared to developed ones [1,2,3,4]. Consequently, any effort to reduce energy consumption can significantly diminish dependence on global energy [5]. Numerous studies focus on energy consumption in residential buildings, including both actual and estimated consumption, as well as CO2 emissions [1,2,3,4,6]. Global changes in residential energy consumption highlight the critical role of the residential energy sector in CO2 emissions, emphasizing the sector’s significant potential for energy savings. Enhancing residential energy efficiency may prove more effective than interventions in other sectors [7].
Recently, global policies and carbon reduction goals have been adopted, coinciding with municipalities taking significant actions to decrease energy consumption and carbon emissions in urban areas. Climate change, financial considerations, and the economic benefits of improving energy efficiency have motivated municipalities to implement long-term energy-sustainability policies [8]. Local governments in the United States have enacted laws requiring owners to report their buildings’ energy consumption annually. This brings transparency to the energy consumption issue in real estate markets and creates opportunities for energy savings [9,10,11]. These initiatives facilitate building owners’ understanding of performance metrics while encouraging responsiveness to market competition, ultimately driving improvements in energy efficiency [10,12,13,14,15]. Effective building energy management requires a comprehensive understanding of a building’s performance, beginning with identifying energy sources and, significantly, the final energy consumption [16]. Key indicators, such as annual CO2 emissions and primary energy consumption, are utilized to measure energy efficiency based on annual energy consumption [17]. Factors influencing energy efficiency include the building’s compatibility with climatic conditions [18], its architectural features [19], its external shading systems [20], and its heat transfer rates.
Machine learning models function as black boxes, meaning they can operate effectively without requiring intricate information regarding building systems. By utilizing input data, these models are capable of discovering the underlying relationships between various input features and output objectives, such as energy performance [5,21,22,23,24,25]. A thorough review of artificial intelligence-based methods for predicting building energy consumption was conducted, detailing these prediction methods’ principles, applications, advantages, and limitations. The analysis of artificial intelligence-based prediction methods was approached from five distinct perspectives: the type of building, the prediction methods employed, the types of energies being predicted, the prediction time scale, and the categories of input data used for predictions. Within the realm of artificial intelligence-based prediction methods, two primary categories can be identified: individual prediction methods and group prediction methods [5]. Singaravel and colleagues evaluated deep learning architecture and component-based modeling approaches to predict buildings’ heating and cooling energy demands. They recognized that the component-based modeling approach represents a form of deep learning engineering, while the deep learning architecture tends to exhibit higher prediction accuracy [26]. In addition, Seyedzadeh and colleagues reviewed four common machine-learning approaches frequently employed to predict and enhance building energy performance. Their review also addressed several preprocessing techniques that are applied to models to improve prediction accuracy [21].
Chou and Tran reviewed machine learning methods for predicting time series energy consumption, utilizing accurate data from residential building patterns. They collected real-time data from an intelligent network implemented within an experimental building, using statistical and machine-learning techniques to assess their performance and effectiveness. This study also included an in-depth analysis of a hybrid model that integrates prediction and optimization techniques [27]. Wei and colleagues explored the traditional artificial intelligence-based models used for energy consumption predictions. They categorized these models and discussed their prediction horizons, application areas, and prediction accuracy levels [28]. In terms of the prediction horizon of these artificial intelligence-based models, it is common for a significant percentage of the models to be employed in predicting annual energy consumption. Overall, artificial intelligence-based models demonstrate robust capabilities across all prediction horizons and application areas at a comprehensive scale.
Ronge and Zmeureanu, specifically emphasizing the applications, data, prediction models, and performance metrics utilized in evaluating models, reviewed studies published since 2000 that incorporated artificial neural networks to predict energy consumption and demand in buildings. Their research findings indicated that most artificial neural network models function as black-box models that utilize a neural network as their predictive mechanism [29]. In a separate study, Nie and colleagues developed an innovative predictive model for simulating and forecasting a building’s electrical energy consumption. This model employed the gradient-boosting regression algorithm, and the results demonstrated that the proposed model outperformed other competing models [30]. Khalil and colleagues systematically reviewed machine learning models, and advanced statistical analyses for predicting building energy consumption [31]. Furthermore, Olu-Ajayi and colleagues conducted a study that compared different machine learning models for predicting building energy demand. The findings from this study indicated that Support Vector Machines (SVMs), Artificial Neural Networks (ANNs), and Random Forest (RF) generally outperformed traditional statistical tools like Linear Regression (LR) and ARIMA. The traditional tools (classical statistical and deterministic methods) are less powerful than modern data-driven methods (ANN, SVM, and RF) for building energy predictions due to their inability to handle non-linearity, multivariate data, and dynamic conditions. While they remain useful for interpretable or long-term forecasts, AI-based tools consistently outperform them in terms of accuracy, especially for short-term predictions [32].
The predictive process in artificial intelligence-based methods typically encompasses four main stages: data collection, preprocessing, model training, and model testing. The meticulous selection of input data significantly influences the accuracy of an artificial intelligence-based predictive model. In general, input data that are impactful and well-correlated are likely to yield better prediction results. During the preprocessing stage, the collected data undergo organization and refinement before being utilized for training artificial intelligence-based predictive models. The subsequent stage involves training the predictive model. Engaging in a training phase that selects the most appropriate parameters to optimize the algorithm’s predictive performance is essential throughout the model development process. Finally, the trained model must be subjected to rigorous testing to ensure its accuracy and reliability [27]. Through the three critical stages—preprocessing, data selection, and data training—the predictive model’s performance can be effectively enhanced through the meticulous preprocessing of data and the extraction of energy consumption features [33].
Artificial intelligence-based predictive models can be categorized into three distinct types based on their prediction components: single models, group models, and ensemble models, with each encompassing various subtypes. Single prediction models use a single learning technique. Ensemble models include multiple prediction models, and hybrid models combine two or more learning techniques.
One of the most widely used machine learning techniques for predicting building energy performance and classifying energy consumption is the ANN, which is classified within the category of single models [5]. Remarkably, even a simple neural network can deliver predictions that are comparable in accuracy to those produced by more complex deep learning models [34]. Lu and colleagues undertook a comprehensive literature review on predicting building energy utilization through artificial neural networks, summarizing 324 relevant studies. This article underscored the twelve distinct ANN architectures utilized in these studies, with Long Short-Term Memory (LSTM) identified as the predominant choice for Recurrent Neural Networks (RNNs). Furthermore, CNN-RNN emerged as an effective established architecture, with both being recommended as benchmark models [35]. Afzal and colleagues sought to predict heating and cooling loads using a Multilayer Perceptron (MLP) neural network with a hybrid approach that integrated MLP with eight metaheuristic algorithms. Their newly developed model, MLP-PSOGWO, demonstrated superior performance, achieving optimal accuracy, reliability, and efficiency [36].
Tsoka and colleagues proposed an innovative approach, employing artificial neural networks to classify the Energy Performance Certificate (EPC) label of buildings with greater efficiency and cost-effectiveness. Their model classified building EPC labels by analyzing input features about the technical and human-driven factors influencing building energy consumption. The findings showed that the EPC classification model could achieve an impressive accuracy rate of 99% when sufficient input data were available. [37]. Al-Baltaqi and Wefki introduced an artificial neural network-based methodology to enhance building energy consumption predictions during the early design phases. Their proposed model was developed utilizing a dataset generated from the energy consumption simulations across various design options with random input variables. This model was rigorously assessed and validated using C#, which was used to create a comprehensive database comprising 12,000 scenarios characterized by diverse building dimensions and features [38,39].
According to extensive research, Artificial Neural Networks (ANNs) are widely preferred for predicting building energy performance because they can model complex non-linear relationships without detailed system knowledge. They consistently demonstrate a high prediction accuracy, often outperforming other machine learning models, like SVM and Random Forest. ANNs are versatile across various building types and time scales, with hybrid models such as CNN-RNN and MLP-PSOGWO showing even greater effectiveness. Therefore, the present study employs artificial neural networks to develop an intelligent model.
The studies by Al-Baltaqi and Wefki [38,39] considered important input parameters and indicators affecting energy consumption, such as building dimensions, window-to-wall ratio (wwr), wall type, slab type, and building orientation. However, they acknowledged that the most crucial factor, the building’s form, was treated as a constant, limiting the model’s generalizability to diverse datasets. Due to the significant role that the form parameter plays in energy consumption, and considering the extensive and diverse production of databases, this will significantly impact the accuracy provided by an artificial intelligence-based model. This research proposes using a parametric structure to generate its database, emphasizing form. This produces 2400 diverse scenarios for each type of area and floor, with different dimensions and features for the building structures, and a different energy simulation for each. Furthermore, given the lack of precise information from Iranian engineers regarding the annual energy consumption during the construction of buildings, there is a need for expertise in the time-consuming processes of energy consumption assessments, including the ability to conduct modelings and simulations with common software, highlighting a crucial gap in the discussion of on assessment and efficiency. Therefore, this research aims to present a model based on artificial neural networks that will be able to, at the initial stage of the design and before the construction of the building, determine, with acceptable approximation, the energy consumption level and category without the need for modeling and simulation, without requiring user expertise, and in an online manner. The research methodology is systematically structured into five distinct steps. First, a modeling and simulation of the energy consumption of six existing buildings (one- to six-story buildings) was conducted. Second, energy consumption was modeled and simulated for the proposed parametric geometric model to generate a comprehensive database. Third, a validation of the simulation results for the proposed parametric geometric model was performed to ensure its accuracy and reliability. Fourth, automated database generation through simulations was carried out to enhance efficiency and consistency. Finally, the development and optimization of the artificial neural network model for energy consumption and grading were undertaken based on the generated database.
2. Methodology
The current investigation is centered on low-rise and medium-rise residential buildings situated in the city of Tabriz. Initially, a volumetric modeling was performed, followed by comprehensive energy simulation to analyze samples of existing residential structures. A parametric model was established after extracting key energy consumption indicators, considering the buildings’ area and floor typology conditions. The obtained results were subjected to validation, creating a database comprising 2400 plans for each typology. The database encompasses 14,400 distinct plans, varying in area, number of floors, and inclusive design specifications, coupled with corresponding energy consumption levels. After data collection, an artificial neural network was trained, and the energy consumption classification model was determined and rigorously tested. The schematic representation of the study process is depicted in Figure 1.
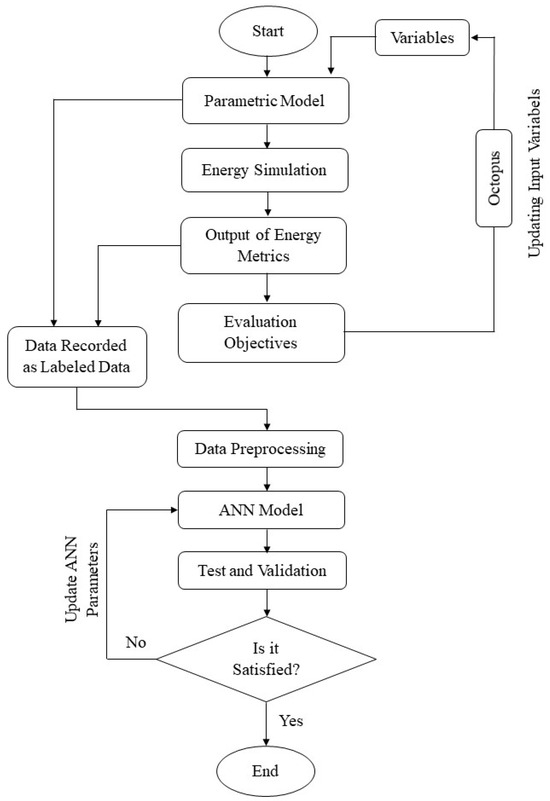
Figure 1.
Flowchart of the proposed method.
2.1. Computational Framework
Rhinoceros 3D 7 and Grasshopper 1.0.0007 constitutes a robust software combination, offering advanced capabilities for computational design. Rhino 3D, a commercial computer-aided design (CAD) and 3D modeling software, synergizes with Grasshopper, a graphical computational tool functioning as a visual programming language based on components. This integration enhances the functionality of the Rhino 3D modeling software [40]. In the context of this research, the modeling phase within the Rhino software environment was conducted through employing the Grasshopper plugin. Subsequently, an energy simulation and assessment were executed within the Grasshopper environment, utilizing the Honeybee and Ladybug plugins. Ladybug 1.7.26, a tool within this computational framework, facilitates the input and analysis of standard weather data, enabling the visualization of various graphs, such as radiation and wind. It further supports analyses encompassing radiation analysis, view analysis, and shadow studies with customizable options. Honeybee 1.7.26 establishes a connection between the Grasshopper/Rhino CAD environment and models, facilitating energy simulations. It employs EnergyPlus/OpenStudio and Radiance for comprehensive modeling and simulations [41]. After the workflow, raw data were assessed by importing standard meteorological files and utilizing the OpenStudio library for energy evaluations. These assessments were conducted using the EnergyPlus 9 finite element energy simulation software. Octopus 0.4, available as a plugin for Grasshopper, allows users to apply evolutionary principles to optimize various functions through a graphical user interface (Octopus plugin. Available: [42]). This plugin simultaneously provides the ability to search for many objectives and generates a wide range of optimized solutions [43].
A search algorithm is essential to generate input data for the artificial intelligence model, encompassing the plans and various building configurations, in a parametric and automated manner. Search algorithms, available as plugins for the Grasshopper environment, persistently strive to optimize a function in a specific direction. In this study, the Octopus plugin was employed for the parametric generation of plans, and a detailed explanation of this task is provided. Data mining, a relatively recent discipline, finds wide applications in data analysis, leading to the development of numerous tools and software for its application. Python 3 is notable for its rich set of additional libraries, many related to machine learning. Orange 3.38.1, an open-source tool, is crucial in developing and testing machine learning models, conducting data analysis, and visualization. Operating through visual programming or script-based programming in Python, Orange boasts extensions and components tailored for machine learning, bioinformatics, text mining, and comprehensive data analysis [44]. In this research, Orange is employed to train and create the artificial neural network model. Figure 2 illustrates the overall flow of the current study using these software tools.
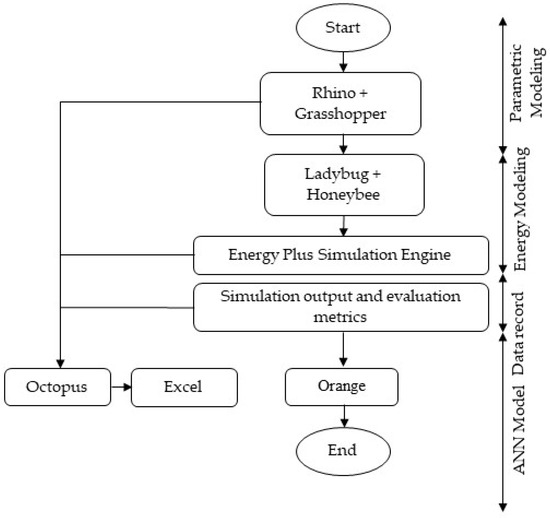
Figure 2.
Flowchart of software tools used in the study.
2.2. Energy Modeling and Simulation of Existing Samples
The primary aim is to extract key indicators that significantly influence energy consumption. Subsequently, the energy simulation results obtained from these reference samples serve as the foundation for validating the outcomes derived from the generated database.
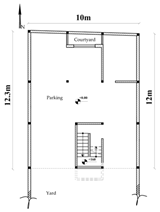
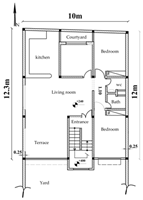
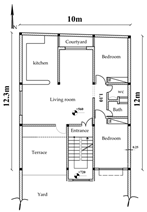
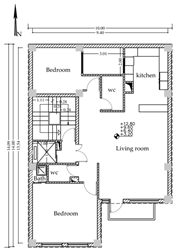
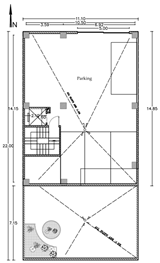
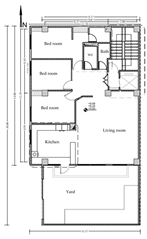
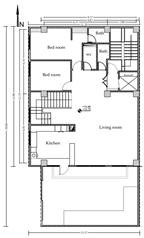
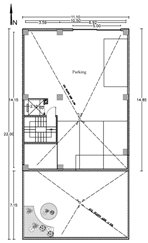
Given the research’s focus on existing residential buildings in Tabriz, six sample buildings—each spanning one to six stories—were chosen as initial samples and reference models. These buildings were meticulously modeled, incorporating details derived from the maps provided by the Tabriz Engineering Organization and adhering to the specified design parameters. The initial step involved solid modeling and transforming the models into energy models. It is worth noting that the modeling and simulation process remained consistent across all six sample buildings. For clarity, the procedural details for a one-story building are elucidated. Figure 3 illustrates the one-story building’s floor plan and 3D energy model, with the plans and models of the two- to six-story buildings also provided.
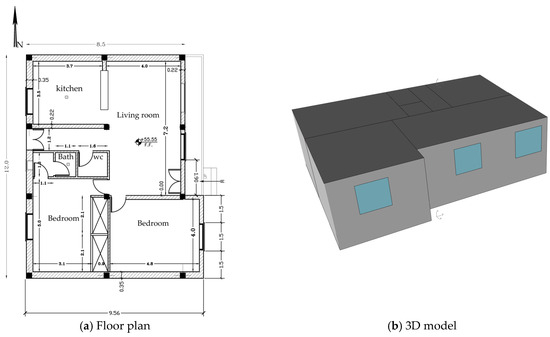
Figure 3.
Floor plan and 3D view of a one-story building; scale 1:100.
2.2.1. Weather Data
The EnergyPlus weather file format (.epw) is a text-based format utilizing comma-separated values. This file encapsulates fundamental information, comprising geographical coordinates such as longitude and latitude, elevation, time zone, annual design, average ground temperature, typical and extreme periods, holiday/daylight-saving periods, dry bulb and dew point temperatures, atmospheric pressure, relative humidity, radiation metrics (horizontal extraterrestrial, normal direct extraterrestrial, horizontal infrared from the sky, global horizontal, normal direct, and diffuse horizontal), global horizontal, diffuse horizontal, zenith, direct normal, wind specifics, sky cover (total, opaque, visible, and ceiling height), current weather conditions, precipitation, aerosol optical depth, and snow metrics (depth and days since last snowfall) [45]. Standard weather files (weather files) pertinent to each city are available for download through https://www.energyplus.net/weather [46].
2.2.2. Simulation Input Parameters
In this research, the input parameters span a variety of factors. Geometry-related parameters include area, perimeter, Volume-to-Surface Ratio (VSR)—indicating the total volume of the building divided by the total area of external walls—and Area-to-Perimeter Ratio (APR)—representing the area of one floor divided by its perimeter. These two indices, coupled with the area and length of the external walls, collectively determine the complexity or simplicity of the building plan shape. Additionally, window-related parameters involve the window-to-wall ratio (WWR) and aspects related to window design, such as window dimensions. Material-related parameters cover thickness, thermal conductivity, specific heat capacity, and thermal resistance. Ventilation system-related parameters include the type of natural ventilation system, the type of mechanical ventilation system, the characteristics of air handling units, pump specifications, setpoint temperatures, and setback temperatures. Lighting-related parameters encompass artificial lighting, density, and the type of artificial lighting control.
2.2.3. Energy Simulation Workflow
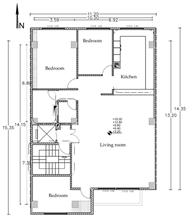
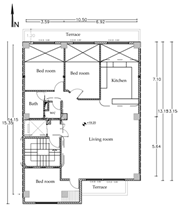
The initial phase involved defining an appropriate physical program for the residential spaces in each zone and specifying the ventilation conditions for each. In the subsequent stage, the windows on the east and west facades of the building were defined based on their respective dimensions. The third stage entails the definition of pertinent materials. Generally, the materials for each building can be specified through two approaches: the first method involves utilizing the recommendations established according to climatic considerations by standards such as ASHRAE, while the second method entails manually modeling materials and adding them to the OpenStudio library for utilization within the EnergyPlus engine in Grasshopper. The latter method models materials based on extant building plans or commonplace materials suitable for the climate and the building’s purpose. In certain instances, pre-existing materials within the OpenStudio library may be employed. In this research, materials were meticulously developed for each component based on the existing building plans and subsequently integrated into the EnergyPlus library. In the fourth stage, natural and mechanical ventilation systems were defined to account for ventilation conditions. The Honeybee plugin assigned internal heat loads, occupancy schedules, and HVAC specifications in Grasshopper. The default ProgramTypes defined internal gains and occupancy patterns without considering occupants’ behavioral variability. An IDEAL HVAC system was applied via Honeybee templates to simplify thermal control and ventilation modeling. The fifth stage involved using EnergyPlus software calculations to compute the illuminance and the duration of sunlight received. Typically, the illuminance for residential buildings is set at 300 lux. In the final stage, an algorithm was linked to the EnergyPlus simulation engine to compute the building’s energy consumption. The outputs encompass features associated with energy consumption, including the total heating energy consumption (sum of the heating and cooling loads), overall energy consumption (sum of the heating, cooling, and lighting loads), and heating energy per square. Buildings with two to six floors were also modeled and simulated using the abovementioned process. The plans and images of the modeled buildings are provided in Table 1.

Table 1.
Reference buildings from two to six stories.
2.3. Proposed Parametric Model
Creating suitable, valid, and extensive training databases is essential to developing the ANN model. This is because the credibility and adequacy of the data directly impact the accuracy of the ANN model. Here, the training data will consist of diverse building plans, varying in form, area, and number of floors. Two solutions exist for generating these building data. The first involves modeling and simulating each building in environments such as Rhino or Grasshopper. However, this approach is time-consuming and may not yield sufficiently diverse building forms. The second solution involves using an algorithm to automatically parametrically generate an extensive set of buildings. This method allows for the rapid production of various building data types. Mutual Information (MI) analysis was employed for sensitivity analyses to identify influential features, enabling the selection of variables with the strongest statistical dependence on energy consumption. In this method, features with higher MI scores are considered more informative and are kept for the model training. As shown in Figure 4, the 15 primary indicators include orientation, shader depth (North, South, East, and West), internal wall area, plan area, perimeter, volume, VSR, APR, and WWR (North, South, East, and West). According to the sensitivity analysis, shading depth and WWR exhibited lower levels of influence. Although their individual MI scores were relatively low, these features may have indirectly contributed to improving the overall predictive capacity of the model when combined with other variables. Neural networks are well-suited to capturing complex, non-linear relationships between features, and the interactions between variables can sometimes enhance performance even when a feature appears weak by itself. The trade-off between model complexity and predictive accuracy was carefully assessed through conducting initial experiments with and without these two features. The results showed a modest but consistent improvement in accuracy when including shadow depth and WWR. Given that the computational cost of including the two additional features in our model framework and hardware settings was minimal, we considered this trade-off acceptable. Therefore, given the model’s performance, we prioritized predictive robustness and retained all 15 core features to capture the full range of building design characteristics.
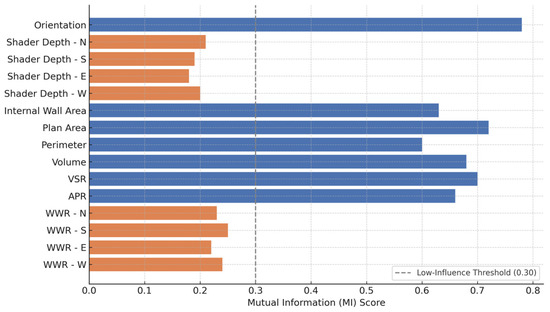
Figure 4.
Sensitivity analysis of input features (MI scores).
Subsequently, a parametric geometric model capable of transforming into diverse forms was proposed. Using the Grasshopper plugin in Grasshopper, an extensive collection of building plans with diverse forms and automatically generated values for each of the mentioned indices was created. Following this, the energy consumption evaluation was performed using the EnergyPlus simulation engine in Grasshopper, providing automated assessments of the energy consumption for each building.
2.3.1. Simulation Variables
Building design options are determined by applying two types of variables: discrete and continuous. A single variable directly controls some indices, while others are influenced by a combination of geometric variables that define the plan. Additionally, certain variables can assume values for either continuous or discrete types. For instance, the Window-to-Wall Ratio (WWR) may range from 1% to 100% or take specific values from a hypothetical list, such as 15%, 25%, or 45%. In this research, discrete variables include geometric plan points, plan scale in terms of its length and width, the orientation, and the internal wall area. Continuous variables encompass plan area, perimeter, volume, VSR, APR, shader depth, and WWR. Refer to Table 2 for details.

Table 2.
Simulation variables.
2.3.2. Modeling and Energy Simulation Workflow
To initiate the modeling, a parametric base plan with geometric shapes capable of transforming into diverse geometric plans was designed. This base plan is controlled by geometric plan points, which are considered part of the geometric variables in the parametric model, as shown in Figure 5.
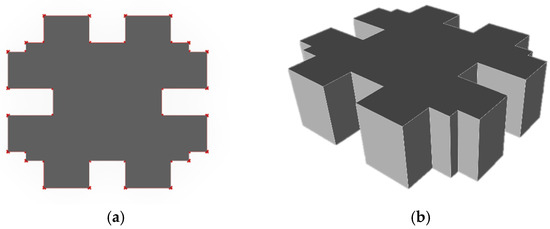
Figure 5.
Geometric plan, (a); model (b).
Energy simulation for this section was performed following the energy simulation process for existing buildings detailed in Section 2.2.3. The properties of common materials in residential buildings in the Tabriz climate were used for material definition. Similarly to that simulation process, in the final stage, the EnergyPlus simulation engine was utilized to calculate the building’s energy consumption.
2.3.3. Validation of Results
Before entering the data generation phase, it is necessary to compare the energy simulation results of the proposed parametric building with the energy simulation results of the reference buildings (existing buildings) to ensure the accuracy and credibility of the data. In this research, reference buildings with one to six floors were remodeled by applying their specifications to the parametric model algorithm for precise validation. To achieve this, the geometric points of the parametric model were adjusted to align with the plan of each building on the parametric plan, and the values for area, perimeter, VSR, APR, window-to-wall ratio, and internal wall area were used during modeling. Subsequently, the modeled buildings underwent energy simulation.
A comparison between the simulation results from the reference buildings and those generated by the parametric model showed less than 5% variance. These compared values are provided in Table 3. This difference implies that the data generated through the proposed parametric model are reliable, establishing a valid database for training an artificial neural network model.

Table 3.
Simulation results of existing buildings and parametric geometric models.
2.4. AI Model Development
This study’s proposed model is designed for general predictive analysis rather than time-series forecasting. It predicts the overall energy consumption of buildings based on their static characteristics (e.g., orientation, area, and WWR) before construction.
2.4.1. Data Preprocessing
The initial phase of developing the AI model consisted of preprocessing the dataset used for training. Various area types within six ranges (40 to 75, 75 to 120, 120 to 140, 140 to 200, 200 to 250, and 250 to 300 square meters) and different floor types, from 1 to 6 floors, were considered based on the floor plan classification standards of the Iran Engineering Organization. Data collection was performed for each area and floor type. A search algorithm was used to generate parametric and automatic data (plans). Search algorithms available as plugins for the Grasshopper environment always strive to optimize a function, and consequently, they tend to converge toward a specific direction. When using these algorithms to generate plans, the plan shapes may converge into a uniform form. However, this research aims to produce diverse and divergent data. Therefore, properly coding the search algorithm was necessary to prevent this convergence. The Octopus plugin in Grasshopper was used for this purpose. A specific feature of Octopus is its ability to optimize multiple objective functions simultaneously.
In this research, the multi-objective capability of Octopus was utilized so that, during the search for plans, the shapes of the plans did not converge towards a uniform shape. For this purpose, symmetric and identical objective functions were used. In this state, Octopus generates a range of solutions between these symmetric functions, covering a broader range of variable lengths. To understand the functionality of this method, consider the following example. In this scenario, the problem involves a vector with a domain from 10− to 10+. Using a numerical slider, any value within this domain can be obtained. The objective is to generate a set of numbers within this domain, specifically between 10− and 10+. The numerical slider, allowing for the selection of any value, is our only variable. By defining a two-sided domain vector objective function, Octopus can be configured to cover the entire range of this domain. The objective functions are defined as follows: the first function maximizes the value shown by the slider, and the second function minimizes the value displayed by the numerical slider. These functions are completely symmetrical and identical. As a result, the algorithm simultaneously attempts to generate solutions for both functions, creating a Pareto front range between these two functions. After optimizing the Pareto front, the resulting boundary covers the entire range of this domain. The generated solutions (the numerical values found by the numerical slider) form a linear range between two symmetrical objective functions. These solutions are from the sixth generation, with 10 solutions each generation, and the slider increment is 0.1. The markers on the axis represent the values of the solutions created within this range. As is evident, the generated solutions cover the entire vector range. Since the two functions are entirely identical and symmetrical, the linear boundary that is created, known as the Pareto boundary, includes all the generated solutions. Therefore, by defining identical and symmetrical objective functions, it is possible to suitably obtain the existing range of variable values. This method was also applied to define the objective functions in the problem of generating plans that will cover the entire length of the variables. For the plan generation problem, the considered functions consisted of two symmetric maximization and minimization energy consumption functions, along with two symmetric sums of the numerical values of variable functions. This approach ensures an appropriate range of plans is obtained.
After applying the specified settings, upon running the Octopus extension, the extension automatically generates 2400 plans (buildings) for each defined spatial and floor type. These plans encompass the values of the defined variables, such as the orientation, volume, area, floor area, APR, VSR, window-to-wall ratio (WWR), shadow depth, and internal wall area of each building, as well as the cooling energy, heating energy, total thermal energy, illumination, and sunlight exposure. All these values are saved as simulation outputs in Excel files.
2.4.2. Model Selection
ANN is a non-linear statistical learning method and a computational system modeled after the interconnections of biological neurons in biological systems, which exhibit activation functions. Typically, artificial neural networks comprise three primary layer types: the input, hidden, and output layers. ANNs may consist of several stacked input and hidden layers. The input layer comprises the independent variables employed to predict the target outcome [5]. The output layer generates the outcomes, which may include predictions, classifications, or other specified outputs [47,48]. Most artificial neural network models are considered black-box models and often use a feedforward neural network architecture [29]. The signal flow is considered unidirectional from the input variables x1, …, xn, as indicated by the arrows, to the output signal flow of neuron (o). The following relationship provides the output signal flow of neuron o:
where () is the weight vector and is referred to as an activation (transfer) function. The variable (net) is the scalar product of the weight and input vectors.
Here, T represents a transfer matrix, and in the simplest case, the output value (o) is calculated as follows:
where is the threshold level. This kind of node is referred to as a linear threshold unit (LTU) [47].
The application of artificial neural networks for modeling structures is intriguing because they do not require detailed data about structural characteristics and can be learned from historical and existing data. The selection of the number and types of input parameters is based on the prediction objective and the desired accuracy. Various structural characteristics exist, with each pursuing specific goals and having their own strengths and weaknesses. However, no uniform structure is systematically provided (not specific to neural network construction, i.e., the number of layers, the neurons, and the activation function). While suitable methods and standard rules exist, they do not exempt the user from the need for an empirical process to select the parameters for determining the desired structure.
A significant number of inputs representing intrinsic characteristics are preferred for the accurate prediction of energy from a single structure [34]. Artificial neural networks have various types, such as multi-layer perceptron, radial basis function neural networks, self-regression neural networks, and general regression neural networks [29,49]. Constructing an artificial neural network involves adjusting these parameters and dividing them into two categories: those determining the artificial neural network’s structure and those specifying how the artificial neural network is trained [50].
2.4.3. ANN Model Architecture
Input layer: The input layer consists of 15 neurons, each representing one of the 15 measured features of the building, based on Table 4. The dataset, consisting of 14,400 samples with annual energy consumption data for each building, was used for model training. The dataset was divided into two subsets with an 80:20 ratio for the data sampling process. Specifically, 80% of the data were allocated as the training set, which was used for model learning and parameter tuning. The remaining 20% comprised the test set, which was used to assess the model’s performance on new, unseen data. This standard partitioning approach ensures an appropriate balance between training and evaluation while mitigating the risk of overfitting. To ensure the reliability and robustness of the results, the random splitting process was repeated 10 times. Across these repetitions, the model consistently achieved similar performance metrics, indicating stability concerning the different data partitions (See Appendix A). Based on this consistency, we proceeded to report representative results, as they reflect the general behavior of the model across various random splits.

Table 4.
Model inputs and output.
Hidden layer: The number of hidden layers in an ANN depends on the problem complexity, with shallow networks having one layer and deep networks having two or more [51]. Networks with one, two, and three layers were tested using ReLU activation, Adam optimizer, and normalized inputs ([0, 1]). Different neuron counts (50–250) were tested to determine the optimal balance between accuracy and computational cost, as an excessive amount of neurons leads to the risk overfitting, despite the low training error rate [51]. Activation functions (ReLU, Identity, Hyperbolic Tangent, and Logistic Sigmoid) and optimizers (Adam, LB, SGD) were compared in terms of performance. Neurons calculate the weighted sum of inputs, which are transformed into output signals using activation functions. These functions include linear and non-linear types, such as sigmoid, hyperbolic tangent, ReLU, identity, and logistic, each suited to specific tasks [51]. Five activation functions (ReLU, Identity, Hyperbolic Tangent, and Logistic Sigmoid) and three optimizers (Adam, LB, and SGD) were tested and compared.
Output layer: Since the target value is continuous and numerical, the output layer consists of a single neuron representing the annual energy consumption without an activation function. Table 4. Subsequently, for the performance evaluation criteria, we used the Mean Squared Error (MSE), Mean Absolute Error (MAE), and R-squared (R2) as three evaluation metrics to assess the accuracy of the developed model.
As shown in Table 4, the 15 input features of the model included orientation, volume, area, perimeter, APR, VSR, internal wall area, WWRs, and shade depth. The model’s output was the building’s annual energy consumption. Ultimately, the model can predict a building’s annual energy consumption solely based on these 15 features. The model output was subsequently used for grading purposes.
2.4.4. Energy Consumption Grading Using KNN
Grading was performed using the K-Nearest Neighbors (KNN) algorithm based on the r value. The KNN is a non-parametric, instance-based supervised learning algorithm commonly applied in classification and regression tasks. It assumes that similar data points exist nearby in the feature space. The algorithm assigns a value (for regression) or a class label (for classification) to a new data point based on the majority class or average of the k-nearest neighbors in the training dataset. The algorithm depends on a user-specified parameter, k, which defines the number of nearest neighbors to be considered during the prediction [52].
According to the Iranian residential building energy label standard ISIRI 14253 [53], after predicting the energy consumption of the building, the energy ratio (R) for that building is calculated based on Table 5 and Table 6. According to Table 5, the energy ratio for small residential buildings is obtained for the Tabriz climate by dividing the energy consumption by 111. For large residential buildings, it is obtained by dividing the energy consumption by 102. The obtained ratio is then input into the energy grading model, determining the energy consumption category of the building.

Table 5.
Classification of the country’s climatic zones and ideal energy consumption indices [53].

Table 6.
The energy consumption category of the building is based on the energy ratio (R) [53].
3. Results
3.1. ANN Model Implementation and Evaluation
The analysis of the selection of the number of hidden layers with the default activation functions and solvers, as shown in Table 7, after examining the error values, showed that a two-layer network is the most suitable choice for the error coefficients, including MSE, MAE, and the R2 of the model correlation for the tested cases, which are presented in this paper. The lowest values for MSE and MAE and the value of R2 closest to 1 were considered.

Table 7.
Error values and R2 for the neural networks with one and two hidden layers. (Part of the process.)
The two-layer network was determined to have 50 to 250 hidden neurons while keeping the activation functions the same. After analyzing the selection of the hidden neurons, as shown in Table 8, the final configuration presented the lowest error with 250 neurons in the first layer and 160 neurons in the second layer.

Table 8.
Error values and R2 for the neural networks with variations in the number of hidden neurons (part of the process).
According to the analysis of the activation functions, in addition to the previous conditions, as shown in Table 9, the final configuration for selecting activation functions presented the lowest error when using the rectified linear unit (ReLU) function combined with Adam’s solver.

Table 9.
Activation functions (Part of the process).
The distribution diagrams in Figure 6 compare the outputs and observed target values for the ANN model in the training phase when applied to buildings of varying story heights, ranging from one-story to six-story structures. These diagrams evaluate the model’s performance using the correlation coefficient R, quantifying the strength of the linear relationship between the outputs and the targets. The diagonal lines in each graph represent the ideal fit, where the predicted values perfectly match the observed ones. The scatter points in all cases lie very close to these lines, demonstrating the ANN’s accuracy in predicting outputs. The R-value for the one-story case is 0.99, indicating a slightly lower accuracy than the other cases. While most data points are clustered around the diagonal line, a few deviations can be observed, suggesting a minor discrepancy due to the variability in the training data for smaller structures; however, an R = 0.99 still signifies excellent performance. In contrast, the R values equal 1 for the two-story to six-story cases, confirming a perfect correlation between the observed and predicted values. The data points in these graphs align almost perfectly with the diagonal line, indicating that the ANN has successfully learned the underlying relationships in the training data for these structures, with minimal error.
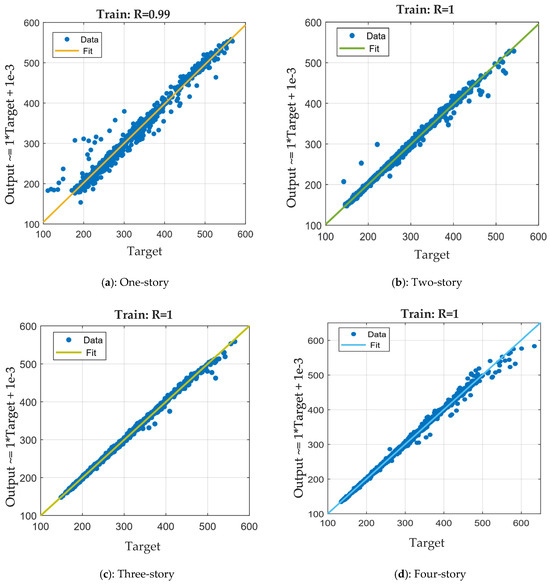
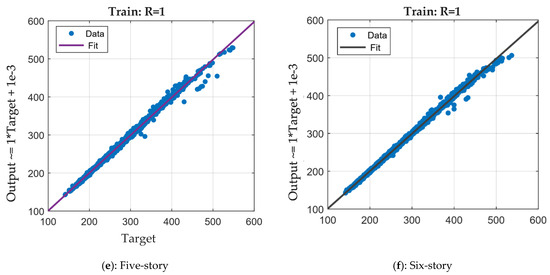
Figure 6.
Distribution diagrams for train observation and prediction values using the ANN.
In the training phase, the ANN demonstrates excellent predictive capabilities across all building heights, with correlation coefficients nearing or reaching unity. However, to confirm the model’s robustness and reliability, further validation of unseen data is essential to rule out overfitting and ensure the model’s general applicability. The distribution diagrams in Figure 7 illustrate the comparative analysis of the outputs and the observed target values for the ANN model in the training phase for the same buildings.
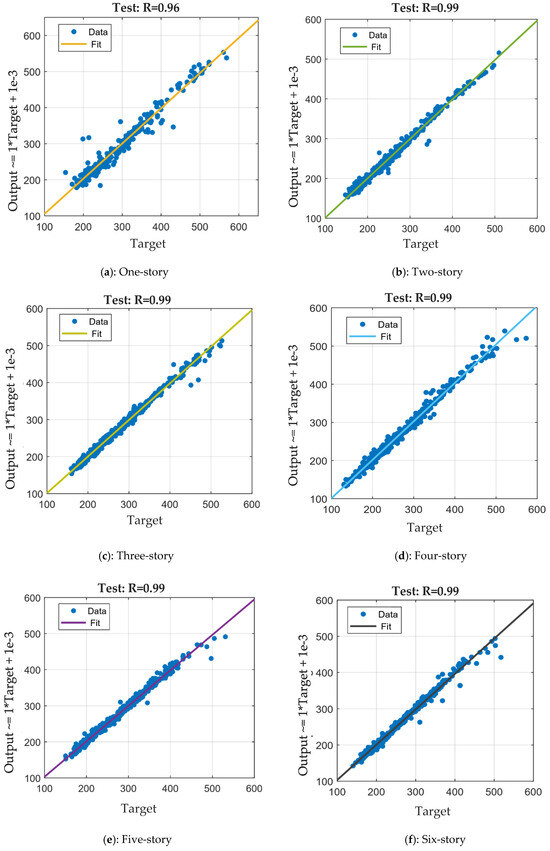
Figure 7.
Distribution diagrams for test observation and prediction values using the ANN.
R2 values range from 0.96 to 0.99, reflecting a high degree of accuracy but a slightly lower performance compared to the training phase. The scatter points correspond to the test data and are closely aligned with these diagonal lines, indicating substantial agreement between the observed and predicted values. The R = 0.96 value indicates slightly lower accuracy for the one-story case than the others, with a noticeable spread of data points around the diagonal line. This suggests that the model’s predictions for one-story buildings are less precise during testing, potentially due to more significant variability in the data or limitations in how the model handles smaller structures.
For the two-story to six-story cases, the R2 = 0.99 indicates excellent predictive performance, with the data points clustered closely around the diagonal lines. These results suggest that the ANN generalizes well for multi-story structures, achieving minimal deviation between the observed and predicted values. The ANN shows excellent predictive capabilities during the testing phase, with consistently high R2 values for multi-story buildings and slightly reduced accuracy for one-story buildings. The results suggest that the model generalizes well to new data, although further investigation into the performance of smaller structures could enhance its overall reliability. While the testing results (R2 values up to 0.99) demonstrate the ANN’s ability to generalize well, they are slightly lower than the perfect R2 values observed in the training phase. This difference suggests the model avoids overfitting and maintains substantial predictive accuracy on unseen data.
3.2. ANN Model Test
Six building samples (one to six stories) were simulated to validate the model’s accuracy in estimating total energy consumption and listing key input variables. These specifications were then entered into an ANN model via an Excel file to predict energy consumption and determine energy grades. The predicted results were compared with the simulation values used to assess model performance. The results of the model performance test are presented in Table 10. This table displays an example of model prediction results, including the actual energy consumption values and the predicted values for six building samples, ranging from one to six stories. The established ANN model predicted the energy consumption of each sample with high accuracy and minimal deviation (below 5%) and determined their energy consumption grades. The characteristics of the training and testing cases for all six models in this table are similar, indicating acceptable results for the network. The current study successfully achieved its intended objective.

Table 10.
Values and testing results 1.
4. Discussion
This research introduces an ANN model for predicting and classifying building energy consumption based on geometric and functional characteristics. It demonstrates that fundamental attributes—area, volume, perimeter, window specifications, shading, orientation, and wall types—can accurately predict energy consumption, achieving a maximum deviation of only 5% compared to EnergyPlus simulations. A systematic sensitivity analysis was conducted to pinpoint the most influential parameters, balancing a comprehensive analysis with user-friendliness for rapid assessments during early design stages.
Fifteen key indicators were identified, including geometric parameters (orientation, volume, area, perimeter, Volume-to-Surface Ratio (VSR), Area-to-Perimeter Ratio (APR)) and envelope features (Window-to-Wall Ratio (WWR)) for each facade, shading depth, and internal wall area). Unlike earlier studies by Al-Baltaqi and Wefki [38,39], this study treats building form as constant; it introduces plan shape complexity (VSR, APR) as dynamic variables. It also aligns with the findings by Tsoka et al. [37] regarding the importance of orientation and envelope properties. Furthermore, this work innovates by treating facade-specific WWR and shading depth as independent variables, allowing for more detailed analysis.
While previous studies, like those of Chou and Tran [27] and Wei et al. [28], emphasized materials and HVAC systems, this study standardizes material properties regionally, isolating the impact of geometric factors, as Afzal et al. [34] suggested. This is in contrast to Nie et al.’s ANN-based studies [30], as well as those of Khalil et al. [31] and Olu-Ajayi et al. [32], which focused on HVAC, occupancy, and non-geometric factors. This research proves that static geometric features alone can achieve high predictive accuracy, reinforcing the findings by Al-Baltaqi and Wefki [38].
A sensitivity analysis using Mutual Information (MI) identified plan shape metrics and orientation as the most influential factors, while shading depth and WWR had moderate impacts.
A significant innovation of this study is the integration of genetic algorithms with ANN. Using parametric modeling, energy simulation, evolutionary optimization, and data processing, the ANN was trained with 260 neurons in the first layer and 160 neurons in the second, utilizing the ReLU activation function and Adam optimizer. The model achieved high precision across multiple metrics and emphasized the critical role of geometric features, an area that is often overlooked. It also incorporates considerations for natural lighting, enhancing its practical relevance.
The final output includes numerical predictions and a classification of energy consumption levels. It also sets the groundwork for generating visual plans and optimizing forms based on the initial designs in future research.
Despite this study’s promising and innovative results in applying artificial intelligence techniques to building modeling, several limitations should be acknowledged. First, the model’s training and validation phases were conducted solely using simulated data. Despite being based on actual buildings, this reliance on simulated datasets may limit the model’s generalizability and accuracy when applied to real-world scenarios. Therefore, future research should incorporate real-world data to enhance the model’s reliability and practical applicability.
Moreover, occupant behavior—an important factor in energy consumption—was not modeled due to computational limitations and the complexity of accurately representing human dynamics. While this simplification helped manage model complexity, future studies should consider incorporating behavioral aspects to enhance realism and accuracy.
5. Conclusions
In this research, we explained how the powerful Energy Consumption Grading model could be used for residential buildings. We developed an Artificial Neural Network model based on a strong database using Octopus, which was employed to create a comprehensive database comprising 14,400 scenarios focusing on different dimensions and factors affecting a building’s energy consumption. The results of the ANN model predict the amount of energy that is consumed before the construction phase of the building. Finally, using the known algorithm, the model determines the degree of energy consumption according to the energy ratio (R-value) classification and provides a strong and efficient predictive model. The model’s test results show that the model has high accuracy. According to the general results, this model eliminates the need for the conventional energy modeling and simulations that are usually performed, removing this time-consuming process. To predict and estimate energy consumption and declare the grade of energy consumption, it is sufficient to use only the leading indicators of the building, which were determined in this research as the input parameters of the ANN model. This model is a potential candidate for implementation in technical and engineering offices, engineering system organizations, and even municipalities. Engineers and designers could use this model as an energy consumption controller and energy consumption grade-determiner before constructing a building.
Author Contributions
Y.S., S.H. and M.M.K.: administration, conceptualization, software, data curation, validation, resources, methodology, investigation, and writing—original draft. M.F. and S.P.: administration, conceptualization, supervision, methodology analysis, and writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The following tables (Table A1, Table A2, Table A3, Table A4, Table A5 and Table A6) summarize the detailed performance metrics of the MLP model—configured with two hidden layers of 200 neurons each, ReLU activation, and the Adam optimizer—across ten independent random train/test splits (20% test size) for each of the six datasets of parametric building models used in this study.

Table A1.
MLP performance over ten random 80/20 splits on the level 1 dataset.
Table A1.
MLP performance over ten random 80/20 splits on the level 1 dataset.
| Split | MSE | MAE | R2 |
|---|---|---|---|
| 1 | 939.0496 | 21.83702 | 0.89035 |
| 2 | 749.8182 | 20.5306 | 0.988976 |
| 3 | 780.7594 | 20.31307 | 0.966402 |
| 4 | 1446.016 | 31.32112 | 0.845466 |
| 5 | 805.7235 | 19.8444 | 0.958779 |
| 6 | 822.5077 | 20.58016 | 0.911912 |
| 7 | 713.2101 | 22.20475 | 0.922691 |
| 8 | 1116.828 | 25.47749 | 0.875345 |
| 9 | 1314.102 | 27.45257 | 0.846268 |
| 10 | 1287.837 | 28.80976 | 0.868285 |

Table A2.
MLP performance over ten random 80/20 splits on the level 2 dataset.
Table A2.
MLP performance over ten random 80/20 splits on the level 2 dataset.
| Split | MSE | MAE | R2 |
|---|---|---|---|
| 1 | 464.0963 | 16.97236 | 0.956078 |
| 2 | 319.1598 | 14.42472 | 0.972284 |
| 3 | 236.7575 | 11.54886 | 0.953113 |
| 4 | 301.3321 | 14.23381 | 0.98236 |
| 5 | 608.8213 | 19.05794 | 0.894096 |
| 6 | 504.7459 | 16.83704 | 0.895332 |
| 7 | 473.9696 | 16.35537 | 0.91134 |
| 8 | 373.1442 | 15.27167 | 0.922211 |
| 9 | 156.7906 | 8.756949 | 0.972593 |
| 10 | 2987.873 | 39.91669 | 0.354073 |

Table A3.
MLP performance over ten random 80/20 splits on the level 3 dataset.
Table A3.
MLP performance over ten random 80/20 splits on the level 3 dataset.
| Split | MSE | MAE | R2 |
|---|---|---|---|
| 1 | 646.2045 | 19.35852 | 0.896962 |
| 2 | 436.3593 | 15.67782 | 0.959128 |
| 3 | 531.051 | 17.39965 | 0.914568 |
| 4 | 566.1927 | 18.10551 | 0.909988 |
| 5 | 307.6571 | 12.73632 | 0.948646 |
| 6 | 666.7583 | 19.57476 | 0.956311 |
| 7 | 545.1042 | 16.77145 | 0.967526 |
| 8 | 854.5338 | 22.51095 | 0.868376 |
| 9 | 702.5794 | 20.27778 | 0.88566 |
| 10 | 7533.805 | 62.61027 | −0.31858 |

Table A4.
MLP performance over ten random 80/20 splits on the level 4 dataset.
Table A4.
MLP performance over ten random 80/20 splits on the level 4 dataset.
| Split | MSE | MAE | R2 |
|---|---|---|---|
| 1 | 514.1374 | 17.71264 | 0.934243 |
| 2 | 628.5542 | 20.27511 | 0.914637 |
| 3 | 635.4107 | 19.24143 | 0.914544 |
| 4 | 821.0995 | 22.36189 | 0.92523 |
| 5 | 343.3422 | 13.97604 | 0.944394 |
| 6 | 934.4415 | 22.9563 | 0.898685 |
| 7 | 955.4811 | 26.99375 | 0.882358 |
| 8 | 932.7975 | 23.17373 | 0.873017 |
| 9 | 507.6461 | 17.30549 | 0.95854 |
| 10 | 1257.501 | 26.80686 | 0.823442 |

Table A5.
MLP performance over ten random 80/20 splits on the level 5 dataset.
Table A5.
MLP performance over ten random 80/20 splits on the level 5 dataset.
| Split | MSE | MAE | R2 |
|---|---|---|---|
| 1 | 774.728 | 22.9731 | 0.85631 |
| 2 | 605.2751 | 19.20743 | 0.8887 |
| 3 | 1012.153 | 26.10465 | 0.812985 |
| 4 | 768.4396 | 21.19448 | 0.854475 |
| 5 | 779.7878 | 22.04807 | 0.863658 |
| 6 | 747.039 | 21.14102 | 0.854186 |
| 7 | 1533.62 | 32.39531 | 0.810655 |
| 8 | 861.8436 | 23.67999 | 0.840125 |
| 9 | 915.7927 | 23.8359 | 0.843062 |
| 10 | 833.6425 | 21.51158 | 0.835395 |

Table A6.
MLP performance over ten random 80/20 splits on the level 6 dataset.
Table A6.
MLP performance over ten random 80/20 splits on the level 6 dataset.
| Split | MSE | MAE | R2 |
|---|---|---|---|
| 1 | 2465.79 | 40.18608 | 0.617101 |
| 2 | 842.8247 | 21.4921 | 0.889756 |
| 3 | 1051.855 | 24.80063 | 0.878674 |
| 4 | 758.6346 | 19.97696 | 0.899484 |
| 5 | 811.8736 | 21.84069 | 0.958785 |
| 6 | 674.8115 | 18.66438 | 0.861743 |
| 7 | 553.5335 | 18.42321 | 0.966595 |
| 8 | 747.5098 | 19.84545 | 0.873888 |
| 9 | 1031.597 | 23.45245 | 0.957008 |
| 10 | 642.9714 | 18.37619 | 0.866949 |
References
- Berardi, U. A cross-country comparison of the building energy consumptions and their trends. Resour. Conserv. Recycl. 2017, 123, 230–241. [Google Scholar] [CrossRef]
- Gaglia, A.G.; Dialynas, E.N.; Argiriou, A.A.; Kostopoulou, E.; Tsiamitros, D.; Stimoniaris, D.; Laskos, K.M. Energy performance of European residential buildings: Energy use, technical and environmental characteristics of the Greek residential sector–energy conservation and CO2 reduction. Energy Build. 2019, 183, 86–104. [Google Scholar] [CrossRef]
- Harvey, L.D.; Korytarova, K.; Lucon, O.; Roshchanka, V. Construction of a global disaggregated dataset of building energy use and floor area in 2010. Energy Build. 2014, 76, 488–496. [Google Scholar] [CrossRef]
- Yoshino, H.; Hong, T.; Nord, N. IEA EBC annex 53: Total energy use in buildings—Analysis and evaluation methods. Energy Build. 2017, 152, 124–136. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- Pablo-Romero, M.d.P.; Pozo-Barajas, R.; Yñiguez, R. Global changes in residential energy consumption. Energy Policy 2017, 101, 342–352. [Google Scholar] [CrossRef]
- Amasyali, K.; El-Gohary, N.M. A review of data-driven building energy consumption prediction studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Kontokosta, C.E. Energy disclosure, market behavior, and the building data ecosystem. Ann. N. Y. Acad. Sci. 2013, 1295, 34–43. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Kontokosta, C.E. Using city benchmarking data to grade buildings on energy performance. Appl. Energy 2019, 233, 244–253. [Google Scholar] [CrossRef]
- Ribeiro, D. Developments in local energy efficiency policy: A review of recent progress and research. Curr. Sustain./Renew. Energy Rep. 2018, 5, 109–115. [Google Scholar] [CrossRef]
- Gao, X.; Malkawi, A. A new methodology for building energy performance benchmarking: An approach based on intelligent clustering algorithm. Energy Build. 2014, 84, 607–616. [Google Scholar] [CrossRef]
- Hsu, D. Improving energy benchmarking with self-reported data. Build. Res. Inf. 2014, 42, 641–656. [Google Scholar] [CrossRef]
- Kontokosta, C.E. A market-specific methodology for a commercial building energy performance index. J. Real Estate Financ. Econ. 2015, 51, 288–316. [Google Scholar] [CrossRef]
- Scofield, J.H. Energy star building benchmarking scores: Good idea, bad science. In Proceedings of the ACEEE Summer Study on Energy Efficiency in Buildings, Pacific Grove, CA, USA, 17–22 August 2014; pp. 267–282. [Google Scholar]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Han, M.; Zhao, X. A review of data-driven approaches for predicting and classifying building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Benavente-Peces, C.; Ibadah, N. Buildings energy efficiency analysis and classification using various machine learning technique classifiers. Energies 2020, 13, 3497. [Google Scholar] [CrossRef]
- Habib, F.; Barzegar, Z.; Hasabani, M.G. Prioritization of Effective Building Energy Consumer Parameters by AHP Deployment. Naqshejahan 2014, 4, 47–53. [Google Scholar]
- Omrany, H.; Marsono, A. Optimization of Building Energy Performance through Passive Design Strategies. Br. J. Appl. Sci. Technol. 2016, 13, 1–16. [Google Scholar] [CrossRef]
- Manzan, M. Genetic optimization of external fixed shading devices. Energy Build. 2014, 72, 431–440. [Google Scholar] [CrossRef]
- Seyedzadeh, S.; Rahimian, F.P.; Glesk, I.; Roper, M. Machine learning for estimating building energy consumption and performance: A review. Vis. Eng. 2018, 6, 5. [Google Scholar] [CrossRef]
- Ahmadnejad, F.; Shahbazi, Y.; Mokhtari Keshavar, M.; Zendeh Laleh, M.; HosseinPour, S.; KhaliliKhoo, N. The Effect of Shader’s Type, Depth and Distance on Optimizing Daylight Autonomy in High Rise Buildings in Cold Climate. Int. J. Archit. Eng. Urban Plan. 2023, 33, 57–73. [Google Scholar] [CrossRef]
- Ghaffari, A.; Shahbazi, Y.; Mokhtari Kashavar, M.; Fotouhi, M.; Pedrammehr, S. Advanced Predictive Structural Health Monitoring in High-Rise Buildings Using Recurrent Neural Networks. Buildings 2024, 14, 3261. [Google Scholar] [CrossRef]
- Shahbazi, Y.; Abdkarimi, M.; Ahmadnejad, F.; Mokhtari Kashavar, M.; Fotouhi, M.; Pedrammehr, S. Comparative Study of Optimal Flat Double-Layer Space Structures with Diverse Geometries through Genetic Algorithm. Buildings 2024, 14, 2816. [Google Scholar] [CrossRef]
- Shahbazi, Y.; Ghofrani, M.; Pedrammehr, S. Aesthetic Assessment of Free-Form Space Structures Using Machine Learning Based on the Expert’s Experiences. Buildings 2023, 13, 2508. [Google Scholar] [CrossRef]
- Singaravel, S.; Suykens, J.; Geyer, P. Deep-learning neural-network architectures and methods: Using component-based models in building-design energy prediction. Adv. Eng. Inform. 2018, 38, 81–90. [Google Scholar] [CrossRef]
- Chou, J.-S.; Tran, D.-S. Forecasting energy consumption time series using machine learning techniques based on usage patterns of residential householders. Energy 2018, 165, 709–726. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Peng, X.; Zeng, F.; Lu, X. Conventional and artificial intelligence-based models for energy consumption forecasting: A review. J. Pet. Sci. Eng. 2019, 181, 106187. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting energy use in buildings using artificial neural networks: A review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef]
- Nie, P.; Roccotelli, M.; Fanti, M.P.; Ming, Z.; Li, Z. Prediction of home energy consumption based on gradient boosting regression tree. Energy Rep. 2021, 7, 1246–1255. [Google Scholar] [CrossRef]
- Khalil, M.; McGough, A.S.; Pourmirza, Z.; Pazhoohesh, M.; Walker, S. Machine Learning, Deep Learning and Statistical Analysis for forecasting building energy consumption—A systematic review. Eng. Appl. Artif. Intell. 2022, 115, 105287. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Owolabi, H.; Akanbi, L.; Ganiyu, S. Data-driven tools for building energy consumption prediction: A review. Energies 2023, 16, 2574. [Google Scholar] [CrossRef]
- Liu, H.; Liang, J.; Liu, Y.; Wu, H. A review of data-driven building energy prediction. Buildings 2023, 13, 532. [Google Scholar] [CrossRef]
- Guyot, D.; Giraud, F.; Simon, F.; Corgier, D.; Marvillet, C.; Tremeac, B. Overview of using artificial neural networks for energy-related applications in the building sector. Int. J. Energy Res. 2019, 43, 6680–6720. [Google Scholar]
- Lu, C.; Li, S.; Lu, Z. Building energy prediction using artificial neural networks: A literature survey. Energy Build. 2022, 262, 111718. [Google Scholar] [CrossRef]
- Afzal, S.; Ziapour, B.M.; Shokri, A.; Shakibi, H.; Sobhani, B. Building energy consumption prediction using multilayer perceptron neural network-assisted models; comparison of different optimization algorithms. Energy 2023, 282, 128446. [Google Scholar] [CrossRef]
- Tsoka, T.; Ye, X.; Chen, Y.; Gong, D.; Xia, X. Explainable artificial intelligence for building energy performance certificate labelling classification. J. Clean. Prod. 2022, 355, 131626. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Wefki, H. Predicting energy consumption for residential buildings using ANN through parametric modeling. Energy Rep. 2021, 7, 2534–2545. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Wefki, H.; Abdrabou, S.M.; Dawood, M.; Ramzy, A. Visualized strategy for predicting buildings energy consumption during early design stage using parametric analysis. J. Build. Eng. 2017, 13, 127–136. [Google Scholar] [CrossRef]
- Boumaraf, H.; İnceoglu, M. Computational analysis for design development evaluation in spatial planning. Eskişehir Tech. Univ. J. Sci. Technol. A-Appl. Sci. Eng. 2022, 23, 94–111. [Google Scholar] [CrossRef]
- LadybugTools. LadybugTools LLC. Available online: https://www.ladybug.tools/ (accessed on 1 July 2024).
- Food4Rhino. Available online: https://www.food4rhino.com/en/app/octopus (accessed on 10 July 2024).
- da Silva, M.A.; Garcia, R.d.P.; Carlo, J.C. Multi-objective optimization algorithms for building performance assessment—A benchmark. Int. J. Archit. Comput. 2024, 14780771241296263. [Google Scholar] [CrossRef]
- Demšar, J.; Curk, T.; Erjavec, A.; Gorup, C.; Hočevar, T.; Milutinovič, M.; Možina, M.; Polajnar, M.; Toplak, M.; Starič, A.; et al. Orange: Data Mining Toolbox in Python. J. Mach. Learn. Res. 2013, 14, 2349–2353. [Google Scholar]
- Ren, Z.; Tang, Z.; James, M. Predictive Weather Files for Building Energy Modelling User Guide; CSIRO: Canberra, Australia, 2021. [Google Scholar]
- Energyplus Weather Data. Available online: https://www.energyplus.net/weather (accessed on 2 July 2024).
- Abraham, A. Handbook of Measuring System Design; Sydenham, P.H., Thorn, R., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005; Available online: https://onlinelibrary.wiley.com/doi/epdf/10.1002/0471497398.mm421 (accessed on 2 July 2024).
- Zhang, G.; Patuwo, B.E.; Hu, M.Y. Forecasting with artificial neural networks: The state of the art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef]
- Trzepieciński, T. The comparison of the multi-layer artificial neural network training methods in terms of the predictive quality of the coefficient of friction of 1.0338 (DC04) Steel Sheet. Materials 2024, 17, 908. [Google Scholar] [CrossRef]
- Kalinić, Z.; Marinković, V.; Kalinić, L.; Liébana-Cabanillas, F.J. Neural network modeling of consumer satisfaction in mobile commerce: An empirical analysis. Expert Syst. Appl. 2021, 175, 114803. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- ISIRI 14253; Residential Building—Criteria for Energy Consumption and Energy Labeling Instruction. Institute of Standards Islamic Republic of Iran: Tehran, Iran, 2011.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).