Probabilistic Prediction Model for Ultimate Conditions Under Compression of FRP-Wrapped Concrete Columns Based on Bayesian Inference

Abstract

The compressive strength and ultimate strain of FRP-confined concrete cylinders are the key indicators for evaluating their mechanical properties. Accurate prediction of compressive strength and ultimate strain is essential for reliability analysis and design of such components. However, the existing ultimate condition under compression models lack sufficient prediction accuracy, and the results exhibit significant uncertainty. This study proposes a Bayesian model updating method based on Markov Chain Monte Carlo (MCMC) sampling to improve the prediction accuracy of the ultimate condition under compression for FRP-confined concrete cylinders and to quantify the uncertainty of the prediction results. First of all, 1016 sets of experimental data on the ultimate condition under compression of FRP-confined concrete cylinders from previous studies were collected. Subsequently, the probabilistic updating model and evaluation system were established based on Bayesian parameter estimation principle, MCMC sampling, WAIC, and DIC. Then, several representative empirical models for predicting the ultimate condition under compression are selected, and their prediction performance is evaluated using the experimental data. Finally, a Bayesian updating problem is established for typical ultimate condition under compression models, and the posterior distributions of model parameters are obtained using MCMC sampling to select the best model, and the prediction performance of the optimal model is assessed using the experimental data. The results show that, compared with existing empirical models, the Bayesian inference-based probabilistic calculation model provides predictions closer to the experimental values, while also reasonably quantifying the uncertainty of the ultimate condition under compression prediction.

1. Introduction

Reinforced concrete (RC) structures are inevitably affected by long-term loading and continuous environmental degradation during their service life, which can impair their mechanical properties. To ensure the overall safety of building structures, strengthening RC structures is crucial. Fiber-reinforced polymer (FRP) is a high-performance composite material composed of fiber reinforcement and a synthetic resin matrix. It possesses characteristics such as high strength, light weight, corrosion resistance, and ease of construction, making it widely used in the construction, retrofitting, and repair of civil engineering structures [1,2,3]. Studies have shown that lateral pressure can effectively constrain the circumferential expansion deformation of concrete. FRP-confined concrete cylinders utilize the high strength and high elastic modulus of FRP materials to subject the concrete to triaxial compression, thereby improving both the strength and ductility of the concrete [4]. Extensive experimental and theoretical research [5,6,7] has confirmed that FRP-confined concrete technology (including FRP wrapping and FRP tube confinement for concrete enhancement) can effectively improve the durability, safety, and mechanical performance of structures, and extend their service life. This technology has demonstrated excellent potential for structural reinforcement and other applications involving FRP-confined concrete.

The ultimate condition under compression typically refers to the state corresponding to the maximum axial compressive load that a concrete component can withstand. It reflects the bearing capacity and the changes in the mechanical behavior of the concrete component before failure. Researchers commonly use two core parameters, namely the ultimate compressive strength and the ultimate compressive strain, to describe the ultimate condition under compression of concrete components. However, due to the significant increase in strength and ultimate strain resulting from the confinement reinforcement provided by FRP materials, the mechanical behavior and ultimate condition under compression of FRP-confined concrete undergo significant changes under loading, and the ductility of FRP-confined concrete shows a significant improvement [8]. Zeng et al. [8] conducted an experimental study on the stress–strain behavior of polyethylene terephthalate (PET) fiber-reinforced polymer (FRP)-confined normal-strength, high-strength, and ultra-high-strength concrete. The results demonstrated that high- and ultra-high-strength concrete confined with PET FRP exhibited strain hardening–softening–hardening behavior. Lim and Ozbakkaloglu [9] found that concrete age has a minimal effect on the compressive strength and strain of FRP-confined concrete, with slight reductions observed as concrete ages beyond 28 days. Liao et al. [10] investigated the compressive behavior of ultra-high-performance concrete (UHPC) confined with FRP. Their study found that the addition of steel fibers significantly enhanced the first peak stress and ultimate strain, improving confinement efficiency and ductility. The research also highlighted the importance of FRP thickness, specimen size, and steel fiber content in determining the stress–strain response of FRP-confined UHPC. In addition, the mechanical behavior of FRP-confined concrete columns with different shapes varies. Zeng et al. [11] investigated the axial compression behavior of PET FRP-confined concrete in square stub columns by considering the effects of confinement thickness, corner radius, and specimen size. Their results showed that increasing the corner radius improves the uniformity of the confinement pressure, enhancing the concrete’s ultimate strength. Ye et al. [12] conducted a review of FRP-confined steel-reinforced concrete (FCSRC) structural members, with a focus on the effects of FRP tube shape. The results showed that square and rectangular FRP tubes are less efficient in confining concrete compared to circular tubes, particularly at the flat sides, which reduces their confinement effectiveness in practical applications. However, existing models struggle to accurately capture the stress reduction phenomenon [13]. To ensure structural safety and the rationality of design, it is necessary to specifically predict the behavior of FRP-confined concrete.

The main issue in the research on FRP-confined concrete cylinders is how to improve the overall mechanical performance of concrete cylinders, specifically, how to accurately predict their compressive strength and ultimate strain. To accurately predict their compressive strength and ultimate strain, many different stress–strain models have been developed. Early studies on FRP-confined concrete stress–strain models typically used steel-confined concrete models to analyze the mechanical behavior of FRP-confined concrete cylinders under axial loads. However, due to the differences in the mechanical properties between steel and FRP materials, this model could not accurately reflect the stress–strain characteristic [14,15,16]. Subsequently, researchers proposed calculation formulas for the ultimate compressive strength, ultimate strain at concrete failure, and stress–strain curves of FRP-confined concrete cylinders, based on studies of GFRP (glass fiber-reinforced polymer) and CFRP (carbon fiber-reinforced polymer). They established stress–strain models for FRP-confined concrete cylinders and identified the main factors affecting the mechanical properties of FRP-confined concrete cylinders, including the circumferential fracture strain of FRP materials, FRP material parameters, the ultimate stress of the core concrete, and the geometric parameters of the cross-section [17]. Furthermore, some studies have proposed calculation formulas for the peak stress, peak strain, ultimate stress, and ultimate strain of FRP-confined concrete cylinders with softening segments, along with corresponding models [18].

FRP-confined concrete stress–strain models are generally divided into three categories: empirical models obtained through regression analysis of experimental data, theoretical models derived from mechanical principles, and design-oriented models. Many existing models are empirical models established through regression analysis, fitting, and the simplification of experimental data. The initial compressive strength model is similar to the empirical model for the compressive strength of FRP-confined concrete proposed by Richart [19] in 1929. Although subsequent models differ in form, their mathematical essence is similar, and the calculation results are relatively stable. However, these models are all based on the fitting of experimental data, and their results represent point estimates for specific parameters, which may have some degree of deviation from the actual ultimate condition under compression. Therefore, the accuracy and completeness of the experimental data play a critical role in the establishment of the model. Additionally, in axial compression tests of FRP-confined concrete cylinders, due to variations in FRP materials, measurement errors, estimation errors, and changes in environmental conditions, it is impossible to precisely predict the ultimate condition under compression of FRP-confined concrete cylinders, and the prediction results exhibit significant uncertainty. These uncertainties are propagated through the model parameter identification process, leading to uncertain model predictions. Consequently, it is necessary to consider these uncertainties through identification of probabilistic parameters. For example, prior probability distributions can be assigned to measurement errors and model parameters, and their posterior probability distributions can be identified through Bayesian inference to quantify the uncertainty in model predictions.

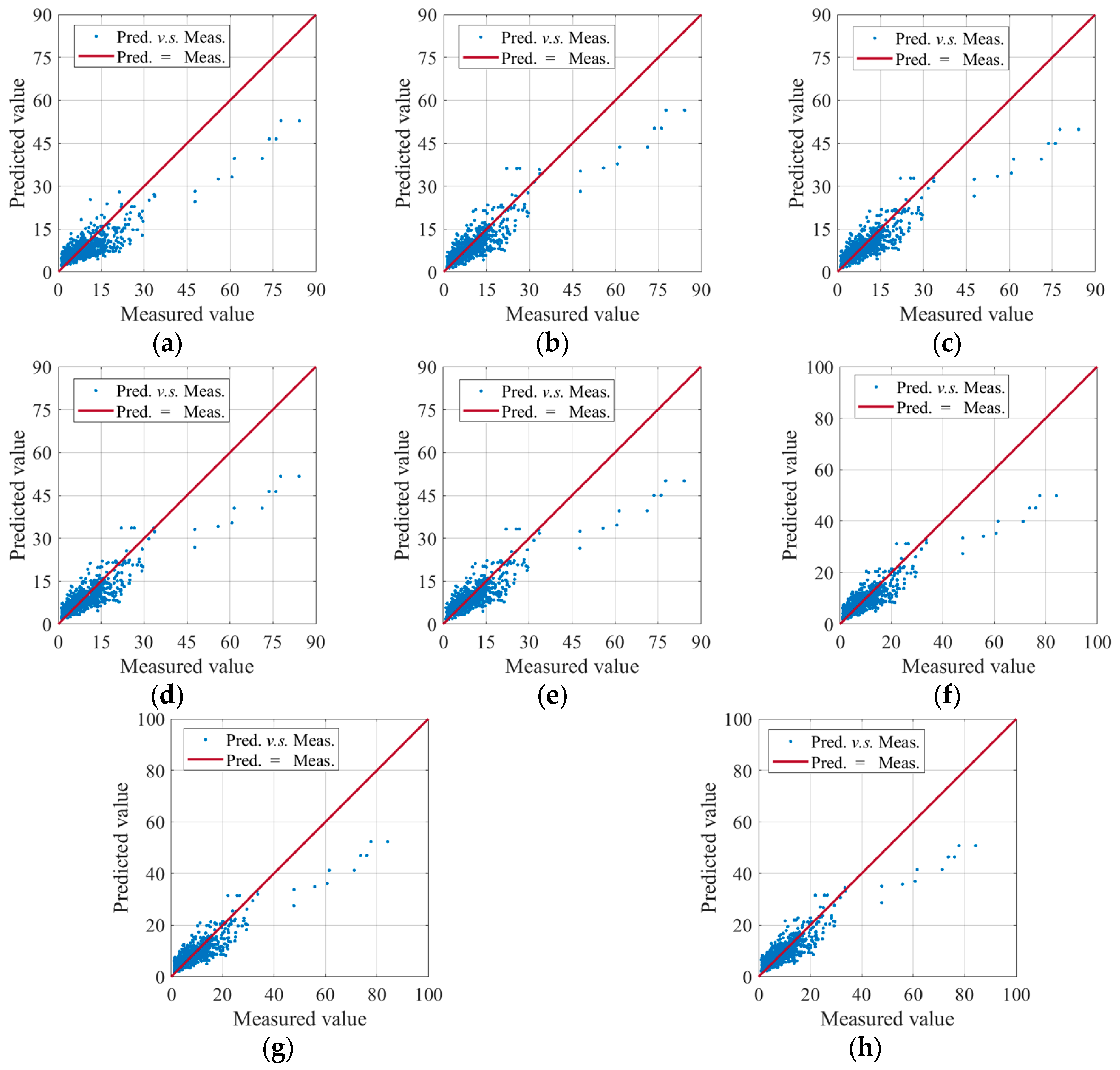
Currently, many researchers have proposed various stress–strain models for FRP-confined concrete cylinders from different perspectives, achieving varying degrees of progress in prediction accuracy. Researchers have conducted experimental studies by controlling different variables and proposed new predictive models for forecasting the compressive strength and ultimate strain of FRP-confined concrete cylinders. However, comprehensive integration and unification of existing data are rarely performed, which limits the applicability of the current models. Furthermore, most existing models are data-driven. While they offer better prediction accuracy compared to traditional models, they are still based on a limited set of experimental data. These models often involve complex or uncertain information, with some parameters needing to be derived from empirical data, making them difficult to obtain through simplified calculation methods. These models are typically expressed in complex or undefined forms, and certain parameters require intricate computational methods, which are not easily obtained through experimentation. Both traditional models and data-driven models are deterministic models, where the predicted compressive strength and ultimate strain of FRP-confined concrete cylinders are given as single values. This overlooks the uncertain relationship between the model inputs and outputs under various unforeseen conditions and fails to reasonably quantify the uncertainty of the prediction results, which does not align with the practical application in engineering.

Bayesian inference has been proven to effectively quantify uncertainty by calculating the posterior distribution. Most of the existing predictive models are empirical formulas developed based on experimental data. These empirical formulas often fail to account for the influence of objective parameters, such as specimen size and fiber type, resulting in limited applicability. This study applies Bayesian inference to calibrate existing models, thereby improving their applicability and prediction accuracy. The results show that the Bayesian method cleverly combines prior information (subjective information) and test data (objective information) to infer the posterior distribution of model parameters. Probability density functions are used to represent parameter estimates, yielding statistical quantities such as mean, variance, and confidence intervals, which better predict the structural performance under load [13]. Moreover, the research results demonstrate that the probability model corrected through Bayesian inference significantly improves the prediction accuracy. It enhances the prediction accuracy of the compressive ultimate condition and the rationality of design decisions for FRP-confined concrete cylinders. The findings can provide a useful reference for engineering applications and future research.

2. Collection of Experimental Data

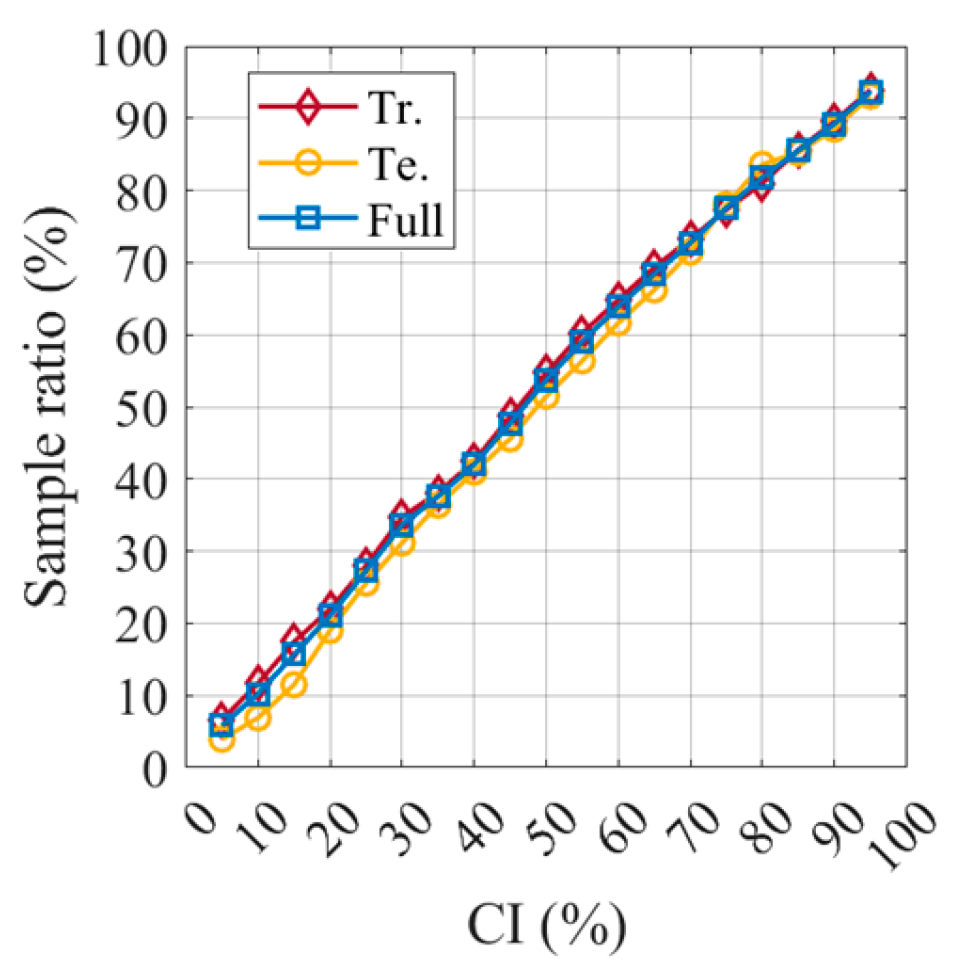
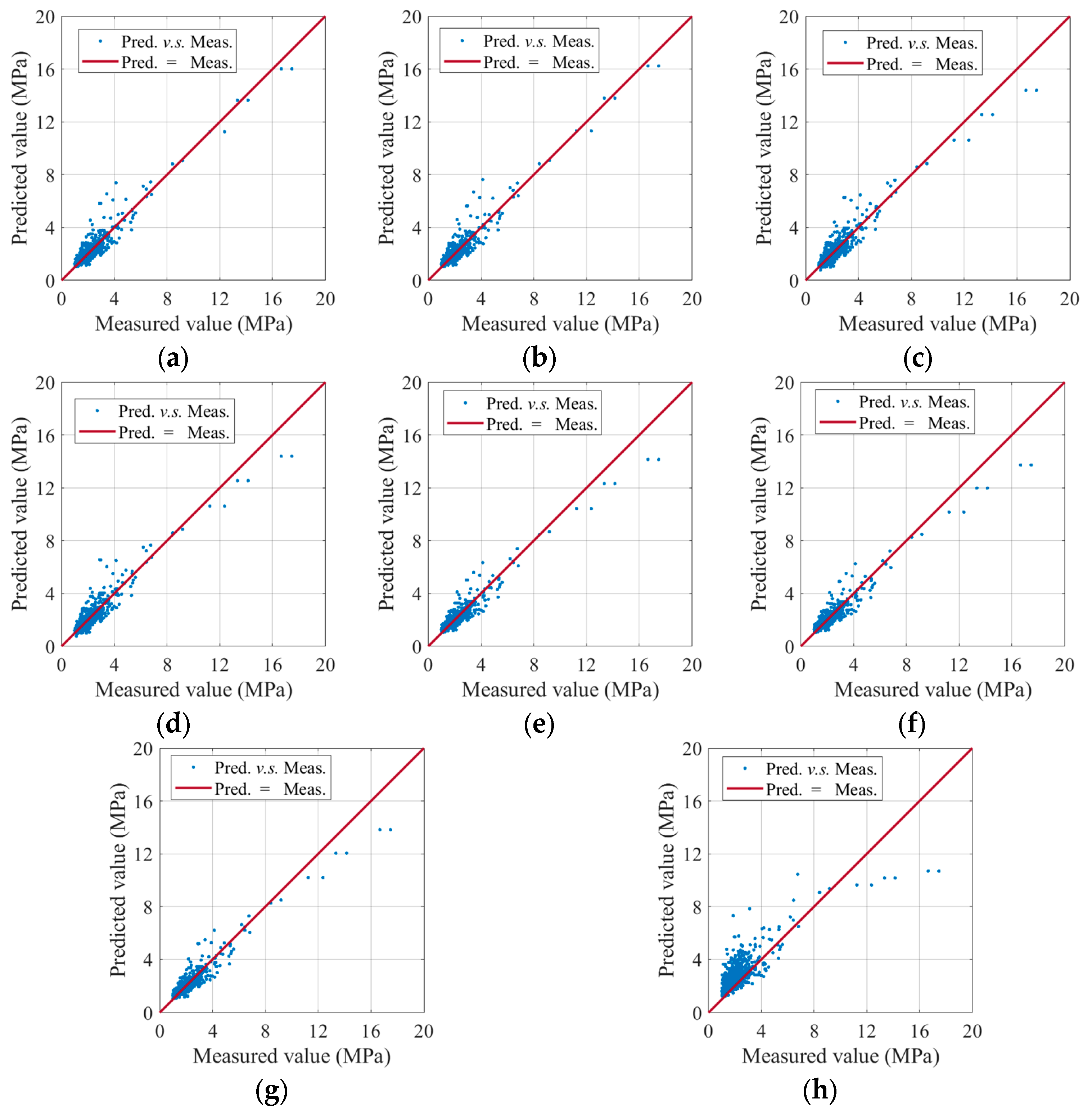
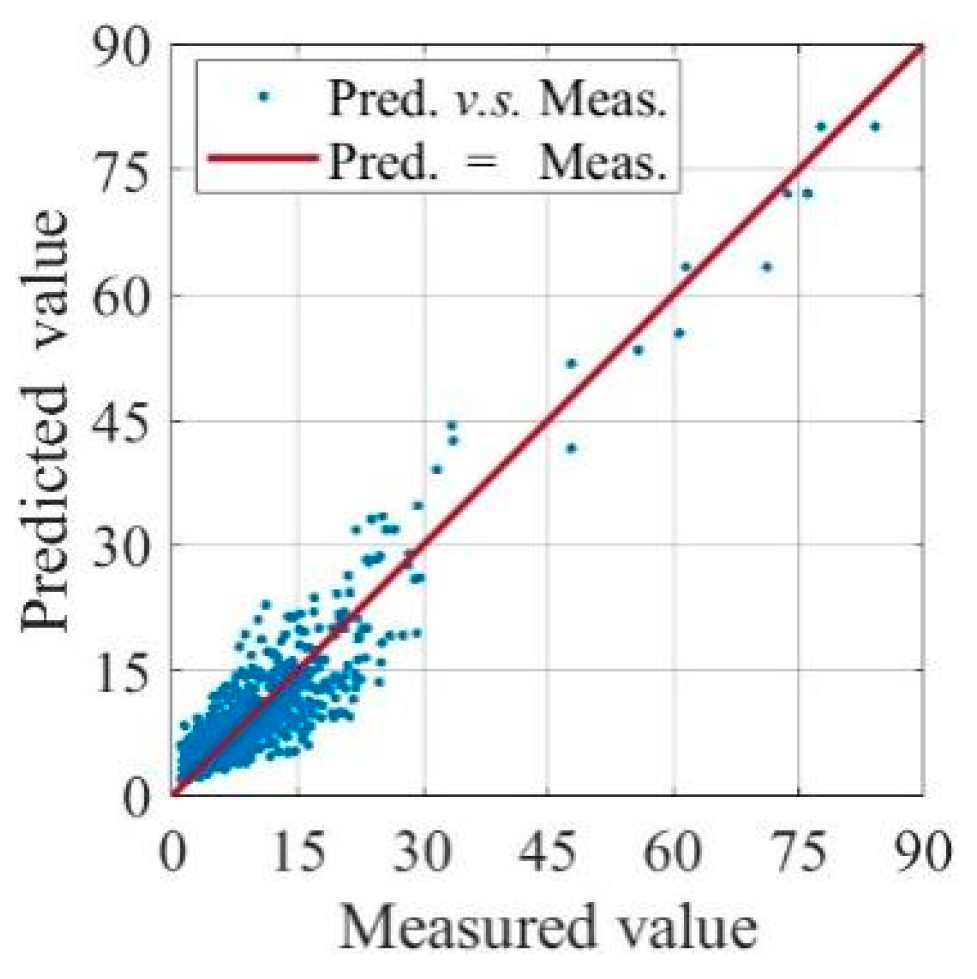
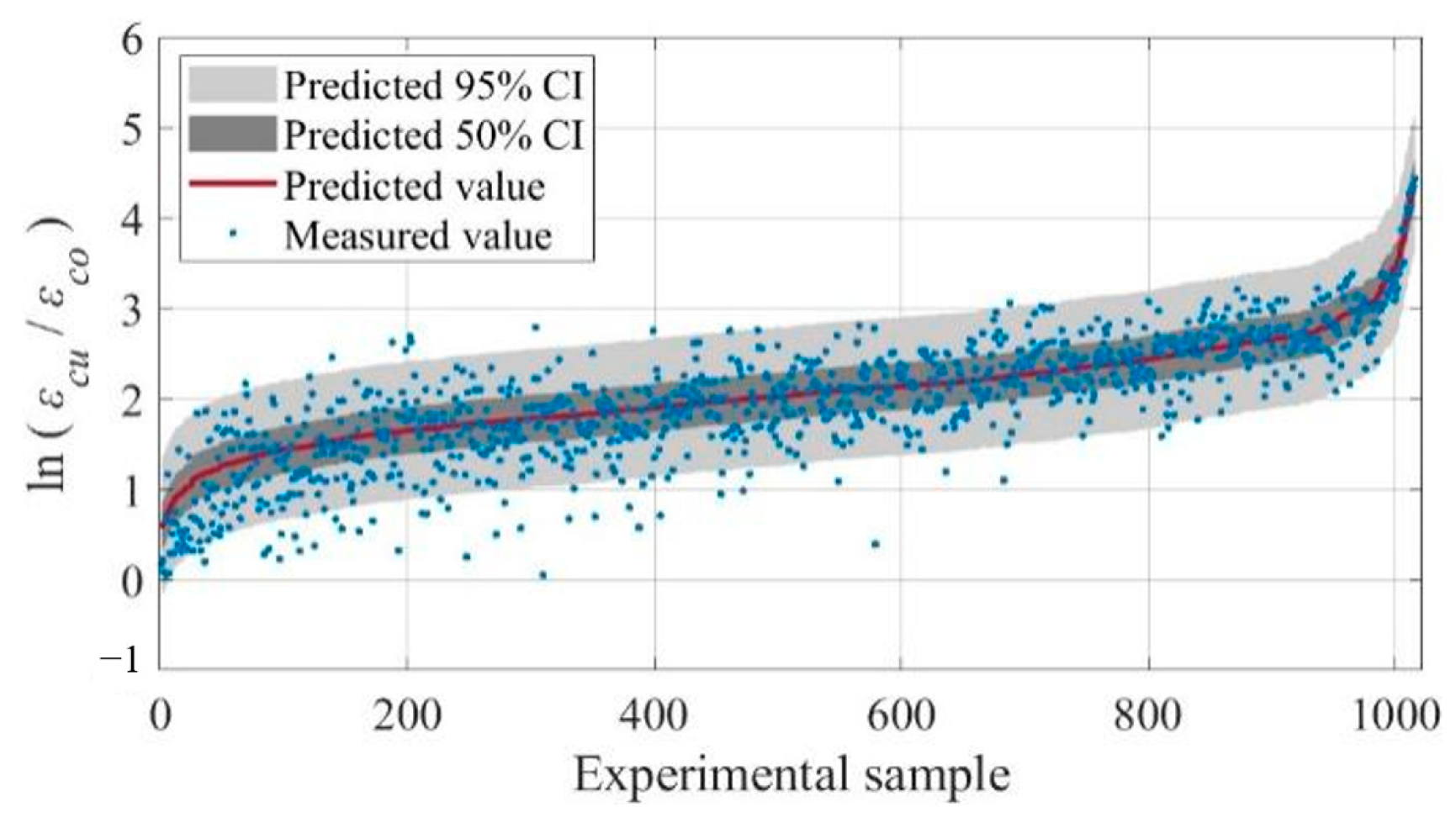
Many studies have conducted uniaxial compression tests on FRP-confined circular concrete cylinders. This study extensively surveys the existing literature and collects 1016 sets of experimental samples on the ultimate condition under compression of FRP-confined circular concrete cylinders [9,15,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91]. Each data set includes the following information: the diameter of the concrete cylinder $D$; the axial compressive strength of the unconfined concrete cylinder $f_{co}^{\prime }$; the axial compressive strength of the FRP-confined concrete cylinder $f_{cc}^{\prime }$; the axial strain of the unconfined concrete cylinder ${\epsilon }_{c0}$; the ultimate strain of the FRP-confined circular concrete cylinder ${\epsilon }_{cu}$; the total thickness of the FRP material $t_f$; the elastic modulus of the FRP material $E_f$; and the circumferential fracture strain of the FRP material ${\epsilon }_{h,rup}$. Furthermore, the collected experimental samples encompass various types of FRP materials, including CFRP, AFRP, BFRP, and GFRP.

The database in this study includes only unreinforced concrete specimens, excluding those with internal transverse or longitudinal reinforcement and those using fully wrapped FRP materials. Specimens with a length-to-diameter ratio greater than three were also excluded. The compressive strength of the unconfined concrete in the specimen ranges from 6.2 to 188.2 MPa, covering some high-strength concrete data. All specimens failed due to the rupture of the FRP material, and specimens that failed prematurely due to other reasons (such as loss of adhesion of the FRP material or excessive eccentricity) were excluded. The loading form applied was concentric axial load, excluding specimens subjected to eccentric or lateral loads. Specimens that failed to accurately record experimental results due to equipment, instrument errors, or insufficient material geometric properties were also excluded.

Table 1. Statistical characteristics of the dataset.

Parameter	Unit	Minimum Value	Maximum Value	Average Value	Standard Deviation	Types of Data
$D$	mm	47.00	406.40	158.28	56.74	Design variables
$f_{co}^{\prime }$	MPa	6.20	188.20	45.75	26.46	Design variables
${\mathit{\epsilon }}_{c0}$	%	0.14	0.70	0.25	0.05	Design variables
$E_f$	GPa	10.30	663.00	170.03	115.29	Design variables
$t_f$	mm	0.06	15.00	0.91	1.23	Design variables
${\epsilon }_{h,rup}$	%	0.10	4.98	1.29	0.64	Design variables
$f_{cc}^{\prime }$	MPa	17.80	372.20	85.50	42.55	Compressive strength

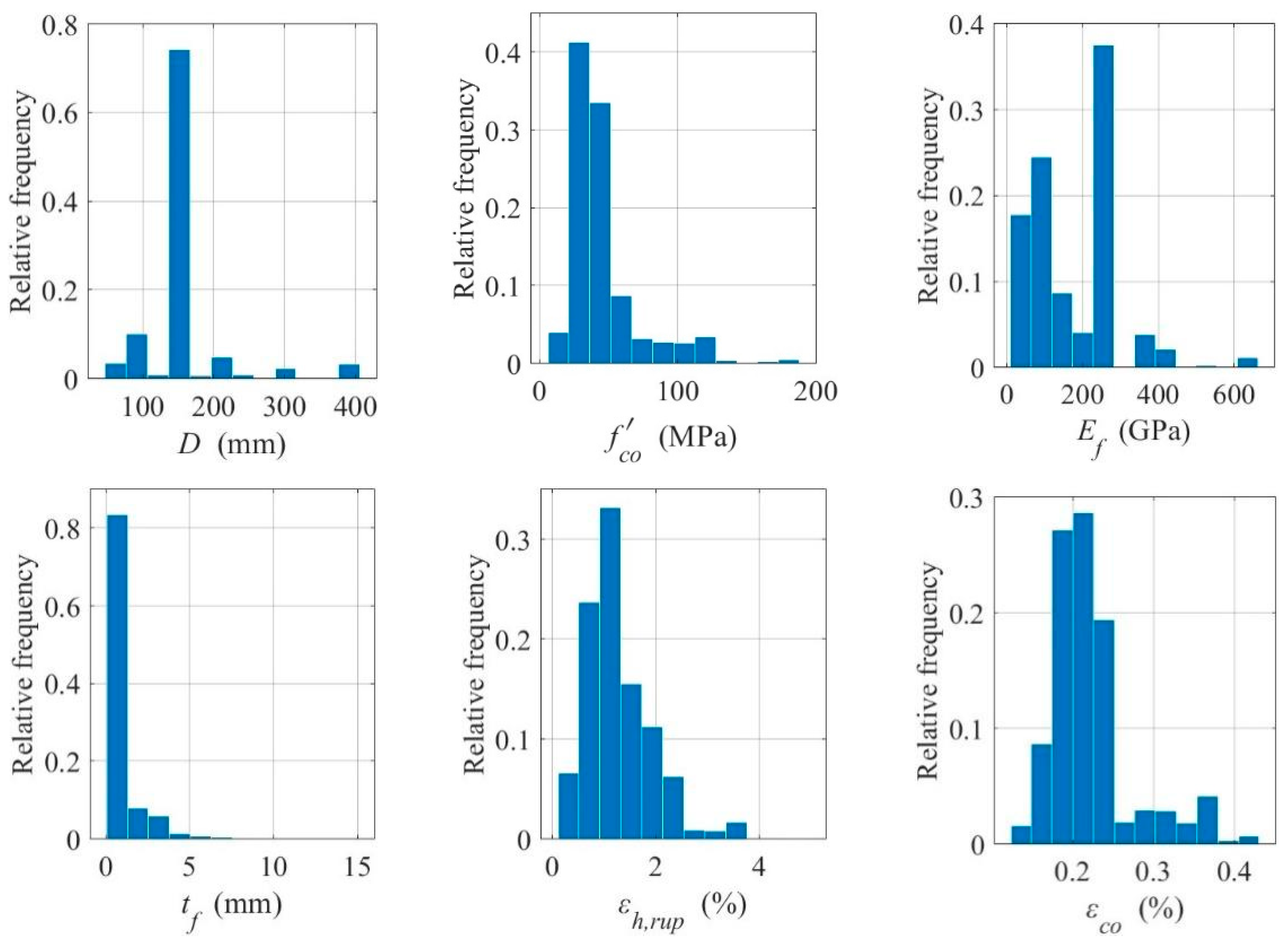
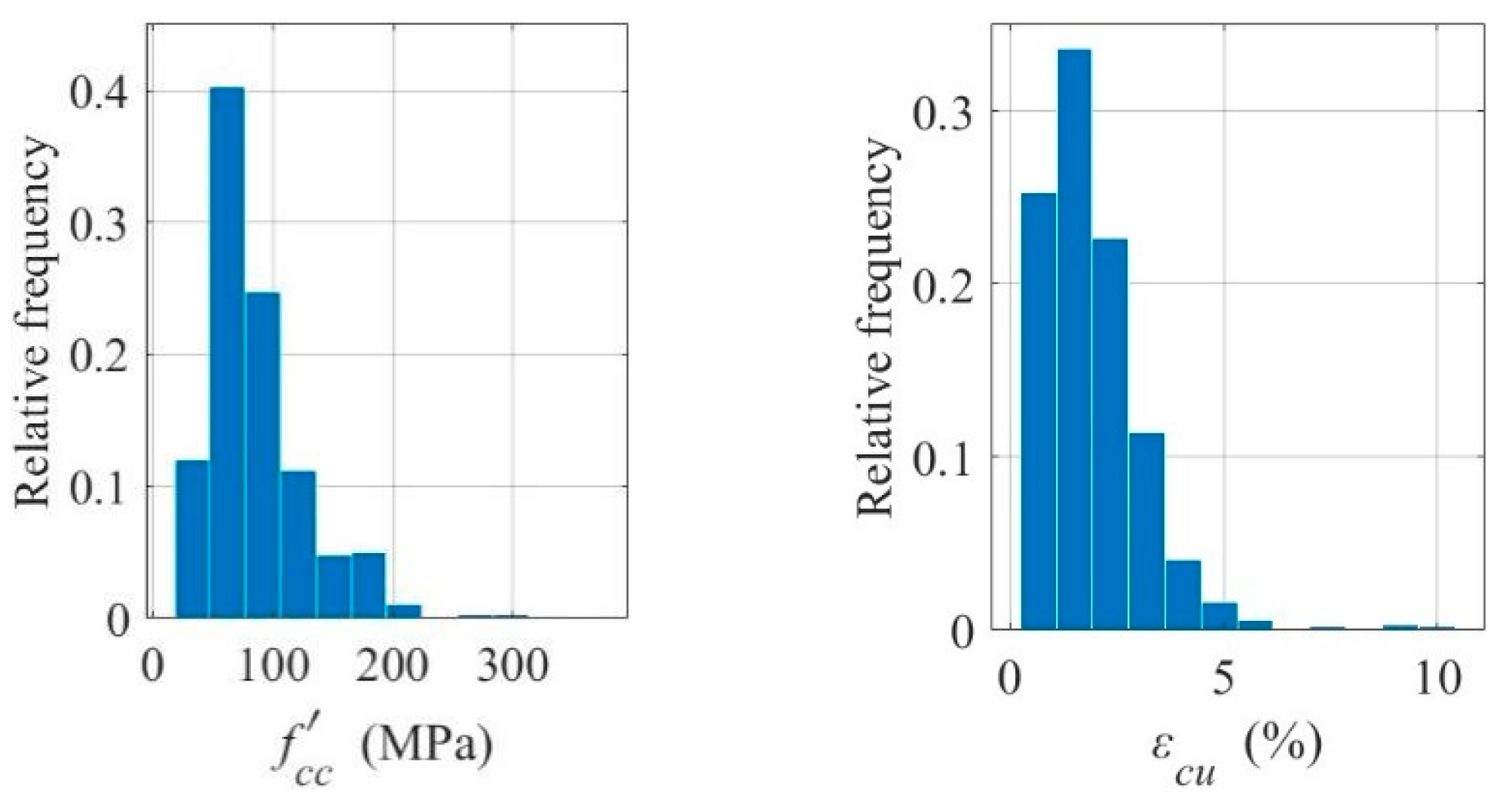
presents the statistical information of the experimental database collected in this study. Figure 1 and Figure 2 show the frequency distribution histograms of the relevant design variables and test variables. As seen from Table 1 and Figure 1 and Figure 2, the design variables included in the current database (such as geometric dimensions and mechanical properties) cover a wide range, indicating its substantial representativeness. In terms of geometric dimensions, the cylinder diameter ranges from 47 to 406.4 mm, and the thickness of the FRP material ranges from 0.06 to 15 mm. Regarding mechanical properties, the elastic modulus of the FRP material ranges from 10.3 to 663 GPa, the compressive strength of unconfined concrete cylinders ranges from 6.21 to 188.2 MPa, and the ultimate strain of unconfined concrete cylinders ranges from 0.12% to 0.43%. Therefore, evaluating compressive strength and ultimate strain based on this database is appropriate, and this database can also be used for probabilistic calibration of models and uncertainty quantification studies.

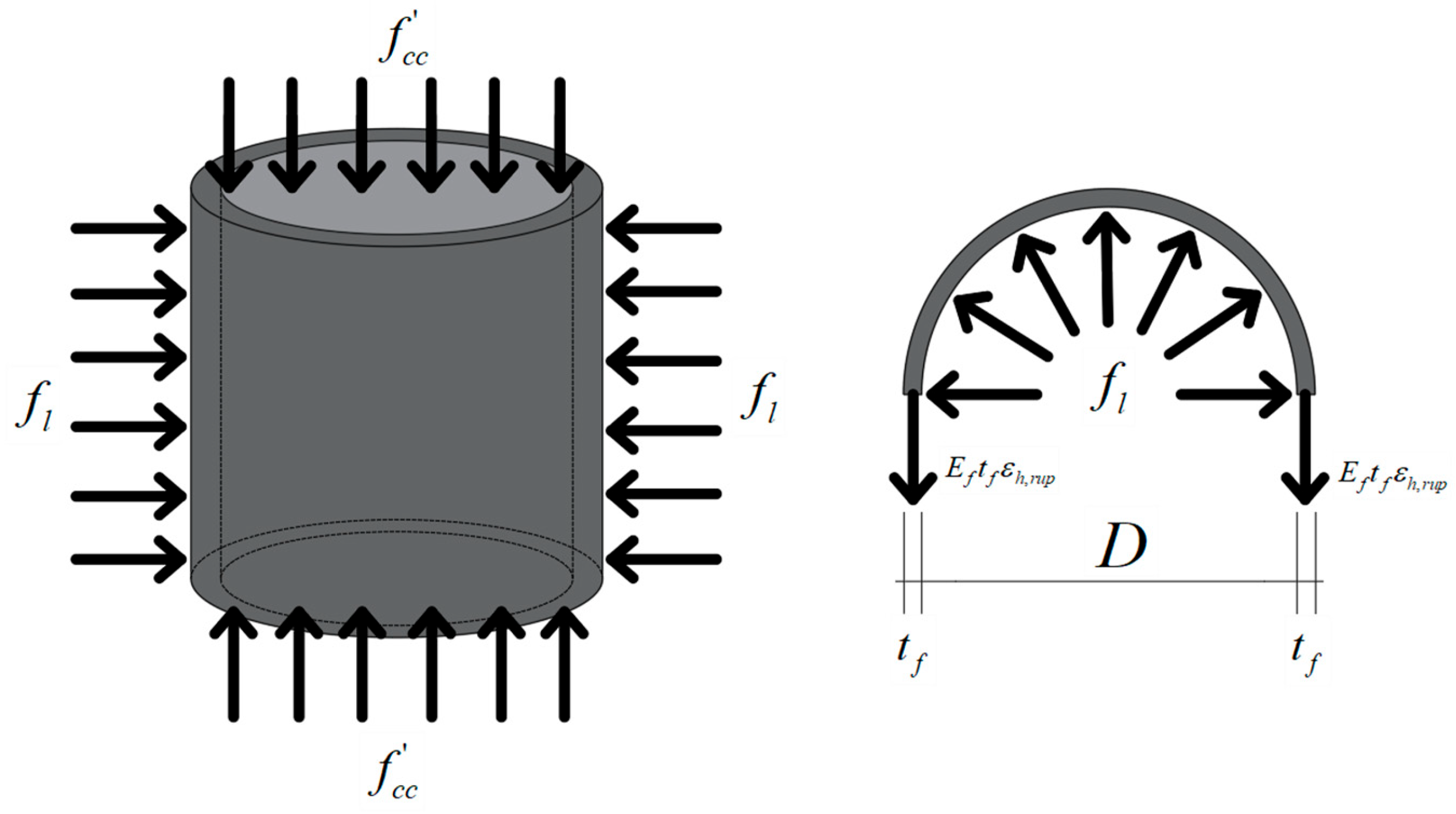
FRP-confined concrete cylinders provide confinement to the internal concrete through the circumferential load applied by the external FRP material, thereby enhancing the overall mechanical performance of the concrete cylinder. Figure 3 illustrates the confinement mechanism of FRP-confined concrete. Scholars around the world have proposed numerous studies on the compressive strength-bearing models for FRP-confined circular concrete cylinders. Existing strength models define several commonly used parameters, including the maximum confinement stress $f_l$, confinement stiffness ratio ${\rho }_k$, and ratio of strain ${\rho }_{\epsilon }$, where ${\rho }_k$ represents the stiffness of the FRP material relative to the core concrete, and ${\rho }_{\epsilon }$ is a measure of the strain capacity of the FRP material. These two parameters were introduced by Teng et al. [92]. Additionally, Keshtegar [93] introduced the lateral stiffness ${\rho }_E$ and area ratio ${\rho }_a$.

Table 2. Mathematical expressions of commonly used parameters in existing models.

Parameters	Displayed Formula
Maximum confinement stress $f_l$	$f_l={\rho }_k{\rho }_{\epsilon }{\displaystyle f_{co}^{\prime }}={\displaystyle \frac{2E_f{t}_f{\epsilon }_{h,rup}}{D}}$
Confinement stiffness ratio ${\rho }_k$	${\rho }_k={\displaystyle \frac{2E_f{t}_f}{\left(f_{co}^{\prime }/{\epsilon }_{co}\right)D}}$
Ratio of strain ${\rho }_{\epsilon }$	${\rho }_{\epsilon }={\displaystyle \frac{{\epsilon }_{h,rup}}{{\epsilon }_{co}}}$
Lateral stiffness ${\rho }_E$	${\rho }_E={\displaystyle \frac{2E_f}{f_{co}^{\prime }/{\epsilon }_{co}}}$
Area ratio ${\rho }_a$	${\rho }_a={\displaystyle \frac{t_f}{D}}$

lists the expressions for these commonly used parameters, where $D$ is the diameter of the circular concrete cylinder, $f_{co}^{\prime }$ is the axial compressive strength of the unconfined concrete cylinder, $f_{cc}^{\prime }$ is the axial compressive strength of the FRP-confined circular concrete cylinder, ${\epsilon }_{c0}$ is the axial strain of the unconfined concrete cylinder, ${\epsilon }_{cu}$ is the ultimate strain of the FRP-confined circular concrete cylinder, $t_f$ is the total thickness of the FRP material, $E_f$ is the elastic modulus of the FRP material, and ${\epsilon }_{h,rup}$ is the circumferential fracture strain of the FRP material.

As shown in the expressions listed in Table 2, the commonly used composite variables in these models are typically formed by a combination of the mechanical properties of the FRP material and the confined concrete, along with the diameter of the concrete. Therefore, these composite variables can also be statistically analyzed using the combination of existing data to determine whether the collected data can be used to evaluate the current ultimate condition prediction models. The confinement ratio $f_l$/$f_{co}^{\prime }$ is a commonly used parameter in existing compressive strength models and is equal to the product of the confinement stiffness ratio ${\rho }_k$ and the ratio of strain ${\rho }_{\epsilon }$. According to the study by Teng et al. [92], the approximate value of 0.002 should not be used to calculate the confinement ratio. Instead, it should be calculated using the following formula (where $f_{co}^{\prime }$ is in MPa):

$${\epsilon }_{co}=9.37\times {10}^{-4}\sqrt[4]{f_{co}^{\prime }}$$

(1)

The statistical information of the commonly used composite parameters in the model is listed in

Table 3. Statistical information of commonly used composite parameters of models.

Parameter	Unit	Minimum Value	Maximum Value	Average Value	Standard Deviation
${\rho }_k$	0.005	0.605	0.064	0.063	Design variables
${\rho }_{\epsilon }$	0.464	26.946	6.096	3.315	Design variables
${\rho }_a$	0.0006	0.099	0.0057	0.0075	Design variables
${\rho }_E$	1.190	91.689	19.745	16.021	Design variables
$f_{cc}^{\prime }/f_{co}^{\prime }$	1.0058	17.468	2.099	1.268	Ratio of strength enhancement
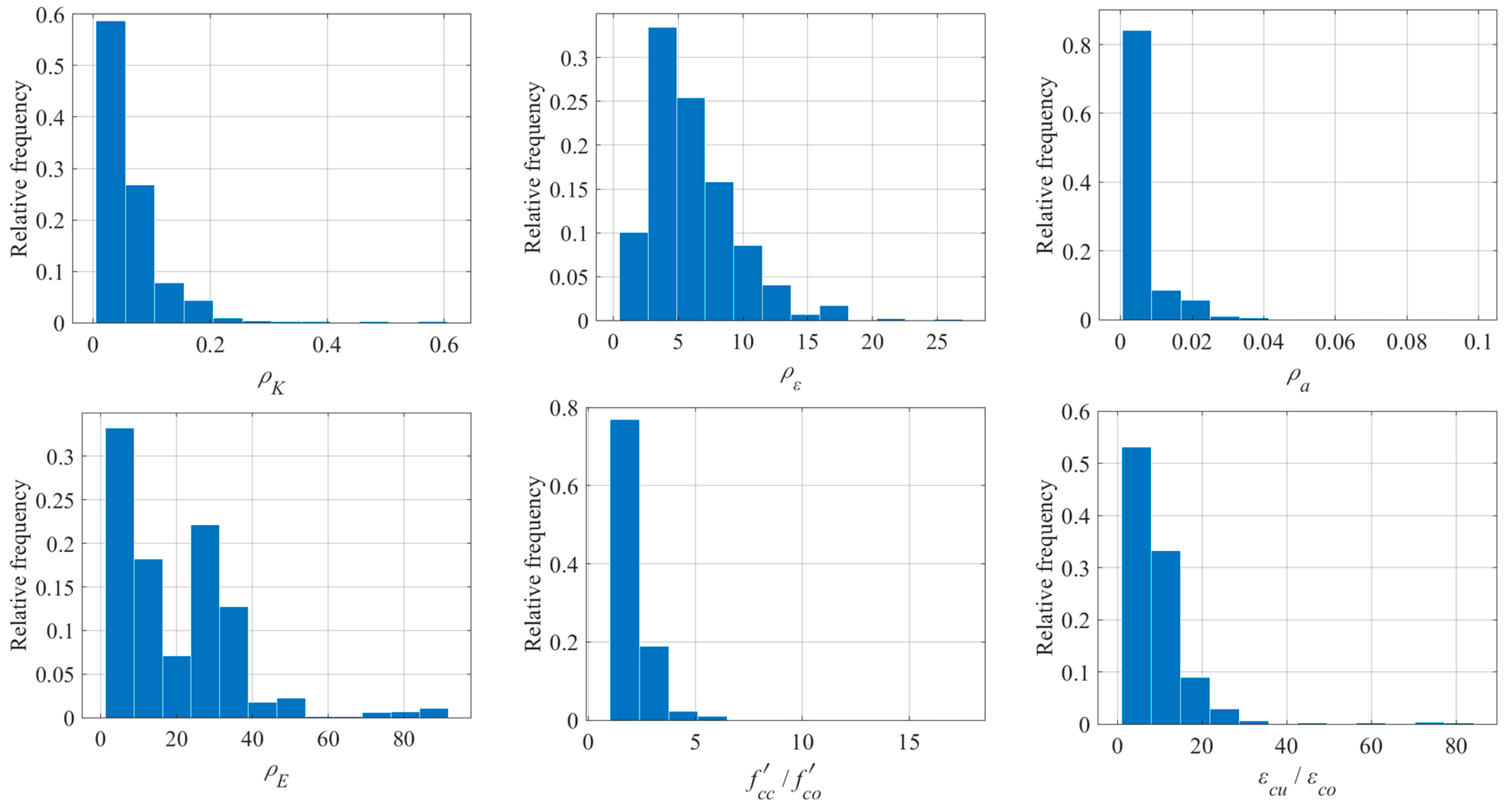
${\epsilon }_{cu}/{\epsilon }_{co}$	1.055	84.156	9.301	7.966	Ratio of strain enhancement

. The table shows that the range of composite design variables in the database is wide, including the confinement stiffness ratio, ratio of strain, area ratio, and confinement stiffness, with ranges of 0.005 to 0.605, 0.464 to 26.946, 0.0006 to 0.099, and 1.190 to 91.689, respectively. The output variables, strength enhancement ratio and strain enhancement ratio, have ranges of 100.58% to 1746.8% and 105.5% to 8415.6%, respectively. It is evident that, after reinforcement with FRP materials, both the strength and ultimate strain of the concrete cylinders have increased to varying extents, indicating that FRP confinement can effectively improve the mechanical properties of the core concrete cylinders. Figure 4 presents the frequency distribution of each composite design variable.

3. Methodology

3.1. Bayesian Parameter Estimation

When performing reliable design of FRP-confined concrete cylinders, most existing models are deterministic, and the prediction results have significant uncertainty. Therefore, it is necessary to develop corresponding probabilistic models, which can typically be expressed by the following equation

$$y=M\left(\mathit{x},\mathit{\theta }\right)+\epsilon$$

(2)

where $y$ represents the output variable; $x=\left(x_1,x_2,\dots \right)$ denotes the corresponding input variable; $M\left(x,\theta \right)$ represents the model prediction term; $\theta$ indicates the parameter vector to be identified; and $\epsilon$ represents the error term, which is caused by various measurement errors. It is typically assumed that $\epsilon$ follows a Gaussian distribution with a mean of 0 and a variance of ${\sigma }^2$.

When applying the above model, several assumptions must be made. In this study, the assumptions of additivity, homoscedasticity, and normality are adopted, implying that the error term is additive, has a constant variance independent of the variables, and follows a normal distribution [94,95,96]. A probabilistic model for the ultimate condition under compression of FRP-confined concrete cylinders can be established by treating the parameters in the model expression $M\left(x,\theta \right)$ as random variables that follow specific probability distributions. Accordingly, the first step is to determine the probability distributions of the model parameters, based on which the probability distribution of the output variable can be predicted.

In the theory of Bayesian inference, unknown parameters are treated as random variables, and probability distributions are used to represent prior assumptions about the parameters before observing the data. This probability distribution is referred to as the prior distribution. By incorporating observed data, our knowledge of the parameters can be updated, resulting in the posterior distribution. In this way, a more accurate inference of the parameter values can be achieved. Given a dataset $\mathcal{D}=\left\{\left(x^{\left(i\right)},y^{\left(i\right)}\right),i=1,2,\dots ,N_e\right\}$ consisting of $N_e$ experimental observations, the posterior probability distribution of the model parameter $\theta$ can be calculated using Bayes’ theorem [97], as follows

$$p\left(\mathit{\theta }\left|\mathcal{D},\mathcal{M}\right.\right)={\displaystyle \frac{p\left(\mathcal{D}\left|\mathit{\theta },\mathcal{M}\right.\right)p\left(\mathit{\theta }\left|\mathcal{M}\right.\right)}{p\left(\mathcal{D}\left|\mathcal{M}\right.\right)}}$$

(3)

where $\mathit{\theta }=\left({\theta }_1,{\theta }_2,\dots ,{\theta }_d\right)$ denotes the vector of model parameters; $\mathcal{M}$ represents the deterministic compressive strength model; $p\left(\mathit{\theta }\left|\mathcal{M}\right.\right)$ is the prior probability distribution of the model parameters; $p\left(\mathit{\theta }\left|\mathcal{D},\mathcal{M}\right.\right)$ is the posterior probability distribution of the model parameters; $p\left(\mathcal{D}\left|\mathit{\theta },\mathcal{M}\right.\right)$ is the likelihood function of the model parameters given the experimental data $\mathcal{D}$; and $p\left(\mathcal{D}\left|\mathcal{M}\right.\right)$ is the Bayesian evidence (also known as the marginal likelihood).

The posterior probability distribution of the parameter $\theta$ is proportional to the product of the likelihood function and the prior probability distribution. This proportional relationship implies that the posterior distribution $p\left(\mathit{\theta }\left|\mathcal{D},\mathcal{M}\right.\right)$ can still be obtained by multiplying the likelihood function $p\left(\mathcal{D}\left|\mathit{\theta },\mathcal{M}\right.\right)$ with the prior distribution $p\left(\mathit{\theta }\left|\mathcal{M}\right.\right)$ [98,99], as expressed by

$$p\left(\mathit{\theta }\left|\mathcal{D},\mathcal{M}\right.\right)\propto p\left(\mathcal{D}\left|\mathit{\theta },\mathcal{M}\right.\right)p\left(\mathit{\theta }\left|\mathcal{M}\right.\right)$$

(4)

In the Bayesian framework, the posterior probability distribution represents the updated probability distribution of the model parameters based on newly acquired information from observed data. However, this approach has certain limitations. For instance, it is often difficult to compute the likelihood function and the normalization constant of the posterior distribution. As a result, directly solving high-dimensional integrals to obtain the posterior probability density of the parameters is generally infeasible. To address this issue, the Markov Chain Monte Carlo (MCMC) method [97] is widely employed to estimate the posterior probability density in Bayesian inference. Assuming that n independent samples $\left\{{\theta }^{\left(1\right)},{\theta }^{\left(2\right)}\dots {\theta }^{\left(n\right)}\right\}$ have been drawn from the posterior distribution $p\left(\mathit{\theta }\left|\mathcal{D},\mathcal{M}\right.\right)$ using the MCMC method, statistical information of the posterior distribution—such as the mean vector and covariance matrix of the model parameter $\theta$ —can be calculated accordingly.

3.2. Model Selection and Evaluation Indicators

When refining existing models, it is often necessary to compare multiple models in order to select the one with the best predictive performance. In general, models with a larger number of parameters and greater complexity tend to exhibit better predictive capabilities. However, to avoid overfitting and excessive parameterization—which may reduce the model’s ability to generalize to new or future data—complex models are typically penalized through certain adjustment criteria. In this study, the Watanabe–Akaike Information Criterion (WAIC) [100] and the Deviance Information Criterion (DIC) [101] are employed to compare the performance of existing models. The model with the lower criterion value is preferred for Bayesian parameter refinement.

The Widely Applicable Information Criterion (WAIC) is a fully Bayesian approach that utilizes the entire posterior distribution.

$$WAIC=-2lppd+2p_{\mathrm{WAIC}}$$

(5)

The parameter expressions in the equation are given as follows:

$$lppd={\displaystyle \sum _{i=1}^n\log }\left({\displaystyle \frac{1}{S}}{\displaystyle \sum _{s=1}^{S}p\left(\left.y_i\right|{\mathit{\theta }}^s\right)}\right)$$

(6)

$$p_{\mathrm{WAIC}}={\displaystyle \sum _{i=1}^n{V}_{s=1}^S}(\log p(\left.y_i\right|{\mathit{\theta }}^s))$$

(7)

The Akaike Information Criterion (AIC) [102] is an indicator used to evaluate the goodness-of-fit of statistical models, based on the concept of entropy. It provides a trade-off between the complexity of the estimated model and its ability to fit the observed data, aiming to identify a model that best explains the data with the lowest number of free parameters. The Deviance Information Criterion (DIC), on the other hand, can be regarded as a partially Bayesian extension of the AIC. Its penalty for model complexity is data-driven. The value of DIC can be calculated as follows:

$$DIC=-2\log p(\left.\mathsf{y}\right|{\widehat{\mathit{\theta }}}_{\mathrm{Bayes}})+2p_{DIC}$$

(8)

The parameter expressions in the equation are given as follows:

$$p_{DIC}=2\left(\log p\left(\left.\mathsf{y}\right|{\widehat{\mathit{\theta }}}_{\mathrm{Bayes}}\right)-{\displaystyle \frac{1}{S}}{\displaystyle \sum _{s=1}^S\log p\left(\left.\mathsf{y}\right|{\mathit{\theta }}^S\right)}\right)$$

(9)

Model comparison enables the selection of models with better predictive performance. To reasonably evaluate the predictive capability of the models, a quantitative assessment was further conducted in this study. Four statistical indicators were employed, including Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), Coefficient of Variation (CV), and Coefficient of Determination (R²). The mathematical expressions of these indicators are given as follows [103,104,105]

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum {\left(x-y\right)}^2}}$$

(10)

$$MAPE={\displaystyle \frac{1}{n}}{\displaystyle \sum \left|\frac{x-y}{x}\right|}\times 100\%$$

(11)

$$R^2(X,Y)={\left({\displaystyle \frac{{\displaystyle \sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}}{\sqrt{{{\displaystyle \sum \left(x-\overline{x}\right)}}^2{\left(y-\overline{y}\right)}^2}}}\right)}^2$$

(12)

$$COV=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum {\left(\frac{x}{y}-\mu \right)}^2}}/\mu \hspace{0.33em},\hspace{0.33em}\mu ={\displaystyle \frac{1}{n}}{\displaystyle \sum \frac{x}{y}}$$

(13)

where $n$ denotes the number of data points; $X$ and $Y$ represent the vectors of experimental and predicted values, respectively; $x$ refers to the experimentally measured compressive strength, $y$ denotes the model-predicted compressive strength; and $\overline{x}$ and $\overline{y}$ are the mean values of the experimental and predicted results, respectively. The coefficient of determination ($R^2$) ranges from 0 to 1. An $R^2$ value of 1 indicates perfect agreement between the predicted and experimental results, whereas $R^2=0$ implies no correlation between them. Although a value of $R^2=1$ reflects a strong linear relationship, it does not guarantee the perfection of the model predictions. Typically, RMSE and MAPE are used to assess the overall prediction error of a model, while a smaller CV value indicates lower dispersion in the predictions and thus higher predictive accuracy.

3.3. Bayesian Model Prediction

Inference based on the posterior probability distribution for model prediction is a commonly used approach. Once the posterior distribution of the model parameters is obtained, probabilistic predictions can be made for a given input variable $x^{\ast }$. In other words, the posterior distribution of the model parameters $\theta$ allows for the computation of the corresponding probability distribution of the output variable $y^{\ast }$ for a specific input. The mean of this distribution can be considered the optimal prediction of y, while its variance provides an estimate of the credible interval (CI) for the response variable.

In Bayesian theory, integration over the posterior probability is required. The marginal integration of the posterior distribution can be expressed as follows:

$$p\left(y^{\ast }\left|{\mathit{x}}^{\ast },\right.\mathcal{D},\mathcal{M}\right)={\displaystyle \int p\left(y^{\ast }\left|{\mathit{x}}^{\ast },\right.\mathit{\theta },\mathcal{M}\right)p\left(\mathit{\theta }\left|\mathcal{D},\mathcal{M}\right.\right)d\mathit{\theta }}$$

(14)

In general, the computation of the posterior probability distribution $p\left(\mathit{\theta }\left|\mathcal{D},\mathcal{M}\right.\right)$ becomes analytically intractable. To address this issue, a Markov Chain Monte Carlo (MCMC) method can be employed to draw a sufficiently large number of independent samples from the posterior distribution. Subsequently, the Monte Carlo Simulation (MCS) method is used to estimate the probability distribution of the parameter $y^{\ast }$ [106]. Specifically, for a given model $\mathcal{M}$, each sample point in the parameter space can be weighted according to its likelihood given the observed data. These sampled parameters can then be used to generate predictions for new input data.

In summary, by randomly sampling from the posterior distribution of the model parameters $\theta$, a corresponding model prediction $M\left(x^{\ast },{\theta }^{\left(i\right)}\right)$ can be obtained for each sample. By incorporating a stochastic error term ε, a predicted value $y^{\ast \left(i\right)}$ can be generated for that specific parameter sample. Repeating this process for all parameter samples yields a set of predicted output values $y^{\ast }$. To better understand the characteristics of the model, statistical features such as the mean and variance of these predicted values can be further computed. In addition, other statistical properties of the predictive distribution—such as quantiles—can also be derived. Once key quantiles, such as the 2.5%, 25%, 75%, and 97.5% percentiles, are obtained, the corresponding 50% and 95% credible intervals can be readily calculated.

4. Results and Discussions

4.1. Evaluation of Existing Deterministic Models

4.1.1. Evaluation of Prediction Models for Compressive Strength

In this study, eight representative models were selected from the literature [92,93,107,108,109,110,111], and their predictive performance was evaluated using an existing database. These eight models are deterministic compressive strength models proposed by different researchers, and their specific formulations are presented in

Table 4. Compressive strength prediction models from different studies.

Vintages	Sources of the Model	Expressions of the Model
1971	Newman [112]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+3.7{\left({\displaystyle \frac{f_l}{f_{co}^{\prime }}}\right)}^{0.86}$
1999	Toutanji [107]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+3.5{\left({\displaystyle \frac{f_l}{f_{co}^{\prime }}}\right)}^{0.85}$
2006	Guralick [108]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=0.616+{\displaystyle \frac{f_l}{f_{co}^{\prime }}}+1.57({\displaystyle \frac{f_l}{f_{co}^{\prime }}}+0.06{)}^{0.5}$
2009	Teng [92]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+3.5({\rho }_k-0.01){\rho }_{\epsilon }$
2013	Ozbakkaloglu [109]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+{\displaystyle \frac{0.0058K_l}{f_{co}^{\prime }}}+3.22({\displaystyle \frac{f_l}{f_{co}^{\prime }}}-{\displaystyle \frac{f_{lo}}{f_{co}^{\prime }}})$
2015	Sadeghian [110]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+(2.77{\rho }_k^{0.77}-0.07){\rho }_{\epsilon }^{0.91}$
2017	Keshtegar I [93]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+(4.63+0.93{\rho }_E^{0.53}{\rho }_{\epsilon }^{1.03})({\rho }_a^{0.82}{\rho }_E^{0.45})$
2017	Keshtegar II [111]	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+(3.23-4.8{\rho }_k^{2.5})({\displaystyle \frac{f_l}{f_{co}^{\prime }}}{)}^{0.95}$

.

Using these eight deterministic models, the axial compressive strength of FRP-confined concrete cylinders can be predicted and subsequently compared with the corresponding experimental results to evaluate the predictive performance of each model. Figure 5 illustrates the comparison between the predicted and experimental values of axial compressive strength for the eight deterministic models. The horizontal axis represents the experimentally measured compressive strength, while the vertical axis denotes the compressive strength predicted by the models. The red diagonal line indicates perfect agreement between predicted and experimental values. The closer the scatter points are to this diagonal line, the more accurate the model’s predictions, indicating a higher precision in estimating the compressive strength.

As shown in Figure 5, the Newman (1971) [112] and Toutanji (1999) [107] models tend to overestimate the axial compressive strength of FRP-confined concrete cylinders, whereas the Guralnick (2006) model [108] generally underestimates the compressive strength. The remaining models exhibit relatively good predictive performance when the compressive strength of the confined concrete is low, with the scatter points distributed symmetrically around the diagonal line. However, when the compressive strength is high, the predictive accuracy of all existing models deteriorates significantly.

In addition, the predictive performance of the eight compressive strength models was quantitatively evaluated. The detailed results of the statistical evaluation for each candidate model are summarized in

Table 5. Detailed evaluation results for the predictive performances of the eight candidate existing models.

Model	RMSE	MAPE (%)	R2	COV (%)
Newman 1971 [112]	0.5786	21.4599	0.791	18.641
Toutanji 1999 [107]	0.5298	19.5738	0.825	18.364
Guralick 2006 [108]	0.6635	14.1431	0.726	18.030
Teng 2009 [92]	0.5076	14.6077	0.839	20.445
Ozbakkaloglu 2013 [109]	0.5221	13.9416	0.830	18.727
Sadeghian 2015 [110]	0.4653	14.1441	0.865	18.794
Keshtegar I 2017 [93]	0.4484	13.3223	0.874	17.213
Keshtegar II 2017 [111]	0.5537	14.3862	0.809	18.522

.

As shown in Table 5, the Newman (1971) [112] model, being the earliest among the candidates, demonstrates relatively poor predictive accuracy. In contrast, the Keshtegar I (2017) model [93] exhibits the best predictive performance overall. This model consistently outperforms the others across all statistical indicators, with the remaining models falling short in at least one metric.

In terms of variability, the Teng (2009) model [92] yields the highest coefficient of variation (COV), reaching 20.445%, whereas the Keshtegar I (2017) model [93] shows the lowest COV, at 17.213%. Overall, among the eight candidate deterministic models, the Keshtegar I (2017) [93] model demonstrates the most reliable and accurate predictive capability.

4.1.2. Evaluation of Prediction Models for Ultimate Strain

In this section, seven representative models were selected from the literature, and their predictive performance was evaluated using an existing database. These seven models are deterministic ultimate strain models proposed by different researchers, and their specific formulations are presented in

Table 6. Ultimate strain prediction models taken from different studies.

Vintages	Sources of the Model	Expressions of the Model
1988	Mander [14]	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+5\left({\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}-1\right)$
1999	Toutanji [107]	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+\left(310.75{\epsilon }_{h,rup}+1.90\right)\left({\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}-1\right)$
2009	Teng [92]	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.75+6.5{\rho }_k^{0.8}{\rho }_{\epsilon }^{1.45}$
2013	Ozbakkaloglu [109]	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=2-{\displaystyle \frac{f_{co}^{\prime }-20}{100}}+0.271{\left({\displaystyle \frac{k_l}{f_{co}^{\prime }}}\right)}^{0.9}\left({\displaystyle \frac{{\epsilon }_{h,rup}}{{\epsilon }_{co}}}\right)$
2015	Sadeghian [110]	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+6.78{\rho }_k^{0.63}{\rho }_{\epsilon }^{1.08}$
2017	Keshtegar I [93]	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+\left(-3.45+5.84{\rho }_E^{0.6}{\rho }_{\epsilon }^{0.69}\right)\left({\rho }_a^{0.57}{\rho }_{\epsilon }^{0.36}\right)$
2017	Keshtegar II [111]	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+\left(7.31+2.06{\rho }_{\epsilon }^{0.8}\right){\left({\displaystyle \frac{f_l}{f_{co}^{\prime }}}\right)}^{0.6}$

.

Using these seven deterministic models, the ultimate strain of FRP-confined concrete cylinders can be predicted and compared with the corresponding experimental results to evaluate the predictive performance of each model. Figure 6 presents the comparison between the predicted and experimental ultimate strain values for the seven deterministic models. The horizontal axis represents the experimentally measured ultimate strain, while the vertical axis denotes the ultimate strain predicted by the models. The red diagonal line indicates perfect agreement between predicted and experimental values. The closer the scatter points lie to this diagonal line, the closer the predicted values are to the experimental results, indicating higher predictive accuracy of the corresponding model for ultimate strain estimation.

As shown in Figure 6, the Mander (1998) [14] and Toutanji (1999) [107] models tend to underestimate the ultimate strain of FRP-confined concrete cylinders under axial loading. The remaining models exhibit better predictive performance at lower compressive strength levels, with the scatter points distributed relatively evenly on both sides of the diagonal line. However, as the compressive strength increases, the predictive accuracy of all existing models for ultimate strain significantly deteriorates. Furthermore, the predictive performance of the seven ultimate strain models was quantitatively evaluated, and the detailed statistical results of the evaluation are summarized in

Table 7. Predictive performance evaluation results for ultimate strain candidate models.

Model	RMSE	MAPE (%)	R2	COV (%)
Mander 1998 [14]	4.7106	38.1816	0.6503	52.4482
Toutanji 1999 [107]	3.6717	33.1218	0.7876	47.0089
Teng 2009 [92]	4.7466	42.2276	0.6450	46.7718
Ozbakkaloglu 2013 [109]	4.7021	32.8525	0.6516	45.8763
Sadeghian 2015 [110]	4.0929	36.6343	0.7360	48.6897
Keshtegar I 2017 [93]	4.1009	36.3297	0.7350	48.0683
Keshtegar II 2017 [111]	4.0982	37.1940	0.7353	48.2143

.

As shown in Table 7, the Teng (2009) model [92] exhibits relatively poor predictive performance, while the Toutanji (1999) model [107] demonstrates superior accuracy compared to the other models. Overall, the Toutanji (1999) model [107] outperforms the rest, as the remaining models show inferior performance in at least one of the evaluated metrics. In terms of model variability, the Mander (1998) model [14] yields the highest coefficient of variation (COV), reaching 52.4482%, whereas the Ozbakkaloglu (2013) model [109] presents the lowest COV value of 45.8763%. In summary, among the seven candidate deterministic models, the Toutanji (1999) model [107] exhibits the best predictive capability. Although both the compressive strength and ultimate strain models tend to show smaller prediction errors at lower concrete strength levels, their overall predictive performance for the collected experimental database remains unsatisfactory. This indicates a significant degree of uncertainty in their predictions. To enable a more reliable design of FRP-confined circular concrete cylinders, it is necessary to calibrate both the compressive strength and ultimate strain models using probabilistic approaches. Such methods can enhance predictive accuracy and provide a rational quantification of the associated uncertainty.

4.2. Bayesian Updating and Selection of the Models

4.2.1. Bayesian Updating and Selection of Prediction Models for Compressive Strength

In the process of model parameter identification based on Bayesian theory, it is essential to first select an appropriate model form. In this study, eight types of parameterized compressive strength models were collected from the existing literature [93,110], and their formulations are summarized in

Table 8. Eight types of existing compressive strength models for parameter identification.

Number	Expressions of the Model
Model 1	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+{\theta }_1{\left({\rho }_k{\rho }_{\epsilon }\right)}^{{\theta }_2}$
Model 2	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+{\theta }_1{\rho }_k^{{\theta }_2}{\rho }_{\epsilon }^{{\theta }_3}$
Model 3	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+({\theta }_1+{\theta }_2{\rho }_k^{{\theta }_3}){\rho }_{\epsilon }^{{\theta }_4}$
Model 4	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+({\theta }_1+{\theta }_2{\rho }_k^{{\theta }_3})({\theta }_4+{\rho }_{\epsilon }^{{\theta }_5})$
Model 5	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+{\theta }_1{\rho }_a^{{\theta }_2}{\rho }_E^{{\theta }_3}{\rho }_{\epsilon }^{{\theta }_4}$
Model 6	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+({\theta }_1+{\theta }_2{\rho }_a^{{\theta }_3}{\rho }_{\epsilon }^{{\theta }_4}){\rho }_E^{{\theta }_5}$
Model 7	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+({\theta }_1+{\theta }_2{\rho }_{\epsilon }^{{\theta }_3}){\rho }_a^{{\theta }_4}{\rho }_E^{{\theta }_5}$
Model 8	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+({\theta }_1+{\theta }_2{\rho }_E^{{\theta }_3}{\rho }_{\epsilon }^{{\theta }_4})({\rho }_a^{{\theta }_5}{\rho }_E^{{\theta }_6})$

.

In general, model parameters $\theta$ can be considered as random variables following a certain probability distribution, which allows the prediction uncertainty of the probabilistic model, as expressed in Equation (2), to be properly interpreted. To determine the most appropriate probability distribution for the model parameters $\theta$, Bayesian inference combined with the Markov Chain Monte Carlo (MCMC) method is adopted in this study.

The collected experimental data are randomly divided into two subsets—a training set and a testing set—in a ratio of 7:3. Given that the existing experimental database contains 1016 samples in total, 711 samples are selected as the training set, and the remaining 305 samples are used as the testing set. The training data are employed for the probabilistic calibration of the compressive strength models, while the testing data are used for evaluating and analyzing the predictive performance of the calibrated models. After data partitioning, a total of 50,000 independent samples are drawn from the posterior distributions of the model parameters using the Delayed Rejection Adaptive Metropolis–Hastings (DRAM) algorithm [113]. The sampling process is implemented via the MatDRAM toolbox [114] on the MATLAB 2023b software platform. Since the selected models are nonlinear in nature, the parameters $\theta$ are assumed to follow uncertain probability distributions. These distributions are characterized by their mean and standard deviation values, which are calculated and presented in

Table 9. Mean values for the posterior samples of the probabilistic model parameters.

Model	Average Value
	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\theta }}_3$	${\mathit{\theta }}_4$	${\mathit{\theta }}_5$	${\mathit{\theta }}_6$
Model 1	2.9740	0.9568
Model 2	3.3492	0.9645	0.9044
Model 3	0.0016	3.3766	0.9687	0.9018
Model 4	0.0028	4.8615	0.9651	−0.5008	0.7837
Model 5	1.4004	0.8021	1.0064	0.8367
Model 6	−0.0036	1.3187	0.7632	0.7942	1.0019
Model 7	−1.1064	2.1373	0.7044	0.7992	1.0031
Model 8	4.9673	0.8331	0.8449	0.9049	0.7830	0.2234

and

Table 10. Standard deviation values for the posterior samples of the probabilistic model parameters.

Model	Standard Deviation
	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\theta }}_3$	${\mathit{\theta }}_4$	${\mathit{\theta }}_5$	${\mathit{\theta }}_6$
Model 1	0.0322	0.0100
Model 2	0.1580	0.0105	0.0227
Model 3	0.0092	0.1772	0.0239	0.0230
Model 4	0.0133	0.7459	0.0239	0.1585	0.0525
Model 5	0.1096	0.0139	0.0099	0.0202
Model 6	0.0022	0.1110	0.0263	0.0335	0.0102
Model 7	0.4623	0.3566	0.0517	0.0137	0.0099
Model 8	1.0180	0.1530	0.1262	0.0390	0.0148	0.1355

, respectively.

When modifying existing models, it is generally necessary to compare multiple candidates in order to select the one with superior predictive performance. In general, models with a greater number of parameters and higher complexity tend to exhibit better predictive accuracy. However, to avoid overfitting and excessive parameterization—which may impair the model’s ability to generalize to future data—penalization adjustments are typically introduced for more complex models. Accordingly, the Akaike Information Criterion (AIC) and the Widely Applicable Deviance Information Criterion (WAIC) scores were calculated for the eight probabilistic models. When comparing Deviance Information Criterion (DIC) and WAIC, WAIC is often preferred due to its robustness in handling multimodal posterior distributions. This is because WAIC is computed using the full posterior distribution, whereas DIC is based on the posterior mean, which can sometimes lead to misleading conclusions. Moreover, DIC may fail in the presence of singular models. Therefore, WAIC is prioritized for model evaluation in this study. The DIC and WAIC scores of the eight selected models, along with the corresponding computational results, are summarized in

Table 11. DIC and WAIC scores for existing compressive strength models.

Model	DIC	WAIC
Model 1	501.73	501.75
Model 2	484.76	485.16
Model 3	488.03	489.05
Model 4	504.27	505.61
Model 5	395.78	396.78
Model 6	396.35	397.56
Model 7	399.99	405.11
Model 8	394.30	397.70

. A visual comparison of these results is illustrated in Figure 7.

The results indicate that all models yield relatively consistent scores across different evaluation criteria, with only minor differences observed. Models with fewer parameters generally perform better in the evaluation, while the model with the largest number of parameters does not achieve the best performance. Considering both the DIC and WAIC scores comprehensively, Model 5 is selected as the preferred model for further modification.

4.2.2. Bayesian Updating and Selection of Prediction Models for Ultimate Strain

Eight types of parameterized ultimate strain models were collected from the existing literature [93,110], and their formulations are summarized in

Table 12. Eight categories of existing ultimate strain models for parameter identification.

Model	Expressions of the Model
Model 1	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+{\theta }_1{\left({\rho }_k{\rho }_{\epsilon }\right)}^{{\theta }_2}$
Model 2	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+{\theta }_1{\rho }_k^{{\theta }_2}{\rho }_{\epsilon }^{{\theta }_3}$
Model 3	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+({\theta }_1+{\theta }_2{\rho }_k^{{\theta }_3}){\rho }_{\epsilon }^{{\theta }_4}$
Model 4	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+({\theta }_1+{\theta }_2{\rho }_k^{{\theta }_3})({\theta }_4+{\rho }_{\epsilon }^{{\theta }_5})$
Model 5	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+{\theta }_1{\rho }_a^{{\theta }_2}{\rho }_E^{{\theta }_3}{\rho }_{\epsilon }^{{\theta }_4}$
Model 6	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+({\theta }_1+{\theta }_2{\rho }_a^{{\theta }_3}{\rho }_{\epsilon }^{{\theta }_4}){\rho }_E^{{\theta }_5}$
Model 7	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+({\theta }_1+{\theta }_2{\rho }_a^{{\theta }_3}){\rho }_E^{{\theta }_4}{\rho }_{\epsilon }^{{\theta }_5}$
Model 8	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+({\theta }_1+{\theta }_2{\rho }_E^{{\theta }_3}{\rho }_{\epsilon }^{{\theta }_4})({\rho }_a^{{\theta }_5}{\rho }_{\epsilon }^{{\theta }_6})$

.

Similarly, by letting $y=\ln ({\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}})$, all the aforementioned models can be expressed in the form of Equation (2). In the following analysis, Bayesian inference combined with the MCMC sampling method will again be employed to determine the posterior probability distributions of the model parameter $\theta$.

Similarly, the collected experimental data are randomly divided into a training set and a testing set, with a ratio of 7:3. Given that the existing experimental database contains a total of 1016 samples, 711 samples are selected for the training set, and the remaining 305 samples are used for the testing set. The training data are utilized for the probabilistic calibration of the ultimate strain models, while the testing data serve for evaluating and analyzing the predictive performance of the calibrated models.

The sampling of posterior distributions follows the same procedure as described in Section 4.2.1. Additionally, the mean and standard deviation of the ultimate strain probabilistic model distributions are computed and presented in

Table 13. The average value of the posterior samples of the ultimate strain probability model parameters.

Model	Average
	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\theta }}_3$	${\mathit{\theta }}_4$	${\mathit{\theta }}_5$	${\mathit{\theta }}_6$
Model 1	19.9106	0.8434
Model 2	9.6535	0.7914	1.1562
Model 3	0.2365	11.1488	0.9250	1.1292
Model 4	0.2909	11.5830	0.9197	0.1468	1.1020
Model 5	3.2953	0.6113	0.8392	1.1363
Model 6	0.2358	2.9695	0.6887	0.9700	1.0948
Model 7	−0.0223	2.4689	0.5142	0.8309	1.1224
Model 8	3.1780	1.9045	0.9365	−0.0671	0.5770	1.1704

and

Table 14. Standard deviation values of posterior samples of ultimate strain probability model parameters.

Model	Average
	${\mathit{\theta }}_1$	${\mathit{\theta }}_2$	${\mathit{\theta }}_3$	${\mathit{\theta }}_4$	${\mathit{\theta }}_5$	${\mathit{\theta }}_6$
Model 1	0.2799	0.0132
Model 2	0.5819	0.0125	0.0285
Model 3	0.0538	0.7830	0.0340	0.0289
Model 4	0.0598	0.9639	0.0340	0.1450	0.0331
Model 5	0.3363	0.0161	0.0116	0.0258
Model 6	0.0582	0.3690	0.0266	0.0356	0.0271
Model 7	0.0157	0.5105	0.0587	0.0122	0.0263
Model 8	1.5997	0.3729	0.0303	0.2807	0.0193	0.2476

, respectively.

Similarly, the DIC and WAIC scores of the eight selected ultimate strain models, along with the corresponding computational results, are summarized in

Table 15. DIC and WAIC scores for existing ultimate strain models.

Model	DIC	WAIC
Model 1	883.98	884.07
Model 2	728.85	729.52
Model 3	753.04	754.63
Model 4	736.98	740.28
Model 5	701.29	703.97
Model 6	735.09	739.44
Model 7	701.62	704.06
Model 8	707.55	726.75

. A visual comparison of these results is illustrated in Figure 8.

The results show that, similar to the compressive strength models, all ultimate strain models yield relatively consistent scores across different evaluation criteria, with only minor differences observed. Models with fewer parameters generally perform better in the evaluation, while the model with the largest number of parameters does not achieve the best performance.

Taking into account both the DIC and WAIC scores, Model 5 is selected as the preferred model for further modification.

4.3. Model Comparisons

4.3.1. Comparisons of Predicting Compressive Strengths

After obtaining the posterior probability distribution of the model parameters, the Monte Carlo Simulation (MCS) method can be employed to predict the probability distribution of the response variable $y(f_{cc}^{\prime }/f_{co}^{\prime })$. Assuming that the parameter $\theta$ follows an uncertain probability distribution, the mean value of the MCS results can be regarded as the optimal prediction of the response variable within the probabilistic framework. Subsequently, the optimal prediction of the compressive strength can be derived using the model expression. Figure 9 presents a comparison between the predicted optimal values of compressive strength obtained from the probabilistic model and the corresponding experimental results. Overall, the scatter points of the revised model’s predictions are symmetrically distributed around the diagonal and exhibit a more concentrated pattern, indicating that the modified model yields predictions that are more consistent with the measured values than the original model. To further evaluate the predictive performance of the probabilistic model, statistical evaluation indicators were also computed for other models after probabilistic updating. The detailed results are summarized in

Table 16. Quantitative evaluation results of probabilistic model prediction performance.

Model	RMSE			MAPE (%)			R2			COV (%)
	Tr.	Te.	Full	Tr.	Te.	Full	Tr.	Te.	Full	Tr.	Te.	Full
1	0.44	0.42	0.44	13.58	13.56	13.57	0.88	0.88	0.88	18.45	18.19	18.36
2	0.44	0.41	0.43	13.36	13.59	13.43	0.88	0.88	0.88	18.21	18.11	18.17
3	0.44	0.41	0.43	13.37	13.61	13.44	0.88	0.89	0.88	18.20	18.11	18.16
4	0.44	0.41	0.43	13.54	13.79	13.62	0.88	0.89	0.88	18.34	18.29	18.31
5	0.39	0.39	0.39	12.80	13.71	13.07	0.91	0.90	0.91	16.48	17.18	16.69
6	0.39	0.39	0.39	12.71	13.52	12.96	0.91	0.90	0.91	16.42	17.19	16.65
7	0.39	0.39	0.39	12.96	13.75	13.20	0.91	0.90	0.91	16.53	17.29	16.76
8	0.38	0.39	0.39	12.94	14.07	13.28	0.91	0.90	0.91	16.32	17.16	16.57

Note: “Tr.” denotes the training set, “Te.” denotes the testing set, and “Full” represents the entire dataset.

.

By comparing the four statistical evaluation metrics presented in Table 5 and Table 16, it is evident that the predictive performance of the revised probabilistic model is significantly improved over the original version. Moreover, the RMSE, MAPE, R², and COV values for all probabilistic models are nearly identical, indicating that their predictive performances are comparable. Based on the model selection results discussed in the previous section, Model 5 was chosen for comparison with the deterministic models presented earlier. The comparison results reveal that, after model updating, the RMSE of the probabilistic prediction was reduced by 13.02% compared to the minimum value before updating, the MAPE decreased by 1.89%, the R² value increased by 3.96%, and the COV was reduced by 3.04%. According to the quantitative results in Table 16, it can be inferred that the revised model predictions are closer to the experimental values, thereby improving the goodness-of-fit, while reducing the model dispersion. Furthermore, the evaluation metrics for the training and testing sets differ only slightly, demonstrating the proposed probabilistic model’s strong generalization capability.

For the probabilistic predictions of compressive strength obtained from the revised model, the percentage of experimental compressive strength data falling within different confidence intervals is illustrated in Figure 10. It can be observed that the differences in sample proportions across various confidence levels are minimal, indicating that the uncertainty quantification of the predictions by the probabilistic model is reasonably accurate.

Figure 11 presents the probabilistic prediction results for Model 5. The prediction output is treated as a random variable, with the 50% and 95% confidence intervals represented by dark-gray- and light-gray-shaded regions, respectively. The red curve indicates the predicted mean values, while the scattered dots correspond to the experimental data. It can be observed that the experimental compressive strength values are evenly distributed on both sides of the predicted mean curve, suggesting that the probabilistic model does not exhibit any systematic tendency to overestimate or underestimate the compressive strength. Moreover, only a few experimental values fall outside the 95% confidence interval, and most of the values lie within the 50% interval. These observations indicate that the proposed probabilistic model is capable of effectively quantifying the uncertainty in predicting the compressive strength of FRP-confined circular concrete cylinders.

In addition, eight existing compressive strength models were selected for comparison, and their specific formulations are listed in

Table 17. Eight types of compressive strength models for parameter identification.

Model	Expressions of the model
Model A	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+3.18{\rho }_k^{0.94}{\rho }_{\epsilon }^{0.94}$
Model B	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+3.48{\rho }_k^{0.96}{\rho }_{\epsilon }^{0.91}$
Model C	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+(2.39{\rho }_k^{0.78}-0.06){\rho }_{\epsilon }$
Model D	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+(1.58{\rho }_k^{0.78}-0.04)({\rho }_{\epsilon }^{1.15}+1.14)$
Model E	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+1.86{\rho }_a^{0.82}{\rho }_E^{0.92}{\rho }_{\epsilon }^{0.89}$
Model F	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+1.87{\rho }_a^{0.81}{\rho }_{\epsilon }^{0.87}{\rho }_E^{0.91}$
Model G	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+(0.85+1.40{\rho }_{\epsilon }){\rho }_a^{0.82}{\rho }_E^{0.91}$
Model H	${\displaystyle \frac{f_{cc}^{\prime }}{f_{co}^{\prime }}}=1+(8.39{\rho }_a^{0.84}+0.01{\rho }_{\epsilon }^{1.40}){\rho }_E^{0.75}$

.

To evaluate the accuracy of these models, their predicted values were compared with the experimental results. Figure 12 illustrates the comparison between the predicted and measured compressive strength values for each model.

As shown in Figure 12, Models A, B, and H tend to overestimate the axial compressive strength of FRP-confined concrete cylinders at lower strength levels. In contrast, the other models do not exhibit a clear tendency to overestimate or underestimate the compressive strength in this range, with the data points relatively evenly distributed on both sides of the diagonal line. However, at higher strength levels, except for Models A and B, which still show a relatively balanced distribution of data points around the diagonal, the remaining models display noticeable inaccuracies in prediction, with a general tendency to underestimate the compressive strength of the concrete.

The quantitative evaluation results for the candidate compressive strength models are summarized in

Table 18. Detailed evaluation results for the predictive performances of the eight candidate models for compressive strength.

Model	RMSE	MAPE (%)	R2	COV (%)
Model A	0.4446	14.3358	0.8770	18.5321
Model B	0.4395	13.9593	0.8798	18.3964
Model C	0.4665	14.0996	0.8646	19.3157
Model D	0.4759	14.2411	0.8591	19.4770
Model E	0.4178	13.6254	0.8914	16.9850
Model F	0.4256	13.6359	0.8873	16.9079
Model G	0.4309	13.7235	0.8845	17.1881
Model H	0.9764	39.0911	0.4068	28.0735

. It can be observed that Model H performs significantly worse than the other models in terms of predictive accuracy. The remaining models show varying levels of accuracy across different evaluation metrics—some models perform well on certain indicators but fall behind on others. Among them, Model E demonstrates the best overall predictive performance, outperforming all other models across most evaluation criteria, with at least three indicators where the remaining models perform worse than Model E. In terms of model dispersion, except for Model H, Model D exhibits the highest coefficient of variation (COV) at 19.4770%, while Model F shows the lowest COV at 16.9079%. Overall, Model E can be considered the most reliable among the candidate models in terms of prediction accuracy.

Therefore, the predictive performance of the revised probabilistic Model 5 is compared with that of Model E. The comparison results show that the RMSE of Model 5 is 6.65% lower than that of Model E, the MAPE is reduced by 4.08%, the R² value is increased by 2.09%, and the COV is reduced by 1.74%. These findings indicate that employing a probabilistic model for predicting the compressive strength of FRP-confined concrete cylinders can effectively improve prediction accuracy while reasonably quantifying the uncertainty associated with the results.

4.3.2. Comparisons of Predicting Ultimate Strains

Similarly, after obtaining the posterior probability distribution of the model parameters, the Monte Carlo Simulation (MCS) method can be employed to predict the probability distribution of the response variable $y({\epsilon }_{cc}/{\epsilon }_{co})$. Assuming that the parameter $\theta$ follows an uncertain probability distribution, the mean value of the MCS results can be considered the optimal prediction of the response variable $y$ in the probabilistic model. Based on the model formulation, the optimal prediction of the ultimate strain can then be obtained. Figure 13 presents a comparison between the predicted optimal values of ultimate strain from the probabilistic model and the corresponding experimental results. Overall, the scatter points of the revised model’s predictions are symmetrically and more tightly distributed around the diagonal, indicating that the revised model yields predictions that are closer to the experimental values than those of the uncorrected model. To further assess the predictive performance of the probabilistic model, statistical evaluation metrics were also computed for other models after probabilistic updating, with detailed results provided in Table 16.

By comparing the four statistical evaluation metrics in Table 7 and

Table 19. Quantitative evaluation results of the prediction performance of ultimate strain probability model.

Model	RMSE			MAPE (%)			R2			COV (%)
	Tr.	Te.	Full	Tr.	Te.	Full	Tr.	Te.	Full	Tr.	Te.	Full
1	4.01	3.60	3.89	41.75	42.98	42.11	0.76	0.75	0.76	52.42	50.25	51.75
2	3.61	3.33	3.53	35.33	36.80	35.77	0.81	0.79	0.80	47.09	47.22	47.12
3	3.56	3.22	3.46	36.70	38.96	37.38	0.81	0.80	0.81	48.77	49.03	48.84
4	3.57	3.22	3.47	36.00	38.10	36.63	0.81	0.80	0.81	48.67	48.66	48.66
5	3.19	3.06	3.15	35.48	36.89	35.90	0.85	0.82	0.84	46.29	44.57	45.76
6	3.16	2.98	3.11	37.04	39.23	37.70	0.85	0.83	0.85	48.22	47.00	47.84
7	3.19	3.07	3.15	35.44	36.70	35.82	0.85	0.82	0.84	45.98	43.87	45.33
8	3.16	3.05	3.13	37.29	39.48	37.95	0.85	0.82	0.85	46.53	46.09	46.40

Note: “Tr.” denotes the training set, “Te.” denotes the testing set, and “Full” represents the entire dataset.

, it is evident that the predictive performance of the revised probabilistic model is significantly improved over the original version. Moreover, the RMSE, MAPE, R², and COV values of all probabilistic models are nearly identical, indicating minimal differences in predictive performance among them. Based on the probabilistic model selection results presented in the previous section, Model 5 was selected for further comparison with the deterministic models. The comparison shows that the RMSE of the revised probabilistic model is reduced by 14.17% compared to the minimum value before updating, the R² value is increased by 7.14%, and the COV is reduced by 0.24%. According to the quantitative results in Table 19, it can be inferred that the predictions from the revised model are closer to the experimental values, indicating both improved goodness-of-fit and reduced model dispersion. Additionally, the differences in evaluation metrics between the training and testing sets are minimal, which demonstrates the strong generalization capability of the proposed probabilistic model.

The R² value increased by 7.14%, while the COV decreased by 0.24% compared to the uncorrected model. Based on the quantitative results presented in Table 19, it can be inferred that the revised model yields predictions that are closer to the experimental values, thereby improving the goodness-of-fit and reducing the prediction dispersion. In addition, the evaluation metrics for the training and testing datasets exhibit only minor differences, which demonstrates the strong generalization capability of the proposed probabilistic model.

For the probabilistic predictions of ultimate strain obtained from the revised model, the percentage of experimental data falling within different confidence intervals is illustrated in Figure 14. It can be observed that the differences in sample proportions across the various confidence levels are minimal, indicating that the probabilistic model provides a reasonable quantification of uncertainty in its predictions.

Figure 15 presents the probabilistic prediction results for Model 5. The prediction is treated as a random variable, with the 50% and 95% confidence intervals represented by dark-gray- and light-gray-shaded areas, respectively. The red curve denotes the predicted mean values, while the scattered points correspond to the experimental data. As shown in the figure, the experimental values of ultimate strain are evenly distributed on both sides of the predicted mean curve, indicating that the probabilistic model does not exhibit any systematic tendency to overestimate or underestimate the ultimate strain. Moreover, only a few experimental values fall outside the 95% confidence interval, and most of them lie within the 50% interval. This demonstrates that the proposed probabilistic model effectively captures the uncertainty associated with the prediction of ultimate strain in FRP-confined circular concrete cylinders.

In addition, eight ultimate strain models were selected for comparison, and their specific formulations are presented in

Table 20. Eight categories of ultimate strain models for parameter identification.

Model	Expressions of the model
Model A	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+15.40{\rho }_k^{0.73}{\rho }_{\epsilon }^{0.73}$
Model B	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+6.47{\rho }_k^{0.65}{\rho }_{\epsilon }^{1.15}$
Model C	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+(7.21{\rho }_k^{0.58}-0.07){\rho }_{\epsilon }^{1.03}$
Model D	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+(6.61{\rho }_k^{0.61}-0.06){\rho }_{\epsilon }^{1.09}$
Model E	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1+(6.48{\rho }_k^{0.59}-0.03)({\rho }_{\epsilon }^{1.07}+0.24)$
Model F	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+5.25{\rho }_a^{0.57}{\rho }_E^{0.62}{\rho }_{\epsilon }^{1.06}$
Model G	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+(0.03+5.97{\rho }_a^{0.61}{\rho }_E^{0.65}){\rho }_{\epsilon }^{1.05}$
Model H	${\displaystyle \frac{{\epsilon }_{cc}}{{\epsilon }_{co}}}=1.5+(-0.09+3.27{\rho }_a^{0.4}){\rho }_E^{0.6}{\rho }_{\epsilon }^{1.04}$

.

The predicted values of the eight models were compared with the experimental results to evaluate the accuracy of each model. Figure 10 illustrates the comparison between the predicted and experimental values.

As shown in Figure 16, when the ultimate strain of the core concrete is relatively low, Model A tends to underestimate the ultimate strain of the concrete, while the other models neither significantly overestimate nor underestimate it, with the scatter points distributed relatively evenly around the diagonal line. However, when the core concrete exhibits higher ultimate strain, all models show reduced predictive accuracy for the ultimate strain, generally tending to underestimate the axial compressive strength of FRP-confined concrete cylinders.

The quantitative evaluation results of the ultimate strain models are summarized in

Table 21. Detailed evaluation results for the predictive performances of the eight candidate models for ultimate strain.

Model	RMSE	MAPE (%)	R2	COV (%)
Model A	4.6446	40.1281	0.6601	53.5498
Model B	3.9633	33.1136	0.7525	47.3828
Model C	4.1716	35.0373	0.7258	47.9544
Model D	4.1045	36.0313	0.7345	48.3149
Model E	4.1617	35.5169	0.7271	48.1133
Model F	4.0713	37.0509	0.7388	48.4655
Model G	4.0010	36.9461	0.7477	48.4765
Model H	3.9568	39.0285	0.7533	47.9821

. It can be observed that Model A exhibits relatively poor predictive performance, as indicated by its higher RMSE and MAPE values and lower R² value. The accuracy of the remaining models varies across different indicators—some models perform well in certain metrics but poorly in others. Among all models, Model H demonstrates the best predictive capability, outperforming the others in terms of overall accuracy, with all remaining models being inferior to it in at least two evaluation metrics. Regarding the degree of dispersion, Model A shows the highest coefficient of variation (COV) at 53.5498%, while Model F has the lowest COV at 47.3828%. Overall, Model H is identified as having the most reliable predictive performance among the evaluated models.

5. Conclusions

This study proposes a Bayesian inference-based method for probabilistic calibration of ultimate state models for FRP-confined circular concrete cylinders under axial compression. The primary objective is to enhance the predictive accuracy of existing models and quantify the associated prediction uncertainties. Representative compressive strength and ultimate strain models were selected from the literature as candidate models, and a comprehensive experimental database comprising 1016 test results for FRP-confined concrete cylinders was compiled. Based on this dataset, the candidate models were evaluated and calibrated. The following conclusions can be drawn from the analysis:

• The evaluation metrics adopted in this study indicate significant discrepancies in the predictive performance of different ultimate state models under axial compression. Among them, the compressive strength model proposed by Keshtegar I (2017) [93] (RMSE = 0.4484, MAPE = 13.3223, R² = 0.874) and the ultimate strain model proposed by Toutanji (1999) [107] (RMSE = 3.6717, MAPE = 33.1218, R² = 0.7876) exhibited relatively higher prediction accuracy. However, the overall performance of these models remains unsatisfactory when applied to the compiled experimental database, indicating substantial prediction uncertainty. Therefore, a probabilistic approach is necessary to calibrate the axial compression ultimate state models.
• To prevent overfitting and over-parameterization—which may hinder the model’s ability to accommodate future data expansion—WAIC and DIC were employed for further comparison of the existing models. To improve predictive accuracy while accounting for inevitable uncertainties, a Bayesian approach was adopted by replacing deterministic model parameters with probabilistic ones. Subsequently, a Bayesian inference-based framework was proposed to calibrate the probabilistic models, where the Markov Chain Monte Carlo (MCMC) algorithm was utilized to generate probabilistic parameter characteristics. The predictive uncertainty of the calibrated models can then be quantified using the Monte Carlo Simulation (MCS) method.
• After Bayesian inference-based calibration, the accuracy of the probabilistic prediction models improved significantly. Compared with the best-performing deterministic model prior to calibration, the RMSE of the calibrated compressive strength model decreased by 13.02%, the MAPE was reduced by 1.89%, the R² value increased by 3.96%, and the COV decreased by 3.04%. For the ultimate strain model, the calibrated version achieved a 14.17% reduction in RMSE, a 7.14% increase in R², and a 0.24% decrease in COV, compared to the lowest values among the original models. These results demonstrate that the calibrated probabilistic models are capable of effectively quantifying the uncertainty in the prediction of the axial compressive strength of FRP-confined concrete cylinders.

Based on the above analysis, the corrected prediction model for the ultimate condition under compression, developed using Bayesian inference, demonstrates a significant improvement in accuracy compared to the uncorrected model. The posterior distribution serves as the basis for model correction, enhancing the accuracy of the prediction results. These improved predictions can provide more reliable references for experimental studies and engineering design, offering a foundation for appropriate adjustments to the design parameters.