Bearing Capacity Prediction of Cold-Formed Steel Columns with Gene Expression Programming
Abstract
1. Introduction
2. Model Parameters
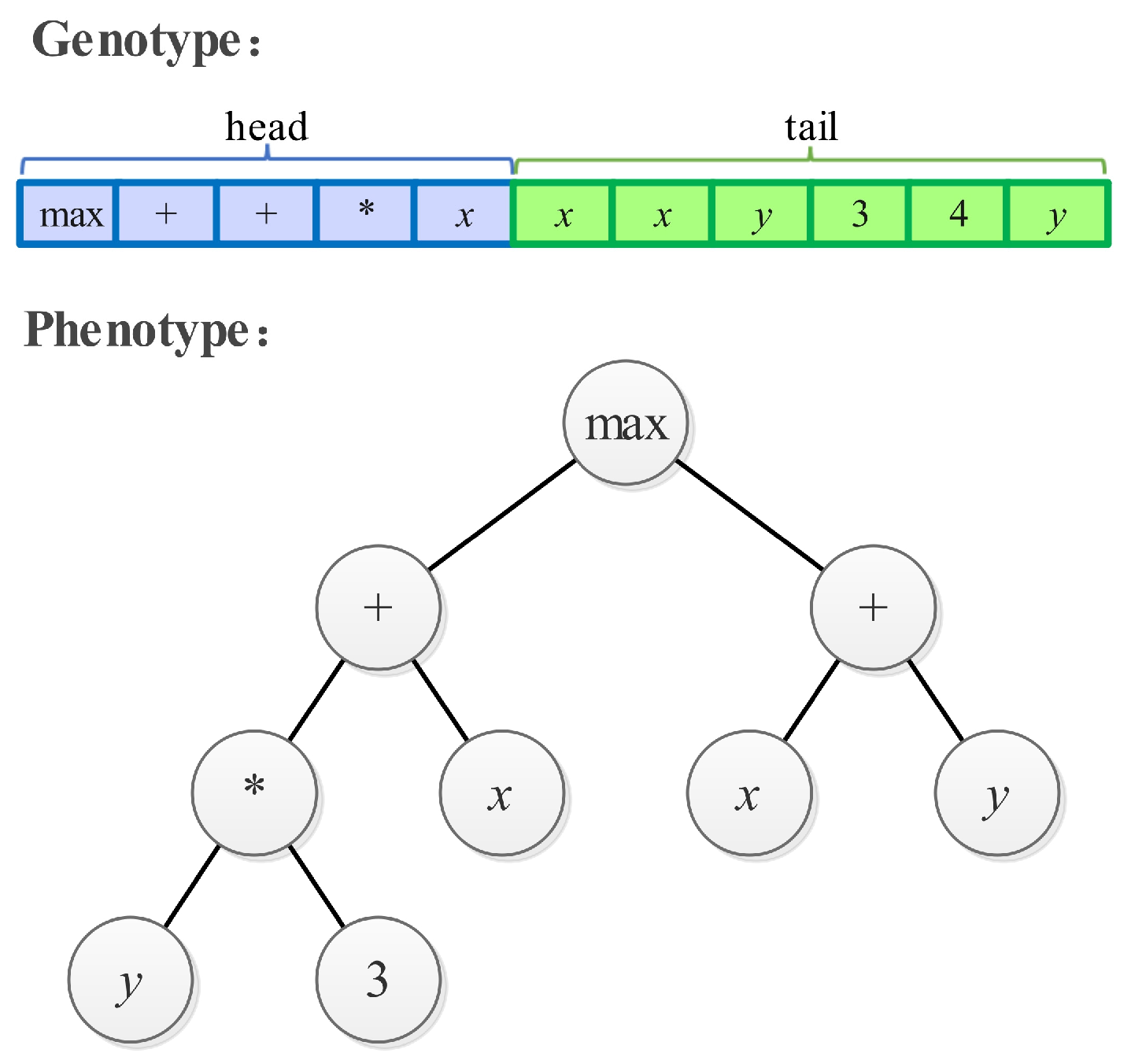
2.1. Gene Expression Programming
2.2. Fitness Function
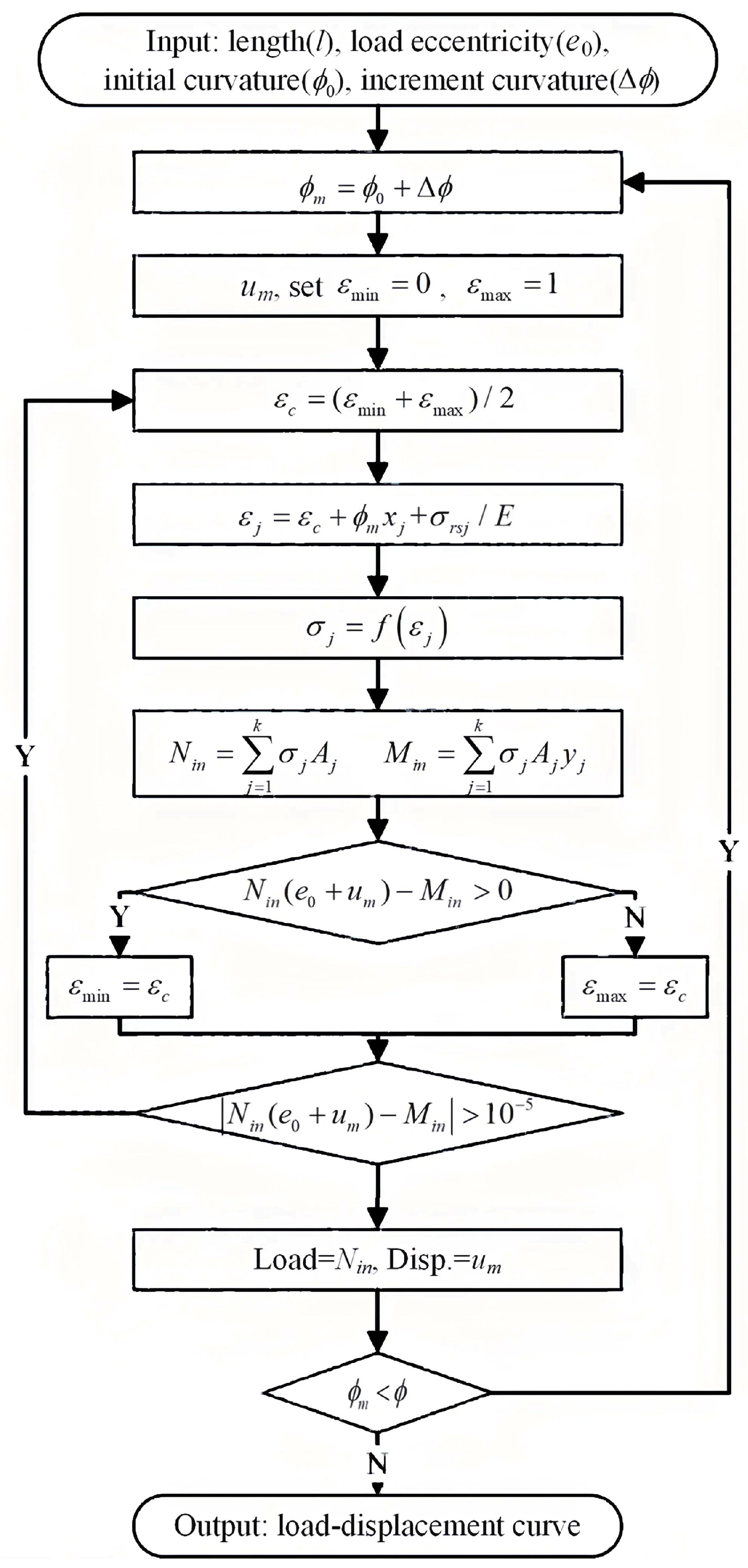
2.3. Modeling Process
3. Buckling Resistance of BCF Thin-Walled Tube Columns Under Axial Compression
3.1. Finite Element Analysis
3.1.1. General
3.1.2. Material Properties
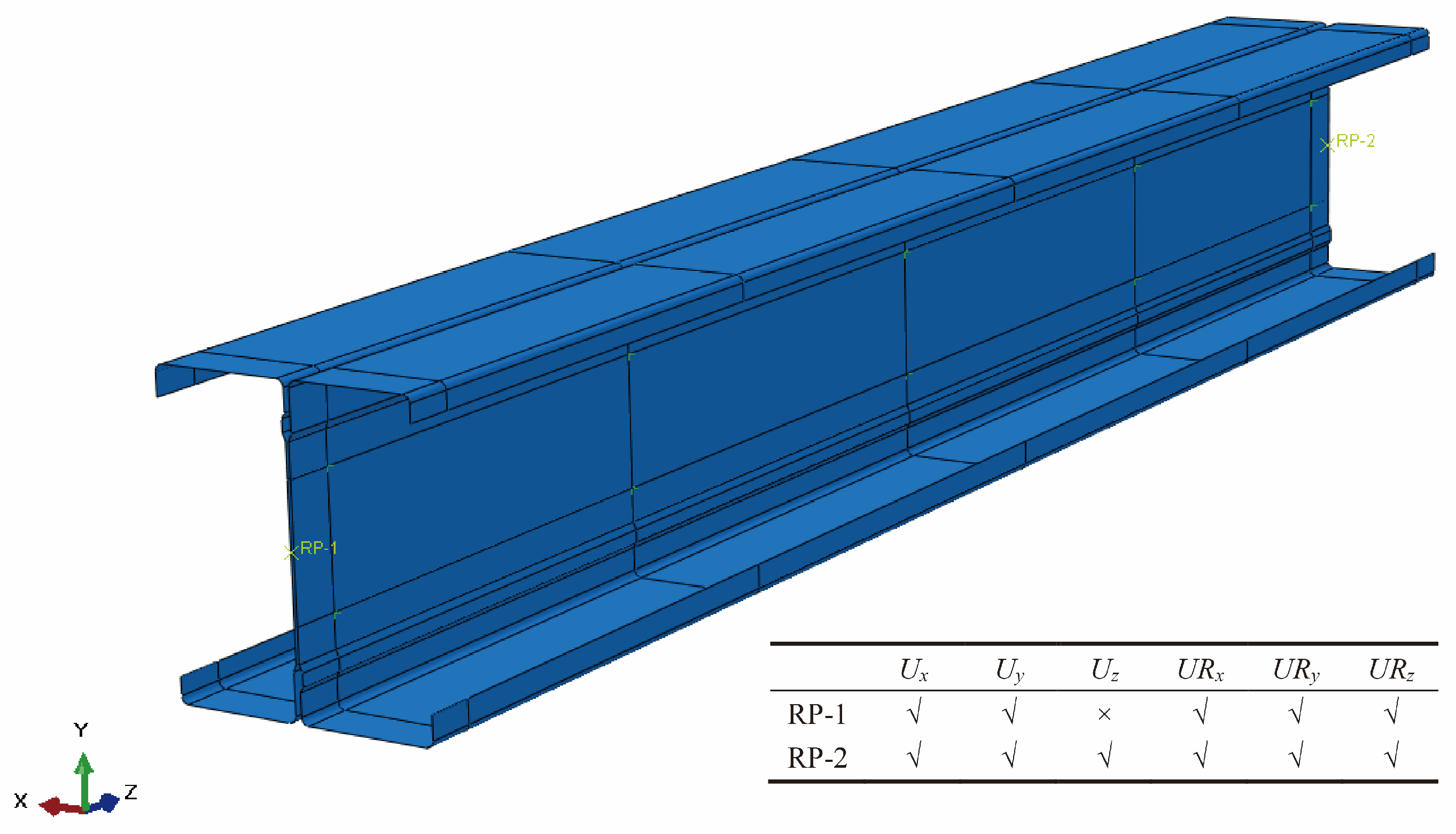
3.1.3. Boundary Conditions and Loading Method
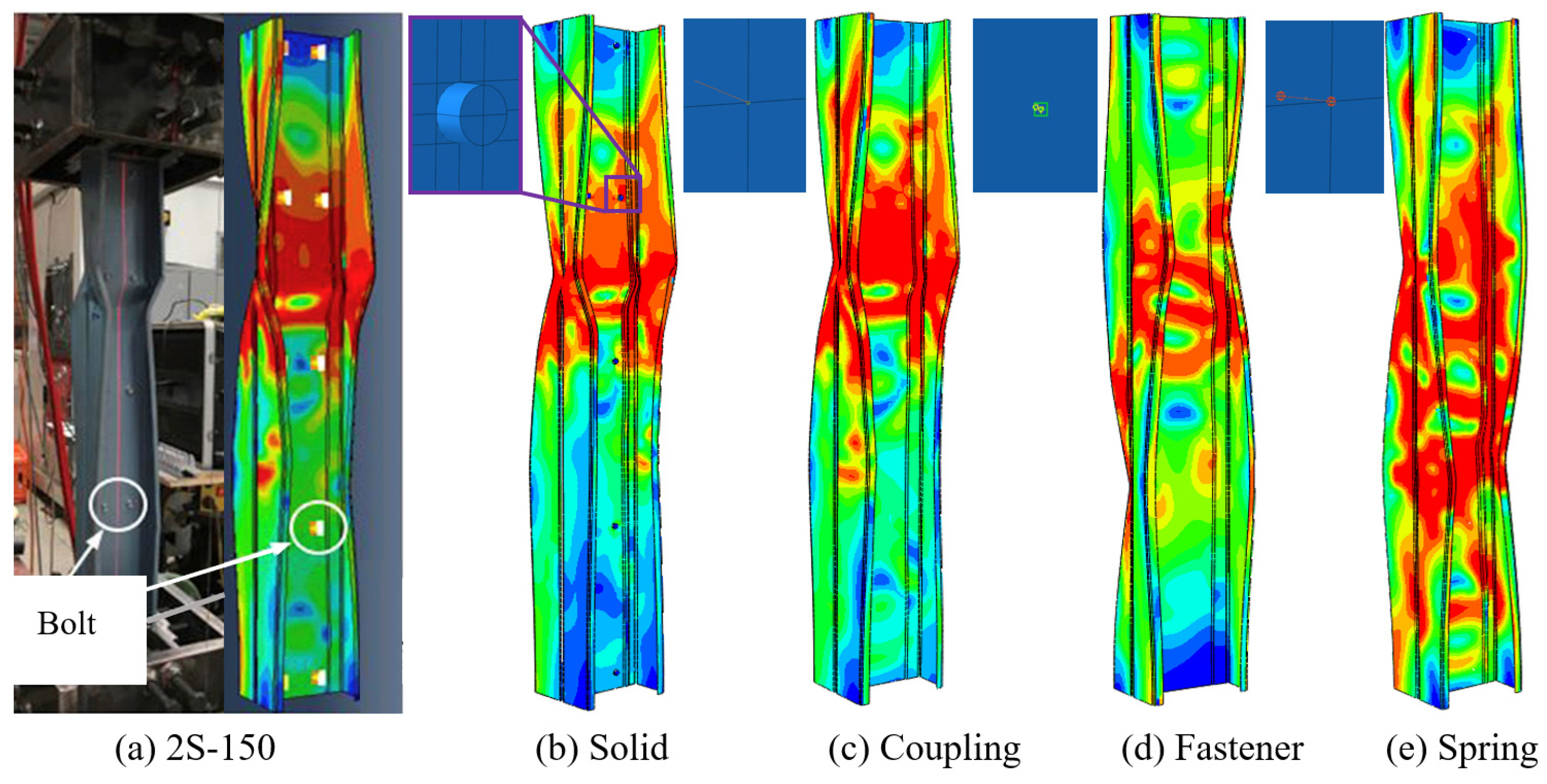
3.1.4. Contact and Bolt Simplification
3.1.5. Initial Geometric Imperfections and Residual Stresses
3.1.6. Mesh Sensitivity Analysis
3.1.7. Verification of FE Model
3.1.8. Parametric Studies
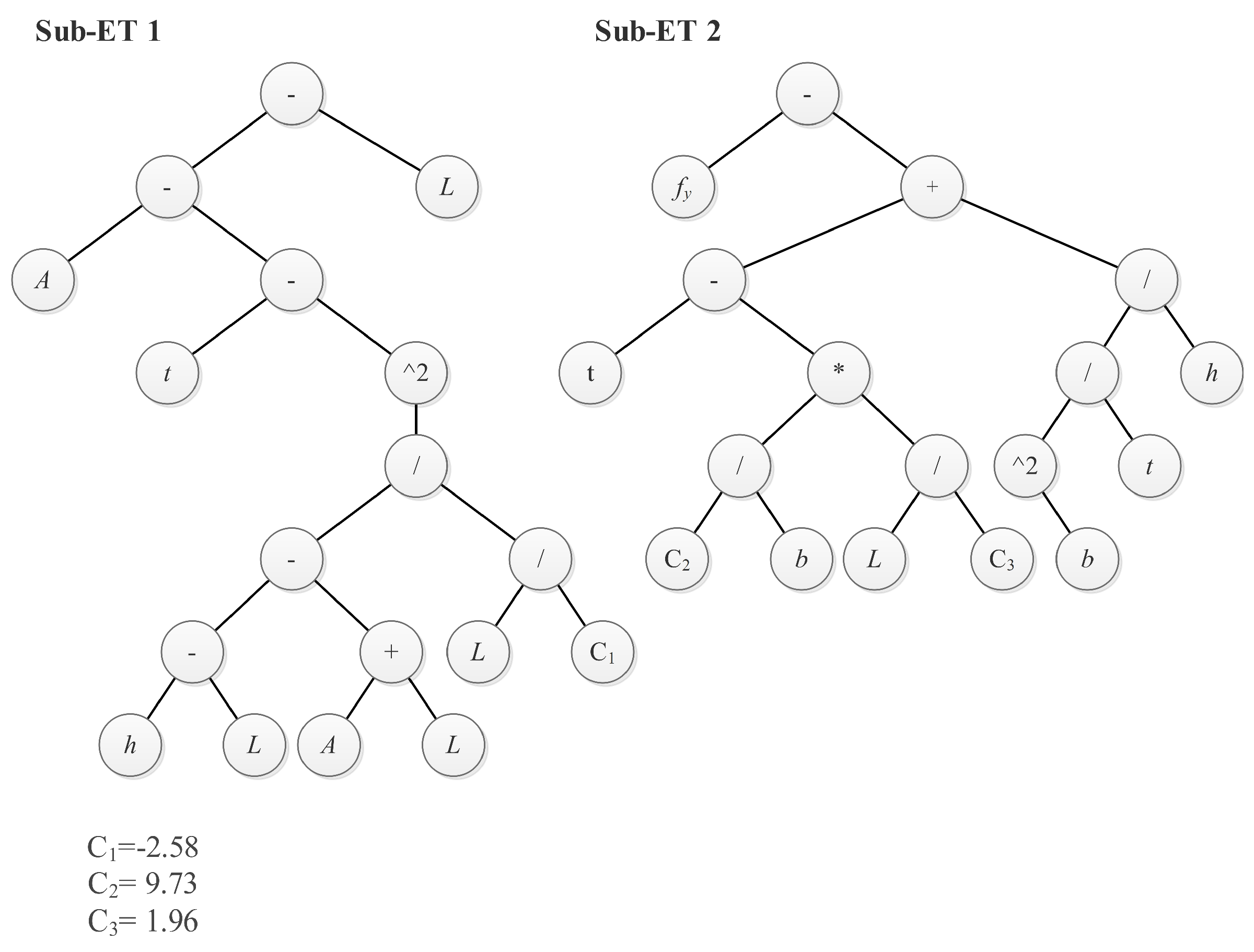
3.2. GEP Model Development
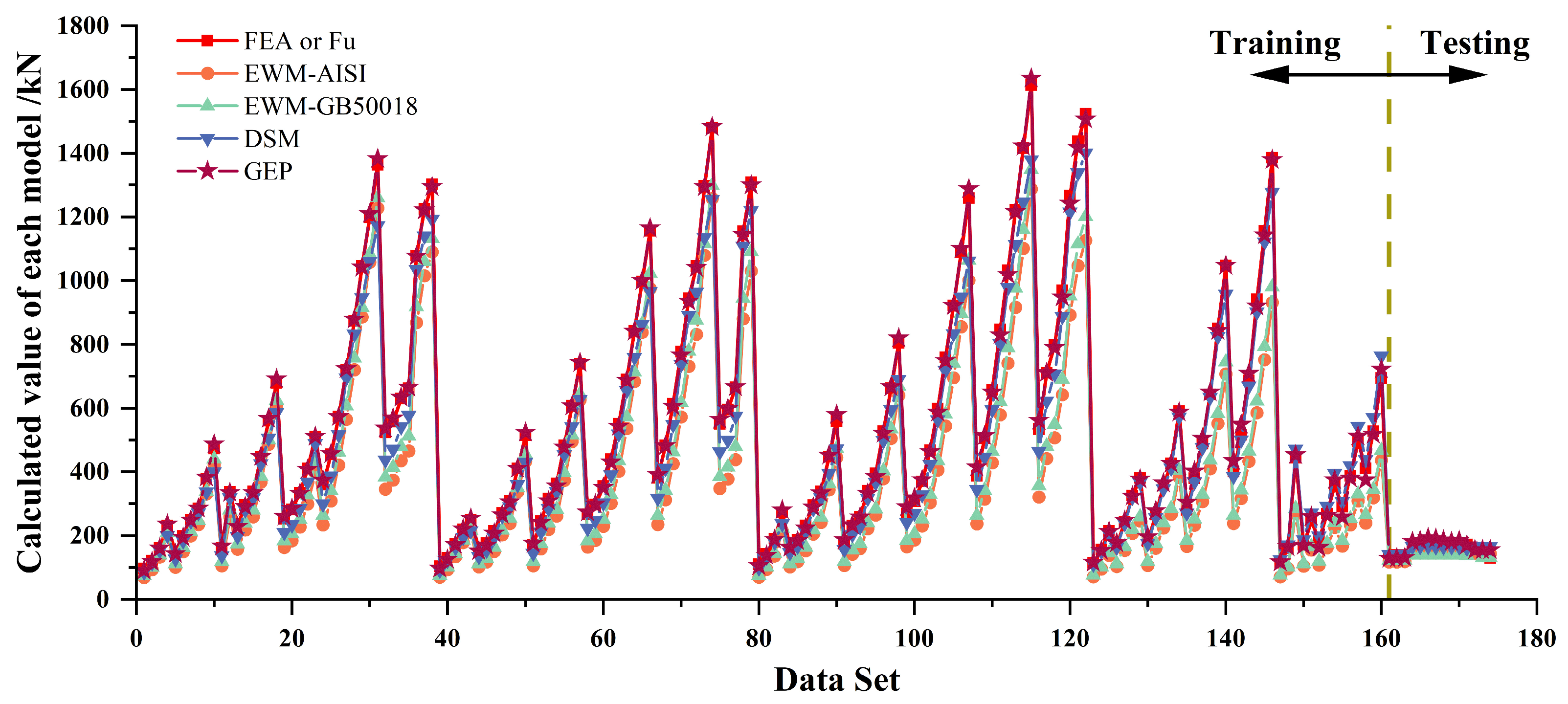
3.3. Performance Analysis and Model Validity
- Effective Width Method
- 2.
- Direct Strength Method
4. Buckling Resistance of Cold-Formed Thick-Walled Steel Columns Under Combined Axial Compression and Bending
4.1. Database
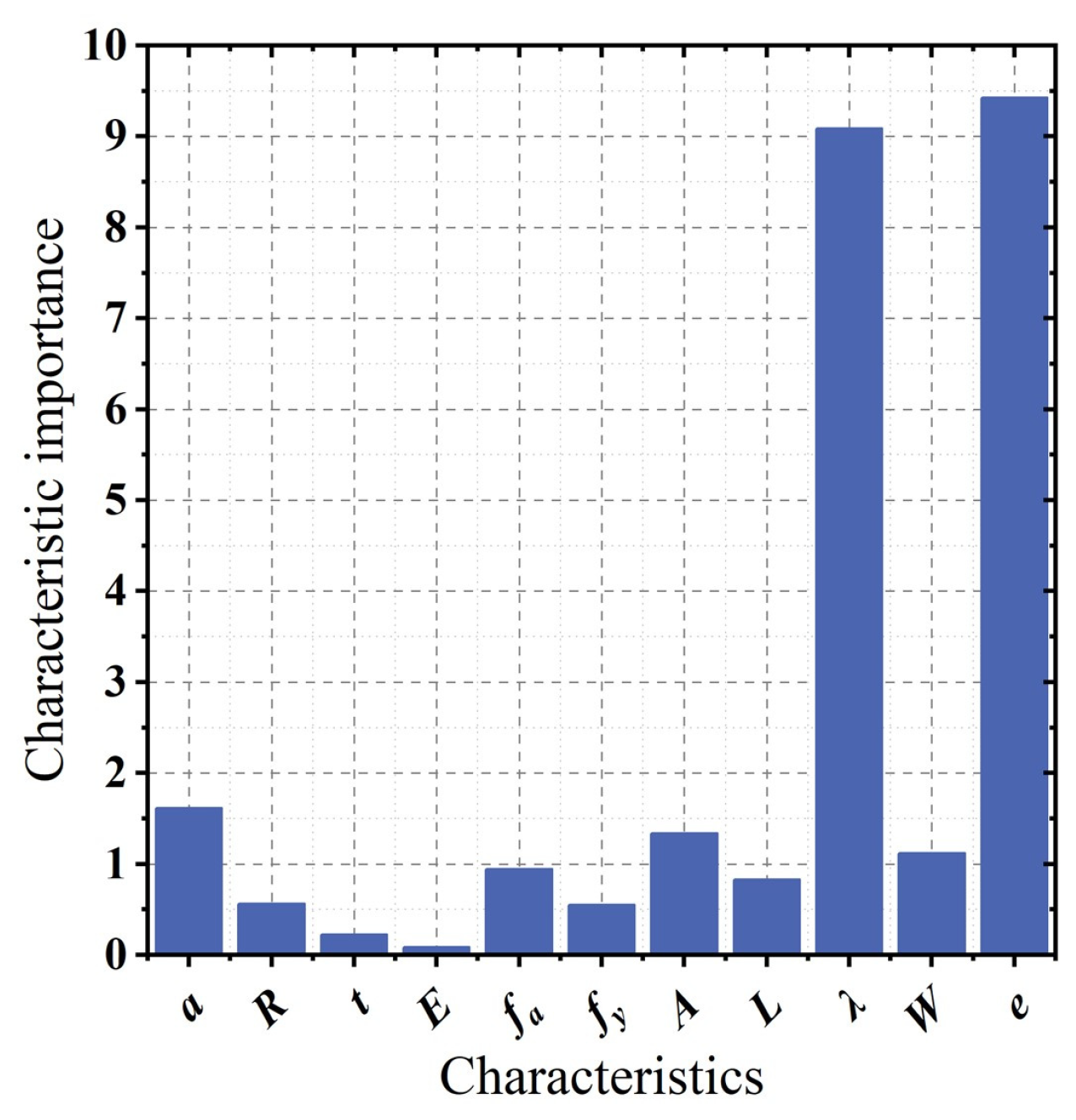
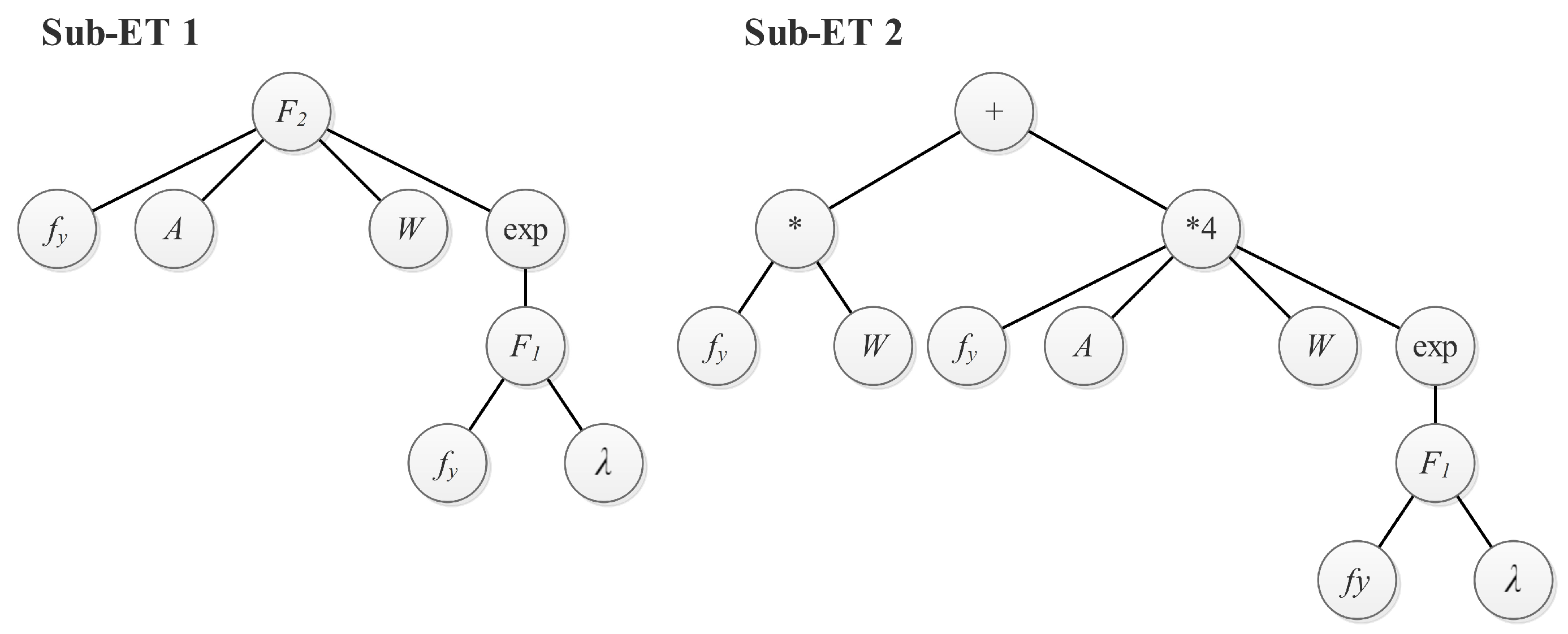
4.2. GEP Model Development
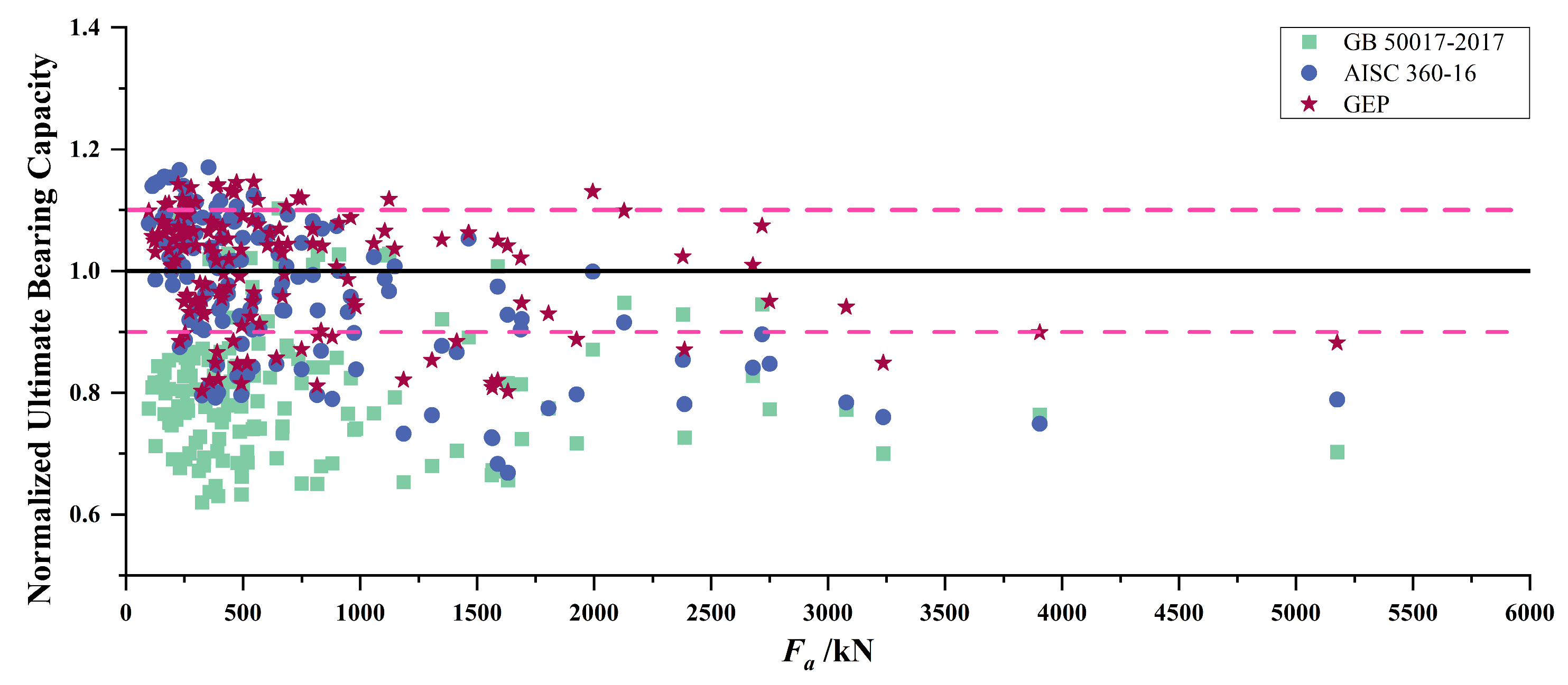
4.3. Validation and Analysis of the GEP Model
- American specification
- 2.
- Chinese specification
5. Conclusions
- The study of the buckling resistance of BCF thin-walled tube columns under axial compression illustrates that the GEP model does not need to consider too many influencing factors (e.g., correlated buckling and elastic critical stress) to avoid excessive second-order errors. Comparing the results calculated by formulae based on GEP with the EWM and DSM calculation results on the test set, we found that the average value of the EWM is about 0.75, and that of the DSM is 0.92, while the average value and R2 of the results calculated using the GEP model exceed 0.95.
- The study of the buckling resistance of cold-formed thick-walled steel columns under combined axial compression and bending illustrates that GEP can be used to construct a mechanical model similar to the existing specifications through an artificially specified mechanical model form. Comparing the results calculated by formulae based on GEP with the experimental data revealed that the average value was 1.007, with an R2 of 0.986.
- All R2 values were greater than 0.95, indicating satisfactory accuracy in predicting the ultimate bearing capacity, and the comparison shows that GEP performs better than the existing design methods.
- GEP performs better in predicting the ultimate load capacity of steel members, which solves the problem that the theoretical model cannot fully reflect the real situation of new steel structural members.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- AISI S100; North American Specification for the Design of Cold-Formed Steel Structural Members. American Iron and Steel Institute: Washington, DC, USA, 2016.
- AS/NZS 4600; Cold-Formed Steel Structures. Australian/New Zealand Standard: Sydney, Australia, 2018.
- Stone, T.A.; LaBoube, R.A. Behavior of cold-formed steel built-up I-sections. Thin-Walled Struct. 2005, 43, 1805–1817. [Google Scholar] [CrossRef]
- Roy, K.; Ting TC, H.; Lau, H.H.; Lim, J.B. Effect of thickness on the behaviour of axially loaded back-to-back cold-formed steel built-up channel sections-Experimental and numerical investigation. Structures 2018, 16, 327–346. [Google Scholar] [CrossRef]
- Hou, G. Experimental Research and Numerical Analysis on Axial Compression Performance of Cold-Formed Non-Thin-Walled Square Hollow Sections; Tongji University: Shanghai, China, 2011. (In Chinese) [Google Scholar]
- Liu, Z.; Liu, H.; Chen, Z.; Zhang, G. Structural behavior of cold-formed thick-walled rectangular steel columns. J. Constr. Steel Res. 2018, 147, 277–292. [Google Scholar] [CrossRef]
- Tong, L.; Hou, G.; Chen, Y.; Zhou, F.; Shen, K.; Yang, A. Experimental investigation on longitudinal residual stresses for cold-formed thick-walled square hollow sections. J. Constr. Steel Res. 2012, 73, 105–116. [Google Scholar] [CrossRef]
- Tenpe, A.R.; Patel, A. Application of genetic expression programming and artificial neural network for prediction of CBR. Road Mater. Pavement Des. 2020, 21, 1183–1200. [Google Scholar] [CrossRef]
- D’Aniello, M.; Güneyisi, E.M.; Landolfo, R.; Mermerdaş, K. Analytical prediction of available rotation capacity of cold-formed rectangular and square hollow section beams. Thin-Walled Struct. 2014, 77, 141–152. [Google Scholar] [CrossRef]
- Cevik, A. A new formulation for web crippling strength of cold-formed steel sheeting using genetic programming. J. Constr. Steel Res. 2007, 63, 867–883. [Google Scholar] [CrossRef]
- Momeni, M.; Hadianfard, M.A.; Bedon, C.; Baghlani, A. Damage evaluation of H-section steel columns under impulsive blast loads via gene expression programming. Eng. Struct. 2020, 219, 110909. [Google Scholar] [CrossRef]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Zhang, X.D.; Li, J. Gene expression programming based on parallel tabu search for improving model accuracy. Appl. Mech. Mater. 2013, 411, 1930–1934. [Google Scholar] [CrossRef]
- Wang, M.; Wan, W. A new empirical formula for evaluating uniaxial compressive strength using the Schmidt hammer test. Int. J. Rock Mech. Min. Sci. 2019, 123, 104094. [Google Scholar] [CrossRef]
- Lu, Q.; Zhou, S.; Tao, F.; Luo, J.; Wang, Z. Enhancing gene expression programming based on space partition and jump for symbolic regression. Inf. Sci. 2021, 547, 553–567. [Google Scholar] [CrossRef]
- ABAQUS. User Manual, version 6.16; DS SIMULIA Corp.: Providence, RI, USA, 2021. [Google Scholar]
- Rokilan, M.; Mahendran, M. Elevated temperature mechanical properties of cold-rolled steel sheets and cold-formed steel sections. J. Constr. Steel Res. 2020, 167, 105851. [Google Scholar] [CrossRef]
- Schafer, B.W.; Peköz, T. Computational modeling of cold-formed steel: Characterizing geometric imperfections and residual stresses. J. Constr. Steel Res. 1998, 47, 193–210. [Google Scholar] [CrossRef]
- Kechidi, S.; Fratamico, D.C.; Schafer, B.W.; Castro, J.M.; Bourahla, N. Simulation of screw connected built-up cold-formed steel back-to-back lipped channels under axial compression. Eng. Struct. 2020, 206, 110109. [Google Scholar] [CrossRef]
- Nie, S.; Zhou, T.; Eatherton, M.R.; Li, J.; Zhang, Y. Compressive behavior of built-up double-box columns consisting of four cold-formed steel channels. Eng. Struct. 2020, 222, 111133. [Google Scholar] [CrossRef]
- Vy, S.T.; Mahendran, M.; Sivaprakasam, T. Built-up back-to-back cold-formed steel compression members failing by local and distortional buckling. Thin-Walled Struct. 2021, 159, 107224. [Google Scholar] [CrossRef]
- Fratamico, D.C.; Torabian, S.; Zhao, X.; Rasmussen, K.J.; Schafer, B.W. Experiments on the global buckling and collapse of built-up cold-formed steel columns. J. Constr. Steel Res. 2018, 144, 65–80. [Google Scholar] [CrossRef]
- GB 50205-2020; Standard for Acceptance of Construction Quality of Steel Structure. China Architecture & Building Press: Beijing, China, 2020. (In Chinese)
- Gardner, L.; Nethercot, D.A. Numerical modeling of stainless steel structural components—A consistent approach. J. Struct. Eng. 2004, 130, 1586–1601. [Google Scholar] [CrossRef]
- Lu, Y. Research on the Instability Mechanism and Bearing Capacity Design Method of Cold-Formed Thin-Walled Steel Double-Leg Split Axial Compression Columns; Changan University: Xi’an, China, 2018. (In Chinese) [Google Scholar]
- Ting, C.H.T. The Behaviour of Axially Loaded Cold-Formed Steel Back-to-Back C-Channel Built-Up Columns. Ph.D. Thesis, Curtin University, Bentley, Australia, 2013. [Google Scholar]
- Wang, Q. Experimental and Theoretical Research on Bearing Capacity of Cold-Formed Thin-Walled Steel Composite Columns with Open Double Legs; Changan University: Xi’an, China, 2009. (In Chinese) [Google Scholar]
- GB 50018-2002; Technical Code of Cold-Formed Thin-Wall Steel Structures. China Architecture & Building Press: Beijing, China, 2002. (In Chinese)
- Zhou, Y.; Huang, D.; Li, T.; Li, Y. Buckling resistance of cold-formed thick-walled steel columns under combined axial compression and bending. J. Build. Eng. 2022, 51, 104300. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Wen, D.H.; Li, Y.Q.; Ma, Y. Distribution patterns of material properties for cross-section of cold-formed thick-walled steel rectangular tubes. J. Tongji Univ. (Nat. Sci.) 2016, 44, 981–990. (In Chinese) [Google Scholar]
- Wang, L.P. Experimental Investigation on Cold-Forming Effect of Thick-Walled Steel Sections; Tongji University: Shanghai, China, 2011. (In Chinese) [Google Scholar]
- Zhu, A.Z. Experimental Investigation of Cold-Formed Effect on Thick-Walled Steel Members and Analysis of the Cold-Formed Residual Stress Field. Master’s Thesis, Wuhan University, Wuhan, China, 2004. (In Chinese). [Google Scholar]
- Liu, D.; Liu, H.; Chen, Z.; Liao, X. Structural behavior of extreme thick-walled cold-formed square steel columns. J. Constr. Steel Res. 2017, 128, 371–379. [Google Scholar] [CrossRef]
- ANSI/AISC 360-16; Specification for Structural Steel Buildings. American Institute of Steel Construction (AISC): Chicago, IL, USA, 2016.
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017. (In Chinese)
- Li, G.W.; Li, Y.Q. Overall stability behavior of axially compressed cold-formed thick-walled steel tubes. Thin-Walled Struct. 2018, 125, 234–244. [Google Scholar] [CrossRef]





| Parameter | Setting | |
|---|---|---|
| General | Chromosomes | 30 |
| Fitness function | Equation (2) | |
| Genetic operators | Mutation rate | 0.044 |
| Inversion rate | 0.1 | |
| IS transposition rate | 0.1 | |
| RIS transposition rate | 0.1 | |
| Gene transposition rate | 0.1 | |
| One-point recombination rate | 0.3 | |
| Two-point recombination rate | 0.3 | |
| Gene recombination rate | 0.1 | |
| Random numerical constant | RNC mutation | 0.00206 |
| DC mutation | 0.00206 | |
| DC inversion | 0.00546 | |
| DC IS transposition | 0.00546 | |
| Constants per gene | 10 | |
| Data type | Floating-point | |
| Value range | −10–10 |
| 2S-150 [20] | Solid | Coupling | Fastener | Spring | |
|---|---|---|---|---|---|
| Load (kN) | 94.88 | 99.79 | 97.91 | 97.62 | 97.75 |
| Error | / | 5.1% | 3.1% | 2.9% | 3% |
| Parameters | Value |
|---|---|
| Web height (h/mm) | 90, 120, 150, 180, 210, 240 |
| Single-member flange width (b/mm) | 0.33 h, 0.4 h, 0.5 h, 0.67 h, h |
| Lip width (d/mm) | 0.5 b |
| Thickness (t/mm) | 1, 1.2, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5 |
| Initial geometric imperfections | b/100 |
| Bolt transverse distance (e) | h/2 |
| Bolt position along the length direction | 0.25 L, 0.5 L, 0.75 L |
| Type | Parameters | Minimum | Maximum |
|---|---|---|---|
| Input | Calculated length (L/mm) | 108 | 288 |
| Input | Single-member flange width (b/mm) | 30 | 210 |
| Lip width (d/mm) | 15 | 40 | |
| Input | Web height (h/mm) | 90 | 240 |
| Input | Thickness (t/mm) | 1 | 5 |
| Input | Outside diameter of rounded corner (R/mm) | 2 | 10 |
| Initial geometric imperfection (Im/mm) | 0.3 | 2.1 | |
| Elastic modulus (E/GPa) | 216 | 216 | |
| Input | Yield strength (fy/MPa) | 235 | 235 |
| Input | Total area (A/mm2) | 352 | 4773.12 |
| Output | Ultimate bearing capacity (FEA/kN) | 96.38 | 1613.7 |
| Model | R2 | RMSE | RAE | Average | SD | |
|---|---|---|---|---|---|---|
| EWM-Train | GB50018-2020 | 0.978 | 143.13 | 0.411 | 0.754 | 0.051 |
| AISI S100 2016 | 0.973 | 171.90 | 0.499 | 0.703 | 0.063 | |
| DSM-Train | 0.990 | 67.13 | 0.169 | 0.923 | 0.069 | |
| GEP-Train | 1.000 | 11.44 | 0.029 | 0.999 | 0.031 | |
| EWM-Test | GB50018-2002 | 0.723 | 47.22 | 1.743 | 0.733 | 0.108 |
| AISI S100 2016 | 0.743 | 42.12 | 1.527 | 0.783 | 0.129 | |
| DSM-Test | 0.823 | 13.35 | 0.417 | 0.967 | 0.100 | |
| GEP-Test | 0.951 | 11.49 | 0.266 | 0.977 | 0.073 | |
| Source | Specimen | L | b | d | h | t | R | Im | E | fy | A | Fu | FGEP | FGEP/Fu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [25] | SC3-140-A1 | 451 | 43.2 | 14.5 | 143.5 | 1.48 | 2.4 | 0.4 | 205 | 305.4 | 748.82 | 130.7 | 128.71 | 0.98 |
| SC3-140-A2 | 451 | 42.8 | 14.9 | 144.4 | 1.48 | 2.4 | 0.4 | 205 | 305.4 | 751.48 | 139.6 | 129.96 | 0.93 | |
| SC3-140-A3 | 451 | 43.4 | 15.3 | 143.1 | 1.48 | 2.4 | 0.4 | 205 | 305.4 | 753.56 | 138.8 | 130.40 | 0.94 | |
| [26] | 90S50L300-1 | 277 | 49.8 | 14.6 | 91.3 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 516.72 | 172.5 | 180.72 | 1.05 |
| 90S50L300-2 | 272 | 49.7 | 14.5 | 91.8 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 516.96 | 171.6 | 184.31 | 1.08 | |
| 90S50L300-3 | 261 | 49.4 | 14.5 | 92.9 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 518.16 | 167.6 | 192.80 | 1.15 | |
| 90S100L300-3 | 262 | 49.7 | 14.6 | 90.8 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 515.04 | 171.2 | 189.93 | 1.11 | |
| 90S100L300-4 | 268 | 49.5 | 14.6 | 90.6 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 513.6 | 173.9 | 184.95 | 1.06 | |
| 90S200L300-1 | 273.5 | 49.4 | 14.6 | 90.7 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 513.36 | 170.3 | 181.08 | 1.06 | |
| 90S200L300-2 | 269.5 | 49.4 | 14.6 | 90.7 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 513.36 | 177.5 | 183.81 | 1.03 | |
| 90S200L300-4 | 280.5 | 48.3 | 14 | 89.5 | 1.2 | 1.5 | 0.5 | 205.72 | 557.5 | 502.32 | 171.9 | 169.64 | 0.99 | |
| [27] | DC450-1 | 450 | 41 | 14 | 140 | 1.6 | 2.4 | 0.4 | 223 | 334.04 | 779.52 | 160 | 154.09 | 0.96 |
| DC450-2 | 450 | 41 | 14 | 140 | 1.6 | 2.4 | 0.4 | 223 | 334.04 | 779.52 | 150 | 154.09 | 1.03 | |
| DC450-3 | 450 | 41 | 14 | 140 | 1.6 | 2.4 | 0.4 | 223 | 334.04 | 779.52 | 130 | 154.09 | 1.18 |
| Specimen | B | H | R | t | fy | E | Grade | L | δ0 | Fu | Fa | Fa/Fu | FGEP | FGEP/Fu |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S108 × 108 × 10-1 | 108 | 108 | 20.5 | 10.1 | 511 | 199 | Q345 | 3620 | 1.34 | 830 | 736 | 0.89 | 787.6 | 0.949 |
| S108 × 108 × 10-2 | 108 | 108 | 20.5 | 10.1 | 511 | 199 | Q345 | 3620 | 1 | 854 | 745 | 0.87 | 787.6 | 0.922 |
| S135 × 135 × 10-1 | 135 | 135 | 21.6 | 10 | 391 | 206 | Q345 | 3495 | 3.6 | 1120 | 1148 | 1.03 | 1271.1 | 1.135 |
| S135 × 135 × 10-2 | 135 | 135 | 21.6 | 10 | 391 | 206 | Q345 | 3495 | 4.15 | 1065 | 1133 | 1.06 | 1271.1 | 1.194 |
| R400 × 200 × 10-1 | 400 | 200 | 24.1 | 10 | 368 | 204 | Q345 | 3345 | 4.24 | 3405 | 3488 | 1.02 | 3747.9 | 1.101 |
| R400 × 200 × 10-2 | 400 | 200 | 24.1 | 10 | 368 | 204 | Q345 | 3345 | 4.41 | 3340 | 3479 | 1.04 | 3747.9 | 1.122 |
| S250 × 250 × 8-1 | 250 | 250 | 22.3 | 7.9 | 395 | 197 | Q345 | 2940 | 2 | 2439 | 2739 | 1.12 | 2587.5 | 1.061 |
| S250 × 250 × 8-2 | 250 | 250 | 22.3 | 7.9 | 395 | 197 | Q345 | 2940 | 7.7 | 2275 | 2572 | 1.13 | 2587.5 | 1.137 |
| S140 × 140 × 10-1 | 140 | 140 | 25 | 10 | 406 | 206 | Q345 | 3110 | 1.36 | 1463 | 1445 | 0.99 | 1430.6 | 0.978 |
| S140 × 140 × 10-2 | 140 | 140 | 25 | 10 | 406 | 206 | Q345 | 4150 | 1.82 | 1130 | 1092 | 0.97 | 1191.7 | 1.055 |
| S200 × 200 × 12-1 | 200 | 200 | 36 | 12 | 368 | 206 | Q235 | 2730 | 1.3 | 2688 | 2740 | 1.02 | 2009.9 | 0.748 |
| S200 × 200 × 12-2 | 200 | 200 | 36 | 12 | 368 | 206 | Q235 | 3480 | 1.66 | 2478 | 2564 | 1.04 | 1937.5 | 0.782 |
| S200 × 200 × 12-3 | 200 | 200 | 36 | 12 | 368 | 206 | Q235 | 4160 | 1.98 | 2233 | 2359 | 1.06 | 1859.8 | 0.833 |
| S200 × 200 × 16-1 | 200 | 200 | 48 | 16 | 453 | 206 | Q345 | 2650 | 1.24 | 4040 | 4383 | 1.09 | 3660.8 | 0.906 |
| S200 × 200 × 16-2 | 200 | 200 | 48 | 16 | 453 | 206 | Q345 | 3380 | 1.59 | 3875 | 3997 | 1.03 | 3477.0 | 0.897 |
| S200 × 200 × 16-3 | 200 | 200 | 48 | 16 | 453 | 206 | Q345 | 4110 | 1.93 | 3630 | 3579 | 0.99 | 3261.4 | 0.898 |
| S150 × 150 × 8-1 | 150 | 150 | 20 | 8 | 503 | 206 | Q345 | 2295 | 1.1 | 1964 | 1853 | 0.94 | 1443.2 | 0.735 |
| S150 × 150 × 8-2 | 150 | 150 | 20 | 8 | 503 | 206 | Q345 | 3150 | 1.51 | 1428 | 1516 | 1.06 | 1310.5 | 0.918 |
| S150 × 150 × 8-3 | 150 | 150 | 20 | 8 | 503 | 206 | Q345 | 4005 | 1.92 | 1140 | 1170 | 1.03 | 1154.5 | 1.013 |
| Type | Parameters | Minimum | Maximum |
|---|---|---|---|
| Input | The long edge (a/mm) | 86 | 350 |
| Outside diameter of rounded corner (R/mm) | 20 | 48 | |
| Thickness (t/mm) | 8 | 16 | |
| Elastic modulus (E/GPa) | 204 | 204 | |
| Input | Average strength (fa/MPa) | 281 | 552.21 |
| Input | Yield strength (fy/MPa) | 235 | 345 |
| Input | Total area (A/mm2) | 2276.24 | 20,277.24 |
| Input | Calculated length (L/mm) | 608.25 | 27,218.23 |
| Input | Slenderness ratio (λ) | 17.01 | 204.03 |
| Input | Plastic section modulus (W/mm3) | 73,264 | 2,679,394 |
| Input | Eccentricity (e/mm) | 0 | 850.76 |
| Output | Ultimate bearing capacity (Fa/kN) | 64.05 | 7702.96 |
| Model | R2 | RMSE | RAE | Average | SD |
|---|---|---|---|---|---|
| AISC 360-16 | 0.978 | 206.05 | 0.171 | 0.967 | 0.117 |
| GB 50017-2017 | 0.970 | 245.67 | 0.269 | 0.823 | 0.101 |
| GEP | 0.986 | 124.47 | 0.136 | 1.007 | 0.092 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, W.; Liu, S. Bearing Capacity Prediction of Cold-Formed Steel Columns with Gene Expression Programming. Buildings 2025, 15, 1597. https://doi.org/10.3390/buildings15101597
Kong W, Liu S. Bearing Capacity Prediction of Cold-Formed Steel Columns with Gene Expression Programming. Buildings. 2025; 15(10):1597. https://doi.org/10.3390/buildings15101597
Chicago/Turabian StyleKong, Wei, and Shouhua Liu. 2025. "Bearing Capacity Prediction of Cold-Formed Steel Columns with Gene Expression Programming" Buildings 15, no. 10: 1597. https://doi.org/10.3390/buildings15101597
APA StyleKong, W., & Liu, S. (2025). Bearing Capacity Prediction of Cold-Formed Steel Columns with Gene Expression Programming. Buildings, 15(10), 1597. https://doi.org/10.3390/buildings15101597





