Experimental and Analytical Study on the Flexural Performance of Layered ECC–Concrete Composite Beams
Abstract
1. Introduction
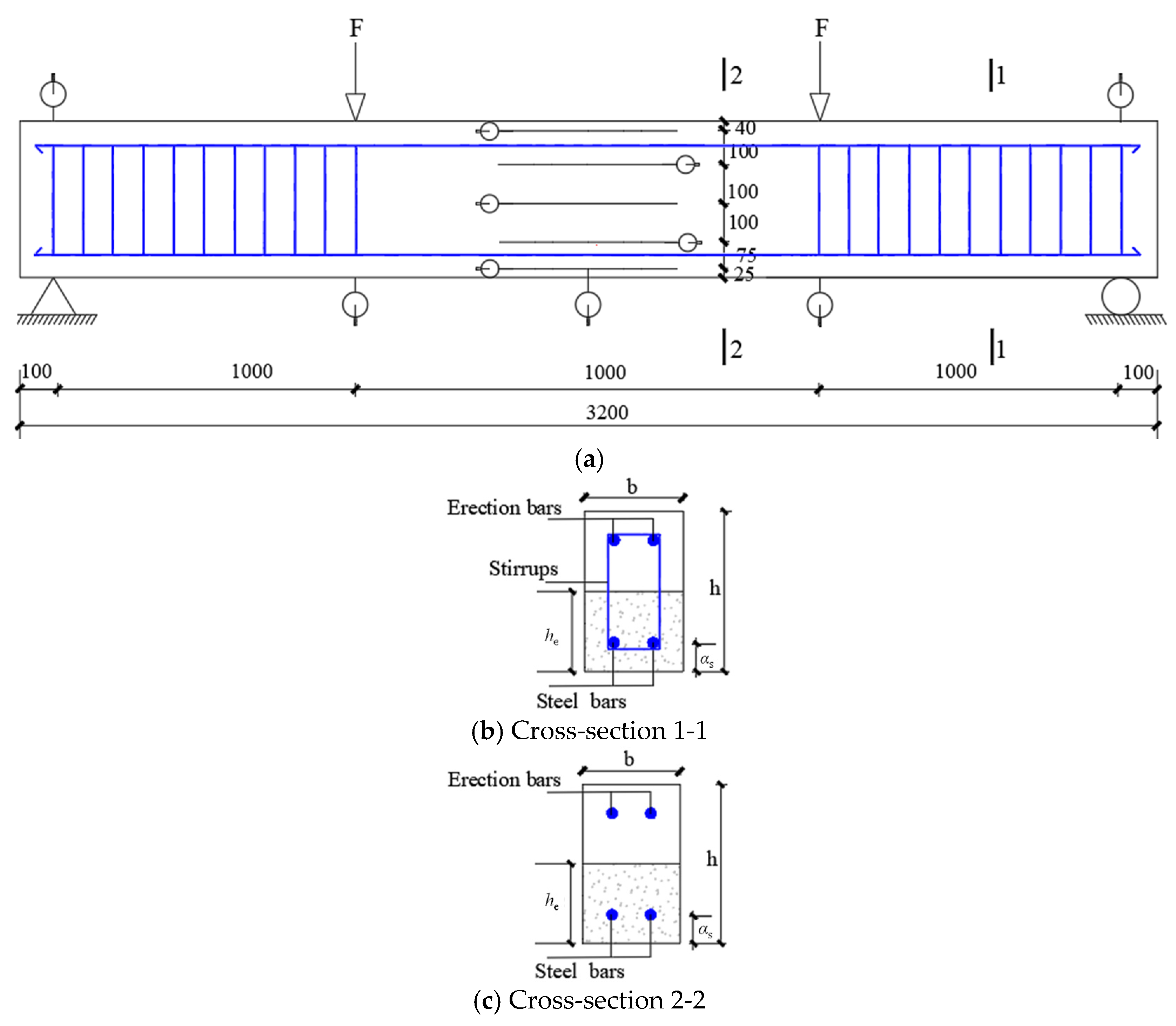
2. Experimental Program
2.1. Specimen Preparation
2.2. Materials Properties
2.3. Test Setup
3. Experimental Results
3.1. Failure Modes
3.2. Strain Development
3.3. Moment-Deflection Curves
3.4. Ductility and Energy Dissipation Capacity
3.5. Crack Propagation
4. Section Analysis of Composite Beams
- (1)
- The tensile stress–strain relationship of ECC can be expressed as follows [15]:
- (2)
- The stress–strain relationship of concrete in compression and tension is applicable to concrete with a cubic compressive strength ranging from 20 to 80 MPa [27]. The compressive stress–strain relationship can be expressed as follows:
- (3)
- The stress–strain relationship of steel bars is simplified as a bilinear model, as shown in Equation (7).
- (4)
- The failure criterion of concrete was that the maximum compressive strain reached the ultimate compressive strain εcu. The failure criteria for ECC and steel bars were that the tensile strain reached the ultimate tensile strain εetu and εsu, respectively.
5. Simplified Methods for Predicting Flexural Capacity, Failure Mode and Deflection
6. Discussion and Conclusions
6.1. Discussion
6.2. Conclusions
- (1)
- This study comprehensively explored the bending performance of ECC–concrete composite beams reinforced with hot-rolled ribbed steel bars. The findings revealed that the longitudinal tensile reinforcement ratio significantly impacted the bending performance, whereas varying the ECC layer thickness within the range of 0.20h~0.32h (h denotes the beam depth) had a relatively small effect on the bending performance of the tested composite beams. Importantly, an adequate ECC layer thickness prevented delamination between the concrete and ECC layers.
- (2)
- Similar failure modes were identified in ECC–concrete composite beams and corresponding control RC beams. The application of ECC in the tensile zone markedly improved the bending bearing capacity and reduced the crack width. Multiple fine cracks with widths less than 0.2 mm appeared in composite beams before the longitudinal tensile reinforcement yield, with an increased reinforcement ratio enhancing crack control. The average crack width at the serviceability limit states of the composite beams was sensitive to the specimen size and steel strength, with the composite beams with high-yield-strength steel bars and large-sized sections exhibiting a larger average crack width at serviceability limit states.
- (3)
- An analytical cross-sectional model, grounded in the equilibrium conditions of the internal force and bending moment, was proposed. It successfully predicted the moment–deflection response of ECC–concrete composite beams, accommodating concrete grades within the range of C20 to C80. The model’s predictions aligned with the experimental results, affirming its accuracy in simulating moment–deflection responses. Interestingly, a size effect was shown for ductility expressed in terms of deflection, showing that the predicted ductility index values of the small composite beams with a depth of 120 mm and a relative pure bending length of 0.2 (the ratio of pure bending length to span length) were generally much lower than the experimental values, while the bearing capacity was not affected by the size effect.
- (4)
- This study introduced a simplified method for predicting the flexural bearing capacity and failure mode of ECC–concrete composite beams. This method demonstrated good agreement with the experimental results. Under serviceability conditions, the ACI 318 code provided reasonable midspan deflection values for composite beams failing in flexure. The proposed simplified methods have practical utility for real-world applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qin, F.J.; Wei, X.Y.; Lu, Y.F.; Zhang, Z.; Di, J.; Yin, Z. Flexural behaviour of high strength engineered cementitious composites (ECC)-reinforced concrete composite beams. Case Stud. Constr. Mater. 2023, 18, e02002. [Google Scholar] [CrossRef]
- Wang, R.; Hu, Z.; Li, Y. Review on the deterioration and approaches to enhance the durability of concrete in the freeze-thaw environment. Constr. Build. Mater. 2022, 321, 126371. [Google Scholar] [CrossRef]
- Atsbha, T.G.; Zhutovsky, S. The effect of external curing methods on the development of mechanical and durability-related properties of normal-strength concrete. Constr. Build. Mater. 2022, 324, 126706. [Google Scholar] [CrossRef]
- Kang, S.T.; Choi, J.I.; Koh, K.T.; Lee, K.S.; Lee, B.Y. Hybrid effects of steel fiber and microfiber on the tensile behavior of ultra-high performance concrete. Compos. Struct. 2016, 145, 37–42. [Google Scholar] [CrossRef]
- Jahami, A.; Dayaa, L.; Assaad, J.J.; Baalbaki, O.; Khatib, J. Flexural strength of structural beams cast using combined normal-weight and lightweight concrete mixtures. Buildings 2024, 14, 3787. [Google Scholar] [CrossRef]
- Zhou, J.; Qian, S.; Ye, Q.; Copuroglu, O.; Breugel, K.; Li, V.C. Improved fiber distribution and mechanical properties of engineered cementitious composites by adjusting the mixing sequence. Cem. Concr. Compos. 2012, 34, 342–348. [Google Scholar] [CrossRef]
- Li, V.; Wang, S.X.; Wu, C. Tensile strain-hardening behavior of PVA-ECC. ACI Mater. J. 2001, 98, 483–492. [Google Scholar]
- Li, V. On engineered cementitious composites (ECC)—A review of the material and its application. J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef]
- Kan, L.; Shi, R.; Zhu, J. Effect of fineness and calcium content of fly ash on the mechanical properties of Engineered Cementitious Composites (ECC). Constr. Build. Mater. 2019, 209, 476–484. [Google Scholar] [CrossRef]
- Arain, M.F.; Wang, M.; Chen, J.; Zhang, H. Study on PVA fiber surface modification for strain-hardening cementitious composites (PVA-SHCC). Constr. Build. Mater. 2019, 197, 107–116. [Google Scholar] [CrossRef]
- Wang, X.F.; Yang, Z.H.; Fang, C.; Han, N.; Zhu, G.; Tang, J.; Xing, F. Evaluation of the mechanical performance recovery of self-healing cementitious materials-its methods and future development: A review. Constr. Build. Mater. 2019, 212, 400–421. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, Z.; Ma, R.; Jiang, Z.; Zhang, Y.; Zhu, H. Insight into the mechanical performance of the UHPC repaired cementitious composite system after exposure to high temperatures. Materials 2021, 14, 4095. [Google Scholar] [CrossRef]
- Zhang, J.; Leung, C.K.Y.; Cheung, Y.N. Flexural performance of layered ECC-concrete composite beam. Compos. Sci. Technol. 2006, 66, 1501–1512. [Google Scholar] [CrossRef]
- Maalej, M.; Li, V.C. Engineered cementitious composites for effective FRP-strengthening of RC beams. Compos. Sci. Technol. 2005, 65, 1120–1128. [Google Scholar] [CrossRef]
- Maalej Li, V.C. Introduction of strain-hardening engineered cementitious composites in design of reinforced concrete flexural members for improved durability. ACI Struct. J. 1995, 92, 167–176. [Google Scholar]
- Maalej, M.; Ahmed, S.F.U.; Paramasivam, P. Corrosion durability and structural response of functionally-graded concrete beams. J. Adv. Concr. Technol. 2003, 1, 307–316. [Google Scholar] [CrossRef]
- Daugevicius, M.; Valivonis, J.; Skuturna, T.; Popov, V. RC Beams strengthened with HPFRCC: Experimental and numerical results. J. Civ. Eng. Manag. 2016, 22, 254–270. [Google Scholar] [CrossRef]
- Wang, N.; Xu, S.L. Flexural response of reinforced concrete beams strengthened with post-poured ultra high toughness cementitious composites layer. J. Cent. South Univ. 2011, 18, 932–939. [Google Scholar] [CrossRef]
- Qin, F.J.; Zhang, Z.G.; Yin, Z.W.; Di, J.; Xu, L.J.; Xu, X.Q. Use of high strength, high ductility engineered cementitious composites (ECC) to enhance the flexural performance of reinforced concrete beams. J. Build. Eng. 2020, 32, 101746. [Google Scholar] [CrossRef]
- Ge, W.J.; Ashour, A.F.; Ji, X.; Cai, C.; Cao, D.F. Flexural behavior of ECC-concrete composite beams reinforced with steel bars. Constr. Build. Mater. 2018, 159, 175–188. [Google Scholar] [CrossRef]
- Maalej, M.; Quek, S.T.; Ahmed, S.F.U.; Zhang, J.; Lin, V.W.J.; Leong, K.S. Review of potential structural applications of hybrid fiber Engineered Cementitious Composites. Constr. Build. Mater. 2012, 36, 216–227. [Google Scholar] [CrossRef]
- Xu, S.L.; Wang, N.; Li, Q.H. Experimental study on the flexural performance of concrete beam strengthened with ultra-high toughness cementitious composites. Chin. Civ. Eng. J. 2010, 43, 17–22. [Google Scholar]
- Zhang, X.F.; Xu, S.L.; Li, H.D. Theoretical analysis of flexural performance of plain concrete beams strengthened with ultra-high toughness cementitious composites. China Civ. Eng. J. 2010, 43, 51–62. [Google Scholar]
- Zhang, J.; Wang, Z.B.; Ju, X.C.; Shi, Z.J. Simulation of flexural performance of layered ECC-concrete composite beam with fracture mechanics model. Eng. Fract. Mech. 2014, 131, 419–438. [Google Scholar] [CrossRef]
- Alca, N.; Alexander, S.D.B.; Macgregor, J.G. Effect of size on flexural behavior of high-strength concrete beams. ACI Struct. J. 1997, 94, 59–67. [Google Scholar]
- Appa, R.G.; Vijayanand, I.; Eligehausen, R. Studies on ductility and evaluation of minimum flexural reinforcement in RC beams. Mater. Struct. 2008, 41, 759–771. [Google Scholar] [CrossRef]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2010.
- Li, Z.H.; Su, X.Z. Experimental Investigation on Flexural Behavior of 500 MPa Reinforced Concrete Beams with and without skin reinforcement. Appl. Mech. Mater. 2013, 368–370, 1668–1673. [Google Scholar] [CrossRef]
- Li, Q.H.; Xu, S.L. Experimental investigation and analysis on flexural performance of functionally graded composite beam crack-controlled by ultrahigh toughness cementitious composites. Sci. China Ser. E Technol. Sci. 2009, 52, 1648–1664. [Google Scholar] [CrossRef]
- Ma, H.; Qian, S.Z.; Zhang, Z.G.; Lin, Z.; Li, V.C. Tailoring Engineered Cementitious Composites with local ingredients. Constr. Build. Mater. 2015, 101, 584–595. [Google Scholar] [CrossRef]
- GBT 50152-2012; Standard for Test Method of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012.
- Li, Z.H.; Wan, S.C.; Ma, C.F.; Guo, X. Flexural behaviour of concrete-basalt FRC beams with steel bars under concentrated load. Structures 2022, 39, 237–252. [Google Scholar] [CrossRef]
- Weiss, W.J.; Güler, K.; Shah, S.P. Localization and size-dependent response of reinforced concrete beams. ACI Struct. J. 2001, 98, 686–695. [Google Scholar]
- Ge, W.J.; Tang, R.; Wang, Y.; Zhang, Z.W.; Sun, C.; Yao, S.; Lu, W. Flexural performance of ECC-concrete composite beams strengthened with carbon fiber sheet. Results Eng. 2022, 13, 100334. [Google Scholar] [CrossRef]
- American Concrete Institute. Building Code Requirements for Structural Concrete (ACI 318-02) and Commentary (ACI 318R-02); ACI Committee 318: Farmington Hills, MI, USA, 2002. [Google Scholar]
- CEB-FIP Model Code 90. Model Code for Concrete Structures, Comite Euro-International du Beton, Bulletin No. 213/214; Thomas Telford Ltd.: London, UK, 1993.











| Specimen ID | As | ρ (%) | Asv | c (mm) | b (mm) | h (mm) | hcr-ECC (mm) | hcr-ECC/h |
|---|---|---|---|---|---|---|---|---|
| RC16-2 | 2B16 | 0.537 | A8@150 | 50 | 200 | 440 | 0 | 0 |
| RC16-3 | 3B16 | 0.806 | A8@150 | 50 | 200 | 440 | 0 | 0 |
| RC25-2 | 2B25 | 1.329 | A8@80 | 50 | 200 | 440 | 0 | 0 |
| RC25-3 | 3B25 | 1.993 | A8@50 | 50 | 200 | 440 | 0 | 0 |
| RCE16-2-1 | 2B16 | 0.568 | A8@150 | 30 | 200 | 400 | 92 | 0.23 |
| RCE16-2-2 | 2B16 | 0.537 | A8@150 | 50 | 200 | 440 | 132 | 0.30 |
| RCE16-2-3 | 2B16 | 0.537 | A8@150 | 50 | 200 | 440 | 90 | 0.20 |
| RCE16-3-1 | 3B16 | 0.852 | A8@150 | 30 | 200 | 400 | 92 | 0.23 |
| RCE16-3-2 | 3B16 | 0.806 | A8@150 | 50 | 200 | 440 | 132 | 0.30 |
| RCE16-3-3 | 3B16 | 0.806 | A8@150 | 50 | 200 | 440 | 90 | 0.20 |
| RCE25-2-1 | 2B25 | 1.405 | A8@80 | 30 | 200 | 400 | 101 | 0.25 |
| RCE25-2-2 | 2B25 | 1.329 | A8@80 | 50 | 200 | 440 | 141 | 0.35 |
| RCE25-2-3 | 2B25 | 1.329 | A8@80 | 50 | 200 | 440 | 108 | 0.27 |
| RCE25-3-1 | 3B25 | 2.107 | A8@50 | 30 | 200 | 400 | 101 | 0.25 |
| RCE25-3-2 | 3B25 | 1.993 | A8@50 | 50 | 200 | 440 | 141 | 0.35 |
| RCE25-3-3 | 3B25 | 1.993 | A8@50 | 50 | 200 | 440 | 108 | 0.27 |
| Bar Type | Diameter (mm) | fy (MPa) | fu (MPa) | E (GPa) |
|---|---|---|---|---|
| HRB400 | 8 | 409 | 526 | 198 |
| HRB400 | 12 | 410 | 511 | 199 |
| HRB500 | 16 | 560 | 686 | 200 |
| HRB500 | 25 | 567 | 596 | 200 |
| Specimen | fcr (mm) | fly (mm) | flu (mm) | Specimen | fcr (mm) | fly (mm) | flu (mm) |
|---|---|---|---|---|---|---|---|
| RC16-2 | 0.48 | 9.05 | 59.50 | RCE16-3-2 | 1.70 | 12.31 | 42.40 |
| RC16-3 | 1.53 | 10.45 | 46.74 | RCE16-3-3 | 1.58 | 12.52 | 43.83 |
| RC25-2 | 1.09 | 13.01 | 33.83 | RCE25-2-1 | 1.05 | 15.05 | 29.85 |
| RC25-3 | 1.23 | 12.95 | 22.92 | RCE25-2-2 | 0.66 | 13.76 | 28.96 |
| RCE16-2-1 | 1.38 | 13.17 | 58.86 | RCE25-2-3 | 0.94 | 13.91 | 29.90 |
| RCE16-2-2 | 1.25 | 12.43 | 54.60 | RCE25-3-1 | 1.47 | 15.37 | 20.46 |
| RCE16-2-3 | 1.21 | 12.15 | 56.32 | RCE25-3-2 | 1.43 | 14.56 | 19.64 |
| RCE16-3-1 | 1.10 | 12.81 | 45.68 | RCE25-3-3 | 1.15 | 14.51 | 21.30 |
| Specimen ID | Mcr (kN·m) | My (kN·m) | Mu (kN·m) | μ | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | Pre. | P/E | Exp. | Pre. | P/E | Exp. | Pre. | P/E | Exp. | Pre. | P/E | |
| RCE16-2-1 | 22.4 | 22.8 | 1.02 | 90.1 | 91.4 | 1.01 | 97.6 | 96.0 | 0.98 | 4.47 | 4.84 | 1.08 |
| RCE16-2-2 | 25.5 | 26.4 | 1.04 | 102.1 | 104.9 | 1.03 | 110.9 | 111.1 | 1.00 | 4.39 | 4.70 | 1.07 |
| RCE16-2-3 | 25.0 | 25.2 | 1.01 | 96.7 | 97.7 | 1.01 | 101.6 | 102.8 | 1.01 | 4.64 | 4.93 | 1.06 |
| RCE16-3-1 | 26.3 | 24.5 | 0.93 | 115.5 | 124.8 | 1.08 | 116.4 | 130.3 | 1.12 | 3.57 | 3.92 | 1.10 |
| RCE16-3-2 | 32.3 | 30.8 | 0.95 | 125.2 | 140.3 | 1.12 | 137.9 | 147.2 | 1.07 | 3.44 | 3.65 | 1.06 |
| RCE16-3-3 | 31.2 | 32.5 | 1.04 | 116.9 | 133.3 | 1.14 | 124.2 | 140.5 | 1.13 | 3.50 | 3.73 | 1.07 |
| RCE25-2-1 | 31.8 | 29.3 | 0.92 | 166.2 | 183.5 | 1.10 | 173.7 | 187.7 | 1.08 | 1.98 | 2.12 | 1.07 |
| RCE25-2-2 | 39.5 | 33.0 | 0.84 | 190.5 | 202.3 | 1.06 | 202.4 | 207.6 | 1.03 | 2.10 | 2.20 | 1.05 |
| RCE25-2-3 | 37.0 | 32.5 | 0.88 | 186.5 | 197.5 | 1.06 | 197.0 | 202.9 | 1.03 | 2.15 | 2.30 | 1.07 |
| RCE25-3-1 | 41.6 | 33.2 | 0.80 | 231.8 | 251.1 | 1.08 | 243.1 | 252.3 | 1.04 | 1.33 | 1.25 | 0.94 |
| RCE25-3-2 | 44.7 | 37.5 | 0.84 | 253.2 | 274.5 | 1.08 | 263.2 | 276.3 | 1.05 | 1.35 | 1.31 | 0.97 |
| RCE25-3-3 | 42.6 | 36.6 | 0.86 | 249.6 | 270.6 | 1.08 | 259.6 | 272.5 | 1.05 | 1.47 | 1.35 | 0.92 |
| CBSA2 [20] | 4.1 | 4.1 | 1.00 | 14.0 | 14.4 | 1.03 | 18.8 | 15.3 | 0.81 | -- | ||
| CBSA3 [20] | 4.0 | 3.1 | 0.78 | 15.8 | 15.8 | 1.00 | 19.4 | 16.9 | 0.87 | -- | ||
| CBSE2 [20] | 3.7 | 4.1 | 1.11 | 16.2 | 16.8 | 1.04 | 19.5 | 17.6 | 0.90 | 5.32 | 3.81 | 0.72 |
| CBSE3 [20] | 3.8 | 3.1 | 0.82 | 17.9 | 18.2 | 1.02 | 19.8 | 19.2 | 0.97 | 3.82 | 3.69 | 0.97 |
| CBSF3 [20] | 3.7 | 3.1 | 0.84 | 20.7 | 21.5 | 1.04 | 23.3 | 22.4 | 0.96 | -- | ||
| UHTCC50 [29] | -- | -- | 4.1 | 4.6 | 1.12 | 4.6 | 4.9 | 1.07 | 3.20 | 3.25 | 1.02 | |
| UHTCC35 [29] | -- | -- | 4.2 | 4.5 | 1.07 | 5.0 | 4.6 | 0.92 | 4.72 | 3.67 | 0.78 | |
| UHTCC25 [29] | -- | -- | 4.0 | 4.3 | 1.08 | 4.4 | 4.4 | 1.00 | 6.59 | 3.92 | 0.59 | |
| UHTCC15 [29] | -- | -- | 3.9 | 3.9 | 1.00 | 4.4 | 4.1 | 0.93 | 5.90 | 4.40 | 0.75 | |
| E-3-S-14 [19] | 17.5 | 14.5 | 0.83 | 60.2 | 63.6 | 1.06 | 66.5 | 67.8 | 1.02 | 3.42 | 4.07 | 1.19 |
| E-6-S-14 [19] | 16.5 | 16.8 | 1.02 | 61.6 | 68.1 | 1.11 | 67.6 | 73.1 | 1.08 | 3.56 | 4.04 | 1.13 |
| E-9-S-14 [19] | 15.7 | 17.4 | 1.11 | 63.1 | 71.7 | 1.14 | 71.0 | 77.5 | 1.09 | 4.02 | 3.95 | 0.98 |
| E-12-S-14 [19] | 14.9 | 16.5 | 1.11 | 66.7 | 74.5 | 1.12 | 79.0 | 80.6 | 1.02 | 4.11 | 3.83 | 0.93 |
| E-6-S-10 [19] | 13.5 | 13.5 | 1.00 | 33.1 | 40.9 | 1.24 | 45.0 | 45.0 | 1.00 | 5.67 | 4.34 | 0.77 |
| E-6-S-18 [19] | 17.0 | 16.6 | 0.98 | 96.0 | 101.7 | 1.06 | 100.2 | 105.7 | 1.05 | 2.35 | 2.64 | 1.12 |
| Average | 0.94 | 1.07 | 1.01 | 0.98 | ||||||||
| COV | 0.11 | 0.05 | 0.07 | 0.16 | ||||||||
| Specimen ID | b (mm) | h (mm) | l0 (mm) | lm (mm) | hcr-ECC (mm) | lm/l0 (mm) |
|---|---|---|---|---|---|---|
| CBSA2 [20] | 150 | 200 | 1400 | 400 | 50 | 0.29 |
| CBSA3 [20] | 150 | 200 | 1400 | 400 | 100 | 0.29 |
| CBSE2 [20] | 150 | 200 | 1400 | 400 | 50 | 0.29 |
| CBSE3 [20] | 150 | 200 | 1400 | 400 | 100 | 0.29 |
| CBSF3 [20] | 150 | 200 | 1400 | 400 | 100 | 0.29 |
| UHTCC50 [29] | 80 | 120 | 2000 | 400 | 50 | 0.20 |
| UHTCC35 [29] | 80 | 120 | 2000 | 400 | 35 | 0.20 |
| UHTCC25 [29] | 80 | 120 | 2000 | 400 | 25 | 0.20 |
| UHTCC15 [29] | 80 | 120 | 2000 | 400 | 15 | 0.20 |
| E-3-S-14 [19] | 200 | 300 | 1700 | 500 | 30 | 0.29 |
| E-6-S-14 [19] | 200 | 300 | 1700 | 500 | 60 | 0.29 |
| E-9-S-14 [19] | 200 | 300 | 1700 | 500 | 90 | 0.29 |
| E-12-S-14 [19] | 200 | 300 | 1700 | 500 | 120 | 0.29 |
| E-6-S-10 [19] | 200 | 300 | 1700 | 500 | 60 | 0.29 |
| E-6-S-18 [19] | 200 | 300 | 1700 | 500 | 60 | 0.29 |
| Specimen ID | Mu (kN·m) | Failure Mode | Specimen ID | Mu (kN·m) | Failure Mode | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | Pre. | P/E | Exp. | Pre. | Exp. | Pre. | P/E | Exp. | Pre. | ||
| RCE16-2-1 | 97.6 | 94.1 | 0.96 | F | F | CBSE2 [20] | 19.5 | 17.5 | 0.90 | -- | F |
| RCE16-2-2 | 110.9 | 107.9 | 0.97 | F | F | CBSE3 [20] | 19.8 | 19.0 | 0.96 | -- | F |
| RCE16-2-3 | 101.6 | 100.5 | 0.99 | F | F | CBSF3 [20] | 23.3 | 22.2 | 0.95 | -- | F |
| RCE16-3-1 | 116.4 | 128.5 | 1.10 | F | F | UHTCC50 [29] | 4.6 | 4.8 | 1.04 | -- | F |
| RCE16-3-2 | 137.9 | 144.2 | 1.05 | F | F | UHTCC35 [29] | 5.0 | 4.5 | 0.90 | F | F |
| RCE16-3-3 | 124.2 | 135.6 | 1.09 | F | F | UHTCC25 [29] | 4.4 | 4.3 | 0.98 | -- | F |
| RCE25-2-1 | 173.7 | 187.1 | 1.08 | F | F | UHTCC15 [29] | 4.4 | 4.0 | 0.91 | -- | F |
| RCE25-2-2 | 202.4 | 206.2 | 1.02 | F | F | E-3-S-14 [19] | 66.5 | 66.6 | 1.00 | F | F |
| RCE25-2-3 | 197.0 | 201.6 | 1.02 | F | F | E-6-S-14 [19] | 67.6 | 70.9 | 1.05 | F | F |
| RCE25-3-1 | 243.1 | 253.6 | 1.04 | F | F | E-9-S-14 [19] | 71.0 | 74.6 | 1.05 | F | F |
| RCE25-3-2 | 263.2 | 277.2 | 1.05 | F | F | E-12-S-14 [19] | 79.0 | 77.6 | 0.98 | F | F |
| RCE25-3-3 | 259.6 | 273.4 | 1.05 | F | F | E-6-S-10 [19] | 45.0 | 42.7 | 0.95 | F | F |
| CBSA2 [20] | 18.8 | 15.1 | 0.81 | -- | F | E-6-S-18 [19] | 100.2 | 105.0 | 1.05 | F | F |
| CBSA3 [20] | 19.4 | 16.7 | 0.86 | -- | F | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gui, C.; Ji, J.; Xu, C.; Li, Z.; Guo, X. Experimental and Analytical Study on the Flexural Performance of Layered ECC–Concrete Composite Beams. Buildings 2025, 15, 1592. https://doi.org/10.3390/buildings15101592
Gui C, Ji J, Xu C, Li Z, Guo X. Experimental and Analytical Study on the Flexural Performance of Layered ECC–Concrete Composite Beams. Buildings. 2025; 15(10):1592. https://doi.org/10.3390/buildings15101592
Chicago/Turabian StyleGui, Chong, Jinlong Ji, Chongfa Xu, Zhihua Li, and Xuan Guo. 2025. "Experimental and Analytical Study on the Flexural Performance of Layered ECC–Concrete Composite Beams" Buildings 15, no. 10: 1592. https://doi.org/10.3390/buildings15101592
APA StyleGui, C., Ji, J., Xu, C., Li, Z., & Guo, X. (2025). Experimental and Analytical Study on the Flexural Performance of Layered ECC–Concrete Composite Beams. Buildings, 15(10), 1592. https://doi.org/10.3390/buildings15101592





