Analytical Solutions for Thermo-Mechanical Coupling Bending of Cross-Laminated Timber Panels
Abstract
1. Introduction
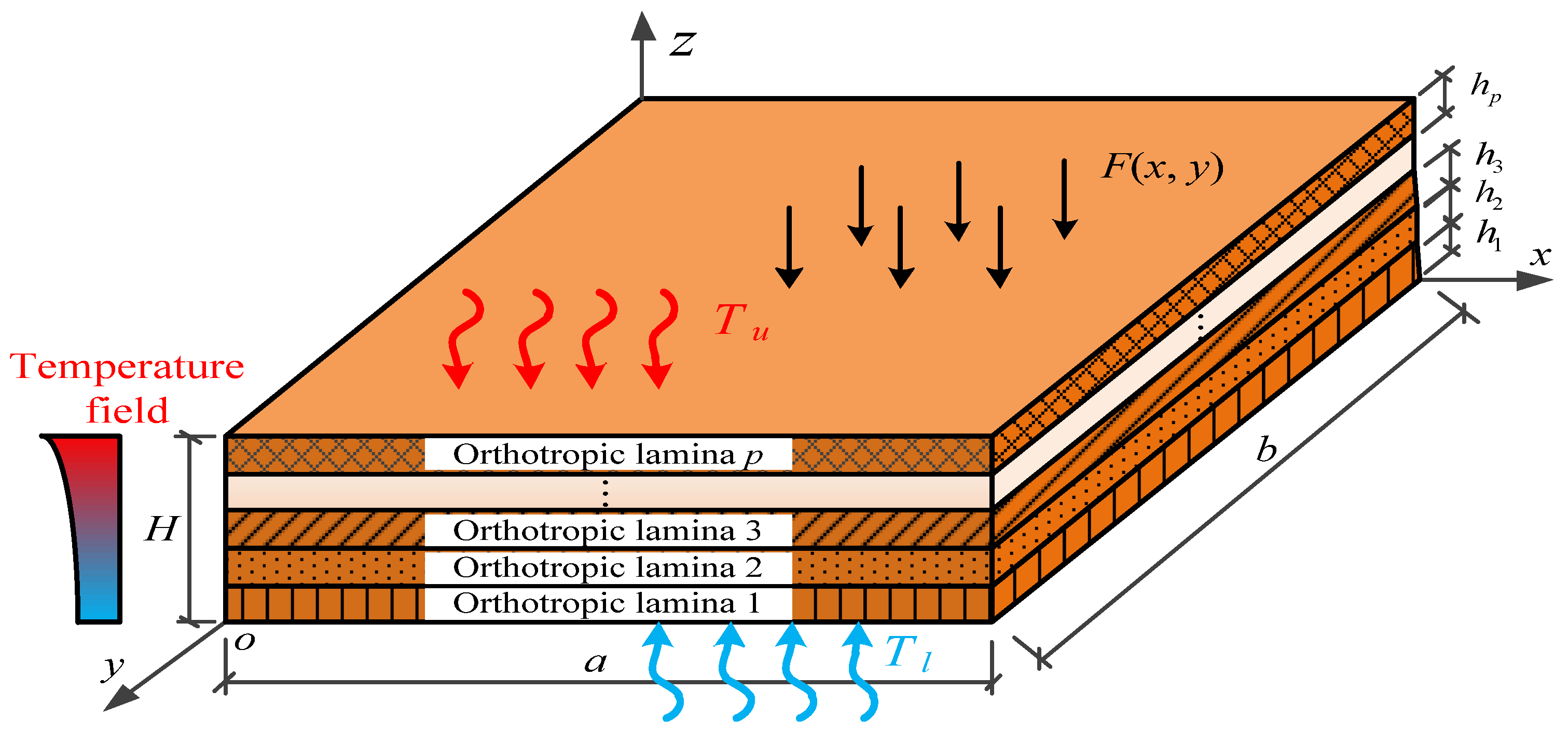
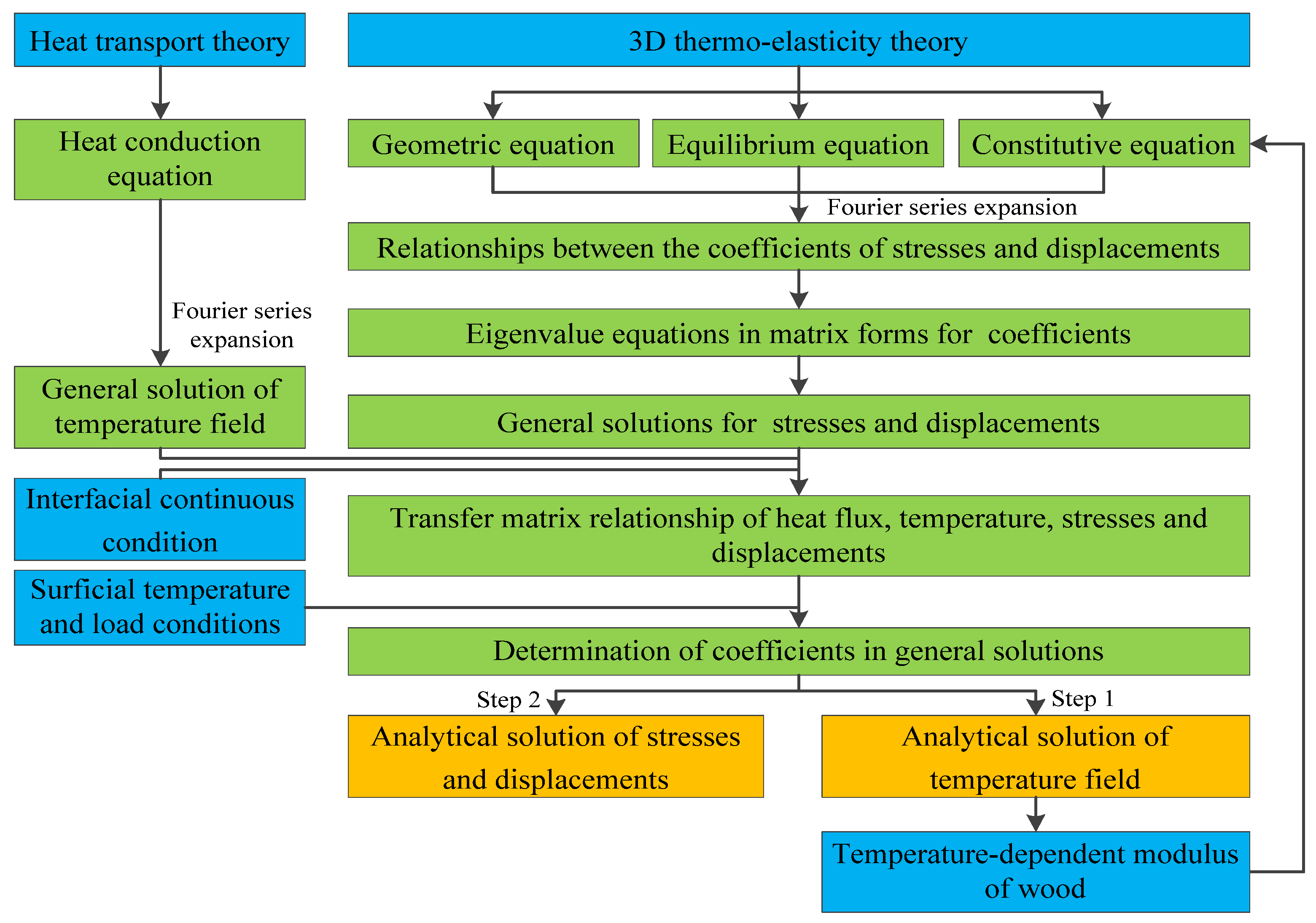
2. Analytical Model for CLT Panel
2.1. General Solutions of Temperature Field
2.2. Temperature-Dependent Properties
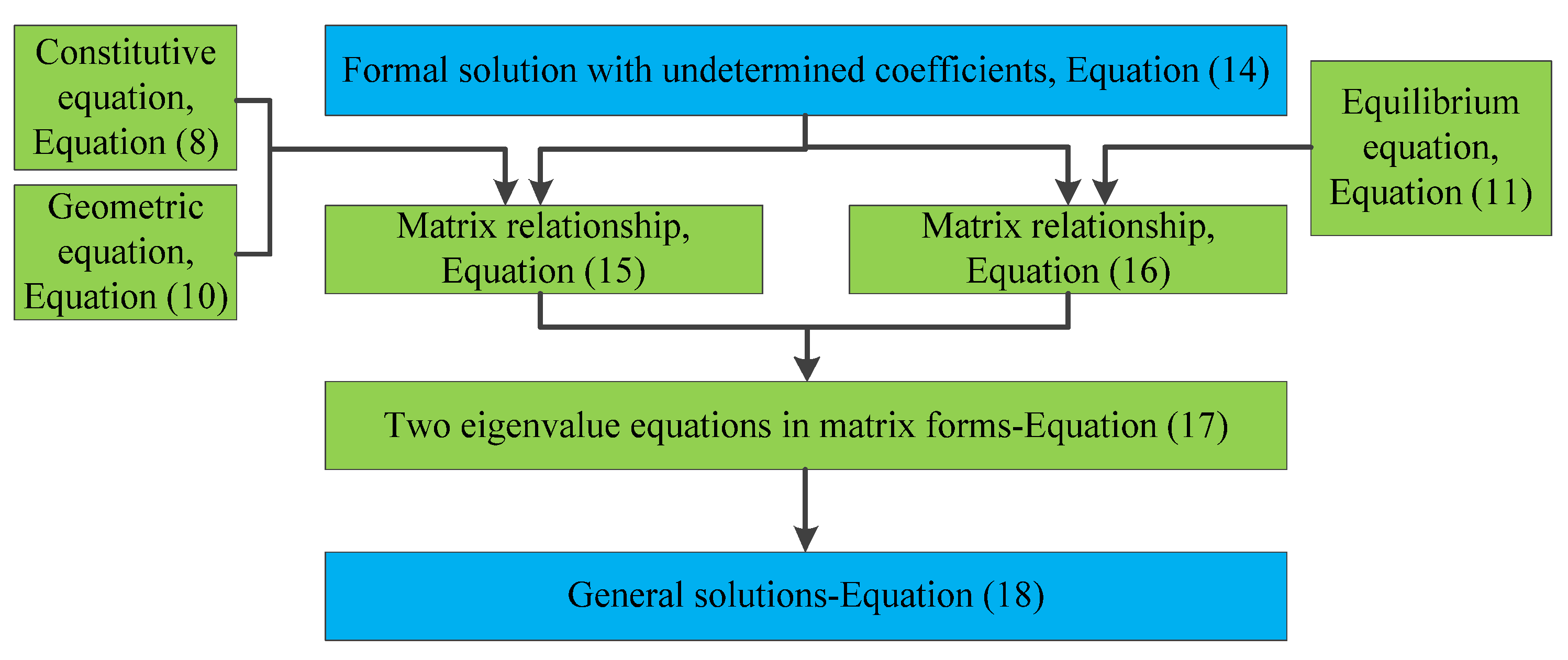
2.3. General Solutions of Stresses and Displacements
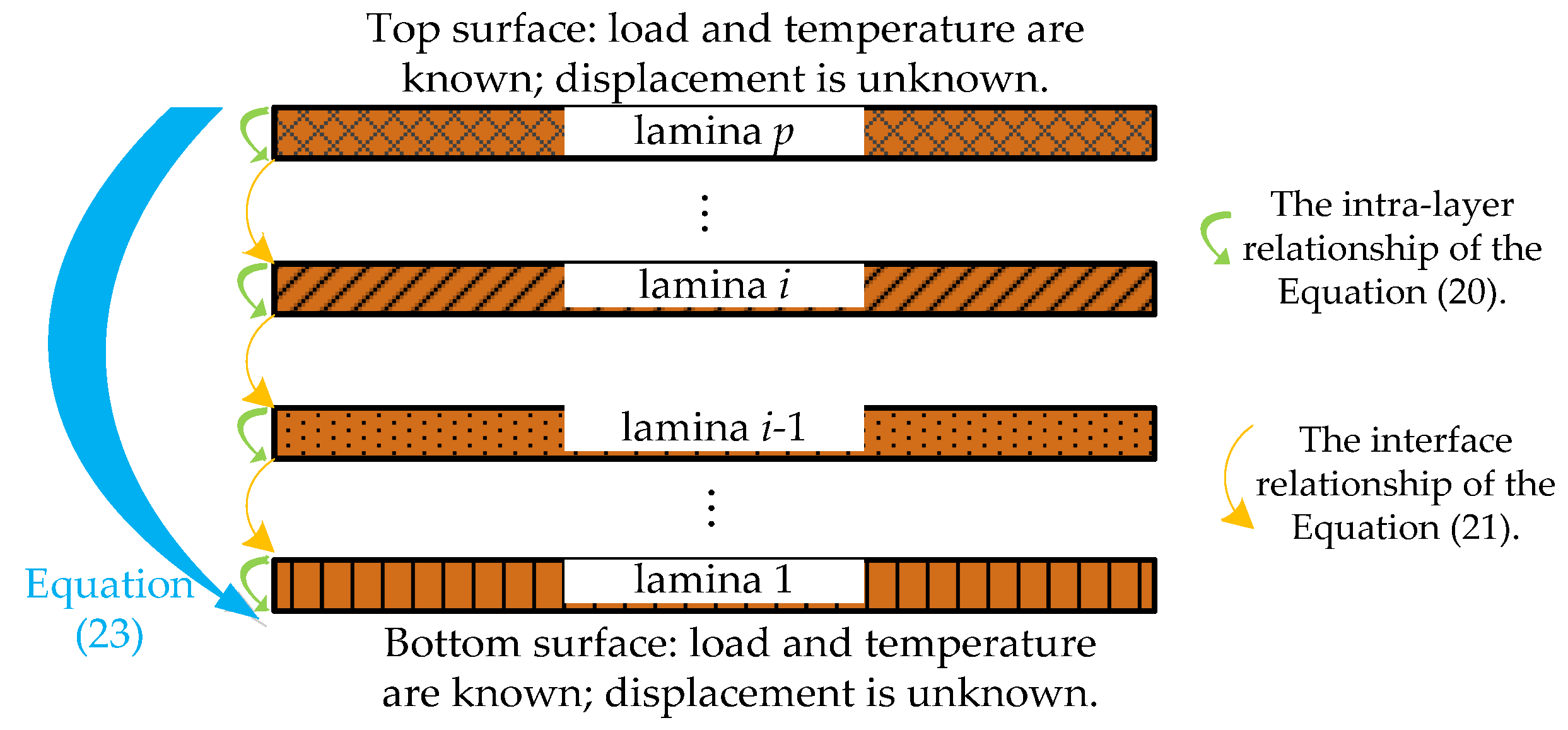
2.4. Determination of Coefficients
3. Example Analysis and Discussion
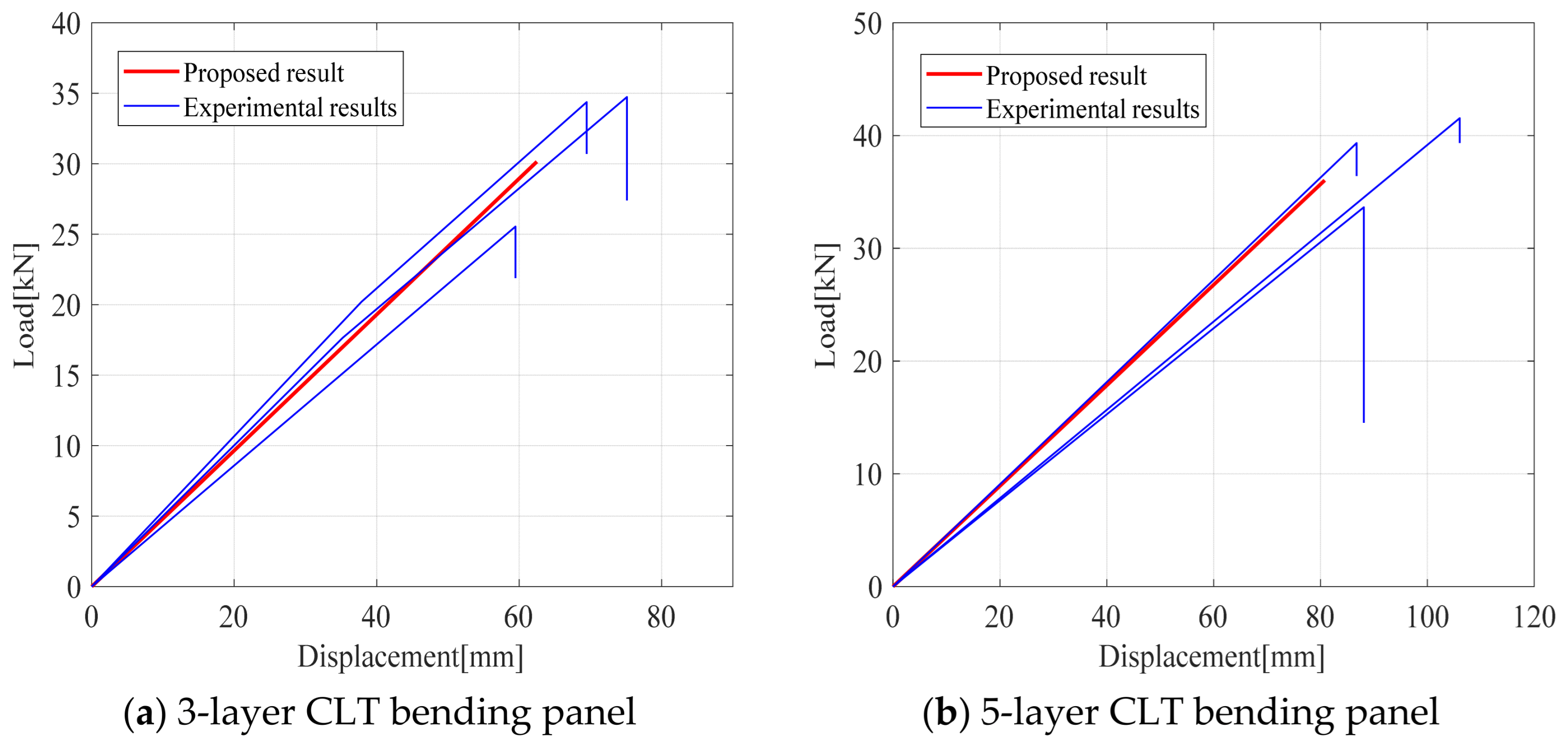
3.1. Comparison Study
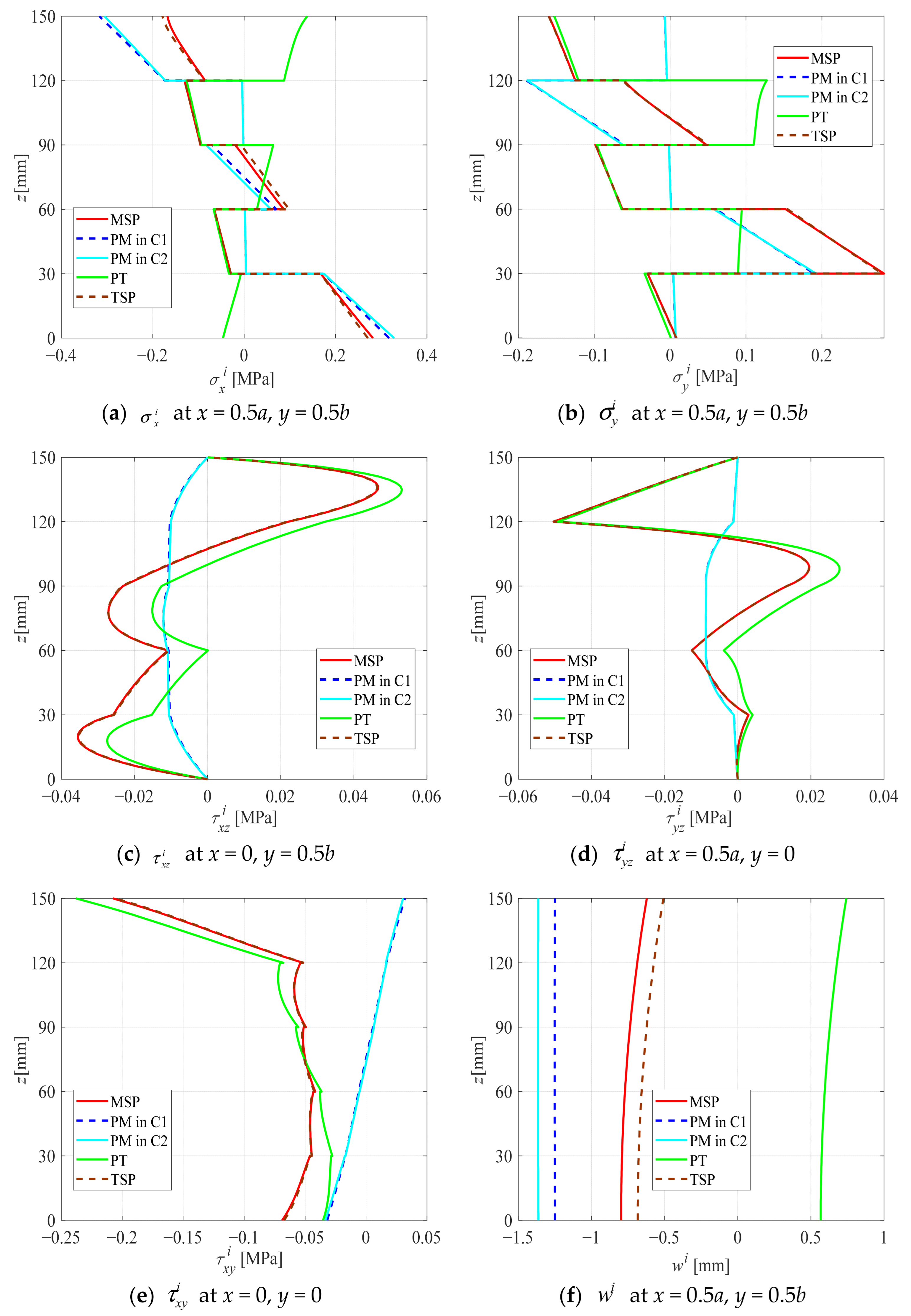
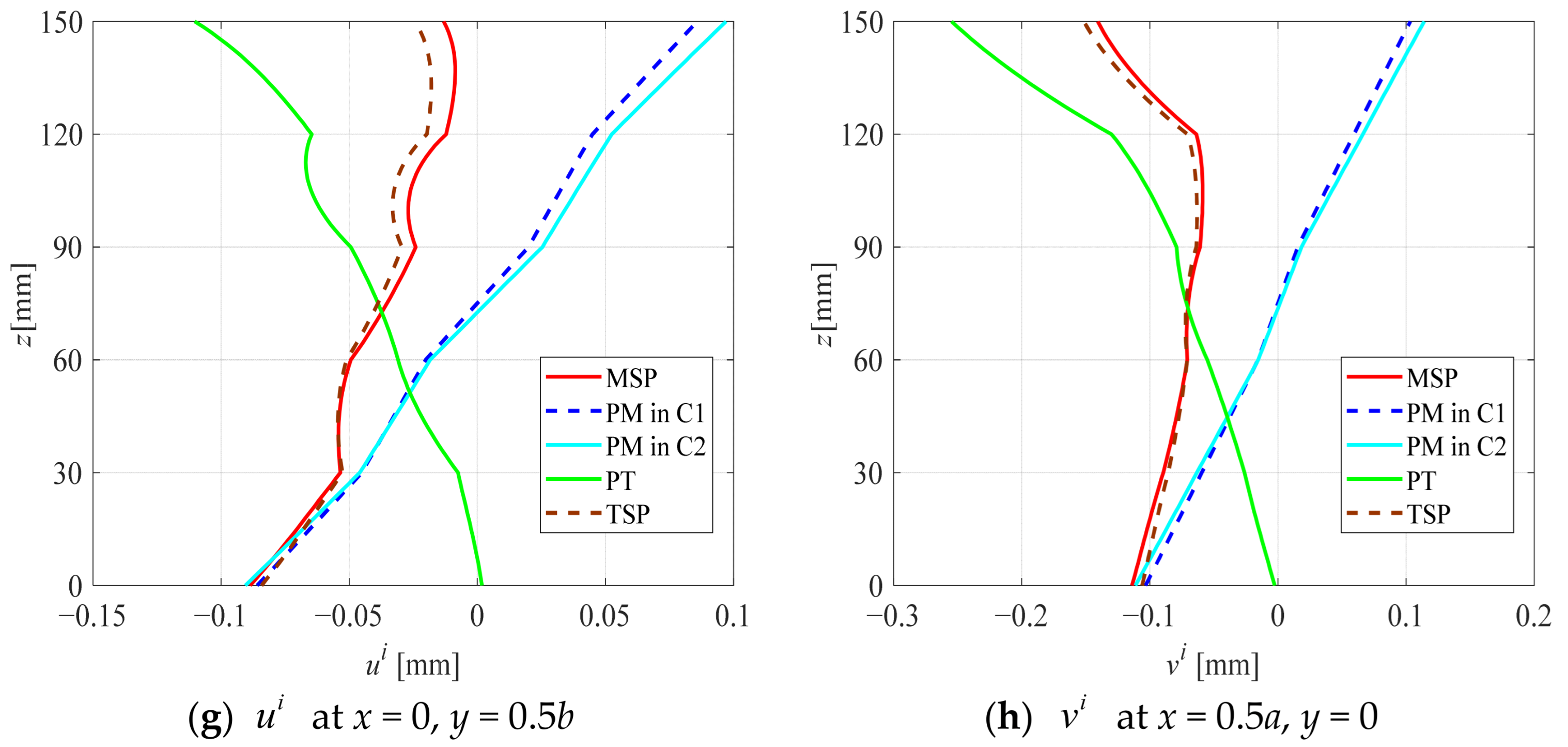
3.2. Decoupling Analysis and Modified Superposition Principle
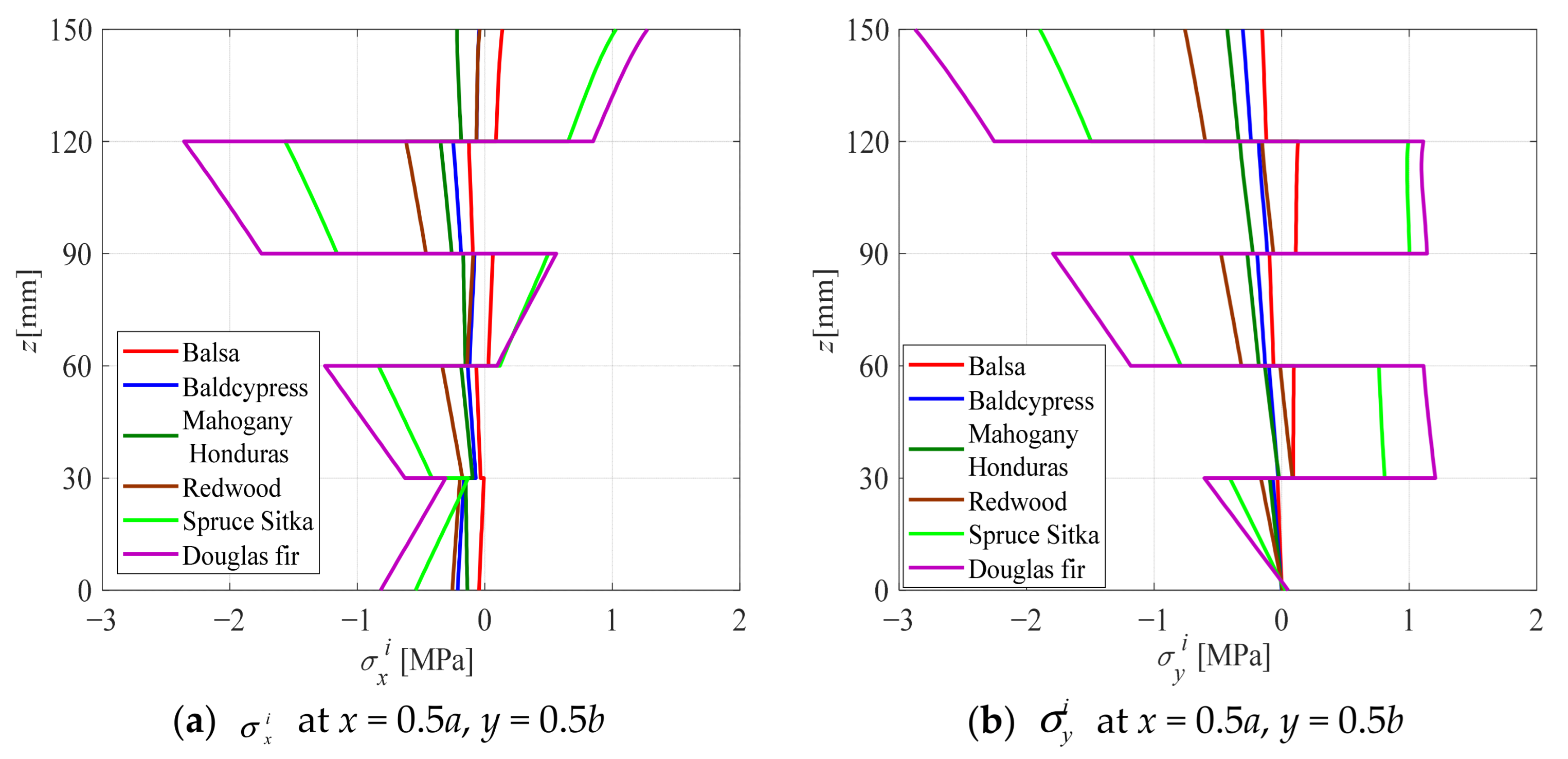
3.3. Influence of Wood Type
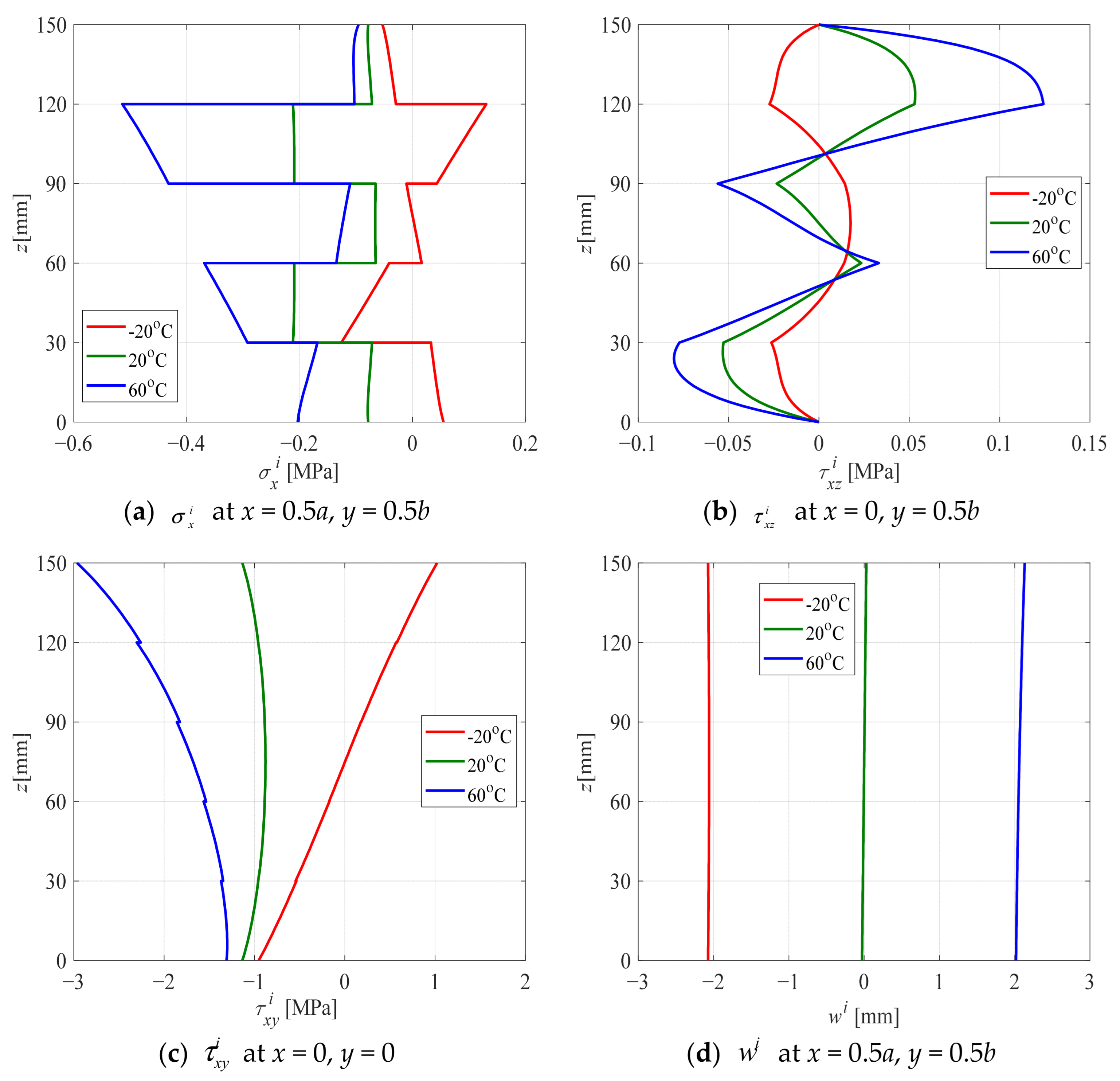
3.4. Influence of Temperature Difference
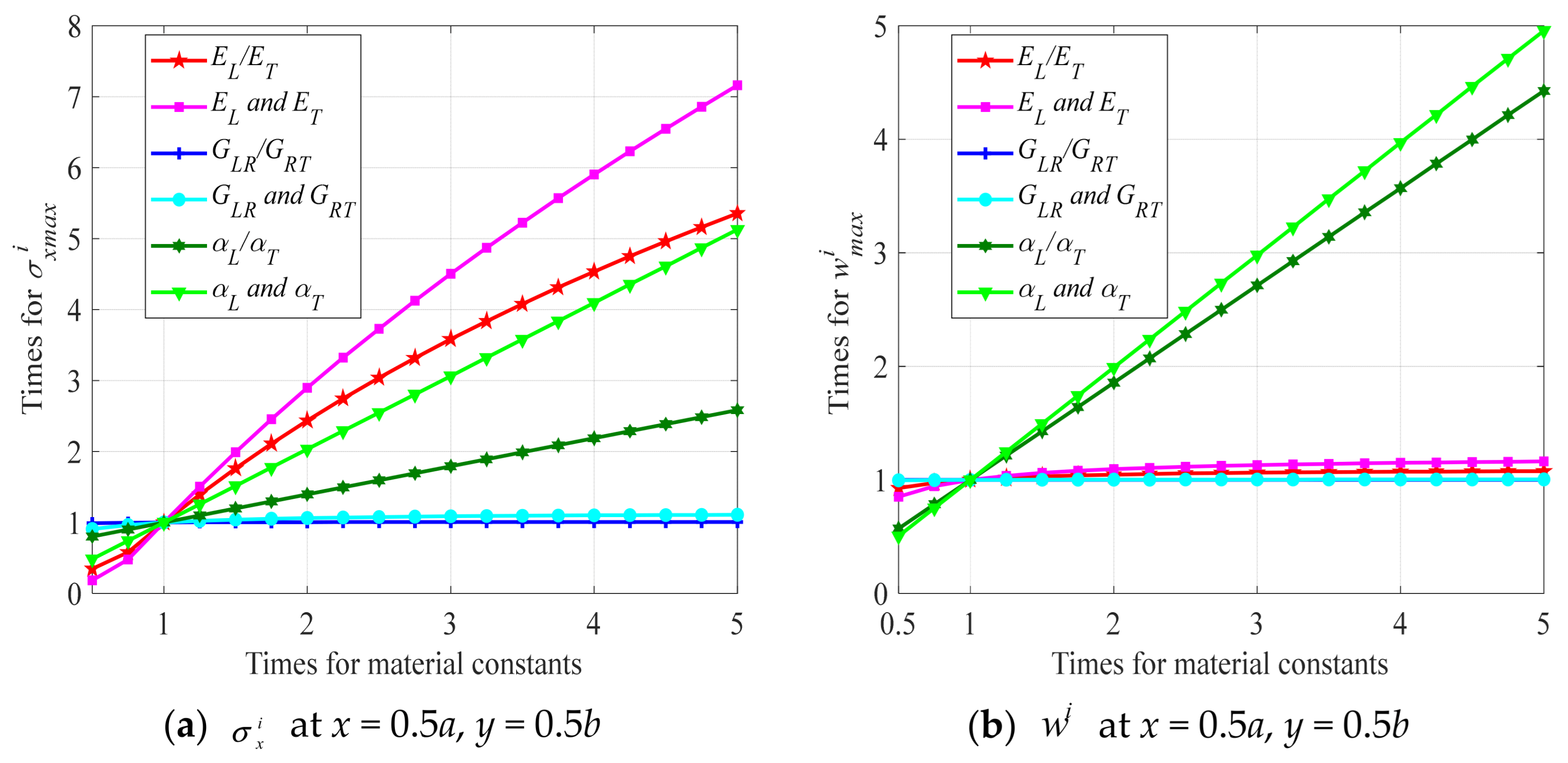
3.5. Influence of Material Constants
4. Conclusions
- The proposed results are close to the experimental ones. The proposed solution aligns well with the finite element results while providing superior computational efficiency. For thinner panels, the solution based on the plane section assumption closely matches the proposed solution; however, discrepancies increase as the panel thickness increases.
- If the temperature at the top surface of the CLT panel is higher than at the bottom, the directions of stress and displacement are generally opposite. This is primarily because the load causes the CLT panel to bend downward, while the temperature difference induces an upward bend. In this case, it can somewhat alleviate the stress and deformation of the CLT panel.
- For load effects, the stresses and displacements exhibit symmetry or anti-symmetry along the mid-plane of the CLT panel. In contrast, for temperature effects, the stresses and displacements are significantly larger near the upper surface, where the temperature is relatively high.
- For different types of wood, thermal stress and displacement are more pronounced near the high-temperature surface, and the directions of thermal stress in adjacent layers are predominantly opposite. Moreover, the thermal stresses mainly increase with absolute values of modulus E, G and the relative value of αL/αT.
- When the temperature field is symmetric along the mid-plane z = H/2, the thermal stress and displacement components exhibit either symmetric or anti-symmetric behavior. However, for an anti-symmetric temperature distribution, the symmetry rules governing thermal stress and displacement are entirely reversed.
- The influencing factors on the normal stress, in descending order of magnitude, are the elastic modulus and thermal expansion coefficients, while shear modulus has little impact on the normal stress. Deflection is mainly affected by thermal expansion coefficients, while it is less affected by modulus.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lineham, S.A.; Thomson, D.; Bartlett, A.I.; Bisby, L.A.; Hadden, R.M. Structural response of fire-exposed cross-laminated timber beams under sustained loads. Fire Saf. J. 2016, 85, 23–34. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Zhu, H.; Yu, F.; Wu, P.; Fang, H. Thermo-mechanical coupled behavior of laminated beams with temperature-dependent viscoelastic interlayers. Eur. J. Mech. A-Solids 2023, 100, 105000. [Google Scholar] [CrossRef]
- Sciomenta, M.; Bedon, C.; Fragiacomo, M. Experimental and Numerical Column Buckling Analysis of Hardwood Cross-Laminated Timber Panels. J. Struct. Eng. 2024, 150, 04024030. [Google Scholar] [CrossRef]
- Xu, B.H.; Zhang, S.D.; Zhao, Y.H.; Bouchair, A.; Zhang, B.S. Mechanical Properties of Adhesive-Free Cross-Laminated Timber. J. Struct. Eng. 2022, 148, 04022135. [Google Scholar] [CrossRef]
- Boccadoro, L.; Zweidler, S.; Steiger, R.; Frangi, A. Bending tests on timber-concrete composite members made of beech laminated veneer lumber with notched connection. Eng. Struct. 2017, 132, 14–28. [Google Scholar] [CrossRef]
- Li, H.; Wang, L.B.; Wei, Y.; Wang, B.J.; Jin, H. Bending and shear performance of cross-laminated timber and glued-laminated timber beams: A comparative investigation. J. Build. Eng. 2022, 45, 103477. [Google Scholar] [CrossRef]
- Santos, P.; Correia, R.; Godinho, L.; Dias, A.M.P.G.; Craveiro, H. Experimental and numerical assessment of a cross-insulated timber panel solution. Eng. Struct. 2021, 235, 112061. [Google Scholar] [CrossRef]
- Mindeguia, J.C.; Mohaine, S.; Bisby, L.; Robert, F.; McNamee, R.; Bartlett, A. Thermo-mechanical behaviour of cross-laminated timber slabs under standard and natural fires. Fire Mater. 2020, 45, 866–884. [Google Scholar] [CrossRef]
- Pieniak, D.; Ogrodnik, P.; Oszust, M.; Niewczas, A. Reliability of the thermal treated timber and wood-based materials in high temperatures. Eksploat. I Niezawodn.-Maint. Reliab. 2013, 15, 18–24. [Google Scholar]
- Santos, P.; Sousa, L.; Godinho, L.; Correia, J.R.; Dias, A.M.P.G. Acoustic and thermal behavior of cross-insulated timber panels. J. Build. Eng. 2021, 44, 103309. [Google Scholar] [CrossRef]
- Fragiacomo, M.; Menis, A.; Clemente, I.; Bochicchio, G.; Ceccotti, A. Fire Resistance of Cross-Laminated Timber Panels Loaded Out of Plane. J. Struct. Eng. 2013, 139, 12. [Google Scholar] [CrossRef]
- Kytka, T.; Gasparík, M.; Sahula LKarami, E.; Teterin, D.; Das, S.; Novák, D.; Kvietková, M.S. Bending characteristics of glued laminated timber depending on the alternating effects of freezing and heating. Constr. Build. Mater. 2022, 350, 128916. [Google Scholar] [CrossRef]
- Chorlton, B.; Gales, J. Mechanical performance of laminated veneer lumber and Glulam beams after short-term incident heat exposure. Constr. Build. Mater. 2020, 263, 120129. [Google Scholar] [CrossRef]
- Pulngern, T.; Udtaranakron, T.; Chanto, K. Physical and mechanical behaviors of thermally modified rubberwood glulam beam under sustained and cyclic loading. Wood Fiber Sci. 2020, 52, 298–312. [Google Scholar] [CrossRef]
- He, M.J.; Sun, X.F.; Ren, H.Q.; Li, Z.; Feng, W. Experimental study on the system effect of bending cross-laminated timber fabricated with Karamatsu larch. Constr. Build. Mater. 2021, 299, 124271. [Google Scholar] [CrossRef]
- Dong, W.C.; Colin, M.R.; Julia, A.S. Cross-laminated secondary timber: Validation of non-destructive assessment of structural properties by full-scale bending tests. Eng. Struct. 2024, 298, 117029. [Google Scholar] [CrossRef]
- Zhang, X.B.; Yang, S.Y.; Fei, B.H.; Qin, D.C.; Yang, J.; Li, H.P.; Wang, X.H. Bending and shear performance of a cross-laminated composite consisting of flattened bamboo board and Chinese fir lumber. Constr. Build. Mater. 2023, 392, 131913. [Google Scholar] [CrossRef]
- Nairn, J.A. Cross laminated timber properties including effects of non-glued edges and additional cracks. Eur. J. Wood Wood Prod. 2017, 75, 973–983. [Google Scholar] [CrossRef]
- Vega, C.R.; Pina, J.C.; Bosco, E.; Flores, E.I.S.; Guzman, C.F.; Yane, S.J. Thermo-mechanical analysis of wood through an asymptotic homogenization approach. Constr. Build. Mater. 2022, 315, 125617. [Google Scholar] [CrossRef]
- Li, C.; Li, S.C.; Yue, K.; Wu, P.; Xiao, Z.P.; Zhang, J. Analytical solutions and optimization design for bending behavior of cross-laminated timber beams considering orthotropy and interface slip. Case Stud. Constr. Mater. 2023, 18, e01948. [Google Scholar] [CrossRef]
- Kim, Y.; Davalos, J.F.; Barbero, E.J. Delamination buckling of FRP layer in laminated wood beams. Compos. Struct. 1997, 37, 311–320. [Google Scholar] [CrossRef]
- Wen, J.; Xiao, Y. The flexural behavior of cross laminated bamboo and timber (CLBT) and cross laminated timber (CLT) beams. Constr. Build. Mater. 2023, 408, 133739. [Google Scholar] [CrossRef]
- Huang, Z.R.; Huang, D.S.; Chui, Y.H.; Chen, Z.F. A layered beam-based model for analyzing the stress of rolling shear for the cross-laminated timber panels under out-of-plane bending. Eng. Struct. 2023, 289, 116290. [Google Scholar] [CrossRef]
- Fabrizio, C.; Sciomenta, M.; Spera, L.; De Santis, Y.; Pagliaro, S.; Di Egidio, A.; Fragiacomo, M. Experimental investigation and beam-theory-based analytical model of cross-laminated timber panels buckling behavior. Arch. Civ. Mech. Eng. 2023, 23, 172. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Popovski, M. Mechanics-based analytical models for balloon-type cross-laminated timber (CLT) shear walls under lateral loads. Eng. Struct. 2020, 208, 109916. [Google Scholar] [CrossRef]
- Gangi, M.J.; Lattimer, B.Y.; Case, S.W. Scale modeling of thermo-structural fire tests of multi-orientation wood laminates. Wood Sci. Technol. 2024, 58, 1285–1322. [Google Scholar] [CrossRef]
- Huang, Z.R.; Bian, Y.L.; Ni, C. A rolling shear analysis-based method for determining the apparent stiffness and bending capacity of CLT panel under out-of-plane load. J. Wood Sci. 2024, 70, 1. [Google Scholar] [CrossRef]
- Wiesner, F.; Bisby, L.A.; Bartlett, A.I.; Hidalgo, J.P.; Santamaria, S.; Deeny, S.; Hadden, R.M. Structural capacity in fire of laminated timber elements in compartments with exposed timber surfaces. Eng. Struct. 2019, 179, 284–295. [Google Scholar] [CrossRef]
- La Scala, A.; Sliwa-Wieczorek, K.; Rizzo, F.; Sabbà, M.F.; Zajac, B. Flexible Polyurethane Adhesives: Predictive Numerical Model Calibration through Experimental Testing at Elevated Temperature. Appl. Sci. 2024, 14, 1943. [Google Scholar] [CrossRef]
- Fernandez-Cabo, J.L.; Diez-Barra, R.; Fernandez-Lavandera, J.; Avila-Jalvo, J.M. Timber composite beams with a discrete connection system. Proc. Inst. Civ. Eng.-Struct. Build. 2013, 166, 57–72. [Google Scholar] [CrossRef]
- Chen, Z.T.; Lu, W.D.; Bao, Y.W.; Zhang, J.; Wang, L.; Yue, K. Numerical Investigation of Connection Performance of Timber-Concrete Composite Slabs with Inclined Self-Tapping Screws under High Temperature. J. Renew. Mater. 2022, 10, 89–104. [Google Scholar] [CrossRef]
- Chiniforush, A.A.; Valipour, H.R.; Bradford, M.A.; Akbarnezhad, A. Long-term behaviour of steel-timber composite (STC) shear connections. Eng. Struct. 2019, 196, 109356. [Google Scholar] [CrossRef]
- Sellitto, A.; Cimmelli, V.A. A Continuum Approach to Thermomass Theory. J. Heat Transf.-Trans. ASME 2012, 134, 112402. [Google Scholar] [CrossRef]
- Peter, N.; Alfred, T.; Dick, S. Springer Handbook of Wood Science and Technology; Springer: Berlin/Heidelberg, Germany, 2023; ISSN 2522-8706. [Google Scholar]
- Adineh, M.; Kadkhodayan, M. Three-dimensional thermo-elastic analysis of multi-directional functionally graded rectangular plates on elastic foundation. Acta Mech. 2017, 228, 881–899. [Google Scholar] [CrossRef]
- Vasil’ev, V.V.; Lurie, S.A. Generalized theory of elasticity. Mech. Solids 2015, 50, 379–388. [Google Scholar] [CrossRef]
- Xu, Y.P.; Zhou, D.; Cheng, Y.K. Elasticity solution of clamped-simply supported beams with variable thickness. Appl. Math. Mech.-Engl. Ed. 2008, 29, 279–290. [Google Scholar] [CrossRef]
- Huang, B.; Chen, J.B.; Hua, L.C.; Yi, L.J.; Ma, T.F.; Wang, J.; Kim, H.S. A stress function based viscoelastic model for relaxation of free edge stresses in composite laminates. Compos. Struct. 2019, 232, 111581. [Google Scholar] [CrossRef]
- He, M.J.; Sun, X.F.; Li, Z.; Feng, W. Bending, shear, and compressive properties of three- and five-layer cross-laminated timber fabricated with black spruce. J. Wood Sci. 2020, 66, 38. [Google Scholar] [CrossRef]
- Foraboschi, P. Three-layered plate: Elasticity solution. Compos. Part B-Eng. 2014, 60, 764–776. [Google Scholar] [CrossRef]

| Material Property | Spruce Sitka | Douglas Fir | Balsa | Bald Cypress | Mahogany Honduras | Redwood |
|---|---|---|---|---|---|---|
| EL | 11,880 | 13,297.7 | 3740 | 10,890 | 11,330 | 10,120 |
| ET | 510.84 | 664.89 | 56.1 | 427.71 | 725.12 | 900.68 |
| ER | 926.64 | 904.24 | 172.04 | 914.76 | 1212.31 | 880.44 |
| GLR | 760.32 | 851.05 | 201.96 | 686.07 | 747.78 | 667.92 |
| GLT | 724.68 | 1037.22 | 138.38 | 588.06 | 974.38 | 779.24 |
| GRT | 35.64 | 93.08 | 18.7 | 76.23 | 317.24 | 111.32 |
| μLR | 0.372 | 0.292 | 0.229 | 0.338 | 0.314 | 0.36 |
| μLT | 0.467 | 0.449 | 0.488 | 0.326 | 0.533 | 0.346 |
| μTL | 0.025 | 0.029 | 0.009 | 0.013 | 0.034 | 0.031 |
| μTR | 0.245 | 0.374 | 0.231 | 0.356 | 0.326 | 0.4 |
| λL | 3 × 10−4 | 3 × 10−4 | 8 × 10−5 | 1.2 × 10−4 | 1.5 × 10−4 | 1.1 × 10−4 |
| λT | 1.2 × 10−4 | 1.2 × 10−4 | 5 × 10−5 | 1 × 10−4 | 1.2 × 10−4 | 1 × 10−4 |
| λR | 1.3 × 10−4 | 1.1 × 10−4 | 5 × 10−5 | 1 × 10−4 | 1.2 × 10−4 | 1 × 10−4 |
| αL | 4 × 10−6 | 5 × 10−6 | 1×10−7 | 5 × 10−6 | 4 × 10−6 | 6 × 10−6 |
| αT | 6 × 10−5 | 7 × 10−5 | 4 × 10−5 | 1.5 × 10−5 | 1.2 × 10−5 | 1.8 × 10−5 |
| αR | 3 × 10−5 | 3 × 10−5 | 2 × 10−5 | 1.1 × 10−5 | 1 × 10−5 | 1.4 × 10−5 |
| Condition | Load Effect | Thermal Deformation | Temperature-Dependent |
|---|---|---|---|
| PM in C1 | ✓ | ||
| PM in C2 | ✓ | ✓ | |
| PT | ✓ | ✓ | |
| MT | ✓ | ✓ | ✓ |
| a/H | Solution | MT Action | PM Action | |||
|---|---|---|---|---|---|---|
| Proposed | FE | Proposed | CPT | FE | ||
| 7 | [MPa] | −40.47 | −41.28 | 15.99 | 18.66 | 16.12 |
| [MPa] | −1.508 | −1.537 | - | - | - | |
| [MPa] | −4.101 | −4.175 | −0.1204 | −0.1200 | −0.1214 | |
| [MPa] | −2.781 | −2.839 | - | - | - | |
| w [mm] | −41.12 | −41.86 | −0.4023 | −0.4628 | −0.4068 | |
| 10 | [MPa] | −77.52 | −79.07 | 35.37 | 36.79 | 35.05 |
| [MPa] | −2.312 | −2.266 | - | - | - | |
| [MPa] | −5.949 | −5.860 | −0.3260 | −0.3253 | −0.3286 | |
| [MPa] | −4.118 | −4.204 | - | - | - | |
| w [mm] | −122.0 | −124.4 | −1.771 | −1.828 | −1.788 | |
| 15 | [MPa] | −172.0 | −175.3 | 76.63 | 77.13 | 75.86 |
| [MPa] | −4.291 | −4.368 | - | - | - | |
| [MPa] | −9.038 | −9.192 | −0.9391 | −0.9373 | −0.9495 | |
| [MPa] | −6.398 | −6.283 | - | - | - | |
| w [mm] | −479.6 | −474.3 | −8.252 | −8.277 | −8.326 | |
| 20 | [MPa] | −305.6 | −311.7 | 116.4 | 116.5 | 117.3 |
| [MPa] | −7.052 | −7.207 | - | - | - | |
| [MPa] | −12.10 | −12.33 | −1.647 | −1.643 | −1.667 | |
| [MPa] | −8.739 | −8.923 | - | - | - | |
| w [mm] | −1360 | −1384 | −19.32 | −19.29 | −19.45 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Li, S.; Yue, K.; Wu, P.; Xiao, Z.; Shu, B. Analytical Solutions for Thermo-Mechanical Coupling Bending of Cross-Laminated Timber Panels. Buildings 2025, 15, 26. https://doi.org/10.3390/buildings15010026
Li C, Li S, Yue K, Wu P, Xiao Z, Shu B. Analytical Solutions for Thermo-Mechanical Coupling Bending of Cross-Laminated Timber Panels. Buildings. 2025; 15(1):26. https://doi.org/10.3390/buildings15010026
Chicago/Turabian StyleLi, Chen, Shengcai Li, Kong Yue, Peng Wu, Zhongping Xiao, and Biqing Shu. 2025. "Analytical Solutions for Thermo-Mechanical Coupling Bending of Cross-Laminated Timber Panels" Buildings 15, no. 1: 26. https://doi.org/10.3390/buildings15010026
APA StyleLi, C., Li, S., Yue, K., Wu, P., Xiao, Z., & Shu, B. (2025). Analytical Solutions for Thermo-Mechanical Coupling Bending of Cross-Laminated Timber Panels. Buildings, 15(1), 26. https://doi.org/10.3390/buildings15010026








