Study of Wind Load Influencing Factors of Flexibly Supported Photovoltaic Panels
Abstract
1. Introduction
2. Materials and Methods
2.1. Analysis Method
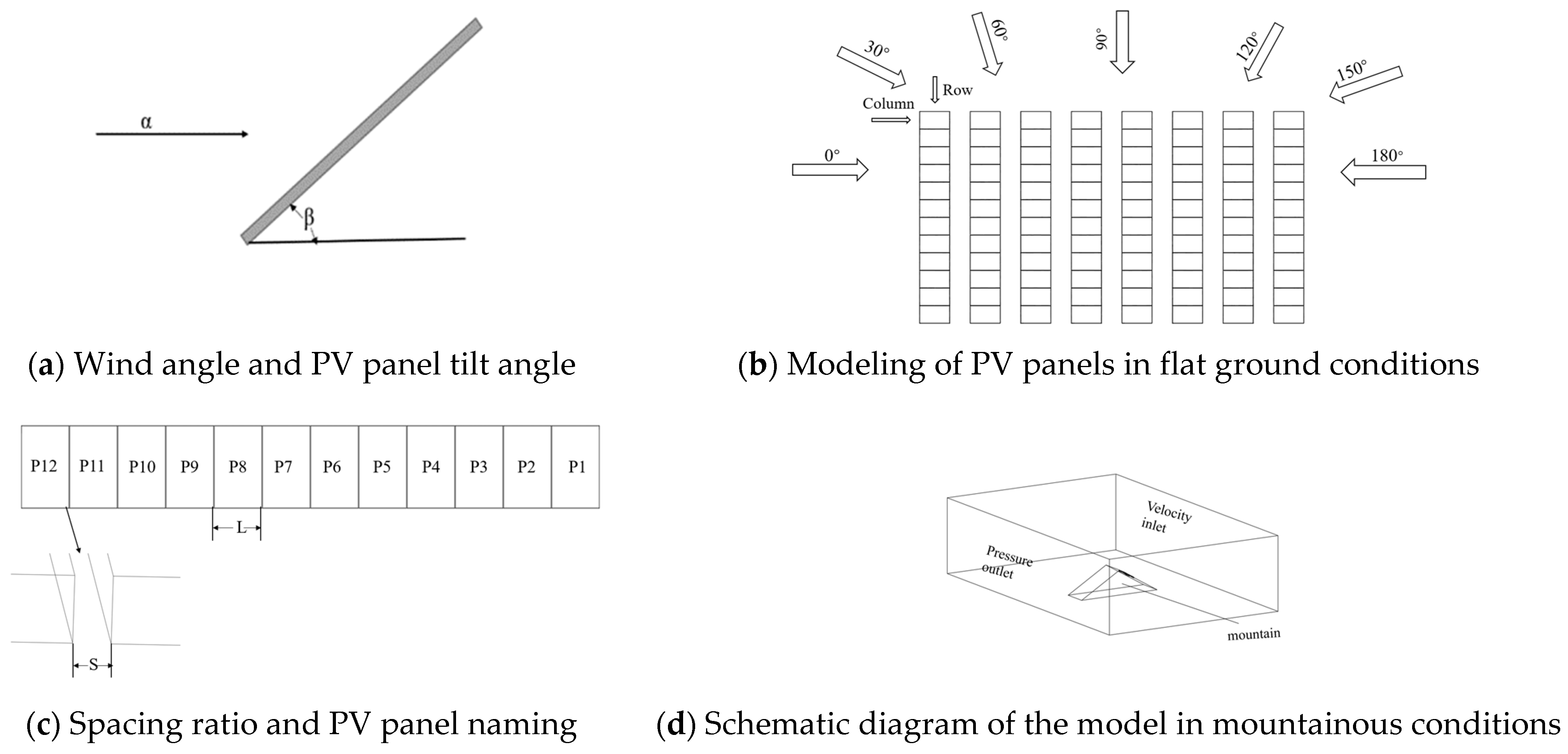
2.2. Model Overview
2.3. Boundary Conditions and Calculation Methods
2.4. Parameter Settings
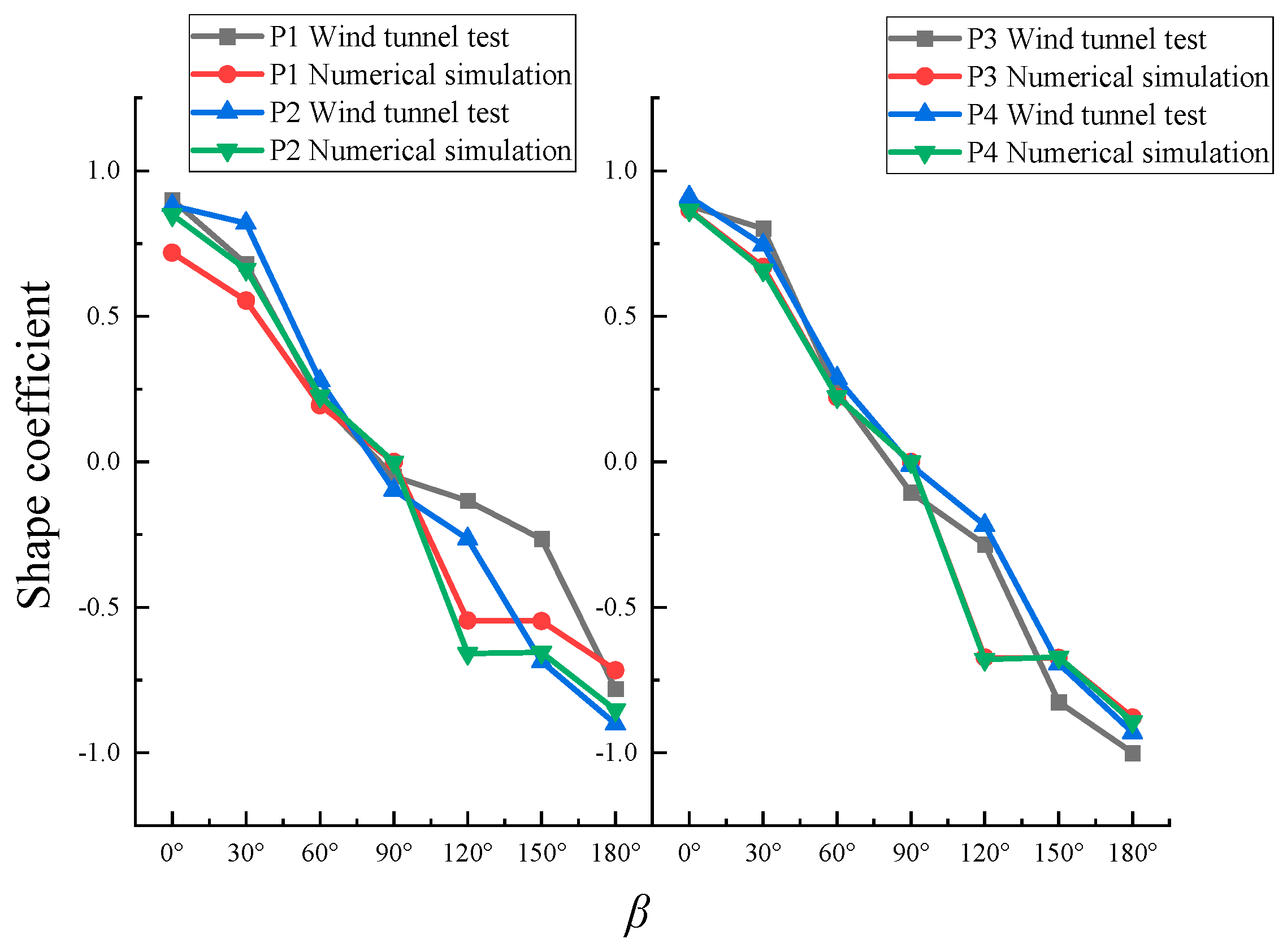
2.5. Verification of Mesh-Independence and Numerical Wind Tunnel Case Validation
3. Numerical Wind Tunnel Simulation Results Analysis
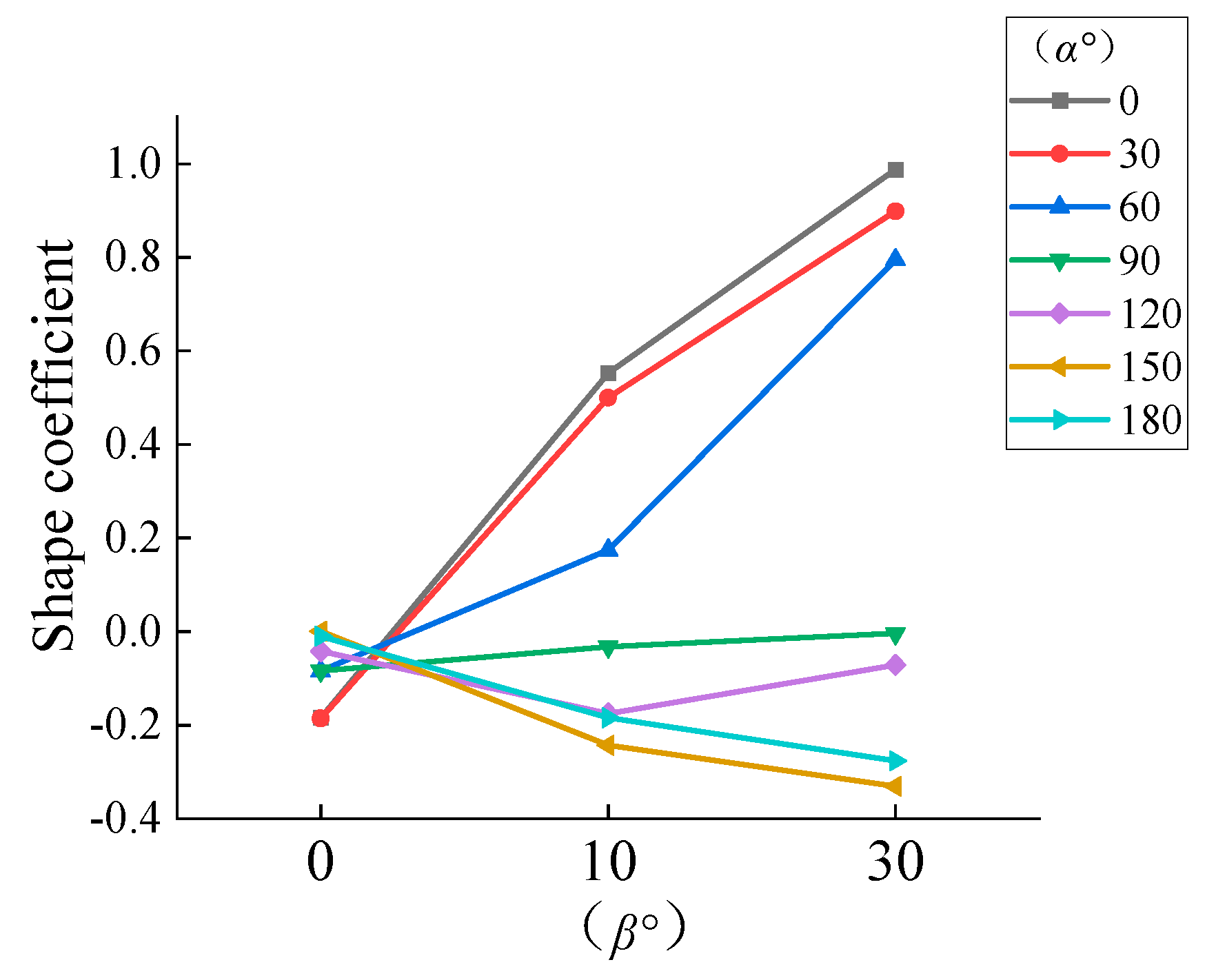
3.1. The Impact of Wind Direction on the Wind Pressure Exerted on a Pliable Group of PV Panels
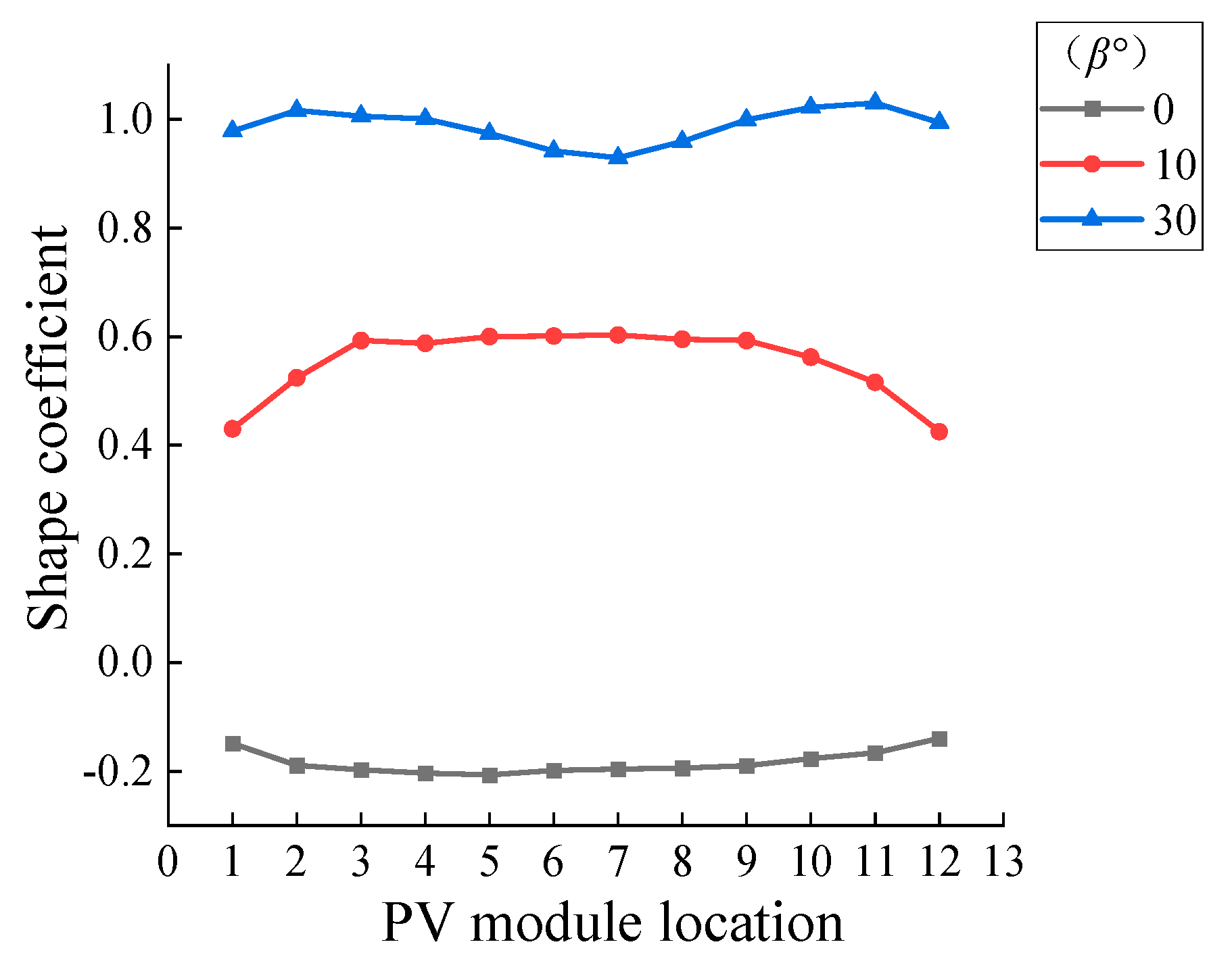
3.2. Effect of Tilt Angle of Flexible PV Panels on Wind Loads
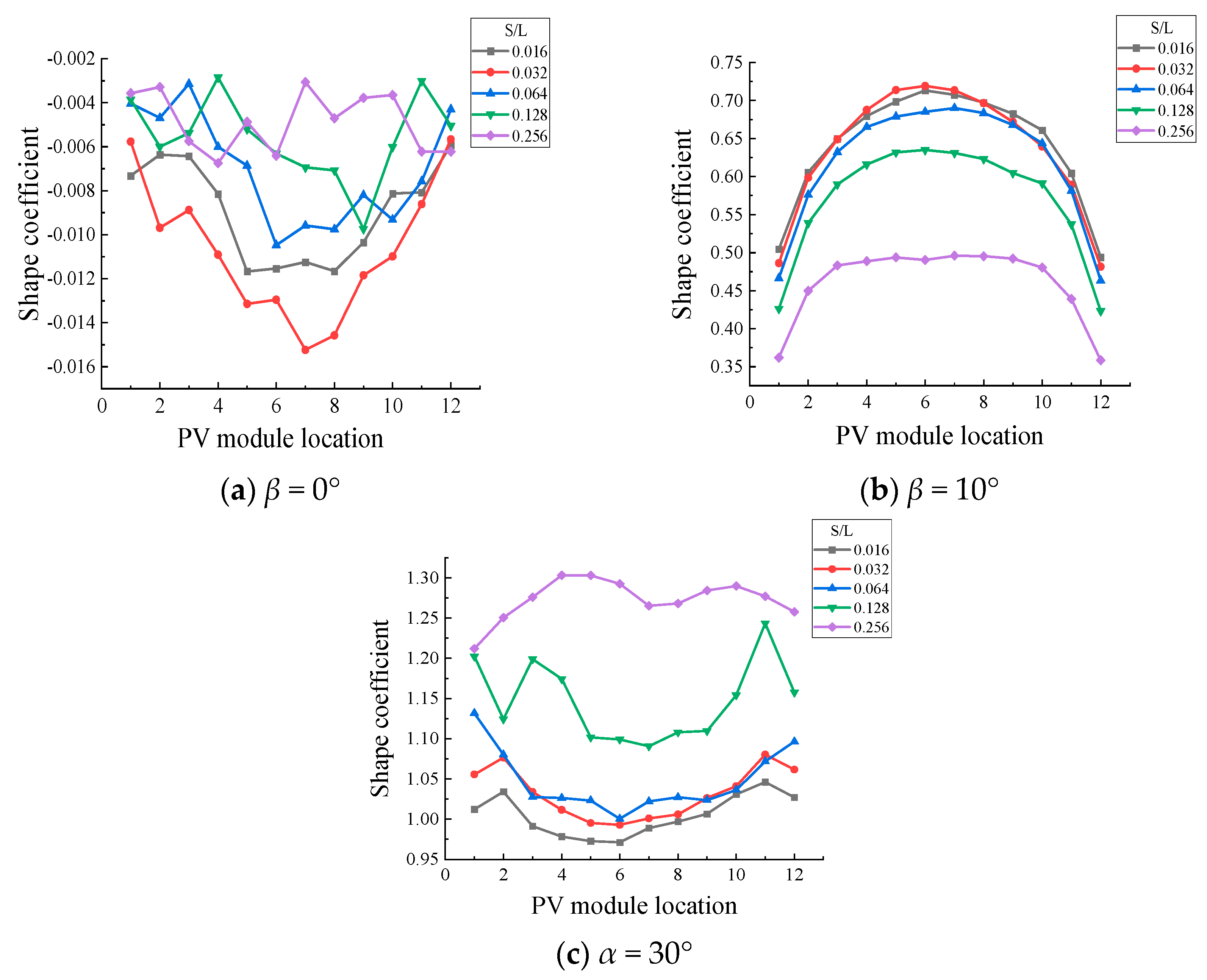
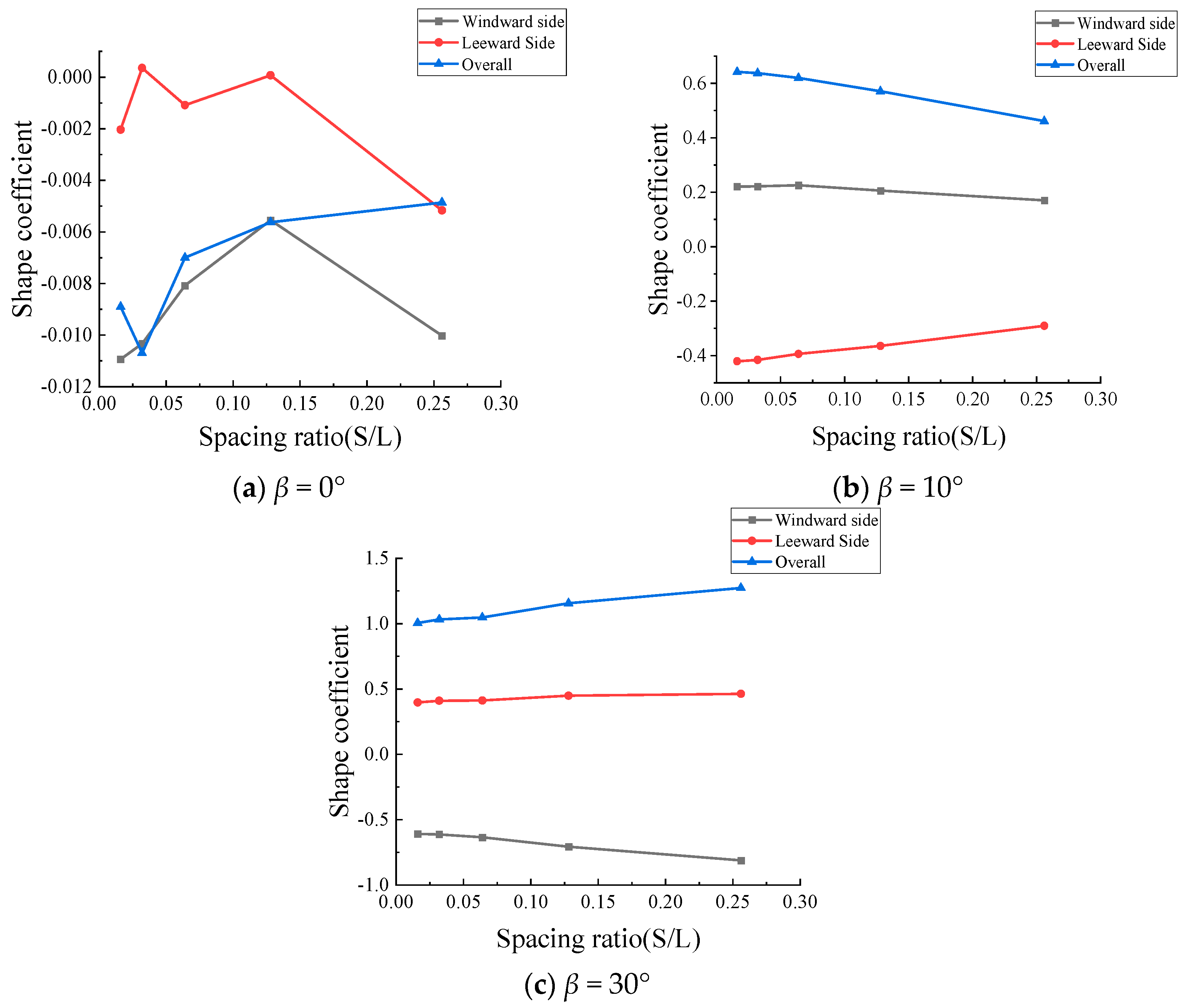
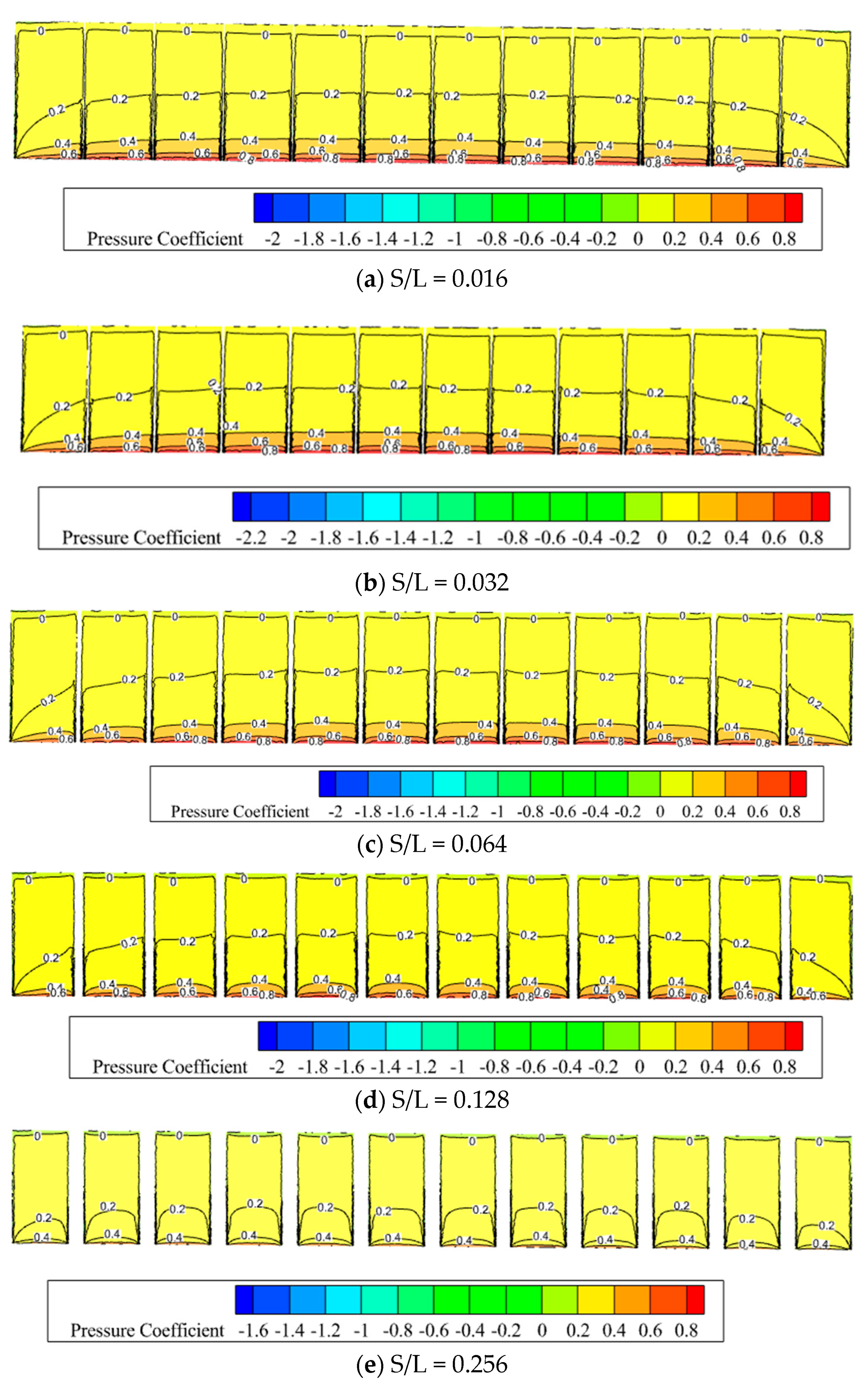
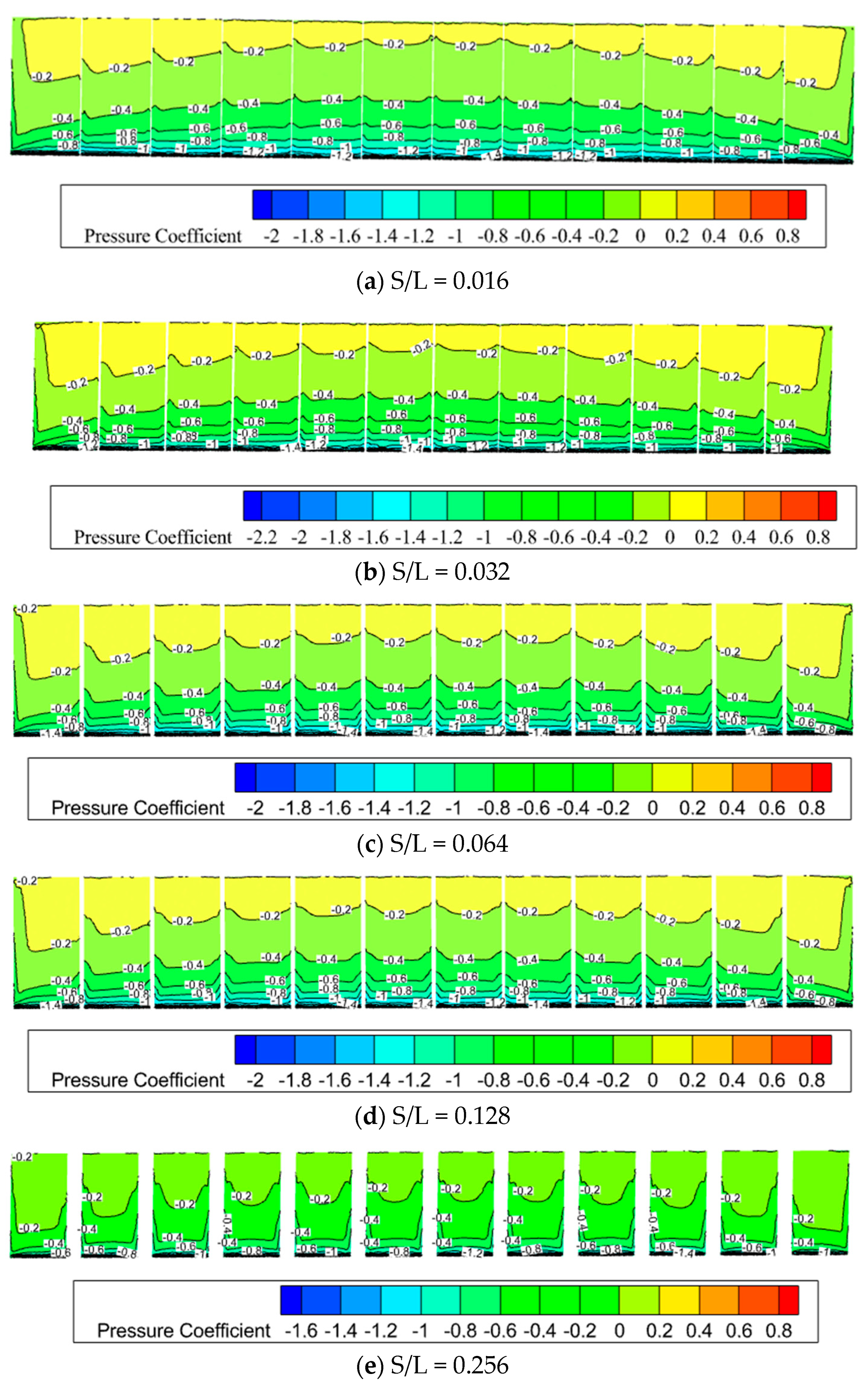
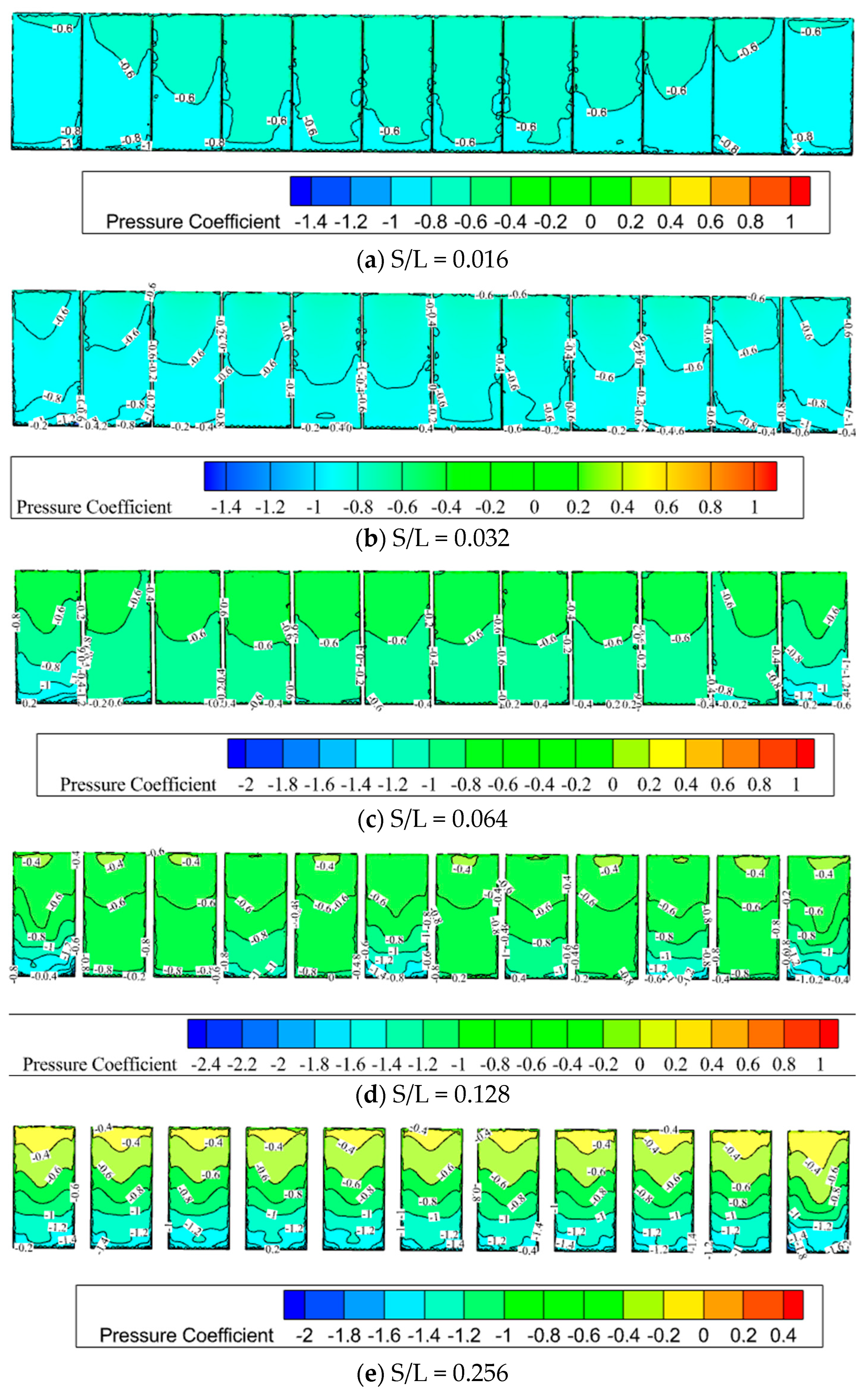
3.3. Effect of Flexible PV Panel Spacing Ratio on Wind Loads
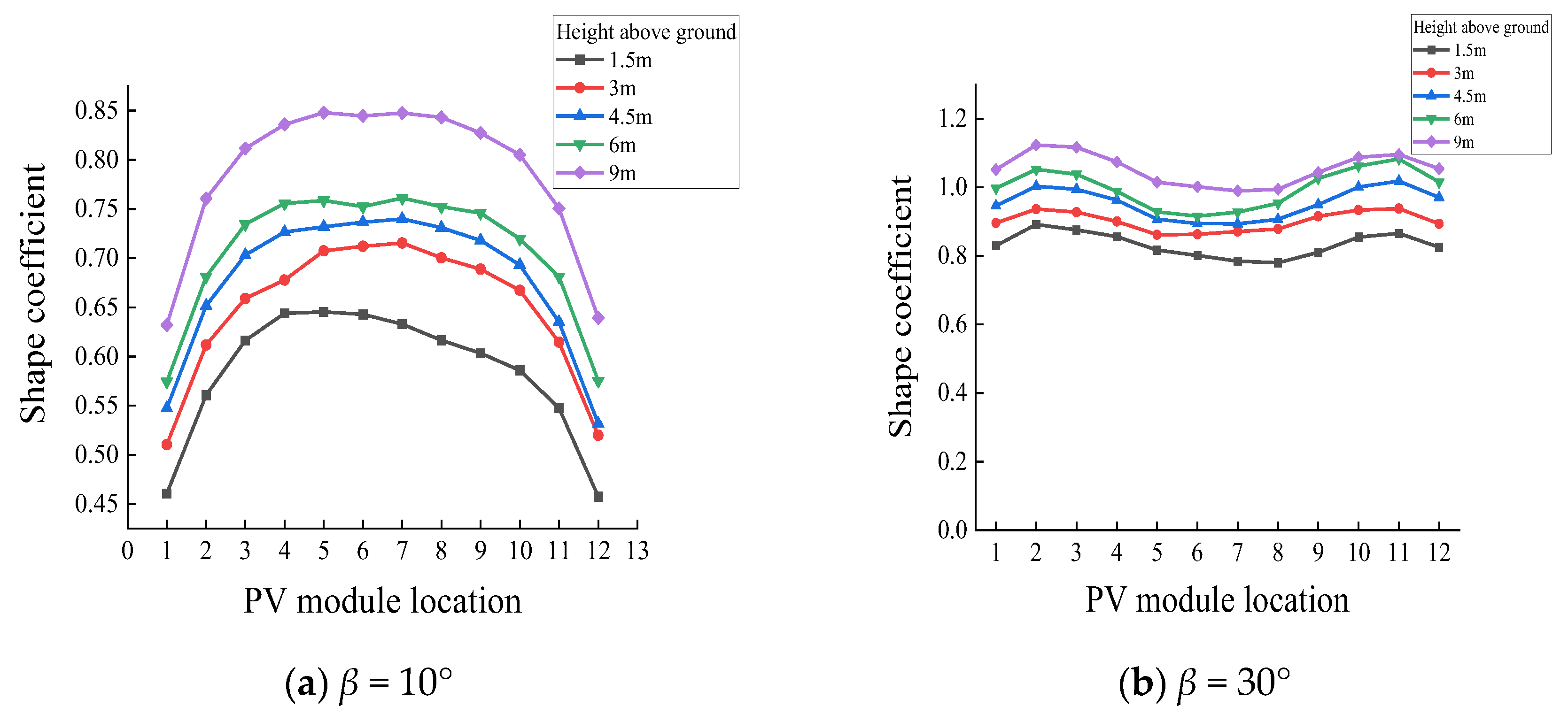
3.4. Effect of Height above Ground on Wind Loads
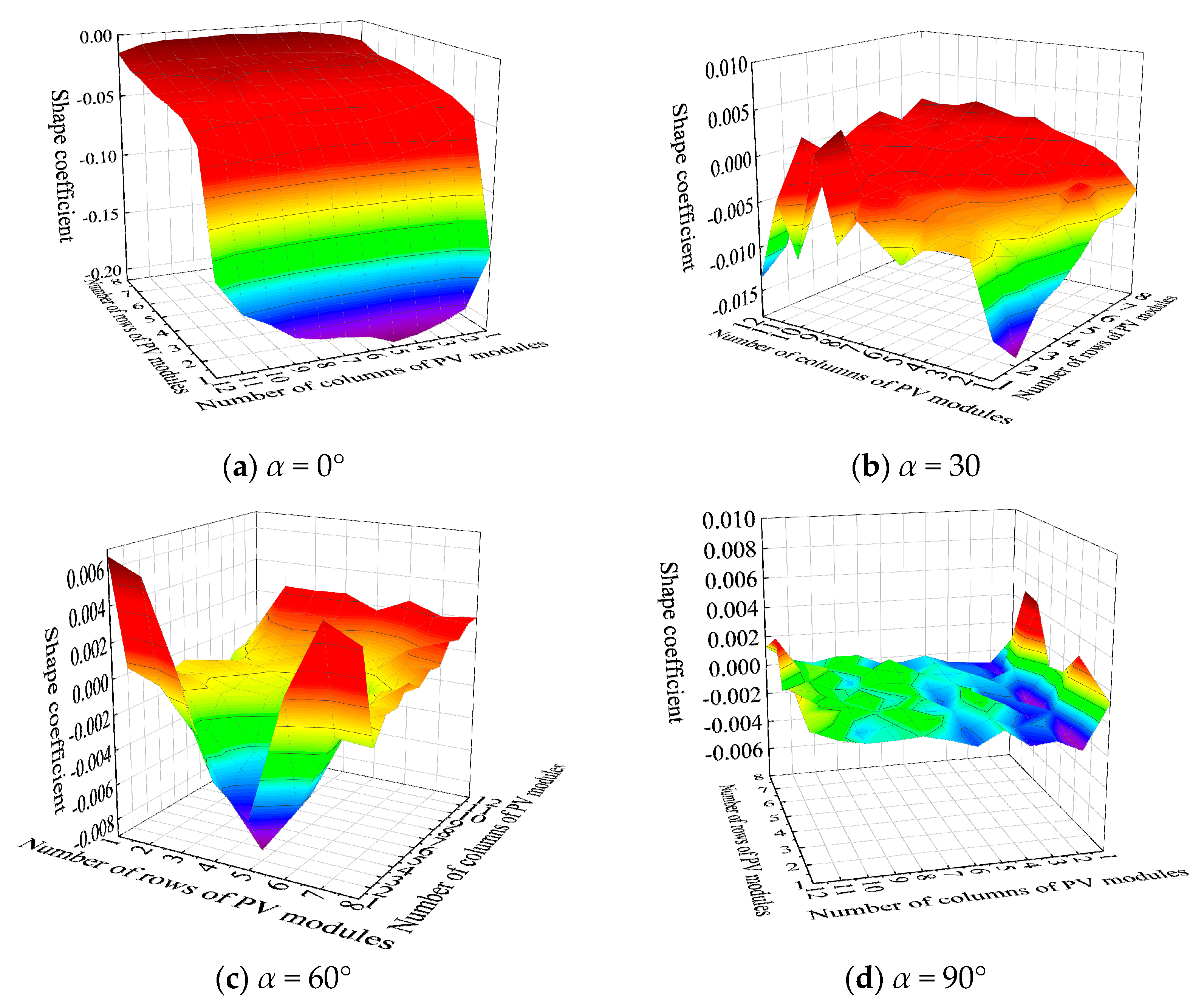
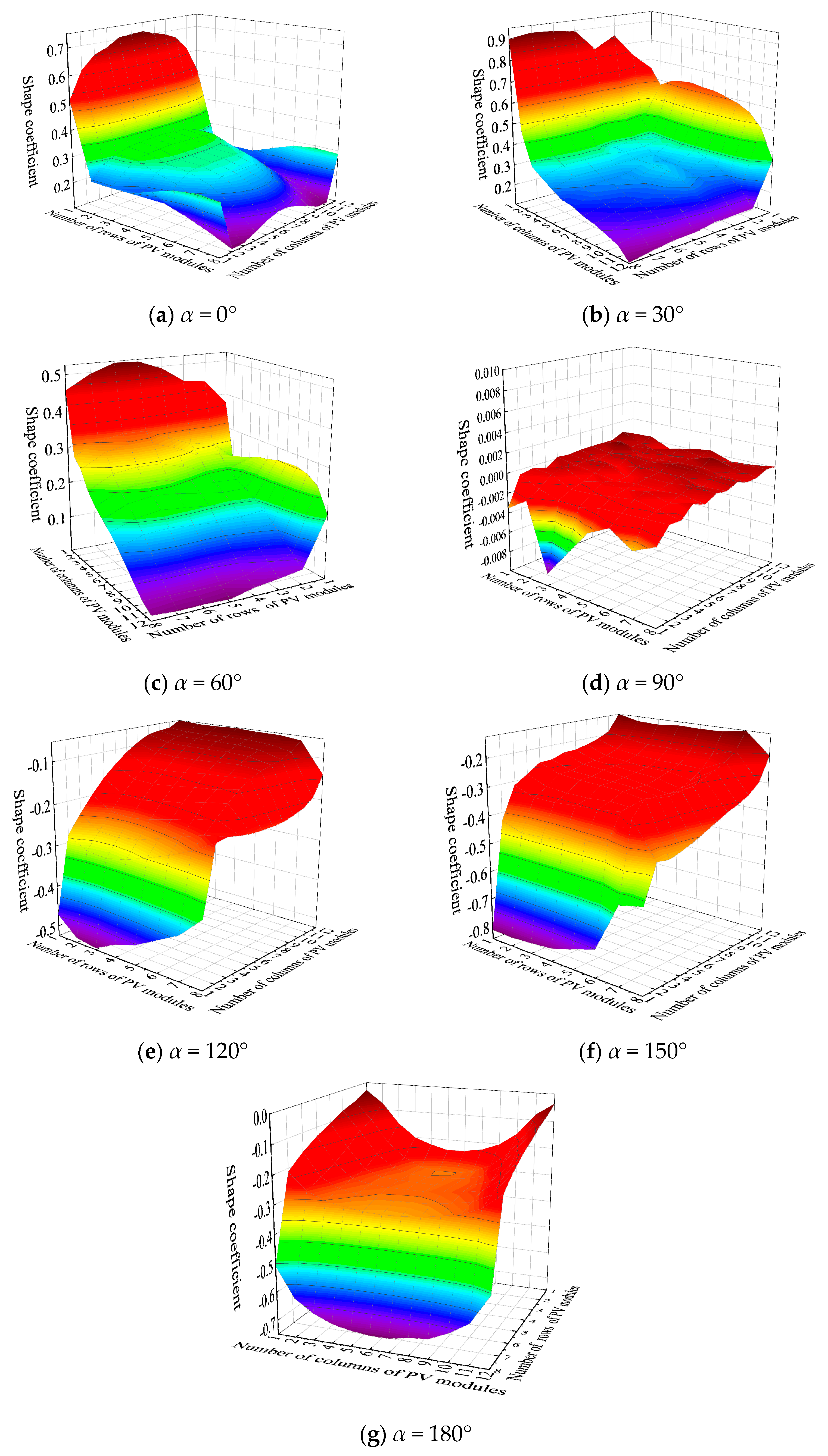
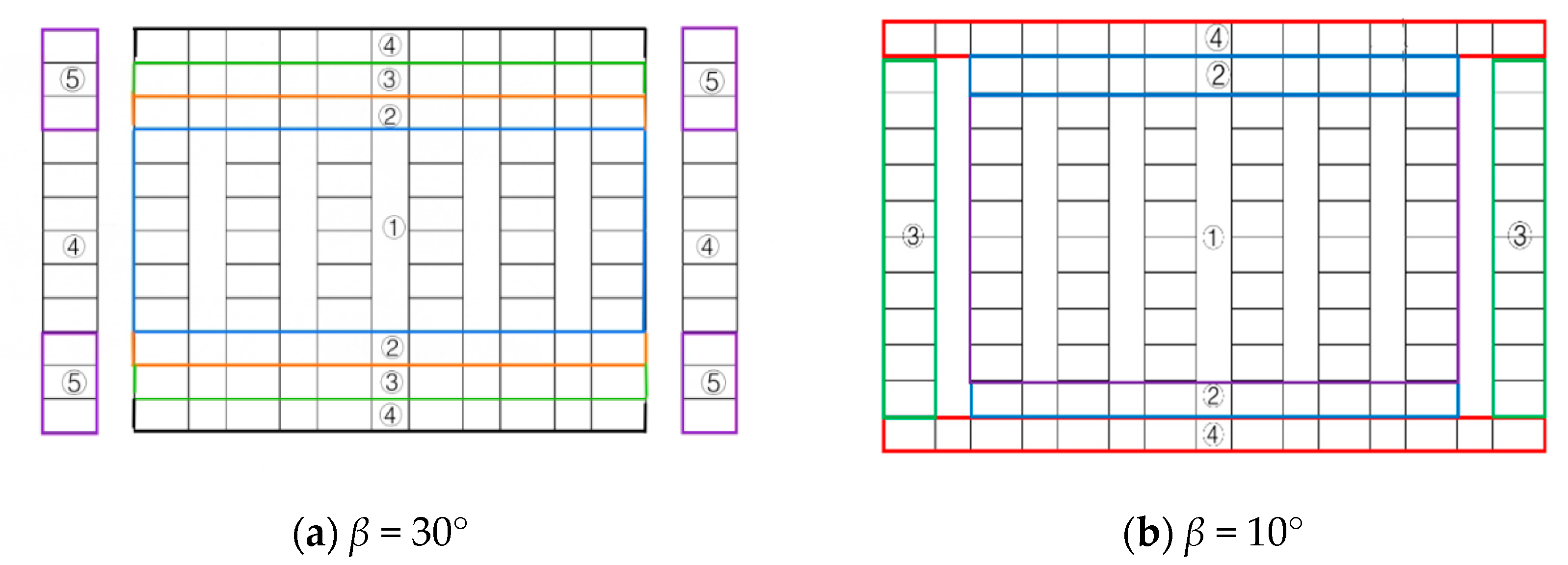
4. Optimization Recommendations for Wind Load Shape Coefficients in Different Regions of PV Panel Arrays
5. Conclusions
- The maximum wind load shape coefficient for PV panels typically occurs near α = 30° or α = 150° on the windward-facing PV panels. The distribution pattern of wind load shape coefficients varies with different tilt angles of the PV panel arrays. Wind load increases almost linearly with the tilt angle, and the sensitivity of wind load to the tilt angle of the PV panels is greater than that of other parameters. In mountainous conditions, wind loads on the middle and upper sections of the PV panels should be prioritized. When designing flexible support structures, special attention should be paid to the impact of changes in the tilt angle on structural wind loads.
- The spacing ratio significantly affects wind loads. The change in wind load shape coefficients with varying spacing ratios is inconsistent across different tilt angles. For PV panels with a tilt angle of β = 0°, the wind pressure distribution remains almost unaffected by changes in the spacing ratio. For β = 10° panels, the contour line where the wind pressure coefficient is greater than or equal to 0.4 shifts from the top (upstream direction) to the bottom of the PV panels as the spacing ratio increases. When β = 30°, the maximum wind pressure coefficient on both the windward and leeward sides shifts from the bottom to the top of the PV panels. The maximum wind pressure coefficient appears at the bottom for β = 0° and β = 10° but at the upper bottom region for β = 30°. Ground clearance height also affects wind loads, with higher clearance resulting in larger wind load shape coefficients. Both the spacing ratio and ground clearance height are critical factors in structural design.
- When estimating wind loads on flexibly supported PV panels, factors such as wind direction angle, tilt angle, ground clearance height, spacing ratio, and location must be considered. The standard wind load estimation for flexible PV arrays can integrate the shape coefficient values for different regions provided in this study with the wind load standard calculation formula that accounts for ground clearance height and spacing ratio. This approach ensures safety while saving materials.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aly, A.; Bitsuamlak, G. Aerodynamics of ground-mounted solar panels: Test model scale effects. J. Wind Eng. Ind. Aerodyn. 2013, 123, 250–260. [Google Scholar] [CrossRef]
- Aly, A.; Bitsuamlak, G. Wind induced pressures on solar panels mounted on residential homes. J. Archit. Eng. 2014, 20, 04013003. [Google Scholar] [CrossRef]
- Kopp, G.A.; Banks, D. Use of wind tunnel test method for obtaining design wind loads on roof-mounted solar arrays. J. Struct. Eng. 2013, 139, 284–287. [Google Scholar] [CrossRef]
- Pratt, R.N.; Kopp, G.A. Velocity measurements around low-profile, tilted, solar arrays mounted on large flat-roofs, for wall normal wind directions. J. Wind Eng. Ind. Aerodyn. 2013, 123, 226–238. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Zisis, I.; Xypnitou, E. Local and overall wind pressure and force coefficients for solar panels. J. Wind Eng. Ind. Aerodyn. 2014, 125, 195–206. [Google Scholar] [CrossRef]
- Warsido, W.P.; Bitsuamlak, G.T.; Barata, J. Influence of spacing parameters on the wind loading of solar array. J. Fluids Struct. 2014, 48, 295–315. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Spatial and temporal assessments of complementarity for renewable energy resources in China. Energy 2019, 177, 262–275. [Google Scholar] [CrossRef]
- Wang, C.; Shuai, J.; Ding, L.; Lu, Y.; Chen, J. Comprehensive benefit evaluation of solar PV projects based on multi-criteria decision grey relation projection method: Evidence from 5 counties in China. Energy 2022, 238, 121654. [Google Scholar] [CrossRef]
- Shafique, M.; Luo, X.; Zuo, J. Photovoltaic-green roofs: A review of benefits, limitations, and trends. Sol. Energy 2020, 202, 485–497. [Google Scholar] [CrossRef]
- Trindade, A.; Cordeiro, L. Automated formal verification of stand-alone solar photovoltaic systems. Sol. Energy 2019, 193, 684–691. [Google Scholar] [CrossRef]
- Glick, A.; Smith, S.E.; Ali, N.; Bossuyt, J.; Recktenwald, G.; Calaf, M.; Cal, R.B. Influence of flow direction and turbulence intensity on heat transfer of utility-scale photovoltaic solar farms. Sol. Energy 2020, 207, 173–182. [Google Scholar] [CrossRef]
- Wittwer, A.R.; Podestá, J.M.; Castro, H.G.; Mroginski, J.L.; Marighetti, J.O.; De Bortoli, M.E.; Paz, R.R.; Mateo, F. Wind loading and its effects on photovoltaic modules: An experimental–Computational study to assess the stress on structures. Sol. Energy 2022, 240, 315–328. [Google Scholar] [CrossRef]
- Alrawashdeh, H.; Stathopoulos, T. Wind loading of rooftop PV panels cover plate: A codification-oriented study. J. Wind. Eng. Ind. Aerodyn. 2023, 240, 105489. [Google Scholar] [CrossRef]
- Dai, S.F.; Liu, H.J.; Yang, J.H.; Peng, H.Y. Wind loads on roof-mounted isolated solar panels of tall buildings through wind tunnel testing. Sol. Energy 2022, 231, 607–622. [Google Scholar] [CrossRef]
- Alrawashdeh, H.; Stathopoulos, T. Critical considerations for modeling roof mounted solar panels in atmospheric wind tunnels. In Proceedings of the 3rd International Conference Coordinating Engineering for Sustainability and Resilience (CESARE’22), Irbid, Jordan, 6–9 May 2022; Volume 1–10. [Google Scholar]
- Alrawashdeh, H.; Stathopoulos, T. Experimental investigation of the wind loading on solar panels: Effects of clearance off flat roofs. J. Struct. Eng. 2022, 148, 04022202. [Google Scholar] [CrossRef]
- Ghazal, T.; Elshaer, A.; Aboshosha, H. Wind load evaluation on storm shelters using wind tunnel testing and North American design codes. Eng. Struct. 2022, 254, 113821. [Google Scholar] [CrossRef]
- Ghazal, T.; Aboutabikh, M.; Aboshosha, H.; Abdelwahab, M. Thunderstorm wind load evaluation on storm shelters using wind tunnel testing. Eng. Struct. 2022, 262, 114350. [Google Scholar] [CrossRef]
- Valentín, D.; Valero, C.; Egusquiza, M.; Presas, A. Failure investigation of a solar tracker due to wind-induced torsional galloping. Eng. Fail. Anal. 2022, 135, 106137. [Google Scholar] [CrossRef]
- Martínez-García, E.; Blanco-Marigorta, E.; Gayo, J.P.; Navarro-Manso, A. Influence of inertia and aspect ratio on the torsional galloping of single-axis solar trackers. Eng. Struct. 2021, 243, 112682. [Google Scholar] [CrossRef]
- Winkelmann, U.; Kämper, C.; Höffer, R.; Forman, P.; Ahrens, M.A.; Mark, P. Wind actions on large-aperture parabolic trough solar collectors: Wind tunnel tests and structural analysis. Renew. Energy 2020, 146, 2390–2407. [Google Scholar] [CrossRef]
- Browne, M.T.L.; Taylor, Z.J.; Li, S.; Gamble, S. A wind load design method for ground-mounted multi-row solar arrays based on a compilation of wind tunnel experiments. J. Wind Eng. Ind. Aerod. 2020, 205, 104294. [Google Scholar] [CrossRef]
- Xu, A.; Ma, W.; Yuan, H.; Lu, L. The effects of row spacing and ground clearance on the wind load of photovoltaic (PV) arrays. Renew. Energy 2024, 220, 119627. [Google Scholar] [CrossRef]
- Yemenici, O.; Aksoy, M.O. An experimental and numerical study of wind effects on a ground-mounted solar panel at different panel tilt angles and wind directions. J. Wind. Eng. Ind. Aerodyn. 2021, 213, 104630. [Google Scholar] [CrossRef]
- Yang, Y.; Gu, M.; Chen, S.; Jin, X. New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering. J. Wind Eng. Ind. Aerod. 2009, 97, 88–95. [Google Scholar] [CrossRef]
- GB 50009-2012; Building Structural Load Specification. Ministry of Housing and Urban-Rural Construction of the People’s Republic of China: Beijing, China, 2012.
- Ye, L.; He, T.; Zhang, X.; Sun, S.; Li, B.; Wang, M. Research on influence of sunlight incident angle difference on power generation capacity of vertically installed PV modules on the facade in different climate zones. Sol. Energy 2023, 1, 35–42. [Google Scholar] [CrossRef]
- Du, H.; Xu, H.W.; Zhang, Y.L.; Lou, W.J. Wind pressure characteristics and wind vibration response of large-span flexible photovoltaic bracket structure. J. Harbin Inst. Technol. 2022, 54, 67–74. [Google Scholar]
- Ma, W.; Chai, X.; Liu, Q.; Xing, K.; Liu, X. Study on effect of bottom flow obstruction on wind load of solar photovoltaic panels. Build. Struct. 2019, 49, 129–134. [Google Scholar]
- NB/T 10115—2018; Code for Structural Design of Photovoltaic Support. Inner Mongolia Electric Power Survey and Design Institute Co., Ltd.: Beijing, China, 2018.
- Zhang, A.; Gao, C.; Shen, C.; Zhang, B. Numerical analysis of wind load characteristics of photovoltaic panels mounted on a roof. Chin. J. Comput. Mech. 2016, 33, 683–688, 737. [Google Scholar]

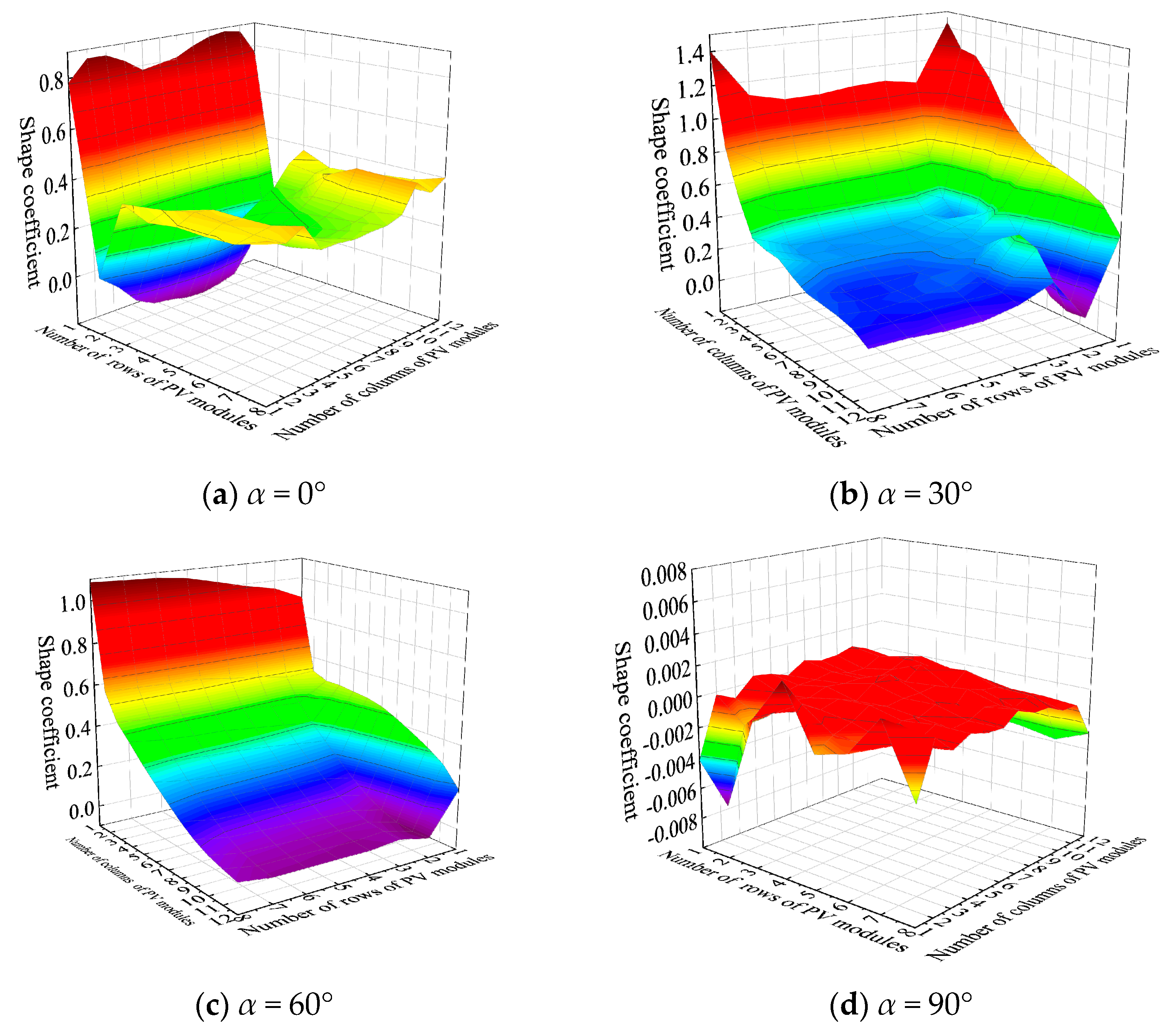
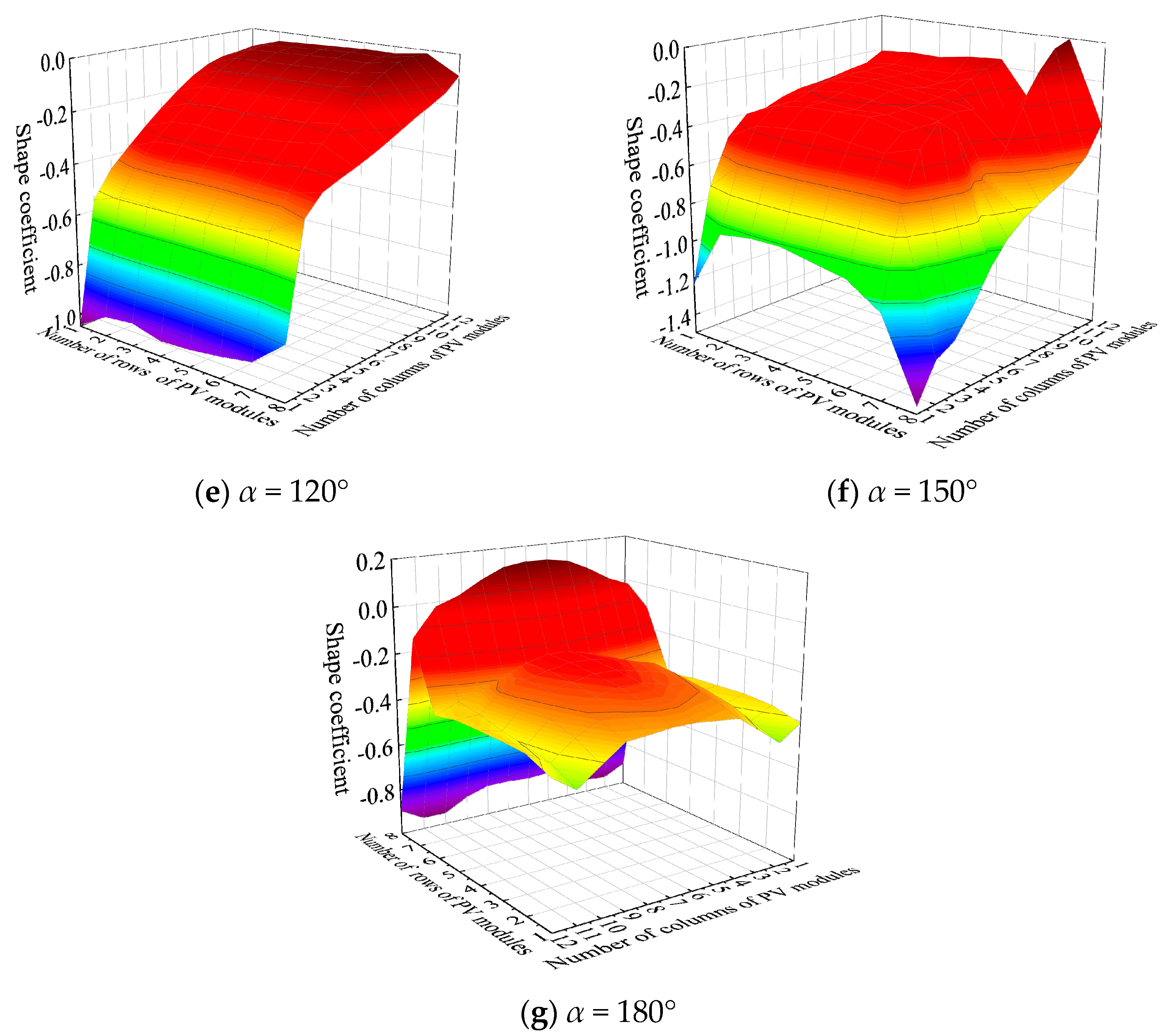
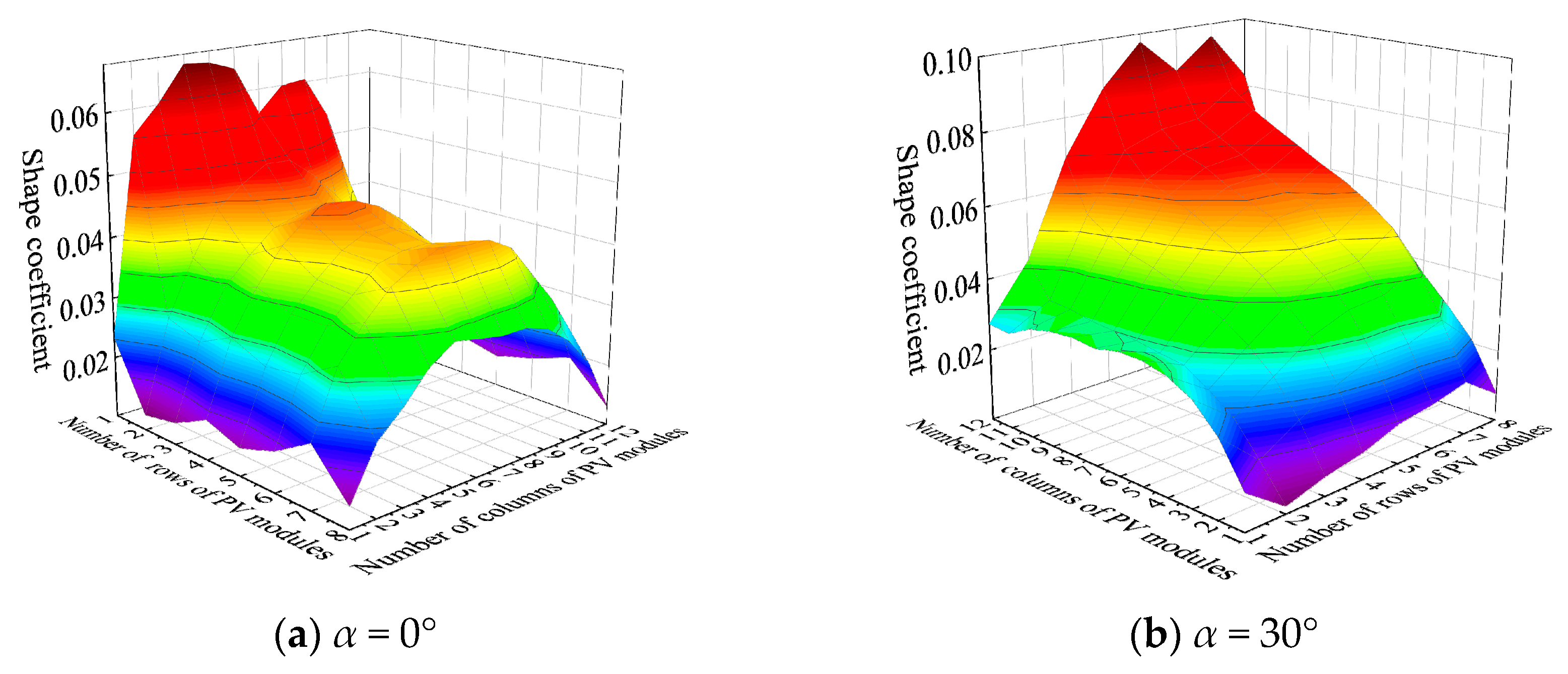
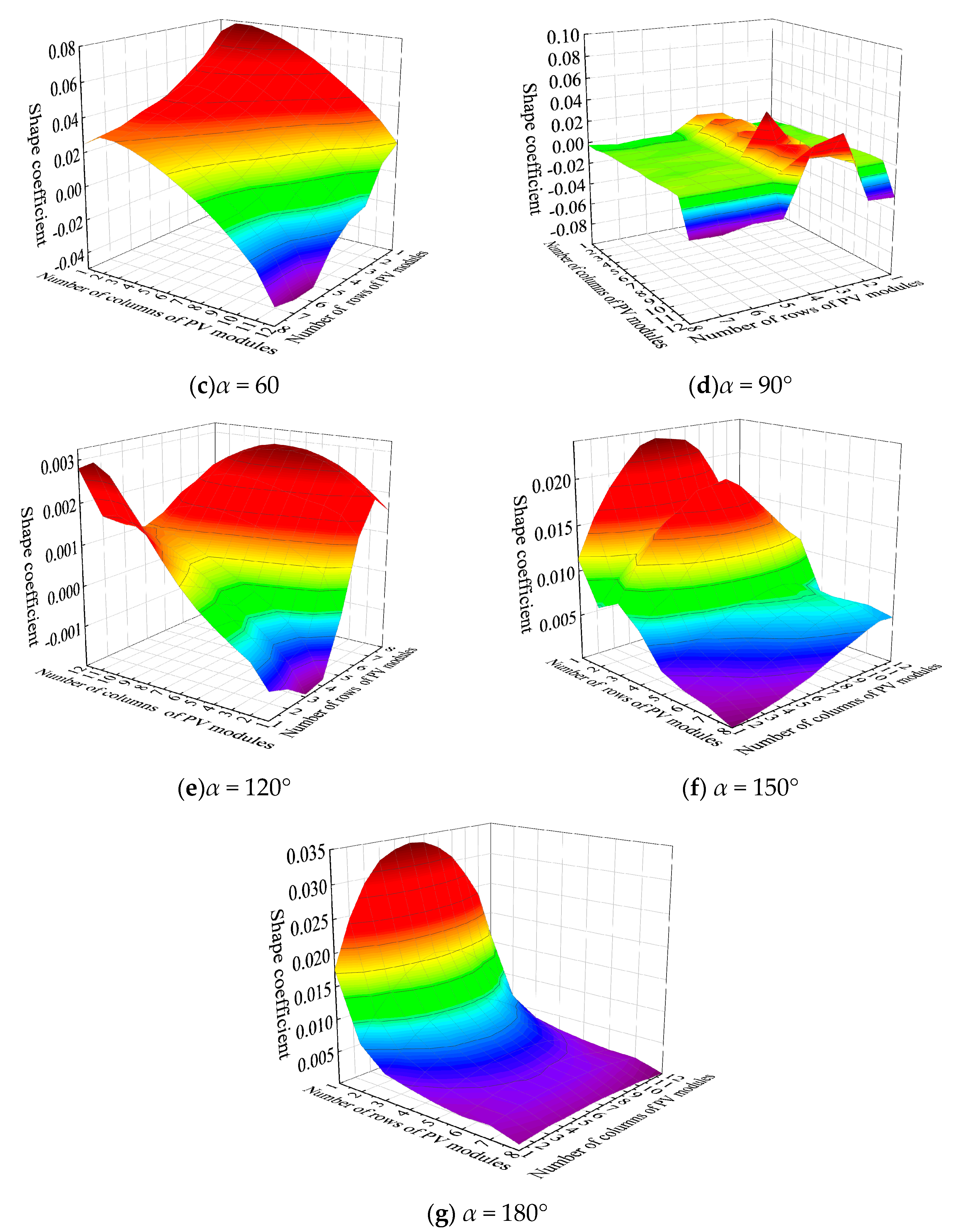

| Drift Angle α | Shape Coefficients | β ≤ 15° | β = 30° |
|---|---|---|---|
| 0° | Simulation value | 0.60 | 0.88 |
| 0° | Standardised value | 0.80 | 1.00 |
| 180° | Simulation value | −0.59 | −0.95 |
| 180° | Standardised value | −0.95 | −1.31 |
| Tilt | Region1 | Region2 | Region3 | Region4 | Region5 |
|---|---|---|---|---|---|
| 30° | 0.40 | 0.35 | 0.50 | 1.00 | 0.90 |
| Tilt | Region1 | Region2 | Region3 | Region4 |
|---|---|---|---|---|
| 10° | 0.37 | 0.50 | 0.70 | 0.95 |
| Heights H | 3 m | 4.5 m | 6 m | 9 m | |
|---|---|---|---|---|---|
| Tilt | 10° | 1.109 | 1.046 | 1.043 | 1.113 |
| β | 30° | 1.083 | 1.058 | 1.047 | 1.055 |
| Spacing Ratio | 0.032 | 0.064 | 0.128 | 0.256 | |
|---|---|---|---|---|---|
| Tilt | 10° | 1.027 | 1.042 | 1.15 | 1.267 |
| β | 30° | 0.992 | 0.964 | 0.889 | 0.718 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Lou, Y. Study of Wind Load Influencing Factors of Flexibly Supported Photovoltaic Panels. Buildings 2024, 14, 1677. https://doi.org/10.3390/buildings14061677
Zhang J, Lou Y. Study of Wind Load Influencing Factors of Flexibly Supported Photovoltaic Panels. Buildings. 2024; 14(6):1677. https://doi.org/10.3390/buildings14061677
Chicago/Turabian StyleZhang, Jian, and Yibing Lou. 2024. "Study of Wind Load Influencing Factors of Flexibly Supported Photovoltaic Panels" Buildings 14, no. 6: 1677. https://doi.org/10.3390/buildings14061677
APA StyleZhang, J., & Lou, Y. (2024). Study of Wind Load Influencing Factors of Flexibly Supported Photovoltaic Panels. Buildings, 14(6), 1677. https://doi.org/10.3390/buildings14061677




