Effects of Steel Fiber Content on Compressive Properties and Constitutive Relation of Ultra-High Performance Shotcrete (UHPSC)
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Mix of UHPSC
2.2. Preparation of Concrete Specimens
2.3. Mechanical Property Test
3. Results and Discussion
3.1. Failure Pattern
3.2. Compressive Strength
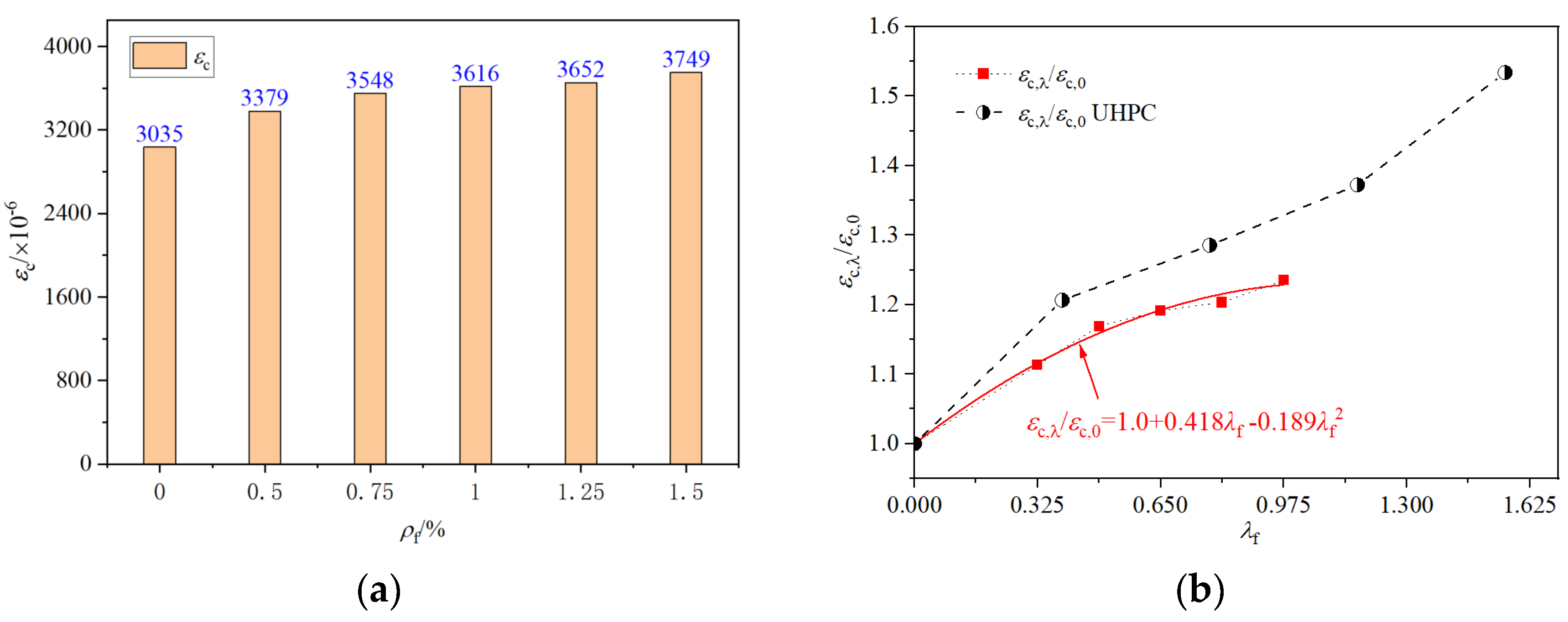
3.3. Peak Strain
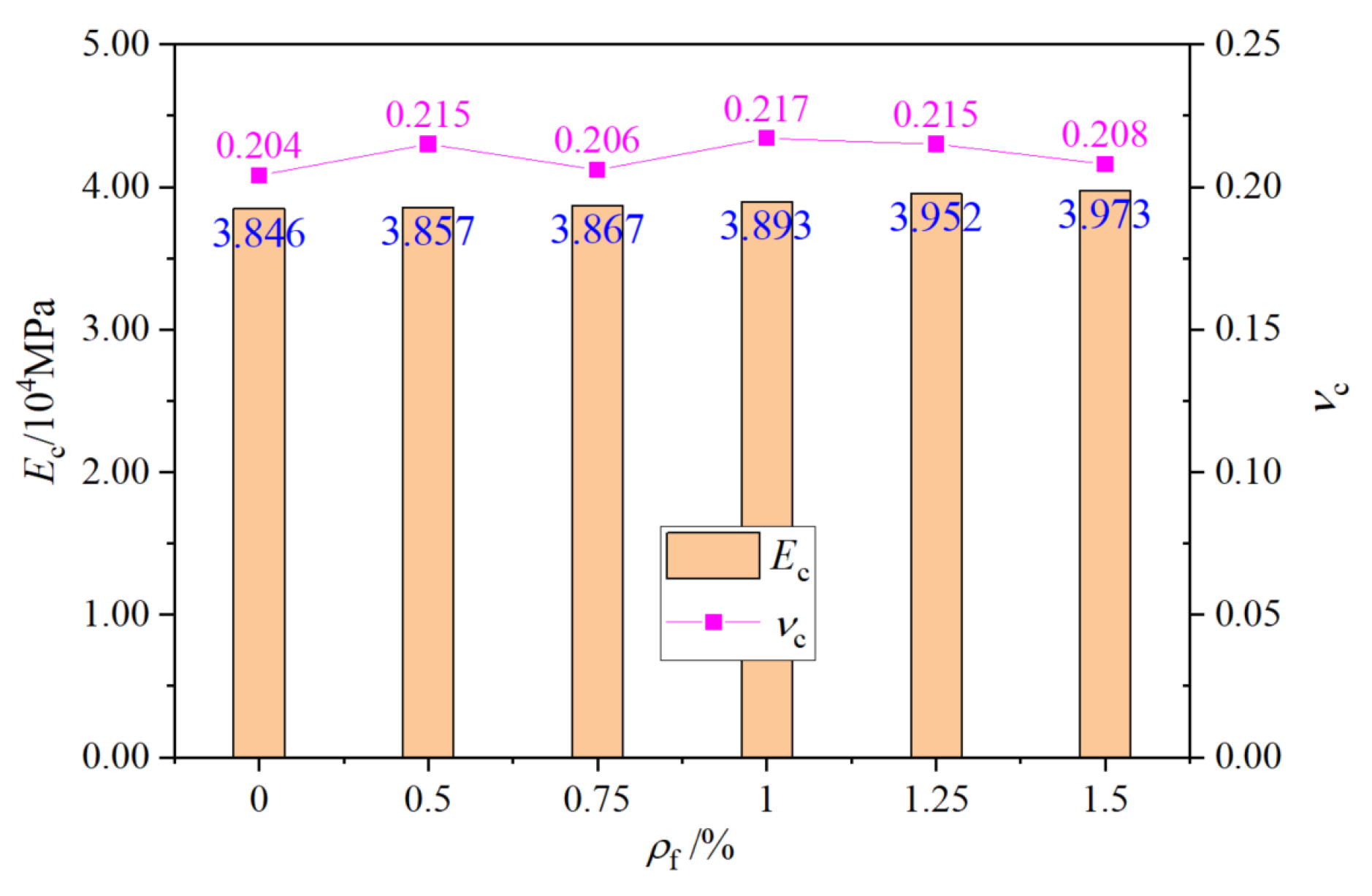
3.4. Elastic Modulus and Poisson’s Ratio
3.5. Compressive Toughness
3.6. Uniaxial Compressive Constitutive Model
4. Conclusions
- (1)
- Before the failure of UHPSC without steel fiber, there was no obvious sign, which belonged to brittle failure. The failure pattern of UHPSC with steel fibers showed the ductile failure characteristics of multiple oblique cracks, showing a complete form of “crack but not broken”. The critical failure surfaces of the prism were all perpendicular to the spraying direction.
- (2)
- The compressive strength, peak strain, and compressive toughness of UHPSC increased with the increase in steel fiber content, but the elastic modulus and Poisson’s ratio did not change significantly. With content of 1.5% steel fibers, its axial compressive strength, peak strain and compressive strain energy were 122.7 MPa, 3749 με and 0.269 MPa, respectively, increased by 14%, 23.5% and 55.5% compared with those without steel fiber.
- (3)
- The peak strain and compressive toughness were higher than that of UHPC, while the elastic modulus of UHPSC was lower than that of UHPC. Based on the experimental data, the relationship between compressive strength, peak strain, compressive toughness and the change in the characteristic value of steel fiber content (λf) were revealed.
- (4)
- Based on the experimental results, the uniaxial compressive constitutive model of UHPSC with different steel fiber content was established, and the variation of the shape coefficients α and β with λf was revealed. The experimental results were in good agreement with the model calculation results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- JGJ/T 372-2016; Technical Specification for Application of Sprayed Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- Cui, Y.; Tan, Z.; Zhou, Z.; Wu, J.; Wang, J. Preparation and application of low rebound liquid alkali-free accelerator for shotcrete. Constr. Build. Mater. 2023, 367, 130220. [Google Scholar] [CrossRef]
- Khooshechin, M.; Tanzadeh, J. Experimental and mechanical performance of shotcrete made with nanomaterials and fiber reinforcement. Constr. Build. Mater. 2018, 165, 199–205. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Li, P.; Pan, G. Rebound Characteristics of Wet-Shotcrete Particle Flow Jet from Wall Based on CFD-DEM. Buildings 2024, 14, 977. [Google Scholar] [CrossRef]
- Takeda, H.; Kawaguchi, T.; Yoshimoto, H.; Fujiwara, S.; Sato, K. Material properties and construction performance of ultra-high strength sprayed concrete. In Tunnels and Underground Cities: Engineering and Innovation Meet Archaeology, Architecture and Art; Peila, D., Viggiani, G., Celestion, T., Eds.; Taylor & Francis Group: Naples, Italy; London, UK, 2019; pp. 3162–3171. [Google Scholar]
- Won, J.P.; Hwang, U.J.; Kim, C.K.; Lee, S.J. Mechanical performance of shotcrete made with a high-strength cement-based mineral accelerator. Constr. Build. Mater. 2013, 49, 175–183. [Google Scholar] [CrossRef]
- Heidarnezhad, F.; Zhang, Q. Shotcrete based 3D concrete printing: State of art, challenges, and opportunities. Constr. Build. Mater. 2022, 323, 126545. [Google Scholar] [CrossRef]
- David, M.; Freund, N.; Dröder, K.; Lowke, D. The effects of nozzle diameter and length on the resulting strand properties for shotcrete 3D printing. Mater. Struct. 2023, 56, 157. [Google Scholar] [CrossRef]
- Rehman, A.U.; Birru, B.M.; Kim, J.H. Set-on-demand 3D Concrete Printing (3DCP) construction and potential outcome of shotcrete accelerators on its hardened properties. Case Stud. Constr. Mat. 2023, 18, e01955. [Google Scholar] [CrossRef]
- Briendl, L.G.; Mittermayr, F.; Röck, R.; Steindl, F.R. The hydration of fast setting spray binder versus (aluminum sulfate) accelerated OPC. Mater. Struct. 2022, 55, 74. [Google Scholar] [CrossRef]
- Kanda, T.; Saito, T.; Sakata, N.; Hiraishi, M. Tensile and Anti-Spalling Proper-ties of Direct Sprayed ECC. J. Adv. Concr. Technol. 2003, 1, 269–282. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, C.; Ma, Y.; Xiao, Y.; Liu, Y. Accelerators for shotcrete–Chemical composition and their effects on hydration, microstructure and properties of cement-based materials. Constr. Build. Mater. 2021, 281, 122557. [Google Scholar] [CrossRef]
- Martinez-Ramirez, S.; Palomo, A. Microstructure studies on Portland cement pastes obtained in highly alkaline environments. Cem. Concr. Res. 2001, 31, 1581–1585. [Google Scholar] [CrossRef]
- Wang, J.; Niu, D.; Zhang, Y. Microstructure and mechanical properties of accelerated sprayed concrete. Mater. Struct. 2016, 49, 1469–1484. [Google Scholar] [CrossRef]
- Lagerblad, B.; Fjällberg, L.; Vogt, C. Shrinkage and durability of shotcrete. In Shotcrete: Elements of a System; Stefan, B., Ed.; CRC Press: London, UK, 2010; pp. 173–180. [Google Scholar]
- Park, H.G.; Sung, S.K.; Park, C.G.; Won, J.P. Influence of a C12A7 mineral-based accelerator on the strength and durability of shotcrete. Cem. Concr. Res. 2008, 38, 379–385. [Google Scholar] [CrossRef]
- Prudencio, L.R., Jr. Accelerating admixtures for shotcrete. Cem. Concr. Compos. 1998, 20, 213–219. [Google Scholar] [CrossRef]
- Cui, J.; He, Z.; Zhang, G.; Cai, X.; Hu, L. Rheology, mechanical properties and pore structure of sprayed ultra-high performance concrete (SUHPC) with viscosity-enhancing agent. Constr. Build. Mater. 2022, 350, 128840. [Google Scholar] [CrossRef]
- Cui, J.; He, Z.; Zhang, G.; Cai, X. Rheological properties of sprayable ultra-high performance concrete with different viscosity-enhancing agents. Constr. Build. Mater. 2022, 321, 126154. [Google Scholar] [CrossRef]
- Cui, J.; He, Z.; Cai, X. Mechanical properties and key intrinsic factors of sprayed ultra-high performance concrete (SUHPC) with alkali-free accelerator. Constr. Build. Mater. 2022, 349, 128788. [Google Scholar] [CrossRef]
- Habel, K.; Viviani, M.; Denarié, E.; Brühwiler, E. Development of the mechanical properties of an Ultra-High Performance Fiber Reinforced Concrete (UHPFRC). Cem. Concr. Res. 2006, 36, 1362–1370. [Google Scholar] [CrossRef]
- Tuan, N.V.; Ye, G.; Breugel, K.V.; Copuroglu, O. Hydration and microstructure of ultra high performance concrete incorporating rice husk ash. Cem. Concr. Res. 2011, 41, 1104–1111. [Google Scholar] [CrossRef]
- Yang, J.; Niu, Y.; Li, Y.; Ding, P.; Zhang, S. Study on constitutive relation of carbon nanotubes shotcrete under uniaxial stress. J. Henan Polytech. Univ. Nat. Sci. 2013, 32, 607–614. (In Chinese) [Google Scholar] [CrossRef]
- Guan, X.; Niu, D.; Wang, J.; Wu, B. Study of Damage Constitutive Model of Shotcrete under Uniaxial Compression. J. China Railw. Soc. 2016, 38, 118–124. (In Chinese) [Google Scholar] [CrossRef]
- Bai, J.; Cheng, Y.; Zheng, Q.; Li, F.; Wu, F. Mechanical characteristics and failure mechanism of dry and wet shotcrete under loading. J. China Coal. Soc. 2020, 45, 2777–2786. (In Chinese) [Google Scholar] [CrossRef]
- Wang, J.; Niu, D.; He, H. Frost durability and stress-strain relationship of lining shotcrete in cold environment. Constr. Build. Mater. 2018, 198, 58–69. [Google Scholar] [CrossRef]
- Yang, F.; Yang, S.; Fu, Y.; Zhang, Y. Stress-strain relationship and damage constitutive model of wet concrete under uniaxial compression. Case Stud. Constr. Mater. 2023, 18, e02154. [Google Scholar] [CrossRef]
- Yang, G. Study on Failure Criterion and Constitutive Relationship of 200 MPa Reactive Powder Concrete. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2005. [Google Scholar]
- Bae, B.I.; Choi, H.K.; Lee, B.S.; Bang, C.H. Compressive behavior and mechanical characteristics and their application to stress-strain relationship of steel fiber-reinforced reactive powder concrete. Adv. Mater. Sci. Eng. 2016, 2016, 6465218. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; He, W.; Wang, D. Uniaxial compression behavior of ultra-high performance concrete with hybrid steel fiber. J. Mater. Civ. Eng. 2016, 28, 06016017. [Google Scholar] [CrossRef]
- Deng, J.; Yang, J.; Chen, B.; Xu, G.; Li, Y. Uniaxial constitutive relation of ultra-high performance fiber reinforced concrete and the effect of steel fiber reinforcement on it. Acta Mater. Compos. Sin. 2024, 41, 911–924. (In Chinese) [Google Scholar] [CrossRef]
- Chang, Y. Investigation on Compressive Stress-Strain Relationship and Application of Ultra-High Performance Concrete Constrained by Stirrups. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2022. [Google Scholar]
- Hu, A. Research on Mechanical Performance of Ultra-High Performance Concrete. Ph.D. Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2022. [Google Scholar]
- Graybeal, B.A. Characterization of the Behavior of Ultrahigh Performance Concrete. Ph.D. Thesis, University of Maryland, College Park, WA, USA, 2005. [Google Scholar]
- Huang, Z.; Tan, B. Research on stress-strain curves of reactive powder concrete with steel-fiber under uniaxial compression. J. China Three Gorges Univ. Nat. Sci. 2007, 29, 415–420. (In Chinese) [Google Scholar] [CrossRef]
- Nie, J. Research on Key Influencing Factors of Mechanical Properties and Expansion of Ultra-High Performance Concrete. Ph.D. Thesis, Changsha University of Science & Technology, Changsha, China, 2020. [Google Scholar]
- Wakjira, T.G.; Kutty, A.A.; Alam, M.S. A novel framework for developing environmentally sustainable and cost-effective ultra-high-performance concrete (UHPC) using advance machine learning and multi-objective optimization techniques. Constr. Build. Mater. 2024, 416, 135114. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Alam, M.S. Peak and ultimate stress-strain model of confined ultra-high-performance concrete (UHPC) using hybrid machine learning model with conditional tabular generative adversarial network. Appl. Soft Comput. 2024, 154, 111353. [Google Scholar] [CrossRef]
- Wakjira, T.G.; Abushanabb, A.; Alam, M.S. Hybrid machine learning model and predictive equations for compressive stress-strain constitutive modelling of confined ultra-high-performance concrete (UHPC) with normal-strength steel and high-strength steel spirals. Eng. Struct. 2024, 304, 117633. [Google Scholar] [CrossRef]
- DBJ43/T325-2017; Technical Specification for Reactive Powder Concrete Structures. Hunan Department of Housing and Urban-Rural Development: Changsha, China, 2017.
- Robins, P.J.; Austin, S.A.; Jones, P.A. Spatial distribution of steel fibres in sprayed and cast concrete. Mag. Concr. Res. 2003, 55, 225–235. [Google Scholar] [CrossRef]
- Wei, D. Study on Fiber Distribution Characteristics and Mechanical Properties of Steel Fiber Shotcrete. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Lee, C.; Kim, H. Orientation factor and number of fibers at failure plane in ring-type steel fiber reinforced concrete. Cem. Concr. Res. 2010, 40, 810–819. [Google Scholar] [CrossRef]
- GB175-2007; Common Portland Cement. Standardization Administration of the People’s Republic of China: Beijing, China, 2007.
- JG/T 568-2019; Aggregate for High Performance Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- CECS13-2009; Standard Test Methods for Fiber Reinforced Concrete. China Association for Engineering Construction Standardization: Beijing, China, 2009.
- GB 50010-2010; Code for Design of Concrete Structures. Standardization Administration of the People’s Republic of China: Beijing, China, 2010.
- JGJ/T 465-2019; Standard for Design of Steel Fiber Reinforced Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- T/CECS 1216-2022; Technical Specification for Application of Ultra High Performance Concrete in Building Engineering. China Association for Engineering Construction Standardization: Beijing, China, 2022.
- Guo, X.; Kang, J.; Zhu, J. Constitutive relationship of ultrahigh performance concrete under uniaxial compression. J. Southeast Univ. Nat. Sci. Ed. 2017, 47, 369–376. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, H.; Hu, F.; Duan, Y.; Liao, J.; Yang, J. Mechanical Properties and Microstructure of Highly Composites with Low-Content Polyvinyl Flowable Geopolymer Alcohol Fiber. Buildings 2024, 14, 449. [Google Scholar] [CrossRef]
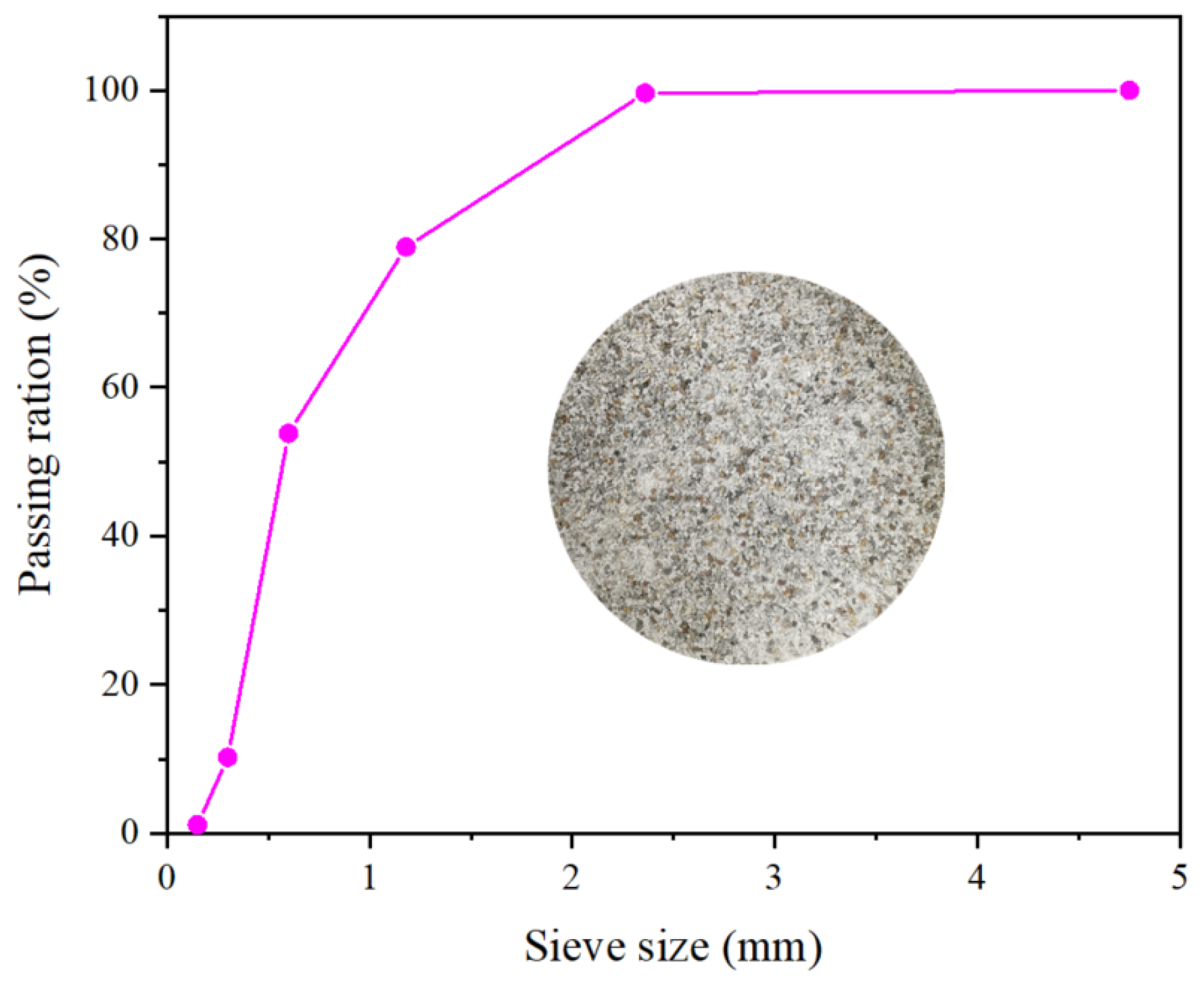
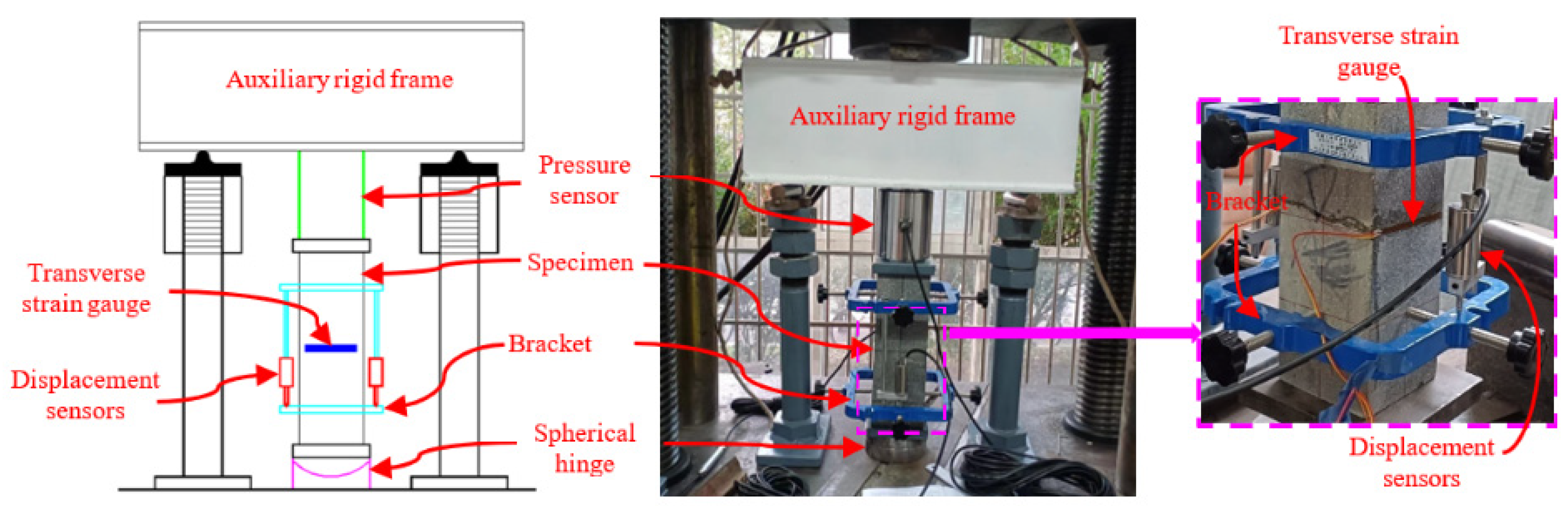

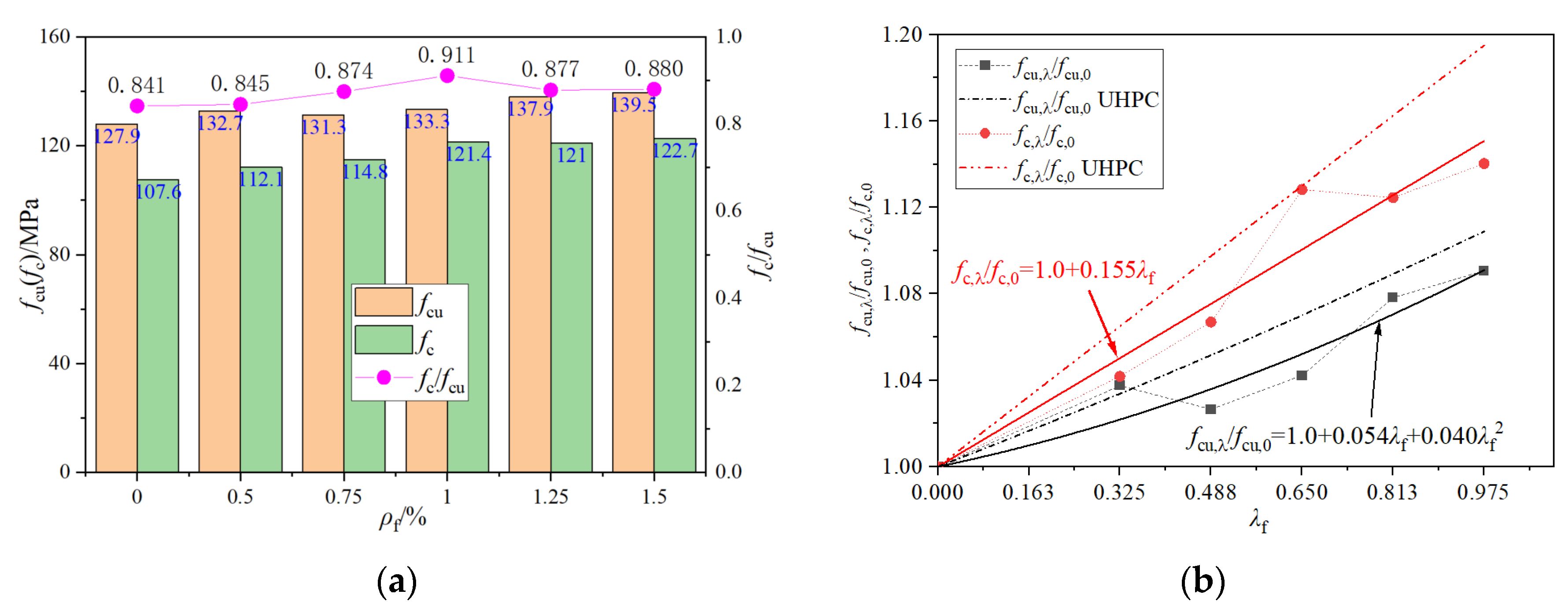
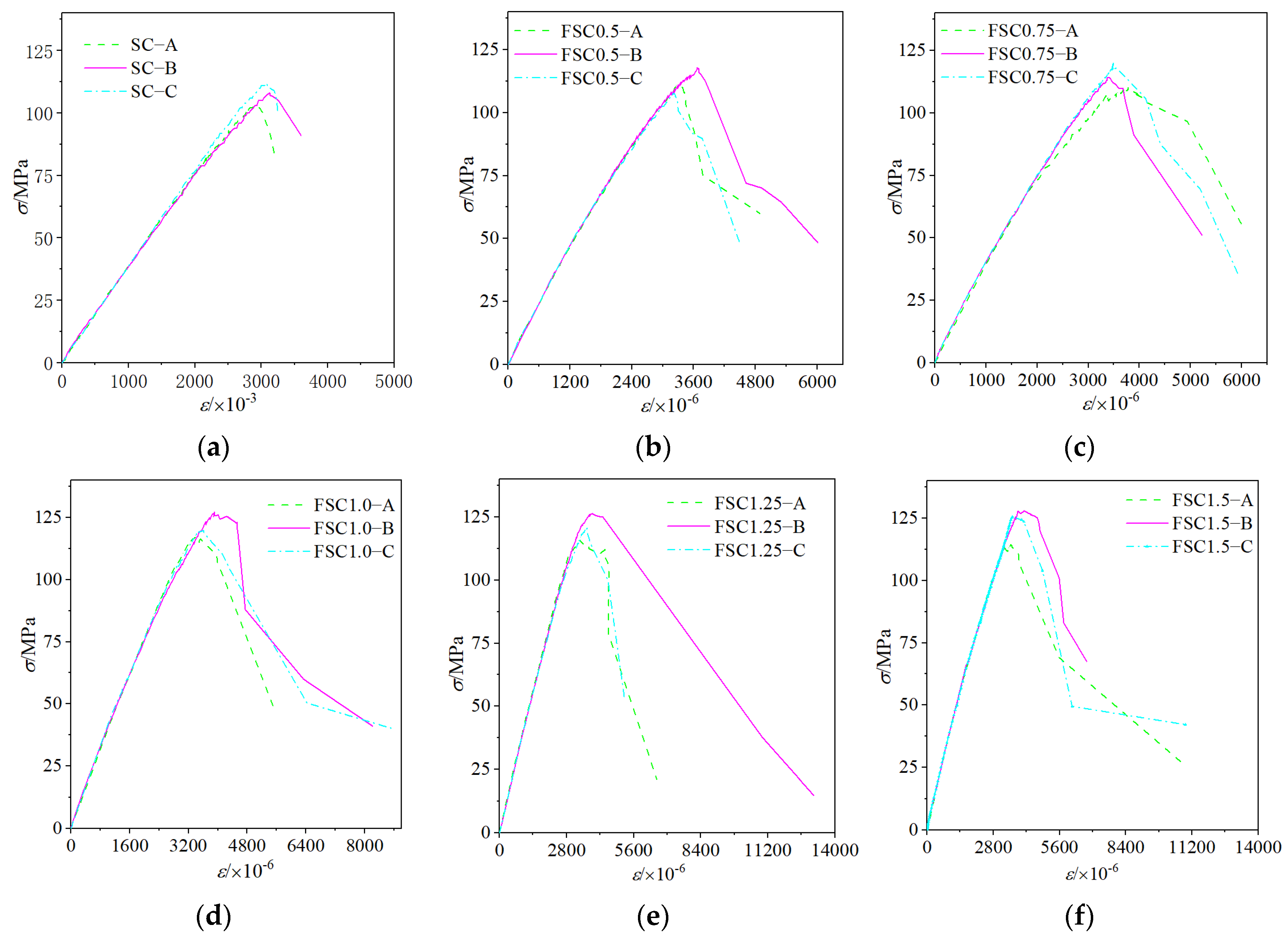

| No. | Steel Fiber (%) | Water | Cement | SF | FA | QS | Superplasticizer | VE |
|---|---|---|---|---|---|---|---|---|
| SC | 0 | 0.295 | 1.0 | 0.128 | 0.103 | 1.282 | 0.005 | 0.077 |
| FSC0.5 | 0.5 | 0.295 | 1.0 | 0.128 | 0.103 | 1.266 | 0.005 | 0.077 |
| FSC0.75 | 0.75 | 0.295 | 1.0 | 0.128 | 0.103 | 1.259 | 0.005 | 0.077 |
| FSC1.0 | 1.0 | 0.295 | 1.0 | 0.128 | 0.103 | 1.251 | 0.005 | 0.077 |
| FSC1.25 | 1.25 | 0.295 | 1.0 | 0.128 | 0.103 | 1.243 | 0.005 | 0.077 |
| FSC1.5 | 1.5 | 0.295 | 1.0 | 0.128 | 0.103 | 1.235 | 0.005 | 0.077 |
| No. | λf | Wc (MPa) | Re | Wc,λ/Wc,0 | Re,λ/Re,0 | ||
|---|---|---|---|---|---|---|---|
| Result | Average | Result | Average | ||||
| SC-A | 0 | 0.158 | 0.173 | 0.528 | 0.529 | 1.000 | 1.000 |
| SC-B | 0.180 | 0.533 | |||||
| SC-C | 0.181 | 0.527 | |||||
| FSC0.5-A | 0.325 | 0.195 | 0.195 * | 0.540 | 0.548 | 1.127 | 1.035 |
| FSC0.5-B | 0.242 | 0.560 | |||||
| FSC0.5-C | 0.188 | 0.544 | |||||
| FSC0.75-A | 0.4875 | 0.245 | 0.227 | 0.587 | 0.557 | 1.310 | 1.052 |
| FSC0.75-B | 0.210 | 0.545 | |||||
| FSC0.75-C | 0.225 | 0.538 | |||||
| FSC1.0-A | 0.65 | 0.226 | 0.249 | 0.556 | 0.567 | 1.439 | 1.071 |
| FSC1.0-B | 0.277 | 0.558 | |||||
| FSC1.0-C | 0.244 | 0.586 | |||||
| FSC1.25-A | 0.8125 | 0.239 | 0.256 | 0.613 | 0.580 | 1.480 | 1.095 |
| FSC1.25-B | 0.281 | 0.568 | |||||
| FSC1.25-C | 0.248 | 0.558 | |||||
| FSC1.5-A | 0.975 | 0.240 | 0.259 * | 0.594 | 0.584 | 1.497 | 1.103 |
| FSC1.5-B | 0.308 | 0.586 | |||||
| FSC1.5-C | 0.259 | 0.571 | |||||
| No. | λf | α | β |
|---|---|---|---|
| SC | 0 | 19.92 | 15.08 |
| FSC0.5 | 0.325 | 9.44 | 8.24 |
| FSC0.75 | 0.4875 | 9.04 | 5.44 |
| FSC1.0 | 0.65 | 6.47 | 4.29 |
| FSC1.25 | 0.8125 | 6.68 | 3.61 |
| FSC1.5 | 0.975 | 7.03 | 3.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, S.; Yang, J.; Liu, Z.; Yang, W.; He, J. Effects of Steel Fiber Content on Compressive Properties and Constitutive Relation of Ultra-High Performance Shotcrete (UHPSC). Buildings 2024, 14, 1503. https://doi.org/10.3390/buildings14061503
Xiao S, Yang J, Liu Z, Yang W, He J. Effects of Steel Fiber Content on Compressive Properties and Constitutive Relation of Ultra-High Performance Shotcrete (UHPSC). Buildings. 2024; 14(6):1503. https://doi.org/10.3390/buildings14061503
Chicago/Turabian StyleXiao, Shijie, Jianyu Yang, Zelin Liu, Weijun Yang, and Jiangang He. 2024. "Effects of Steel Fiber Content on Compressive Properties and Constitutive Relation of Ultra-High Performance Shotcrete (UHPSC)" Buildings 14, no. 6: 1503. https://doi.org/10.3390/buildings14061503
APA StyleXiao, S., Yang, J., Liu, Z., Yang, W., & He, J. (2024). Effects of Steel Fiber Content on Compressive Properties and Constitutive Relation of Ultra-High Performance Shotcrete (UHPSC). Buildings, 14(6), 1503. https://doi.org/10.3390/buildings14061503








